Effect of Fiber Type on the Thermomechanical Performance of High-Density Polyethylene (HDPE) Composites with Continuous Reinforcement
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Operational Conditions
2.2. Material Characterization Overview
2.3. Differential Scanning Calorimetry (DSC)
2.4. Thermomechanical Analysis (TMA)
2.5. Dynamic Mechanical Analysis (DMA)
2.5.1. Strain Sweep Test
2.5.2. Temperature Ramp Test
2.5.3. Frequency Sweep Test
2.5.4. Stress Relaxation Test
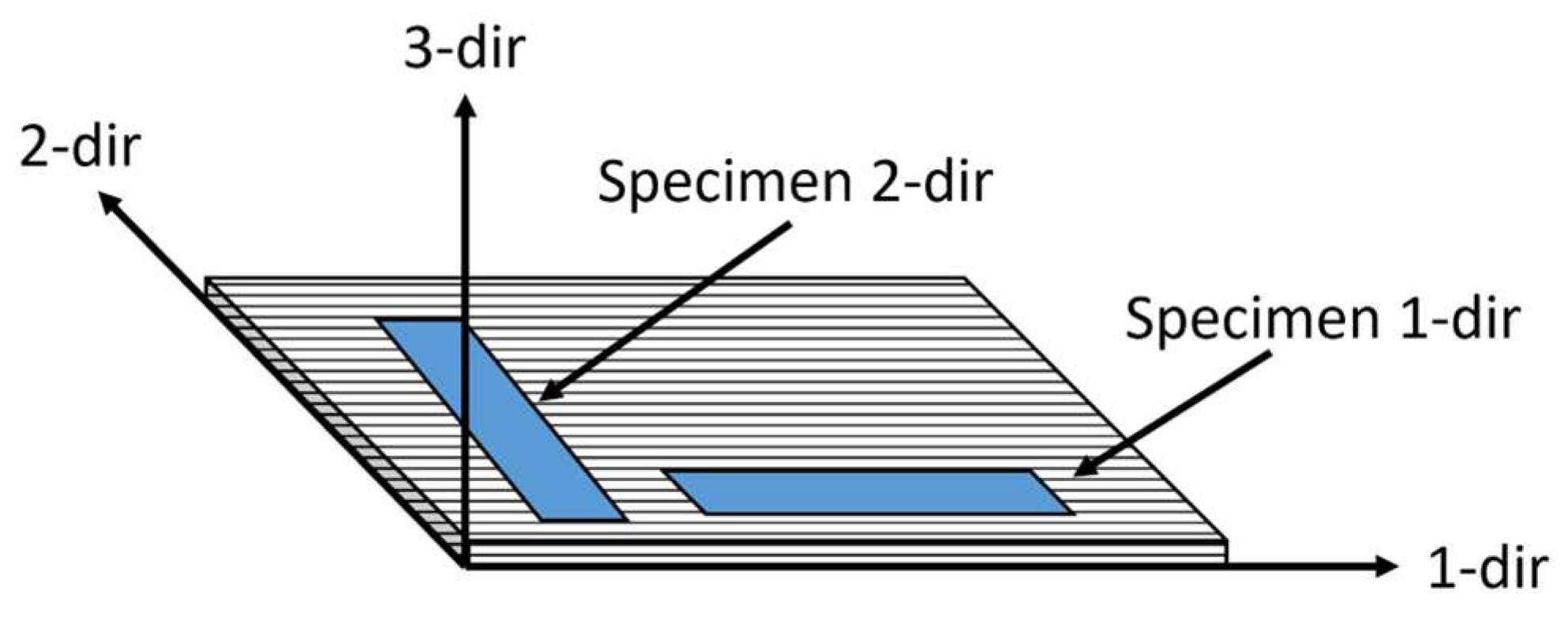
2.6. Manufacturing of Specimens
2.7. Conditioning of Specimens
2.8. Modeling the Viscoelastic Behavior
2.8.1. Time–Temperature Superposition (TTS) Principle
2.8.2. Modeling Stress Relaxation
3. Results and Discussion
3.1. DSC Results
3.1.1. Raw Material
3.1.2. Consolidated Panels
3.1.3. Crystallinity Percentage Calculation
3.2. TMA Results
3.3. DMA Results
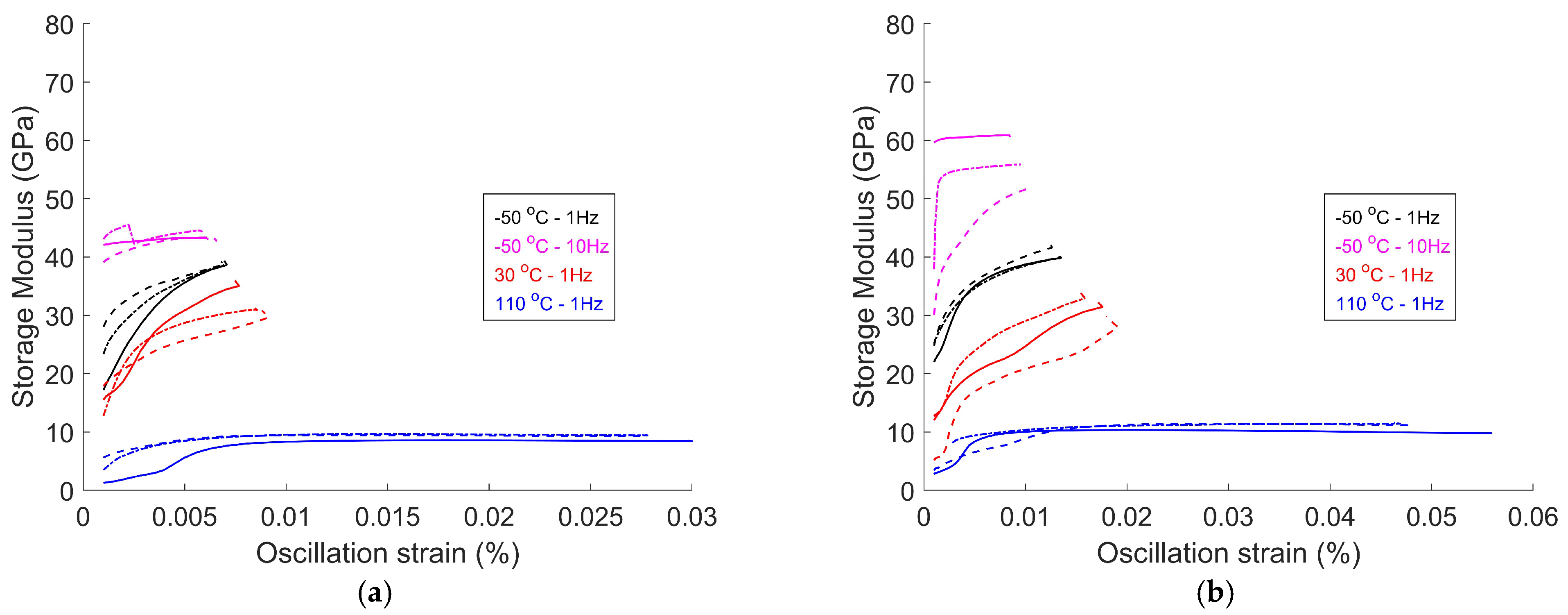
3.3.1. Strain Sweep
3.3.2. Temperature Ramp Test
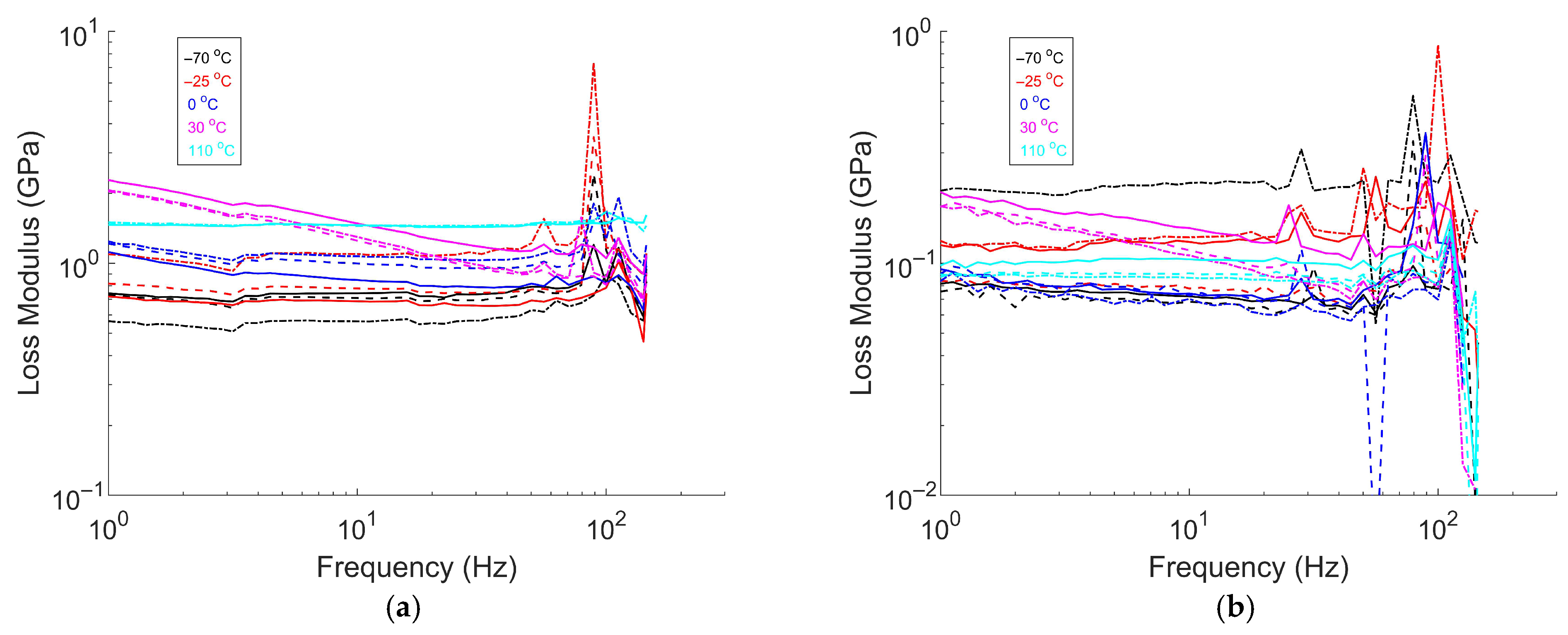
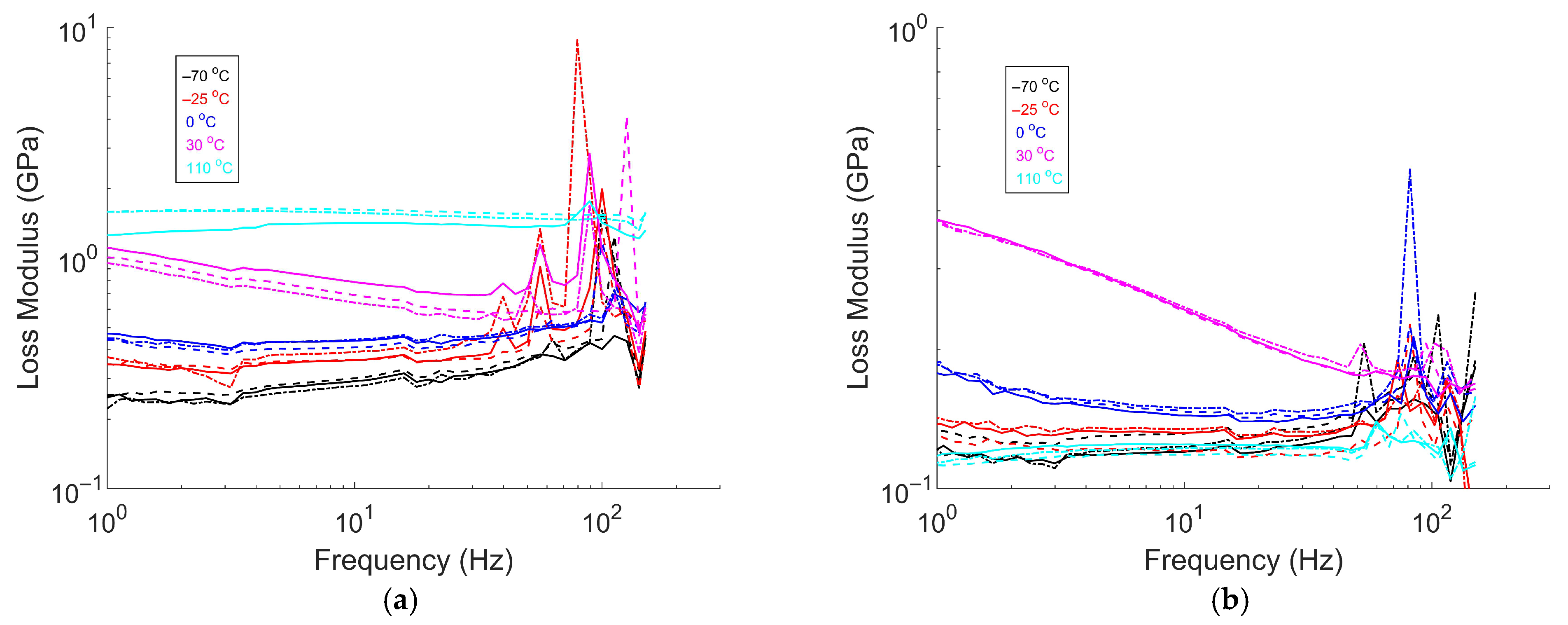
3.3.3. Frequency Sweep Test



3.3.4. Stress Relaxation Test
3.4. Comparative Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Prony Series Parameters for Stress Relaxation Test
| Parameters | GF/HDPE | UHMWPE/HDPE |
|---|---|---|
| 0.0809 | 0.1143 | |
| 0.3046 | 0.0470 | |
| 0.0473 | 0.0903 | |
| 0.0099 | 2.58 × 10−4 | |
| 8.22 × 10−7 | 3.02 × 105 | |
| 8.3309 | 11.5157 |
| Parameters | GF/HDPE | UHMWPE/HDPE |
|---|---|---|
| 0.2713 | 0.0728 | |
| 2.57 × 10−7 | 0.0491 | |
| 0.0078 | 0.0473 | |
| 0.0543 | 0.0553 | |
| 0.0401 | 0.0476 | |
| 1.72 × 10−6 | 9.18 × 10−6 | |
| 0.0389 | 4.36 × 10−4 | |
| 0.0011 | 4.66 × 104 | |
| 0.0279 | 24.1081 | |
| 2.7118 | 0.0785 |
References
- Yano, O.; Yamaoka, H. Cryogenic properties of polymers. Prog. Polym. Sci. 1995, 20, 585–613. [Google Scholar] [CrossRef]
- Sapi, Z.; Butler, R. Properties of cryogenic and low temperature composite materials—A review. Cryogenics 2020, 111, 103190. [Google Scholar] [CrossRef]
- Carter, J.B. Vibration and Aeroelastic Prediction of Multi-Material Structures Based on 3D-Printed Viscoelastic Polymers. Master’s Thesis, Miami University, Oxford, OH, USA, 2021. [Google Scholar]
- Bonning, B.; Blackburn, C.J.; Stretz, H.A.; Wilson, C.D.; Johnson, W.R. Superposition-based predictions of creep for polymer films at cryogenic temperatures. Cryogenics 2019, 104, 102979. [Google Scholar] [CrossRef]
- Kalia, S.; Fu, S.-Y. Polymers at Cryogenic Temperatures; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Slifka, A.J.; Smith, D.R. Thermal expansion of an E-glass/vinyl ester composite from 4 to 293 K. Int. J. Thermophys. 1997, 18, 1249–1256. [Google Scholar] [CrossRef]
- Pan, Z.; Sun, B.; Gu, B. Thermo-mechanical numerical modeling on impact com- pressive damage of 3-D braided composite materials under room and low tem- peratures. Aerosp. Sci. Technol. 2016, 54, 23–40. [Google Scholar] [CrossRef]
- Yamanaka, A.; Kashima, T.; Tsutsumi, M.; Ema, K.; Izumi, Y.; Nishijima, S. Thermal Expansion Coefficient of Unidirectional High-Strength Polyethylene Fiber Reinforced Plastics at Low Temperature. J. Compos. Mater. 2007, 41, 165–174. [Google Scholar] [CrossRef]
- Hua, Y.; Ni, Q.-Q.; Yamanaka, A.; Teramoto, Y.; Natsuki, T. The Development of Composites with Negative Thermal Expansion Properties Using High Performance Fibers. Adv. Compos. Mater. 2011, 20, 463–475. [Google Scholar] [CrossRef]
- Nielsen, L.E.; Landel, R.F. Mechanical Properties of Polymers and Composites; Marcel Dekker: New York, NY, USA, 1975. [Google Scholar]
- Kim, Y.; Kim, M.S.; Jeon, H.J.; Kim, J.H.; Chun, K.W. Mechanical Performance of Polymer Materials for Low-Temperature Applications. Appl. Sci. 2022, 12, 12251. [Google Scholar] [CrossRef]
- He, Y.; Yang, S.; Liu, H.; Shao, Q.; Chen, Q.; Lu, C.; Jiang, Y.; Liu, C.; Guo, Z. Reinforced carbon fiber laminates with oriented carbon nanotube epoxy nanocomposites: Magnetic field assisted alignment and cryogenic temperature mechanical properties. J. Colloid Interface Sci. 2018, 517, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Quintana, J.L.C.; Redmann, A.; Capote, G.A.M.; Perez-Irizarry, A.; Bechara, A.; Osswald, T.A.; Lakes, R. Viscoelastic properties of fused filament fabrication parts. Addit. Manuf. 2019, 28, 704–710. [Google Scholar] [CrossRef]
- Sun, W.; Vassilopoulos, A.P.; Keller, T. Effect of thermal lag on glass transition temperature of polymers measured by DMA. Int. J. Adhes. Adhes. 2014, 52, 31–39. [Google Scholar] [CrossRef]
- Raghavan, J.; Meshii, M. Creep of Polymer Composites. Compos. Sci. Technol. 1997, 57, 1673–1688. [Google Scholar] [CrossRef]
- Jiang, L.; Zhou, Y.; Jin, F. Design of short fiber-reinforced thermoplastic composites: A review. Polym. Compos. 2022, 43, 4835–4847. [Google Scholar] [CrossRef]
- Dasari, S.; Patnaik, S.; Prusty, R.K. Temperature-dependent inter-laminar fracture behavior of waste short carbon fiber embedded glass fiber/epoxy composites. Polym. Compos. 2023, 44, 6793–6810. [Google Scholar] [CrossRef]
- Gupta, A.; Hasanov, S.; Fidan, I. Thermal characterization of short carbon fiber reinforced high temperature polymer material produced using the fused filament fabrication process. J. Manuf. Process. 2022, 80, 515–528. [Google Scholar] [CrossRef]
- Qiao, Y.; Fring, L.D.; Pallaka, M.R.; Simmons, K.L. A Review of the Fabrication Methods and Mechanical Behavior of Continuous Thermoplastic Polymer Fiber-Thermoplastic Polymer Matrix Composites. Polym. Compos. 2022, 44, 694–733. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A. Tensile behavior and modeling of short fiber-reinforced polymer composites including temperature and strain rate effects. J. Thermoplast. Compos. Mater. 2016, 30, 1414–1437. [Google Scholar] [CrossRef]
- Abouhamzeh, M.; Dijk, Y.L.M.; Gratzl, T. Viscoelastic modelling of fibre-reinforced thermoplastics in hygrothermal circumstances. Mech. Time-Depend. Mater. 2022, 27, 973–987. [Google Scholar] [CrossRef]
- Quintana, J.L.C.; Tomlinson, S.; Lopez-Anido, R.A. Thermomechanical and Viscoelastic Characterization of Continuous GF/PETG Tape for Extreme Environment Applications. J. Compos. Sci. 2024, 8, 392. [Google Scholar] [CrossRef]
- McConville, J.C.; Miller, K.S. Research, Development, Test and Evaluation of Material for Worldwide Use; Department of the Army: Washington, DC, USA, 2020. [Google Scholar]
- A & C Plastics, Inc. Common Uses of High-Density Polyethylene. 2024. Available online: https://www.acplasticsinc.com/informationcenter/r/common-uses-of-hdpe (accessed on 1 April 2025).
- PolyAlto, G. The Advantages and Applications of HDPE. 2024. Available online: https://blogue.polyalto.com/en/the-advantages-and-applications-of-hdpe (accessed on 5 April 2025).
- ASTM E793-24; Standard Test Method for Enthalpies of Fusion and Crystallization by Differential Scanning Calorimetry. ASTM International: West Conshohocken, PA, USA, 2024.
- ASTM D3418-21; Standard Test Method for Transition Temperatures and Enthalpies of Fusion and Crystallization of Polymers by Differential Scanning Calorimetry. ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM E1269-11; Standard Test Method for Determining Specific Heat Capacity by Differential Scanning Calorimetry. ASTM International: West Conshohocken, PA, USA, 2011.
- PerkinElmer. A Beginner’s Guide to Differential Scanning Calorimetry DSC. 2010. Available online: https://www.s4science.at/wordpress/wp-content/uploads/2018/10/DSC-Beginners-Guide.pdf (accessed on 9 September 2024).
- ASTM E831-25; Standard Test Method for Linear Thermal Expansion of Solid Materials by Thermomechanical Analysis. ASTM International: West Conshohocken, PA, USA, 2025.
- ASTM D5023-23; Standard Test Method for Plastics: Dynamic Mechanical Properties: In Flexure (Three-Point Bending). ASTM International: West Conshohocken, PA, USA, 2023.
- ASTM D7028-07(2024); Standard Test Method for Glass Transition Temperature (DMA Tg) of Polymer Matrix Composites by Dynamic Mechanical Analysis (DMA). ASTM International: West Conshohocken, PA, USA, 2024.
- ASTM E1640-23; Standard Test Method for Assignment of the Glass Transition Temperature by Dynamic Mechanical Analysis. ASTM International: West Conshohocken, PA, USA, 2023.
- ASTM D2990-17; Standard Test Methods for Tensile, Compressive, and Flexural Creep and Creep-Rupture of Plastics. ASTM International: West Conshohocken, PA, USA, 2017.
- Clough, R.W.; Penzien, J. Dynamics of Structures; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- ASTM D618-21; Standard Practice for Conditioning Plastics for Testing. ASTM International: West Conshohocken, PA, USA, 2021.
- Osswald, T.A.; Menges, G. Material Science of Polymers for Engineers; Hanser: Munich, Germany, 2012. [Google Scholar]
- Chen, T. Determining a Prony Series for a Viscoelastic material From Time Varying Strain Data. 2000. Available online: https://ntrs.nasa.gov/citations/20000052499 (accessed on 1 May 2025).
- Rudnik, E.; Dobkowski, Z. Thermal degradation of UHMWPE. J. Therm. Anal. 1997, 49, 471–475. [Google Scholar] [CrossRef]
- Khalil, Y.; Hopkinson, N.; Kowalski, A.; Fairclough, J.P.A. Characterisation of UHMWPE polymer poder for laser sintering. Materials 2019, 12, 3496. [Google Scholar] [CrossRef]
- Salkhi Khasraghi, S.; Rezaei, M. Preparation and characterization of UHMWPE/HDPE/MWCNT melt-blended nanocomposites. Thermoplast. Compos. Mater. 2015, 28, 305–326. [Google Scholar] [CrossRef]
- Roiron, C.; Laine, E.; Grandidier, J.-C.; Garois, N.; Vix-Guter, C. A Review of the Mechanical and Physical Properties of Polyethylene Fibers. Textiles 2021, 1, 86–151. [Google Scholar] [CrossRef]
- Ratner, S.; Pegoretti, A.; Migliaresi, C.; Weinberg, A.; Marom, G. Relaxation processes and fatigue behavior of crosslinked UHMWPE fiber compacts. Compos. Sci. Technol. 2005, 65, 87–94. [Google Scholar] [CrossRef]
- Dayyoub, T.; Maksimkin, A.V.; Kaloshkin, S.; Kolesnikov, E.; Chukov, D.; Dyachkova, T.P.; Gutnik, I. The Structure and Mechanical Properties of the UHMWPE Films Modified by the Mixture of Graphene Nanoplates with Polyaniline. Polymers 2019, 11, 23. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Zhang, C.; Chen, X.-X.; Li, A.; Zhang, Y.-F. Thermal, Mechanical and Electrical Properties of Carbon Fiber Fabric and Graphene Reinforced Segmented Polyurethane Composites. Nanomaterials 2021, 11, 1289. [Google Scholar] [CrossRef] [PubMed]
- Bahlouli, S.; Belaadi, A.; Makhlouf, A.; Alshahrani, H.; Khan, M.K.A.; Jawaid, M. Effect of Fiber Loading on Thermal Properties of Cellulosic Washingtonia Reinforced HDPE Biocomposites. Polymers 2023, 15, 2910. [Google Scholar] [CrossRef]
- Paul, S.A.; Boudenne, A.; Ibos, L.; Candau, Y.; Joseph, K.; Thomas, S. Effect of fiber loading and chemical treatments on thermophysical properties of banana fiber/polypropylene commingled composite materials. Compos. Part A 2008, 39, 1582–1588. [Google Scholar] [CrossRef]
- Awad, A.H.; El Gamasy, R.; Abd El Wahab, A.; Abdellatif, M.H. Mechanical and physical properties of PP and HDPE. Eng. Sci. 2019, 4, 34–42. [Google Scholar] [CrossRef]
- Anu, M.; Pillai, S.S. Structure, thermal, optical, and dielectric properties of SnO2 nanoparticles-filled HDPE polymer. Solid. State Commun. 2022, 341, 114577. [Google Scholar] [CrossRef]
- Tarani, E.; Arvanitidis, I.; Christofilos, D.; Bikiaris, D.N.; Chrissafis, K.; Vourlias, G. Calculation of the degree of crystallinity of HDPE/GNPs nanocomposites by using various experimental techniques: A comparative stud. J. Mater. Sci. 2023, 58, 1621–1639. [Google Scholar] [CrossRef]
- Koffi, A.; Mijiyawa, F.; Koffi, D.; Erchiqui, F.; Toubal, L. Mechanical Properties, Wettability and Thermal Degradation of HDPE/Birch Fiber Composite. Polymers 2021, 13, 1459. [Google Scholar] [CrossRef]
- Ziaee, S.; Kerr-Anderson, E.; Johnson, A.; Eastep, D.; Abdel-Magid, B. Effect of High Fiber Content on Properties and Performance of CFRTP Composites. J. Compos. Sci. 2024, 8, 364. [Google Scholar] [CrossRef]
- Deng, B.; Chen, L.; Zhong, Y.; Li, X.; Wang, Z. The effect of temperature on the structural evolution of ultra-high molecular weight polyethylene films with pre-reserved shish crystals during the stretching process. Polymer 2023, 267, 125690. [Google Scholar] [CrossRef]
- Tsinas, Z.; Orski, S.V.; Bentley, V.R.C.; Lopez, L.G.; Al-Sheikhly, M.; Forster, A.L. Effects of Thermal Aging on Molar Mass of Ultra-High Molar Mass Polyethylene Fibers. Polymers 2022, 14, 1324. [Google Scholar] [CrossRef]
- Deepthi, M.V.; Sharma, M.; Sailaja, R.R.N.; Anantha, P.; Sampathkumaran, P.; Seetharamu, S. Mechanical and thermal characteristics of high density polyethylene-fly ash cenospheres composites. Mater. Des. 2010, 31, 2051–2060. [Google Scholar] [CrossRef]
- Steven, M.K. The UHMWPE Handbook Ultra-High Molecular Weight Polyethylene in Total Joint Replacement; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- JPS Composite Materials. E-Glass & S-Glass. Available online: https://jpscm.com/products/e-glass-s-glass/ (accessed on 1 March 2025).
- Barbero, E.J. Introduction to Composite Materials Design, 3rd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Otex Specialty Narrow Fabrics. The Core Differences Between UHMWPE & Kevlar. Available online: https://osnf.com/uhmwpe-vs-kevlar/ (accessed on 15 December 2024).
- Plastics Europe. Polyolefins. Available online: https://plasticseurope.org/plastics-explained/a-large-family/polyolefins/#:~:text=The%20density%20of%20HDPE%20can,and%20tensile%20strength%20than%20LDPE (accessed on 15 May 2025).
- Poel, G.V.; Mathot, V.B.F.; Ye, P. Crystallization Temperature vs. Cooling Rate: The Link with “Real-Life” Polymer Processes; PerkinElmer: Shelton, CT, USA, 2011. [Google Scholar]
- Yu, M.; Qi, L.; Cheng, L.; Min, W.; Mei, Z.; Gao, R.; Sun, Z. The Effect of Cooling Rates on Thermal, Crystallization, Mechanical and Barrier Properties of Rotational Molding Polyamide 11 as the Liner Material for High-Capacity High-Pressure Vessels. Molecules 2023, 28, 2425. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Gandhi, U.; Perez, C.; Osswald, T.; Vallury, S.; Yang, A. Method to account for the fiber orientation of the initial charge on the fiber orientation of finished part in compression molding simulation. Compos. Part A Appl. Sci. Manuf. 2017, 10, 244–254. [Google Scholar] [CrossRef]
- MatWeb-Material Property Data. C-Glass Fiber, Generic. Available online: https://www.matweb.com/search/datasheet.aspx?MatGUID=462fd1da8ad245b2ad40093889016448&ckck=1 (accessed on 7 May 2025).
- Omnexus. Coefficient of Linear Thermal Expansion. Available online: https://omnexus.specialchem.com/polymer-property/coefficient-of-linear-thermal-expansion (accessed on 1 November 2024).
- Professional Plastics. Thermal Properties of Plastic Materials. Available online: https://www.professionalplastics.com/professionalplastics/ThermalPropertiesofPlasticMaterials.pdf (accessed on 10 December 2024).
- Zhang, X.; Wang, Y.; Lu, C.; Cheng, S. Interfacial adhesion study on UHMWPE fiber-reinforced composites. Polym. Bull. 2011, 67, 527–540. [Google Scholar] [CrossRef]
- Dynamica Rope. Physical Properties of Dyneema Fibers. Available online: https://pelicanrope.com/content/PDFs/Dyneema-Comprehensive-factsheet-UHMWPE.pdf (accessed on 15 February 2024).
- Rama Sreekanth, P.S.; Subramani, K. Influence of MWCNTs and gamma irradiation on thermal characteristics of medical grade UHMWPE. Bull. Mater. Sci. 2014, 37, 347–356. [Google Scholar] [CrossRef]
- Deng, S.; Hou, M.; Ye, L. Temperature-dependent elastic moduli of epoxies measured by DMA and their correlations to mechanical testing data. Polym. Test. 2007, 26, 803–813. [Google Scholar] [CrossRef]
- Kumar, S.D.; Samvel, R.; Aramindh, M.; Vibin, R.A.; Poovarasu, E.; Prasad, M.S.S. Ballistic studies on synthetic fibre reinforced polymer composites and it’s applications–A brief review. Mater. Today Proc. 2023; in press. [Google Scholar]
- Sahu, S.K.; Badgayan, N.D.; Sreekanth, P.R. Rheological Properties of HDPE based Thermoplastic Polymeric Nanocomposite Reinforced with Multidimensional Carbon-based Nanofillers. Biointerface Res. Appl. Chem. 2022, 12, 5709–5715. [Google Scholar]
- Dupaix, R.B.; Boyce, M.C. Finite strain behavior of poly(ethylene terephthalate) (PET) and poly(ethylene terephthalate)-glycol (PETG). Polymer 2005, 46, 4827–4838. [Google Scholar] [CrossRef]
- Yi, C.; Xu, J.; Tian, L.; Zhang, C. Temperature and Strain Rate Related Deformation Behavior of UHMWPE Fiber-Reinforced Composites. Polymers 2024, 16, 1250. [Google Scholar] [CrossRef]
- Edinne, G.D.; Ramdane, Y.; Nouredine, O.; Nadir, B. Modal analysis of biocomposite materials beams reinforced by Washingtonia Filifera natural fibers. J. Vibroeng 2022, 24, 1502–1511. [Google Scholar] [CrossRef]
- Bharath, H.S.; Waddar, S.; Bekinal, S.I.; Jeyaraj, P.; Doddamani, M. Effect of axial compression on dynamic response of concurrently printed sandwich. Compos. Struct. 2021, 259, 113223. [Google Scholar] [CrossRef]
- Bharath, H.S.; Sawardekar, A.; Waddar, S.; Jeyaraj, P.; Doddamani, M. Mechanical behavior of 3D printed syntactic foam composites. Compos. Struct. 2020, 254, 112832. [Google Scholar] [CrossRef]
- Xing, Y.; Sun, D.; Deng, Z. An Analysis of the Vibration Transmission Properties of Assemblies Using Honeycomb Paperboard and Expanded Polyethylene. Materials 2023, 16, 6554. [Google Scholar] [CrossRef]
- Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Kroon, M.; Gortz, J.; Islam, S.; Andreasson, E.; Petersson, V.; Jutemar, E.P. Experimental and theoretical study of stress relaxation in high-density polyethylene. Acta Mech. 2024, 235, 2455–2477. [Google Scholar] [CrossRef]
- Saeed, U.; Al-Turaif, H.; Siddiqui, M.E. Stress relaxation performance of glass fiber-reinforced high-density polyethylene composite. Polym. Polym. Compos. 2021, 29, 705–713. [Google Scholar] [CrossRef]
- THS Industrial Textiles. Non-Combustibility of Glass Fibre. 2025. Available online: https://www.thstextiles.co.uk/info-centre/technical-guides/non-combustibility-of-glass-fibre/ (accessed on 9 June 2025).









| Material | Name | Manufacturer | Fiber Content | Thickness (mm) |
|---|---|---|---|---|
| GF/HDPE | GF-HDPE-46-51-296 | A+ Composites | 46 vol. % | 0.205 |
| UHMWPE/HDPE | UHMWPE-HDPE-50-51-235 | A+ Composites | 50 vol. % | 0.235 |
| Temperature Daily High (°C) | Design Type | Daily Cycle | Ambient Relative Humidity (%RH) |
|---|---|---|---|
| −57 | Extreme Cold | Extreme Cold (C4) | Tending toward saturation |
| −37 | Cold | Cold (C2) | Tending toward saturation |
| −6 | Basic | Mild Cold (C0) | Tending toward saturation |
| 24 | Basic | Constant High Humidity (B1) | 95–100 |
| 49 | Hot | Hot Dry (A1) | 3–8 |
| Test | Temperature (°C) | Strain % | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Stress Relaxation | −70 | −50 | −25 | 0 | 15 | 30 | 45 | 60 | 0.01 |
| Material | Pressure, MPa, (psi) | Processing Temperature, °C (°F) | Dwell Time (min) |
|---|---|---|---|
| GF/HDPE | 0.18 (26) | 140 (284) | 3 |
| UHMWPE/HDPE | 0.14 (20) | 135 (275) | 3 |
| Material (n **) | Tm-matrix (°C) | ΔHfusion (J/g) | Tm-fiber (°C) | ΔHfusion-fiber (J/g) |
|---|---|---|---|---|
| GF/HDPE (5) | 126.4 ± 0.4 | 45 ± 5 | - | - |
| UHMWPE/HDPE (4) | 126.8 ± 0.2 | 83 ± 3 | 144.7 ± 0.3 | 110 ± 4 |
| Material (n **) | Tcrystallization (°C) | ΔHcrystallization (J/g) | Tm-matrix (°C) | ΔHfusion (J/g) |
|---|---|---|---|---|
| GF/HDPE (5) | 117.0 ± 0.1 | 52 ± 5 | 127.8 ± 0.2 | 48 ± 4 |
| UHMWPE/HDPE (4) | 116.3 ± 0.1 | 165 ± 5 | 128.3 ± 0.2 | 167 ± 4 |
| Material (n **) | Tm-matrix (°C) | ΔHfusion (J/g) | Tm-fiber (°C) | ΔHfusion-fiber (J/g) |
|---|---|---|---|---|
| UHMWPE/HDPE (3) | 128.5 ± 0.2 | 79 ± 1 | 144.9 ± 0.3 | 98 ± 3 |
| Material (n **) | Tcrystallization (°C) | ΔHcrystallization (J/g) | Tm-matrix (°C) | ΔHfusion (J/g) |
|---|---|---|---|---|
| UHMWPE/HDPE (3) | 116.2 ± 0.1 | 159 ± 2 | 128.4 ± 0.2 | 166 ± 1 |
| Material | GF/HDPE | UHMWPE/HDPE |
|---|---|---|
| Fiber wt.% | 69.7 | 50.2 |
| % (raw material) | 50 | 57 |
| % (raw material) | - | 38 |
| % (consolidated panel) | 59 | 54 |
| % (consolidated panel) | - | 34 |
| Material (n **) | CTE 1-dir (με/C) | CTE 2-dir (με/C) | CTE 3-dir (με/C) |
|---|---|---|---|
| GF/HDPE (3) | 10 ± 1 | 83 ± 5 | 88 ± 6 |
| UHMWPE/HDPE (3) | −2 ± 9 (6) | 149 ± 9 (4) | 156 ± 9 |
| Material | Strain % | Activation Energy, Ea (kJ/mol) | Reference Temperature, Tref (°C) | R2 |
|---|---|---|---|---|
| GF/HDPE | 0.01 | 95.96 | 30.55 | 0.50 |
| UHMWPE/HDPE | 0.01 | 83.24 | 30.35 | 0.62 |
| Material | R2-Value Prony3 | R2-Value Prony5 |
|---|---|---|
| GF/HDPE | 0.99 | 0.99 |
| UHMWPE/HDPE | 0.97 | 0.98 |
| Property | GF/HDPE | UHMWPE/HDPE | ||||
|---|---|---|---|---|---|---|
| 1-dir | 2-dir | 3-dir | 1-dir | 2-dir | 3-dir | |
| Melting Temperature, Tm (°C) | 127.8 ± 0.2 | 128.3 ± 0.2 | ||||
| Processing Temperature, Tprocessing (°C) | Tprocessing > 127.8 ± 0.2 | 128.3 ± 0.2 < Tprocessing < 144.7 ± 0.3 | ||||
| CTE (με/°C) | 10 ± 1 | 83 ± 5 | 88 ± 6 | −2 ± 9 | 149 ± 9 | 156 ± 9 |
| Storage Modulus, E′ (GPa) @ −57 °C | 36 ± 3 | 8.7 ± 0.3 | - | 40 ± 2 | 3.9 ± 0.5 | - |
| Storage Modulus, E′ (GPa) @ −37 °C | 35 ± 2 | 8.2 ± 0.3 | - | 39 ± 2 | 3.8 ± 0.3 | - |
| Storage Modulus, E′ (GPa) @ −6 °C | 34 ± 2 | 7.1 ± 0.3 | - | 36 ± 1 | 3.5 ± 0.2 | - |
| Storage Modulus, E′ (GPa) @ 24 °C | 32 ± 2 | 5.4 ± 0.1 | - | 31 ± 1 | 2.9 ± 0.2 | - |
| Storage Modulus, E′ (GPa) @ 49 °C | 28 ± 2 | 3.6 ± 0.1 | - | 25 ± 1 | 2.3 ± 0.2 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colón Quintana, J.L.; Tomlinson, S.; Lopez-Anido, R.A. Effect of Fiber Type on the Thermomechanical Performance of High-Density Polyethylene (HDPE) Composites with Continuous Reinforcement. J. Compos. Sci. 2025, 9, 450. https://doi.org/10.3390/jcs9080450
Colón Quintana JL, Tomlinson S, Lopez-Anido RA. Effect of Fiber Type on the Thermomechanical Performance of High-Density Polyethylene (HDPE) Composites with Continuous Reinforcement. Journal of Composites Science. 2025; 9(8):450. https://doi.org/10.3390/jcs9080450
Chicago/Turabian StyleColón Quintana, José Luis, Scott Tomlinson, and Roberto A. Lopez-Anido. 2025. "Effect of Fiber Type on the Thermomechanical Performance of High-Density Polyethylene (HDPE) Composites with Continuous Reinforcement" Journal of Composites Science 9, no. 8: 450. https://doi.org/10.3390/jcs9080450
APA StyleColón Quintana, J. L., Tomlinson, S., & Lopez-Anido, R. A. (2025). Effect of Fiber Type on the Thermomechanical Performance of High-Density Polyethylene (HDPE) Composites with Continuous Reinforcement. Journal of Composites Science, 9(8), 450. https://doi.org/10.3390/jcs9080450









