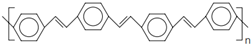Electrical Properties of Composite Materials: A Comprehensive Review
Abstract
1. Introduction
- Metallic composites, in which metallic fillers are used to reinforce polymers and improve conductivity.
- Ceramic composites, encompassing both dielectric and conductive uses.
- Polymeric composites, emphasizing both extrinsically and intrinsically conductive polymers.
- The role of nanomaterials like graphene, carbon nanotubes, and silver nanoparticles is highlighted in nanocomposites.
2. Composite Science and Engineering
2.1. Particle Reinforcement
2.1.1. Large Particle Composites
2.1.2. Dispersion-Strengthened Composites
2.2. Fiber-Reinforced Composites
2.3. Structural Composites
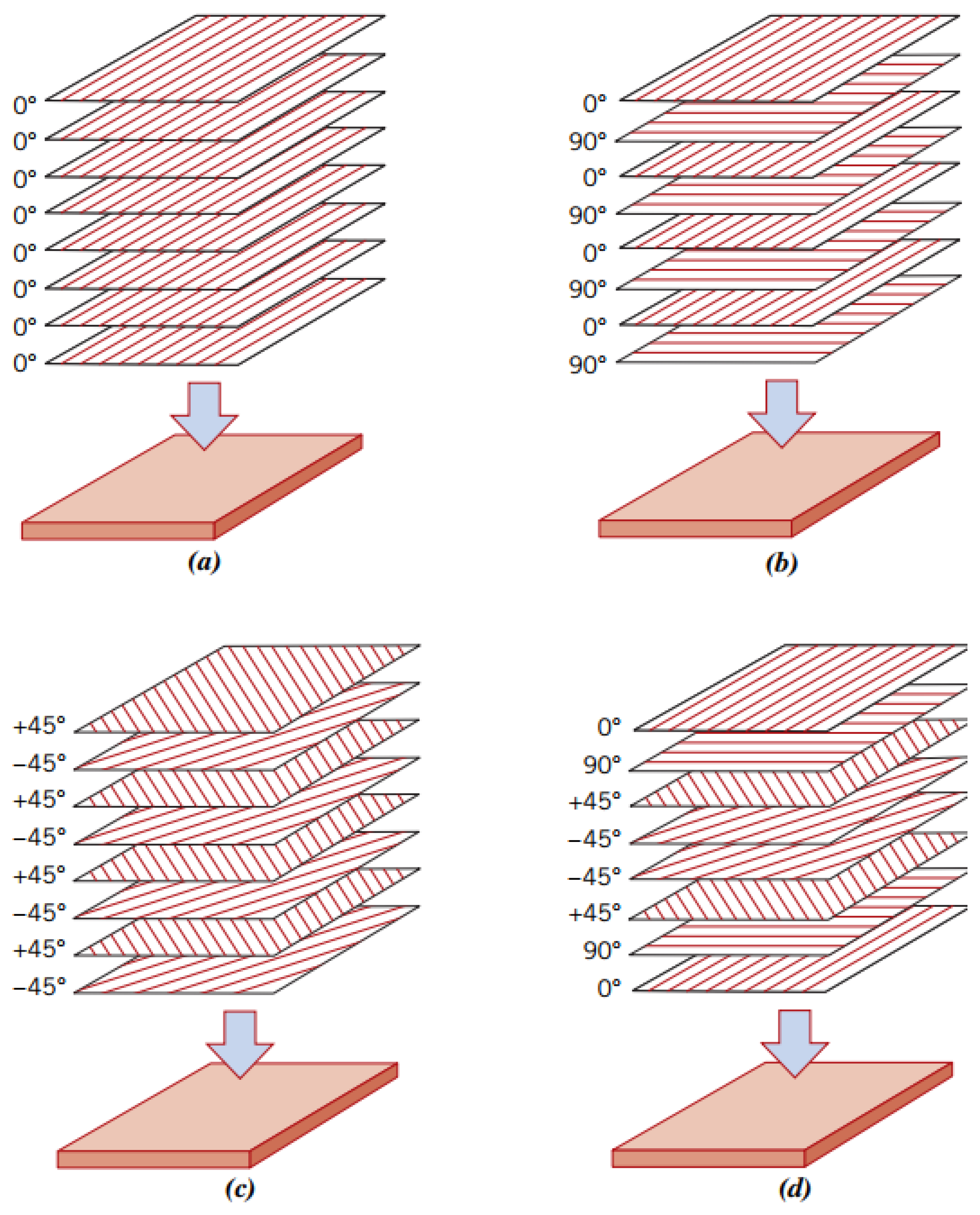
2.3.1. Laminated Composites
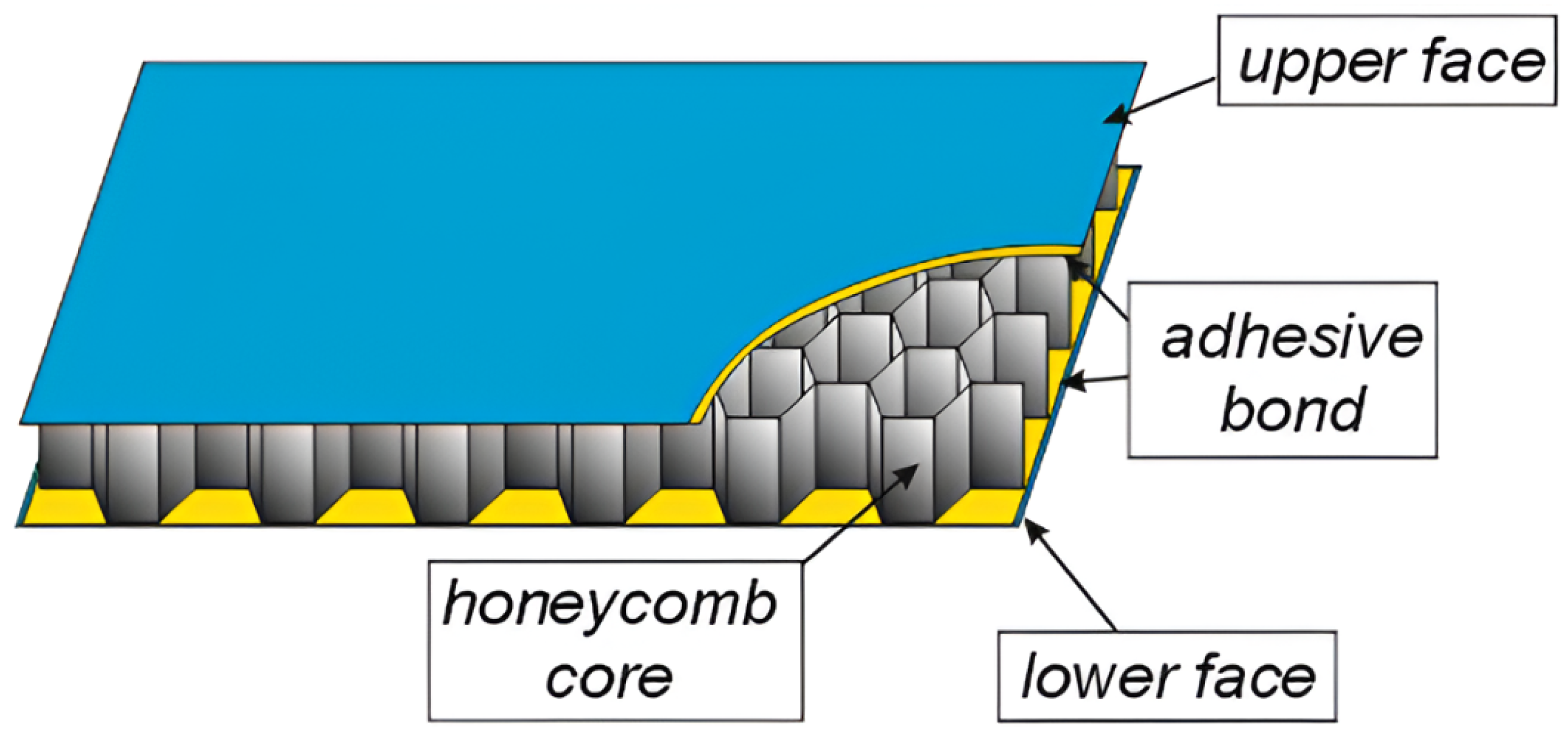
2.3.2. Sandwich Panels
2.3.3. Nanocomposites
3. Electrical Properties
3.1. Ohm’s Law and Conductivity
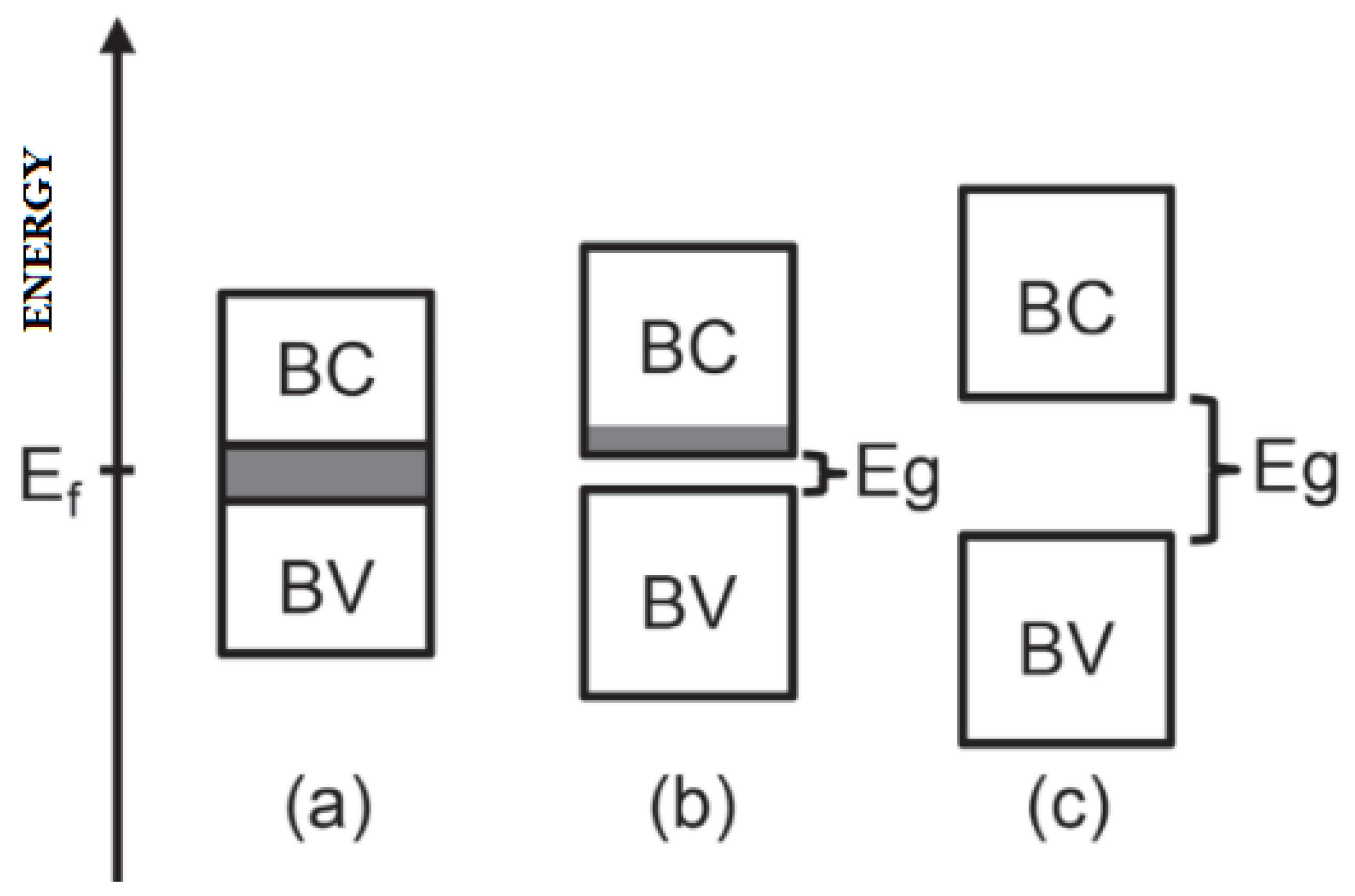
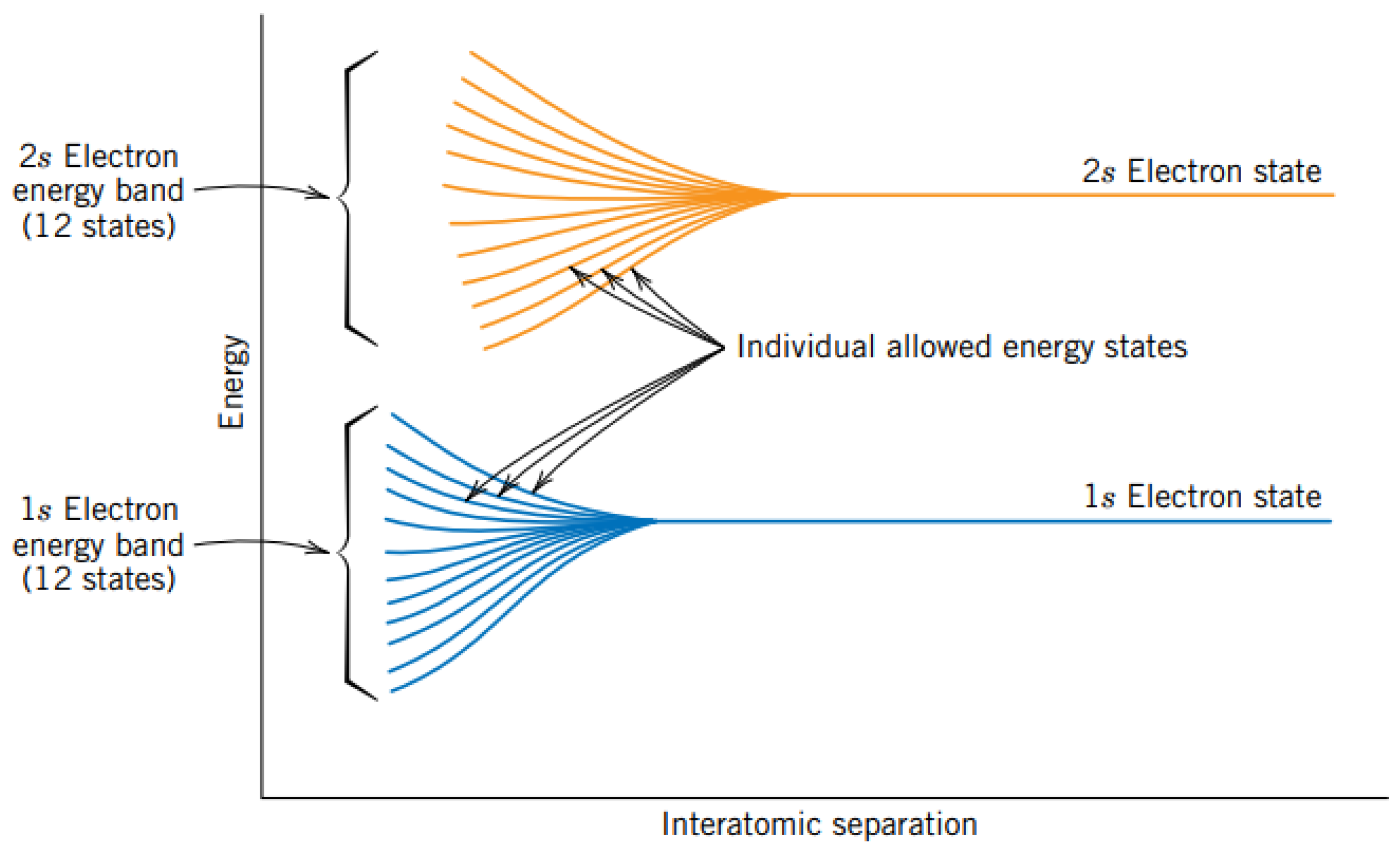
3.2. Energy Bands in Solids
3.3. Electron Mobility
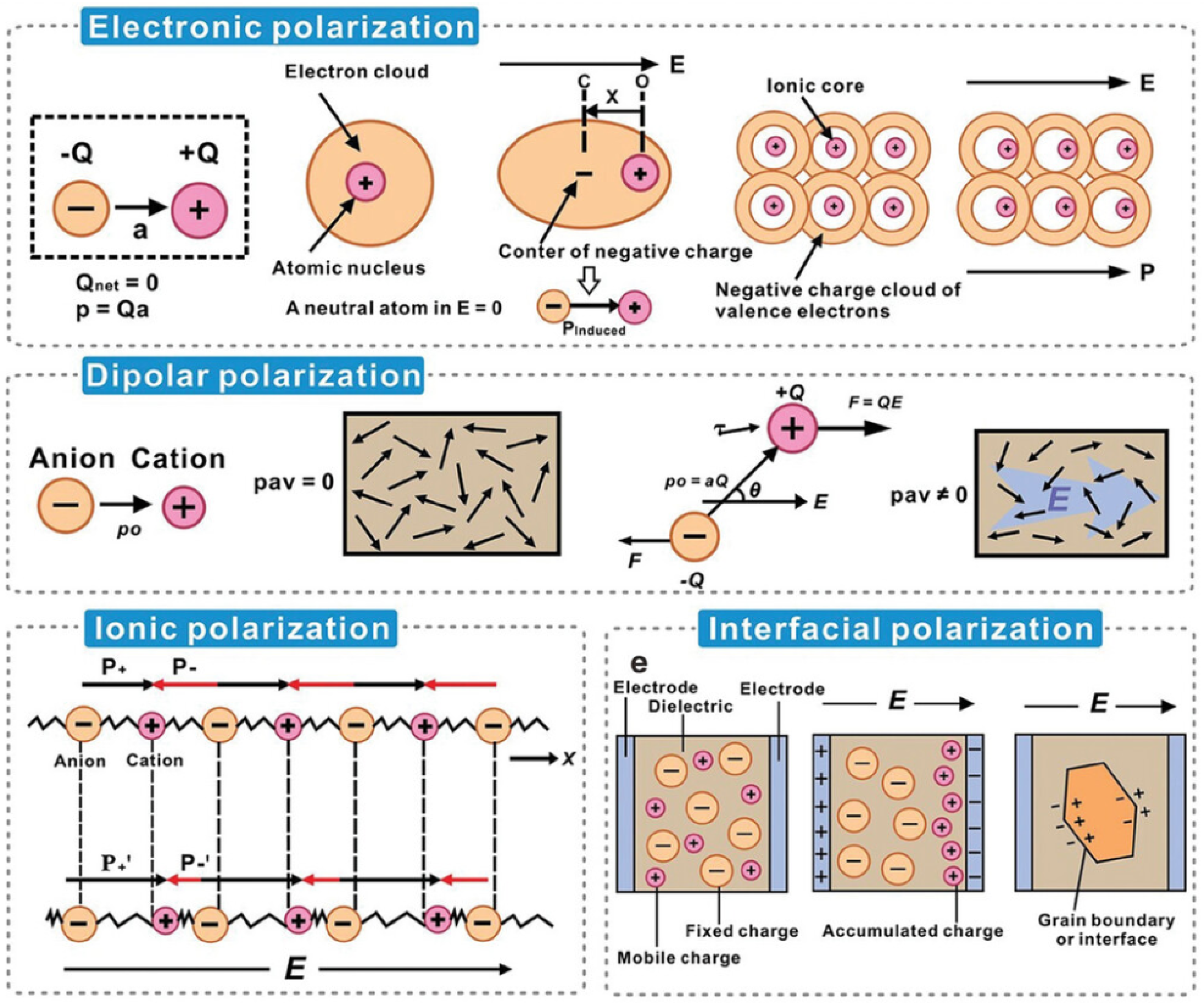
3.4. Dielectric Properties
Electrophysical Characteristics of Dielectrics
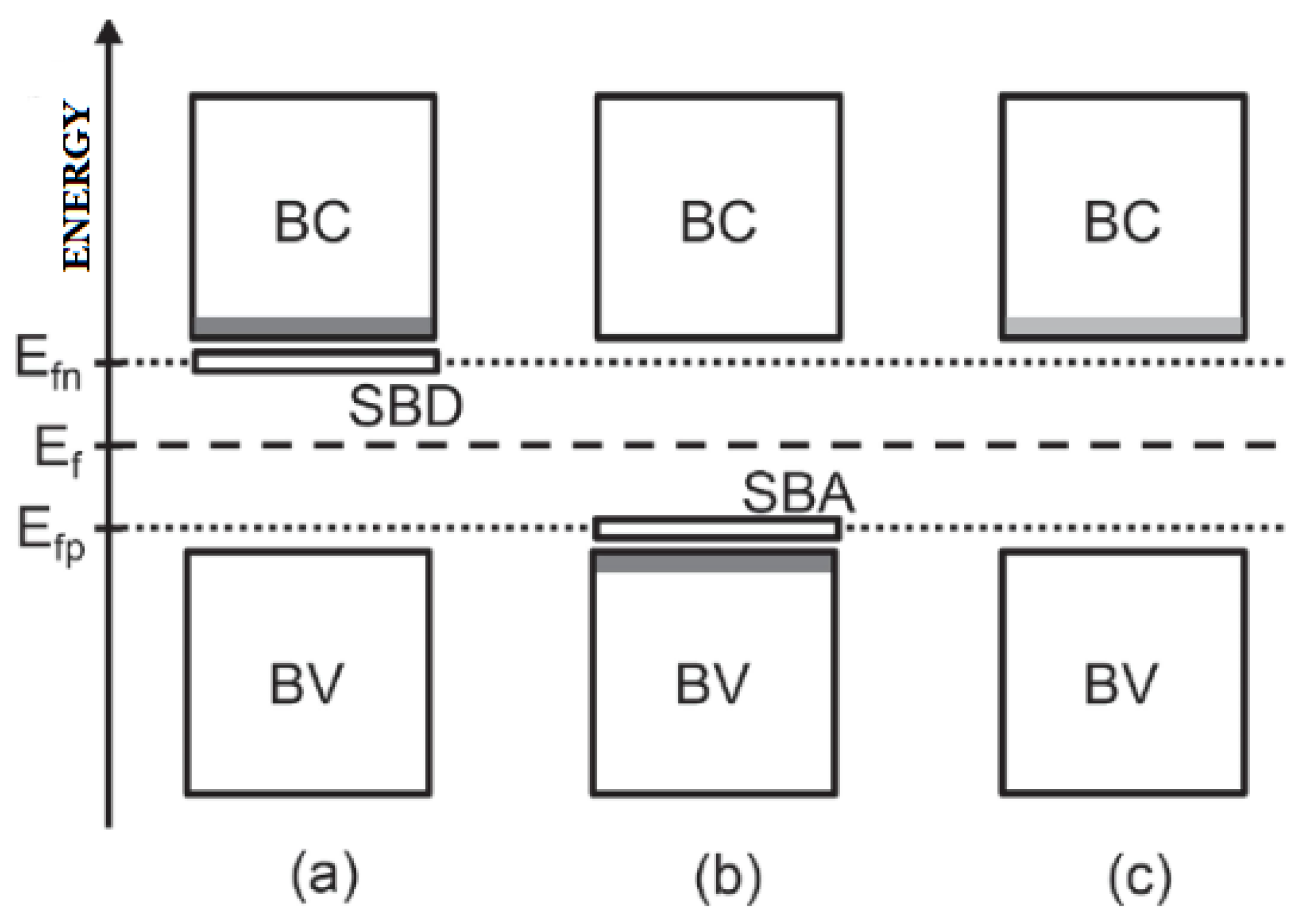
3.5. Semiconductivity
3.5.1. Intrinsic
3.5.2. Extrinsic
4. Electrical Properties of Composite Materials
4.1. Metallic Composites
4.2. Ceramic Composites
4.2.1. Conductivity
4.2.2. Dielectric
4.3. Polymeric Composites
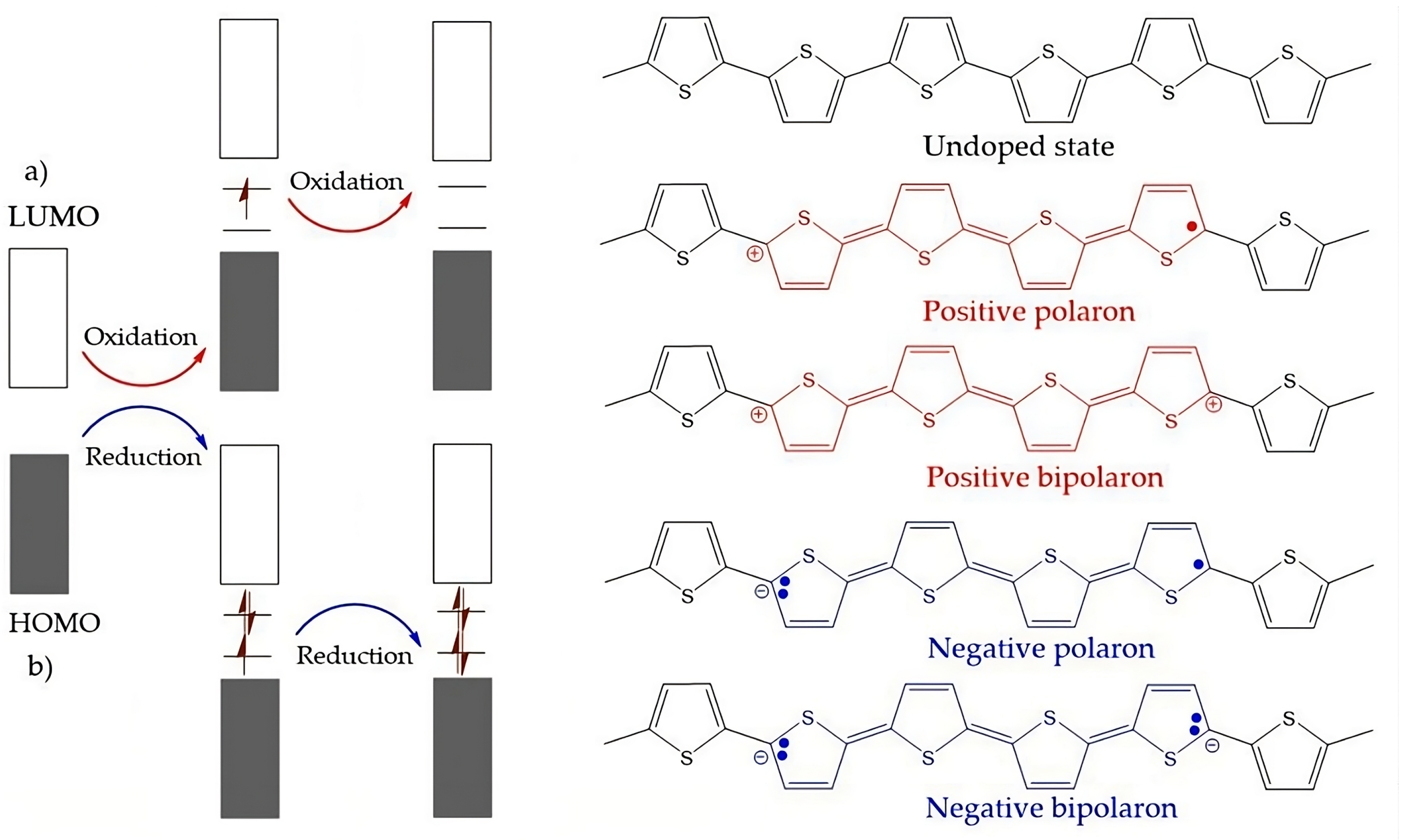
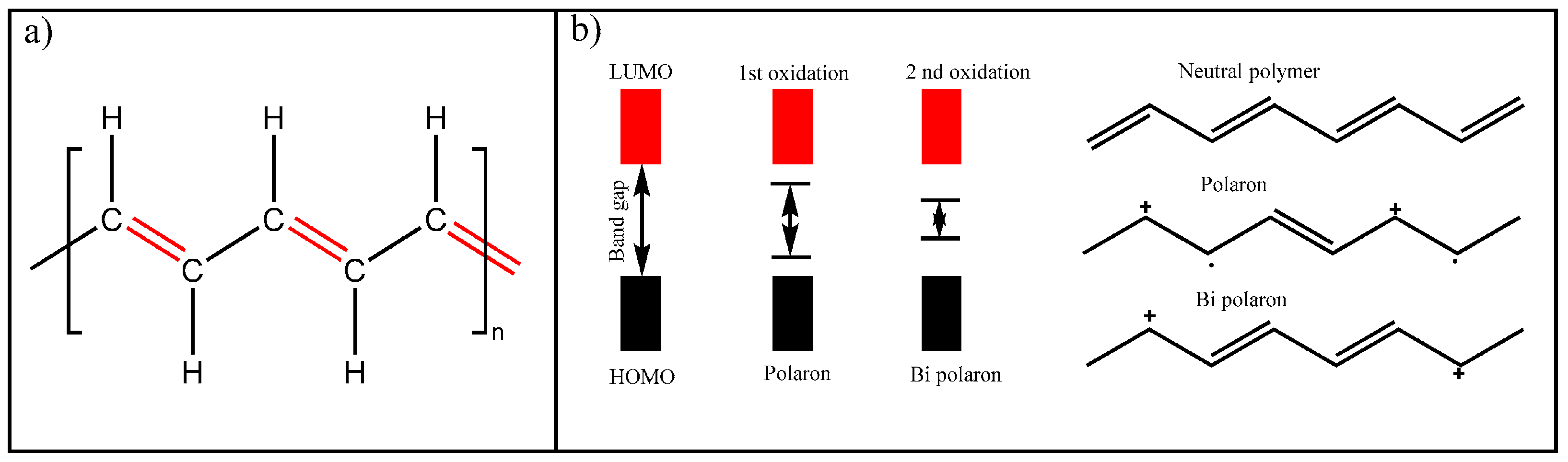
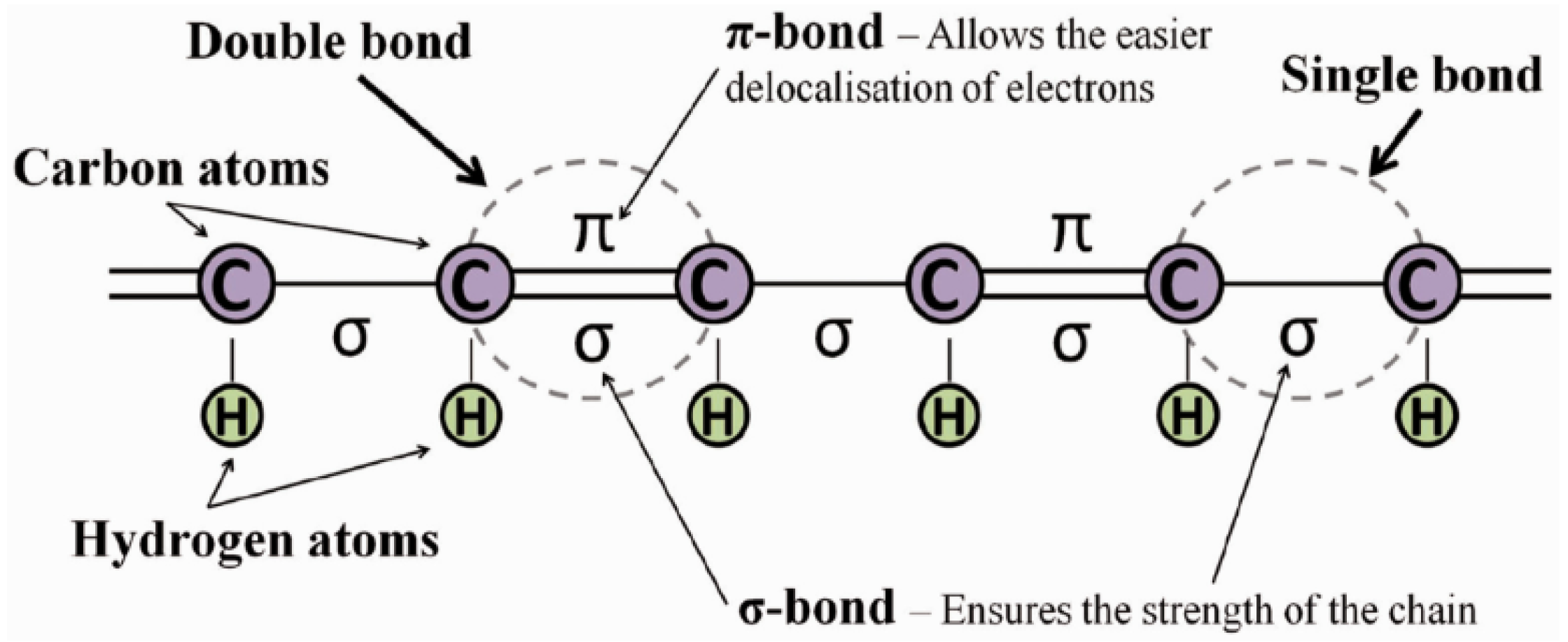
- To achieve high electronic mobility, the molecule must have a linear structure with hybridized carbon centers forming the “backbone” that permits electrons in the orbitals to delocalize.
- In order to increase electron conductivity and create an overlap of bonds, the molecule must have extended conjugation and a continuous matrix of “p” orbitals that can align.
- It is essential to introduce dopants or charge carriers because the charge they create gives the polymer conductivity. By decreasing the gaps between particles, increasing the doping level increases conductivity by creating more charges in the polymer.
Electrical Properties
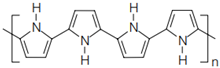
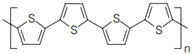
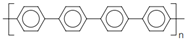
4.4. Types of Conductive Polymers
4.4.1. Intrinsically Conductive Polymers-ICPs
4.4.2. Extrinsically Conductive Polymers-ECPs
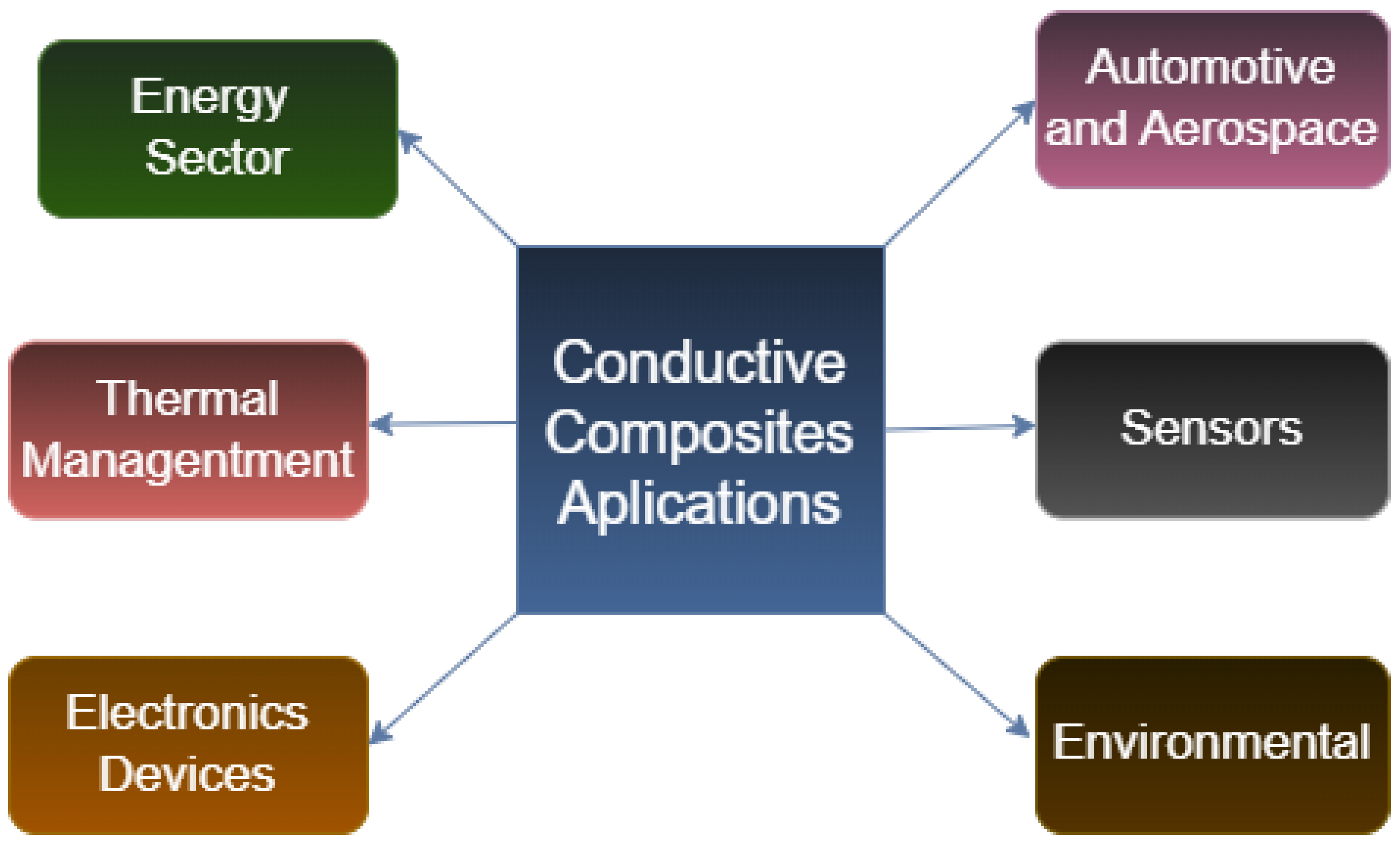
4.5. Applications of Conductive Polymers
4.6. Composites with Nano-Reinforcements
- Ceramic matrix nanocomposites (CMNC);
- Polymer matrix nanocomposites (PMNC);
- Metal matrix nanocomposites (MMNC).
4.6.1. Carbon Nanotubes
4.6.2. Graphene and Derivatives
4.6.3. Electrical Properties
5. Prospects
6. Conclusions
- A variety of composite-type materials covered in the review included metal, ceramic, and polymer-based composites, as well as nanocomposites with nanoscale reinforcements.
- Impact of Metallic Nanoparticles: the analysis showed that adding metallic nanoparticles can greatly improve polymer composites’ electrical conductivity, mostly because they create conductive networks inside the matrix.
- Significance of Dielectric and Electrical Behavior: a thorough explanation of electrical conductivity and dielectric characteristics was given, with a focus on how these characteristics are affected by the interactions between composite materials in different scenarios.
- Contribution to the Literature: This review makes a significant contribution to the academic community by compiling current and pertinent studies, acting as a reference and a stimulant for more in-depth, focused research.
- Potential Applications: The electrical behavior of the composites investigated in this work provides opportunities for use in important fields like environmental technologies, biomedical devices, and electronics.
- Hybrid Composites: the creation of systems that combine various fillers, like metallic particles, with graphene or carbon nanotubes to enable multifunctionality and take advantage of synergistic effects.
- Sustainable Materials: In order to lessen the environmental impact, it will be more crucial to incorporate biodegradable or bio-based matrices with environmentally friendly conductive fillers.
- Electrically conductive composites are anticipated to be essential in the development of wearable technology, flexible electronics, and intelligent sensors that can react to chemical, mechanical, or thermal stimuli.
- Advanced processing methods: precise control over filler dispersion and composite architecture will be made possible by the application of additive manufacturing (such as 3D printing) and nano-engineering techniques.
- Interface Optimization: To improve electrical pathways and long-term stability, future research will probably concentrate on customizing the interface between the matrix and conductive filler.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Atomic Force Microscopy |
| ICP | Extrinsically Conductive Polymers |
| ICP | Intrinsically Conductive Polymers |
| LM | Liquid Metals |
| SEM | Scanning Electron Microscopy |
| WC-Co | Tungsten carbide-cobalt |
| Aluminum | |
| Copper | |
| Conductive Polymers | |
| Cytosine | |
| e | Electron |
| Electron-Volt | |
| Gallium | |
| Germanium | |
| Graphene Oxide | |
| Lithium Sulfide | |
| Avogadro’s number | |
| Nickel | |
| Polyacetylene | |
| Polyaniline | |
| Polyethylene | |
| Polypyrrole | |
| Polystyrene | |
| Polythiophene | |
| Polyvinyl Chloride | |
| Polyvinyl Alcohol | |
| Silicon | |
| Silicon Carbide | |
| Drift velocity | |
| Yttrium Oxide | |
| Electric permeability | |
| Electron mobility | |
| Mean electron velocity | |
| Electrical resistivity | |
| Electrical conductivity | |
| Mean free path | |
| Dielectric constant |
References
- Simões, S. High-performance advanced composites in multifunctional material design: State of the art, challenges, and future directions. Materials 2024, 17, 5997. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, R.; Isano, Y.; Ota, H. Stretchable composites with electrical conductivity. Flex. Print. Electron. 2025, 10, 013001. [Google Scholar] [CrossRef]
- Dhingra, A.; Kumar, R.; Thakur, O.; Pandey, R. Advancements in hexaferrite composite materials for electromagnetic interference shielding solutions. Sustain. Mater. Technol. 2025, 44, e01333. [Google Scholar] [CrossRef]
- Islam, M.; Hossain, M.S.; Adak, B.; Rahman, M.M.; kubra Moni, K.; Nur, A.S.; Hong, H.; Younes, H.; Mukhopadhyay, S. Recent advancements in carbon-based composite materials as electrodes for high-performance supercapacitors. J. Energy Storage 2025, 107, 114838. [Google Scholar] [CrossRef]
- Amin, A.S.; Caidi, A.; Lange, T.; Radev, I.; Sandbeck, D.J.S.; Philippi, W.; Kräenbring, M.A.; Öztürk, M.; Peinecke, V.; Lerche, D.; et al. Key Control Characteristics of Carbon Black Materials for Fuel Cells and Batteries for a Standardized Characterization of Surface Properties. Part. Part. Syst. Charact. 2025, 42, 2400069. [Google Scholar] [CrossRef]
- Faniband, B.; Chandra, S.S.; Pattar, J.; Rao, H.A.; Sreekanth, R.; Mahendra, K.; Murugendrappa, M.; Nataraja, S.K.; Nagaraja, M. Exploring the charge transport mechanism, electrical conductivity, and dielectric properties of polyaniline/tin sulfide nanocomposites. Polym. Compos. 2025, 46, 8076–8087. [Google Scholar] [CrossRef]
- Elbakyan, L.; Zaporotskova, I. Polypropylene Modified with Carbon Nanomaterials: Structure, Properties and Application (A Review). Polymers 2025, 17, 517. [Google Scholar] [CrossRef]
- Barra, A.; Ferreira, N.M.; Poças, F.; Ruiz-Hitzky, E.; Nunes, C.; Ferreira, P. Boosting through-plane electrical conductivity: Chitosan composite films with carbon-sepiolite and multiwalled carbon nanotubes. Carbon 2025, 231, 119691. [Google Scholar] [CrossRef]
- Lai, F.; Getzner, L.; Rotaru, A.; Molnár, G.; Cobo, S.; Bousseksou, A. Drastic Enhancement of Electrical Conductivity of Metal–Organic Frameworks Displaying Spin Crossover. Chem. Mater. 2025, 37, 636–643. [Google Scholar] [CrossRef]
- Lalire, T.; Longuet, C.; Taguet, A. Electrical properties of graphene/multiphase polymer nanocomposites: A review. Carbon 2024, 225, 119055. [Google Scholar] [CrossRef]
- Reghat, M.; Mirabedini, A.; Tan, A.M.; Weizman, Y.; Middendorf, P.; Bjekovic, R.; Hyde, L.; Antiohos, D.; Hameed, N.; Fuss, F.K.; et al. Graphene as a piezo-resistive coating to enable strain monitoring in glass fiber composites. Compos. Sci. Technol. 2021, 211, 108842. [Google Scholar] [CrossRef]
- Sahu, N.; Rizwan, A. Multifunctional Composite Materials: Innovations And Applications. Int. J. Compos. Mater. 2024, 10, 28–34. [Google Scholar]
- Sabet, M. Innovations in Carbon Nanotube Polymer Composites: Electrical, Thermal, and Mechanical Advancements for Aerospace and Automotive Applications. Synth. Met. 2024, 310, 117794. [Google Scholar] [CrossRef]
- Zhou, H.; Li, H.; Li, L.; Liu, T.; Chen, G.; Zhu, Y.; Zhou, L.; Huang, H. Structural composite energy storage devices—A review. Mater. Today Energy 2022, 24, 100924. [Google Scholar] [CrossRef]
- Van den Brink, W.; Van de Vrie, G.; Nawijn, M. Modelling and simulation of damage in woven fabric composites on meso-macro level using the independent mesh method. Int. J. Mater. Eng. Innov. 2013, 4, 84–100. [Google Scholar] [CrossRef]
- Aboudi, J.; Arnold, S.M.; Bednarcyk, B.A. Micromechanics of Composite Materials: A Generalized Multiscale Analysis Approach; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Gu, H.; Liu, C.; Zhu, J.; Gu, J.; Wujcik, E.K.; Shao, L.; Wang, N.; Wei, H.; Scaffaro, R.; Zhang, J.; et al. Introducing advanced composites and hybrid materials. Adv. Compos. Hybrid Mater. 2018, 1, 1–5. [Google Scholar] [CrossRef]
- Campbell, F.C. Structural Composite Materials; ASM International: Materials Park, OH, USA, 2010. [Google Scholar]
- González, C.; Vilatela, J.; Molina-Aldareguía, J.; Lopes, C.; LLorca, J. Structural composites for multifunctional applications: Current challenges and future trends. Prog. Mater. Sci. 2017, 89, 194–251. [Google Scholar] [CrossRef]
- Clyne, T.W.; Hull, D. An Introduction to Composite Materials; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Carlsson, L.A.; Adams, D.F.; Pipes, R.B. Experimental Characterization of Advanced Composite Materials; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- da Silva Chagas, N.P.; de Oliveira Aguiar, V.; da Costa Garcia Filho, F.; da Silva Figueiredo, A.B.H.; Monteiro, S.N.; Huaman, N.R.C.; Marques, M.d.F.V. Ballistic performance of boron carbide nanoparticles reinforced ultra-high molecular weight polyethylene (UHMWPE). J. Mater. Res. Technol. 2022, 17, 1799–1811. [Google Scholar] [CrossRef]
- An, X.; Li, F.; Kan, L.; Zhang, W.; Wang, J.; Jin, X.; Wang, Y.; Li, J.; Zhu, H.; Qi, W.; et al. High entropy alloy particle reinforced 6061 aluminum matrix composites: An investigation of mechanical strength and thermoelectric properties. J. Alloys Compd. 2025, 1010, 177424. [Google Scholar] [CrossRef]
- Vesco, S.; Salvi, D.; Almonti, D. High performance particle-reinforced epoxy composites with industrial grade graphite, GNPs and hBN: A comparative study. Int. J. Adv. Manuf. Technol. 2024, 136, 1379–1391. [Google Scholar] [CrossRef]
- Saravana Kumar, M.; Pulikkalparambil, H.; Ishfaq, K.; Ramasamy, S.; Romanovski, V.; Salah, B. Elevating green materials sustainability through the integration of ceramic particles. Polym. Compos. 2025. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Z.; Bi, S.; Sun, Q.; Lu, Y. Design and regulation of electromagnetic parameters of THz absorbing epoxy resin composite film for 6G electronic packaging. Mater. Today Phys. 2025, 51, 101655. [Google Scholar] [CrossRef]
- Ma, Q.; Dong, K.; Li, F.; Jia, Q.; Tian, J.; Yu, M.; Xiong, Y. Additive manufacturing of polymer composite millimeter-wave components: Recent progress, novel applications, and challenges. Polym. Compos. 2024, 46, 14–37. [Google Scholar] [CrossRef]
- Singhal, V.; Shelly, D.; Saxena, A.; Gupta, R.; Verma, V.K.; Jain, A. Study of the Influence of Nanoparticle Reinforcement on the Mechanical and Tribological Performance of Aluminum Matrix Composites—A Review. Lubricants 2025, 13, 93. [Google Scholar] [CrossRef]
- Khan, W.S.; Asmatulu, R. Nanotechnology Safety in Energy Industry; Elsevier eBooks: Amsterdam, The Netherlands, 2025; pp. 187–205. [Google Scholar]
- Callister, W.D., Jr.; Rethwisch, D.G. Callister’s Materials Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Oliveira, M.S.; da Costa Garcia Filho, F.; Pereira, A.C.; Nunes, L.F.; da Luz, F.S.; de Oliveira Braga, F.; Colorado, H.A.; Monteiro, S.N. Ballistic performance and statistical evaluation of multilayered armor with epoxy-fique fabric composites using the Weibull analysis. J. Mater. Res. Technol. 2019, 8, 5899–5908. [Google Scholar] [CrossRef]
- Yang, J.M.; Ma, C.L.; Chou, T.W. Fiber inclination model of three-dimensional textile structural composites. J. Compos. Mater. 1986, 20, 472–484. [Google Scholar] [CrossRef]
- Monteiro, S.N.; Lopes, F.P.D.; Ferreira, A.S.; Nascimento, D.C.O. Natural-fiber polymer-matrix composites: Cheaper, tougher, and environmentally friendly. JOM 2009, 61, 17–22. [Google Scholar] [CrossRef]
- Seychal, G.; Van Renterghem, L.; Ocando, C.; Bonnaud, L.; Raquez, J.M. Towards sustainable reprocessable structural composites: Benzoxazines as biobased matrices for natural fibers. Compos. Part B Eng. 2024, 272, 111201. [Google Scholar] [CrossRef]
- Miracle, D.B.; Donaldson, S.L.; Henry, S.D.; Moosbrugger, C.; Anton, G.J.; Sanders, B.R.; Hrivnak, N.; Terman, C.; Kinson, J.; Muldoon, K.; et al. ASM Handbook; ASM International: Materials Park, OH, USA, 2001; Volume 21. [Google Scholar]
- Staab, G. Laminar Composites; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Tariolle, S.; Thévenot, F.; Chartier, T.; Besson, J. Properties of reinforced boron carbide laminar composites. J. Eur. Ceram. Soc. 2005, 25, 3639–3647. [Google Scholar] [CrossRef]
- Kreja, I. A literature review on computational models for laminated composite and sandwich panels. Open Eng. 2011, 1, 59–80. [Google Scholar] [CrossRef]
- Omanović-Mikličanin, E.; Badnjević, A.; Kazlagić, A.; Hajlovac, M. Nanocomposites: A brief review. Health Technol. 2020, 10, 51–59. [Google Scholar] [CrossRef]
- de Carvalho, D.B.; da Costa Lima, R.; dos Santos Aguilera, L.; de Biasi, R.S.; da Silva Figueiredo, A.B.H. Ballistic resistance and microwave absorbing properties of a composite made of aramid fabric impregnated with polyethylene glycol and hematite nanoparticles. Obs. Econ. Latinoam. 2024, 22, e3739. [Google Scholar] [CrossRef]
- Patel, Y.; Sun, P.H.; Llumiquinga, B.; Bao, N.; Duran, A.; Nicholas, C.; Mohanty, R.; Cho, N.; Tse, S.; Singer, J. Enhancing Thermal Conductivity and Flame Resistance of Carbon Fiber Composites Using CNT-Infused Multiphase Graphene Resins; Cambridge University Press: Cambridge, UK, 2025. [Google Scholar]
- Bogue, R. Nanocomposites: A review of technology and applications. Assem. Autom. 2011, 31, 106–112. [Google Scholar] [CrossRef]
- Solymar, L.; Walsh, D.; Syms, R.R. Electrical Properties of Materials; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Kittel, C.; McEuen, P. Introduction to Solid State Physics; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Tenny, K.M.; Keenaghan, M. Ohms Law; Europe PMC: Cambridge, UK, 2017. [Google Scholar]
- Weber, B.; Mahapatra, S.; Ryu, H.; Lee, S.; Fuhrer, A.; Reusch, T.; Thompson, D.; Lee, W.; Klimeck, G.; Hollenberg, L.C.; et al. Ohm’s law survives to the atomic scale. Science 2012, 335, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Herman, F. Theoretical investigation of the electronic energy band structure of solids. Rev. Mod. Phys. 1958, 30, 102. [Google Scholar] [CrossRef]
- Ferrari, A.M.; Orlando, R.; Rérat, M. of the Ultraviolet-Visible (UV-vis) Absorption Spectrum, Electron-Loss Function, and Reflectivity of Solids. J. Chem. Theory Comput. 2023, 11, 3245–3258. [Google Scholar] [CrossRef]
- Baccaro, A.L.; Gutz, I.G. Fotoeletrocatálise em semicondutores: Dos princípios básicos até sua conformação à nanoescala. Química Nova 2018, 41, 326–339. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Huang, N.Y.; Xu, Q. Metal halide perovskite materials in photocatalysis: Design strategies and applications. Coord. Chem. Rev. 2023, 481, 215031. [Google Scholar] [CrossRef]
- Katzbaer, R.R.; dos Santos Vieira, F.M.; Dabo, I.; Mao, Z.; Schaak, R.E. Band Gap Narrowing in a High-Entropy Spinel Oxide Semiconductor for Enhanced Oxygen Evolution Catalysis. J. Am. Chem. Soc. 2023, 145, 6753–6761. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, Z.; Guan, R.; Cheng, X.; Shang, Q.; Sun, Y. Regulation of the band structure and water solubility of perylene imide derivatives based on bay-substitution to accelerate the transport of photogenerated carriers with TiO2. Chem. Eng. J. 2023, 470, 144293. [Google Scholar] [CrossRef]
- Ko, H.; Wi, Y.; Koo, J.; Rim, M.; Hyeong, J.; Yoo, M.J.; Jeong, Y.; Chaudhary, G.; Kang, D.G.; Jeong, K.U. Recyclable Low Dielectric Polymers with High Thermal Conductivity for Copper-Clad Laminated Film for High-Frequency Applications. Adv. Funct. Mater. 2025, 2422633. [Google Scholar] [CrossRef]
- Cheng, Y.; Gong, H.; Zhang, M.; Ji, Q.; Zhang, G.; Zhang, X.; Zhang, Z. Overcoming Energy Storage-Loss Trade-Offs in Polymer Dielectrics Through the Synergistic Tuning of Electronic Effects in π-Conjugated Polystyrenes. Adv. Sci. 2025, 12, 2415738. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Tan, H.; Zhong, H.; Zhou, J.; Xu, A.; Luo, H.; Guo, R.; Chen, S. High energy density of poly(vinylidene fluoride)-based all organic dielectric composites via using functional polymethacrylate filler. J. Energy Storage 2025, 110, 115313. [Google Scholar] [CrossRef]
- Patel, A.; Upadhyaya, T.; Girjashankar, P.R.; Swati, M.; Kumar, O.P. Enhanced isolation in aperture fed dielectric resonator MIMO antennas for 5G Sub 6 GHz applications. Sci. Rep. 2025, 15, 10653. [Google Scholar] [CrossRef]
- Aljelawy, S.S.; Al-Bermany, E.; Abdulridha, A.R. Opto-electrical dielectrics and conductivity behavior of vinyl polymers reinforced with chitosan@ graphene oxide nanomaterials for optoelectronic and biological activity. Eur. Phys. J. Plus 2025, 140, 94. [Google Scholar] [CrossRef]
- García-Hernández, Z.; Molina-Ramírez, O.; Rivera-Salinas, J.E.; Sifuentes-Nieves, I.; González-Morones, P.; Hernández-Hernández, E. Boron nitride: The key material in polymer composites for electromobility. Polym. Compos. 2025, 46, 1976–2029. [Google Scholar] [CrossRef]
- Adachi, S. Properties of Semiconductor Alloys: Group-IV, III-V and II-VI Semiconductors; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Miracle, D. Metal matrix composites–from science to technological significance. Compos. Sci. Technol. 2005, 65, 2526–2540. [Google Scholar] [CrossRef]
- Ghandour, A.A.; Selmy, A.; Megahed, M.; Kabeel, A.; Ibrahim, A. Performance analysis of 3D orthogonal polymeric composites reinforced with metallic and glass fibrous z-binders of varying sizes. Polym. Compos. 2025, 46, 6670–6680. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, Z.; Li, X.; Ji, Y.; Yang, Z.; Yin, T.; Long, J.; Li, C. High-Temperature Electrical Insulation Degradation Mechanism in TiN/Ti (C, N)/Al2O3 Composite Ceramic Films. Ceram. Int. 2025, 51, 31219–31229. [Google Scholar] [CrossRef]
- Li, Y.; Xiong, T.; Ge, L.; Liu, D.; Ma, W.; Gang, S.; Li, X.; Jiang, Q.; Luo, Y.; Yang, J. Highly-Effective Thermoelectric Cooling for Power Semiconductor Devices Packed with Thermal-Expansion Offset and Flame Retardancy Epoxy Resin. Adv. Funct. Mater. 2025, 22, 2420944. [Google Scholar] [CrossRef]
- Rihan, M.; Hassan, A.; Ebnalwaled, K.; Nasrat, L.S. Electrical Insulators Based on Polymeric Materials: Toward New Cutting-edge Enhancements. SVU Int. J. Eng. Sci. Appl. 2025, 6, 86–92. [Google Scholar] [CrossRef]
- Bakkiyaraj, M.; Kumar, R.D.S.; Kumar, L.H.; Abdul Munaf, R.N. Mechanical Behavior and Applications of Hybrid Polymer Composites Reinforced with Natural Fibers: A Narrative Theoretical Review. Solid State Phenom. 2025, 369, 17–36. [Google Scholar] [CrossRef]
- Umer, U.; Abidi, M.H.; Almutairi, Z.; Aboudaif, M.K. A Multi-Phase Analytical Model for Effective Electrical Conductivity of Polymer Matrix Composites Containing Micro-SiC Whiskers and Nano-Carbon Black Hybrids. Polymers 2025, 17, 128. [Google Scholar] [CrossRef] [PubMed]
- Kausar, A. Composites/Nanocomposites of natural rubber with carbonaceous micro-/nano-reinforcements—research trends and scientific distinctions. Polymer Plast. Technol. Mater. 2025, 64, 138–157. [Google Scholar] [CrossRef]
- Chung, D.D. Composites get smart. Mater. Today 2002, 5, 30–35. [Google Scholar] [CrossRef]
- Kumar, B.; Fellner, J. Polymer–ceramic composite protonic conductors. J. Power Sources 2003, 123, 132–136. [Google Scholar] [CrossRef]
- Kashfipour, M.A.; Mehra, N.; Zhu, J. A review on the role of interface in mechanical, thermal, and electrical properties of polymer composites. Adv. Compos. Hybrid Mater. 2018, 1, 415–439. [Google Scholar] [CrossRef]
- Yadav, S.; Sharma, A. Importance and challenges of hydrothermal technique for synthesis of transition metal oxides and composites as supercapacitor electrode materials. J. Energy Storage 2021, 44, 103295. [Google Scholar] [CrossRef]
- Xiao, J.; Li, H.; Zhang, H.; He, S.; Zhang, Q.; Liu, K.; Jiang, S.; Duan, G.; Zhang, K. Nanocellulose and its derived composite electrodes toward supercapacitors: Fabrication, properties, and challenges. J. Bioresour. Bioprod. 2022, 7, 245–269. [Google Scholar] [CrossRef]
- Khan, M.E.; Mohammad, A.; Yoon, T. State-of-the-art developments in carbon quantum dots (CQDs): Photo-catalysis, bio-imaging, and bio-sensing applications. Chemosphere 2022, 302, 134815. [Google Scholar] [CrossRef]
- Ye, M.; Gao, X.; Hong, X.; Liu, Q.; He, C.; Liu, X.; Lin, C. Recent advances in quantum dot-sensitized solar cells: Insights into photoanodes, sensitizers, electrolytes and counter electrodes. Sustain. Energy Fuels 2017, 1, 1217–1231. [Google Scholar] [CrossRef]
- Iacob, M.; Tugui, C.; Tiron, V.; Bele, A.; Vlad, S.; Vasiliu, T.; Cazacu, M.; Vasiliu, A.L.; Racles, C. Iron oxide nanoparticles as dielectric and piezoelectric enhancers for silicone elastomers. Smart Mater. Struct. 2017, 26, 105046. [Google Scholar] [CrossRef]
- Kosedag, E.; Ekici, R. Low-velocity and ballistic impact resistances of particle reinforced metal–matrix composites: An experimental study. J. Compos. Mater. 2022, 56, 991–1002. [Google Scholar] [CrossRef]
- Uddin, S.M.; Mahmud, T.; Wolf, C.; Glanz, C.; Kolaric, I.; Volkmer, C.; Höller, H.; Wienecke, U.; Roth, S.; Fecht, H.J. Effect of size and shape of metal particles to improve hardness and electrical properties of carbon nanotube reinforced copper and copper alloy composites. Compos. Sci. Technol. 2010, 70, 2253–2257. [Google Scholar] [CrossRef]
- Khan, J.B.; Smith, A.C.; Tuohy, P.M.; Gresil, M.; Soutis, C.; Lambourne, A. Experimental electrical characterisation of carbon fibre composites for use in future aircraft applications. IET Sci. Meas. Technol. 2019, 13, 1131–1138. [Google Scholar] [CrossRef]
- Gibson, R.F. A review of recent research on mechanics of multifunctional composite materials and structures. Compos. Struct. 2010, 92, 2793–2810. [Google Scholar] [CrossRef]
- Huang, Y.; Kormakov, S.; He, X.; Gao, X.; Zheng, X.; Liu, Y.; Sun, J.; Wu, D. Conductive Polymer Composites from Renewable Resources: An Overview of Preparation, Properties, and Applications. Polymers 2019, 11, 187. [Google Scholar] [CrossRef]
- Sharmila, T.B.; Antony, J.V.; Jayakrishnan, M.; Beegum, P.S.; Thachil, E.T. Mechanical, thermal and dielectric properties of hybrid composites of epoxy and reduced graphene oxide/iron oxide. Mater. Des. 2016, 90, 66–75. [Google Scholar] [CrossRef]
- Ighalo, J.O.; Adeniyi, A.G. Utilization of recycled polystyrene and aluminum wastes in the development of conductive plastic composites: Evaluation of electrical properties. In Handbook of Environmental Materials Management; PHI Learning Pvt. Ltd.: Delhi, India, 2020; pp. 1–9. [Google Scholar]
- Abdulkareem, S.; Adeniyi, A. Recycling copper and polystyrene from solid waste stream in developing conductive composites. J. Solid Waste Technol. Manag. 2019, 45, 39–44. [Google Scholar] [CrossRef]
- Pargi, M.N.F.; Teh, P.L.; Hussiensyah, S.; Yeoh, C.K.; Abd Ghani, S. Recycled-copper-filled epoxy composites: The effect of mixed particle size. Int. J. Mech. Mater. Eng. 2015, 10, 1–10. [Google Scholar] [CrossRef]
- Mamunya, Y.P.; Davydenko, V.; Pissis, P.; Lebedev, E. Electrical and thermal conductivity of polymers filled with metal powders. Eur. Polym. J. 2002, 38, 1887–1897. [Google Scholar] [CrossRef]
- Kurt, E.; Özçelik, C.Y.; Yetgin, S.; Ömürlü, F.Ö.; Balköse, D. Preparation and characterization of flexible polyvinylchloride-copper composite films. Polym. Polym. Compos. 2013, 21, 139–144. [Google Scholar] [CrossRef]
- Xu, Y.; Su, Y.; Xu, X.; Arends, B.; Zhao, G.; Ackerman, D.N.; Huang, H.; Reid, S.P.; Santarpia, J.L.; Kim, C.; et al. Porous liquid metal–elastomer composites with high leakage resistance and antimicrobial property for skin-interfaced bioelectronics. Sci. Adv. 2023, 9, eadf0575. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Han, S.I.; Jung, D.; Hwang, H.J.; Lim, C.; Bae, S.; Park, O.K.; Tschabrunn, C.M.; Lee, M.; Bae, S.Y.; et al. Highly conductive, stretchable and biocompatible Ag–Au core–sheath nanowire composite for wearable and implantable bioelectronics. Nat. Nanotechnol. 2018, 13, 1048–1056. [Google Scholar] [CrossRef] [PubMed]
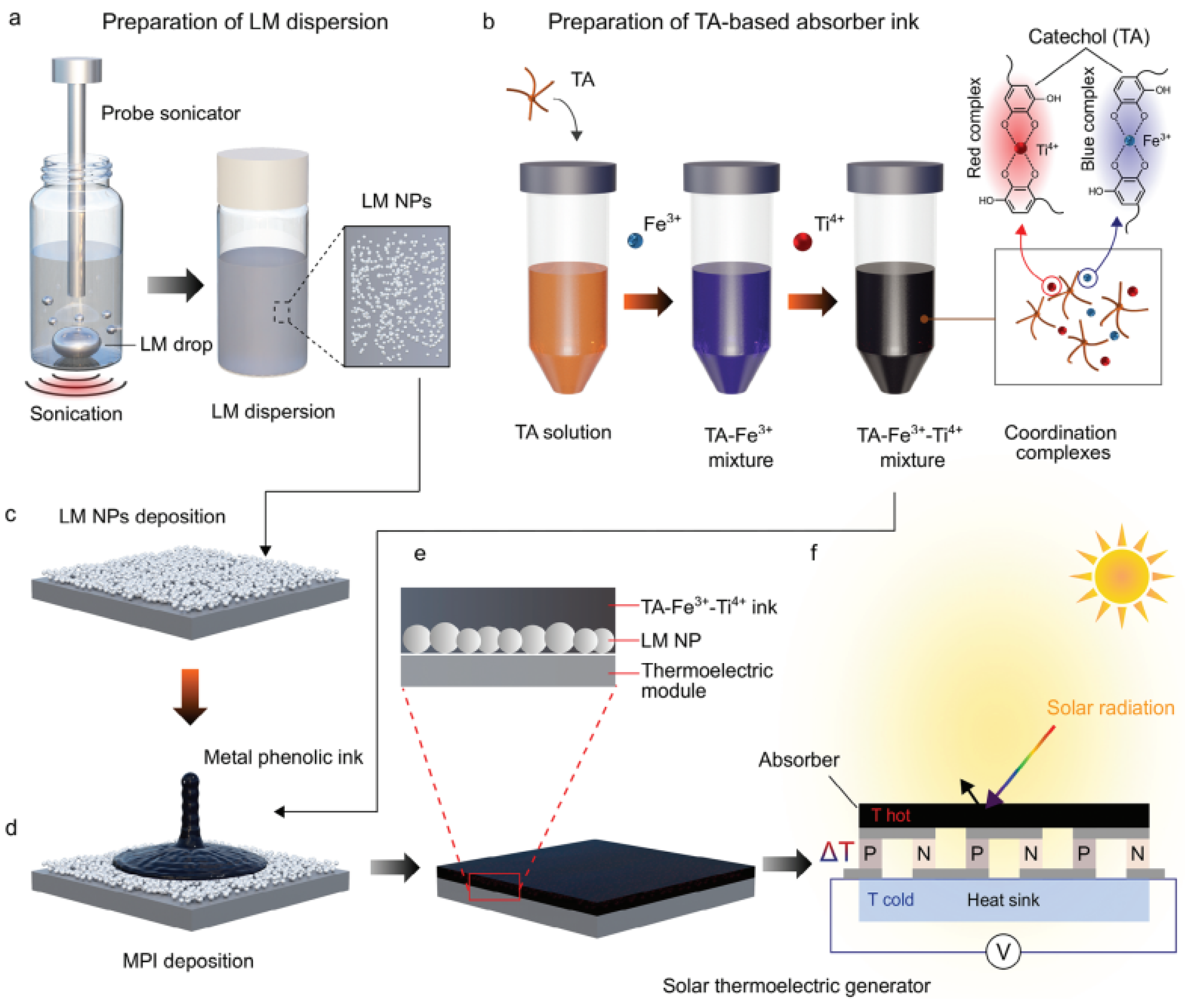
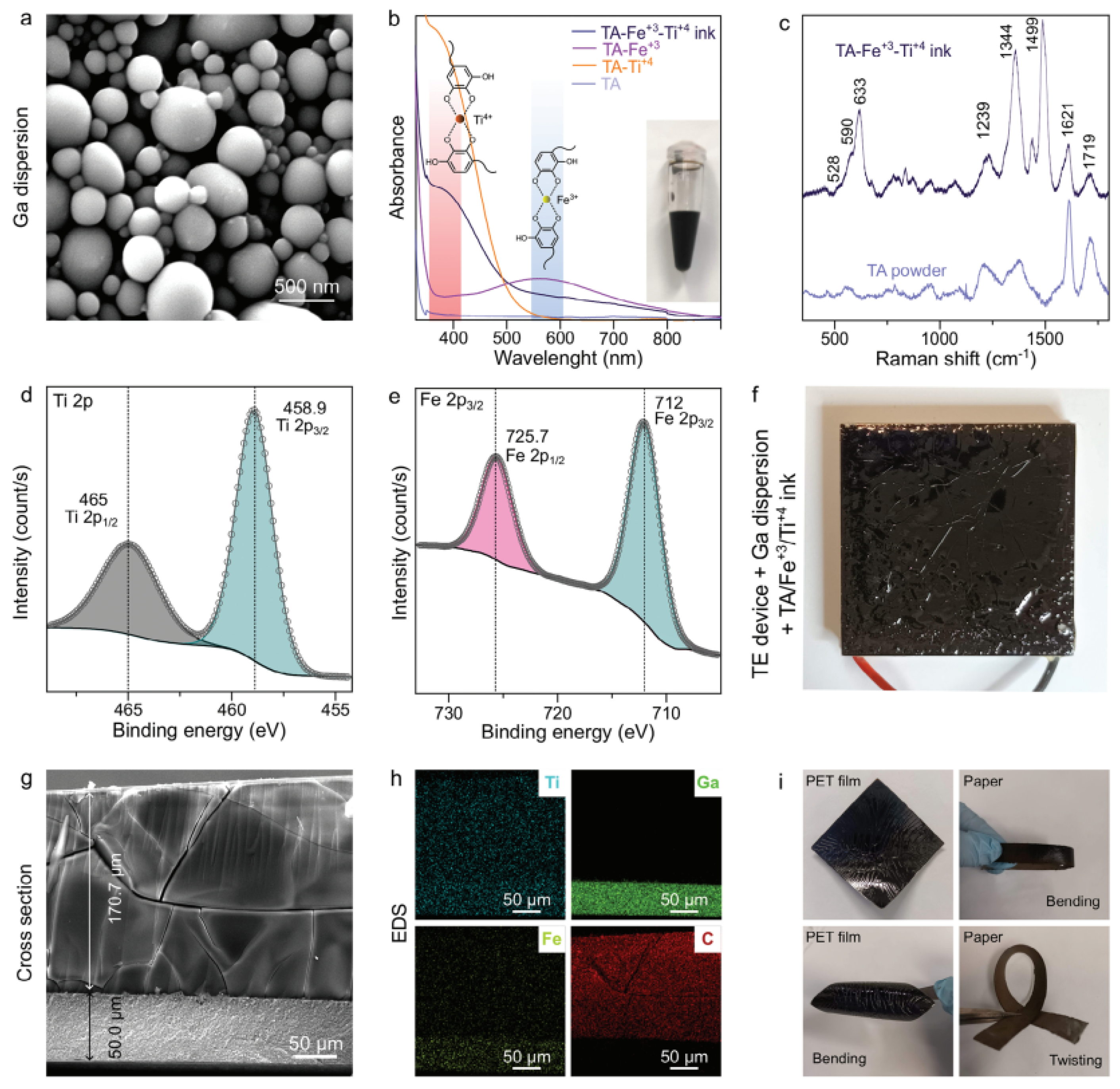
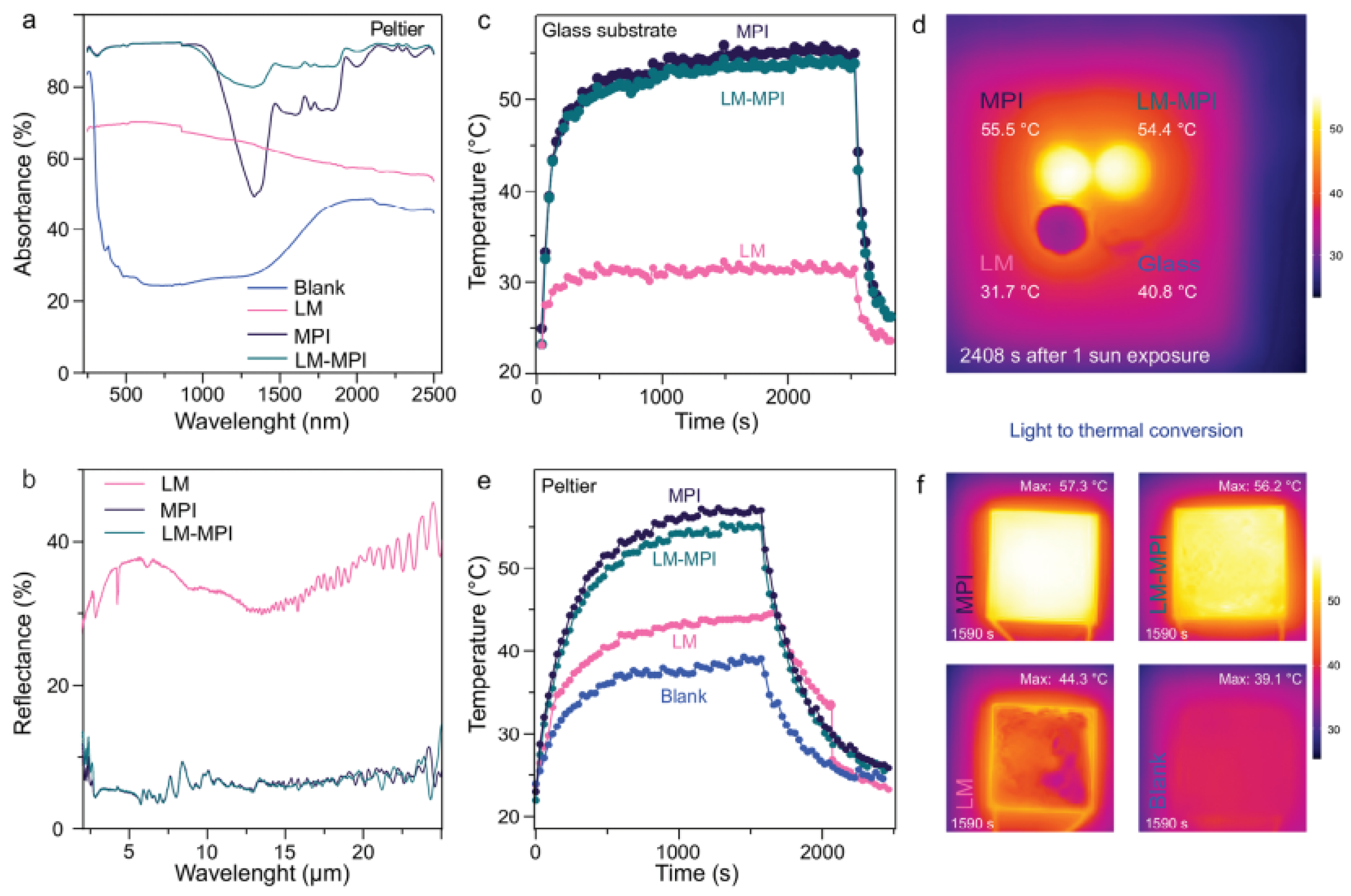
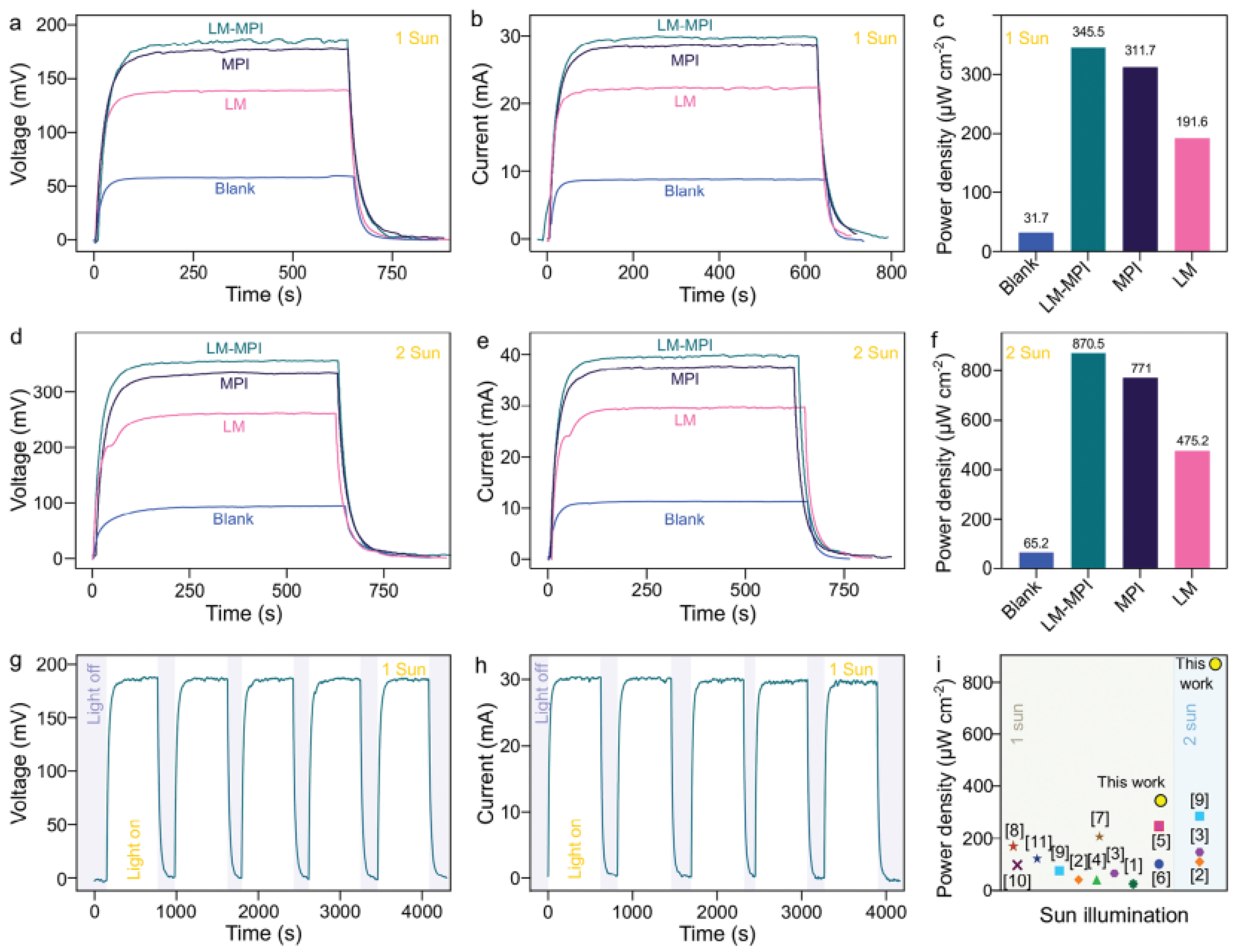
- Flores, N.; Centurion, F.; Zheng, J.; Baharfar, M.; Kilani, M.; Ghasemian, M.B.; Allioux, F.M.; Tang, J.; Tang, J.; Kalantar-Zadeh, K.; et al. Polyphenol-Mediated Liquid Metal Composite Architecture for Solar Thermoelectric Generation. Adv. Mater. 2024, 36, 2308346. [Google Scholar] [CrossRef]
- Rana, D.; Xavier, V.; Jana, S.S.; Maiti, T.; Thiruvenkatam, V.; Balani, K. Elevated Temperature Thermal and Electrical Properties of Carbon Nanotubes, Graphite and Graphene Reinforced (Zr-Ta-W-Ti) C-SiC Based High Entropy Carbide Ceramics. Mater. Today Commun. 2024, 38, 108434. [Google Scholar] [CrossRef]
- Wan, X.; Wu, Y.; Lai, S.; Weng, A.; Jah, T.N.; Du, Z.; Chen, D.; Ding, G.; Cheng, G. Thermal stability and electrical properties of polyaniline/waterborne polyurethane composites by using in-situ polymerization. Synth. Met. 2024, 302, 117545. [Google Scholar] [CrossRef]
- Hu, W.; Li, Y.; Zhang, W.; Ma, Z.; Feng, Y.; Liu, C.; Li, C.; Yu, L.; Liu, Y. Excellent mechanical, thermal and electrical properties of ultrafine W-Cu alloys via freeze-drying technology. Scr. Mater. 2024, 239, 115805. [Google Scholar] [CrossRef]
- Lobato, C.N.; Esposito, V.; Pryds, N.; Christensen, D. How efficient are thermoelectric materials?—An assessment of state-of-the-art individual and segmented thermoelectric materials. Mater. Today Energy 2024, 43, 101564. [Google Scholar] [CrossRef]
- Tiryaki, H.; Yusuf, A.; Ballikaya, S. Determination of electrical and thermal conductivities of n-and p-type thermoelectric materials by prediction iteration machine learning method. Energy 2024, 292, 130597. [Google Scholar] [CrossRef]
- Rajesh, C. Applications of ceramic matrix composites. In Technical Organic and Inorganic Fibres from Natural Resources; Elsevier: Amsterdam, The Netherlands, 2025; pp. 741–763. [Google Scholar]
- Gupta, A.; Morscher, G.N. Electrical resistance of non-oxide ceramic matrix composites: Health monitoring and design considerations. Ceram. Int. 2025, 51, 8930–8940. [Google Scholar] [CrossRef]
- Long, L.; Zhang, Y.; Zhu, H.; Nie, Y.; Zhou, W.; Li, Y. In situ growth of the Y3Si2C2 interphase in SiCf-reinforced mullite ceramics for enhanced electromagnetic wave absorption. J. Am. Ceram. Soc. 2025, 108, e20506. [Google Scholar] [CrossRef]
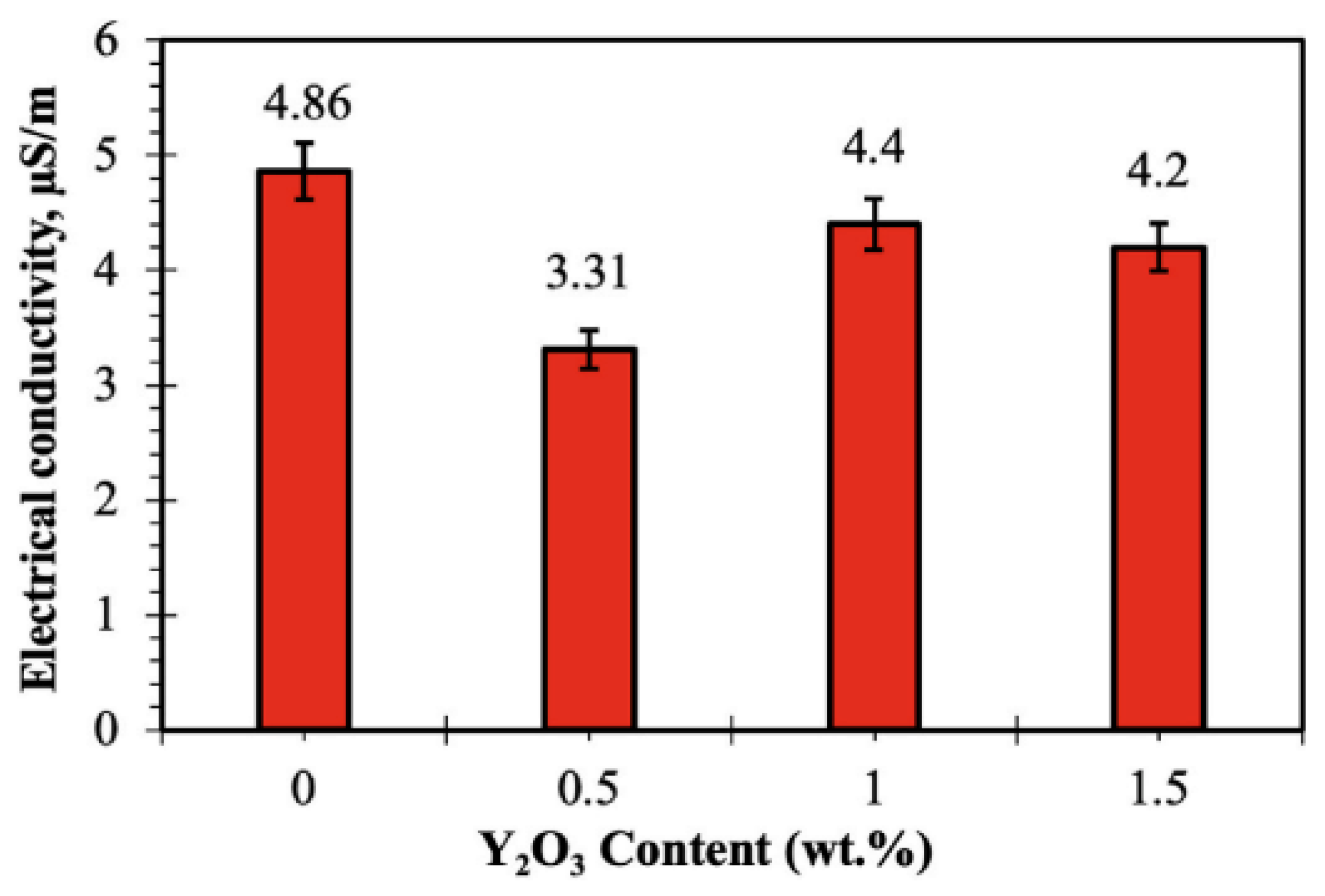
- Abd-Elaziem, W.; Hamada, A.; Allam, T.; Mohammed, M.M.; Abd-El Hamid, M.; Samah, S.; Wasfy, D.; Darwish, M.A.; El-Kady, Y.O.A.E.; Elkatatny, S. Enhancement of mechanical and physical properties of Cu–Ni composites by various contents of Y2O3 reinforcement. J. Mater. Res. Technol. 2024, 30, 473–484. [Google Scholar] [CrossRef]
- Abd-Elaziem, W.; Liu, J.; Ghoniem, N.; Li, X. Effect of nanoparticles on creep behaviour of metals: A review. J. Mater. Res. Technol. 2023, 26, 3025–3053. [Google Scholar] [CrossRef]
- Paton, N.E. Materials for advanced space propulsion systems. Mater. Sci. Eng. A 1991, 143, 21–29. [Google Scholar] [CrossRef]
- Qin, J.; Wu, Y.; Yu, M.; Liu, B.; Liu, H.; Weiss, K.P.; Li, L.; Li, H.; Niu, E.; Bruzzone, P. Manufacture of ITER feeder sample conductors. Fusion Eng. Des. 2013, 88, 1461–1464. [Google Scholar] [CrossRef]
- Hamid, F.S.; El-Kady, O.A.E.; Essa, A.R.S.; El-Nikhaily, A.E.G.; Elsayed, A.; Abd-Elaziem, W. Synthesis and characterization of titanium carbide and/or alumina nanoparticle reinforced copper matrix composites by spark plasma sintering. J. Mater. Eng. Perform. 2022, 31, 5583–5592. [Google Scholar] [CrossRef]
- Mu, Z.; Geng, H.R.; Li, M.M.; Nie, G.L.; Leng, J.F. Effects of Y2O3 on the property of copper based contact materials. Compos. Part B Eng. 2013, 52, 51–55. [Google Scholar] [CrossRef]
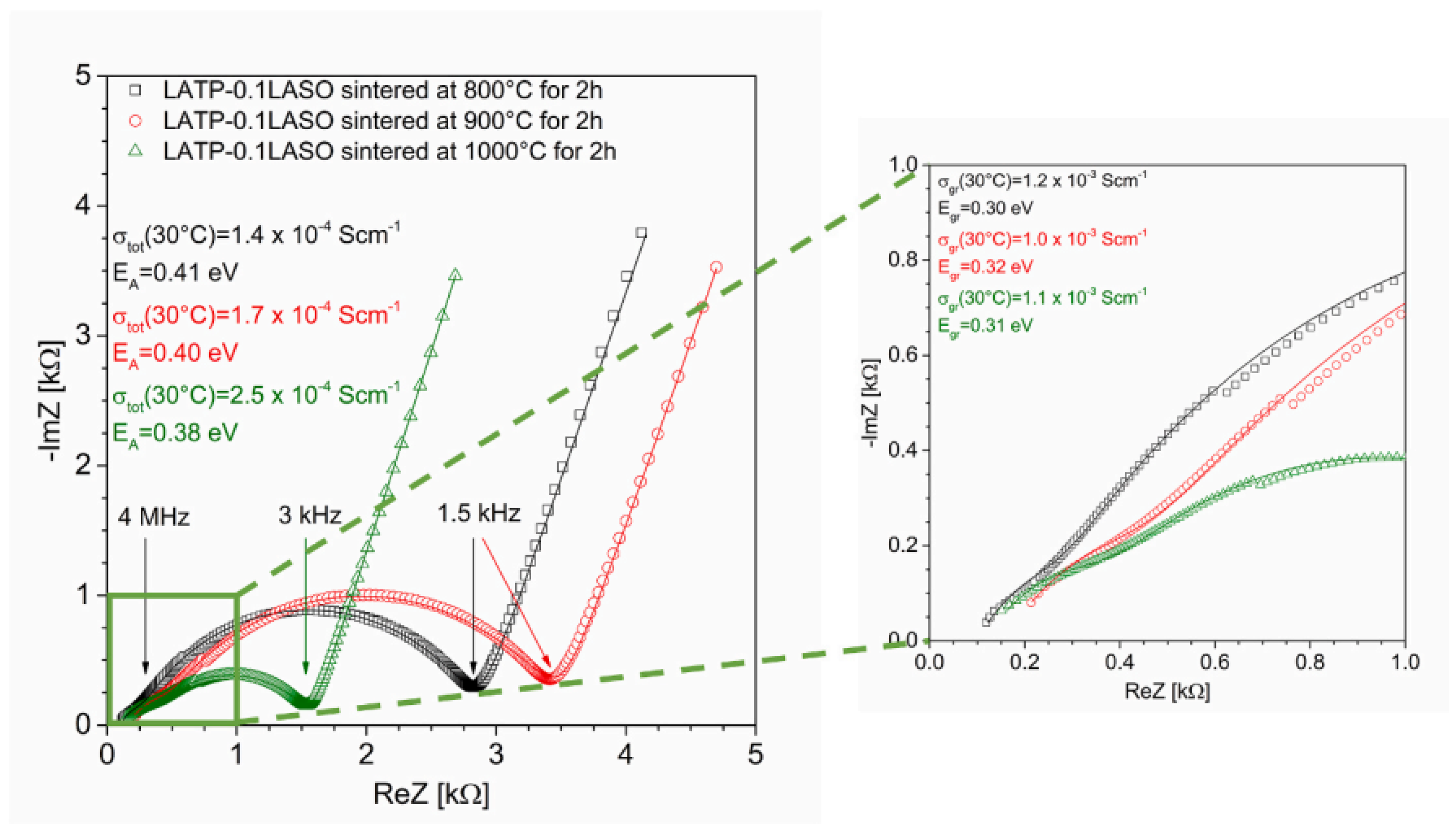
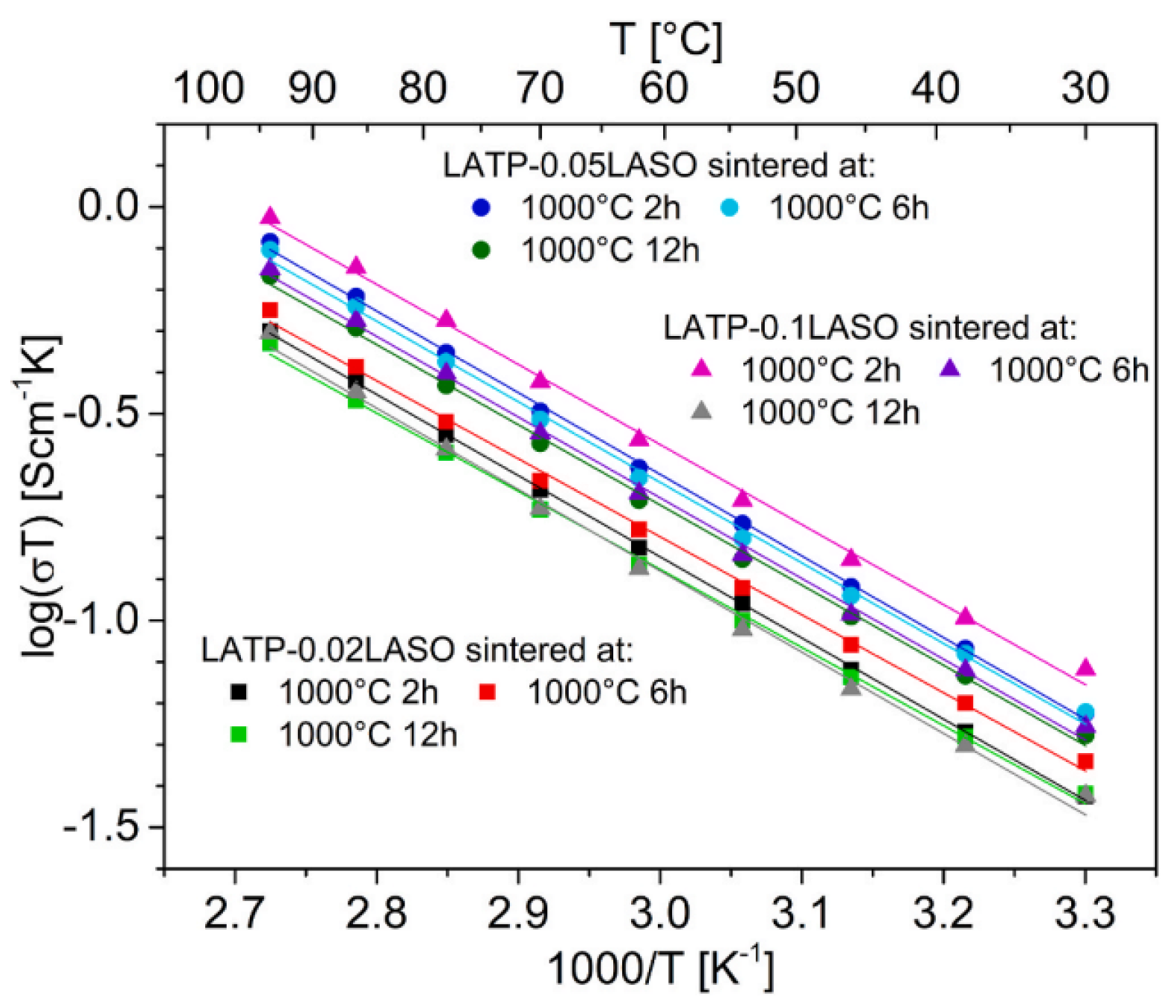
- Kwatek, K.; Ślubowska-Walkusz, W.; Nowiński, J.; Krawczyńska, A.; Sobrados, I.; Diez-Gomez, V.; Sanz, J. Effect of addition of LiAlSiO4 on microstructure, phase composition, and electrical properties of Li1.3Al0.3Ti1.7(PO4)3–based solid electrolyte. Ceram. Int. 2024, 50, 12450–12458. [Google Scholar] [CrossRef]
- Kundu, S.; Kraytsberg, A.; Ein-Eli, Y. Recent development in the field of ceramics solid-state electrolytes: I—oxide ceramic solid-state electrolytes. J. Solid State Electrochem. 2022, 26, 1809–1838. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, J.; Fan, L.; Zhang, J.; Li, X. Recent advances in Li1+xAlxTi2−x(PO4)3 solid-state electrolyte for safe lithium batteries. Energy Storage Mater. 2019, 19, 379–400. [Google Scholar] [CrossRef]
- Reddy, M.V.; Julien, C.M.; Mauger, A.; Zaghib, K. Sulfide and oxide inorganic solid electrolytes for all-solid-state Li batteries: A review. Nanomaterials 2020, 10, 1606. [Google Scholar] [CrossRef]
- Mauger, A.; Julien, C.M.; Paolella, A.; Armand, M.; Zaghib, K. Building better batteries in the solid state: A review. Materials 2019, 12, 3892. [Google Scholar] [CrossRef]
- Gu, R.; Kang, J.; Guo, X.; Li, J.; Yu, K.; Ma, R.; Xu, Z.; Jin, L.; Wei, X. Microstructure and ionic conductivity of Li0.5−xLa0.5(Ti1−xNbx)O3 solid-state electrolytes. J. Alloys Compd. 2022, 896, 163084. [Google Scholar] [CrossRef]
- Yu, K.; Tian, Y.; Gu, R.; Jin, L.; Ma, R.; Sun, H.; Xu, Y.; Xu, Z.; Wei, X. Ionic conduction, colossal permittivity and dielectric relaxation behavior of solid electrolyte Li3xLa2/3−xTiO3 ceramics. J. Eur. Ceram. Soc. 2018, 38, 4483–4487. [Google Scholar] [CrossRef]
- Koishi, M.; Kotobuki, M. Preparation of Y-doped Li7La3Zr2O12 by co-precipitation method. Ionics 2022, 28, 2065–2072. [Google Scholar] [CrossRef]
- Il’ina, E.; Raskovalov, A.; Antonov, B.; Pankratov, A.; Reznitskikh, O. Composite electrolytes ceramic Li7La3Zr2O12/glassy Li2O-Y2O3-SiO2. Mater. Res. Bull. 2017, 93, 157–161. [Google Scholar] [CrossRef]
- Il’ina, E.; Pershina, S.; Antonov, B.; Pankratov, A.; Vovkotrub, E. The influence of the glass additive Li2O-B2O3-SiO2 on the phase composition, conductivity, and microstructure of the Li7La3Zr2O12. J. Alloys Compd. 2018, 765, 841–847. [Google Scholar] [CrossRef]
- Kaur, G.; Singh, M.D.; Sivasubramanian, S.C.; Dalvi, A. Investigations on enhanced ionic conduction in ionic liquid dispersed sol-gel derived LiTi2(PO4)3. Mater. Res. Bull. 2022, 145, 111555. [Google Scholar] [CrossRef]
- Sharma, S.; Kaur, G.; Dalvi, A. Improving Interfaces in All-Solid-State Supercapacitors Using Polymer-Added Activated Carbon Electrodes. Batteries 2023, 9, 81. [Google Scholar] [CrossRef]
- Jiménez, R.; Sobrados, I.; Martínez-Chaparro, S.; del Campo, A.A.; Calzada, M.L.; Sanz, J.; Tsai, S.Y.; Lin, M.R.; Fung, K.Z.; Kazakevicius, E.; et al. Preparation and characterization of large area Li-NASICON electrolyte thick films. Inorganics 2019, 7, 107. [Google Scholar] [CrossRef]
- Kwatek, K.; Nowiński, J. The lithium-ion-conducting ceramic composite based on LiTi2(PO4)3 with addition of LiF. Ionics 2019, 25, 41–50. [Google Scholar] [CrossRef]
- Zhao, G.; Suzuki, K.; Seki, T.; Sun, X.; Hirayama, M.; Kanno, R. High lithium ionic conductivity of γ-Li3PO4-type solid electrolytes in Li4GeO4–Li4SiO4–Li3VO4 quasi-ternary system. J. Solid State Chem. 2020, 292, 121651. [Google Scholar] [CrossRef]
- Okumura, T.; Taminato, S.; Takeuchi, T.; Kobayashi, H. Minimizing the grain boundary resistance of Li-ion-conducting oxide electrolyte by controlling liquid-phase formation during sintering. ACS Appl. Energy Mater. 2018, 1, 6303–6311. [Google Scholar] [CrossRef]
- Koedtruad, A.; Patino, M.A.; Ichikawa, N.; Kan, D.; Shimakawa, Y. Crystal structures and ionic conductivity in Li2OHX (X = Cl, Br) antiperovskites. J. Solid State Chem. 2020, 286, 121263. [Google Scholar] [CrossRef]
- Yang, Y.; Han, J.; DeVita, M.; Lee, S.S.; Kim, J.C. Lithium and chlorine-rich preparation of mechanochemically activated antiperovskite composites for solid-state batteries. Front. Chem. 2020, 8, 562549. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Avdeev, M.; Yun, H.; Kim, S.J. LiTa2PO8: A fast lithium-ion conductor with new framework structure. J. Mater. Chem. A 2018, 6, 22478–22482. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, J.; Ma, L.; Zhai, D.; Wei, B.; Yang, H.; He, C. Electronic structure and geometric construction modulation of carbon-based single/dual atom catalysts for electrocatalysis. Energy Rev. 2024, 3, 100075. [Google Scholar] [CrossRef]
- Huang, B.; Xu, B.; Zhang, J.; Li, Z.; Huang, Z.; Li, Y.; Wang, C.A. Li-ion conductivity and stability of hot-pressed LiTa2PO8 solid electrolyte for all-solid-state batteries. J. Mater. Sci. 2021, 56, 2425–2434. [Google Scholar] [CrossRef]
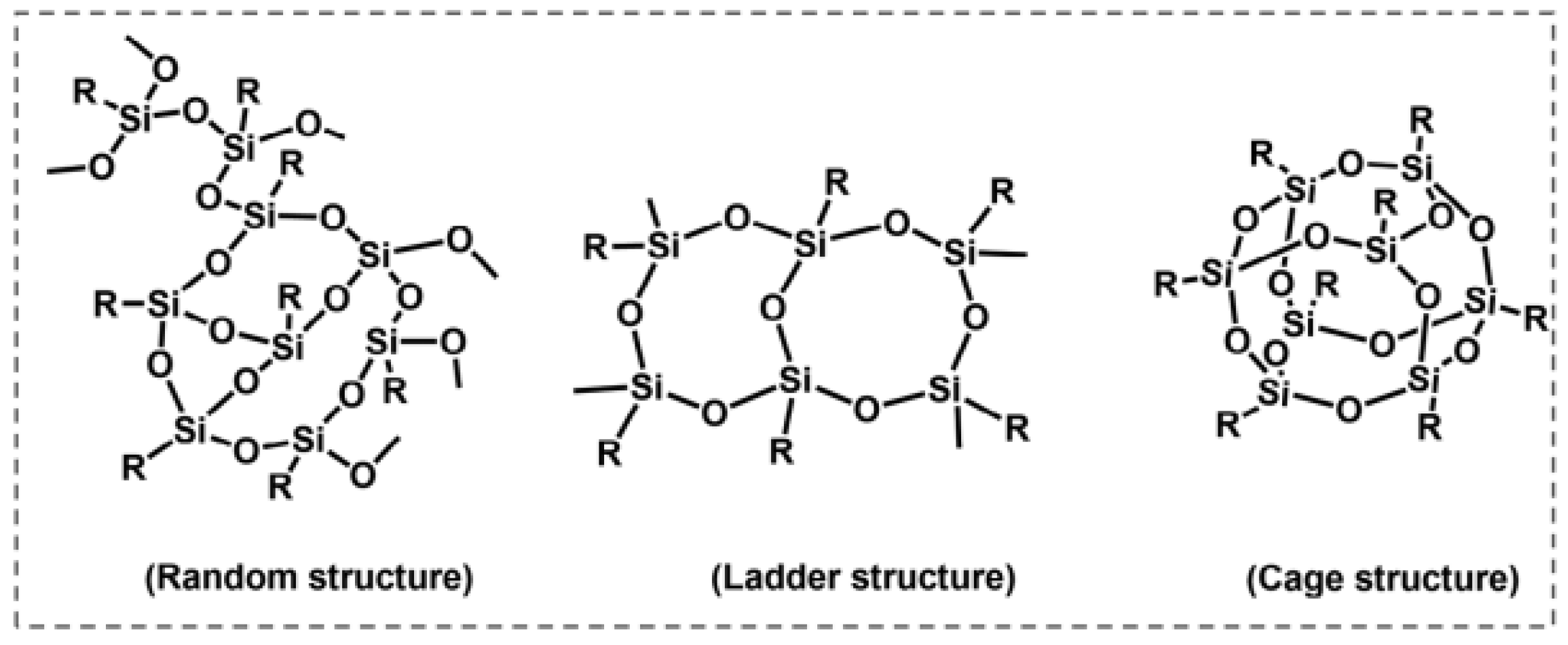
- Miao, L.; Zhan, L.; Liao, S.; Li, Y.; He, T.; Yin, S.; Wu, L.; Qiu, H. The Recent Advances of Polymer-POSS Nanocomposites with Low Dielectric Constant. Macromol. Rapid Commun. 2024, 45, 2300601. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, Y.; Huang, S.; Fu, J.; Zhou, Y.; Li, M.; Meng, L.; Zhang, X.; Liang, J.; Ran, Z.; et al. Dielectric polymers with mechanical bonds for high-temperature capacitive energy storage. Nat. Mater. 2025, 24, 1–8. [Google Scholar] [CrossRef]
- Shanmugasundram, H.P.P.V.; Jayamani, E.; Soon, K.H. Classification, theories, and methodologies concerning bio-based polymer dielectric composites. Renew. Sustain. Energy Rev. 2025, 209, 115026. [Google Scholar] [CrossRef]
- Ahbab, N.; Naz, S.; Xu, T.B.; Zhang, S. A Comprehensive Review of Piezoelectric PVDF Polymer Fabrications and Characteristics. Micromachines 2025, 16, 386. [Google Scholar] [CrossRef]
- Mehrabova, M.; Babayev, E.; Kerimov, F.; Asadov, M.; Hasanov, N.; Shamilov, F.; Musayev, Y. Study of mechanical properties of the composition based on low-density polyethylene modified with carbon nanotubes. Reliab. Theory Appl. 2025, 20, 410–419. [Google Scholar]
- Du, B.; Xiao, M. Polypropylene Film. In Polypropylene Film for HVDC Capacitors; Springer: Berlin, Germany, 2025; pp. 19–48. [Google Scholar]
- Chen, J.; Pei, Z.; Chai, B.; Jiang, P.; Ma, L.; Zhu, L.; Huang, X. Engineering the dielectric constants of polymers: From molecular to mesoscopic scales. Adv. Mater. 2024, 36, 2308670. [Google Scholar] [CrossRef]
- Tadesse, M.G.; Ahmmed, A.S.; Lübben, J.F. Review on Conductive Polymer Composites for Supercapacitor Applications. J. Compos. Sci. 2024, 8, 53. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, M. Supercapacitors. Towards Next Generation Energy Storage Technologies: From Fundamentals to Commercial Applications; John Wiley & Sons: Hoboken, NJ, USA, 2024; pp. 331–368. [Google Scholar]
- Phogat, P.; Sharma, S.; Jha, R.; Singh, S. Electrochemical Capacitors: EDLCs and Pseudocapacitors. In Electrochemical Devices: Principles to Applications; Springer: Berlin, Germany, 2024; pp. 225–255. [Google Scholar]
- Srividhya, G.; Ponpandian, N. Pseudocapacitance: Mechanism and Characteristics Check for updates. In Pseudocapacitors: Fundam. High Perform. Energy Storage Devices; Springer: Berlin, Germany, 2024; p. 39. [Google Scholar]
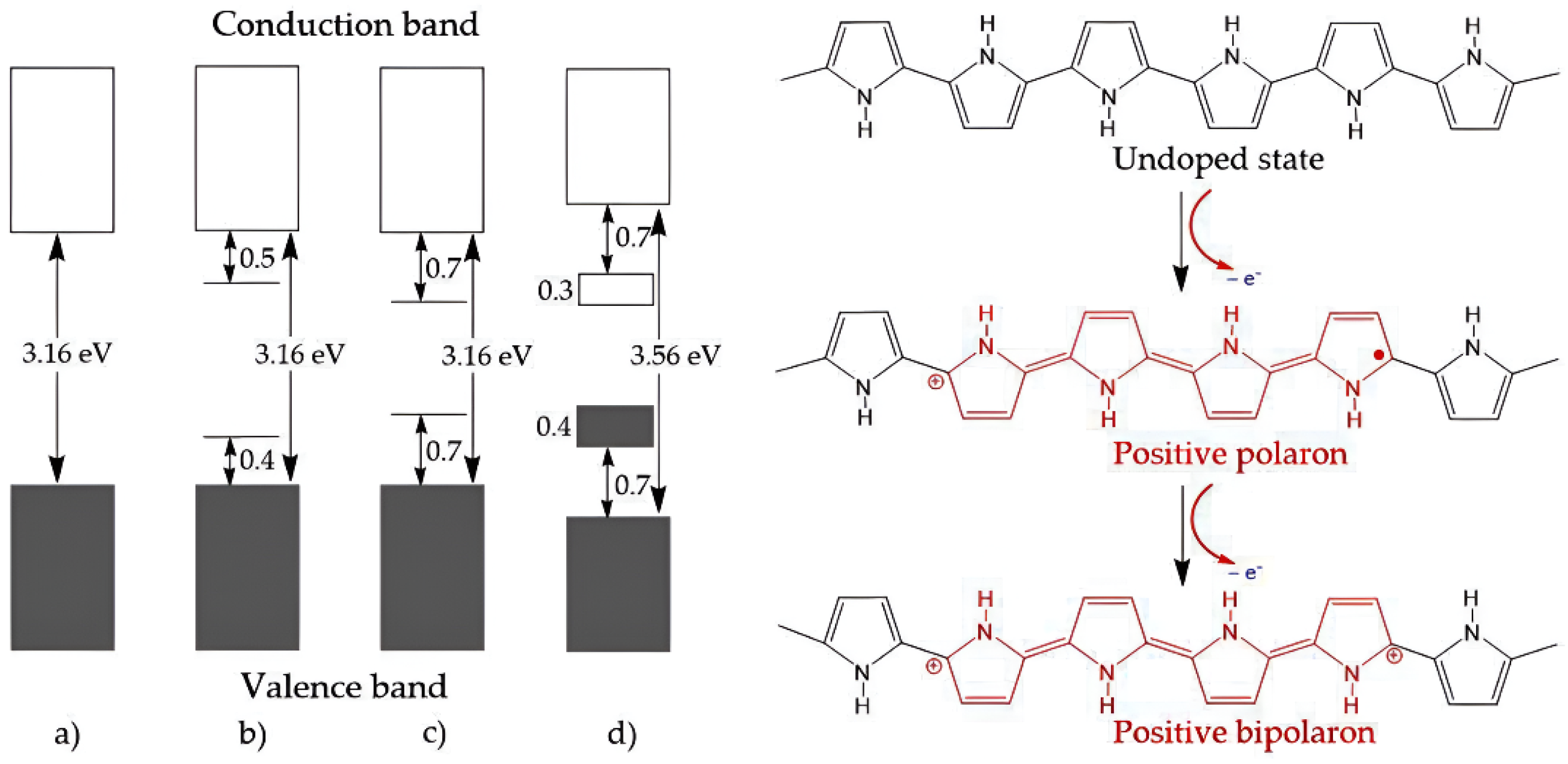
- Le, T.H.; Kim, Y.; Yoon, H. Electrical and electrochemical properties of conducting polymers. Polymers 2017, 9, 150. [Google Scholar] [CrossRef] [PubMed]
- Parkhutik, V.; Patil, R.; Harima, Y.; Matveyeva, E. Electrical conduction mechanism in conjugated polymers studied using Flicker noise spectroscopy. Electrochim. Acta 2006, 51, 2656–2661. [Google Scholar] [CrossRef]
- Yoon, S.E.; Park, J.; Kwon, J.E.; Lee, S.Y.; Han, J.M.; Go, C.Y.; Choi, S.; Kim, K.C.; Seo, H.; Kim, J.H.; et al. Improvement of Electrical Conductivity in Conjugated Polymers through Cascade Doping with Small-Molecular Dopants. Adv. Mater. 2020, 32, 2005129. [Google Scholar] [CrossRef]
- Zarean Mousaabadi, K.; Ensafi, A.A.; Fazel-Zarandi, R.; Vahabi, A. Conducting polymers, types, properties, and applications in electroluminescence, separation, and mass spectroscopy. J. Iran. Chem. Soc. 2024, 21, 1–26. [Google Scholar] [CrossRef]
- Faez, R.; Reis, C.; Freitas, P.D.; Kosima, O.K.; Ruggeri, G.; De Paoli, M. Polímeros condutores. Química Nova na Esc. 2000, 11, 13–18. [Google Scholar]
- Bobade, R.S. Polythiophene composites: A review of selected applications. J. Polym. Eng. 2011, 31, 209–215. [Google Scholar] [CrossRef]
- Tran, H.D.; Li, D.; Kaner, R.B. One-Dimensional Conducting Polymer Nanostructures: Bulk Synthesis and Applications. Adv. Mater. 2009, 21, 1487–1499. [Google Scholar] [CrossRef]
- Romero-Fierro, D.; Bustamante-Torres, M.; Bravo-Plascencia, F.; Magaña, H.; Bucio, E. Polymer-Magnetic Semiconductor Nanocomposites for Industrial Electronic Applications. Polymers 2022, 14, 2467. [Google Scholar] [CrossRef]
- Sharma, S.; Sudhakara, P.; Omran, A.A.B.; Singh, J.; Ilyas, R.A. Recent Trends and Developments in Conducting Polymer Nanocomposites for Multifunctional Applications. Polymers 2021, 13, 2898. [Google Scholar] [CrossRef]
- Stenger-Smith, J.D. Intrinsically electrically conducting polymers. Synthesis, characterization, and their applications. Prog. Polym. Sci. 1998, 23, 57–79. [Google Scholar] [CrossRef]
- Jianyong, O. Recent advances of intrinsically conductive polymers. Acta Phys. Chim. Sin 2018, 34, 1211–1220. [Google Scholar]
- Grancarić, A.M.; Jerković, I.; Koncar, V.; Cochrane, C.; Kelly, F.M.; Soulat, D.; Legrand, X. Conductive polymers for smart textile applications. J. Ind. Text. 2018, 48, 612–642. [Google Scholar] [CrossRef]
- Banerjee, S.; Kar, K.K. Conducting polymers as electrode materials for supercapacitors. In Handbook of Nanocomposite Supercapacitor Materials II: Performance; Springer: Berlin, Germany, 2020; pp. 333–352. [Google Scholar]
- Yu, T.; Li, S.; Zhang, L.; Li, F.; Pan, H.; Zhang, D. Design and construction of conductive polymer PPy anchored NiCo bi-metal sulfide composite electrode materials for high-performance hybrid supercapacitor and electrochemical hydroquinone sensor. J. Energy Storage 2024, 87, 111427. [Google Scholar] [CrossRef]
- Yuan, Z.; Yamamoto, H.; Kanehashi, S.; Shimomura, T. MEH-PPV/SBS composite films: Localization and luminescence properties of conductive polymers with microphase separation. Polym. Adv. Technol. 2024, 35, e6209. [Google Scholar] [CrossRef]
- Khade, V.; Wuppulluri, M. A comparative study on rigid and flexible magnetoelectric composites. J. Adv. Dielectr. 2024, 14, 2340001. [Google Scholar] [CrossRef]
- Lv, D.; Shen, W.; Tan, R.; Song, W. Conductive Polymers in Gas Sensors. Org. Inorg. Mater. Based Sens. 2024, 2, 631–673. [Google Scholar]
- Mulyono, T.; Siswoyo, A.; Lestari, P.B.; Zulfikar, Z.; Mufliha, Y.M. Development of A Resistive Sensor Array Based on Graphene and Conducting Polymer Composites for Coffee Aroma Classification. In Proceedings of the E3S Web of Conferences, Qingdao, China, 13–15 June 2024; Volume 481, p. 06012. [Google Scholar]
- Biglari, N.; Zare, E.N. Conjugated polymer-based composite scaffolds for tissue engineering and regenerative medicine. Alex. Eng. J. 2024, 87, 277–299. [Google Scholar] [CrossRef]
- Hosny, M.; Abdel-Aziz, M.; Zoromba, M.S.; Al-Hossainy, A. Design and synthesis of high-performance polymer blend solar cell. J. Mater. Res. Technol. 2024, 28, 4199–4211. [Google Scholar] [CrossRef]
- Nagao, Y. Proton-Conducting Polymers: Key to Next-Generation Fuel Cells, Electrolyzers, Batteries, Actuators, and Sensors. ChemElectroChem 2024, 11, e202300846. [Google Scholar] [CrossRef]
- Dua, S.; Arora, N.; Prakashaiah, B.; Saxena, R.C.; Ganguly, S.K.; Senthilkumar, T. Conjugated polymer-based composites for anti-corrosion applications. Prog. Org. Coatings 2024, 188, 108231. [Google Scholar] [CrossRef]
- Rikhari, B.; Saranya, K.; Kalaiyarasan, M.; Rahaman, M.; Periyasami, G.; Pandiaraj, S.; Thiruvengadam, M.; Pugalmani, S.; Rajakumar, G. Bioactive conductive polymer-coated titanium to support osseointegration. Biomass Convers. Biorefinery 2024, 14, 10699–10712. [Google Scholar] [CrossRef]
- Balaji, R.; Sasikumar, M. Graphene based strain and damage prediction system for polymer composites. Compos. Part A Appl. Sci. Manuf. 2017, 103, 48–59. [Google Scholar] [CrossRef]
- Akbar, A.R.; Tian, W.; Qadir, M.B.; Khaliq, Z.; Liu, Z.; Tahir, M.; Hu, Y.; Xiong, C.; Yang, Q. A novel ternary composite aerogel for high-performance supercapacitor. Colloids Surfaces A Physicochem. Eng. Asp. 2021, 610, 125644. [Google Scholar] [CrossRef]
- Schmidt, D.; Shah, D.; Giannelis, E.P. New advances in polymer/layered silicate nanocomposites. Curr. Opin. Solid State Mater. Sci. 2002, 6, 205–212. [Google Scholar] [CrossRef]
- Wang, R.M.; Zheng, S.R.; Zheng, Y.G. Polymer Matrix Composites and Technology; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Gomes Souza, F., Jr.; Bhansali, S.; Pal, K.; Silveira Maranhão, F.d.; Santos Oliveira, M.; Valladão, V.S.; Brandão e Silva, D.S.; Silva, G.B. A 30-Year Review on Nanocomposites: Comprehensive Bibliometric Insights into Microstructural, Electrical, and Mechanical Properties Assisted by Artificial Intelligence. Materials 2024, 17, 1088. [Google Scholar] [CrossRef]
- Tong, Z.; Lv, C.; Bai, G.; Yin, Z.; Zhou, Y.; Li, J. A review on applications and challenges of carbon nanotubes in lithium-ion battery. Carbon Energy 2024, 7, e643. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, H.; Hu, N.; Zhu, F.; Zhang, Y.; Yang, M.; Li, P.; Li, H. Recent advances in carbon nanotubes-based organic thermoelectric composites-a mini review. Mater. Today Nano 2025, 29, 100590. [Google Scholar] [CrossRef]
- Bocanegra-Bernal, M.H.; Reyes-Rojas, A.; Esparza-Ponce, H.E.; Aguilar-Elguézabal, A. Skepticism regarding the use of carbon nanotubes as reinforcing agent in ceramics for biomedical applications: A critical review. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2025, 239, 1051–1067. [Google Scholar] [CrossRef]
- Mathew, C.; Boby, A.; P, R.V.; Mohamed, S.N.; Singaravelu, D.L. Effect of multi-walled carbon nanotubes on the properties of Composite Bipolar Plate for Polymer Electrolyte Membrane Fuel Cells. Eng. Res. Express 2025, 7, 015552. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Lacey, S.D.; Xu, L.; Xie, H.; Li, T.; Danner, V.A.; Hu, L. Reduced graphene oxide film with record-high conductivity and mobility. Mater. Today 2018, 21, 186–192. [Google Scholar] [CrossRef]
- Din, I.U.; Bathusha, M.S.; Khan, K.A. Effects of liquid rubber-modified epoxy on the fracture toughness of rGO-Coated fabric piezoresistive composites. Compos. Commun. 2025, 56, 102368. [Google Scholar] [CrossRef]
- Rouabah, N.; Boudine, B.; Nazir, R.; Zaabat, M.; Sebais, M.; Halimi, O.; Soltani, M.; Chala, A. Structural, optical and photocatalytic properties of PVC/CdS nanocomposites prepared by soft chemistry method. J. Inorg. Organomet. Polym. Mater. 2021, 31, 1102–1110. [Google Scholar] [CrossRef]
- Ragab, H.; Diab, N.; Obeidat, S.T.; Alghamdi, A.M.; Khaled, A.M.; Farea, M.; Morsi, M. Improving the optical, thermal, mechanical, electrical properties and antibacterial activity of PVA-chitosan by biosynthesized Ag nanoparticles: Eco-friendly nanocomposites for food packaging applications. Int. J. Biol. Macromol. 2024, 264, 130668. [Google Scholar] [CrossRef]




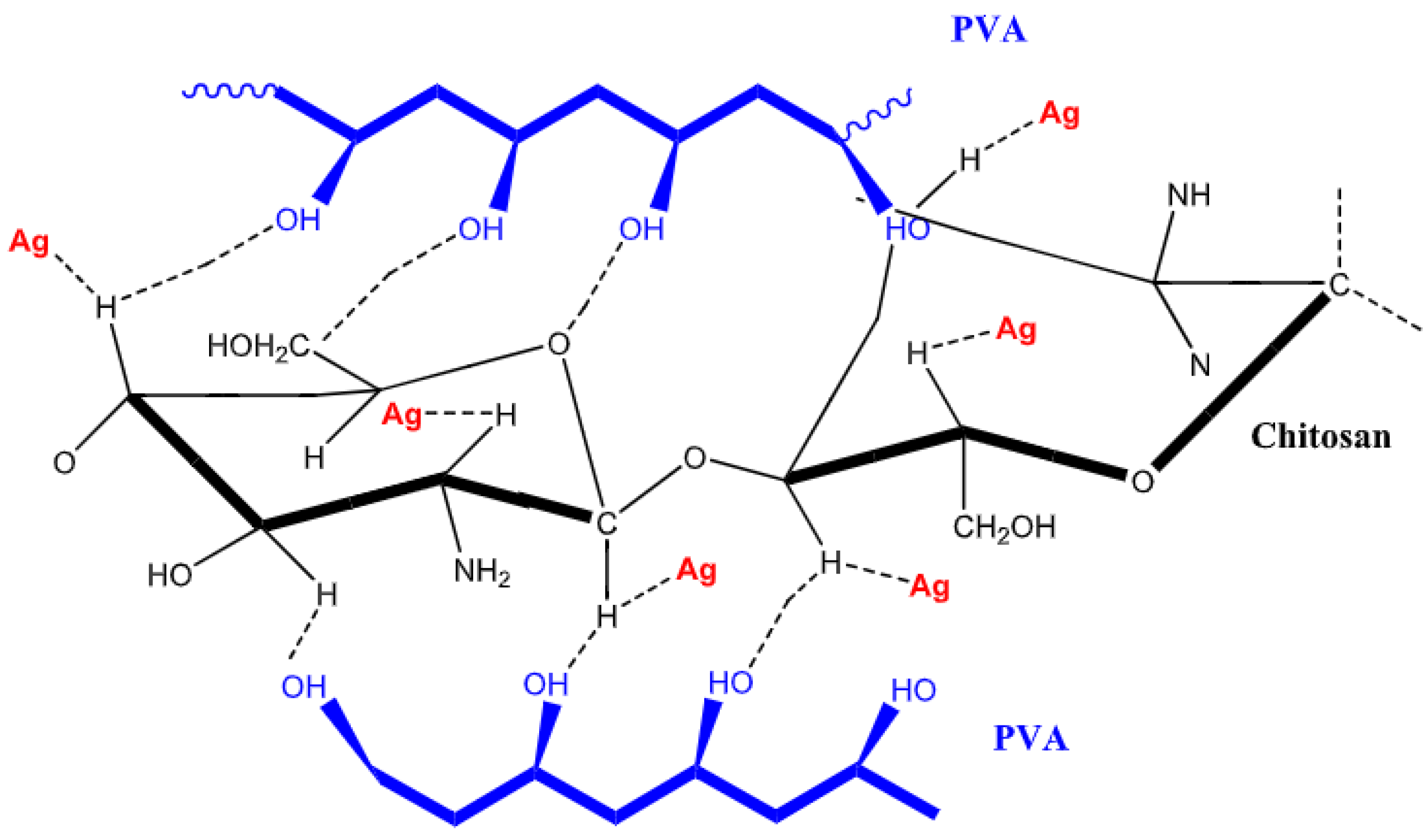
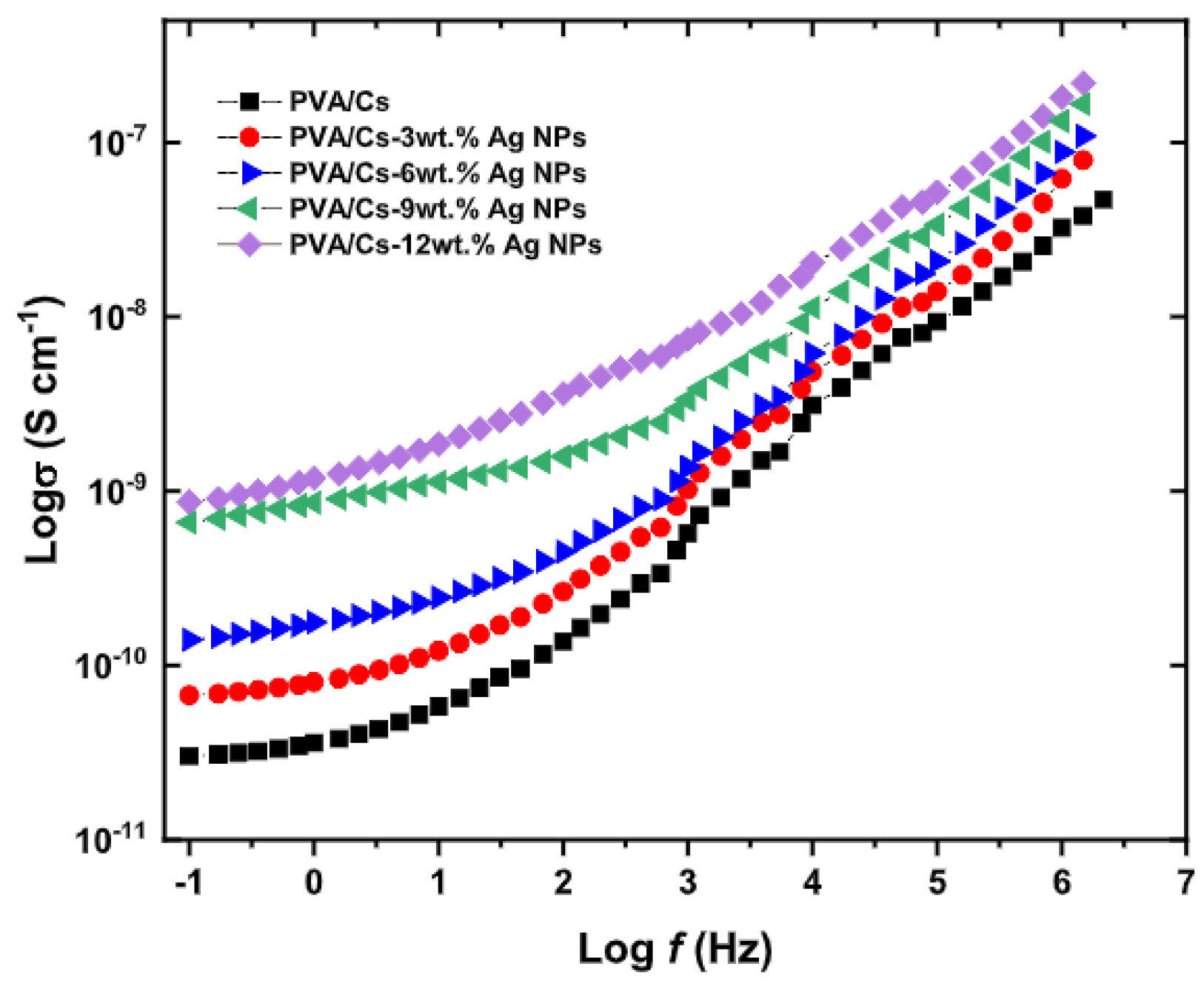
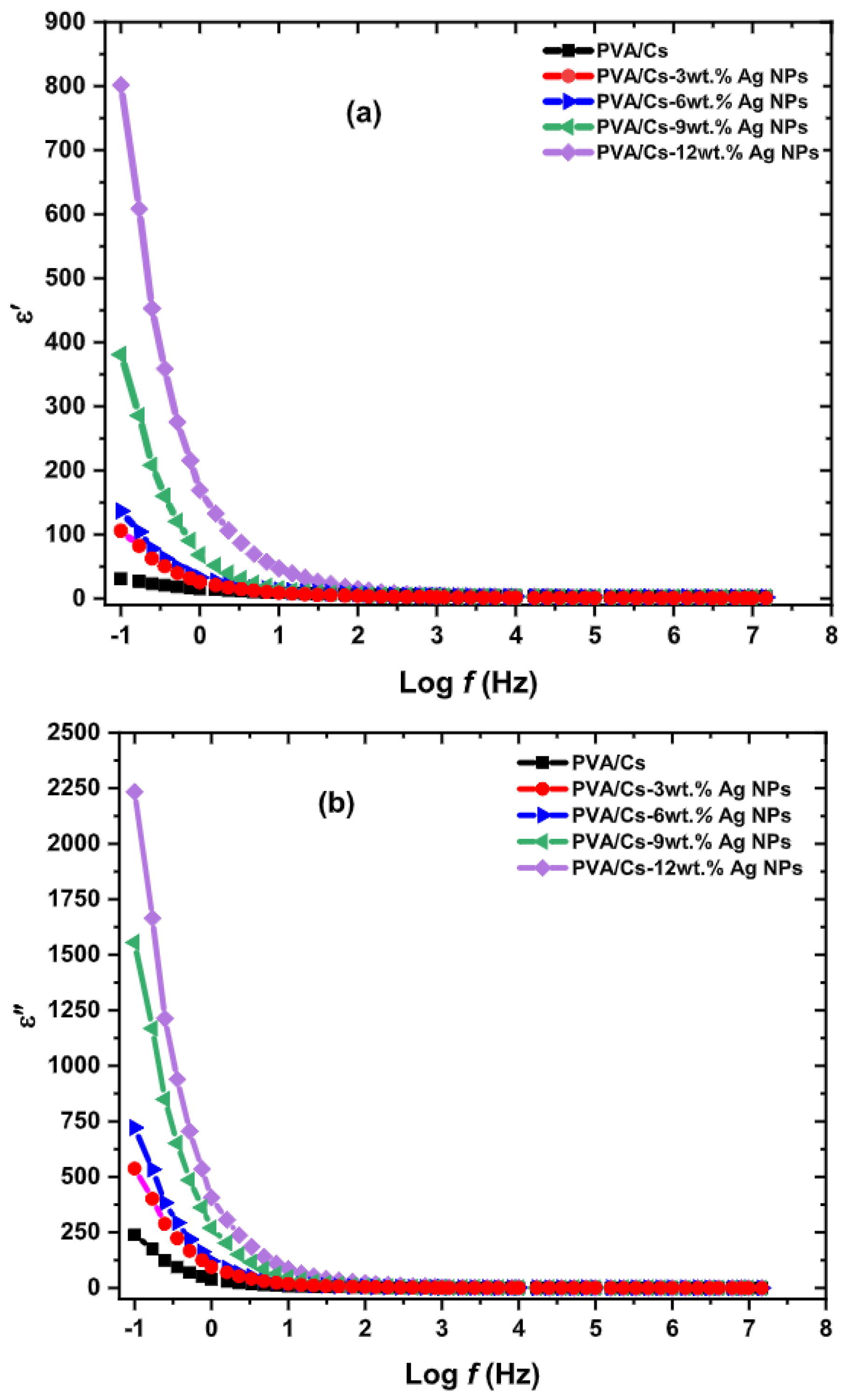
| Composite | Applications | Refs. |
|---|---|---|
| Metallic | Various electronic components and household appliances | [60,61] |
| Ceramic | Electrical insulators, sensors, and semiconductor devices | [62,63] |
| Polymeric | Lightweight electrical cables and insulators for electronic components | [64,65] |
| Nano-reinforcements | Can improve electrical conductivity and other composite properties | [66,67] |
| Composite | Metal Content | Electrical Conductivity (S/cm) | Ref. |
|---|---|---|---|
| Pure Cu | 100 wt% | [80] | |
| Pure Al | 100 wt% | [80] | |
| Pure Ni | 100 wt% | [80] | |
| Fe/EP/GO | 5 phr | [81] | |
| Al/PS | 40 wt% | [82] | |
| Cu/PS | 40 wt% | [83] | |
| Cu/EP | 40 wt% | ≈ | [84] |
| Ni/EP | 45 vol% | [85] | |
| Cu/EP | 45 vol% | [85] | |
| Cu/PVC | 45 vol% | [85] | |
| Ni/PVC | 45 vol% | [85] | |
| Cu/PVC | 18.7 wt% | [86] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, T.J.; Azevedo, A.M.d.; Monteiro, S.N.; Araujo-Moreira, F.M. Electrical Properties of Composite Materials: A Comprehensive Review. J. Compos. Sci. 2025, 9, 438. https://doi.org/10.3390/jcs9080438
Lopes TJ, Azevedo AMd, Monteiro SN, Araujo-Moreira FM. Electrical Properties of Composite Materials: A Comprehensive Review. Journal of Composites Science. 2025; 9(8):438. https://doi.org/10.3390/jcs9080438
Chicago/Turabian StyleLopes, Thomaz Jacintho, Ary Machado de Azevedo, Sergio Neves Monteiro, and Fernando Manuel Araujo-Moreira. 2025. "Electrical Properties of Composite Materials: A Comprehensive Review" Journal of Composites Science 9, no. 8: 438. https://doi.org/10.3390/jcs9080438
APA StyleLopes, T. J., Azevedo, A. M. d., Monteiro, S. N., & Araujo-Moreira, F. M. (2025). Electrical Properties of Composite Materials: A Comprehensive Review. Journal of Composites Science, 9(8), 438. https://doi.org/10.3390/jcs9080438