Kinetic Analysis of Thermal Degradation of Styrene–Butadiene Rubber Compounds Under Different Aging Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
- Original Unaged Sample (OUS): This baseline sample represents the original material in its unaltered, as-supplied state, and serves as a control to identify property changes due to aging.
- Laboratory-Stored Sample (LSS): Stored for 25 years under controlled laboratory conditions (23 °C ± 2 °C, 50% ± 5% relative humidity, and 1 atmosphere pressure), this sample was used to study the effects of natural, long-term aging without exposure to operational stressors.
- Operationally Aged Sample (OAS): Exposed over 25 years to high-voltage electrical installations, this sample experienced continuous thermal fluctuations due to seasonal temperature changes and mechanical vibrations caused by wind, providing insights into material behavior under real-world operational stresses.
2.2. Thermogravimetric Analysis
2.3. SEM/EDX Analysis
3. Theoretical Approach
3.1. Thermal Kinetic Analysis
3.2. The Kissinger–Akahira–Sunose (KAS) Method
3.3. The Flynn–Wall–Ozawa (FWO) Method
3.4. The Friedman Method
3.5. Lifetime of Thermal Decomposition
3.6. Thermodynamic Analysis
4. Results and Discussion
4.1. Thermal Analysis
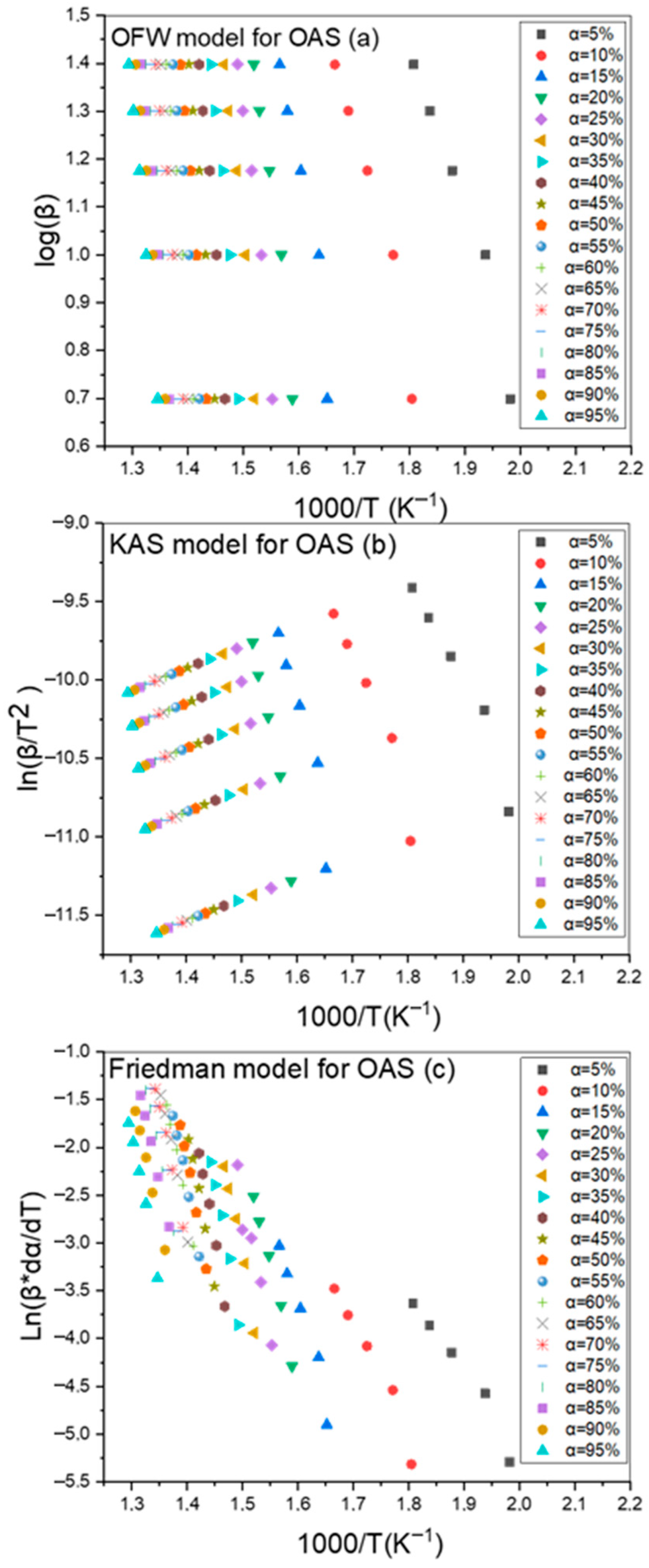
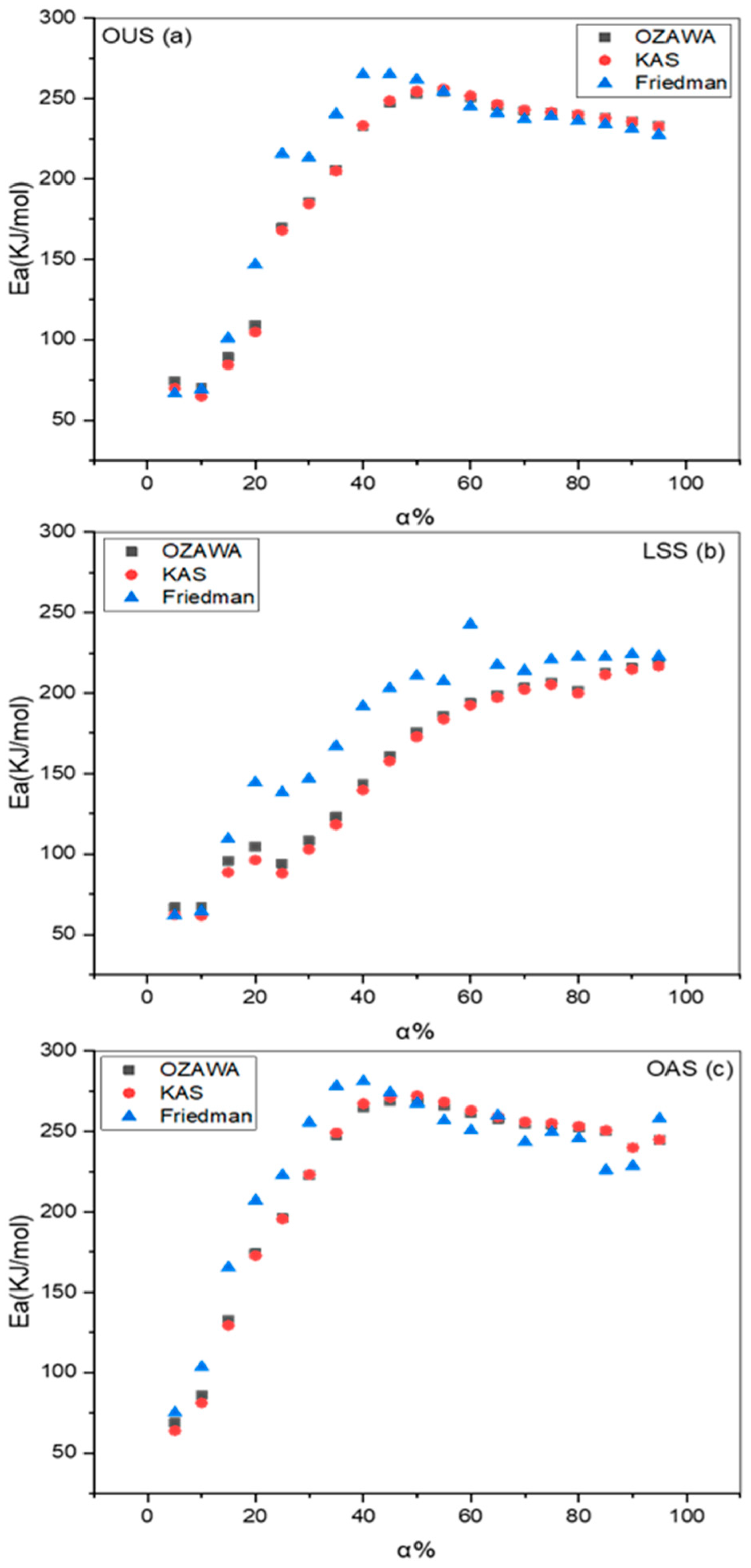
4.2. Determination of Activation Energy
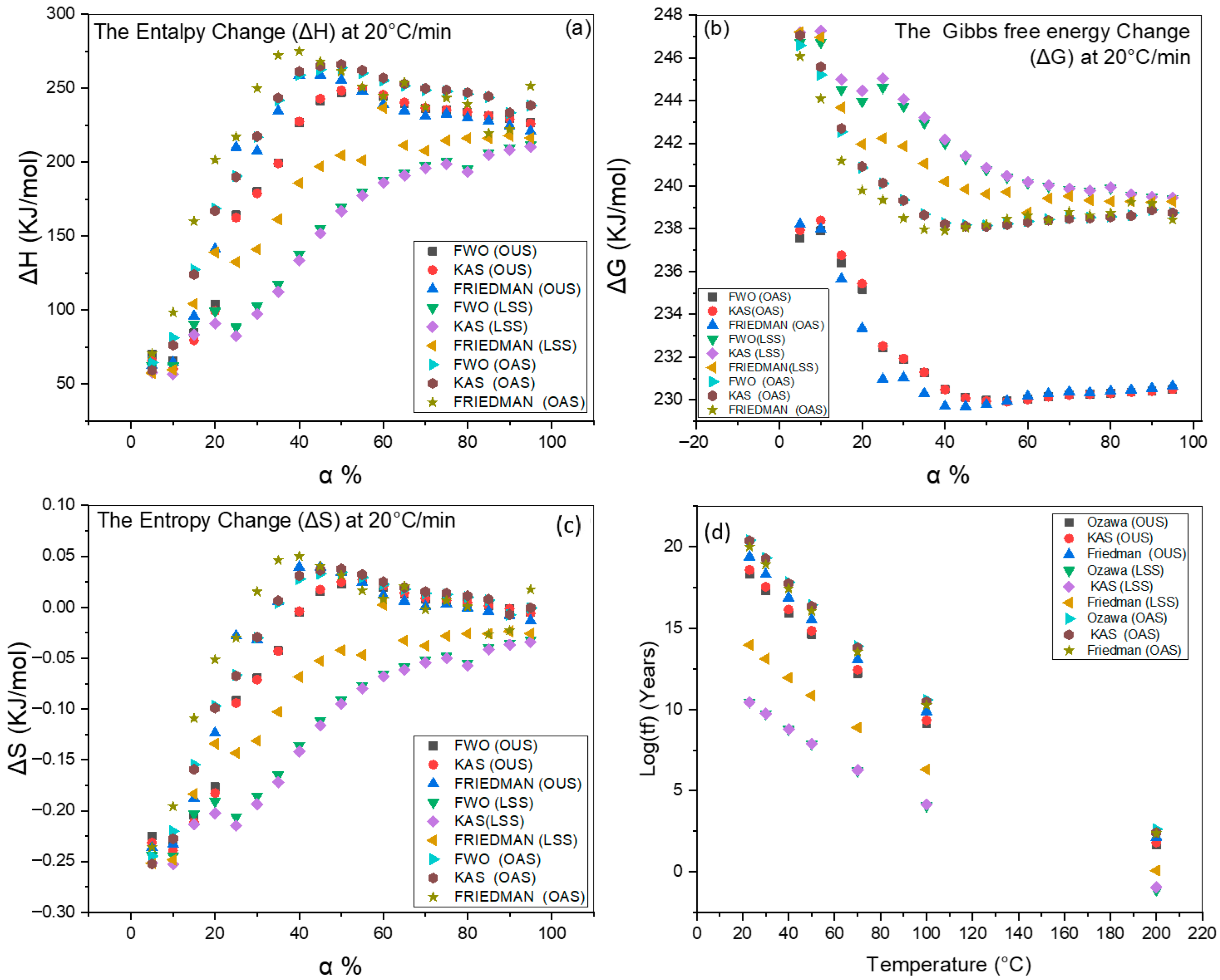
4.3. Determination of Thermodynamic Parameters
4.4. Lifetime of Thermal Degradation
4.5. Microstructural and Compositional Analysis
4.6. Electrical Conductivity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASTM | American Society for Testing and Materials |
| DTGA | Derivative Thermogravimetric Analysis |
| DMA | Dynamic Mechanical Analysis |
| DSC | Differential Scanning Calorimetry |
| EDX | Energy-Dispersive X-ray Spectroscopy |
| FWO | Flynn–Wall–Ozawa (iso-conversional kinetic method) |
| GC-MS | Gas Chromatography–Mass Spectrometry |
| KAS | Kissinger–Akahira–Sunose (iso-conversional kinetic method) |
| LSS | Laboratory-Stored Sample |
| OAS | Operationally Aged Sample |
| OUS | Original Unaged Sample |
| SEM | Scanning Electron Microscopy |
| SBR | Styrene–Butadiene Rubber |
| TGA | Thermogravimetric Analysis |
References
- Li, C.; Li, L.; Yellezuome, D.; Cai, J.; Liu, R.; Hu, J. Physicochemical investigation and thermogravimetric analysis of bamboo and poplar wood residues and tire rubber waste: Kinetic and thermodynamic analyses. Ind. Crops Prod. 2023, 206, 117715. [Google Scholar] [CrossRef]
- Toiserkani, H. Fabrication and characterization of epoxidized natural rubber nanocomposites reinforced with mercapto-functionalized nano-zirconia filler. Polym. Compos. 2023, 44, 8063–8074. [Google Scholar] [CrossRef]
- Bensalem, K.; Eesaee, M.; Hassanipour, M.; Elkoun, S.; David, E.; Agbossou, K.; Nguyen-Tri, P. Lifetime estimation models and degradation mechanisms of elastomeric materials: A critical review. Polym. Degrad. Stab. 2024, 220, 110644. [Google Scholar] [CrossRef]
- Ikpeseni, S.C.; Orugba, H.O.; Efetobor, U.J.; Sada, S.O.; Ekpu, M.; Amagre, M.E.; Owamah, H.I. Pyrolysis characteristics and kinetics of the thermal degradation of elephant grass (Pennisetum purpureum): A comparative analysis using the Flynn–Wall–Ozawa and the Kissinger–Akahira–Sunose methods. Environ. Dev. Sustain. 2023, 27, 10549–11056. [Google Scholar] [CrossRef]
- Tayefi, M.; Eesaee, M.; Hassanipour, M.; Elkoun, S.; David, E.; Nguyen-Tri, P. Recent progress in the accelerated aging and lifetime prediction of elastomers: A review. Polym. Degrad. Stab. 2023, 214, 110379. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, X.; Cai, J. Modified Friedman isoconversional kinetic method for effective activation energies of waste tires rubber pyrolysis. React. Kinet. Mech. Catal. 2024, 137, 1987–2001. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Lin, J. Natural rubber/styrene–butadiene rubber blend composites potentially applied in damping bearings. Polymers 2024, 16, 1945. [Google Scholar] [CrossRef]
- Alfannakh, H.; Alnaim, N.; Ibrahim, S.S. Thermal stability and non-isothermal kinetic analysis of ethylene–propylene–diene rubber composite. Polymers 2023, 15, 1890. [Google Scholar] [CrossRef]
- Cai, J.; Yang, X.; Jiao, R.; He, X.; Cao, X.; Xu, F.; Hou, Z.; Ma, Z.; Zhang, X. Effect of pulverized coal/carbon black hybrid fillers on mechanical properties and thermal stability of styrene-butadiene rubber composites. J. Appl. Polym. Sci. 2024, 141, e55363. [Google Scholar] [CrossRef]
- Sreethu, T.K.; Jana, S.; Jana, N.R.; Naskar, K. Influence of active, nano, and functionalized zinc oxide particles on the mechanical, cytotoxicity, and thermal stability of carbon-black-filled SBR/NR blends. Polym. Eng. Sci. 2023, 63, 2354–2370. [Google Scholar] [CrossRef]
- Ding, D.; Xu, W.; Qin, Z.; Cheng, Z.; Zhang, Z.; Qiao, M. Improvement of flame retardancy and thermal conductivity of SBR by piperazine-pyrophosphate-modified boron nitride synergistic expandable graphite. Iran Polym. J. 2024, 33, 209–222. [Google Scholar] [CrossRef]
- Saha, T.; Bhowmick, A.K. High-temperature degradation of butadiene-based model elastomers by reactive molecular dynamics simulation. J. Appl. Polym. Sci. 2020, 137, 48592. [Google Scholar] [CrossRef]
- Luo, G.; Wang, W.; Xie, W.; Tang, Y.; Xu, Y.; Wang, K. Co-pyrolysis of corn stover and waste tire: Pyrolysis behavior and kinetic study based on Fraser–Suzuki deconvolution procedure. J. Anal. Appl. Pyrolysis 2022, 168, 105743. [Google Scholar] [CrossRef]
- Ammineni, S.P.; Lingaraju, D.; Nagaraju, C. The effects of physical aging on the quasi-static and dynamic viscoelastic properties of nitrile butadiene rubber. Mech. Time-Depend. Mater. 2023, 27, 765–789. [Google Scholar] [CrossRef]
- Jovičić, M.; Bera, O.; Stojanov, S.; Pavličević, J.; Govedarica, D.; Bobinac, I.; Hollo, B.B. Effects of recycled carbon black generated from waste rubber on the curing process and properties of new natural rubber composites. Polym. Bull. 2023, 80, 5047–5069. [Google Scholar] [CrossRef]
- Bahrololoumi, A.; Mohammadi, H.; Moravati, V.; Dargazany, R. A Physically-Based Model for Thermo-Oxidative and Hydrolytic Aging of Elastomers. Int. J. Mech. Sci. 2021, 194, 106193. [Google Scholar] [CrossRef]
- Johlitz, M.; Diercks, N.; Lion, A. Thermo-oxidative ageing of elastomers: A modelling approach based on a finite strain theory. Int. J. Plast. 2014, 63, 138–151. [Google Scholar] [CrossRef]
- Rybiński, P.; Mirkhodjaev, U.Z.; Żukowski, W.; Bradło, D.; Gawlik, A.; Zamachowski, J.; Marzec, A.; Szadkowski, B. The effect of the lignocellulosic filler on the reduction of fire hazard of styrene-butadiene rubber composites, including the reduction of smoke, PCDD/F, PAH emissions and toxicity during its thermal decomposition. Polym. Test. 2023, 118, 107900. [Google Scholar] [CrossRef]
- Amrhar, R.; Eesaee, M.; Nguyen-Tri, P. Identification of the Elements of an Industrial Rubber of Unknown Formulation. In Materials for Sustainable Environmental, Energy, and Bioresource Applications; M2EBA 2023; Nguyen-Tri, P., Ed.; Springer Proceedings in Earth and Environmental Sciences; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, X.; Hou, G.; Zhang, Z.; Liu, G. Natural aging life prediction of rubber products using artificial bee colony algorithm to identify acceleration factor. Polymers 2022, 14, 3439. [Google Scholar] [CrossRef]
- Saadatkhah, N.; Garcia, A.C.; Ackermann, S.; Leclerc, P.; Latifi, M.; Samih, S.; Patience, G.S.; Chaouki, J. Experimental methods in chemical engineering: Thermogravimetric analysis—TGA. Can. J. Chem. Eng. 2020, 98, 34–43. [Google Scholar] [CrossRef]
- Hamouda, I.; Eesaee, M.; Nguyen-Tri, P. Elastomer service life: The role of thermal and mechanical test data in predictive analysis. In Materials for Sustainable Environmental, Energy, and Bioresource Applications; Nguyen-Tri, P., Ed.; Springer: Cham, Switzerland, 2024; pp. 154–166. [Google Scholar] [CrossRef]
- Kasmiarno, L.D.; Panannangan, J.K.; Steven, S.; Rizkiana, J.; Hernowo, P.; Achmad, F.; Muraza, O.; Prakoso, T.; Istyami, A.N.; Pratiwi, M.; et al. Exploration of bio-hydrocarbon gases production via pyrolysis of fresh natural rubber: Experimental and volatile state kinetic modeling studies. J. Anal. Appl. Pyrolysis 2024, 177, 106275. [Google Scholar] [CrossRef]
- Ke, Q.; Wu, C.; Chen, X. Model-free cure kinetics of additional liquid silicone rubber. Thermochim. Acta 2020, 688, 178584. [Google Scholar] [CrossRef]
- Mallick, D.; Sharma, P.; Bora, B.J.; Baruah, D.; Bhowmik, R.; Barbhuiya, S.A.; Balakrishnan, D. Mechanistic investigation of pyrolysis kinetics of water hyacinth for biofuel employing isoconversional method. Sustain. Energy Technol. Assess. 2023, 57, 103175. [Google Scholar] [CrossRef]
- Abenojar, J.; Aparicio, G.M.; Butenegro, J.A.; Bahrami, M.; Martínez, M.A. Decomposition kinetics and lifetime estimation of thermoplastic composite materials reinforced with rCFRP. Materials 2024, 17, 2054. [Google Scholar] [CrossRef] [PubMed]
- Enciso, B.; Abenojar, J.; Aparicio, G.; Martínez, M. Decomposition kinetics and lifetime estimation of natural fiber reinforced composites: Influence of plasma treatment and fiber type. J. Ind. Text. 2019, 177, 106275. [Google Scholar] [CrossRef]
- Wan, H.; Huang, Z. Pyrolysis and oxidative thermal decomposition investigations of tennis-ball rubber wastes through kinetic and thermodynamic evaluations. Materials 2023, 16, 2328. [Google Scholar] [CrossRef]
- Smook, L.A.; Chatra, S.K.R.; Lugt, P.M. Evaluating the oxidation properties of lubricants via non-isothermal thermogravimetric analysis: Estimating induction times and oxidation stability. Tribol. Int. 2022, 171, 107569. [Google Scholar] [CrossRef]
- Jovanović, S.; Samaržija-Jovanović, S.; Jovanović, V.; Marković, G.; Vujaković, J.; Marinović-Cincović, M. Use of recycled rubber in carbon black as a filler in ternary blends of NR/BR/SBR for the automotive tire industry. J. Vinyl Addit. Technol. 2024, 30, 1341–1356. [Google Scholar] [CrossRef]
- Rantuch, P. The thermal degradation of polymer materials. In Ignition of Polymers; Springer Series on Polymer and Composite Materials; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Zhong, B.; Dong, H.; Luo, Y. Antioxidant-modified graphene oxide for robust and highly aging-resistant rubber composites. Compos. Commun. 2023, 37, 101443. [Google Scholar] [CrossRef]
- Hu, Q.; Chen, Q.; Song, P.; Gong, X.; Chen, J.; Zhao, Y. Performance of thermal-oxidative aging on the structure and properties of ethylene-propylene-diene-monomer (EPDM) vulcanizates. Polymers 2023, 15, 2329. [Google Scholar] [CrossRef]
- Wang, K.; Shan, T.; Zang, H.; Zhan, J.; Yang, S.; Tian, X.; Wang, C.; Peng, Z. Kinetic, thermodynamic and synergistic effects of pyrolysis of natural rubber, styrene-butadiene rubber and butadiene rubber. Fuel 2024, 372, 132088. [Google Scholar] [CrossRef]
- Wang, J.; Qi, X.; Dong, X.; Zhang, K.; Luo, S. Mechanistic insights into co-pyrolysis of waste tires and waste lubricating oil: Kinetics and thermal behavior study. Energy Sources Part A 2023, 45, 8568–8583. [Google Scholar] [CrossRef]
- Osorio-Vargas, P.; Lick, I.D.; Sobrevía, F.; Correa-Muriel, D.; Menares, T.; Manrique, R.; Casella, M.L.; Arteaga-Pérez, L.E. Thermal behavior, reaction pathways and kinetic implications of using a Ni/SiO2 catalyst for waste-tire pyrolysis. Waste Biomass Valor. 2021, 12, 6465–6479. [Google Scholar] [CrossRef]
- Jansen, A.A.; Van der Walt, I.J.; Crouse, P.L. Waste-tyre pyrolysis and gasification via the reverse Boudouard reaction: Derivation of empirical kinetics from TGA data. Thermochim. Acta 2022, 708, 179104. [Google Scholar] [CrossRef]
- Qu, B.; Li, A.; Qu, Y.; Wang, T.; Zhang, Y.; Wang, X.; Gao, Y.; Fu, W.; Ji, G. Kinetic analysis of waste-tire pyrolysis with metal-oxide and zeolitic catalysts. J. Anal. Appl. Pyrolysis 2020, 152, 104949. [Google Scholar] [CrossRef]
- Paran, S.M.; Naderi, G.; Movahedifar, E.; Jouyandeh, M.; Formela, K.; Colom, X.; Cañavate, J.; Saeb, M.R. Isothermal vulcanization and non-isothermal degradation kinetics of XNBR/Epoxy/XNBR-g-halloysite-nanotube nanocomposites. Materials 2021, 14, 2872. [Google Scholar] [CrossRef]
- Rammohan, D.; Kishore, N.; Uppaluri, R.V.S. Kinetics and thermodynamics investigation of pyrolysis of butyl-rubber tube waste. Eur. J. Sustain. Dev. Res. 2023, 7, em0215. [Google Scholar] [CrossRef]
- Mong, G.R.; Liew, C.S.; Idris, R.; Woon, K.S.; Chong, W.W.F.; Chiong, M.C.; Lim, J.W.; Chong, C.T.; Lee, C.T.; Wong, K.Y.; et al. Effective waste management through co-pyrolysis of EFB and tire waste: Mechanistic and synergism analysis. J. Environ. Manag. 2024, 368, 122172. [Google Scholar] [CrossRef]
- Nobis, C.; Mancini, M.; Fischlschweiger, M. Modelling binder degradation in the thermal treatment of spent lithium-ion batteries by coupling discrete-element method and isoconversional kinetics. Batteries 2024, 10, 63. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.; Erkens, S.; Skarpas, A. Experimental characterization of storage stability of crumb-rubber-modified bitumen with warm-mix additives. Constr. Build. Mater. 2020, 249, 118840. [Google Scholar] [CrossRef]
- Cvetinović, D.; Milutinović, N.; Erić, A.; Škobalj, P.; Andjelković, J.; Bakić, V. Optimisation of the operating parameters of a thermal-plasma system for converting PCB-containing waste by thermodynamic modelling. Energy Convers. Manag. 2023, 292, 117358. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, X.; Liu, H.; Zhang, H.; Song, M.; Liu, J.; Luo, Z. Precisely tailoring the thermodynamic compatibility between single-walled carbon nanotubes and styrene-butadiene rubber via fully atomistic molecular-dynamics simulation and theoretical approach. Comput. Mater. Sci. 2021, 186, 109995. [Google Scholar] [CrossRef]
- Rubiera, F.; Pevida, C.; Pio, D.T.; Tarelho, L.A. Thermodynamic analysis of biomass gasification using Aspen Plus: Comparison of stoichiometric and non-stoichiometric models. Energies 2021, 14, 189. [Google Scholar] [CrossRef]
- Alam, M.N.; Kumar, V.; Lee, J.; Park, S. Styrene-butadiene-rubber-based nanocomposites toughened by carbon nanotubes for wide and linear electromechanical-sensing applications. Polym. Compos. 2024, 45, 2485–2499. [Google Scholar] [CrossRef]
- Plota, A.; Masek, A. Lifetime prediction methods for degradable polymeric materials—A short review. Materials 2020, 13, 4507. [Google Scholar] [CrossRef] [PubMed]
- Burelo, M.; Franco-Urquiza, E.A.; Martínez-Franco, E.; Moreno-Núñez, B.A.; Gómez, C.M.; Stringer, T.; Treviño-Quintanilla, C.D. Effect of thermal aging on polyurethane degradation and the influence of unsaturations in the hard segment. J. Polym. Sci. 2025, 63, 2639–2650. [Google Scholar] [CrossRef]
- Ammineni, S.P.; Lingaraju, D.; Nagaraju, C. Estimating shelf life and degradation mechanisms of nitrile-butadiene rubber for viscoelastic dampers. J. Elastomers Plast. 2024, 56, 434–453. [Google Scholar] [CrossRef]
- Lee, Y.S.; Ha, K. Effects of acrylonitrile content on thermal characteristics and thermal-aging properties of carbon-black-filled NBR composite. J. Elastomers Plast. 2020, 53, 402–416. [Google Scholar] [CrossRef]
- Aghapour, A.A.; Alizadeh, N.; Khorsandi, H. Biological degradation and mineralization of tetracycline antibiotic using SBR equipped with a vertical axially rotating biological bed (SBR-VARB). Biodegradation 2023, 34, 325–340. [Google Scholar] [CrossRef]
- Dileep, P.; Poornima, M.; Jacob, S.; Rappai, J.P.; Dominic, M. Accelerator-functionalized nanosilica for vulcanization efficiency and thermal resistance of SBR. Mater. Today Proc. 2022, 51, 2599–2603. [Google Scholar] [CrossRef]
- Lessa Belone, M.C.; Kokko, M.; Sarlin, E. Degradation of common polymers in a sewage-sludge purification process developed for microplastic analysis. Environ. Pollut. 2021, 269, 116235. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Kim, J.; Jeong, M.H.; Ahn, K.H.; Lee, H.L.; Youn, H.J. Visualization of styrene-butadiene-rubber latex and large-scale analysis of the microstructure of lithium-ion-battery anodes. J. Power Sources 2023, 557, 232552. [Google Scholar] [CrossRef]
- Peidayesh, H.; Špitalský, Z.; Chodák, I. Electrical conductivity of rubber composites with varying cross-link density under cyclic deformation. Polymers 2022, 14, 3640. [Google Scholar] [CrossRef] [PubMed]
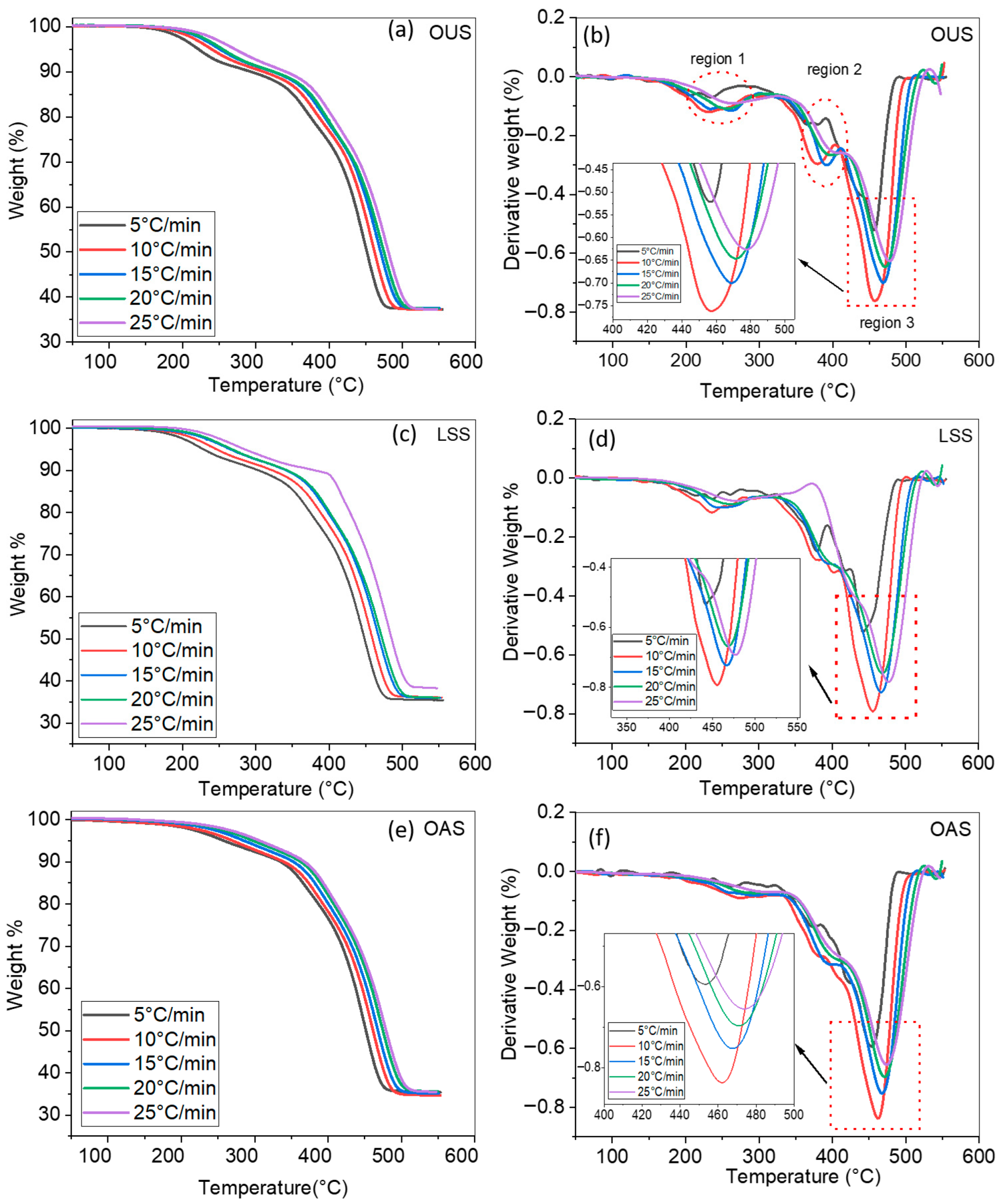







| Sample | TOnset °C | T50 (°C) | Tmax (°C) |
|---|---|---|---|
| OUS | 350 | 460 | 475 |
| LSS | 370 | 455 | 470 |
| OAS | 360 | 465 | 478 |
| FWO | KAS | Friedman | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameters | OUS | LSS | OAS | OUS | LSS | OAS | OUS | LSS | OAS |
| Ea | 200.94 | 156.64 | 221.79 | 200.16 | 153.17 | 221.91 | 209.95 | 180.63 | 228.84 |
| LCL | 170.73 | 131.46 | 193.74 | 169.95 | 127.98 | 193.87 | 179.75 | 155.45 | 200.80 |
| SCS | 231.14 | 181.82 | 249.84 | 230.36 | 178.35 | 249.96 | 231.14 | 205.81 | 256.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamouda, I.; Tayefi, M.; Eesaee, M.; Hassanipour, M.; Nguyen-Tri, P. Kinetic Analysis of Thermal Degradation of Styrene–Butadiene Rubber Compounds Under Different Aging Conditions. J. Compos. Sci. 2025, 9, 420. https://doi.org/10.3390/jcs9080420
Hamouda I, Tayefi M, Eesaee M, Hassanipour M, Nguyen-Tri P. Kinetic Analysis of Thermal Degradation of Styrene–Butadiene Rubber Compounds Under Different Aging Conditions. Journal of Composites Science. 2025; 9(8):420. https://doi.org/10.3390/jcs9080420
Chicago/Turabian StyleHamouda, Imen, Masoud Tayefi, Mostafa Eesaee, Meysam Hassanipour, and Phuong Nguyen-Tri. 2025. "Kinetic Analysis of Thermal Degradation of Styrene–Butadiene Rubber Compounds Under Different Aging Conditions" Journal of Composites Science 9, no. 8: 420. https://doi.org/10.3390/jcs9080420
APA StyleHamouda, I., Tayefi, M., Eesaee, M., Hassanipour, M., & Nguyen-Tri, P. (2025). Kinetic Analysis of Thermal Degradation of Styrene–Butadiene Rubber Compounds Under Different Aging Conditions. Journal of Composites Science, 9(8), 420. https://doi.org/10.3390/jcs9080420






