Abstract
Conventional adhesively bonded joints, such as single-lap, curved-lap, wavy-lap, double-lap, stepped-lap, and scarf joints, are widely used for aerospace, automotive, and medical applications. These adhesively bonded joints exhibit different load transfer mechanisms and stress distributions within adhesive layers, which depend primarily on their geometries and mechanical properties of bonded materials. As such, joint geometry and material properties play a critical role in determining the capability of the joints to withstand high loads, resist fatigue, and absorb energy under impact loading. This paper investigates the effects of geometry and material dissimilarity on the performance of both conventional bonded and interlocking joints under tensile loading based on the information available in the literature. In addition, bonding and load transfer mechanisms were analysed in detail. It was found that stress concentration often occurs at free edges of the adhesive layer due to geometric discontinuities, while most of the load is carried by these regions rather than its centre. Sharp corners further intensify resulting stresses, thereby increasing the risk of joint failure. Adhesives typically resist shear loads better than peel loads, and stiffness mismatches between adherents induce an asymmetric stress distribution. Nonetheless, similar materials promote symmetric load sharing. Among conventional joints, scarf joints provide the most uniform load distribution. In interlocking joints such as dovetail, T-slot, gooseneck, and elliptical types, the outward bending of the female component under tension can lead to mechanical failure.
1. Introduction
Weight reduction and multi-material structures are increasingly critical, and the demand for reliable joining techniques between dissimilar materials such as polymers, composites and metals continues to grow at a rapid pace [1]. However, manufacturing components from multiple materials poses significant challenges, particularly in terms of joining techniques. Generally speaking, the joints are the weakest point in mechanical design [2]. Specifically, dissimilar materials are usually difficult to join effectively due to significantly different physio-chemical and mechanical properties [3]. Many joining techniques are available for dissimilar material joining such as welding, mechanical fasteners, adhesive bonding, and interlocking.
Arc, gas, resistance welding [4,5], and laser welding [6,7] methods utilise electrical energy to generate heat, which melts joining materials and creates a molten pool. In this molten state, the atoms of joining materials mix, and upon cooling, a metallurgical bond is formed as the materials solidify. However, in dissimilar material joining such as metal–polymer and metal–composite joining, significant differences in melting temperatures between base materials often yield typical defects such as voids cavities and thermal degradation [8], which is the case for polymer-based components. Consequently, these fusion welding techniques are generally unsuitable for joining dissimilar materials, especially when polymers and composites are involved [9].
The other welding techniques used for joining dissimilar materials include ultrasonic welding, friction stir welding, and friction spot welding. Unlike fusion welding, ultrasonic and friction stir methods do not melt joining materials, but instead soften the interfaces through localised heating [10]. Ultrasonic welding applies high-frequency mechanical vibrations ranging from 20 to 70 kHz [11], while friction stir and friction spot welding utilise a rotating tool to generate frictional heat and plastic deformation [10]. However, ultrasonic welding is typically limited to thin materials, whereas friction stir welding is primarily applicable to soft and medium-strength materials due to pin wear and tear [12]. Since these solid-state processes rely predominantly on mechanical interlocking and diffusion rather than full metallurgical fusion, the resulting chemical bonding strength may be comparatively lower than that achieved in fusion welding [13]. In addition, these joints increase the risk of fibre damage in composite materials.
Mechanical fasteners such as rivets and clinching require the drilling of holes or forced penetration in both joining materials, which locally weaken the structure and cause fibre breakage. Under loading, rivets and bolts introduce localised stress concentrations around the holes, increasing the risk of crack initiation, delamination, and plastic deformation in base materials [14,15]. Furthermore, the addition of mechanical fasteners increases overall assembly weight, which is undesirable for lightweight composite structures such as drones and automotive components [16].
Adhesive bonding can be used for joining any materials with uniform stress distributions and aesthetic features without the addition of weight [17]. Despite having many advantages, adhesive bonding has potential drawbacks like a high sensitivity to peel stress [18]. Under impact loading, this is prone to decreasing joint strength and reliability [19,20]. Therefore, the adhesive joint was further strengthened by metal rivets in aerospace applications to ensure the safety in case of adhesive failure [21].
Interlocking joints consist of two or more components assembled through slot-type engagement. Once assembled, these joints can resist external loads based on mechanical properties of base materials. However, interlocking joints often require additional fasteners or adhesives to maintain assembly integrity, particularly under complex loading conditions. In traditional timber construction, this is typically achieved using nails or bolts [22]. Common interlocking designs include mortise-and-tenon, dovetail, finger, elliptical, and T-slot joints, which have been widely implemented in timber house construction [22] and composite structures [23]. Nowadays, these joints can also be fabricated easily using additive manufacturing [22,23] or advanced cutting machines based on electrical discharge machining (EDM) [24] and computer numerical control (CNC) [25].
The integration of adhesive bonding and interlocking techniques has shown great promise in enhancing joint performance while simultaneously reducing structural weight [23,24,25]. Adhesive bonding contributes to increased stiffness and uniform stress distribution, while interlocking mechanisms enable to achieve favourable mechanical strength and resistance to failure. Furthermore, inherent brittleness of adhesives under certain conditions can also be mitigated by mechanical interlocking features [26]. In the case that interlocking engagement restricts the motion in only one direction, adhesive bonding can be applied to secure the joint in the remaining direction, resulting in a synergistic hybrid joining approach [23,27]. This method is particularly relevant to composite science, as it enables to enhance damage tolerance, multi-directional load resistance, and better preservation of fibre integrity in composite structures. Therefore, adhesively bonded interlocking joints contribute directly to the design and optimisation of advanced composite assemblies used in aerospace, automotive, and structural applications, in good alignment with broader goals of composite materials engineering.
Therefore, a comprehensive review of the literature is essential to evaluate how joint geometry and material dissimilarity influence the mechanical performance of adhesively bonded and interlocked joints. While existing review studies focus on the effects of adhesive types [28], chemical bonding [29], reinforcement [30], surface texture [31], geometries [16], and their applications [32,33,34,35,36,37], there is limited insight into holistic stress distribution analysis and failure mechanisms due to geometrical and material dissimilarity effects. This knowledge is critical for advancing lightweight, high-strength, and cost-efficient solutions in aerospace, automotive, and other engineering sectors. This review aims to investigate the effects of geometry and material dissimilarity on adhesively bonded joints and interlocking joints through a stress analysis in adhesive layers and interlocking joint interfaces.
The main contribution of this review is to provide a detailed understanding of stress distributions in both adhesively bonded joints and interlocking joints with various geometries. By systematically analysing how stress is transferred and concentrated in these configurations, the review offers critical insights that can guide the design of more effective hybrid joints. In particular, this knowledge enables researchers to strategically combine adhesive bonding and interlocking features to develop joints with enhanced strength, stiffness, and damage tolerance—optimised for dissimilar material systems.
2. Adhesive Bonding
Adhesive bonding mechanism in dissimilar joints involves the combination, diffusion, Van der Waals interactions, molecular interactions, adsorption (thermodynamic), mechanical interlocking, chemical bonding (covalent), and electrostatic force [1]. This combination of forces reacts from the atomic level to the macro level [38,39,40,41]. Sina et al. [42] reported that adhesive bonding mechanisms could occur on three scales, namely mechanical interlocking and electrostatic forces acting on a microscopic scale, as opposed to diffusion, wettability, and weak boundary layer acting on the molecular scale. On the other hand, chemical bonding is generally built at the atomic level [43]. The combined strengths of all these mechanisms determine the joint strength. It also depends on surface treatment, curing process, adhesive type, and material properties of substrates.
Mechanical interlocking often takes place when the liquid adhesive fills the micro-level roughness (including voids and cavities) of adherents under certain compressive pressure and curing temperature. After the adhesive fills the micro-roughness of the substrates at the desired level, the temperature is removed, and the cooling process is initiated. The adhesive hardens in the voids and cavities under the cooling process [44]. This interaction with respect to the roughness of adhesives and adherents creates typical mechanical interlocking with different shapes, as shown in Figure 1. Mechanical interlocking theory has been investigated in many previous studies [43,45,46,47]. The interlocking increases the adhesive bonding strength. Therefore, many surface treatment methods were used for advancing mechanical interlocking by creating a rough surface on adherents. In addition, the rough surface amplifies the bonding area, wettability, and interlocking. The surface treatment eliminates the contaminants from the surface of adherents and further creates more surface energy.
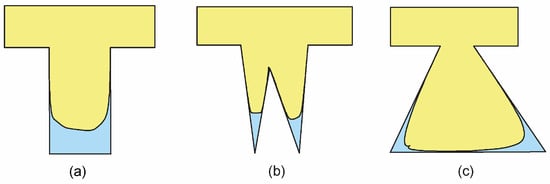
Figure 1.
Schematic diagram of mechanical interlocking: (a) rectangular interlock, (b) triangle interlock, and (c) trapezoidal interlock, adapted with permission from Ref. [48], Copyright 2025, S.-J. Park & M.-K. Seo.
There are many types of chemical bonding, such as covalent, ionic, and intermolecular bonds (hydrogen and Van der Waals forces) [49]. Intermolecular bonds make a positive contribution in the curing process of adhesive-bonding joints. Such bonding forces are relatively weak when compared with covalent, polar, and ionic bonding counterparts [50,51]. A covalent bond is deemed overall the strongest since atoms share electrons, resulting in a strong and stable chemical link between the adhesive and the substrate [52] accordingly. An ionic bonding occurs when charged cations and anions attract each other, generating an electrostatic interaction between the adhesive and the metal or polymer surface. Metals create oxide layers that release metal cations when exposed to an adhesive. Some adhesives contain negatively charged functional groups such as carboxyl, phosphate, and sulphate, which can bond ionically to metal cations. To increase the covalent bonding, researchers used silane coupling agents to create silane–oxide–metal covalent bonds [50].
Chemical and physical interactions at material interfaces vary widely in strength. In particular, bond energies depend on the nature of the bonding mechanism. Covalent bonds, such as carbon–carbon (C–C) bonds, are among the strongest bonds in nature with energies around 350 kJ/mol. Whereas ion–ion interactions like those between Na+ and Cl− are even stronger, reaching approximately 450 kJ/mol. In contrast, ion–dipole interactions (e.g., Na+ and CF3H) exhibit moderate bond energies of approximately 33 kJ/mol [51]. Dipole–dipole interactions, such as those between CF3H molecules, are much weaker at only 2 kJ/mol. Hydrogen bonding, although weaker than covalent or ionic bonding, remains significant particularly in polymers and biological systems with typical bond energies about 24 kJ/mol, as seen in H2O···H2O interactions. These differences in bonding strength significantly influence the mechanical performance and stability of multi-material joints, especially in polymer–metal and composite systems [51].
According to adsorption theory, during the adhesive bonding, molecules of adhesive and metal attract each other if the intimate contact is less than 0.1 nm. Consequently, such a molecular force in close contact is also known as Van der Waals force [52]. The close contact of molecules depends on the wettability of adhesives [53]. Good wettability ensures intimate contact with micro voids and cavities. The poor wettability, on the other hand, covers smaller areas, and thereby the adhesive cannot deeply penetrate into substrate surfaces according to Figure 2.
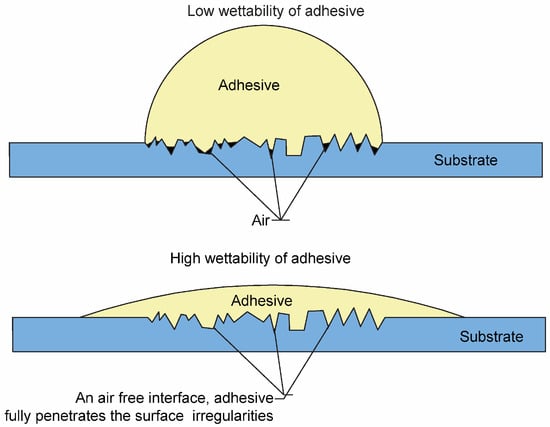
Figure 2.
Low and high wettability of adhesive, redrawn from Ref. [52].
The electrostatic theory indicates that when the adhesive deeply penetrates into the adherent surface, being less than 0.5 nm into the interface of adhesive and adherents, the two charged layers are created. One layer is charged positively, and the other one undergoes negative charge. These opposing charged forces of layers attract each other and enhance the bond strength, but such electrostatic forces are much weaker than corresponding Van der Waals forces [43,52].
The molecular transfer of individual material to another one can be achieved through the interface, with the direct influence arising from certain temperatures and forces without breaking molecular chains according to diffusion theory [54]. Since polymers with long molecular chains are able to move, as illustrated in Figure 3, diffusion theory can be well established between polymer matrices and adhesive interfaces rather than between less favourable adhesive and metal interfaces [49].
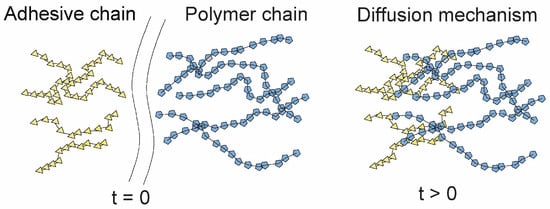
Figure 3.
Schematic diagram of diffusion mechanism, redrawn from Refs. [52,55].
Adhesive bonding undergoes four different failing modes, namely cohesion, adhesion, cohesion–adhesion, and peel failure, as shown in Figure 4. Cohesion failure occurs when the adhesive layer cracks or breaks [19]. Adhesion failure often takes place when adhesives are separated from adherent surfaces, while cohesion–adhesion failure is a combination of adhesion and cohesion failure.
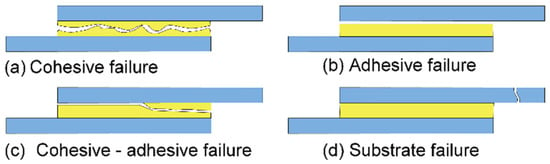
Figure 4.
Adhesive bonding failure modes: (a) cohesion failure, (b) adhesion failure, (c) cohesion–adhesion failure, and (d) substrate failure, redrawn from Ref. [56].
The adhesive layer itself shows certain stress distribution behaviour for all joints. Three common phenomena have been detected in all adhesively bonded joints. Firstly, the adhesive layer typically experiences higher stress concentrations at the free edges due to adhesive layer discontinuity [57]. Secondly, the adhesive layer undergoes high shear stress on the edge areas when compared with the central region under tensile loading [58]. This phenomenon occurs because the adhesive layer transfers the load, starting from the edge region towards the centre, leading to a non-uniform stress distribution known as the shear lag effect of adhesives. It is increased when the stiffness of adherents becomes significantly different. Additionally, sharp corners in the joint design can further exacerbate stress concentrations in the adhesive layer. Although such phenomena are consistent across all adhesive joints, the degree of stress concentration varies depending on joint geometry [3].
3. Geometry and Material Dissimilarity Effects on Adhesive Bonded Joints
The geometry of an adhesive joint plays a pivotal role in determining how loads are transferred across different bonded components, as well as how resulting stresses are distributed within the adhesive layer. Different geometrical configurations influence the concentration and type of stresses, which is the particular case for shear, peel, and normal stresses at critical joint regions [59]. Poorly designed geometries can lead to localised stress concentrations, often prone to premature failure, while optimal shapes can enhance load transfer efficiency and durability. Therefore, a better understanding on the impact of joint geometry is essential to improving the mechanical performance and reliability of adhesively bonded joints [60], particularly when dealing with dissimilar materials. This gives rise to further complexity due to mismatches in stiffness and thermal expansion.
3.1. Single-Lap Joint (SLJ)
Single-lap joint (SLJs) consists of two adherents overlapping in parallel with the adhesive applied in the overlapping region, as shown in Figure 5. This configuration, while simple and commonly used, yields eccentric loading, which significantly affects the stress distribution in the adhesive layer.
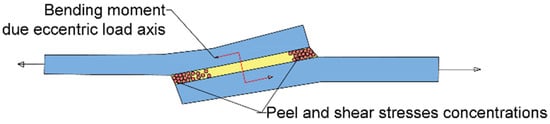
Figure 5.
Eccentric load axis and its effects acting on adhesive layer.
Under tensile loading, the adhesive layer in SLJs primarily undergoes shear and peel stresses. Due to the eccentricity in the load path, a bending moment is generated accordingly, which in turn induces peel stresses near the overlap ends. Additionally, shear stresses are not uniformly distributed, but tend to be much higher near free edges of the joint in a gradually decreasing trend towards the centre. This observation stems from the typical shear lag effect for the load being transferred progressively through the adhesive starting, from overlap edges.
Moreover, the free edge of an adhesive layer is a critical region where discontinuity leads to typical stress concentration. Both peel and shear stresses are accumulated in this region, often leading to crack initiation and premature failure. A typical stress distribution of adhesive layer is shown in Figure 6.
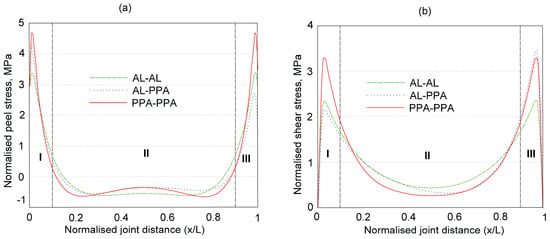
Figure 6.
Normalised peel (a) and shear (b) stress distributions in the joints with epoxy adhesive. Al—aluminium; PPA—polyphthalamide, regions I and III represent the edge area of the adhesive layer, region II presents the middle region, adapted with permission from Ref. [61], Copyright, A. Y. Kanani, et al.
When similar materials are used for the adherents, the stress distribution across the bond line is symmetric. However, for dissimilar adherents, such as a polymer and aluminium, the stress distribution becomes asymmetric due to the differences in material stiffness shown in Figure 6 [62,63]. Stiffness mismatch results in uneven deformation, increasing peel stresses at the interface of the less stiff adherend. For instance, in a polyphthalamide–aluminium (PPA-Al) joint, peel stresses are typically higher on the polymer side where crack initiation tends to occur first. Similarly, Zou et al. [64] investigated a titanium–composite single-lap joint under tensile loading. It was found that crack initiation was manifested at the adhesive–composite interface near the free edge, as illustrated in Figure 7. It has been shown that dissimilar joints exhibit higher peak shear stress than similar ones, as mentioned earlier [61].
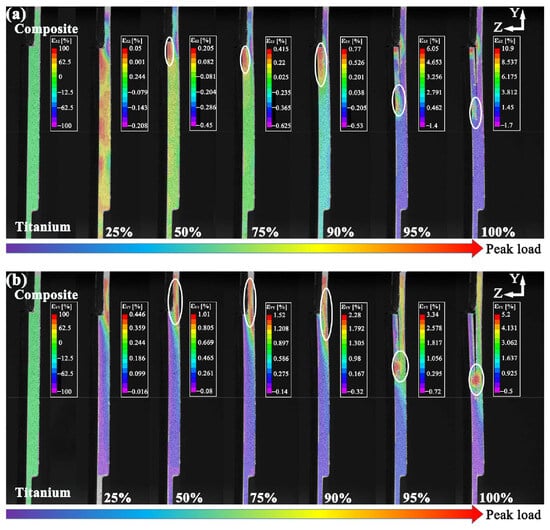
Figure 7.
Z-direction and Y-direction strain fields of dissimilar joints at different load levels: (a) Z-direction strain field; (b) Y-direction strain field, reprinted with permission from Ref. [64], Copyright 2025, T. Zou et.al.
To enhance joint performance, increasing adherend thickness can mitigate adherend deformation and improve load-bearing capacity. However, this also amplifies the bending moment, and hence the peel stress in the adhesive layer.
From an engineering point of view, substrate failure is more desired when compared with either adhesive or cohesive failure. This is because substrates, especially metals and composites, are generally stronger and more prone to easy optimisation by increasing thickness. On the contrary, joint strength cannot be significantly enhanced with increasing adhesive thickness, which may even be reduced instead. The enhancement of adhesion strength is associated with material compatibility, surface preparation, curing conditions, as well as stress distribution.
On the other hand, overlap length also play a significant role in stress distribution. The bonded area is enlarged by increasing the overlap, leading to the improvement in joint strength. The flip side is that the stress concentration is increased at the edges, despite the stress reduction in the centre of the bond line [65]. Beyond a certain overlap length, the edge stresses reach the adhesive strength limit with resulting failure, despite a further increase in overlap. For example, previous study on Al-PPA joints [61] reported load capacities of 2200 and 3600 N with corresponding overlaps of 12.5 and 50 mm respectively. This fourfold increase in overlap resulted in only a 1.6-fold increase in strength with a clear sign of adverse returns [66]. The free ends of SLJs are well established as primary regions towards stress concentration, which makes them most likely to be crack initiation sites. In dissimilar joints, interfacial failure is often initiated between the adhesive and the weaker adherend (typically the polymer). Owing to inherently low surface energy, adhesive wetting and bond strength can be limited, even after surface treatments. In contrast, metals possess higher surface energy to assist in stronger bonds with adhesives [67].
SLJs often exhibit adhesive, cohesive, substrate, or mixed-mode failures near the free edges in the presence of high shear and peel stress concentrations. In metal–composite joints, two primary interfaces are involved, namely metal–adhesive and adhesive–composite interfaces. Mechanical failure typically initiates at the adhesive–composite interface due to inherently low surface energy and poor wettability of polymer composites, which result in weaker adhesion strength when compared with metal–adhesive interface [68]. Nevertheless, metal–adhesive failure may also occur if the metal surface is inadequately treated or if the curing process is suboptimal. When advanced surface treatment and proper curing protocols are applied, cohesive failure within the adhesive layer becomes more dominant, which is indicative of improved interfacial bonding [69]. Additionally, depending on the material system and laminate stacking sequence, composite substrates may also induce delamination failure under loading conditions.
3.2. Curved Single-Lap Joint
A curved single-lap joint (CSLJ) is a modified version of conventional single-lap joint where bonded adherents are curved instead of flat. Depending on the direction of curvature, CSLJs can be divided into axially inward curved, axially outward curved, or circumferentially curved, as illustrated in Figure 8. Among these, circumferentially CSLJs have been employed in aircraft fuselage constructions due to their ability to conform to cylindrical surfaces. On the other hand, axial curved joints have been investigated to improve the mechanical performance of conventional SLJs by enhancing the stress distribution [70,71,72].

Figure 8.
Different types of curved single-lap joints: (a) axially inward curved, (b) axially outward curved, and (c) circumferentially curved, redrawn from Refs. [70,71,72].
This geometry has been explored primarily in aerospace and marine applications, such as fuselage structures of aircraft and ship hulls, where the curvature helps to form streamlines and potentially reduce stress concentrations. Several studies [70,71,72] have examined the mechanical behaviour of CSLJs under tensile loading.
Longitudinal curved single-lap joints with curvature radii of 105, 132 and 155 mm were also tested under tensile loading [58]. Corresponding results showed that CSLJs consistently outperformed flat SLJs in terms of peak load [58]. Notably, the use of an outside curved configuration significantly reduced peel and shear stress concentrations. It was reported that 53.5% reduction in peel stress and a 71.6% reduction in shear stress occurred when compared with those of standard flat SLJs [72]. Furthermore, CSLJs with much larger radii, namely 1000, 2000, and 3000 mm, were also analysed to assess load-bearing capacity under tensile loads. While the joint with a 1000 mm radius showed a comparable performance to a flat SLJ, 3000 mm radius configuration exhibited slightly higher peak load and greater displacement under loading [73]. These results, along with the peel stress comparisons illustrated in Figure 9, underscore the advantages of curved-lap joints to achieve more uniform stress. It has also been confirmed that increasing curvature contributes to a corresponding rise in peak load capacity [74].
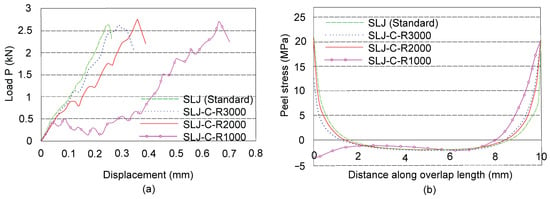
Figure 9.
Load–displacement curves (a) and peel stress distributions (b) of SLJ and curved single-lap joints. SLJ—standard single-lap joint; SLJ-C-R3000—curved SLJ with curvature radius of 3000 mm; SLJ-C-R2000—curvature radius of 2000 mm; SLJ-C-R1000—curvature radius of 1000 mm, adapted with permission from Ref. [73], Copyright 2025, Y. Liu, et al.
To date, no peer-reviewed studies have been published on the application of curved single-lap joints for dissimilar material systems. This presents a notable research gap in the literature and offers a great opportunity for future research, particularly considering the potential of curvature to mitigate the stress concentration in hybrid joints.
3.3. Wavy-Lap Joint
A wavy-lap joint is a modified adhesive joint geometry where the bonding surface follows a wave-like sinusoidal pattern rather than a flat mode. This design intends to improve the load distribution and reduce stress concentrations at the joint edges. A wavy-lap joint can be categorised into two different types, namely, a straight wavy lap (SWL) and a reverse wavy lap (RWL), as illustrated in Figure 10 [75,76].
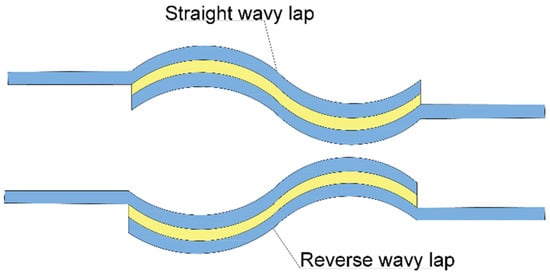
Figure 10.
SWJ–straight wavy lap; RWJ–reverse wavy lap joint, redrawn from Ref. [35].
Several studies have investigated the mechanical performance of a wavy-lap joint. Zeng and Sun [77] experimentally analysed the tensile performance and failure mechanisms of RWJs. Their results demonstrated that wavy geometry effectively induced a stress redistribution from free edges toward the centre of the bonded area, thereby reducing critical peel and shear stress concentrations. This redistribution led to an 87% increase in failure load and a 13-fold improvement in fatigue life when compared with that of conventional single-lap joints (SLJs). The predominant failure mode of RWJs was cohesive and more abrupt than the failure observed in SLJs. In the subsequent study, Ávila et al. [78] examined the performance of RWJs using composite adherents and reported 41% improvement in failure load, further validating the efficiency of this geometry in load redistribution.
Nosouhi et al. [35] conducted comparative tests on SWJs, RWJs, and SLJs under tensile loading. Their findings revealed that RWJs consistently outperformed both SWJs and SLJs, with a peak load of 8.5 kN for RWJs, and corresponding values of 6.5 and 6 kN for SLJs and SWJs respectively. The high load-bearing capacity is due to compressive stresses formed at the free edges of RWJs. Conversely, SWJs performed worse than SLJs, with a lower tensile load of approximately 1 kN. Numerical simulations carried out by Nosouhi et al. [35] further examined the stress distribution of adhesive layers in different joint geometries. SWJs generated higher peel and shear stresses when compared with SLJs and RWJs. While both SWJs and RWJs exhibited compressive stresses in the middle of the adhesive layer, only RWJs induced compressive stress at free edges in order to assist in the suppression of failure initiation at critical locations presented in Figure 11.
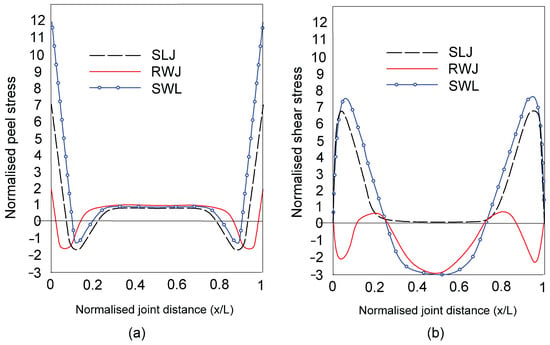
Figure 11.
Adapted stress distributions of adhesive layers: (a) normal stress and (b) shear stress, redrawn from Ref. [35].
Ayatollahi et al. [79] evaluated tensile and fatigue performances of aluminium reverse wavy joints. RWJs yielded a 48.8% increase in peak load, as opposed to SLJs, along with a more uniform stress distribution. The stresses were more concentrated in the middle of the bond line, while critical edge stresses were significantly reduced.
To date, no peer-reviewed studies have been performed to examine the application of wavy-lap joints in dissimilar material bonding, underpinning significant opportunities for future research, particularly in hybrid structures involving metals and polymers or composites.
3.4. Stepped-Lap Joint
The stepped-lap joint consists of multiple overlapping steps, created between two bonded adherents. These steps may be uniform or vary in size depending on design requirements, as depicted in Figure 12.
Figure 12.
One-stepped lap joint.
This joint configuration allows the bonding of components to take place in a collinear manner, thus minimising an eccentric load path that typically generates bending moments and peel stresses in single-lap joints. As a result, peel stress in stepped-lap joints is significantly reduced, leading to overall enhanced joint performance. The fatigue and tensile performances of stepped-lap joints have been extensively studied under various loading conditions, including bending [80], uniaxial tension [81,82], tensile performance estimation [83], variable-step scenarios, and adhesive thickness [84], as well as multi-step configurations [85]. Additional investigations have also addressed the behaviour of dissimilar material systems [86] for stress distribution using a slip model [87], along with bi-adhesive applications [88]. Akpinar et al. [89] conducted an experimental and numerical comparison of single-lap, one-stepped, and three-stepped lap joints made from AA2024-T3 aluminium. The three-stepped joint yielded 68% and 54% increases in peak load when compared with single-lap and one-stepped joints. This phenomenon is attributed to even more uniform stress distributions, according to Figure 13.
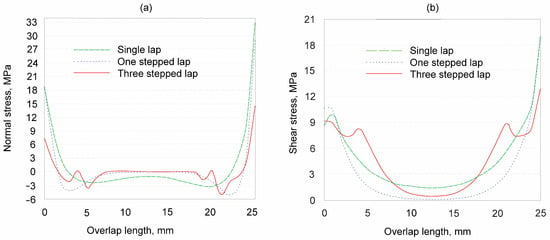
Figure 13.
Stress distributions in the adhesive layer: (a) normal stress and (b) shear stress, Adapted with permission from Ref. [89], Copyright 2025, S. Akpinar.
According to the stress curves, it can be seen that increasing the number of steps reduces normal stress concentrations at the two free edges by redistributing the load among the corners of each step. While small stress concentrations occur at inner sharp corners, the absence of an eccentric load path eliminates large peel stresses, thus reducing the risk of premature adhesive failure. Shear and normal stress distributions across the adhesive layer are asymmetric even in symmetrical composite joints. This asymmetry can be explained by the experimental setup, which means that one side of the specimen is fixed in the test grip, while the opposite side is subjected to tensile loading with an uneven load transfer.
Further studies confirmed that increasing the number of steps improved fatigue performance. Cracks typically initiate from vertically bonded sections, particularly from internal corners where adhesive meets the step edge [81]. The effect of step length was also evaluated, and a stepped-lap joint with uniform step lengths exhibited a 49% increase in peak load, as compared to non-uniform step designs under tensile loading [90]. DIC methods were used to identify stress concentration zones and crack initiation points in metal–polymer stepped-lap joints. Relevant results showed that polymer–adhesive interface experienced significantly higher stress concentration than metal–adhesive counterpart, which makes the polymer constituent more prone to crack initiation particularly at the free edges [3].
3.5. Double-Lap Joint (DLJ)
A double-lap joint (DLJ) is an adhesive joint configuration in which a central adherend is bonded on both sides by two outer adherends. The overlap region is symmetrically distributed across the central layer, as illustrated in Figure 14. This geometry provides better alignment under tensile loading and minimises bending moments, thereby reducing peel stress concentration often detected in single-lap joints.

Figure 14.
Adhesively bonded double-lap joint.
In a comparative study, Shin and Lee [91] investigated stress concentrations at the overlap ends in SLJs and DLJs for composite–aluminium interfaces. Their results indicated that DLJ provided a more uniform stress distribution and achieved approximately twice the peak load of an equivalent SLJ with the same bond length [91]. This finding was well aligned with Kinloch’s experimental results, which confirmed the excellent tensile strength of DLJs for aluminium joints [92]. Francesco Marchione [33] compared his numerical and analytical results with the studies of Tsai [93] and Volkerson [94]. While the study conducted by Tsai [90] reported symmetric stress distributions across both adhesive layers, Francesco [33] and Volkersen [94] found the asymmetry in the stress distribution, particularly near the overlap edges, as shown in Figure 15 [33].
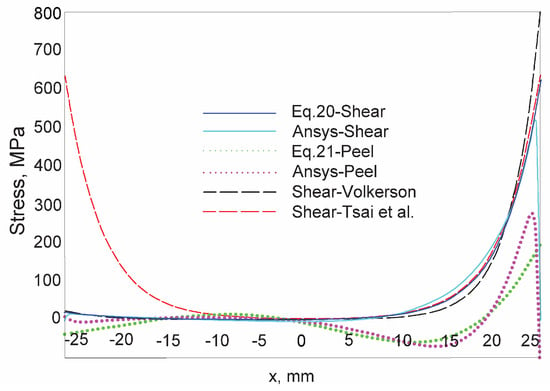
Figure 15.
Stress distribution of double-lap joint, adapted with permission from Ref. [33], copyright 2025, F. Marchione.
Further support for asymmetric stress patterns was provided by Santos et al. [95] and Gonçalves et al. [96], which have numerically demonstrated that although peel and normal stresses are of equal magnitude in the two adhesive layers, the distribution within each layer remains asymmetric due to unequal load paths and moment directions. In particular, the right side of the adhesive layer experiences higher peel stress because of a counterclockwise bending moment acting at the overlap end, thus resulting in crack initiation at that edge. In contrast, left side undergoes compressive stresses due to the inward bending moment applied toward the adhesive layer and the central adherend as shown in Figure 13. This compressive action strengthens the adhesive interface and delays joint failure [97,98].
Overall, a double-lap joint offers a substantial improvement over single-lap joint in terms of stress uniformity and load-bearing capability. However, the presence of asymmetric stress distribution, particularly in dissimilar material joints, highlights the essential requirement for careful joint design. Despite the evident advantages of DLJ, a direct experimental and numerical comparison between scarf, stepped- and double-lap joints remains scarce in the previous studies. To our best knowledge, such comparative studies are quite limited in published work with a clear sign of the promising research direction in the future.
3.6. Scarf Joint
A scarf joint is a particular type of adhesively bonded configuration where overlapping ends of adherents are tapered to create a smooth and angled interface. This joint geometry is defined by the scarf angle (α), the overlap length (a), and the thicknesses of the materials being joined (tₐ and tₚ), according to Figure 16.

Figure 16.
Scarf joint illustration, adapted with permission from Ref. [34], Copyright 2025, D. L. Alves et al.
The tensile performance of dissimilar metal–composite scarf joints has been investigated both experimentally and numerically, with a major focus on the influence of scarf angle. Alves et al. [34] demonstrated that a 10° scarf joint delivered the highest tensile strength compared to joints with scarf angles of 20°, 30°, 40° and 50°, outperforming them by 30.3%, 89.3%, 136.9% and 231.7% respectively. Similarly, Liu and Liu [99] reported that a composite scarf joint with a 10° angle was approximately twice as strong as joints with 30° and 45° angles. These findings support the conclusion that smaller scarf angles result in a higher load-bearing capacity. This performance trend is explained by the stress distribution analysis shown in Figure 17.
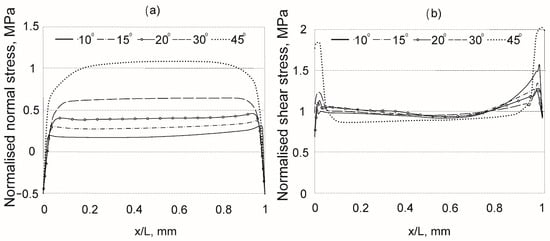
Figure 17.
Stress distribution of composite-metal scarf joint: (a) normal stress; (b) shear stress, adapted with permission from Ref. [34], Copyright 2025, D. L. Alves et al.
As the scarf angle increases, normal stresses become more concentrated in the centre of the bond line, while shear stresses are accumulated near free edges. This imbalance in stress distribution promotes crack initiation and final adhesive failure. The adhesive or cohesive failure starts in the area with high stress concentration. When it comes to composite scarf joints, failure becomes more complex due to the laminate direction and adhesion between laminates. Oshima et al. [100] studied composite joints under tensile loading and revealed adhesive, interlaminar, and intralaminar failures, as shown in Figure 18.
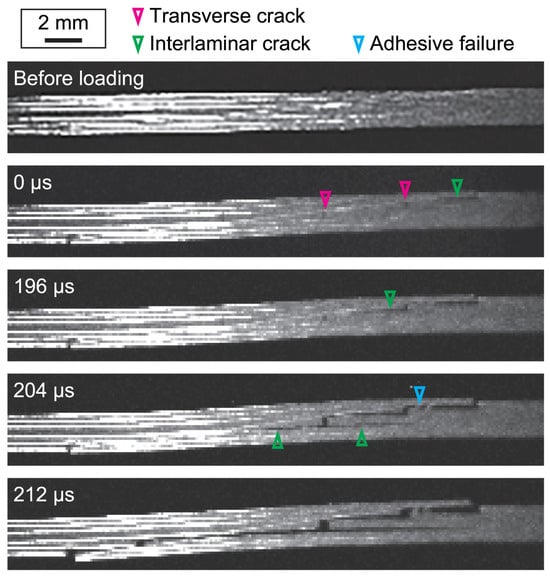
Figure 18.
Damage in composite scarf joints immediately before final failure with different configurations, reprinted with permission from Ref. [100], Copyright 2025, S. Oshima & S. Kobayashi.
Moreover, Kim et al. [101] compared scarf and one-stepped lap joints with equal overlap length and adhesive thickness. The scarf joint achieved a tensile strength of 219 MPa, which was nearly three times higher than that observed for the stepped-lap joint at 72 MPa. Similarly, Kanani et al. [3] compared single-lap, one-stepped, three-stepped, and scarf joints across various overlap lengths and consistently found the scarf joint to exhibit a superior performance in all cases.
Figure 19 compares normal and shear stress distributions in the scarf, single-lap, one-stepped (half-splice), as well as three-stepped lap joints [3]. The scarf joint exhibited the most uniform distribution. For example, the normalised normal stress at the free ends of the scarf joint was approximately 0.2 MPa, as opposed to 7 MPa in single-lap, 8 MPa in one-stepped, as well as 3 MPa in three-stepped joints. In the central region, the scarf joint maintained normal stress near zero, indicating excellent stress diffusion. In contrast, stepped-lap joints, particularly the three-stepped configuration, showed elevated stress levels due to geometric discontinuities. Even though one-stepped and single-lap joints demonstrated more uniform central stress than the stepped version, their overall stress levels remained higher than those induced in scarf joints.
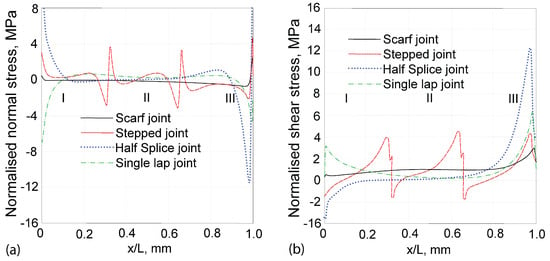
Figure 19.
Normalised normal stress (a) and normalised shear stress (b) distributions in the adhesive layers of scarf, stepped-, half-splice, and single-lap joints, adapted with permission from Ref. [3], Copyright 2025, A. Y. Kanani, et al.
The asymmetry in stress distribution, especially in dissimilar joints, arises from the mismatch in stiffness between the adherents. Additionally, thermal residual stresses during adhesive curing, caused by differences in the coefficient of thermal expansion and variations in chemical bonding strength due to distinct surface chemistries, further contribute to interfacial stress concentrations and early failure risk. Despite uniform stress distribution of scarf joint, crack initiation still typically occurs at free edges of the adhesive interface. However, scarf geometry allows the joint to sustain higher loads in the elastic region before yielding, resulting in higher yield strength when compared with stepped- or single-lap joints.
Scarf and stepped-lap patching are among the most widely adopted methods for repairing physically damaged composite structures in aircrafts and wind turbine blades [102]. A typical scarf patch features circular conical frustum geometry, generally designed with an optimised scarf angle ranging from 1° to 3° in order to minimise shear and peel stress concentrations at the free edges [103]. Marques et al. [104] demonstrated that reducing the scarf angle increased the repair strength, using scarf angles of 2.42°, 1.71°, 1.45°, and 1.09°. However, very shallow scarf angles significantly enlarge the repair area and necessitate the removal of a considerable amount of healthy parent materials, which is particularly problematic in thick composite structures [105]. Consequently, scarf repairs have noticeable drawbacks, including substantial material removal and high associated costs. As a result, recent studies have focused on maximising mechanical performance recovery while minimising the volume of removed parent materials.
To address this issue, Pitanga et al. [106] investigated combined stepped-scarf repairs using the configurations of 1:2/1:20, 1:2/1:30, and a reference 1:20 straight scarf. Their results showed that the 1:20 joint exhibited the highest strength, while the 1:30/1:2 scarf configuration achieved approximately 64% of the tensile strength for the 1:20 straight scarf, along with only 40% of its length. Additionally, the same configuration reached up to 75% of the tensile strength for the 1:20 joint, implying a promising performance with less parent material removal. While stepped repairs offer the advantage of conserving more base materials, they typically yield lower strength recovery. Wu et al. [107] further confirmed that scarf repairs were mechanically superior to stepped repairs.
Common stepped repair configurations, including step ratios of 1/60, 1/45 and 1/30, are generally defined as the ratio between step thickness and overlap length [108]. Damghani et al. [108] compared stepped-lap joints with five ratios of 1/10, 1/20, 1/30, 1/45 and 1/60 to evaluate their ability to restore the stiffness and strength of repaired composites. Their findings showed that shorter overlap lengths were correlated with reduced strength recovery. The 1/20 joint restored only 66% of the original strength, whereas the 1/60 joint achieved 77%. More interestingly, the 1/20 joint exhibited the highest stiffness recovery at 95%, which slightly outperformed the 1/60 joint at 91%. Overall, both scarf and stepped repairs can sustain high mechanical loads, with scarf joints offering slightly higher strength at the expense of increased material removal. In contrast, multiple overlapping steps in stepped repairs help reduce material loss while still maintaining a reasonable level of strength restoration [108].
In composite structures, defects vary widely in shape, size and orientation, which are in range from circular impact damage to elongated delamination, thereby making circular repair patches unsuitable in many situations. When damage is distributed along the length of a component, the determination of optimal patch design becomes more complex, especially when considering load directions, force magnitudes, fibre orientations, the number of plies, and adhesive properties. The interaction of these factors induces significant design complexity, making manual approaches impractical. As a result, engineers increasingly rely on advanced optimisation techniques, including parametric optimisation, topology optimisation and machine learning-based methods. They are generally employed to identify optimal patch configurations that minimise parent material removal while maximising mechanical performance under specific loading conditions.
For instance, Pierce and Falzon et al. [109] developed a MATLAB-based parametric tool that showed 36–40% reduction in bonding region size and 17–22% strength improvement using optimised fibre-oriented scarf joints. Psarras et al. [110] introduced an integrated Python–Abaqus algorithm to automate the design and evaluation of elliptical stepped patches, modifying scarf angles and step lengths based on maximum stress and fibre orientation criteria. Their results demonstrated that elliptical patches achieved higher strength-to-volume efficiency than conservative circular counterparts. These parametric studies indicate that optimisation strategies focusing on patch geometry and ply orientation can significantly enhance repair efficiency by improving load distribution and reducing peak stress without compromising structural integrity.
Ren et al. [111] introduced a concurrent optimisation framework that integrates structural topology design with continuous fibre deposition path planning for the additive manufacturing of fibre-reinforced polymer composites. The input parameters included load conditions, volume fraction constraints, and fibre orientation continuity, while the design space encompassed both material layouts and feasible toolpath strategies. Using a level-set-based topology optimisation algorithm combined with toolpath generation techniques, the study ensured that fibre continuity was preserved along structurally optimal paths. The results demonstrated improved mechanical performance such as higher stiffness and more effective load transfer, as compared to traditional methods that treat topology and toolpath planning independently. This approach highlights the potential of coupling material architecture and manufacturing constraints for the efficient design of high-performance composite structures.
4. Geometrical Effects on Interlocking Joints
Interlocking joints present a unique and increasingly valuable solution in structural and mechanical design, particularly in applications where conventional bonding methods may be limited or undesired. Unlike conventional adhesive or welded joints, interlocking mechanisms rely on geometry-based load transfer, yielding enhanced mechanical interdependence between parts. This makes them especially suitable for particular scenarios requiring disassembly, modularity, or hybrid material integration, such as lightweight transport structures [112,113], composite assemblies [114], and additively manufactured components [115,116]. Interlocking joints reduce the reliance on adhesives, which are often sensitive to temperature, chemical degradation, and surface preparation. They also enable the joining effect of materials with incompatible thermal or chemical properties, thereby expanding design flexibility. Furthermore, with the growing demand for sustainable and recyclable products, interlocking mechanisms pave a pathway for mechanical bonding without permanent alteration of materials, thus facilitating repairability and recyclability. As advanced materials and digital manufacturing techniques evolve, the exploration of interlocking joints opens up new routes to customisable, high-performance, and eco-conscious structural solutions [117,118,119,120].
4.1. T-Slot Joint
T-slot joint is widely used in structural and modular assemblies, particularly in machine tool bases, CNC frames, and laboratory automation systems. Its popularity stems from the ease of assembly, reusability, adjustability, and ability to withstand repetitive loading. Common applications include mounting systems for metalworking lathes, aluminium extrusion frameworks and modular mechanical platforms. Brown et al. [118] utilised conventional T-slot joints to be compared with genetically optimised geometries under tensile and shear loading conditions. The results indicated that Pareto-optimised T-slot joints outperformed conventional designs in terms of load-bearing capacity and stress distribution. Finite element analysis (FEA) showed that conventional T-slot joints developed severe stress concentrations at key transition zones, particularly at points A and B, where the male and female parts are engaged exhibited in Figure 20 [118].
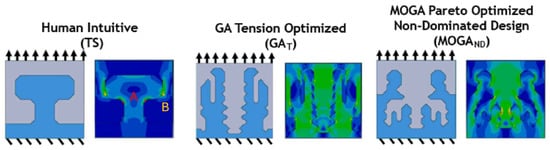
Figure 20.
T-slot joint configurations: (TS) T-slot human intuitive joint; (GA) tension-optimised; (MOGA) Pareto-optimised, reprinted with permission from Ref. [118], Copyright 2025, N. K. Brown et al.
Young et al. [120] focused on T-slot joints within interlocking metasurfaces. Their analysis revealed that a dominant failure mechanism was associated with the outward bending of a female component, which led to a non-uniform stress distribution and asymmetric deformation across the interface, as shown in Figure 21. This compromised structural integrity of the joint, leading to early interlocking failure.
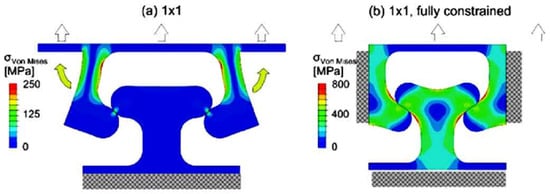
Figure 21.
T-slot joint stress analysis under tensile loading: (a) one side constrained and (b) fully constrained, reprinted with permission from Ref. [120], licenced under CC BY 4.0, B. Young et al.
Despite its robust interlocking mechanism, the limited contact area of T-slot joint, particularly at the neck, contributes to stress concentration and susceptibility to the bending failure of the female section. As a result, mechanical properties of joining materials, such as yield strength and stiffness, play a critical role in determining the joint performance. In a comparative study, Jin et al. [121] evaluated the tensile strength of dovetail and T-slot joints in dissimilar metal systems, specifically Inconel (i.e., a nickel-based superalloy) and stainless steel. The dovetail joint demonstrated a significantly superior performance, achieving a tensile strength of approximately 640 MPa. In comparison, T-slot joint failed at approximately 300 MPa due to the bending of the female part and interfacial stress concentration. More interestingly, in a diagonal tensile loading scenario, Maleki et al. [122] found that T-slot joint performed slightly better than dovetail joint, highlighting that loading direction and geometry alignment can play a significant role in determining joint efficiency.
4.2. Dovetail Joint
Dovetail joint is a conventional interlocking configuration known for its exceptional tensile strength and resistance to separation, primarily due to its trapezoidal geometry. Historically employed in carpentry and cabinetry, this joint design has evolved, with advanced applications including jet engine components, dental prosthetics [123,124], and modular construction systems with the characteristics of high precision, good durability, and vibration resistance. The dovetail joint was studied in civil engineering such as cellular structural plates for lightweight floor and sandwich structures [125], joining rafter and timber collar beams [126,127], seismic performance of dovetail root structures [128], lattice shell structures with dovetail root [129], prefabricated concrete plates joining [130], furniture parts joining [131], as well as dovetail friction stir joining dissimilar materials [132].
The performance of dovetail joints depends primarily on their geometric parameters, such as the angle, length, and neck width. Qin et al. [114] reported that composite dovetail joints were tested with dovetail angles ranging from 66° to 86°, resulting in the highest tensile strength identified at 71°. Similarly, Atar et al. [133] evaluated timber dovetail joints at angles of 75°, 78°, 81°, 84°, and 87°, and detected the optimal strength at 84° and the lowest strength at 75°.
These findings suggest that no universal dovetail angle warrants the maximum strength across all material types. Instead, the ideal geometry must be tailored to mechanical properties of the adherents, particularly their stiffness, Young’s modulus, and resistance to deformation. Stiffer materials can accommodate larger dovetail angles and wider necks, both of which contribute to enhanced load-bearing capacity. Dovetail joints undergo a combination of tensile, compressive, shear, and bending stresses during loading, leading to inherently complex stress analysis. However, Qin et al. [114] performed specific simulations to visualise stress concentration zones within the male (tenon) and female (mortise) components under axial tensile loading. As shown in Figure 22, a normal force (Fₙ) acts perpendicularly to the inner wall of the mortise, along with the peak stress at point B around the inner corner of the mortise. The stress at this point intensifies with steeper slope angles with the improvement in interlocking resistance. Conversely, tenon neck undergoes tensile stress, while point A at the outer edge experiences a combination of compressive and shear stresses. These areas (points A and B) are generally considered as the weakest regions for crack initiation.
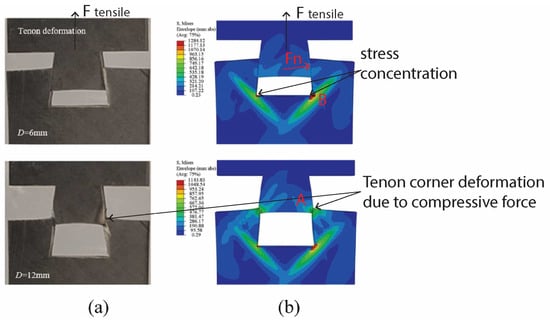
Figure 22.
Stress concentration points A and B under tensile loading: (a) experimental picture; (b) numerical analysis, reprinted with permission from Ref. [114], Copyright 2025, Y. Qin et al.
In many cases, mechanical failure may occur, either within the interlocking interface or in the substrate material itself. For timber dovetails, grain direction plays a pivotal role in governing crack paths and load resistance. As shown in Figure 23, substrate failure in mortise and tenon joints is often driven by shear forces along the grain and normal forces exerted to the mortise walls [134].

Figure 23.
Substrate failure of dovetail joint: (a) CFRP mortise failure; (b) timber tenon failure; (c) timber failure through grain direction [114].
Overall, a dovetail joint remains one of the most mechanically efficient interlocking geometries, especially when carefully tailored to mechanical properties of the materials. Its capacity for multi-directional load transfer, geometric adaptability, and structural integration makes it a compelling option in both conventional and modern assembly applications.
4.3. Dovetail-Adapted Joint
Dovetail-adapted joint has a geometric variation from conventional dovetail joint. Its defined feature consists of a longer and curved neck, which is different from the standard trapezoidal form. In a comparative experimental study, a dovetail-adapted joint was tested against other interlocking geometries including omega-adapted, conventional dovetail, T-slot, T-slot-adapted, and arrow-shaped joints [132], as shown in Figure 24.
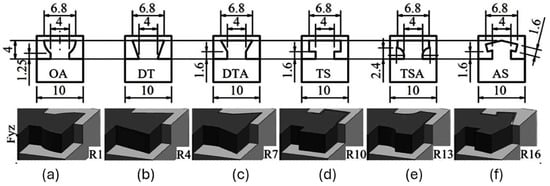
Figure 24.
Interlocking joints: (a) OA-omega adapted, (b) DT-dovetail, (c) DTA-dovetail adapted, (d) TS-T slot, (e) TSA-T shaped adapted, and (f) AS–arrow shape, reprinted from Ref. [132], licensed under CC BY 4.0, V. Ermolai. et al.
The load is primarily transferred through the neck, while the interlocking contact surfaces resist the disengagement. Among all the configurations tested, dovetail-adapted joints exhibited the highest ultimate tensile strength at 10.22 MPa, which was followed by the T-slot joint at 9.59 MPa, the dovetail joint at 9.49 MPa, the omega-adapted joint at 9.45 MPa, the T-slot adapted joint at 9.32 MPa, as well as the arrow-shaped joint at 8.88 MPa. The results indicate that neck geometry is specifically modified by its elongation as gooseneck design can significantly enhance the load-bearing capacity of the joint.
The stress concentration zones in dovetail-adapted joints were observed primarily at the outer edges of the tenon and along the neck region. Compared to the conventional dovetail joint, the longer neck in gooseneck geometry allows for greater deformation, which assists in more uniform load distribution and the possible reduction in brittle failure. This behaviour was confirmed through strain analysis with the specific strain measured at 1.77% for gooseneck joint and 1.61% for conventional dovetail joint [132].
4.4. Ellipse Joint
Elliptical interlocking joint is characterised by a protruding or recessed elliptical geometry, which provides mechanical engagement under axial or transverse loading. This design offers enhanced stiffness due to its elongated contact profile, making it effective in load redistribution and joint stability under tensile loads. The interlocking concept and corresponding stress responses are illustrated in Figure 25 [56].
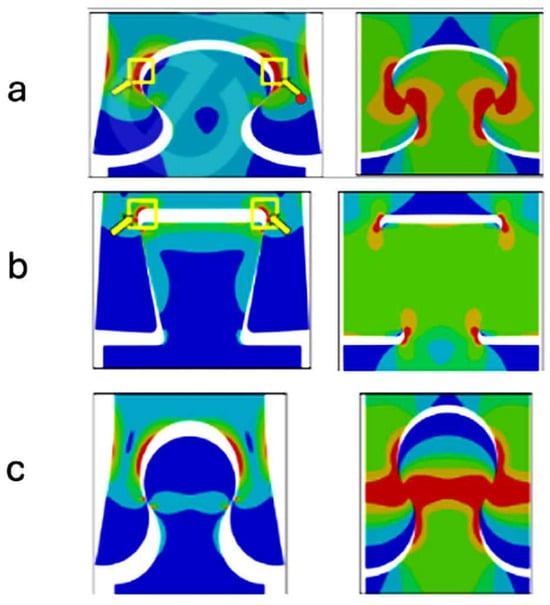
Figure 25.
Stress distribution of dovetail, circle and elliptical joints under tensile loading: (a) elliptical joint; (b) dovetail joint; (c) circle joint, reprinted from Ref. [56], licensed under CC BY 4.0, Y. Liu.
In a comparative numerical study, elliptical, circular, and dovetail joints were evaluated under tensile loading while constraining the bending deformation of the female part [56]. The dovetail joint, as discussed earlier, exhibited stress concentrations at the inner corners of the female groove and along the neck of the male component. Similarly, elliptical joint showed significant stress accumulation near the interior corners of the female interface, as illustrated by yellow squares in Figure 25a,b. Elliptical joint demonstrated the highest stiffness primarily due to its wider lateral contact region, which distributes stress more effectively perpendicularly in relation to the loading direction. In contrast, a circular joint exhibited greater resilience and load-bearing capacity as its geometry facilitates smoother stress flow along the load direction.
Mechanical performance of elliptical and circular joints made from acrylonitrile butadiene styrene (ABS) was compared elsewhere [25]. The relevant results confirmed that elliptical joint was both stiffer and stronger than circular counterpart under similar loading conditions. Furthermore, elliptical angle defined by the degree of arc in the interlock profile was shown to significantly influence the failure mode. The joints with angles greater than 190° typically failed across the neck, while joints with the angles at approximately 100° failed along both sides of the male component [25].
5. Discussion
This review highlights the significant role of geometry and material dissimilarity effects in determining mechanical performance of adhesively bonded and interlocked joints.
5.1. Stress Distribution and Failure Mechanisms in Bonded Joints
Adhesively bonded joints are highly efficient in distributing the load across large surface areas, though they suffer from localised stress concentrations, particularly at free edges with crack initiation. Several key phenomena were observed across different bonded geometries. Firstly, the adhesive layer does not uniformly transfer load, leading to asymmetric stress distributions. Most of the load transfers through the edge area rather than the middle section of the bond, known as the shear lag effect for the adhesive, especially in dissimilar material joints where stiffness mismatch enhances non-uniform stress distribution. Secondly, all adhesive bonds are weak under peel stress and become stronger under shear stress. For instance, Araldite 2011 adhesive offers 4 times stronger shear strength than peel strength. Therefore, joint design must ensure that joint geometry experiences shear stress rather than peel stress. Thirdly, discontinuities and sharp corners of adhesive layers inside the steps generate localised stress concentration, again leading to typical adhesive failure. As such, joint discontinuities and sharp corners must be avoided for the improvement in joint strength.
A single-lap joint presents an eccentric load axis that induces the bending moment. The bending moment elevates the peel stress at the free edges prone to mechanical failure. A single-lap joint is widely used in aerospace and automobile industries because the substrates are thin and easy-to-apply adhesives. Thin adherents cause negligible bending moments and peel stress. Single-lap bonded joints are particularly not suitable for bonding thick adherents because the adherents generate high peel stress at the free edges under tensile loading. In addition, single-lap joints have been studied extensively with broad availability.
While stepped-lap joints reduce stress at free edges, they induce stress singularities at each step to accelerate crack initiation. Scarf joints exhibit the most uniform stress distribution, making them stronger under tensile loading [3]. Scarf joints transfer the load across the whole bond line with uniform stress. The load increase contributes to the intensification of stress concentration along the bond line, but not on the free edges. When the subjected load is increased to the single-lap, stepped-lap, and butt joints, stress concentration becomes more pronounced at free edges and step corners, leading to adhesive failure.
Wavy joints perform well only in one direction, such as tensile or compressive stress. Reverse wavy joints show higher load-bearing capacity with 32% increase when compared with SLJs due to the compressive stress imposed on free edges. However, reverse wavy joint under compressive loading loses the compressive stress at the free edges due to geometries, and free edges undergo typical tensile stress. In addition, their higher displacement under loading makes them less stiff than other geometries [35]. In particular, a double-lap joint eliminates the bending moment of middle substrates, but the two outer adherents create bending moments, resulting in peel stress at the one free edge. However, the joint is stronger than a single-lap joint. The double-strapped lap joint fully eliminates the bending moment and induces no negative effect from the geometrical point of view. The two outer substrates apparently contribute to the weight and cost of production.
5.2. Interlocking Joints: Strengths and Limitations
Interlocking joints eliminate adhesive dependency and instead rely on material engagement through contact pressure and friction. The strength comparison of interlocking joints is challenging due to the variation in input parameters, material types, and specimen sizes used in experimental and numerical studies. However, failure modes can be well compared based on the stress concentration and deformation of interlocking joints.
Almost all interlocking joints, consisting of female and male parts, suffer from the bending of female part outward, while the male part undergoes high stress along neck sections. The dovetail joints experience stress concentration at the mortise inside the corners, prone to localised crack initiation [114]. Gooseneck joints outperform dovetail joints by spreading strain along the extended neck with failure delay [56]. T-slot joints can suffer from bending-induced failure in the female part, particularly in an unconstrained condition [115]. Elliptical joints exhibit higher stiffness, whereas Yin–Yang joints promote symmetric load transfer, thus improving mechanical resilience [56]. Although interlocking joints avoid adhesive failure risk, their primary limitation is stress localisation at contact edges and bending deformation in the female part.
The above-mentioned interlocking joints facilitate only one interlocking function with various geometries, intensifying the neck sections of the male part. Therefore, the interlocking joint, which eliminates the bending of female part and shares the load of the neck section, is desirable as it increases joint performance. Mimic interlocking joints could offer multiple interlocking features and remove female part bending, but become difficult to fabricate and implement in specific applications. However, interlocking joints combined with the adhesive bonding is a promising solution because the adhesive can restrict the bending of female parts, and the neck section enables to share the load with other bonded areas. In return, adhesive-bonded joints diminish catastrophic failure due to interlocking features.
6. Summary
This review systematically examined the influence of joint geometry and material dissimilarity on mechanical performance of adhesively bonded and interlocked joints. The findings highlight that geometry plays a pivotal role in optimising stress distribution, enhancing load-bearing capacity and mitigating premature failure.
Key insights identified in this review comprise the following: Firstly, localised stress concentration commonly occurs at free edges and geometric transitions in bonded joints, as well as at neck regions and inside the corners in interlocking joints. Secondly, adhesives perform better under shear stress instead of peel stress. Eccentric loading in overlapped joints induces peel stress at free edges. Thirdly, load transfer occurs predominantly at adhesive edges, thus resulting in higher stress at the edge region rather than at the centre of the bond line. Lastly, scarf joints are well aligned with adhesive properties, outperforming stepped-lap, single-lap, and butt joints in load-bearing capacity.
Future direction should focus on the design of scarf-like bonded joints to minimise edge stresses, the development of interlocking geometries with smoother stress paths along with minimisation of bending for female part to enhance failure resistance, as well as the exploration of hybrid joints in combination of adhesive bonding and mechanical interlocking for enhanced joint performance. All these strategies are anticipated to contribute positively to more robust and reliable joint solutions in aerospace, automotive and other engineering applications in the future.
Author Contributions
K.D.: writing, formal analysis, validation; Y.D. and A.P.: conceptualization, writing—review and editing; supervision; resource; A.K.B.: writing—review and editing, formal analysis, validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw/processed data used to produce the results will be made available by the corresponding author upon reasonable request.
Acknowledgments
The authors acknowledge the use of artificial intelligence tools (ChatGPT, OpenAI) to improve the language and clarity of the manuscript. All content was reviewed and approved by the authors, who take full responsibility for the integrity and accuracy of the work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pramanik, A.; Basak, A.K.; Dong, Y.; Sarker, P.K.; Uddin, M.S.; Littlefair, G.; Dixit, A.R.; Chattopadhyaya, S. Joining of carbon fibre reinforced polymer (CFRP) composites and aluminium alloys—A review. Compos. Part A Appl. Sci. Manuf. 2017, 101, 1–29. [Google Scholar] [CrossRef]
- Pramanik, A.; Garg, D.; Basak, A.K.; Prakash, C.; Shankar, S.; Chattopadhyaya, S. Tensile Behaviour of Steel Joints Implemented by Bolts and Adhesive. Arch. Adv. Eng. Sci. 2025, 1–8. [Google Scholar] [CrossRef]
- Kanani, A.Y.; Hou, X.; Laidlaw, R.; Ye, J. The effect of joint configuration on the strength and stress distributions of dissimilar adhesively bonded joints. Eng. Struct. 2021, 226, 111322. [Google Scholar] [CrossRef]
- Szallies, K.; Bielenin, M.; Schricker, K.; Bergmann, J.P.; Neudel, C. Single-side resistance spot joining of polymer-metal hybrid structures. Weld. World 2019, 63, 1145–1152. [Google Scholar] [CrossRef]
- Nagatsuka, K.; Xiao, B.; Wu, L.; Natata, K.; Saeki, S.; Kitamoto, Y.; Iwamoto, Y. Dissimilar materials joining of metal/carbon fibre reinforced plastic by resistance spot welding. Weld. Int. 2018, 32, 505–512. [Google Scholar] [CrossRef]
- Schricker, K.; Bergmann, J.P.; Hopfeld, M.; Spieß, L. Effect of thermoplastic morphology on mechanical properties in laser-assisted joining of polyamide 6 with aluminum. Weld. World 2021, 65, 699–711. [Google Scholar] [CrossRef]
- Jiao, J.; Xu, J.; Jing, C.; Sheng, L.; Ru, H.; Xia, H. Laser welding process and strength enhancement of carbon fiber reinforced thermoplastic composites and metals dissimilar joint: A review. Chin. J. Aeronaut. 2023, 36, 13–31. [Google Scholar] [CrossRef]
- Li, T.; Bi, X.; Li, R. A strategy for bonding immiscible Mg/steel by laser-TIG butt fusion welding and lattice distortion on the Fe/Mg interface matching. Mater. Des. 2022, 219, 110763. [Google Scholar] [CrossRef]
- Yang, J.; Oliveira, J.; Li, Y.; Tan, C.; Gao, C.; Zhao, Y.; Yu, Z. Laser techniques for dissimilar joining of aluminum alloys to steels: A critical review. J. Mater. Process. Technol. 2022, 301, 117443. [Google Scholar] [CrossRef]
- Bose, S.; Chelladurai, H.; Ponappa, K. A review on recent developments in ultrasonic welding of polymers and polymeric composites. Weld. World 2024, 68, 1881–1903. [Google Scholar] [CrossRef]
- Fan, Z.; Bai, K.; Chen, C. The application of ultrasound in Joining: Principles, processes and properties. J. Manuf. Process. 2023, 101, 269–299. [Google Scholar] [CrossRef]
- Liu, J.; Wu, B.; Wang, Z.; Li, C.; Chen, G.; Miao, Y. Microstructure and mechanical properties of aluminum-steel dissimilar metal welded using arc and friction stir hybrid welding. Mater. Des. 2023, 225, 111520. [Google Scholar] [CrossRef]
- Cooke, K.O.; Atieh, A.M. Current trends in dissimilar diffusion bonding of titanium alloys to stainless steels, aluminium and magnesium. J. Manuf. Mater. Process. 2020, 4, 39. [Google Scholar] [CrossRef]
- Basak, A.K.; Pramanik, A.; Shankar, S.; Mohanraj, T.; Prakash, C. Effect of support and adhesive tape to reduce delamination of carbon fiber reinforced polymer during drilling. Prog. Compos. Mater. 2025, 1, 5. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y.; Lou, M.; Zhao, H.; Li, Y. Flow drill screw (FDS) technique: A state-of-the-art review. J. Manuf. Process. 2023, 103, 23–52. [Google Scholar] [CrossRef]
- Yousefi Kanani, A.; Green, S.; Hou, X.; Ye, J. Hybrid and adhesively bonded joints with dissimilar adherends: A critical review. J. Adhes. Sci. Technol. 2021, 35, 1821–1859. [Google Scholar] [CrossRef]
- Machado, J.; Nunes, P.; Marques, E.; da Silva, L.F. Numerical study of similar and dissimilar single lap joints under quasi-static and impact conditions. Int. J. Adhes. Adhes. 2020, 96, 102501. [Google Scholar] [CrossRef]
- Burhan, M.; Ullah, Z.; Kazancı, Z.; Catalanotti, G. A critical review on free edge delamination fracture criteria. Mech. Adv. Mater. Struct. 2024, 31, 13542–13555. [Google Scholar] [CrossRef]
- Basak, A.K.; Bajwa, D.S.; Pramanik, A. Fatigue Behaviour of Mechanical Joints: A Review. Metals 2024, 15, 25. [Google Scholar] [CrossRef]
- Machado, J.; Marques, E.; da Silva, L.F. Adhesives and adhesive joints under impact loadings: An overview. J. Adhes. 2018, 94, 421–452. [Google Scholar] [CrossRef]
- Maggiore, S.; Banea, M.D.; Stagnaro, P.; Luciano, G. A review of structural adhesive joints in hybrid joining processes. Polymers 2021, 13, 3961. [Google Scholar] [CrossRef] [PubMed]
- Bego, M.; Lobaš Kukavičić, I.; Martinović, S.; Puljas, V. Historical Application of Dovetail Corner Joints with Practical Example. Drv. Ind. 2025, 76, 99–111. [Google Scholar] [CrossRef]
- Ding, Y.; Abdullah, A.M.; Dunn, M.; Yu, K. Design of interfaces to promote the bonding strength between dissimilar materials. J. Manuf. Process. 2022, 76, 786–795. [Google Scholar] [CrossRef]
- Lin, E.; Li, Y.; Ortiz, C.; Boyce, M.C. 3D printed, bio-inspired prototypes and analytical models for structured suture interfaces with geometrically-tuned deformation and failure behavior. J. Mech. Phys. Solids 2014, 73, 166–182. [Google Scholar] [CrossRef]
- Xing, Y.; Yang, C.; Sun, S.-Y.; Zhao, Z.-L.; Feng, X.-Q.; Yang, J.; Gao, H. Mechanics of elliptical interlocking sutures in biological interfaces. Acta Biomater. 2025, 192, 90–100. [Google Scholar] [CrossRef]
- Mirkhalaf, M.; Dastjerdi, A.K.; Barthelat, F. Overcoming the brittleness of glass through bio-inspiration and micro-architecture. Nat. Commun. 2014, 5, 3166. [Google Scholar] [CrossRef]
- Cordisco, F.A.; Zavattieri, P.D.; Hector, L.G., Jr.; Carlson, B.E. Mode I fracture along adhesively bonded sinusoidal interfaces. Int. J. Solids Struct. 2016, 83, 45–64. [Google Scholar] [CrossRef]
- Marchione, F. Structural Adhesive Joints: State of the Art, Challenges, and Future Perspectives. Int. J. Eng. Trans. C Asp. 2025, 38, 2018–2025. [Google Scholar] [CrossRef]
- Ishida, H. A review of recent progress in the studies of molecular and microstructure of coupling agents and their functions in composites, coatings and adhesive joints. Polym. Compos. 1984, 5, 101–123. [Google Scholar] [CrossRef]
- Kupski, J.; De Freitas, S.T. Design of adhesively bonded lap joints with laminated CFRP adherends: Review, challenges and new opportunities for aerospace structures. Compos. Struct. 2021, 268, 113923. [Google Scholar] [CrossRef]
- Naat, N.; Boutar, Y.; Naïmi, S.; Mezlini, S.; Da Silva, L.F.M. Effect of surface texture on the mechanical performance of bonded joints: A review. J. Adhes. 2023, 99, 166–258. [Google Scholar] [CrossRef]
- Demir, K.; Bayramoglu, S.; Akpinar, S. The fracture load analysis of different support patches in adhesively bonded single-lap joints. Theor. Appl. Fract. Mech. 2020, 108, 102653. [Google Scholar] [CrossRef]
- Marchione, F. Stress distribution in double-lap adhesive joints: Effect of adherend reinforcement layer. Int. J. Adhes. Adhes. 2021, 105, 102780. [Google Scholar] [CrossRef]
- Alves, D.; Campilho, R.; Moreira, R.; Silva, F.; Da Silva, L. Experimental and numerical analysis of hybrid adhesively-bonded scarf joints. Int. J. Adhes. Adhes. 2018, 83, 87–95. [Google Scholar] [CrossRef]
- Nosouhi, F.; Farahani, M.; Ansari, M. Experimental and numerical study on the composite adhesive joint reinforcement using wavy edge. J. Adhes. Sci. Technol. 2018, 32, 1007–1017. [Google Scholar] [CrossRef]
- Brito, R.F.N.; Campilho, R.D.S.G.; Moreira, R.D.F.; Sánchez-Arce, I.J.; Silva, F.J.G. Composite stepped-lap adhesive joint analysis by cohesive zone modelling. Procedia Struct. Integr. 2021, 33, 665–672. [Google Scholar] [CrossRef]
- Han, S.; Guang, X.; Li, Z.; Li, Y. Joining processes of CFRP-Al sheets in automobile lightweighting technologies: A review. Polym. Compos. 2022, 43, 8622–8633. [Google Scholar] [CrossRef]
- Ravichandran, B.; Balasubramanian, M. Joining methods for Fiber Reinforced Polymer (FRP) composites—A critical review. Compos. Part A Appl. Sci. Manuf. 2024, 186, 108394. [Google Scholar] [CrossRef]
- Singh, Y.; Kumar, J.; Singh, I.; Rakesh, P.K. Joining behavior of natural fiber reinforced polymer composites. In Joining Processes for Dissimilar and Advanced Materials; Rakesh, P., Paulo Davim, J., Eds.; Woodhead Publishing: Cambridge, UK, 2022; pp. 33–63. [Google Scholar]
- Lee, L.-H. Adhesive Bonding; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Horiuchi, S.; Terasaki, N.; Miyamae, T. Interfacial Phenomena in Adhesion and Adhesive Bonding; Springer Nature: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Ebnesajjad, S.; Landrock, A.H. Adhesive applications and bonding processes. In Adhesives Technology Handbook; William Andrew Publishing: Boston, MA, USA, 2015; pp. 206–234. [Google Scholar] [CrossRef]
- Ebnesajjad, S.; Landrock, A.H. (Eds.) Introduction and Adhesion Theories. In Adhesives Technology Handbook, 3rd ed.; William Andrew Publishing: Boston, MA, USA, 2015; pp. 1–18. [Google Scholar] [CrossRef]
- Falsafi, A. The science and mechanics of adhesion: An industrial view. Dent. Mater. 2023, 39, 682–685. [Google Scholar] [CrossRef]
- Adams, R.D. Adhesive Bonding: Science, Technology and Applications; Woodhead Publishing: Sawston, UK, 2021. [Google Scholar]
- Omar, H.A.; Yusoff, N.I.M.; Mubaraki, M.; Ceylan, H. Effects of moisture damage on asphalt mixtures. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 600–628. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, W.; Li, B.; Zhu, J.; Wang, C.; Song, G.; Wu, G.; Yang, X.; Huang, Y.; Ma, L. Recent advances of interphases in carbon fiber-reinforced polymer composites: A review. Compos. Part B Eng. 2022, 233, 109639. [Google Scholar] [CrossRef]
- Park, S.-J.; Seo, M.-K. Solid-solid interfaces. Interface Sci. Technol. 2011, 18, 253–331. [Google Scholar]
- Nugroho, W.T.; Dong, Y.; Pramanik, A. Mechanical and Shape Memory Properties of Additively Manufactured Polyurethane (PU)/Halloysite Nanotube (HNT) Nanocomposites. Nanomaterials 2024, 14, 1373. [Google Scholar] [CrossRef]
- Aziz, T.; Ullah, A.; Fan, H.; Jamil, M.I.; Khan, F.U.; Ullah, R.; Iqbal, M.; Ali, A.; Ullah, B. Recent progress in silane coupling agent with its emerging applications. J. Polym. Environ. 2021, 29, 3427–3443. [Google Scholar] [CrossRef]
- Sundriyal, P.; Pandey, M.; Bhattacharya, S. Plasma-assisted surface alteration of industrial polymers for improved adhesive bonding. Int. J. Adhes. Adhes. 2020, 101, 102626. [Google Scholar] [CrossRef]
- Petrie, E.M. Adhesive bonding of textiles: Principles, types of adhesive and methods of use. In Joining Textiles; Jones, I., Stylios, G.K., Eds.; Woodhead Publishing: Sawston, UK, 2013; pp. 225–274. [Google Scholar] [CrossRef]
- Young, T. III. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Xie, M.; Zhan, L.; Ma, B.; Hui, S. Classification of fiber metal laminates (FMLs), adhesion theories and methods for improving interfacial adhesion: A review. Thin-Walled Struct. 2024, 198, 111744. [Google Scholar] [CrossRef]
- Fourche, G. An overview of the basic aspects of polymer adhesion. Part I: Fundamentals. Polym. Eng. Sci. 1995, 35, 957–967. [Google Scholar] [CrossRef]
- Liu, Y. Fatigue Debonding Behaviour in Composite Joints: Experimental and Numerical Investigations. Ph.D. Thesis, Coventry University, Coventry, UK, 2019. Available online: https://pureportal.coventry.ac.uk/en/studentTheses/fatigue-debonding-behaviour-in-composite-joints-experimental-and- (accessed on 9 July 2025).
- Cognard, J.Y. Numerical analysis of edge effects in adhesively-bonded assemblies application to the determination of the adhesive behaviour. Comput. Struct. 2008, 86, 1704–1717. [Google Scholar] [CrossRef]
- Huang, J.; Zeng, J.; Bai, Y.; Cheng, Z.; Wang, Y.; Zhao, Q.; Liang, D. Effect of adhesive layer properties on the shear strength of single-lap structures of dissimilar materials based on the cohesive zone model. J. Mech. Sci. Technol. 2021, 35, 133–143. [Google Scholar] [CrossRef]
- Akhavan-Safar, A.; Ramezani, F.; Delzendehrooy, F.; Ayatollahi, M.; Da Silva, L. A review on bi-adhesive joints: Benefits and challenges. Int. J. Adhes. Adhes. 2022, 114, 103098. [Google Scholar] [CrossRef]
- de Queiroz, H.F.; Banea, M.D. Methods to increase the mechanical performance of composite adhesive joints: An overview with focus on joints with natural fibre composite adherends. J. Compos. Mater. 2022, 56, 3993–4010. [Google Scholar] [CrossRef]
- Kanani, A.Y.; Liu, Y.; Hughes, D.J.; Ye, J.; Hou, X. Fracture mechanisms of hybrid adhesive bonded joints: Effects of the stiffness of constituents. Int. J. Adhes. Adhes. 2020, 102, 102649. [Google Scholar] [CrossRef]
- Ribeiro, T.; Campilho, R.; da Silva, L.F.; Goglio, L. Damage analysis of composite–aluminium adhesively-bonded single-lap joints. Compos. Struct. 2016, 136, 25–33. [Google Scholar] [CrossRef]
- Jiang, W.; Qiao, P. An improved four-parameter model with consideration of Poisson’s effect on stress analysis of adhesive joints. Eng. Struct. 2015, 88, 203–215. [Google Scholar] [CrossRef]
- Zou, T.; Fu, J.; Qin, J.; Li, L.; Liu, Z. Failure analysis of composite-to-titanium single lap adhesive joints subjected to tensile loading. Eng. Fail. Anal. 2021, 129, 105734. [Google Scholar] [CrossRef]
- Peres, L.M.C.; Arnaud, M.F.T.D.; Silva, A.F.M.V.; Campilho, R.D.S.G.; Machado, J.J.M.; Marques, E.A.S.; dos Reis, M.Q.; Da Silva, L.F.M. Geometry and adhesive optimization of single-lap adhesive joints under impact. J. Adhes. 2022, 98, 677–703. [Google Scholar] [CrossRef]
- Akpinar, S.; Hacısalihoglu, İ.; Çalık, A. The effect of geometry on joint strength in adhesively bonded joints with the same adhesive area. Mech. Adv. Mater. Struct. 2024, 31, 2635–2647. [Google Scholar] [CrossRef]
- Stuparu, F.A.; Apostol, D.A.; Constantinescu, D.M.; Picu, C.R.; Sandu, M.; Sorohan, S. Local evaluation of adhesive failure in similar and dissimilar single-lap joints. Eng. Fract. Mech. 2017, 183, 39–52. [Google Scholar] [CrossRef]
- Ghanem, A.; Lang, Y. Introduction to Polymer Adhesion. 2017. Available online: https://www.researchgate.net/publication/387340948_Participation_of_Polymer_Materials_in_the_Structure_of_Piezoelectric_Composites (accessed on 9 July 2025).
- Rhee, K.; Lee, S.; Choi, N.; Park, S. Treatment of CFRP by IAR method and its effect on the fracture behavior of adhesive bonded CFRP/aluminum composites. Mater. Sci. Eng. A 2003, 357, 270–276. [Google Scholar] [CrossRef]
- Parida, S.K.; Murmu, A.M.; Hari, V.; Ayar, V.S.; Das, R. 3D FE adhesion failure analyses of adhesive bonded single lap joint made with functionally modulus graded curved adherends. Int. J. Interact. Des. Manuf. 2024, 19, 4103–4112. [Google Scholar] [CrossRef]
- Temiz, S.; Akpinar, S.; Aydin, M.D.; Sancaktar, E. Increasing single-lap joint strength by adherend curvature-induced residual stresses. J. Adhes. Sci. Technol. 2013, 27, 244–251. [Google Scholar] [CrossRef]
- Pires, V.D.C.; Ribeiro, F.C.C.; Carbas, R.J.C.; Marques, E.A.S.; da Silva, L.F.M. The reduction of stress concentrations in adhesive joints with the use of curved aluminum adherends. Mech. Adv. Mater. Struct. 2024, 31, 10962–10973. [Google Scholar] [CrossRef]
- Liu, Y.; Lemanski, S.; Zhang, X. Parametric study of size, curvature and free edge effects on the predicted strength of bonded composite joints. Compos. Struct. 2018, 202, 364–373. [Google Scholar] [CrossRef]
- Correia, J.; Campilho, R.; Rocha, R.; Liu, Y.; Ramalho, L. Parametric study of composite curved adhesive joints. Int. J. Adv. Manuf. Technol. 2020, 111, 2957–2970. [Google Scholar] [CrossRef]
- Fessel, G.; Broughton, J.; Fellows, N.; Durodola, J.; Hutchinson, A. A numerical and experimental study on reverse-bent joints for composite substrates. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 2192. [Google Scholar]
- Campilho, R.; Pinto, A.; Banea, M.D.; Silva, R.; da Silva, L.F. Strength improvement of adhesively-bonded joints using a reverse-bent geometry. J. Adhes. Sci. Technol. 2011, 25, 2351–2368. [Google Scholar] [CrossRef]
- Zeng, Q.; Sun, C. Fatigue performance of a bonded wavy composite lap joint. Fatigue Fract. Eng. Mater. Struct. 2004, 27, 413–422. [Google Scholar] [CrossRef]
- Avila, A.F.; Bueno, P.d.O. Stress analysis on a wavy-lap bonded joint for composites. Int. J. Adhes. Adhes. 2004, 24, 407–414. [Google Scholar] [CrossRef]
- Ayatollahi, M.; Samari, M.; Razavi, N.; Da Silva, L. Fatigue performance of adhesively bonded single lap joints with non-flat sinusoid interfaces. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1355–1363. [Google Scholar] [CrossRef]
- Demiral, M.; Kadioglu, F. Damage Characteristics of a Step Lap Joint Exposed to Flexural Loading for Its Different Configurations. Polymers 2023, 15, 2458. [Google Scholar] [CrossRef]
- Demiral, M.; Mamedov, A. Fatigue Performance of a Step-Lap Joint under Tensile Load: A Numerical Study. Polymers 2023, 15, 1949. [Google Scholar] [CrossRef] [PubMed]
- Gavgali, E.; Sahin, R.; Akpinar, S. An investigation of the fatigue performance of adhesively bonded step-lap joints: An experimental and numerical analysis. Int. J. Adhes. Adhes. 2021, 104, 102736. [Google Scholar] [CrossRef]
- Ekladious, A.; Wang, J.; Chowdhury, N.; Chiu, W.K. Mechanical performance of hybrid double- and step-lap joints in primary metallic aircraft structures: An experimental and numerical approach. Compos. Part C Open Access 2025, 16, 100554. [Google Scholar] [CrossRef]
- Bayramoglu, S.; Akpinar, S.; Çalik, A. Numerical analysis of elasto-plastic adhesively single step lap joints with cohesive zone models and its experimental verification. J. Mech. Sci. Technol. 2021, 35, 641–649. [Google Scholar] [CrossRef]
- Sonwani, H.; Ramji, M.; Sidhardh, S. An energy-based analytical model for adhesively bonded stepped and simple-lap joined CFRP laminates. Int. J. Fract. 2024, 247, 225–252. [Google Scholar] [CrossRef]
- Sawa, T.; Ichikawa, K.; Shin, Y.; Kobayashi, T. A three-dimensional finite element stress analysis and strength prediction of stepped-lap adhesive joints of dissimilar adherends subjected to bending moments. Int. J. Adhes. Adhes. 2010, 30, 298–305. [Google Scholar] [CrossRef]
- Biscaia, H.C.; Micaelo, R.; Cornetti, P.; Almeida, R. Numerical bond assessment of carbon-epoxy stepped-lap joints. Eng. Fract. Mech. 2023, 289, 109413. [Google Scholar] [CrossRef]
- Carvalho, D.F.T.; Campilho, R.; Vargas, A.S.; Moreira, R.D.F.; Madani, K. Parametric cohesive zone analysis of bi-adhesive single-step joints. SN Appl. Sci. 2023, 5, 377. [Google Scholar] [CrossRef]
- Akpinar, S. The strength of the adhesively bonded step-lap joints for different step numbers. Compos. Part B Eng. 2014, 67, 170–178. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Soltani, P.; Reinicke, T. Effects of steps on the load bearing capacity of 3D-printed single lap joints. J. Mater. Res. Technol. 2023, 23, 1834–1847. [Google Scholar] [CrossRef]
- Shin, K.C.; Lee, J.J. Bond parameters to improve tensile load bearing capacities of co-cured single and double lap joints with steel and carbon fiber-epoxy composite adherends. J. Compos. Mater. 2003, 37, 401–420. [Google Scholar] [CrossRef]
- Kinloch, A.J. Adhesion and Adhesives: Science and Technology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Tsai, M.; Oplinger, D.; Morton, J. Improved theoretical solutions for adhesive lap joints. Int. J. Solids Struct. 1998, 35, 1163–1185. [Google Scholar] [CrossRef]
- Volkersen, O. Die Nietkraftverteilung in zugbeanspruchten Nietverbindungen mit konstanten Laschenquerschnitten. Luftfahrtfor Schung 1938, 15, 41–47. [Google Scholar]
- Santos, T.F.; Campilho, R.D.S.G. Numerical modelling of adhesively-bonded double-lap joints by the eXtended Finite Element Method. Finite Elem. Anal. Des. 2017, 133, 1–9. [Google Scholar] [CrossRef]
- Gonçalves, D.C.; Sánchez-Arce, I.J.; Ramalho, L.D.; Campilho, R.D.; Belinha, J. Introductory application of a natural neighbour meshless elastic formulation to double-lap adhesive joints. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 55. [Google Scholar] [CrossRef]
- Amidi, S.; Wang, J. An analytical model for interfacial stresses in double-lap bonded joints. J. Adhes. 2019, 95, 1031–1055. [Google Scholar] [CrossRef]
- Kurennov, S.; Barakhov, K.; Poliakov, O. An improved analytical model for interfacial stresses in double-lap bonded joints. AIP Conf. Proc. 2023, 2840, 030004. [Google Scholar]
- Liu, P.F.; Liu, J.W. Finite element analysis of competitive damage mechanisms of composite scarf adhesive joints by considering thickness effect. Theor. Appl. Fract. Mech. 2022, 119, 103347. [Google Scholar] [CrossRef]
- Oshima, S.; Kobayashi, S. Experimental and numerical investigation of mesoscopic damage accumulation in adhesively bonded composite scarf joints. Compos. Part A Appl. Sci. Manuf. 2024, 179, 108036. [Google Scholar] [CrossRef]
- Kim, G.; Kulkarni, S.; Lee, H.; Denos, B. Step and scarf joint elastic and failure behavior comparison under tensile and flexural loading. J. Reinf. Plast. Compos. 2023, 44, 36–44. [Google Scholar] [CrossRef]
- Ghazali, E.; Dano, M.-L.; Gakwaya, A.; Amyot, C.-O. Experimental and numerical studies of stepped-scarf circular repairs in composite sandwich panels. Int. J. Adhes. Adhes. 2018, 82, 41–49. [Google Scholar] [CrossRef]
- Pipes, R.; Adkins, D. Strength and Mechanics of Bonded Scarf Joints for Repair of Composite Materials; Contract Report; 1982. Available online: https://ntrs.nasa.gov/citations/19830007088 (accessed on 9 July 2025).
- Marques, T.P.Z.; Mayer, S.; Cândido, G.M.; Rezende, M.C. Fractographic analysis of scarf repaired carbon/epoxy laminates submitted to tensile strength. Eng. Fail. Anal. 2021, 124, 105374. [Google Scholar] [CrossRef]
- Rasane, A.; Kumar, P.; Khond, M. Optimizing the size of a CFRP patch to repair a crack in a thin sheet. J. Adhes. 2017, 93, 1064–1080. [Google Scholar] [CrossRef]
- Pitanga, M.Y.; Cioffi, M.O.H.; Voorwald, H.J.C.; Wang, C.H. Reducing repair dimension with variable scarf angles. Int. J. Adhes. Adhes. 2021, 104, 102752. [Google Scholar] [CrossRef]
- Wu, C.; Chen, C.; He, L.; Yan, W. Comparison on damage tolerance of scarf and stepped-lap bonded composite joints under quasi-static loading. Compos. Part B Eng. 2018, 155, 19–30. [Google Scholar] [CrossRef]
- Damghani, M.; Bolanos, S.; Chahar, A.; Matthews, J.; Atkinson, G.A.; Murphy, A.; Edwards, T. Design, novel quality check and experimental test of an original variable length stepped scarf repair scheme. Compos. Part B Eng. 2022, 230, 109542. [Google Scholar] [CrossRef]
- Pierce, R.S.; Falzon, B.G. Modelling the size and strength benefits of optimised step/scarf joints and repairs in composite structures. Compos. Part B Eng. 2019, 173, 107020. [Google Scholar] [CrossRef]
- Psarras, S.; Giannoutsou, M.-P.; Kostopoulos, V. A Design Optimization Study of Step/Scarf Composite Panel Repairs, Targeting the Maximum Strength and the Minimization of Material Removal. J. Compos. Sci. 2024, 8, 248. [Google Scholar] [CrossRef]
- Ren, H.; Wang, D.; Liu, G.; Rosen, D.W.; Xiong, Y. Concurrent optimization of structural topology and toolpath for additive manufacturing of continuous fiber-reinforced polymer composites. Comput. Methods Appl. Mech. Eng. 2024, 430, 117227. [Google Scholar] [CrossRef]
- Shen, Z.; Huang, Z.; Wang, J.; Zheng, L.; Qian, H.; Zhu, Q. Investigation of fretting fatigue performance for IN718 dovetail joint in very high cycle regime. Int. J. Fatigue 2025, 195, 108874. [Google Scholar] [CrossRef]
- Guo, K.; Yuan, H. Nonlocal fretting fatigue assessment for dovetail joints. Int. J. Fatigue 2024, 185, 108337. [Google Scholar] [CrossRef]
- Qin, Y.; Xiong, C.; Zhu, X.; Yin, J.; Zhang, Y.; Fan, Z.; Liu, Z.; Zhang, W. Strength analysis of carbon-fiber dovetail tenon connections under quasi-static tension. Structures 2024, 67, 106925. [Google Scholar] [CrossRef]
- Kusumah, A.M.; Bintara, R.D.; Suprayitno. The Strength Analysis of Dovetail Joint on 3D Printed Part Polylactic Acid Using Computer Simulation. In Recent Advances in Mechanical Engineering: Select Proceedings of ICOME 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 179–185. [Google Scholar]
- De Pasquale, G.; Altunok, F.E. Multiphase modeling of matrix/fiber-related damaging mechanism in multimaterial additively manufactured joints with 3D interlocking. Eng. Fail. Anal. 2025, 170, 109272. [Google Scholar] [CrossRef]
- Bolmin, O.; Young, B.; Leathe, N.; Noell, P.J.; Boyce, B.L. Interlocking metasurfaces. J. Mater. Sci. 2023, 58, 411–419. [Google Scholar] [CrossRef]
- Brown, N.K.; Young, B.; Clark, B.; Bolmin, O.; Boyce, B.L.; Noell, P.J. Optimized design of interlocking metasurfaces. Mater. Des. 2023, 233, 112272. [Google Scholar] [CrossRef]
- Elsayed, A.; Guleria, T.; Atli, K.C.; Bolmin, O.; Young, B.; Noell, P.J.; Boyce, B.L.; Elwany, A.; Arroyave, R.; Karaman, I. Active interlocking metasurfaces enabled by shape memory alloys. Mater. Des. 2024, 244, 113137. [Google Scholar] [CrossRef]
- Young, B.; Bolmin, O.; Boyce, B.; Noell, P. Synergistic strengthening in interlocking metasurfaces. Mater. Des. 2023, 227, 111798. [Google Scholar] [CrossRef]
- Jin, Q.-Y.; Nam, H.; Jo, H.; Park, J.; Kang, H.J.; Kim, D.J.; Lee, W. Design of dissimilar material joint for defect-free multi-material additive manufacturing via laser-directed energy deposition. Heliyon 2024, 10, e29666. [Google Scholar] [CrossRef] [PubMed]
- Maleki, S.; Derikvand, M.; Dalvand, M.; Ebrahimi, G. Load-carrying capacity of mitered furniture corner joints with dovetail keys under diagonal tension load. Turk. J. Agric. For. 2012, 36, 636–643. [Google Scholar] [CrossRef]
- Harding, A.; Pramanik, A.; Basak, A.K.; Prakash, C.; Shankar, S. Application of additive manufacturing in the biomedical field- A review. Ann. 3D Print. Med. 2023, 10, 100110. [Google Scholar] [CrossRef]
- Fadzil, A.F.b.A.; Pramanik, A.; Basak, A.K.; Prakash, C.; Shankar, S. Role of surface quality on biocompatibility of implants—A review. Ann. 3D Print. Med. 2022, 8, 100082. [Google Scholar] [CrossRef]
- Shuang, X.; Qingtian, D.; Xinbo, L.; Jiabao, Z.; Jinpeng, W.; Zhirong, Y. Energy absorption and deformation of cellular structures with dovetail joints. Mech. Res. Commun. 2025, 143, 104353. [Google Scholar] [CrossRef]
- Karolak, A.; Jasieńko, J. Experimental research on tensile dovetail joint between rafter and collar beam. Eng. Struct. 2024, 307, 117854. [Google Scholar] [CrossRef]
- Hu, W.; Luo, M.; Liu, Y.; Xu, W.; Caglar Konukcu, A. Experimental and numerical studies on the mechanical properties and behaviors of a novel wood dowel reinforced dovetail joint. Eng. Fail. Anal. 2023, 152, 107440. [Google Scholar] [CrossRef]
- Bai, F.; Fan, Z.; Xue, J.; Wu, C.; Hu, C.; Li, J. Experimental study on seismic performance and deformation damage of loose dovetail-tenon joints in ancient timber structures. Structures 2023, 54, 541–555. [Google Scholar] [CrossRef]
- Mashrah, W.; Chen, Z.; Boufendassa, R.; Liu, H. Numerical Parametric Study on Hysteresis Performance of the Novel Dovetail Joint for Single-layer Grid Shells Subjected to Out-of-Plane Bending Moment. KSCE J. Civ. Eng. 2023, 27, 3952–3970. [Google Scholar] [CrossRef]
- Du, L.; Qi, J.; Cheng, Z.; Wang, J. Finite element modeling of UHPC slabs with dovetail joints and steel wire mesh using an innovative interfacial treating method. Structures 2022, 37, 745–755. [Google Scholar] [CrossRef]
- Kamboj, G.; Gaff, M.; Smardzewski, J.; Haviarová, E.; Borůvka, V.; Sethy, A.K. Numerical and experimental investigation on the elastic stiffness of glued dovetail joints. Constr. Build. Mater. 2020, 263, 120613. [Google Scholar] [CrossRef]
- Ermolai, V.; Sover, A.; Andrei Boca, M.; Mihalache, A.; Ionuț Irimia, A.; Hrițuc, A.; Slătineanu, L.; Nagîț, G.; Cosmin Stavarache, R. Mechanical behavior of macroscopic interfaces for 3D printed multi-material samples made of dissimilar materials. Mech. Ind. 2024, 25, 24. [Google Scholar] [CrossRef]
- Atar, M.; Keskin, H.; Peker, H.; Ustündağ, A.; Togay, A.; Candan, Z. Impacts of different joint angles and adhesives on diagonal tension performances of box-type furniture. BioResources 2010, 5, 343–355. [Google Scholar] [CrossRef]
- Jeong, G.; Park, M.; Park, J.; Hwang, K. Predicting load-carrying capacity of dovetail connections using the stochastic finite element method. Wood Fiber Sci. 2012, 44, 430–439. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).