Thermal and Volumetric Signatures of the Mullins Effect in Carbon Black Reinforced Styrene-Butadiene Rubber Composites
Abstract
1. Introduction
2. Materials and Experiments
2.1. Materials
2.2. Tensile Tests Combining In-Situ Infra-Red Thermography and Digital Image Correlation
2.3. Analysis of the Heat Sources
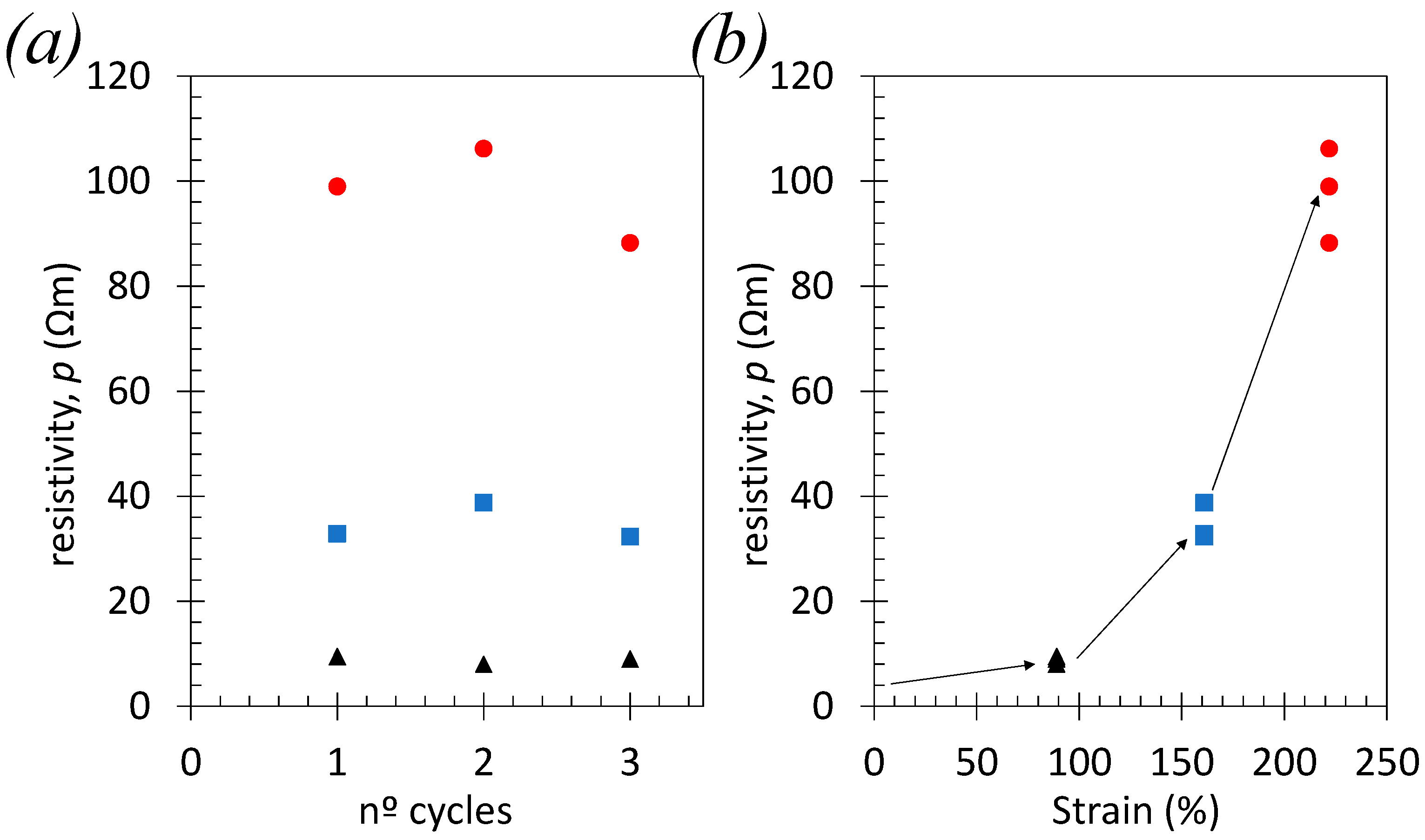
2.4. Electrical Conductivity Measurements
3. Results and Discussion
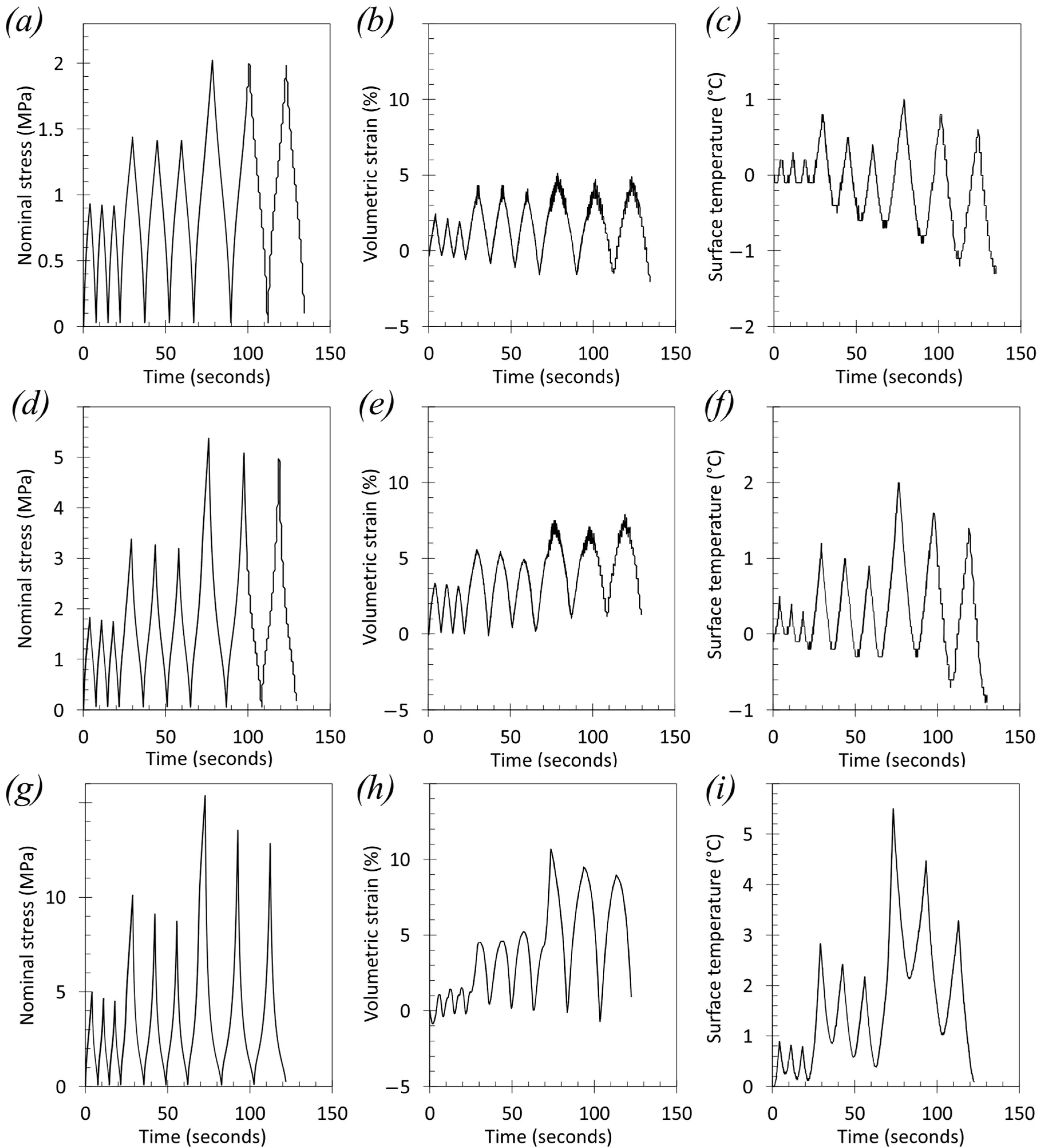
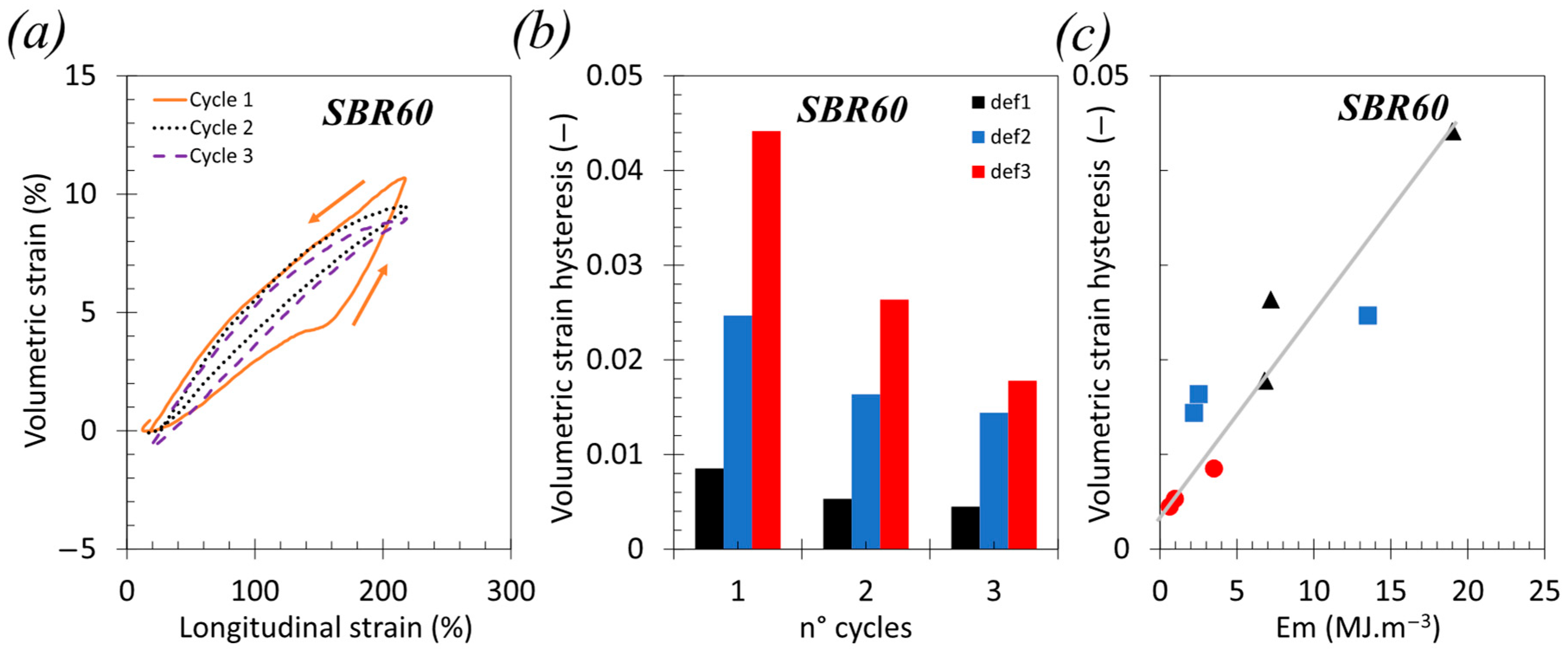
3.1. Mechanical, Thermal and Volumetric Strain Responses
3.2. Heat Source and Dissipation Energy Rate
3.3. Role of Voiding in Dissipative Mechanisms in Highly Filled SBR650
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sirisinha, C.; Sae-oui, P.; Suchiva, K.; Thaptong, P. Properties of tire tread compounds based on functionalized styrene butadiene rubber and functionalized natural rubber. J. Appl. Polym. Sci. 2020, 137, 48696. [Google Scholar] [CrossRef]
- Feyzullahoğlu, E. Abrasive wear, thermal and viscoelastic behaviors of rubber seal materials used in different working conditions. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 64–73. [Google Scholar] [CrossRef]
- Choi, S.-S.; Park, B.-H.; Song, H. Influence of filler type and content on properties of styrene-butadiene rubber (SBR) compound reinforced with carbon black or silica. Polym. Adv. Technol. 2004, 15, 122–127. [Google Scholar] [CrossRef]
- Mullins, L. Softening of Rubber by Deformation. Rubber Chem. Technol. 1969, 42, 339–362. [Google Scholar] [CrossRef]
- Ogden, R.W.; Roxburgh, D.G. A pseudo–elastic model for the Mullins effect in filled rubber. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1999, 455, 2861–2877. [Google Scholar] [CrossRef]
- Denora, I.; Marano, C. Stretch-induced softening in filled elastomers: A review on Mullins effect related anisotropy and thermally induced recovery. Polym. Test. 2024, 133, 108399. [Google Scholar] [CrossRef]
- Merckel, Y.; Diani, J.; Brieu, M.; Gilormini, P.; Caillard, J. CHARACTERIZATION OF THE MULLINS EFFECT OF CARBON-BLACK FILLED RUBBERS. Rubber Chem. Technol. 2011, 84, 402–414. [Google Scholar] [CrossRef]
- Mai, T.-T.; Morishita, Y.; Urayama, K. Induced anisotropy by Mullins effect in filled elastomers subjected to stretching with various geometries. Polymer 2017, 126, 29–39. [Google Scholar] [CrossRef]
- Zhang, H.; Scholz, A.K.; de Crevoisier, J.; Vion-Loisel, F.; Besnard, G.; Hexemer, A.; Brown, H.R.; Kramer, E.J.; Creton, C. Nanocavitation in Carbon Black Filled Styrene–Butadiene Rubber under Tension Detected by Real Time Small Angle X-ray Scattering. Macromolecules 2012, 45, 1529–1543. [Google Scholar] [CrossRef]
- Zhang, H.; Scholz, A.K.; Vion-Loisel, F.; Merckel, Y.; Brieu, M.; Brown, H.; Roux, S.; Kramer, E.J.; Creton, C. Opening and Closing of Nanocavities under Cyclic Loading in a Soft Nanocomposite Probed by Real-Time Small-Angle X-ray Scattering. Macromolecules 2013, 46, 900–913. [Google Scholar] [CrossRef]
- Diani, J.; Fayolle, B.; Gilormini, P. A review on the Mullins effect. Eur. Polym. J. 2009, 45, 601–612. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. Constitutive modelling of rubbers: Mullins effect, residual strain, time-temperature dependence. Int. J. Mech. Sci. 2021, 210, 106735. [Google Scholar] [CrossRef]
- Govindjee, S.; Simo, J. A micro-mechanically based continuum damage model for carbon black-filled rubbers incorporating Mullins’ effect. J. Mech. Phys. Solids 1991, 39, 87–112. [Google Scholar] [CrossRef]
- Zhu, P.; Zhong, Z. Constitutive modelling for the mullins effect with permanent set and induced anisotropy in particle-filled rubbers. Appl. Math. Model. 2021, 97, 19–35. [Google Scholar] [CrossRef]
- Clough, J.M.; Creton, C.; Craig, S.L.; Sijbesma, R.P. Covalent Bond Scission in the Mullins Effect of a Filled Elastomer: Real-Time Visualization with Mechanoluminescence. Adv. Funct. Mater. 2016, 26, 9063–9074. [Google Scholar] [CrossRef]
- Karásek, L.; Meissner, B.; Asai, S.; Sumita, M. Percolation Concept: Polymer-Filler Gel Formation, Electrical Conductivity and Dynamic Electrical Properties of Carbon-Black-Filled Rubbers. Polym. J. 1996, 28, 121–126. [Google Scholar] [CrossRef]
- Diaz, R.; Diani, J.; Gilormini, P. Physical interpretation of the Mullins softening in a carbon-black filled SBR. Polymer 2014, 55, 4942–4947. [Google Scholar] [CrossRef]
- Mohanraj, G.T.; Chaki, T.K.; Chakraborty, A.; Khastgir, D. Effect of some service conditions on the electrical resistivity of conductive styrene–butadiene rubber–carbon black composites. J. Appl. Polym. Sci. 2004, 92, 2179–2188. [Google Scholar] [CrossRef]
- Nasr, G.M. Vulcanization conditions: How they affect the electrical conductivity of SBR loaded with the percolation concentration of FEF-black. Polym. Test. 1996, 15, 585–591. [Google Scholar] [CrossRef]
- Flaifel, M.H. An Approach Towards Optimization Appraisal of Thermal Conductivity of Magnetic Thermoplastic Elastomeric Nanocomposites Using Response Surface Methodology. Polymers 2020, 12, 2030. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, Y.; Mai, T.-T.; Yamaguchi, M.; Tsunoda, K.; Urayama, K. Investigating Multiaxial Mullins Effect of Carbon-Black-Reinforced Elastomers Using Electrical Resistivity Measurements. ACS Appl. Polym. Mater. 2022, 4, 1139–1149. [Google Scholar] [CrossRef]
- Vieweg, S.; Unger, R.; Heinrich, G.; Donth, E. Comparison of dynamic shear properties of styrene–butadiene vulcanizates filled with carbon black or polymeric fillers. J. Appl. Polym. Sci. 1999, 73, 495–503. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhang, A.; Wang, L. Carbon Black–Filled Styrene Butadiene Rubber Masterbatch Based on Simple Mixing of Latex and Carbon Black Suspension: Preparation and Mechanical Properties. J. Macromol. Sci. Part B 2015, 54, 1541–1553. [Google Scholar] [CrossRef]
- George, S.C.; Thomas, S. Carbon-Black-Filled SBR Composites: The Effect of Rubber-Filler Interaction on Transport. J. Macromol. Sci. 2000, 39, 175–195. [Google Scholar] [CrossRef]
- Han, J.-J.; Yang, T.-T.; Yang, C.-W.; Huang, L.-Z.; Song, K.; Sun, G.-A.; Wei, C.-S.; Xu, J.-Z.; Li, Z.-M.; Liu, D. The maximum-strain and strain-interval dependences of microstructural evolution underneath the Mullins effect. Compos. Part A Appl. Sci. Manuf. 2023, 172, 107586. [Google Scholar] [CrossRef]
- Yang, C.-W.; Yang, T.-T.; Huang, L.-Z.; Han, J.-J.; Sun, G.-A.; Xu, J.-Z.; Li, Z.-M.; Liu, D. Correlation between the hierarchical structure evolution and Mullins effect of filled rubber under variable amplitude loading. Polymer 2023, 277, 125988. [Google Scholar] [CrossRef]
- Zhan, L.; Qu, S.; Xiao, R. A Review on the Mullins Effect in Tough Elastomers and Gels. Acta Mech. Solida Sin. 2024, 37, 181–214. [Google Scholar] [CrossRef]
- Candau, N.; Oguz, O.; Peuvrel-Disdier, E.; Bouvard, J.-L.; Maspoch, M.L.; Corvec, G.; Pradille, C.; Billon, N. Heat source and voiding signatures of Mullins damage in filled EPDM. Polym. Test. 2020, 91, 106838. [Google Scholar] [CrossRef]
- Candau, N.; Oguz, O.; Peuvrel-Disdier, E.; Bouvard, J.-L.; Pradille, C.; Billon, N. Strain-induced network chains damage in carbon black filled EPDM. Polymer 2019, 175, 329–338. [Google Scholar] [CrossRef]
- Candau, N.; Oguz, O.; Peuvrel-Disdier, E.; Bouvard, J.-L.; Pradille, C.; Billon, N. Strain and filler ratio transitions from chains network to filler network damage in EPDM during single and cyclic loadings. Polymer 2020, 197, 122435. [Google Scholar] [CrossRef]
- Candau, N.; Oguz, O.; Peuvrel-Disdier, E.; Bouvard, J.-L.; Maspoch, M.L.; Corvec, G.; Pradille, C.; Billon, N. Effect of the Strain Rate on Damage in Filled EPDM during Single and Cyclic Loadings. Polymers 2020, 12, 3021. [Google Scholar] [CrossRef]
- Caruthers, J.M.; Hooley, C.J.; Cohen, R.E. Time and strain dependent thermal expansion of carbon-black filled SBR elastomers. Polym. Eng. Sci. 1978, 18, 668–673. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dargazany, R. A Data-Driven Model to Predict Constitutive and Failure Behavior of Elastomers Considering the Strain Rate, Temperature, and Filler Ratio. J. Appl. Mech. 2023, 90, 051010. [Google Scholar] [CrossRef]
- Candau, N.; Vives, E.; Fernández, A.I.; Maspoch, M.L. Elastocaloric effect in vulcanized natural rubber and natural/wastes rubber blends. Polymer 2021, 236, 124309. [Google Scholar] [CrossRef]
- Samaca Martinez, J.R.; Le Cam, J.-B.; Balandraud, X.; Toussaint, E.; Caillard, J. Filler effects on the thermomechanical response of stretched rubbers. Polym. Test. 2013, 32, 835–841. [Google Scholar] [CrossRef]
- Candau, N.; Zimny, A.; Vives, E.; Maspoch, M.L. Elastocaloric waste/natural rubber materials with various crosslink densities. Polymers 2023, 15, 2566. [Google Scholar] [CrossRef]
- Candau, N.; Fernandes, J.P.C.; Vives, E.; Mudarra Lopez, M.; Neira-Viñas, M.; Maspoch, M.L. Heat exchange and damage of carbon black-filled styrene-butadiene rubber under uniaxial cyclic loading. J. Appl. Polym. Sci. 2024, 141, e55972. [Google Scholar] [CrossRef]
- Samaca Martinez, J.R.; Le Cam, J.-B.; Balandraud, X.; Toussaint, E.; Caillard, J. New elements concerning the Mullins effect: A thermomechanical analysis. Eur. Polym. J. 2014, 55, 98–107. [Google Scholar] [CrossRef]
- Loukil, M.T.; Corvec, G.; Robin, E.; Miroir, M.; Le Cam, J.-B.; Garnier, P. Stored energy accompanying cyclic deformation of filled rubber. Eur. Polym. J. 2018, 98, 448–455. [Google Scholar] [CrossRef]
- Le Cam, J.-B.; Toussaint, E. Cyclic volume changes in rubber. Mech. Mater. 2009, 41, 898–901. [Google Scholar] [CrossRef]
- de Crevoisier, J.; Besnard, G.; Merckel, Y.; Zhang, H.; Vion-Loisel, F.; Caillard, J.; Berghezan, D.; Creton, C.; Diani, J.; Brieu, M.; et al. Volume changes in a filled elastomer studied via digital image correlation. Polym. Test. 2012, 31, 663–670. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Busfield, J.J.C.; Thomas, A.G. Electrical and mechanical behavior of filled elastomers. I. The effect of strain. J. Polym. Sci. Part B Polym. Phys. 2003, 41, 2079–2089. [Google Scholar] [CrossRef]
- Busfield, J.J.C.; Thomas, A.G.; Yamaguchi, K. Electrical and mechanical behavior of filled rubber. III. Dynamic loading and the rate of recovery. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 1649–1661. [Google Scholar] [CrossRef]





| Sample Code | SBR5 | SBR30 | SBR60 |
|---|---|---|---|
| SBR | 100 | 100 | 100 |
| CB N347 (phr) | 5 | 30 | 60 |
| CB N347 (wt.%) | 4.8 | 24.1 | 37.5 |
| 6PPD (phr) | 1.9 | 1.9 | 1.9 |
| Stearic acid (phr) | 2 | 2 | 2 |
| ZnO (phr) | 2.5 | 2.5 | 2.5 |
| Sulfur (phr) | 1.6 | 1.6 | 1.6 |
| CBS (phr) | 1.6 | 1.6 | 1.6 |
| Density (g.cm−3) | 0.95 | 1.12 | 1.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Candau, N.; Corvec, G.; León-Albiter, N.; Mudarra Lopez, M. Thermal and Volumetric Signatures of the Mullins Effect in Carbon Black Reinforced Styrene-Butadiene Rubber Composites. J. Compos. Sci. 2025, 9, 393. https://doi.org/10.3390/jcs9080393
Candau N, Corvec G, León-Albiter N, Mudarra Lopez M. Thermal and Volumetric Signatures of the Mullins Effect in Carbon Black Reinforced Styrene-Butadiene Rubber Composites. Journal of Composites Science. 2025; 9(8):393. https://doi.org/10.3390/jcs9080393
Chicago/Turabian StyleCandau, Nicolas, Guillaume Corvec, Noel León-Albiter, and Miguel Mudarra Lopez. 2025. "Thermal and Volumetric Signatures of the Mullins Effect in Carbon Black Reinforced Styrene-Butadiene Rubber Composites" Journal of Composites Science 9, no. 8: 393. https://doi.org/10.3390/jcs9080393
APA StyleCandau, N., Corvec, G., León-Albiter, N., & Mudarra Lopez, M. (2025). Thermal and Volumetric Signatures of the Mullins Effect in Carbon Black Reinforced Styrene-Butadiene Rubber Composites. Journal of Composites Science, 9(8), 393. https://doi.org/10.3390/jcs9080393







