Experimental and Simulation Analysis on Wet Slip Performance Between Tread Rubber and Road Surface
Abstract
1. Introduction
2. Materials and Methods
2.1. Tread Rubber Sample
2.2. Test Equipment
2.3. Test Methods
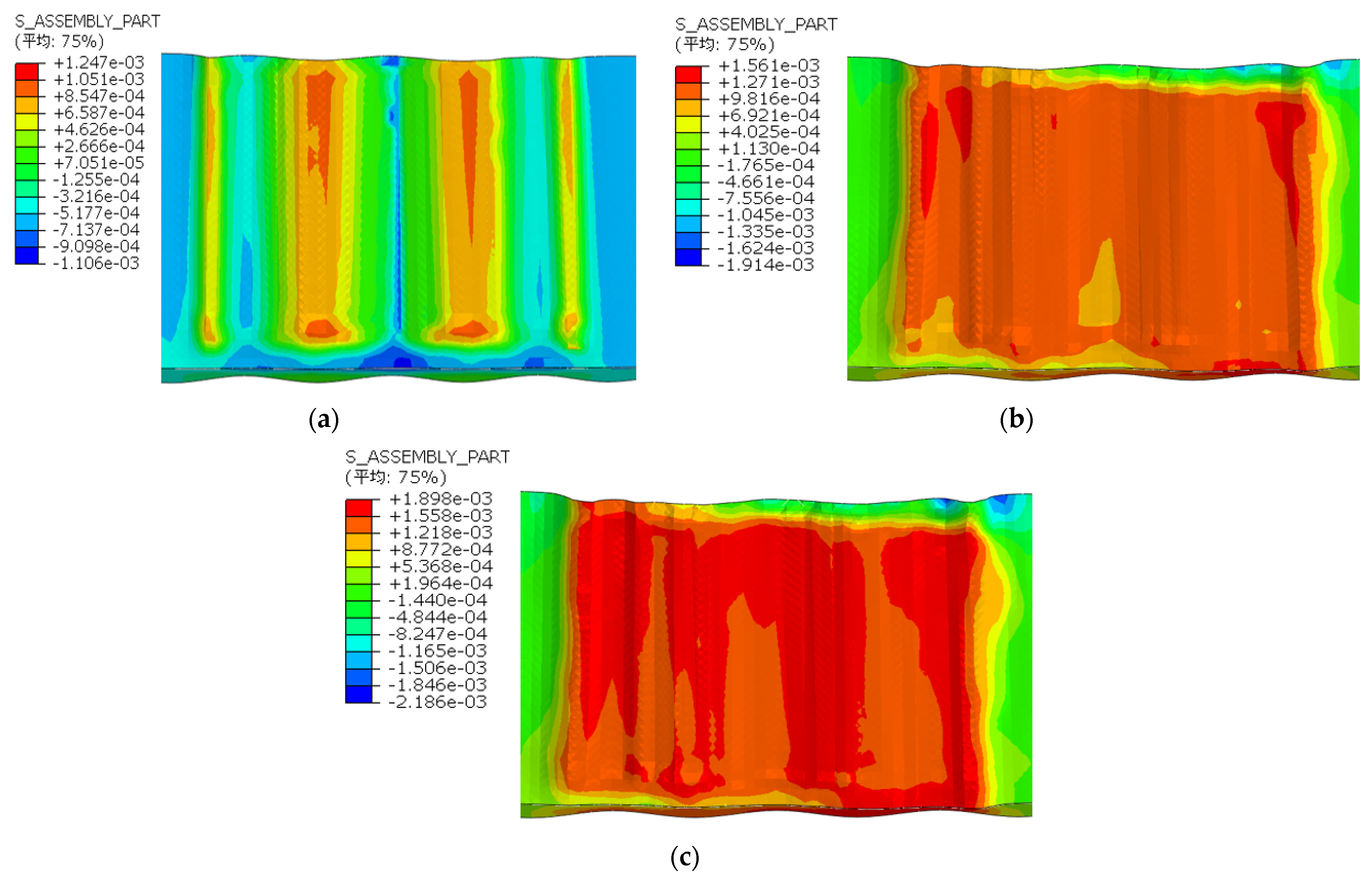
2.4. Simulation Modeling
2.4.1. Geometric Model
2.4.2. Mesh Model
3. Results and Discussion
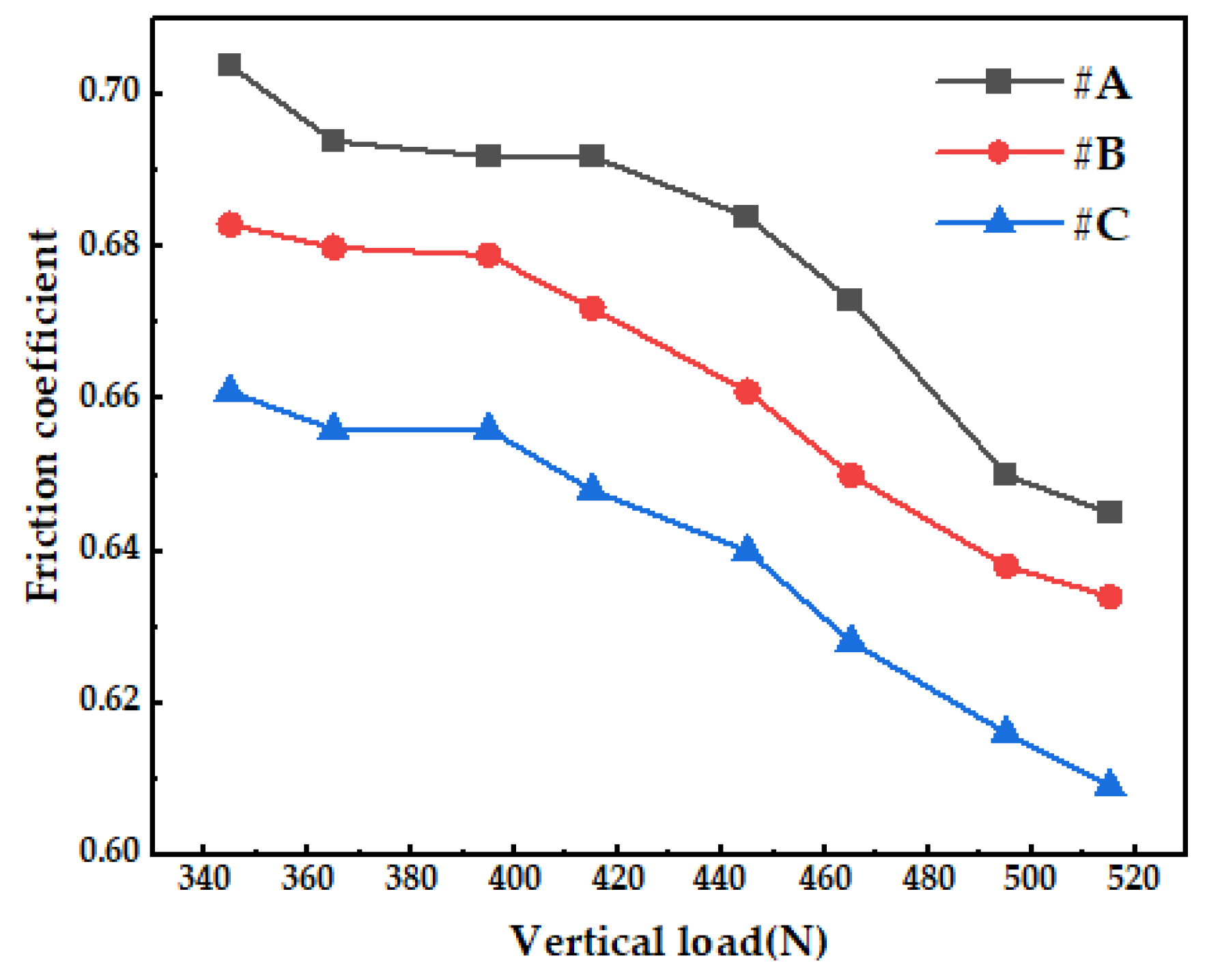
3.1. Effect of Vertical Load
3.2. Effect of Slip Speed
3.3. Effect of Water Film Thickness
3.4. Analysis of Orthogonal Test Results
4. Conclusions
- The wet slip performance of tread rubber and road surface in wet slip conditions is contingent on a number of factors, including vertical load, slip speed, and water film thickness, within the established range of test conditions. With an increase in vertical load applied to the rubber sample, the internal stress of the water film in contact with the bottom surface of the sample is increasing, the water film on the rubber sample of the support reaction force increases, while the coefficient of friction of the wet slip decreases with rising vertical load.
- The friction coefficient of the rubber block in the wet slip condition is obviously lower than that in the dry grinding condition, with a decrease of approximately 26%. Furthermore, the fluctuation of the friction coefficient change is minimal with increasing water film thickness. Within the parameters of the low-speed test interval allowed by the equipment, it was observed that the friction coefficient exhibited an increase in proportion to the rise in slip speed. And at very low speeds, the effect of the increase in speed on the friction coefficient is particularly obvious.
- The weights of the influence factors on the friction coefficient of each influence factor are vertical load > slip speed > water film thickness. These results are derived through polar analysis of the orthogonal test results. The results of the analysis of variance (ANOVA) and significance analysis show that the vertical load on the tread has a very significant effect on the coefficient of friction of wet slip, the slip speed has a significant effect on the coefficient of friction, and the thickness of the water film on the road surface has a non-significant effect on the coefficient of friction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, H.C.; Wang, G.L.; Jiang, Z.; Chen, X.P. Numerical Analysis Method for Friction Characteristics of Tire-pavement under Wet Slip Condition. J. Mech. Eng. 2020, 56, 177–185. [Google Scholar]
- Do, M.T.; Cerezo, V.; Beautru, Y.; Kane, M. Modeling of the connection road surface microtexture/water depth/friction. Wear Int. J. Sci. Technol. Frict. Lubr. Wear 2013, 302, 1426–1435. [Google Scholar] [CrossRef]
- Sabey, B.E. Pressure Distributions beneath Spherical and Conical Shapes pressed into a Rubber Plane, and their Bearing on Coefficients of Friction under Wet Conditions. Proc. Phys. Soc. 1958, 71, 979–988. [Google Scholar] [CrossRef]
- Deleau, F.; Mazuyer, D.; Koenen, A. Sliding friction at elastomer/glass contact: Influence of the wetting conditions and instability analysis. Tribol. Int. 2009, 42, 149–159. [Google Scholar] [CrossRef]
- Licher, J.; Schmerwitz, F.; Soleimani, M.; Junker, P. Experimental investigation of the tire wear process using camera-assisted observation assessed by numerical modeling. Tribol. Int. 2023, 189, 108918. [Google Scholar] [CrossRef]
- Zhao, H.D.; Wu, M.Z.; Wu, S.T. Variation of asphalt pavement friction coefficient with change of water film thickness. J. Civ. Aviat. Univ. China 2015, 33, 47–52. [Google Scholar]
- Greenwood, J.A.; Tabor, D. The Friction of Hard Sliders on Lubricated Rubber: The Importance of Deformation Losses. Proc. Phys. Soc. 1958, 71, 989–1001. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Tartaglino, U.; Albohr, O.; Tosatti, E. Rubber friction on wet and dry road surfaces: The sealing effect. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 71, 035428. [Google Scholar] [CrossRef]
- Persson, B.N.J. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef]
- Ji, T.J.; Huang, X.M.; Liu, Q.Q. Part hydroplaning effect on pavement friction coefficient. J. Traffic Transp. Eng. 2003, 3, 10–12. [Google Scholar]
- Zhu, Y.G.; Liu, X.J.; Wang, W.; Liu, K. A Study on Tire Wet Traction Performance with Consideration of Road Roughness and Hydrodynamic Action. Automot. Eng. 2007, 29, 616–619, 629. [Google Scholar]
- Zhao, L.R.; Zhao, H.D.; Cai, J.W. Tire-pavement friction modeling considering pavement texture and water film. Int. J. Transp. Sci. Technol. 2024, 14, 99–109. [Google Scholar] [CrossRef]
- Guo, K.H.; Wu, H.D.; Lu, D. Brush model for steady-state side-slip of tire on icy road. J. Jilin Univ. (Eng. Technol. Ed.) 2007, 37, 253–258. [Google Scholar]
- Zhang, L.; Cai, Z.; Wang, L.; Zhang, R.; Liu, H. Coupled Eulerian-Lagrangian finite element method for simulating soil-tool interaction. Biosyst. Eng. 2018, 175, 96–105. [Google Scholar] [CrossRef]
- Zeng, H.; Zhao, C.; Chen, S.; Xu, W.; Zang, M. Numerical simulations of tire-soil interactions: A Comprehensive Review. Arch. Comput. Methods Eng. 2023, 30, 4801–4829. [Google Scholar] [CrossRef]
- Armin, A.; Fotouhi, R.; Szyszkowski, W. On the FE modeling of soil–blade interaction in tillage operations. Finite Elem. Anal. Des. 2014, 92, 1–11. [Google Scholar] [CrossRef]
- Jiang, B.Y.; Wang, H. An integrated analytical model for friction characteristics of aircraft tire on wet runway pavement. Tribol. Int. 2023, 185, 108501. [Google Scholar] [CrossRef]
- Ma, B.; Xu, H.G.; Liu, H.F. Effects of road surface fractal and rubber characteristics on tire sliding friction factor. J. Jilin Univ. (Eng. Technol. Ed.) 2013, 43, 317–322. [Google Scholar]
- Seta, E.; Nakajima, Y.; Kamegawa, T.; Ogawa, H. Hydroplaning analysis by FEM and FVM: Effect of tire rolling and tire pattern on hydroplaning. Tire Sci. Technol. 2000, 28, 140–156. [Google Scholar] [CrossRef]
- Ong, G.P.; Fwa, T.F. Mechanistic Interpretation of Braking Distance Specifications and Pavement Friction Requirements. Transp. Res. Rec. 2010, 2155, 145–157. [Google Scholar] [CrossRef]
- Zhou, H.C.; Chen, L.; Zhai, H.H.; Lei, L.L. Reserch on Flow Field and Influencing Factors of Tire Hydroplaning Based on CFD Method. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2017, 36, 110–116. [Google Scholar]
- Yang, J.; Wang, H.P.; Wu, Q. Numerical simulation on skid resistance property of wet asphalt pavement. J. Chang. Univ. (Nat. Sci. Ed.) 2016, 36, 25–32. [Google Scholar]
- Indriasari; Kaewsakul, W.; Dierkes, W.K.; Blume, A. Defining Key Factors in Carbon Black-Filled NR/BR Compounds for Balancing Aircraft Tire Tread Properties. J. Compos. Sci. 2019, 3, 47. [Google Scholar] [CrossRef]
- Liu, C.Z.; Chen, G.; Liu, H.Z.; Ma, Q.; Xu, C.W.; Meng, H.; Wang, G.L. Tire grounding mechanical UA model on wet roads. J. Jilin Univ. (Eng. Technol. Ed.) 2024, 54, 1501–1511. [Google Scholar]











| Sample Number | A | B | C |
|---|---|---|---|
| Hardness (HA) | 61 | 69 | 62 |
| Tensile strength (MPa) | 17.84 | 18.33 | 21.42 |
| Tensile elongation (%) | 490.01 | 593.87 | 604.19 |
| Factor | Test Conditions |
|---|---|
| Vertical load (N) | 345, 365, 395, 415, 445, 465, 495, 515 |
| Slip speed (mm/min) | 50, 100, 150, 200, 250, 300, 350, 400, 450, 500 |
| Water film thickness (mm) | 0 mm (Dry pavement), 1, 2, 3, 4, 5, 6, 7, 8 |
| Level | Factor | ||
|---|---|---|---|
| x1 (N) | x2 (mm/min) | x3 (mm) | |
| 1 | 265 | 20 | 2 |
| 2 | 345 | 100 | 5 |
| 3 | 415 | 400 | 8 |
| Test Number | Test Parameter | Test Indicator | ||
|---|---|---|---|---|
| x1 | x2 | x3 | Friction Coefficient | |
| 1 | 1 | 1 | 1 | 0.380 |
| 2 | 1 | 2 | 3 | 0.409 |
| 3 | 1 | 3 | 2 | 0.389 |
| 4 | 2 | 1 | 3 | 0.491 |
| 5 | 2 | 2 | 2 | 0.486 |
| 6 | 2 | 3 | 1 | 0.441 |
| 7 | 3 | 1 | 2 | 0.548 |
| 8 | 3 | 2 | 1 | 0.489 |
| 9 | 3 | 3 | 3 | 0.517 |
| x1 | x2 | x3 | ||
|---|---|---|---|---|
| K1j | 1.178 | 1.419 | 1.31 | 1.383 |
| K2j | 1.418 | 1.384 | 1.417 | 1.398 |
| K3j | 1.554 | 1.347 | 1.423 | 1.369 |
| k1j | 0.393 | 0.473 | 0.437 | 0.461 |
| k2j | 0.473 | 0.461 | 0.472 | 0.466 |
| k3j | 0.518 | 0.449 | 0.474 | 0.456 |
| Rj | 0.125 | 0.0240 | 0.0377 | 0.00967 |
| Source of Variance | Sum of Squared Deviations | Degrees of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| x1 | 0.0242 | 2 | 0.0121 | 172.323 | 0.00577 | ** |
| x2 | 0.00269 | 2 | 0.00135 | 19.219 | 0.0495 | * |
| x3 | 0.000864 | 2 | 0.000432 | 6.163 | 0.139 | No |
| Inaccuracy | 0.00014 | 2 | 7.01 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, Y.; Su, B.; Lin, G.; Wang, Y.; Huang, G.; Wu, J. Experimental and Simulation Analysis on Wet Slip Performance Between Tread Rubber and Road Surface. J. Compos. Sci. 2025, 9, 394. https://doi.org/10.3390/jcs9080394
Wan Y, Su B, Lin G, Wang Y, Huang G, Wu J. Experimental and Simulation Analysis on Wet Slip Performance Between Tread Rubber and Road Surface. Journal of Composites Science. 2025; 9(8):394. https://doi.org/10.3390/jcs9080394
Chicago/Turabian StyleWan, Yang, Benlong Su, Guochang Lin, Youshan Wang, Gege Huang, and Jian Wu. 2025. "Experimental and Simulation Analysis on Wet Slip Performance Between Tread Rubber and Road Surface" Journal of Composites Science 9, no. 8: 394. https://doi.org/10.3390/jcs9080394
APA StyleWan, Y., Su, B., Lin, G., Wang, Y., Huang, G., & Wu, J. (2025). Experimental and Simulation Analysis on Wet Slip Performance Between Tread Rubber and Road Surface. Journal of Composites Science, 9(8), 394. https://doi.org/10.3390/jcs9080394






