Prediction of Mechanical and Fracture Properties of Lightweight Polyurethane Composites Using Machine Learning Methods
Abstract
1. Introduction
2. Experimental Details
2.1. Materials
2.2. Fabrication of Composites
2.3. Experimental Methods
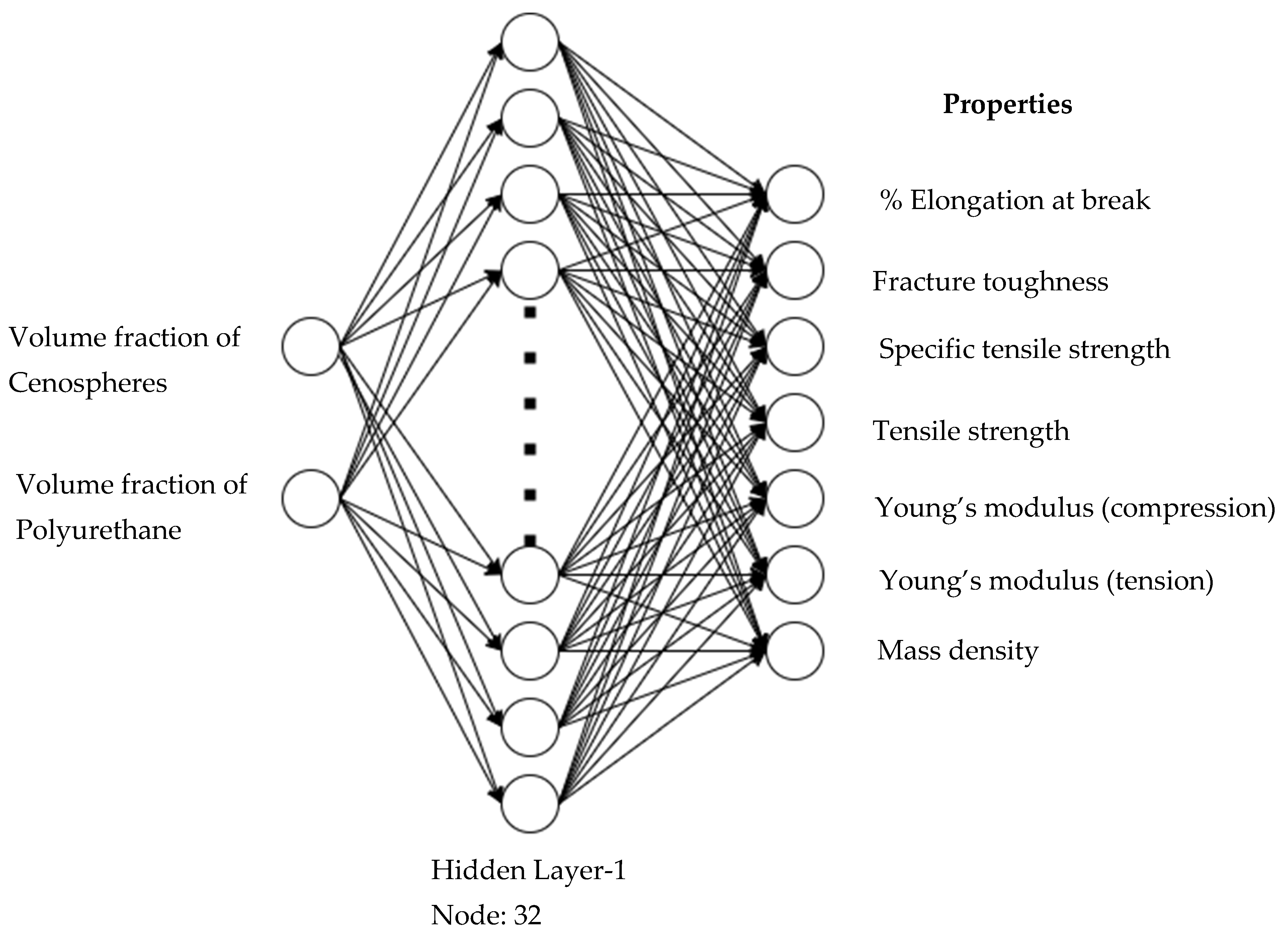
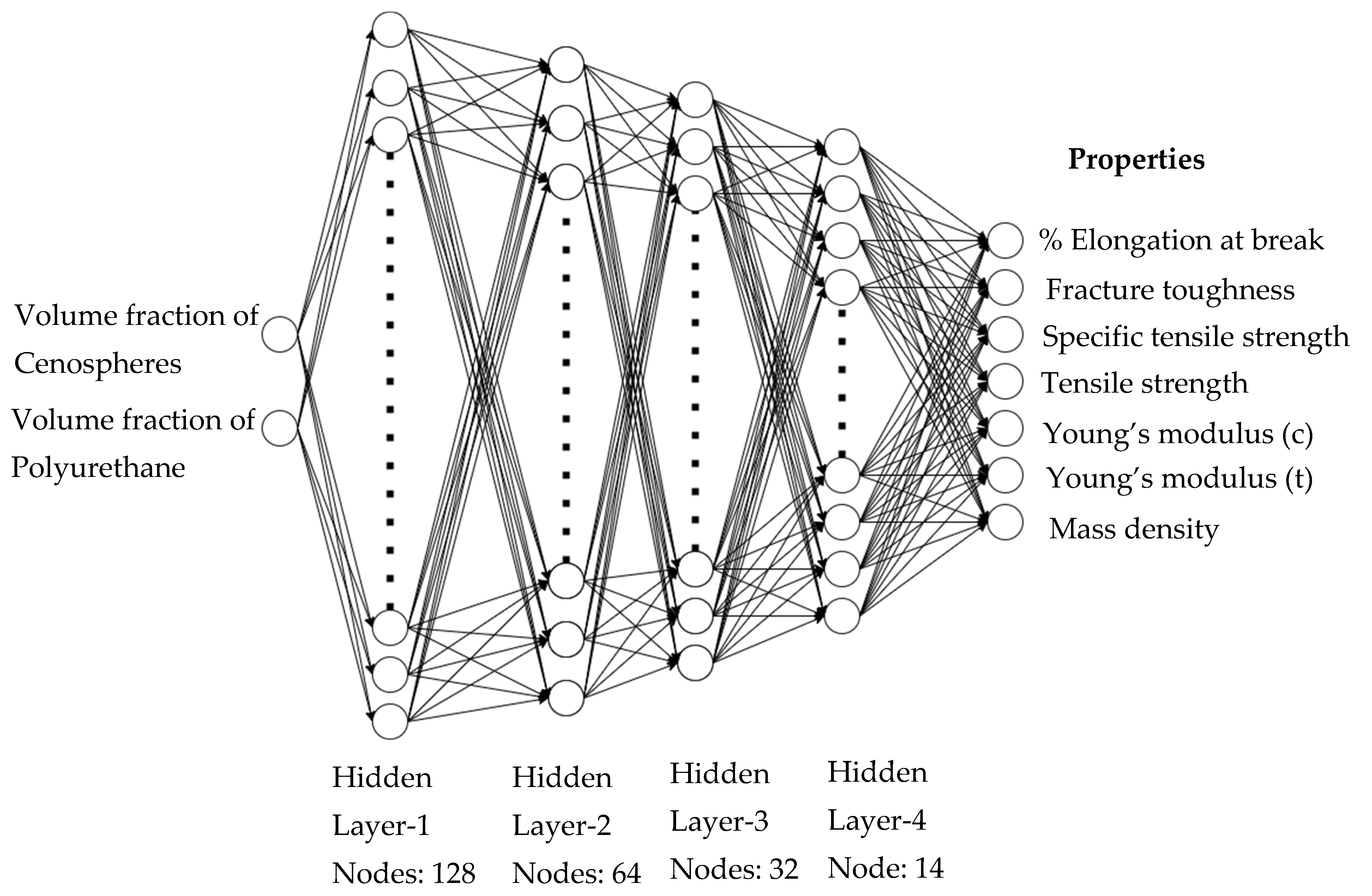
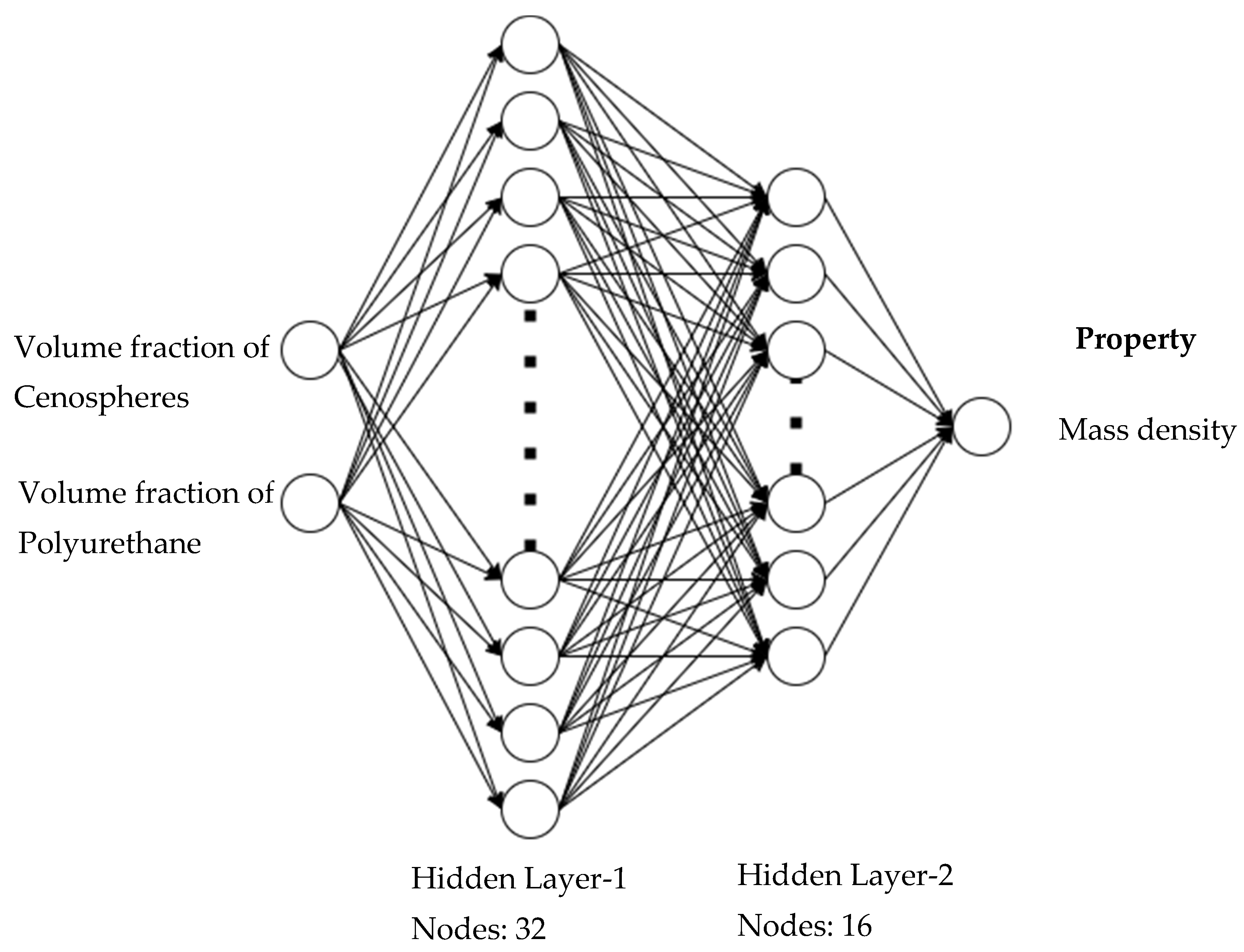
2.4. Artificial Neutral Network and Deep Learning Models
3. Results
3.1. Experimental Results
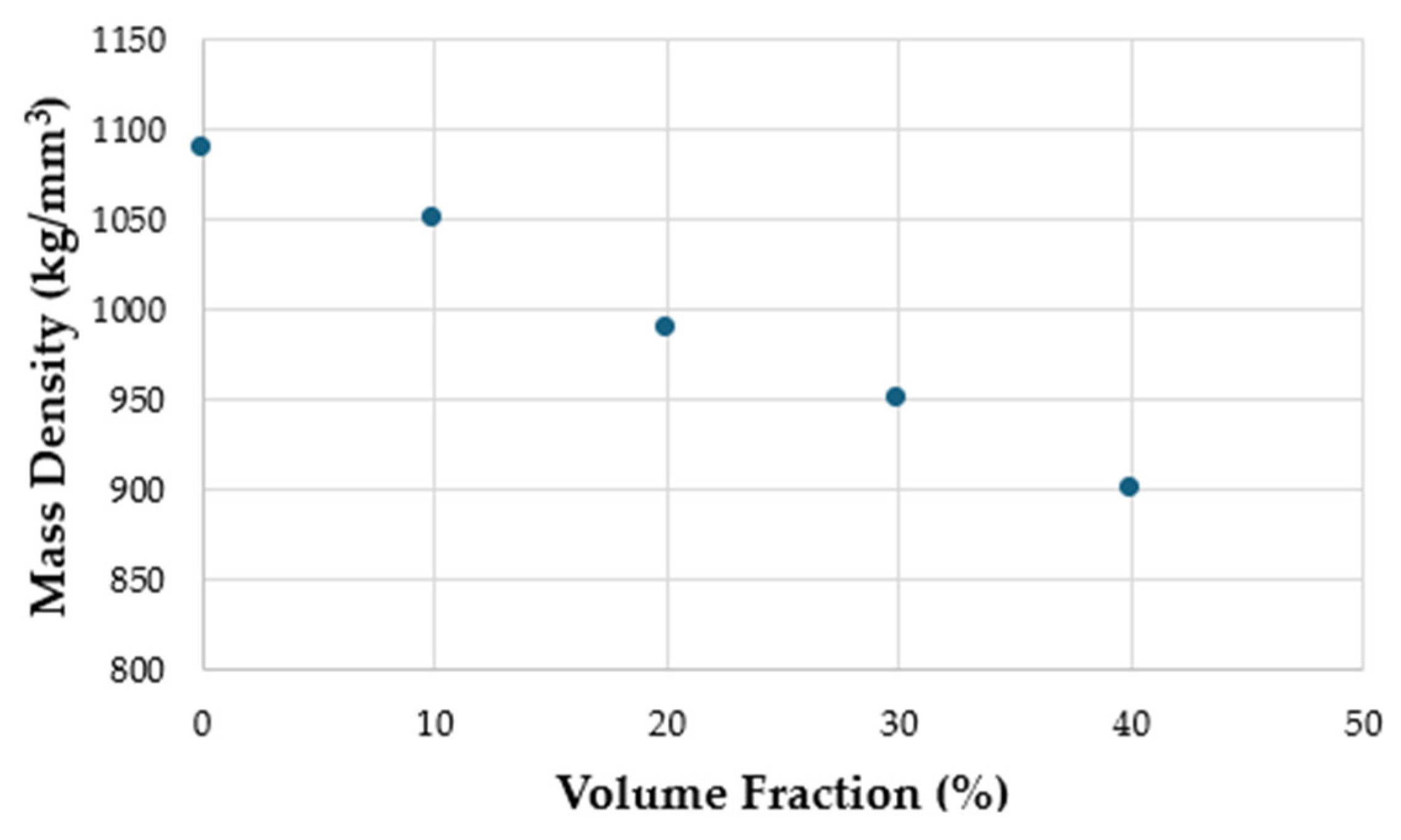
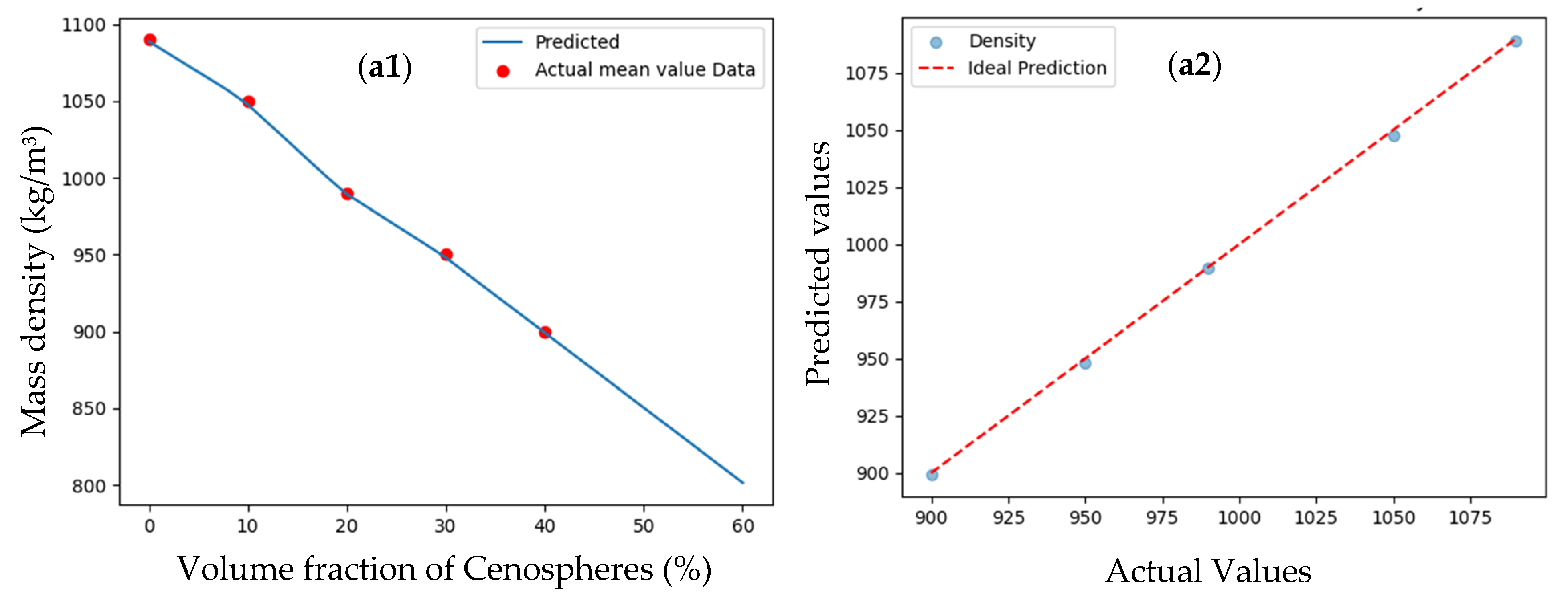
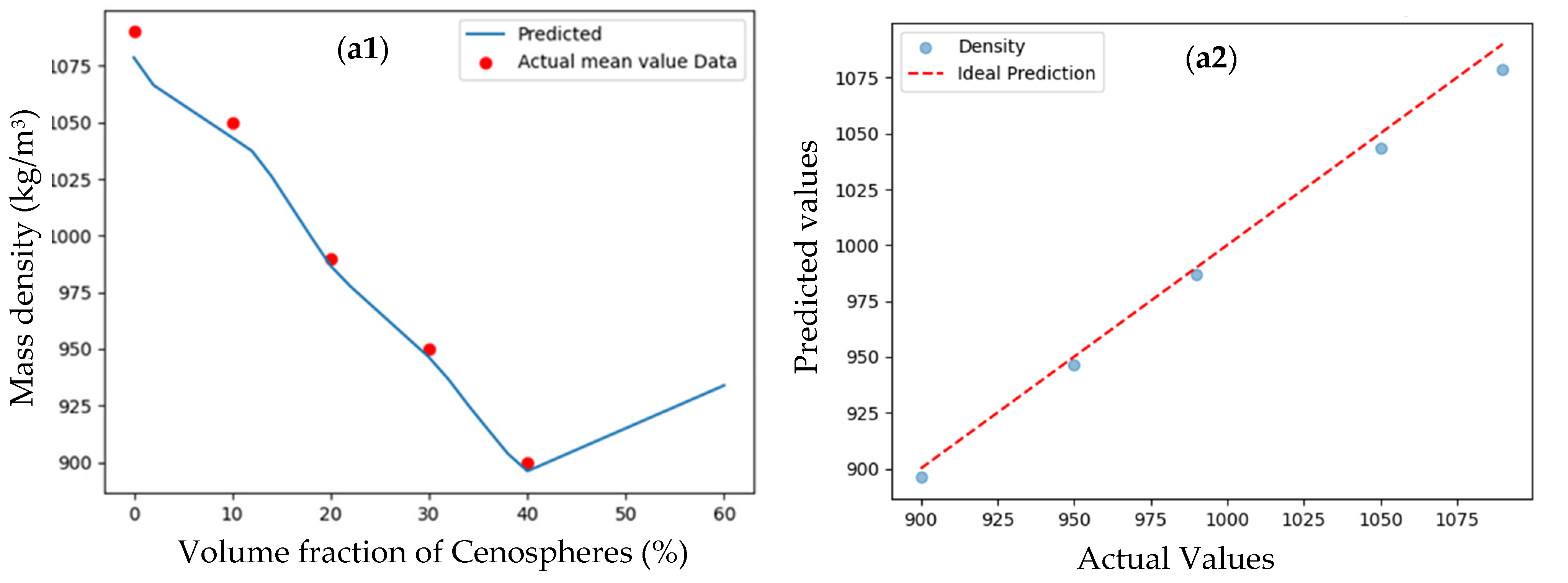
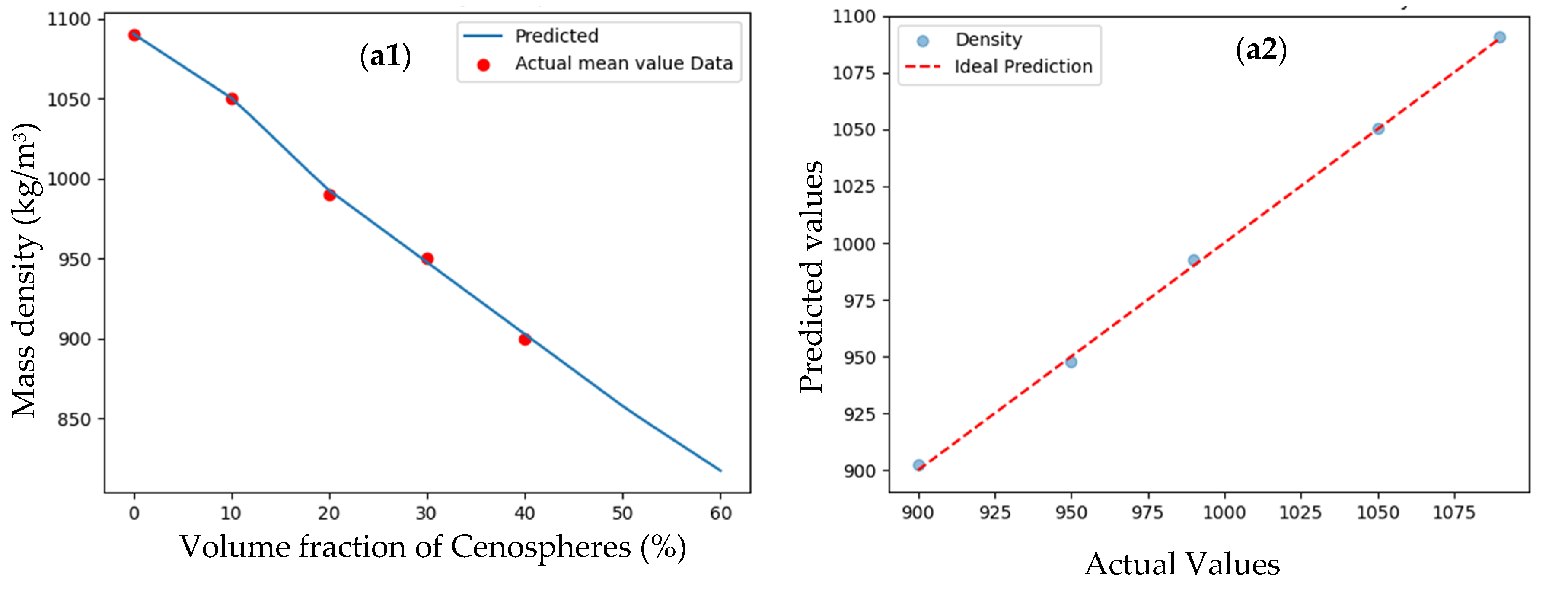
3.1.1. Mass Density
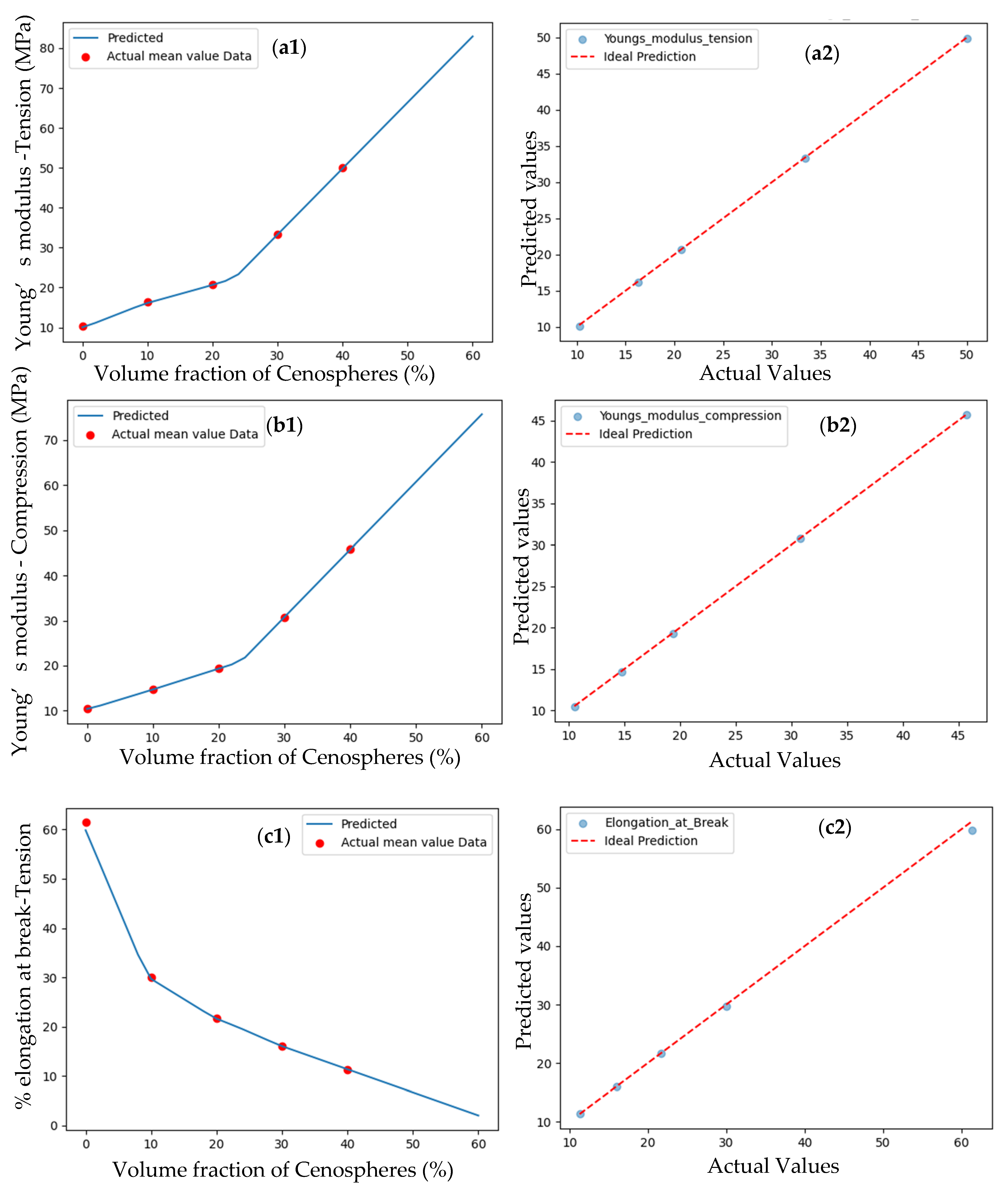
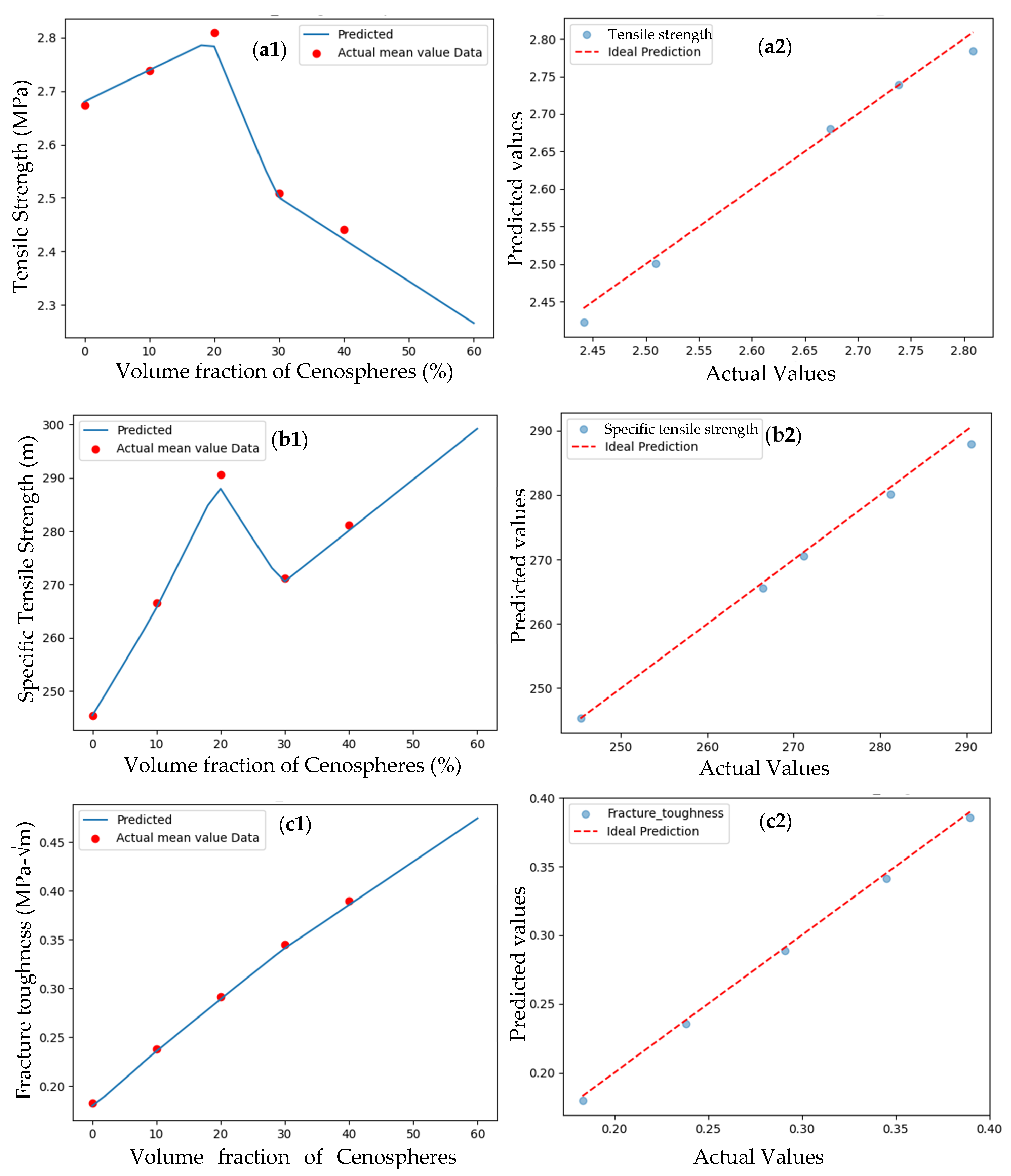
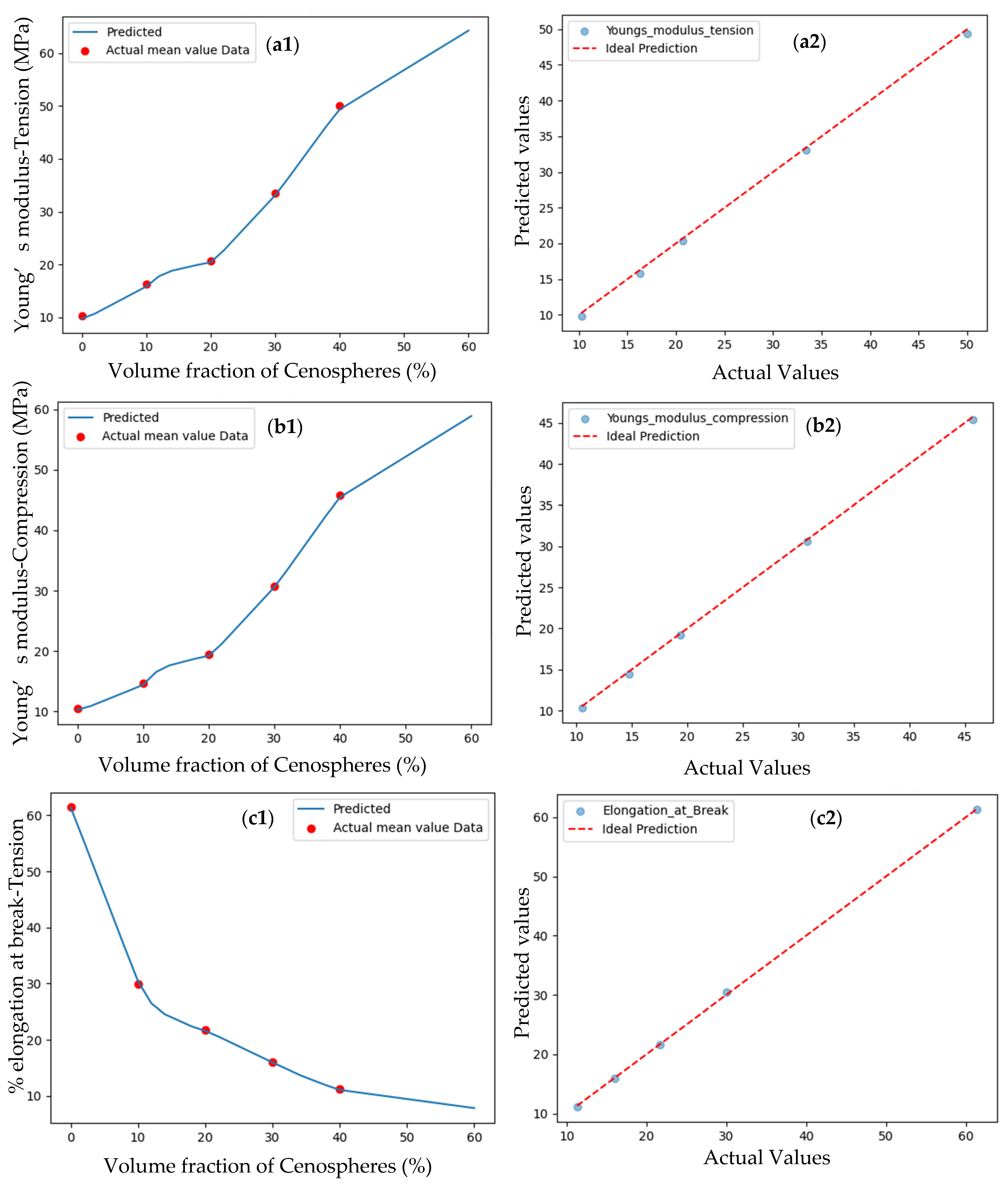
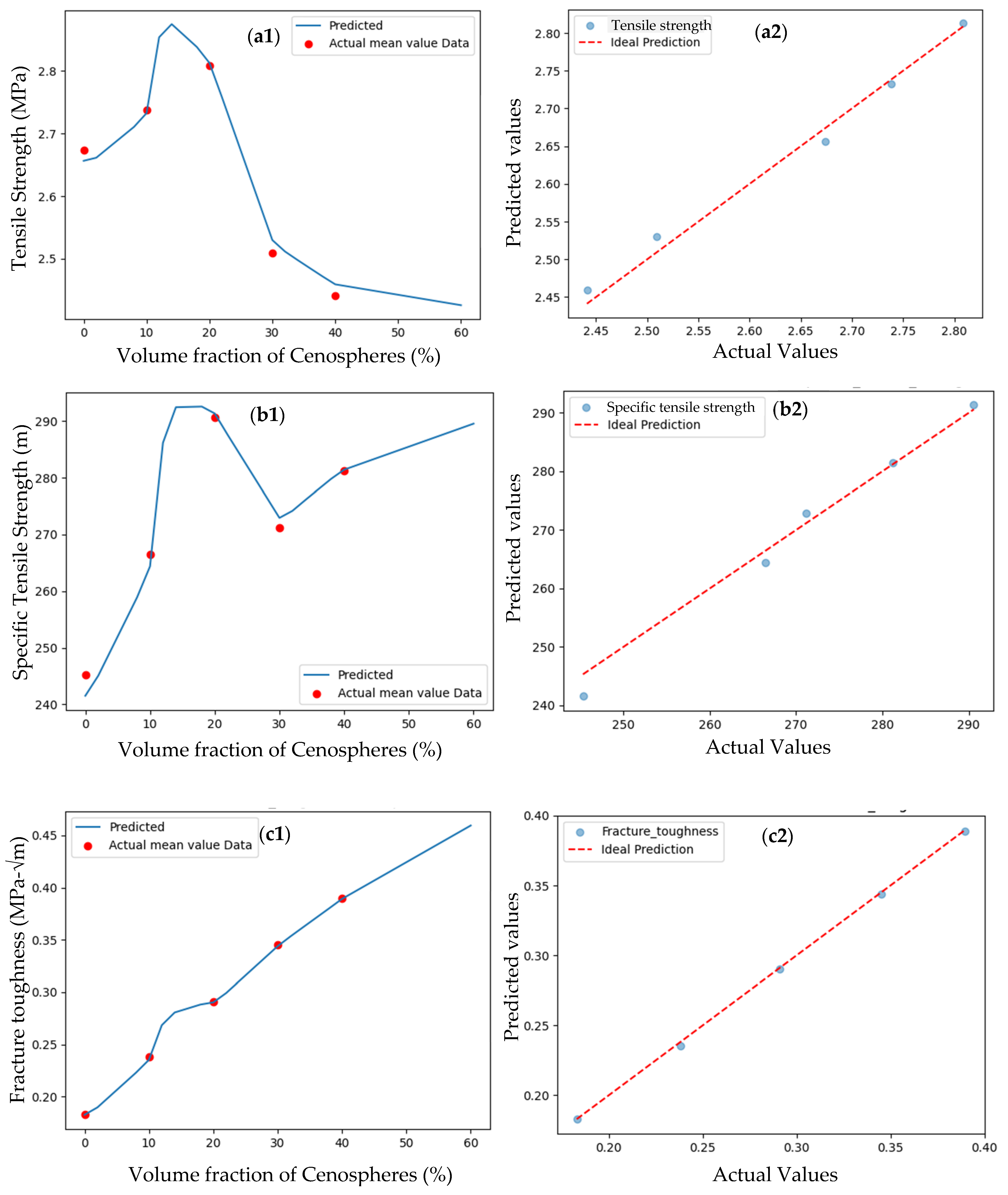
3.1.2. Mechanical and Fracture Properties
3.1.3. Results of Shallow ANN Model
3.1.4. Results of Non-Linear DNN Model
3.1.5. Mass Density Prediction of DNN Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Atiqah, A.; Mastura, M.T.; Ahmed Ali, B.A.; Jawaid, M.; Sapuan, M. A Review on Polyurethane and its Polymer Composites. Curr. Org. Synth. 2017, 14, 233–248. [Google Scholar] [CrossRef]
- Kausar, A. Polyurethane Composite Foams in High-Performance Applications: A Review. Polym. Plast. Technol. Eng. 2018, 57, 346–369. [Google Scholar] [CrossRef]
- Ahiwar, D.; Telang, A.; Purohit, R.; Namdev, A. A short review on polyurethane polymer composite. Mater. Today 2022, 62, 3804–3810. [Google Scholar]
- Sounik, D.; McCullough, D.; Clemons, J.; Liddle, J. Dynamic Impact Testing of Polyurethane Energy Absorbing (EA) Foams. In SAE Technical Paper 940879; SAE International: Warrendale, PA, USA, 1994. [Google Scholar]
- Patel, J.; Stojko, S. Characterising polyurethane foam as impact absorber in transport packages. Packag. Transp. Storage Secur. Radioact. Mater. 2013, 21, 25–30. [Google Scholar] [CrossRef]
- Bates, S.R.G.; Farrow, I.R.; Trask, R.S. 3D printed polyurethane honeycombs for repeated tailored energy absorption. Mater. Design 2016, 112, 172–183. [Google Scholar] [CrossRef]
- McClory, C.; McNally, T.; Brennan, G.P.; Erskine, J. Thermosetting polyurethane multiwalled carbon nanotube composites. J. Appl. Polym. Sci. 2007, 105, 1003–1011. [Google Scholar] [CrossRef]
- Wu, G.-M.; Liu, G.-F.; Chen, J.; Kong, Z.-W. Preparation and properties of thermoset composite films from two-component waterborne polyurethane with low loading level nanofibrillated cellulose. Prog. Org. Coat. 2017, 106, 170–176. [Google Scholar] [CrossRef]
- Yang, G.; Song, J.; Hou, X. Fabrication of highly hydrophobic two-component thermosetting polyurethane surfaces with silica nanoparticles. Appl. Surf. Sci. 2018, 439, 772–779. [Google Scholar] [CrossRef]
- Chalivendra, V.; Shukla, A.; Bose, A.; Parameswaran, V. Processing and mechanical characterization of lightweight polyurethane composites. J. Mater. Sci. 2003, 38, 1631–1643. [Google Scholar] [CrossRef]
- Faria, D.L.; Junior, L.M.; Resende, A.A.; Lopes, D.E.; Mended, L.M.; Martins, M.A.; Marconcini, J.M.; Junior, J.B.G. Physical and mechanical properties of polyurethane thermoset matrices reinforced with green coconut fibres. J. Compos. Mater. 2020, 54, 4841–4852. [Google Scholar] [CrossRef]
- Gao, L.; Tang, Q.; Chen, Y.; Wnag, Z.; Guo, W. Investigation of novel lightweight phenolic foam-based composites reinforced with flax fiber mats. Polym. Compos. 2016, 39, 1809–1817. [Google Scholar] [CrossRef]
- Latere Dwan’isa, J.-P.; Mohanty, A.K.; Misra, M.; Drzal, L.T.; Kazemizadeh, M. Novel soy oil based polyurethane composites: Fabrication and dynamic mechanical properties evaluation. J. Mater. Sci. 2004, 39, 1887–1890. [Google Scholar] [CrossRef]
- Yu, S.; Li, X.; Zhao, Y.; Zou, M. A Novel Lightweight Polyurethane Composite for Application on Ultra-High-Voltage Insulator Core Filler. Polymers 2020, 12, 2737. [Google Scholar] [CrossRef]
- Chen, C.; Gu, G.X. Machine learning for composite materials. MRS Commun. 2021, 9, 556–566. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Sharma, A.; Mukhopadhyay, T.; Rangappa, S.M.; Siengchin, S.; Kushvaha, V. Advances in computational intelligence of polymer composite materials: Machine learning assisted modeling, analysis and design. Arch. Comput. Methods Eng. 2022, 29, 3341–3385. [Google Scholar] [CrossRef]
- Wang, Y.; Soutis, C.; Ando, D.; Sutou, Y.; Narita, F. Application of deep neural network learning in composites design. Eur. J. Mater. 2022, 2, 117–170. [Google Scholar] [CrossRef]
- Shyam, S.; Kaul, S.; Kalsara, N.; Babu, T.N. Mechanical behaviour and microscopic analysis of epoxy and E-glass reinforced banyan fibre composites with the application of artificial neural network and deep neural network for the automatic prediction of orientation. J. Compos. Mater. 2021, 55, 213–234. [Google Scholar] [CrossRef]
- Zazoum, B.; Triki, E.; Bachri, A. Modeling of Mechanical Properties of Clay-Reinforced Polymer Nanocomposites Using Deep Neural Network. Materials 2020, 13, 4266. [Google Scholar] [CrossRef]
- Baek, K.; Hwang, T.; Lee, W.; Chung, H.; Cho, M. Deep learning aided evaluation for electromechanical properties of complexly structured polymer nanocomposites. Compos. Sci. Tech. 2022, 228, 109661. [Google Scholar] [CrossRef]
- Niaki, M.H.; Pashaian, M.; Ahangari, M.G. Experimental assessment of the efficiency of deep learning method in predicting the mechanical properties of polymer concretes and composites. J. Build. Eng. 2023, 76, 107107. [Google Scholar] [CrossRef]
- Varughese, J.Y.; Sreekanth, M.S. Influence of silane and polyethylene glycol functionalization of boron nitride nanosheets on mechanical and thermal properties of epoxy nanocomposites: Machine and deep learning forecasting. Polym. Compos. 2024, 46, 2190–2208. [Google Scholar] [CrossRef]
- Chai, X.; Sue, Y.; Lin, Z.; Qiu, C.; Liu, X.; Zhang, X.; Yang, J.; Ouyang, Q.; Zhang, D. Mechanical property prediction and configuration effect exploration of particulate reinforced metal matrix composites via an interpretable deep learning approach. Mater. Sci. Eng. A 2025, 925, 147880. [Google Scholar] [CrossRef]
- Ngu, L.-N.; Wu, H.; Zhang, D.-K. Characterization of Ash Cenospheres in Fly Ash from Australian Power Stations. Energy Fuels 2007, 21, 3437–3445. [Google Scholar] [CrossRef]
- Ranjbar, N.; Kuenzel, C. Cenospheres: A review. Fuel 2017, 207, 1–12. [Google Scholar] [CrossRef]
- Danish, A.; Mosaberpanah, M.A. Formation mechanism and applications of cenospheres: A review. J. Mater. Sci. 2020, 55, 4539–4557. [Google Scholar] [CrossRef]
- Available online: https://bariteworld.com/industrial-minerals-products/cenospheres/ (accessed on 10 May 2025).
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 4th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Fu, S.-Y.; Feng, X.-Q.; Lauke, B.; Mai, Y.-W. Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–polymer composites. Compos. B Eng. 2008, 19, 933–961. [Google Scholar] [CrossRef]
- Guth, E. Theory of Filler Reinforcement. J. Appl. Phys. 1945, 16, 20–25. [Google Scholar] [CrossRef]

| Parameter | Values/Tools Investigated | Selected Value/Tool |
|---|---|---|
| Learning Rates | 0.0001, 0.001, 0.01 | 0.001 |
| Neurons | 8, 16, 32, 64, 128, 256, 512 | 32 |
| Activations | sigmoid, ReLU | ReLU |
| Batch Sizes | 8, 16, 32, 64 | 16 |
| Dropout Rates | 0, 0.2, 0.4 | 0 |
| Initializers | glorot_uniform, he_normal | glorot_uniform |
| Regularizers | None, l1(0.01), l2(0.01) | l1(0.01) |
| Optimizer | SGD, RMSprop, ADAM | ADAM |
| Loss | mae, root_mean_squared_error, mse, R2_score | mse |
| Epochs | 50, 100, 200 | 100 |
| Parameter | Values/Tools Investigated | Selected Value/Tool |
|---|---|---|
| Learning Rates | 0.0001, 0.001, 0.01 | 0.001 |
| Neuron Layer no 1 | 8, 14, 16, 32, 64, 128, 256, 512 | 128 |
| Neuron Layer no 2 | 8, 14, 16, 32, 64, 128, 256, 512 | 64 |
| Neuron Layer no 3 | 8, 14, 16, 32, 64, 128, 256, 512 | 32 |
| Neuron Layer no 4 | 8, 14, 16, 32, 64, 128, 256, 512 | 14 |
| Activations | sigmoid, ReLU | ReLU |
| Batch Sizes | 8, 16, 32, 64 | 16 |
| Dropout Rates | 0, 0.2, 0.4 | 0 |
| Initializers | glorot_uniform, he_normal | glorot_uniform |
| Regularizers | None, l1(0.01), l2(0.01) | l1(0.01) |
| Optimizer | SGD, RMSprop, ADAM | ADAM |
| Loss | mae, root_mean_squared_error, mse, R2_score | mse |
| Epochs | 50, 100, 200 | 100 |
| Parameter | Values/Tools Investigated | Selected Value/Tool |
|---|---|---|
| Learning Rates | 0.0001, 0.001, 0.01 | 0.001 |
| Neuron Layer no 1 | 8, 14, 16, 32, 64, 128, 256, 512 | 32 |
| Neuron Layer no 2 | 8, 14, 16, 32, 64, 128, 256, 512 | 16 |
| Activations | sigmoid, ReLU | ReLU |
| Batch Sizes | 8, 16, 32, 64 | 16 |
| Dropout Rates | 0, 0.2, 0.4 | 0 |
| Initializers | glorot_uniform, he_normal | glorot_uniform |
| Regularizers | None, l1(0.01), l2(0.01) | l1(0.01) |
| Optimizer | SGD, RMSprop, ADAM | ADAM |
| Loss | mae, root_mean_squared_error, mse, r2_score | mse |
| Epochs | 50, 100, 200 | 100 |
| Volume Fraction of Particles (%) | Tensile Young’s Modulus (MPa) | Compression Young’s Modulus (MPa) | Tensile Strength (MPa) | Specific Tensile Strength (m) | % Elongation at Break Under Tension | Fracture Toughness (MPa·√m) |
|---|---|---|---|---|---|---|
| 0 | 10.24 ± 0.94 | 10.5 ± 0.64 | 2.67 ± 0.18 | 245.29 ± 16.44 | 61.42 ± 5.05 | 0.18 ± 0.008 |
| 10 | 16.32 ± 0.88 | 14.72 ± 1.18 | 2.74 ± 0.11 | 266. 47 ± 11.42 | 29.97 ± 3.36 | 0.23 ± 0.013 |
| 20 | 20.67 ± 1.27 | 19.42 ± 0.75 | 2.81 ± 0.24 | 290.58 ± 25.17 | 21.70 ± 3.23 | 0.29 ± 0.021 |
| 30 | 33.43 ± 2.42 | 30.77 ± 0.96 | 2.51 ± 0.15 | 271. 18 ± 16.45 | 16.02 ± 2.55 | 0.34 ± 0.027 |
| 40 | 50.05 ± 2.53 | 45.77 ± 1.12 | 2.44 ± 0.07 | 281. 17 ± 8.72 | 11.31 ± 1.68 | 0.38 ± 0.033 |
| Shallow ANN | Non-Linear DNN | DNN | |
|---|---|---|---|
| Parameter | Value | ||
| Mean Absolute Error (MAE) | 1.27 | 1.34 | 1.75 |
| Root Mean Square Error (RMSE) | 1.95 | 1.96 | 2.03 |
| Mean Square Error | 3.81 | 3.84 | 4.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narkhede, N.N.; Chalivendra, V. Prediction of Mechanical and Fracture Properties of Lightweight Polyurethane Composites Using Machine Learning Methods. J. Compos. Sci. 2025, 9, 271. https://doi.org/10.3390/jcs9060271
Narkhede NN, Chalivendra V. Prediction of Mechanical and Fracture Properties of Lightweight Polyurethane Composites Using Machine Learning Methods. Journal of Composites Science. 2025; 9(6):271. https://doi.org/10.3390/jcs9060271
Chicago/Turabian StyleNarkhede, Nikhilesh Nishikant, and Vijaya Chalivendra. 2025. "Prediction of Mechanical and Fracture Properties of Lightweight Polyurethane Composites Using Machine Learning Methods" Journal of Composites Science 9, no. 6: 271. https://doi.org/10.3390/jcs9060271
APA StyleNarkhede, N. N., & Chalivendra, V. (2025). Prediction of Mechanical and Fracture Properties of Lightweight Polyurethane Composites Using Machine Learning Methods. Journal of Composites Science, 9(6), 271. https://doi.org/10.3390/jcs9060271







