Deep Artificial Neural Network Modeling of the Ablation Performance of Ceramic Matrix Composites in the Hydrogen Torch Test

Abstract

In recent years, there has been increasing interest in new materials such as ceramic matrix composites (CMCs) for power generation and aerospace propulsion applications through hydrogen combustion. This study employed a deep artificial neural network (DANN) model to predict the ablation performance of CMCs in the hydrogen torch test (HTT). The study was conducted in three phases to increase the accuracy of the model’s predictions. Initially, to predict the thermal behavior of ceramic composites, two linear machine learning models were used known as Lasso and Ridge regression. In the second step, four decision tree-based ensemble machine learning models, namely random forest, gradient boosting regression, extreme gradient boosting regression, and extra tree regression, were used to improve the prediction accuracy metrics, including root mean square error (RMSE), mean absolute error (MAE), correlation coefficient (R² score), and mean absolute percentage error (MAPE), relative to the previously introduced linear models. Finally, to forecast the thermal stability of CMCs with time, an optimized DANN model with two hidden layers having rectified linear unit activation function was developed. The data collection procedure involved preparing CMCs with continuous Yttria-Stabilized Zirconia (YSZ) fibers and silicon carbide (SiC) matrix using a polymer infiltration and pyrolysis (PIP) technique. The samples were exposed to a hydrogen flame at a high heat flux of 183 W/cm² for a duration of 10 min. A good agreement between the DANN model’s predictions and experimental data with an R² score of 0.9671, RMSE of 16.45, an MAE of 14.07, and an MAPE of 3.92% confirmed the acceptability of the developed neural network model in this study.

1. Introduction

Ablation resistance of materials is important because it allows them to preserve structural integrity and protect underlying components when exposed to severe temperatures and oxidative conditions [1]. This feature is essential in high-temperature applications such as aerospace propulsion systems, thermal protection systems (TPSs) for space vehicles, missile nozzles, and hypersonic flight structures. Under these applications, materials are subjected to high heat fluxes, rapid temperature fluctuations, and chemically adverse surroundings. Without good ablation resistance, materials could decay, corrode, or collapse catastrophically, creating risks and endangering mission success [2].

Ceramic matrix composites (CMCs) are the most suitable material for extreme conditions due to their remarkable thermal stability [3]. High melting temperatures, strong resistance to oxidation, corrosion, ablation, little creep, and advantageous thermal cycling behavior are some of the characteristics of CMCs [4]. As a result, CMCs have a significant amount of ability to satisfy these requirements to qualify them to be used in hydrogen combustion engines. CMCs and other high-temperature ceramics are being explored for applications requiring resilience at elevated temperatures. They are traditionally made by the melt infiltration technique. Nevertheless, the large porosity and brittle structures of CMCs made with this technique make them unable to endure strong mechanical and thermal demands. Alternatively, continuous fibers are used to reinforce the polymer-derived ceramic matrix, resulting in ceramic matrix composites with enhanced fracture toughness.

The main distinction of hydrogen flame from that of acetylene is the flame temperature. Hydrogen flame has an adiabatic flame temperature of 2207 °C [5]. On the other hand, the oxy-acetylene torch has an adiabatic flame temperature of 3500 °C [6]. While the oxy-acetylene torch test reaches higher flame temperatures, the hydrogen torch test (HTT) is more representative of combustion conditions in hydrogen-fueled systems, providing relevant data for applications in hydrogen-based power generation or propulsion. Furthermore, hydrogen offers more variety and precision in industrial applications and can be more affordable, particularly when produced from renewable energy sources. Thus, our study intended to find the applicability of CMC in a hydrogen gas turbine engine by exposing the material against HTT and observing its effect through machine learning modeling.

In recent years, materials informatics has rapidly expanded into a variety of material domains, including ceramic matrix composite materials [7]. Machine learning has the potential to reduce labor and material costs when compared to traditional experimental procedures [8,9,10]. Additionally, it can also speed up numerical methods by training on experimental results [11,12,13]. Therefore, it is possible to predict mechanical and thermal characteristics of composite materials by using machine learning (ML) techniques [14]. These algorithms are very good at finding patterns and connections within datasets, which helps them to respond correctly to novel and unexpected inputs or to generate precise predictions [15,16]. Machine learning’s capacity to learn from data, generalize to new circumstances, and provide dependable results without explicit instructions is one of its core strengths [17,18]. Zhang et al. [19] emphasizes the rising importance of ML and data-driven techniques in materials science and engineering, notably for expediting material discovery, design, and optimization. It addresses breakthroughs in inverse design, phase stability modeling, and thermoelectric material prediction, demonstrating how generative models and computational tools supplement traditional approaches for exploring novel materials and optimizing their characteristics for a variety of applications.

Yuan et al. [20] used regression machine models based on Ridge and Lasso to forecast the cross-ply composite laminates’ equivalent axial modulus when they showed matrix cracking. The impact-buckling reactions of double-strap adhesive-bonded joints (ABJs) with carbon fiber reinforced polymer (CFRP) straps, sandwich composite adherends, and room-cured structural epoxy are examined by Mottaghian et al. [21]. The axial impact behaviors of the joints at energy levels of 5J, 10J, and 20J were observed by experimental tests. To mimic failure mechanisms, a finite element model was created and verified against experimental data utilizing continuum and zero-thickness cohesive elements. Furthermore, 13 design characteristics impacting the dynamic reactions of the ABJs were taken into consideration for developing machine learning models deep neural networks. Yuan et al. [22] developed a data-driven method that makes use of a multi-layer perceptron (MLP) algorithm and pixelated stacking sequence to forecast stiffness loss caused by matrix cracking in laminated composites. To determine the structure-property relationship of polymer nanocomposites, Baek et al. [18] designed two different types of deep neural networks (DNNs). They showed that DNNs perform better than traditional models when assessing the electromechanical properties of polypropylene matrix composites with dispersed spherical SiC nanoparticles. Remarkably, a straightforward graph convolution network outperformed a sophisticated neural network in terms of efficiency and usability, demonstrating its appropriateness for evaluating nanoparticle aggregation and dispersion while maintaining accuracy. By reducing the need for experiments, Shi et al. [23] attempted to improve material design by using a machine learning technique for developing an efficient prediction model for shielding effectiveness in carbon-based conductive particles/polymer nanocomposites. The final prediction model, which is based on a Weighted Average Ensemble of five base models, performs better than the individual models (Kernel ridge regression, support vector machines, random forest regression, extra tree regression, and gradient boosting trees) and offers important insights into key factors influencing EMI, helping to direct the development of new materials and lower expenses. Despite the advantages of being lightweight and strong, CFRPs have a complicated design parameter space, which makes typical optimization techniques expensive and labor-intensive. A machine learning-assisted multiscale modeling approach was suggested as a solution to this problem. It effectively predicts the mechanical properties of CFRPs by fusing inexpensive ML models with molecular dynamics simulations, demonstrating good agreement with experimental data, and providing a workable method for CFRP design. Nguyen et al. [24] designed an artificial neural network (ANN) model with 10,419 data points from cone calorimetry measurements on 14 sets of laminates based on phenol with different flame retardants to predict the heat release characteristics of composite materials. Without having to take into consideration mechanistic interactions, the Bayesian regularized ANN with Gaussian prior (BRANNGP) outperformed Multiple Linear Regression (MLR) in terms of predictive accuracy. It was able to accurately estimate the heat release rate-time curve, peak heat release value, and total heat release. Six machine learning regression techniques, including decision trees, random forests, support vector machines, gradient boosting, extreme gradient boosting, and adaptive boosting, were developed by Deb et al. [25] to predict the ablation performance of ceramic matrix composites in the oxy-acetylene torch test. Gradient boosting and extreme gradient boosting models outperformed the others, indicating that machine learning is a useful tool for forecasting the ablation behavior of ceramic matrix composites.

Ablation performance refers to the ceramic matrix composite’s heat shielding or thermal insulation performance when exposed to a hydrogen torch. Our study was to determine heat shielding or thermal insulation effectiveness of CMCs indirectly by measuring back-surface temperatures during exposure. Most of the previous literature utilized oxy-acetylene torch tests for analyzing the ablation performance of CMCs. To predict the structural and electro-mechanical characteristics of composite materials, machine learning prediction models were widely used in the literature [26,27]. Predicting the thermal characteristics of CMCs at very high temperatures, however, is a field of research that needs further study. Evaluating the durability of high-temperature ceramics in extreme environmental conditions such as HTT requires the prediction of their thermal stability in those conditions. Therefore, this study investigated applications of YSZ fiber mats to reinforce SiC and expose them to a hydrogen flame torch test. The purpose was to collect experimental data that would offer valuable insights into the thermal performance and structural integrity of ceramic matrix composites when exposed to high heat flux through data driven modeling. Although the back-surface temperature distribution of CMCs was the primary input variable in our study, the thermal response of YSZ/SiC ceramic matrix composites under HTT was characterized by highly nonlinear deterioration processes. Rapid changes in thermal gradients produce complicated temperature fluctuations that linear regression or ensemble tree-based models could not effectively describe [28]. Therefore, an optimized DANN model was developed as a first attempt in the literature to evaluate and predict the ablation performance of CMCs in HTTs. Three different stages were considered in the improvement of machine learning models’ prediction accuracy. To forecast the thermal behavior of ceramic composites in hydrogen exposed torch test, two linear machine learning models were first used Lasso and Ridge regression. The objective of the second stage was to improve the prediction accuracy above the linear regression models by utilizing four decision tree-based ensemble machine learning models including random forest (RF), gradient boosting regression (GBR), extreme gradient boosting regression (XGBR), and extra tree regression (ETR). Finally, to forecast the ablation performance of the CMCs, an improved DANN model with two hidden layers was developed. Then the model’s accuracy was confirmed by the significant agreement between the DANN model’s thermal data predictions and the experimental data. This work presented a DANN model-based innovative framework for the ablation performance prediction model of CMCs under HTT.

2. Materials and Methods

2.1. Material Selection

Yttria-Stabilized Zirconia (YSZ) twill-weave fiber mats were obtained from Zircar Zirconia, Inc. (Florida, NY, USA), along with a YSZ rigidizing agent made of sub-micron YSZ particles in an aqueous acetate solution. Rigidizing agent was required to improve the structural robustness of the porous preform due to the intrinsic low tensile strength of the raw ceramic fiber. Eight layers of YSZ twill-weave fiber mats were immersed in a YSZ rigidizer solution and then distributed evenly using a serrated roller. The layers were manually stacked in a ${\left[0\right]}_8$ sequence using a hand layup technique. The laminate was dried in an autoclave at 149 °C for 2 h with a vacuum of −20 inHg. This method produced a porous preform structure made entirely of YSZ, but with substantially higher mechanical integrity than the individual fiber mats. Furthermore, Starfire Systems, Inc. (Schenectady, NY, USA) provided the SMP-10 preceramic polymer, which was used as the ceramic precursor. The SMP-10, a commercially available polycarbosilazane precursor, served as the principal matrix-forming component in the composite. The fiber mats were impregnated with the liquid SMP-10 resin using vacuum-assisted impregnation, which ensured complete penetration of the porous fiber architecture. Following impregnation, the composites went through a pyrolysis stage in an inert atmosphere using Nitrogen (N) at 950 °C, where they were kept for 2 h after heating at a rate of 2.6 °C/min. After the 2-h hold, they were cooled to room temperature at a rate of 2.6 °C per minute. At the time, the SMP-10 was pyrolyzed to a silicon carbide (SiC) ceramic matrix. The polymer infiltration and pyrolysis (PIP) procedure was repeated to improve matrix density and decrease porosity, resulting in a strong CMC structure.

Table 1. Material properties of the YSZ rigidizing agent.

YSZ Rigidizer (ZR-RIG)
Melting Point (°C)	2590
Specific Gravity	1.87
Solids Content (Weight %)	50
Cured Nominal Chemical Composition (Weight %)
ZrO2	90
Y2O3	10
Trace Inorganics	<0.3

and

Table 2. Material properties of the YSZ twill-woven fiber.

YSZ Woven Fiber (ZYW-15)
Nominal Thickness (mm)	0.381
Bulk Density (g/cc)	1.02
Porosity (%)	87
Melting Point (°C)	2590
Tensile Strength (g/cm width)	154
Continuous Maximum Use Limit (°C)	2200

list all the characteristics of the YSZ materials and rigidizing agents respectively as disclosed by the manufacturer. Because of the high concentration of zirconium oxide, which provides excellent resilience in high-temperature, oxidizing conditions, YSZ components are recognized for their remarkably high melting points and service temperatures [29]. As a result, these materials are commonly used as thermal barrier coatings.

2.2. Experimental Setup

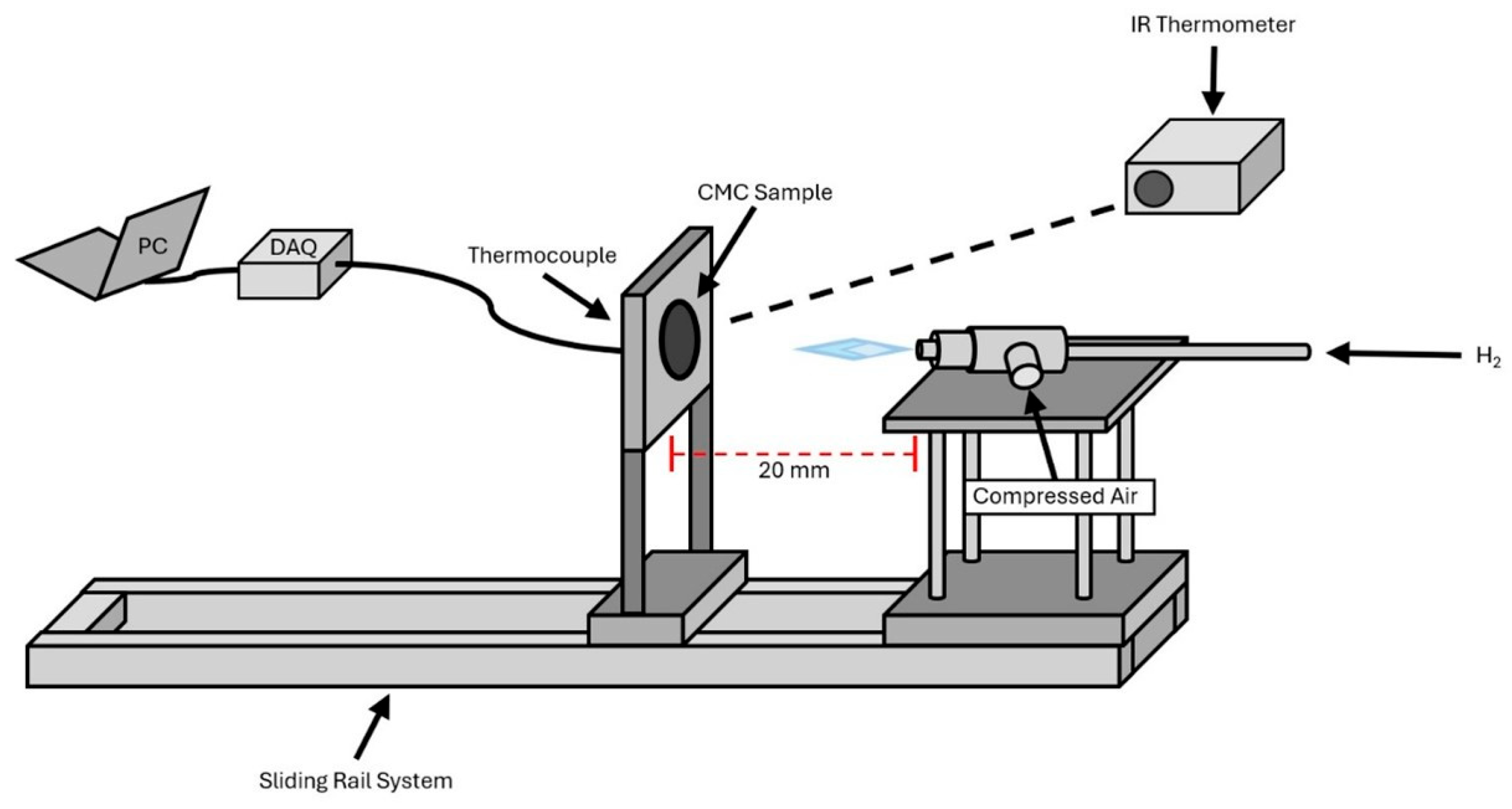
A bench-top torch testing rig was designed and built to expose the CMC samples to a hydrogen flame of constant heat flux as shown in Figure 1. A circular foil heat flux gauge (TG 1000-1, Vatell Corporation, Christiansburg, VA, USA) was used to map the heat flux output of the torch setup at various distances from the torch tip. The CMC samples were loaded onto the sample holder and held in place by a stainless-steel faceplate with a circular opening slightly smaller than the diameter of the samples. A spring-loaded K-type thermocouple (OMEGA Engineering, Norwalk, CT, USA) was positioned on the center of the back side of the sample to measure back-face temperature, while an infrared radiation thermometer (IR-HAQNE, CHINO Corporation, Torrance, CA, USA) was used to record the temperature of the flame-exposed front face of the sample. The sample was loaded into the holder and pushed the maximum distance from the torch tip on the sliding track. Additionally, a thick stainless-steel plate was placed in between the torch and sample to protect the sample from any pre-heating while the torch was ignited, and the flame allowed it to stabilize. After the flame was stabilized and the data acquisition systems got ready, the stainless-steel plate was removed, and the sample holder was pushed along the sliding track before stopping 20 mm from the tip of the torch, where the flame imparted a heat flux of 183 W/cm². Then the samples were exposed to the hydrogen flame torch for 10 continuous minutes before the test ended.

Testing was conducted following the ASTM E285 standard [30]. In the HTT, the CMC sample was moved towards the flame at a regulated pace of 5 cm/s before stopping 20 mm from the tip of the torch and the constant heat flux (183 W/m²) was produced to the CMC surface. To precisely quantify the thermal energy given to the CMC material and assure the consistency throughout the torch experiments, a heat flux gauge was used to profile the output of the hydrogen torch at set distances from the nozzle, ranging from 10 mm to 120 mm in 10 mm increments. Before each test session, the heat flux was revalidated at the 20 mm testing distance. This distance, with a heat flux of 183 W/cm², was chosen to provide sufficient thermal energy to the sample while retaining clear IR thermometer visibility and preventing flame disturbance.

The highest temperature attained throughout the test was 1412 °C, which was reliably recorded at the CMC surface under steady-state circumstances. After three experimental runs, it was found that the optimal torch test condition was to position the sample 20 mm from the hydrogen torch tip, resulting in a measured heat flux of 183 W/cm². This arrangement was chosen because it produced strong thermal loading while keeping a consistent flame and providing a clear line of sight for the infrared thermometer. The torch used 45 psi of hydrogen and 23 psi of air to produce a flame temperature of roughly 2000 °C in fuel-rich circumstances.

This optimal environment produced consistent and dependable data for the development of our machine-learning models, which is the major goal of this study. Therefore, the machine learning models were developed on this single set of optimized experimental findings to provide the data consistency required for successful machine learning model training. The samples before and after the HTT are shown in Figure 2.

2.3. Data Preparation

Machine learning models greatly benefit from preprocessing experimental data, which includes cleaning and organizing it. This is because better data quality leads to more efficient extraction of insightful information. Missing values, noise, inconsistencies, and redundancy are just a few of the many problems that can trouble raw experimental data and negatively impact subsequent procedures. To improve the predicted accuracy of the machine learning models in this study, we removed three missing HTT thermal data. The “train-test split methodology” was employed in this research to evaluate the performance of the developed machine learning models [21]. The dataset was split into two subsets: a training dataset, which contains 70% of the total data (417 sets), was used to train the machine learning models, and a testing dataset, which contains the remaining 30% (180 sets), was used to assess the accuracy of the models. This method was used to estimate the model’s performance using new data that was not used for training. Cross-validation was used to mitigate potential overfitting problem [22]. With this method, the data were divided into a predetermined number of folds. The model was then trained on the remaining folds as a validation set, and its accuracy and generalization performance were assessed [25]. We utilized a five-fold cross-validation approach to evaluate the overall efficacy of the machine learning models for this research. The training set is split up into equal-sized groups, at random. Five trials were used in a five-fold cross-validation in this investigation. The model was trained on four of the five folds for each trial, while the fifth fold was used for evaluation [23]. The highest scores of these five assessments were used in developing the final model. In addition, the model hyperparameters were chosen and determined using a grid search technique. All eight machine learning models received the same training methodology.

2.4. Deep Artificial Neural Networks

Artificial neural networks (ANNs) are computational models that simulate how neurons interact in the brain, drawing inspiration from biological neural networks. These networks are made up of linked components called neurons that function similarly to their biological counterparts in terms of communication with the outside world or other neurons. An input layer, one or more hidden layers, and an output layer make up the usual architecture of an ANN [31]. Neurons in hidden layers process the incoming data; these neurons are completely linked to networks since they are connected to all other neurons in the preceding and following layers. The model’s predictions are generated by the output layer. An ANN is called a deep neural network (DNN) if it has more than two hidden layers [32,33]. One well-known ANN type is the multi-layer perceptron (MLP) neural network. MLP can handle non-linear regression issues because each neuron’s activation function in the hidden layers performs non-linear mapping of input data. Increasing the number of hidden layers and neurons within each layer will increase the model’ s complexity [34,35].

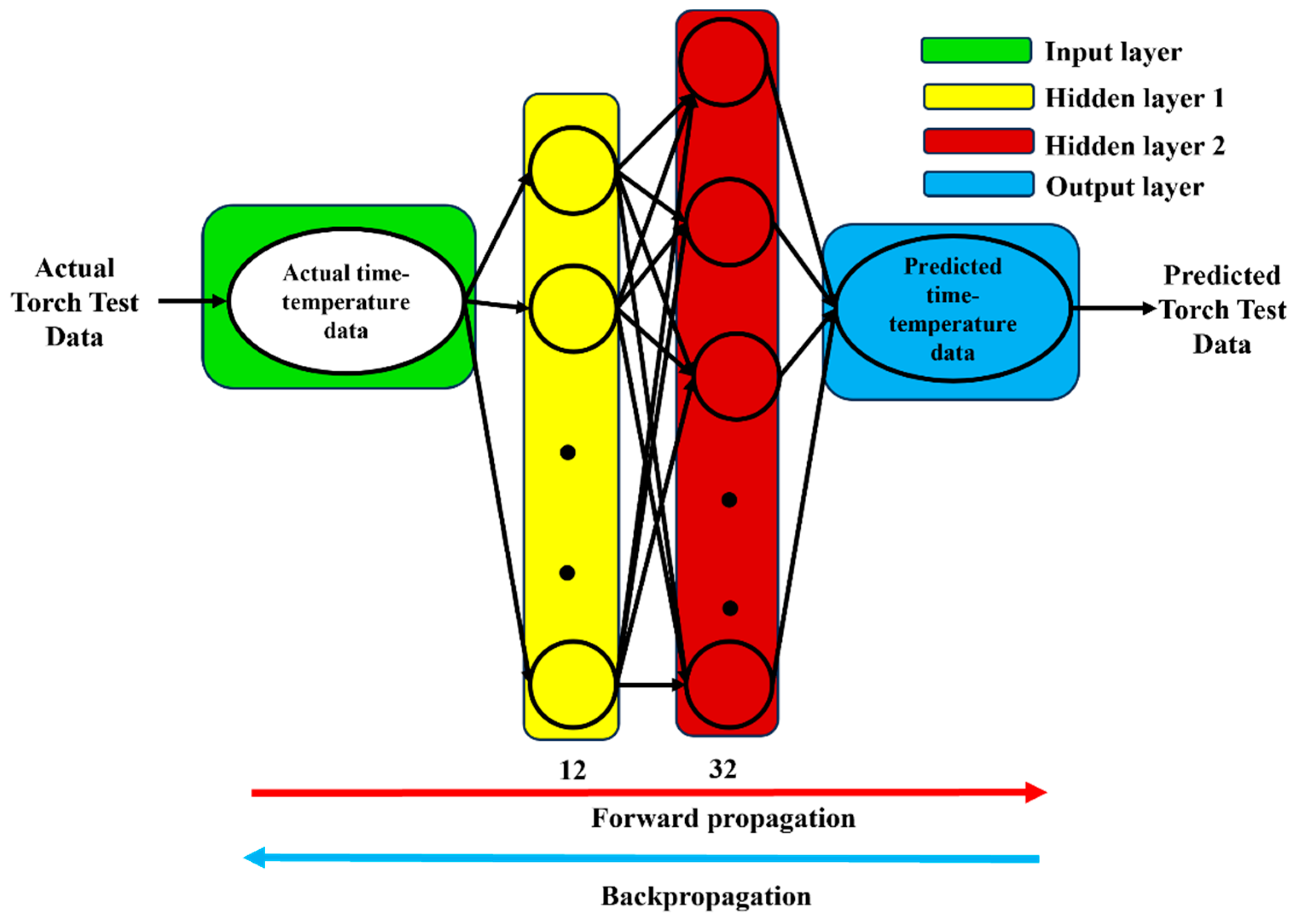
The schematic layout of the DANN model developed for this study is shown in Figure 3. As this is the first research to use the MLP neural network model to forecast the ablation performance of ceramic matrix composites in a HTT, several factors are investigated for the model. A whole cycle of MLP training utilizing the whole training dataset is called an epoch, and the maximum number of epochs is assigned to 100 for this study. To determine the best configuration for the HTT dataset, methodical computation was carried out. It was discovered that the optimum arrangement to build the neural network for our HTT datasets consisted of one to ten hidden layers. Using this method, the investigation began with a simple design with one hidden layer and raised the number of layers gradually up to ten depending on performance assessment and accuracy gains in every simulation stage. Similarly, each layer’s neuronal count was iterated from 1 to 100 based on how each neuron affected the training and validation procedures. The “Keras” and “TensorFlow” modules in Python 3.0 using the T4 GPU hardware accelerator at Google Colab were used to implement the optimized neural network model. Keras is a Python-based high-level neural network Application Programming Interface that offers a simple and flexible interface for developing deep learning models. It serves as a wrapper for backend engines like TensorFlow, enabling quick model creation and experimentation [36]. Google created TensorFlow, a comprehensive end-to-end framework for machine learning and deep learning workloads. It efficiently computes large-scale neural networks using dataflow graphs and supports CPU and GPU execution. Keras was utilized in this study to build and maintain the deep artificial neural network (DANN) architecture, while TensorFlow served as the backend engine for executing and improving the model’s training and inference procedures [37].

To precisely capture the thermal data from the output neuron, a linear activation function was implemented in the output layer of the optimized DANN model. The optimized DANN model had two hidden layers. Each neuron in the hidden layer used the ReLU (rectified linear unit) activation function. The number of hidden layers ranged from one to ten, with each layer comprising between one to one hundred neurons. ReLU, sigmoid, and tanh activation functions were examined, and ReLU had the greatest prediction ability. Learning rates ranging from [0.001, 0.01, 0.1, 0.2, 0.3, 1.0] were investigated. The experimental data used input neurons to pass the HTT data information to the neurons in the hidden layers during forward propagation, accumulating weights, and bias values. Afterwards, the output layer neuron forecasted the temperature information. After calculating the mean square error between the predicted and experimental data, the backpropagation method was utilized to update the weights in the hidden layer neurons. By following the forward and back propagation method, the optimized DANN model was able to determine the minimum error between the prediction and the experimental data of the HTT.

2.5. Ensemble Machine Learning Modeling

An ensemble of decision trees known as random forest (RF) regression was trained using random subset of the bootstrapped data, and following bootstrap aggregations, their predictions were accumulated [38]. Random forest is an ensemble learning approach that creates numerous decision trees during training and then combines their predictions to improve accuracy and prevent overfitting. Each tree is trained on a random portion of the data and predictions are calculated by averaging the results of all trees. In this work, row sampling with replacement was used to gather a subset (bootstrap sampled) of the whole HTT dataset. Subsequently, a portion of the HTT data was processed through separate base learner trees. To predict the thermal data in the HTT, grid search (a technique for hyperparameter optimization that systematically evaluates different parameter combinations) and the bootstrap aggregation method from scikit learn were used. Seventy percent of the training data and the five-fold cross validation technique (dividing data into five parts to iteratively train on four parts and validate on one) were used to optimize the model. Lastly, 30% of the data from the torch test was used to compute the model’s performance. For random forest regression, we examined the number of estimators in the range [100, 300, 500, 1000], the learning rate from [0.001, 0.01, 0.1, 0.2, 0.3, 1.0], and tree depths of [5, 10, 20] using bootstrap sampling.

In an ensemble learning technique, gradient boosting regression (GBR) is used to develop a series of weak learners (decision trees), each of which seeks to capture the residuals (the differences between predicted and actual values) of the models that came before it [39]. Initially, the ablation performance data of the ceramic matrix composites was predicted using a simple model. The basic model’s mistakes or residuals were then put into the decision tree (DT) model. Eventually, the anticipated errors decreased using serially connected DT models to produce the final predicted thermal performance data. The optimal hyperparameters for GBR modeling were found using the grid search technique. The learning rate (controls how much the model adjusts with each new tree) and the trees’ maximum depth (the maximum number of levels a decision tree can have) were two hyperparameters that were adjusted to enhance the HTT ablation performance prediction model. For gradient boosting regression (GBR), the number of estimators was set to [100, 300, 500, 1000], the learning rates from [0.001, 0.01, 0.1, 0.2, 0.3, 1.0], and the maximum depths were [5, 10, 20].

To decrease overfitting and enhance efficiency, the extreme gradient boosting regression (XGBR) technique uses a more regularized (which helps prevent overfitting by penalizing model complexity, making it more efficient and robust) gradient tree-boosting algorithm than gradient boosting regression. Similarity weight (which measures how similar the data points in a node are, helping to decide if the node should be split further) and gains (represent the improvement in prediction accuracy by splitting a node, indicating how much better the model becomes by adding that split) were determined at the leaf node to help in the building of the XGBR model and to forecast the residuals from the first tree. After using the decision trees sequence to estimate the data from the HTT, the residuals or errors were subsequently decreased. The ablation performance prediction model was adjusted using the grid search approach from scikit learn by adding a learning rate of 0.001, 0.01, 0.1, 0.2, 0.3, and 1 to overcome the overfitting issue. In extreme gradient boosting regression (XGBR), we used the learning rate from [0.001, 0.01, 0.1, 0.2, 0.3, 1.0], the number of trees from [100, 300, 500, 1000], and the depths from [5, 10, 20].

Based on trees such as random forest regression, the extra tree regression (ETR) method generates a series of top-down unpruned trees. Unlike a bootstrap aggregating method, extra trees build the trees utilizing all the training data. During the splitting procedure, n features (a subset of all features) in total are randomly selected as split candidates at each node. The cutting locations for each selected feature are also selected randomly [40]. In the current study, the grid search strategy was utilized from scikit learn to enhance the CMC ablation performance prediction model through the usage of decision trees at a predetermined depth. For extra tree regression (ETR), we examined estimator counts of [100, 300, 500, 1000], maximum depths of [5, 10, 20], and learning rates of [0.001, 0.01, 0.1, 0.2, 0.3, 1.0].

2.6. Linear Regression Modeling

Ridge regression is a kind of biased estimating regression approach that improves the conventional least squares method by handling collinear data also known as multicollinear. It works especially well and consistently when fitting data that are not well-conditioned. Ridge regression introduces bias to stabilize the estimates and increase dependability, in contrast to the least squares technique, which maintains an unbiased estimation. This results in regression coefficients that are more resilient in the face of multicollinearity, but at the expense of some accuracy and information. The regularization term’s coefficient α in Ridge regression is the parameter that lessens the effect of ill-conditioned data. In this study, the model’s sensitivity to outliers was determined by this α parameter; the greater the α value, the less sensitive the model is to outliers. Through feature selection procedures, particularly Lasso (Least Absolute Shrinkage and Selection Operator) and cross-validation (CV), the optimum value of α was determined.

2.7. Error Function Calculations

A range of metrics, including a comparison of the system’s output with real data was used to assess the performance of an intelligent expert system [8]. For evaluating the effectiveness of the system, mean square error (MSE) and root mean square error (RMSE) were measured [41,42]. The MSE was used as a loss function in the machine learning models that were developed for this investigation. By calculating the average squared difference between the expected and experimental outcomes, it determined how well the developed machine model matches the experimental torch test data [43]. It can be expressed by using the following equation:

$$MSE={\displaystyle \frac{1}{k}}{\sum }_{m=1}^k{\left(x_{em}-x_{pm}\right)}^2$$

(1)

where k is the number of data points, $x_{em}$ is the value of experimental data, and $x_{pm}$ is the value of model predicted data. The RMSE is the root of the mean square error [44]. The following equation can express it:

$$RMSE=\sqrt{{\displaystyle \frac{1}{k}} {\sum }_{m=1}^k{(x_{em}-x_{pm})}^2}$$

(2)

where k is the number of data points, $x_{em}$ is the value of experimental data, and $x_{pm}$ is the value of model predicted data. A statistical metric called the coefficient of determination, or $R^2$, was used to assess how well a machine learning model fits the experimental data. It measured the degree of agreement between the actual data points and the predictions made by the machine learning model. It can be expressed by the following equation:

$$R^2=1-{\displaystyle \frac{{\sum }_{m=1}^K{(x_{em}-x_{pm})}^2}{{\sum }_{m=1}^K{(x_{em}-\overline{x})}^2}}$$

(3)

where $\overline{x}$ is the average actual temperature data of HTT. To assess how well the machine learning models are performing, the test datasets mean absolute error (MAE) and mean absolute percentage error (MAPE) are examined. They are expressed by the following equations, respectively:

$$MAE={\displaystyle \frac{1}{k}} {\sum }_{m=1}^k\left|x_{em}-x_{pm}\right|$$

(4)

$$MAPE={\displaystyle \frac{1}{k}} {\sum }_{m=1}^k{\displaystyle \frac{\left|x_{em}-x_{pm}\right|}{\left|x_{em}\right|}}\times 100$$

(5)

3. Results and Discussion

3.1. Hydrogen Torch Test Results

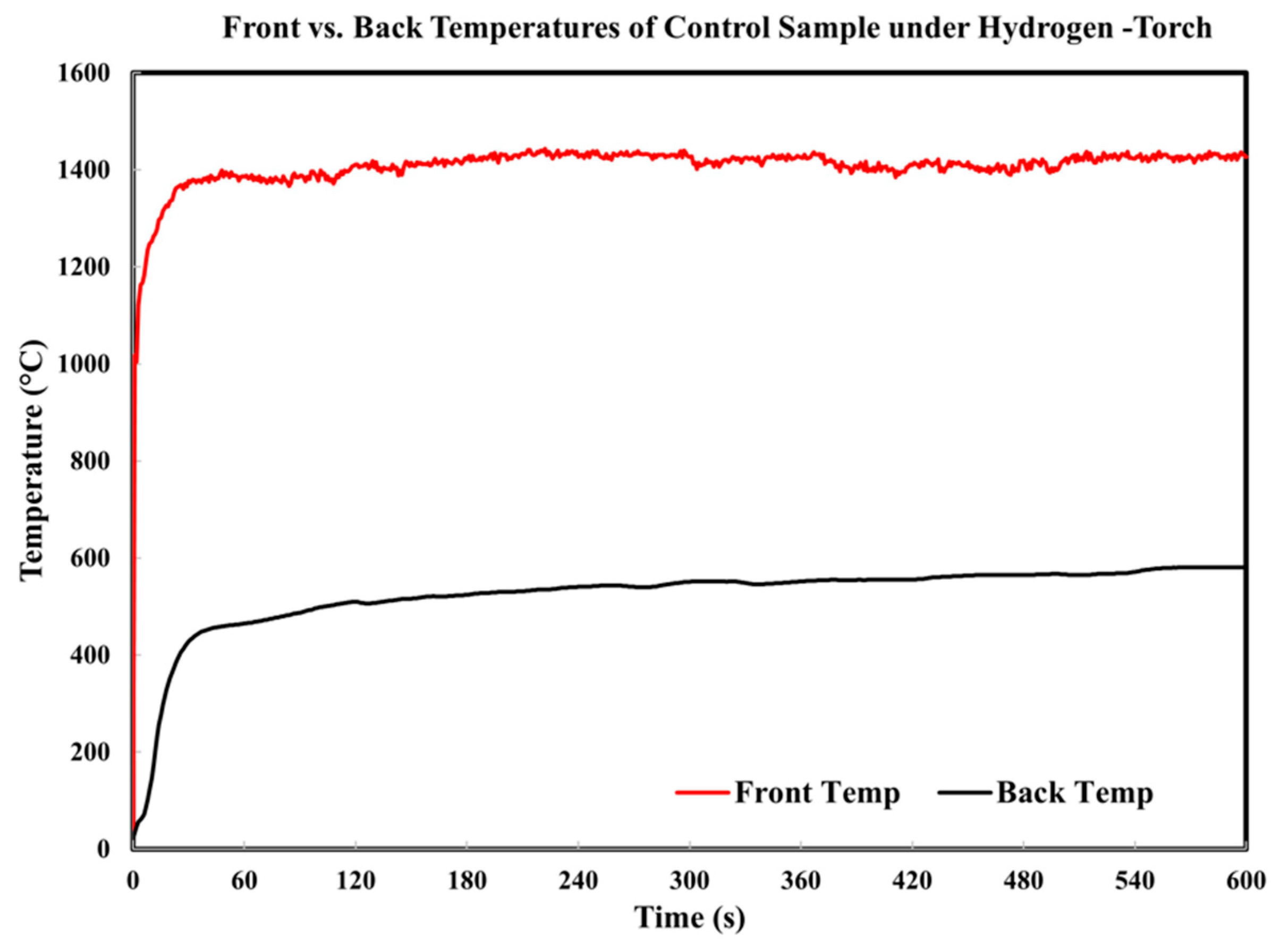
The CMC samples performed consistently and favorably when subjected to the HTT. In all cases, the front temperature of the samples stabilized within 45 s to a temperature of around 1400 °C, while the back temperature was kept considerably lower, staying below 600 °C throughout the duration of torch exposure as provided in Figure 4. Furthermore, the CMC samples retained structural integrity even after 10 min of continuous exposure, experiencing no delamination, burn-through, or loss of thickness (Figure 5). Rather than losing mass over the duration of testing, all samples exhibited a mass gain after the torch test. This implies that the SiC matrix of the CMCs reacted with Oxygen to form protective deposits of glassy silica, SiO₂, on the flame-exposed surface of the composite, further improving the thermal performance of the material.

Electron microscopy was used to characterize the CMC samples before and after hydrogen flame exposure. The high-temperature flame appeared to melt the SiC matrix and cause it to flow and fill gaps previously observed on the surface of the sample, while the YSZ fibers remained physically unchanged. Darker colored deposits were observed on the flame-exposed surfaces of the samples, which were hypothesized to be Silica (SiO₂) plaques formed because of the passive oxidation of the SiC matrix, which is known to occur at certain temperatures and partial pressures of oxygen [45]. EDS spectral mapping provides insight on the elemental distribution on the surface of the flame-damaged sample. After the HTT, the oxygen concentration increased dramatically from 29.6 to 41.5 wt%, whereas the silicon content declined somewhat from 27.1 to 21.8 wt%. High-temperature oxidation leads to the creation of silicon dioxide (SiO₂), as evidenced by the significant rise in oxygen content and retention of silicon.

In ceramic matrix composites, both front and back temperatures are significant. While the front face temperature reveals surface stability and initial resistance to heat, the back face temperature provides insights into internal heat penetration and potential degradation. The performance of both faces under heat exposure is essential to evaluate composite integrity in high-temperature applications. Thus, the focus of this study is to develop machine learning prediction models to predict the back temperature of ceramic matrix composites in HTTs.

3.2. Deep Artificial Neural Network Modeling Results

To efficiently train machine learning models and evaluate their accuracy, this study used a split of 70% training data and 30% testing data. The choice to employ this split was based on the results found from the cross-validation techniques, even though other percentages (80/20, 60/40) for the training and testing data were investigated as well. Furthermore, a five-fold cross-validation technique was used to confirm the stability of the selected split. This technique involves splitting the data into five groups and repeatedly utilizing each subset as training and testing data. This method provided reliability in the chosen training and testing data percentage for validating the model’s performance across various data subsets. We began with a simple neural network design and worked gradually up to more complex configurations. To determine their effect on model performance, this research included varying the number of hidden layers and the number of neurons in each layer.

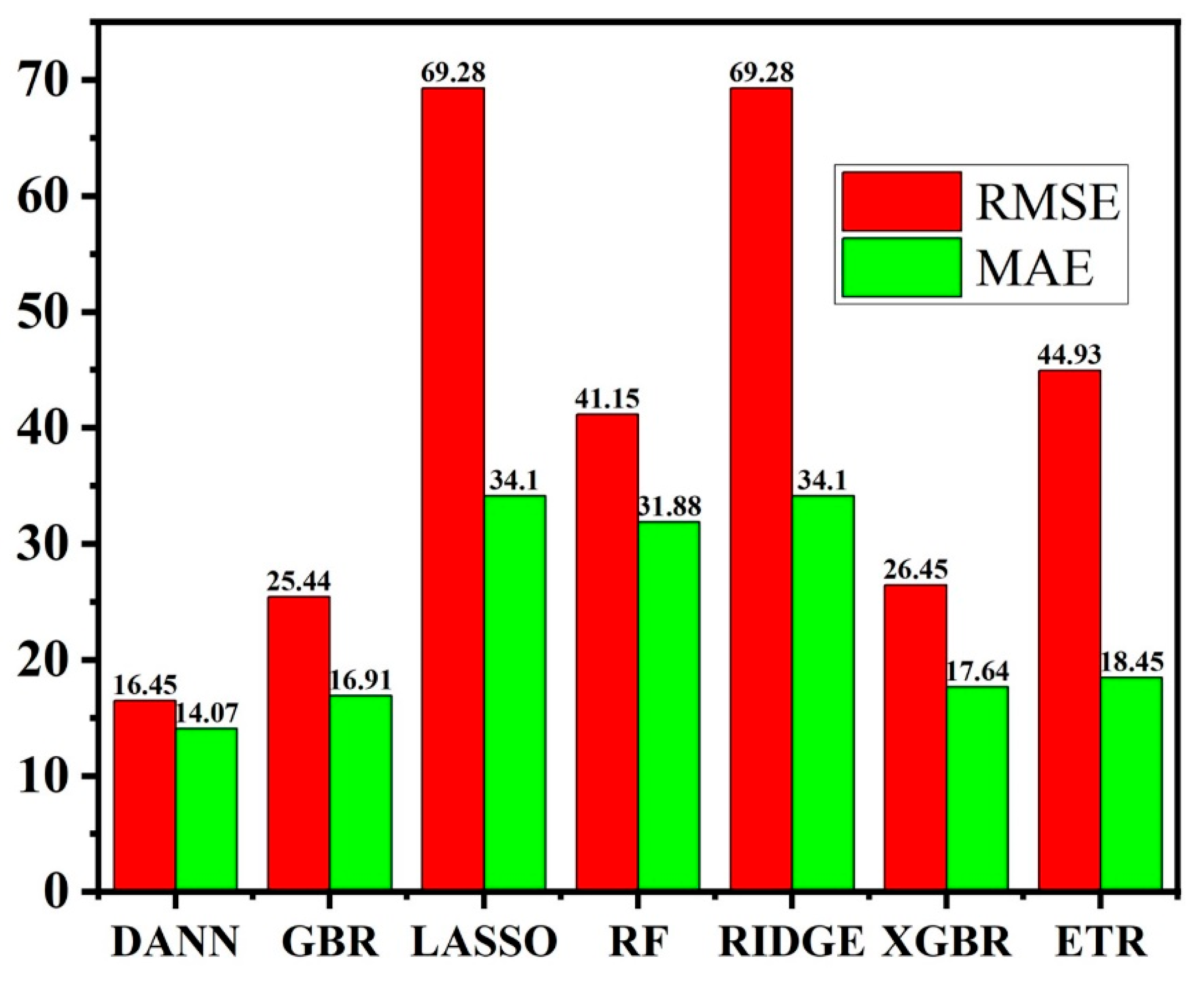
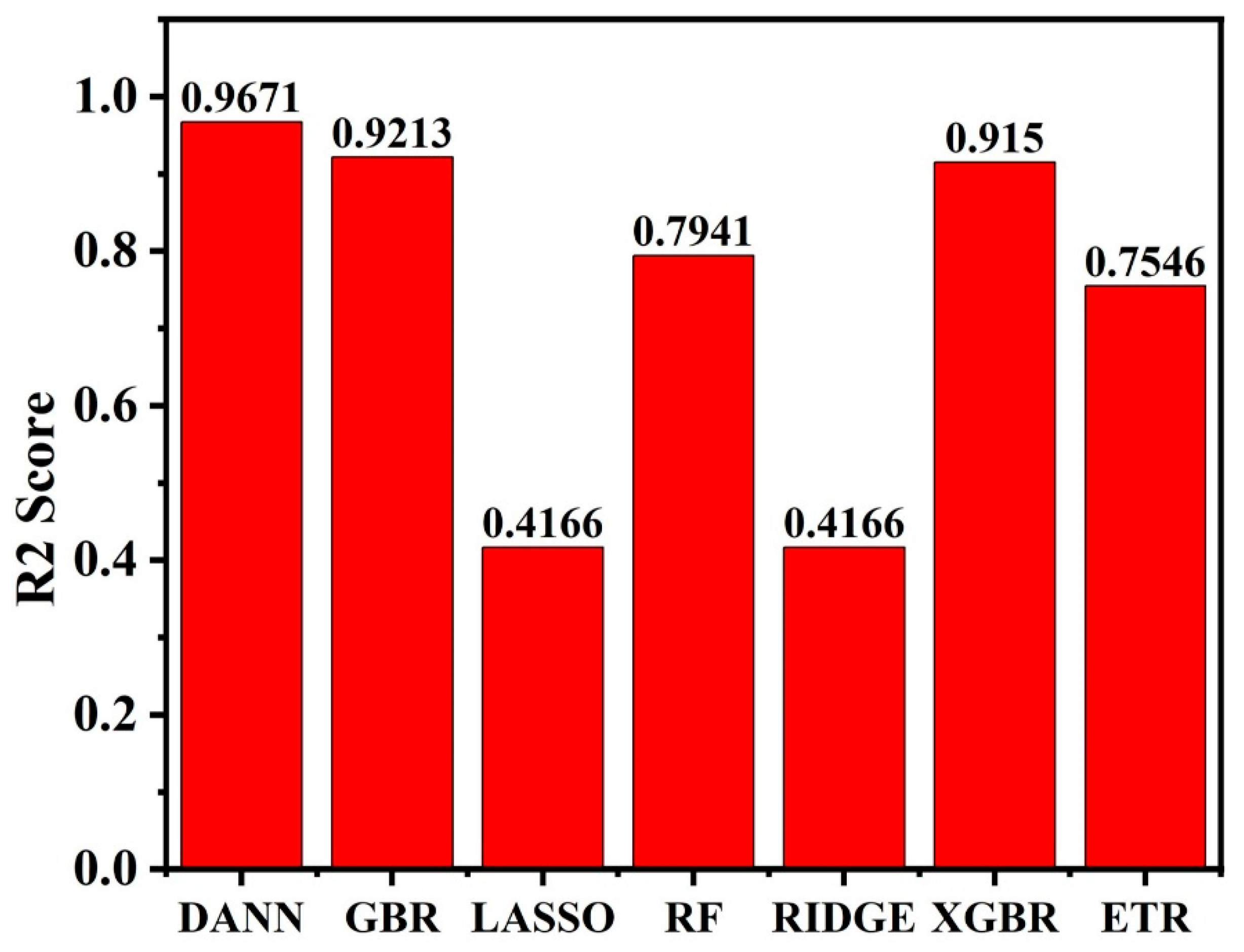
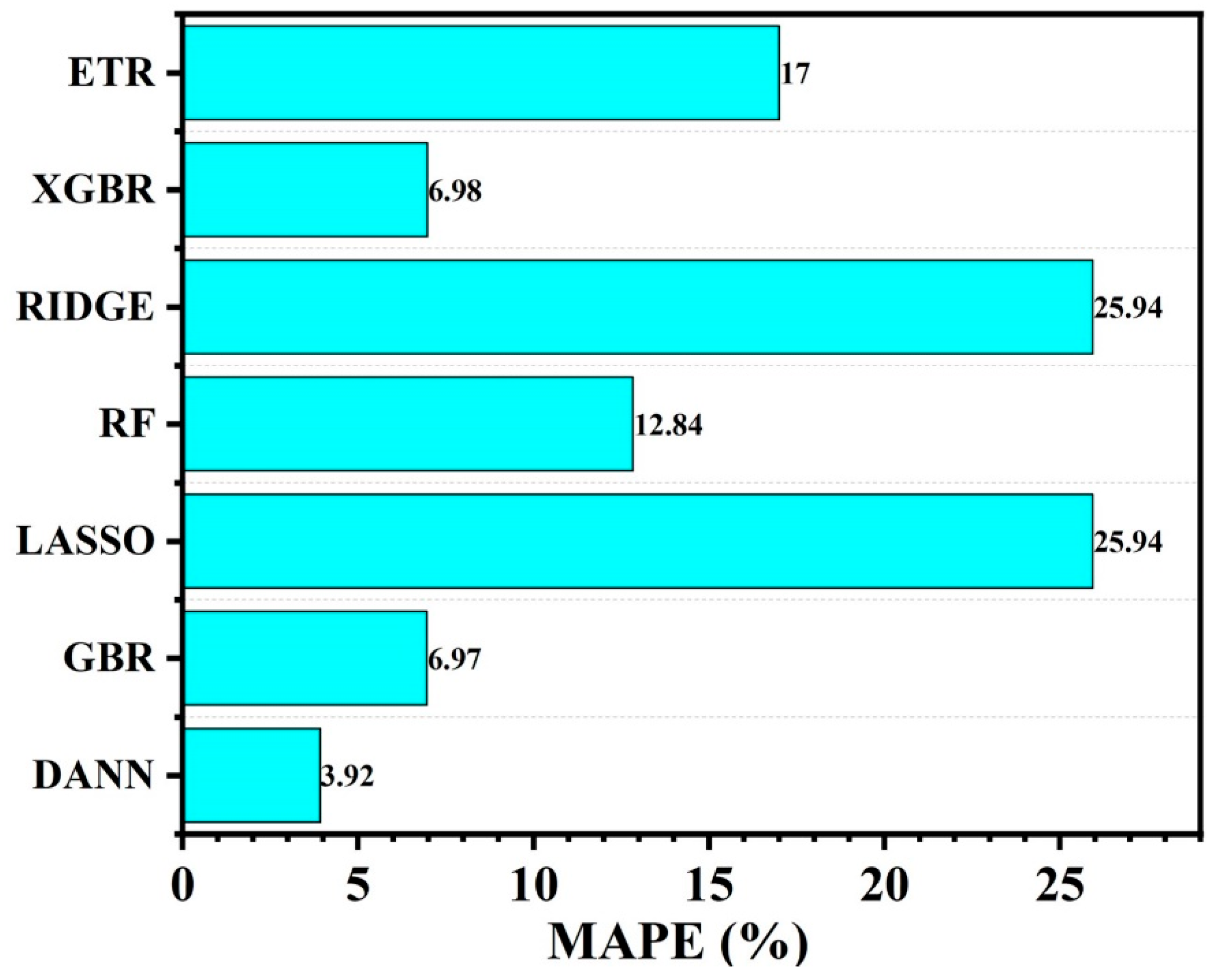
The deep neural network model’s findings showed that for neurons in the hidden layers, the rectified linear unit (ReLU) activation function performed better than the sigmoid and Tanh functions. With a learning rate α = 0.0001 and ReLU activation function, the best multi-layer perceptron (MLP) configuration had an R² score of 0.9671, an RMSE of 16.45, an MAE of 14.07, and a MAPE of 3.92%. The configuration with two hidden layers, having 12 neurons in the first layer and 32 neurons in the second layer yielding the highest R-squared and the lowest MAPE, indicating that it was the optimized deep neural network model. The first hidden layer, which included 12 neurons, achieved a perfect equilibrium between preventing overfitting and capturing the intricacy of the input data. If there are too many neurons in the model, it may become overfitted and perform badly on untried data, whereas there are too few neurons in the model, which might result in underfitting, where the model misses significant patterns. More complex and higher-order representations of the input data could be learned by the model, which included 32 neurons in the second hidden layer. A comprehensive and methodical hyperparameter tuning approach was used to the selection of 12 neurons in the first hidden layer and 32 neurons in the second hidden layer [41]. The configuration with the highest R-squared and lowest MAPE values offered the best balance between predictive performance and model complexity. This was found through additional testing of the deep neural network model using 10 hidden layers and up to 100 neurons in each hidden layer. However, as the deep neural network model becomes more complicated, the average time cost increased.

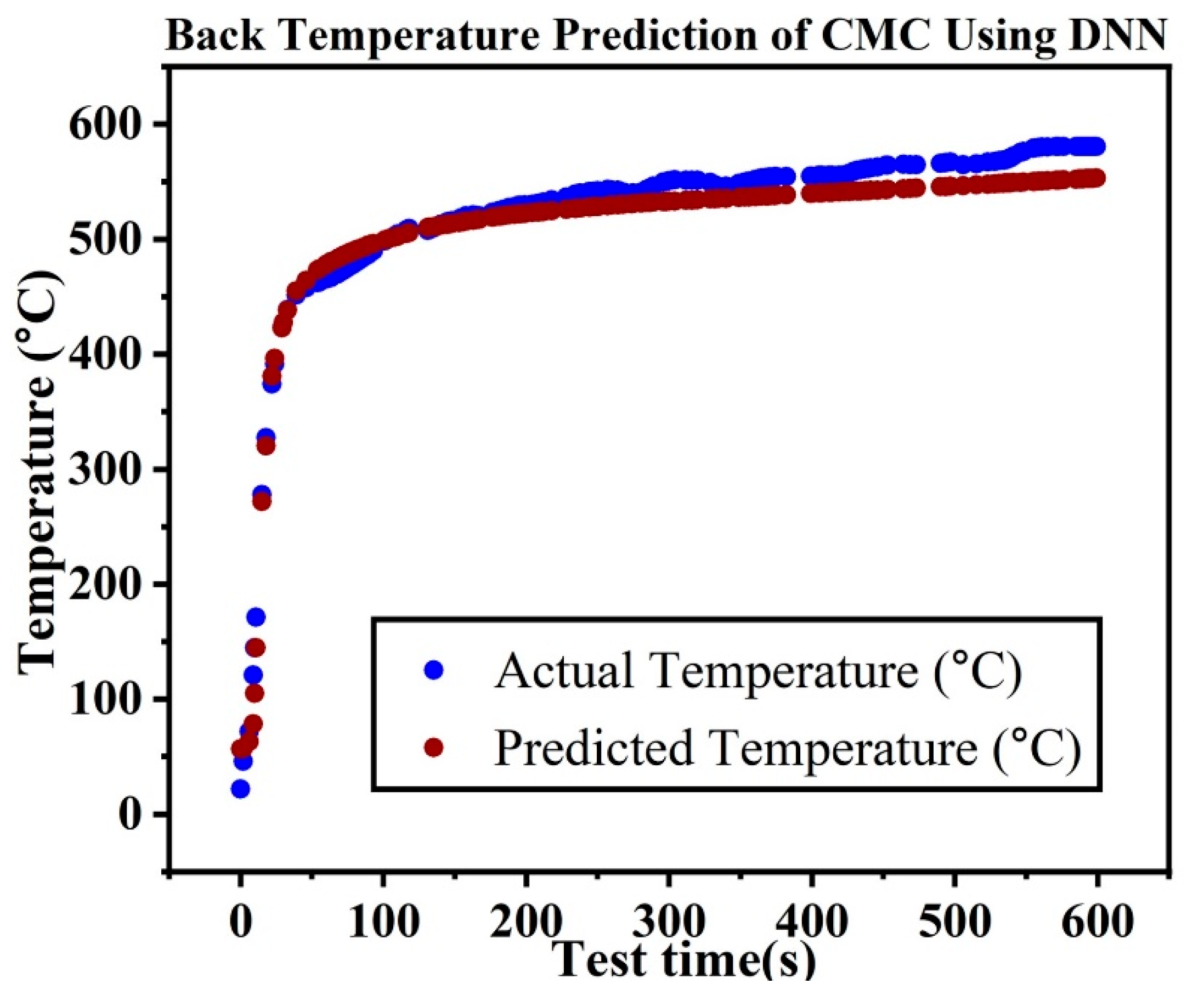
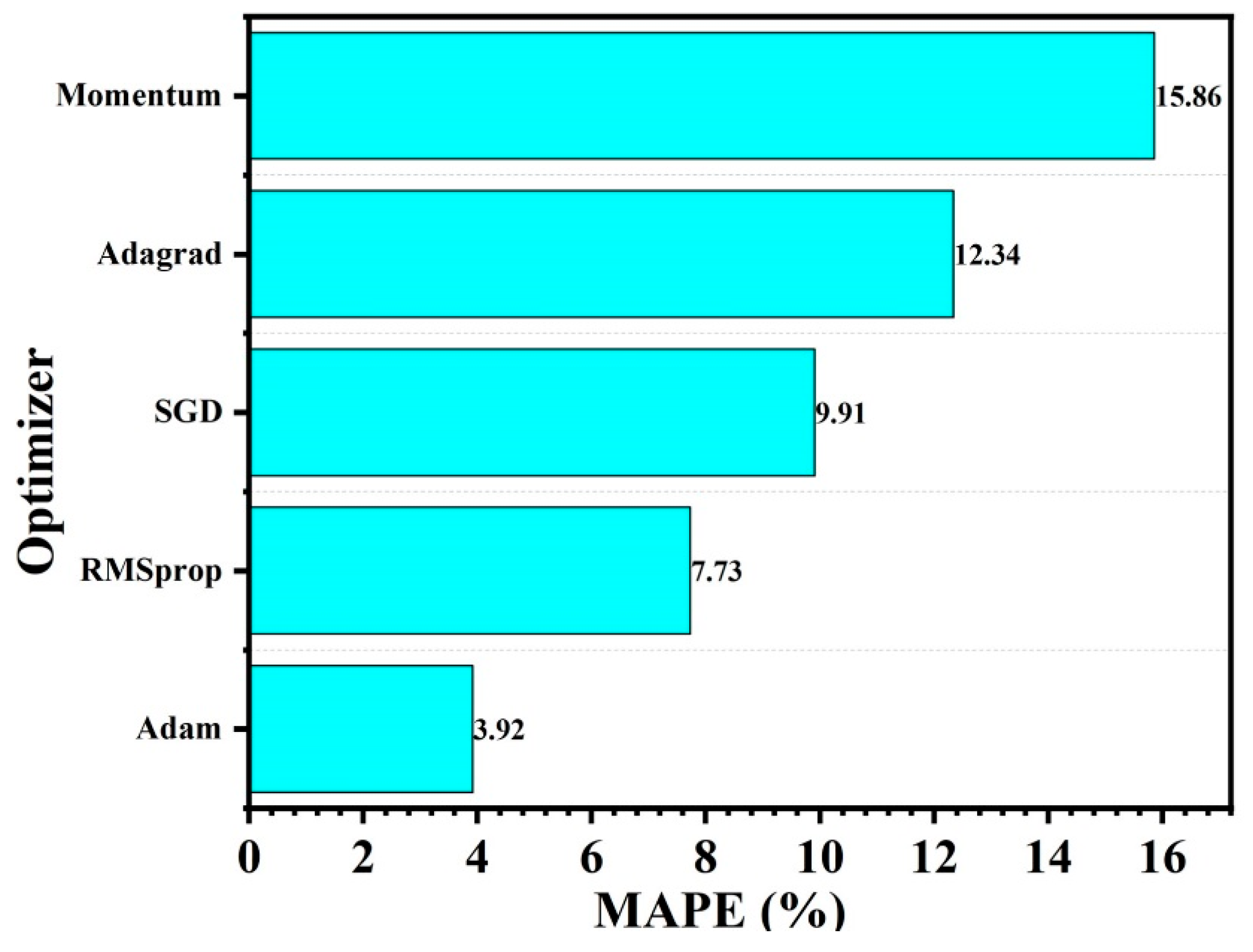
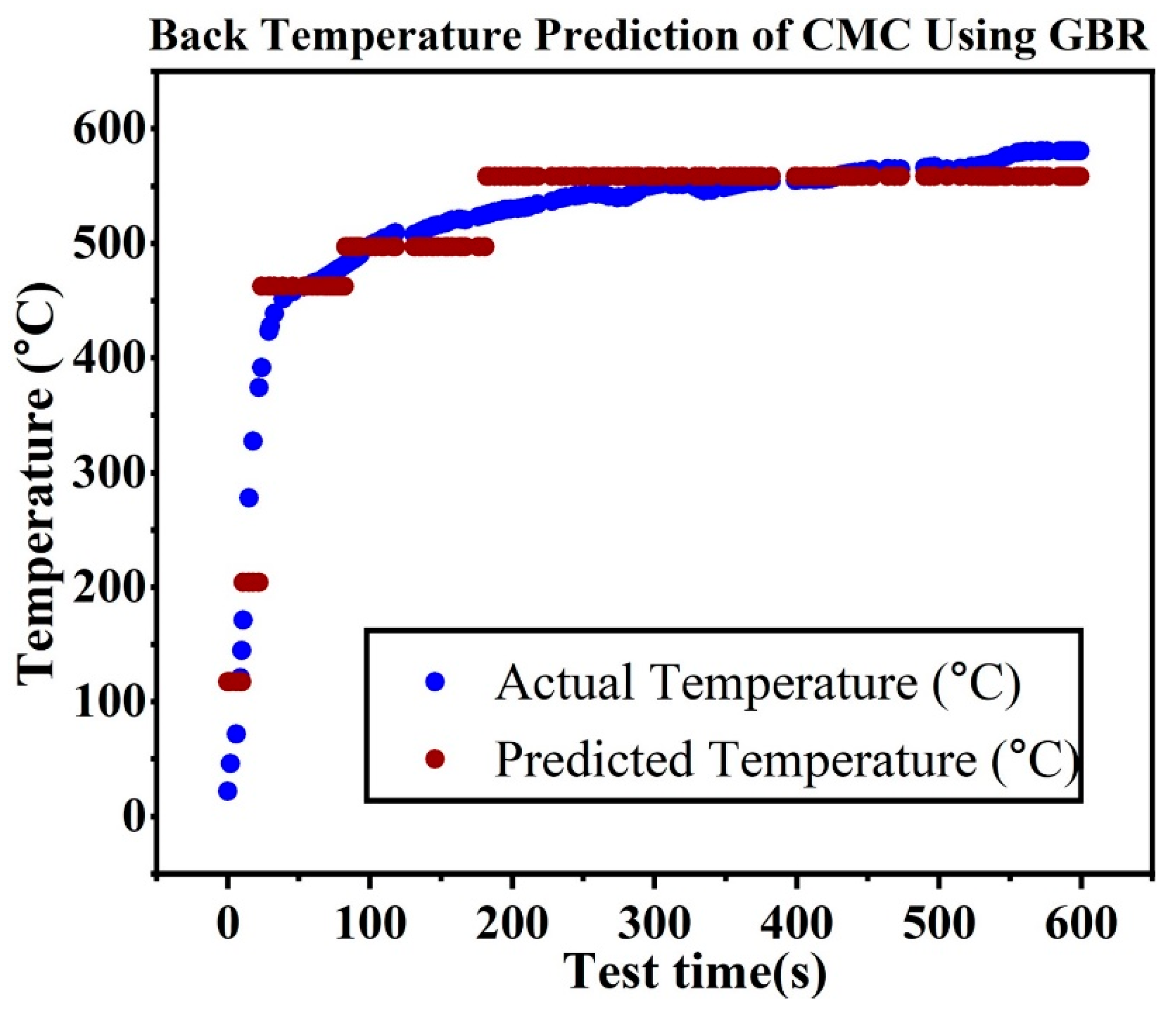
Numerous optimization techniques are available using neural networks. But choosing the best optimizer for a particular application is essential. Stochastic Gradient Descent (SGD), Momentum, Adagrad, RMSprop, and Adam were the five optimizers that we examined in this study. Throughout the HTT, the DANN model showed differing levels of accuracy at various points in time. There were some differences between actual and predicted temperatures in the early phases since the model has some difficulty with quick temperature swings. Nevertheless, over time, the model’s predictions demonstrated a great capacity to accurately represent the thermal behavior of ceramic matrix composites during extended exposure, as seen by how well they match real temperatures in both the mid- and late stages (Figure 6). Using measures including MAE, RMSE, R², and MAPE, we assessed the DANN model’s predictive performance with each optimizer. 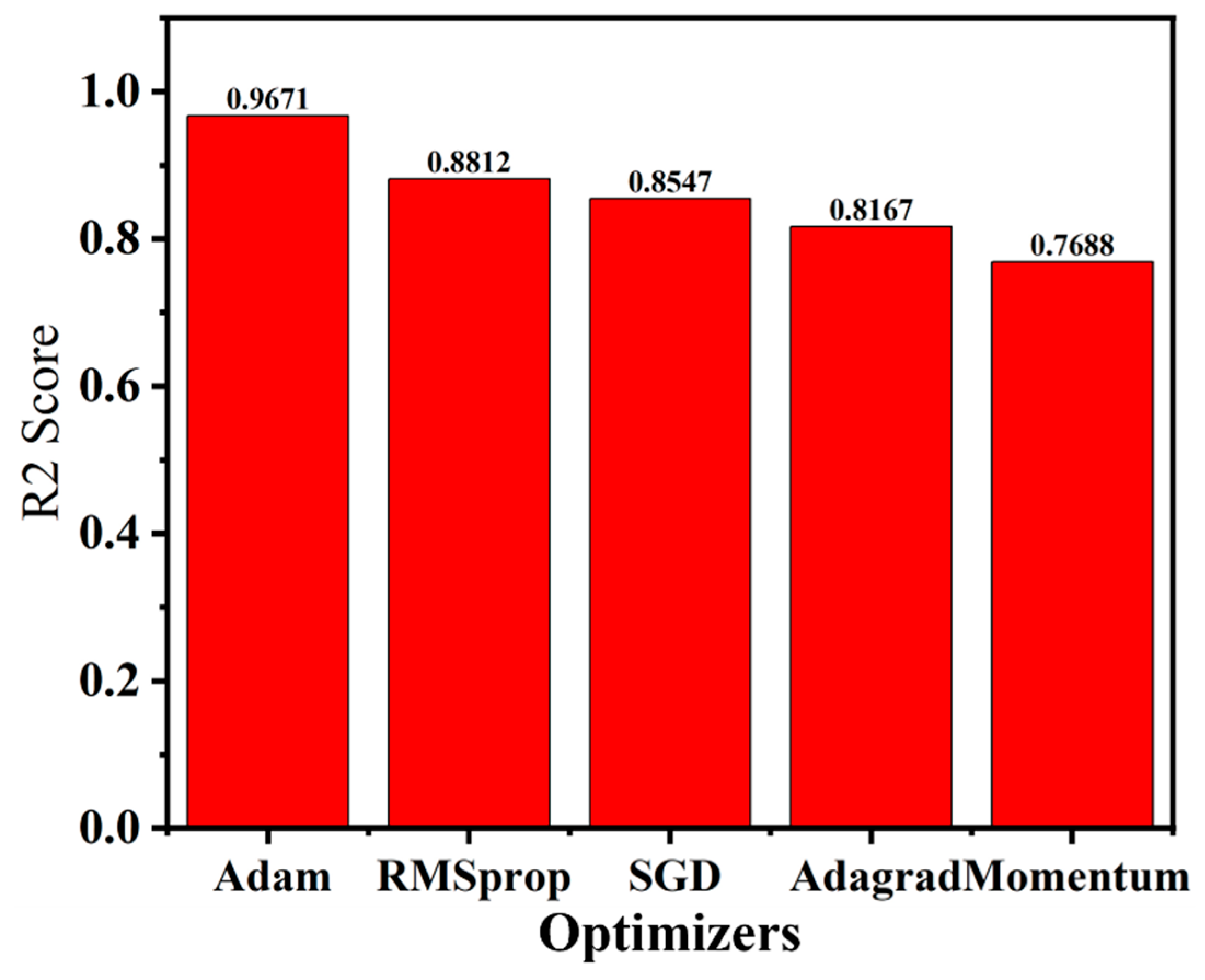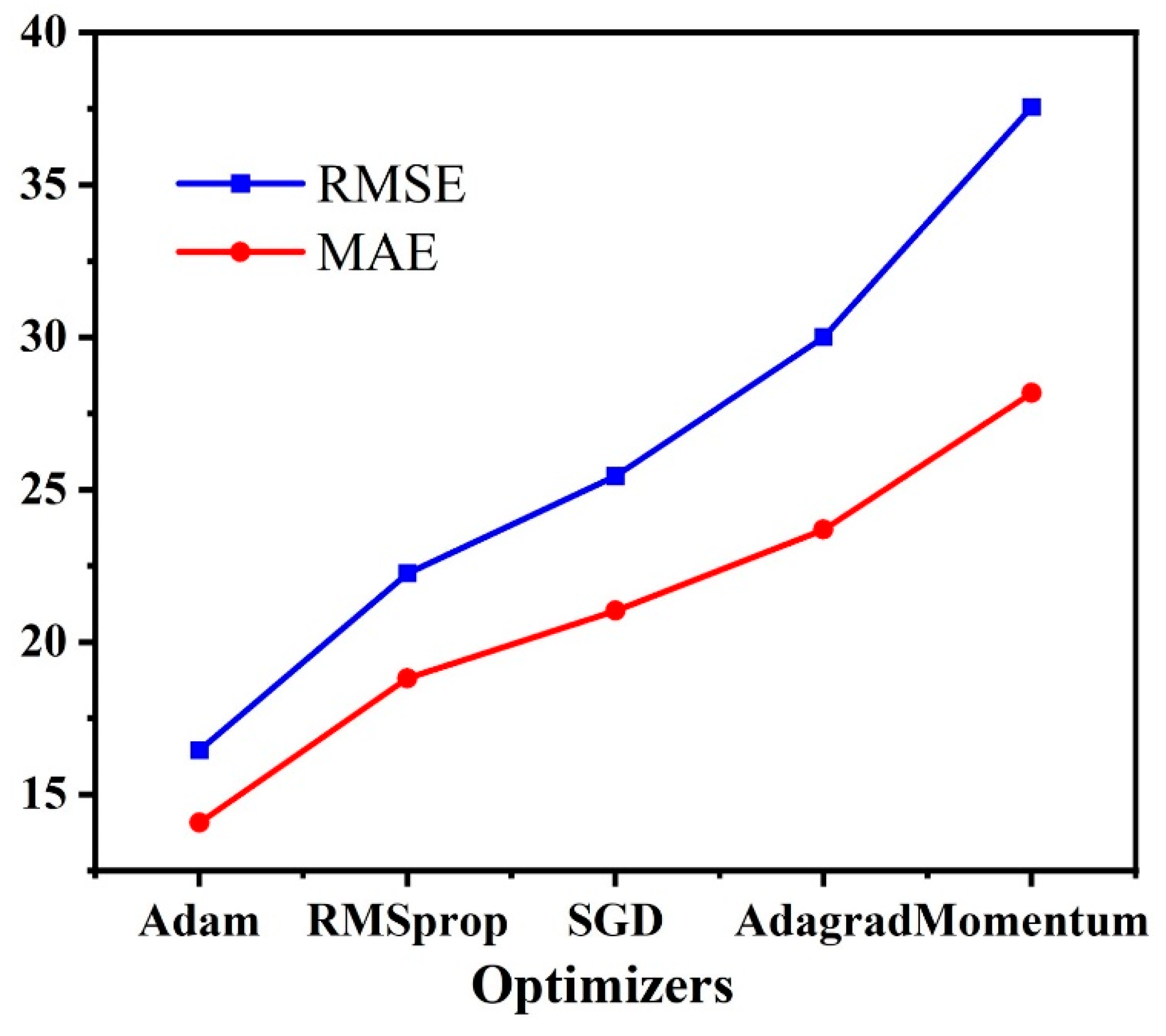Figure 7, Figure 8 and Figure 9 show the outcomes of this comparison. The Adam optimizer enabled the RMSE and MAE to attain their respective minimum value of 16.45 and 14.07, suggesting that the Adam optimizer-based DANN model exhibited the best predictive performance regarding accuracy than the other optimizers. Furthermore, the R² value reached a maximum of 0.9671, indicating a high degree of agreement between the actual and predicted values. Notably, the DANN model with the Adam optimizer also attained an MAPE of 3.92%, demonstrating its usefulness in terms of computing efficiency. When forecasting the ablation performance of ceramic matrix composites in HTTs, the Adam optimizer resulted greater nonlinear correlation and a lower difference between actual and predicted values.

3.3. Performance Comparison with Linear and Ensemble Machine Learning Models

To address the systematic comparison of model classes (linear, ensemble, deep), we first assessed performance using linear regression approaches (Lasso and Ridge). These established a baseline understanding of the linear relationships between temperature characteristics and ablation outcomes. Next, we moved on to ensemble tree-based models (random forest, gradient boosting, and so on), which captured non-linear correlations more accurately but still restricted in their ability to acquire deeper functional representations from limited thermal data. Finally, we used a deep artificial neural network (DANN) that surpassed all previous models in terms of error metrics and coefficient of correlation. This rigorous comparison not only supports the increased complexity necessary to appropriately describe ablation response, but it also assured that our model selection was based on empirical performance trends rather than intuition.

Following the completion of the five-fold cross-validation in every machine learning process, the HTT dataset was randomly split into a 70% training set and a 30% testing set. The assessment outcomes of the seven machine learning models developed for this study on the testing set are shown in

Table 3. Performance accuracy results of different machine learning models.

Model	RMSE	MAE	R2	MAPE
DANN	16.45	14.07	0.97	3.92
GBR	25.44	16.91	0.92	6.97
LASSO	69.28	34.10	0.42	25.94
RF	41.15	31.88	0.79	12.84
RIDGE	69.28	34.10	0.42	25.94
XGBR	26.45	17.64	0.91	6.98
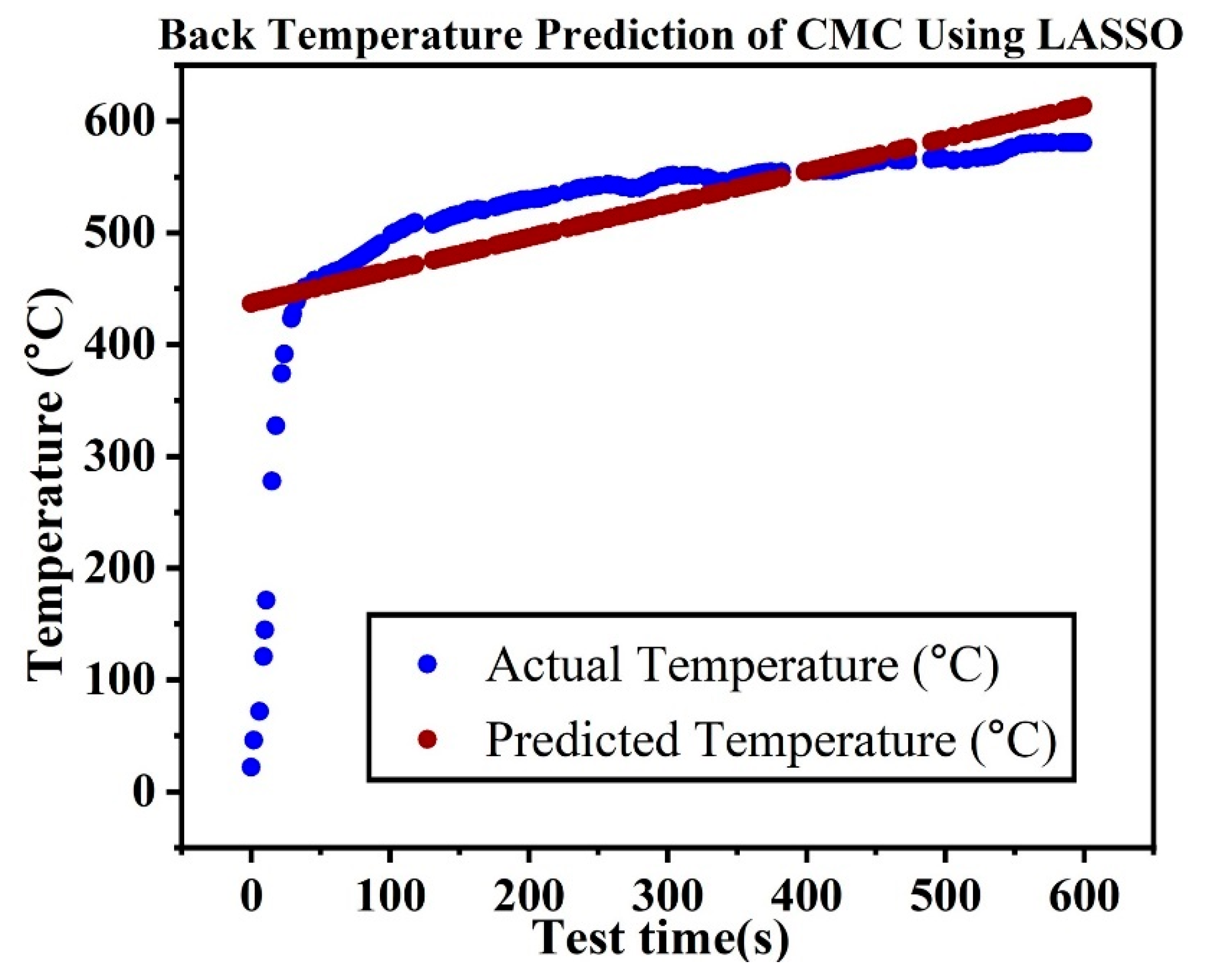
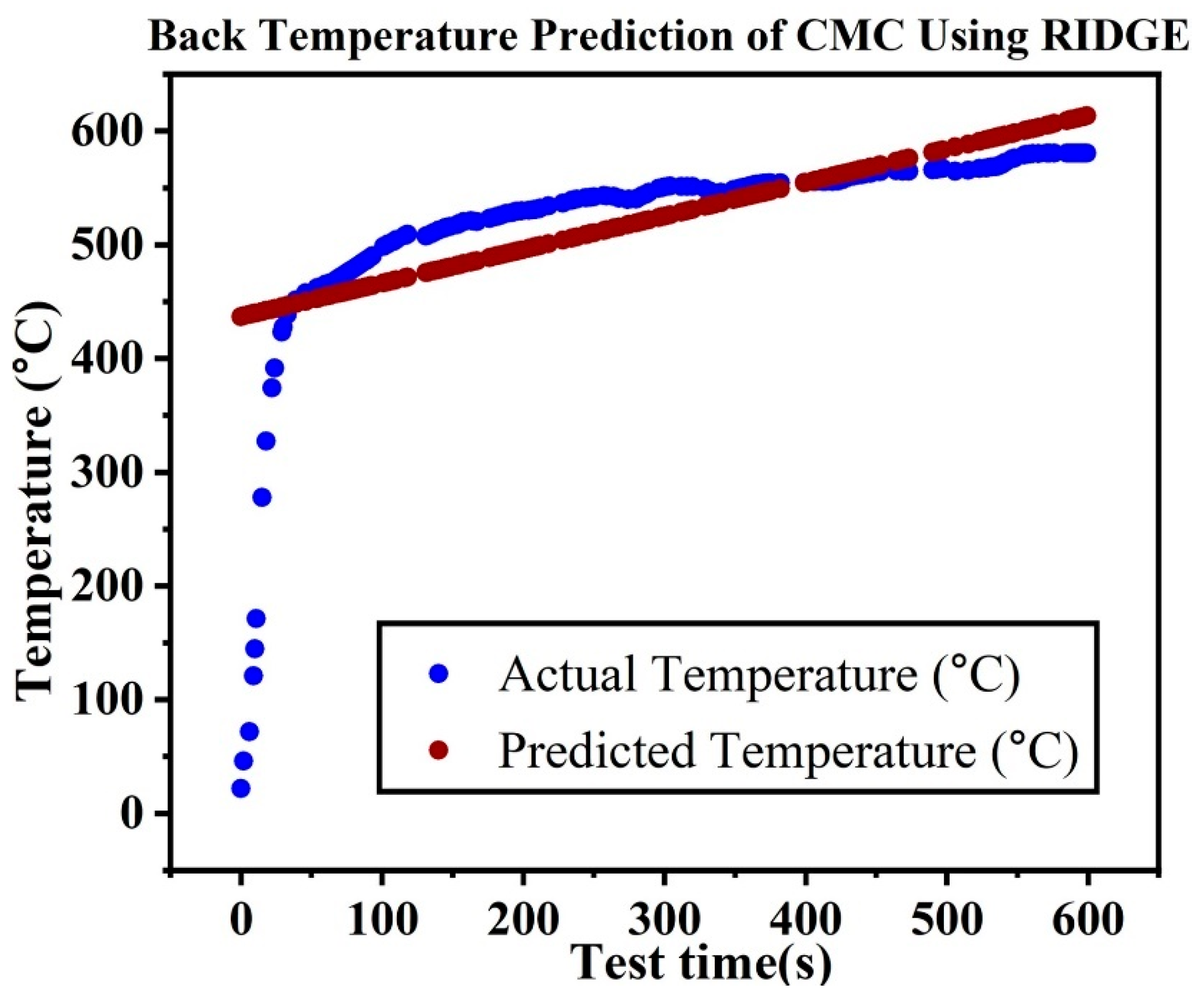
ETR	44.93	18.45	0.75	17.00

. The performance of the basic linear Lasso, Ridge Regressor, model was quite low as shown in Figure 10 and Figure 11 respectively, showing the need for more sophisticated machine learning models for this study. Lasso and Ridge regression models have difficulty predicting the time-temperature data from the HTT because of their linear nature. These models are not well adapted to capture the intricate, non-linear patterns seen in the HTT data because they presume a linear connection between the input characteristics and the target variable. These linear models do not capture the complex interactions and non-linearities involved in the ablation performance of ceramic matrix composites, which results in poor predicting performance. Neural networks and ensemble techniques are examples of advanced models that are better suited to handle non-linear data.

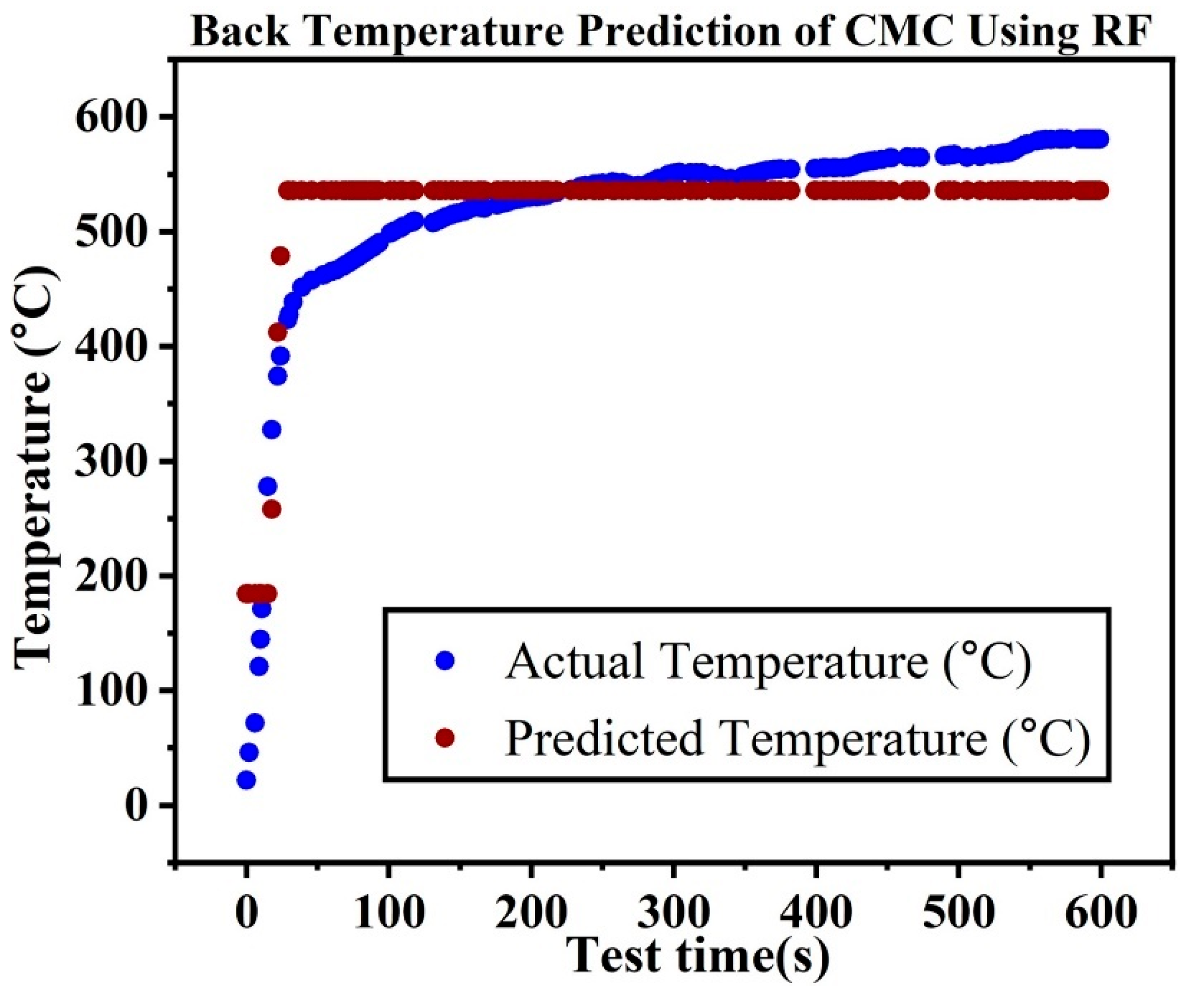
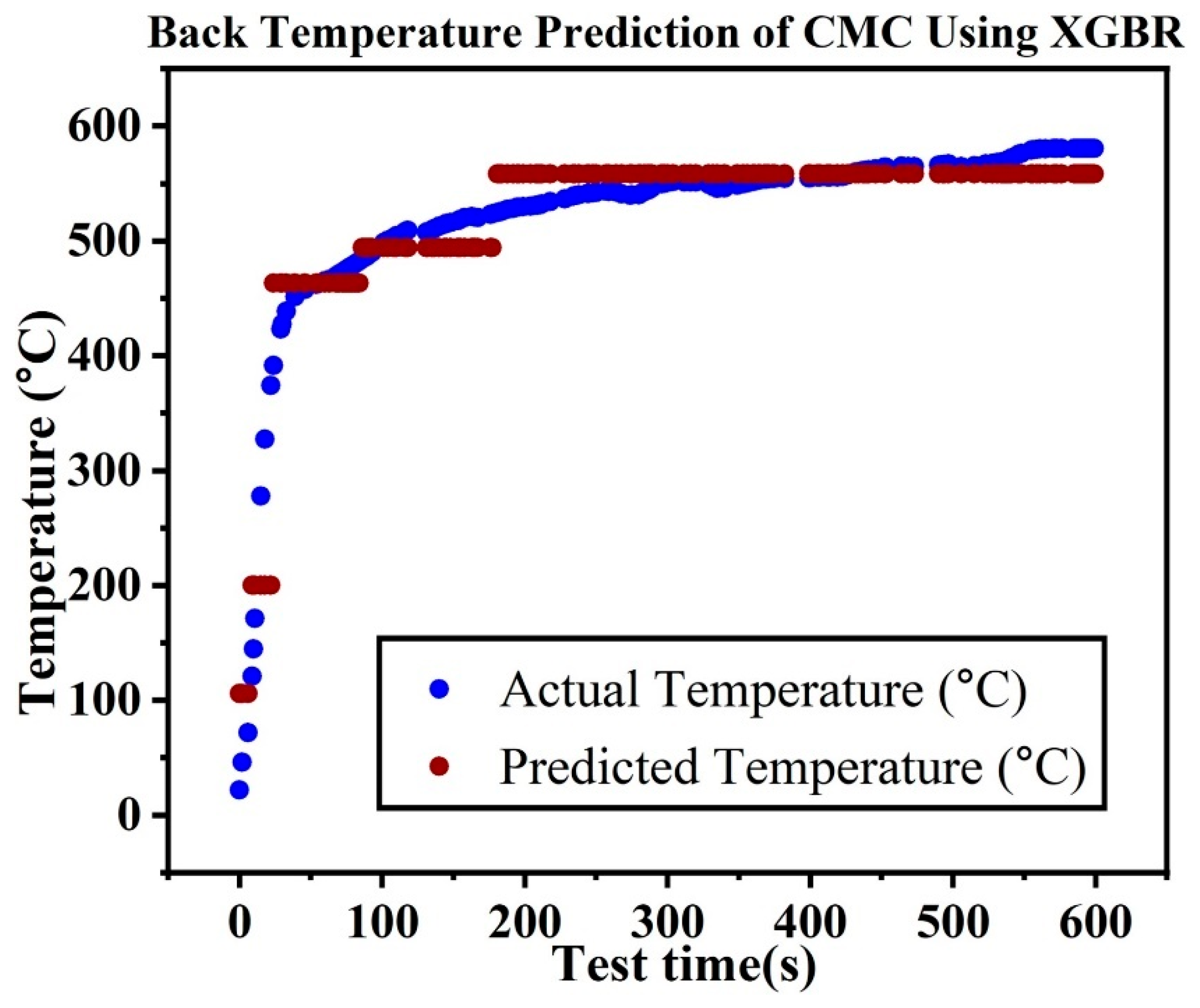
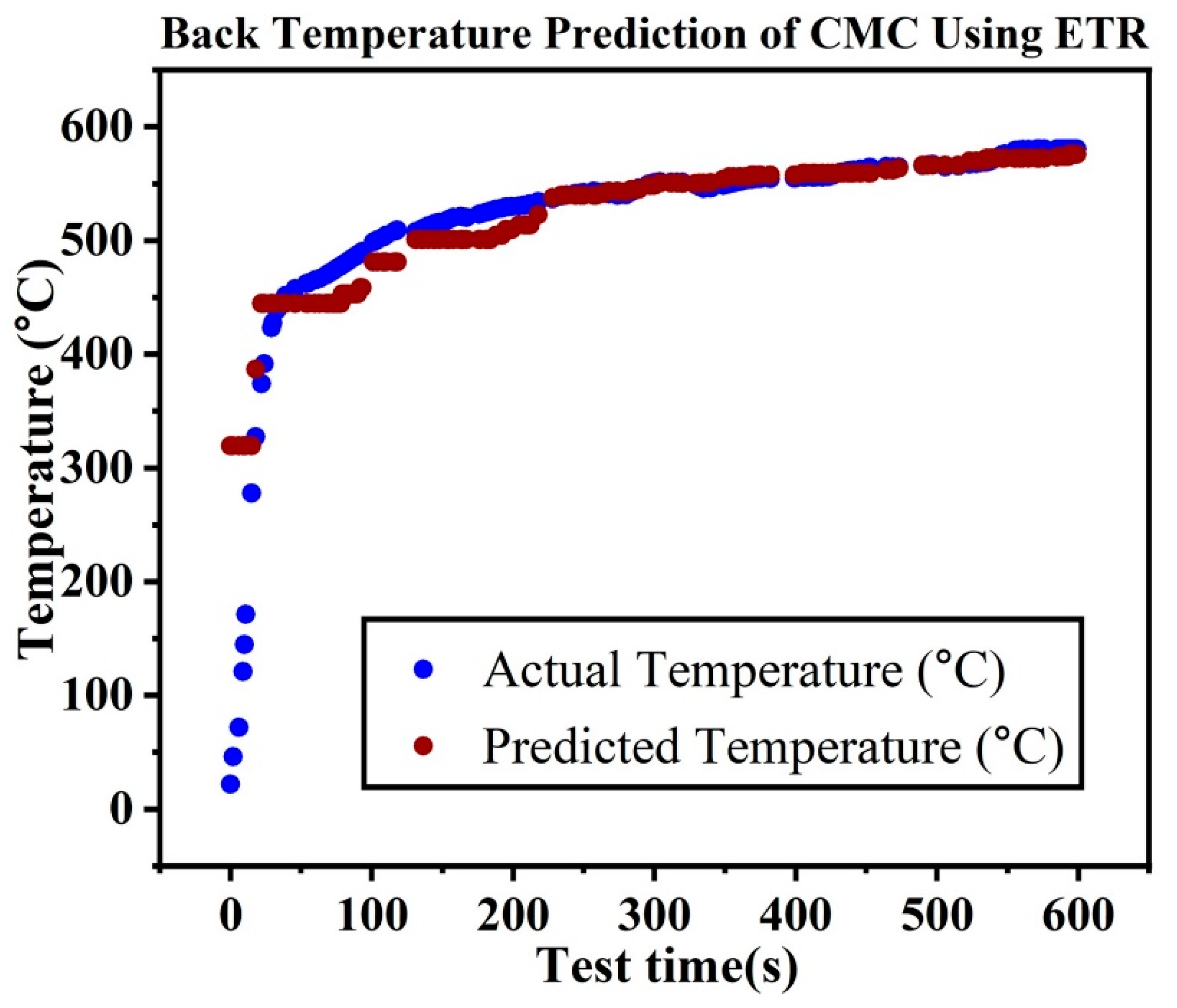
Four decision tree ensemble machine learning models were developed: random forest regression (RFR), extreme gradient boosting regression (XGBR), extra tree regression (ETR), and gradient boosting regression as provided the results in Figure 12, Figure 13, Figure 14 and Figure 15 respectively. The RMSE, MAE, R² score, and MAPE of the test data for each model, as indicated in Figure 16, Figure 17 and Figure 18, supported our study finding that the DANN model performed better than the ensemble and linear models. When compared to the DANN model, ensemble machine learning models like XGBR, GBR, RFR, and ETR performed badly because they had trouble capturing the complex, non-linear correlations observed in the HTT data. Although merging several weak learners might enhance prediction performance than linear machine learning modeling, ensemble techniques frequently had trouble handling extremely complex and high-dimensional data. The deep hierarchical structure that ensemble models lack in comparison to DANNs makes it difficult for them to automatically identify and extract small characteristics from the data, which leads to less precise predictions about the ablation performance of ceramic matrix composites.

Due to the improved capacity to capture complicated non-linear correlations in data through several layers of neurons, DANN perform better than ensemble machine learning models such as XGBR, GBR, RFR, and ETR. DANNs are better able to generalize from high-dimensional and large-scale datasets because of their hierarchical structure, which enables them to automatically learn and extract significant characteristics. When compared to ensemble approaches, DANNs provide more accurate and reliable prediction performance because of their superior regularization techniques and adaptive optimizers, which increase training efficiency and reduce overfitting. We can conclude from the HTT that the ceramic matrix composites’ ablation performance was most accurately predicted by the DANN model.

4. Conclusions

The application of machine learning approaches was introduced for the first time in the literature to predict the ablation behavior of ceramic matrix composites through HTT. The results showed that training a DANN model with 70% of the HTT data produced better performance accuracy. In addition to overcoming the shortcomings of standard ensemble decision tree-based machine learning methods (RF, GBR, XGBR, and ETR), the DANNs performed better in forecasting the thermal behavior of ceramic composites under hydrogen torch conditions than typical linear machine learning (Lasso and Ridge) systems. Nonetheless, the limitation of the DANN model developed in this study was its inability to clarify the basic physical laws guiding the ablation behavior of ceramic composites. By using machine learning approaches with a physics background, this constraint could be lessened. Additionally, our dataset was collected using a controlled hydrogen torch test settings with a fixed gas flow rate, constant heat flux, and constant exposure period. However, the present model might serve as a foundation for gradually improving prediction capabilities for neural network-based models using future datasets that encompass a variety of experimental conditions and long-duration ablation testing. But this study highlighted the important significance of neural network modeling in predicting the operational lifetime of ceramic matrix composites in demanding applications like hydrogen-based combustion chambers of gas turbine engines. The DANN model also established an efficient method for predicting thermal characteristics of ceramic matrix composites using HTT data.