Eco-Friendly Magnetically Active Textiles: Influence of Magnetic Fields, Pumpkin Seed Oil, and Propolis Microparticles on Complex Dielectric Permittivity Components

Abstract

This study presents the fabrication and characterization of magnetically active textiles using cotton fibers impregnated with suspensions of pumpkin seed oil, carbonyl iron microparticles, and propolis microparticles. The textiles were utilized to manufacture planar capacitors, enabling an investigation of the effects of static magnetic fields and the introduced microparticles on the components of complex dielectric permittivity. The results reveal that the dielectric properties of the fabricated textiles are highly sensitive to the applied magnetic field intensity, the frequency of the alternating electric field, and the composition of the impregnating suspension. The experimental findings suggest that the dielectric loss and permittivity can be finely tuned by adjusting the magnetic flux density and the proportion of propolis microparticles. The multifunctional nature of these magnetically responsive textiles, combined with the bioactive properties of the incorporated natural components, opens promising pathways for applications in smart textiles, biomedical devices, and sensor technologies.

1. Introduction

Smart textiles with tunable physical properties, responsive to electric, magnetic, or mechanical stimuli, have gained increasing attention for technological and healthcare applications [1,2,3]. Integrating sensors into fabrics enables remote monitoring of vital parameters [4,5], while electromagnetic field-assisted localized heating has shown promise for cancer therapy using fibers decorated with magnetite nanoparticles [6,7,8,9,10,11,12].

The use of textile fibers in this context is highly advantageous, as they serve both as monitoring tools and therapeutic agents [13]. Ref. [14] presents an approach where nano-microfibers decorated with magnetite nanoparticles and chemotherapeutic substances were developed. The resulting medical device is precisely directed to the tumor site, releasing well-defined amounts of therapeutic agents in response to the local pH environment. However, a drawback of this method is the need for multiple treatment cycles, leading to the gradual loss of magnetizable material. To address this issue, Ref. [15] proposes the use of textiles decorated with magnetite nanoparticles, where the therapeutic substance is absorbed directly into the tumoral tissue.

Recent advancements have replaced chemotherapeutic agents in smart textiles with natural compounds. Cotton bandages incorporating honey, carbonyl iron microparticles (CIMs), and turmeric have demonstrated tunable electrical conductivity under magnetic fields, modulated by CIM concentration and field intensity [16]. Although turmeric reduces conductivity, the application of medium-frequency electric fields enables efficient heating, enhancing the thermal activation and penetration of bioactive compounds through the skin [17].

This study aims to develop advanced smart textiles with tunable electromagnetic properties. Therefore, cotton fabric (CF) is soaked with pumpkin seed oil (PSO), propolis microparticles (PMs), and CIMs. PSO was chosen for its antibacterial properties [18]. Furthermore, it has cardioprotective, anti-atherosclerotic, and anticancer properties, while also stimulating fat metabolism in tissues [19]. PMs provide additional therapeutic benefits, including antiallergic, antioxidant, anticancer, antidiabetic, and anti-inflammatory effects [20,21]. When ingested, they also demonstrate anti-anemic properties [22].

The primary objective is to investigate how the composition of these textiles and the application of an external magnetic field and a medium-frequency electric field influence their dielectric properties. The focus is on their capacitance, dielectric permittivity, and loss tangent. To achieve this, we fabricated three types of textile-based capacitors with varying proportions of CIMs, PSO, and PMs, then systematically analyzed their dielectric response under different frequencies and magnetic flux densities. The experimental results demonstrate that both material composition and external fields significantly modulate the dielectric properties, enabling tunable electrical behavior. These textile-based composites are intended for use in applications such as wearable sensors, field-tunable capacitive devices, electromagnetic shielding, or localized bioelectronic actuation, where remote or adaptive control of dielectric properties is advantageous.

2. Manufacturing of Magnetically Active Textile Fabrics

2.1. Materials and Main Physical Characteristics

The materials required for the manufacture of magnetically active textile fabrics are the following:

• CF, for commercial use, with dimensions 50 mm × 50 mm × 0.6 mm. Optical microscopy shows that the structure of CF consists of interwoven cotton threads (Figure 1a). Each thread in the fabric is made up of microfibers. The relative humidity of the ambient environment of 65 % the mass density of CF is ${\rho }_{\mathrm{CF}}=0.346$ g/cm³.
• PSO purchased from BIODAC-Timisoara, Romania. At 24 °C the bulk density of PSO is ${\rho }_{\mathrm{PSO}}=0.679$ g/cm³.
• CIMs (code C3518) were purchased from Sigma-Aldrich, Germany. They have an iron content of at least 97 %. The mass density is ${\rho }_{\mathrm{CIMs}}=7.860$ g/cm³, and the average diameter about 5 $\mathsf{\mu }$ m.
• Raw propolis from Comana Natural Park (Romania). After grinding, PMs are obtained, with a mass density ${\rho }_{\mathrm{PMs}}=0.758$ g/cm³. The optical microscopy image (Figure 1b) reveals that the PMs exhibit irregular shapes and relatively broad size distribution, with particle diameters centered around 0.25 mm. The microparticles are non-spherical, with rough surfaces and some tendency to form loose agglomerates. Such morphological features are typical for mechanically ground natural propolis and may influence the homogeneity of particle distribution within the PSO matrix. The relatively large particle size (as compared with CIMs) and irregular shape are expected to impact the interfacial polarization effects observed in the dielectric response of the smart textiles.

All the above mass densities are for a temperature of 24 °C.

2.2. Magnetic Properties of CIMs

The magnetic behavior of CIMs used in this study is characterized by soft magnetic properties, with a relative saturation magnetization of approximately 200 Am²/kg and a rapid approach to saturation for magnetic field intensities up to 530 kA/m, as reported in Ref. [23]. These particles exhibit low coercivity and remanence, making them suitable for applications involving alternating or static magnetic fields.

2.3. Manufacturing of Magnetorheological Suspensions (MRSs) and of Smart Textiles (STs)

The MRSs were prepared by mixing CIMs, PSO, and PMs in the proportions given in

Table 1. Volumes V and volume fractions $\Phi$ of components CIMs, PSO, and PMs in MRS_i ($i=1,2,3$), together with the relative saturation magnetization $\mathit{M}\mathit{s}$ (at $H=525$ kA/m) of MRS_i.

	VCIMs (cm3)	VPSO (cm3)	VPMs (cm3)	${\Phi }_{\mathbf{CIMs}}$ (vol.%)	${\Phi }_{\mathbf{PSO}}$ (vol.%)	${\Phi }_{\mathbf{PMs}}$ (vol.%)	$\mathit{Ms}$ (Am2/kg)
MRS1	1.50	3.50	0.00	30.00	70.00	0.00	60
MRS2	1.50	2.50	1.00	30.00	50.00	20.00	60
MRS3	1.50	1.50	2.00	30.00	30.00	40.00	60

. The mixtures formed are homogenized for about 120 s at 14.000 rpm. The CF was then soaked in each suspension to obtain the corresponding ST samples, with proportions given in

Table 2. Volumes V and volume fractions $\Phi$ of components CF, CIMs, PSO, and PMs in ST_i ($i=1,2,3$), together with the relative saturation magnetization $Ms$ (at $H=525$ kA/m) of ST_i, and their thicknesses $h_0$.

	VCF (cm3)	VCIMs (cm3)	VPSO (cm3)	VPMs (cm3)	${\Phi }_{\mathbf{CF}}$ (vol.%)	${\Phi }_{\mathbf{CIMs}}$ (vol.%)	${\Phi }_{\mathbf{PSO}}$ (vol.%)	${\Phi }_{\mathbf{PMs}}$ (vol.%)	$\mathit{Ms}$ (Am2/kg)	${\mathit{h}}_0$ (mm)
ST1	1.50	0.60	1.40	0.00	43.00	17.00	40.00	0.00	10.2	0.65
ST2	1.50	0.60	1.00	0.40	43.00	17.00	29.00	11.00	10.2	0.69
ST3	1.50	0.60	0.60	0.80	43.00	17.00	17.00	23.00	10.2	0.74

.

2.4. Magnetic and Structural Properties of MRSs

To obtain the relative saturation magnetization $M{s}_{\mathrm{MRSs}}$ of the MRSs, we use the following relation [24]: ${\mu }_{0}M{s}_{\mathrm{MRSs}}={\mu }_0{\Phi }_{\mathrm{CIMs}}M{s}_{\mathrm{CIMs}}$ with ${\Phi }_{\mathrm{CIMs}}$ being given in Table 1, and ${\mu }_0$ is the vacuum magnetic constant. Then, using the relative saturation magnetization for CIMs, i.e., $M{s}_{\mathrm{CIMs}}\simeq 200$ Am²/Kg [23] in the above equation, we obtain $M{s}_{\mathrm{MRSs}}=60$ Am²/Kg (Table 1).

In the absence of a magnetic field, CIMs and PMs are randomly distributed within the PSO matrix (Figure 2a), with CIMs clustering around larger PMs due to interfacial interactions. Upon magnetic field application, CIMs align into chain-like structures along the field lines [25], while PMs remain randomly distributed (Figure 2b). Their spatial arrangement is maintained due to the lack of direct magnetic forces acting on them, while local changes in viscosity and particle movement may result in minor adjustments in their positioning. This dynamic restructuring highlights the competition between magnetic forces driving the alignment of CIMs and the passive behavior of the non-magnetic inclusions.

2.5. Magnetic and Structural Properties of STs

The relative saturation magnetization of STs is calculated using the above formula in the form: ${\mu }_{0}M{s}_{\mathrm{STs}}={\mu }_0{\Phi }_{\mathrm{CIMs}}M{s}_{\mathrm{MRSs}}$, where ${\Phi }_{\mathrm{CIMs}}=17$ vol.% is the volume fraction of CIMs in STs (Table 2). The thicknesses $h_0$ of STs were measured using a digital micrometer with a precision of 0.01 mm. The average values are listed in Table 2. Each value was averaged over three measurements taken at different points of the sample.

Optical microscopy reveals that MRS primarily accumulates in the spaces between the yarns of CF rather than uniformly coating individual fibers (Figure 3). This structural arrangement is governed by a combination of capillary action, surface wetting, and viscous flow dynamics. Cotton, being a highly porous and hydrophilic material, promotes the absorption of the liquid matrix through capillary forces, drawing the mixture into the gaps between yarns where the fiber intersections create small reservoirs. The distribution of the suspension is further influenced by the interfacial energy between the oil-based fluid and the cotton fibers; if the surface energy of the fibers is lower than that of the liquid, the suspension tends to accumulate in regions where it can minimize interfacial tension. Additionally, the viscosity of the suspension affects its ability to penetrate the fabric structure—if sufficiently low, it spreads easily, but if too high, it may remain localized in larger voids. As the liquid matrix is absorbed, the solid microparticles (propolis and carbonyl iron) follow the flow path but may experience filtering effects, where larger particles are more likely to remain trapped in wider pores, while finer ones distribute more evenly throughout the fabric. This results in a non-uniform but structured impregnation, where the active components are concentrated in the inter-yarn spaces, potentially enhancing their release and interaction with the skin when STs are applied.

3. Dielectric Properties

To investigate the dielectric properties of STs, we use them as dielectric materials in a parallel-plate capacitor configuration, with two copper plates serving as electrodes. The primary dielectric properties analyzed include the complex dielectric permittivity (${\epsilon }^{*}$), comprising both the real part (${\epsilon }^{\prime }$), which represents the material’s ability to store electrical energy, and the imaginary part (${\epsilon }^{″}$), which accounts for dielectric losses. The loss tangent (D = $tan\delta$), defined as the ratio of the imaginary to the real part of permittivity, is evaluated to determine energy dissipation due to dielectric losses. Furthermore, we measure the electrical resistance (R) and derive the electrical conductivity ($\sigma$) of the STs to understand their resistive behavior under an applied alternating electric field. The influence of an external static magnetic field on these dielectric parameters is also explored, allowing us to characterize potential magnetodielectric effects. By systematically analyzing these properties, we aim to gain insight into the tunability of the STs for applications in sensors, medical textiles, and smart materials.

3.1. Materials for Manufacturing the Capacitors

For the manufacture of capacitors, the following materials are used:

• A simple copper-clad glass-textolite board, with dimensions 100 mm × 75 mm × 0.8 mm, from Electronic Light Tech (Romania). The board is based on a type FR4 epoxy resin and reinforced with glass fiber, with one side covered with a copper layer. The thickness of this layer is 35 μm.
• STs obtained in Section 2.3.
• Self-adhesive insulating tape from 3M (USA). The tape is for general surgical use and is in the form of rolls. A roll of this tape has a length of 9.5 m, a width of 5 cm, and a thickness of 0.20 mm.

3.2. Steps for Manufacturing the Capacitors

The main steps for manufacturing the capacitors are as follows:

• Six pieces are cut from the textolite board, with dimensions 50 mm × 50 mm × 0.8 mm.
• On each board, two electrical conductors are soldered with lead alloy.
• Between two boards with electrically conductive surfaces, the ST_i (with $i=1,2,3$) are fixed one by one.
• To obtain a good electrical contact between the copper electrodes and the STs surfaces, the electrode–ST assembly is pressed and consolidated with the self-adhesive tape.

The plate distance in the capacitors is defined by the thickness $h_0$ of the impregnated textile layer, as listed in Table 2. To ensure reproducibility, each sample was pressed between copper plates using a consistent wrapping force from adhesive tape.

3.3. Experimental Setup

The experimental installation used to study the influence of the magnetic field and PMs on the components and the complex dielectric permittivity modulus has the overall configuration shown in Figure 4. The installation consists of a homemade direct current electromagnet, a direct current source (DCS; RXN-3020D type, from Shenzhen Ever Good Electronic Co., China), the impedance meter Br (E7-20 type, from MNIPI, Rep. Belarus), and the gaussmeter Gs (DX-102 type, from Dexing-Magnetic, China) with a Hall probe, h. The electromagnet consists of a coil fixed on a magnetic core. For values $0\le I\left({\mathrm{A}}_{\mathrm{dc}}\right)\le 4.5$ of the current intensity through the electromagnet coil, between the magnetic poles N and S, located at a distance of 5 mm apart from each other, the values B of the magnetic flux density can be continuously increased up to the maximum of 420 mT. For voltages of 30 V_dc at its terminals, it delivers an electric current with maximum intensities of 20 A_dc. The equivalent components are measured when connected to an inductive or capacitive load, for frequencies between 25 Hz and 1 MHz. The effective voltage of the alternating signal applied to the inductive or capacitive load can be adjusted in the range 0.4–1.0 V_dc.

3.4. Relative Dielectric Permittivity of Capacitors with STs

For the study of relative dielectric permittivity ${ϵ}^{\prime }$ of STs in an alternating electric field superimposed on a static magnetic field we introduce, in turn, the capacitors between the N and S poles together with the Hall probe. On the impedance meter panel, we set the alternating voltage to the effective value $U_{\mathrm{eff}}=1$ V. On the same panel, we set the frequency f of the alternating voltage to the 10, 20, 30, 40, and 50 kHz. For each value of f, the values of B are increased from 0 to 390 mT in steps of 30 mT. In these conditions, the capacitance C and D are measured after the application of the magnetic field. For these measurements, the impedance meter is connected to the capacitor terminals and fixed on the parallel measuring module for electrical circuit elements.

Then, ${ϵ}^{\prime }$ is calculated from the measured capacitance using the standard formula for a parallel-plate capacitor: ${ϵ}^{\prime }=C{h}_0/\left({ϵ}_{0}S\right)$, where $h_0$ is given in Section 3.1, and for each capacitor, ${ϵ}_0=8.854\times {10}^{-12}$ F/m and $S=2.5\times {10}^{-3}{\mathrm{m}}^2$ are the common area of the plates. These numerical values give:

$${ϵ}^{\prime }=\left\{\begin{array}{cc}0.029380\left({\mathrm{pF}}^{-1}\right)C\left(\mathrm{pF}\right)\hfill & \mathrm{for}{\mathrm{ST}}_1\hfill \\ 0.031188\left({\mathrm{pF}}^{-1}\right)C\left(\mathrm{pF}\right)\hfill & \mathrm{for}{\mathrm{ST}}_2,\hfill \\ 0.033448\left({\mathrm{pF}}^{-1}\right)C\left(\mathrm{pF}\right)\hfill & \mathrm{for}{\mathrm{ST}}_3\hfill \end{array}\right.$$

(1)

where the measured capacitances correspond to ST₁, ST₂ and respectively ST₃. Capacitance data are not shown here, as they directly scale with ${ϵ}^{\prime }$ (see Equation (1)).

The values obtained for ${ϵ}^{\prime }$ are graphically represented in Figure 5. The results reveal a clear dependence on both frequency and material composition. In all cases, ${ϵ}^{\prime }$ decreases with increasing frequency, a common behavior in dielectric materials where dipole polarization mechanisms become less effective at higher frequencies [26]. The differences in ${ϵ}^{\prime }$ values among the three STs can be primarily attributed to variations in the amounts of PSO and PMs. ST₁, which contains the highest volume of PSO and no PMs (Table 2), exhibits the highest ${ϵ}^{\prime }$ across all frequencies. In contrast, ST₃, with the lowest PSO content and the highest amount of PMs, shows the lowest ${ϵ}^{\prime }$ values. ST₂, which has an intermediate composition, has ${ϵ}^{\prime }$ values between those of ST₁ and ST₃. The higher ${ϵ}^{\prime }$ in ST₁ suggests that PSO contributes significantly to the dielectric properties of the system. Oils generally have a high dielectric constant, which enhances charge storage capability. In contrast, the presence of PMs in ST₂ and ST₃ appears to reduce ${ϵ}^{\prime }$, likely due to interfacial polarization effects or disruptions in the dielectric uniformity caused by the solid particles. These microparticles may introduce microstructural inhomogeneities that hinder charge storage, effectively lowering the overall permittivity of the material.

Figure 5 also shows that the ${ϵ}^{\prime }$ of all three smart textiles (ST₁, ST₂, and ST₃) significantly depend on the applied magnetic flux density (B). This suggests that increasing B enhances charge storage in the textile systems. The dependence is strongest for ST₃, indicating that the interaction between the magnetic field and the dielectric properties is most pronounced in the textile with the highest PM content and lowest PSO content. ST₁ and ST₂ also show significant dependencies on B, implying that magnetodielectric effects play a crucial role in modulating ${ϵ}^{\prime }$ in these materials. This strong dependence of ${ϵ}^{\prime }$ on B can be attributed to the presence of CIMs, which induce magnetodielectric effects through mechanisms such as field-induced polarization enhancement or modifications in the internal electric field distribution. The alignment of iron microparticles under an applied magnetic field may lead to increased polarization of the surrounding dielectric medium, thereby increasing the effective permittivity of the system. Additionally, magnetically induced charge redistribution at the interfaces between PSO, PMs, and the conductive iron particles may contribute to an increase in ${ϵ}^{\prime }$.

3.5. Loss Tangent of Capacitors with STs

The loss tangent D characterizes the energy dissipation in a dielectric material and provides insight into polarization and conduction losses. The measured values for all three smart textiles (ST₁, ST₂, and ST₃) exhibit a decreasing trend with increasing frequency (Figure 6), indicating a dominant dielectric relaxation mechanism. At lower frequencies, dipoles and charge carriers have sufficient time to align with the applied electric field, leading to greater energy dissipation. As frequency increases, their response time is insufficient, reducing overall losses. No relaxation peaks are observed in any of the systems, suggesting that the dominant loss mechanisms are steady-state polarization and conduction rather than discrete frequency-dependent relaxation processes.

The composition of the textiles significantly influences the magnitude of dielectric losses. ST₁, which contains the highest volume of PSO and no PMs, exhibits intermediate values across all frequencies, confirming that an oil-rich composition enhances charge storage efficiency while minimizing dissipation. ST₂, with a moderate amount of PMs, shows consistently higher losses than ST₁, likely due to increased interfacial polarization at the interfaces between the oil and solid microparticles. ST₃, which has the highest concentration of PMs and the lowest oil content, exhibits generally the lowest loss tangent values across all frequencies, indicating that interfacial charge trapping and polarization losses dominate in this system.

A strong correlation between D and the applied magnetic flux density (B) is observed in all three systems (Figure 6), suggesting the presence of magnetodielectric effects. The presence of CIMs in the textiles may contribute to increased losses through magnetoresistance effects, which affect charge carrier dynamics, and through eddy current losses in the iron particles under an alternating electric field.

The observed field-dependent modulation of ${ϵ}^{\prime }$ and D indicates that these materials could serve as flexible dielectric layers in tunable capacitive sensors of soft magneto-electronic systems.

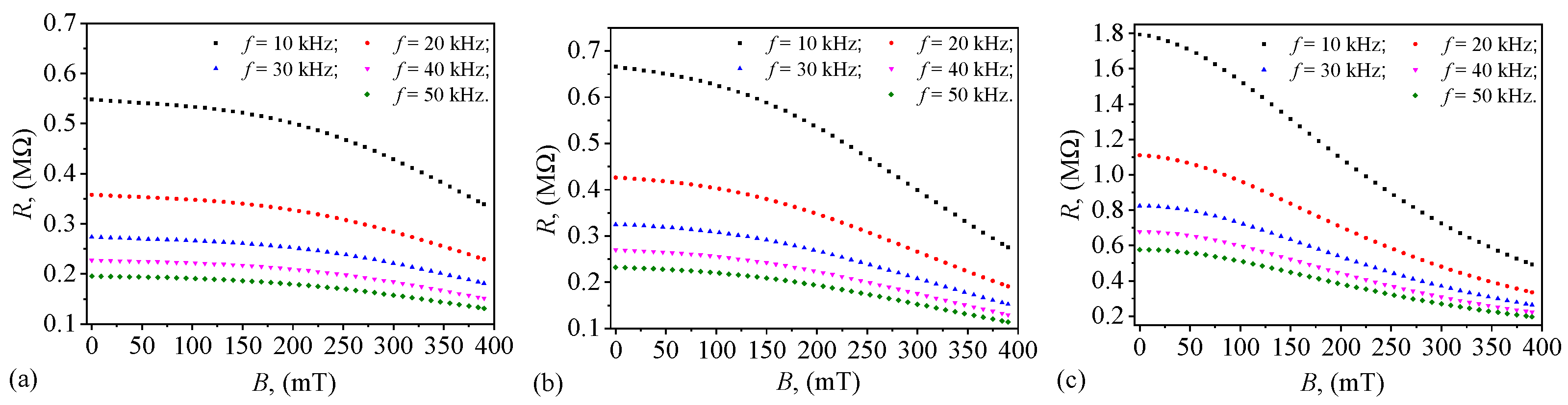
3.6. Resistance of Capacitors with STs

The results obtained in Figure 5 and Figure 6, respectively, suggest that from an electrical point of view, the capacitors can be represented as an electric dipole formed by a capacitor electrically connected in parallel with a resistor. Then, from the calculation relation of a planar electric capacitor and the calculation relation of a linear resistor and, respectively, using the definition of the loss tangent, the calculation formula for the resistor resistance is given by [27]:

$$R(\mathrm{M}\Omega )={\displaystyle \frac{159}{f\left(\mathrm{kHz}\right)C\left(\mathrm{pF}\right)D}}.$$

(2)

Then, the resistance measurements for ST₁, ST₂, and ST₃ are presented in Figure 7. The results show they exhibit distinct trends, complementing the previously analyzed capacitance and loss tangent behaviors. The resistance decreases with increasing frequency for all three textiles, which is expected in dielectric materials where conduction effects become less dominant at higher frequencies.

ST₁ consistently shows the lowest resistance values, indicating that the oil-dominated composition supports better charge transport or reduced interfacial barriers. In contrast, ST₃ exhibits significantly higher resistance across all frequencies, suggesting that the presence of solid microparticles introduces additional barriers to charge movement, leading to increased resistive losses. ST₂, which has an intermediate composition, shows resistance values between those of ST₁ and ST₃, reinforcing the role of PMs in increasing resistivity. This effect is likely due to interfacial charge trapping and disrupted charge percolation pathways in the composite structure. The higher standard deviation of average resistance observed in ST₃ suggests greater heterogeneity in resistive behavior, possibly due to variations in charge transport across different regions of the material.

4. Discussions

The findings of this study not only confirm the expected dielectric behavior of the manufactured STs but also reveal additional insights into their tunability, interaction mechanisms, and potential technological impact. Beyond the direct experimental observations, several aspects require further exploration to deepen the understanding of these materials’ behavior in real-world applications.

4.1. Synergistic Role of Magnetic and Dielectric Properties

One key observation is the ability of CIMs to modulate dielectric properties in the presence of a magnetic field. While previous studies have explored magnetodielectric effects in various composite materials, the unique integration of biocompatible components such as PSO and PMs provides new insights. The results indicate that the reorganization of CIMs under an applied field alters charge distribution within the textile, indirectly influencing capacitance and loss tangent.

A more detailed microscopic investigation could clarify whether this behavior is purely due to magnetic realignment or if additional interfacial effects—such as localized charge trapping or microstructural polarization anisotropy—are contributing. Future studies incorporating imaging techniques like scanning electron microscopy coupled with energy-dispersive X-ray spectroscopy could provide a more detailed picture of how the internal structure of these materials evolves in response to an applied field.

4.2. Interfacial Interactions and Charge Distribution

Another intriguing aspect is the nonlinear variation in dielectric loss with PM content. While the presence of PMs generally reduces capacitance, its influence on dielectric loss appears more complex. The results suggest that at certain concentrations, PMs contribute to energy dissipation, possibly by disrupting charge pathways or introducing additional sites for interfacial polarization.

The role of PSO as a dielectric modifier is also worth further investigation. It is well known that oils can influence charge carrier mobility in composite systems, but the exact contribution of PSO to dielectric behavior remains partially speculative. A systematic comparison with other bio-oils could help differentiate between effects specific to PSO and general trends observed in oil-impregnated textiles. Such comparative studies could be explored in future research, providing deeper insights into the influence of different natural additives on the dielectric properties of STs.

4.3. Time-Dependent and Environmental Effects

The study primarily focuses on the immediate response of STs to electromagnetic fields, but long-term stability remains an open question. Factors such as the following could all impact their real-world performance:

• Oxidation or degradation of PSO over time;
• Possible migration or aggregation of CIMs and PMs under repeated exposure to varying magnetic fields;
• Changes in the ST’s mechanical flexibility due to repeated stress cycles.

Future experiments should consider aging studies under different environmental conditions (e.g., humidity, temperature variations) to determine whether these materials maintain their tunability over extended use.

4.4. Towards a More Predictive Model

Finally, the experimental results provide valuable data for developing a predictive theoretical model of magnetodielectric effects in hybrid bio-based materials. The observed trends suggest that capacitance and loss tangent could be described using a generalized effective medium approximation, incorporating magnetically induced structural realignment, frequency-dependent polarization relaxation, and interfacial charge redistribution effects.

Models based on the dipolar approximation have been used to describe dielectric behaviour in composite materials [28,29]. Improving or extending these models by incorporating field-dependent dipolar interactions and charge redistribution mechanisms would lead to a more predictive framework. This allows for a more precise tuning of ST properties.

5. Conclusions

This study successfully demonstrates the fabrication and characterization of magnetically active STs composed of cotton fabric impregnated with CIMs, PSO, and PMs. The integration of these components enables tunable dielectric properties.

The experimental findings highlight the potential of these STs for applications in wearable electronics, biomedical devices, and electromagnetic shielding. The results reveal that the dielectric response of the STs is highly dependent on frequency, composition, and magnetic field strength.

Relative dielectric permittivity decreases with increasing frequency due to reduced dipole polarization, while the presence of PSO enhances charge storage, increasing dielectric permittivity. Conversely, the inclusion of PMs reduces dielectric permittivity, likely due to interfacial polarization effects and microstructural inhomogeneities. The presence of CIMs introduces magnetodielectric effects, which enable dynamic tuning of electrical properties under an applied magnetic field. This effect is most pronounced in ST₃, where a higher PM content leads to stronger field-dependent behavior. The analysis of electrical conductivity and resistance further supports these observations. ST₁, which contains the highest proportion of PSO, exhibits lower resistance and better charge transport properties, making it suitable for applications that require efficient energy storage and minimal dielectric losses. In contrast, ST₃, with a higher PM content, displays greater resistivity, suggesting an increased level of charge trapping and reduced electrical conductivity. The loss tangent follows a decreasing trend with frequency, with ST₁ demonstrating the lowest dielectric losses, indicating that low-loss STs can be designed for high-performance energy storage and sensing applications.

These findings suggest a broad range of technological applications for these STs. Their tunable dielectric permittivity makes them ideal for flexible capacitors and bioelectronic sensors in wearable electronics. The incorporation of bioactive components such as PSO and PMs provides additional functionality, making these materials promising candidates for biomedical applications, including wound healing and controlled drug delivery. Additionally, their magnetodielectric tunability suggests their potential use in electromagnetic shielding and reconfigurable RF devices, where adaptive field-dependent responses are desirable.

To maximize the potential of these materials, future research should focus on microscopic structural analysis using advanced imaging techniques such as scanning electron microscopy and energy-dispersive X-ray spectroscopy to better understand the underlying charge transport mechanisms. Long-term stability studies are also necessary to evaluate the durability of these textiles under mechanical stress and environmental exposure. Additionally, theoretical modeling should be developed to describe the interplay between magnetic field effects, interfacial polarization, and charge redistribution, providing a predictive framework for optimizing textile performance. Further exploration of alternative bioactive components may expand their functionality and broaden their applicability in biomedical and electronic applications.

Overall, this study highlights the multifunctional and adaptive nature of magnetically active textiles. By strategically adjusting material composition and external magnetic fields, their electrical properties can be customized for diverse real-world applications. These results open promising avenues for the next generation of intelligent, responsive, and eco-friendly textile-based devices.