Effects of Key Parameters on Thermal Conductivity of Carbon Nanotube–Epoxy Composites by Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Molecular Dynamics Simulation
2.1. Simulation Details
2.2. Computational Details
3. Results and Discussion
3.1. Thermal Properties of Epoxy Matrix
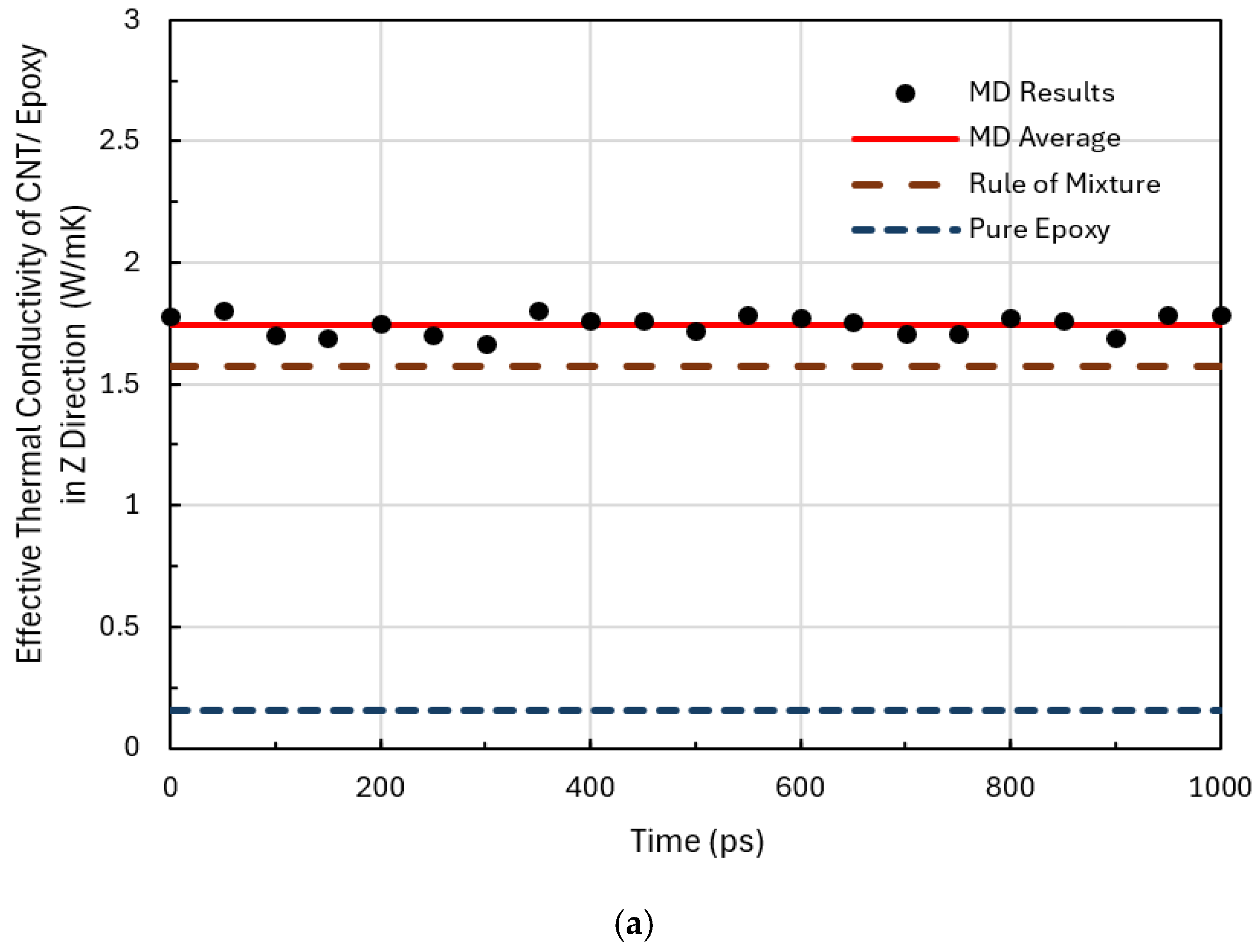
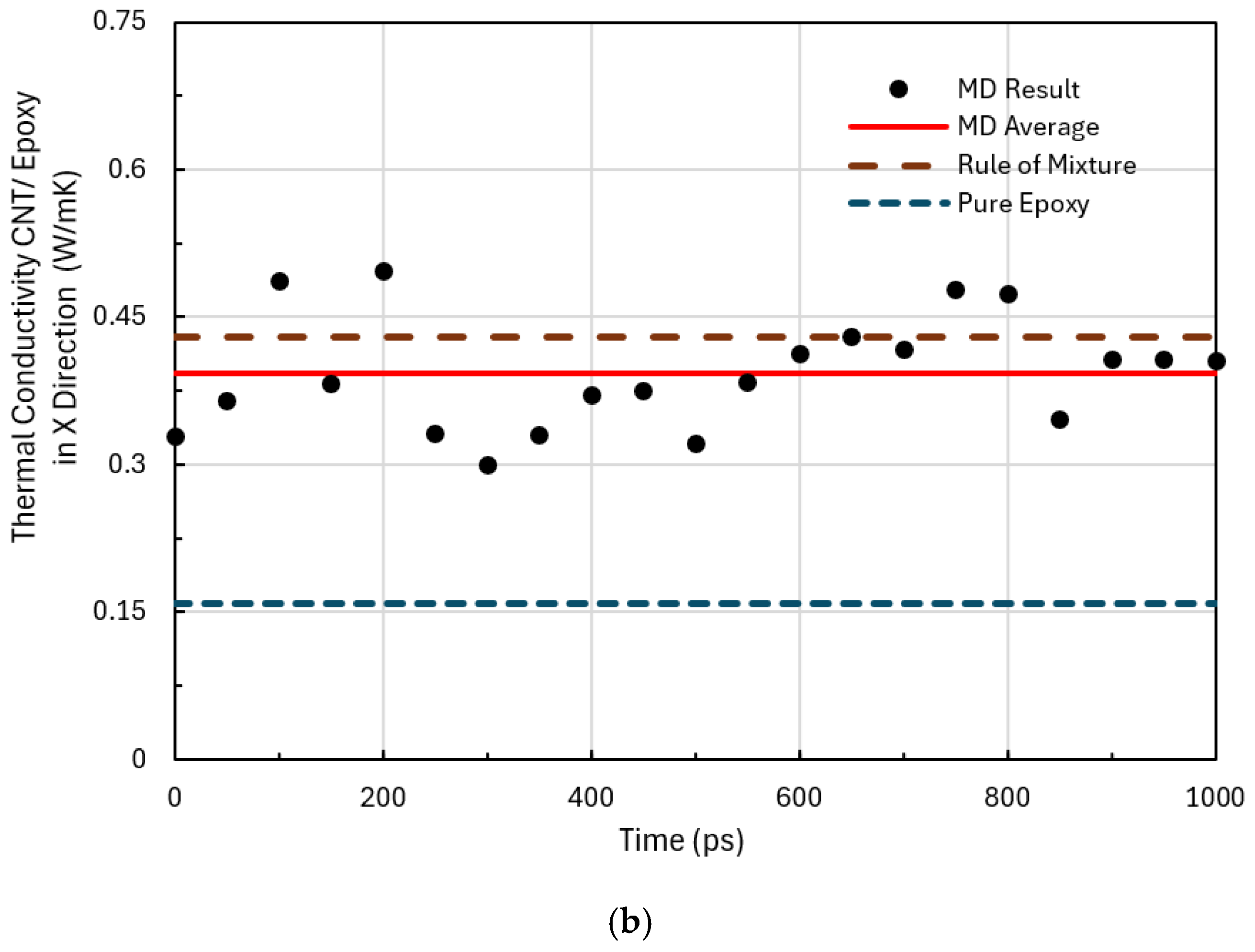
3.2. Thermal Properties of CNT-Reinforced Epoxy Composites (CRECs)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chung, S.; Lin, J. Thermal conductivity of epoxy resin composites filled with combustion synthesized h-BN particles. Molecules 2016, 21, 670. [Google Scholar] [CrossRef] [PubMed]
- Hussain, A.R.J.; Alahyari, A.A.; Eastman, S.A.; Thibaud-Erkey, C.; Johnston, S.; Sobkowicz, M.J. Review of polymers for heat exchanger applications: Factors concerning thermal conductivity. Appl. Therm. Eng. 2017, 113, 1118–1127. [Google Scholar]
- Kumanek, B.; Janas, D. Thermal conductivity of carbon nanotube networks: A review. J. Mater. Sci. 2019, 54, 7397–7427. [Google Scholar]
- Lee, D.; Yoo, J.; Kim, H.; Kang, B.; Park, S. Electrical and Thermal Properties of Carbon Nanotube Polymer Composites with Various Aspect Ratios. Materials 2022, 15, 1356. [Google Scholar] [CrossRef]
- Gérard, J.; Perret, P.; Chabert, B. Study of carbon/epoxy interface (or interphase): Effect of surface treatment of carbon fibers on the dynamic mechanical behavior of carbon/epoxy unidirectional composites. In Composite Materials; Springer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Najmi, L.; Hu, Z. Molecular dynamics simulations of effects of geometric parameters and temperature on mechanical properties of single-walled carbon nanotubes. J. Compos. Sci. 2024, 8, 293. [Google Scholar] [CrossRef]
- Demiroglu, S.; Singaravelu, V.; Seydibeyoğlu, M.Ö.; Misra, M.; Mohanty, A.K. The use of nanotechnology for fibre-reinforced polymer composites. In Composites Science and Engineering; Woodhead Publishing: Cambridge, UK, 2017; pp. 277–297. [Google Scholar]
- Li, Y.C.; Chu, N.; Jin, F.L.; Park, S.J. Recent advances in improvement of thermal conductivity of epoxy-based nanocomposites through addition of fillers. Polymer 2024, 313, 127678. [Google Scholar]
- Benega, M.A.G.; Silva, W.M.; Schnitzler, M.C.; Andrade, R.J.E.; Ribeiro, H. Improvements in thermal and mechanical properties of composites based on epoxy-carbon nanomaterials—A brief landscape. Polym. Test. 2021, 98, 107180. [Google Scholar]
- Siddiqui, V.U.; Sapuan, S.M.; Hassan, M.R. Innovative dispersion techniques of graphene nanoplatelets (GNPs) through mechanical stirring and ultrasonication: Impact on morphological, mechanical, and thermal properties of epoxy nanocomposites. Def. Technol. 2025, 43, 13–25. [Google Scholar]
- Das, C.; Tamrakar, S.; Kiziltas, A.; Xie, X. Incorporation of biochar to improve mechanical, thermal and electrical properties of polymer composites. Polymers 2021, 13, 2663. [Google Scholar] [CrossRef]
- Moghanlou, M.R.; Azizian-Farsani, E.; Mahmoudi, A.; Khonsari, M.M. Optimization of FDM parameters for enhanced mechanical properties of chopped carbon fiber-reinforced polymer composites. Prog. Addit. Manuf. 2024, 10, 2073–2088. [Google Scholar]
- Arash, B.; Wang, Q.; Varadan, V. Mechanical properties of carbon nanotube/polymer composites. Sci. Rep. 2014, 4, 6479. [Google Scholar] [CrossRef] [PubMed]
- Young, R.J.; Liu, M.; Kinloch, I.A.; Li, S.; Zhao, X.; Vallés, C.; Papageorgiou, D.G. The mechanics of reinforcement of polymers by graphene nanoplatelets. Compos. Sci. Technol. 2018, 154, 110–116. [Google Scholar] [CrossRef]
- Najmi, L.; Hu, Z. Review on Molecular Dynamics Simulations of Effects of Carbon Nanotubes (CNTs) on Electrical and Thermal Conductivities of CNT-Modified Polymeric Composites. J. Compos. Sci. 2023, 7, 165. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, B.; Chen, S.; Shao, Y.H.; Hammond, P. Layer-by-layer assembly of all carbon nanotube ultrathin films for electrochemical applications. J. Am. Chem. Soc. 2009, 131, 671–679. [Google Scholar] [CrossRef]
- Najmi, L.; Zebarjad, S.; Janghorban, K. Effects of Carbon Nanotubes on the Compressive and Flexural Strength and Mi-croscopic Structure of Epoxy Honeycomb Sandwich Panels. Polym. Sci. Ser. B 2023, 65, 220–229. [Google Scholar] [CrossRef]
- Aqel, A.; El-Nour, K.M.M.A.; Ammar, R.A.A.; Al-Warthan, A. Carbon nanotubes, science and technology part (I) structure, synthesis and characterisation. Arab. J. Chem. 2012, 5, 1–23. [Google Scholar] [CrossRef]
- Shundo, A.; Yamamoto, S.; Tanaka, K. Network formation and physical properties of epoxy resins for future practical applications. JACS Au 2022, 2, 1522–1542. [Google Scholar] [CrossRef]
- Gojny, F.H.; Wichmann, M.H.G.; Köpke, U.; Fiedler, B.; Schulte, K. Carbon nanotube-reinforced epoxy-composites: Enhanced stiffness and fracture toughness at low nanotube content. Compos. Sci. Technol. 2004, 64, 2363–2371. [Google Scholar] [CrossRef]
- Nurazzi, N.M.; Asyraf, M.R.M.; Khalina, A.; Abdullah, N.; Sabaruddin, F.A.; Kamarudin, S.H.; Ahmad, S.; Mahat, A.M.; Lee, C.L.; Aisyah, H.A.; et al. Fabrication, functionalization, and application of carbon nanotube-reinforced polymer composite: An overview. Polymers 2021, 13, 1047. [Google Scholar] [CrossRef]
- King, J.A.; Barton, R.L.; Hauser, R.A.; Keith, J.M. Synergistic effects of carbon fillers in electrically and thermally conductive liquid crystal polymer based resins. Polym. Compos. 2008, 29, 421–428. [Google Scholar] [CrossRef]
- Choi, S.; Zhang, Z.; Yu, W.; Lockwood, F.; Grulke, E. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Biercuk, M.; Llaguno, M.; Radosavljevic, M.; Hyun, J.; Johnson, A.; Fischer, J. Carbon nanotubes for thermal management. Appl. Phys. Lett. 2002, 80, 2767–2769. [Google Scholar] [CrossRef]
- Shen, Z.; Bateman, S.; Wu, D.; McMahon, P.; Dell’Olio, M.; Gotama, J. The effects of carbon nanotubes on mechanical and thermal properties of woven glass fibre reinforced polyamide nanocomposites. Compos. Sci. Technol. 2009, 69, 239–244. [Google Scholar]
- Azizian-Farsani, E.; Mahmoudi, A.; Khonsari, M.M.; Moghanlou, M.R. Accelerated fatigue characterization of additively manufactured continuous carbon fiber reinforced thermoplastic: A thermodynamic approach. Compos. Part A Appl. Sci. Manuf. 2025, 192, 108805. [Google Scholar]
- Das, A.; Stöckelhuber, K.; Jurk, R.; Saphiannikova, M.; Fritzsche, J.; Lorenz, H.; Klüppel, M.; Heinrich, G. Modified and unmodified multiwalled carbon nanotubes in high performance solution-styrene–butadiene and butadiene rubber blends. Polymer 2008, 49, 5276–5283. [Google Scholar]
- Najmi, L.; Hu, Z. Effects of carbon nanotubes on thermal behavior of epoxy resin composites. J. Compos. Sci. 2023, 7, 313. [Google Scholar] [CrossRef]
- Jian, W.; Wang, X.; Lu, H.; Lau, D. Molecular dynamics simulations of thermodynamics and shape memory effect in CNT-epoxy nanocomposites. Compos. Sci. Technol. 2021, 211, 108849. [Google Scholar]
- Guo, Y.; Liu, J.; Lu, Y.; Dong, D.; Wang, W.; Zhang, L. A combined molecular dynamics simulation and experimental method to study the compatibility between elastomers and resins. RSC Adv. 2018, 8, 14401–14413. [Google Scholar]
- Chan, H.; Nordlund, K.; Peltola, J.; Gossmann, H.-J.; Ma, N.; Srinivasan, M.; Benistant, F.; Chan, L. The effect of interatomic potential in molecular dynamics simulation of low energy ion implantation. Nucl. Instrum. Methods Phys. Res. B 2005, 228, 240–244. [Google Scholar]
- Hernandez, S. Molecular Dynamic Simulation of Thermo-Mechanical Properties of Ultra-Thin Poly (Methyl Meth-Acrylate) Films. Ph.D. Thesis, Texas A&M University, Brazos County, TX, USA, 2010. [Google Scholar]
- Najmi, L.; Hu, Z. Effects of Topological Parameters on Thermal Properties of Carbon Nanotubes via Molecular Dynamics Simulation. J. Compos. Sci. 2024, 8, 37. [Google Scholar] [CrossRef]
- Clancy, T.; Frankland, S.; Hinkley, J.; Gates, T. Multiscale modeling of thermal conductivity of polymer/carbon nanocomposites. Int. J. Therm. Sci. 2010, 49, 1555–1560. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase Applications—Overview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Rajasekaran, G.; Kumar, R.; Parashar, A. Tersoff potential with improved accuracy for simulating graphene in molecular dynamics environment. Mater. Res. Express 2016, 3, 035011. [Google Scholar] [CrossRef]
- Tersoff, J. Empirical interatomic potential for carbon, with applications to amorphous carbon. Phys. Rev. 1988, 61, 2879–2882. [Google Scholar]
- Uvarov, N.F. Estimation of composites conductivity using a general mixing rule. Solid State Ion. 2000, 136–137, 1267–1272. [Google Scholar]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar]
- Nejatolahi, M.; Golneshan, A.; Kamali, R.; Sabbaghi, S. Nonequilibrium versus equilibrium molecular dynamics for calculating the thermal conductivity of nanofluids. J. Therm. Anal. Calorim. 2021, 144, 1467–1481. [Google Scholar] [CrossRef]
- Chang, C.; Okawa, D.; Garcia, H.; Majumdar, A.; Zettl, A. Breakdown of Fourier’s Law in Nanotube Thermal Conductors. Phys. Rev. Lett. 2008, 101, 075903. [Google Scholar]
- Lussetti, E.; Terao, T.; Müller-Plathe, F. Nonequilibrium Molecular Dynamics Calculation of the Thermal Conductivity of Amorphous Polyamide-6,6. J. Phys. Chem. B 2007, 111, 11516–11523. [Google Scholar]
- Ezquerro, C.S.; Laspalas, M.; Chiminelli, A.; Serrano, F.; Valero, C. Interface Characterization of Epoxy Resin Nanocomposites: A Molecular Dynamics Approach. Fibers 2018, 6, 54. [Google Scholar] [CrossRef]
- Keryvin, V.; Méchin, P.; Fabing, E.; Pillin, I.; Mahé-Flahaut, K.; Palabe, A.L. Counter-intuitive effect of the degree of cure of epoxy resins on the compressive strength of continuous fibre composites. Compos. Part B Eng. 2024, 287, 111836. [Google Scholar]
- Shams, A.; Papon, E.; Shinde, P.; Bara, J. Degree of Cure, Microstructures, and Properties of Carbon/Epoxy Composites Processed via Frontal Polymerization. Polymers 2024, 16, 1493. [Google Scholar] [CrossRef] [PubMed]
- Daissè, G.; Marcon, M.; Zecchini, M.; Wan-Wendner, R. Cure-dependent loading rate effects on strength and stiffness of particle-reinforced thermoset polymers. Polymer 2022, 259, 125326. [Google Scholar]
- Du, Y.; Zhao, G.; Shi, G.; Wang, Y.; Li, W.; Ren, S. Effect of crosslink structure on mechanical properties, thermal stability and flame retardancy of natural flavonoid based epoxy resins. Eur. Polym. J. 2022, 162, 110877. [Google Scholar]
- Delhommelle, J.; Millié, P. Inadequacy of the Lorentz-Berthelot combining rules for accurate predictions of equilibrium properties by molecular simulation. Mol. Phys. 2001, 99, 619–625. [Google Scholar]
- Alamusi, N.; Hu, N.; Jia, B.; Arai, M.; Yan, C.; Li, J.; Liu, Y.; Atobe, S.; Fukunaga, H. Prediction of thermal expansion properties of carbon nanotubes using molecular dynamics simulations. Comput. Mater. Sci. 2012, 54, 249–254. [Google Scholar] [CrossRef]
- Brown, E.N.; White, S.R.; Sottos, N.R. Fatigue crack propagation in microcapsule toughened epoxy. J. Mater. Sci. 2006, 41, 6266–6273. [Google Scholar] [CrossRef]
- Garrett, K.W.; Rosenberg, H.M. The thermal conductivity of epoxy-resin/powder composite materials. J. Phys. D Appl. Phys. 1974, 7, 1247–1258. [Google Scholar]
- Licari, J.J. Coating Materials for Electronic Applications: Polymers, Processing, Reliability, Testing; William Andrew Publishing: Norwich, NY, USA, 2003; Volume 22, pp. 20647–20655. [Google Scholar]
- Wan, X.; Demir, B.; An, M.; Walsh, T.R.; Yang, N. Thermal conductivities and mechanical properties of epoxy resin as a function of the degree of cross-linking. Int. J. Heat Mass Transf. 2021, 180, 121821. [Google Scholar]
- Choi, J.; Song, H.; Jung, J.; Yu, J.; You, N.-H.; Goh, M. Effect of crosslink density on thermal conductivity of epoxy/carbon nanotube nanocomposites. J. Appl. Polym. Sci. 2017, 134, 44253. [Google Scholar] [CrossRef]
- Zhao, Y.; Kikugawa, G.; Kawagoe, Y.; Shirasu, K.; Okabe, T. Molecular-scale investigation on relationship between thermal conductivity and the structure of crosslinked epoxy resin. Int. J. Heat Mass Transf. 2022, 198, 123429. [Google Scholar]
- Wang, H.; Xiao, E.; Fan, T.; Li, X.; Xiao, W. Calculations of factors that affect thermal conductivity in epoxy composites with hybrid carbon nanotube and graphene nanoplatelet. Mater. Res. Express 2020, 7, 025031. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, J.; Jiang, D.; Wang, S.; Gu, Y.; Li, M.; He, Y. Interaction between carbon nanotubes with functional groups and epoxy resin and its effect on thermal properties of carbon nanotubes/epoxy composites. J. Compos. Mater. 2022, 56, 1287–1298. [Google Scholar] [CrossRef]
- Ciecierska, E.; Boczkowska, A.; Kurzydlowski, K.; Rosca, I.D.; Van Hoa, S. The effect of carbon nanotubes on epoxy matrix nanocomposites. J. Therm. Anal. Calorim. 2013, 111, 1019–1024. [Google Scholar] [CrossRef]
- Xiao, W.; Luo, X.; Ma, P.; Zhai, X.; Fan, T.; Li, X. Structure factors of carbon nanotubes on the thermal conductivity of carbon nanotube/epoxy composites. AIP Adv. 2018, 8, 035107. [Google Scholar] [CrossRef]
- Russ, M.; Rahatekar, S.S.; Koziol, K.; Farmer, B.; Peng, H.-X. Length-dependent electrical and thermal properties of carbon nanotube-loaded epoxy nanocomposites. Compos. Sci. Technol. 2013, 81, 42–47. [Google Scholar] [CrossRef]
- Jakubinek, M.B.; White, M.A.; Mu, M.; Winey, K.I. Temperature dependence of thermal conductivity enhancement in single-walled carbon nanotube/polystyrene composites. Appl. Phys. Lett. 2010, 96, 083105. [Google Scholar] [CrossRef]
- Wu, L.K.; Ying, J. Effect of CNT arrays on electrical and thermal conductivity of epoxy resins. Adv. Mater. Res. 2014, 1043, 27–30. [Google Scholar]
- Gardea, F.; Lagoudas, D.C. Characterization of electrical and thermal properties of carbon nanotube/epoxy composites. Compos. Part B Eng. 2014, 56, 611–620. [Google Scholar]
- Hone, J.; Whitney, M.; Zettl, A. Thermal conductivity of single-walled carbon nanotubes. Synth. Met. 1999, 103, 2498–2499. [Google Scholar]
- Struzziero, G.; Remy, B.; Skordos, A.A. Measurement of thermal conductivity of epoxy resins during cure. J. Appl. Polym. Sci. 2019, 136, 47015. [Google Scholar] [CrossRef]
- Peng, L.; Zeng, F.; Mikhalchan, A.; Tran, T.; Jewell, D.; Duong, H.; Marconnet, A. Continuous Carbon Nanotube-Based Fibers and Films for Applications Requiring Enhanced Heat Dissipation. ACS Appl. Mater. Interfaces 2016, 8, 19359–19366. [Google Scholar]
- Marconnet, A.; Yamamoto, N.; Panzer, M.; Wardle, B.; Goodson, K. Thermal Conduction in Aligned Carbon Nanotube-Polymer Nanocomposites with High Packing Density. ACS Nano 2011, 5, 4818–4825. [Google Scholar] [CrossRef] [PubMed]
- Sarode, A.; Ahmed, Z.; Basarkar, P.; Bhargav, A.; Banerjee, D.A. A molecular dynamics approach of the role of carbon nanotube diameter on thermal interfacial resistance through vibrational mismatch analysis. Int. J. Therm. Sci. 2017, 122, 33–38. [Google Scholar] [CrossRef]
- Kamae, T.; Drzal, L.T. Mechanical and thermal properties of high volume-fraction carbon nanotube/epoxy composites, and property enhancement by UV ozone treatment of carbon nanotubes. Polym. Compos. 2023, 44, 7855–7864. [Google Scholar] [CrossRef]
- Kadhim, B.; Salim, F.; Muhsen, H. Thermal properties of carbon nanotubes reinforced epoxy resin nano composites. J. Nanotechnol. 2011, 22, 276–290. [Google Scholar]
- Jacquet, E.; Trivaudey, F.; Varchon, D. Calculation of the transverse modulus of a unidirectional composite material and of the modulus of an aggregate. Application of the rule of mixtures. Compos. Sci. Technol. 2000, 60, 345–350. [Google Scholar] [CrossRef]
- Ji, T.; Feng, Y.; Qin, M.; Feng, W. Thermal conducting properties of aligned carbon nanotubes and their polymer composites. Compos. Part A Appl. Sci. Manuf. 2016, 91, 351–369. [Google Scholar] [CrossRef]

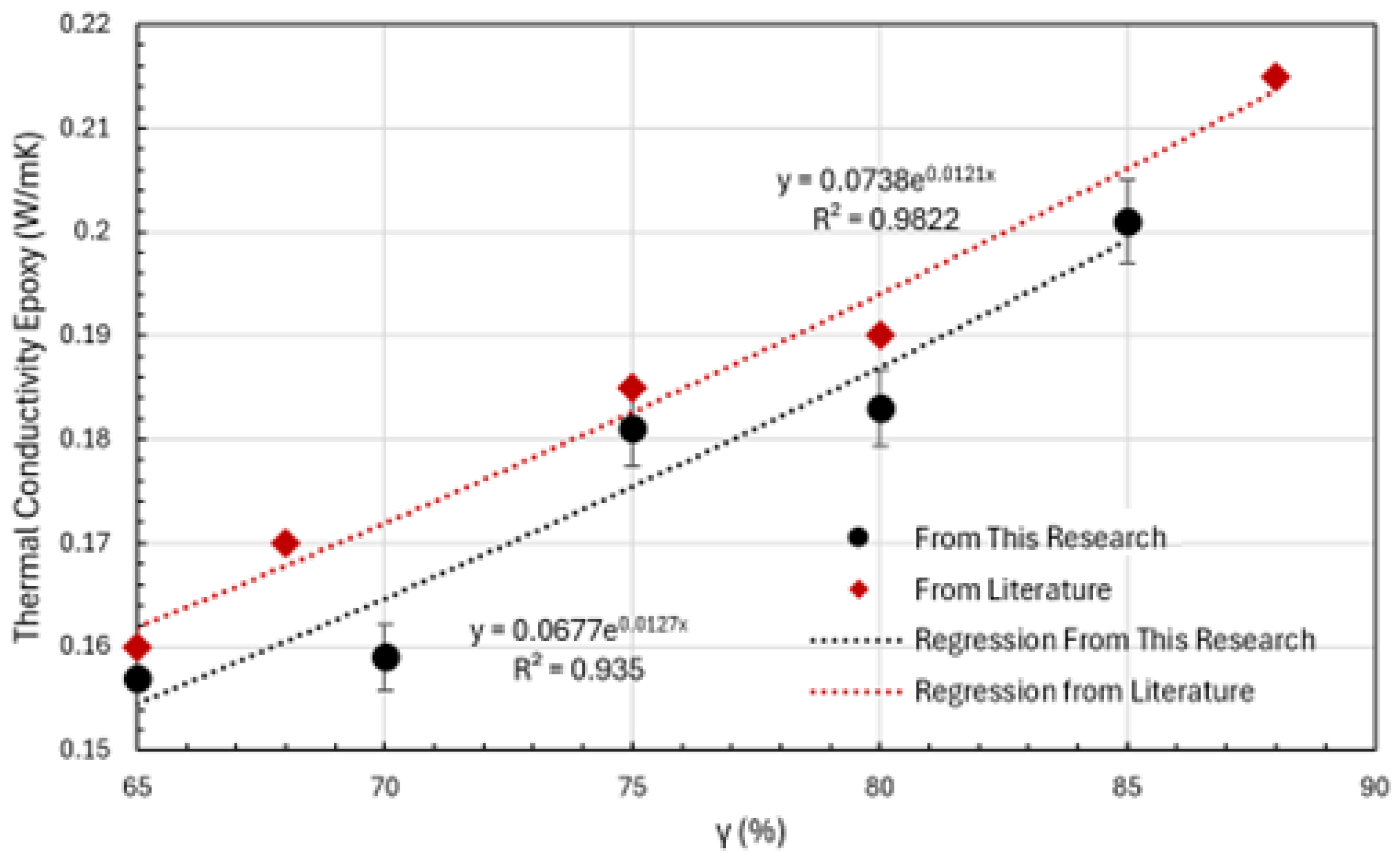



| γ (%) | 65 | 70 | 75 | 80 | 85 | Note |
|---|---|---|---|---|---|---|
| λ from MD Simulation | 0.157 ±0.0031 | 0.159 ±0.0032 | 0.181 ±0.0031 | 0.183 ±0.0036 | 0.201 ±0.0040 | This Study |
| γ (%) | 65 | 68 | 75 | 80 | 88 | Note |
| λ from Literature | 0.16 | 0.17 | 0.185 | 0.19 | 0.215 | [1,51,52] |
| γ (%) | 65 | 70 | 75 | 80 | Note |
|---|---|---|---|---|---|
| λ from MD Simulation | 1.67 ±0.0167 | 1.74 ±0.0174 | 1.78 ±0.0178 | 1.79 ±0.0179 | This Study |
| γ (%) | 68 | 75 | 80 | 85 | Note |
| λ from Literature | 0.16 | 0.17 | 0.185 | 0.19 | [55,56,57] |
| L (nm) | 0 | 2 | 4 | 6 | 8.1 | 10 | 20 | Note |
|---|---|---|---|---|---|---|---|---|
| λ from MD Simulation | 0.159 ±0.004 | 1.20 ±0.036 | 1.69 ±0.050 | 1.74 ±0.052 | 1.75 ±0.052 | 1.75 ±0.050 | 1.75 ±0.052 | This Study |
| L (nm) | 0 | 2 | 4.2 | 6 | 8 | 16 | 24 | Note |
| λ from Literature | 0.17 | 1.38 | 1.73 | 1.79 | 1.8 | 1.8 | 1.8 | [58,59,60] |
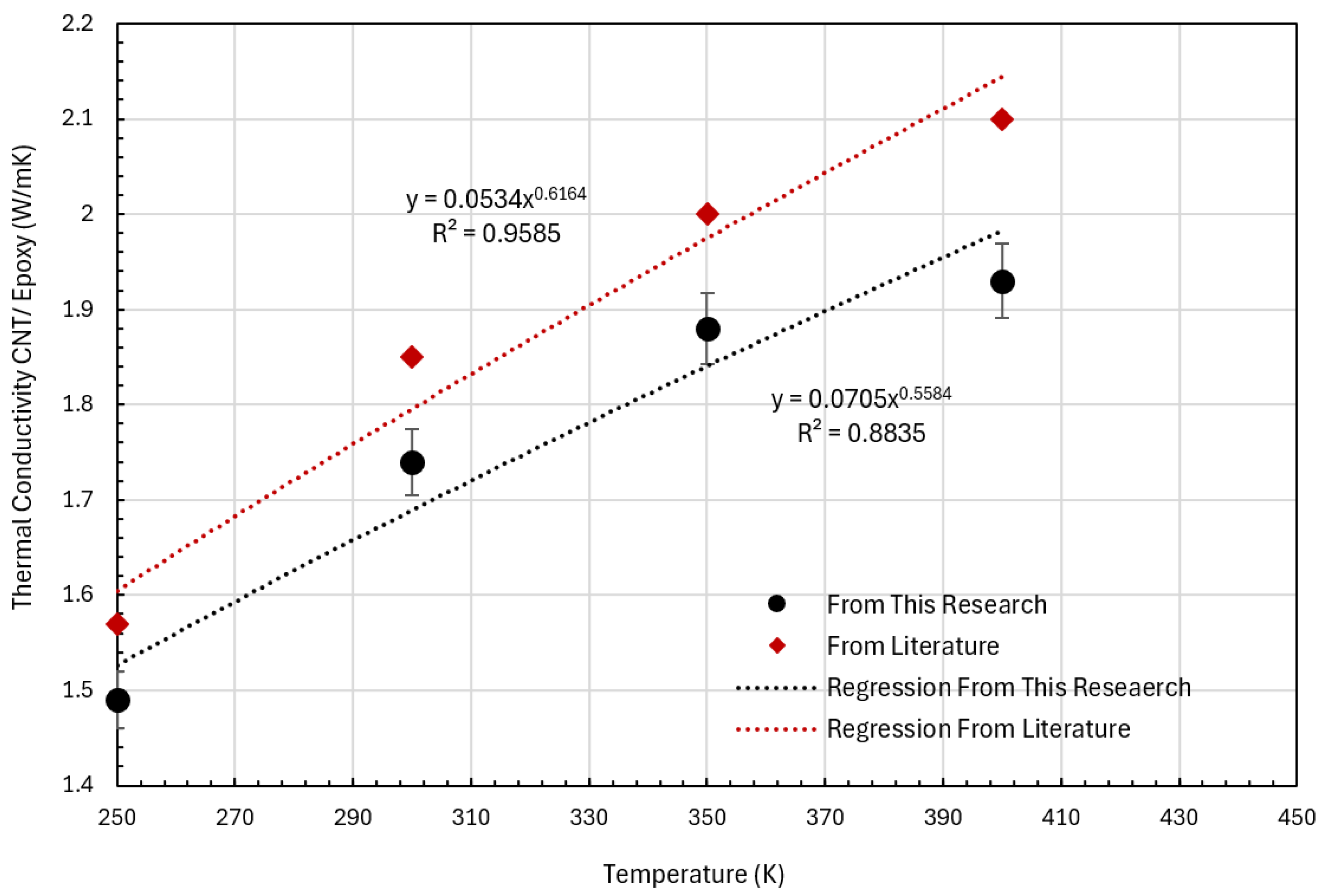
| T (k) | 250 | 300 | 350 | 400 | Note |
|---|---|---|---|---|---|
| λ from MD Simulation | 1.49 ±0.030 | 1.74 ±0.035 | 1.88 ±0.038 | 1.93 ±0.038 | This Study |
| λ from Literature | 1.57 | 1.85 | 2 | 2.1 | [61,62] |
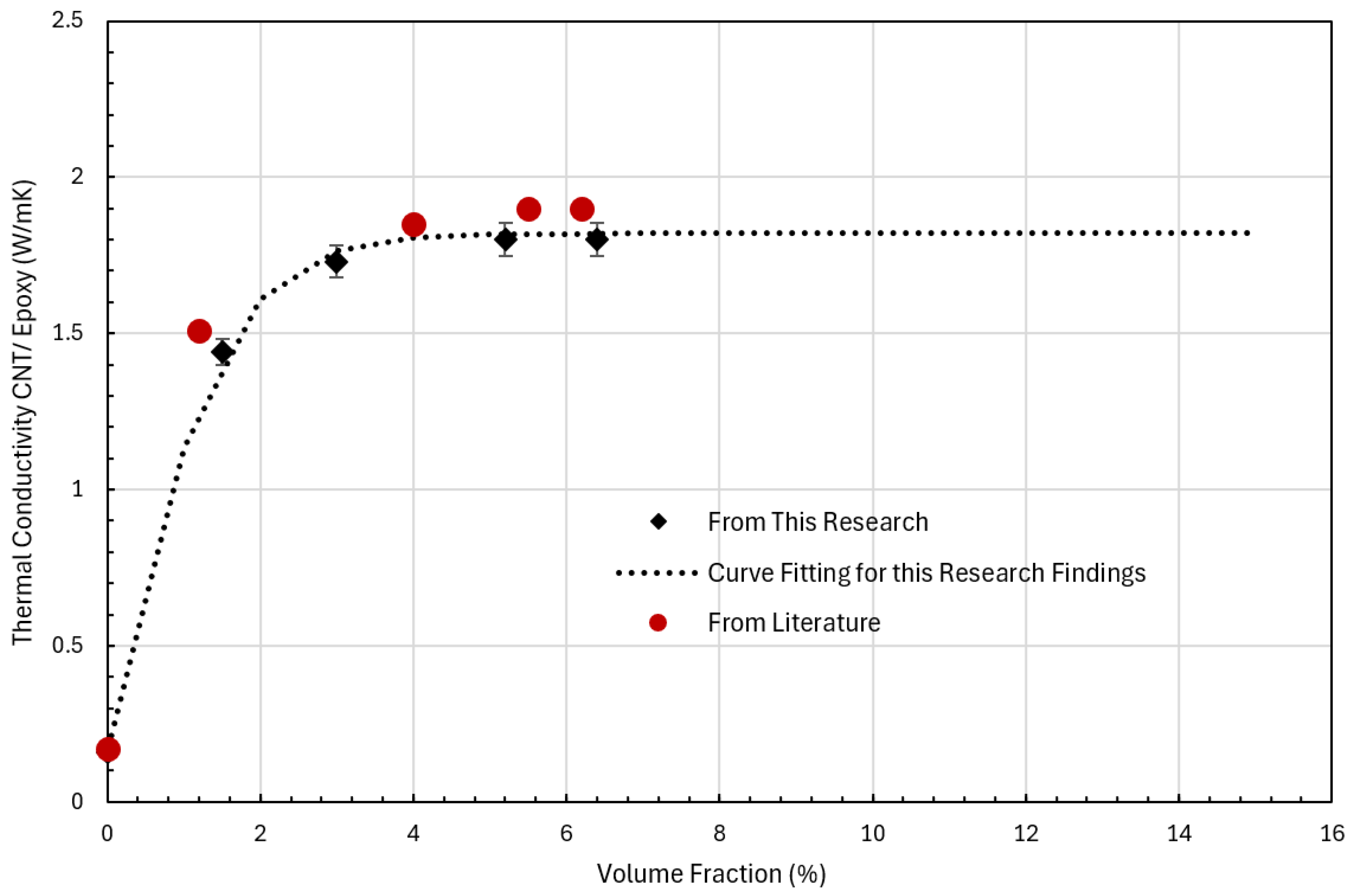
| f (%) | 0 | 1.5 | 3 | 5.2 | 6.4 | Note |
|---|---|---|---|---|---|---|
| λ from MD Simulation | 0.159 ±0.004 | 1.44 ±0.043 | 1.73 ±0.051 | 1.80 ±0.055 | 1.80 ±0.057 | This Study |
| f (%) | 0 | 1.2 | 4 | 5.5 | 6.2 | Note |
| λ from Literature | 0.17 | 1.51 | 1.85 | 1.9 | 1.9 | [64,65,66,68,69,70] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najmi, L.; Hu, Z. Effects of Key Parameters on Thermal Conductivity of Carbon Nanotube–Epoxy Composites by Molecular Dynamics Simulations. J. Compos. Sci. 2025, 9, 159. https://doi.org/10.3390/jcs9040159
Najmi L, Hu Z. Effects of Key Parameters on Thermal Conductivity of Carbon Nanotube–Epoxy Composites by Molecular Dynamics Simulations. Journal of Composites Science. 2025; 9(4):159. https://doi.org/10.3390/jcs9040159
Chicago/Turabian StyleNajmi, Lida, and Zhong Hu. 2025. "Effects of Key Parameters on Thermal Conductivity of Carbon Nanotube–Epoxy Composites by Molecular Dynamics Simulations" Journal of Composites Science 9, no. 4: 159. https://doi.org/10.3390/jcs9040159
APA StyleNajmi, L., & Hu, Z. (2025). Effects of Key Parameters on Thermal Conductivity of Carbon Nanotube–Epoxy Composites by Molecular Dynamics Simulations. Journal of Composites Science, 9(4), 159. https://doi.org/10.3390/jcs9040159







