Size-Dependent Flexural Analysis of Thick Microplates Using Consistent Couple Stress Theory
Abstract
1. Introduction
2. Solution Procedure Based on Couple Stress Theory
2.1. Governing Equations
2.2. Analytical Solution
2.2.1. System of Equations
2.2.2. Determination of Coefficients, aij
- In Equations (A1), (A11) and (A24), the same coefficients of can be obtained. Thus, one can obtain .
- In Equations (A4), (A14) and (A21), the same coefficients of can be obtained. Thus, one can obtain .
- In Equations (A3), (A13) and (A26), although the coefficients of are different, these equations are identical.
- In Equations (A6), (A16) and (A23), although the coefficients of are different, these equations are identical.
- In Equations (A2), (A12) and (A25), the same coefficients of can be obtained. Thus, one can obtain .
- In Equations (A5), (A15) and (A22), the same coefficients of can be obtained. Thus, one can obtain .
- In Equations (A8), (A18) and (A30), although the coefficients of are different, these equations are identical.
- In Equations (A10), (A20) and (A28), the same coefficients of can be obtained.
- In Equations (A9), (A19) and (A27), the same coefficients of can be obtained.
- Solving the equations, the coefficients are determined as follows:
2.2.3. Boundary Conditions
- Bottom surface: .
- Top surface: .
3. Classical Plate Theory
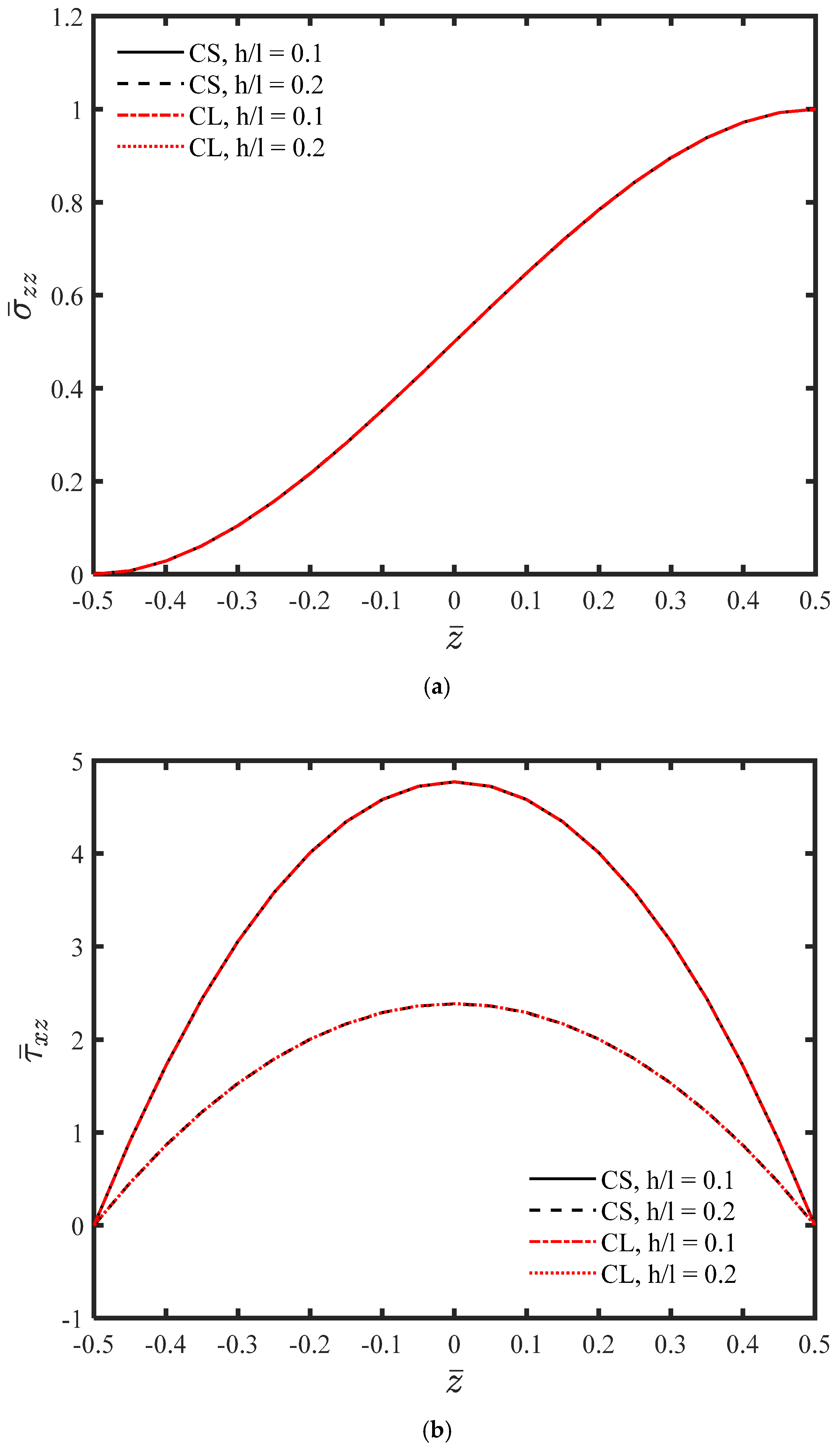
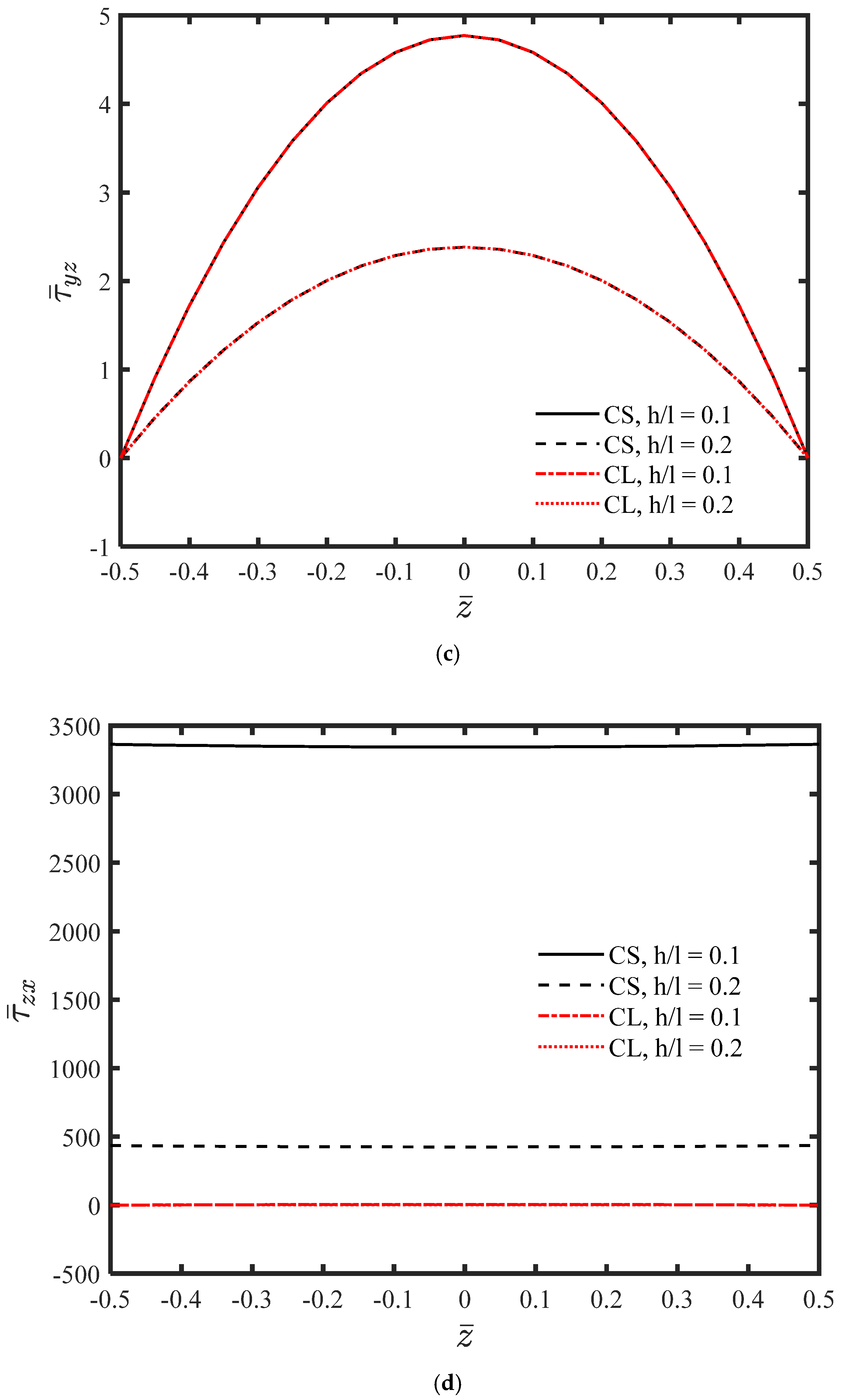
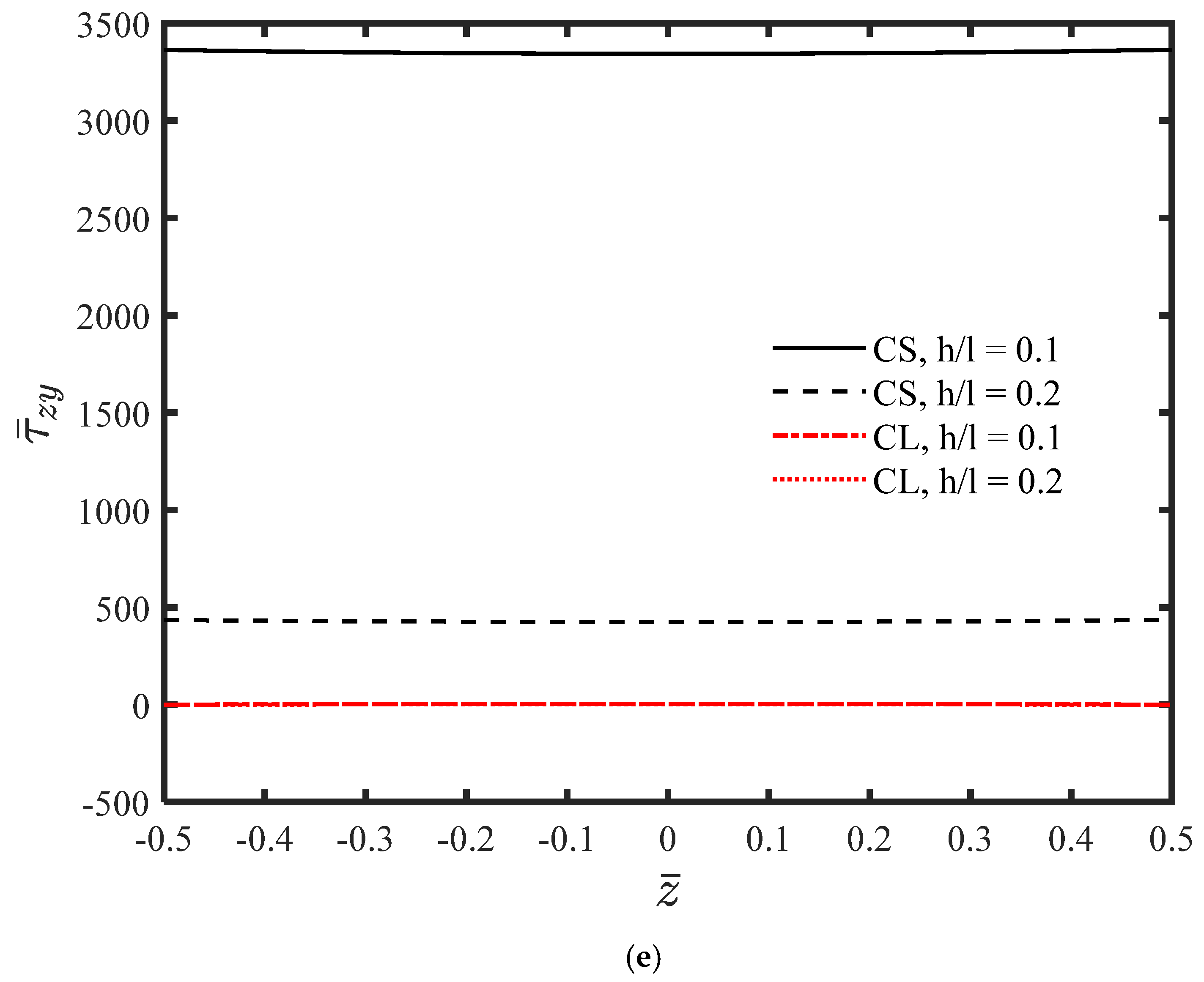
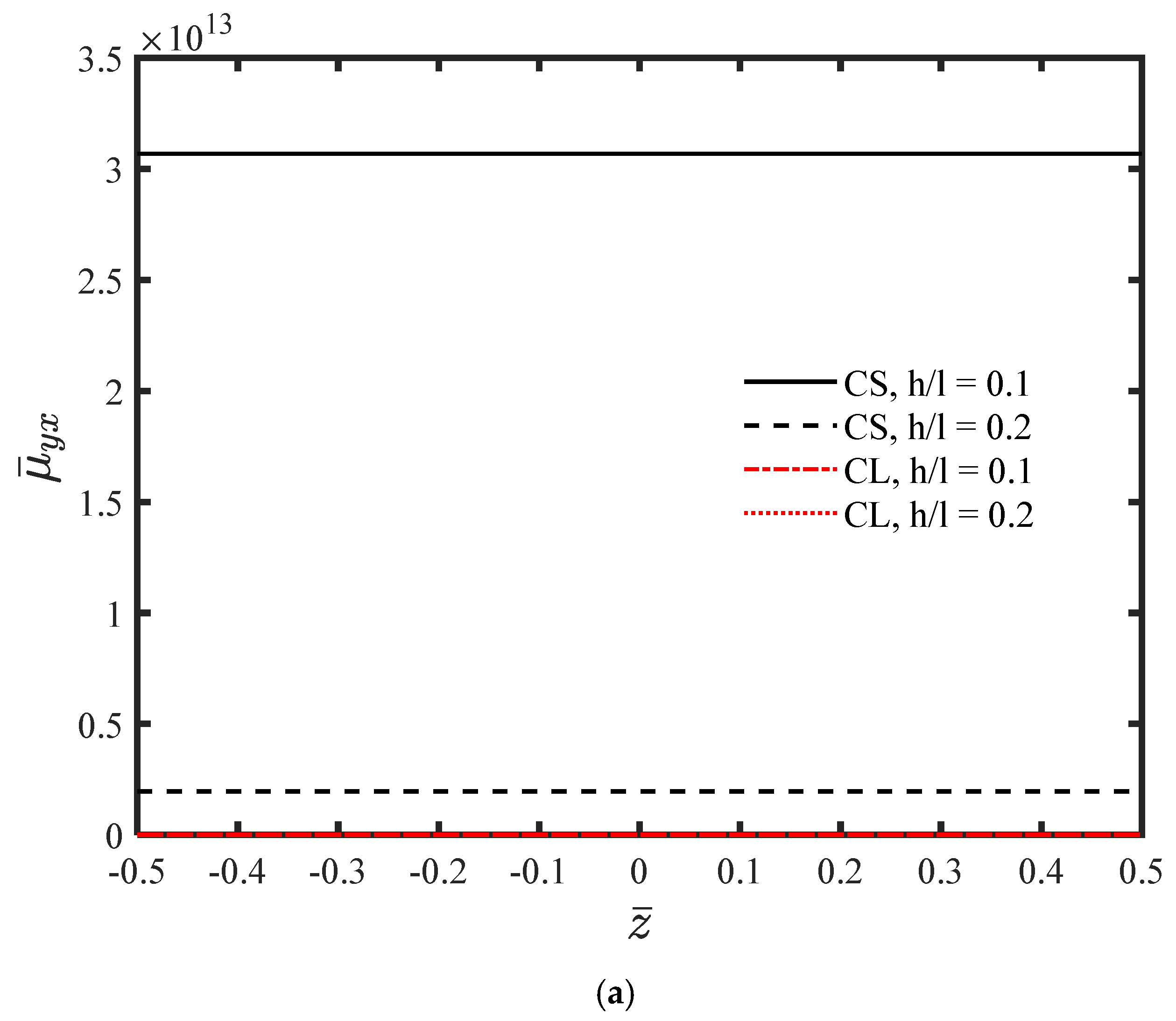
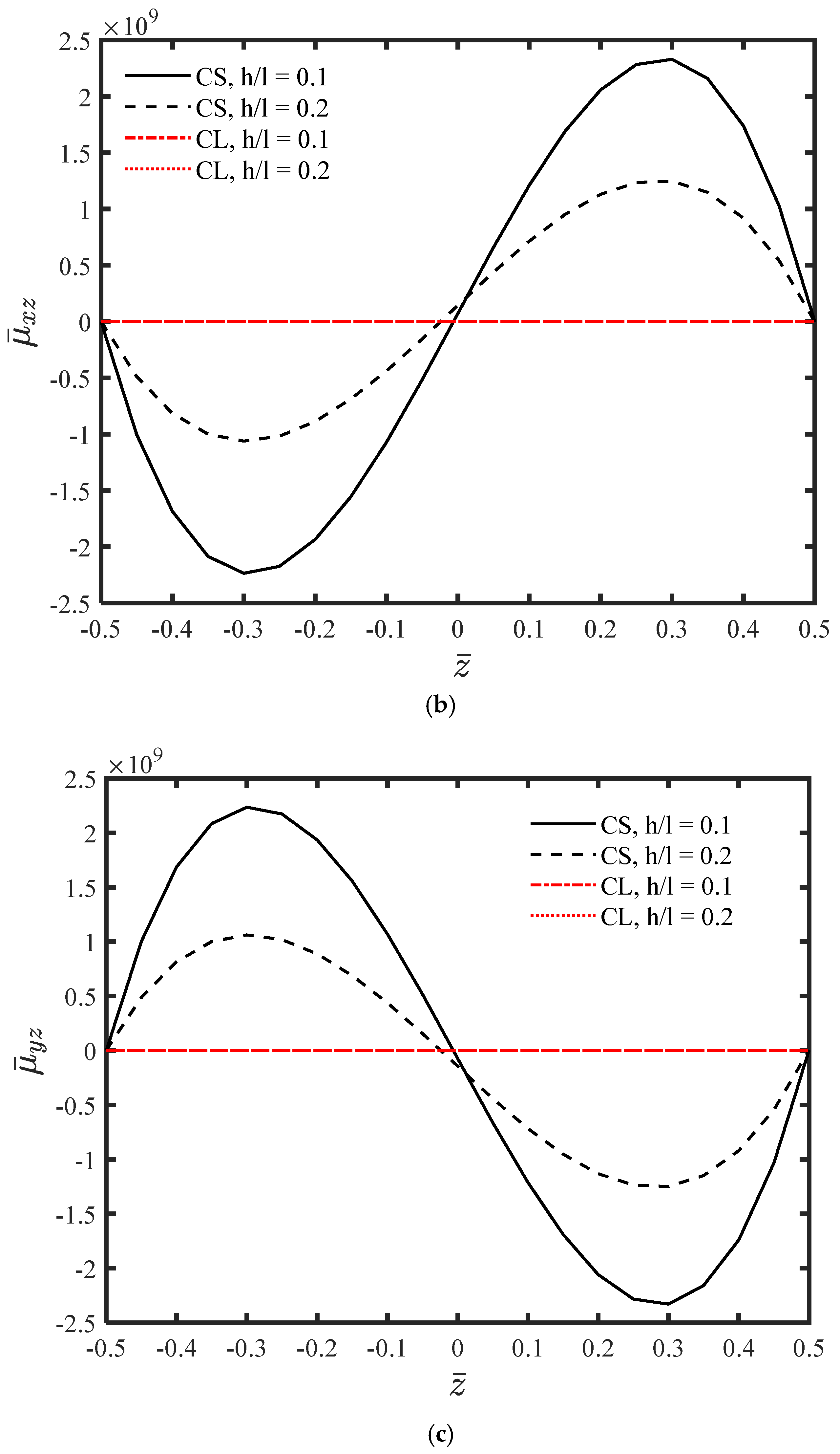
4. Numerical Results and Discussion
5. Conclusions
- 1-
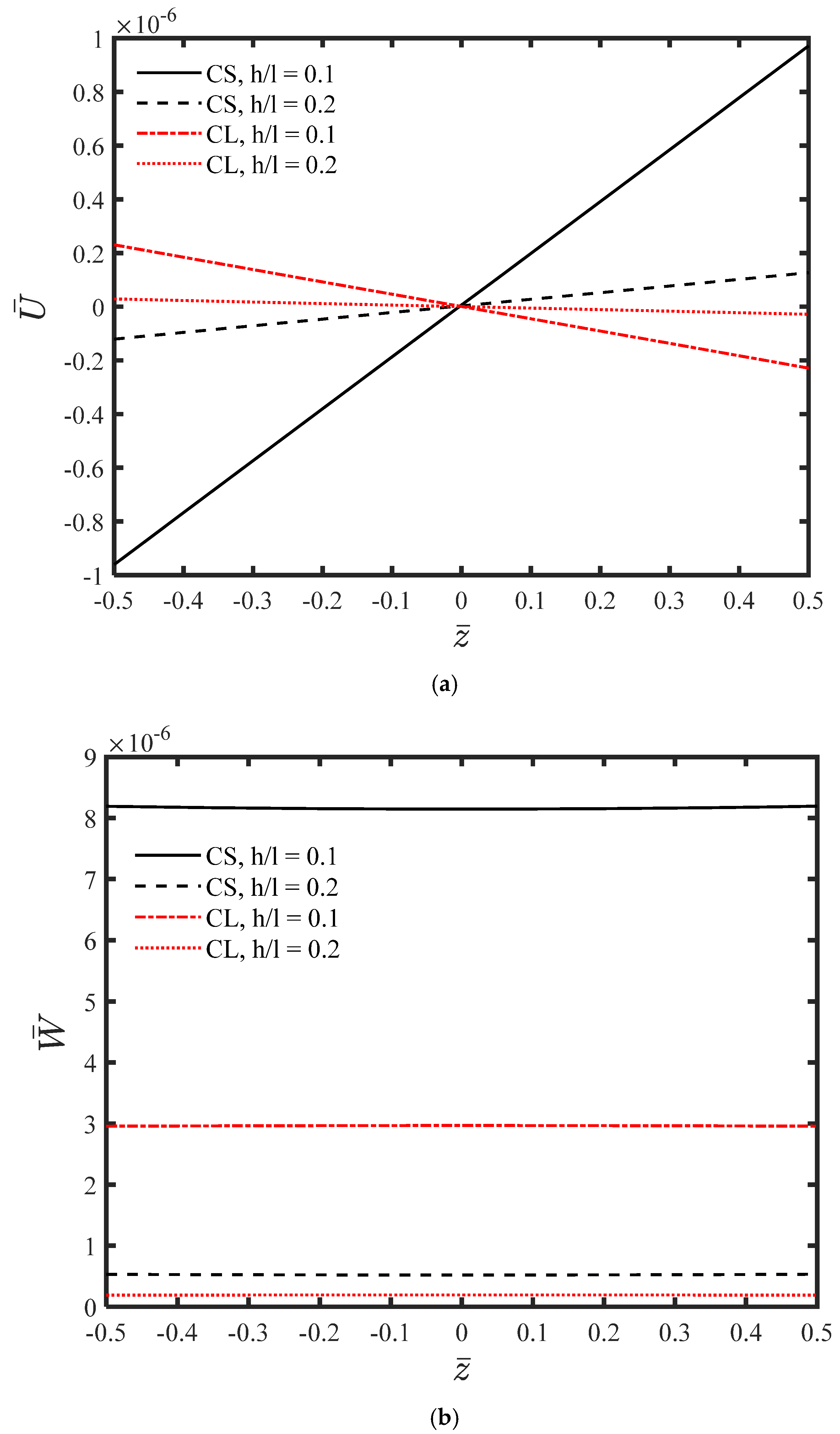
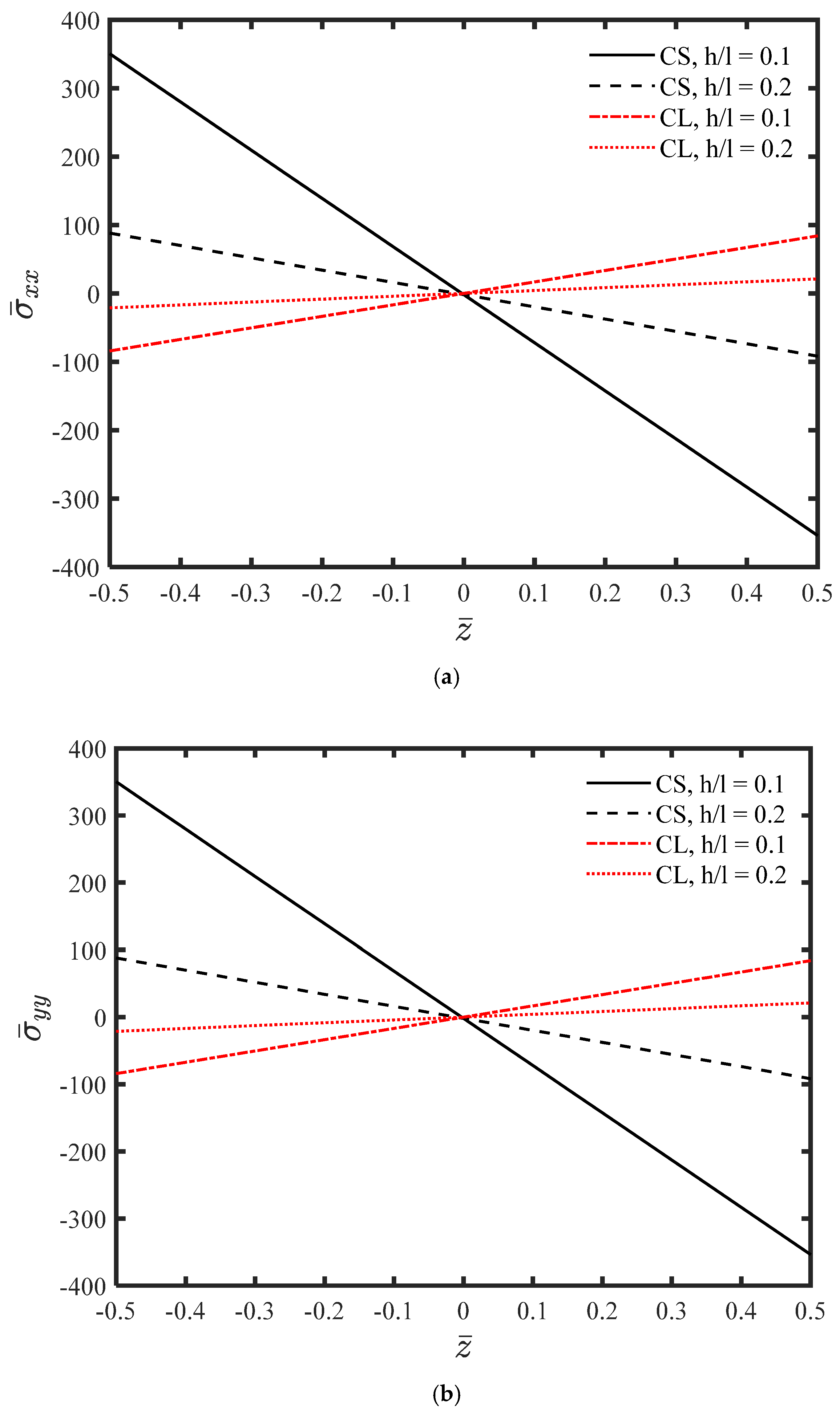
- The material length-scale parameter has a significant influence on the bending behavior of the microplate and cannot be neglected.
- 2-
- The microplate is more flexible and experiences higher stress levels compared to classical elasticity predictions.
- 3-
- The absolute values of displacements decrease as the thickness of the microplate increases.
- 4-
- For a constant h/l ratio, the displacements calculated using couple stress theory are greater than those predicted by classical theory.
- 5-
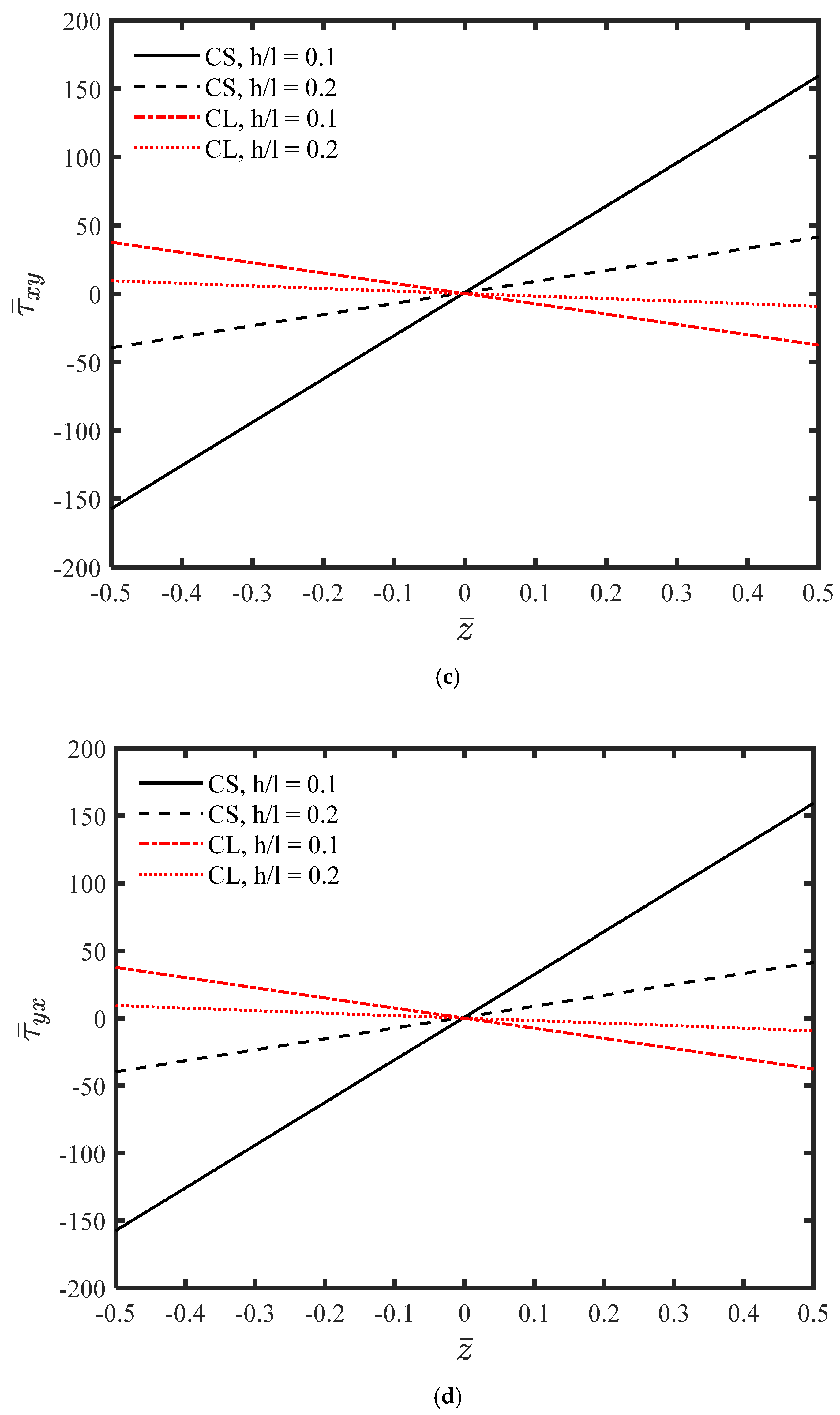
- As the thickness of the microplate increases, the absolute values of stresses decrease.
- 6-
- Unlike classical theories, and are not identical.
- 7-
- Compared to classical elasticity theory, the out-of-plane stresses attain larger values, and these components increase further as the thickness decreases.
- 8-
- An increase in thickness results in a reduction in the absolute value of .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mcfarland, A.W.; Colton, J.S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J. Micromech. Microeng. 2005, 15, 1060–1067. [Google Scholar] [CrossRef]
- Lei, J.; He, Y.; Guo, S.; Li, Z.; Liu, D. Size-dependent vibration of nickel cantilever microbeams: Experiment and gradient elasticity. AIP Adv. 2016, 6, 105202. [Google Scholar] [CrossRef]
- Kandaz, M.; Dal, H. A comparative study of modified strain gradient theory and modified couple stress theory for gold microbeams. Arch. Appl. Mech. 2018, 88, 2051–2070. [Google Scholar] [CrossRef]
- Shaban, M.; Mazaheri, H. Size-dependent electro-static analysis of smart micro-sandwich panels with functionally graded core. Acta Mech. 2020, 232, 111–133. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Akgöz, B. New static and dynamic analyses of macro and nano FGM plates using exact three-dimensional elasticity in thermal environment. Compos. Struct. 2018, 192, 626–641. [Google Scholar] [CrossRef]
- Ansari, R.; Norouzzadeh, A.; Shakouri, A.H.; Bazdid-Vahdati, M.; Rouhi, H. Finite element analysis of vibrating micro-beams and -plates using a three-dimensional micropolar element. Thin-Walled Struct. 2018, 124, 489–500. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Eshel, N.N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Park, S.K.; Gao, X.L. Bernoulli-Euler beam model based on a modified couple stress theory. J. Micromech. Microeng. 2006, 16, 2355–2359. [Google Scholar] [CrossRef]
- Asghari, M.; Ahmadian, M.T.; Kahrobaiyan, M.H.; Rahaeifard, M. On the size-dependent behavior of functionally graded micro-beams. Mater. Des. 2010, 31, 2324–2329. [Google Scholar] [CrossRef]
- Reddy, J.N. Microstructure-dependent couple stress theories of functionally graded beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
- Gao, X.L.; Mahmoud, F.F. A new Bernoulli-Euler beam model incorporating microstructure and surface energy effects. Z. Angew. Math. Phys. 2014, 65, 393–404. [Google Scholar] [CrossRef]
- Sßimsßek, M.; Reddy, J.N. Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory. Int. J. Eng. Sci. 2013, 64, 37–53. [Google Scholar] [CrossRef]
- Jabbari Behrouz, S.; Rahmani, O.; Hosseini, S.A. On nonlinear forced vibration of nano cantilever-based biosensor via couple stress theory. Mech. Syst. Signal Process. 2019, 128, 19–36. [Google Scholar] [CrossRef]
- Gan, N.; Wang, Q. Topology optimization design for buckling analysis related to the size effect. Math. Mech. Solids 2021, 27, 10812865211066608. [Google Scholar] [CrossRef]
- Reddy, J.N.; Berry, J. Nonlinear theories of axisymmetric bending of functionally graded circular plates with modified couple stress. Compos. Struct. 2012, 94, 3664–3668. [Google Scholar] [CrossRef]
- Tsiatas, G.C. A new Kirchhoff plate model based on a modified couple stress theory. Int. J. Solids Struct. 2009, 46, 2757–2764. [Google Scholar] [CrossRef]
- Ashoori, A.R.; Sadough Vanini, S.A. Thermal buckling of annular microstructure-dependent functionally graded material plates resting on an elastic medium. Compos. Part B Eng. 2016, 87, 245–255. [Google Scholar] [CrossRef]
- Ashoori, A.R.; Sadough Vanini, S.A. Nonlinear thermal stability and snap-through behavior of circular microstructure-dependent FGM plates. Eur. J. Mech. A/Solids 2016, 59, 323–332. [Google Scholar] [CrossRef]
- Beni, Y.T.; Mehralian, F.; Zeighampour, H. The modified couple stress functionally graded cylindrical thin shell formulation. Mech. Adv. Mater. Struct. 2016, 23, 791–801. [Google Scholar] [CrossRef]
- Ma, H.M.; Gao, X.L.; Reddy, J.N. A non-classical Mindlin plate model based on a modified couple stress theory. Acta Mech. 2011, 220, 217–235. [Google Scholar] [CrossRef]
- Alinaghizadeh, F.; Shariati, M.; Fish, J. Bending analysis of size-dependent functionally graded annular sector microplates based on the modified couple stress theory. Appl. Math. Model. 2017, 44, 540–556. [Google Scholar] [CrossRef]
- Jung, W.Y.; Han, S.C. Static and eigenvalue problems of Sigmoid Functionally Graded Materials (S-FGM) micro-scale plates using the modified couple stress theory. Appl. Math. Model. 2015, 39, 3506–3524. [Google Scholar] [CrossRef]
- Eshraghi, I.; Dag, S.; Soltani, N. Consideration of spatial variation of the length scale parameter in static and dynamic analyses of functionally graded annular and circular micro-plates. Compos. Part B Eng. 2015, 78, 338–348. [Google Scholar] [CrossRef]
- Eshraghi, I.; Dag, S.; Soltani, N. Bending and free vibrations of functionally graded annular and circular micro-plates under thermal loading. Compos. Struct. 2016, 137, 196–207. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Coupled size-dependent behavior of shear deformable microplates. Acta Mech. 2016, 227, 757–775. [Google Scholar] [CrossRef]
- Chen, W.; Li, X. A new modified couple stress theory for anisotropic elasticity and microscale laminated Kirchhoff plate model. Arch. Appl. Mech. 2014, 84, 323–341. [Google Scholar] [CrossRef]
- He, D.; Yang, W.; Chen, W. A size-dependent composite laminated skew plate model based on a new modified couple stress theory. Acta Mech. Solida Sin. 2017, 30, 75–86. [Google Scholar] [CrossRef]
- Li, Q.; Niu, X.; Pan, Z. Size-dependent effects of graded porous micro-/nanocircular plates on thermal vibration based on modified couple stress theory. Mech. Based Des. Struct. Mach. 2025, 1–27. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Couple stress theory for solids. Int. J. Solids Struct. 2011, 48, 2496–2510. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R. Size-dependent piezoelectricity. Int. J. Solids Struct. 2013, 50, 2781–2791. [Google Scholar] [CrossRef]
- Alashti, R.A.; Abolghasemi, A.H. A Size-dependent Bernoulli-Euler Beam Formulation based on a New Model of Couple Stress Theory. Int. J. Eng. 2014, 27, 951–960. [Google Scholar] [CrossRef]
- Fakhrabadi, M.M.S.; Yang, J. Comprehensive nonlinear electromechanical analysis of nanobeams under DC/AC voltages based on consistent couple-stress theory. Compos. Struct. 2015, 132, 1206–1218. [Google Scholar] [CrossRef]
- Seyyed Fakhrabadi, M.M. Prediction of small-scale effects on nonlinear dynamic behaviors of carbon nanotube-based nano-resonators using consistent couple stress theory. Compos. Part B Eng. 2016, 88, 26–35. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Comparison of theoretical elastic couple stress predictions with physical experiments for pure torsion. arXiv 2016, arXiv:1605.02556, 1–25. [Google Scholar]
- Tadi Beni, Y. Size-dependent electromechanical bending, buckling, and free vibration analysis of functionally graded piezoelectric nanobeams. J. Intell. Mater. Syst. Struct. 2016, 27, 2199–2215. [Google Scholar] [CrossRef]
- Keivani, M.; Koochi, A.; Abadyan, M. A new model for stability analysis of electromechanical nano-actuator based on Gurtin-Murdoch and consistent couple-stress theories. J. Vibroeng. 2016, 18, 1406–1416. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Hadi, A.; Farajpour, A. Consistent couple-stress theory for free vibration analysis of Euler-Bernoulli nano-beams made of arbitrary bi-directional functionally graded materials. Struct. Eng. Mech. 2017, 63, 161–169. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Hajesfandiari, A.; Zhang, H.; Dargush, G.F. Size-dependent couple stress Timoshenko beam theory. arXiv 2017, arXiv:1712.08527, 1–48. [Google Scholar]
- Fattahian Dehkordi, S.; Tadi Beni, Y. Electro-mechanical free vibration of single-walled piezoelectric/flexoelectric nano cones using consistent couple stress theory. Int. J. Mech. Sci. 2017, 128–129, 125–139. [Google Scholar] [CrossRef]
- Ajri, M.; Fakhrabadi, M.M.S.; Rastgoo, A. Analytical solution for nonlinear dynamic behavior of viscoelastic nano-plates modeled by consistent couple stress theory. Lat. Am. J. Solids Struct. 2018, 15, 1–23. [Google Scholar] [CrossRef]
- Amin Hadi, M.Z.N.; Rastgoo, A.; Hosseini, M. Buckling analysis of FGM Euler-Bernoulli nano-beams with 3D-varying properties based on consistent couple-stress theory. Steel Compos. Struct. 2018, 26, 663–672. [Google Scholar] [CrossRef]
- Wu, C.-P.; Hu, H.-X. A unified size-dependent plate theory for static bending and free vibration analyses of micro- and nano-scale plates based on the consistent couple stress theory. Mech. Mater. 2021, 162, 104085. [Google Scholar] [CrossRef]
- Kutbi, M.A.; Zenkour, A.M. Modified couple stress model for thermoelastic microbeams due to temperature pulse heating. J. Comput. Appl. Mech. 2022, 53, 83–101. [Google Scholar] [CrossRef]
- Zhang, R.; Bai, H.; Chen, X. The Consistent Couple Stress Theory-Based Vibration and Post-Buckling Analysis of Bi-directional Functionally Graded Microbeam. Symmetry 2022, 14, 602. [Google Scholar] [CrossRef]
- Wu, C.P.; Lyu, Y.S. An asymptotic consistent couple stress theory for the three-dimensional free vibration analysis of functionally graded microplates resting on an elastic medium. Math. Methods Appl. Sci. 2023, 46, 4891–4919. [Google Scholar] [CrossRef]
- Wu, C.P.; Huang, Z. A unified consistent couple stress beam theory for functionally graded microscale beams. Steel Compos. Struct. 2024, 51, 103–116. [Google Scholar] [CrossRef]
- Huang, H.; Guan, W.; He, X. Modal displacement analyses of Lamb waves in micro/nano-plates based on the consistent couple stress theory. Ultrasonics 2024, 138, 107272. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.A. 3D static bending analysis of functionally graded piezoelectric microplates resting on an elastic medium subjected to electro-mechanical loads using a size-dependent Hermitian C2 finite layer method based on the consistent couple stress theory. Mech. Based Des. Struct. Mach. 2024, 52, 3799–3841. [Google Scholar] [CrossRef]
- Shang, Y.; Sun, M.; Cen, S.; Li, C.F. Computational homogenization of flexoelectric composites within the consistent couple stress theory. Comput. Methods Appl. Mech. Eng. 2025, 437, 117762. [Google Scholar] [CrossRef]
- Sadd, M.H. Elasticity: Theory, Applications, and Numerics, 3rd ed.; Academic Press: Cambridge, MA, USA, 2014; ISBN 9780124081369. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Fundamental solutions for isotropic size-dependent couple stress elasticity. Int. J. Solids Struct. 2013, 50, 1253–1265. [Google Scholar] [CrossRef]
- Shaban, M. Elasticity Solution for Static Analysis of Sandwich Structures with Sinusoidal Corrugated Cores. J. Stress Anal. 2016, 1, 23–31. [Google Scholar]
- Pagano, N.J. Exact Solutions for Rectangular Bidirectional Composites and Sandwich Plates. J. Compos. Mater. 1970, 4, 20–34. [Google Scholar] [CrossRef]
| Elasticity Theory | Classical Plate Theory | |||||
|---|---|---|---|---|---|---|
| 9.61 × 10−7 | 9.61 × 10−7 | 8.19 × 10−6 | 4.46 × 104 | 4.46 × 104 | 1.97 × 10−9 | |
| 1.21 × 10−7 | 1.21 × 10−7 | 5.31 × 10−7 | 4.46 × 104 | 4.46 × 104 | 4.91 × 10−10 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaban, M.; Minaeii, S.; Kalhori, H. Size-Dependent Flexural Analysis of Thick Microplates Using Consistent Couple Stress Theory. J. Compos. Sci. 2025, 9, 142. https://doi.org/10.3390/jcs9030142
Shaban M, Minaeii S, Kalhori H. Size-Dependent Flexural Analysis of Thick Microplates Using Consistent Couple Stress Theory. Journal of Composites Science. 2025; 9(3):142. https://doi.org/10.3390/jcs9030142
Chicago/Turabian StyleShaban, Mahdi, Saeid Minaeii, and Hamed Kalhori. 2025. "Size-Dependent Flexural Analysis of Thick Microplates Using Consistent Couple Stress Theory" Journal of Composites Science 9, no. 3: 142. https://doi.org/10.3390/jcs9030142
APA StyleShaban, M., Minaeii, S., & Kalhori, H. (2025). Size-Dependent Flexural Analysis of Thick Microplates Using Consistent Couple Stress Theory. Journal of Composites Science, 9(3), 142. https://doi.org/10.3390/jcs9030142






