Modal Parameter Identification and Comfort Assessment of GFRP Lightweight Footbridges in Relation to Human–Structure Interaction
Abstract
:1. Introduction and Background
2. Summary of the Examined Lightweight Footbridges
3. Modal Testing, Vibration and Comfort Analysis Methods
3.1. iDynamics Based Smartphone Accelerometer Data Collection
3.2. First and Second Measurement Sets of Heel Tests
3.3. Modal Analysis
3.3.1. First Natural Flexural Frequency
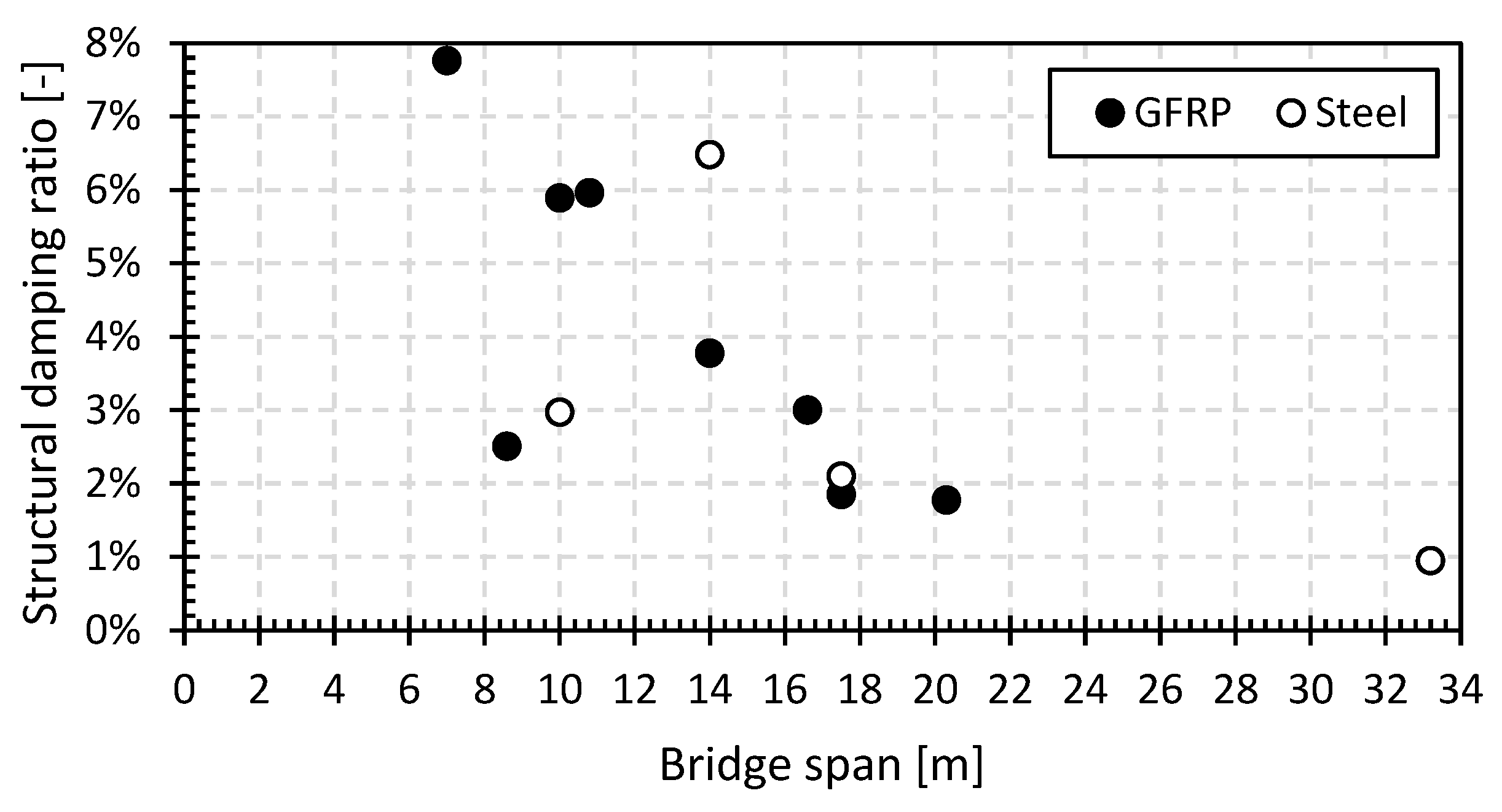
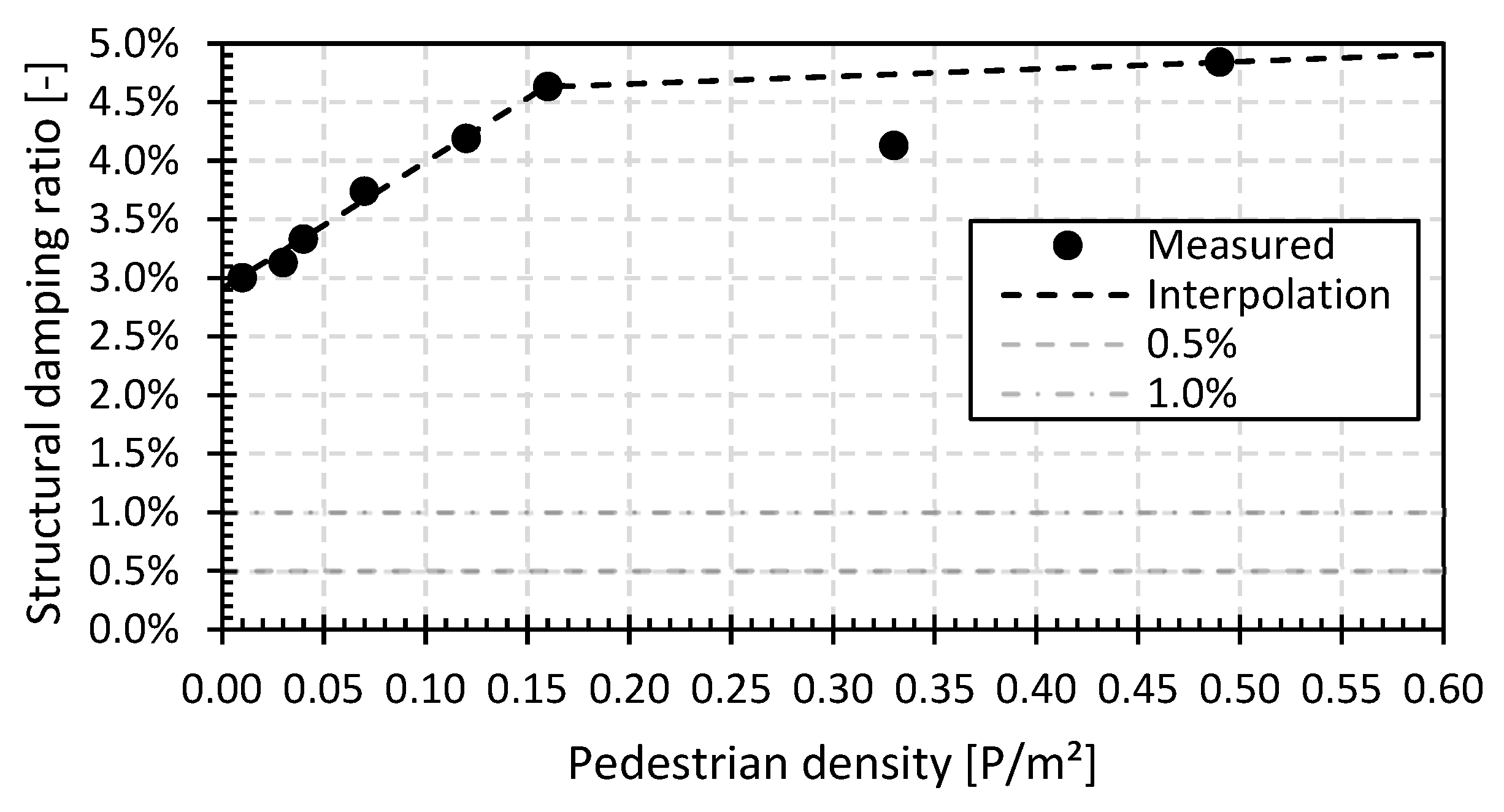
3.3.2. Structural Damping Ratio
3.4. Comfort Analysis of Lightweight GFRP and Steel Footbridges
4. Results of Parameter Identification of Lightweight GFRP and Steel Footbridges
4.1. Heel Tests: First Measurement Set
4.1.1. First Natural Flexural Frequency
4.1.2. Structural Damping Ratio
4.2. Heel Test: Second Measurement Set
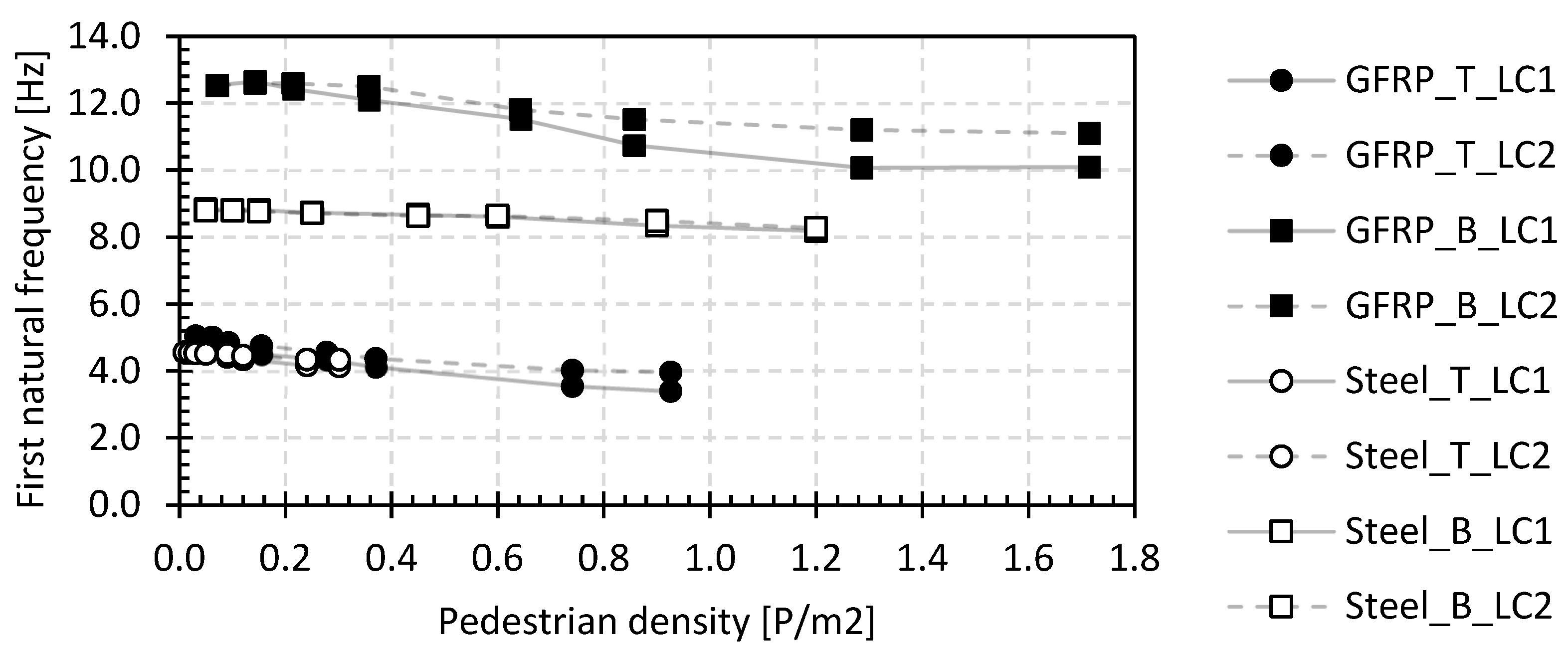
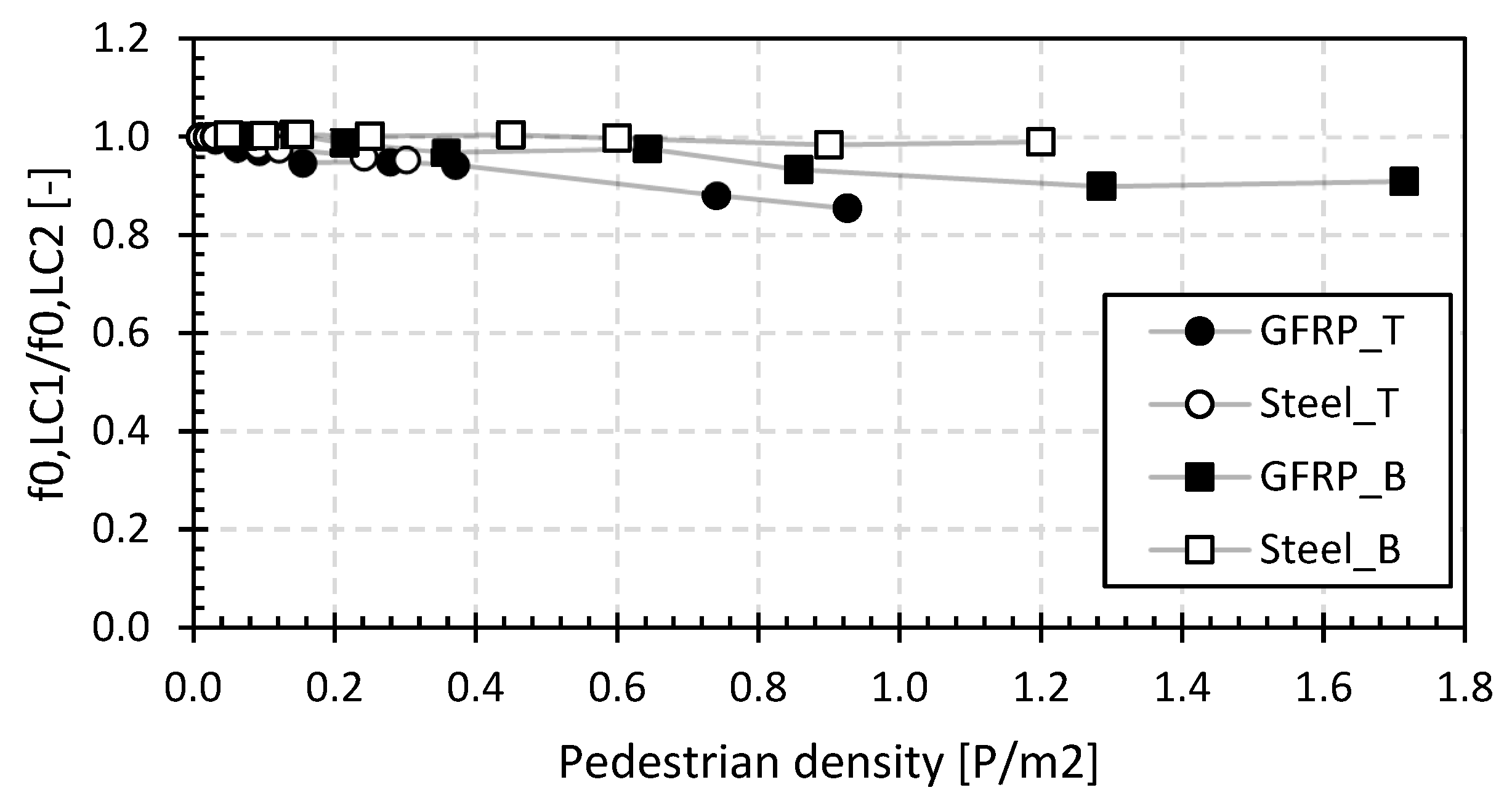
4.2.1. First Natural Flexural Frequency
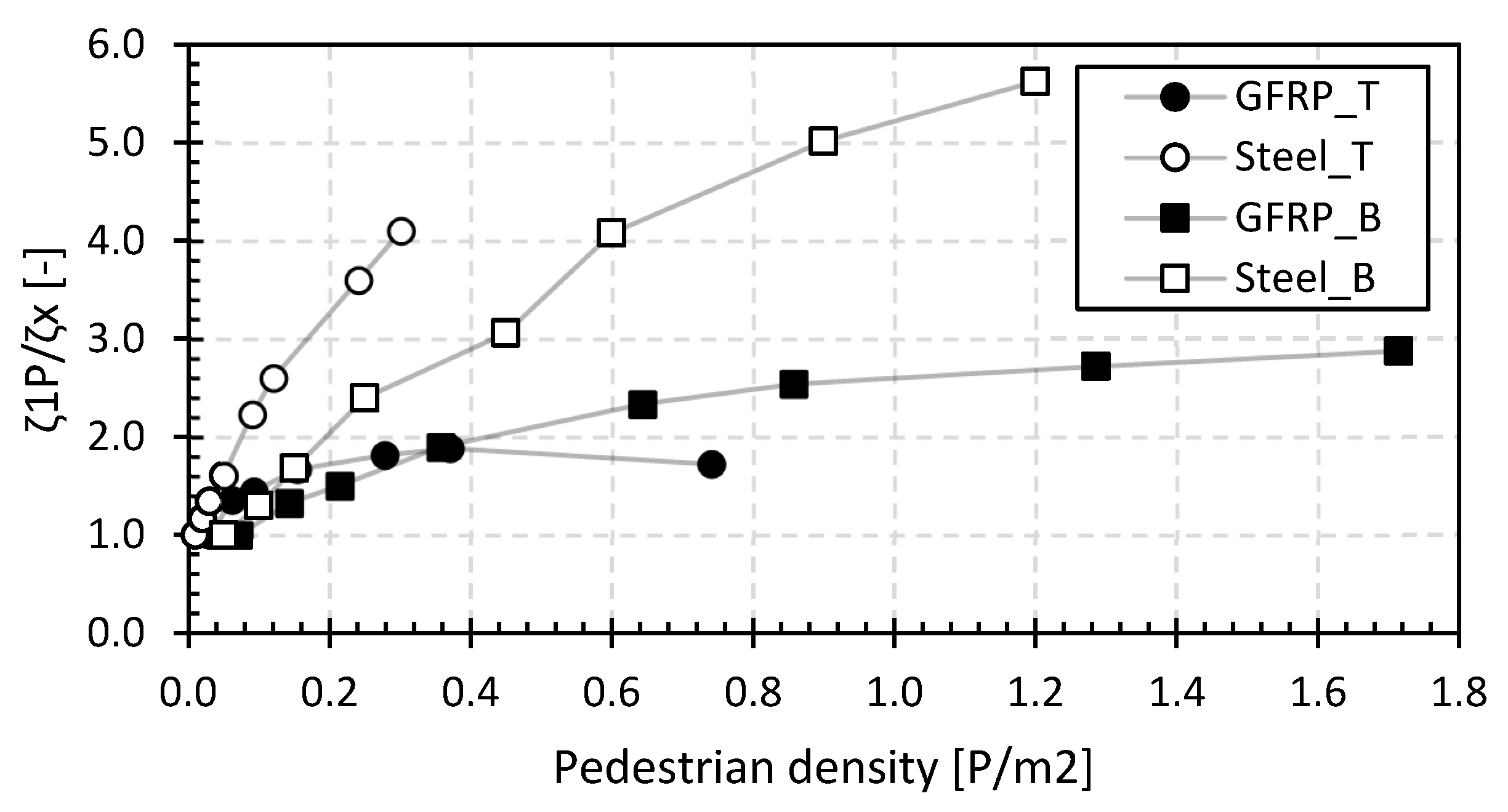
4.2.2. Structural Damping Ratio
4.3. Dynamic Vibration Tests
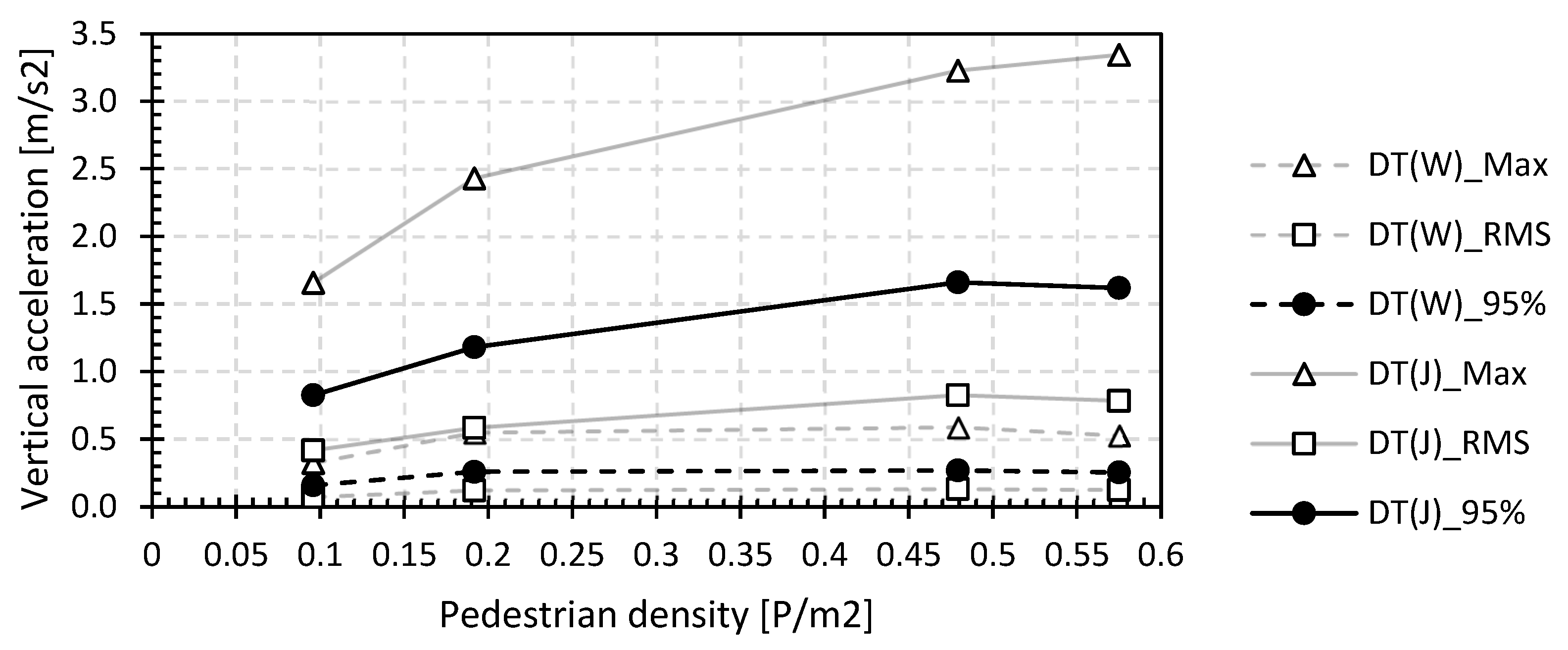
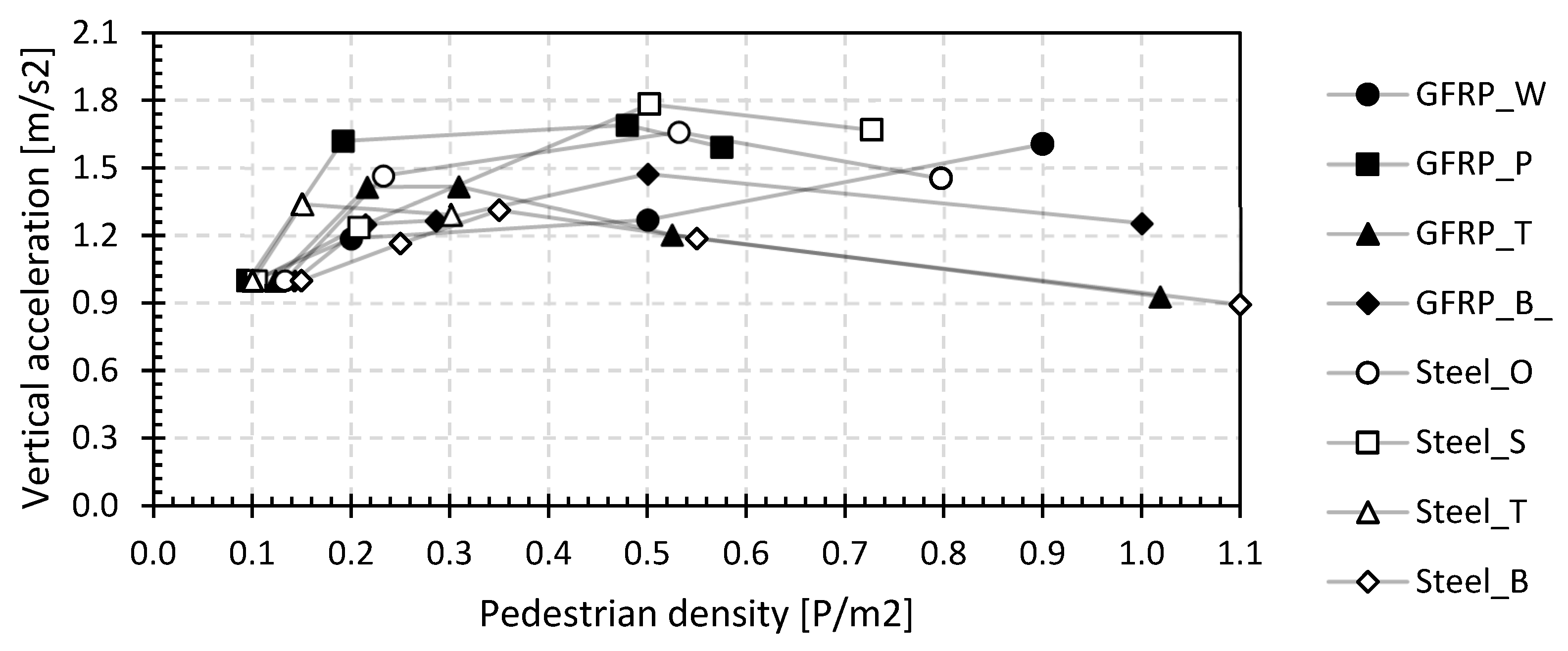
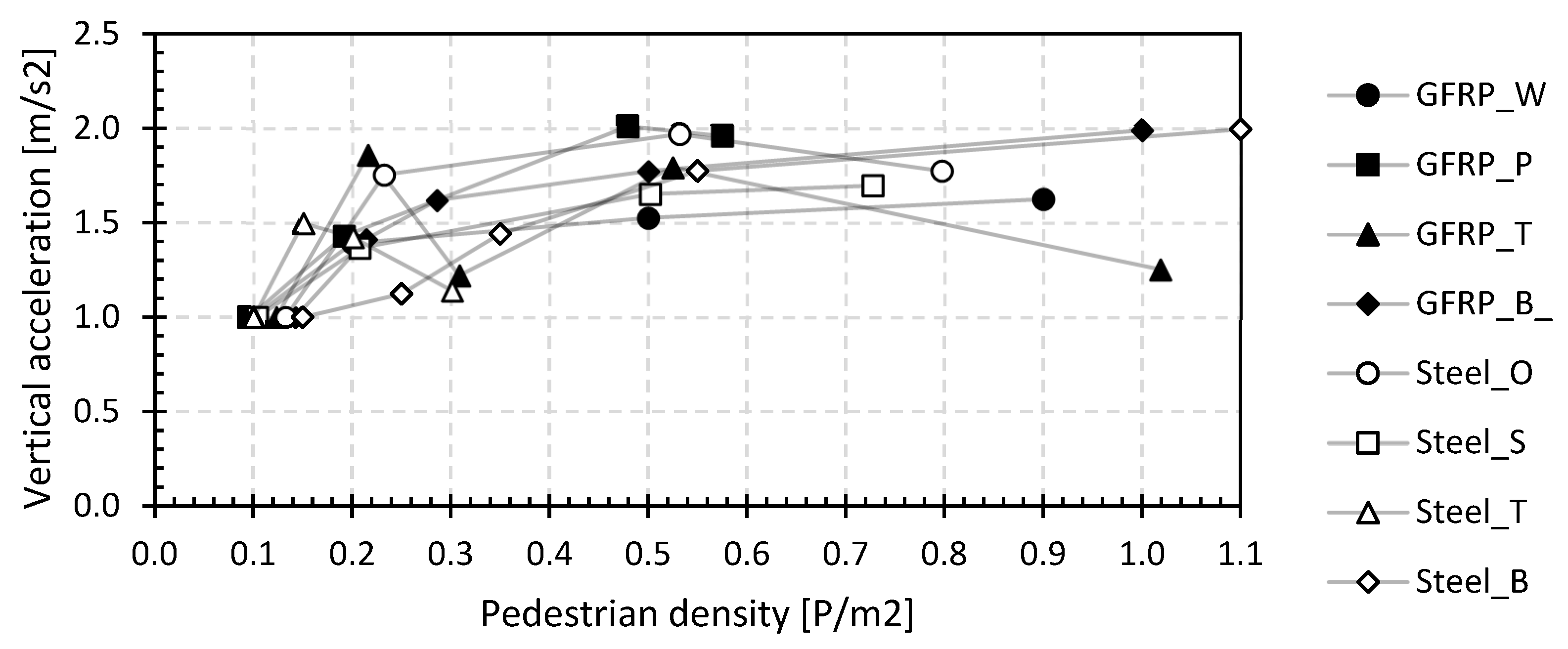
4.3.1. Comfort Assessment during Walking
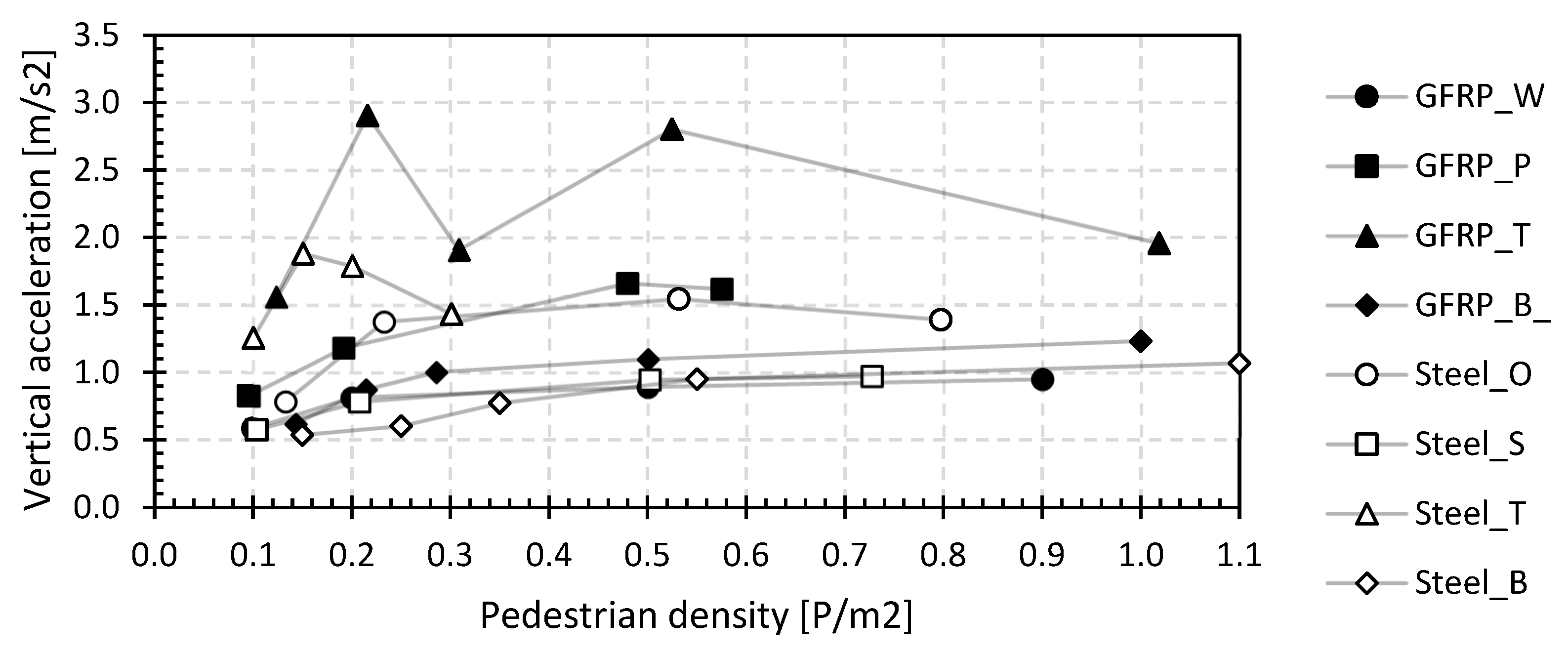
4.3.2. Comfort Assessment during Jogging
5. Discussion of the Modal Parameters and Comfort Assessment
5.1. General Observations
5.2. Relation between Modal Parameters and Vertical Accelerations
6. Analytical Comparison
6.1. First Natural Flexural Frequency
6.2. Comfort Analysis
7. Conclusions
- The basic value of the first natural flexural frequencies for the GFRP footbridges is between 3.8 Hz and 12.5 Hz, and for the steel footbridges, it is between 4.5 Hz and 8.8 Hz. The first natural frequency will decrease by 2% to 20% with increasing pedestrian densities up to 0.5 P/m2. The initial values of the structural damping ratio with only the operator on the bridge deck are between 3.0% and 8.0% for the GFRP footbridges and between 1.0% and 6.5% for the steel footbridges. The structural damping ratio will increase by a factor between 1.5 and 5.5 with increasing pedestrian density at 0.5 P/m2. In addition, the position of the pedestrians on the bridge deck has a small but noticeable influence on the increase in the structural damping ratio. The position of the pedestrians on the bridge deck influences the dynamic loading pattern and, consequently, the bridge’s response. For example, a large group of pedestrians walking in unison or concentrated in a specific area can cause localized dynamic loading and excite specific modes of vibration in the bridge. This can lead to localized areas of higher structural damping. Furthermore, pedestrians positioned near structural members or sensitive regions of the bridge may cause higher dynamic responses in those areas, affecting the overall damping behaviour of the structure. These observations point at significant human–structure interaction for small lightweight footbridges.
- The vertical accelerations are acceptable for the walking load case (CC1) but quickly become unacceptable for the jogging load case (CC3 and CC4). In the international guidelines, only the accelerations for walking are considered. As a result of the increasing damping, the experimentally measured 95 percentile vertical acceleration values do not increase proportionally with increasing pedestrian density, contradicting international guidelines. Excluding human–structure interaction therefore leads to uneconomic designs of lightweight footbridges. Despite the high basic first natural flexural frequency (f0 > 5 Hz) of some of the tested lightweight GFRP and steel footbridges, the comfort will be minimal (CK3) or even worse for the jogging load case. The statement of Eurocode 0, declaring that no check of the vibrations should be carried out if the first natural flexural frequency is larger than 5 Hz, is therefore not valid for these lightweight footbridges. It is recommended to always carry out an in situ check of the vibration behaviour and comfort.
- Good agreement between calculated and measured first natural flexural frequency values for the GFRP bridge in Puurs can be obtained by the analytical formula from the Dutch guideline CUR96:2019. Following the current guidelines in combination with the recommended damping ratios (0.5% and 1.0%) for GFRP bridges stated in CUR96:2019 clearly overestimates the vertical accelerations for the walking load case. However, if experimentally obtained pedestrian density-dependent structural damping ratio values are used, better agreement can be obtained between the analytically predicted and the experimentally measured maximum acceleration values for the walking load case.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Živanović, S.; Wei, X.; Russell, J.; Mottram, J.T. Vibration Performance of Two FRP Footbridge Structures in the United Kingdom. In Proceedings of the Footbridge 2017, Berlin, Germany, 6–8 September 2017. [Google Scholar] [CrossRef]
- Živanović, S.; Pavic, A.; Reynolds, P. Vibration serviceability of footbridges under human-induced excitation: A literature review. J. Sound Vib. 2005, 279, 1–74. [Google Scholar] [CrossRef]
- Živanović, S. Benchmark footbridge for vibration serviceability assessment under the vertical component of pedestrian load. J. Struct. Eng. 2012, 138, 1193–1202. [Google Scholar] [CrossRef]
- Ahmadi, E.; Caprani, C.; Živanović, S.; Evans, N.; Heidarpour, A. A framework for quantification of human-structure interaction in vertical direction. J. Sound Vib. 2018, 432, 351–372. [Google Scholar] [CrossRef]
- Bassoli, E.; Van Nimmen, K.; Vincenzi, L.; Van Den Broeck, P. A spectral load model for pedestrian excitation including vertical human-structure interaction. Eng. Struct. 2018, 156, 537–547. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W. Energy dissipation from vibrating floor slabs due to human-structure interaction. Shock Vib. 2001, 8, 315–332. [Google Scholar] [CrossRef]
- Heinemann, P.; Kasperski, M. Damping Induced by Walking and Running. Procedia Eng. 2017, 199, 2826–2831. [Google Scholar] [CrossRef]
- Dallard, P.; Fitzpatrick, A.J.; Flint, A.; Le Bourva, S.; Low, A.; Ridsdill Smith, R.M.; Willford, M. The London Millennium Footbridge. Struct. Eng. 2001, 79, 17–33. [Google Scholar]
- Dallard, P.; Fitzpatrick, T.; Flint, A.; Low, A.; Ridsdill Smith, R.; Willford, M.; Roche, M. London Millennium Bridge: Pedestrian Induced Lateral Vibration. J. Bridg. Eng. 2001, 6, 412–417. [Google Scholar] [CrossRef]
- Tuakta, C. Use of Fiber Reinforced Polymer Composite in Bridge Structures. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Zyjewski, A.; Chróścielewski, J.; Pyrzowski, Ł. The use of fibre-reinforced polymers (FRP) in bridges as a favourable solution for the environment. E3S Web Conf. 2017, 17, 00102. [Google Scholar] [CrossRef]
- Wan, B. Using fiber-reinforced polymer (FRP) composites in bridge construction and monitoring their performance: An overview. In Advanced Composites in Bridge Construction and Repair; Elsevier Inc.: Amsterdam, The Netherlands, 2014; pp. 3–29. [Google Scholar] [CrossRef]
- Van Den Einde, L.; Zhao, L.; Seible, F. Use of FRP composites in civil structural applications. Constr. Build. Mater. 2003, 17, 389–403. [Google Scholar] [CrossRef]
- Chróścielewski, J.; Miśkiewicz, M.; Pyrzowski, Ł.; Sobczyk, B.; Wilde, K. A novel sandwich footbridge—Practical application of laminated composites in bridge design and in situ measurements of static response. Compos. Part B Eng. 2017, 126, 153–161. [Google Scholar] [CrossRef]
- De Corte, W.; Uyttersprot, J.; Van Paepegem, W. The structural behavior of tiled laminate GFRP composites, a class of robust materials for civil applications. In Proceedings of the 20th IABSE Congress 2019 ’The Evolving Metropolis’, New York, NY, USA, 4–6 September 2019. [Google Scholar]
- De Corte, W.; Jansseune, A.; Van Paepegem, W.; Peeters, J. Structural behaviour and robustness assessment of an InfraCore® inside bridge deck specimen subjected to static and dynamic local loading. In Proceedings of the 21st International Conference on Composite Materials, Xi’an, China, 20–25 August 2017. [Google Scholar]
- De Corte, W.; Uyttersprot, J. FRP Bridges in the Flanders Region: Experiences from the C-Bridge Project. Appl. Sci. 2022, 12, 10897. [Google Scholar] [CrossRef]
- Tuwair, H.; Drury, J.; Volz, J. Testing and evaluation of full scale fiber-reinforced polymer bridge deck panels incorporating a polyurethane foam core. Eng. Struct. 2019, 184, 205–216. [Google Scholar] [CrossRef]
- De Corte, W.; Jansseune, A.; Van Paepegem, W.; Peeters, J. Elastic properties and failure behavior of tiled laminate composites. Key Eng. Mater. 2018, 774, 564–569. [Google Scholar] [CrossRef]
- Karbhari, V.M. Material Considerations in FRP Rhabilitation of concrete structures. J. Mater. Civ. Eng. 2001, 13, 90–97. [Google Scholar] [CrossRef]
- Sonnenschein, R.; Gajdosova, K.; Holly, I. FRP Composites and their Using in the Construction of Bridges. Procedia Eng. 2016, 161, 477–482. [Google Scholar] [CrossRef]
- Valbona, M.; Haghani, R.; Harryson, P. Bridge decks of fibre reinforced polymer (FRP): A sustainable solution. Constr. Build. Mater. 2014, 50, 190–199. [Google Scholar] [CrossRef]
- Stankiewicz, B. Composite GFRP deck for bridge structures. Procedia Eng. 2012, 40, 423–427. [Google Scholar] [CrossRef]
- Vovesný, M.; Rotter, T. GFRP bridge deck panel. Procedia Eng. 2012, 40, 492–497. [Google Scholar] [CrossRef]
- Kim, Y.J. State of the practice of FRP composites in highway bridges. Eng. Struct. 2019, 179, 1–8. [Google Scholar] [CrossRef]
- Piras, S.; Chin, K. Footbridge design for pedestrian induced vibrations. In Proceedings of the Concrete NZ Conference 2018, Claudelands, Hamilton, New Zealand, 11–13 October 2018; Volume 3. [Google Scholar]
- Shahabpoor, E.; Pavic, A.; Racic, V. Structural vibration serviceability: New design framework featuring human-structure interaction. Eng. Struct. 2017, 136, 295–311. [Google Scholar] [CrossRef]
- Ahmadi, E.; Caprani, C.; Živanović, S.; Heidarpour, A. Assessment of human-structure interaction on a lively lightweight GFRP footbridge. Eng. Struct. 2019, 199, 109687. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Lombaert, G.; de Roeck, G.; Van Den Broeck, P. Human-induced vibrations of footbridges: The effect of vertical human-structure interaction. Conf. Proc. Soc. Exp. Mech. Ser. 2016, 4, 299–307. [Google Scholar] [CrossRef]
- Ellis, B.R.; Ji, T. Human-structure interaction in vertical vibrations. Proc. Inst. Civ. Eng. Struct. Build. 1997, 122, 1–9. [Google Scholar] [CrossRef]
- Friehe, M.; Heinemeyer, C.; Feldmann, M. Design of highly sensitive floors for human induced vibrations. Procedia Eng. 2017, 199, 2796–2801. [Google Scholar] [CrossRef]
- Mohammed, A.S.; Pavic, A. Effect of Walking people on Dynamic Properties of Floors. Procedia Eng. 2017, 199, 2856–2863. [Google Scholar] [CrossRef]
- Gomez, D.; Dyke, S.J.; Rietdyk, S. Structured uncertainty for a pedestrian-structure interaction model. J. Sound Vib. 2020, 474, 115237. [Google Scholar] [CrossRef]
- Gheitasi, A.; Ozbulut, O.E.; Usmani, S.; Alipour, M.; Harris, D.K. Experimental and analytical vibration serviceability assessment of an in-service footbridge. Case Stud. Nondestruct. Test. Eval. 2016, 6, 79–88. [Google Scholar] [CrossRef]
- Shahabpoor, E.; Pavic, A.; Racic, V. Interaction between Walking Humans and Structures in Vertical Direction: A Literature Review. Shock Vib. 2016, 2016, 3430285. [Google Scholar] [CrossRef]
- Gallegos-Calderón, C.; Naranjo-Pérez, J.; Díaz, I.M.; Goicolea, J.M. Identification of a Human-Structure Interaction Model on an Ultra-Lightweight FRP Footbridge. Appl. Sci. 2021, 11, 6654. [Google Scholar] [CrossRef]
- Creasy, T. Sheet Forming in Polymer Matrix Composites; Woodhead Publishing Limited: Sawston, UK, 2012. [Google Scholar] [CrossRef]
- Tamura, Y.; Suganuma, S.Y. Evaluation of amplitude-dependent damping and natural frequency of buildings during strong winds. J. Wind. Eng. Ind. Aerodyn. 1996, 59, 115–130. [Google Scholar] [CrossRef]
- Sachse, R.; Pavic, A.; Reynolds, P. Parametric study of modal properties of damped two-degree-of-freedom crowd-structure dynamic systems. J. Sound Vib. 2004, 274, 461–480. [Google Scholar] [CrossRef]
- Wei, X.; Živanović, S.; Russell, J.; Mottershead, J.E. Subsystem identification in structures with a human occupant based on composite frequency response functions. Mech. Syst. Signal Process. 2019, 120, 290–307. [Google Scholar] [CrossRef]
- Pimentel, R.L. Vibrational Performance of Pedestrian Bridges due to Human-Induced Loads. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 1997. [Google Scholar]
- Živanović, S.; Díaz, I.M.; Pavić, A. Influence of walking and standing crowds on structural dynamic properties. In Proceedings of the IMAC XXVII Conference & Exposition on Structural Dynamics, Orlando, FL, USA, 9–12 February 2009. [Google Scholar]
- Shahabpoor, E.; Pavic, A.; Racic, V.; Zivanovic, S. Effect of group walking traffic on dynamic properties of pedestrian structures. J. Sound Vib. 2017, 387, 207–225. [Google Scholar] [CrossRef]
- Dacol, V.; Caetano, E.; Correia, J.R. Modal identification and damping performance of a full-scale GFRP-SFRSCC hybrid footbridge. Struct. Control. Health Monit. 2022, 29, e3137. [Google Scholar] [CrossRef]
- Wei, X.; Wan, H.P.; Russell, J.; Živanović, S.; He, X. Influence of mechanical uncertainties on dynamic responses of a full-scale all-FRP footbridge. Compos. Struct. 2019, 223, 110964. [Google Scholar] [CrossRef]
- Gomez, D.; Rietdyk, S.; Dyke, S.J. Spatio-temporal assessment of gait kinematics in vertical pedestrian-structure interaction. Structures 2021, 31, 1199–1206. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. Vibration serviceability of footbridges: Evaluation of the current codes of practice. Eng. Struct. 2014, 59, 448–461. [Google Scholar] [CrossRef]
- Boniface, V.; Bui, V.; Bressolette, P.; Charles, P.; Cespedes, X.; Consigny, F.; Cremona, C.; Delavaud, C.; Dieleman, L.; Duclos, T.; et al. SETRA: Assessment of Vibrational Behaviour of Footbridges under Pedestrian Loading; Association Française de Génie Civil: Paris, France, 2006. [Google Scholar]
- Dey, P.; Narasimhan, S.; Walbridge, S. Calibrating Pedestrian-Bridge Standards for Vibration Serviceability. J. Bridg. Eng. 2018, 23, 1–17. [Google Scholar] [CrossRef]
- Feldmann, M.; Heinemeyer, C.; Lukic, M.; Caetano, E.; Cunha, Á.; Goldack, A.; Keil, A.; Schlaich, M.; Smith, A.; Hechler, O.; et al. Human Induced Vibrations of Steel Structures (HiVoSS): Design of Footbridges—RFS2-CT-2007-00033; Publications Office of the European Union: Luxembourg, 2008. [Google Scholar] [CrossRef]
- Wei, X.; Russell, J.; Živanović, S.; Mottram, J.T. Measured dynamic properties for FRP footbridges and their critical comparison against structures made of conventional construction materials. Compos. Struct. 2019, 223, 110956. [Google Scholar] [CrossRef]
- Ligthart, R. Forecast of the Dynamic Behaviour of FRP. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Wei, X.; Živanović, S. Frequency response function-based explicit framework for dynamic identification in human-structure systems. J. Sound Vib. 2018, 422, 453–470. [Google Scholar] [CrossRef]
- Uyttersprot, J.; De Corte, W.; Ingelbinck, B. Influence of SLS design requirements on the material consumption and self-weight of web-core sandwich panel FRP composite footbridges. Compos. Struct. 2021, 262, 18. [Google Scholar] [CrossRef]
- Gallegos-Calderón, C.; Naranjo-Pérez, J.; Renedo, C.M.C.; Díaz, I.M. A frequency-domain approach to model vertical crowd-structure interaction in lightweight footbridges. J. Sound Vib. 2023, 557, 117750. [Google Scholar] [CrossRef]
- Ahmadi, E.; Caprani, C.; Živanović, S.; Heidarpour, A. Experimental validation of moving spring-mass-damper model for human-structure interaction in the presence of vertical vibration. Structures 2021, 29, 1274–1285. [Google Scholar] [CrossRef]
- Caprani, C.C.; Ngan, J.W.; Ahmadi, E.; Zhang, S.H.; Bai, Y.; Satasivam, S. Design, construction and performance of the Monash pultruded glass fibre-reinforced polymer footbridge. Structures 2023, 51, 970–984. [Google Scholar] [CrossRef]
- EN 1990:2002; Basis of Structural Design. Vol. 1. European Committee For Standardization: Brussels, Belgium, 2011.
- Brownjohn, J.M.W.; Bocian, M.; Hester, D.; Quattrone, A.; Hudson, W.; Moore, D.; Goh, S.; Lim, M.S. Footbridge system identification using wireless inertial measurement units for force and response measurements. J. Sound Vib. 2016, 384, 339–355. [Google Scholar] [CrossRef]
- PCB Piezotronics, Inc. Model 393B04 Seismic, Miniature (50 gm), Ceramic Flexural ICP ® Accelerometr, 1V/g, 0.06 to 450: Installation and Operating Manual. Available online: https://www.pcbpiezotronics.fr/wp-content/uploads/393B04.pdf (accessed on 30 January 2023).
- Feng, M.; Fukuda, Y.; Mizuta, M.; Ozer, E. Citizen sensors for SHM: Use of accelerometer data from smartphones. Sensors 2015, 15, 2980–2998. [Google Scholar] [CrossRef]
- Zhao, X.; Yu, Y.; Li, M.; Ou, J. Cloud-structural health monitoring based on smartphone. Vibroengineering Procedia 2015, 5, 241–246. [Google Scholar]
- Yu, Y.; Han, R.; Zhao, X.; Mao, X.; Hu, W.; Jiao, D.; Li, M.; Ou, J. Initial validation of mobile-structural health monitoring method using smartphones. Int. J. Distrib. Sens. Networks 2015, 11, 274391. [Google Scholar] [CrossRef]
- Gonzalez, R.; Huerta, M.; Sagbay, G.; Clotet, R.; Rivas, D.; Pérez, A.; Ordonez, E.; Rivas, D. Structural Health Monitoring using WifiPhones. In Proceedings of the IEEE Colombian Conference on Communication and Computing (IEEE COLCOM 2015), Popayan, Colombia, 13–15 May 2015. [Google Scholar] [CrossRef]
- Castellanos-Toro, S.; Marmolejo, M.; Marulanda, J.; Cruz, A.; Thomson, P. Frequencies and damping ratios of bridges through Operational Modal Analysis using smartphones. Constr. Build. Mater. 2018, 188, 490–504. [Google Scholar] [CrossRef]
- Cahill, P.; Quirk, L.; Dewan, P.; Pakrashi, V. Comparison of smartphone accelerometer applications for structural vibration monitoring. Adv. Comput. Des. 2019, 4, 1–13. [Google Scholar] [CrossRef]
- Ghent University. C-Bridge: Roadmap into Design, Guidelines and Execution of Composite Bridges in Flanders 2018. Available online: https://www.ugent.be/ea/structural-engineering/en/research/schoonmeersen/projects/cbridge.htm (accessed on 12 September 2022).
- Uyttersprot, J.; De Corte, W. Measured dynamic properties of web-core sandwich panel FRP composite footbridges and their relation to pedestrian comfort analysis. Compos. Struct. 2021, 259, 113236. [Google Scholar] [CrossRef]
- Russell, J.M.; Wei, X.; Živanović, S.; Kruger, C. Vibration serviceability of a GFRP railway crossing due to pedestrians and train excitation. Eng. Struct. 2020, 219, 110756. [Google Scholar] [CrossRef]
- Bai, Y.; Keller, T. Modal parameter identification for a GFRP pedestrian bridge. Compos. Struct. 2008, 82, 90–100. [Google Scholar] [CrossRef]
- Manual—TU Kaiserslautern. Available online: https://www.bauing.uni-kl.de/en/sdt/idynamics/manual#c100082 (accessed on 30 January 2023).
- Kögel, C.; Agne, P.; Feldbusch, A.; Sadegh-Azar, H. Schwingungsuntersuchungen mit dem Smartphone und Tablet/Vibration measurements and analysis with smartphones and tablet PCs. Bauingenieur 2017, 92, 200–211. [Google Scholar] [CrossRef]
- Land van Teirlinck|Vlaamse Landmaatschappij. Available online: https://www.vlm.be/nl/projecten/Paginas/Land_van_Teirlinck.aspx (accessed on 30 January 2023).
- Natuurpark Alsembergse Beemd Heringericht Voor Mens en Natuur|Belgium. Available online: https://anteagroup.be/projecten/alsembergse-beemd (accessed on 30 January 2023).
- Feldbusch, A.; Sadegh-Azar, H.; Agne, P. Vibration analysis using mobile devices (smartphones or tablets). Procedia Eng. 2017, 199, 2790–2795. [Google Scholar] [CrossRef]
- DIN 4150-2; Deutshe Norm. Structural Vibration—Part 2: Human Exposure to Vibration in Buildings. DIN German Institute for Standardization: Berlin, Germany, 1999.
- Etter, D.M.; Gough, T.A.; Cheng, Y.F. Direct computation of second-oredr coefficients for bandpass and bandstop digital filters. Signal Process. 1990, 19, 27–41. [Google Scholar] [CrossRef]
- Ellis, G. Filters in Control Systems. In Control System Design Guide; Elsevier Inc.: Amsterdam, The Netherlands, 2012; pp. 165–183. [Google Scholar] [CrossRef]
- Chaparro, L.F. Introduction to the Design of Discrete Filters. In Signals and Systems Using MATLAB; Academic Press: Boston, MA, USA, 2011. [Google Scholar] [CrossRef]
- Chen, W.-K. Filters: Digital Filters. In Passive, Active, and Digital Filters, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2009; pp. 205–2017. [Google Scholar]
- Heinemeyer, C.; Butz, C.; Keil, A.; Schlaich, M.; Goldack, A.; Trometer, S.; Lukić, M.; Chabrolin, B.; Lemaire, A.; Martin, P.-O.; et al. JRC Scientific and Technical Reports—EUR 23984 EN: Design of Lightweight Footbridges for Human Induced Vibrations; European Commission—Joint Research Centre: Aachen, Germany, 2009. [Google Scholar] [CrossRef]
- Van Hauwermeiren, J.; Van Nimmen, K.; Van Den Broeck, P. Canada Bridges Bruges Part I: Downstream Bridge Operational Modal Analysis Human-Induced Vibrations Report BWM-2019-03; KU Leuven: Leuven, Belgium, 2019. [Google Scholar]
- Drygala, I.J.; Polak, M.A.; Dulinska, J.M. Vibration serviceability assessment of GFRP pedestrian bridges. Eng. Struct. 2019, 184, 176–185. [Google Scholar] [CrossRef]
- He, W.; Xie, W.P. Characterization of stationary and walking people on vertical dynamic properties of a lively lightweight bridge. Struct. Control Health Monit. 2018, 25, e2123. [Google Scholar] [CrossRef]
- Hawryszków, P.; Pimentel, R.; Silva, F. Vibration effects of loads due to groups crossing a lively footbridge. Procedia Eng. 2017, 199, 2808–2813. [Google Scholar] [CrossRef]
- Kasperski, M. Damping induced by pedestrians. In Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Van Der Steen, C. CUR96:2019 Vezelversterkte Kunststoffen in Bouwkundige en Civieltechnische Draagconstructies—In Dutch; CROW: Delft, The Netherlands, 2019. [Google Scholar]
- Van Nimmen, K.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. The impact of vertical human-structure interaction on the response of footbridges to pedestrian excitation. J. Sound Vib. 2017, 402, 104–121. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Maes, K.; Živanovi, S.; Lombaert, G.; De Roeck, G.; Van Den Broeck, P. Identification and Modelling of Vertical Human-Structure Interaction. In The Society for Experimental Mechanics; Caicedo, J., Pakzad, S., Eds.; Springer: Cham, Switzerland, 2015; Volume 2, pp. 319–330. [Google Scholar] [CrossRef]




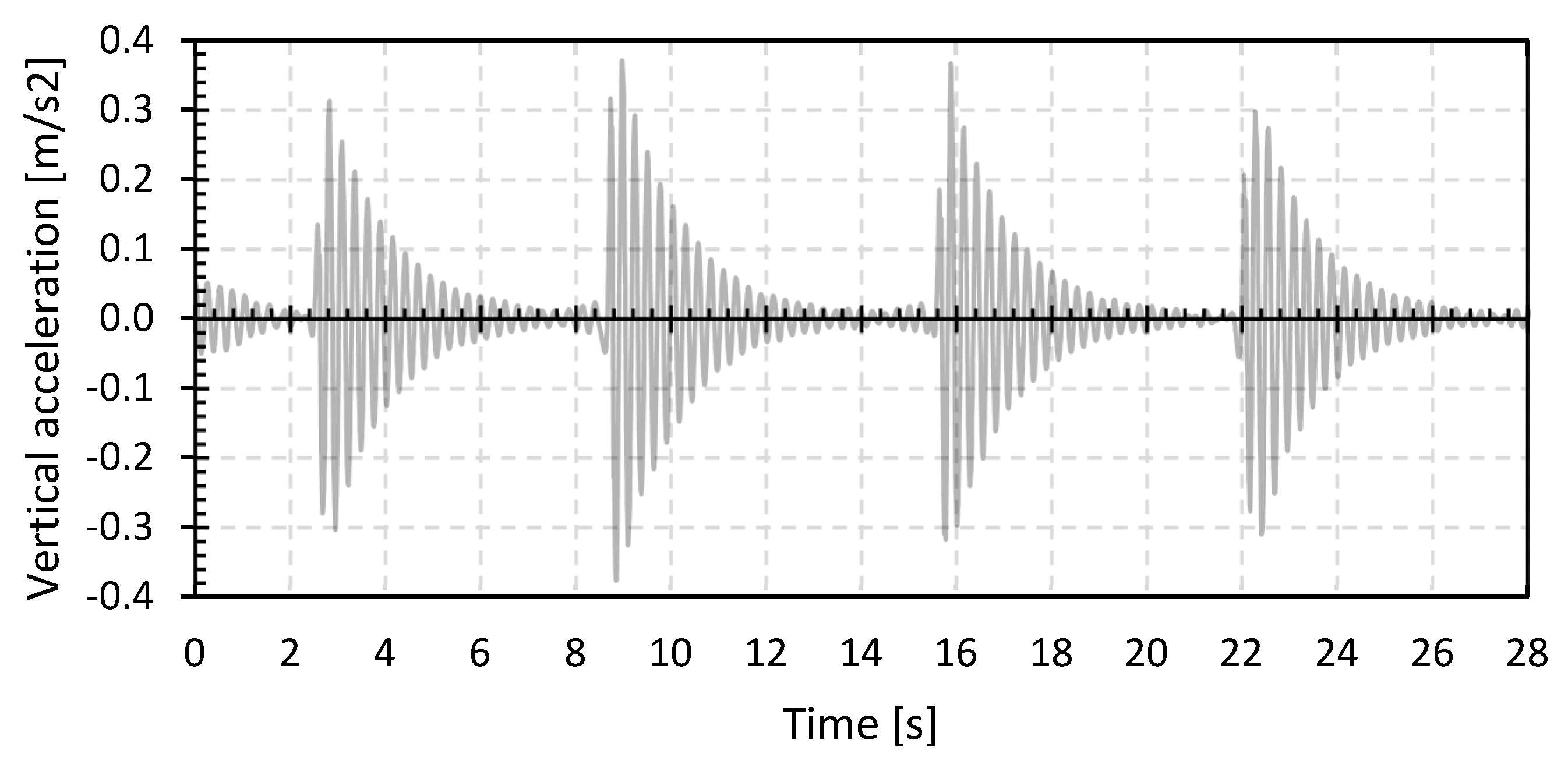
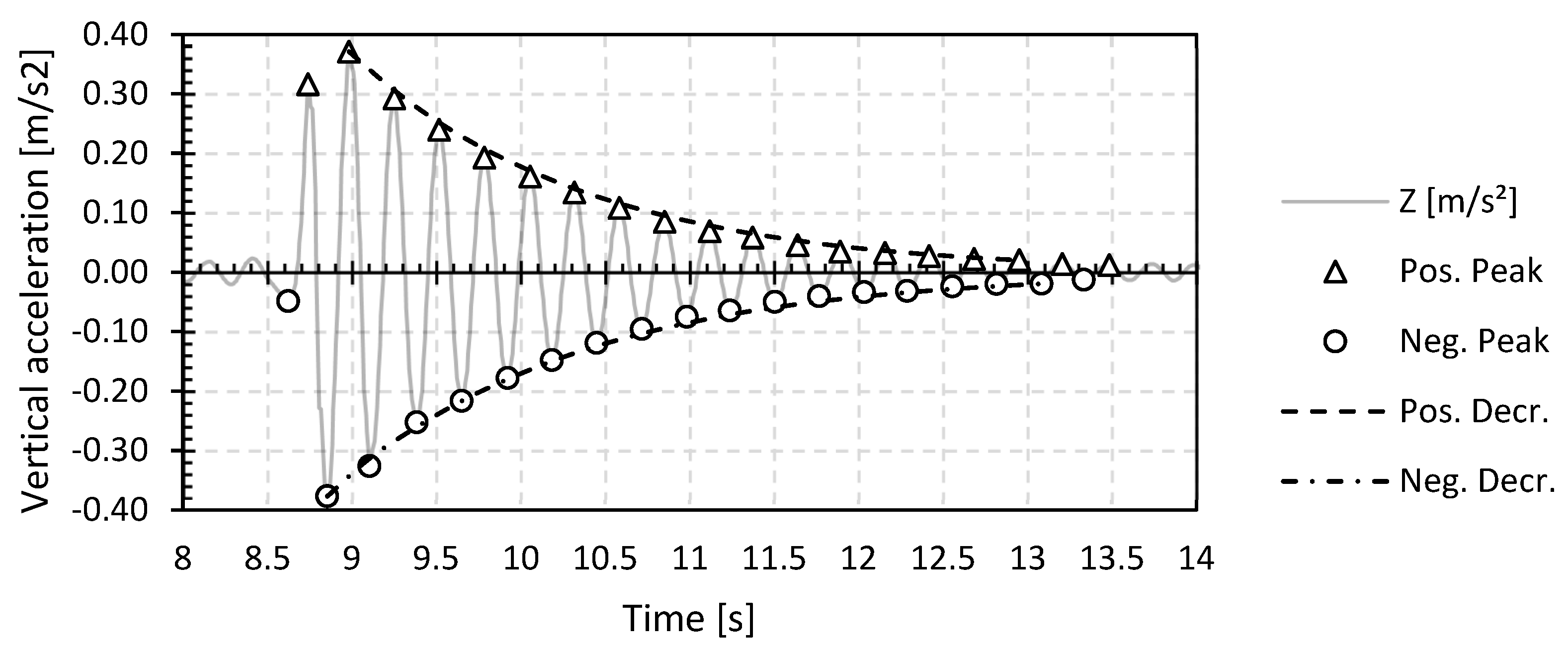



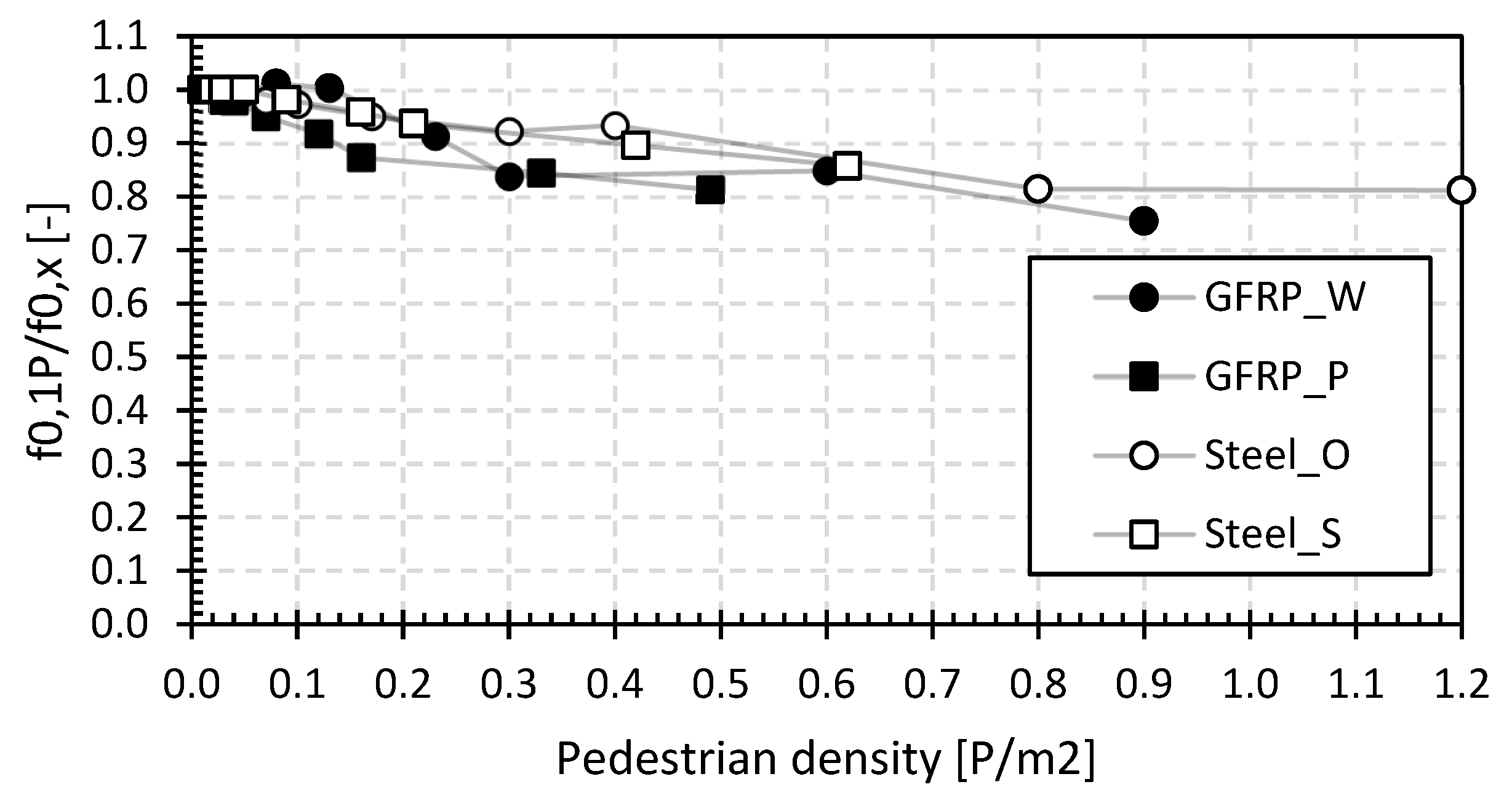
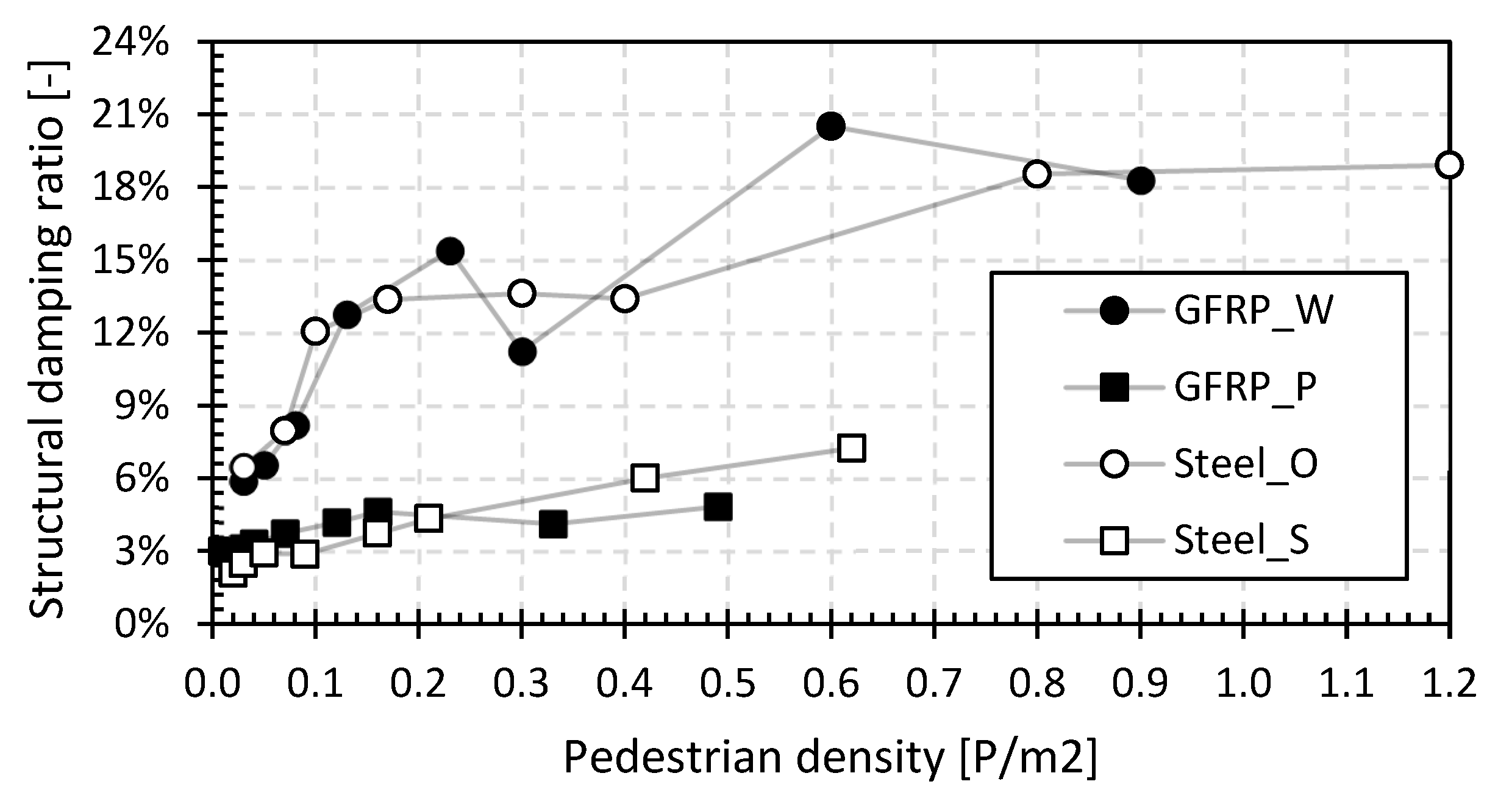








| No. | Set | Year | Location | Material | Abbreviation | Length L (m) | Width W (m) | Surface Area A (m2) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2020 | Waregem | GFRP | GFRP_W | 10.00 | 4.00 | 40.00 |
| 2 | 1 | 2019 | Puurs | GFRP | GFRP_P | 16.60 | 4.20 | 69.72 |
| 3 | 1 | 2017 | Oudenaarde | Steel | Steel_O | 14.00 | 2.15 | 30.10 |
| 4 | 1 | 2017 | Sinaai | Steel | Steel_S | 17.50 | 3.30 | 57.75 |
| 5 | 2 | 2018 | Tremelo | GFRP | GFRP_T | 10.80 | 3.00 | 32.40 |
| 6 | 2 | 2012 | Tremelo | Steel | Steel_T | 33.20 | 3.00 | 99.60 |
| 7 | 2 | 2018 | Beersel | GFRP | GFRP_B | 7.00 | 2.00 | 14.00 |
| 8 | 2 | 2020 | Beersel | Steel | Steel_B | 10.00 | 2.20 | 22.00 |
| No. | MC | Bridge | # Pedestrians (-) (Pedestrian Density (P/m2)) | ||||
|---|---|---|---|---|---|---|---|
| DT1 | DT2 | DT3 | DT4 | DT5 | |||
| 1 | 1 | GFRP_W | 4 (0.10) | 8 (0.20) | 20 (0.50) | 36 (0.90) | - |
| 2 | 1 | GFRP_P | 4 (0.06) | 7 (0.10) | 16 (0.23) | 24 (0.34) | - |
| 3 | 1 | Steel_O | 7 (0.23) | 14 (0.47) | 35 (1.16) | 42 (1.40) | - |
| 4 | 1 | Steel_S | 6 (0.10) | 12 (0.21) | 29 (0.50) | 42 (0.73) | - |
| 5 | 2 | GFRP_T | 4 (0.12) | 7 (0.22) | 10 (0.31) | 17 (0.52) | 33 (1.02) |
| 6 | 2 | Steel_T | 10 (0.10) | 15 (0.15) | 20 (0.20) | 25 (0.25) | 30 (0.30) |
| 7 | 2 | GFRP_B | 2 (0.14) | 3 (0.21) | 4 (0.29) | 7 (0.50) | 14 (1.00) |
| 8 | 2 | Steel_B | 3 (0.14) | 5 (0.23) | 7 (0.32) | 11 (0.50) | 22 (1.00) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uyttersprot, J.; De Corte, W.; Van Paepegem, W. Modal Parameter Identification and Comfort Assessment of GFRP Lightweight Footbridges in Relation to Human–Structure Interaction. J. Compos. Sci. 2023, 7, 348. https://doi.org/10.3390/jcs7090348
Uyttersprot J, De Corte W, Van Paepegem W. Modal Parameter Identification and Comfort Assessment of GFRP Lightweight Footbridges in Relation to Human–Structure Interaction. Journal of Composites Science. 2023; 7(9):348. https://doi.org/10.3390/jcs7090348
Chicago/Turabian StyleUyttersprot, Jordi, Wouter De Corte, and Wim Van Paepegem. 2023. "Modal Parameter Identification and Comfort Assessment of GFRP Lightweight Footbridges in Relation to Human–Structure Interaction" Journal of Composites Science 7, no. 9: 348. https://doi.org/10.3390/jcs7090348
APA StyleUyttersprot, J., De Corte, W., & Van Paepegem, W. (2023). Modal Parameter Identification and Comfort Assessment of GFRP Lightweight Footbridges in Relation to Human–Structure Interaction. Journal of Composites Science, 7(9), 348. https://doi.org/10.3390/jcs7090348






