Resilience of Medium-to-High-Rise Ductile Coupled Shear Walls Located in Canadian Seismic Zones and Strengthened with Externally Bonded Fiber-Reinforced Polymer Composite: Nonlinear Time History Assessment
Abstract
1. Introduction
2. Canadian Seismic Design Provisions for Ductile Walls
2.1. Force-Based Design Provisions
2.2. Capacity Design Provisions
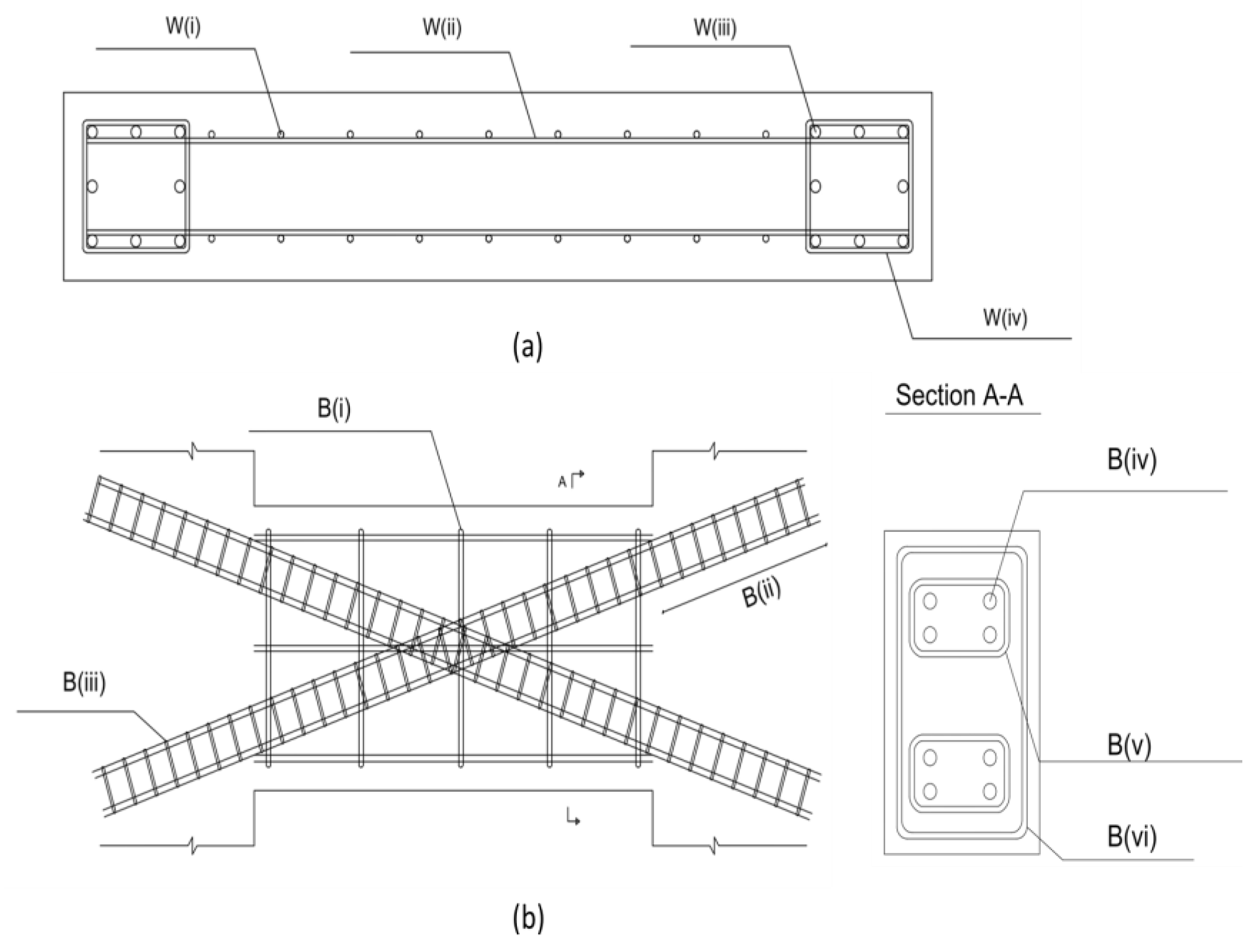
3. Details and Geometry of the Case Study
4. Seismic Strengthening of CSWs with EB-FRP Sheets
4.1. Provisions for the Design of EB-FRP Sheets
4.2. Strengthening Schemes
5. Nonlinear Time History Analysis
5.1. CSWs Assumptions for Nonlinear Analysis
5.1.1. Member Modeling
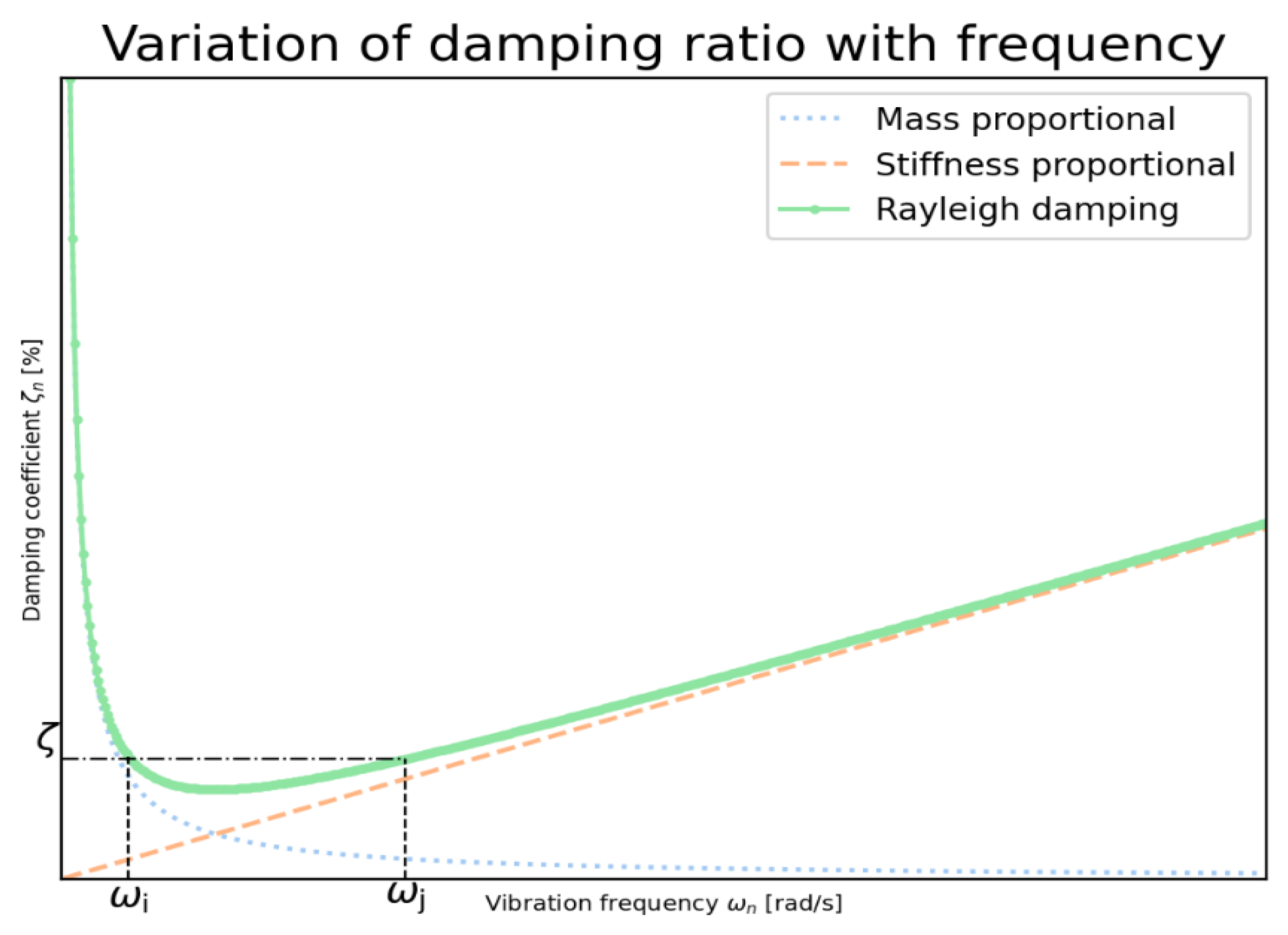
5.1.2. Damping Modeling
5.1.3. Hysteresis Modeling
6. Ground Motion Selection and Scaling
7. Results and Discussion
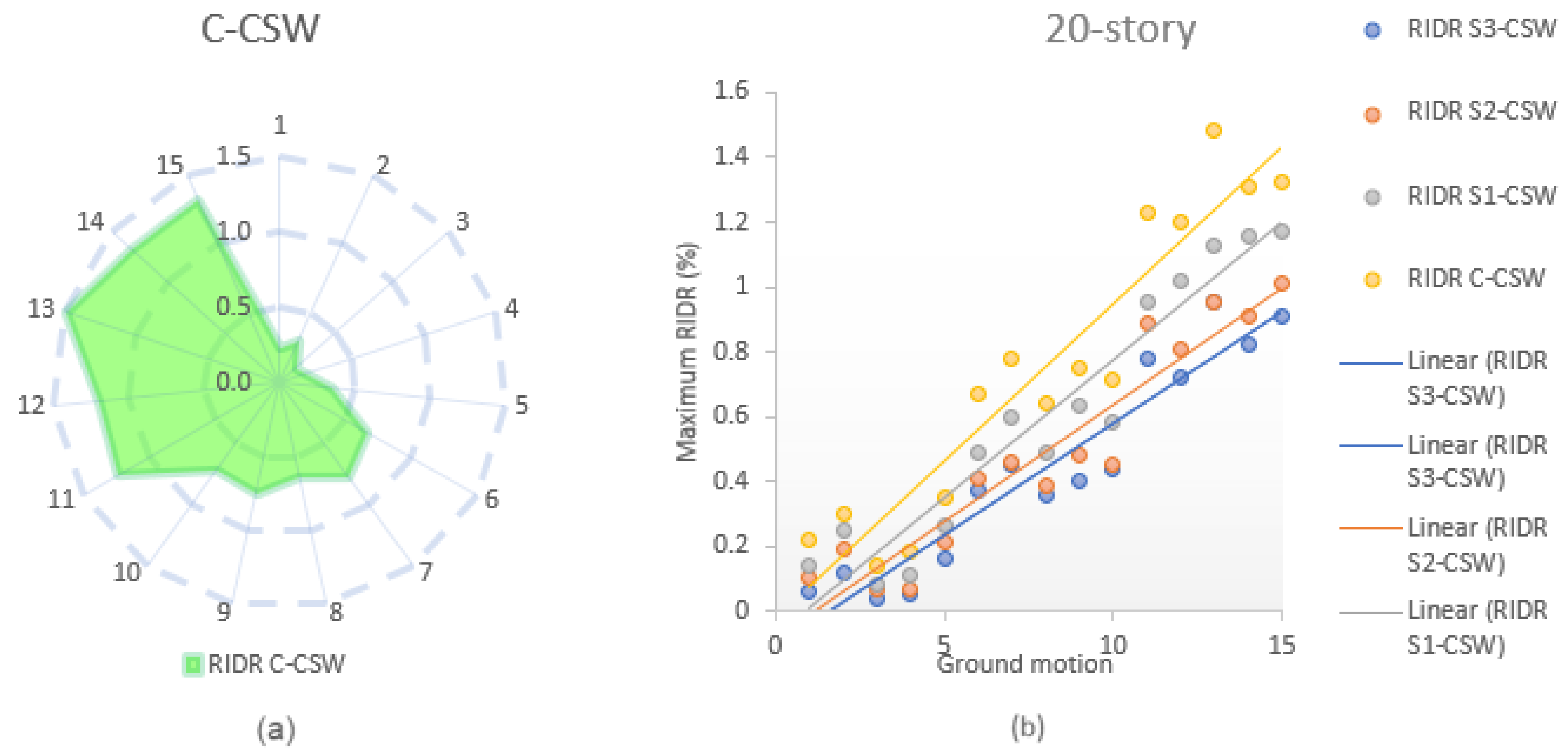
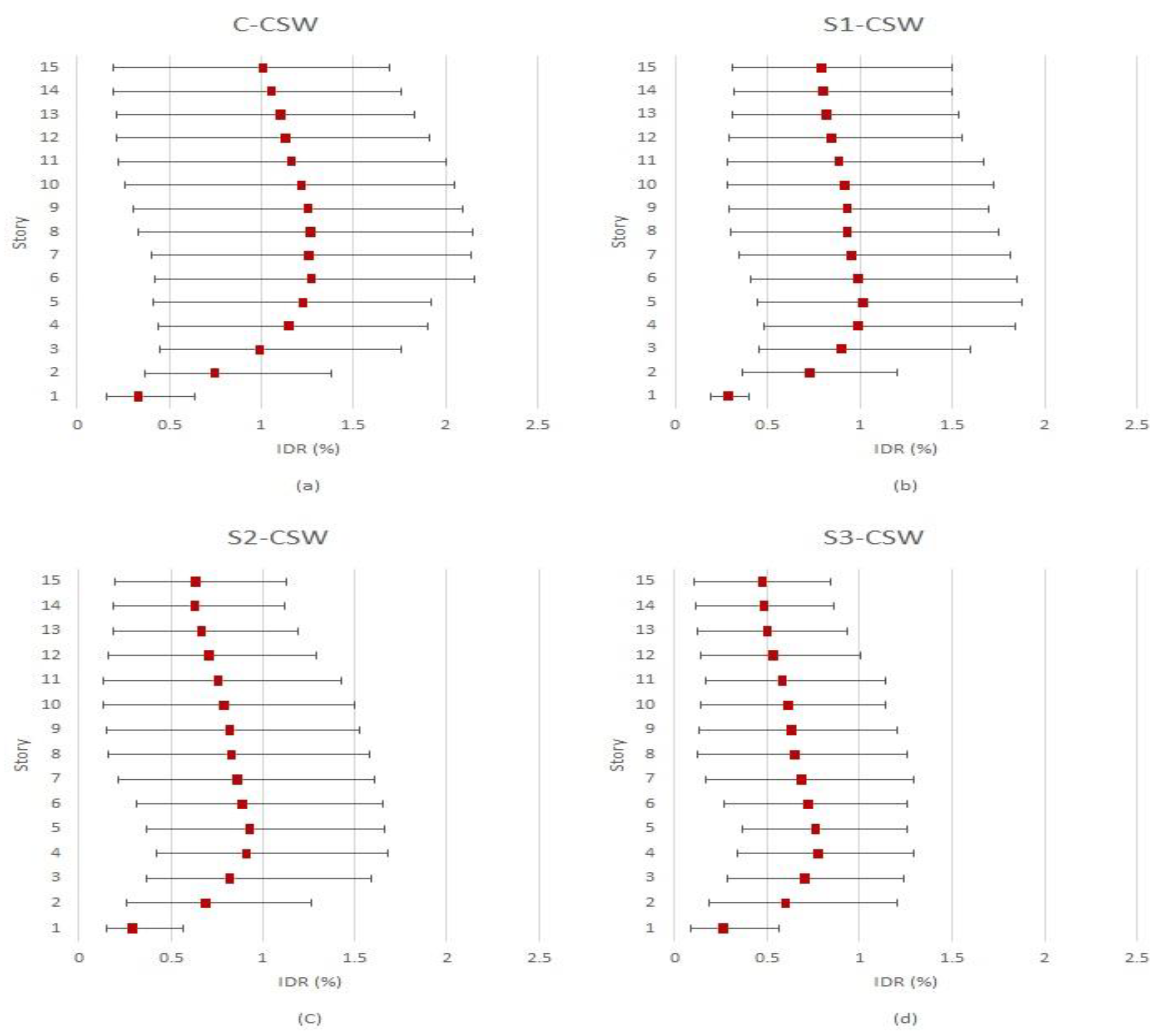
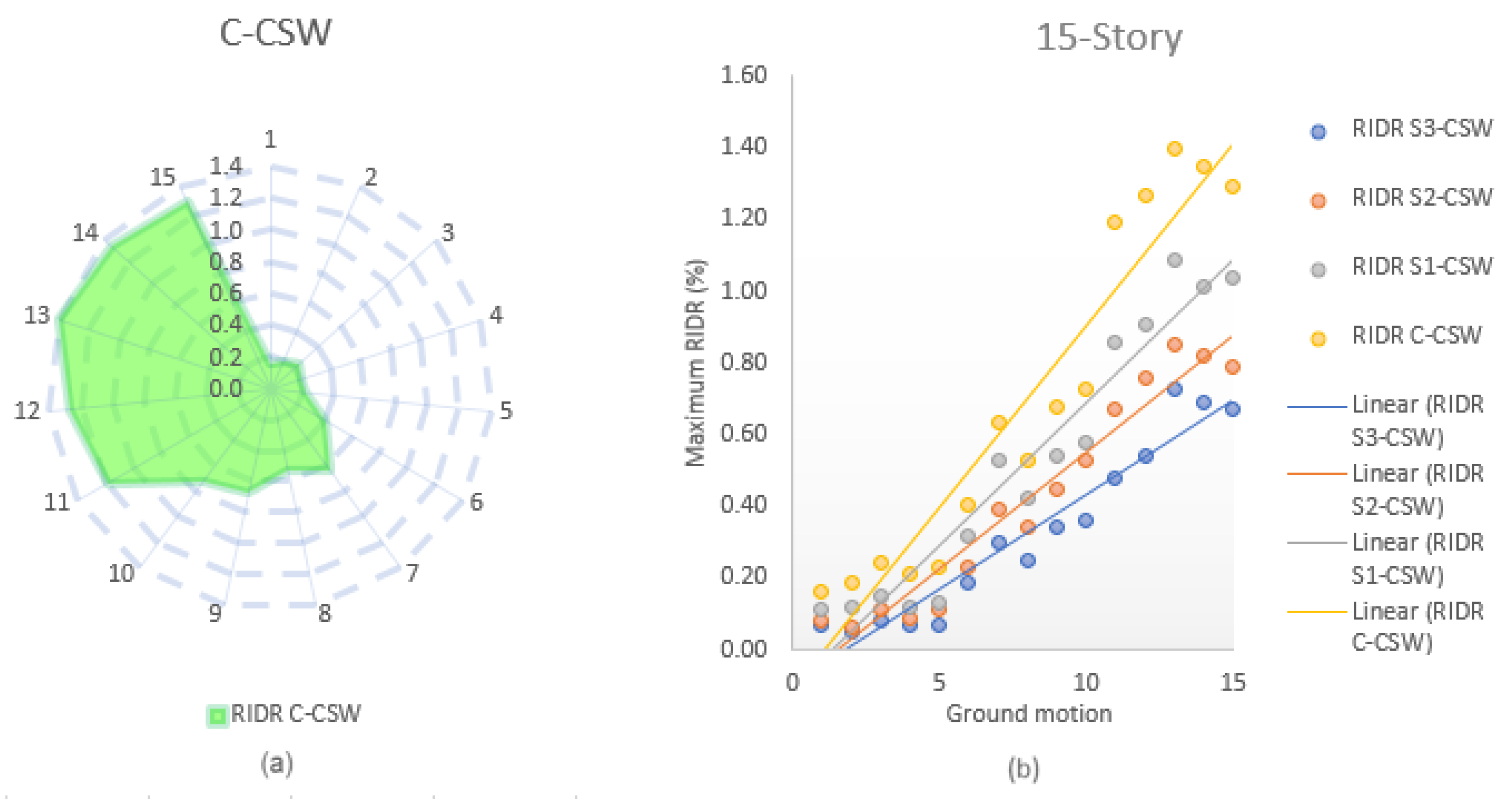
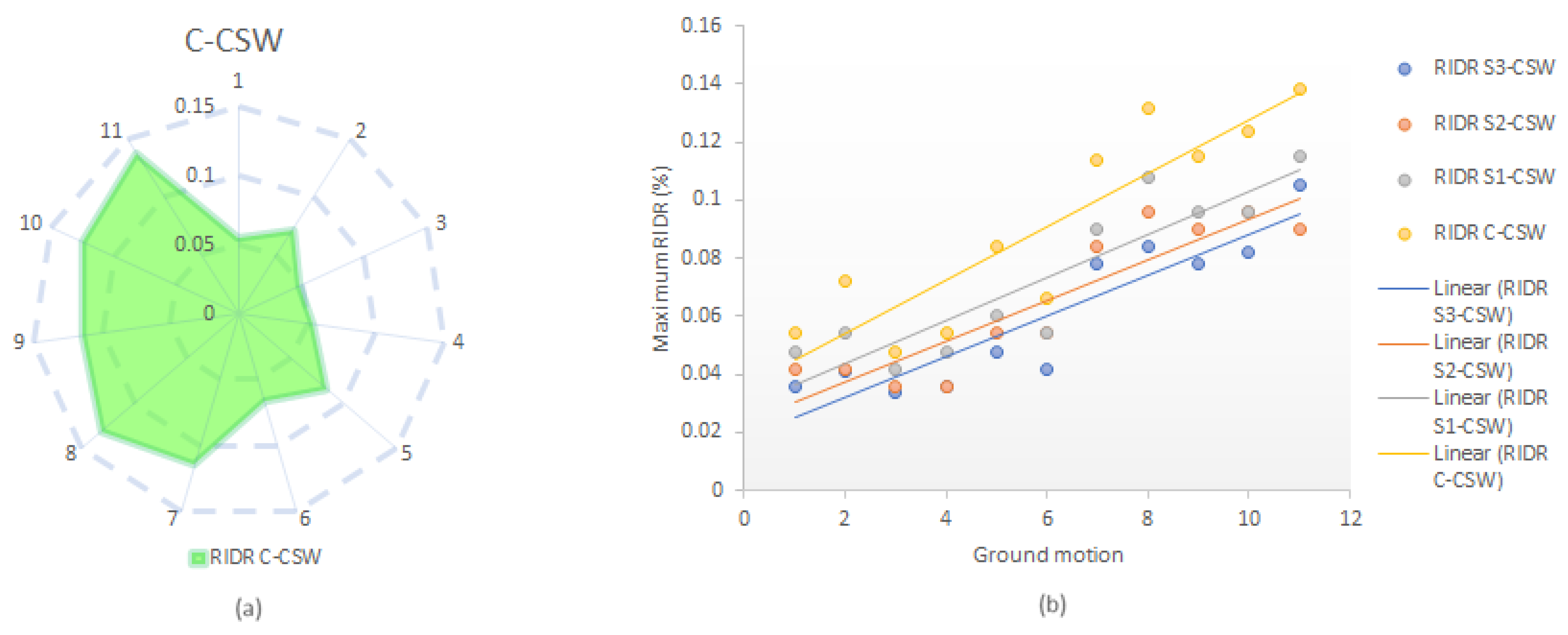
7.1. Residual Inter-Story Drift Ratio
7.1.1. Western Canada
7.1.2. Eastern Canada
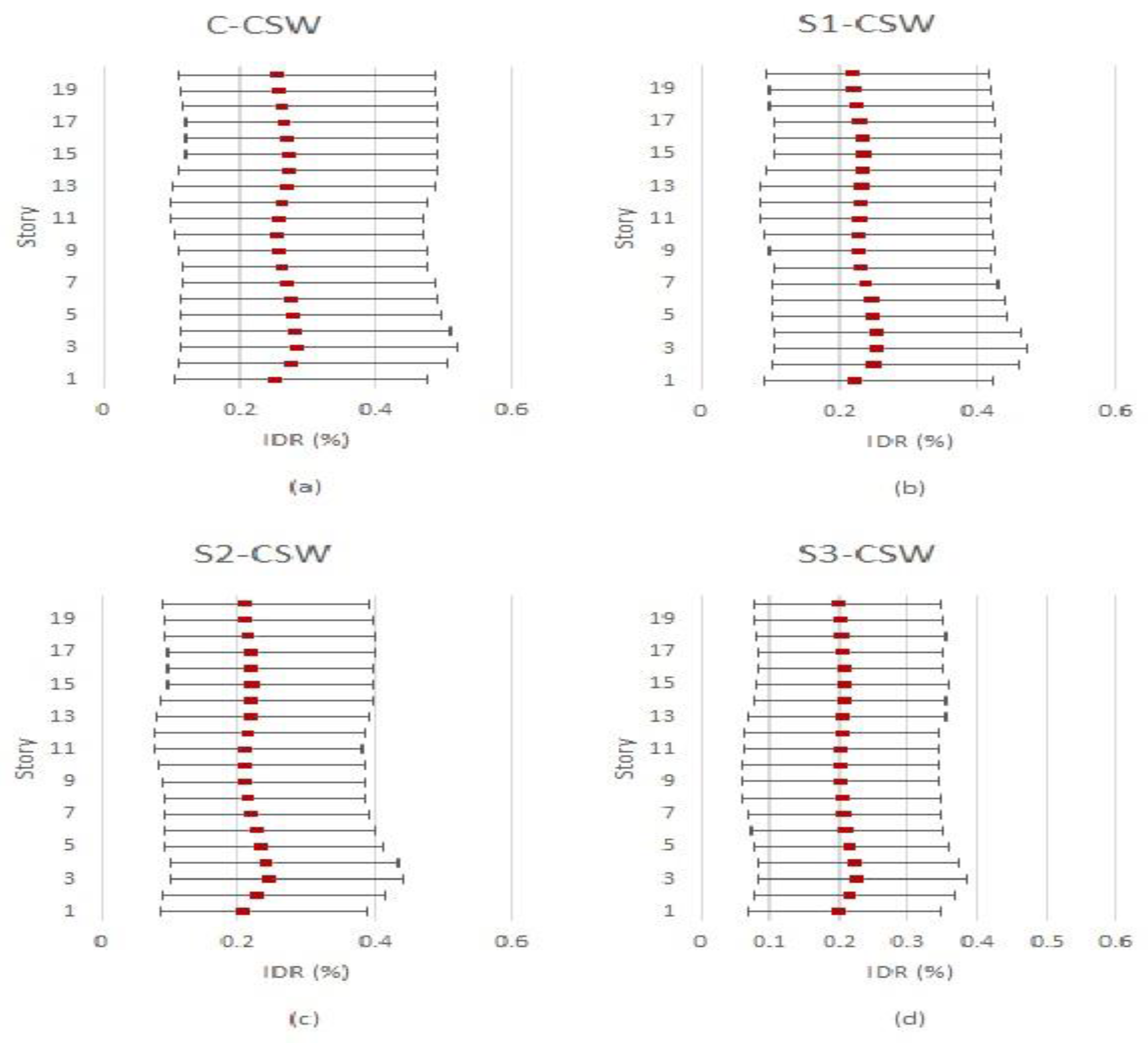
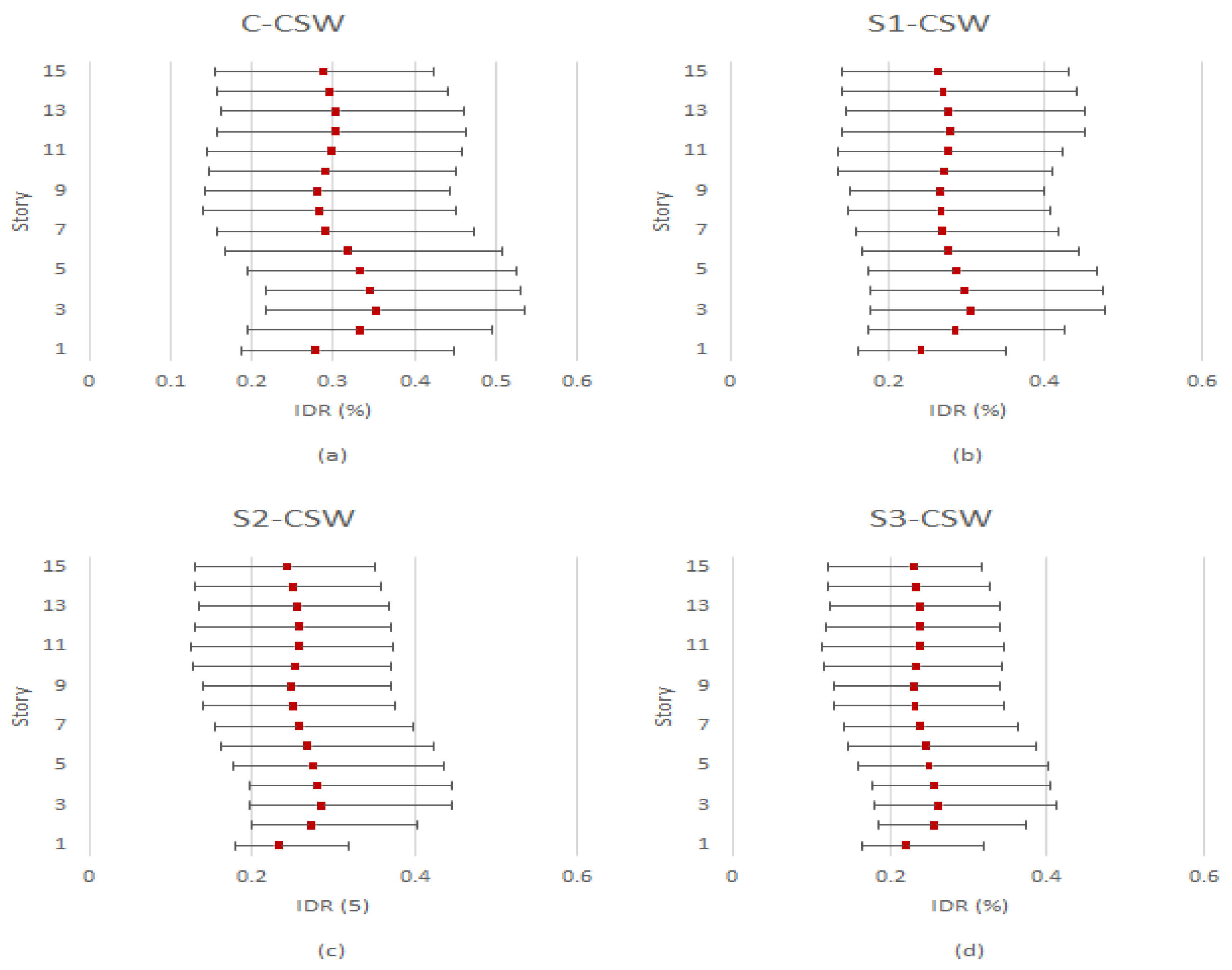
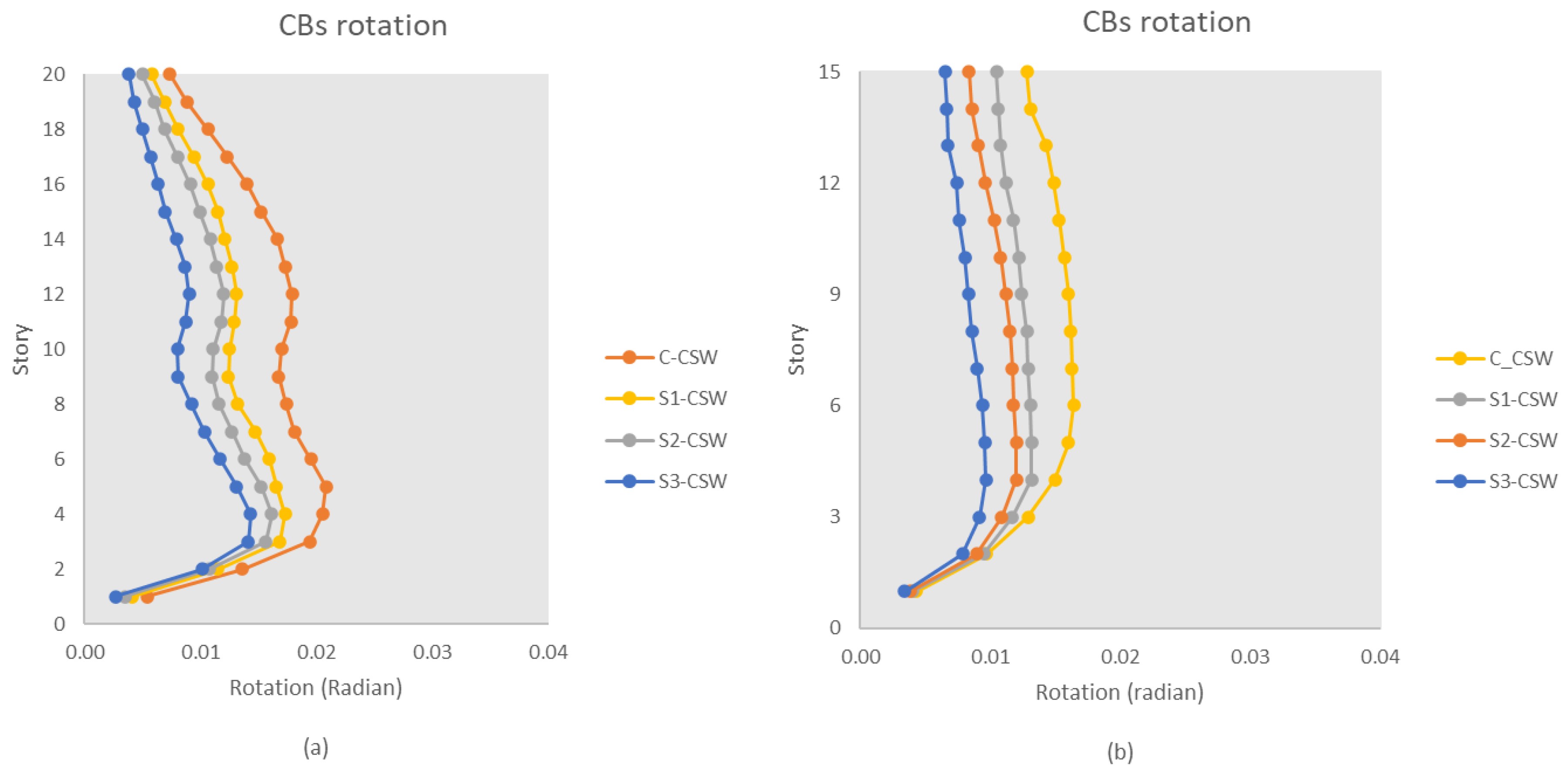
7.2. Beam Rotation
7.2.1. Western Canada
7.2.2. Eastern Canada
7.3. Shear Demand in Wall Piers
7.4. Bending Moment Demand in Wall Piers
8. Conclusions
- EB-FRP sheets are a viable option for reducing the RIDR in existing modern CSWs (14–53%). The proposed strengthening schemes were evaluated, and it was found that S3-CSW was the most effective in decreasing the RIDR in CSWs. However, it was also observed that the efficiency of the proposed configurations decreased as the height of the shear walls increased. Notably, the RIDR in western Canada was significantly higher compared with eastern Canada.
- The predominant cause of the RIDR among CSWs in western Canada can be attributed to Cascadia events, compared with other seismic sources. Apart from their long duration, which could induce structural fatigue, the low frequency of such events could result in resonance in high-rise buildings with longer vibration periods.
- Based on the behavior of 15-story and 20-story CSWs in eastern Canada, it is not deemed reasonable nor cost-effective to apply EB-FRP sheets on the CSWs in this region due to their predominantly elastic behavior and absence of significant residual displacement. Nonetheless, it was observed that, for the eastern CSWs, higher modes had an impact, displaying the potential formation of a second plastic hinge in the upper stories (60–70% of the wall height).
- The S3-CSW performed better in reducing the IDR and CB rotation. This can be attributed to the higher flexural strength resulting from the three layers of vertical EB-FRP sheets, coupled with the confinement caused by the FRP wrapping. Moreover, the horizontal FRP sheets enhanced the shear strength of CSWs, thereby preventing brittle shear failure. The fully wrapped FRP sheets also increased the debonding failure resistance of vertical FRP sheets, which further contributed to the system’s overall effectiveness. Also, the research findings indicate the effectiveness of using EB-FRP sheets in mitigating the fluctuation of the IDR cross height of CSWs.
- Applying EB-FRP sheets to CSWs resulted in a slight increase in base shear and bending moment demand. Among the various strengthening schemes employed, it was observed that S3-CSW had the highest impact on increasing the shear force and bending moment demand in CSWs. This increase was found to be more pronounced in the CSWs located in eastern Canada, attributable to the relatively larger share of EB-FRP sheets in the overall stiffness of the reinforced walls compared with western Canada. However, the improvement in the shear and bending resistance of CSWs due to the EB-FRP sheets far outweighed the increase in demand.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Afefy, H.M. Seismic retrofitting of reinforced-concrete coupled shear walls: A review. Pract. Period. Struct. Des. Constr. 2020, 25, 03120001. [Google Scholar] [CrossRef]
- Paulay, T.; Santhakumar, A.R. Ductile behavior of coupled shear walls. J. Struct. Div. 1976, 102, 93–108. [Google Scholar] [CrossRef]
- Franchi, A.; Napoli, P.; Crespi, P.; Giordano, N.; Zucca, M. Unloading and reloading process for the earthquake damage repair of ancient Masonry columns: The case of the Basilica di Collemaggio. Int. J. Archit. Herit. 2022, 16, 1683–1698. [Google Scholar] [CrossRef]
- Elnady, M. Seismic Rehabilitation of RC Structural Walls. Ph.D. Thesis, McMaster University, Hamilton, ON, USA, 2008. [Google Scholar]
- Arabzadeh, H.; Galal, K. Effectiveness of FRP wraps for retrofitting of existing RC shear walls. In Proceedings of the 11th Canadian Conference on Earthquake Engineering, Victoria, BC, Canada, 21–24 July 2015; pp. 21–24. [Google Scholar]
- Arabzadeh, H.; Galal, K. Seismic collapse risk assessment and FRP retrofitting of RC coupled C-shaped core walls using the FEMA P695 methodology. J. Struct. Eng. 2017, 143, 04017096. [Google Scholar] [CrossRef]
- Sakr, M.A.; El-Khoriby, S.R.; Khalifa, T.M.; Nagib, M.T. Modeling of RC shear walls strengthened by FRP composites. Struct. Eng. Mech. 2017, 61, 407–417. [Google Scholar] [CrossRef]
- Layssi, H.; Cook, W.D.; Mitchell, D. Seismic response and CFRP retrofit of poorly detailed shear walls. J. Compos. Constr. 2012, 16, 332–339. [Google Scholar] [CrossRef]
- El-Sokkary, H.; Galal, K. Seismic behavior of RC shear walls strengthened with fiber-reinforced polymer. J. Compos. Constr. 2013, 17, 603–613. [Google Scholar] [CrossRef]
- Lavorato, D.; Bergami, A.V.; Fiorentino, G.; Fiore, A.; Santini, S.; Nuti, C. Experimental tests on existing RC beams strengthened in flexure and retrofitted for shear by C-FRP in presence of negative moments. Int. J. Adv. Struct. Eng. 2018, 10, 211–232. [Google Scholar] [CrossRef]
- Honarparast, S.; Chaallal, O. Non-linear time history analysis of reinforced concrete coupled shear walls: Comparison of old design, modern design and retrofitted with externally bonded CFRP composites. Eng. Struct. 2019, 185, 353–365. [Google Scholar] [CrossRef]
- Honarparast, S.; El-Saikaly, G.; Chaallal, O. Externally bonded carbon fiber–reinforced polymer composites for seismic retrofit of reinforced concrete coupling beams designed according to old codes. Adv. Struct. Eng. 2019, 22, 1412–1425. [Google Scholar] [CrossRef]
- El-Sokkary, H. Nonlinear behaviour of FRP-retrofitted RC coupled shear walls. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 47, pp. 324–337. [Google Scholar]
- Fathalla, E.; Rajapakse, R.; Mihaylov, B.I. Modeling the shear behavior of deep beams strengthened with FRP sheets. Eng. Struct. 2022, 260, 114232. [Google Scholar] [CrossRef]
- Pecker, A. Advanced Earthquake Engineering Analysis; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Wu, X. A Study of Nonlinear Time History Analysis vs. Current Codes Analysis Procedure of Comparing Linear Dynamic Demand with Nonlinear Static Capacity for Ordinary Standard Bridge. In Challenges and Advances in Sustainable Transportation Systems; ASCE: Reston, VA, USA, 2014; pp. 467–480. [Google Scholar]
- McNeice, D. Performance-Based Design of a 30-Storey Coupled wall Structure. Ph.D. Thesis, University of South Carolina, Columbia, SC, USA, 2004. [Google Scholar]
- National Building Code of Canada (NBCC). Institute for Research in Construction; National Research Council of Canada: Ottawa, ON, Canada, 1941. Available online: https://nrc-publications.canada.ca/eng/view/object/?id=cf6ad19a-6e99-438a-af92-3eee7561156b (accessed on 30 May 2023).
- National Building Code of Canada (NBCC). Institute for Research in Construction; National Research Council of Canada: Ottawa, ON, Canada, 2015. Available online: https://nrc.canada.ca/en/certifications-evaluations-standards/codes-canada/codes-canada-publications/national-building-code-canada-2015 (accessed on 30 May 2023).
- Boivin, Y.; Paultre, P. Seismic performance of a 12-storey ductile concrete shear wall system designed according to the 2005 National building code of Canada and the 2004 Canadian Standard Association standard A23.3. Can. J. Civ. Eng. 2010, 37, 1–16. [Google Scholar] [CrossRef]
- Ye, L.; Lu, X.; Zhao, S. Analysis on seismic damage of buildings in the Wenchuan earthquake. J. Build. Struct. 2008, 29, 1–9. [Google Scholar]
- Bruneau, M.; Reinhorn, A. Overview of the resilience concept. In Proceedings of the 8th US National Conference on Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006; Volume 2040, pp. 18–22. [Google Scholar]
- Adey, B.; Hajdin, R.; Brühwiler, E. Effect of common cause failures on indirect costs. J. Bridge Eng. 2004, 9, 200–208. [Google Scholar] [CrossRef]
- Brookshire, D.S.; Chang, S.E.; Cochrane, H.; Olson, R.A.; Rose, A.; Steenson, J. Direct and indirect economic losses from earthquake damage. Earthq. Spectra 1997, 13, 683–701. [Google Scholar] [CrossRef]
- Forcellini, D. A new methodology to assess indirect losses in bridges subjected to multiple hazards. Innov. Infrastruct. Solut. 2019, 4, 10. [Google Scholar] [CrossRef]
- de Oliveira, L.B.; de Azevedo, A.R.; Marvila, M.T.; Pereira, E.C.; Fediuk, R.; Vieira, C.M.F. Durability of geopolymers with industrial waste. Case Stud. Constr. Mater. 2022, 16, e00839. [Google Scholar] [CrossRef]
- Abbaszadeh, A.; Chaallal, O. Enhancing resilience and self-centering of existing RC coupled and single shear walls using EB-FRP: State-of-the-art review and research needs. J. Compos. Sci. 2022, 6, 301. [Google Scholar] [CrossRef]
- Chancellor, N.B.; Eatherton, M.R.; Roke, D.A.; Akbaş, T. Self-Centering seismic lateral force resisting systems: High performance structures for the city of tomorrow. Buildings 2014, 4, 520–548. [Google Scholar] [CrossRef]
- Bedriñana, L.A.; Tani, M.; Kono, S.; Nishiyama, M. Evaluation of the Seismic Performance of Unbonded Post-Tensioned Precast Concrete Walls with Internal and External Dampers. II: Design Criteria and Numerical Research. J. Struct. Eng. 2022, 148, 04022106. [Google Scholar] [CrossRef]
- Holden, T.; Restrepo, J.; Mander, J.B. Seismic performance of precast reinforced and prestressed concrete walls. J. Struct. Eng. 2003, 129, 286–296. [Google Scholar] [CrossRef]
- Marriott, D.; Pampanin, S.; Palermo, A. Quasi-static and pseudo-dynamic testing of unbonded post-tensioned rocking bridge piers with external replaceable dissipaters. Earthq. Eng. Struct. Dyn. 2009, 38, 331–354. [Google Scholar] [CrossRef]
- Lecce, L. Shape Memory Alloy Engineering: For Aerospace, Structural and Biomedical Applications; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Wang, B.; Zhu, S.; Chen, K.; Huang, J. Development of superelastic SMA angles as seismic-resistant self-centering devices. Eng. Struct. 2020, 218, 110836. [Google Scholar] [CrossRef]
- Yang, C.-S.W.; DesRoches, R.; Leon, R.T. Design and analysis of braced frames with shape memory alloy and energy-absorbing hybrid devices. Eng. Struct. 2010, 32, 498–507. [Google Scholar] [CrossRef]
- Soares, M.M.; Palermo, D.; Cortes-Puentes, W.L. Modelling of mid-rise concrete shear walls reinforced with superelastic shape memory alloys: Nonlinear analysis. Eng. Struct. 2021, 247, 113049. [Google Scholar] [CrossRef]
- Qian, H.; Wang, X.; Li, Z.; Zhang, Y. Experimental study on re-centering behavior and energy dissipation capacity of prefabricated concrete frame joints with shape memory alloy bars and engineered cementitious composites. Eng. Struct. 2023, 277, 115394. [Google Scholar] [CrossRef]
- Noureldin, M.; Memon, S.A.; Gharagoz, M.; Kim, J. Performance-based seismic retrofit of RC structures using concentric braced frames equipped with friction dampers and disc springs. Eng. Struct. 2021, 243, 112555. [Google Scholar] [CrossRef]
- Naeem, A.; Kim, J. Seismic performance evaluation of a spring viscous damper cable system. Eng. Struct. 2018, 176, 455–467. [Google Scholar] [CrossRef]
- Shen, J.; Huang, Z.; Song, X.; Yao, Y. Deformation performance analysis of concrete shear wall with CFRP grids based on the modified uniaxial shear-flexural model. J. Build. Eng. 2022, 54, 104621. [Google Scholar] [CrossRef]
- Song, X.; Huang, Z.; Shen, J.; Yao, Y. Experimental study on cyclic behavior of hybrid CFRP grids-steel shear walls. In Structures; Elsevier: Amsterdam, The Netherlands, 2020; Volume 28, pp. 496–511. [Google Scholar]
- Zhao, Q.; Zhao, J.; Dang, J.-T.; Chen, J.-W.; Shen, F.-Q. Experimental investigation of shear walls using carbon fiber reinforced polymer bars under cyclic lateral loading. Eng. Struct. 2019, 191, 82–91. [Google Scholar] [CrossRef]
- Sadeghian, A. Seismic Deformations of Taller Reinforced Concrete Shear Walls Located in Eastern Canada; Ecole Polytechnique: Montreal, QC, Canada, 2018. [Google Scholar]
- National Building Code of Canada (NBCC). Institute for Research in Construction; National Research Council of Canada: Ottawa, ON, Canada, 2020. Available online: https://nrc-publications.canada.ca/eng/view/object/?id=515340b5-f4e0-4798-be69-692e4ec423e8 (accessed on 30 May 2023).
- CAN-A23.3-19; Design of Concrete Structures for Buildings. National Standard of Canada: Rexdale, ON, Canada, 2019.
- Canada, C.A.O.; Association, C.S. Concrete Design Handbook, 4th ed.; Cement Association of Canada: Ottawa, ON, Canada, 2016. [Google Scholar]
- Analysis Reference Manual for SAP2000 Ultimate v. 21.0.2; CSi: Berkeley, CA, USA, 2017.
- Honarparast, S.; Chaallal, O. Seismic performance of coupled shear walls designed according to old and new codes and retrofitted with Eb-CFRP composites. J. Earthq. Eng. 2022, 26, 1875–1898. [Google Scholar] [CrossRef]
- Manohar, S.; Madhekar, S. Seismic design of RC buildings. In Springer Transactions in Civil and Environmental Engineering; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Mohammadi, H.; Esfahani, M.; Riyazi, M. Behavior of coupling beams strengthened with carbon fiber reinforced polymer sheets. Int. J. Eng. 2007, 20, 49–58. [Google Scholar]
- Committee, A. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures (ACI 440.2 R-17); American Concrete Institute: Farmington Hills, MI, USA, 2017. [Google Scholar]
- Teng, J.; Chen, J.-F.; Smith, S.T.; Lam, L. FRP: Strengthened RC Structures; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- NRCC. Structural Commentaries (User’s Guide—NBC 2015: Part 4 of Division B); NRCC: Ottawa, ON, Canada, 2015. [Google Scholar]
- Carr, A. RUAUMOKO, Computer Program Library; Department of Civil Engineering, University of Canterbury: Christchurch, New Zealand, 2004. [Google Scholar]
- Harries, K.A. Seismic Design and Retrofit of Coupled Walls Using Structural Steel. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 1995. [Google Scholar]
- Smith, B.S.; Coull, A. Tall Building Structures: Analysis and Design; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Giberson, M.F. Two nonlinear beams with definitions of ductility. J. Struct. Div. 1969, 95, 137–157. [Google Scholar] [CrossRef]
- Jury, R.D. Seismic Load Demands on Columns of Reinforced Concrete Multistorey Frames. Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 1978. [Google Scholar]
- Boivin, Y. Assessment of the Seismic Performance of a 12-Storey Ductile Concrete Shear Wall System Designed according to the NBCC 2005 and the CSA A23. 3 2004 Standard; Université de Sherbrooke: Sherbrooke, QC, Canada, 2006. [Google Scholar]
- Carr, A.J. Ruaumoko Manual, Volume 2: User Manual for the 2-Dimensional Version Ruaumoko2D; University of Canterbury: Christchurch, New Zealand, 2008. [Google Scholar]
- Imbsen Software Systems. XTRACT—Cross-Sectional X sTRuctural Analysis of ComponenTs v2.6.0. Imbsen Software Systems. 2004.
- Mander, J.B.; Priestley, M.J.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-oriented stress–strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Zhijun, L. Seismic Vulnerability of RC Frame and Shear Wall Structures in Singapore. Ph.D. Thesis, National University of Singapore, Singapore, 2006. [Google Scholar]
- Dong, P. Effect of Varying Hysteresis Models and Damage Models on Damage Assessment of r/c Structures under Standard Design Level Earthquakes Obtained Using a New Scaling Method. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2003. [Google Scholar]
- Choi, K.-S.; Kim, H.-J. Strength demand of hysteretic energy dissipating devices alternative to coupling beams in high-rise buildings. Int. J. High-Rise Build. 2014, 3, 107–120. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced concrete elements subjected to shear. ACI J. 1986, 83, 219–231. [Google Scholar]
- Petrini, L.; Maggi, C.; Priestley, M.N.; Calvi, G.M. Experimental verification of viscous damping modeling for inelastic time history analyzes. J. Earthq. Eng. 2008, 12, 125–145. [Google Scholar] [CrossRef]
- Hall, J.F. Problems encountered from the use (or misuse) of Rayleigh damping. Earthq. Eng. Struct. Dyn. 2006, 35, 525–545. [Google Scholar] [CrossRef]
- Otani, S. SAKE: A computer program for inelastic response of R/C frames to earthquakes. Civ. Eng. Stud. SRS-413 1974. [Google Scholar]
- Saiidi, M.; Sozen, M.A. Simple and complex models for nonlinear seismic response of reinforced concrete structures. Civ. Eng. Stud. SRS-465 1979. [Google Scholar]
- Benazza, T. Non-Linear Behavior of Coupled Shear Wall Systems under Seismic Events; University of Quebec Montreal: Montreal, QC, Canada, 2012. [Google Scholar]
- Adams, J.; Allen, T.; Halchuk, S.; Kolaj, M. Canada’s 6th Generation Seismic Hazard Model, as Prepared for the 2020 National Building Code of Canada. 12th Can. Conf. Earthq. Eng. 2019. [Google Scholar]
- McGuire, R.K. Probabilistic seismic hazard analysis and design earthquakes: Closing the loop. Bull. Seismol. Soc. Am. 1995, 85, 1275–1284. [Google Scholar] [CrossRef]
- Tremblay, R.; Atkinson, G.M. Comparative study of the inelastic seismic demand of eastern and western Canadian sites. Earthq. Spectra 2001, 17, 333–358. [Google Scholar] [CrossRef]
- Atkinson, G.M. The high-frequency shape of the source spectrum for earthquakes in eastern and western Canada. Bull. Seismol. Soc. Am. 1996, 86, 106–112. [Google Scholar] [CrossRef]
- Adams, J.; Atkinson, G. Development of seismic hazard maps for the proposed 2005 edition of the National Building Code of Canada. Can. J. Civ. Eng. 2003, 30, 255–271. [Google Scholar] [CrossRef]
- Atkinson, G.M. Earthquake time histories compatible with the 2005 National building code of Canada uniform hazard spectrum. Can. J. Civ. Eng. 2009, 36, 991–1000. [Google Scholar] [CrossRef]
- Tremblay, R.; Atkinson, G.M.; Bouaanani, N.; Daneshvar, P.; Léger, P.; Koboevic, S. Selection and scaling of ground motion time histories for seismic analysis using NBCC 2015. In Proceedings of the 11th Canadian Conference on Earthquake Engineering, Victoria, BC, Canada, 21–24 July 2015; Volume 99060. [Google Scholar]
- ASCE/SEI 7-22; Minimum Design Loads and Associated Criteria for Buildingsand Other Structures. ASCE: Reston, VA, USA, 2022.
- Adebar, P.; Dezhdar, E.; Yathon, J. Accounting for higher mode shear forces in concrete wall buildings: 2014 CSA A23.3. In Proceedings of the The 11th Canadian Conference on Earthquake Engineering, Victoria, BC, Canada, 21–24 July 2015. [Google Scholar]
- White, T.; Adebar, P. Estimating rotational demands in high-rise concrete wall buildings. In Proceedings of the 13th World Conference on Earthquake Engineering, Victoria, BC, Canada, 1–6 August 2004; pp. 1–6. [Google Scholar]
- El-Sokkary, H.; Galal, K.; Ghorbanirenani, I.; Léger, P.; Tremblay, R. Shake table tests on FRP-rehabilitated RC shear walls. J. Compos. Constr. 2013, 17, 79–90. [Google Scholar] [CrossRef]











| Type of Ductile Wall | Force Modification Factor | |
|---|---|---|
| Coupled wall | = 4 | = 1.7 |
| Partially coupled wall | = 3.5 | = 1.7 |
| Shear wall | = 3.5 | = 1.6 |
| Element | Property | Effective Property |
|---|---|---|
| Diagonally reinforced CB | Moment of inertia | = 0.25 |
| Shear area | = 0.45 | |
| Wall | Flexural stiffness | = |
| Axial stiffness | = |
| W (i) (mm) | W (ii) (mm) | W (iii) (mm) | W (iv) (mm) | Section Dimension (mm) | ||
|---|---|---|---|---|---|---|
| West | 20-story | 15M @200 | 10M @200 | 8M 30 in PH region 8M 25 out of PH region | 10M @150 | 8250 × 400 |
| 15-story | 10M @200 | 10M @250 | 4M 25 in PH region 4M 20 out of PH region | 10M @200 | 8250 × 400 | |
| East | 20-story | 15M @200 | 10M @250 | 6M 25 in PH region 6M 20 out of PH region | 10M @150 | 8250 × 400 |
| 15-story | 10M @200 | 10M @250 | 4M 20 in PH region 4M 15 out of PH region | 10M @200 | 8250 × 400 |
| B (i) (mm) | B (ii) (mm) | B (iii) (mm) | B (iv) (mm) | B (v) (mm) | B (vi) (mm) | Section Dimension (mm) | ||
|---|---|---|---|---|---|---|---|---|
| West | 20-story | 10M @250 | 1500 mm stories 1–7 1300 mm stories 8–16 850 mm stories 17–20 | 10M @80 | 25M stories 1–7 20M stories 8–16 15M stories 17–20 | 10M @100 | 10M @200 | 750 × 400 |
| 15-story | 10M @250 | 1300 mm stories 1–5 850 mm stories 6–10 700 mm stories 11–15 | 10M @100 | 20M stories 1–5 15M stories 6–10 10M stories 11–15 | 10M @150 | 10M @250 | 750 × 400 | |
| East | 20-story | 10M @250 | 1100 mm stories 1–5 950 mm stories 6–13 700 mm stories 14–20 | 10M @100 | 25M stories 1–5 20M stories 6–3 15M stories 14–20 | 10M @100 | 10M @200 | 750 × 400 |
| 15-story | 10M @250 | 900 mm stories 1–4 750 mm stories 5–10 700 mm stories 11–15 | 10M @120 | 20M stories 1–4 15M stories 5–10 10M stories 11–15 | 10M @150 | 10M @250 | 750 × 400 |
| Ultimate tensile strength (MPa) | 1355 |
| Tensile modulus, (MPa) | 115,700 |
| Elongation at break (%) | 0.95 |
| Thickness per ply (mm) | 1.3 |
| Scenario | Rec. No. | M | R (km) | PGA (g) | Duration (s) | Period Range (s) | Event Type |
|---|---|---|---|---|---|---|---|
| 1 | West 1 | 6.5 | 8.8 | 0.475 | 49.30 | 0.2–0.8 | Crustal |
| West 2 | 6.5 | 11.2 | 0.483 | 49.30 | |||
| West 3 | 6.5 | 10.8 | 0.503 | 49.30 | |||
| West 4 | 6.5 | 12.3 | 0.497 | 53.63 | |||
| West 5 | 6.5 | 14.6 | 0.559 | 53.63 | |||
| 2 | West 6 | 7.5 | 16.4 | 0.391 | 102.02 | 0.3–1.5 | In-slab |
| West 7 | 7.5 | 18.1 | 0.430 | 102.02 | |||
| West 8 | 7.5 | 21.6 | 0.351 | 102.02 | |||
| West 9 | 7.5 | 35.7 | 0.289 | 93.39 | |||
| West 10 | 7.5 | 48.4 | 0.423 | 93.39 | |||
| 3 | West 11 | 9 | 112.4 | 0.137 | 309.42 | 1–4 | Cascadia subduction |
| West 12 | 9 | 112.4 | 0.132 | 309.42 | |||
| West 13 | 9 | 156.7 | 0.173 | 309.42 | |||
| West 14 | 9 | 156.7 | 0.146 | 309.42 | |||
| West 15 | 9 | 200 | 0.167 | 309.42 |
| Scenario | Rec. No. | M | R (km) | PGA (g) | Duration (s) | Period Range (s) | Event Type |
|---|---|---|---|---|---|---|---|
| 1 | East 1 | 6 | 10.7 | 0.322 | 43.59 | 0.2–1 | Crustal |
| East 2 | 6 | 12.8 | 0.645 | 43.59 | |||
| East 3 | 6 | 20.8 | 0.423 | 43.59 | |||
| East 4 | 6 | 21.6 | 0.451 | 47.53 | |||
| East 5 | 6 | 26.3 | 0.301 | 47.53 | |||
| 2 | East 6 | 7 | 13.8 | 0.478 | 51.12 | 0.5–2.42 | Crustal |
| East 7 | 7 | 20.6 | 0.410 | 51.12 | |||
| East 8 | 7 | 50.3 | 0.308 | 51.12 | |||
| East 9 | 7 | 62.6 | 0.331 | 57.35 | |||
| East 10 | 7 | 95.5 | 0.248 | 57.35 | |||
| East 11 | 7 | 94.2 | 0.299 | 57.35 |
| Base Shear Demand (kN) | |||||
|---|---|---|---|---|---|
| S3-CSW | S2-CSW | S1-CSW | C-CSW | ||
| Vancouver | 20-story | 1126 | 1081 | 1048 | 969 |
| 15-story | 736 | 691 | 670 | 603 | |
| Montreal | 20-story | 1158 | 1110 | 1077 | 963 |
| 15-story | 633 | 606 | 588 | 494 | |
| Base Bending Moment (kN.m) | |||||
|---|---|---|---|---|---|
| S3-CSW | S2-CSW | S1-CSW | C-CSW | ||
| Vancouver | 20-story | 5346 | 5181 | 4972 | 4843 |
| 15-story | 3729 | 3564 | 3454 | 3212 | |
| Montreal | 20-story | 2806 | 2754 | 2651 | 2486 |
| 15-story | 2134 | 2046 | 1958 | 1804 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbaszadeh, A.; Chaallal, O. Resilience of Medium-to-High-Rise Ductile Coupled Shear Walls Located in Canadian Seismic Zones and Strengthened with Externally Bonded Fiber-Reinforced Polymer Composite: Nonlinear Time History Assessment. J. Compos. Sci. 2023, 7, 317. https://doi.org/10.3390/jcs7080317
Abbaszadeh A, Chaallal O. Resilience of Medium-to-High-Rise Ductile Coupled Shear Walls Located in Canadian Seismic Zones and Strengthened with Externally Bonded Fiber-Reinforced Polymer Composite: Nonlinear Time History Assessment. Journal of Composites Science. 2023; 7(8):317. https://doi.org/10.3390/jcs7080317
Chicago/Turabian StyleAbbaszadeh, Ali, and Omar Chaallal. 2023. "Resilience of Medium-to-High-Rise Ductile Coupled Shear Walls Located in Canadian Seismic Zones and Strengthened with Externally Bonded Fiber-Reinforced Polymer Composite: Nonlinear Time History Assessment" Journal of Composites Science 7, no. 8: 317. https://doi.org/10.3390/jcs7080317
APA StyleAbbaszadeh, A., & Chaallal, O. (2023). Resilience of Medium-to-High-Rise Ductile Coupled Shear Walls Located in Canadian Seismic Zones and Strengthened with Externally Bonded Fiber-Reinforced Polymer Composite: Nonlinear Time History Assessment. Journal of Composites Science, 7(8), 317. https://doi.org/10.3390/jcs7080317





