Effect of Nanoparticles and Their Anisometry on Adhesion and Strength in Hybrid Carbon-Fiber-Reinforced Epoxy Nanocomposites

Abstract

Carbon-fiber-reinforced plastics are composite materials with record-high specific strength, which depends on the efficiency of stress redistribution between the reinforcing fibers by the polymer matrix. The problem is the accurate assessment of adhesion in the carbon fiber–polymer matrix system since it affects the overall strength of the composite. This paper provides a novel electrochemical method for determining adhesion by estimating the critical length of carbon fibers that protrude above the fracture surface of the fiber-reinforced composite using their electrical conductivity and insulating properties of the polymer matrix. The method has been successfully applied to evaluate adhesion in carbon plastics having an epoxy matrix filled with nanoparticles of different anisometry: carbon nanotubes, organomodified montmorillonite, or detonation nanodiamonds. In addition to adhesion measurements, the effect of nanoparticles on the viscosity of epoxy binder, its impregnation efficiency of carbon fibers, curing, glass transition, and tensile strength of fiber-reinforced composites was estimated. Nanodiamonds at a mass fraction of 0.1% proved to be the most effective for improving the quality of epoxy carbon plastics, increasing fiber–matrix adhesion by 2.5 times, tensile strength by 17%, and not decreasing the glass transition temperature.

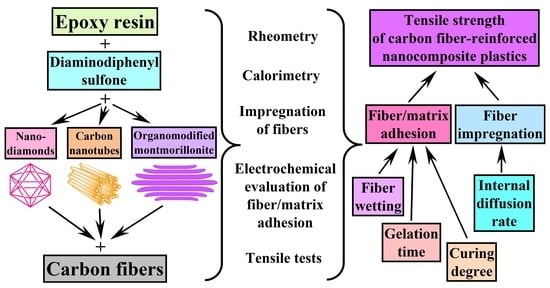
1. Introduction

The filling of polymers with nanoscale particles has become a usual method of improving their properties [1,2,3,4]. Over the past three decades, a wide variety of types of nanoparticles, both natural and synthetic, have been considered for modifying polymers [5]. Researchers focused maximum attention on such particles as montmorillonite [6,7], graphene [8,9,10,11,12], carbon nanotubes [13,14,15,16,17], silicon nanotubes [18], nanocellulose [19,20], boron nitride [17], and fumed silica [21,22]. This particular focus is due to the anisometric structure of these particles, which are plates, fibers, or fractal aggregates. Compared to spherical particles, anisometric ones increase the mechanical properties of composites more strongly at the same volume fraction [23,24]. The advantage of nanoparticles is their well-developed high-energy surface, whose adsorption of macromolecular chains can improve the mechanical properties of the polymer. In this case, modification of polymer properties requires only relatively small amounts of nanoparticles due to their high specific surface area. However, the high surface energy of nanoparticles also results in their strong aggregation [25,26], as interparticle interactions are more energetically favorable than those between inorganic particles and organic molecules [27]. Because of this problem, the surface of polar (high-energy) nanoparticles is often modified either by chemical functionalization or by using a surfactant to improve their affinity to non-polar organic matrices and facilitate their disaggregation in them [28,29,30,31].

Despite the high properties of nanocomposites, they cannot replace traditional composites in all cases. An example is reinforced plastics, whose dispersed phase is a continuous or very long fiber oriented in one direction [32,33]. Fiber reinforcement makes it possible to achieve the highest mechanical properties of polymer composites. In this case, carbon, aramid, silicate, or other fibers having both high strength and high modulus bear the load, while the mission of the polymer matrix is to redistribute the stresses evenly between the load-bearing fibers. The interfacial adhesion between the fiber and the polymer matrix determines the efficiency of stress redistribution, eventually affecting the strength properties of the reinforced composite [34,35,36]. The small interfacial adhesion can cause delamination of the continuous matrix from the fiber surface, forcing the fiber to cease its function as a load-bearing framework with instant destruction of the composite due to the much lower strength of the polymer matrix compared to the reinforcing fiber. High polymer–fiber interfacial adhesion is essential, but this does not mean that the cohesive properties of the polymer matrix itself do not matter. During the manufacturing of a reinforced composite and its operation, it is always possible that internal stresses will appear at the fiber–polymer boundary, causing the formation of cracks, their growth, and the resulting destruction of the material [37,38]. Therefore, the cohesive strength of the matrix is also necessary, as its increase can enhance the strength and durability of the reinforced composite itself. In turn, since nanoparticles are the best to improve the cohesion strength, it is logical to use a nanocomposite polymer matrix that will then include reinforcing continuous fibers. Such a design representing a hybrid fiber-reinforced polymer nanocomposite can provide the highest mechanical properties to the polymer material.

As a polymer matrix for reinforced plastic, epoxy resin is the most convenient [39,40]. Firstly, it has a relatively low viscosity, allowing the impregnation of fibers with it without high temperatures and pressures. Secondly, it exhibits strong adhesion to low- and high-polar surfaces, allowing, among other things, for obtaining epoxy nanocomposites made with many types of nanoparticles [41,42,43]. The problem is a high increase in the viscosity of epoxy resin after the addition of nanoparticles, which can impair the impregnation of the reinforcing fiber with the nanocomposite epoxy binder and thus deteriorate the mechanical properties of the cured reinforced plastic. Moreover, the viscosity increases more when using anisometric disaggregated nanoparticles that improve the strength properties of the polymer matrix more strongly [44], making the choice of the type of nanoparticle (spherical, fibrous, or plate-like) not apparent when using them to produce a hybrid fiber-reinforced plastic with a nanocomposite matrix. The increase in the strength of the nanocomposite matrix is indirectly accompanied by a rise in its viscosity, potentially impairing the impregnation of the reinforcing fiber. In turn, the deterioration of fiber impregnation will increase the porosity and reduce the adhesion between the fiber and the polymer matrix, thereby lowering the strength of the resulting reinforced plastic. Consequently, nanoparticles can improve the performance of the reinforced plastic by increasing the cohesive strength of its matrix and degrade it by worsening impregnation and interfacial adhesion. Recently, there are many works on obtaining hybrid composites, i.e., containing two or more reinforcing agents, e.g., reinforcing fibers and dispersed nanoparticles [45,46,47,48,49,50,51]. All these works show a positive effect of nanoparticles (mainly graphene, alumina, or silica) on the mechanical properties of fiber-reinforced plastics at some concentrations of nanoparticles and usually using a single type of them. In other words, there are no studies investigating the effect of nanoparticle anisometry on the efficiency of improving the properties of fiber-reinforced plastics, due to which the role of anisometry remains off-limits.

This study examines three types of nanoparticles with different shapes to produce a nanocomposite epoxy matrix. Firstly, these are sphere-like detonation nanodiamonds (DND) [52]. Their peculiarity is both the highly developed surface and the abundance of various functional surface groups (methyl, hydroxyl, carbonyl, carboxyl, and others), which would promote good adhesion both with the epoxy matrix and with the reinforcing fiber if they come into contact. Nanodiamonds have previously improved the strength properties of many polymer matrices, while their production contributes to the rational disposal of weapons-grade explosives [53]. The second is functionalized carbon nanotubes (CNT) capped with carboxyl and hydroxyl groups to facilitate their disaggregation and improve interaction with epoxy resin, as previously shown in many studies [54]. The third is organomodified montmorillonite (OMMT), whose modification with surfactant also helps to facilitate the disaggregation of its clay particles in polymer matrices [55,56]. Carbon fibers (CF) will be reinforcing fibers as they provide the highest increase in the strength properties of the composite and have critical applications in marine, aerospace, and nuclear engineering for producing hulls and vessels of different configurations [57,58]. Thus, this work aims to investigate the effect of nanodiamonds, carbon nanotubes, and organomodified nanoclay on the ability of epoxy resin to impregnate the carbon fibers, the epoxy adhesion to them, and the strength of the cured hybrid carbon-fiber-reinforced nanocomposite.

2. Materials and Methods

2.1. Materials

The epoxy binder was a diglycidyl ether of bisphenol A (DGEBA, an epoxy equivalent weight: 203 g/eq) and 4,4′-diaminodiphenyl sulfone as its hardener (DDS, an amine hydrogen equivalent weight: 62 g/eq). The DGEBA/DDS mass ratio was 70/30, which corresponded to the role of DDS as a trifunctional hardener [59]. The choice of the binder composition results from the affordability of this epoxy resin and the high heat deflection temperature of the product of its interaction with this hardener, which is essential for high-grade fiber-reinforced composites [60,61]. The filler-containing resin and hardener were mixed at 80 °C just before the impregnation and curing of the specimens.

There were three types of nanofillers used separately. Detonation nanodiamonds (Electrokhimpribor, Lesnoy, Russia) had a specific surface area of 350 m²/g and an elementary particle size of 3 nm. Multiwalled carbon nanotubes (Taunit-M, Nanotechcentr, Tambov, Russia) had a specific surface area of 300 m²/g and an outer diameter of 8–15 nm and were functionalized using hot nitric acid by the manufacturer [62]. Organomodified montmorillonite (Cloisite 30B, Southern Clay Products, Gonzales, TX, USA) had a specific surface area of 750 m²/g and was treated with bis(2-hydroxyethyl)methyl(octadecyl)ammonium chloride by the manufacturer. The mixing of nanoparticles and hardener-free epoxy resin was on a dispersing instrument (Ultra-Turrax T10, IKA, Staufen, Germany) at a rotor speed of 30,000 rpm (rotor diameter: 6.1 mm, rotor–stator gap: 0.25 mm, shear rate: about 38,000 s⁻¹) for a total of 30 min (three runs for 10 min each with breaks of 5 min) at 20 °C. The nanoparticle mass fraction in the obtained dispersions was 0.1% or 1%.

Carbon fiber bundle UKN-5000 produced by LLC “Argon” (Balakovo, Russia) consisted of 5000 filaments with a diameter of 8 µm. The linear density of the bundle was 456 tex (mass in grams with one-kilometer length), whereas Young’s modulus and tensile strength of the filament were 210 GPa and 2.5 GPa, respectively. There was no additional treatment of the fiber. Single-bundle plastics were produced by impregnating the carbon fibers of the bundle with an epoxy binder in a bath at 100 °C. The prepregs thus obtained were wound onto the frame one by one without any mutual contact and then cured in an upright position, allowing the excess binder to flow down freely. All samples were cured at 180 °C for 3 h.

2.2. Standard Methods

The size distribution of nanoparticles was determined by dynamic light scattering on an analyzer Zetasizer Nano ZS (Malvern Instruments, Worcestershire, UK) at a scattering angle of 173°, a laser wavelength of 632.8 nm, a mass fraction of nanoparticles in their dispersion in the hardener-free epoxy resin of 0.1 %, and a temperature of 90 °C. For each dispersion in three independent replicates, the time dependence of the light scattering intensity was registered for 3 min, and the experiment was repeated ten times to obtain ten correlograms, which were averaged for computation of the distribution of the diffusion coefficient and the corresponding effective hydrodynamic diameter of particles. The viscosity of the pure epoxy resin to convert the diffusion coefficient distribution to the particle size distribution was measured preliminarily on a rotational rheometer at 90 °C (see below).

For assessing the impregnation of the carbon fiber bundle with an epoxy binder, a drop of binder was applied to the bundle stretched horizontally on the frame and then placed in an oven at 180 °C (Figure 1). After curing, the boundary of the impregnated part of the bundle was determined as its rigid section. This section was cut off, and its length and weight were measured. The size of the binder drop was chosen as big as to leave a portion of the epoxy polymer not absorbed into the bundle after curing (before weighing, the unabsorbed binder drop was removed). At least ten samples were used to evaluate the impregnation of each binder composition.

The viscosity (η) of nanoparticle dispersions was measured on a rotational rheometer Physica MCR 301 (Anton Paar, Graz, Austria) using a cone–plate measuring unit (plate diameter: 40 mm, cone–plate angle: 1°) by a stepwise increase in shear rate ($\dot{\gamma }$) from 0.01 s⁻¹ to 100 s⁻¹ at 20 °C. The viscosity growth of fiber-free epoxy binders was evaluated at a constant shear rate of 1 s⁻¹ and a temperature (T) of 180 °C. Gel time (t_g) was determined by extrapolating the reciprocal value of viscosity (1/η) to zero. In addition, time dependences of complex modulus of rigidity (E) were measured by dynamic mechanical analysis (DMA) during the curing of carbon prepregs consisting of a single impregnated bundle using damped oscillations with a frequency of about 1 Hz at 180 °C. The characteristic cross-linking time (τ_DMA) for an e-fold increase in the complex modulus was determined by fitting the obtained data using an exponential function. The glass transition temperature (T_g) of the cured carbon plastics composed of a single bundle was determined at a temperature rise rate of 5 °C/min and a frequency of damping oscillations of about 1 Hz. All experiments were repeated three times. The rheological characteristics were calculated using the standard equations [63].

Heat changes during the curing of fiber-free binders were evaluated using a differential scanning calorimeter MDSC 2920 (TA Instruments, New Castle, DE, USA) at 180 °C. In addition, the glass transition of cured fiber-free binders was estimated on the same calorimeter at a temperature increase rate of 5 °C/min.

The tensile strength tests of carbon plastics with a length of 100 mm were carried out on a machine Instron 1122 (Norwood, MA, USA) at a stretching speed of 0.2 mm/min. The strength of plastics was calculated to the cross-sectional area of carbon fibers included in them. At least 20 samples of one series were used in the tests. After breaking the plastics, they were used to evaluate carbon–binder adhesion using an LCR meter E7-22 (CHY Firemate, Tainan City, Taiwan) and an original electrochemical method developed in this work and described below.

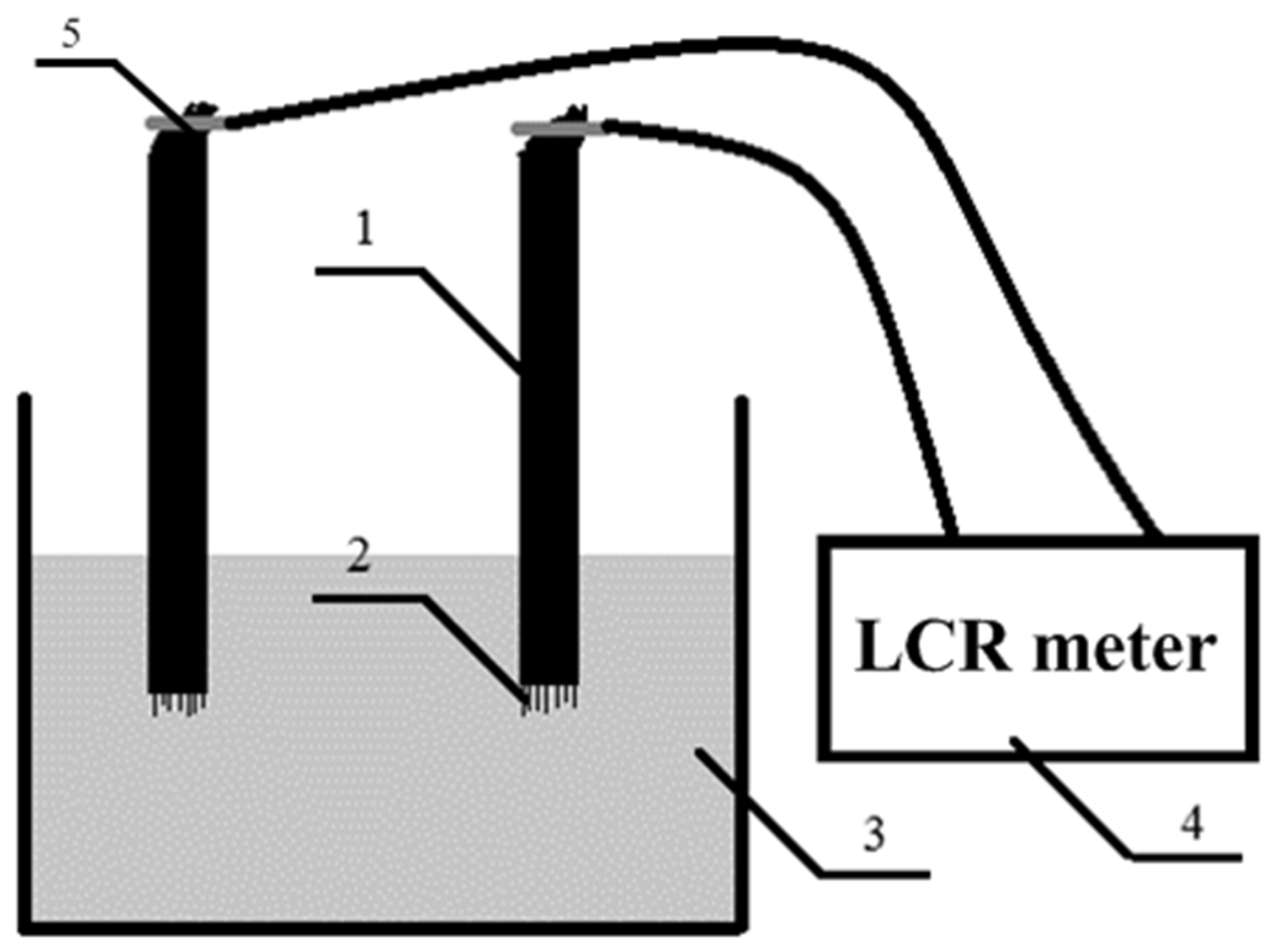
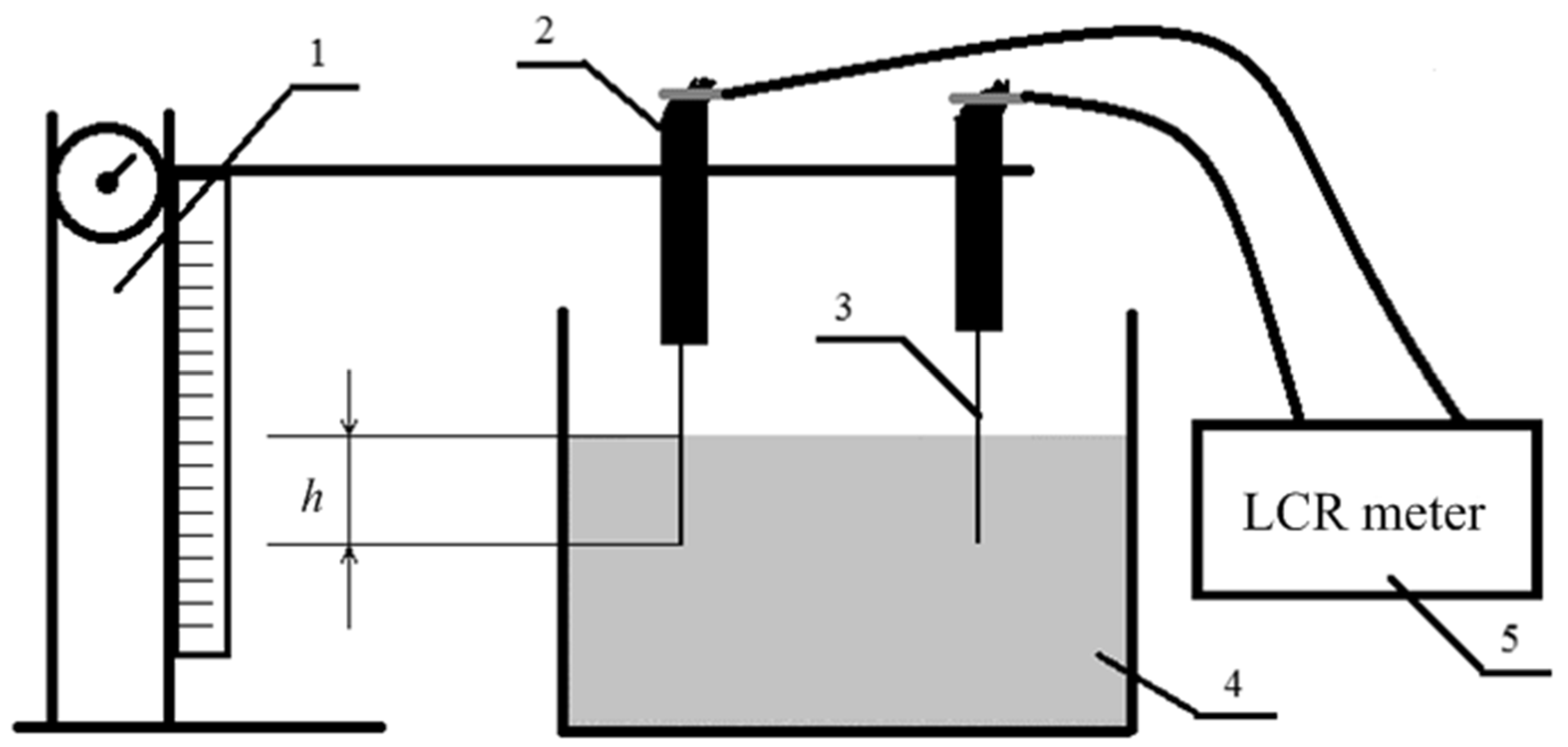
2.3. Electrochemical Method for Assessing Adhesion between Carbon Fibers and a Polymer Matrix

2.3.1. The Base of the Method

After the tensile test and fracture of the carbon plastic, its fibers protrude from the polymer matrix in the fracture zone (Figure 2). The length of the protruding fibers corresponds to the fiber’s critical length, characterizing the strength of the fiber–binder adhesion bond [64]. The knowledge of the fiber’s critical length allows for the calculation of the adhesion strength using the following formula:

$${\sigma }_{\mathrm{A}}=\frac{Ed\epsilon }{4h},$$

(1)

where σ_A is the fiber–binder adhesion strength, E is the Young modulus of fibers, d is the fiber diameter, ε is the fiber strain at breaking, and h is the critical length of the fibers, i.e., the height of their protrusion from the polymer matrix at the place of fracture.

Thus, it is necessary to determine the length of the protruding fibers to assess their adhesion to different polymer matrices, which is too time-consuming for dozens of specimens and involves human subjectivity when processing their photographs. However, carbon fiber conducts electricity, while the usual polymer matrix is a dielectric whose conductivity is incommensurably less than that of carbon fibers. This feature can be used to measure the length of protruding carbon fibers.

The non-fractured end of a carbon plastic was cleaned from the epoxy matrix by burning it out and then connected as an electrode directly to the LCR meter (Figure 3). The plastic’s other end, which represents the fracture area, was immersed in the electrolyte solution (saturated NaCl solution in water). In this case, the carbon fibers protruding from the matrix at the point of plastic’s fracture provide electrical contact: the greater their length, the greater the electrical conductance should be. After a plastic specimen was broken in the tensile test, its two pieces were used for evaluating adhesion in a considered fiber–binder system. The distance between the plastics acting as electrodes was 2 cm. For measuring the impedance by the LCR meter, an alternating current with a frequency of 120 Hz or 1000 Hz was used to prevent electrolysis of the electrolyte. However, this scheme requires calibration before use for linking the impedance value and the length of the protruding carbon fibers.

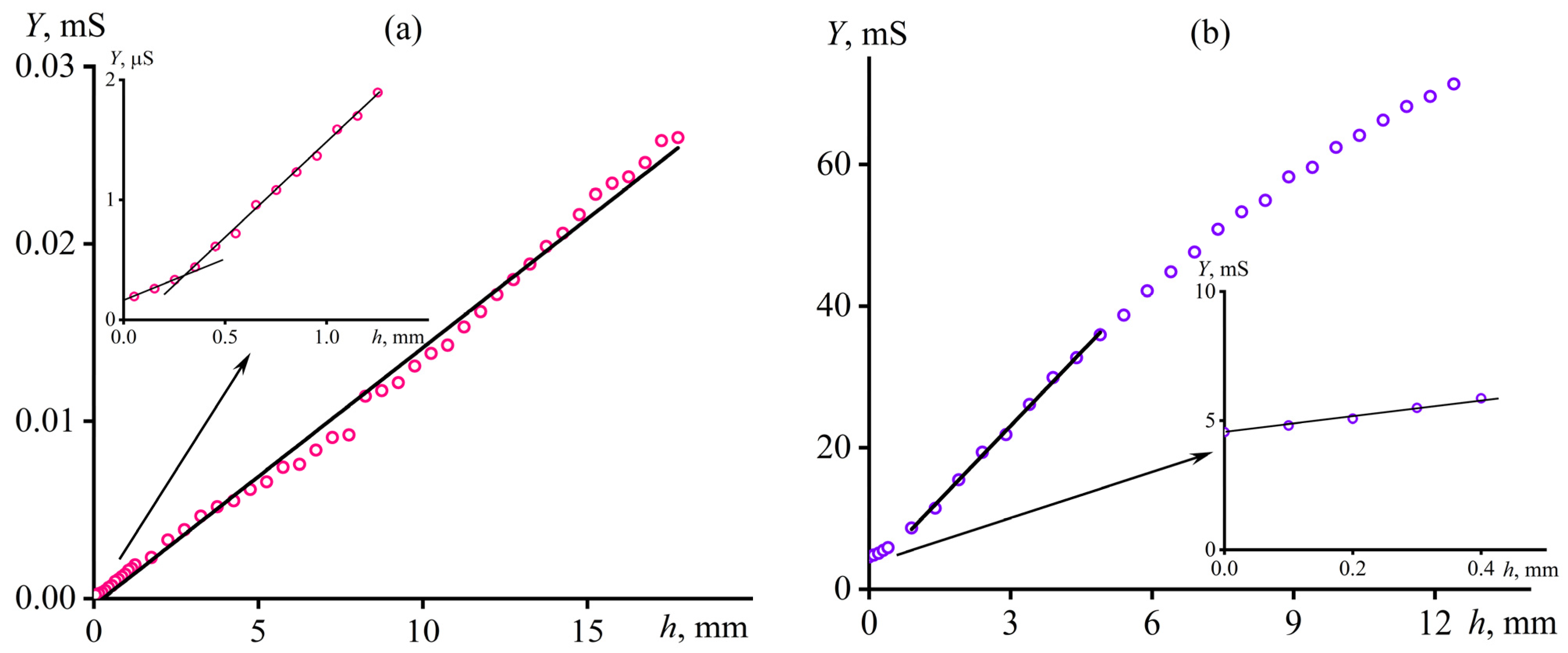
2.3.2. Calibration of the Method

Let us first consider the behavior of carbon filaments and bundles as electrodes placed in the electrolyte, i.e., when they are used instead of plastics in the measuring scheme shown in Figure 3. The overall resistance of the electrochemical cell consists of the resistance of the electrolyte solution and the bulk and surface resistances of the carbon fibers. In this case, it is possible to assume the conductance of the filaments’ surface is much lower than the conductance of other circuit elements due to the limited contact area between the carbon fibers and the electrolyte. Initially, let us analyze a system where one of the electrodes has a much larger contact area with the electrolyte solution.

Figure 4 presents the dependence of the cell’s admittance (consisting of conductance and susceptance) on the depth of immersion of the electrode with a small surface—a carbon filament—into the electrolyte. The second electrode was a multifilament bundle immersed in the electrolyte to a fixed value of 25 mm, and the experiment was conducted at two alternating current (AC) frequencies. As can be seen from the figure, the admittance of the cell increases as the electrode is immersed deeper in the solution. Moreover, the total admittance turned out to be dependent on the AC frequency. It is known that the impedance (consisting of resistance and reactance) of electrodes from carbon fibers increases with decreasing AC frequency, which indicates the behavior of electrodes as capacitors in the low-frequency region [65]. In our case, the lower of the considered frequencies (120 Hz) provides a smoother and more monotonous increase in the admittance as the contact area of the electrode with the electrolyte increases. Perhaps the non-monotonicity of the cell response at higher AC frequency (1 kHz) is caused by the proximity of this frequency to the capacitor resonance frequency, which is determined by the capacitor inductance and capacitance, i.e., the contact area of the electrode and electrolyte. To avoid non-monotonicity, we will use an AC frequency of 120 Hz for further tests.

Regardless of the AC frequency, the cell’s admittance grows up to a certain depth of electrode immersion (about 8–9 mm) and then reaches the plateau region and changes little with a further increase of the immersed electrode’s area. A situation is likely achieved in this case where the surface resistance of the second electrode becomes comparable to the resistance of the other circuit elements. However, the correct application of the proposed scheme (Figure 3) to determine the length of carbon fibers at the point of the plastic’s fracture requires much higher resistance of the electrode surface compared to the resistances of other cell elements.

Let us consider a cell with two multifilament electrodes (carbon bundles): the depth of the first will be fixed, while that of the second will be varied. Regardless of the immersion depth of the first electrode (3.5 mm or 25 mm), the dependences of the cell’s admittance on the immersion depth of the second one come from the same point on the ordinate axis (Figure 5). Therefore, the cell’s resistance at the minimum immersion of the second electrode can be assumed to be equal to the resistance of this electrode, i.e., to the resistance of the set of carbon filament ends of the carbon bundle.

In the case of a shallow immersion depth of the first electrode (3.5 mm), the dependence of the cell’s admittance can be divided into two rectilinear sections. These sections represent a situation where the immersion depth and hence the contact area with the electrolyte of one of the electrodes is much greater than that of the other. In this case, an increase in the immersion depth of the first electrode down to 25 mm leads to a more intense growth of the admittance with an increase in the contact surface area of the second electrode. In other words, the admittance of the cell can be assumed to depend only on the contact area of the electrode and electrolyte, and this dependence is linear.

Now let us estimate the dependence of the admittance on the immersion depth of single carbon filaments into the electrolyte. We used two identical electrodes with equal contact areas with the electrolyte and gradually changed this area by their simultaneous immersion in the electrolyte to a known depth (h) fixed with a cathetometer (Figure 6). In this case, the dependence of admittance on the immersion depth is linear when two elementary filaments are used as electrodes (Figure 7a). The slope allows for finding the relationship between admittance and depth of immersion of single filaments:

Y ~ 1.45 μS/mm·h.

(2)

When using two carbon fiber bundles as electrodes, the dependence of the cell’s admittance is linear if their immersion depth is less than 6 mm (Figure 7b). It is likely that with a greater immersion depth of the electrodes (higher contact area), their surface resistance becomes comparable with the resistance of other circuit elements. However, this does not matter in our case, as the length of the carbon fibers at the fracture zone of the carbon-fiber-reinforced plastic cannot exceed 6 mm. Thus, the admittance of a cell from two bundles can be written as

Y ~ 6950 μS/mm·h.

(3)

The ratio between Equations (2) and (3) is 4800, which is close to the nominal number of filaments in the bundle equal to 5000 as per the manufacturer’s technical specification. In addition, the dependence of admittance does not come from the zero point because of the admittance of filament ends (see the insets in Figure 7). Once the total number of filaments in the bundle is known, this allows for calculating the admittance of the end surface of the elementary filament. According to the experiment with two bundle electrodes (the inset in Figure 7b), the admittance of the filament end is equal to 1 μS (approx. 20 kS/m²). Perhaps this value is severely overestimated due to the capillary rise of the electrolyte between the bundle filaments. If we calculate the admittance of the filament end using its surface area, Equation (2), and the assumption of isotropic conductivity of carbon fiber, it is equal to 0.002 μS (40 S/m²). Both calculated values contradict the results of the experiment with two filament electrodes (the inset in Figure 7a). When extrapolating the admittance of this cell to zero electrode immersion, we get a value of 0.16 μS (3.2 kS/m²), which we will accept as the admittance of the filament end.

Further, when the plastic fractures, each of the resultant surfaces will have about half of the total number of filaments in the bundle. Then, the following equation can be proposed to determine the average length of filaments protruding from the surface of two symmetrical plastic electrodes immersed in the electrolyte solution according to the scheme of Figure 3:

h = 0.287·Y − 110,

(4)

where h is the average length of the protruding carbon fibers equal to their critical length (in μm), and Y is the cell’s admittance at 120 Hz (in μS).

By way of example, if we apply the obtained Equation (4) to process the experimental data on measuring the admittance of an electrochemical cell (Figure 3) involving fractured carbon plastics based on an unmodified epoxy binder (Figure 2), we obtain the average length of fibers protruding from the fracture surface equal to 240 ± 45 μm. Indeed, this value matches the results of hand-counted processing of microphotographs of the fracture surface of this plastic, which give a value of 220 ± 60 μm. Thus, Equation (4) will allow for calculating the fiber’s critical length, which will help in determining the adhesion between carbon fibers and cured epoxy binder according to Equation (1).

3. Results and Discussion

3.1. Properties of Nanoparticle Dispersions in Epoxy Resin

According to the results of dynamic light scattering, the average hydrodynamic diameters of particles are 0.28, 0.32, and 1.32 μm for carbon nanotubes, nanodiamonds, and organoclay, respectively (Figure 8). Therefore, submicron aggregates of elementary nanotubes and nanodiamonds are present in the epoxy medium. At the same time, the size of clay particles corresponds to the longitudinal dimension of the elemental montmorillonite plates and may indicate the absence of aggregation among clay tactoids.

Both pure epoxy resin and dispersions of nanoparticles in it exhibit weak shear-thinning behavior since their viscosities decrease slightly with increasing shear rate (Figure 9). The addition of 1% particles increases the low-shear viscosity from 50 Pa·s to either 58 Pa·s, 62 Pa·s, or 88 Pa·s in the case of CNT, OMMT, or DND, respectively. Thus, zero-dimensional nanodiamond particles have the smallest size and the most substantial effect on viscosity. Meanwhile, the effect of two-dimensional clay particles and one-dimensional carbon nanotube particles on the viscosity of the epoxy resin is almost the same, despite the smaller hydrodynamic diameter of nanotubes. Generally, the higher the anisometry of the particles, the grander the increase in viscosity of their dispersion would be expected. In turn, this means that zero-dimensional nanodiamonds mutually aggregate to form fractal high-dimensional particles and hence effectively increase the viscosity of the epoxy resin. At the same time, dispersions have no yield stress, indicating that there is no agglomeration of particles to form a three-dimensional structural network [66,67].

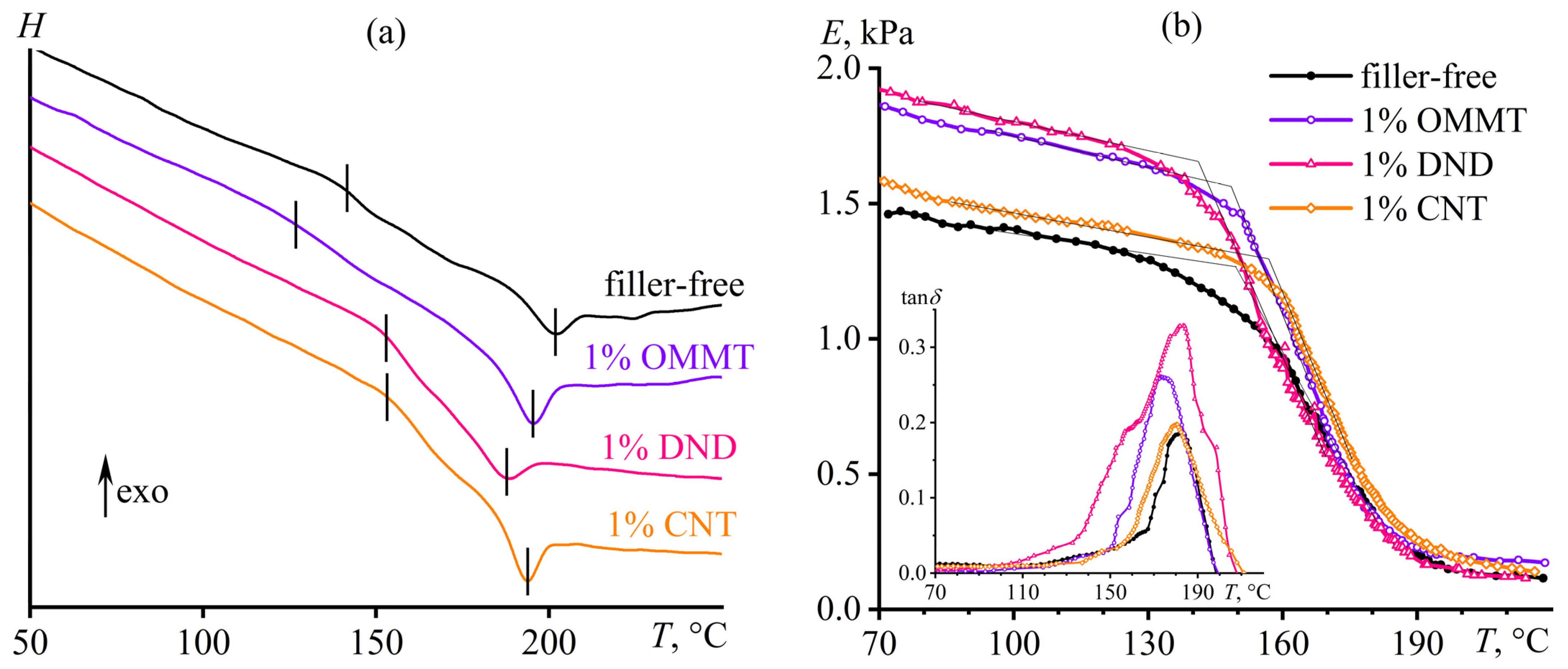
3.2. Effect of Nanoparticles on the Curing of Epoxy Binder

The addition of nanoparticles can affect not only the viscosity of the epoxy binder but also the rate and completeness of its curing. The kinetics of curing epoxy resins with amine hardeners have been studied in detail [60], and we will limit ourselves to general observations. During curing, the binder’s viscosity increases (Figure 10a) until it reaches an infinitely high value due to the formation of a three-dimensional network of chemical cross-links. The time of achieving this viscosity can be considered the gel time. Measurement of viscosity growth curves of fiber-free epoxy binders showed that the introduction of nanoparticles could both accelerate and slow down the binder’s gel time (t_g,

Table 1. Effect of fillers on the curing characteristics of epoxy binder.

Filler	tg, min	τDMA, min	ΔH, J/g	A1, J·g−1·s−1	A2, J·g−1·s−1	A1/(A1 + A2), %	τDSC,1, min	τDSC,2, min
0%	18.7	35.8	437	1.20	0.084	93.5	7.6	32.1
0.1% DND	20.0	35.1	482	2.24	0.136	94.3	7.3	27.6
1% DND	18.0	60.1	416	1.04	0.094	91.7	7.9	33.7
0.1% OMMT	20.6	131	467	2.33	0.171	93.2	7.2	25.7
1% OMMT	18.6	74.8	471	1.27	0.129	90.8	7.3	24.5
0.1% CNT	19.0	98.2	454	2.42	0.129	94.9	7.2	27.2
1% CNT	21.3	56.8	478	0.82	0.116	87.6	8.7	35.1

). The decrease in gel time can result from chemical interactions of the binder’s molecules with the surface functional groups of nanodiamonds and carbon nanotubes or with the hydroxyethyl or ammonium groups of OMMT’s surfactant. Meanwhile, the increase in gel time may result from an increase in the viscosity of the reaction medium by the suspended filler particles. In our case, the fillers slow gel formation by 1–2 min (Table 1), and more strongly in the case of carbon nanotubes, whose dispersion has the lowest viscosity compared to the others and should decelerate the curing less. This may indirectly indicate a chemical interaction of the epoxy binder with nanodiamonds and organoclay, resulting in a lower delay in gel formation despite a more significant increase in viscosity with these fillers. The same conclusion is further supported by the slight acceleration of curing when the concentration of nanodiamonds and organoclay was increased from 0.1% to 1%.

Nanoparticles have a more significant effect on the curing rate of epoxy binder after it reaches the gel point, which can be traced by the time dependence of the reduced complex modulus (Figure 10b), i.e., the modulus of rigidity (E) normalized to its limiting value (E_max). All fillers slow the curing, whose rate can be quantified by the characteristic time of cross-linking τ_DMA:

$$\frac{E_{\mathrm{m}\mathrm{a}\mathrm{x}}-E}{E_{\mathrm{m}\mathrm{a}\mathrm{x}}}·100\%=a+b{·e}^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{\mathrm{D}\mathrm{M}\mathrm{A}}$}\right.},$$

(5)

where a and b are the fitting parameters. At this stage of curing, filler particles can adsorb growing polymer chains on their surface or act as defects within the spatial network of the epoxy gel. In other words, they can shift the glass transition of the cross-linking binder in time, changing the moment when the diffusion rate of the reacting components sharply declines. In our case, the particles slow the growth of the complex modulus, i.e., delay the glass transition. The most potent effect is observed for 0.1% content of organoclay or carbon nanotubes, probably due to their role as large-scale structural defects. Meanwhile, 1% of these fillers or 0.1–1% of nanodiamonds have a less pronounced effect, possibly due to some acceleration of cross-linking, which may occur as judged by a slight decrease in gel time (t_g, Table 1).

Differential scanning calorimetry (DSC) curves allow for estimating the completeness of cross-linking and its rate (Figure 10c). The reaction heat passes through a maximum followed by a decrease in curing intensity due to a reduction in the concentration of the reacting functional groups and increasing viscosity of the samples. The addition of nanodiamonds to the binder has a minimal effect on cross-linking, whereas organoclay intensifies it at the initial stage of curing, probably due to the reactivity of the hydroxyl and ammonium groups of the clay’s organic modifier. On the contrary, carbon nanotubes slow the curing, which agrees with their effect of increasing the gel time (see Figure 10a). Generally, all fillers increase the curing time according to the DSC data, which is consistent with the DMA findings. Quantitatively, the cross-linking rate can be expressed in characteristic times by approximating the descending sections of the DSC curves by exponential functions. It turns out that it requires two characteristic times τ_DSC:

$$H=A_1{·e}^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{\mathrm{D}\mathrm{S}\mathrm{C},1}$}\right.}+A_2{·e}^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{\mathrm{D}\mathrm{S}\mathrm{C},2}$}\right.},$$

(6)

where H is the heat flow, while A₁ and A₂ are the fitting parameters.

For the unmodified epoxy binder, times τ_DSC,1 and τ_DSC,2 are 7.6 min and 32.1 min with fitting parameters A₁ and A₂ of 1.2 and 0.084 J·g⁻¹·s⁻¹, respectively (Table 1). It can be assumed that the first time characterizes the reaction in the initial stage of curing when its rate is determined by the concentration of the reacting substances, i.e., until diffusion restrictions arise. In the second (final) stage of curing, its rate slows down and is determined by the diffusion rate of the reacting substances because of the increase in the internal friction inside the reaction medium. The rate of this stage is characterized by the second characteristic time, τ_DSC,2. The higher value of the fitting parameter A₁ for the first time, τ_DSC,1, indicates a proportionally larger quantity of reacted functional groups at the initial stage of curing. Absolute values of the fitting parameters are not informative, and therefore, it is better to compare the nominal share of reaction groups that have reacted in the initial stage of curing before a drop in the diffusion rate. The nominal share of reacted functional groups of the unmodified binder at the first curing stage is about 93.5% (Table 1).

As little as 0.1% of nanoparticles accelerate the curing (reduce τ_DSC) and can slightly increase the share of functional groups reacting before diffusion restrictions arise (from 93.5% up to 94.9%, see Table 1). On the contrary, 1% particles decrease the percentage of groups reacting in the first curing stage (down to 87.6%), i.e., they lead to earlier diffusion restrictions and can also lower the cross-linking rate by increasing τ_DSC. Fillers can slow down the curing of the binder due to kinetic limitations, a possible increase in the quantity of reacting groups, or an increase in the completeness of curing. The total thermal effect of curing (ΔH, Table 1) allows for estimating the possibility of the latter options. The data indicate that binders with a longer gel time have a greater heat effect and hence more curing completeness. This is consistent with the identified fitting parameters A₁ and A₂, according to which most functional groups react before the appearance of diffusion restrictions that are intensified upon reaching the gel point. It seems apparent that 0.1% of a filler, even having a reactive surface, cannot significantly increase the total thermal effect of the curing, nor can it act as a cross-linking catalyst since the gel time becomes longer in its presence. Therefore, a possible influence of nanoparticles can consist of inhibiting the formation of cross-links between the growing epoxy macromolecules, which ensures the binder stays in the liquid state for longer, hence resulting in a fuller reaction of functional groups. The specific mechanism may involve preferential adsorption of higher molecular weight chains on the nanoparticle surface with desorption of oligomeric molecules into the reacting volume and the appearance of steric difficulties for branching the adsorbed chains.

Thus, nanoparticles in the epoxy binder increase its viscosity and do not reduce the gel time but may increase the time required for curing.

3.3. Effect of Nanoparticles on the Impregnation of Carbon Fibers with Epoxy Binder

An increase in the viscosity of the epoxy binder can worsen its penetration into the bundle from carbon fibers. The impregnation of reinforcing fibers was evaluated without applying external influence according to the scheme of Figure 1. The carbon fiber bundle was impregnated with epoxy binder due to capillary forces after applying a drop of binder on its surface at curing temperature (180 °C). Other things being equal, the length of the impregnated part of the bundle should be determined by the impregnation time (i.e., the gel time), the binder’s viscosity, and the interfacial tension at the fiber–binder interface.

As the nanoparticle content in the epoxy medium increases, the length of the impregnated segment of the carbon bundle passes through the maximum (Figure 11a). Organoclay, being a modifier, provides the lengthiest impregnation zone, while carbon nanotubes provide the shortest. This result is unexpected since the binders with OMMT and DND have almost the same viscosity, while the gel time of the binder containing 1% CNT is the longest (see Figure 9 and Table 1). At the same time, the filling of the epoxy binder with nanoparticles reduces its penetration into carbon fibers (Figure 11b). Perhaps this may be caused by the increased viscosity of the modified binder, which prevents filling the fiber pores with the binder. However, the binder containing 1% DND has the highest viscosity but not less impregnation efficiency than other systems. Thus, the binder’s viscosity and gel time do not appear to be the main factors determining the effectiveness of carbon fiber impregnation.

Fiber impregnation can also be influenced by the interaction between the fiber and the binder, as a smaller wetting angle should provide a thinner layer of binder covering the fiber surface. The epoxy binder is polar, while carbon fiber is not but can have aldehyde, carbonyl, and carboxyl groups on its surface [68]. The surface of DND is chemically heterogeneous and has polar functional groups and non-polar areas of the diamond lattice. Carbon nanotubes have a partly similar heterogeneous structure, and their functionalization leads to the appearance of hydroxyl and carboxyl groups on their edges and in the places of surface defects. In turn, the charged surface of montmorillonite adsorbs a surfactant whose non-polar groups are oriented away from the surface. Therefore, we can assume that all of these nanofillers are interfacial-active, i.e., they can be adsorbed on the interface between the epoxy matrix and the carbon fiber. In any case, nanoclays and nanodiamonds can produce Pickering emulsions through adsorption at the oil–water interface [69,70].

Thus, it seems that nanoparticles at low concentrations improve impregnation due to a possible increase in fiber wetting with the binder, while a higher concentration of nanoparticles increases the binder’s viscosity and impairs impregnation. Washburn’s equation explains this effect [71]:

$$l={\left(\frac{\gamma rt\cos \theta }{2\eta }\right)}^{0.5},$$

(7)

where γ is the surface tension, r is the average pore radius (in our case, the pores consist of the spaces between the carbon fibers in their bundle), t is the impregnation time (approximately equal to the gel time t_g), θ is the contact angle between the binder and the carbon fiber, and η is the viscosity that gradually increases due to cross-linking (see Figure 10a). An increase in the viscosity of the epoxy binder reduces the length of the impregnated part of the carbon fiber bundle, whereas improving wetting (reducing the contact angle) conversely increases this length. The improvement in wettability should also increase the adhesion between the binder and the carbon fiber, and its assessment can serve as indirect evidence to support the above conclusion.

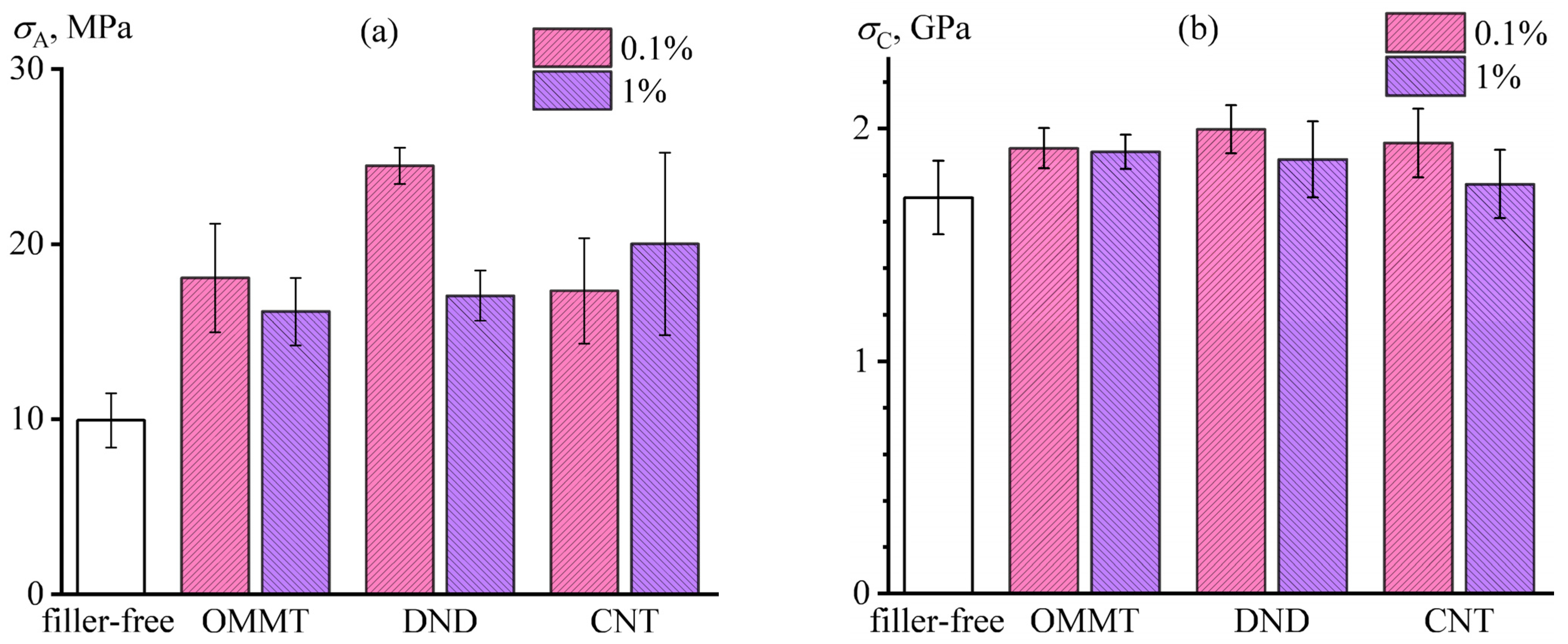
3.4. Adhesion and Strength in the Carbon Fiber–Epoxy Nanocomposite Matrix System

The effect of nanoparticles on the interphase boundary between the carbon fiber and epoxy polymer can be determined by evaluating the adhesive interaction for them. In all cases, nanoparticles increase the fiber–matrix adhesive strength (Figure 12a) calculated using Equation (1) and fiber critical length determined by the electrochemical method (Figure 3). Of the fillers used to make 1% compositions, carbon nanotubes provide the best adhesion to carbon fibers. However, a binder with 0.1% nanodiamonds yields a more interesting result of a 2.5-fold increase in adhesive strength. It is most likely that this effect is caused by surface phenomena at the fiber–binder interface, as the binder of this formulation exhibited neither specific rheological properties nor impregnation efficiency. Moreover, the increase in adhesive strength for systems with nanodiamonds is many times greater than the standard deviation, whose value is significantly lower than for other tested composites.

An improvement in adhesion to a substrate upon filling an epoxy binder with particles has been observed before [72], and the increase in adhesive interaction passed through a maximum with increasing filler content regardless of its nature [73,74,75]. A possible explanation for the increase in adhesion is the adsorption of nanoparticles on the fiber–binder interface, i.e., when they play the role of an intermediate layer between the fiber and the polymer matrix. Another possibility is that the nanoparticles modify the epoxy polymer, whose chains can become less branched and oriented due to adsorption on the particle surfaces. The smaller branching and orientation of the macromolecular chains should increase the specific number of contacts between their functional groups and the fiber’s surface, thereby increasing adhesion strength.

Tensile testing of carbon plastics showed the highest strength for composites having the best fiber–binder adhesion, i.e., containing 0.1% nanodiamonds (Figure 12b). In this case, the strength gain is 17% compared to the nanoparticle-free composite, despite the simultaneous increase in adhesive strength by 2.5 times for this system. The tensile strength of fiber-reinforced plastics is determined primarily by that of the carbon fibers, on which the added nanoparticles can have no effect. The polymer matrix redistributes stresses between the reinforcing fibers, and improved stress redistribution due to increased fiber–matrix adhesion in the presence of nanoparticles gives this small but significant (p < 0.01) improvement in tensile strength. Generally, the strength of plastics increases substantially in all cases of adding nanoparticles (p < 0.05), and the best effects appear when using their 0.1% mass fraction. It is likely that the increase in strength results from improved adhesion while adding as little as 0.1% nanoparticles (Figure 12a), whose mass fraction of 1% raises the viscosity of the binder (see Figure 9), impairs the impregnation of carbon fibers (Figure 11), and thus reduces the strength of the fiber-reinforced composite (Figure 12b). Moreover, the same nanoparticles in high concentrations can act as defects, reducing the uniformity of cross-links in the cured polymer and consequently deteriorating its resistance to high temperatures. Let us consider the effect of nanoparticles on the glass transition temperature and stiffness of composites.

3.5. Glass Transition in Cured Composites

The filler-free cross-linked epoxy polymer exhibits the glass transition in a broad temperature range reaching 60 °C (shown by the vertical lines in Figure 13a). Probably, this extended temperature range results from the structural microheterogeneity of the cured epoxy polymer. Microheterogeneity may result from the diversity of the initial epoxy molecules, whose polymerization degree ranges from one to four. In this respect, the molecules of the initial epoxy resin with a higher molecular weight will form sections of the gel network with a larger cross-linking spacing and, consequently, higher flexibility and a lower glass transition temperature. In addition, the irregularity of cross-linking may be caused by the high curing rate and the participation of some hardener’s tertiary amino groups in the curing to form a more locally branched network, simultaneously ignoring a part of the secondary amino groups and increasing the distance between some cross-links [76].

The addition of organomodified montmorillonite shifts the glass transition region of the fiber-free epoxy binder towards lower temperatures, which may be a consequence of a decrease in cross-linking density due to both the adsorption of epoxy reaction centers on the clay surface and the plasticizing effect of the surfactant contained in this filler. Nanodiamonds and nanotubes increase the lower temperature of the glass transition range, which may be the result of reduced flexibility of the long macromolecular sections between the cross-links due to their adsorption on the surface of the particles. In addition, the particles in all cases decrease the higher temperature of the glass transition range, which indicates a decrease in cross-linking density and agrees with the reduction of branching of the growing macromolecules in the presents of the filler particles.

According to DMA data, the rigidity modulus of carbon-fiber-reinforced plastic based on the nanoparticle-free epoxy binder starts to decrease at 149 °C (Figure 13b; the determination of the onset point was with intersecting tangents). This temperature is the beginning of the transition of the cured composite from a glass to a rubber-like state. The introduction of organoclay into the binder composition does not change the onset temperature of reduction of mechanical properties, while nanodiamonds and carbon nanotubes reduce and increase this temperature by 8 °C, respectively. At the same time, the greater rigidity of the carbon plastic in the glassy state is provided by the matrix filled with nanodiamonds and organoclay, while carbon nanotubes only slightly increase the rigidity modulus compared to the nanoparticle-free composite. In this respect, a decrease in the onset temperature of the rigidity declining for the nanodiamond-containing composite goes with a higher initial rigidity. Generally, nanoparticles affect the rigidity of plastics analogously to their impact on the plastics’ tensile strength (see Figure 12b).

The glass transition temperature of carbon plastics can also be estimated based on the position of the maximum of the loss tangent (see inset to Figure 13b). This temperature can be considered the end of the transition of a composite from a glass to a rubber-like state. Together with the onset temperature of rigidity modulus falling, they represent the glass–rubbery transition temperature interval for carbon plastics under study (

Table 2. Temperature interval of the glass–rubber transition of carbon-fiber-reinforced epoxy plastics containing nanoparticles (in °C).

c, wt %	Filler-Free	OMMT	DND	CNT
0.1	149–181	151–181	148–182	159–181
1		148–175	141–183	157–180

). There is no significant change in the end temperature of this transition upon the addition of nanoparticles, except for 1% organoclay that reduces the end temperature, possibly due to the plasticizing effect of the incorporated surfactant, which does not affect the rigidity modulus at the same time (see Figure 13b). Thus, the effect of nanoparticles on the glass transition temperature is complex, resulting from the extended glass transition of the cured epoxy matrix, the ability of adsorption of its chains and reaction centers on the fibers’ and nanoparticles’ surfaces, and the possibility of particles and fibers mutually interacting. Summarizing, both organoclay and nanodiamonds can reduce the glass transition temperature at their high concentrations, while carbon nanotubes increase it even at low content.

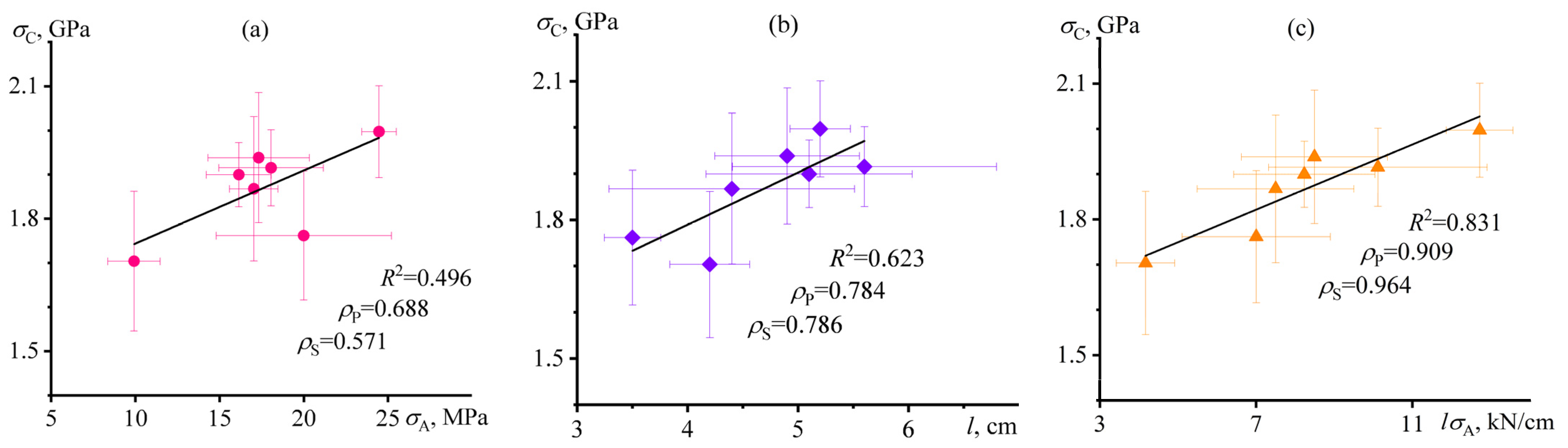
3.6. Mutual Correlations of Characteristics of Carbon-Fiber-Reinforced Nanocomposite Plastics

The glass transition temperature and strength properties are essential for fiber-reinforced plastics as construction materials. However, analysis of the effect of the characteristics of the epoxy nanocomposite binder on the glass transition temperature did not reveal any significant correlations (p > 0.1 for all evaluated properties). Further, nanoparticles have an insignificant effect on the Young modulus (93 ± 8 GPa for all tested specimens, p > 0.1) and breaking strain (2.0 ± 0.2%, p > 0.1) of cured plastics for correlation analysis. Of the performance properties of plastics, only their tensile strength remains for examination.

The search for mutual correlations between the tensile strength and characteristics of the binder and the obtained carbon plastics revealed two significant relationships. Firstly, the strength moderately correlated with the adhesion between the carbon fiber and the polymer matrix (Figure 14a). In this case, the Pearson correlation coefficient (ρ_P = 0.688, p < 0.1) is higher than the Spearman one (ρ_S = 0.571, p > 0.1), indicating a positive linear correlation between strength and adhesion. Secondly, a stronger linear correlation exists for the tensile strength and the length of the carbon bundle impregnated with the epoxy binder (Figure 14b, ρ_P = 0.784, p < 0.05), i.e., with a measure of the effectiveness of the fiber impregnation. If we consider the dependence of the tensile strength on both parameters simultaneously using their product as an independent variable, the correlation becomes very strong (Figure 14c; ρ_S = 0.964; hereafter, the larger of the two coefficients is presented) and probably slightly nonlinear since ρ_S > ρ_P (p < 0.01 for both coefficients). The increase in correlation indicates the mutual independence of adhesion and impregnation efficiency, which is also proved by the small values of their correlation coefficients (ρ_S = 0.286, p > 0.1). Thus, these two parameters independently increase the strength of carbon plastics and must be somehow related to the properties of the epoxy binder.

The search for mutual correlations reveals the relationship between adhesion strength and three parameters: the time of gelation (t_g, ρ_S = 0.750, p < 0.1), the thermal effect of curing (ΔH, ρ_S = 0.714, p < 0.1), and the binder mass fraction in the impregnated fiber (w, ρ_P = −0.803, p < 0.05). Most likely, the increase in gel time allows the binder to penetrate longer and, consequently, deeper into the surface irregularities and pores of the carbon fiber, thereby enlarging the adhesion contact area and hence adhesive strength. The increase in the thermal effect of curing may be related to a boost in curing degree or the formation of new chemical bonds between the surface groups of nanoparticles and the epoxy matrix. Both of these factors can contribute to the growth of adhesion to the fiber if some of the covalent bonds formed by the epoxy matrix are with the surface groups of the carbon fiber or if the nanoparticles adsorb on the fiber–matrix interface, acting as some interphase layer. The third-detected negative strong linear correlation is unusual: the lower the impregnation degree, the higher the adhesion. This seems absurd at first glance since anyone would expect the opposite: an increase in adhesive strength at a higher mass fraction of the binder in the resulting plastic. The explanation may lie in the fact that the assessment of impregnation was under the action of capillary forces in our case. The epoxy binder coats the carbon fibers, and one would expect that the larger the contact angle at the binder–fiber interface, the thicker the binder layer would be on them. Thus, a decrease in the binder mass fraction in the impregnated carbon fiber bundle indirectly indicates a reduction in the wetting angle, increasing the thermodynamic work of adhesion according to the Young–Dupré equation [30,31,43].

As for the relative effectiveness of the impregnation (its length), it found only one—but very strong and negative—correlation with both characteristic curing times τ_DSC,1 and τ_DSC,2 (ρ_P = −0.906 for both parameters, p < 0.01). There is again a surprising correlation: the lower the characteristic curing time, the faster the cross-linking and the better the impregnation of fibers. Anyone would expect the opposite: the slower the curing, the more time the binder has for impregnation and spreading (see Equation (7)). It is hard to interpret this situation correctly. Perhaps this may be related to the internal diffusion rate in the binder. The higher the diffusion rate, the faster both the cross-linking proceeds and the binder spreads over the fiber surface. According to the Rabinowitch model [77], the overall rate constant of a chemical small-molecule reaction depends on the chemically controlled rate and diffusion rate constants as k⁻¹ = k_react⁻¹ + k_diff⁻¹, i.e., represents their harmonic mean [78]. In turn, the diffusion rate constant is proportional to the average diffusion coefficient of the reacting entities: k_diff ~ D [79]. Thus, the higher the diffusion rate, the faster the cross-linking and the shorter the gel time, i.e., the time for impregnation. The impregnation length of the fibers is related to time and the diffusion coefficient as l = (Dt)^0.5 [80], meaning that a higher diffusion rate improves impregnation and simultaneously worsens it indirectly due to decreased impregnation time. However, the curing rate depends on both the diffusion rate and the rate of chemical interaction between the reagents, indicating that an increase in the diffusion rate results in a less pronounced decrease in the gel time, a higher product Dt, and hence an improvement in fiber impregnation. In this case, the internal diffusion rate of the binder molecules is not directly related to its viscosity as a heterogeneous dispersion containing nanoparticles. In other words, nanoparticles can increase the viscosity of the binder as a whole, simultaneously accelerating the internal diffusion of its molecules. The acceleration comes from enhanced micro-convection caused by nanoparticles due to their Brownian motion, and this effect is used to create nanofluids for heat transfer [81].

To summarize, the main reason for increased fiber–matrix adhesion is improved wetting of the carbon fiber by the epoxy binder, which suggests surface and/or interface activity of the nanoparticles, i.e., their adsorption at the air–binder and/or fiber–binder boundaries with enhanced fiber impregnation due to a reduced contact angle and a probable increase in the thermodynamic work of adhesion. An additional potential reason for increased adhesion is the formation of chemical bonds between the nanoparticles adsorbed on the fiber and the epoxy matrix. The strength of fiber-reinforced plastics rises primarily due to improved fiber impregnation due to accelerated internal diffusion by the nanoparticles: epoxy binder penetrates better between the fibers and into the pores of the fibers, thereby increasing the specific fiber–matrix contact area. An additional reason for higher tensile strength is the increased fiber–matrix adhesion.

Thus, to enhance the strength of reinforced plastics, the binder must have a high internal diffusion rate, exhibit good wetting of the fiber surface, and cure not too fast but to a maximum degree. The presence of nanoparticles in the binder modifies these characteristics, thereby increasing the strength of the plastics. Judging indirectly by τ_DSC,1 and τ_DSC,2 (see Table 1), all the nanoparticles improve the internal diffusion at their low concentration of 0.1%. Further, nanoparticles raise the curing enthalpy and slow down gel formation (0.1% DND, 0.1–1% OMMT, and 1% CNT are especially effective). Since the mass fraction of 0.1% is more effective in the case of nanodiamonds, the improvement of cross-linking is most likely due to the adsorption/desorption of growing macromolecules on the nanoparticles’ surfaces with a change in the spatial configuration of the gel network rather than because of chemical reactions between the nanoparticles and the epoxy medium. As particles having less anisometry (DND) are in a grander number in space for comparable volume fraction and nano-dimensional size, they affect more macromolecules and are more effective. Next, all types of nanoparticles improve the wetting of the fiber surface, judging by the decrease in the mass fraction of binder in the impregnated fiber (Figure 11b), although 1% CNT, 1% OMMT, and 0.1% DND work better. It is possible that nanodiamonds are better in this case and at low concentrations due to their lower anisometry, i.e., they can arrange more densely at the interfacial boundary in contrast to carbon nanotubes or montmorillonite plates. Since all four parameters are improved simultaneously only with 0.1% DND in the binder, this composition increases the tensile strength of plastics the most (Figure 12b).

4. Conclusions

The main novelty of this work is a new method for evaluating the adhesion between carbon fiber and polymer matrix by measuring the electrical conductivity of the fracture surface of the fiber-reinforced composite and using the electroconductivity of the fibers and insulating properties of the polymer. In addition, a novelty is a parallel comparative study of the effect of three types of particles with different anisometry (0D nanodiamonds, 1D carbon nanotubes, and 2D clay nanoplates) on the adhesion of the epoxy matrix to the carbon fiber and the strength of the resulting fiber-reinforced plastics with a deep analysis of the causes for changes in the properties. As a result, the study of rheological, thermophysical, adhesion, and strength properties of carbon-fiber-reinforced plastics with the epoxy matrix containing nanoparticles revealed the following:

• The measurement of electrical conduction of fractured carbon single-bundle plastics allows for evaluating the adhesion between the carbon fiber and the dielectric polymer matrix, which correlates with plastics’ tensile strength.
• Nanoparticles can increase the tensile strength of carbon-fiber-reinforced plastics by improving the impregnation of the carbon fiber with the binder and enhancing fiber–matrix adhesion, which may be due to improved fiber wetting with the nanocomposite binder, accelerated internal diffusion of binder molecules by nanoparticles, slowing the cross-linking of the binder, and increasing the curing degree.
• For improving the tensile strength of fiber-reinforced plastics, the concentration of nanoparticles should be low to avoid increased binder viscosity and deterioration of fiber impregnation. Moreover, isometric particles are more effective than anisometric nanotubes and nanoplates, possibly due to easier adsorption on the surface of carbon fibers.
• The maximum strengthening effect results from filling the epoxy binder with 0.1% detonation nanodiamonds, which increase the fiber–matrix adhesion and plastic’s tensile strength by 150% and 17%, respectively, creating novel hybrid carbon-fiber-reinforced epoxy nanocomposite with higher performance.

The advantage of the hybrid carbon-fiber-reinforced epoxy nanocomposite over the traditional carbon-fiber-reinforced composite is a 17% improvement in strength. Although this growth does not look like a large number at first glance, it is significant. Potential applications for the novel hybrid plastic lie in obtaining hull material for airplanes, rockets, ships, racing cars, drones, and the like. In this respect, improved strength means the possibility of using thinner structural elements of the vehicles, which reduces their weight and results in higher payloads, higher speed characteristics, and fuel savings, especially in the case of aerospace machines. A drawback of the material is the increase in cost due to the relatively high price of nanoparticles, but this will more than pay for itself due to the lightening vehicles and reduced fuel consumption for their operation. Further serious engineering calculations are necessary for specific conclusions. Since the introduction of nanoparticles is carried out directly into the epoxy resin, and this does not significantly change its viscosity, the production of hybrid plastics is easily scalable and does not require a change in the technological scheme of manufacturing the existing epoxy carbon-fiber-reinforced composites. The change in their production will only consist of replacing pure epoxy resin with the nanoparticle-containing one. Moreover, all the types of nanoparticles considered are produced on an industrial scale, i.e., their production is well established, the particles themselves are available, and their properties are reproducible from one batch to the next.

The potential limitations of this study are the assumption of uniform nanoparticle dispersion and the sensitivity of the results to the specific experimental conditions and parameters. In this respect, an increase in the stretching rate of plastics will raise their measured strength and, indirectly, the estimated value of fiber–matrix adhesion. In addition, the anisometry of the particles may differ from the integers (0D, 1D, and 2D) due to their aggregation. Moreover, further research is needed on structural observation and evaluation of the carbon fiber–nanoparticles–polymer matrix interphase. A separate issue is the evaluation of the environmental impact of the proposed materials, including any potential toxicity or ecological risks associated with the use or disposal of the nanoparticles. Since the nanoparticles are placed in the cross-linked polymer matrix with good adhesion properties, they cannot leave out and act separately. At the same time, this means that the microplastic particles that may be formed from the hybrid nanocomposite will contain nanoparticles, which may further exacerbate their detrimental effects on living organisms. All polymer nanocomposites require rational disposal after the expiration of their service life in the products they contain. In this regard, the disposal of nanoparticles should be carried out together with the epoxy matrix and carbon fibers, and the reuse of hybrid composites is impossible due to the cross-linked state of its matrix. In turn, this means that these composites will require grinding and further use of the resulting powder as a filler for obtaining new composite materials, which may include road bitumen and disperse-filled polymer composites, and this also requires further research.