Abstract
Moisture absorption of composites with nanoscale carbon additives such as carbon nanotubes, carbon nanofibers, graphite nanoplatelets, and carbon black is investigated using thermogravimetric data and a non-Fickian hindered diffusion (Langmuir-type) model. The moisture absorption parameters are determined using this model for six different types of carbon/epoxy nanocomposites. The absorption behaviors obtained at different humidity levels and thermal environments are recovered by minimizing the error between the experimental data and model predictions, thus enabling the accurate determination of the moisture equilibrium level. The absorption behavior and the weight gain of all nanocomposites are shown to be accurately represented by this model over the entire absorption period. The presence of carbon nanomaterials is found to induce varying levels of non-Fickian behavior, governed by the nondimensional hindrance coefficient. This behavior is enhanced with the nanomaterial content and separate from the slight non-Fickian behavior of all neat epoxy samples. The molecular bonding during diffusion, as well as the interfacial moisture storage, could be among the reasons for non-Fickian behavior and should be included in the absorption models for accurate characterization of carbon/epoxy nanocomposites.
1. Introduction
Nanocomposites of thermoset polymers have a wide range of desirable mechanical, thermal, and electrical properties. Due to these enhanced properties and their low density, nanocomposites have been used in a wide variety of industries, including aerospace [1,2], automotive [2,3], and energy [4,5]. In particular, thermosets contain nanoscale fillers or additives at different concentrations to reduce cost or to enhance electrical [3,6] mechanical [7,8,9] and/or barrier [8,10,11,12,13] properties. The type (i.e., nanofibers, nanotubes, and nano-glass spheres) and the amounts of nanofillers used usually determine the extent of property enhancement.
Most composite products are exposed to wet or humid environments for extended periods, resulting in considerable moisture absorption. Polymers readily absorb and retain moisture, which in turn plasticizes the resin, causes swelling and may induce considerable residual stresses and delamination in the material [2,14,15]. These microstructural changes often alter the physical and mechanical properties of the composites, and therefore adversely affect their service life [14,16,17,18,19,20].
Recent progress in carbon nanoparticles (i.e., graphene, carbon nanotube, carbon nanofiber) makes them excellent candidates for performance improvements in polymers [21,22,23]. The addition of carbon nanoparticles in polymers often improves properties but may cause degradation in their long-term durability due to environmental damage. Khoramishad and Alizahed [23] reported a 20–30% increase in tensile strength and a 12–23% increase in stiffness via multi-walled carbon nanotube (MWCNT) addition to epoxy. However, the mechanical properties of these MWCNT/epoxy composites decreased back to the level of neat epoxy when saturated with moisture. Liu et al. [22] reported that 60-day immersion in distilled water results in 42% and 6% decrease in tensile strength of epoxy and graphene oxide reinforced epoxy, respectively. Similarly, Glaskova-Kuzmian et al. [24] found moisture-induced reductions of 29%, 21%, 18%, and 6% in the flexural modulus of epoxy, carbon nanotube/epoxy, glass fiber-reinforced epoxy and carbon nanotube/glass fiber-reinforced epoxy composites, respectively. Both the amount of absorbed moisture and the resulting property degradation are clearly influenced by the amount and type of reinforcing nanoparticles.
Zulfli et al. [21] demonstrated that maximum moisture content absorbed by carbon nanotube/glass fiber-reinforced epoxy is increased by the nanotube content. The addition of 0.5 wt %, 1 wt %, and 1.5 wt % nanotube to glass fiber-reinforced epoxy increased the maximum moisture the composite can absorb by 12%, 22%, and 44%, respectively. On the other hand, the addition of graphene oxide to epoxy was reported to decrease the maximum moisture level [22]. Depending on the type and amount of nanoparticles, nanocomposites may absorb higher [21,25] or lower [8,22,24,26] amounts of moisture. Consequently, accurate prediction of the absorbed moisture is essential for the life cycle design of structural composites.
Several models have been developed to characterize the moisture absorption behavior of polymers and their composites. These models range from the Fickian diffusion [27,28] to more sophisticated anomalous non-Fickian absorption models [29,30,31,32,33]. If the absorption dynamics of a composite is fully understood, then it would be possible to estimate variations in its properties due to the presence of moisture [34,35,36].
For a one-dimensional, classical Fickian diffusion, the diffusivity, D, and the moisture saturation level, , fully characterize the absorption dynamics. However, many composite parts do not follow Fickian behavior, and thus require non-Fickian models with additional absorption parameters [29,31,37]. Varying levels of molecular bonding between water and the polymer network in thermoset polymers, as well as the interfacial moisture storage in composites, result in the continuation of moisture uptake at a lower rate and over a longer period. Fickian-based models cannot explain such anomalous behavior caused by molecular bonding and interfacial storage.
In this article, moisture absorption behaviors of various carbon/epoxy nanocomposites are characterized by using the non-Fickian hindered diffusion model. The published data are used to determine the effect of six different carbon nanomaterials. Changes in the absorption dynamics and maximum absorption levels due to two different types of carbon nanotubes, two different types of carbon nanofibers, graphite nanoplatelets, and carbon black, are identified at different volume fractions. The model predictions quantitatively reveal the changes in absorption behavior and illustrate the discernable effects of having different types of carbon nanomaterials dispersed in an epoxy nanocomposite.
2. Moisture Absorption Theory
In the commonly used Fickian model, absorption of water molecules is entirely based on diffusion, driven by the spatial concentration gradient. During the initial stages of one-dimensional Fickian absorption, the weight of absorbed moisture increases linearly with the square root of time. After the initial linear uptake, the absorption gradually slows down and eventually stops as saturation is reached [27]. However, most high-performance thermosetting polymers such as epoxy and bismaleimide resins exhibit a non-Fickian behavior [29,30,31,32,33]. Several models have been used to characterize this non-Fickian behavior, such as the coupled diffusion-relaxation [29], dual-diffusivity [30], and time-varying diffusion coefficient [31] models. Of particular importance is the Langmuir model [32], which has been recently extended to the three-dimensional, anisotropic hindered diffusion model (HDM) [38,39]. The Langmuir-type absorption model and the HDM were reported to be very accurate in describing the non-Fickian absorption [6,33,40], and were successful in predicting this anomalous behavior in thermoset-based adhesives, composites and molding compounds [6,10,32,33,40,41,42,43,44,45].
The HDM considers both the diffusivity of the polymer and water-polymer affinity by separating the water molecules into two different states: mobile (free to diffuse due to concentration gradient) and bound (not free to diffuse through the polymer network). Thus, the moisture concentration is expressed as the sum of these two distinct components: bound moisture concentration and mobile moisture concentration. The one-dimensional moisture intake is then described by two coupled differential equations:
where, is the diffusion coefficient, is the rate for mobile molecules to become bound, is the rate for bound molecules to become mobile,represents the mobile molecules per unit volume, and represents the bound molecules per unit volume. The coefficients and account for the interaction between the polymer network and the water molecule, which could hinder the diffusion process. In this framework, after the initial diffusion-driven uptake, the absorption often continues at a slower rate until moisture saturation is reached as:
where and are the equilibrium bound and mobile moisture content, respectively. Equation (2) indicates that, when the polymer is fully saturated, the ratio of the bound to mobile moisture can be represented by a nondimensional hindrance coefficient, .
The hindered diffusion model characterizes the liquid absorption behavior using four distinct absorption parameters. The diffusion coefficient, or diffusivity, is the migration rate of diffusing liquid molecules into the penetrated medium. It determines the speed of initial concentration-driven moisture intake. The maximum moisture content, on the other hand, defines the maximum amount of liquid that the medium can absorb and retain. Additionally, statistical parameters (i.e., the rate for mobile molecules to become bound, ; the rate for bound molecules to become mobile, and their ratio, hindrance coefficient, ), describe the chemical interactions between the liquid penetrant and the medium. The values of all absorption parameters are dependent on the type of the penetrant, the absorbing medium, and the temperature.
It is important to note that at saturation, both mobile and bound moisture reach their maximum values, and , respectively. Although the ratio of the bound to mobile moisture (i.e., ) varies throughout the absorption, at saturation, this becomes, , which is identical to The hindrance coefficient is zero for a Fickian diffusion, but it can be much larger for polymers with greater water affinity [33,43,46,47].
For a one-dimensional absorption into a fully immersed part of thickness, h, the analytical solutions of bound moisture concentration and unbound moisture concentration are given in Equations (3) and (4).
where,
In order to obtain the total weight fraction of the absorbed moisture, the sum of the bound moisture concentration and the unbound moisture concentration can be integrated over the composite thickness as:
In Equation (6), is the weight percent of absorbed moisture and is the weight percent of the saturation moisture.
3. Materials, Sample Preparation, and Moisture Absorption Experiments
In this study, experimental moisture absorption data for six different types of carbon/epoxy nanocomposites published in four different articles are used to identify the effect of various carbon nanomaterials [9,48,49,50]. In most cases, the moisture absorption behavior was analyzed with the simpler Fickian model, thus neglecting the interaction and possible bonding between the water molecules and the polymer. Thus, the non-Fickian absorption effects, often becoming more prominent at later stages of the absorption, have not been fully addressed. The data presented in these four articles, when viewed collectively, represent a broader viewpoint of the absorption of carbon/epoxy nanocomposites, as the experiments were carried out under different humidity and temperature conditions over different periods of time. Although the individual material components and the sample preparation methods are detailed in each article, a brief summary of the relevant points of materials and experimental methods is given below.
3.1. Carbon Nanotube/Epoxy and Carbon Nanofiber/Epoxy Samples
Prolongo et al. [48] fabricated carbon nanotube/epoxy (CNT/epoxy) and carbon nanofiber/epoxy (CNF/epoxy) composites using diglycidyl ether of bisphenol A (DGEBA) epoxy and 4,40-methylenedianiline (DDM) hardener. The CNTs were produced by the catalytic carbon vapor deposition method, functionalized with amino-groups (<0.5% w/w) by Nanocyl (NC3152). Amino functionalization of CNTs makes covalent bonding to polymers possible, thus enhancing polymer additive interface and increasing the mechanical performance [51]. CNFs are produced by electrospinning. The CNTs and CNFs had average lengths of <1 µm and ~35 µm, respectively. The CNTs had an average diameter of 10 nm, whereas the average diameter of CNFs varied between 20–100 nm. Nanocomposite samples were manufactured by first dispersing the CNTs (0.10 or 0.25 wt %) or CNFs (0.25 wt % or 1.0 wt %) in chloroform, followed by adding epoxy and mixing at 150 rpm for 30 min. at 45 °C. After sonicating the mixture for 45 min. and removing chloroform at 90 °C, the DDM hardener was added and the composite parts were cured at 150 °C for 3 h and post-cured at 180 °C for 1 h. The manufactured samples absorbed moisture at 55 °C and 95% relative humidity.
In another study with carbon nanofibers, Saha and Bal [49] fabricated CNF/epoxy composites using CNF (L = 10–40 µm and d = 200–500 nm; Nanostructured & Amorphous Materials, Inc.), Ciba-Geigy, araldite LY-556 based in bisphenol, an epoxy resin and an aliphatic primary amine hardener (HY-951). Nanocomposites were manufactured by first mixing CNF with ethanol solution to disperse individual nanofibers, followed by evaporating the ethanol and mixing the CNF powder with epoxy. After 6 h sonication, the hardener was added, and the solution was mixed for 5 min. The material was cast into a mold, cured first at room temperature and then at 90 °C for 6 h. The edges of the manufactured samples were sealed and then immersed into water for 6 months.
Starkova et al. [9] used a DGEBA-based L135i/H137i epoxy system (Momentive Specialty Chemicals) and as-produced multiwall carbon nanotubes (Baytubes C150P) to produce CNT/epoxy nanocomposites. The nanotubes in this study were non-functionalized and had open ends. The composite samples were prepared by first mixing and dispersing the required amount of CNT with resin using lab-scale three-roll-mill and adding amine hardener (H137i). The suspension was then mixed at 200–600 rpm under vacuum for 10 min., followed by curing at 22 °C for 24 h and post-curing at 80 °C for 15 h. The cured samples were polished into 2.2 × 10 × 110 mm bar-shaped samples and conditioned at 20 °C and 98% relative humidity.
3.2. Graphite Nanoplatelets/Epoxy and Carbon Black/Epoxy Samples
In a complementary study, Starkova et al. [50] used a DGEBA-based epoxy resin Araldite LY556 and triamine curing agent Jeffamine T-403 to produce nanocomposites. The nanocomposite parts contained either Printex XE2 carbon black with an average particle size of 30 nm or Punto Quantico S. r.1 graphite nanoplatelets with an average flake thickness of 12–15 nm and a planar size of 20–50 µm. Both Printex XE2 carbon black and Punto Quantico graphite nanoplatelets are conductive and used for electronically conductive coatings, plastics and rubber. The high BET surface area of Printex XE2 carbon black (1000 m2/g) increases the gas adsorption on the particle surface. This phenomenon can be related to the moisture absorption, since the moisture diffuses in molecular form. The samples were fabricated by first manually mixing the nano-filler into the resin and then by using a three-roll-mill to improve the dispersion. Subsequently, the hardener was added, and the mixture was degassed at room temperature, followed by curing at 80 °C for 4 h and post-curing at 120 °C for 8 h. Samples of 2.0–2.4 mm thickness were prepared and immersed in distilled water at 50 °C.
3.3. Determination of Absorption Parameters from Gravimetric Data
Both Fickian and hindered diffusion models contain a specific set of material properties generally referred to as “absorption parameters” or “diffusion parameters”, which are needed for the characterization of liquid absorption in a particular polymer or composite. The one-dimensional Fickian diffusion model uses only two parameters: diffusion coefficient, , and the maximum amount of liquid that can be absorbed, . When the edge effects and/or anisotropy are present, different directions might have different diffusion coefficients, usually referred to as through-the-thickness diffusion coefficient, , and planar diffusion coefficients, and. When the diffusion is non-Fickian, the hindered diffusion model introduces two additional parameters: the rate of bound molecules becoming mobile, , and the rate of mobile molecules becoming bound, .
One of the robust methods to determine these absorption parameters has been proposed by Aktas et al. [28]. This method can simultaneously identify all the absorption parameters from the experimental data by using a gradient optimization technique. In identifying the unknown model parameters, the error to be minimized is given as:
where and are theoretically predicted and experimentally measured weight gains, respectively, and m is the total number of weight gain data collected. In order to improve the accuracy of finding the model parameters, using a large number of weight gain data would be beneficial. The error, , is calculated by the summation of individual errors from each point of the weight gain data.
In this paper, an iterative steepest descent method [28] is used to determine the set of absorption parameters. The error minimization procedure is implemented by adjusting the absorption parameters in the opposite direction of the gradient vector at each iteration. The iterative process can be expressed as,
where is a coefficient vector chosen to accelerate the convergence, is the number of iterations, is the absorption parameters to be recovered (e.g., for Langmuir diffusion model), and is the number of absorption parameters (e.g., = 2 for Fickian and = 4 for Langmuir diffusion model). An important advantage of this optimization procedure is its minimization of by adjusting the value of each absorption parameter at every step according to their individual effect on . The computational effort needed for this method can be reduced by using a recent approach developed by Guloglu et al. [33], where the initial guess for the parameters are taken from faster but approximate solutions of the same data set.
4. Results and Discussion
Figure 1 shows the moisture absorption behavior of CNT/epoxy nanocomposites kept at 95% relative humidity in an environmental chamber at 55 °C for almost 600 h [48]. With the addition of carbon nanotubes, the nanocomposite samples absorbed less moisture and the initial rate of absorption is reduced for those samples with 0.1 % and 0.25% CNT. The rapid initial moisture intake gradually slows down at around after 100 h of humidity exposure. Although the rate of absorption is significantly lower after 400 h (i.e., , the samples continue absorbing moisture. This small but discernible secondary absorption slope is an indication of non-Fickian behavior. Hence, even if the experiments were stopped before the samples approached full saturation, the maximum absorption amount could be viewed as an unknown and should be determined simultaneously with the other model parameters. Such an approach enables more accurate characterization of the absorption behavior, particularly for nanocomposites with prominent non-Fickian absorption. Figure 1 also shows that the one-dimensional solution of the hindered diffusion model perfectly captures all the salient features of the absorption behavior for the neat epoxy as well as the two other samples with carbon nanotubes.
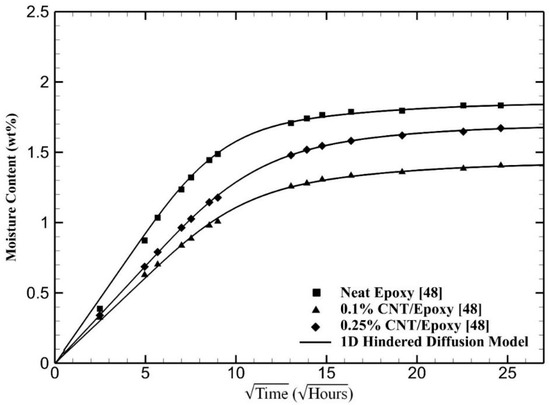
Figure 1.
Prediction of the moisture absorption of carbon nanotube (CNT)/epoxy nanocomposites using the one-dimensional hindered diffusion model. Experimental data are from Prolongo et al. [48].
Figure 2 shows the moisture uptake of the samples with 0.1% and 0.25% carbon nanofibers (CNF) together with the hindered diffusion model predictions. Similar to Figure 1, the absorption behavior of nanocomposites with CNT shows a considerable reduction of both the initial rate and total moisture intake. Moreover, the model predictions can very accurately recover the experimental data for all samples. The nanocomposites with CNT and CNT show similar absorption characteristics and exhibit non-Fickian behavior.
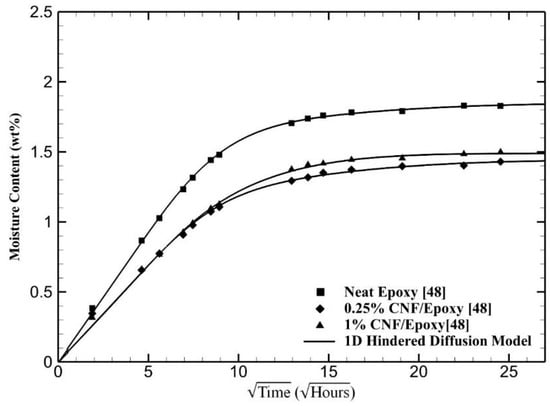
Figure 2.
Prediction of the moisture absorption of carbon nanofiber (CNF)/epoxy nanocomposites by the one-dimensional hindered diffusion model. Experimental data are from Prolongo et al. [48].
Table 1 gives the moisture absorption parameters obtained from the hindered diffusion model. The maximum absorption amounts and the other parameters given in Table 1 were directly obtained from the optimization method described in Section 3.3. The model results reveal that the neat epoxy is slightly non-Fickian with a hindrance coefficient, µ = 0.1. The addition of CNT and CNF increases the non-Fickian behavior evidenced by the increased µ. The sample that has the most nanomaterials at 1% CNF also has the highest µ at 0.25. A hindrance coefficient of 0.25 implies that the ratio of bound to unbound moisture at saturation is 0.25, thus indicating that a considerable amount of absorbed moisture is stored at the CNF/epoxy interface at saturation.

Table 1.
Moisture absorption parameters of carbon nanotube (CNT)/epoxy and carbon nanofiber (CNF)/epoxy nanocomposites.
Figure 3 shows absorption and model prediction results from another set of CNF/epoxy nanocomposite samples. The samples were immersed in water for six months at room temperature [49]. For this case, three different CNF contents were used in addition to the neat epoxy resin. Similar to Figure 2, the presence of CNF reduced the initial rate and the saturation moisture content compared to neat epoxy. Figure 3 shows that the model successfully recovered the experimental data for all CNF/epoxy samples regardless of the CNF content. Moreover, compared to Figure 1, the absorption data extends over a longer time period, making it easier to discern the absorption behavior after the quasi-equilibrium, which is primarily dominated by molecular interactions. In fact, all samples exhibit clear non-Fickian behavior, indicated by the secondary slopes after 2500 h of immersion.
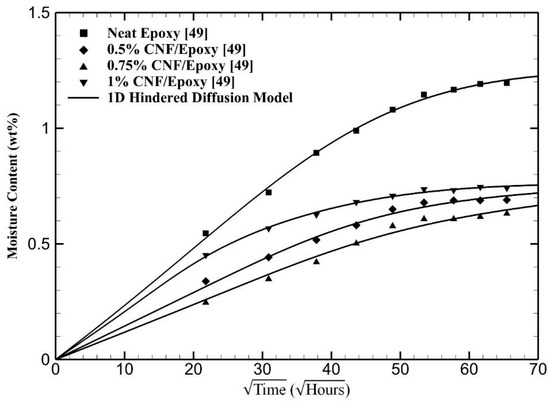
Figure 3.
Prediction of the moisture absorption of CNF/epoxy nanocomposites by the one-dimensional hindered diffusion model. Experimental data are from Saha and Bal [49].
Table 2 lists the absorption parameters recovered by the hindered diffusion model for the samples given in Figure 3. The neat epoxy sample has a hindrance coefficient of 0.145, which is slightly more non-Fickian than the epoxy sample shown in Figure 1 and Figure 2. Table 2 also shows that the hindrance coefficient is positively correlated with the CNF content, leading to a strongly non-Fickian behavior of µ = 0.493 when the CNT content is increased to 1%. This behavior can be discerned by the careful observation of Figure 3. As the CNF content is increased to 1%, the initial absorption rate becomes higher than the samples with lower CNF content. However, the absorption rate slows down at later stages, resulting in a lower saturation level. This indicates that the moisture uptake at later stages is mostly driven by the presence of molecular exchange between the diffused moisture and the storage at the CNF interface.

Table 2.
Moisture absorption parameters of neat epoxy and CNF/epoxy nanocomposites.
Moisture absorption for another type of CNT/epoxy samples and the model predictions are shown in Figure 4. These samples were conditioned at 98% relative humidity at 20 °C for nearly 10 months [9]. Again, the hindered diffusion model accurately recovered the absorption behavior of both the neat epoxy and the nanocomposite. Since these experiments were carried out longer than those given in Figure 1, Figure 2 and Figure 3, the difference between the absorption behavior of neat epoxy and the 0.5% CNT sample became clearer. As in the previous samples, the rate of initial moisture uptake is lower for the 0.5% CNT sample. However, the neat epoxy saturates faster, reaching the saturation level earlier than the nanocomposite. In contrast, the presence of CNT promotes further moisture intake at later stages, despite an initially lower absorption level. Eventually, the CNT/epoxy samples would absorb more moisture than the neat epoxy, where interfacial bound moisture plays a significant role in this non-Fickian behavior.
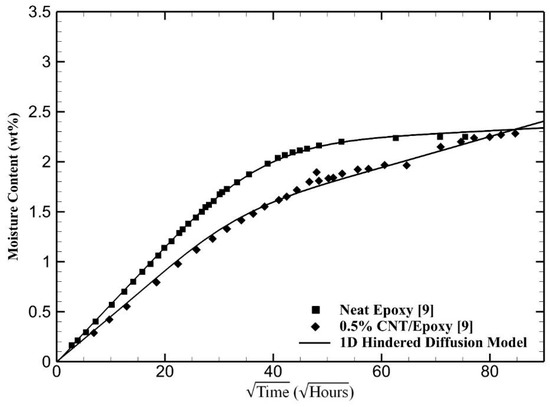
Figure 4.
Prediction of the moisture absorption of CNT/epoxy nanocomposites by the one-dimensional hindered diffusion model. Experimental data are from Starkova et al. [9].
Table 3 gives the model parameters for both cases shown in Figure 4. This CNT/epoxy sample exhibits the highest level of non-Fickian behavior, with a hindrance coefficient of 1.15. The neat epoxy, however, shows a modest level of non-Fickian behavior with a hindrance coefficient of 0.256. The CNT/epoxy sample is expected to absorb a high level of moisture, reaching a total weight gain of 3.43% at saturation.

Table 3.
Moisture absorption parameters for the neat epoxy and the CNT/epoxy nanocomposite.
Figure 5 shows the moisture absorption and the model predictions for the samples containing 0.5% graphite nanoplatelets (GnP) compared to the neat epoxy resin used in this case. The nanocomposite samples were immersed in water at 50 °C for almost two years, whereas the epoxy samples were immersed a shorter time, as they seem to have reached saturation earlier [50]. The predictions of the model are observed to be very accurate for both cases over the entire immersion period. The effect of 0.5% graphite nanoplatelets is significant and somewhat similar to those of CNT and CNF given earlier. The lower initial moisture uptake appears again for this nanocomposite, yet the moisture absorption continues further and exceeds that of neat epoxy during the initial stages of the immersion. Since the absorption tests continued much longer than the experiments given for other cases, a higher amount of water absorption and a longer time required for saturation are clearly observed for this nanocomposite.
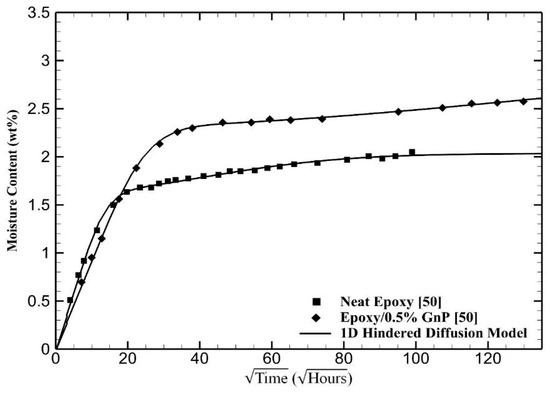
Figure 5.
Prediction of the moisture absorption of a neat epoxy sample and a graphite nanoplatelets (GnP)/epoxy nanocomposite by the one-dimensional hindered diffusion model. Experimental data are from Starkova et al. [9].
Figure 6 shows the moisture absorption of the same epoxy system that contains 0.5% carbon black (CB). The immersion experiments for the neat epoxy and carbon black were carried out up to 14 months where the moisture absorption rates seem to have significantly slowed down. The model predictions successfully recover and explain the absorption behavior of the CB/epoxy nanocomposite. More importantly, the CB, similar to GnP, promotes increased moisture uptake. However, unlike GnP, the CB/epoxy sample gives the false impression of approaching the saturation level earlier, shown by the longer plateau region after the initial diffusion-dominant absorption. However, after the long plateau, a considerable secondary absorption rate appears at . This behavior further corroborates that the carbon/epoxy nanocomposites can become strongly non-Fickian due to nanoparticles, even at very low concentrations. The hindered diffusion model is able to fully explain and mimic the water uptake throughout the entire absorption process.
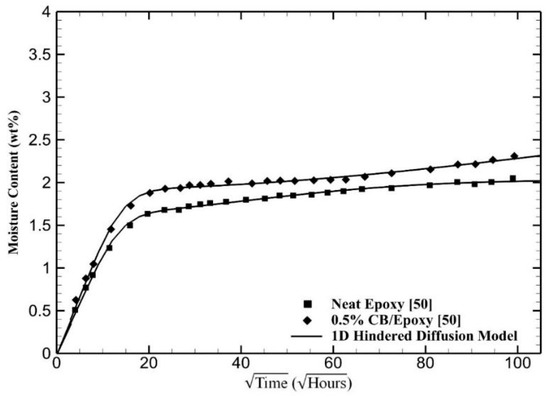
Figure 6.
Prediction of the moisture absorption of a neat epoxy and a carbon black (CB)/epoxy nanocomposite by the one-dimensional hindered diffusion model. Experimental data are from Starkova et al. [50].
Table 4 lists the model parameters recovered for the neat epoxy, GnP/epoxy, and CB/epoxy nanocomposites. Both nanocomposites absorb considerably more moisture at saturation, predicted to be 3.17% and 3.47% for GnP and CB, respectively. These values are higher than those CNT and CNFs dispersed in similar epoxy resins. Geometrical factors may explain this difference, where the platelets and carbon black could provide an increased interfacial surface for molecular bonding and moisture storage compared to nanotubes and nanofibers with a high aspect ratio.

Table 4.
Moisture absorption parameters of GnP/epoxy and CB/epoxy nanocomposites.
The results indicate that each carbon-based nanofiller has a unique effect on the moisture absorption parameters. In general, the addition of carbon-based nanofillers resulted in an increase in the hindrance coefficient in all material systems when compared to the respective neat epoxy. The increasing hindrance coefficient implies that a higher amount of unbound (diffused) moisture becomes bound when the moisture equilibrium is reached. Clearly, a higher hindrance coefficient means the nanocomposite is becoming more non-Fickian, which is also corroborated by the moisture absorption curves.
Further insight can be gained by considering that the carbon-based nanofillers themselves do not absorb moisture. Yet, their presence, even in very low amounts, creates large interfacial spaces within the nanocomposite that can store moisture. Moreover, there could be molecular interaction and bonding between the moisture and the nanofiller, which contributes to the bound moisture levels. Hence, the combination of interfacial moisture storage and molecular bonding may explain the increase in the hindrance coefficient as the additive volume fraction is increased.
Another small but important effect of increasing the nanofiller content is the change in diffusivity of the nanocomposite. The diffusion of water molecules through the nanocomposite is affected by the reduction of the polymer volume due to the nanofillers. Since usually small amounts of nanofillers are mixed with the polymer, a small reduction in diffusivity is expected. One approach in modeling the effect of carbon fillers on the diffusivity of the nanocomposite may be to use a “rule of mixture”, where the bulk polymer diffusivity is reduced proportionally with the additive volume fraction. At this point, there is not sufficient experimental data to test the predictive capability of such micromechanics models, but the results presented here confirm that the hindered diffusion model is able to describe a broad spectrum of highly non-Fickian absorption behavior, often observed in carbon-based nanocomposites.
5. Conclusions
The moisture absorption behavior of several epoxy-based nanocomposites containing different types of carbon, such as carbon nanotubes, carbon nanofibers, graphite nanoplatelets, and carbon black, is investigated using the non-Fickian hindered diffusion model. The moisture absorption data from six different nanocomposites are shown to be accurately described by this theoretical model over the entire absorption time periods.
All neat epoxy parts are shown to be weakly non-Fickian, displaying a small but discernible secondary slope after the initial diffusion-driven absorption. The non-Fickian region becomes more apparent after the quasi-equilibrium plateau and is governed primarily by the exchange between bound and unbound water molecules. As the carbon content is increased, the hindrance effects are shown to become more prevalent, thus delaying the moisture saturation. These effects are observed to be characterized by the nondimensional hindrance coefficient, the ratio of bound to unbound moisture at saturation. The increased level of hindrance indicates that the moisture intake at saturation becomes increasingly bound moisture, which would accumulate at the carbon/epoxy interface. This effect is even more pronounced for nanoparticles with larger surface areas such as graphite nanoplatelets and carbon black, compared to high aspect ratio carbon nanofibers or nanotubes.
It is important to realize that the carbon nanoparticles, even at very low concentrations, act as possible moisture storage sites, promoting delayed but increased moisture uptake later in the absorption cycle. This delayed response may not be observed in experiments that are terminated early due to a lower initial absorption rate, with an extended, intermediate plateau often seen in carbon/epoxy nanocomposites.
Author Contributions
Conceptualization, G.E.G. and M.C.A.; Formal Analysis, G.E.G.; Writing—original draft, G.E.G.; Writing—review & editing, M.C.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
References
- Soares-Pozzi, A.C.; Dibbern-Brunelli, D. Study of the influence of saline solutions in carbon/epoxy composite by luminescence, Raman and UATR/FT-IR spectroscopy. J. Mater. Sci. 2016, 51, 9342–9355. [Google Scholar] [CrossRef]
- Sugita, Y.; Winkelmann, C.; La Saponara, V. Environmental and chemical degradation of carbon/epoxy lap joints for aerospace applications, and effects on their mechanical performance. Compos. Sci. Technol. 2010, 70, 829–839. [Google Scholar] [CrossRef]
- Kotrotsos, A.; Vavouliotis, A.; Tsantzalis, S.; Kostopoulos, V. Effect of CNT modified matrix of epoxy CFRPs on hydrothermal behaviour of material. Evaluation of water uptake using electrical resistance measurements. Plast. Rubber Compos. 2014, 43, 122–129. [Google Scholar] [CrossRef]
- Jefferson, G.D.; Farah, B.; Hempowicz, M.L.; Hsiao, K.T. Influence of hygrothermal aging on carbon nanofiber enhanced polyester material systems. Compos. Part B Eng. 2015, 78, 319–323. [Google Scholar] [CrossRef]
- Alzamora Guzman, V.; Brøndsted, P. Effects of moisture on glass fiber-reinforced polymer composites. J. Compos. Mater. 2015, 49, 911–920. [Google Scholar] [CrossRef]
- Barink, M.; Mavinkurve, A.; Janssen, J. Predicting non-Fickian moisture diffusion in EMCs for application in micro-electronic devices. Microelectron. Reliab. 2016, 62, 45–49. [Google Scholar] [CrossRef]
- Guermazi, N.; Haddar, N.; Elleuch, K.; Ayedi, F.H. Effect of filler addition and weathering conditions on the performance of PVC/CaCO3 composites. Polym. Compos. 2015, 37, 2171–2183. [Google Scholar] [CrossRef]
- Garg, M.; Sharma, S.; Mehta, R. Carbon nanotube-reinforced glass fiber epoxy composite laminates exposed to hygrothermal conditioning. J. Mater. Sci. 2016, 51, 8562–8578. [Google Scholar] [CrossRef]
- Starkova, O.; Buschhorn, S.T.; Mannov, E.; Schulte, K.; Aniskevich, A. Water transport in epoxy/MWCNT composites. Eur. Polym. J. 2013, 49, 2138–2148. [Google Scholar] [CrossRef]
- Korobkov, V.A.; Krylova, Y.E.; Kasatkina, T.B.; Levashov, A.S.; Gorokhov, R.V.; Bukov, N.N.; Startseva, L.T.; Krotov, A.S.; Startsev, O.V. Diffusion of moisture in an epoxy coating with a disperse mineral filler. Polym. Sci. Ser. D 2016, 9, 351–357. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Christiansen, J.; Gupta, R.K.; Shah, A.P. Model for anomalous moisture diffusion through a polymer–Clay nanocomposite. J. Polym. Sci. Part B Polym. Phys. 2002, 476–492. [Google Scholar] [CrossRef]
- Kumar, A.; Roy, S. Modeling of anomalous moisture diffusion in nanographene reinforced thermoset polymers. Compos. Struct. 2015, 122, 1–7. [Google Scholar] [CrossRef]
- Al-Qadhi, M.; Merah, N.; Gasem, Z.M. Mechanical properties and water uptake of epoxy-clay nanocomposites containing different clay loadings. J. Mater. Sci. 2013, 48, 3798–3804. [Google Scholar] [CrossRef]
- Kim, D.H.; Kim, H.S. Waterproof characteristics of nanoclay/epoxy nanocomposite in adhesively bonded joints. Compos. Part B Eng. 2013, 55, 86–95. [Google Scholar] [CrossRef]
- Akil, H.M.; Santulli, C.; Sarasini, F.; Tirillò, J.; Valente, T. Environmental effects on the mechanical behaviour of pultruded jute/glass fibre-reinforced polyester hybrid composites. Compos. Sci. Technol. 2014, 94, 62–70. [Google Scholar] [CrossRef]
- Aktas, L.; Hamidi, Y.; Altan, M. Effect of moisture on the mechanical properties of resin transfer molded composites - Part I: Absorption. J. Mater. Process. Manuf. Sci. 2002, 10, 239–254. [Google Scholar] [CrossRef]
- Aktas, L.; Hamidi, Y.; Altan, M.C. Effect of moisture on the mechanical properties of resin transfer molded composites - Part II: Desorption. J. Mater. Process. Manuf. Sci. 2002, 10, 255–267. [Google Scholar] [CrossRef]
- Dhakal, H.N.; Zhang, Z.Y.; Richardson, M.O.W. Effect of water absorption on the mechanical properties of hemp fibre reinforced unsaturated polyester composites. Compos. Sci. Technol. 2007, 67, 1674–1683. [Google Scholar] [CrossRef]
- Agubra, V.A.; Mahesh, H.V. Environmental degradation of E-glass/nanocomposite under the combined effect of UV radiation, moisture, and rain. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 1024–1029. [Google Scholar] [CrossRef]
- Sridhar, R.; Narasimha Murthy, H.N.; Karthik, B.; Vishnu Mahesh, K.R.; Krishna, M.; Ratna, P. Moisture diffusion through nanoclay/vinylester processed using twin-screw extrusion. J. Vinyl Addit. Technol. 2014, 20, 152–159. [Google Scholar] [CrossRef]
- Zulfli, N.M.; Bakar, A.A.; Chow, W.S. Mechanical and water absorption behaviors of carbon nanotube reinforced epoxy/glass fiber laminates. J. Reinf. Plast. Compos. 2013, 32, 1715–1721. [Google Scholar] [CrossRef]
- Liu, H.-K.; Wang, Y.-C.; Huang, T.-H. Moisture Effect on Mechanical Properties of Graphene/Epoxy Nanocomposites. J. Mech. 2016, 32, 673–682. [Google Scholar] [CrossRef]
- Khoramishad, H.; Alizadeh, O. Effects of silicon carbide nanoparticles and multi-walled carbon nanotubes on water uptake and resultant mechanical properties degradation of polymer nanocomposites immersed in hot water. Polym. Compos. 2018, 39, E883–E890. [Google Scholar] [CrossRef]
- Glaskova-Kuzmina, T.; Aniskevich, A.; Martone, A.; Giordano, M.; Zarrelli, M. Effect of moisture on elastic and viscoelastic properties of epoxy and epoxy-based carbon fibre reinforced plastic filled with multiwall carbon nanotubes. Compos. Part A Appl. Sci. Manuf. 2016, 90, 522–527. [Google Scholar] [CrossRef]
- Lee, B.L.; Yang, T.W.; Wilusz, E. Moisture effects on isobutylene-isoprene copolymer-based composite barrier. I: Moisture diffusion and detection. Polym. Eng. Sci. 1996, 36, 1217–1231. [Google Scholar] [CrossRef]
- Jana, S.; Zhong, W.-H. FTIR study of ageing epoxy resin reinforced by reactive graphitic nanofibers. J. Appl. Polym. Sci. 2007, 106, 3555–3563. [Google Scholar] [CrossRef]
- Fick, A. Ueber Difusion. Ann. Phys. 1855. [Google Scholar] [CrossRef]
- Aktas, L.; Hamidi, Y.K.; Altan, M.C. Combined edge and anisotropy effects on Fickian mass diffusion in polymer composites. J. Eng. Mater. Technol. 2004, 126, 427. [Google Scholar] [CrossRef]
- Berens, A.R.; Hopfenberg, H.B. Diffusion and relaxation in glassy polymer powders: 2. Separation of diffusion and relaxation parameters. Polymer 1978, 19, 489–496. [Google Scholar] [CrossRef]
- Jacobs, P.M.; Jones, E.R. Diffusion of moisture into two-phase polymers—Part 2 Styrenated polyester resins. J. Mater. Sci. 1989, 24, 2343–2347. [Google Scholar] [CrossRef]
- Roy, S.; Xu, W.X.; Park, S.J.; Liechti, K.M. Anomalous Moisture Diffusion in Viscoelastic Polymers: Modeling and Testing. J. Appl. Mech. 2000, 67, 391. [Google Scholar] [CrossRef]
- Carter, H.G.; Kibler, K.G. Langmuir-type model for anomalous moisture diffusion in composite resins. J. Compos. Mater. 1978, 12, 118–131. [Google Scholar] [CrossRef]
- Guloglu, G.E.; Hamidi, Y.K.; Altan, M.C. Fast recovery of non-fickian moisture absorption parameters for polymers and polymer composites. Polym. Eng. Sci. 2016, 57, 921–931. [Google Scholar] [CrossRef]
- Regazzi, A.; Léger, R.; Corn, S.; Ienny, P. Modeling of hydrothermal aging of short flax fiber reinforced composites. Compos. Part A Appl. Sci. Manuf. 2016, 90, 559–566. [Google Scholar] [CrossRef]
- Youssef, Z.; Jacquemin, F.; Gloaguen, D.; Guillén, R. A multiscale hygroviscoelastic approach to predicting the internal stresses in composite materials. Mech. Compos. Mater. 2010, 46, 201–210. [Google Scholar] [CrossRef]
- Peret, T.; Clement, A.; Freour, S.; Jacquemin, F. Numerical transient hygro-elastic analyses of reinforced Fickian and non-Fickian polymers. Compos. Struct. 2014, 116, 395–403. [Google Scholar] [CrossRef]
- Maggana, C.; Pissis, P. Water sorption and diffusion in an epoxy resin system. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 1165–1182. [Google Scholar] [CrossRef]
- Grace, L.R.; Altan, M.C. Characterization of anisotropic moisture absorption in polymeric composites using hindered diffusion model. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1187–1196. [Google Scholar] [CrossRef]
- Grace, L.R.; Altan, M.C. Non-Fickian three-dimensional hindered moisture absorption in polymeric composites: Model development and validation. Polym. Compos. 2013, 34, 1144–1157. [Google Scholar] [CrossRef]
- Glaskova, T.I.; Guedes, R.M.; Morais, J.J.; Aniskevich, A.N. A comparative analysis of moisture transport models as applied to an epoxy binder. Mech. Compos. Mater. 2007, 43, 377–388. [Google Scholar] [CrossRef]
- Scott, P.; Lees, J.M. Water, salt water, and alkaline solution uptake in epoxy thin films. J. Appl. Polym. Sci. 2013, 130, 1898–1908. [Google Scholar] [CrossRef]
- Joliff, Y.; Belec, L.; Chailan, J.F. Modified water diffusion kinetics in an unidirectional glass/fibre composite due to the interphase area: Experimental, analytical and numerical approach. Compos. Struct. 2013, 97, 296–303. [Google Scholar] [CrossRef]
- Popineau, S.; Rondeau-Mouro, C.; Sulpice-Gaillet, C.; Shanahan, M.E.R. Free/bound water absorption in an epoxy adhesive. Polymer 2005, 46, 10733–10740. [Google Scholar] [CrossRef]
- LaPlante, G.; Ouriadov, A.V.; Lee-Sullivan, P.; Balcom, B.J. Anomalous moisture diffusion in an epoxy adhesive detected by magnetic resonance imaging. J. Appl. Polym. Sci. 2008, 109, 1350–1359. [Google Scholar] [CrossRef]
- Grace, L.R.; Altan, M.C. Three-dimensional anisotropic moisture absorption in quartz-reinforced bismaleimide laminates. Polym. Eng. Sci. 2013, 54, 137–146. [Google Scholar] [CrossRef]
- Grace, L.R. Projecting long-term non-Fickian diffusion behavior in polymeric composites based on short-term data: A 5-year validation study. J. Mater. Sci. 2016, 51, 845–853. [Google Scholar] [CrossRef]
- Helbling, C.S.; Karbhari, V.M. Investigation of the sorption and tensile response of pultruded E-glass/vinylester composites subjected to hygrothermal exposure and sustained strain. J. Reinf. Plast. Compos. 2008, 27, 613–638. [Google Scholar] [CrossRef]
- Prolongo, S.G.; Gude, M.R.; Ureña, A. Water uptake of epoxy composites reinforced with carbon nanofillers. Compos. Part A Appl. Sci. Manuf. 2012, 43, 2169–2175. [Google Scholar] [CrossRef]
- Saha, S.; Bal, S. Long term hydrothermal effect on the mechanical and thermo-mechanical properties of carbon nanofiber doped epoxy composites. J. Polym. Eng. 2018, 38, 251. [Google Scholar] [CrossRef]
- Starkova, O.; Chandrasekaran, S.; Schnoor, T.; Sevcenko, J.; Schulte, K. Anomalous water diffusion in epoxy/carbon nanoparticle composites. Polym. Degrad. Stab. 2019, 164, 127–135. [Google Scholar] [CrossRef]
- Ramanathan, T.; Fisher, F.T.; Ruoff, R.S.; Brinson, L.C. Amino-Functionalized Carbon Nanotubes for Binding to Polymers and Biological Systems. Chem. Mater. 2005, 17, 1290–1295. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).