Abstract
Due to increasing costs and growing environmental concerns pertaining to the construction of structures, an alternative form of reinforcement has been proposed through our studies; through a new beam design methodology, referred to as triple composite beams, glass can be used as a cost-competitive and more environmentally friendly macro-scale compressive reinforcement. The cost competitiveness of glasses derives from their large compressive strength (in general 1000 MPa; >1100 MPa for fused quartz). To support the triple composite design architecture, equations have been developed using Euler–Bernoulli beam theory and the method of transformed sections and compared against finite element modeling determined stresses. Our results show that the average stress was more accurate but less precise than fully considering binder, assuming the binder did not contribute to the cross-section of the beam. The paper concludes by presenting a flexural reinforcement utilization ratio (R), which predicts the ability of a reinforcement-binder combination to utilize the reinforcement to maximum stress effectively while ignoring bonding strength. This R ratio suggests that while concrete is a low cost, it cannot be used in a glass-reinforced beam as the concrete is too stiff compared to the glass.
1. Introduction
The first known use of composite materials is the use of straw in clay bricks to increase their tensile strength, which is thousands of years old [1]. The production of steel-reinforced concrete began in the 1800s [2] and continues to be one of the most common composite materials. Additional improvements to composites were made during the 1940s and 1950s for military applications [3]. In general, composites attempt to improve the function of an engineered device by improving the properties of the materials by which it is composed. In fact, part of what brought about composite research in the mid-20th century was interest in finding a method of harnessing the crystal strengths predicted by solid-state theory [4]. While there has been a general transition in composite interest from macro-scale mixtures to micro- and nano-scale mixtures [5], the relative importance of composites as a material for mechanical and civil applications has generally increased over time [6]. Composites in and of themselves are interesting in that composite design must incorporate the configuration, manufacturing method, and analysis methods all simultaneously, to provide an effective product. As an example, Ref. [7] specifically studied the bonding strengths that can occur when plastic is injection molded to steel reinforcement. In many regards, composite manufacturing techniques drive the availability of more complex designs [3]. For example, reinforced concrete has unique analysis procedures, has specially designed reinforcement (ribs on the reinforcement bar, for example), and is arranged so that the beams can be poured in an open-top form.
The composites proposed in this study are modeled primarily using the Euler–Bernoulli beam theory and the method of transformed sections. Moreover, Ref. [8] provides details on how the method of transformed sections is applied to engineering problems.
Much of this paper assumes a glass compressive strength of 1000 MPa. This is a substantial strength when the glass is compared to many other mechanical components. Due to the disparity between this strength and other typical materials, additional investigating was conducted; Ref. [9] indicates that in general, the strength of glass is up to 1000 MPa, Ref. [10] indicates that the compressive strength of fused quartz is >1100 MPa, and Ref. [11] indicated that the dynamic compressive strength of borosilicate glass exceeded 2000 MPa in their testing. So, this paper assumes a glass compressive strength of 1000 MPa.
There are four primary ways in which composites are formulated using current manufacturing methods, which are summarized in Figure 1. These would be Figure 1a distributed composites (particles and/or fibers, of which there are many subtypes, as indicated by [3,5]), Figure 1b sheet composites (laminates), Figure 1c sandwich composites [2], and Figure 1d rod composites. Each type of composite has its own advantages and disadvantages. This paper deals primarily with sandwich and rod composites (referred to as macro-scale composites), as they are most applicable to triple composite beams under bending moment loading. Distributed composites are typically the easiest to manufacture, as they are constructed by essentially a mixture of solid within solid, such as glass fibers distributed within a polymer.
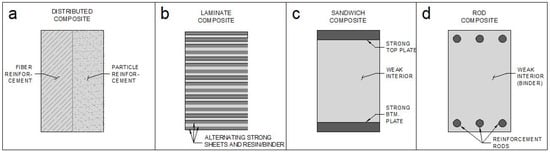
Figure 1.
The types of composites: (a) Fiber/particle reinforcement distributed throughout the interior of a component. (b) Laminate composites, which alternate different materials between layers. (c) Sandwich composites. (d) Rod composites; these are representative of reinforced concrete.
Sandwich and rod composites have been explored by others. For example, precast concrete sandwich panels are a sandwich composite which can be seen as an example of the type of behavior that can occur in sandwich composites, as shown by [12]. Ref. [13] provides an example of a steel-concrete-steel composite used for blast shielding. Reinforced concrete is the classical example of a rod composite.
To better understand why sandwich and rod composites are preferred for beams, consider the beam cross-sections shown in Figure 2. In Figure 2a, there is a random assortment of stiffer particles distributed in the beam’s cross-section. When transforming this beam using the transformed section method and Euler–Bernoulli beam theory, the stiffer particles increase the width of the equivalent beam approximately uniformly across the depth of the beam. In Figure 2b, the sandwich composite, which has the stiffer material placed at the extremities, increases the width at a distance far from the neutral axis. This increased width greatly increases the beam’s strength due to the increased geometric second moment of area. Figure 2c has the superior shape of Figure 2b, but includes a cover (the small portions at the top and bottom of Figure 2c), material which protects the reinforcement rods. The glass-polymer composite beams proposed in this paper will be either sandwich or rod composite beams.
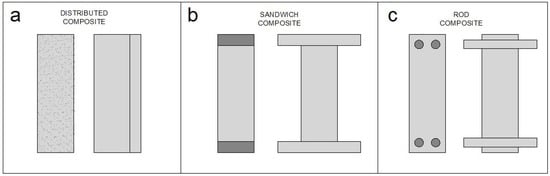
Figure 2.
A comparison of the cross-section of different composite materials when transformed using the transformed sections method with Euler–Bernoulli beam theory. (a) The distributed particles sum to a increase in width in the transformed (right-side) section. (b) With sandwich composites, the stiffer material is placed at the extreme top and bottom, allowing the contributed area to increase the width at the extremities. (c) Rod composites have top and bottom cover included to allow for reinforcement protection.
Distributed composites (as detailed in Figure 2a) do have design cases for which they are superior to sandwich and rod composites. These design cases are referred to as general cases; that is, the increased strength across the depth of the beam allows the beam to withstand more varied loading conditions. For example, case Figure 2a resists axial loading and bending across both bending moment axes without requiring anisotropic manufacturing conditions as would be required for the beams shown in Figure 2b,c. As such, constructing a beam in configuration Figure 2a typically has a lower cost relative to Figure 2b,c. To extrapolate on this, composites are shown as a sliding scale of complexity in Figure 3. In this figure, the designs become increasingly complex from left to right. This causes an increase in specialized strength (e.g., strength in bending across a single axis) and increased labor costs due to the additional work required to install each additional composite material, such as chairs/fixtures for tensile reinforcement in steel-reinforced concrete beams. However, this allows for more efficient use of materials, which offsets the negatives of the increases in labor costs.
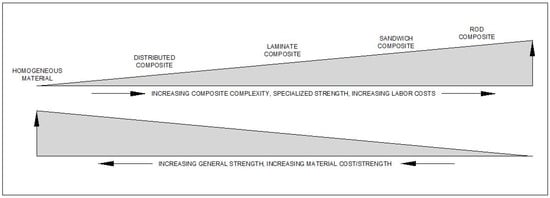
Figure 3.
As material moves from being a homogenized material to an increasingly complex composite, several changes are made. While the strength becomes more specialized so too does the cost of construction per additional compositing item added. This, however, is offset by decreasing material costs per strength. The relative increases in specialized strength for beams greatly outweighs the disadvantage of the increased labor costs. An additional example is fiber-reinforced concrete; while it does have superior general strength, it cannot outperform steel-reinforced concrete for flexural requirements due to the advantages of locating the reinforcement at the extremities of a beam section.
The interactions between dissimilar materials are where new properties for composites are found [14], though the bonding strength does pose challenges. The presence and necessity of bond strength are noted here, the primary contribution of this work is the use of glass as compressive reinforcement in macro-scale composites. The direct approach to modeling bonding strengths is to examine the geometry between elements [14]. Accordingly, what is unique to compressive forces when dealing with composites is an increase in frictional forces that occur at the interface of two materials placed in compression. This can be thought of as the binding material having a hole through it; when placed in compression, the binder will try to squeeze this cavity tighter, shrinking the diameter of the hole. The reinforcement within said hole simultaneously is trying to increase in diameter due to Poisson’s ratio. This dual-action between two materials placed in compression allows for greater frictional forces to occur between the two materials as the loading is increased. Therefore, it can be thought of that the compressive forces within the compressive reinforcement must transmit across the surface of the reinforcement as a shear force, which is resisted by a frictional force that occurs due to the squeezing action between the two materials. While these bonding strengths are beyond the scope of this paper, these forces will be modeled and will play a larger role when samples of triple composite beams are tested to failure.
Attempting to incorporate glass into structural applications isn’t novel. Glass has at many times been utilized due to its transparent properties. With regard to attempting to composite glass, the works of P.C. Louter et al. are of note [15,16,17,18]. A generic arrangement representative of their work is shown in Figure 4. In this figure, steel tensioners are placed at the top and bottom of the beam and post-tensioned, placing the beam in compression. Despite this, when the beam becomes loaded it quickly builds tension and the allowed capacity is limited to ½ the strength of glass, a point which coincides with the beam failing in tension at the top and compression at the bottom surface. However, the applications specifically sought by the type of design represented in Figure 4 differs from what is sought in this paper; instead of beams that specifically are translucent, the goal of this paper is to establish beams that can utilize the maximum theoretical strengths of glasses. An additional aspect is that beams that have glass throughout their depth tend to be significantly more expensive due to the relatively high cost of glass per unit area.
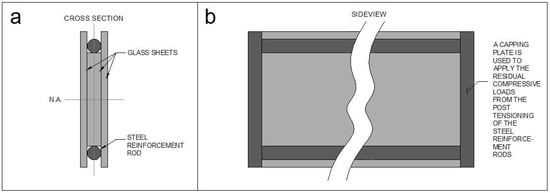
Figure 4.
A typical post-tensioned glass composite is shown. These are constructed so that the view through the glass is minimally obstructed while providing increased load capacity to the glass beam through the post-tensioning of the steel rods.
The aims and objectives of this research are to introduce the concept of a polymer beam that utilizes glass as compressive reinforcement, as a lower-cost and more environmentally friendly alternative to structural elements that are currently available on the marketplace. As is discussed in subsequent sections, glass, when compared on a per strength basis, outperforms both steel and concrete. This work intends to provide justification for further study of such polymer beams that utilize glass as compressive reinforcement and steel as tensile reinforcement. To summarize, what is specifically being described in this paper is the application of glass reinforcement into structural beams. Strength per cost ratios for glasses, when the glasses are only considered to be loaded in compression, outperform many other typical engineering materials for structural applications, such as steel, aluminum, concrete, etc. The following section helps explain the specific means by which glass outperforms these alternative materials.
2. An Explanation of the Potential Economics and Environmental Improvements of Glass Reinforcement
Novel to this paper is the concept of including glass as a reinforcing element with the purpose of attempting to offset the use of concrete or other binders in reinforced composite beams. These glass-concrete-steel or glass-polymer-steel beams are referred to in this paper as triple composite beams as there are three elements to these beams. Each beam element plays a vital role: steel in tension, glass in compression, and a binder to hold the reinforcement together. To achieve the advantages of glass, it must be produced at a low cost while guaranteeing a high compressive strength. This has been tested; our initial experimentation created low-quality glasses by melting a mixture of glass making materials (silica, soda ash, and lime) within a steel sleeve and allowing the mixture to cool insulated only by sand surrounding the composite material. Despite the simplistic production method, this low-quality glass had a failure stress of 208 MPa (30 ksi). These glasses are regarded as “as tested” in subsequent context. While the testing fell short of the 1000 MPa (144 ksi) that was anticipated [9,10], a leading cause could have been the testing arrangement, which did not guarantee a perpendicular loading of the glass sample. Loading could not be guaranteed to be perpendicular due to the difficulty of cutting the steel-sleeve into which the low-quality glass was cast.
Additionally, this paper uses comparison tools between glasses and many common structural materials, such as concrete and steel. Preliminary calculations suggest that glass can be produced at a price of approximately $0.12 per kilogram. The actual prices of soda-lime glass were researched and found to be $0.17 per kilogram, which is 70% of the calculated value. This value of $0.12 per kilogram takes into account the energy required to melt the glass making components as well as the costs of the silica, soda ash, and lime as required for making the soda-lime glass. It also assumes a 10% thermal efficiency and a cost of $0.10 per kilowatt-hr. Soda-lime glass can be produced at a lower cost than other glasses [19] due to soda and lime acting to lower the glass melting temperature significantly. However, bulk metallic glasses may provide superior mechanical properties at lower costs [20,21,22], etc.
Glass is specifically assumed to remain in compression when describing glass as a reinforcement in this paper. This requirement is held as if the glass is directly compared with concrete or steel under tensile loading, the assumed glass strength has to be reduced. An example of this can be found in Ref. [23], which indicates that glasses have a strength of around 50–200 MPa and a relative cost per volume index of 2.5. Conversely, these tables indicate that typical steels have a strength of 300 MPa at a cost per volume index of 1.0; this would mean that steel greatly outperforms glass. However, these charts typically make broad assumptions about materials, so the glasses referenced are silica glass (a more costly to produce glass), not soda-lime glass as is used for the triple composite beams. They also assume the glass is not loaded exclusively in compression and is manufactured to quality necessary to make the glass translucent.
Regardless, even at such a low strength, given the manufacturing technique (which did not include any annealing step), a low-quality glass may be able to function cost-effectively as a reinforcement. It is difficult to compare data on glass manufacturing techniques from others due to the requirements necessary for most glass manufacturing. For instance, most glass manufacturing focuses on producing glass that is translucent, smooth, and able to withstand small (relative to steel) tensile loading. All three of these requirements would be unnecessary for the glass reinforcement proposed in this paper as the translucence does not matter, the glass needs to have a rough exterior (which can be provided by casting it against silica in a sand-mold) to help transfer loading between the glass and binder, and the glass need only be strong in compression.
Based on the specific details outlined above, Table 1 was developed. This table indicates that glass may provide a marginal improvement in cost (10%) over concrete (assuming an “as tested” strength and a cost of $0.17 per kilogram).

Table 1.
The cost of materials required to resist 100 Mn applied to a variable cross-sectional area (i.e., axially loaded) and at a unit length of 1 m. The sections are divided by the loading types for the given materials so as not to directly compare compression-only to other material types.
- The costs listed in this table reflect the most up to date information as found researching material prices. Prices fluctuate, and accordingly, so do price indices. Steel prestressing cable price: [24]; Recycled soda-lime glass: [25]; Virgin soda-lime glass [26].
- The theoretical glass strength was set to 1000 MPa, the as-tested glass strength was 217 MPa (based on our research), and the concrete strength was assumed to be 27.6 MPa (4 ksi, an industry-standard concrete strength).
To obtain Table 1, a load of 100 Mn was applied to an arbitrary surface area made of a material. Due to the strength of the material, a particular surface area can be assumed for this loading, assuming the load is equally distributed across the member. Then, an arbitrary length of 1 m is assumed. By doing this, a volume can be determined, by which the mass can be calculated using the material’s density. This weight of the material is compared against the material’s cost, creating a cost per 100 Mn of load (in USD $/100 Mn). While the definition of the shape is arbitrary, since all materials were applied with the same criteria, a basis for comparison on a cost per load basis can be formed. Following this procedure, the cost per loading of glass can be highlighted. The calculated cost for the arbitrary loading and length was found to be $42.84 for glass, and $218.93 for concrete. This means that glass costs 20% the cost of concrete to withstand an equal load. A superior description may be provided by developing a formula for this specific price index. The index would be:
where ρ is the density, σult is the ultimate strength, which may be substituted with the yield (σy) for a given application, cmi is the cost to mass (essentially the unit price) for a product, and asci is the axial strength to cost index.
Admittedly, this analysis highlights the theoretical advantages of glass, but fails to extrapolate on the disadvantages found with glass design. For instance, glass becomes exceedingly difficult to design for if the design is based on glass reaching its theoretical compressive strength. The difficulty stems from the abnormally small cross-sectional surface areas (for example, glass requires only 2.8% of the cross-sectional area of concrete for equal strengths), especially when considering a material that must bond effectively to the surrounding binder. It is likely that the bond strength itself will control the design for triple composite beams.
There are additional benefits to glass. Glass provides a more environmentally friendly material when compared on a per strength basis to concrete. These advantages are highlighted in Table 2 and Table 3. For Table 2, the percentages of material that is required to be transported and mined, if considering designs of equivalent strength, are shown for glass and concrete. Glass, whether virgin, recycled, as tested or at theoretical strength, outperforms concrete at least 10 fold concerning the quantity of material that must be mined or transported.

Table 2.
The required weight from Table 1, for the compression only materials, is used to compare the transportation and mining requirements for each material. This is done to show that glass, having a higher strength to mass, greatly outperforms concrete. This would help to reduce the amount of greenhouse gas emissions developed during the transportation of materials.

Table 3.
The embodied energy (an estimate of the energy to produce a material, which correlates with fossil fuel usage during the manufacturing of the material) and CO2 generated for concrete and glasses are shown. Glass outperforms concrete in certain situations.
Table 3 highlights the advantages with regard to embodied energy and CO2 generated. These environmental qualities are of increasing importance. Comparisons should be made on a per strength basis, as it allows for a more realistic real environmental impact for each material. The testing of glass produced in preliminary testing has indicated an embodied energy of 92% that of concrete, while the theoretical strength of glass would allow a reduction of 80% of the embodied energy. The advantages regarding CO2 developed indicate that in order to reduce CO2 generated, the glass is required to be recycled or near the theoretical strength. Virgin glass with the reduced weight does pose a disadvantage by producing quadruple the CO2 generated by an equivalent strength component made of concrete.
- The embodied energies for concrete and glass were 1.9 MJ/kg and 12.7 MJ/kg, respectively [27].
- The kilograms of CO2 generated per kilogram of the material was 0.15 for concrete, 4.4 for non-recycled (virgin) glass, and 0.73 for recycled glass [28].
To summarize, glass outperforms concrete in all cases except in the case of using virgin glass for the “as tested” glass strengths. So, in this case, it may be superior to utilize recycled glass to produce glass structural reinforcement. As can be observed from the Table 1, Table 2 and Table 3, the prices of the proposed materials in many regards meet or beat the traditional materials. This means that, although it often is not considered as such, the glass may be able to reduce the use of concrete in reinforced concrete beams or be placed into a new polymer-based-binder composite beam that allows for further cost reductions.
3. Stress Equations for Triple Composite Beams Using Euler–Bernoulli Beam Theory and the Transformed Sections Method
The specific design selected for this paper is a beam which features glass as a compressive reinforcement that works in conjunction with a tensile material and a binder. This triple-composite-beam arrangement allows for a superior material to be provided for the compression face of a beam similar to the method in which superior tensile reinforcement is used in concrete beams. This is proposed in an attempt to provide superior cost-effectiveness for a beam.
Example designs are shown in Figure 5. In this figure, Figure 5a shows the beams utilized for finite element modeling (FEM). These beams have a simplistic shape and arrangement though, due to the low Young’s modulus of the binder they perform similarly to the beams shown in Figure 5b,c. Figure 5b is a design that features rods in both faces but may have issues with slenderness. Conversely, Figure 5c shows a T-section with a glass top plate, which reduces the likelihood of slenderness being an issue in the beam. A capping material (cover) may be necessary for the beam shown in Figure 5c.
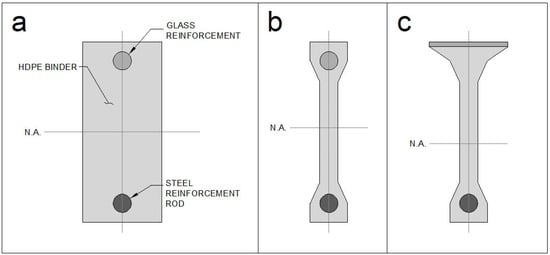
Figure 5.
(a) The beams considered in this study, which feature a purposefully wide section to limit alternate failure modes. (b) An alternate design featuring rod-type reinforcement at the top and bottom. (c) Another alternative, but a sheet of glass is placed as top reinforcement.
Future designs may allow for tensioning of the glass reinforcement but as mentioned before, the as tested glasses have not had their tensile strengths checked and are assumed to be extremely weak due to the prevalence of cracks in the as tested glass. In order to place the glass in a constant residual compressive load, it must first be tensioned, then the tension must be released after the binder has solidified. Post-tensioning designs will have to be researched at a later time.
Equations were developed for triple composite beams to establish a comprehensive method for analysis. These equations were developed using the “transformed section” method with Euler–Bernoulli beam theory. The transformed section method involves converting the cross-section of a beam to an alternate, nonexistent beam that has an equivalent second area moment. This nonexistent beam is used to determine the capacity of the beam and the stresses, though materials that have been converted must be transformed back to the original material. The conversion ratio for the materials is based on Young’s modulus of each material.
Due to the wide range of materials possible for composites, a single set of equations cannot be employed for triple composite beams as the binders considered (concrete and polymers) behave considerably differently. Therefore, Section 3.1, Section 3.2 and Section 3.3 all have specific analysis assumptions that were used in determining the section maximum stresses and properties. These are summarized in Figure 6. In this figure, Figure 6a shows the beam to be analyzed, Figure 6b shows the assumed geometric shape under the binderless assumption, Figure 6c shows the geometric shape under the compression only binder assumption, and Figure 6d shows the cross-section when considering full binder.
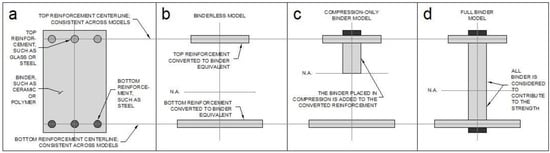
Figure 6.
A summary of the binder models considered. (a) The general arrangement of the beams considered. (b) The binderless model, where the reinforcement is converted to binder-material; due to the differential Young’s moduli between the materials. (c) The compression-only binder model, which is commonly used for the concrete design. (d) In cases where the binder still contributes significantly to the beam’s flexural stiffness, the full binder model may need to be used. Note the dark gray regions at the top (c and d) and bottom (d), which denotes cover regions. These small components contribute little strength, with the true intention being protection for the reinforcement.
3.1. Binderless Beams
Binderless beams are constructed typically of a binder with a relatively small Young’s modulus when compared to the reinforcement’s Young’s modulus. Hence, the equations developed in this section are for nonstiff binder materials that allow the neglection of the binder when considering the bending properties of the beam. Conversely, if a beam’s binder has a relatively large stiffness, the binderless assumption may not be appropriate. The concept of a binderless beam in and of itself is incorrect, as a beam without an interior section would cease to function as a complete entity; only the top reinforcement would become loaded. What is specifically meant as a “binderless beam” is the lack of consideration of the binder when calculating the geometric, second moment of area. The second moment of area is key as this value is inversely proportional to the stress due to the bending moment. The binderless assumption, which is, by definition, what makes it a binderless beam, artificially removes the binder from consideration, resulting in a more conservative design. The advantage of disregarding the binder is that the stress analysis for the beam becomes significantly less complicated. For example, the equations that define the stresses in a binderless beam are (based on the method of transformed sections presented in [29]):
These stress equations are analytically derived from the method of transformed sections. This theory has been extrapolated and worked by many others, such as [8]. Inherent to the method of transformed sections is an assumption that Euler–Bernoulli beam theory is followed.
Where yb is the distance from the neutral axis to the bottom reinforcement, yt is the distance from the neutral axis to the top reinforcement, At is the area of the top reinforcement, nt/b is the ratio of Young’s modulus of the top reinforcement to the binder, d is the distance between the top and bottom reinforcement (i.e., depth), Ab is the area of the bottom reinforcement, nb/b is Young’s modulus ratio of the bottom reinforcement to the binder, I* is the second moment of area of the transformed section, M is the applied bending moment, σr,t,x is the normal stress of the top reinforcement in the x-direction, σb,t,x is the normal stress of the top binder in the x-direction, σr,b,x is the normal stress of the bottom reinforcement in the x-direction, and σb,b,x is the normal stress of the binder at the bottom in the x-direction. While the binder is not considered to contribute to the second moment of area, it can still have maximum stress calculated which will be larger than the maximum stress in analyses that consider the contributions of the binder. The advantage of this arrangement of equations is that the method of designing a beam with a different top and bottom reinforcement can be made significantly easier using this set of equations.
3.2. Compression Only Binder Beams
Compression only binder beams are considered next, which are typically ceramic-like materials (such as concrete) which are assumed to only develop compressive loads. This results in the following series of stress equations:
where tc is the top cover distance. Note that Equations (6) and (8) also apply in this section, though (7) has been modified to include a top cover (see (14) above) and (9) is neglected. There is no calculation for the binder tension on the bottom half of the beam, as it is assumed that the binder is a ceramic material and fails immediately upon the development of tension (an assumption often used in the concrete analysis, though concrete does have a minimal tensile strength).
3.3. Beams Considering Full Binder
Beams that consider the binder to remain intact during analysis prove more challenging to determine properties for. This occurs due to the complexity of meeting the requirements of the first moment of the area being equal on either side of the neutral axis while having a relationship of the centroids of the reinforcement to the measurement for the depth, d. First, the locations of the centroids of the top and bottom sections must be found while maintaining a depth that is equivalent:
The above equations are most easily solved through iterative techniques, to establish values of the reinforcement locations that equal the depth, d (the requirement of Equation (16)). The easiest way to do this is to assume a value of yt, solving for a value of yb through Equation (16), then solving Equation (15). If the assumed yt value was correct, then the left and right sides of the Equation (15) will be equal.
Once the reinforcement locations relative to the central axis are found, the moment of inertia is calculated through:
Now, the stresses can be calculated using Equations (6), (8), (14) and the following, additional equation:
4. Finite Element Modeling for Triple Composite Beams
A comprehensive Finite Element Modeling (FEM) study was conducted to verify the stresses calculated using the formula developed. Figure 7 shows the dimensions of the beam and cross-sections considered for analysis. Finite element analysis was conducted using the following parameters: fixed-fixed supported beam, 3.048-m length (10 feet), 254 mm depth (10 inches, between reinforcement centroids), beam width of 152 mm (6 inches), loading of 10.5 kN per meter (720 pounds per foot, input as a 10 psi pressure on the top surface of the beams in ANSYS), top reinforcement had an area of 484 square mm (0.75 square inches), bottom reinforcement had an area of 484 square mm (0.75 square inches), top and bottom cover (for the rod-beam only) was 25 mm (1 inch) from the surface to reinforcement centroid, Young’s modulus for steel was 200 GPa, Young’s modulus of HDPE was 0.8 GPa [30], and Young’s modulus of glass was 70 GPa [31]. The critical section considered for analysis was the center of the beam (five feet from each fixed face of the beam). The section was utilized to prevent localized discrepancies that are sometimes caused at supports in finite element models.
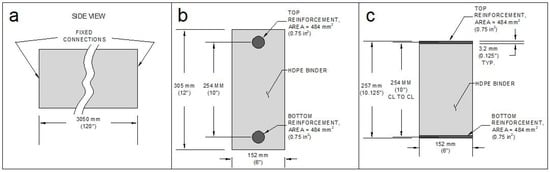
Figure 7.
The dimensions utilized for the FEM of the triple composite beams. (a) Side view showing the length of the beam. (b) The configuration used for rod-type reinforced models. (c) The configuration used for double-plate reinforced beams. Note that the reinforcement spacing was maintained between cross-sections (b and c) to provide comparable stresses between the two cross-sections.
Finite Element Analysis (FEA) was conducted through Ansys 2019 R1 using the static structural analysis tool. Examples of the models can be seen in Figure 8, Figure 9 and Figure 10. Figure 8 shows the double-plate beam model at an isometric view. Figure 9 shows the double-plate cross-section near the center and some normal stress values. Figure 10 shows the same cross-section as 9, but for the double rod.
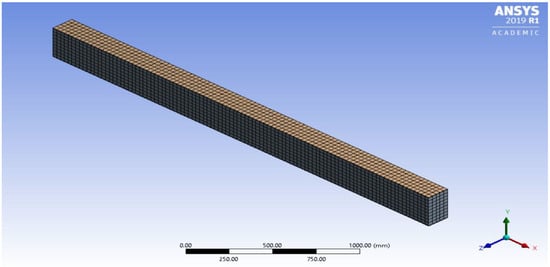
Figure 8.
The mesh of the double plate beam is shown.
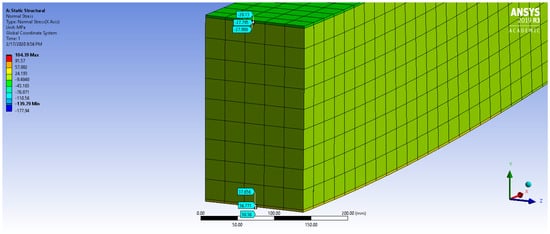
Figure 9.
A section cut near the center of the beam for the double-plate configuration with glass reinforcement in the top plate and steel in the bottom. Probe values are shown in MPa.
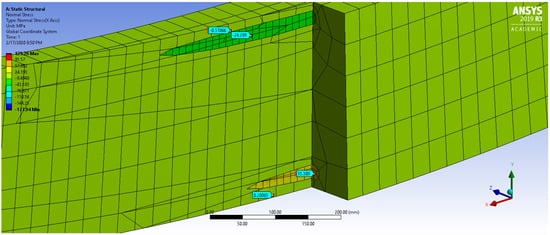
Figure 10.
A section cut near the center of the beam for the double-rod configuration with glass reinforcement in the top plate and steel in the bottom. Probe values are shown in MPa.
In all cases, the model was utilized for two different analyses; one analysis had steel as reinforcement in the top and bottom reinforcement while the second analysis had glass replace the steel in the top reinforcement only. In all cases considered, HDPE was assumed to be the binder for the beam.
Table 4 summarizes the measurements taken from the FEM and compares them to the calculations conducted using equations developed in this paper.

Table 4.
The FEM stresses are compared against all-binder and no binder assumptions. The percent error for both against the FEM results is also presented.
The table highlights some corollary data. The equations developed typically produce values that have a smaller magnitude than the FEM determined stresses. Additionally, given the materials and their differing Young’s modulli, the binderless assumption is generally a superior predictor of the stresses in the reinforcement as it is either at a value closer to the FEM determined value or is above the FEM value. However, at times the all-binder assumption is superior in calculating stresses in the binder. The differences in the binder stress calculations are typically quite large. While this may appear concerning, given the materials used, HDPE is very unlikely to fail, even in these conditions. Additionally, the values of the stress in the binder are significantly smaller than that of the reinforcement, so a small discrepancy in stress in the reinforcement can contribute a large variation in the stress in the binder. It should be specifically expressed that these results are for these particular materials. The results would likely be appreciably different if Young’s moduli ratios between the reinforcement and binder grew close to 1.0; at lower ratios, the binder contributes more significantly to the beam strength. Otherwise, the beams designed may be far too conservative, a consideration for some of the values in Table 4 (e.g., the binderless assumption predicts greater stress in the glass, by 30% and 18% for the double-plate and double-rod configurations).
To further explain the differences, Table 5 was created. Table 5 uses select data from Table 4 and organizes it in a way that allows for a superior interpretation. Table 5 only looks at the reinforcement stresses of each condition, and includes the average errors and the standard deviation of error. What this table explains is that while the average stress of the binderless assumption is lower, the binderless assumption has a significantly large standard deviation when compared to the all-binder assumption. This means that it may be more appropriate to consider all-binder, and provide a comfortable safety factor equivalent in value to the negative percentage error.

Table 5.
A select subset of Table 4 in which the differences in reinforcement stress can be better comprehended for comparison purposes.
5. Establishment of the Flexural Reinforcement Utilization Factor
There is a maximum stress that is theoretically possible for the reinforcement of a composite beam. This specific ratio, referred to as the Flexural Reinforcement Utilization Ratio (R) is:
This ratio, in and of itself, heavily influences how the materials that compose a composite beam will function due to the application of bending moment. For instance, at a value of 1.0, the R ratio indicates that the binder and reinforcement are of equivalent transformed loading. This means that the reinforcement and the binder will become loaded to failure at the same instant. This beam would be best analyzed using a full binder type analysis. In a case where the value of R is less than 1.0, this is a potentially negative configuration of reinforcement. In this situation, the reinforcement will never be fully stressed prior to the binder failing. This particular situation exists for glass and concrete. To explain this, first consider glass to have a Young’s modulus of 70 GPa (the average, according to [31]). Next, concrete’s Young’s modulus is considered as 24.8 GPa (calculated according to ACI 318-08, Section 8.5 [32]). Under these circumstances, the utilization ratio, R, is:
This means that for a glass-concrete composite, glass can only be stressed at a maximum to 7.6% of its theoretical strength. This results in a poor utilization of glass (and therefore, a less efficient beam), but there are strategies to reduce this issue; by modifying the glass (to be stiffer, i.e., to have a greater Young’s modulus) and the concrete (by utilizing lightweight concrete with a higher failure load), this utilization percentage can be increased. Hence, by changing to a glass with Young’s modulus of 90 GPa (the upper limit, according to [31]), concrete with a unit weight of 1550 kg/m3, and a strength of 42 MPa, the ratio becomes:
By changing these material properties, the glass can be stressed up to a maximum of 22.2% of the theoretical maximum glass strength. While this represents an improvement, there will be additional costs associated with the improved concrete and glass properties. It is possible to rearrange the R equation accordingly:
This arrangement helps to express the maximum stress allowed in the reinforcement in cases where R is less than 1.0. So, for the glass-concrete example above, it can be said that:
This value closely matches the stress that was determined to be the “as tested” glass strength for the first set of experiments (217 MPa), which utilized a low-quality glass. This means that glass, in this case, doesn’t have to reach the theoretical maximum of 1000 MPa to be considered possible for reinforcement when using a concrete binder. For confirmation, the R values for glass-HDPE and steel-HDPE are:
And for steel and HDPE:
As the ratio becomes too large, other factors will begin to dictate the strength of the reinforcement-binder couple, factors that are not accounted for, to any extent, in the equations above. Some examples include bonding stresses exceeding acceptable values for the binder interfacing with the reinforcement, or buckling of the reinforcement itself.
6. Conclusions
This paper introduces the idea of using low-quality cast glass as a compressive reinforcement replacement for concrete, with the goal of easing the detriment of increasing construction costs. Due to the relatively high cost per cross-sectional area, glass must be paired with a binder and used as a compressive reinforcement. By involving three different materials into a single beam and applying the transformed sections method using Euler–Bernoulli beam theory, a series of equations were developed that allow for direct calculation of the maximum stresses (for both reinforcement and binder) in a variety of design cases based on material properties between the binder and reinforcement materials.
The transformed sections method was tested against finite element models that were developed to replicate the design cases. This resulted in the binderless assumption proving superior when only considering average stresses, as it estimates stresses to be within 2% (on average) of the FEM stresses. However, the all-binder assumption results in more precision, as the standard deviation is much smaller (2% vs. 10% with the binderless assumption); the all-binder assumption resulted in estimated stresses at values, on average, 10% lower than the FEM suggested. The binderless assumption does have some advantages in that it is much quicker to estimate values and maximize the efficiency of a cross-section due to its simplistic nature.
This paper proves, on a theoretical basis, that glass and steel-reinforced polymers can be more cost-effective than both reinforced concrete and steel structures when considering the development of stresses according to Euler–Bernoulli beam theory and the method of transformed sections. Future studies will focus on the additional testing of samples. Physical samples need to be fabricated and tested to failure. This will likely take many iterations as there are many ways for a composite beam to fail. One such failure mode is from a bonding failure; in this case, the glass or steel would debond from the binding material. This would be particularly detrimental to the glass as it may place the glass in tension, where it has little strength. Reinforcement buckling, lateral torsional buckling, and shear failure are a few other failure modes. As such, this paper is simply the first in a series of investigations into the possibility of these triple composite beams.
Author Contributions
Conceptualization, J.C., R.G.; methodology, J.C.; software, J.C.; formal analysis, J.C.; investigation, J.C., R.G.; writing—original draft preparation, J.C.; writing—review and editing, R.G.; supervision, R.G.; project administration, R.G.; funding acquisition, R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Quagliarini, E.; Lenci, S. The influence of natural stabilizers and natural fibres on the mechanical properties of ancient Roman adobe bricks. J. Cult. Herit. 2010, 11, 309–314. [Google Scholar] [CrossRef]
- Kalpakjian, S.; Schmid, S.R. Manufacturing Processes for Engineering Materials, 6th ed.; Pearson: London, UK, 2016. [Google Scholar]
- Mazumdar, S. Composites Manufacturing: Materials, Product, and Process Engineering; CrC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Scala, E.P. A brief history of composites in the US—the dream and the success. JOM 1996, 48, 45–48. [Google Scholar] [CrossRef]
- Gibson, R.F. Principles of Composite Material Mechanics; CRC Press: London, UK, 2016. [Google Scholar]
- Bush, S.; Ashby, M.; Swindells, N.; Bullough, R.; Ellison, G.; Lindblom, Y.; Cahn, R.; Barnes, J. Technology of the 1990s: Advanced Materials and Predictive Design: Discussion. Philos. Trans. R. Soc. A 1987, 322, 404–407. [Google Scholar]
- Ramani, K.; Moriarty, B. Thermoplastic bonding to metals via injection molding for macro-composite manufacture. Polym. Eng. Sci. 1998, 38, 870–877. [Google Scholar] [CrossRef]
- Hamilton, R.; Tennyson, S.; Hamilton, W. Analysis by the transformed-section method. In Proceedings of the 2001 American Society for Engineering Education Annual Conference & Exposition, Albuquerque, NM, USA, 24–27 June 2001. [Google Scholar]
- Bos, F.; Louter, C.; Veer, F. Challenging Glass: Conference on Architectural and Structural Applications of Glass, Faculty of Architecture, Delft University of Technology, May 2008; IOS Press: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Northolt, M.G. Compressive strength and glass transition temperature. J. Mater. Sci. 1981, 16, 2025–2028. [Google Scholar] [CrossRef]
- Chojnacki, J.T.; Chen, W.W. Mechanical Response of Borosilicate and Soda-Lime Glass Under Dynamic Triaxial Compression. JDBM 2016, 2, 251–258. [Google Scholar] [CrossRef]
- Benayoune, A.; Samad, A.A.; Trikha, D.; Ali, A.A.; Ellinna, S. Flexural behaviour of pre-cast concrete sandwich composite panel–experimental and theoretical investigations. Constr. Build. Mater. 2008, 22, 580–592. [Google Scholar] [CrossRef]
- Liew, J.R.; Wang, T. Novel steel-concrete-steel sandwich composite plates subject to impact and blast load. Adv. Struct. Eng. 2011, 14, 673–687. [Google Scholar] [CrossRef]
- Khoddam, S.; Tian, L.; Sapanathan, T.; Hodgson, P.D.; Zarei-Hanzaki, A. Latest developments in modeling and characterization of joining metal based hybrid materials. Adv. Eng. Mater. 2018, 20, 1800048. [Google Scholar] [CrossRef]
- Louter, P. Adhesively bonded reinforced glass beams. HERON 2007, 52, 31. [Google Scholar]
- Louter, C.; Cupać, J.; Lebet, J.-P. Exploratory experimental investigations on post-tensioned structural glass beams. J. Facade Des. Eng. 2014, 2, 3–18. [Google Scholar] [CrossRef]
- Bedon, C.; Louter, C. Finite-element numerical simulation of the bending performance of post-tensioned structural glass beams with adhesively bonded cfrp tendons. Am. J. Eng. Appl. Sci. 2016. [Google Scholar] [CrossRef][Green Version]
- Santarsiero, M.; Louter, C.; Nussbaumer, A. Laminated connections for structural glass applications under shear loading at different temperatures and strain rates. Constr. Build. Mater. 2016, 128, 214–237. [Google Scholar] [CrossRef]
- Le Bourhis, E. Glass: Mechanics and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Ma, H.; Xu, J.; Ma, E. Mg-based bulk metallic glass composites with plasticity and high strength. Appl. Phys. Lett. 2003, 83, 2793–2795. [Google Scholar] [CrossRef]
- Bruck, H.; Christman, T.; Rosakis, A.; Johnson, W. Quasi-static constitutive behavior of Zr41. 25Ti13. 75Ni10Cu12. 5Be22. 5 bulk amorphous alloys. Scr. Metall. Mater. 1994, 30, 429–434. [Google Scholar] [CrossRef]
- Bruck, H.A.; Rosakis, A.J.; Johnson, W.L. The dynamic compressive behavior of beryllium bearing bulk metallic glasses. J Mater. Res. 1996, 11, 503–511. [Google Scholar] [CrossRef]
- Ashby, M.F. Materials Selection in Mechanical Design; Elsevier Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Available online: https://www.alibaba.com/trade/search?fsb=y&IndexArea=product_en&CatId=&SearchText=steel+prestressed+cable (accessed on 21 November 2019).
- Available online: https://www.alibaba.com/trade/search?IndexArea=product_en&CatId=&fsb=y&viewtype=&tab=&SearchText=recycled+glass+cullet (accessed on 21 November 2019).
- Available online: https://www.alibaba.com/products/soda_lime_glass_sheet.html?IndexArea=product_en&sort_type=TRALV (accessed on 21 November 2019).
- Available online: http://www.yourhome.gov.au/materials/embodied-energy (accessed on 22 February 2020).
- Available online: https://winnipeg.ca/finance/findata/matmgt/documents/2012/682-2012/682-2012_Appendix_H-WSTP_South_End_Plant_Process_Selection_Report/Appendix%207.pdf (accessed on 22 February 2020).
- Hibbeler, R.C. Mechanics of Materials; Prentice Hall: Upper New Jersey River, NJ, USA, 2008. [Google Scholar]
- Available online: https://www.engineeringtoolbox.com/young-modulus-d_417.html (accessed on 21 November 2019).
- Available online: http://valleydesign.com/soda-lime-glass.htm (accessed on 21 November 2019).
- ACI. Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary; ACI: Rome, Italy, 2008. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).