Determination of Annealing Temperature of Thin-Walled Samples from Al-Mn-Mg-Ti-Zr Alloys for Mechanical Properties Restoration of Defective Parts After SLM
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Thin-Walled Samples Fabrication
2.3. Mechanical Properties, Microhardness, and Roughness Analysis
2.4. Test Methods
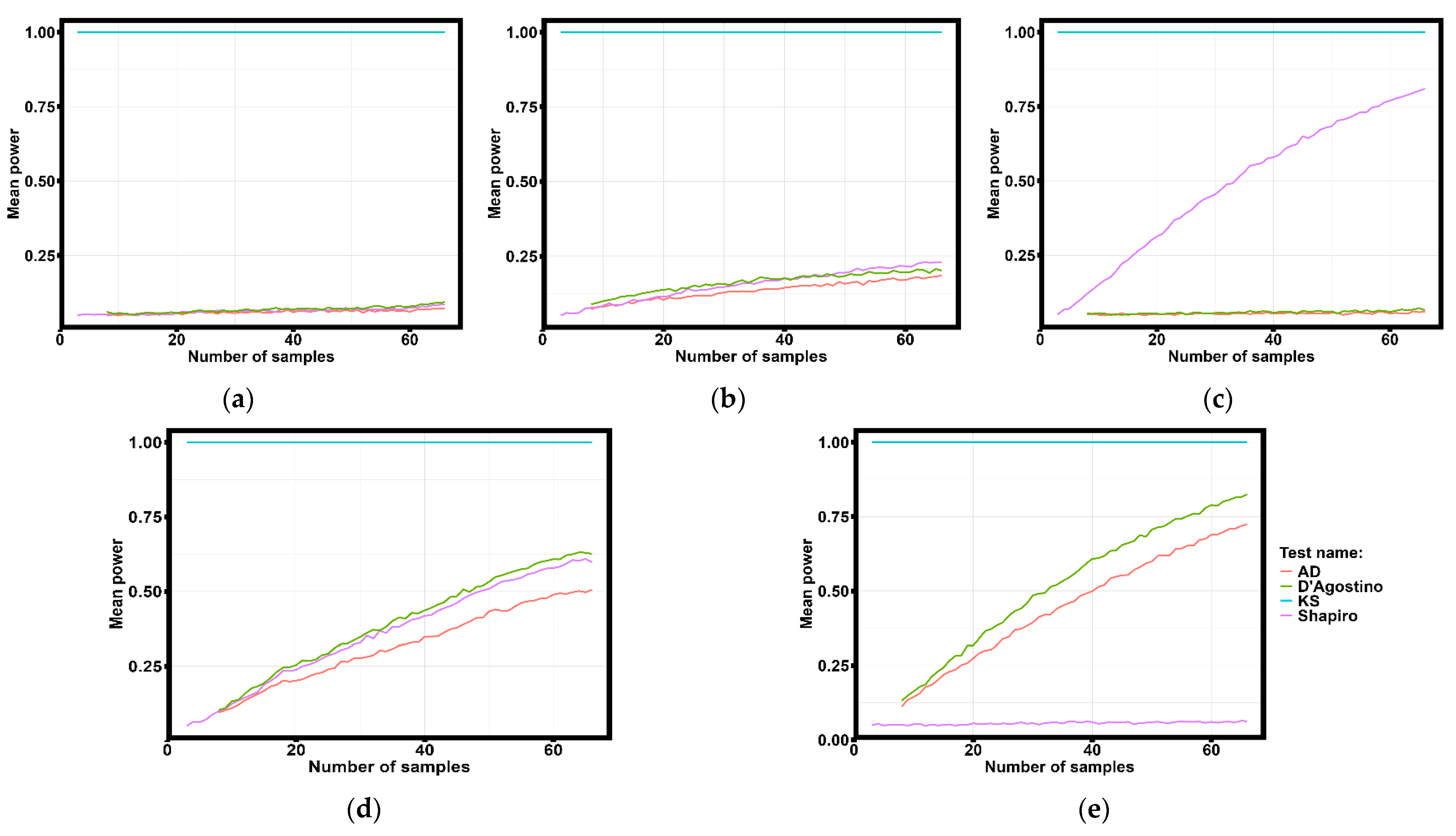
2.5. Statistical Analysis Methods
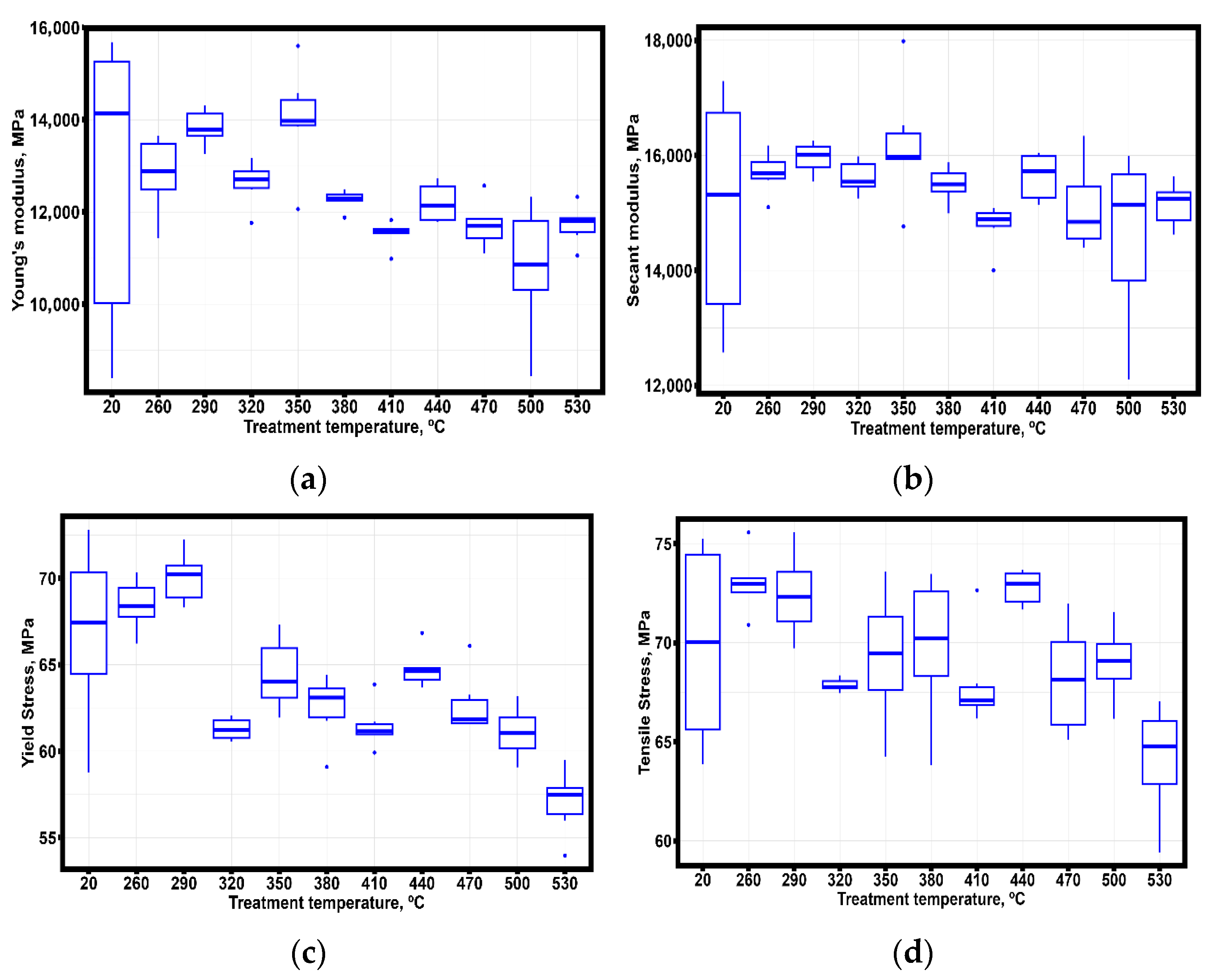
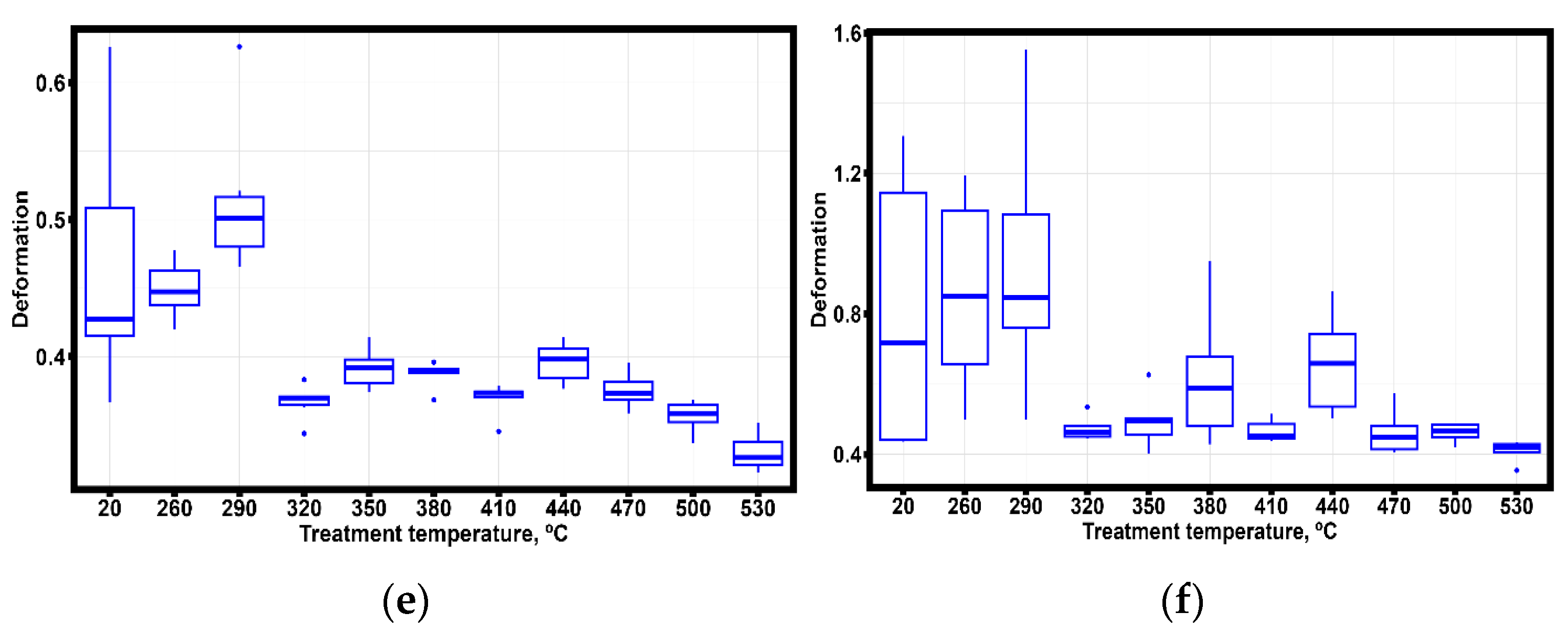
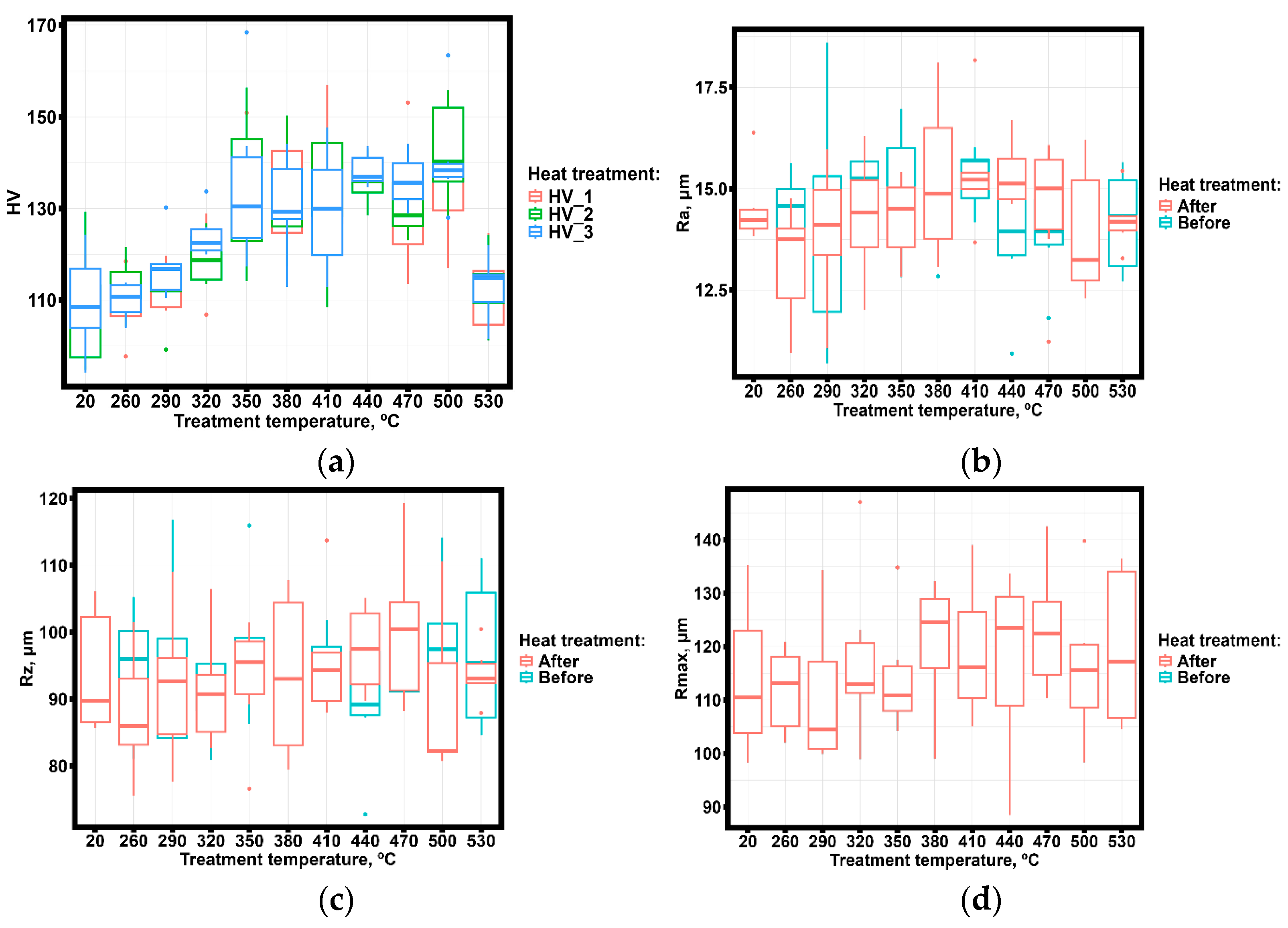
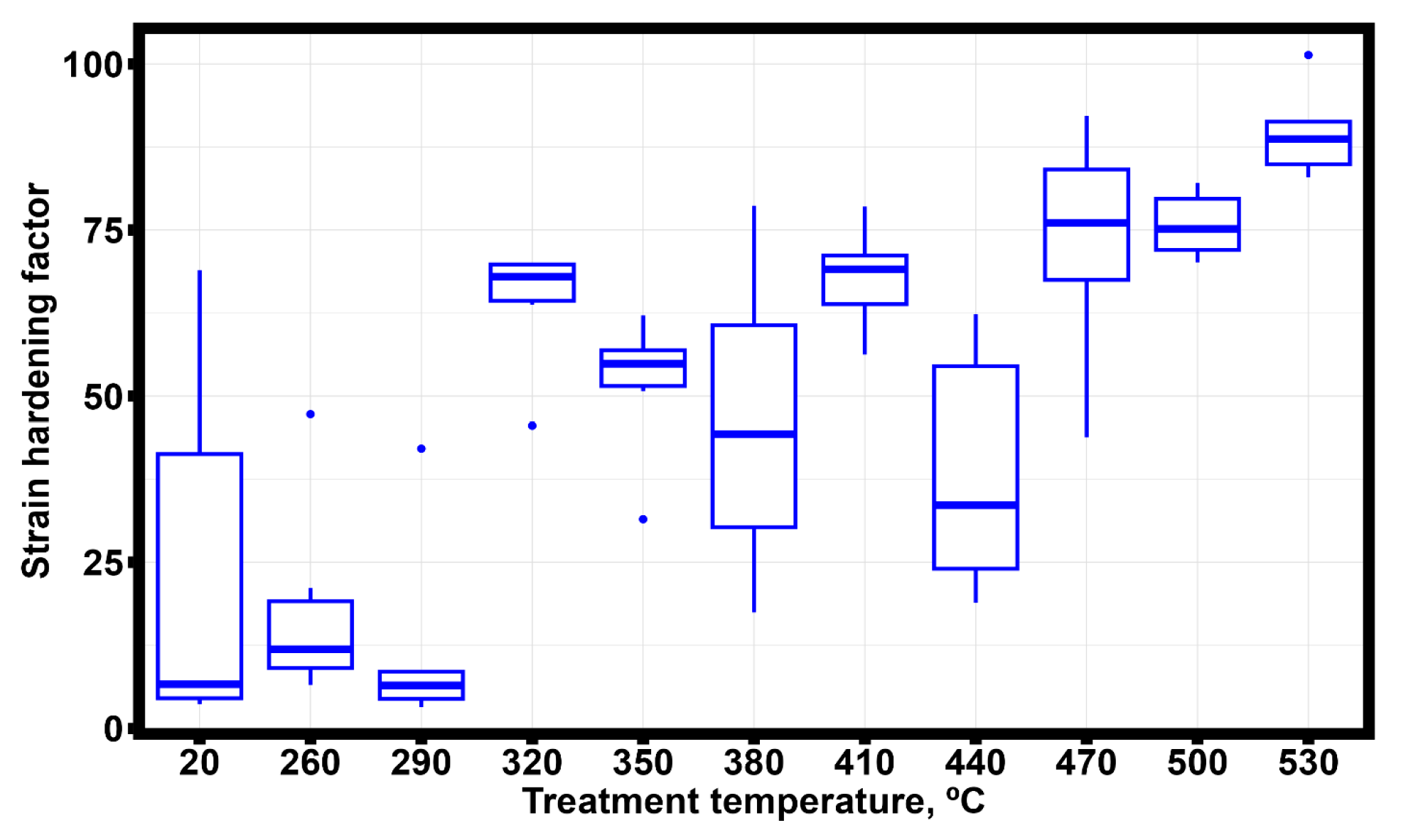
3. Results and Discussion
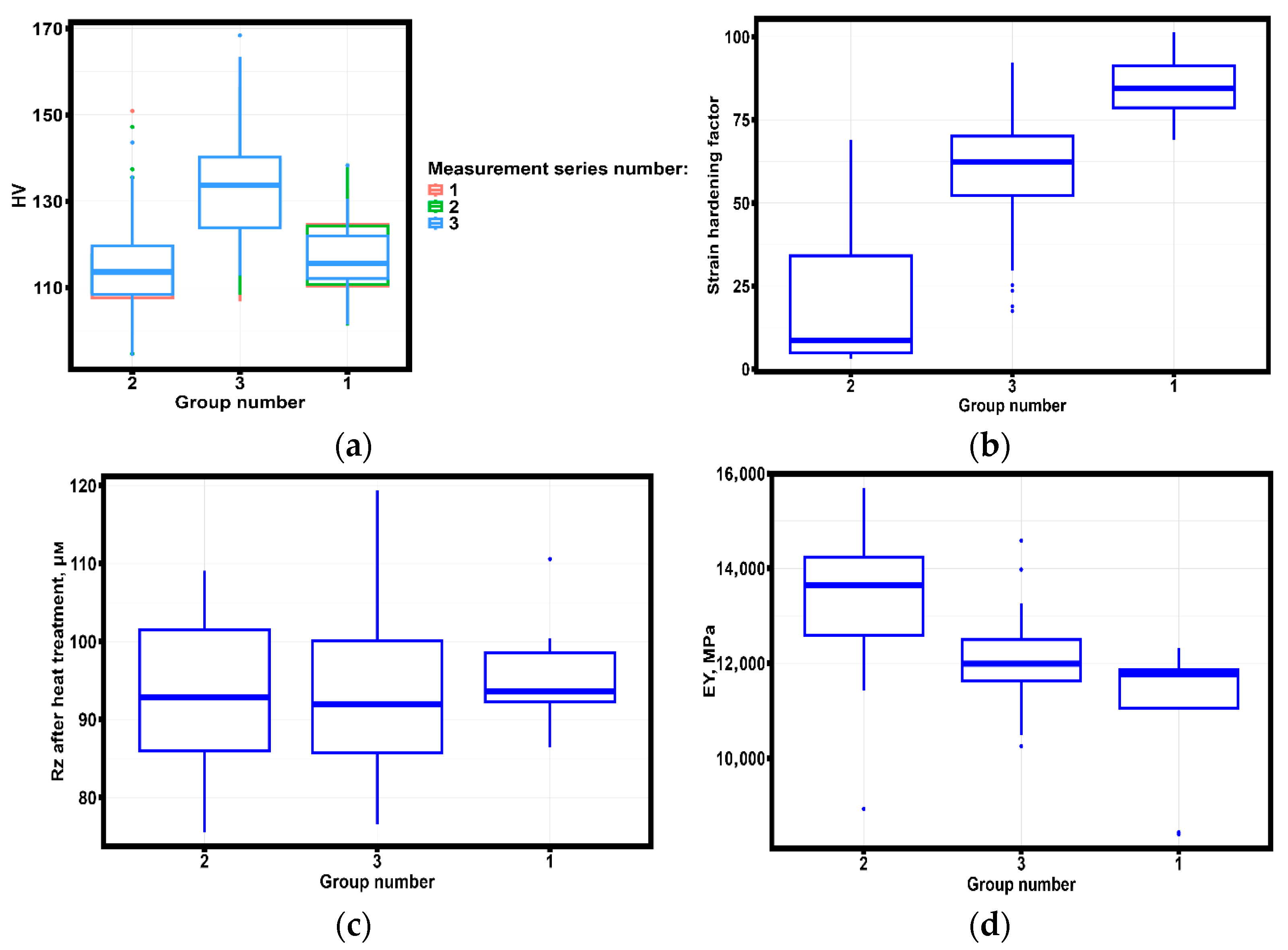
3.1. Experimental Results of the Samples
3.2. Statistical Analysis of Results
3.3. Discussion
4. Conclusions
- Heat treatment of thin-walled samples obtained using SLM technology from an Al-Mn-Mg-Ti-Zr alloy at a temperature of 530 °C for one hour allows maximum strain hardening to be achieved.
- Heat treatment at 530 °C for one hour of thin-walled samples significantly reduced the number of observed microcracks and macropores.
- At a heat treatment temperature of 530 °C for one hour, titanium and zirconium are released from the solid solution in combination with dispersion strengthening due to the formation of intermetallic phases.
- The nonlinear change in microhardness shows a peak in hardness in the treatment range of 320–500 °C and a decrease at 530 °C, which may be associated with the formation of nanoscale inclusions of intermetallic phases of the composition Al3 (Ti, Zr) inclusions with an L12 crystallographic structure and a subsequent increase in their size. This conclusion is consistent with the direct and inverse Hall–Petch law.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Symbol | Abbreviation | ||
| T | annealing temperature, [°C] | HV_1 | First series of Vickers microhardness measurement |
| EY | Young’s modulus, [MPa] | HV_2 | Second series of Vickers microhardness measurement |
| ET | Secant modulus, [MPa] | HV_3 | Third series of Vickers microhardness measurement |
| σ0.2 | Yield strength, [MPa] | Criter. | Criterion |
| σB | ultimate tensile strength, [MPa] | Norm. | Normal |
| εB | tensile strain [%] | LgNor. | Log-Normal |
| ε0.2 | yield strain, [%] | Log. | Logistic |
| Ra | arithmetic average roughness, [μm] | Exp. | Exponential |
| Rz | Ten-point Height of Irregularities, [μm] | D | Kolmogorov–Smirnov parameter |
| Rmax | Maximum Roughness Depth, [μm] | № | Sample number |
References
- ISO/ASTM 52900:2015 [ASTM F2792]; International Organization for Standardization. Additive Manufacturing-General Principles-Terminology. ISO: Geneva, Switzerland, 2015.
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Tecnologies. In 3D Printing, Rapid Prototyping and Direct Digital Manufacturing, 2nd ed.; Springer: New York, NY, USA, 2015; Volume 648. [Google Scholar] [CrossRef]
- Borgue, R. 3D printing: The dawn of a new era in manufacturing? Assem. Autom. 2013, 33, 307–311. [Google Scholar] [CrossRef]
- Tofail, S.A.M.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- Lee, J.M.; Sing, S.L.; Zhou, M.M.; Yeong, W.Y. 3D bioprinting processes: A perspective on classification and terminology. Int. J. Bioprint. 2018, 4, 151. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic componentseprocess, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Haubrich, J.; Gussone, J.; Barriobero-Vila, P.; Kürnsteiner, P.; Jägle, E.A.; Raabe, D.; Schell, N.; Requena, G. The role of lattice defects, element partitioning and intrinsic heat effects on the microstructure in selective laser melted Ti-6Al-4V. Acta Mater. 2019, 167, 136–148. [Google Scholar] [CrossRef]
- Tian, Q. The development status of selective laser melting technology (SLM). J. Phys. Conf. Ser. 2021, 1798, 012045. [Google Scholar] [CrossRef]
- Kaufman, J.G. Properties of Aluminum Alloys: Tensile, Creep, and Fatigue Data at High and Low Temperatures; ASM International: Warren, MI, USA, 1999. [Google Scholar]
- Polmear, I.J.; Couper, M.J. Design and development of an experimental wrought aluminum alloy for use at elevated temperatures. Metall. Trans. A 1988, 19, 1027–1035. [Google Scholar] [CrossRef]
- Wang, G.S.; Liu, K.; Wang, S.L. Evolution of Elevated-Temperature Strength and Creep Resistance during Multi-Step Heat Treatments in Al-Mn-Mg Alloy. Materials 2018, 11, 1158. [Google Scholar] [CrossRef]
- Van Dalen, M.E.; Gyger, T.; Dunand, D.C.; Seidman, D.N. Effects of Yb and Zr microalloying additions on the microstructure and mechanical properties of dilute Al–Sc alloys. Acta Mater. 2011, 59, 7615–7626. [Google Scholar] [CrossRef]
- Lai, J.; Zhang, Z.; Chen, X.-G. The thermal stability of mechanical properties of Al–B4C composites alloyed with Sc and Zr at elevated temperatures. Mater. Sci. Eng. A 2012, 532, 462–470. [Google Scholar] [CrossRef]
- Farkoosh, A.R.; Grant Chen, X.; Pekguleryuz, M. Dispersoid strengthening of a high temperature Al–Si–Cu–Mg alloy via Mo addition. Mater. Sci. Eng. A 2015, 620, 181–189. [Google Scholar] [CrossRef]
- Liu, K.; Ma, H.; Chen, X.-G. Enhanced elevated-temperature properties via Mo addition in Al-Mn-Mg 3004 alloy. J. Alloys Compd. 2017, 694, 354–365. [Google Scholar] [CrossRef]
- Mikhaylovskaya, A.V.; Portnoy, V.K.; Mochugovskiy, A.G.; Zadorozhnyy, M.Y.; Tabachkova, N.Y.; Golovin, I.S. Effect of homogenisation treatment on precipitation, recrystallisation and properties of Al–3% Mg–TM alloys (TM = Mn, Cr, Zr). Mater. Design 2016, 109, 197–208. [Google Scholar] [CrossRef]
- Engler, O.; Liu, Z.; Kuhnke, K. Impact of homogenization on particles in the Al–Mg–Mn alloy AA 5454–Experiment and simulation. J. Alloys Compd. 2013, 560, 111–122. [Google Scholar] [CrossRef]
- Radetić, T.; Popović, M.; Romhanji, E. Microstructure evolution of a modified AA5083 aluminum alloy during a multistage homogenization treatment. Mater. Charact. 2012, 65, 16–27. [Google Scholar] [CrossRef]
- Engler, O.; Miller-Jupp, S. Control of second-phase particles in the Al-Mg-Mn alloy AA 5083. J. Alloys Compd. 2016, 689, 998–1010. [Google Scholar] [CrossRef]
- Engler, O.; Kuhnke, K.; Hasenclever, J. Development of intermetallic particles during solidification and homogenization of two AA 5xxx series Al-Mg alloys with different Mg contents. J. Alloys Compd. 2017, 728, 669–681. [Google Scholar] [CrossRef]
- Cadek, J. Creep in precipitation- and dispersion-strengthened alloys (a review). Met. Mater. 1991, 29, 385–398. [Google Scholar]
- Knipling, K.E.; Dunand, D.C.; Seidman, D.N. Criteria for developing castable, creep-resistant aluminum-based alloys—A review. Int. J. Mater. Res. 2022, 97, 246–265. [Google Scholar] [CrossRef]
- Zhu, A.W.; Gable, B.M.; Shiflet, G.J.; Starke, E.A., Jr. The Intelligent Design of High Strength, Creep-Resistant Aluminum Alloys. MSF 2002, 396–402, 21–30. [Google Scholar] [CrossRef]
- Knipling, K.E.; Dunand, D.C. Creep resistance of cast and aged Al–0.1 Zr and Al–0.1 Zr–0.1 Ti (at.%) alloys at 300–400 °C. Scr. Mater. 2008, 59, 387–390. [Google Scholar] [CrossRef]
- Krug, M.E.; Dunand, D.C. Modeling the creep threshold stress due to climb of a dislocation in the stress field of a misfitting precipitate. Acta Mater. 2011, 59, 5125–5134. [Google Scholar] [CrossRef]
- Marquis, E.A.; Dunand, D.C. Model for creep threshold stress in precipitation-strengthened alloys with coherent particles. Scr. Mater. 2002, 47, 503–508. [Google Scholar] [CrossRef]
- Kittel, C.; McEuen, P. Introduction to Solid State Physics; Global, Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; 720p. [Google Scholar]
- Abuzin, Y.A.; Nikitin, N.Y. Determination of promising areas of research in the field of aluminum-based alloys using the electronic theory of metals. Non-Ferr. Met. 2012, 4, 74–77. [Google Scholar]
- Nikitin, N.Y. A first-principles investigation of the effect of relaxation on the alloy formation in the aluminum-3d-transition-metal system. Phys. Met. Metallogr. 2012, 113, 427–437. [Google Scholar] [CrossRef]
- Huang, H.; Huang, Y.; Zhang, H. Dissolution and Precipitation Behavior of the γ′ Phase During Heat Treatment of the Nickel-Based High-Temperature Alloy K444. JOM 2025, 77, 7655–7667. [Google Scholar] [CrossRef]
- Grigoriev, S.; Nikitin, N.; Yanushevich, O.; Krikheli, N.; Khmyrov, R.; Strunevich, D.; Soloninkin, M.; Pinargote, N.W.S.; Peretyagin, P.; Smirnov, A. Mechanical properties variation of samples fabricated by fused deposition additive manufacturing, as a function of filler percentage and structure for different plastics. Sci. Rep. 2024, 14, 28344. [Google Scholar] [CrossRef]
- Nandhakumar, R.; Venkatesan, K. A process parameters review on selective laser melting-based additive manufacturing of single and multi-material: Microstructure, physical properties, tribological, and surface roughness. Mater. Today Comm. 2023, 35, 105538. [Google Scholar] [CrossRef]
- Pal, S.; Drstvensek, I.; Brajlih, T. Physical Behaviors of Materials in Selective Laser Melting Process, Chapter 21. In DAAAM International Scientific Book; Katalinic, B., Ed.; DAAAM International: Vienna, Austria, 2018; pp. 239–256. [Google Scholar] [CrossRef]
- Zhang, X.; Yocom, C.J.; Mao, B.; Liao, Y. Microstructure evolution during selective laser melting of metallic materials: A review. J. Laser Appl. 2019, 31, 031201. [Google Scholar] [CrossRef]
- Li, R.; Shi, Y.; Wang, Z.; Wang, L.; Liu, J.; Jiang, W. Densification behavior of gas and water atomized 316L stainless steel powder during selective laser melting. Appl. Surf. Sci. 2010, 256, 4350–4356. [Google Scholar] [CrossRef]
- Eos. info. Available online: https://www.eos.info/var/assets/03_system-related-assets/material-related-contents/metal-materials-and-examples/metal-material-datasheet/titan/ti64/eos_ti64_9011-0014_9011-0039_m290_mds_06-22_en.pdf (accessed on 17 October 2025).
- Agile-Manufacturing.com. Available online: https://agile-manufacturing.com/wp-content/uploads/2017/11/aluminum.pdf (accessed on 17 October 2025).
- Grigoriev, S.N.; Nikitin, N.; Yanushevich, O.; Kriheli, N.; Kramar, O.; Khmyrov, R.; Idarmachev, I.; Peretyagin, P. Experimental and Statistical Analysis of the Effect of Heat Treatment on Surface Roughness and Mechanical Properties of Thin-Walled Samples Obtained by Selective Laser Melting from the Material AlSi10Mg. Materials 2023, 16, 7326. [Google Scholar] [CrossRef]
- DIN 50125; Testing of Metallic Materials—Tensile Pieces. DIN Standards Committee for Materials Testing (NMP): Berlin, Germany, 2016.
- Liu, C.; Liu, T.; Wang, T.; Liu, W.; Ma, Y. Effects of heat treatment on the microstructure and properties of graded-density powder aluminum alloys. Metal Sci. Heat Treat. 2022, 63, 590–598. [Google Scholar] [CrossRef]
- Kammer, C. Aluminum and aluminum alloys. In Springer Handbook of Materials Data, 2nd ed.; Warlimont, H., Martienssen, W., Eds.; Springer International Publishing: New York, NY, USA, 2018; pp. 161–197. [Google Scholar]
- Snopiński, P.; Woźniak, A.; Pagáč, M. Microstructural Evolution, Hardness, and Strengthening Mechanisms in SLM AlSi10Mg Alloy Subjected to Equal-Channel Angular Pressing (ECAP). Materials 2021, 14, 7598. [Google Scholar] [CrossRef]
- ASTM E92-17; Standard Test Methods for Vickers Hardness and Knoop Hardness of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2017.
- Shelekhov, E.V.; Sviridova, T.A. Programs for X-ray analysis of polycrystals. Metal Sci. Heat Treat. 2000, 42, 309–313. [Google Scholar] [CrossRef]
- Grazulis, S.; Chateigner, D.; Downs, R.T.; Yokochi, A.T.; Quiros, M.; Lutterotti, L.; Manakova, E.; Butkus, J.; Moeck, P.; Bail, A. Crystallography open database an open-accesscollection of crystal structures. J. Appl. Cryst. 2009, 42, 726–729. [Google Scholar] [CrossRef]
- Beyer, H. Tukey, John W.: Exploratory Data Analysis. Addison-Wesley Publishing Company Reading, Mass.—Menlo Park, Cal., London, Amsterdam, Don Mills, Ontario, Sydney 1977, XVI, 688 S. Biom. J. 1981, 23, 413–414. [Google Scholar] [CrossRef]
- Rossi, R.J. Mathematical Statistics: An Introduction to Likelihood Based Inference; John Wiley & Sons: Hoboken, NJ, USA, 2018; 422p. [Google Scholar] [CrossRef]
- Akaike, H. On entropy maximization principle. In Applications of Statistics; Krishnaiah, P.R., Ed.; North-Holland: Amsterdam, The Netherlands, 1977; p. 27. [Google Scholar]
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Akaike Information Criterion Statistics; D. Reidel: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Neath, A.A.; Cavanaugh, J.E. The Bayesian information criterion: Background, derivation, and applications. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 199–203. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality. Biom. Trust 1965, 52, 591–611. [Google Scholar] [CrossRef]
- D’agostino, R.B.; Pearson, E.S. Tests for Departure from Normality. Empirical Results for the Distributions of b2 and √b1. Biometrika 1973, 60, 613–622. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Sulla determinazione empirica di une legge di distribuzione. G. Ist. Ital. Attuari 1933, 4, 83–91. [Google Scholar]
- Anderson, T.W. On the Distribution of the Two-Sample Cramer-von Mises Criterion. Ann. Math. Statist. 1962, 33, 1148–1159. [Google Scholar] [CrossRef]
- Araújo-Neto, V.G.; Sebold, M.; Castro, E.F.; Feitosa, V.P.; Giannini, M. Evaluation of physico-mechanical properties and filler particles characterization of conventional, bulk-fill, and bioactive resin-based composites. J. Mech. Behav. Biomed. Mater. 2021, 115, 104288. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Dunnett, C.W. New tables for multiple comparisons with a control. Biometrics 1964, 20, 482–491. [Google Scholar] [CrossRef]
- Bonferroni, C.E. Teoria Statistica Delle Classi e Calcolo Delle Probabilità; Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commerciali di Firenze: Florence, Italy, 1936. [Google Scholar]
- Nielsen, F. Introduction to HPC with MPI for Data Science; Springer: New York, NY, USA, 2016. [Google Scholar]
- Pearson, K. VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. In Studies in Individual Differences: The Search for Intelligence; Jenkins, J.J., Paterson, D.G., Eds.; Appleton-Century-Crofts: New York, NY, USA, 1961; pp. 45–58. [Google Scholar] [CrossRef]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences; Thomson Brooks/Cole Publishing Co.: Pacific Grove, CA, USA, 1996. [Google Scholar]
- Grigoriev, S.N.; Nikitin, N.Y.; Frolov, A.; Shapovalov, P.; Medeltsev, A.; Voronov, M.; Khmyrov, R.; Idarmachev, I.; Peretyagin, P. Modeling of Tensile Stress Distribution Considering Anisotropy of Mechanical Properties of Thin-Walled AlSi10Mg Samples Obtained by Selective Laser Melting. J. Manuf. Mater. Process. 2024, 8, 235. [Google Scholar] [CrossRef]
- Lu, C.; Danzer, R.; Fischer, F.D. Fracture statistics of brittle materials: Weibull or normal distribution. Phys. Rev. E 2002, 65, 067102. [Google Scholar] [CrossRef]
- Waqar, S.; Guo, K.; Sun, J. Evolution of residual stress behavior in selective laser melting (SLM) of 316L stainless steel through preheating and in-situ re-scanning techniques. Opt. Laser Technol. 2022, 149, 107806. [Google Scholar] [CrossRef]
- Weibull, W. Fatigue Testing and Analysis of Results; Pergamon Press: New York, NY, USA, 1961; p. 236. [Google Scholar]
- Razumovskiy, V.I.; Ruban, A.V.; Razumovskii, I.M.; Lozovoi, A.Y.; Butrim, V.N.; Vekilov, Y.K. The effect of alloying elements on grain boundary and bulk cohesion in aluminum alloys: An ab initio study. Scr. Mater. 2011, 65, 926–929. [Google Scholar] [CrossRef]
- Razumovskiy, V.I.; Razumovskii, I.M.; Ruban, A.V.; Butrim, V.N.; Vekilov, Y.K. The influence of alloying elements on grain boundary and bulk cohesion in aluminum alloys: Ab initio study. Adv. Mater. Res. 2012, 409, 417–422. [Google Scholar] [CrossRef]
- Razumovskiy, V.I.; Vekilov, Y.K.; Razumovskii, I.M.; Ruban, A.V.; Butrim, V.N.; Mironenko, V.N. Effect of alloying elements and impurities on interface properties in aluminum alloys. Phys. Solid State 2011, 53, 2189–2193. [Google Scholar] [CrossRef]
- Spierings, A.B.; Dawson, K.; Kern, K.; Palm, F.; Wegener, K. SLM-processed Sc- and Zr- modified Al-Mg alloy: Mechanical properties and microstructural effects of heat treatment. Mater. Sci. Eng. A 2017, 701, 264–273. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Shi, Y.; Fei, Q.; Zhao, N.; Ni, C.; Wu, J.; Dong, Y.; Dai, T.; Ding, H.; et al. An SLM-processed Er-and Zr-modified Al–Mg alloy: Microstructure and mechanical properties at room and elevated temperatures. Mater. Sci. Eng. A 2023, 883, 145485. [Google Scholar] [CrossRef]
- Bharat, B.; Nosonovsky, M. Scale effect in mechanical properties and tribology. In Nanotribology and Nanomechanics: An Introduction; Springer International Publishing: New York, NY, USA, 2017; pp. 549–589. [Google Scholar]
- Kempf, A.; Hilgenberg, K. Influence of heat treatments on AlSi10Mg specimens manufactured with different laser powder bed fusion machines. Mater. Sci. Eng. A 2021, 818, 141371. [Google Scholar] [CrossRef]
- Mertens, A.; Delahaye, J.; Dedry, O.; Vertruyen, B.; Tchuindjang, J.T.; Habraken, A.M. Microstructure and properties of SLM AlSi10Mg: Under-standing the influence of the local thermal history. Procedia Manuf. 2020, 47, 1089–1095. [Google Scholar] [CrossRef]
- Maamoun, A.H.; Elbestawi, M.; Dosbaeva, G.K.; Veldhuis, S.C. Thermal post-processing of AlSi10Mg parts produced by Selective Laser Melting using recycled powder. Addit. Manuf. 2018, 21, 234–247. [Google Scholar] [CrossRef]
- Naik, S.N.; Stephen, M.W. The Hall–Petch and inverse Hall–Petch relations and the hardness of nanocrystalline metals. J. Mater. Sci. 2020, 55, 2661–2681. [Google Scholar] [CrossRef]
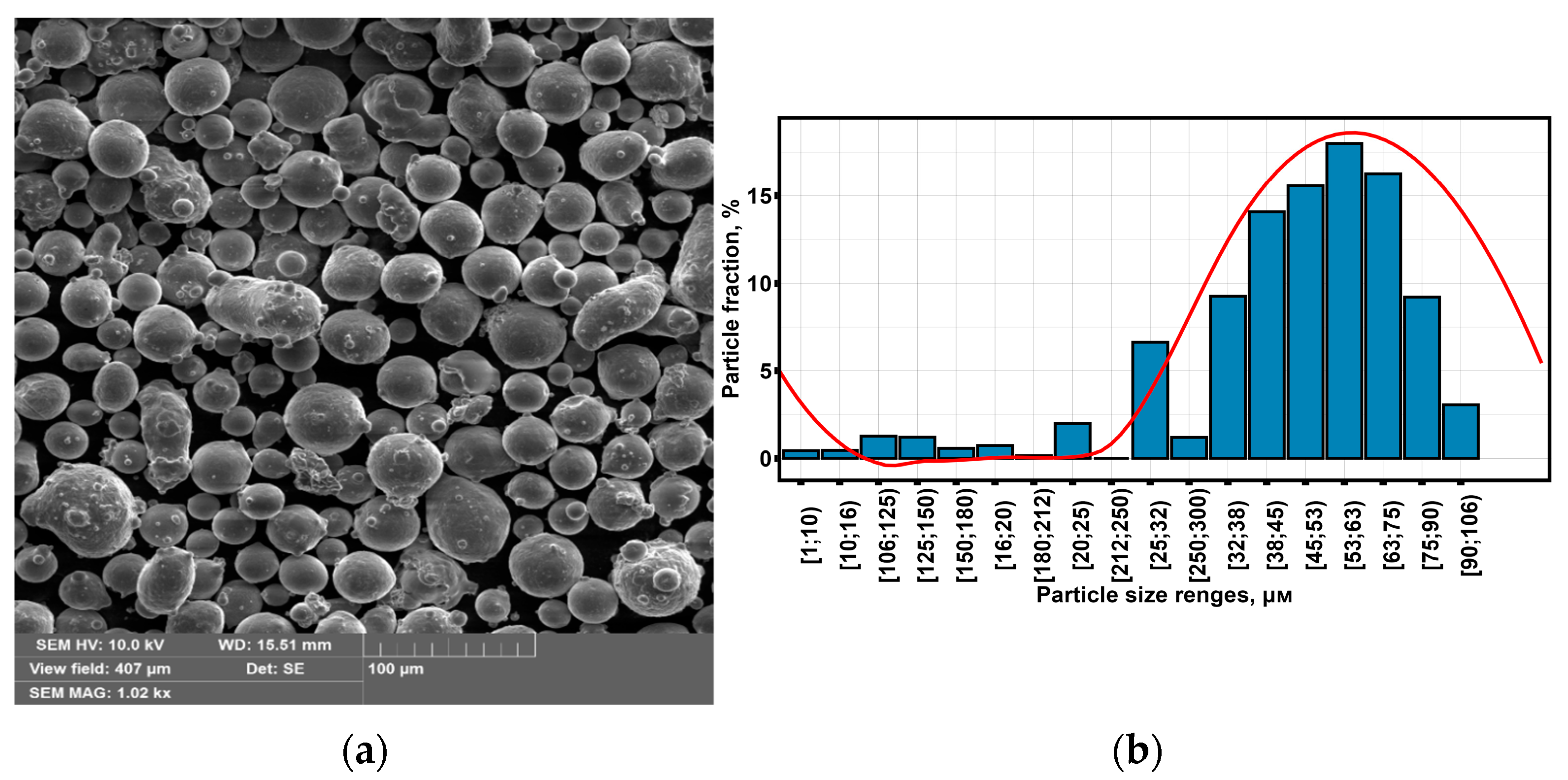


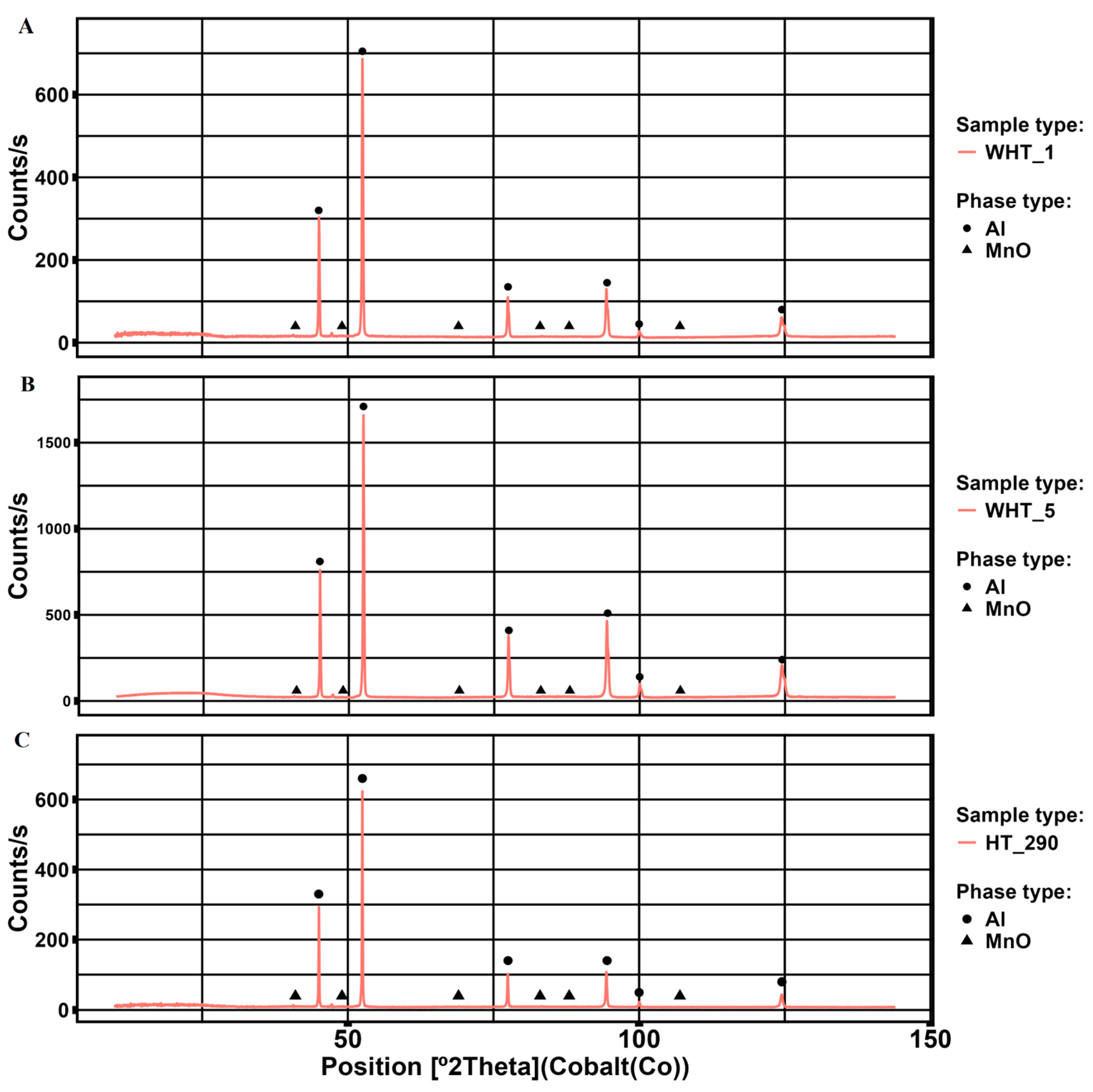
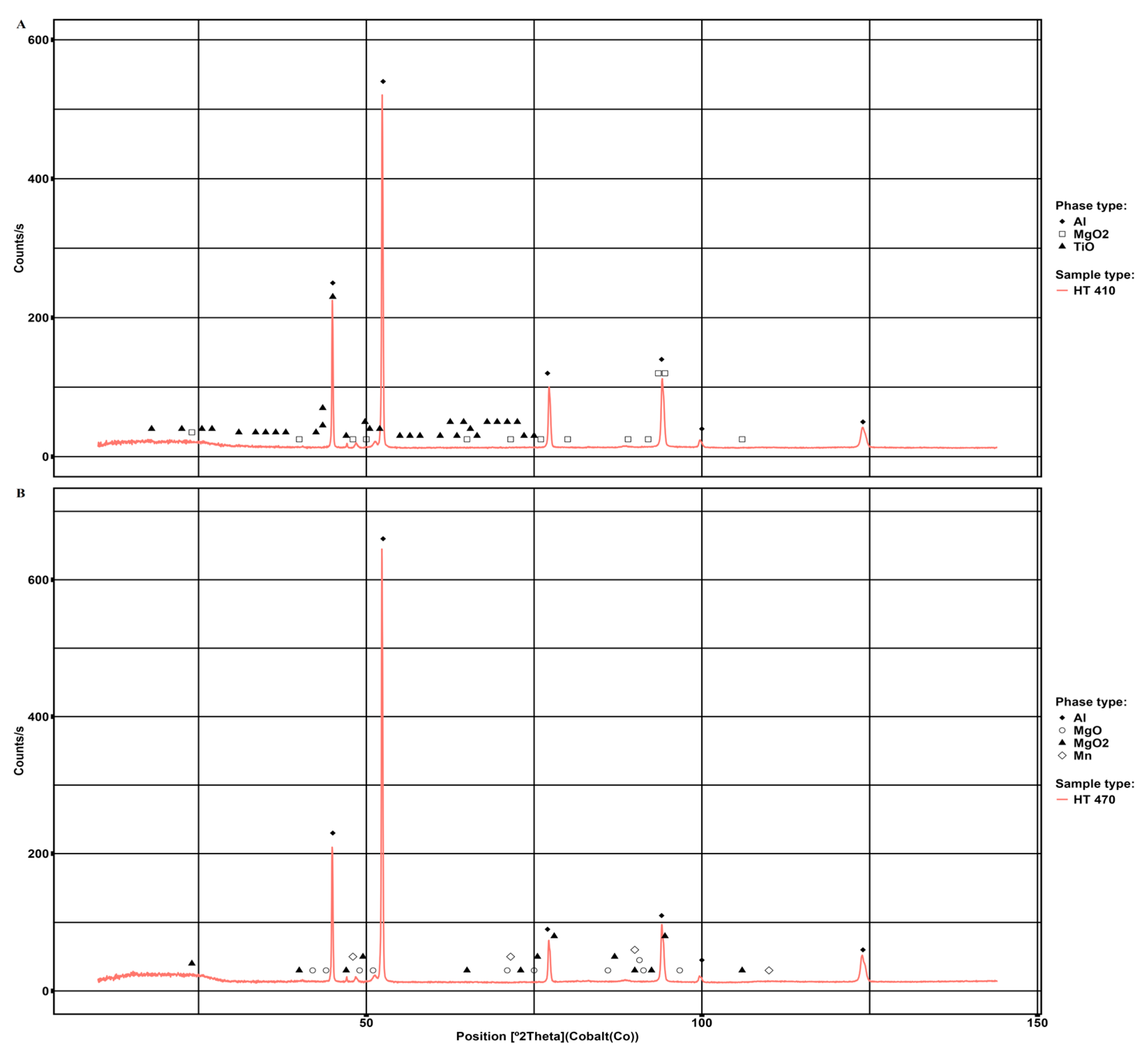
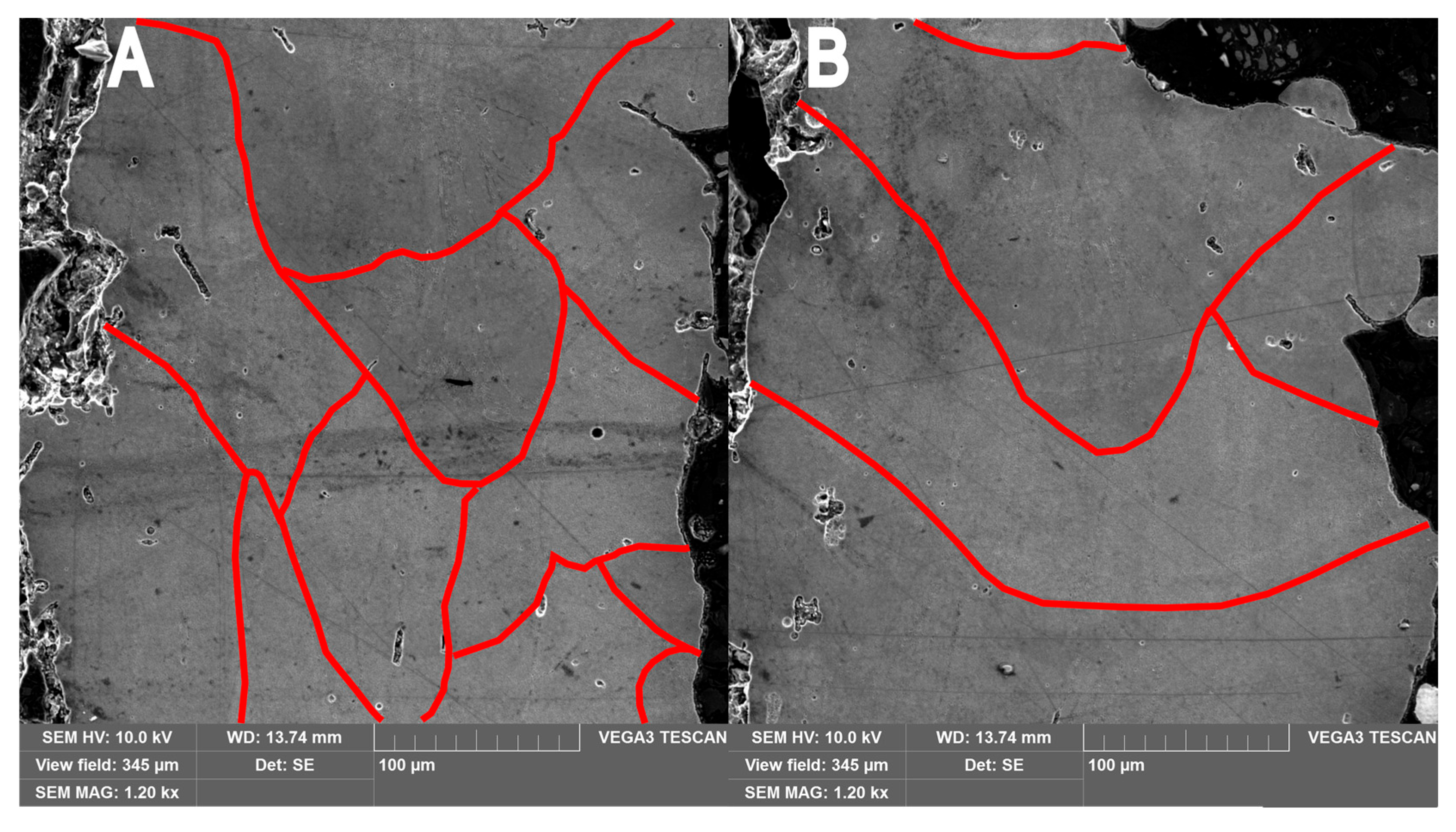
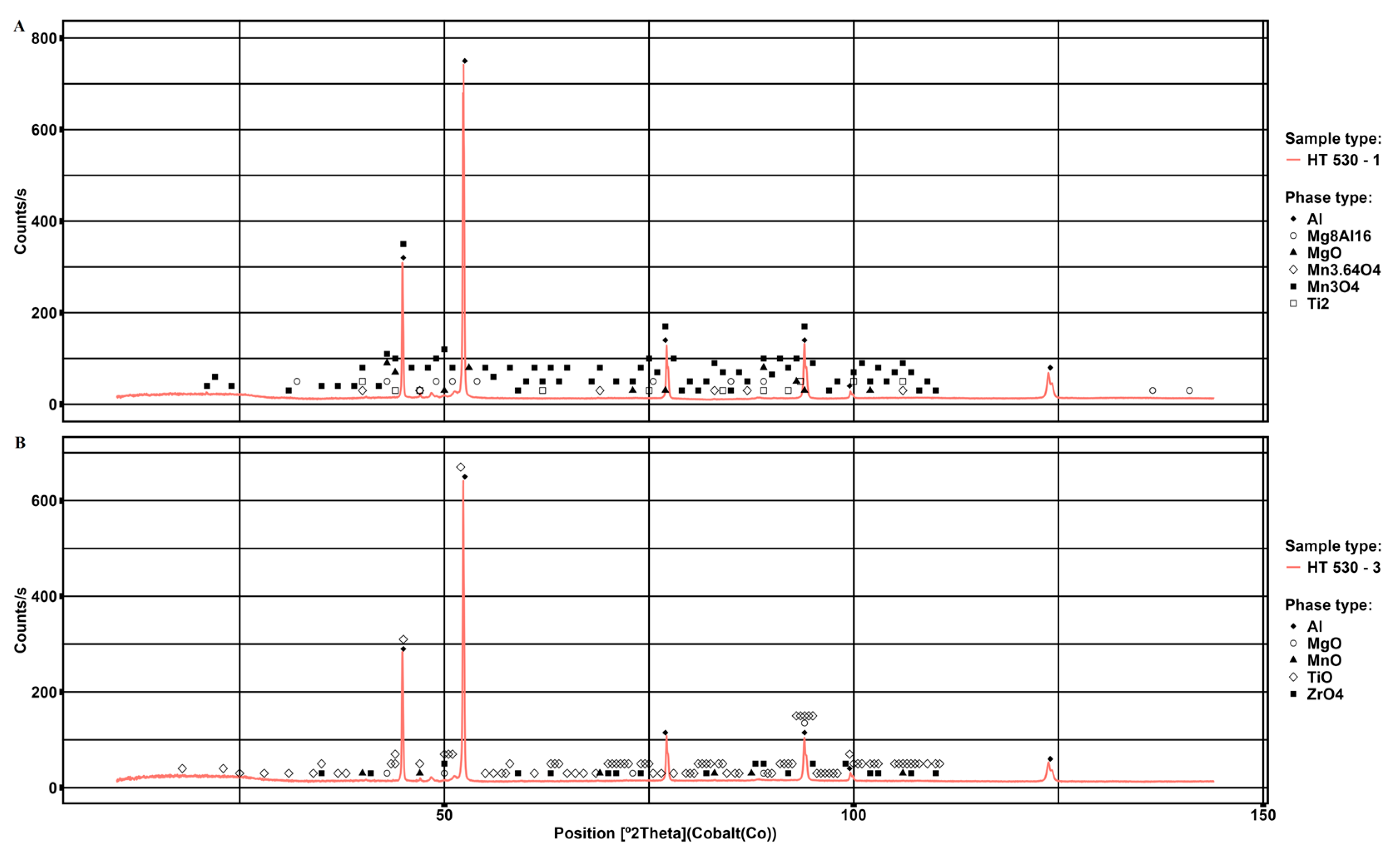

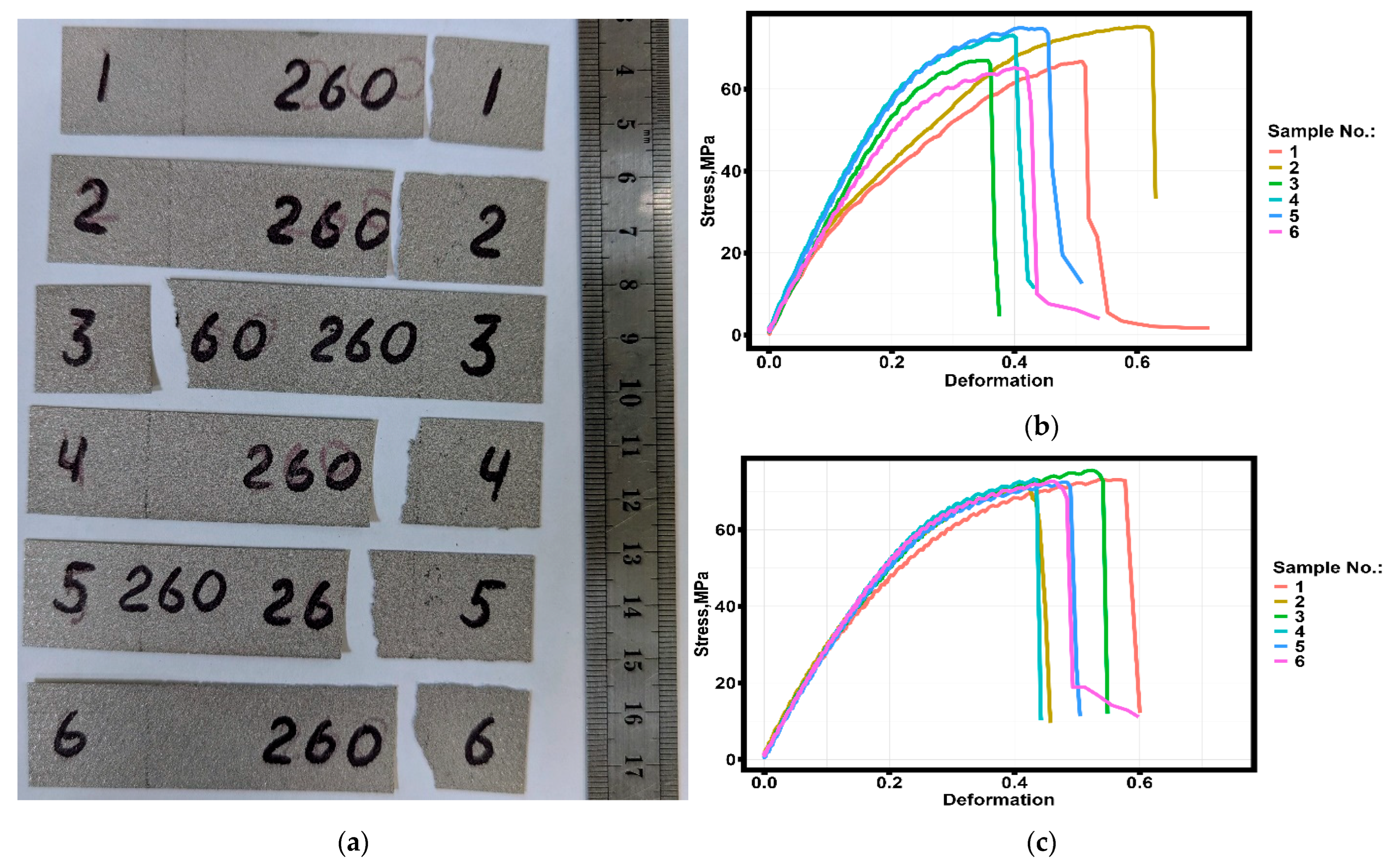
| Measurement Series | Element Content, % wt. | ||||
|---|---|---|---|---|---|
| Al | Mn | Mg | Zr | Ti | |
| 1 | 94.34 | 3.04 | 2.39 | 0.14 | 0.09 |
| 2 | 93.97 | 3.53 | 2.27 | 0.11 | 0.12 |
| 3 | 93.61 | 3.78 | 2.41 | 0.09 | 0.11 |
| Laser Power, W | Spot Diameter, μm | Scan Speed, mm/s | Average Particle Size, μm | Thickness Layer, μm | Atmosphere | Platform Temperature, °C |
|---|---|---|---|---|---|---|
| 400 | 100 | ~7000 | 90 | 20 | Argon | 35 |
| Step | Abrasive | Time, min |
|---|---|---|
| Grinding | SiC (sanding paper 180P) | 1 |
| SiC (sanding paper 800P) | 1 | |
| SiC (sanding paper 1200P) | 1 | |
| Polishing | Diamond paste slurry: 9 MKM | 4 |
| Diamond paste slurry: 3 MKM | 3 | |
| Diamond paste slurry: 1 MKM | 2 | |
| Chemical etching | Keller’s reagent | — |
| T | EY | ET | σ0.2 | σB | εB | ε0.2 |
|---|---|---|---|---|---|---|
| - | 12,776.500 ±3295.888 | 15,083.680 ±2009.623 | 66.869 ±5.114 | 69.877 ±5.126 | 0.803 ±0.410 | 0.466 ±0.096 |
| 260 | 12,816.200 ±844.506 | 15,693.180 ±362.379 | 68.457 ±1.486 | 73.030 ±1.513 | 0.861 ±0.282 | 0.449 ±0.021 |
| 290 | 13,830.600 ±390.981 | 15,955.300 ±272.271 | 70.061 ±1.477 | 72.434 ±2.111 | 0.940 ±0.366 | 0.515 ±0.058 |
| 320 | 12,624.810 ±483.839 | 15,617.230 ±289.902 | 61.270 ±0.640 | 67.857 ±0.332 | 0.473 ±0.034 | 0.367 ±0.013 |
| 350 | 14,009.450 ±1156.348 | 16,189.620 ±1051.402 | 64.449 ±2.078 | 69.284 ±3.338 | 0.495 ±0.075 | 0.392 ±0.015 |
| 380 | 12,269.020 ±210.441 | 15,493.390 ±313.333 | 62.523 ±1.922 | 69.801 ±3.623 | 0.618 ±0.192 | 0.387 ±0.010 |
| 410 | 11,524.460 ±283.668 | 14,770.560 ±396.665 | 61.451 ±1.321 | 67.956 ±2.370 | 0.467 ±0.031 | 0.369 ±0.012 |
| 440 | 12,202.780 ±429.954 | 15,636.570 ±409.780 | 64.761 ±1.104 | 72.798 ±0.870 | 0.659 ±0.144 | 0.396 ±0.015 |
| 470 | 11,721.180 ±504.737 | 15,091.690 ±752.384 | 62.704 ±1.778 | 68.182 ±2.777 | 0.461 ±0.064 | 0.375 ±0.013 |
| 500 | 10,789.990 ±1408.964 | 14,600.230 ±1516.584 | 61.079 ±1502 | 68.994 ±1844 | 0.463 ±0.027 | 0.357 ±0.012 |
| 530 | 11,727.070 ±424.822 | 15,145.230 ±383.635 | 57.068 ±1.895 | 64.107 ±2.835 | 0.410 ±0.030 | 0.330 ±0.014 |
| T | Before Annealing, μm | After Annealing, μm | ||||
|---|---|---|---|---|---|---|
| Ra | Rz | Rmax | Ra | Rz | Rmax | |
| 260 | 14.408 ±0.971 | 93.559 ±9.990 | 111.892 ±8.094 | 13.185 ±1.471 | 87.780 ±9.264 | 108.369 ±22.602 |
| 290 | 14.105 ±2.894 | 93.074 ±13.879 | 110.716 ±13.960 | 13.938 ±1.706 | 91.890 ±11.111 | 114.843 ±11.632 |
| 320 | 14.645 ±1.528 | 91.271 ±6.353 | 117.631 ±16.349 | 14.309 ±1.513 | 91.408 ±8.681 | 108.221 ±11.031 |
| 350 | 15.061 ±1.464 | 97.751 ±10.108 | 114.300 ±11.022 | 14.284 ±1.027 | 92.960 ±9.054 | 113.142 ±17.563 |
| 380 | 15.402 ±1.269 | 96.658 ±7.386 | 120.633 ±12.498 | 15.225 ±1.967 | 93.548 ±12.394 | 121.983 ±28.169 |
| 410 | 15.293 ±0.769 | 95.954 ±4.055 | 119.123 ±12.900 | 15.444 ±1.476 | 96.056 ±9.410 | 118.419 ±18.536 |
| 440 | 13.728 ±1.574 | 90.125 ±10.612 | 117.430 ±17.373 | 15.357 ±0.806 | 97.466 ±6.698 | 118.456 ±12.875 |
| 470 | 13.997 ±1.346 | 95.423 ±5.493 | 123.366 ±11.815 | 14.487 ±1.800 | 100.425 ±11.656 | 119.877 ±12.952 |
| 500 | 14.108 ±0.953 | 98.126 ±9.591 | 116.231 ±14.169 | 13.903 ±1.686 | 89.612 ±12.520 | 109.916 ±13.766 |
| 530 | 14.198 ±1.286 | 96.750 ±11.517 | 119.667 ±15.311 | 14.228 ±0.704 | 93.777 ±4.160 | 112.182 ±8.903 |
| T | HV_1 | HV_2 | HV_3 |
|---|---|---|---|
| - | 109.923 ± 7.852 | 108.120 ± 13.070 | 109.595 ± 10.934 |
| 260 | 107.970 ± 6.659 | 112.833 ± 6.042 | 109.900 ± 4.021 |
| 290 | 113.433 ± 5.366 | 111.933 ± 6.659 | 117.200 ± 7.194 |
| 320 | 120.567 ± 7.887 | 119.383 ± 5.626 | 124.267 ± 5.133 |
| 350 | 130.117 ± 10.974 | 134.300 ± 16.065 | 135.450 ± 18.544 |
| 380 | 133.367 ± 11.303 | 132.150 ± 11.454 | 130.717 ± 11.199 |
| 410 | 135.417 ± 12.979 | 133.583 ± 14.617 | 129.683 ± 13.406 |
| 440 | 137.950 ± 3.348 | 135.850 ± 5.000 | 138.350 ± 3.662 |
| 470 | 130.483 ± 13.691 | 130.383 ± 6.406 | 136.050 ± 5.852 |
| 500 | 133.967 ± 10.129 | 142.367 ± 11.3945 | 140.767 ± 11.890 |
| 530 | 111.650 ± 8.918 | 112.450 ± 7.748 | 112.818 ± 7.113 |
| Parameter | Criter. | Distribution Law | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Norm. | LgNor. | Log. | Gamma | Weibull | Exp. | Gumbel | Cauchy | ||
| EY | Akaike | 543.022 | 546.942 | 539.581 | 545.189 | 546.899 | 770.173 | 561.671 | 550.118 |
| Bayes | 547.401 | 551.322 | 543.960 | 549.568 | 551.278 | 772.362 | 566.050 | 554.497 | |
| ET | Akaike | 487.725 | 492.355 | 478.043 | 490.666 | 487.627 | 798.782 | 519.767 | 482.978 |
| Bayes | 492.104 | 496.734 | 482.423 | 495.045 | 492.007 | 800.971 | 524.146 | 487.357 | |
| σ0.2 | Akaike | 376.311 | 375.531 | 378.407 | 375.713 | 385.520 | 682.351 | 380.241 | 398.717 |
| Bayes | 380.690 | 379.911 | 382.786 | 380.093 | 389.900 | 684.540 | 384.620 | 403.097 | |
| σB | Akaike | 357.990 | 359.246 | 361.612 | 358.778 | 356.914 | 693.824 | 373.096 | 392.362 |
| Bayes | 362.369 | 363.625 | 365.999 | 363.157 | 361.294 | 696.014 | 377.475 | 396.741 | |
| ε0.2 | Akaike | −176.865 | −191.149 | −188.262 | −186.863 | −157.173 | 13.121 | −205.074 | −196.006 |
| Bayes | −172.486 | −186.770 | −183.882 | −182.484 | −152.793 | 15.311 | −200.695 | −191.627 | |
| εB | Akaike | 11.803 | −24.168 | 2.234 | −14.018 | 4.100 | 67.544 | −26.774 | −31.021 |
| Bayes | 16.182 | −19.789 | 6.613 | −9.639 | 8.479 | 69.734 | −22.394 | −26.642 | |
| HV_1 | Akaike | 539.507 | 538.563 | 542.762 | 538.660 | 545.670 | 770.359 | 541.664 | 568.507 |
| Bayes | 543.887 | 542.942 | 547.142 | 543.040 | 550.049 | 772.548 | 546.043 | 572.887 | |
| HV_2 | Akaike | 546.838 | 546.405 | 550.042 | 546.297 | 552.062 | 771.179 | 550.850 | 577.117 |
| Bayes | 551.218 | 550.784 | 554.421 | 550.676 | 556.441 | 773.369 | 555.230 | 581.497 | |
| HV_3 | Akaike | 543.861 | 542.396 | 545.455 | 542.613 | 553.211 | 772.274 | 545.954 | 572.888 |
| Bayes | 548.241 | 546.776 | 549.835 | 546.992 | 557.590 | 774.464 | 550.333 | 577.267 | |
| Ra * | Akaike | 239.457 | 242.814 | 239.040 | 241.443 | 241.777 | 486.966 | 256.755 | 261.134 |
| Bayes | 243.836 | 247.194 | 243.420 | 245.822 | 246.157 | 489.156 | 261.135 | 265.513 | |
| Ra ** | Akaike | 241.394 | 243.092 | 240.343 | 242.265 | 246.914 | 486.481 | 254.274 | 258.246 |
| Bayes | 245.773 | 247.471 | 244.722 | 246.644 | 251.293 | 488.671 | 258.654 | 262.625 | |
| Rz * | Akaike | 479.917 | 479.245 | 481.351 | 479.281 | 488.437 | 734.804 | 485.079 | 506.335 |
| Bayes | 484.296 | 483.624 | 485.730 | 483.661 | 492.817 | 736.994 | 489.458 | 510.714 | |
| Rz ** | Akaike | 489.237 | 487.736 | 491.981 | 488.052 | 497.673 | 733.049 | 489.731 | 517.015 |
| Bayes | 493.617 | 492.115 | 496.360 | 492.431 | 502.053 | 735.239 | 494.111 | 521.395 | |
| Rmax * | Akaike | 529.931 | 528.558 | 533.977 | 528.815 | 536.285 | 762.389 | 530.644 | 561.836 |
| Bayes | 534.311 | 532.937 | 538.356 | 533.194 | 540.664 | 764.578 | 535.024 | 566.215 | |
| Rmax ** | Akaike | 555.467 | 550.152 | 555.052 | 551.536 | 568.393 | 759.734 | 548.390 | 577.165 |
| Bayes | 559.846 | 554.531 | 559.431 | 555.915 | 572.772 | 761.924 | 552.770 | 581.544 | |
| Parameter | Kolmogorov–Smirnov Statistics | |
|---|---|---|
| p-Value | D * | |
| EY | <0.0000001 | 1.000 |
| ET | <0.0000001 | 1.000 |
| σ0.2 | <0.0000001 | 1.000 |
| σB | <0.0000001 | 1.000 |
| ε0.2 | <0.0000001 | 0.624 |
| εB | <0.0000001 | 0.641 |
| HV_1 | <0.0000001 | 1.000 |
| HV_2 | <0.0000001 | 1.000 |
| HV_3 | <0.0000001 | 1.000 |
| Ra * | <0.0000001 | 1.000 |
| Ra ** | <0.0000001 | 1.000 |
| Rz * | <0.0000001 | 1.000 |
| Rz ** | <0.0000001 | 1.000 |
| Rmax * | <0.0000001 | 1.000 |
| Rmax ** | <0.0000001 | 1.000 |
| Parameter | Comparable Groups | p-Value |
|---|---|---|
| EY | 290–410 °C | 0.0106 |
| 350–410 °C | 0.0150 | |
| 290–500 °C | 0.0078 | |
| 350–500 °C | 0.0112 | |
| ET | 290–410 °C | 0.0489 |
| σ0.2 | 290–320 °C | 1.261 × 10−2 |
| 290–410 °C | 1.897 × 10−2 | |
| 290–500 °C | 9.948 × 10−3 | |
| 20–530 °C | 6.915 × 10−3 | |
| 260–530 °C | 1.855 × 10−4 | |
| 290–530 °C | 1.889 × 10−5 | |
| 440–530 °C | 1.690 × 10−2 | |
| σB | 260–530 °C | 0.003 |
| 290–530 °C | 0.010 | |
| 440–530 °C | 0.003 | |
| ε0.2 | 290–320 °C | 1.219 × 10−2 |
| 290–410 °C | 3.416 × 10−2 | |
| 20–500 °C | 3.610 × 10−2 | |
| 260–500 °C | 4.459 × 10−3 | |
| 290–500 °C | 4.831 × 10−4 | |
| 20–530 °C | 2.208 × 10−3 | |
| 260–530 °C | 1.910 × 10−4 | |
| 290–530 °C | 1.474 × 10−5 | |
| εB | 260–530 °C | 0.001 |
| 290–530 °C | 0.001 | |
| 440–530 °C | 0.013 | |
| HV_1 | 260–410 °C | 0.037 |
| 20–440 °C | 0.011 | |
| 260–440 °C | 0.004 | |
| 290–440 °C | 0.041 | |
| 260–500 °C | 0.046 | |
| 440–530 °C | 0.031 | |
| HV_2 | 20–500 °C | 0.010 |
| 260–500 °C | 0.024 | |
| 290–500 °C | 0.030 | |
| 500–530 °C | 0.021 | |
| HV_3 | 20–440 °C | 0.023 |
| 260–440 °C | 0.009 | |
| 260–470 °C | 0.021 | |
| 20–500 °C | 0.021 | |
| 260–500 °C | 0.008 | |
| 500–530 °C | 0.046 |
| Group 1 | Group 2 | Group 3 | |||
|---|---|---|---|---|---|
| № | T, °C | № | T, °C | № | T, °C |
| 1 | 20 | 2 | 20 | 6 | 20 |
| 4 | 380 | 3 | 20 | 1 | 320 |
| 4 | 500 | 4 | 20 | 2 | 320 |
| 1 | 530 | 5 | 20 | 3 | 320 |
| 2 | 530 | 1 | 260 | 4 | 320 |
| 3 | 530 | 2 | 260 | 5 | 320 |
| 4 | 530 | 3 | 260 | 6 | 320 |
| 5 | 530 | 4 | 260 | 3 | 350 |
| 6 | 530 | 5 | 260 | 4 | 350 |
| --- | --- | 6 | 260 | 5 | 350 |
| --- | --- | 1 | 290 | 6 | 350 |
| --- | --- | 2 | 290 | 1 | 380 |
| --- | --- | 3 | 290 | 2 | 380 |
| --- | --- | 4 | 290 | 3 | 380 |
| --- | --- | 5 | 290 | 5 | 380 |
| --- | --- | 6 | 290 | 6 | 380 |
| --- | --- | 1 | 350 | 1 | 410 |
| --- | --- | 2 | 350 | 2 | 410 |
| --- | --- | 1 | 440 | 3 | 410 |
| --- | --- | 2 | 470 | 4 | 410 |
| --- | --- | --- | --- | 5 | 410 |
| --- | --- | --- | --- | 6 | 410 |
| --- | --- | --- | --- | 1 | 470 |
| --- | --- | --- | --- | 3 | 470 |
| --- | --- | --- | --- | 4 | 470 |
| --- | --- | --- | --- | 5 | 470 |
| --- | --- | --- | --- | 6 | 470 |
| --- | --- | --- | --- | 1 | 500 |
| --- | --- | --- | --- | 2 | 500 |
| --- | --- | --- | --- | 3 | 500 |
| --- | --- | --- | --- | 5 | 500 |
| --- | --- | --- | --- | 6 | 500 |
| Alloy | YS, MPa | TS, MPa | EY, GPa |
|---|---|---|---|
| Al-Mn-Mg-Ti-Zr for a temperature of 530 °C for 1 h (thin-walled < 500 μm) | 57.068 ± 1.895 | 64.107 ± 2.835 | 11.727± 0.424 |
| AlSi10Mg for a temperature of 440 °C and a time of 1 h (<500 μm) [38] | 106.627 ± 2.314 | 167.986 ± 4.032 | --- |
| Al-Mg alloyed with Sc and Zr [69] | 482.000 ± 4.100 (493.000 ± 13.000) | 523.000 ± 18.600 (547.000 ± 4.600) | 76.200 ± 1.700 (74.900 ± 1.200) |
| Al-Mg alloyed with Er and Zr [70] | 70.000 (62.000) | 107.000 (102.000) | 24.500 (28.400) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikitin, N.; Khmyrov, R.; Podrabinnik, P.A.; Pinargote, N.W.S.; Smirnov, A.; Idarmach, I.; Tarasova, T.V.; Grigoriev, S.N. Determination of Annealing Temperature of Thin-Walled Samples from Al-Mn-Mg-Ti-Zr Alloys for Mechanical Properties Restoration of Defective Parts After SLM. J. Manuf. Mater. Process. 2025, 9, 371. https://doi.org/10.3390/jmmp9110371
Nikitin N, Khmyrov R, Podrabinnik PA, Pinargote NWS, Smirnov A, Idarmach I, Tarasova TV, Grigoriev SN. Determination of Annealing Temperature of Thin-Walled Samples from Al-Mn-Mg-Ti-Zr Alloys for Mechanical Properties Restoration of Defective Parts After SLM. Journal of Manufacturing and Materials Processing. 2025; 9(11):371. https://doi.org/10.3390/jmmp9110371
Chicago/Turabian StyleNikitin, Nikita, Roman Khmyrov, Pavel A. Podrabinnik, Nestor Washington Solis Pinargote, Anton Smirnov, Idarmachev Idarmach, Tatiana V. Tarasova, and Sergey N. Grigoriev. 2025. "Determination of Annealing Temperature of Thin-Walled Samples from Al-Mn-Mg-Ti-Zr Alloys for Mechanical Properties Restoration of Defective Parts After SLM" Journal of Manufacturing and Materials Processing 9, no. 11: 371. https://doi.org/10.3390/jmmp9110371
APA StyleNikitin, N., Khmyrov, R., Podrabinnik, P. A., Pinargote, N. W. S., Smirnov, A., Idarmach, I., Tarasova, T. V., & Grigoriev, S. N. (2025). Determination of Annealing Temperature of Thin-Walled Samples from Al-Mn-Mg-Ti-Zr Alloys for Mechanical Properties Restoration of Defective Parts After SLM. Journal of Manufacturing and Materials Processing, 9(11), 371. https://doi.org/10.3390/jmmp9110371








