Time and Spatially Resolved Operando Small-Angle X-ray Scattering Measurements during Injection Moulding of Plastics
Abstract
:1. Introduction
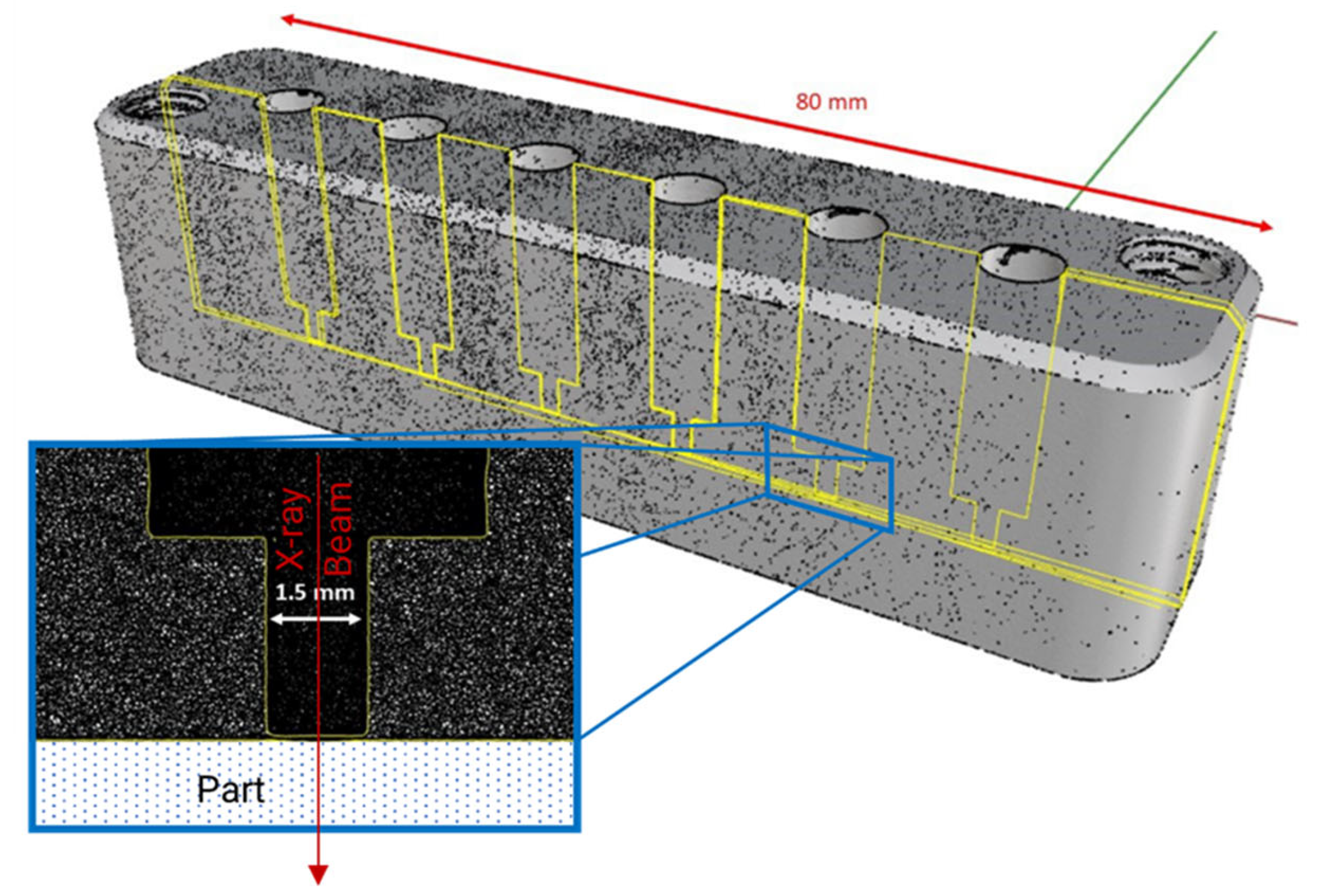
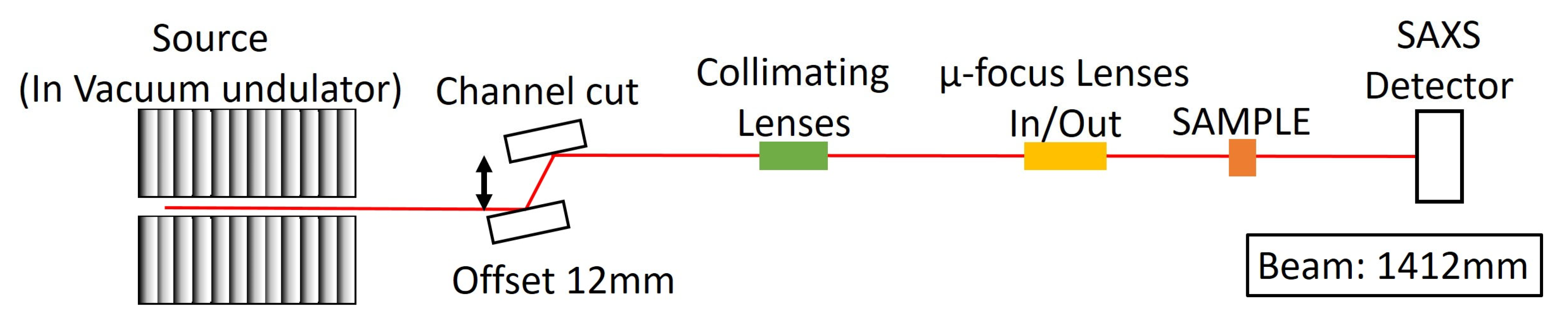
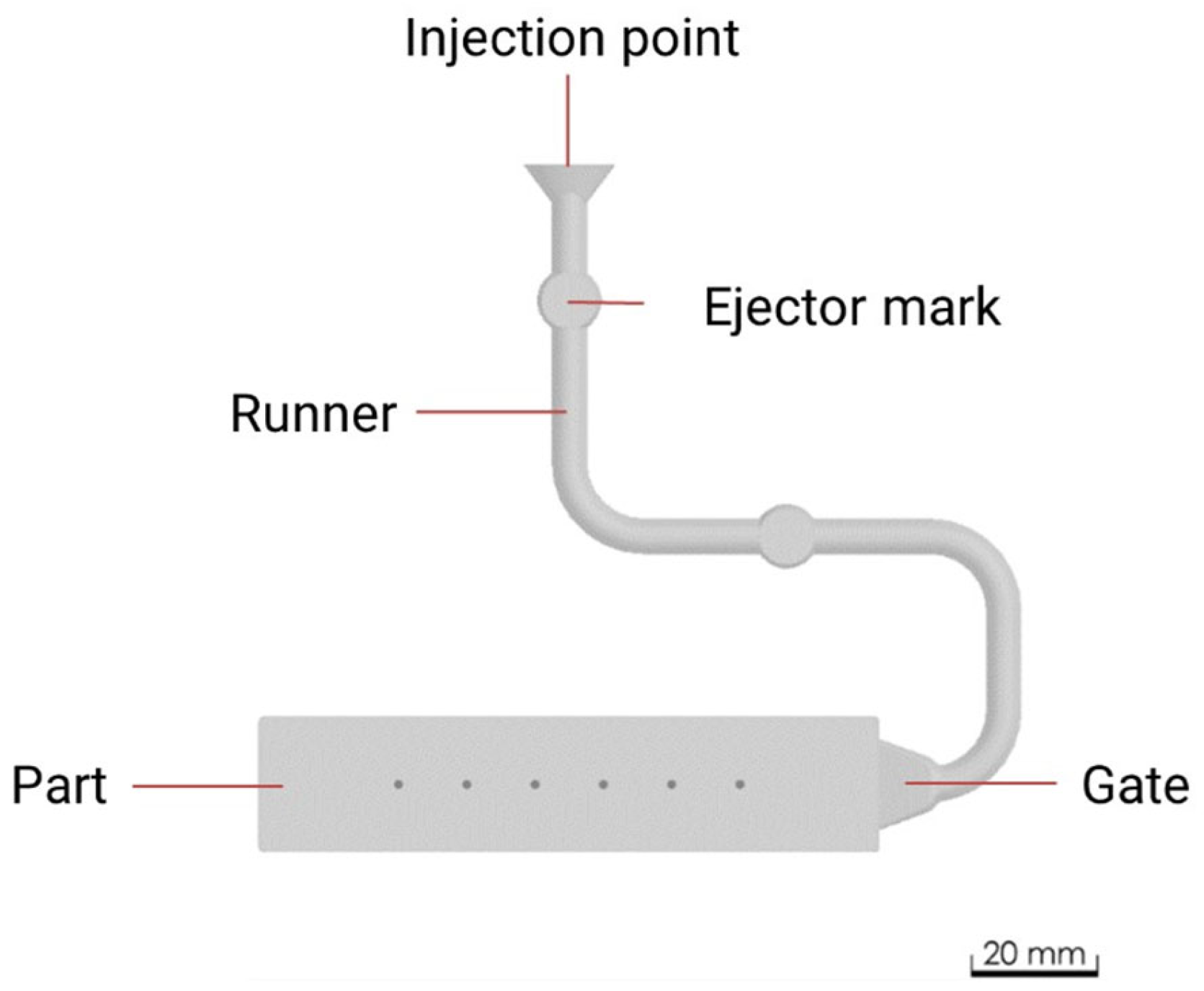
2. Materials and Methods
3. Results
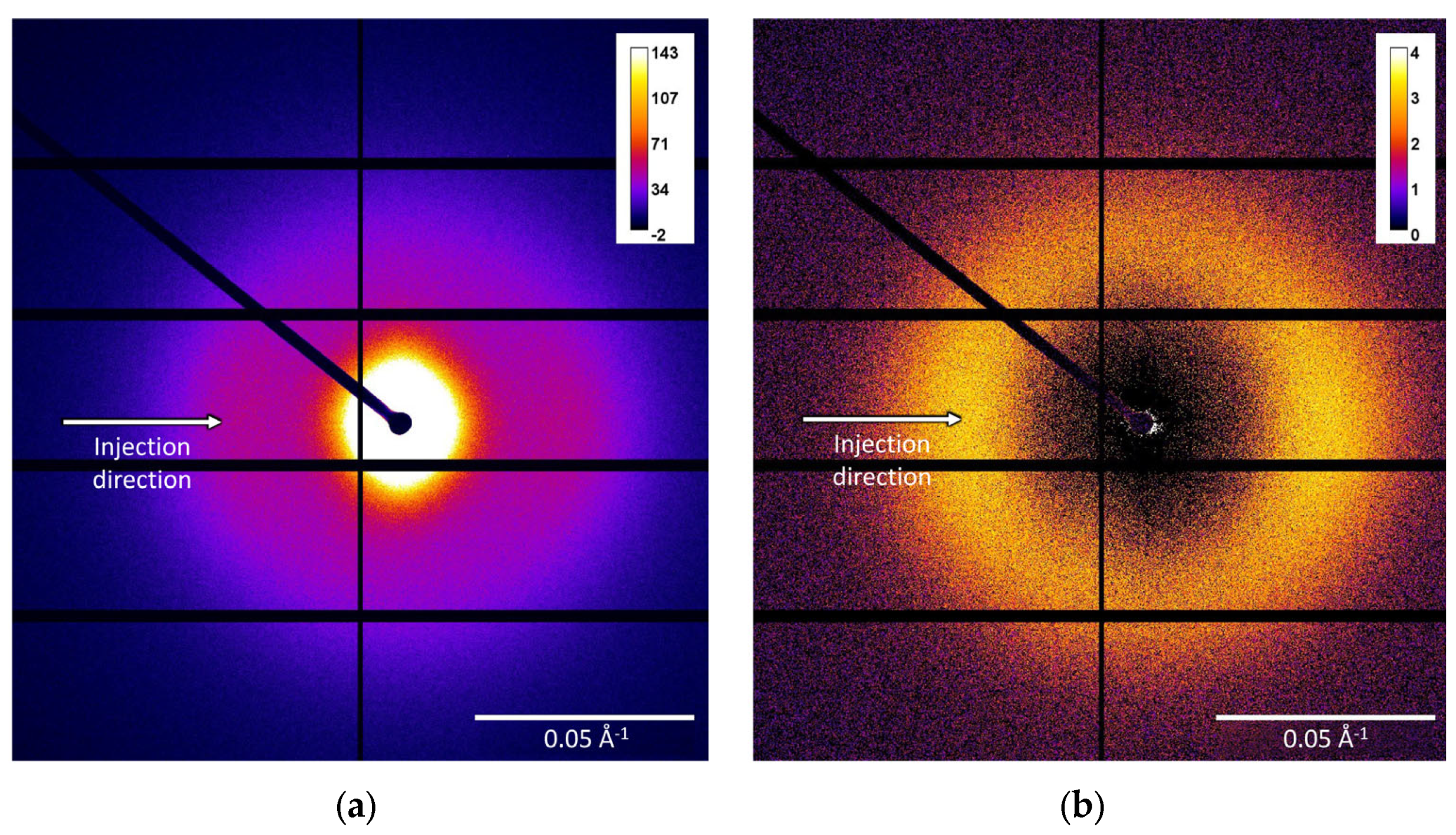
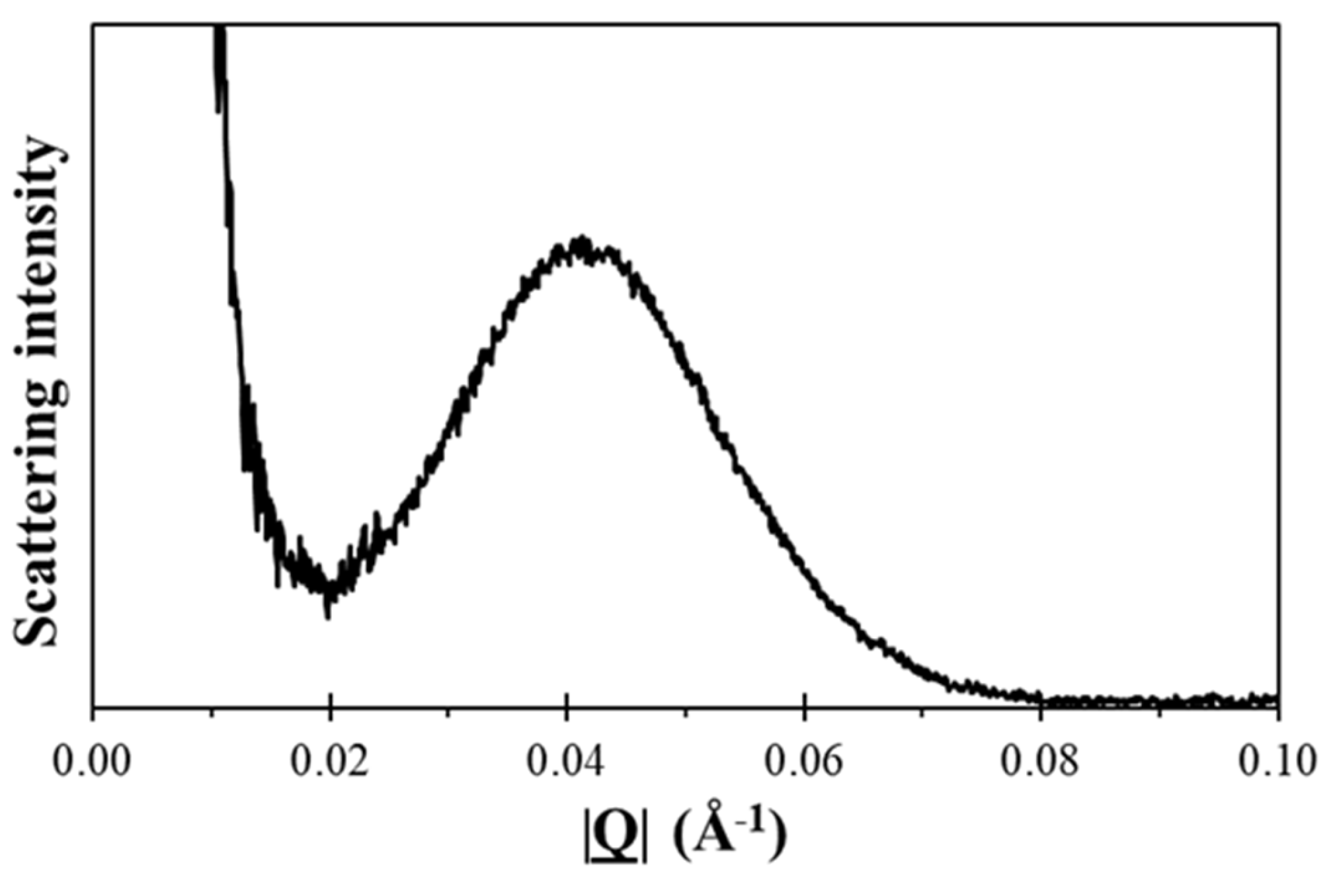
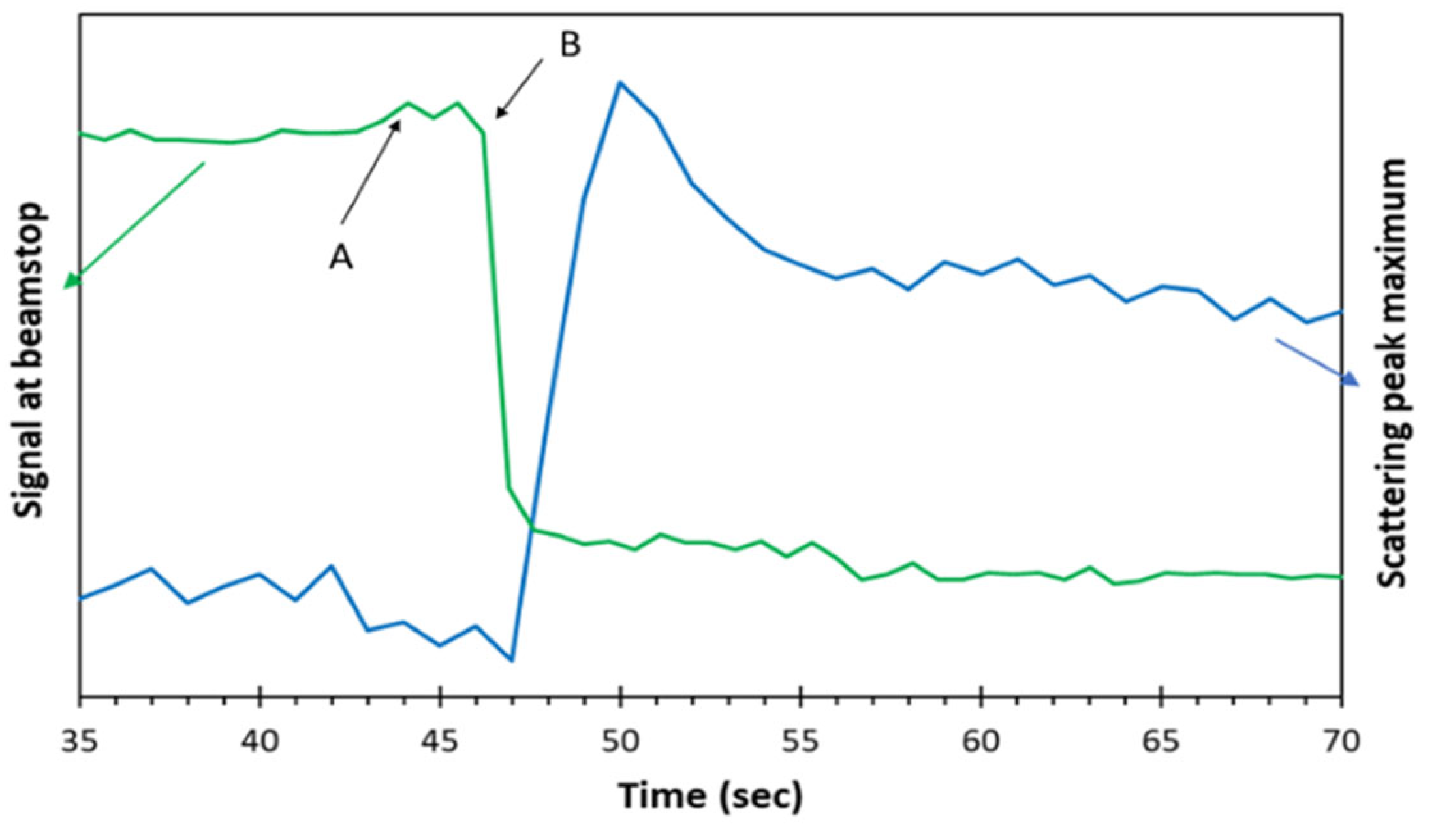
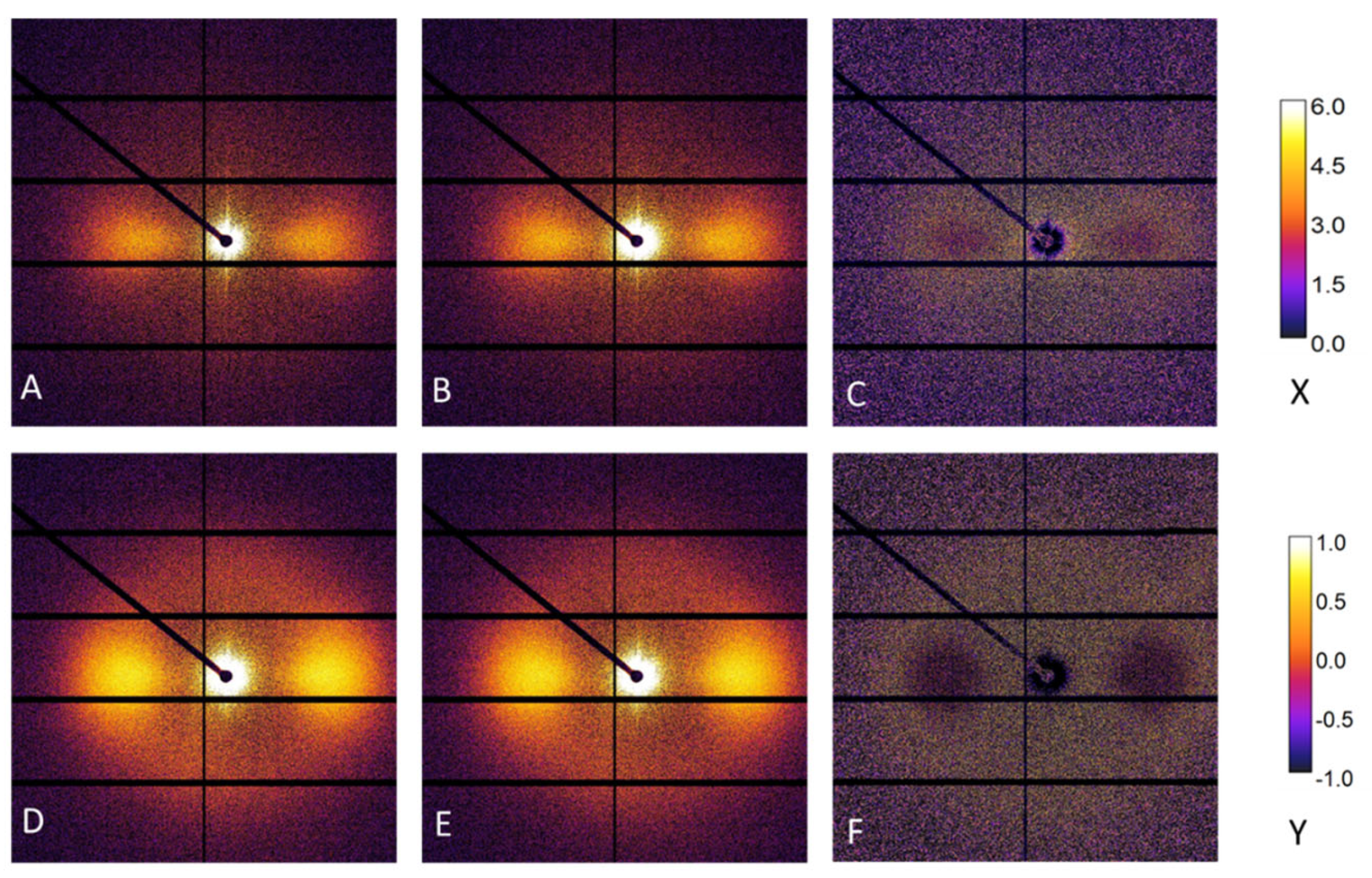
3.1. Basic Observations
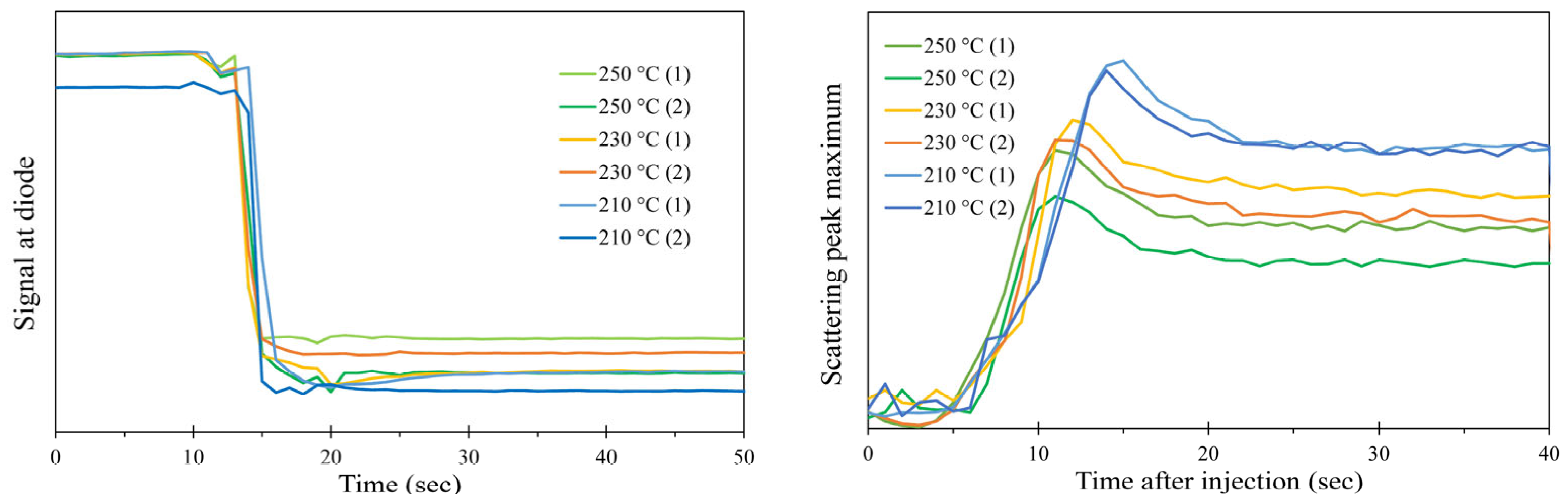
3.2. Reproducibility
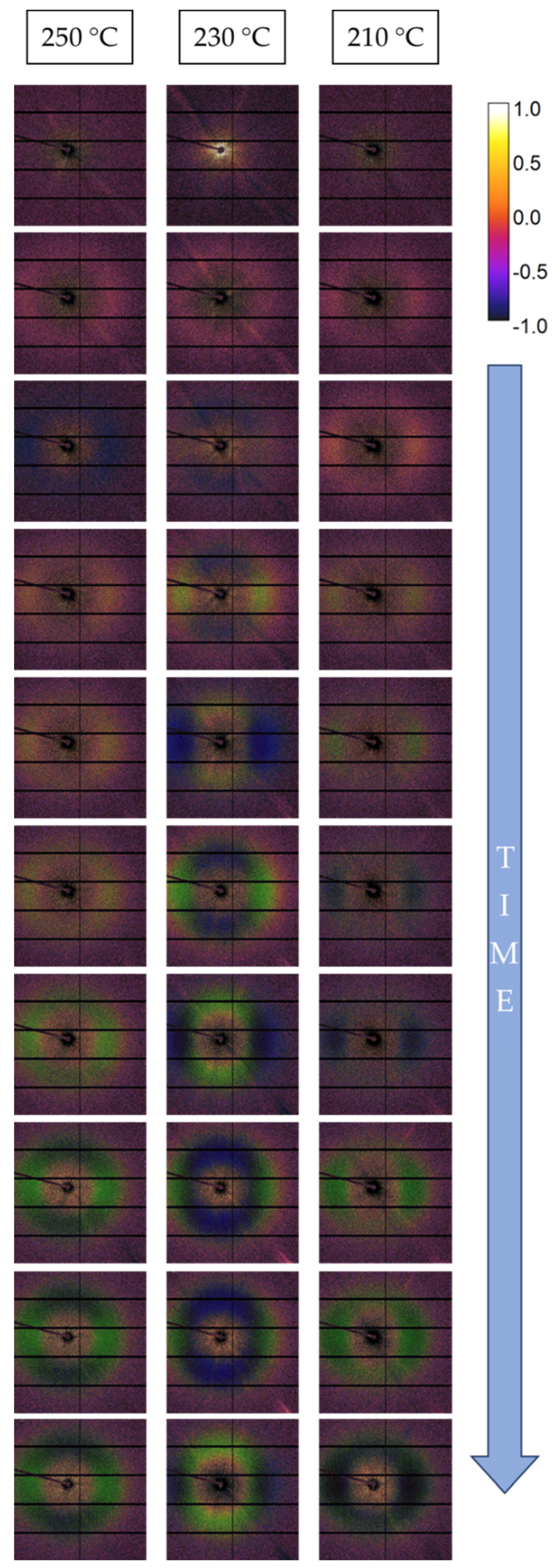
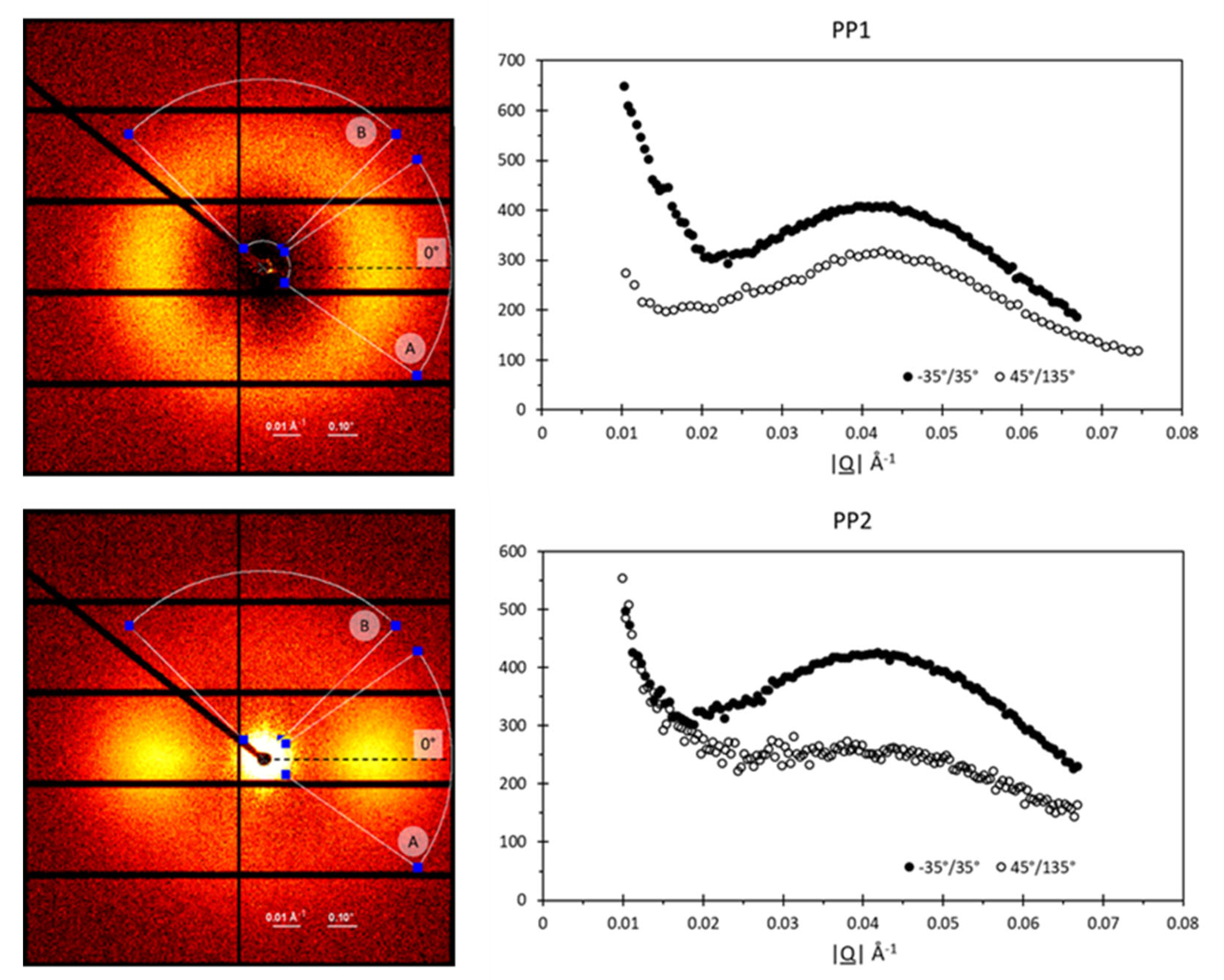
3.3. Spatial Variations
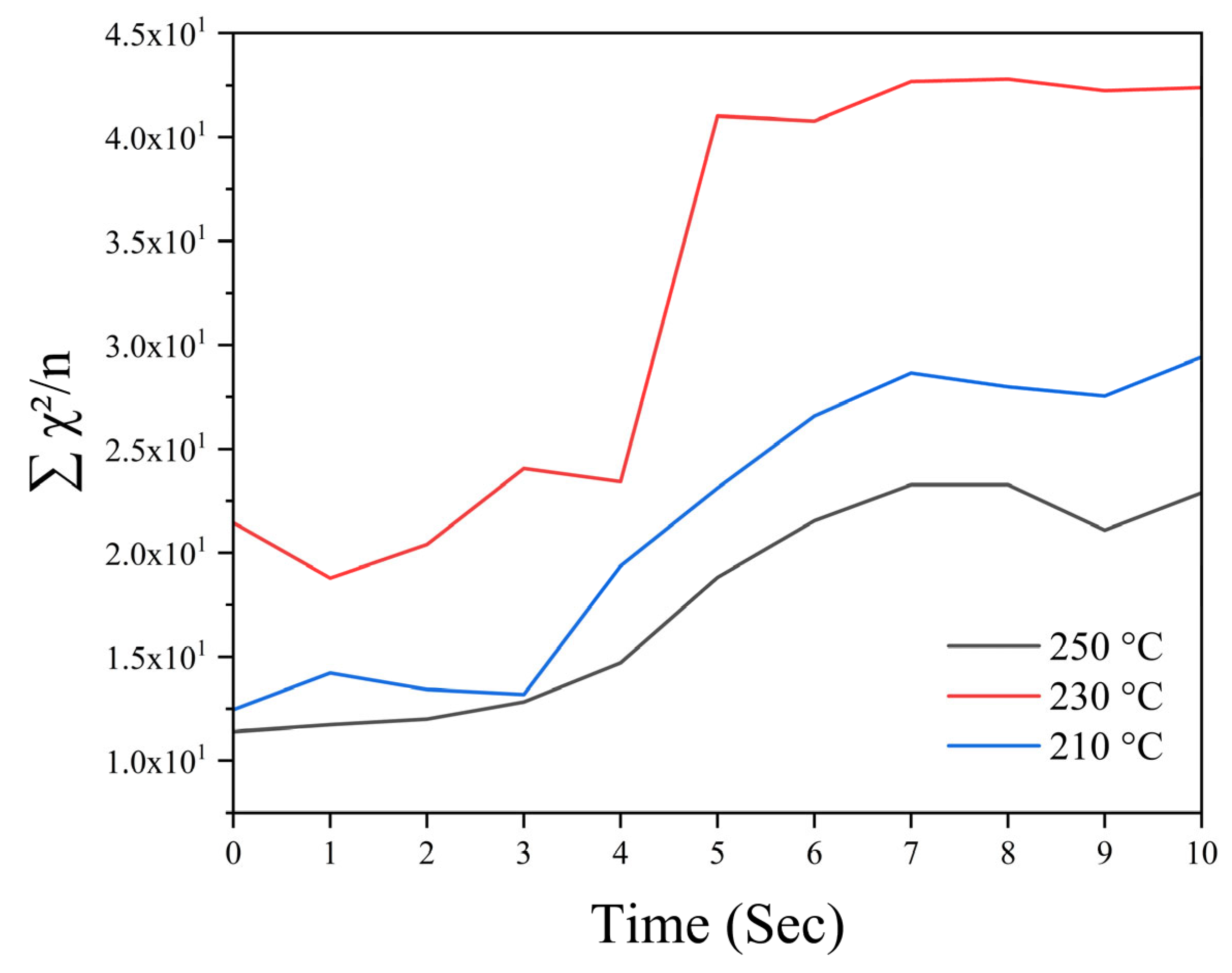
3.4. Time Variation
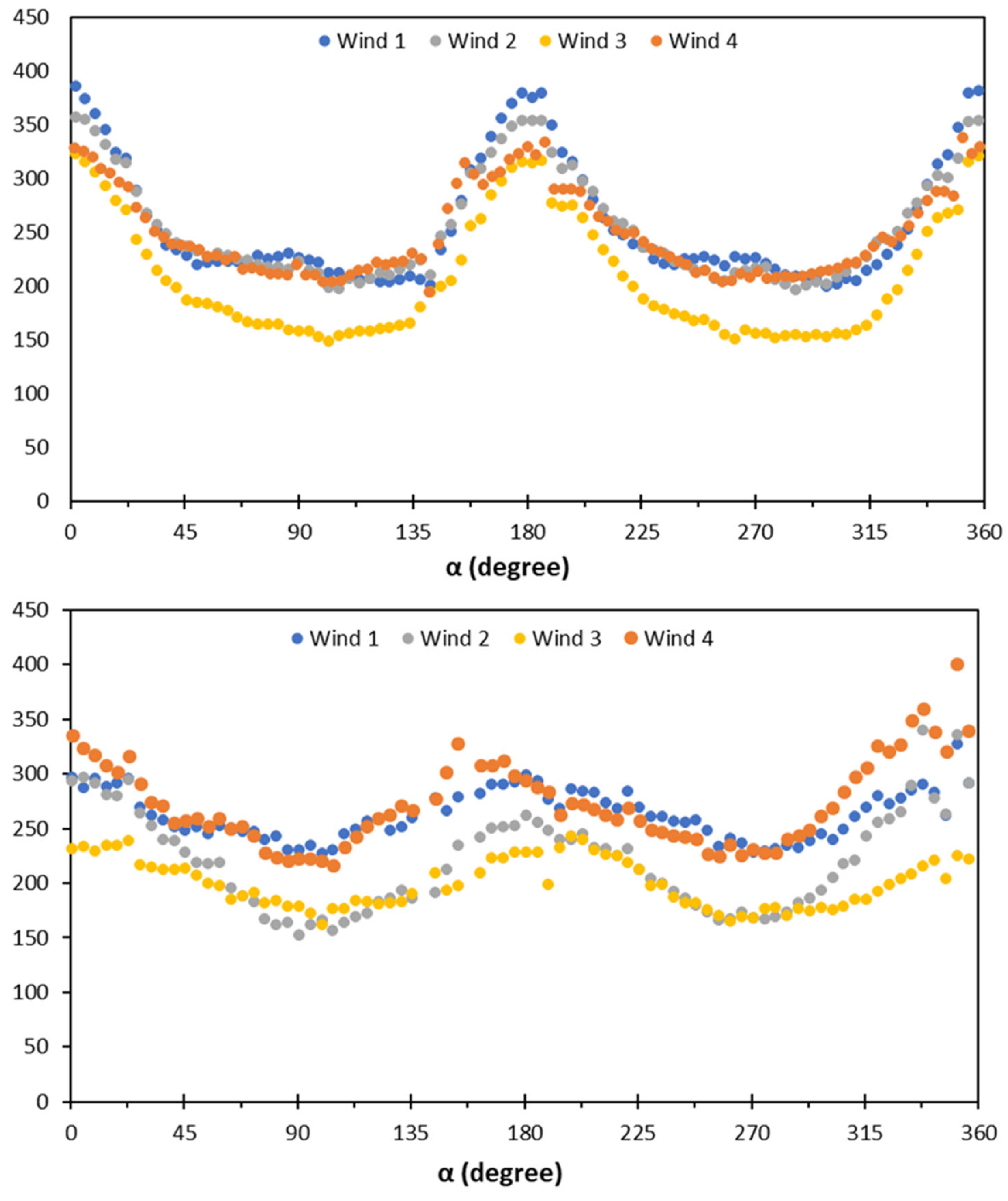
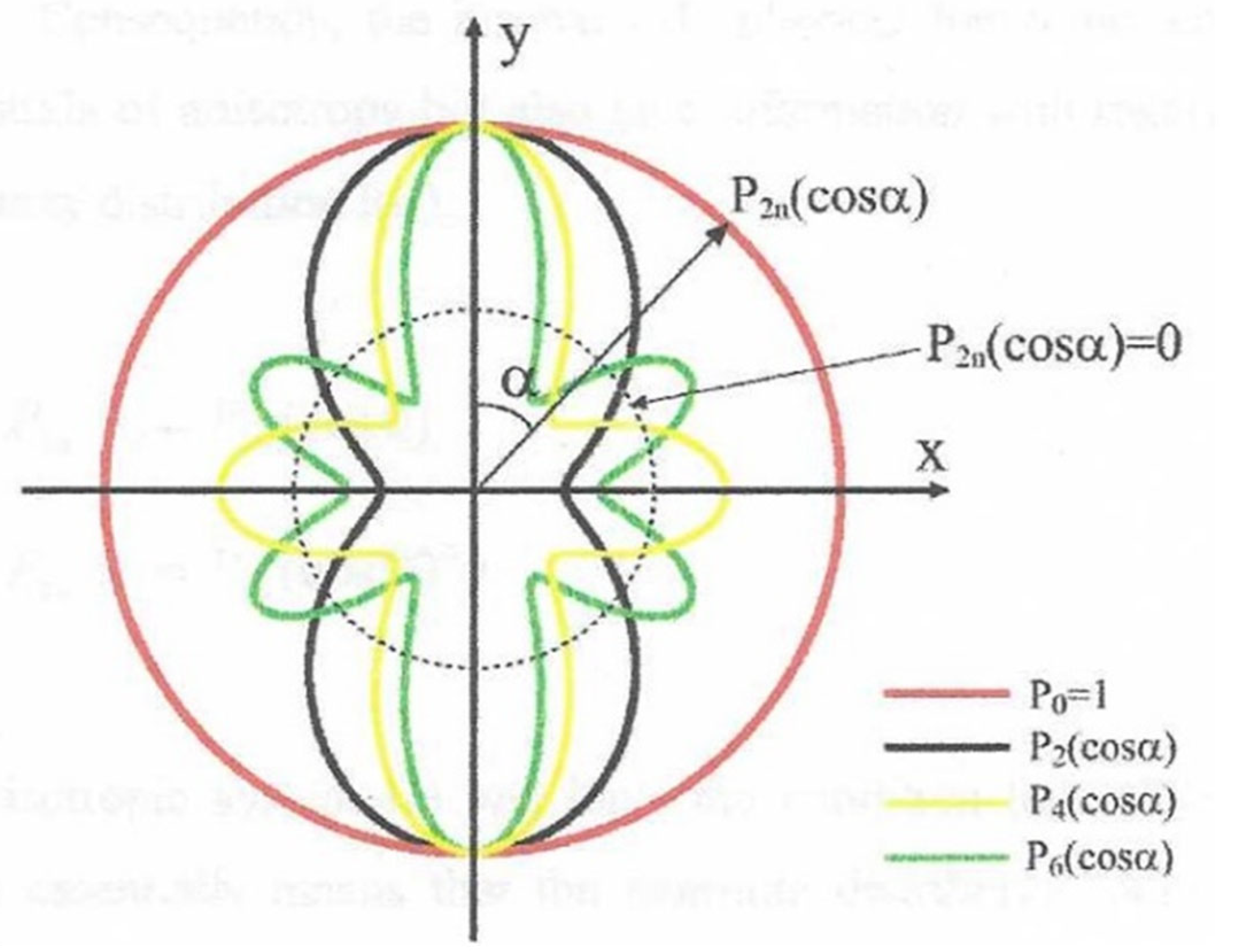
3.5. Preferred Crystal Orientation
4. Discussion
5. Conclusions
- We have successfully developed and tested operando X-ray scattering measurements during injection moulding. We are able to obtain useful quantitative data on the rate of crystallisation, local temperature variations, and the pattern of preferred orientation of the lamellar crystals.
- We are able to operate on a 1 s data cycle time, and the possibilities of reducing this to 0.5 s are promising.
- The design of the injection moulding unit enables modifications to be made easily and controls the processing parameter.
- On this basis of these validation experiments, we are poised to perform defined injection moulding cycles to test specific aspects of the process of transforming molten plastic into a shaped, moulded solid product.
- These validation experiments have confirmed that the microscopic characteristics of the process of transforming molten plastic to solid plastic are reproducible with successive moulding cycles, and this opens up the possibility of exploring spatial variations within the mould cavity using the predetermined window locations.
- We have been able to obtain quantitative time-resolving data that can be compared with the predictions of computer simulations.
- We now have a quantitative test bed with which to explore new avenues and new procedures in the injection moulding of plastics; the opportunities for multiscale active feedback are exciting and move us closer to the realisation of a multiscale digital twin for injection moulding.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ebnesajjad, S. Injection Moulding. In Melt Processible Fluoroplastics; Chapter 7; Ebnesajjad, S., Ed.; Andrew Publishing: Norwich, UK, 2003; pp. 151–193. ISBN 13: 9781884207969. [Google Scholar]
- Hyatt, S.; Hyatt, J.W. Improvement in Processes and Apparatus for Manufacturing Pyroxyline. U.S. Patent 133,229, 19 November 1872. [Google Scholar]
- Mitchell, P. (Ed.) Tool and Manufacturing Engineers Handbook: Plastic Part Manufacturing; Society of Manufacturing Engineers: Southfield, MI, USA, 1996; Available online: https://books.google.pt/books?id=Q4X1ovFVBvoC&printsec=frontcover&hl=pt-PT&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false (accessed on 30 July 2023).
- Sailors, H.R.; Hogan, J.P. History of Polyolefins. J. Macromol. Sci. Part A Chem. 1981, 15, 1377–1402. [Google Scholar] [CrossRef]
- Mandelkern, L. The Relation between Structure and Properties of Crystalline Polymers. Polym. J. 1985, 17, 337–350. [Google Scholar] [CrossRef]
- Hu, T.; Hua, W.-Q.; Zhong, G.-J.; Wang, Y.-D.; Gao, Y.-T.; Hong, C.-X.; Li, Z.-M.; Bian, F.-G.; Xiao, T.-Q. Nondestructive and Quantitative Characterization of Bulk Injection-Molded Polylactide Using SAXS Microtomography. Macromolecules 2020, 53, 6498–6509. [Google Scholar] [CrossRef]
- Björn, L.; Mazza, R.M.; Andreasson, E.; Linell, F.; Lutz-Bueno, V.; Guizar-Sicairos, M.; Jutemar, E.P.; Liebi, M. Scanning Small-Angle X-ray Scattering of Injection-Molded Polymers: Anisotropic Structure and Mechanical Properties of Low-Density Polyethylene. ACS Appl. Polym. Mater. 2023, 5, 6429–6440. [Google Scholar] [CrossRef]
- Elwell, M.J.; Mortimer, S.; Ryan, A.J. A Synchrotron SAXS Study of Structure Development Kinetics during the Reactive Processing of Flexible Polyurethane Foam. Macromolecules 1994, 27, 5428–5439. [Google Scholar] [CrossRef]
- Stanford, J.L.; Powell, J.R.; Wilkinson, A.N. Structural composites formed by reaction injection moulding. In FRC 2000–Composites for the Millennium; Gibson, A.G., Ed.; Woodhead Publishing: Sawston, UK, 2000; pp. 191–199. ISBN 9781855735507. [Google Scholar] [CrossRef]
- Mateus, A.; Bartolo, P.; Mitchell, G.R. In-situ time-resolving small-angle X-ray scattering studies of reaction kinetics and morphology in reaction injection moulding. 2010; Unpublished work. [Google Scholar]
- Kolb, R.; Seifert, S.; Stribeck, N.; Zachmann, H. Investigation of the high speed spinning process of poly(ethylene terephthalate) by means of synchrotron X-ray diffraction. Polymer 2000, 41, 2931–2935. [Google Scholar] [CrossRef]
- Van Drongelen, M.; Cavallo, D.; Balzano, L.; Portale, G.; Vittorias, I.; Bras, W.; Alfonso, G.C.; Peters, G.W.M. Structure Development of Low-Density Polyethylenes During Film Blowing: A Real-Time Wide-Angle X-ray Diffraction Study. Macromol. Mater. Eng. 2014, 299, 1494–1512. [Google Scholar] [CrossRef]
- Troisi, E.; van Drongelen, M.; Caelers, H.; Portale, G.; Peters, G. Structure evolution during film blowing: An experimental study using in-situ small angle X-ray scattering. Eur. Polym. J. 2016, 74, 190–208. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, W.; Zhao, H.; Ji, Y.; Meng, L.; Wang, D.; Li, L. In-situ tracking polymer crystallization during film blowing by synchrotron radiation X-ray scattering: The critical role of network. Polymer 2020, 198, 122492. [Google Scholar] [CrossRef]
- Li, Y.-W.; Liu, G.-F.; Wu, H.-J.; Zhou, P.; Hong, C.-X.; Li, N.; Bian, F.-G. BL19U2: Small-angle X-ray scattering beamline for biological macromolecules in solution at SSRF. Nucl. Sci. Tech. 2020, 31, 117. [Google Scholar] [CrossRef]
- Liao, T.; Zhao, X.; Yang, X.; Coates, P.; Whiteside, B.; Barker, D.; Thompson, G.; Lai, Y.; Jiang, Z.; Men, Y. In situ synchrotron small angle X-ray scattering investigation of structural formation of polyethylene upon micro-injection molding. Polymer 2021, 215, 123390. [Google Scholar] [CrossRef]
- Costa, A.A.; Gameiro, F.; Potêncio, A.; da Silva, D.P.; Carreira, P.; Martinez, J.C.; Pascoal-Faria, P.; Mateus, A.; Mitchell, G.R. Evaluating the Injection Moulding of Plastic Parts Using In Situ Time-Resolved Small-Angle X-ray Scattering Techniques. Polymers 2022, 14, 4745. [Google Scholar] [CrossRef] [PubMed]
- González Fernánde, J.B.; Colldelram, C.; Ferrer, S.; Fontserè Recuenco, A.; Gevorgyan, A.A.; Gonzalez, N.; Jover-Mañas, G.; Kamma-Lorger, C.; Llonch, M.L.; Malfois, M.; et al. Mechanical Engineering Design of Synchrotron Radiation Equipment and Instrumentation. In Proceedings of the MEDSI2018, Paris, France, 28 June 2018; JACoW Publishing: Geneva, Switzerland, 2018. ISBN 978-3-95450-207-3. [Google Scholar] [CrossRef]
- Ishige, R. Precise structural analysis of polymer materials using synchrotron X-ray scattering and spectroscopic methods. Polym. J. 2020, 52, 1013–1026. [Google Scholar] [CrossRef]
- Zhao, X.; Liao, T.; Yang, X.; Coates, P.; Whiteside, B.; Barker, D.; Thompson, G.; Jiang, Z.; Men, Y. Mold temperature- and molar mass-dependent structural formation in micro-injection molding of isotactic polypropylene. Polymer 2022, 248, 124797. [Google Scholar] [CrossRef]
- Mohan, S.; Olley, R.H.; Vaughan, A.S.; Mitchell, G.R. Evaluating Scales of Structure in Polymers. In Controlling the Morphology of Polymers: Multiple Scales of Structure and Processing; Mitchell, G.R., Tojeira, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-319-39320-9. [Google Scholar]
- Párizs, R.D.; Török, D.; Ageyeva, T.; Kovács, J.G. Multiple In-Mold Sensors for Quality and Process Control in Injection Molding. Sensors 2023, 23, 1735. [Google Scholar] [CrossRef]
- Shin, S. New era of synchrotron radiation: Fourth-generation storage ring. AAPPS Bull. 2021, 31, 21. [Google Scholar] [CrossRef]
- Bilderback, D.H.; Batterman, B.W.; Bedzyk, M.J.; Finkelstein, K.; Henderson, C.; Merlini, A.; Schildkamp, W.; Shen, Q.; White, J.; Blum, E.B.; et al. Performance of a hard X-ray undulator at CHESS. Rev. Sci. Instrum. 1989, 60, 1419–1425. [Google Scholar] [CrossRef]
- 6082 Aluminium Alloy 6082-T6 T651 AlMgSi1 (AlSi1MgMn–3.2315) Properties. Available online: https://www.theworldmaterial.com/ (accessed on 30 July 2023).
- UAI—Babyplast. Available online: https://www.babyplast.com/en/product-line/uai/ (accessed on 30 July 2023).
- Costa, A.A.; Gameiro, F.; Olivereria, L.; da Silva, D.P.; Carreira, P.; Martínez, J.C.; Martinho, P.G.; Mateus, A.; Mitchell, G.R. Industrially relevant Injection Moulding Apparatus for Operando Time-Resolving Small-Angle X-ray Scattering Measurements. J. Manuf. Process. 2023. submitted. [Google Scholar]
- Keller, A.; Kolnaar, H. Flow-Induced Orientation and Structure Formation. Mater. Sci. Technol. 1997, 18, 187–268. [Google Scholar]
- Pinheiro, J.; Abdulghani, S.; Pascoal-Faria, P.; Sousa, D.; Carreira, P.; Viana, T.; Kamma-Lorger, C.S.; Mitchell, G. Tools to define and evaluate morphology mapping, a route to complex structures using direct digital manufacturing. AIP Conf. Proc. 2019, 2116, 230003. [Google Scholar] [CrossRef]
- Lovell, R.; Mitchell, G.R. Molecular orientation distribution derived from an arbitrary reflection. Acta Crystallogr. Sect. A 1981, 37, 135–137. [Google Scholar] [CrossRef]
- Mitchell, G.R.; Saengsuwan, S.; Bualek-Limcharoen, S. Evaluation of preferred orientation in multi-component polymer systems using X-ray scattering procedures. In Scattering Methods and the Properties of Polymer Materials; Progress in Colloid and Polymer Science; Stribeck, N., Smarsly, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 130. [Google Scholar]
- Da Silva, D.P.; Holt, J.J.; Pratumshat, S.; Pascoal-Faria, P.; Mateus, A.; Mitchell, G.R. Crystallisation from Anisotropic Polymer Melts. In Polymer Crystallization: Methods, Characterization, and Applications; Chapter 10; Parameswaranpillai, J., Jacob, J., Krishnasamy, S., Jayakumar, A., Hameed, N., Eds.; Wiley-VCH: Weinheim, Germany, 2023; pp. 225–284. ISBN 9783527350810. [Google Scholar]
- Muszyński, P.; Poszwa, P.; Mrozek, K.; Zielinski, M.; Dalewski, P.; Kowal, M. Design and Simulation Study of the Induction Heated Injection Mold with Sliders. Materials 2021, 14, 7476. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, R.; Martinez, A.; Mercado, D.; Carbonel, A.; Aisa, J. Rapid heating injection moulding: An experimental surface temperature study. Polym. Test. 2021, 93, 106928. [Google Scholar] [CrossRef]
- Mitchell, G.R. Neutron Diffraction of Polymers and Other Soft Matter. In Essentials of Neutron Techniques for Soft Matter; Imae, T., Kanaya, T., Furusaka, M., Eds.; Wiley: Hoboken, NJ, USA, 2011; ISBN 10: 0-470-40252. [Google Scholar]
- Mitchell, G.R. X Ray Scattering from Non Crystalline and Liquid Crystalline Polymers in Comprehensive Polymer Science; Allen, G., Bevington, J., Eds.; Pergamon Press: Oxford, UK, 1989; Volume 1, pp. 687–729, Chapter 31. [Google Scholar]
- Mofakhami, E.; Tencé-Girault, S.; Perrin, J.; Scheel, M.; Gervat, L.; Ovalle, C.; Laiarinandrasana, L.; Fayolle, B.; Miquelard-Garnier, G. Microstructure-mechanical properties relationships in vibration welded glass-fiber-reinforced polyamide 66: A high-resolution X-ray microtomography study. Polym. Test. 2020, 85, 106454. [Google Scholar] [CrossRef]
- ALBA II—En. Available online: https://www.cells.es/en/science-at-alba/alba-ii-upgrade (accessed on 30 July 2023).
- Reichert, H.; Honkimäki, V. High-Energy X-ray Scattering and Imaging. In Synchrotron Light Sources and Free-Electron Lasers; Jaeschke, E., Khan, S., Schneider, J., Hastings, J., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]



| Acronym | Manufacturer | Grade | MFI g/10 min at 230 °C | Notes |
|---|---|---|---|---|
| PP1 | Lyndon Basel | MOPLEN HP 500N | 12 | General purpose suitable for food contact applications. |
| PP2 | Repsol | ISPLEN PR595C2M | 45 | Phthalate free random copolymer which is clarified and contains antistatic additives. |
| PP3 | SABIC | 595A | 47 | Designed for Automotive applications. |
| Parameter | Value | Units |
|---|---|---|
| Part weight | 5 | G |
| Shot size | 12.991 | cm3 |
| 1st Injection Pressure | 40 | Bar |
| 1st Injection Time | 2 | S |
| 2nd Injection Pressure | 30 | Bar |
| 2nd Injection Time | 6 | S |
| 1st Injection speed | 55 | % a |
| 2nd Injection speed | 45 | % a |
| Cooling time | 2 | S |
| Cycle time | 22.30 | S |
| D2n | PP1 | PP2 |
|---|---|---|
| D2 | 0.26 | 0.50 |
| D4 | 0.05 | −0.28 |
| D6 | 0.00 | −0.26 |
| Lp (Å) | PP1 | PP2 |
|---|---|---|
| −35°/35° | 113 | 106 |
| 45°/135° | 121 | 116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arioli, M.; Massano, A.P.; da Silva, D.P.; Gameiro, F.A.; Carreira, P.; Malfois, M.; Matias, J.; Pascoal-Faria, P.; Mateus, A.; Mitchell, G.R. Time and Spatially Resolved Operando Small-Angle X-ray Scattering Measurements during Injection Moulding of Plastics. J. Manuf. Mater. Process. 2023, 7, 176. https://doi.org/10.3390/jmmp7050176
Arioli M, Massano AP, da Silva DP, Gameiro FA, Carreira P, Malfois M, Matias J, Pascoal-Faria P, Mateus A, Mitchell GR. Time and Spatially Resolved Operando Small-Angle X-ray Scattering Measurements during Injection Moulding of Plastics. Journal of Manufacturing and Materials Processing. 2023; 7(5):176. https://doi.org/10.3390/jmmp7050176
Chicago/Turabian StyleArioli, Matteo, Anabela Paiva Massano, Daniel P. da Silva, Fábio A. Gameiro, Pedro Carreira, Marc Malfois, João Matias, Paula Pascoal-Faria, Artur Mateus, and Geoffrey R. Mitchell. 2023. "Time and Spatially Resolved Operando Small-Angle X-ray Scattering Measurements during Injection Moulding of Plastics" Journal of Manufacturing and Materials Processing 7, no. 5: 176. https://doi.org/10.3390/jmmp7050176
APA StyleArioli, M., Massano, A. P., da Silva, D. P., Gameiro, F. A., Carreira, P., Malfois, M., Matias, J., Pascoal-Faria, P., Mateus, A., & Mitchell, G. R. (2023). Time and Spatially Resolved Operando Small-Angle X-ray Scattering Measurements during Injection Moulding of Plastics. Journal of Manufacturing and Materials Processing, 7(5), 176. https://doi.org/10.3390/jmmp7050176













