Effect of Process Variables on Interface Friction Characteristics in Strip Drawing of AA 5182 Alloy and Its Formability in Warm Deep Drawing †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Strip Drawing Tests
2.2. Warm Deep Drawing Simulation
2.2.1. Friction Conditions
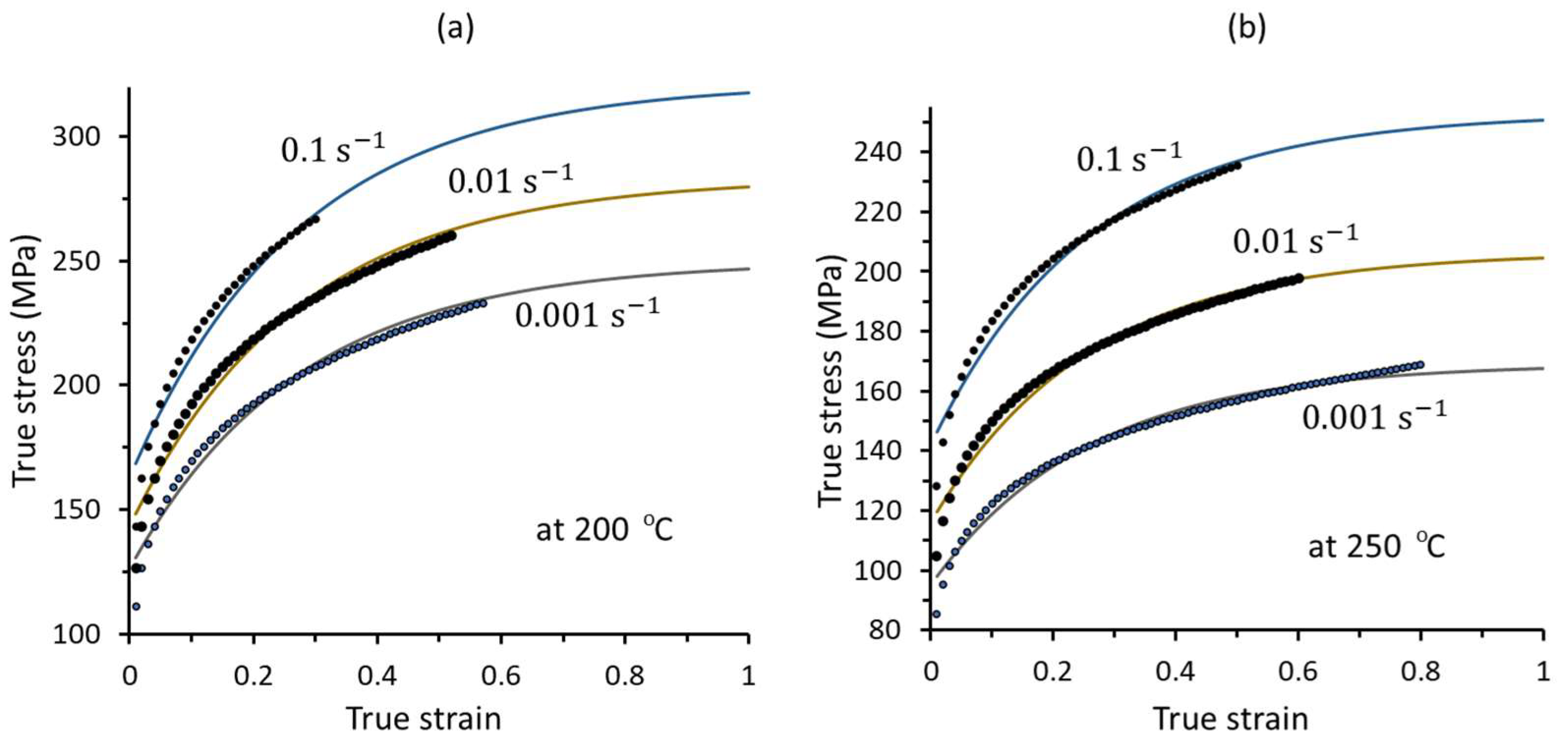
2.2.2. Material Model
2.3. Deep Drawing Experiments
3. Results and Discussion
3.1. Effect of Process Variables on Friction in Strip Drawing Tests
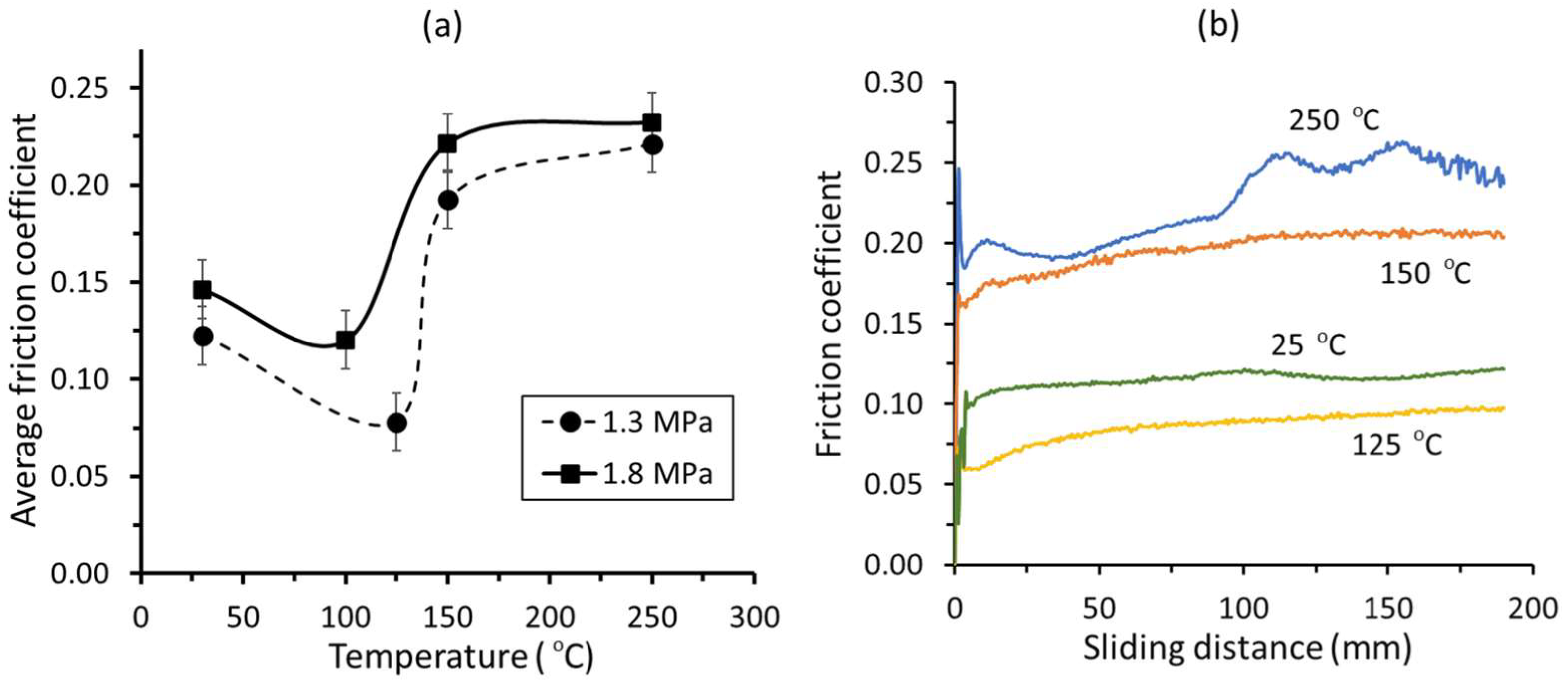
3.1.1. Effect of Temperature
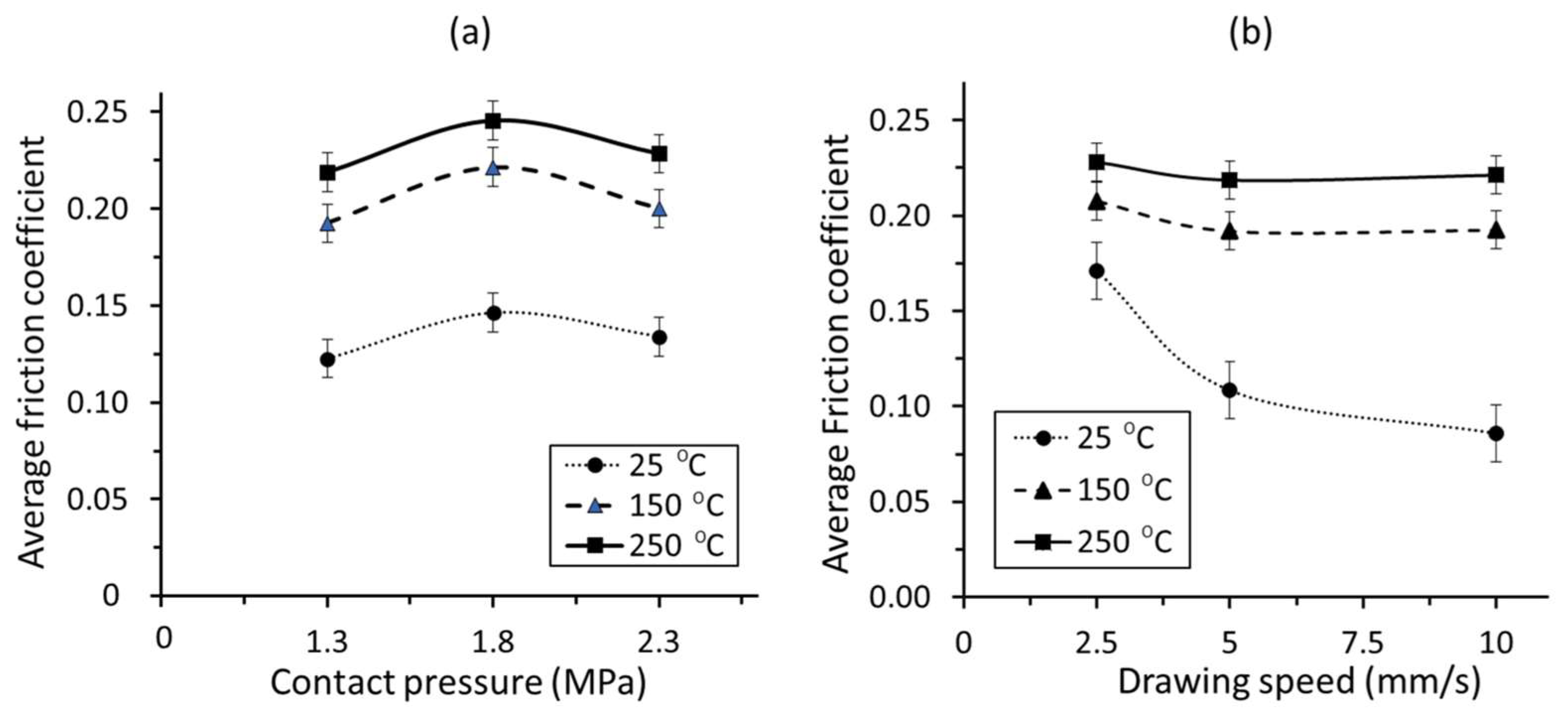
3.1.2. Effect of Contact Pressure
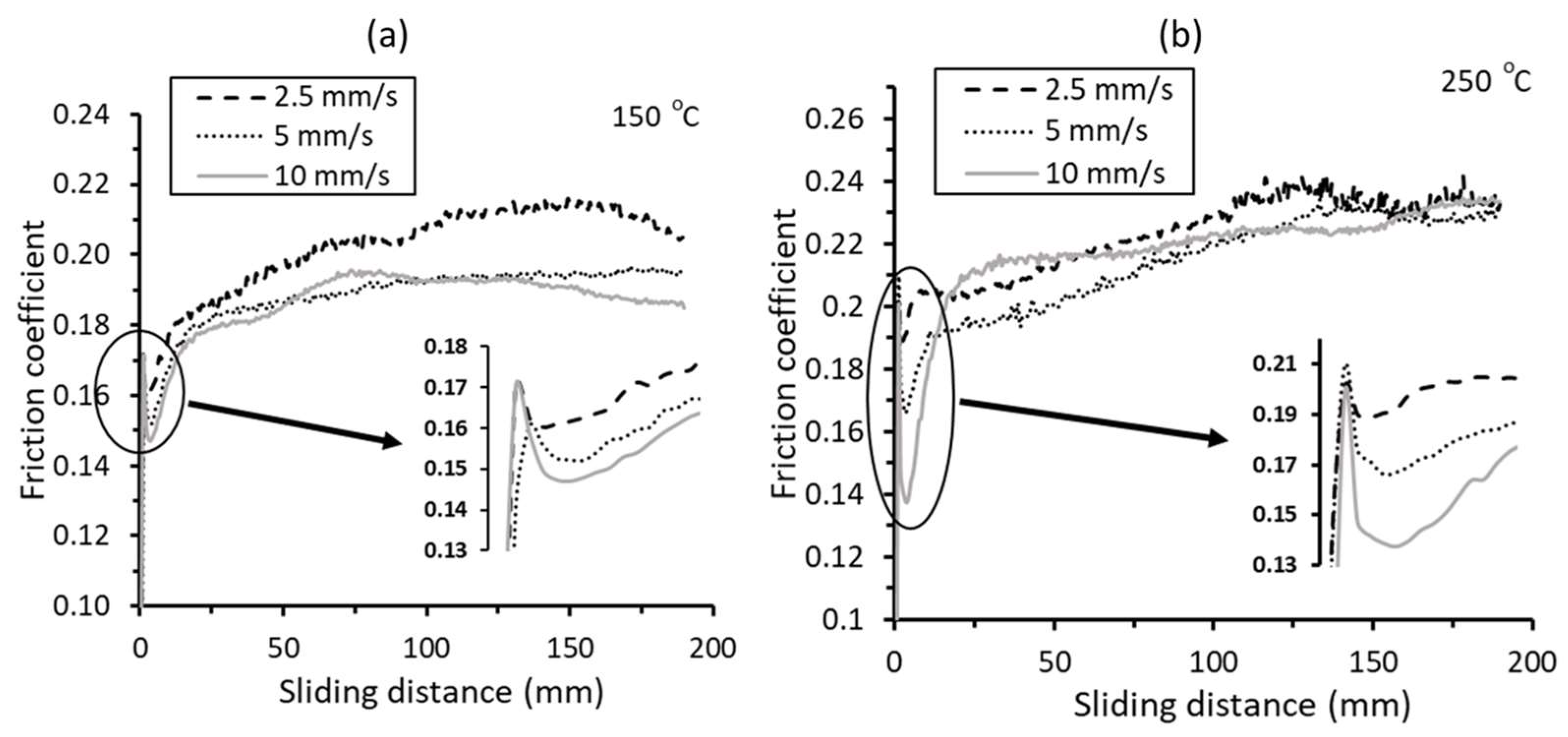
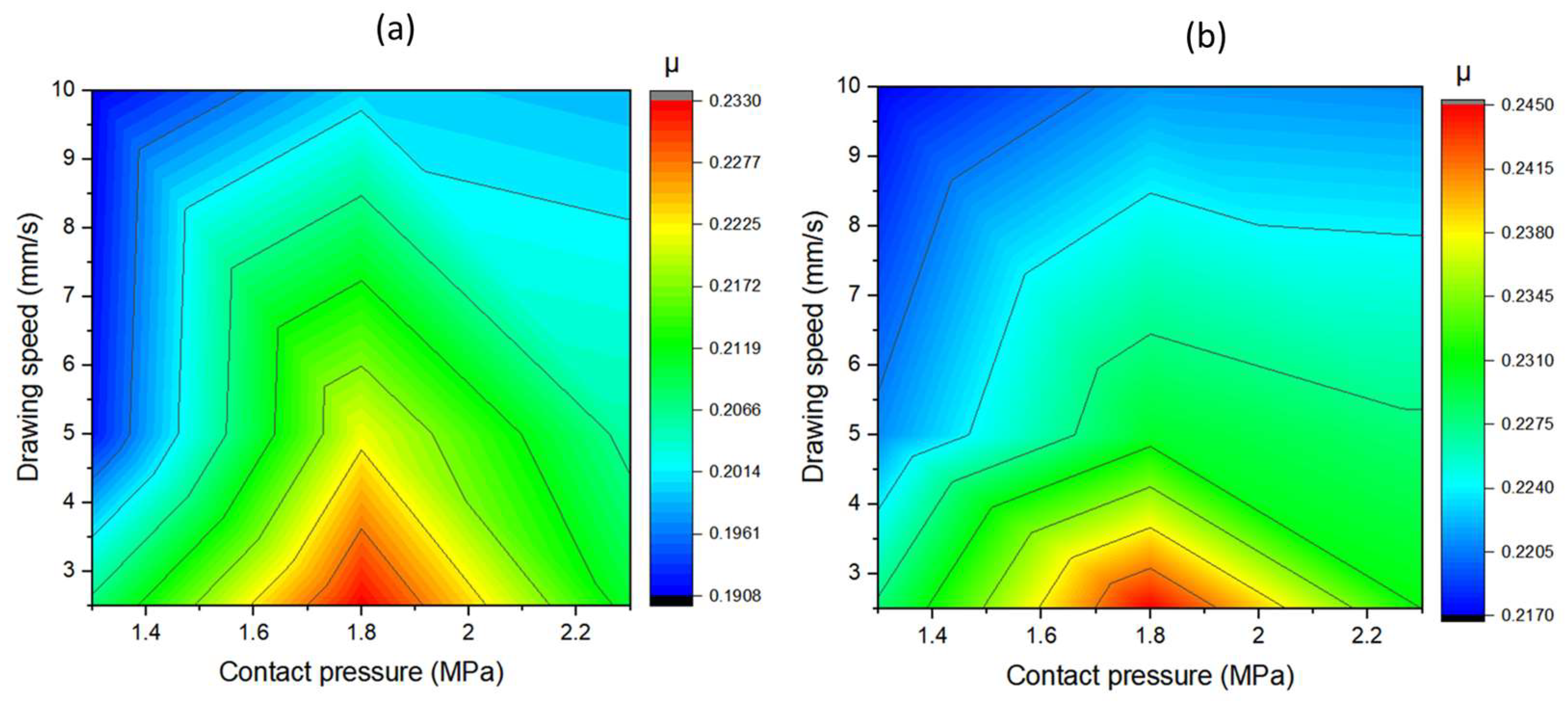
3.1.3. Effect of Drawing Speed
3.2. Prediction of Effect of Friction in Warm Deep Drawing by FE Simulations
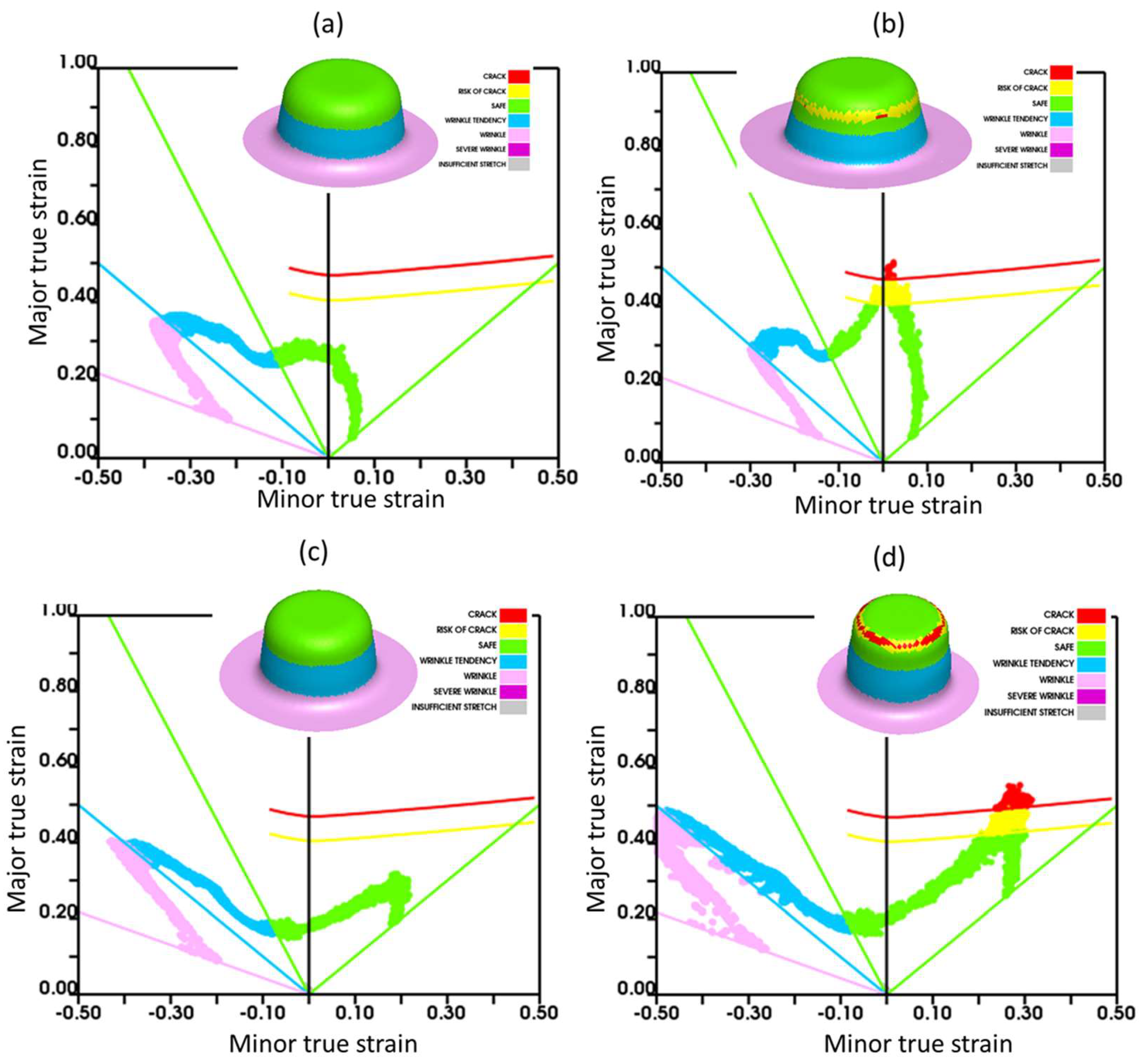
3.2.1. Prediction of Drawability
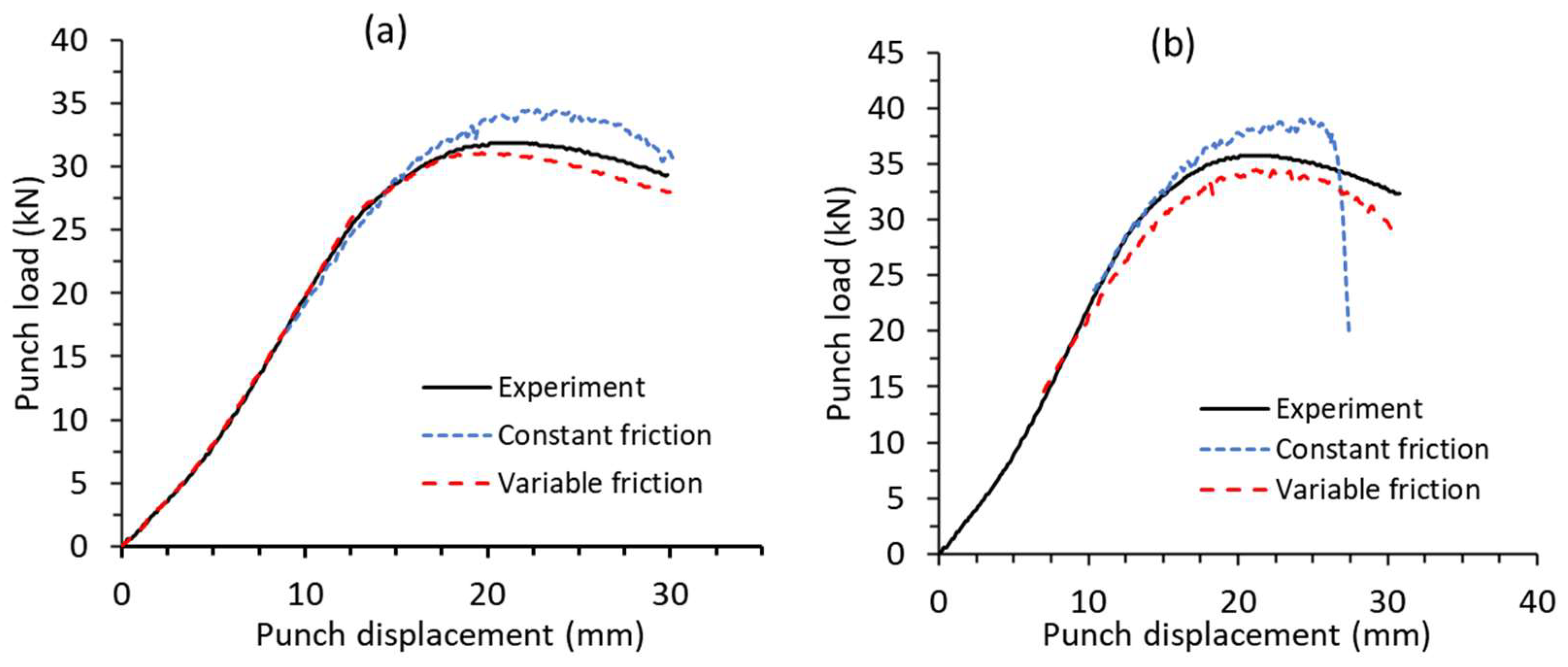
3.2.2. Predictions of Load–Displacement Curves
3.2.3. Prediction of Shear Stress Distribution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prasad Rambabu, N.; Eswara Prasad, V.V.K.; Wanhill, R.J.H. Aerospace Materials and Material Technologies; Springer: Singapore, 2017; Volume 1, p. 586. [Google Scholar] [CrossRef]
- Benedyk, J.C. Aluminum Alloys for Lightweight Automotive Structures; Woodhead Publishing Limited: Sawston, UK, 2010; ISBN 9781845694630. [Google Scholar]
- Marciniak, Z.; Duncan, J.L.; Hu, S.J. 2—Sheet Deformation Processes. In Mechanics of Sheet Metal Forming, 2nd ed.; Marciniak, Z., Duncan, J.L., Hu, S.J., Eds.; Butterworth-Heinemann: Oxford, UK, 2002; pp. 14–29. ISBN 978-0-7506-5300-8. [Google Scholar]
- Altan, T.; Tekkaya, A.E. Sheet Metal Forming Processes and Applications; ASM International: Novelty, OH, USA, 2012; pp. 83–98. ISBN 978-1-61503-844-2. [Google Scholar]
- Tisza, M.; Lukács, Z. High Strength Aluminum Alloys in Car Manufacturing. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012033. [Google Scholar] [CrossRef]
- Jang, D.H.; Kim, W.J. Warm Temperature Deformation Behavior and Processing Maps of 5182 and 7075 Aluminum Alloy Sheets with Fine Grains. Met. Mater. Int. 2018, 24, 455–463. [Google Scholar] [CrossRef]
- Satish, D.R.; Kumar, D.R.; Merklein, M. Effect of Temperature and Punch Speed on Forming Limit Strains of AA5182 Alloy in Warm Forming and Improvement in Failure Prediction in Finite Element Analysis. J. Strain Anal. Eng. Des. 2017, 52, 258–273. [Google Scholar] [CrossRef]
- Adamus, J.; Więckowski, W.; Lacki, P. Analysis of the Effectiveness of Technological Lubricants with the Addition of Boric Acid in Sheet Metal Forming. Materials 2023, 16, 5125. [Google Scholar] [CrossRef]
- Lachmayer, R.; Behrens, B.A.; Ehlers, T.; Müller, P.; Althaus, P.; Oel, M.; Farahmand, E.; Gembarski, P.C.; Wester, H.; Hübner, S. Process-Integrated Lubrication in Sheet Metal Forming. J. Manuf. Mater. Process. 2022, 6, 121. [Google Scholar] [CrossRef]
- Wu, Y.; Recklin, V.; Groche, P. Strain Induced Surface Change in Sheet Metal Forming: Numerical Prediction, Influence on Friction and Tool Wear. J. Manuf. Mater. Process. 2021, 5, 29. [Google Scholar] [CrossRef]
- Noder, J.; George, R.; Butcher, C.; Worswick, M.J. Friction Characterization and Application to Warm Forming of a High Strength 7000-Series Aluminum Sheet. J. Mater. Process. Technol. 2021, 293, 117066. [Google Scholar] [CrossRef]
- Prakash, V.; Kumar, D.R. Performance Evaluation of Bio-Lubricants in Strip Drawing and Deep Drawing of an Aluminium Alloy. Adv. Mater. Process. Technol. 2020, 8, 1044–1057. [Google Scholar] [CrossRef]
- Więckowski, W.; Adamus, J.; Dyner, M. Sheet Metal Forming Using Environmentally Benign Lubricant. Arch. Civil. Mech. Eng. 2020, 20, 51. [Google Scholar] [CrossRef]
- Tenner, J.; Andreas, K.; Radius, A.; Merklein, M. Numerical and Experimental Investigation of Dry Deep Drawing of Aluminum Alloys with Conventional and Coated Tool Surfaces. Procedia Eng. 2017, 207, 2245–2250. [Google Scholar] [CrossRef]
- Januszkiewicz, K.R.; Riahi, A.R.; Barakat, S. High Temperature Tribological Behaviour of Lubricating Emulsions. Wear 2004, 256, 1050–1061. [Google Scholar] [CrossRef]
- Tatipala, S.; Pilthammar, J.; Sigvant, M.; Wall, J.; Johansson, C.M. Introductory Study of Sheet Metal Forming Simulations to Evaluate Process Robustness. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012111. [Google Scholar] [CrossRef]
- Ben Said, L.; Allouch, M.; Wali, M.; Dammak, F. Numerical Formulation of Anisotropic Elastoplastic Behavior Coupled with Damage Model in Forming Processes. Mathematics 2023, 11, 204. [Google Scholar] [CrossRef]
- Barlat, F.; Lian, K. Plastic Behavior and Stretchability of Sheet Metals. Part I: A Yield Function for Orthotropic Sheets under Plane Stress Conditions. Int. J. Plast. 1989, 5, 51–66. [Google Scholar] [CrossRef]
- Banabic, D.; Kuwabara, T.; Balan, T.; Comsa, D.S. An Anisotropic Yield Criterion for Sheet Metals. J. Mater. Process. Technol. 2004, 157–158, 462–465. [Google Scholar] [CrossRef]
- Zabala, A.; de Argandoña, E.S.; Cañizares, D.; Llavori, I.; Otegi, N.; Mendiguren, J. Numerical Study of Advanced Friction Modelling for Sheet Metal Forming: Influence of the Die Local Roughness. Tribol. Int. 2022, 165, 107259. [Google Scholar] [CrossRef]
- Sigvant, M.; Hol, J.; Chezan, T.; van den Boogaard, T. Friction modelling in sheet metal forming simulations: Application and validation on an U-Bend product. In Proceedings of the 8th Forming Technology Forum Zurich, Advanced Constitutive Models in Sheet Metal Forming; Hora, P., Ed.; Institute of Virtual Manufacturing: Zurich, Switzerland, 2015; pp. 135–142. ISBN 978-3-906031-98-9. [Google Scholar]
- Hol, J.; Wiebenga, J.H.; Stock, J.; Wied, J.; Wiegand, K.; Carleer, B. Improving Stamping Simulation Accuracy by Accounting for Realistic Friction and Lubrication Conditions: Application to the Door-Outer of the Mercedes-Benz C-Class Coupé. J. Phys. Conf. Ser. 2016, 734, 032091. [Google Scholar] [CrossRef]
- Bay, N.; Olsson, D.D.; Andreasen, J.L. Lubricant Test Methods for Sheet Metal Forming. Tribol. Int. 2008, 41, 844–853. [Google Scholar] [CrossRef]
- Kim, H.S.; Koç, M.; Ni, J.; Ghosh, A. Finite Element Modeling and Analysis of Warm Forming of Aluminum Alloys—Validation through Comparisons with Experiments and Determination of a Failure Criterion. J. Manuf. Sci. Eng. 2006, 128, 613–621. [Google Scholar] [CrossRef]
- Voce, E. The Relationship between Stress and Strain for Homogeneous Deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Cowper, G.R.; Symonds, P.S. Strain Hardening and Strain Rate Effect in the Impact Loading of Cantilever Beams; Division of Applied Mathematics, Brown University: Providence, RI, USA, 1957. [Google Scholar]
- Prakash, V.; Kumar, D.R. Numerical Simulation of Warm Deep Drawing Incorporating Strain Rate Effect in Sheet Material Properties. Mater. Today Proc. 2019, 18, 2595–2602. [Google Scholar] [CrossRef]
- Swift, H.W. Drawing Tests for Sheet Metal. Proc. Inst. Automob. Eng. 1939, 34, 10–1243. [Google Scholar]
- Dieter, G.E. Mechanical Metallurgy; SI Metric; McGraw-Hill: London, UK, 1988; pp. 539–546. [Google Scholar]
- Costa, H.L.; Hutchings, I.M. Hydrodynamic Lubrication of Textured Steel Surfaces under Reciprocating Sliding Conditions. Tribol. Int. 2007, 40, 1227–1238. [Google Scholar] [CrossRef]
- Kasaei, M.M.; Oliveira, M.C. Influence of the Contact with Friction on the Deformation Behavior of Advanced High Strength Steels in the Nakajima Test. J. Strain Anal. Eng. Des. 2022, 57, 193–207. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Punch diameter | 50 mm |
| Punch corner radius | 10 mm |
| Die diameter | 56 mm |
| Die corner radius | 6 mm |
| Blank diameters | 105 mm, 110 mm, 115 mm and 120 mm |
| Blank thickness | 1.15 mm |
| Initial blank holding pressure | 0.6 MPa |
| Punch travel (maximum) | 50 mm |
| Punch speed | 10 mm/s |
| Temperature | a (MPa) | b (MPa) | d | C (s−1) | P |
|---|---|---|---|---|---|
| 200 °C | 249.8 | 123.5 | 3.6 | 4.36 | 3.03 |
| 250 °C | 169.2 | 73.9 | 3.8 | 0.74 | 2.88 |
| Temperature | YS (MPa) | UTS (MPa) | r0 | r45 | r90 |
|---|---|---|---|---|---|
| 200 °C | 117 | 156 | 0.64 | 0.81 | 0.75 |
| 250 °C | 98 | 114 | 0.68 | 0.84 | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrivastava, A.; Digavalli, R.K. Effect of Process Variables on Interface Friction Characteristics in Strip Drawing of AA 5182 Alloy and Its Formability in Warm Deep Drawing. J. Manuf. Mater. Process. 2023, 7, 175. https://doi.org/10.3390/jmmp7050175
Shrivastava A, Digavalli RK. Effect of Process Variables on Interface Friction Characteristics in Strip Drawing of AA 5182 Alloy and Its Formability in Warm Deep Drawing. Journal of Manufacturing and Materials Processing. 2023; 7(5):175. https://doi.org/10.3390/jmmp7050175
Chicago/Turabian StyleShrivastava, Archit, and Ravi Kumar Digavalli. 2023. "Effect of Process Variables on Interface Friction Characteristics in Strip Drawing of AA 5182 Alloy and Its Formability in Warm Deep Drawing" Journal of Manufacturing and Materials Processing 7, no. 5: 175. https://doi.org/10.3390/jmmp7050175
APA StyleShrivastava, A., & Digavalli, R. K. (2023). Effect of Process Variables on Interface Friction Characteristics in Strip Drawing of AA 5182 Alloy and Its Formability in Warm Deep Drawing. Journal of Manufacturing and Materials Processing, 7(5), 175. https://doi.org/10.3390/jmmp7050175











