Machine-Learning-Based Thermal Conductivity Prediction for Additively Manufactured Alloys
Abstract
:1. Introduction
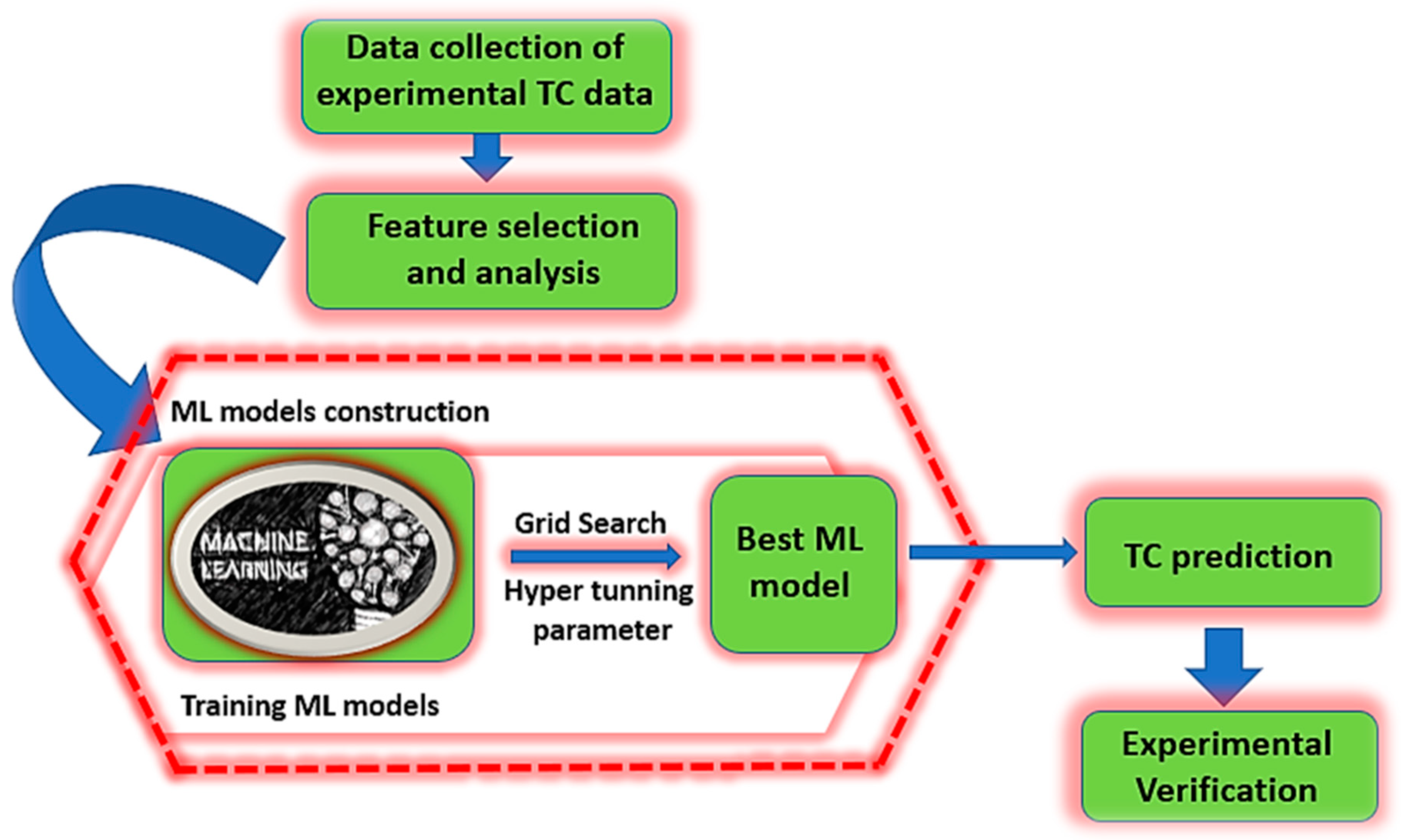
2. Machine Learning Methods
2.1. Establishment of an Alloy TC Database
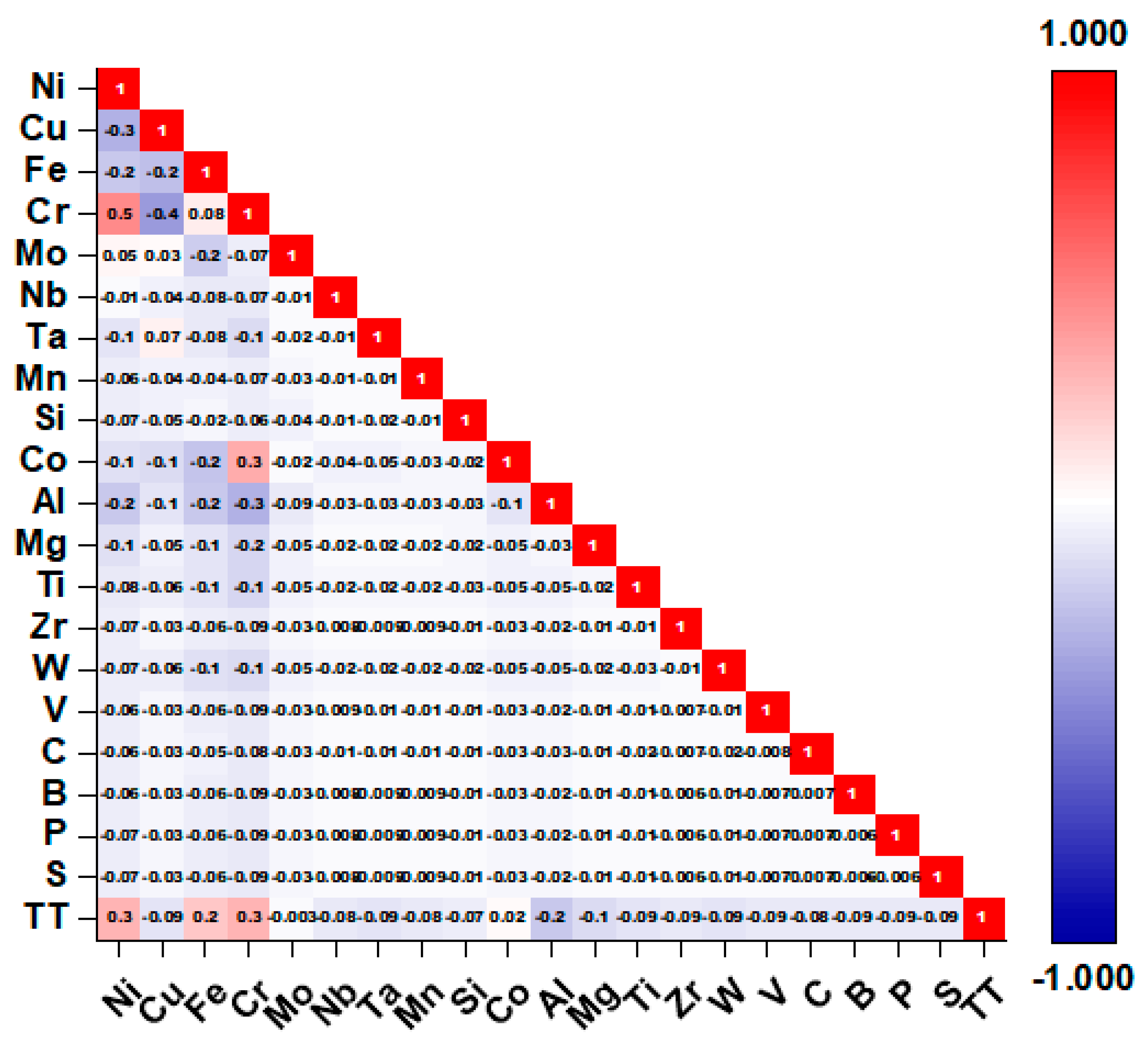
2.2. Feature Selection and Analysis
2.3. ML Methods
3. Results and Discussion
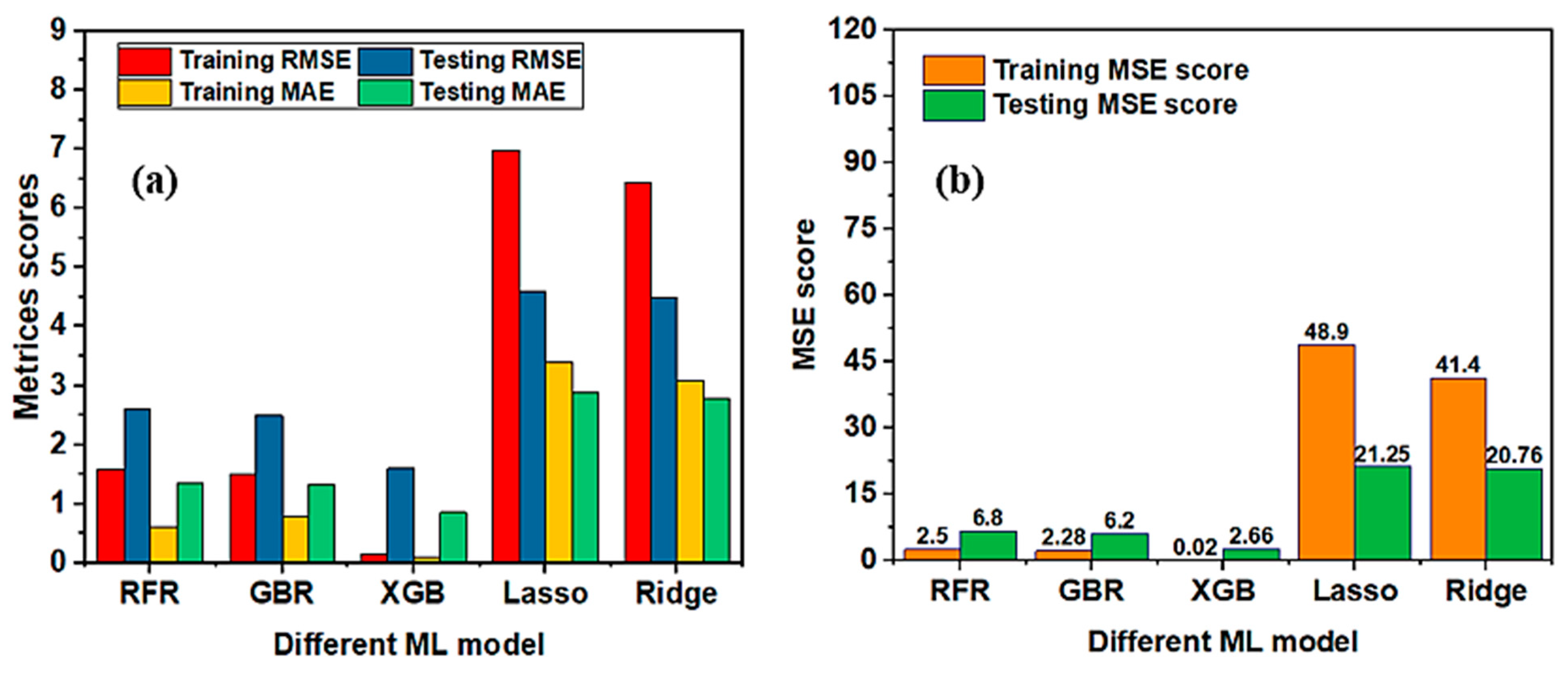
3.1. ML Models and Evaluation
3.2. Additional Testing of the XGB Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, Z.Q.; Wang, J.G.; Guan, Z.P.; Ma, P.K.; Zhao, P.; Li, Z.J.; Lu, T.S.; Yan, R.F. Effect of short T6 heat treatment on the thermal conductivity and mechanical properties of different casting processes Al-Si-Mg-Cu Alloys. Metals 2021, 11, 1450. [Google Scholar]
- Li, S.; Yang, X.; Hou, J.; Du, W.J. A review on thermal conductivity of magnesium and its alloys. J. Magnes. Alloys 2020, 8, 78–90. [Google Scholar]
- Zhang, C.; Du, Y.; Liu, S.; Liu, Y.; Sundman, B.J.T.A. Thermal conductivity of Al–Cu–Mg–Si alloys: Experimental measurement and CALPHAD modeling. Thermochim. Acta 2016, 635, 8–16. [Google Scholar]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; Du Plessis, A. Metal additive manufacturing in aerospace. Mater. Des. 2021, 209, 110008. [Google Scholar]
- Niknam, S.A.; Mortazavi, M.; Li, D. Additively manufactured heat exchangers: A review on opportunities and challenges. Int. J. Adv. Manuf. Technol. 2021, 112, 601–618. [Google Scholar]
- Pan, H.; Pan, F.; Yang, R.; Peng, J.; Zhao, C.; She, J.; Gao, Z.; Tang, A. Thermal and electrical conductivity of binary magnesium alloys. J. Mater. Sci. 2014, 49, 3107–3124. [Google Scholar]
- Miura, A.; Osada, T.; Kawagishi, K.; Uchida, K.I. Thermal transport properties of Ni–Co-based superalloy. AIP Adv. 2020, 10, 125118. [Google Scholar]
- Cheng, H.H.; Huang, D.S.; Lin, M.T. Heat dissipation design and analysis of high power LED array using the finite element method. Microelectron. Reliab. 2012, 52, 905–911. [Google Scholar]
- Li, W.; Mingo, N.; Lindsay, L.; Broido, D.A.; Stewart, D.A.; Katcho, N.A. Thermal conductivity of diamond nanowires from first principles. Phys. Rev. B 2012, 85, 195436. [Google Scholar]
- Ward, A.; Broido, D.; Stewart, D.A.; Deinzer, G. Ab initio theory of the lattice thermal conductivity in diamond. Phys. Rev. B 2009, 80, 125203. [Google Scholar]
- Shiomi, J.; Esfarjani, K.; Chen, G. Thermal conductivity of half-Heusler compounds from first-principles calculations. Phys. Rev. B 2011, 84, 104302. [Google Scholar]
- Broido, D.A.; Malorny, M.; Birner, G.; Mingo, N.; Stewart, D.A. Intrinsic lattice thermal conductivity of semiconductors from first principles. Appl. Phys. Lett. 2007, 91, 231922. [Google Scholar]
- Ward, A.; Broido, D.A. Intrinsic phonon relaxation times from first-principles studies of the thermal conductivities of Si and Ge. Phys. Rev. B 2010, 81, 085205. [Google Scholar]
- Esfarjani, K.; Chen, G.; Stokes, H.T. Heat transport in silicon from first-principles calculations. Phys. Rev. B 2011, 84, 085204. [Google Scholar]
- Eliassen, S.N.; Katre, A.; Madsen, G.K.; Persson, C.; Løvvik, O.M.; Berland, K. Lattice thermal conductivity of TixZr yHf1− x− y NiSn half-Heusler alloys calculated from first principles: Key role of nature of phonon modes. Phys. Rev. B 2017, 95, 045202. [Google Scholar]
- Ding, G.; Gao, G.Y.; Yao, K.L. Examining the thermal conductivity of the half-Heusler alloy TiNiSn by first-principles calculations. J. Phys. D Appl. Phys. 2015, 48, 235302. [Google Scholar]
- Lampin, E.; Palla, P.L.; Francioso, P.A.; Cleri, F. Thermal conductivity from approach-to-equilibrium molecular dynamics. J. Appl. Phys. 2013, 114, 033525. [Google Scholar]
- Liu, X.; Zhang, J.; Pei, Z. Machine learning for high-entropy alloys: Progress, challenges and opportunities. Prog. Mater. Sci. 2022, 131, 101018. [Google Scholar]
- Zhou, Z.; Zhou, Y.; He, Q.; Ding, Z.; Li, F.; Yang, Y. Machine learning guided appraisal and exploration of phase design for high entropy alloys. Npj. Comput. Mater. 2019, 5, 128. [Google Scholar]
- Zhou, Y.; Srinivasan, P.; Körmann, F.; Grabowski, B.; Smith, R.; Goddard, P.; Duff, A.I. Thermodynamics up to the melting point in a TaVCrW high entropy alloy: Systematic abinitio study aided by machine learning potentials. Phys. Rev. B 2022, 105, 214302. [Google Scholar]
- Schleder, G.R.; Padilha, A.C.; Acosta, C.M.; Costa, M.; Fazzio, A. From DFT to machine learning: Recent approaches to materials science—A review. J. Phys. Mater. 2019, 2, 032001. [Google Scholar]
- Schmidt, J.; Marques, M.R.; Botti, S.; Marques, M.A. Recent advances and applications of machine learning in solid-state materials science. Npj. Comput. Mater. 2019, 5, 83. [Google Scholar]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar]
- Raccuglia, P.; Elbert, K.C.; Adler, P.D.; Falk, C.; Wenny, M.B.; Mollo, A.; Zeller, M.; Friedler, S.A.; Schrier, J.; Norquist, A.J. Machine-learning-assisted materials discovery using failed experiments. Nature 2016, 533, 73–76. [Google Scholar]
- Chen, L.; Tran, H.; Batra, R.; Kim, C.; Ramprasad, R. Machine learning models for the lattice thermal conductivity prediction of inorganic materials. Comput. Mater. Sci. 2019, 170, 109155. [Google Scholar] [CrossRef]
- Jaafreh, R.; Kang, Y.S.; Hamad, K. Interfaces. Lattice thermal conductivity: An accelerated discovery guided by machine learning. ACS Appl. Mater Interfaces 2021, 13, 57204–57213. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B.; Podryabinkin, E.V.; Roche, S.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. Machine-learning interatomic potentials enable first-principles multiscale modeling of lattice thermal conductivity in graphene/borophene heterostructures. Mater. Horiz. 2020, 7, 2359–2367. [Google Scholar] [CrossRef]
- Tewari, A.; Dixit, S.; Sahni, N.; Bordas, S.P. Machine learning approaches to identify and design low thermal conductivity oxides for thermoelectric applications. Data-Centric Eng. 2020, 1, e8. [Google Scholar] [CrossRef]
- Miyazaki, H.; Tamura, T.; Mikami, M.; Watanabe, K.; Ide, N.; Ozkendir, O.M.; Nishino, Y. Machine learning based prediction of lattice thermal conductivity for half-Heusler compounds using atomic information. Sci. Rep. 2021, 11, 13410. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Kondo, Y.; Kakimoto, M.A.; Yang, B.; Yamada, H.; Kuwajima, I.; Lambard, G.; Hongo, K.; Xu, Y.; Shiomi, J.; et al. Machine-learning-assisted discovery of polymers with high thermal conductivity using a molecular design algorithm. Npj. Comput. Mater. 2019, 5, 66. [Google Scholar] [CrossRef]
- Gradl, P.; Tinker, D.C.; Park, A.; Mireles, O.R.; Garcia, M.; Wilkerson, R.; Mckinney, C.J. Performance. Robust metal additive manufacturing process selection and development for aerospace components. J. Mater. Eng. Perform. 2022, 31, 6013–6044. [Google Scholar] [CrossRef]
- Gradl, P.R.; Mireles, O.R.; Protz, C.S.; Garcia, C.P. Metal Additive Manufacturing for Propulsion Applications; Timothy, C., Lieuwen, T.C., Eds.; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2022. [Google Scholar]
- Zeng, C.; Guo, S.; Gradl, P.R.; Belcher, T. Thermophysical Properties of Select AM Alloys. In Metal Additive Manufacturing for Propulsion Applications; Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2022; pp. 775–824. [Google Scholar]
- Joseph, J.; Hodgson, P.; Jarvis, T.; Wu, X.; Stanford, N.; Fabijanic, D.M. Effect of hot isostatic pressing on the microstructure and mechanical properties of additive manufactured AlxCoCrFeNi high entropy alloys. Mater. Sci. Eng. A 2018, 733, 59–70. [Google Scholar] [CrossRef]
- Hafenstein, S.; Werner, E. Pressure dependence of age-hardenability of aluminum cast alloys and coarsening of precipitates during hot isostatic pressing. Mater. Sci. Eng. A 2019, 757, 62–69. [Google Scholar] [CrossRef]
- Lario, J.; Vicente, Á.; Amigó, V.J.M. Evolution of the microstructure and mechanical properties of a Ti35Nb2Sn alloy post-processed by hot isostatic pressing for biomedical applications. Mater. Sci. Eng. A 2021, 11, 1027. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, Y. Quench rates in air, water, and liquid nitrogen, and inference of temperature in volcanic eruption columns. Earth Planet. Sci. Lett. 2002, 200, 315–330. [Google Scholar] [CrossRef]
- Nishibata, T.; Kojima, N. Effect of quenching rate on hardness and microstructure of hot-stamped steel. J. Alloys Compd. 2013, 577, S549–S554. [Google Scholar] [CrossRef]
- Zeng, C.; Zhang, B.; Hemmasian Ettefagh, A.; Wen, H.; Yao, H.; Meng, W.J.; Guo, S. Mechanical, thermal, and corrosion properties of Cu-10Sn alloy prepared by laser-powder-bed-fusion additive manufacturing. Addit. Manuf. 2020, 35, 101411. [Google Scholar] [CrossRef]
- Chen, Y.; Zeng, C.; Ding., H.; Emanet, S.; Gradl, P.R.; Ellis, D.L.; Guo, S. Thermophysical properties of additively manufactured (AM) GRCOP-42 and GRCOP-84. Mater. Today Commun. 2023, 36, 106665. [Google Scholar] [CrossRef]
- Rodgers, J.L.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Yang, C.; Ren, C.; Jia, Y.; Wang, G.; Li, M.; Lu, W. A machine learning-based alloy design system to facilitate the rational design of high entropy alloys with enhanced hardness. Acta Mater. 2022, 222, 117431. [Google Scholar] [CrossRef]
- Khakurel, H.; Taufique, M.; Roy, A.; Balasubramanian, G.; Ouyang, G.; Cui, J.; Johnson, D.D.; Devanathan, R. Machine learning assisted prediction of the Young’s modulus of compositionally complex alloys. Sci. Rep. 2021, 11, 17149. [Google Scholar] [CrossRef]
- Yang, K.; Xu, X.; Yang, B.; Cook, B.; Ramos, H.; Krishnan, N.; Smedskjaer, M.M.; Hoover, C.; Bauchy, M. Predicting the Young’s modulus of silicate glasses using high-throughput molecular dynamics simulations and machine learning. Sci. Rep. 2019, 9, 8739. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y. Multiple predicting K-fold cross-validation for model selection. J. Nonparametr. Stat. 2018, 30, 197–215. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, É. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- LaValle, S.M.; Branicky, M.S.; Lindemann, S.R. On the relationship between classical grid search and probabilistic roadmaps. Int. J. Robot. Res. 2004, 23, 673–692. [Google Scholar] [CrossRef]
- Huang, X.; Jin, C.; Zhang, C.; Zhang, H.; Fu, H. Machine learning assisted modelling and design of solid solution hardened high entropy alloys. Mater. Des. 2021, 211, 110177. [Google Scholar] [CrossRef]
- Huang, W.; Martin, P.; Zhuang, H.L. Machine-learning phase prediction of high-entropy alloys. Acta Mater. 2019, 169, 225–236. [Google Scholar] [CrossRef]
- Lee, S.Y.; Byeon, S.; Kim, H.S.; Jin, H.; Lee, S. Deep learning-based phase prediction of high-entropy alloys: Optimization, generation, and explanation. Mater. Des. 2021, 197, 109260. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. 2012, 25, 1–9. [Google Scholar]
- Sun, Y.; Hu, W. Novel machine learning framework for thermal conductivity prediction by crystal graph convolution embedded ensemble. SmartMat 2022, 3, 474–481. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, S.; Wang, Z.; Ni, J. Identification of crystalline materials with ultra-low thermal conductivity based on machine learning study. J. Phys. Chem. C 2020, 124, 8488–8495. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. 2017, 30, 4768–4777. [Google Scholar]
- Wang, G.; Li, Y. Effects of alloying elements and temperature on thermal conductivity of ferrite. J. Appl. Phys. 2019, 126, 125118. [Google Scholar] [CrossRef]
- Chen, L.; Lü, S.; Guo, W.; Li, J.; Wu, S. High thermal conductivity of highly alloyed Mg-Zn-Cu alloy and its mechanism. J. Alloys Compd. 2022, 918, 165614. [Google Scholar] [CrossRef]
- Choi, S.W.; Kim, Y.M.; Kim, Y.C.; Kang, C.S. Technology. Effects of alloying elements on mechanical and thermal characteristics of Al-6wt-% Si-0.4 wt-% Mg–(Cu) foundry alloys. Mater. Sci. Technol. 2019, 35, 1365–1371. [Google Scholar] [CrossRef]
- Qin, R.; Yan, R.F.; Guan, Z.P.; Zhang, G.Q.; Song, J.W.; Ren, M.W.; Wang, J.G. Effect of vanadium on Fe-rich phase, mechanical properties and thermal conductivity of hypoeutectic Al–Si alloy. Mater. Res. Express. 2021, 8, 026518. [Google Scholar] [CrossRef]
- Heo, J.; Hashimoto, N.; Oka, H.; Noto, H. Improvement of thermal conductivity by adding tungsten and/or copper wire in F82H. J. Nucl. Sci. Technol. 2022, 59, 216–221. [Google Scholar] [CrossRef]
- Moore, J.; McElroy, D.; Graves, R.S. Thermal conductivity and electrical resistivity of high-purity copper from 78 to 400 K. Can. J. Phys. 1967, 45, 3849–3865. [Google Scholar] [CrossRef]
- Brandt, R.; Neuer, G. Electrical resistivity and thermal conductivity of pure aluminum and aluminum alloys up to and above the melting temperature. Int. J. Thermophys. 2007, 28, 1429–1446. [Google Scholar] [CrossRef]
- Ho, C.Y.; Powell, R.W.; Liley, P.E. Thermal conductivity of the elements: A comprehensive review. J. Phys. Chem. Ref. Data 1974, 1, 11974. [Google Scholar]
- Tritt, T.M. Thermal Conductivity: Theory, Properties, and Applications; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
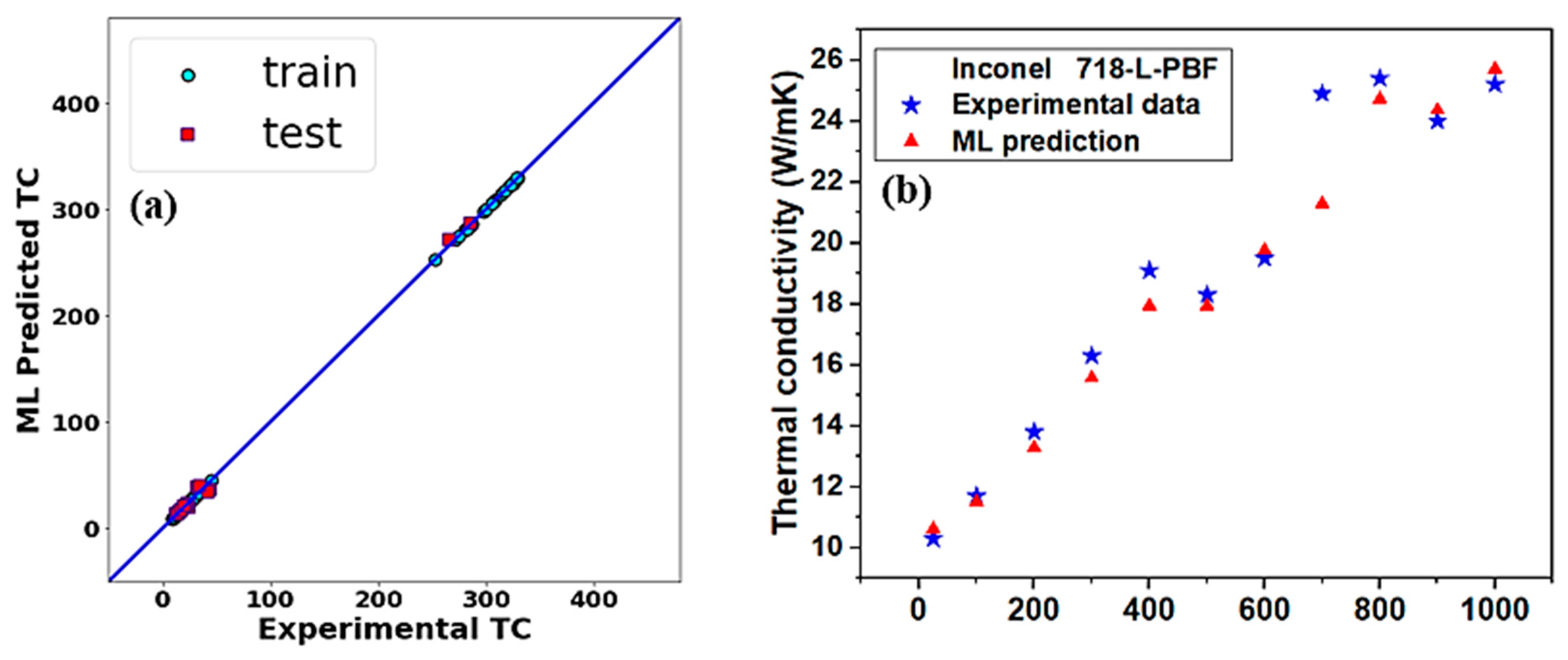
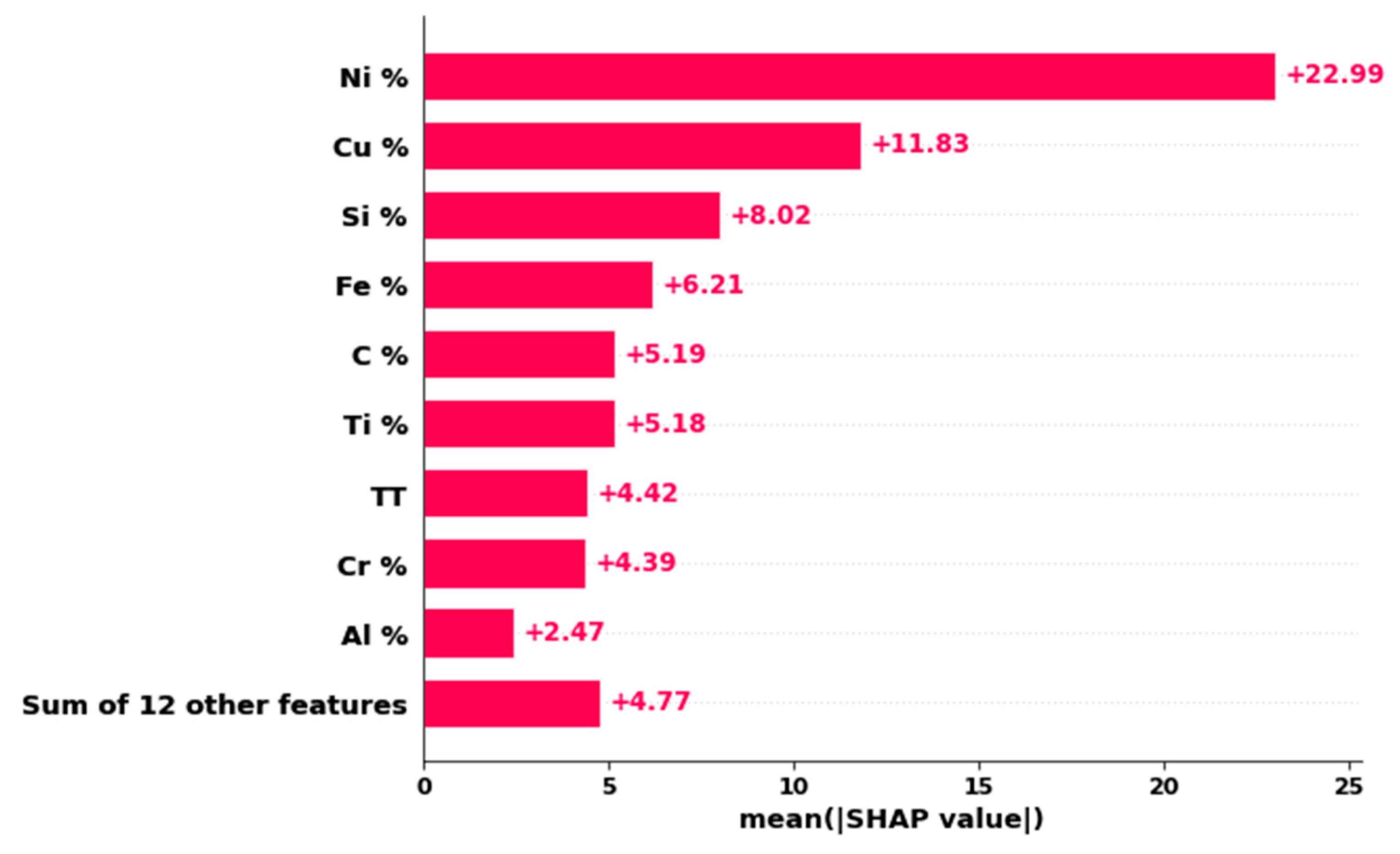
| Alloy | Process | Heat Treatment Procedures a |
|---|---|---|
| GRCop-42 | L-PBF | HIP b |
| GRCop-84 | L-PBF | HIP b |
| C-18150 | L-PBF | Sol (1000 °C for 9 h) |
| Inconel 625 | L-PBF | SR (1066 °C for 90 min) + HIP b + Sol (1177 °C for 60 min, quench) |
| Inconel 625 | LP-DED | SR (1066 °C for 90 min) + HIP b + Sol (1177 °C for 60 min, quench) |
| Inconel 625 | Wrought | Anneal (1010 °C for 60 min), quench |
| Inconel 718 | L-PBF | SR (1066 °C for 90 min) + HIP b + Sol (1066 °C for 60 min, quench) + Age (760 °C for 10 h, cool to 649 °C hold until total aging time of 20 h) |
| Inconel 939 | L-PBF | SR (1066 °C for 90 min) + HIP b + Sol (1090 °C for 4 h, quench) + Age (1000 °C for 6 h, quench + 800 °C for 4 h, air cooling) |
| Hastelloy X | L-PBF | SR (1066 °C for 90 min) + HIP b + Sol (1177 °C for 180 min, quench) |
| Hastelloy X | LP-DED | SR (1066 °C for 90 min) + HIP b + Sol (1177 °C for 180 min, quench) |
| Hastelloy X | Wrought | Hot rolled, anneal (1177 °C for 20 min), water quench |
| Haynes 230 | L-PBF | SR (1066 °C for 90 min) + HIP b + Sol (1177 °C for 60 min, quench) |
| Haynes 230 | LP-DED | SR (1066 °C for 90 min) + HIP b + Sol (1177 °C for 60 min, quench) |
| Haynes 230 | Wrought | Hot rolled, Sol (1204 °C for 30 min), quench |
| Haynes 282 | L-PBF | SR (1066 °C for 90 min) + HIP b + Sol (1135 °C for 60 min, quench) + Age (1010 °C for 120 min, cool to 788 °C hold until total aging time of 10 h, quench) |
| SS 316L | LP-DED | SR (899 °C for 120 min) + HIP b + Sol (1100 °C for 120 min, quench) |
| 15-5, H1150 | LP-DED | SR (649 °C for 60 min) + HIP b + Sol (1050 °C for 60 min, air cool) + Age (621 °C for 60 min, air cool) |
| 17-4, H1150 | LP-DED | SR (649 °C for 60 min) + HIP b + Sol (1050 °C for 60 min, air cool) + Age (621 °C for 60 min, air cool) |
| NASA HR-1 | LP-DED 350W | SR (1066 °C for 90 min) + HIP b + Sol (1066 °C for 60 min, quench) + Age (691 °C for 16 h, cool to 621 °C hold until total aging time of 32 h) |
| JBK-75 | LP-DED | SR (982 °C for 90 min) + HIP b + Sol (982 °C for 60 min, quench) + Age (718 °C for 16 h) |
| CoCr | LP-DED | SR (1052 °C for 120 min) + HIP b + Sol (1100 °C for 120 min, quench) + Age (802 °C for 25 h, quench; 1000 °C for 60 min, quench) |
| Thermal Conductivity (W/(mK)) at Different Testing Temperatures (°C) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| alloy | Process | 25 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| GRCop-42 | L-PBF | 327.5 | 328.7 | 329.4 | 328.4 | 325 | 322.1 | 316.9 | 305.8 | - | - | - |
| GRCop-84 | L-PBF | 286.4 | 285.5 | 286 | 285 | 282.5 | 279.8 | 274.6 | 265.9 | - | - | - |
| C-18150 | L-PBF | 271.2 | 284.4 | 297.8 | 305.4 | 308.9 | 322.9 | 324.4 | 314.3 | 299.7 | 281.7 | 252.4 |
| Inconel 625 | L-PBF | 10.3 | 11.7 | 13.9 | 16.6 | 19.5 | 18.7 | 20.6 | 23 | 23 | 24.6 | 25.6 |
| Inconel 625 | LP-DED | 10.6 | 12.1 | 14.4 | 17.2 | 20.2 | 19.2 | 21 | 23.4 | 23 | 25.1 | 26.4 |
| Inconel 625 | Wrought | 10.4 | 11.6 | 13.5 | 16.5 | 19.4 | 18.6 | 20.6 | 22.9 | 23 | 24.9 | 25.4 |
| Inconel 939 | L-PBF | 10.4 | 11.8 | 13.5 | 16 | 18.4 | 18.3 | 20.3 | 21.8 | 23.2 | 25 | 25.6 |
| Inconel 718 | L-PBF | 10.3 | 11.7 | 13.8 | 16.3 | 19.1 | 18.3 | 19.5 | 24.9 | 25.4 | 24.0 | 25.2 |
| Hastelloy X | L-PBF | 11.1 | 12.8 | 15.3 | 17.9 | 21 | 20.6 | 23.7 | 26.3 | 29.5 | 28.8 | 29.4 |
| Hastelloy X | LP-DED | 10.5 | 12.1 | 14.5 | 17.1 | 19.9 | 19.5 | 22.4 | 24.8 | 28.7 | 27 | 27.9 |
| Hastelloy X | Wrought | 10.6 | 12.2 | 14.6 | 17.2 | 20.2 | 19.7 | 22.5 | 24.8 | 27.9 | 27.2 | 27.6 |
| Haynes 230 | L-PBF | 8.8 | 10.2 | 12.4 | 15 | 17.7 | 17.2 | 19 | 21.4 | 21.9 | 23.8 | 25.2 |
| Haynes 230 | LP-DED | 9.2 | 10.6 | 12.8 | 15.5 | 18.5 | 17.8 | 19.6 | 22 | 22.1 | 24.4 | 25.7 |
| Haynes 230 | Wrought | 9.1 | 10.5 | 12.8 | 15.5 | 18.4 | 17.8 | 19.5 | 21.7 | 22.6 | 24.6 | 26.3 |
| Haynes 282 | L-PBF | 10.9 | 12.3 | 14.4 | 16.8 | 19.6 | 19.1 | 20.9 | 23.3 | 23.4 | 25.2 | 26 |
| SS 316L | LP-DED | 13.3 | 14.9 | 17.2 | 19.5 | 22.1 | 22.6 | 28.9 | 31.7 | 42 | 32.4 | 31.4 |
| 15-5, H1150 | LP-DED | 16.1 | 17.7 | 19.6 | 21.2 | 22.6 | 21.9 | 24 | 31.5 | 44.8 | 33.7 | 32 |
| 17-4, H1150 | LP-DED | 15.2 | 16.7 | 18.5 | 20.1 | 21.6 | 21 | 22.4 | 30.6 | 43.6 | 32.8 | 31.3 |
| NASA HR-1 | LP-DED | 11.1 | 13 | 15.8 | 18.3 | 20.4 | 19.7 | 22.5 | 24.8 | 22.6 | 23.6 | 24.5 |
| JBK-75 | LP-DED | 12.3 | 13.9 | 16.2 | 18.8 | 21.5 | 21.4 | 26.3 | 28.8 | 36 | 29.3 | 29.2 |
| CoCr | LP-DED | 12 | 13.5 | 15.6 | 17.7 | 19.7 | 21.4 | 23.7 | 26 | 28.5 | 31.2 | 34.4 |
| GRCop-42-1 | L-PBF | 316.3 | 312.5 | 318.0 | 315.4 | 310.9 | 305.7 | 298.8 | 288.5 | - | - | - |
| GRCop-42-2 | L-PBF | 320.5 | 318.2 | 317.2 | 314.7 | 310.3 | 305.5 | 299.9 | 289.8 | - | - | - |
| GRCop-42-3 | L-PBF | 325.3 | 331.3 | 330.3 | 327.8 | 323.5 | 318.4 | 312.3 | 302.3 | - | - | - |
| GRCop-42-4 | L-PBF | 329.5 | 329.7 | 327.4 | 324.2 | 319.6 | 314.2 | 307.9 | 297.5 | - | - | - |
| GRCop-42-5 | L-PBF | 328.2 | 327.7 | 324.9 | 321.8 | 317.2 | 311.9 | 305.7 | 295.4 | - | - | - |
| GRCop-42-6 | L-PBF | 325.6 | 322.5 | 319.4 | 315.7 | 311.2 | 305.5 | 297.9 | 288.5 | - | - | - |
| GRCop-42-7 | L-PBF | 342.6 | 341.6 | 340.2 | 337.1 | 332.4 | 327.3 | 321.4 | 310.5 | - | - | - |
| GRCop-84-1 | L-PBF | 308.5 | 304.8 | 303.3 | 300.5 | 296.6 | 292.3 | 285.8 | 275.3 | - | - | - |
| GRCop-84-2 | L-PBF | 291.4 | 288.5 | 287.5 | 285.2 | 281.6 | 277.2 | 271.4 | 262.1 | - | - | - |
| Element | GRCop-42-1 | GRCop-42-2 | GRCop-42-3 | GRCop-42-4 | GRCop-42-5 | GRCop-42-6 | GRCop-42-7 | GRCop-42-8 | GRCop-84-1 | GRCop-84-2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ag | 0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 |
| Al | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.07 | 0.04 | 0.06 | 0.01 | 0.03 |
| Co | 0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 |
| Cr | 3.25 | 3.30 | 3.29 | 3.37 | 3.26 | 3.28 | 3.28 | 3.38 | 6.61 | 6.59 |
| Fe | 0.01 | <0.01 | <0.01 | <0.01 | 0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 |
| Nb | 2.65 | 2.82 | 2.77 | 2.81 | 2.65 | 2.92 | 2.73 | 2.92 | 5.68 | 5.47 |
| Ni | 0.03 | <0.01 | <0.01 | 0.01 | 0.02 | <0.01 | 0.01 | <0.01 | <0.01 | <0.01 |
| O | 0.08 | 0.05 | 0.04 | 0.06 | 0.1 | 0.05 | 0.08 | 0.05 | 0.13 | 0.12 |
| P | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | <0.005 | 0.011 |
| Si | 0.02 | 0.01 | <0.01 | 0.03 | 0.04 | 0.01 | <0.01 | 0.02 | <0.01 | <0.01 |
| ML Model | Train R2 Score | Test R2 Score |
|---|---|---|
| RF | 0.9997 | 0.9228 |
| GBR | 0.9997 | 0.9086 |
| XGB | 0.9999 | 0.9618 |
| Ridge | 0.9948 | 0.6953 |
| Lasso | 0.9956 | 0.7023 |
| Parameters | Hyperparameter Value | Tuned Hyperparameter |
|---|---|---|
| Learning rate | [0.01, 0.1, 0.5] | 0.1 |
| max_depth | [3, 4, 5, 6, 8] | 6 |
| n_estimators | [100, 500, 900] | 900 |
| Subsample | [0.5, 0.7, 1.0] | 0.5 |
| Colsample_bytree | [0.3, 0.4, 0.6] | 0.4 |
| Gamma | [0, 1, 4] | 0 |
| Hyperparameter | Space Searching | Tuned Hyperparameter |
|---|---|---|
| max_depth | (1, 6) | 4.16 |
| learning_rate | (0.01, 0.4), | 0.4 |
| n_estimators | (100, 700), | 448.06 |
| subsample | (0.1, 1), | 0.1 |
| colsample_bytree | (0.1, 1), | 1 |
| min_child_weight | (1, 4), | 1.0 |
| gamma | (0, 4) | 0 |
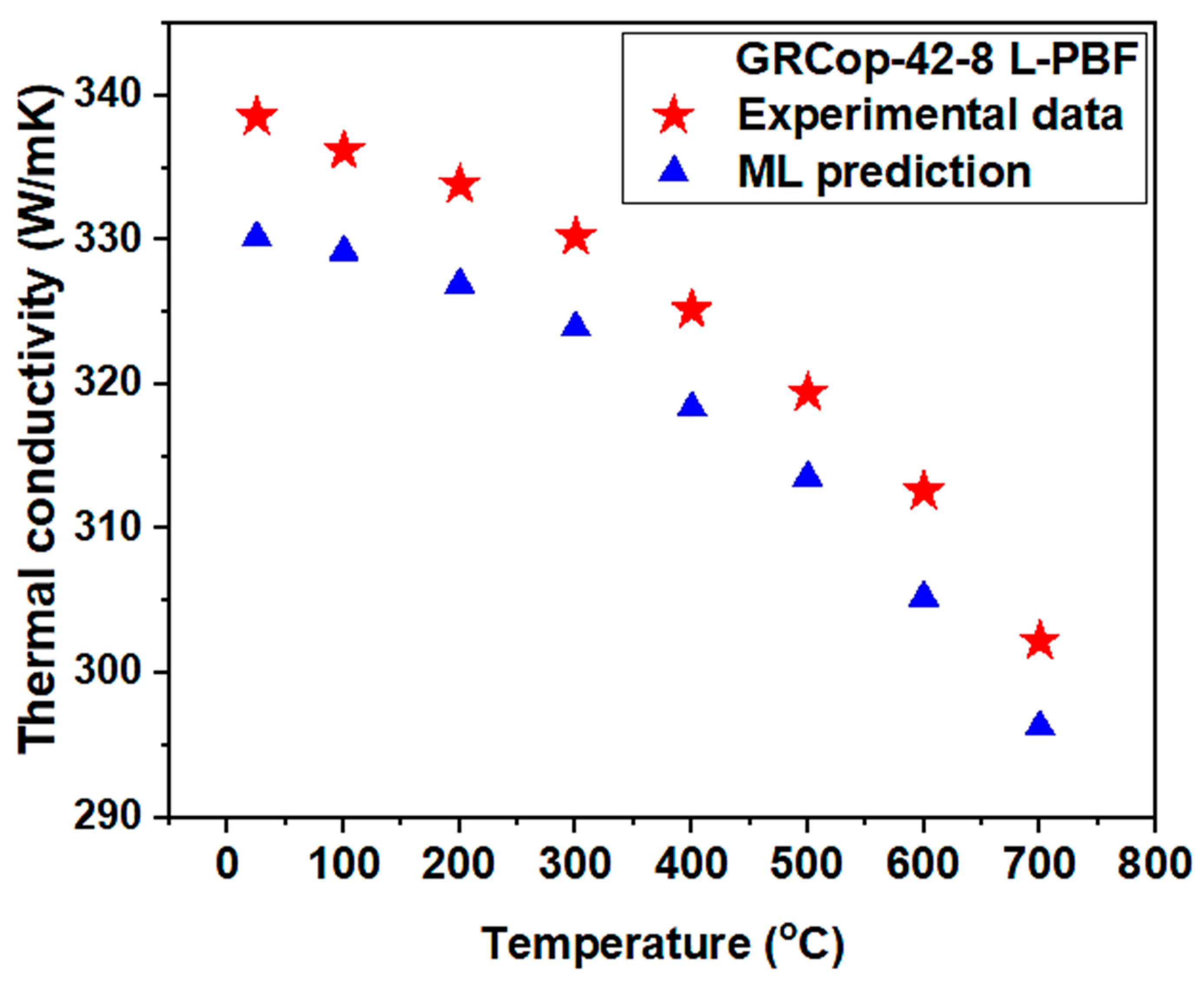
| Testing Temperature (°C) | Experimental TC (W/mK) | TC Predicted Using XGB Model (W/mK) | Error % |
|---|---|---|---|
| 25 | 338.536 | 330.21 | 2.45 |
| 100 | 336.187 | 329.21 | 2.08 |
| 200 | 333.851 | 326.96 | 2.06 |
| 300 | 330.246 | 323.96 | 1.9 |
| 400 | 325.17 | 318.39 | 2.08 |
| 500 | 319.44 | 313.58 | 1.83 |
| 600 | 312.59 | 305.27 | 2.34 |
| 700 | 302.2228 | 296.31 | 1.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhandari, U.; Chen, Y.; Ding, H.; Zeng, C.; Emanet, S.; Gradl, P.R.; Guo, S. Machine-Learning-Based Thermal Conductivity Prediction for Additively Manufactured Alloys. J. Manuf. Mater. Process. 2023, 7, 160. https://doi.org/10.3390/jmmp7050160
Bhandari U, Chen Y, Ding H, Zeng C, Emanet S, Gradl PR, Guo S. Machine-Learning-Based Thermal Conductivity Prediction for Additively Manufactured Alloys. Journal of Manufacturing and Materials Processing. 2023; 7(5):160. https://doi.org/10.3390/jmmp7050160
Chicago/Turabian StyleBhandari, Uttam, Yehong Chen, Huan Ding, Congyuan Zeng, Selami Emanet, Paul R. Gradl, and Shengmin Guo. 2023. "Machine-Learning-Based Thermal Conductivity Prediction for Additively Manufactured Alloys" Journal of Manufacturing and Materials Processing 7, no. 5: 160. https://doi.org/10.3390/jmmp7050160
APA StyleBhandari, U., Chen, Y., Ding, H., Zeng, C., Emanet, S., Gradl, P. R., & Guo, S. (2023). Machine-Learning-Based Thermal Conductivity Prediction for Additively Manufactured Alloys. Journal of Manufacturing and Materials Processing, 7(5), 160. https://doi.org/10.3390/jmmp7050160











