Numerical Study on the Temperature-Dependent Viscosity Effect on the Strand Shape in Extrusion-Based Additive Manufacturing
Abstract
1. Introduction
2. Numerical Simulation
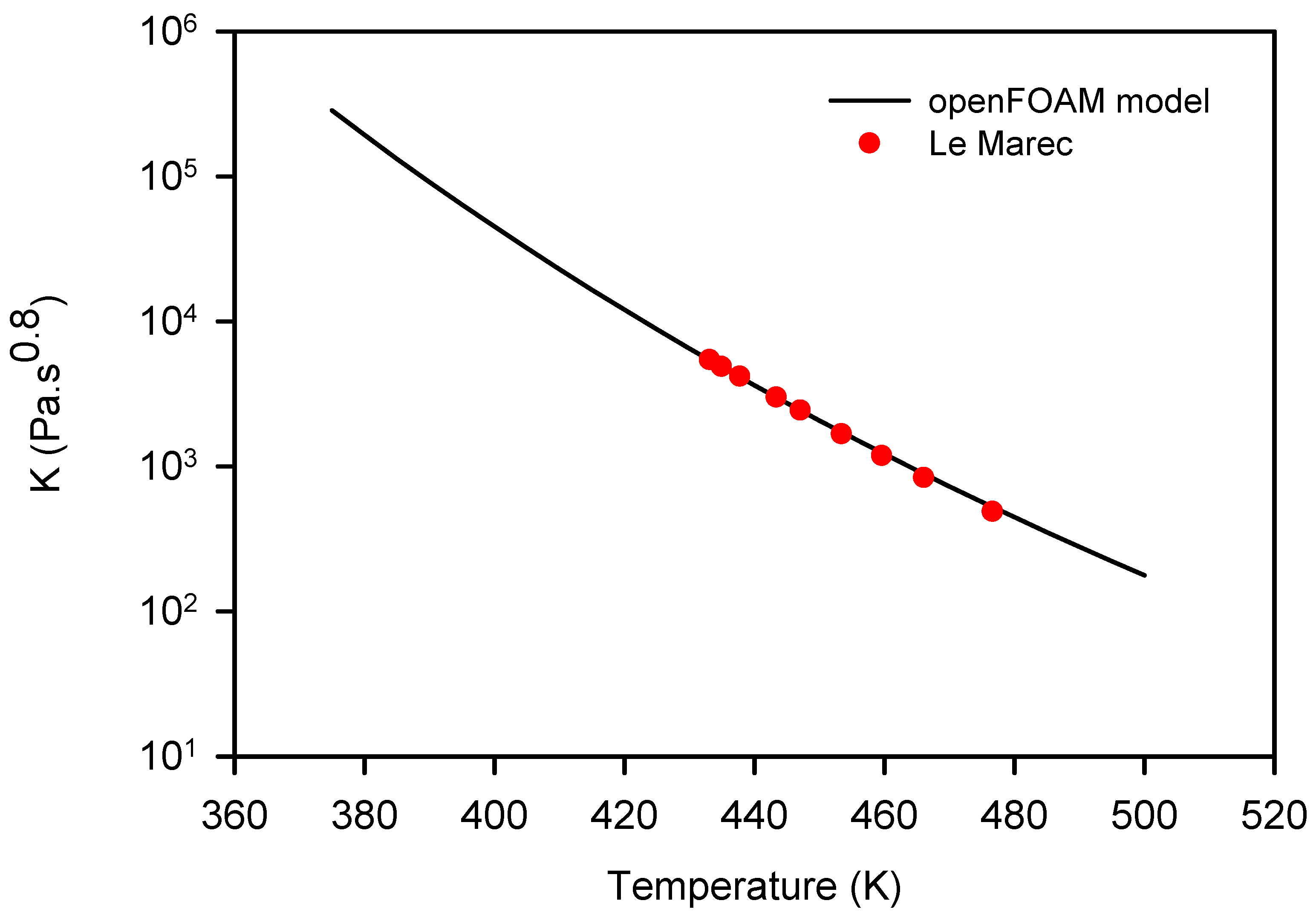
2.1. Governing Equations
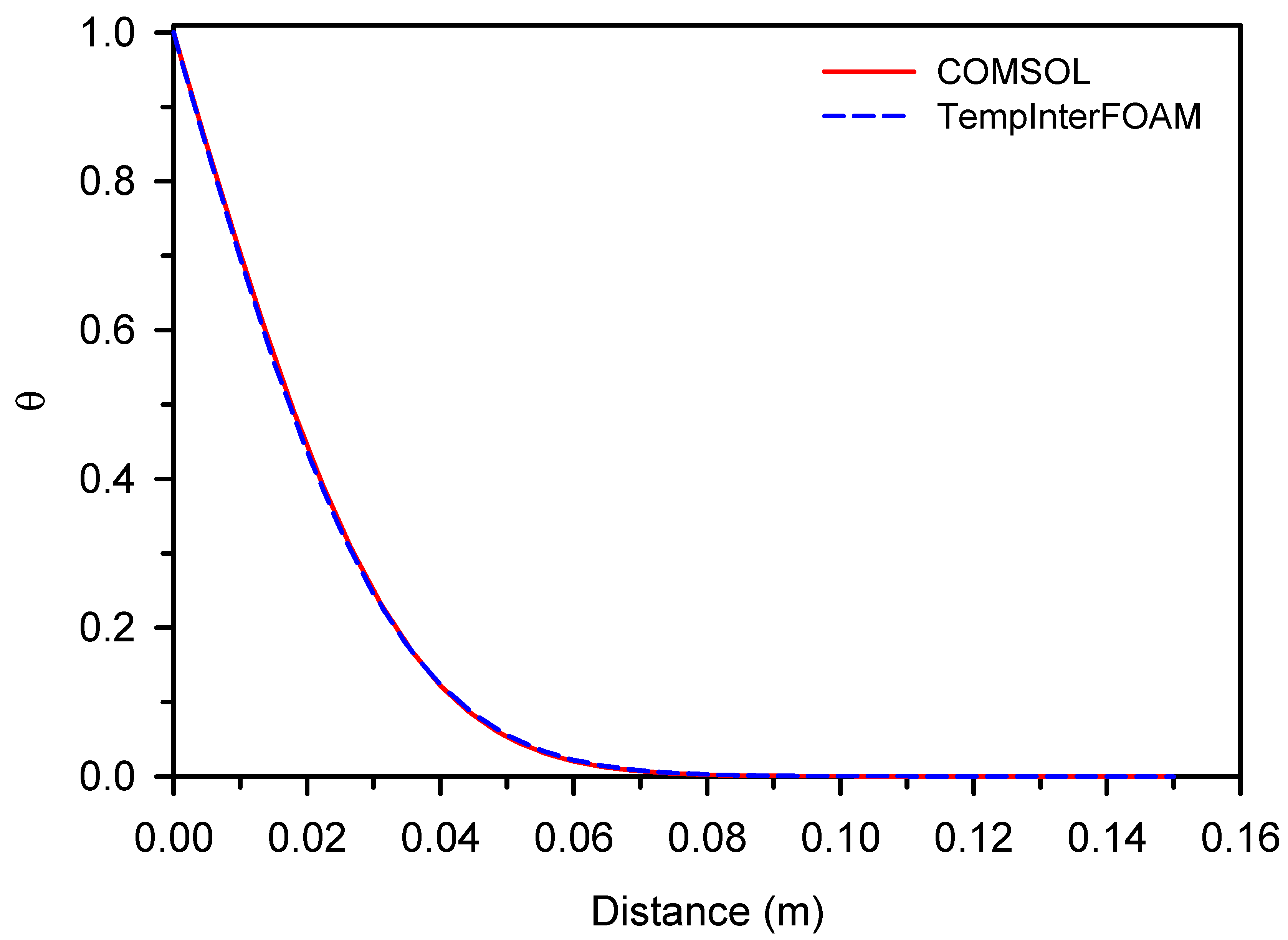
2.2. Numerical Model Solver
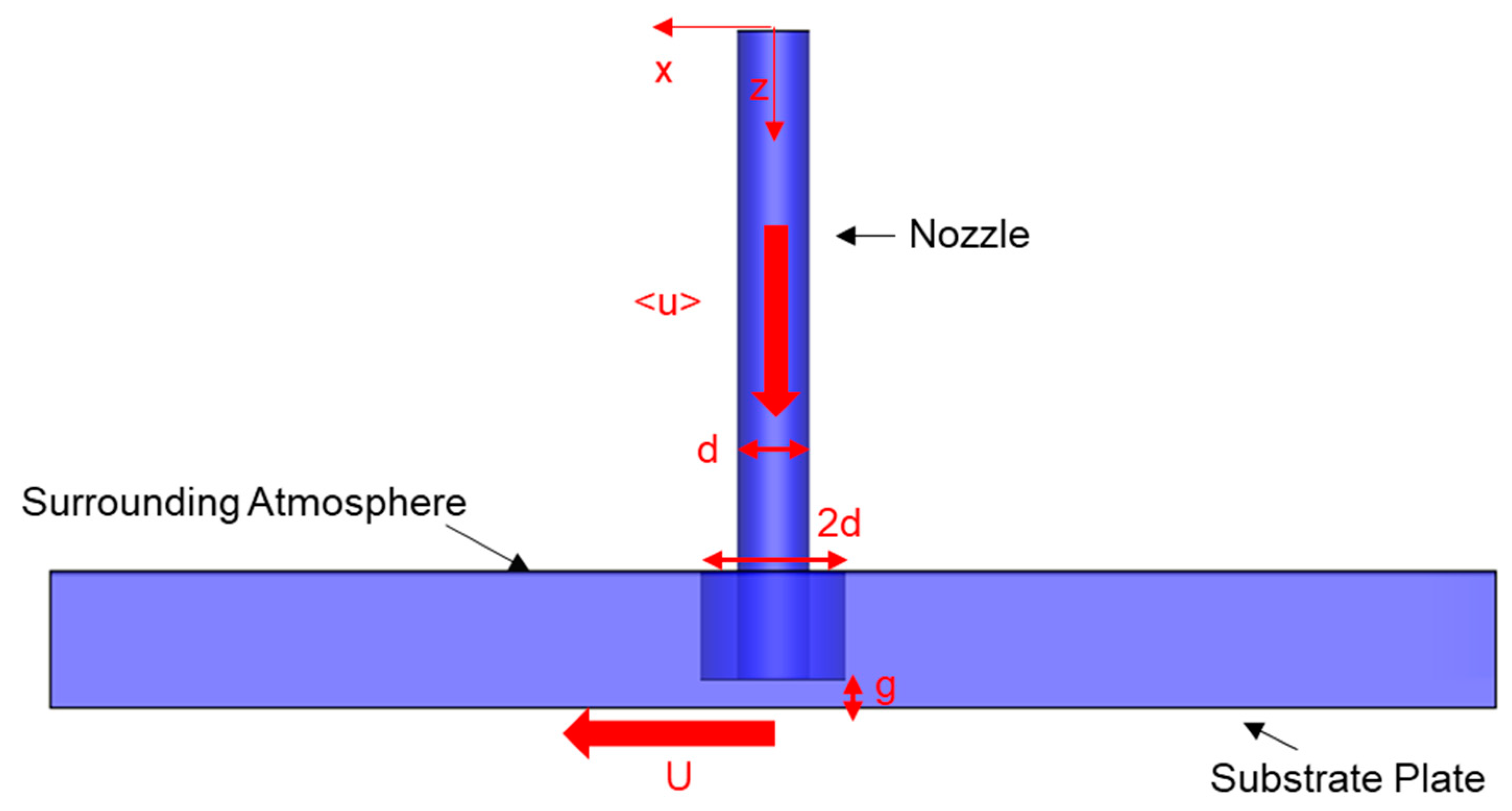
2.3. System Description
3. Results and Discussion
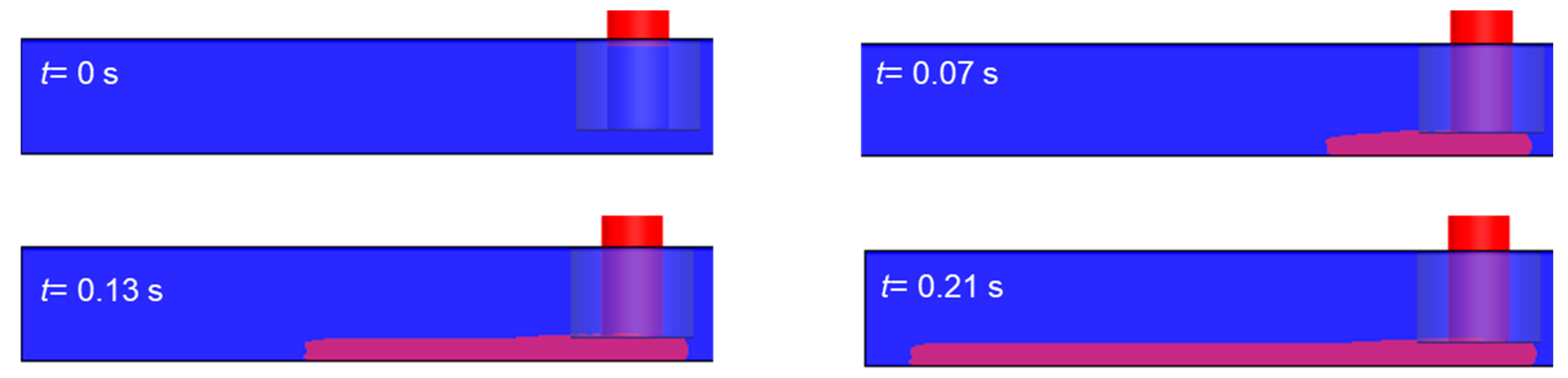
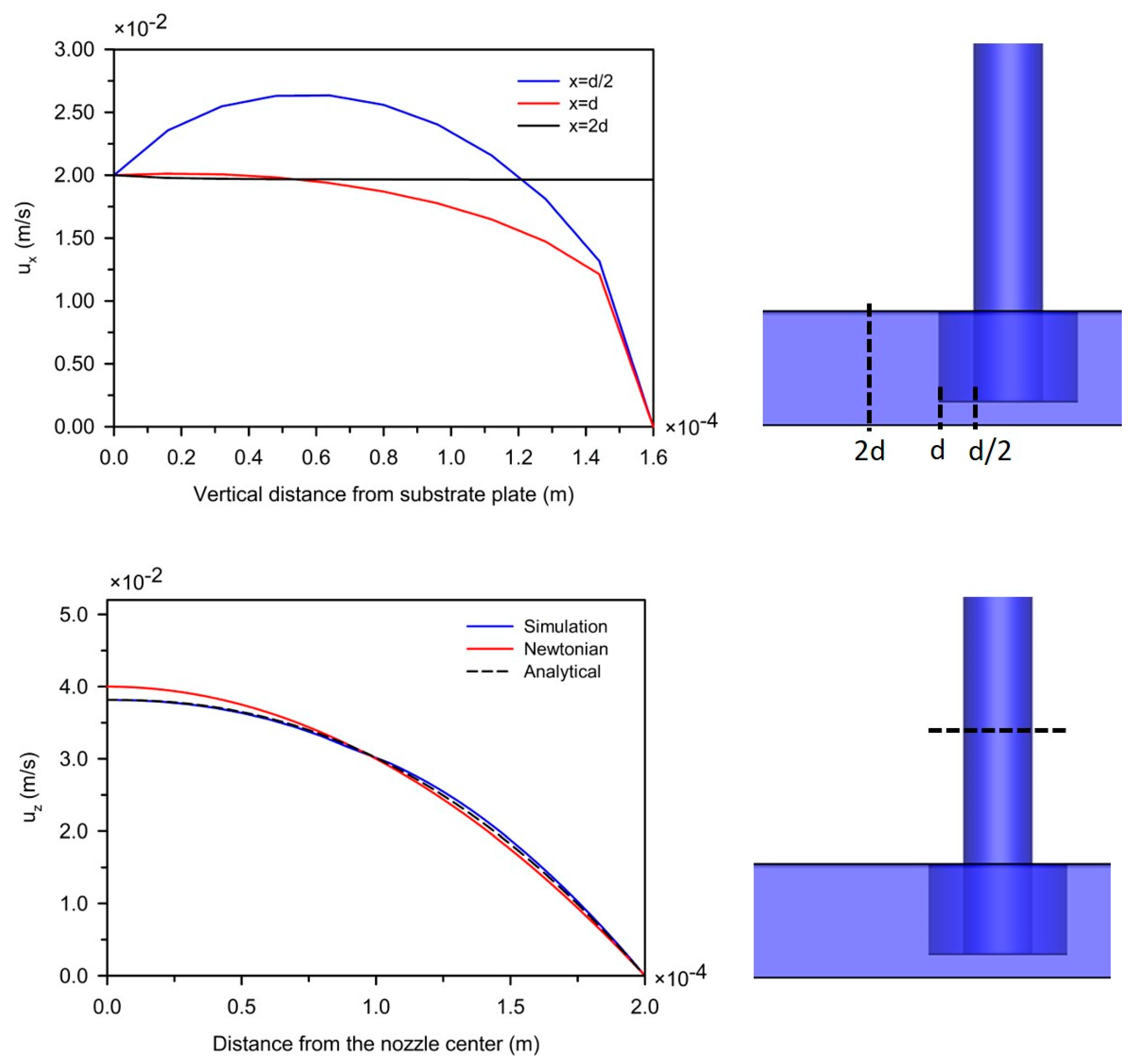
3.1. Simulation of the Extrusion Process
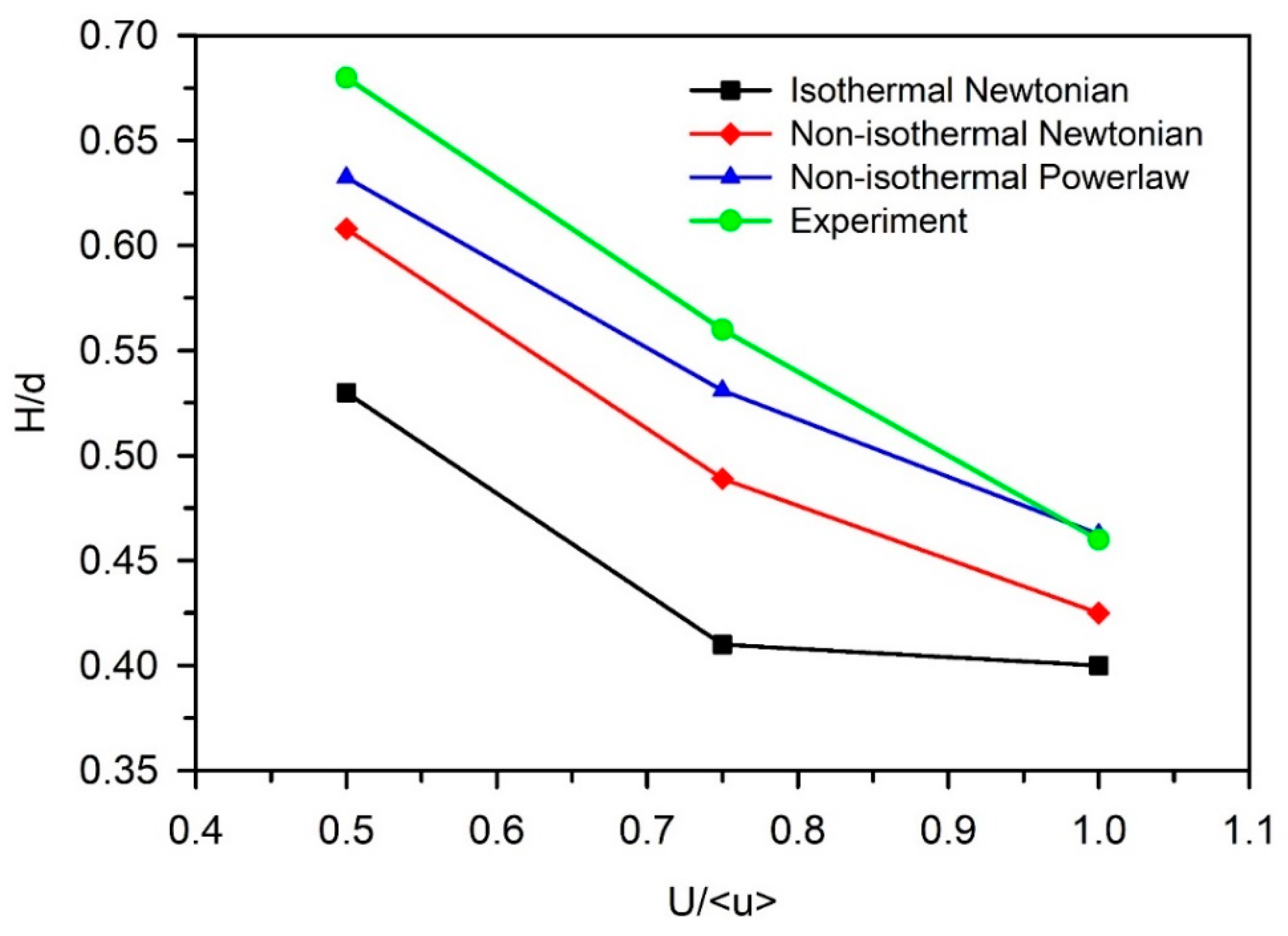
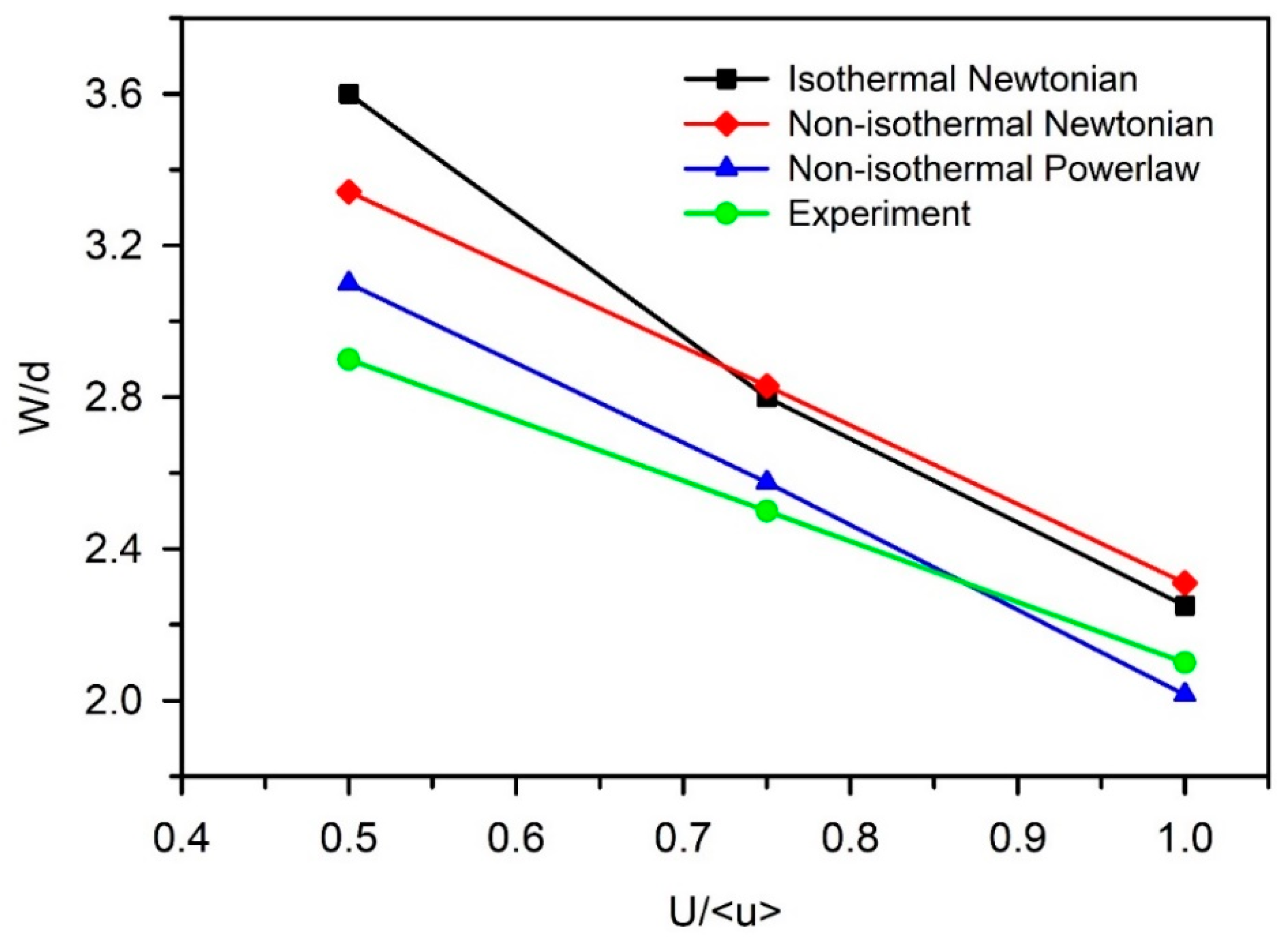
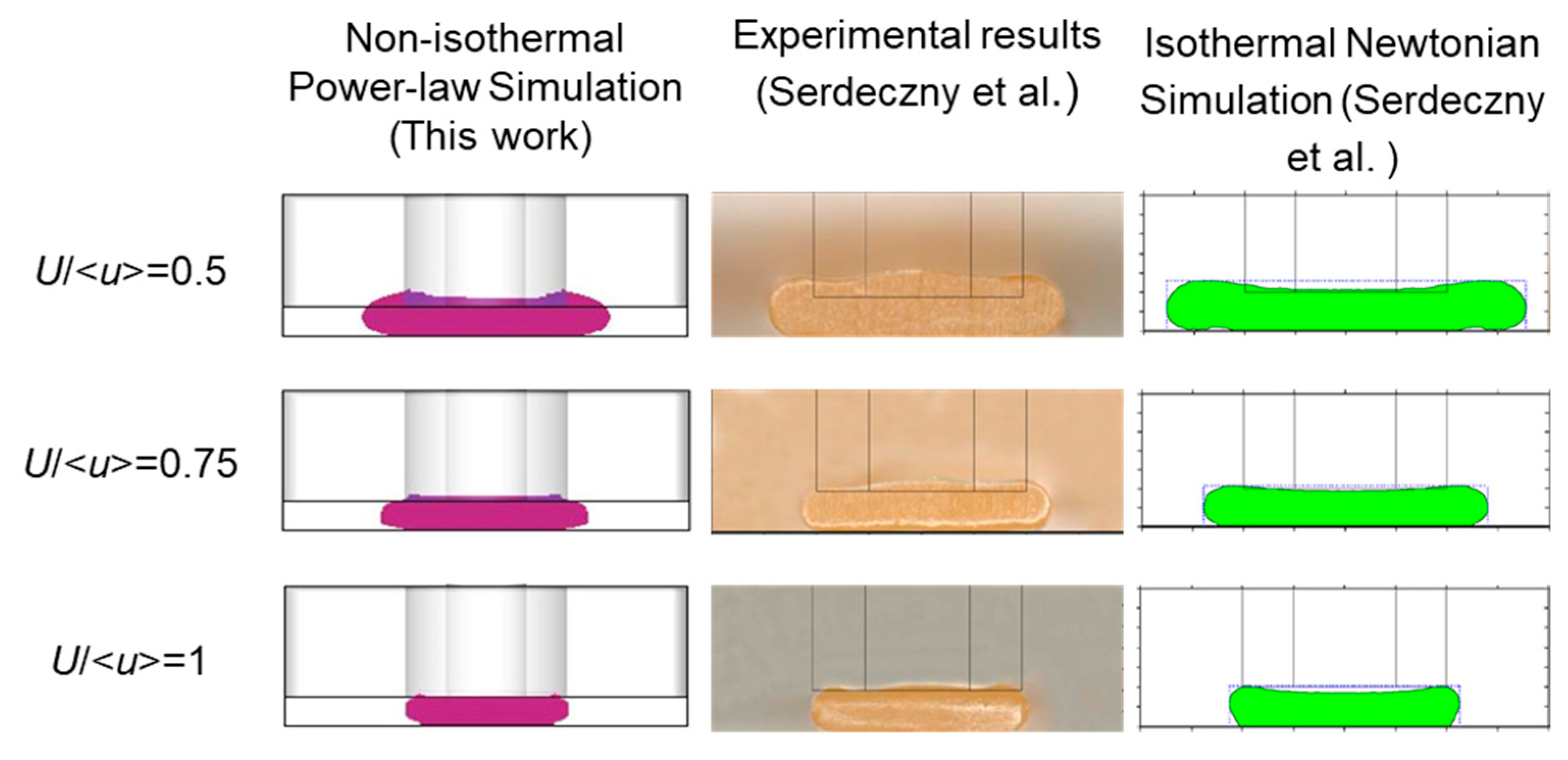
3.2. The Effect of the Viscosity Model on the Relation between Strand Shape and U/<u>
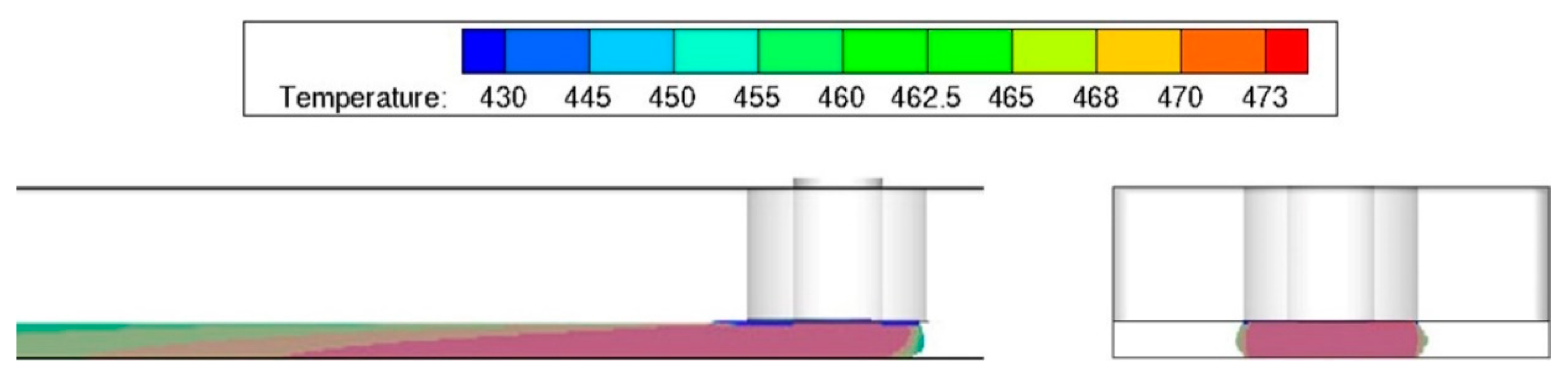
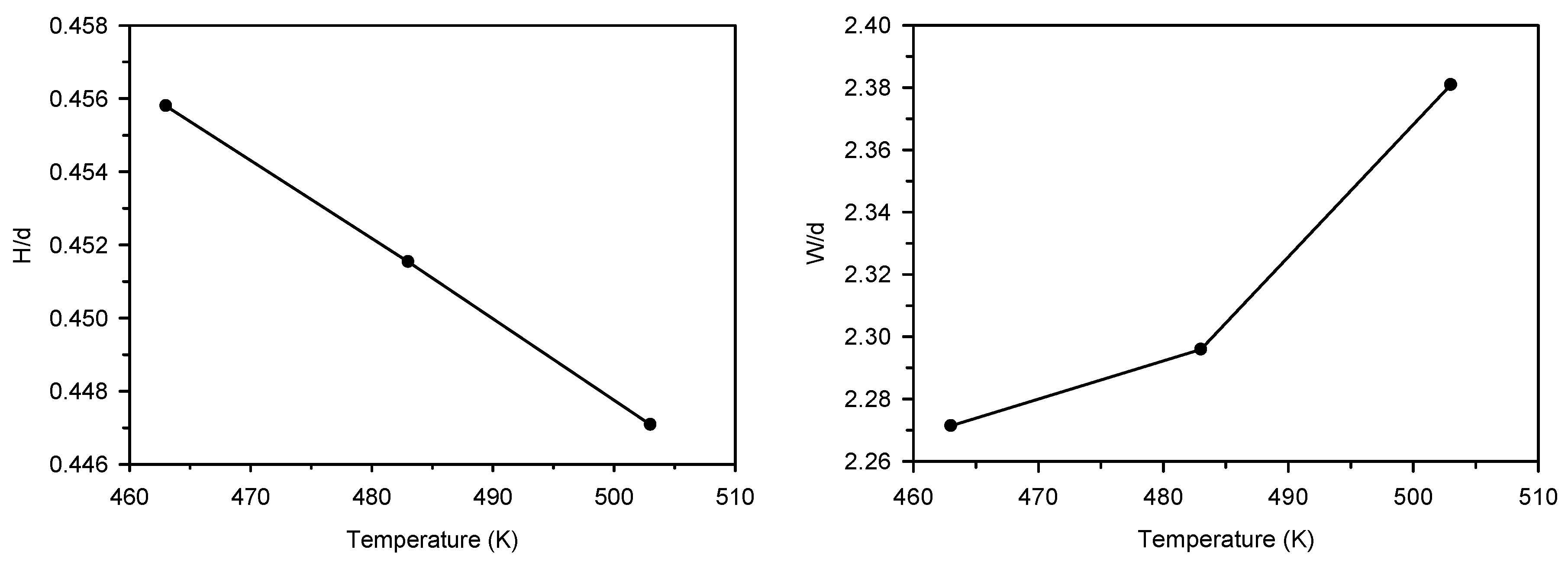
3.3. The Effect of the Nozzle Temperature on the Strand Shape
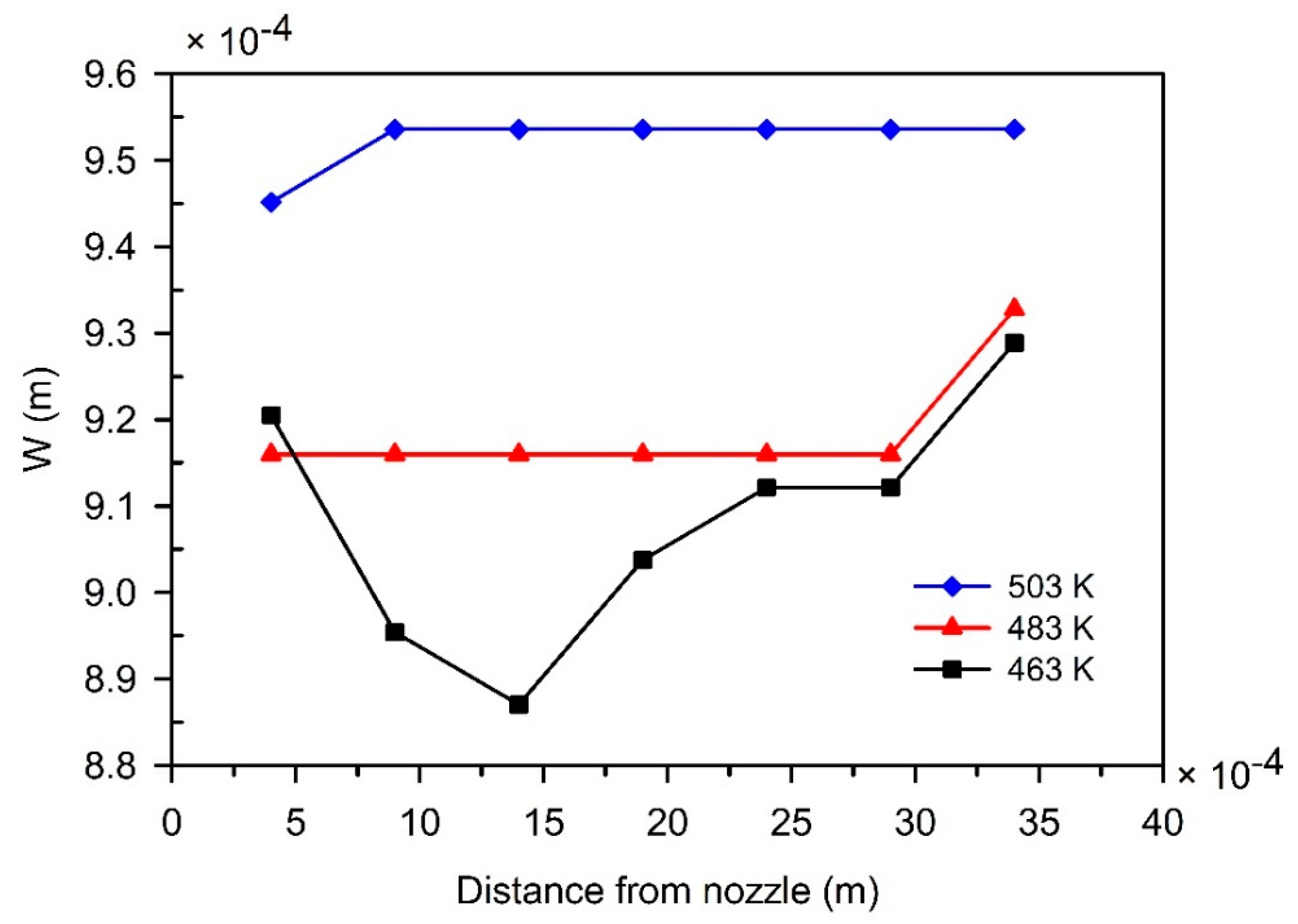
3.4. The Effect of the Nozzle Temperature on the Strand Uniformity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Horn, T.J.; Harrysson, O.L.A. Overview of current additive manufacturing technologies and selected applications. Sci. Prog. 2012, 95, 255–282. [Google Scholar] [CrossRef] [PubMed]
- Pourali, M.; Peterson, A.M. Thermal Modeling of Material Extrusion Additive Manufacturing. In Polymer-Based Additive Manufacturing: Recent Developments; ACS Publications: Washington, DC, USA, 2019; pp. 115–130. [Google Scholar]
- Gilmer, E.L.; Mansfield, C.; Gardner, J.M.; Siochi, E.J.; Baird, D.G.; Bortner, M.J. Characterization and Analysis of Polyetherimide: Realizing Practical Challenges of Modeling the Extrusion-Based Additive Manufacturing Process. In Polymer-Based Additive Manufacturing: Recent Developments; ACS Publications: Washington, DC, USA, 2019; pp. 69–84. [Google Scholar]
- Garg, A.; Tai, K.; Savalani, M. State-of-the-art in empirical modelling of rapid prototyping processes. Rapid Prototyp. J. 2014, 20, 164–178. [Google Scholar] [CrossRef]
- Bellini, A. Fused Deposition of Ceramics: A Comprehensive Experimental, Analytical and Computational Study of Material Behavior, Fabrication Process and Equipment Design. Ph.D. Thesis, Drexel University, Philadelphia, PA, USA, 2002. [Google Scholar]
- Brenken, B.; Barocio, E.; Favaloro, A.J.; Kunc, V.; Pipes, R.B. Development and validation of extrusion deposition additive manufacturing process simulations. Addit. Manuf. 2019, 25, 218–226. [Google Scholar] [CrossRef]
- D’Amico, T.; Peterson, A.M. An adaptable FEA simulation of material extrusion additive manufacturing heat transfer in 3D. Addit. Manuf. 2018, 21, 422–430. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Barocio, E.; Tejada-Ortigoza, V.; Pipes, R.B.; Rodriguez, C.; Roman-Flores, A. Characterization of the Mechanical Properties of FFF Structures and Materials: A Review on the Experimental, Computational and Theoretical Approaches. Materials 2019, 12, 895. [Google Scholar] [CrossRef]
- Huang, B.; Singamneni, S. Adaptive slicing and speed- and time-dependent consolidation mechanisms in fused deposition modeling. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 228, 111–126. [Google Scholar] [CrossRef]
- Huang, B.; Singamneni, S. Raster angle mechanics in fused deposition modelling. J. Compos. Mater. 2014, 49, 363–383. [Google Scholar] [CrossRef]
- Ramanath, H.S.; Chua, C.K.; Leong, K.F.; Shah, K.D. Melt flow behaviour of poly-ε-caprolactone in fused deposition modelling. J. Mater. Sci. Mater. Electron. 2007, 19, 2541–2550. [Google Scholar] [CrossRef]
- Mostafa, N.; Syed, H.M.; Igor, S.; Andrew, G. A study of melt flow analysis of an ABS-Iron composite in fused deposition modelling process. Tsinghua Sci. Technol. 2009, 14, 29–37. [Google Scholar] [CrossRef]
- Heller, B.; Smith, D.E.; Jack, D.A. Effects of extrudate swell and nozzle geometry on fiber orientation in Fused Filament Fabrication nozzle flow. Addit. Manuf. 2016, 12, 252–264. [Google Scholar] [CrossRef]
- Comminal, R.; Serdeczny, M.P.; Pedersen, D.B.; Spangenberg, J. Numerical modeling of the strand deposition flow in extrusion-based additive manufacturing. Addit. Manuf. 2018, 20, 68–76. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Pedersen, D.B.; Spangenberg, J. Experimental validation of a numerical model for the strand shape in material extrusion additive manufacturing. Addit. Manuf. 2018, 24, 145–153. [Google Scholar] [CrossRef]
- Santana, L.; Alves, J.L.; Netto, A.D.C.S. A study of parametric calibration for low cost 3D printing: Seeking improvement in dimensional quality. Mater. Des. 2017, 135, 159–172. [Google Scholar] [CrossRef]
- Bartikian, M.; Ferreira, A.; Gonçalves-Ferreira, A.; Neto, L.L. 3D printing anatomical models of head bones. Surg. Radiol. Anat. 2018, 41, 1205–1209. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chou, K. A parametric study of part distortions in fused deposition modelling using three-dimensional finite element analysis. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 222, 959–968. [Google Scholar] [CrossRef]
- Rosas, L.F.V. Characterization of Parametric Internal Structures for Components Built by Fused Deposition Modeling. Master’s Thesis, University of Windsor, Windsor, ON, Canada, 2013. [Google Scholar]
- Dabiri, S.; Schmid, S.; Tryggvason, G. Fully Resolved Numerical Simulations of Fused Deposition Modeling. In Proceedings of the ASME 2014 International Manufacturing Science and Engineering Conference collocated with the JSME 2014 International Conference on Materials and Processing and the 42nd North American Manufacturing Research Conference, Detroit, MI, USA, 9–13 June 2014. [Google Scholar] [CrossRef]
- McIlroy, C.; Olmsted, P.D. Deformation of an amorphous polymer during the fused-filament-fabrication method for additive manufacturing. J. Rheol. 2017, 61, 379–397. [Google Scholar] [CrossRef]
- Liu, J.; Anderson, K.L.; Sridhar, N. Direct Simulation of Polymer Fused Deposition Modeling (FDM)—An Implementation of the Multi-Phase Viscoelastic Solver in OpenFOAM. Int. J. Comput. Methods 2019, 17, 1844002. [Google Scholar] [CrossRef]
- Xia, H.; Lu, J.; Tryggvason, G. A numerical study of the effect of viscoelastic stresses in fused filament fabrication. Comput. Methods Appl. Mech. Eng. 2019, 346, 242–259. [Google Scholar] [CrossRef]
- Phan, D.D.; Swain, Z.R.; Mackay, M.E. Rheological and heat transfer effects in fused filament fabrication. J. Rheol. 2018, 62, 1097–1107. [Google Scholar] [CrossRef]
- Le Marec, P.E.; Quantin, J.-C.; Ferry, L.; Benezet, J.-C.; Guilbert, S.; Bergeret, A. Modelling of PLA melt rheology and batch mixing energy balance. Eur. Polym. J. 2014, 60, 273–285. [Google Scholar] [CrossRef]
- Mackay, M.E. The importance of rheological behavior in the additive manufacturing technique material extrusion. J. Rheol. 2018, 62, 1549–1561. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R.; Roenby, J. Performance of interFoam on the simulation of progressive waves. arXiv 2018, arXiv:1804.01158. [Google Scholar] [CrossRef]
- Comminal, R.B.; Hattel, J.H.; Spangenberg, J. Numerical simulations of planar extrusion and fused filament fabrication of non-Newtonian fluids. Nord. Rheol. Soc. Annu. Trans. 2017, 25, 263–270. [Google Scholar]
- Turner, B.N.; Strong, R.; Gold, S.A. A review of melt extrusion additive manufacturing processes: I. Process design and modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Ang, T.; Sultana, F.; Hutmacher, D.W.; Wong, Y.; Fuh, J.; Mo, X.; Loh, H.; Burdet, E.; Teoh, S. Fabrication of 3D chitosan–hydroxyapatite scaffolds using a robotic dispensing system. Mater. Sci. Eng. C 2002, 20, 35–42. [Google Scholar] [CrossRef]
- Trachtenberg, J.; Placone, J.K.; Smith, B.T.; Fisher, J.P.; Mikos, A.G. Extrusion-based 3D printing of poly(propylene fumarate) scaffolds with hydroxyapatite gradients. J. Biomater. Sci. Polym. Ed. 2017, 28, 532–554. [Google Scholar] [CrossRef]
- Jamróz, W.; Kurek, M.; Łyszczarz, E.; Szafraniec-Szczęsny, J.; Knapik-Kowalczuk, J.; Syrek, K.; Paluch, M.; Jachowicz, R. 3D printed orodispersible films with Aripiprazole. Int. J. Pharm. 2017, 533, 413–420. [Google Scholar] [CrossRef]
- Chaidas, D.; Kitsakis, K.; Kechagias, J.; Maropoulos, S. The impact of temperature changing on surface roughness of FFF process. IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 12033. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behdani, B.; Senter, M.; Mason, L.; Leu, M.; Park, J. Numerical Study on the Temperature-Dependent Viscosity Effect on the Strand Shape in Extrusion-Based Additive Manufacturing. J. Manuf. Mater. Process. 2020, 4, 46. https://doi.org/10.3390/jmmp4020046
Behdani B, Senter M, Mason L, Leu M, Park J. Numerical Study on the Temperature-Dependent Viscosity Effect on the Strand Shape in Extrusion-Based Additive Manufacturing. Journal of Manufacturing and Materials Processing. 2020; 4(2):46. https://doi.org/10.3390/jmmp4020046
Chicago/Turabian StyleBehdani, Behrouz, Matthew Senter, Leah Mason, Ming Leu, and Joontaek Park. 2020. "Numerical Study on the Temperature-Dependent Viscosity Effect on the Strand Shape in Extrusion-Based Additive Manufacturing" Journal of Manufacturing and Materials Processing 4, no. 2: 46. https://doi.org/10.3390/jmmp4020046
APA StyleBehdani, B., Senter, M., Mason, L., Leu, M., & Park, J. (2020). Numerical Study on the Temperature-Dependent Viscosity Effect on the Strand Shape in Extrusion-Based Additive Manufacturing. Journal of Manufacturing and Materials Processing, 4(2), 46. https://doi.org/10.3390/jmmp4020046




