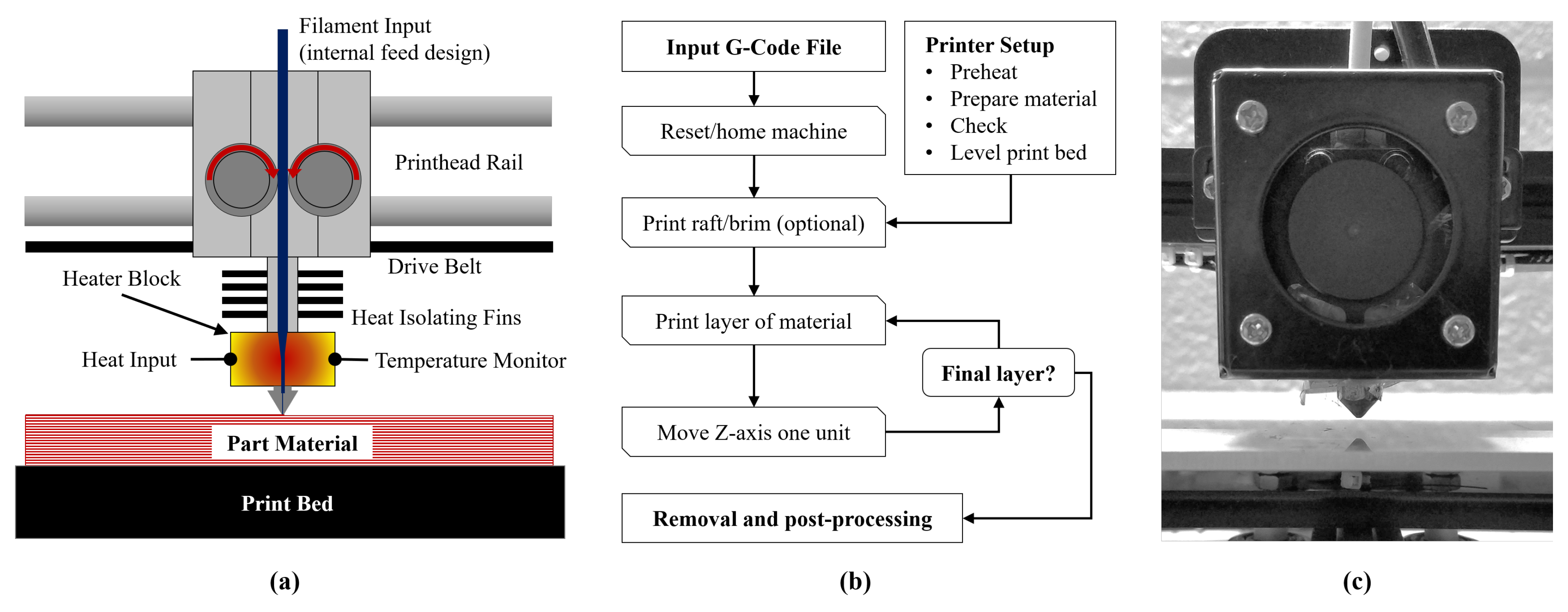
Figure 1.
Fused deposition modeling (FDM) (
a) process, (
b) work-flow, and (
c) extruder carriage example [
30].
Figure 1.
Fused deposition modeling (FDM) (
a) process, (
b) work-flow, and (
c) extruder carriage example [
30].
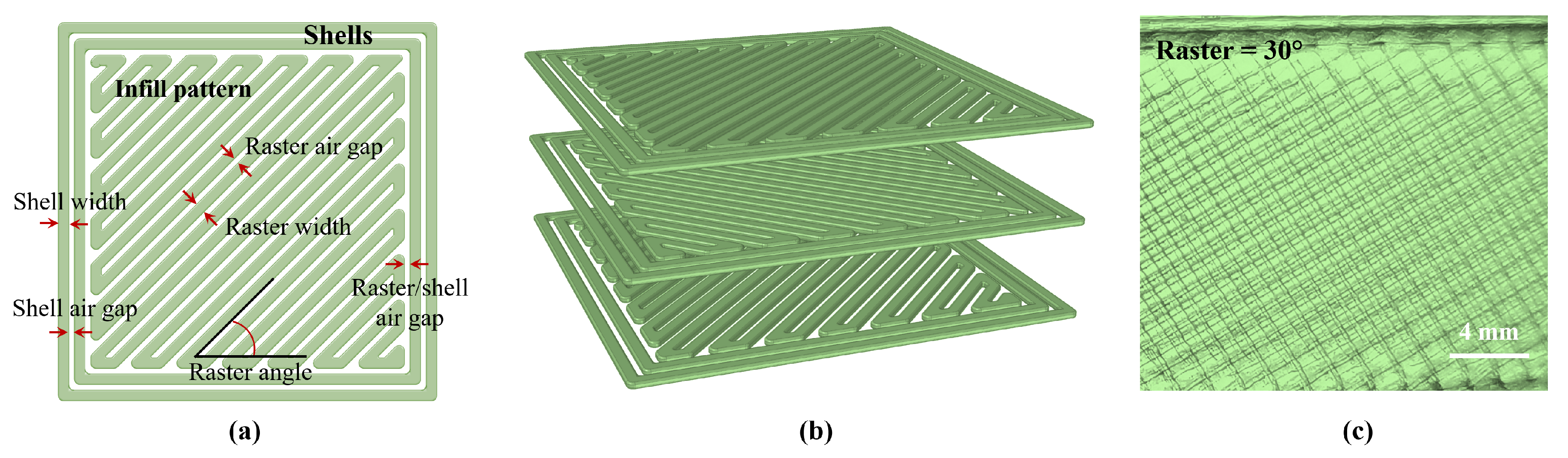
Figure 2.
Rectilinear infill pattern for (a) a single layer, (b) multiple layers, and (c) observed in a manufactured sample at a raster angle of and 100% density.
Figure 2.
Rectilinear infill pattern for (a) a single layer, (b) multiple layers, and (c) observed in a manufactured sample at a raster angle of and 100% density.
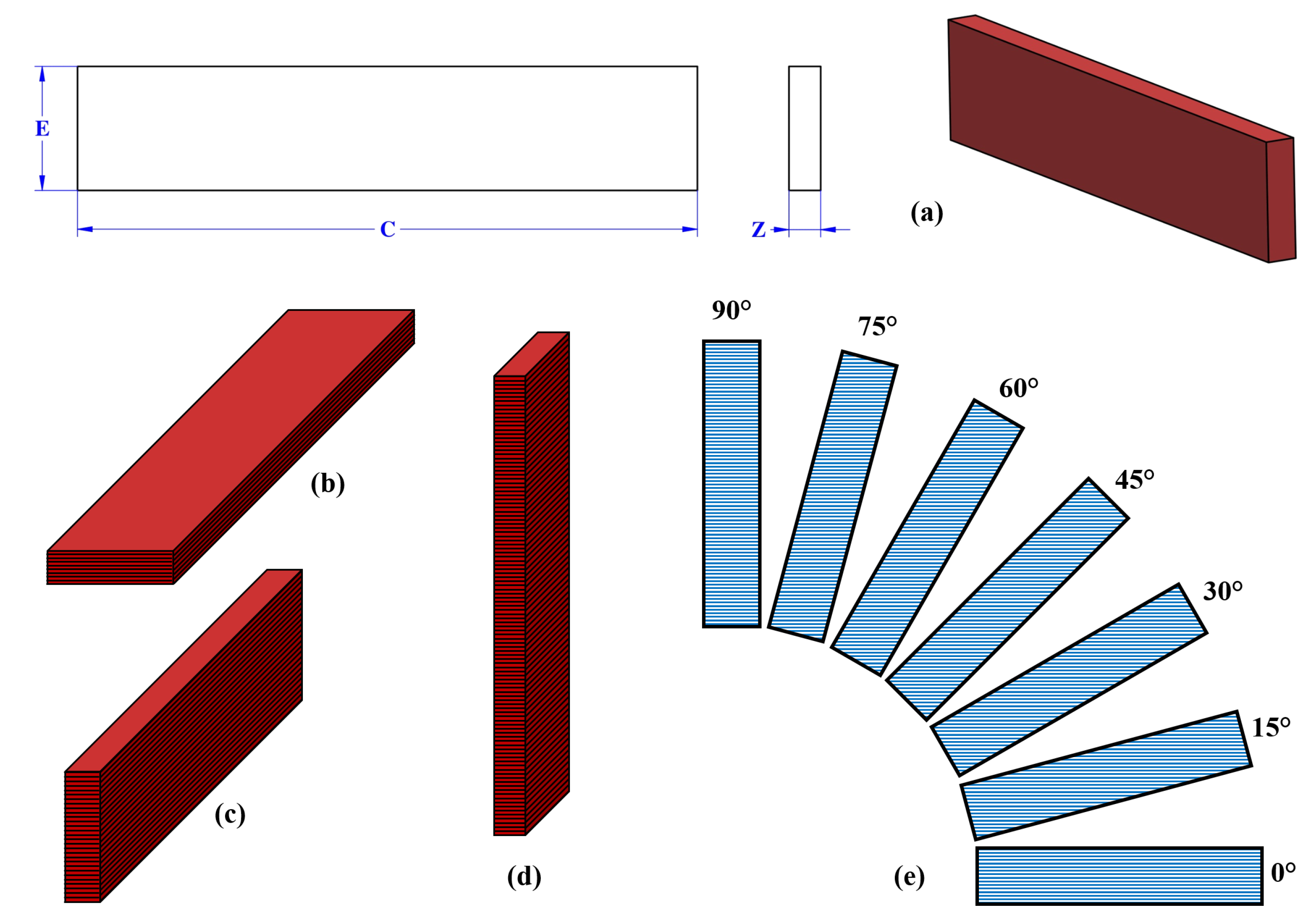
Figure 3.
Specimen configurations: (a) standard geometry, (b) flat printing orientation, (c) horizontal printing orientation, (d) vertical printing orientation, and (e) raster angles.
Figure 3.
Specimen configurations: (a) standard geometry, (b) flat printing orientation, (c) horizontal printing orientation, (d) vertical printing orientation, and (e) raster angles.
Figure 4.
ABS specimen set for one replication of measurements.
Figure 4.
ABS specimen set for one replication of measurements.
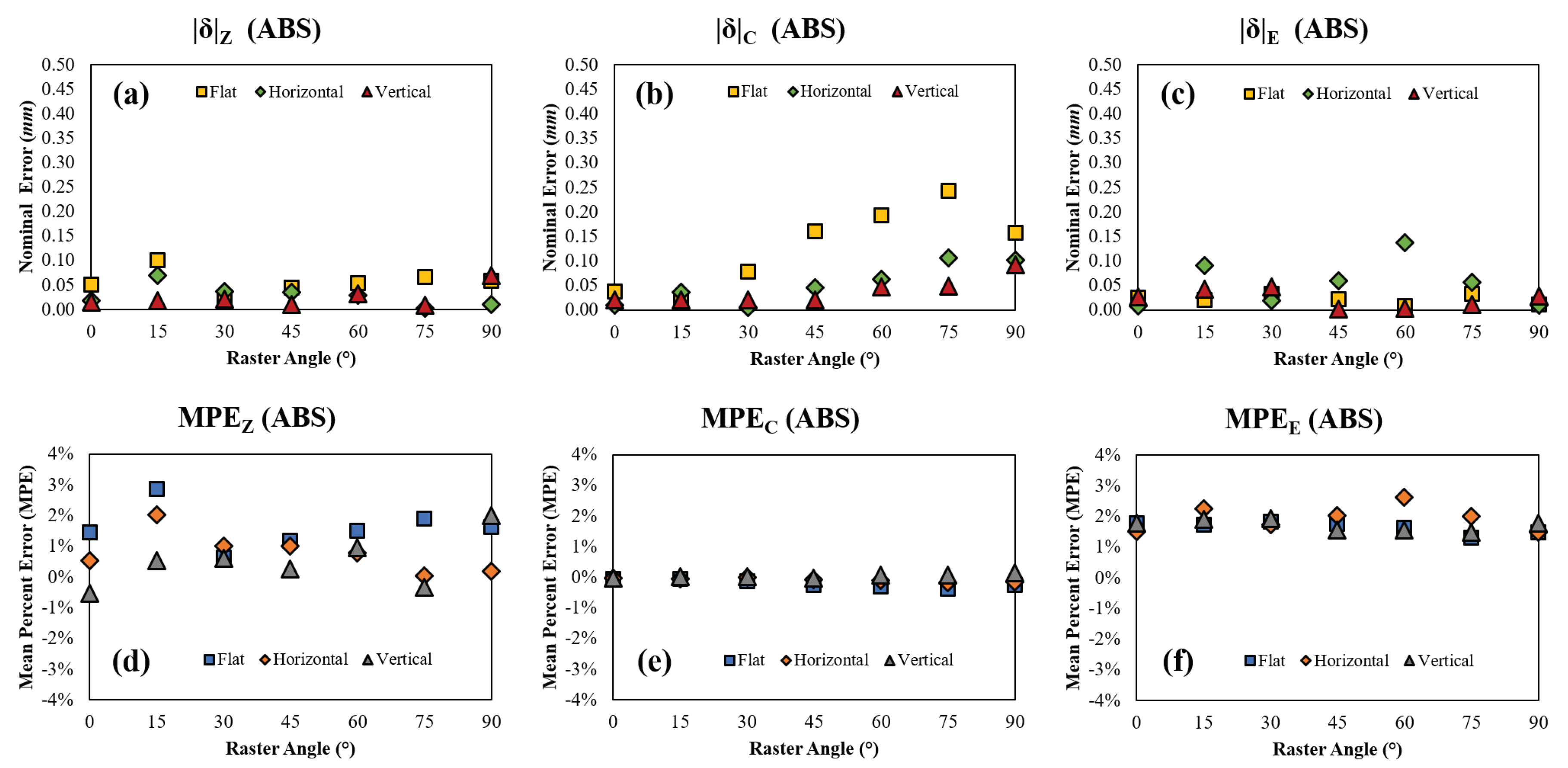
Figure 5.
ABS (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 5.
ABS (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 6.
PLA specimen set for one replication of measurements.
Figure 6.
PLA specimen set for one replication of measurements.
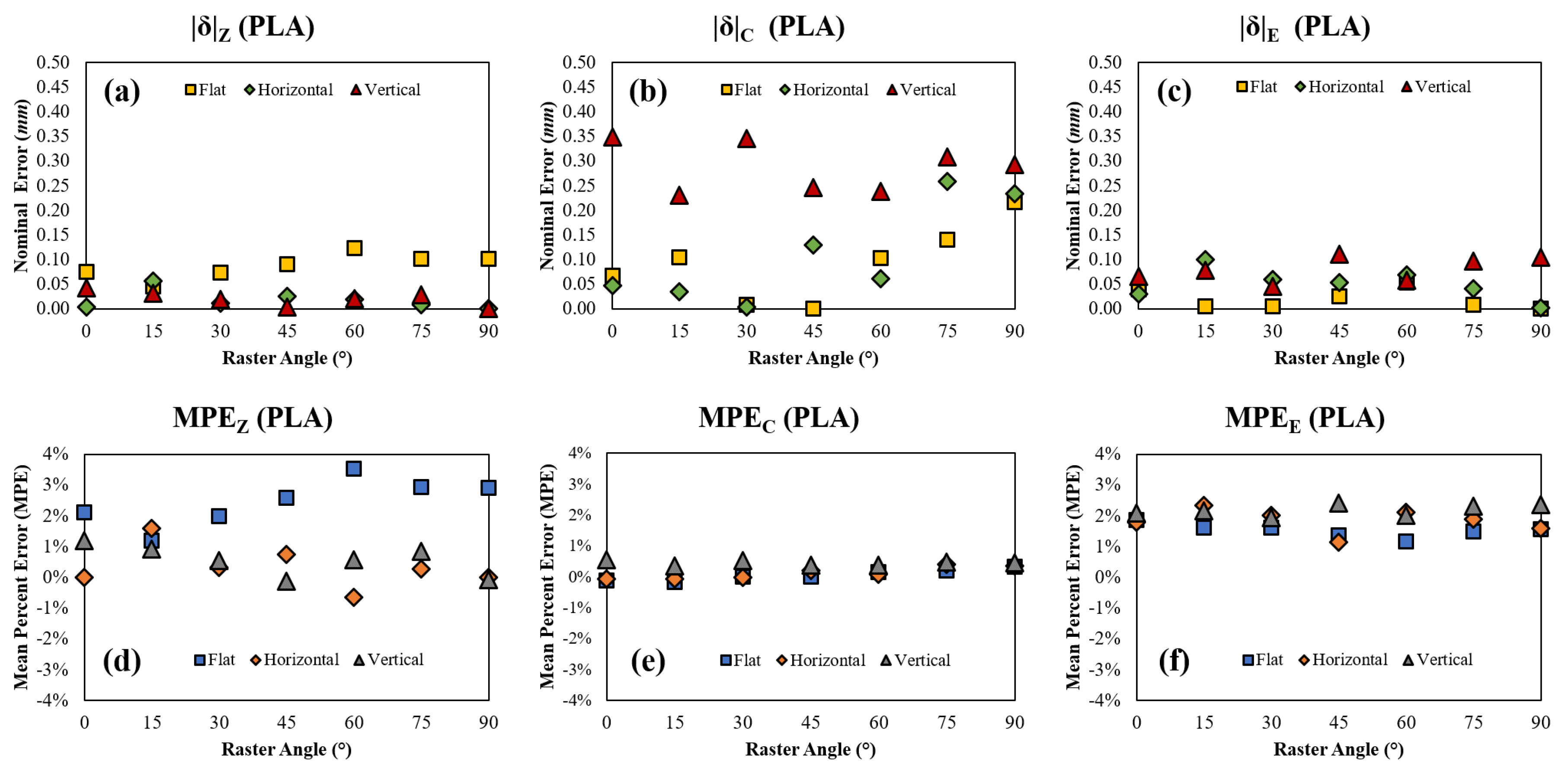
Figure 7.
PLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 7.
PLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 8.
HTPLA specimen set for one replication of measurements.
Figure 8.
HTPLA specimen set for one replication of measurements.
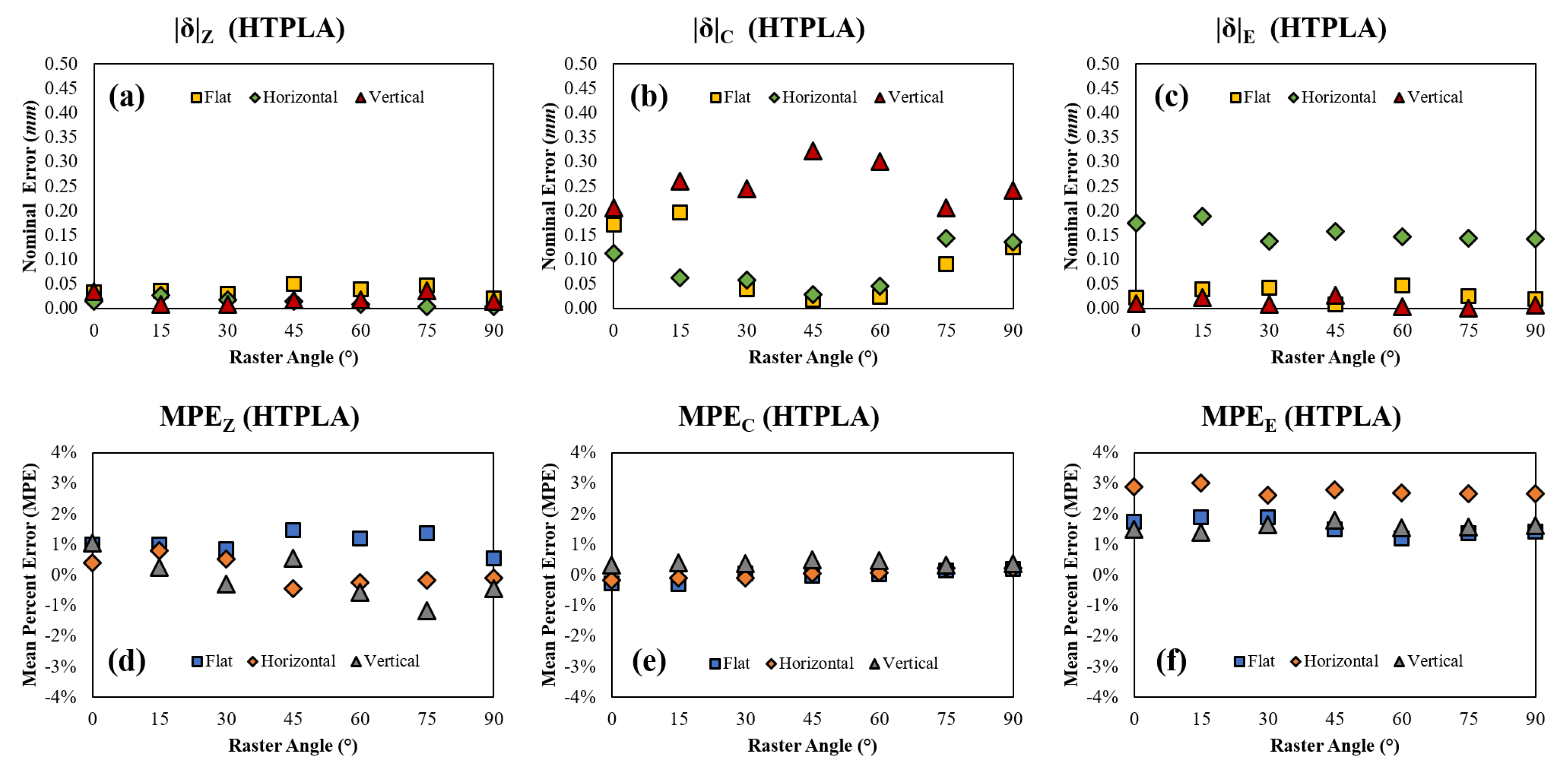
Figure 9.
HTPLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 9.
HTPLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 10.
HIPS specimen set for one replication of measurements.
Figure 10.
HIPS specimen set for one replication of measurements.
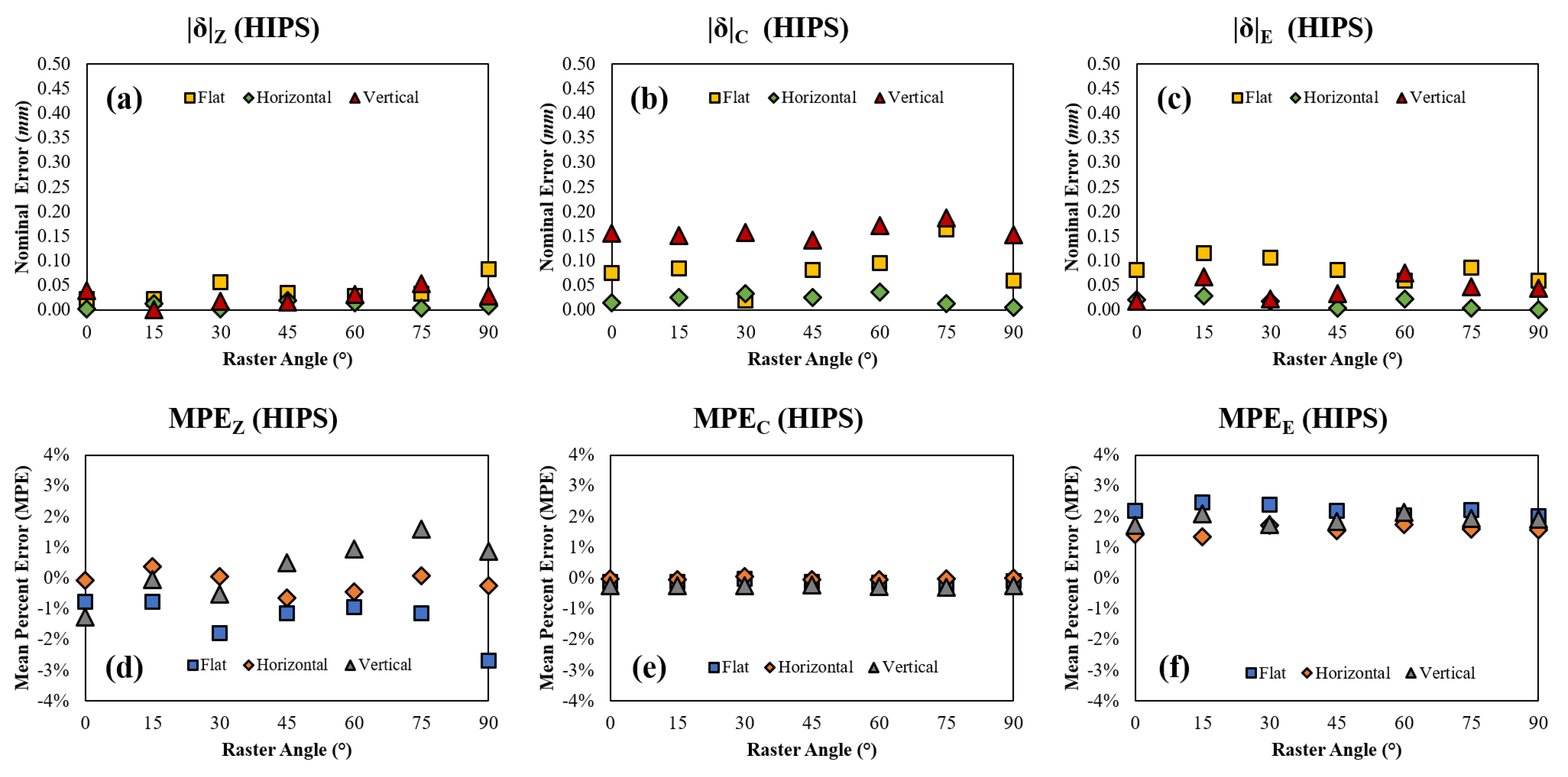
Figure 11.
HIPS (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 11.
HIPS (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 12.
Nylon specimen set for one replication of measurements.
Figure 12.
Nylon specimen set for one replication of measurements.
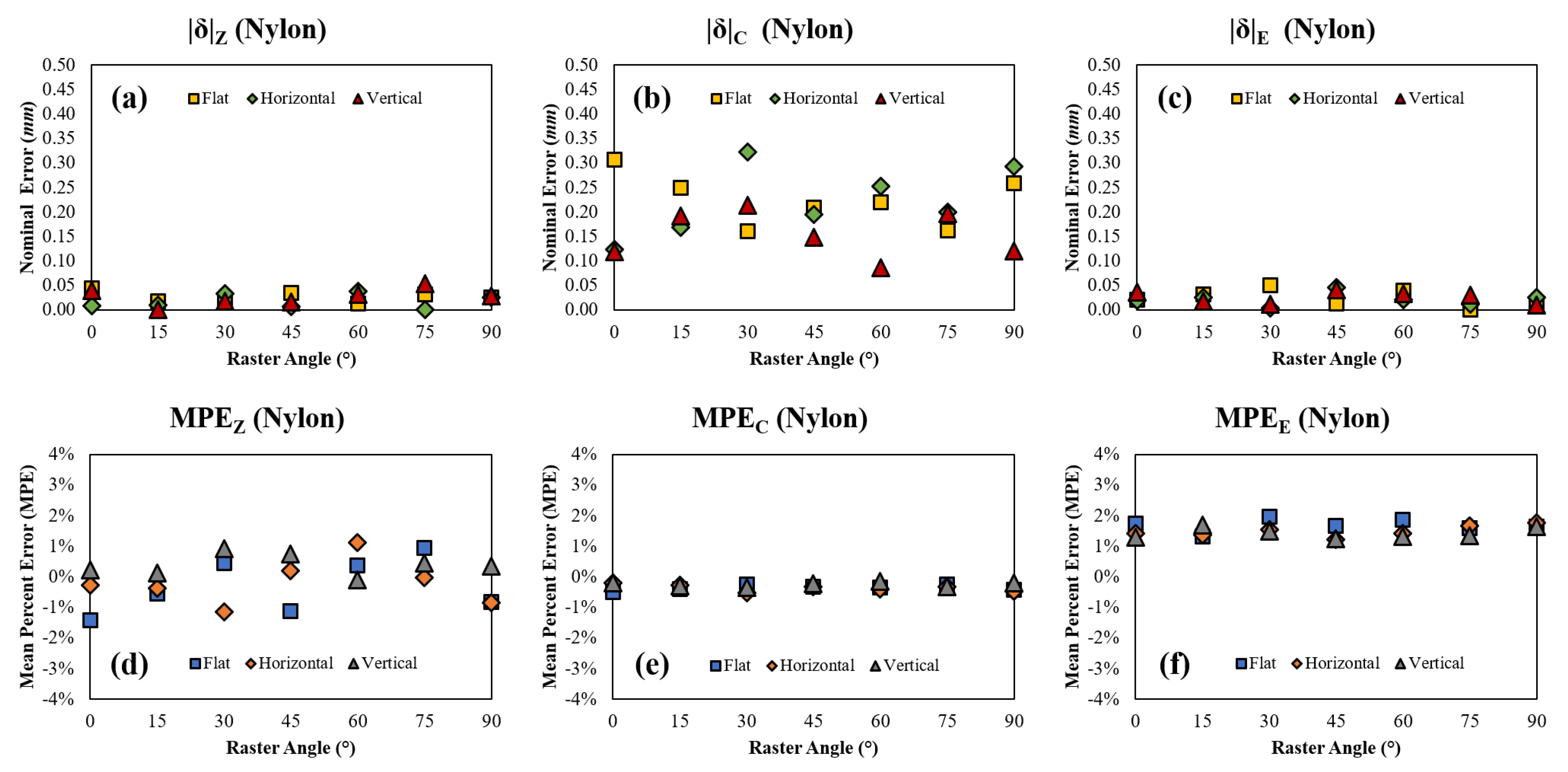
Figure 13.
Nylon (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 13.
Nylon (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 14.
PETG specimen set for one replication of measurements.
Figure 14.
PETG specimen set for one replication of measurements.
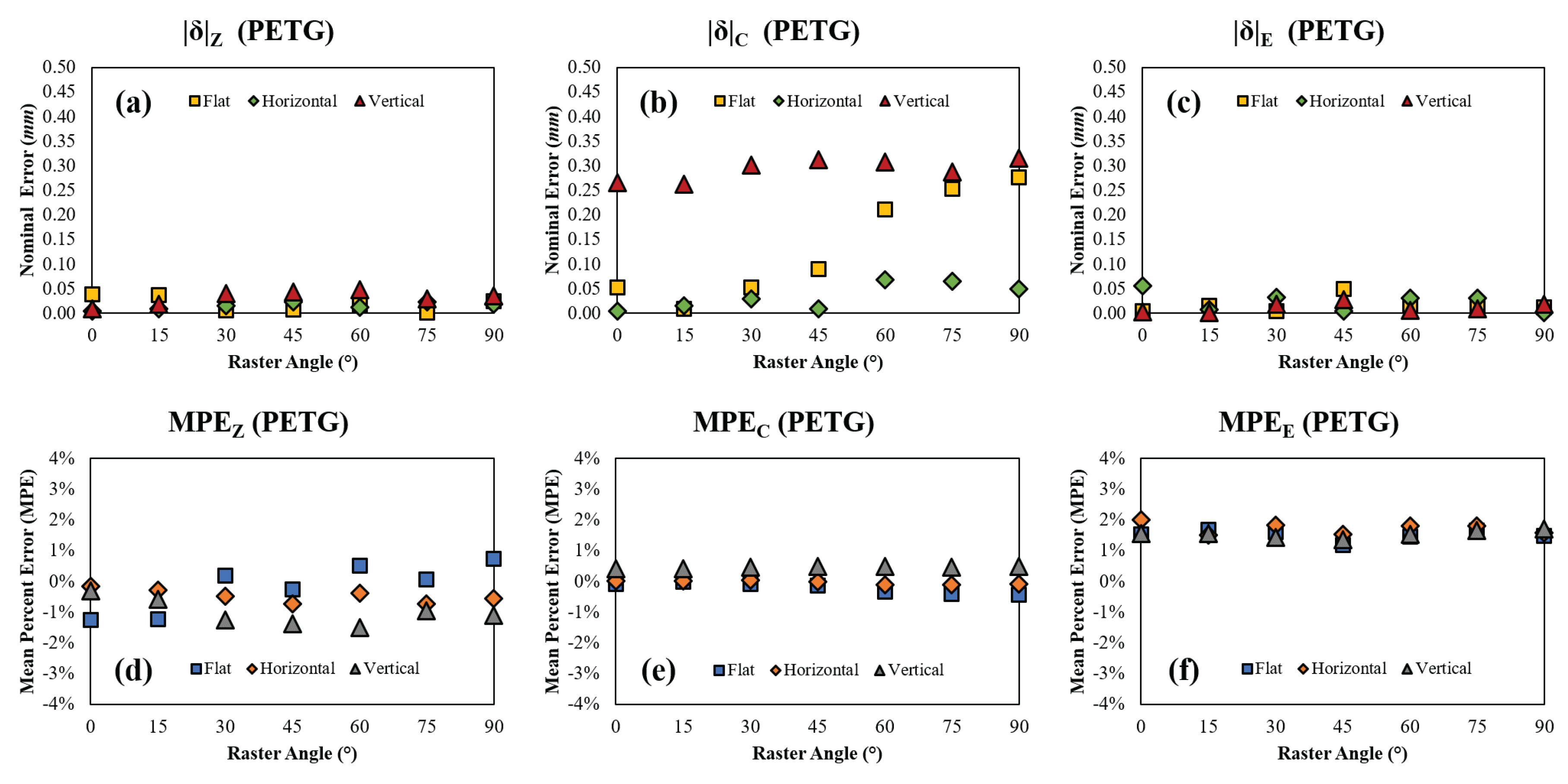
Figure 15.
PETG (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 15.
PETG (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 16.
PC specimen set for one replication of measurements.
Figure 16.
PC specimen set for one replication of measurements.
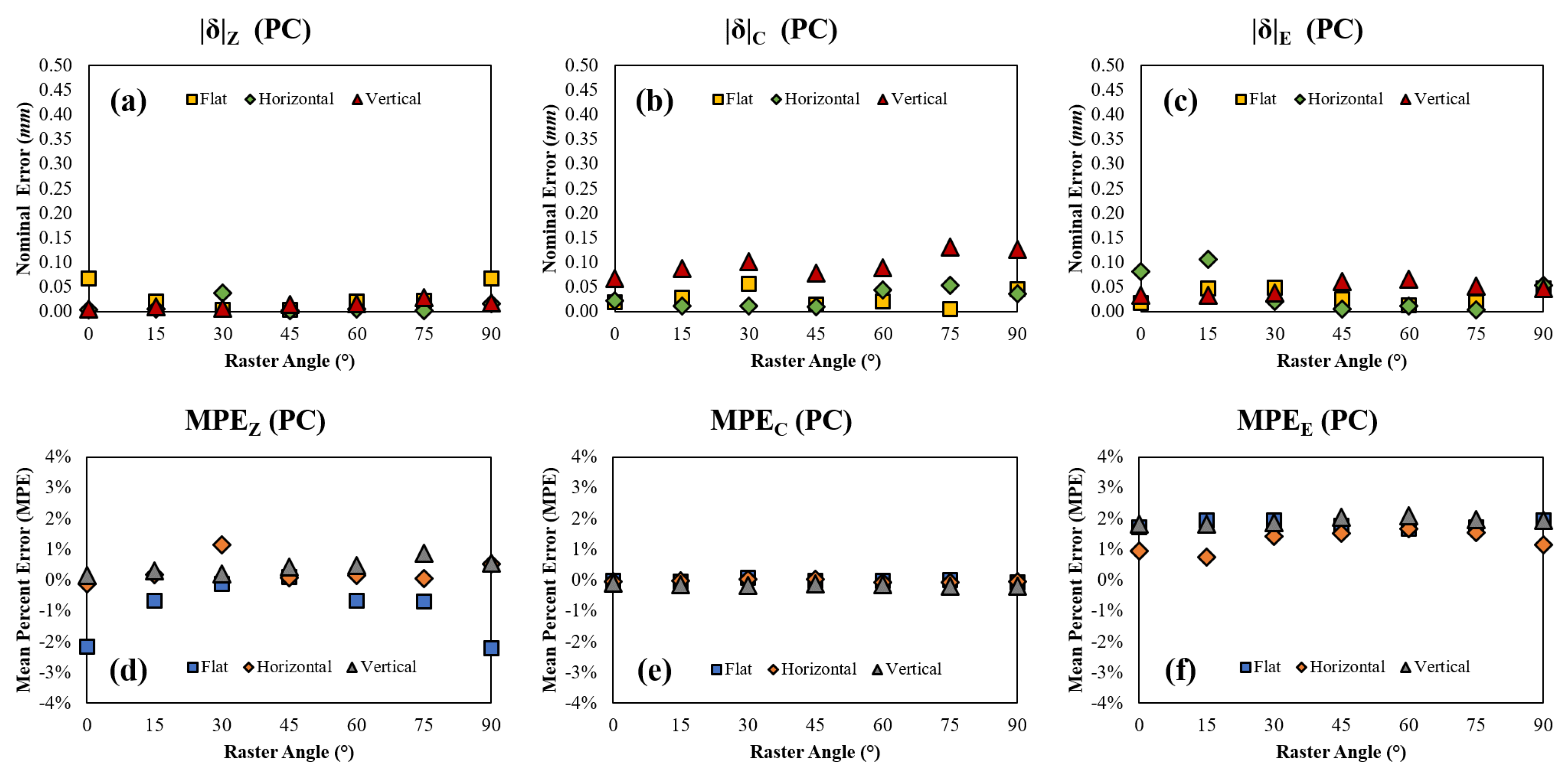
Figure 17.
PC (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 17.
PC (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 18.
APLA specimen set for one replication of measurements.
Figure 18.
APLA specimen set for one replication of measurements.
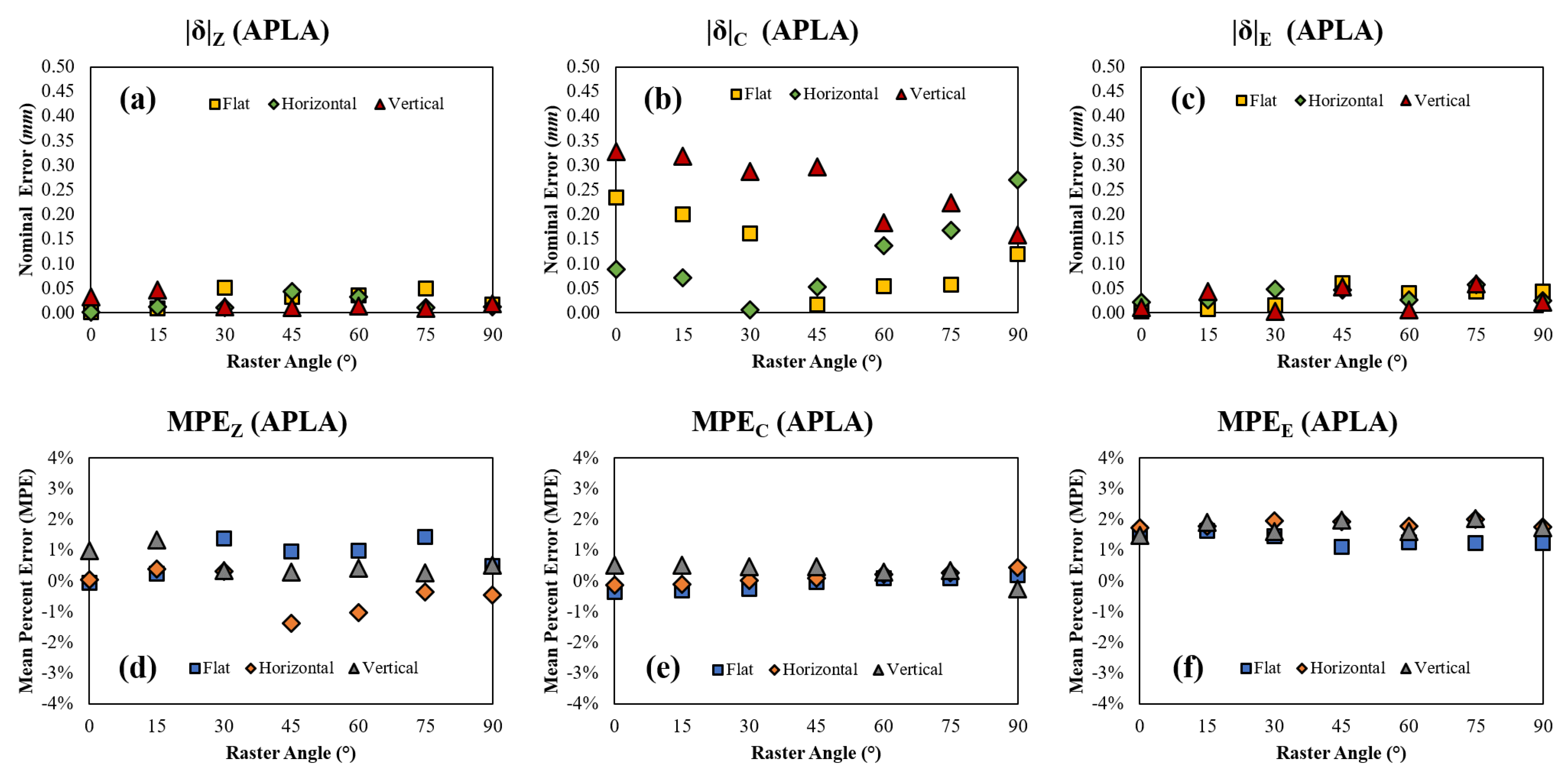
Figure 19.
APLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 19.
APLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 20.
CPLA specimen set for one replication of measurements.
Figure 20.
CPLA specimen set for one replication of measurements.
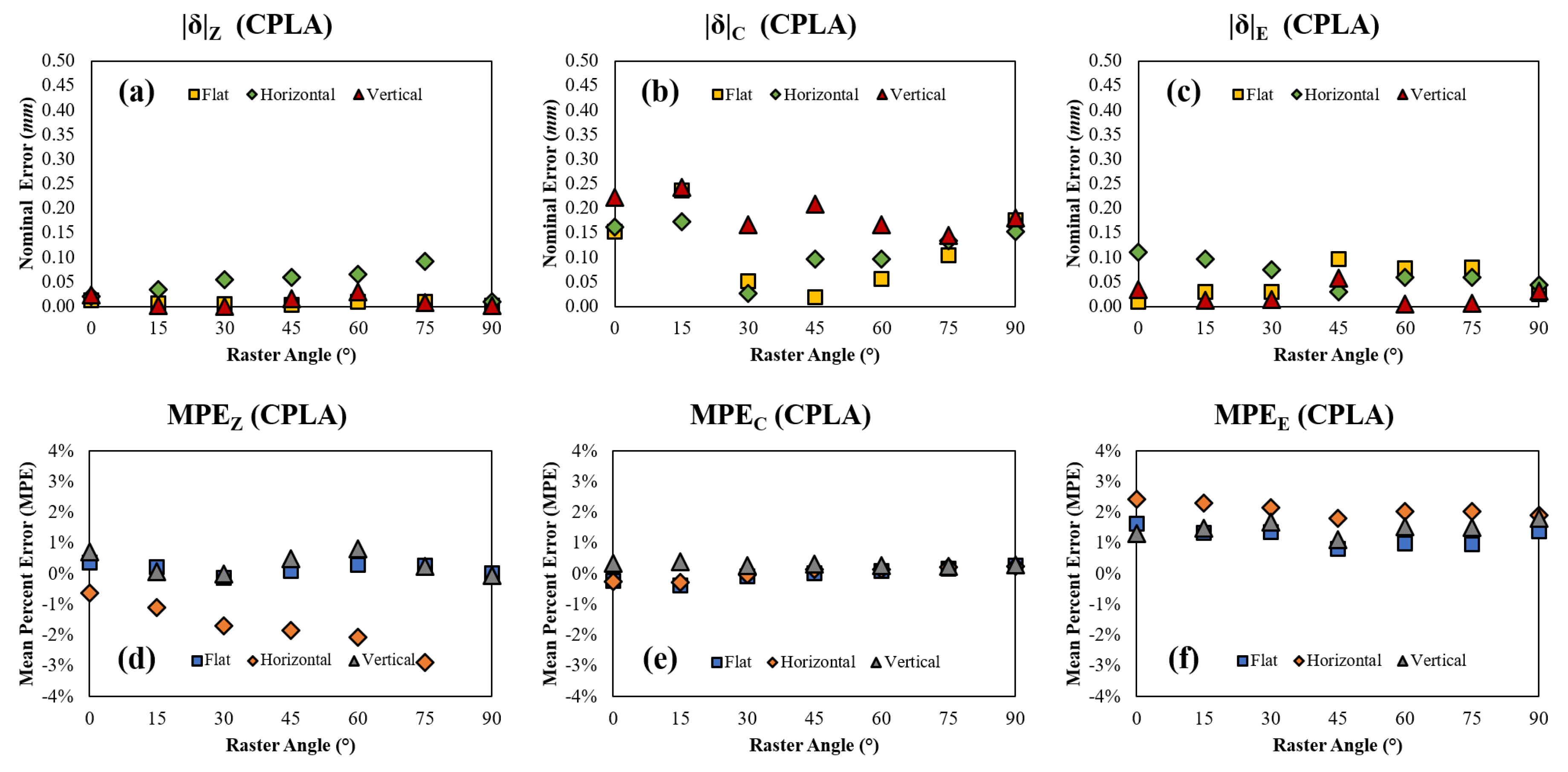
Figure 21.
CPLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 21.
CPLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 22.
WPLA specimen set for one replication of measurements.
Figure 22.
WPLA specimen set for one replication of measurements.
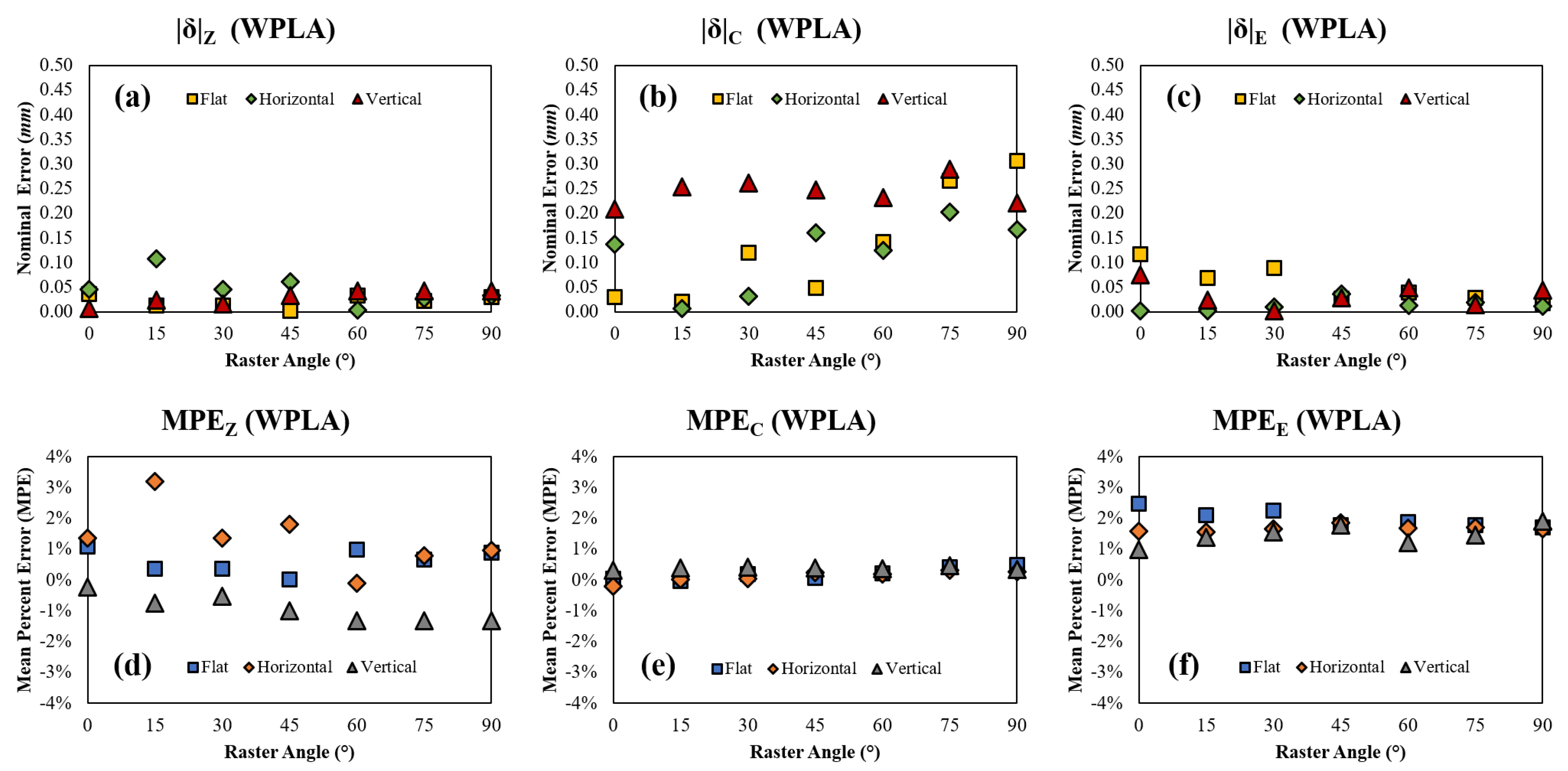
Figure 23.
WPLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 23.
WPLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 24.
CFPLA specimen set for one replication of measurements.
Figure 24.
CFPLA specimen set for one replication of measurements.
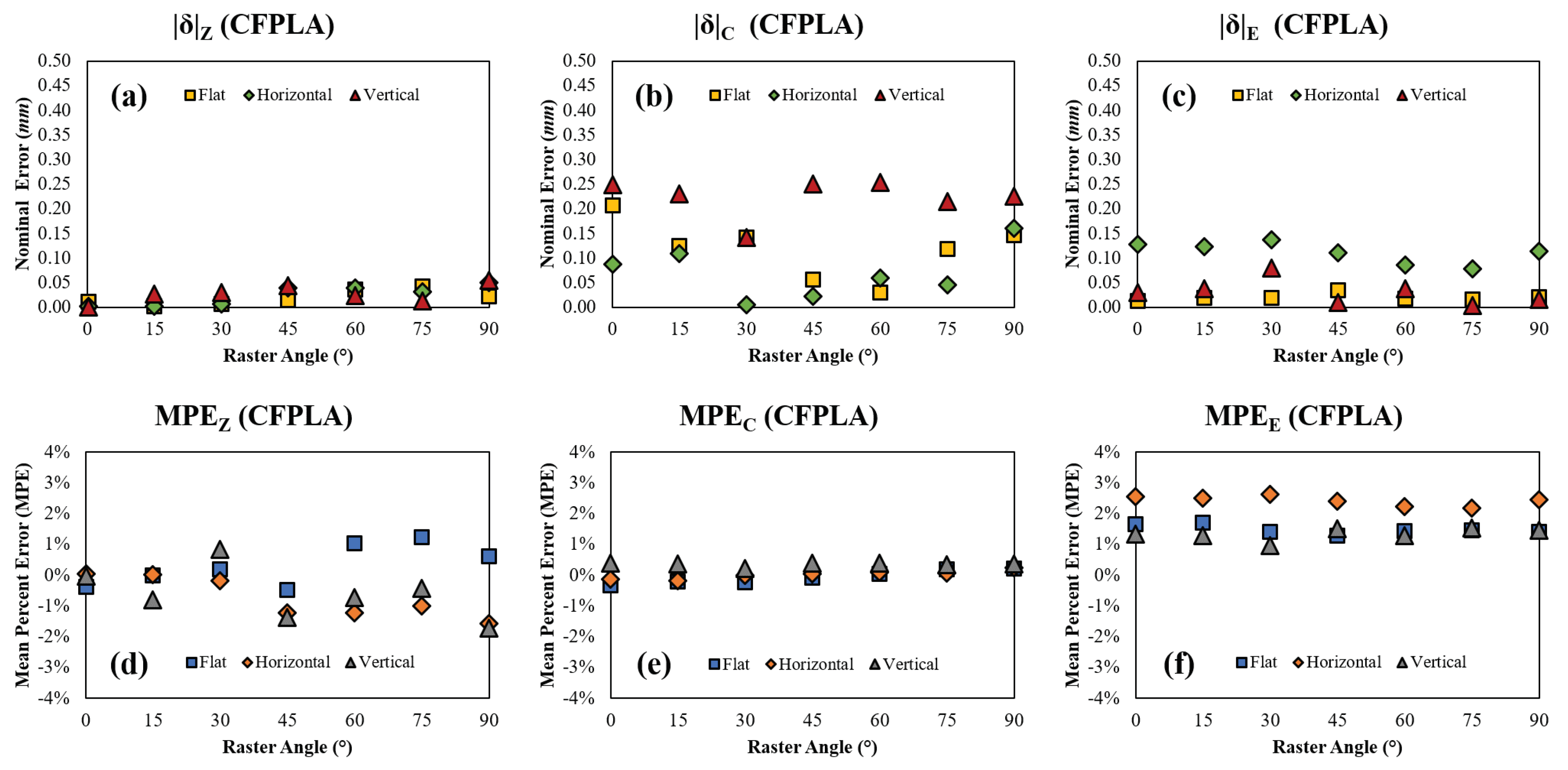
Figure 25.
CFPLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
Figure 25.
CFPLA (a) nominal error in Z, (b) nominal error in C, (c) nominal error in E, (d) mean percent error in Z, (e) mean percent error in C, and (f) mean percent error in E with respect to raster angle and orientation.
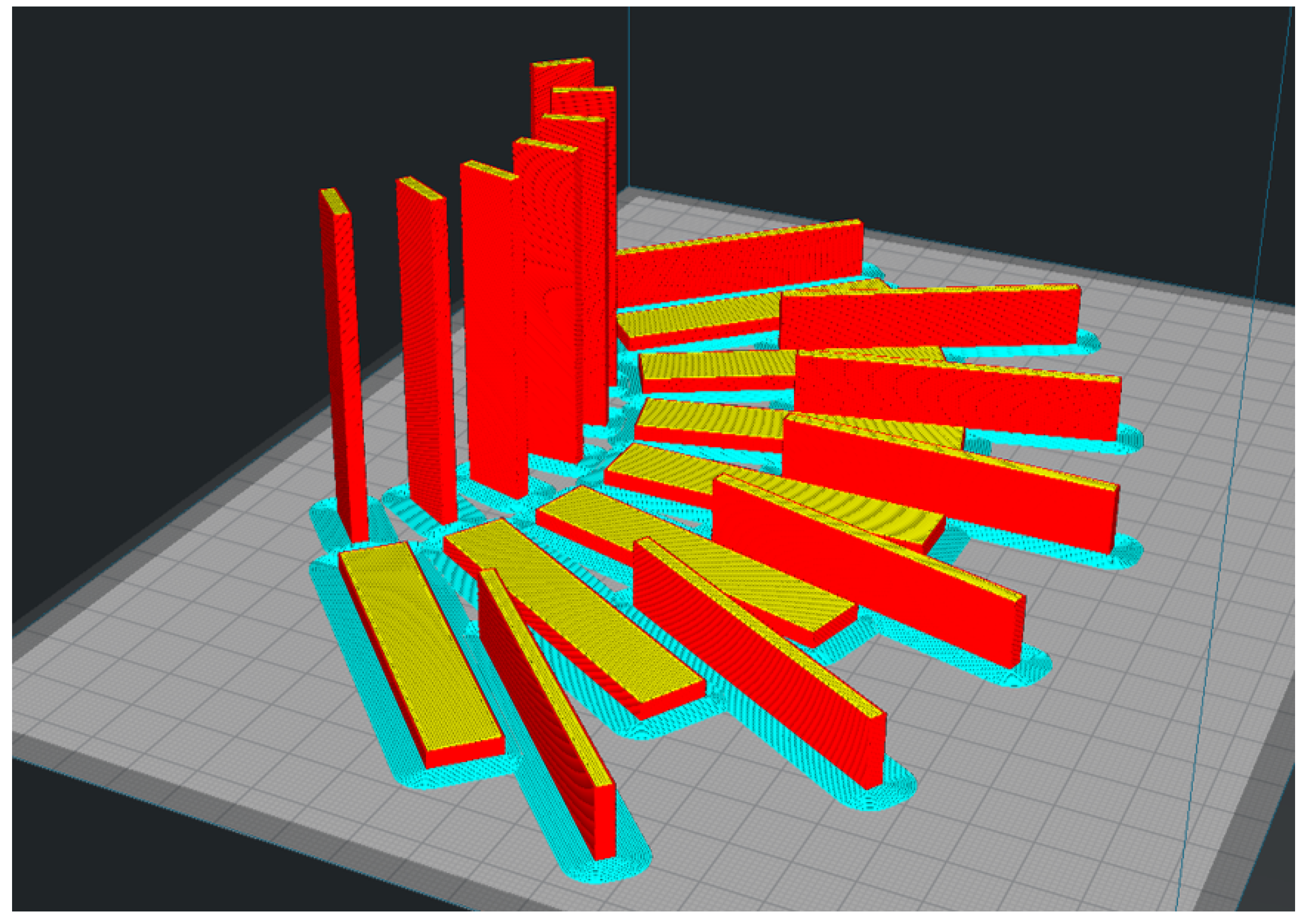
Figure 26.
Pre-processed batch of samples showing orientation, angle, and raft and layer settings; note the shell (red) and the infill (yellow) regions in the parts for the different orientations.
Figure 26.
Pre-processed batch of samples showing orientation, angle, and raft and layer settings; note the shell (red) and the infill (yellow) regions in the parts for the different orientations.
Figure 27.
Vernier calipers (a) tared before measuring, (b) measuring Z, (c) measuring C, and (d) measuring E of a sample.
Figure 27.
Vernier calipers (a) tared before measuring, (b) measuring Z, (c) measuring C, and (d) measuring E of a sample.
Figure 28.
Examples of (a) brass and (b) tool steel extrusion nozzles shown at the same scale.
Figure 28.
Examples of (a) brass and (b) tool steel extrusion nozzles shown at the same scale.
Table 1.
Materials, composition, and source.
Table 1.
Materials, composition, and source.
| Material | Composition | Filament Source/Brand |
|---|
| 1 | ABS | Acrylonitrile butadiene styrene | Hatchbox ABS |
| 2 | PLA | Polylactic acid | Hatchbox PLA |
| 3 | HTPLA | High-temperature PLA | MakerGeeks Raptor PLA |
| 4 | HIPS | High-impact polystyrene | Monoprice premium natural |
| 5 | Nylon | Synthetic polyamide | eSUN ePA |
| 6 | PETG | Polyethylene terephthalate glycol-enhanced | Inland white |
| 7 | PC | Polycarbonate | eSUN black PC |
| 8 | APLA | PLA + 40% aluminum powder | SainSmart aluminum |
| 9 | CPLA | PLA + 5% copper powder | GizmoDorks copper |
| 10 | WPLA | PLA + 30% wood fiber | Hatchbox wood |
| 11 | CFPLA | PLA + 15% chopped carbon fibers | 3DSolutech carbon fiber |
Table 2.
Mean, , SE, MPE, and for ABS as a function of print orientation and raster angle.
Table 2.
Mean, , SE, MPE, and for ABS as a function of print orientation and raster angle.
| Material: ABS (all dimensions in mm unless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.30 | 0.05 | 0.034 | 1.45% | 63.46 | 0.04 | 0.024 | −0.06% | 12.73 | 0.03 | 0.014 | 1.77% | 0.07 |
| F | | 3.35 | 0.10 | 0.040 | 2.86% | 63.48 | 0.02 | 0.065 | −0.03% | 12.72 | 0.02 | 0.015 | 1.74% | 0.10 |
| F | | 3.28 | 0.03 | 0.043 | 0.64% | 63.42 | 0.08 | 0.029 | −0.12% | 12.73 | 0.03 | 0.018 | 1.83% | 0.09 |
| F | | 3.29 | 0.04 | 0.042 | 1.19% | 63.34 | 0.16 | 0.033 | −0.25% | 12.72 | 0.02 | 0.013 | 1.75% | 0.17 |
| F | | 3.30 | 0.05 | 0.040 | 1.50% | 63.31 | 0.19 | 0.033 | −0.31% | 12.71 | 0.01 | 0.023 | 1.63% | 0.20 |
| F | | 3.32 | 0.07 | 0.040 | 1.89% | 63.26 | 0.24 | 0.047 | −0.38% | 12.67 | 0.03 | 0.026 | 1.31% | 0.25 |
| F | | 3.31 | 0.06 | 0.043 | 1.64% | 63.34 | 0.16 | 0.038 | −0.25% | 12.69 | 0.01 | 0.013 | 1.48% | 0.17 |
| H | | 3.27 | 0.02 | 0.015 | 0.53% | 63.49 | 0.01 | 0.015 | −0.02% | 12.69 | 0.01 | 0.018 | 1.50% | 0.02 |
| H | | 3.32 | 0.07 | 0.027 | 2.02% | 63.46 | 0.04 | 0.014 | −0.06% | 12.79 | 0.09 | 0.024 | 2.26% | 0.12 |
| H | | 3.29 | 0.04 | 0.036 | 1.02% | 63.50 | 0.00 | 0.014 | −0.01% | 12.72 | 0.02 | 0.015 | 1.73% | 0.04 |
| H | | 3.29 | 0.04 | 0.031 | 1.01% | 63.45 | 0.05 | 0.015 | −0.07% | 12.76 | 0.06 | 0.021 | 2.04% | 0.08 |
| H | | 3.28 | 0.03 | 0.033 | 0.79% | 63.44 | 0.06 | 0.012 | −0.10% | 12.84 | 0.14 | 0.026 | 2.63% | 0.15 |
| H | | 3.25 | 0.00 | 0.024 | 0.04% | 63.39 | 0.11 | 0.015 | −0.17% | 12.76 | 0.06 | 0.015 | 2.01% | 0.12 |
| H | | 3.26 | 0.01 | 0.038 | 0.19% | 63.40 | 0.10 | 0.030 | −0.16% | 12.69 | 0.01 | 0.033 | 1.49% | 0.10 |
| V | | 3.24 | 0.01 | 0.026 | −0.52% | 63.48 | 0.02 | 0.042 | −0.03% | 12.73 | 0.03 | 0.013 | 1.78% | 0.04 |
| V | | 3.27 | 0.02 | 0.023 | 0.54% | 63.52 | 0.02 | 0.028 | 0.03% | 12.74 | 0.04 | 0.015 | 1.91% | 0.05 |
| V | | 3.27 | 0.02 | 0.016 | 0.62% | 63.52 | 0.02 | 0.037 | 0.03% | 12.75 | 0.05 | 0.011 | 1.94% | 0.06 |
| V | | 3.26 | 0.01 | 0.019 | 0.28% | 63.48 | 0.02 | 0.029 | −0.03% | 12.70 | 0.00 | 0.018 | 1.56% | 0.02 |
| V | | 3.28 | 0.03 | 0.022 | 0.96% | 63.55 | 0.05 | 0.049 | 0.07% | 12.70 | 0.00 | 0.014 | 1.55% | 0.06 |
| V | | 3.24 | 0.01 | 0.023 | −0.32% | 63.55 | 0.05 | 0.054 | 0.08% | 12.69 | 0.01 | 0.018 | 1.49% | 0.05 |
| V | | 3.32 | 0.07 | 0.030 | 2.01% | 63.59 | 0.09 | 0.044 | 0.15% | 12.73 | 0.03 | 0.009 | 1.79% | 0.12 |
Table 3.
Mean, , SE, MPE, and for PLA as a function of print orientation and raster angle.
Table 3.
Mean, , SE, MPE, and for PLA as a function of print orientation and raster angle.
| Material: PLA (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.33 | 0.08 | 0.044 | 2.10% | 63.43 | 0.07 | 0.014 | −0.11% | 12.74 | 0.04 | 0.019 | 1.87% | 0.11 |
| F | | 3.30 | 0.05 | 0.045 | 1.20% | 63.40 | 0.10 | 0.017 | −0.17% | 12.71 | 0.01 | 0.028 | 1.62% | 0.11 |
| F | | 3.32 | 0.07 | 0.052 | 1.98% | 63.51 | 0.01 | 0.012 | 0.01% | 12.71 | 0.01 | 0.016 | 1.62% | 0.07 |
| F | | 3.34 | 0.09 | 0.043 | 2.58% | 63.50 | 0.00 | 0.011 | 0.00% | 12.67 | 0.03 | 0.019 | 1.37% | 0.09 |
| F | | 3.37 | 0.12 | 0.043 | 3.54% | 63.60 | 0.10 | 0.031 | 0.16% | 12.65 | 0.05 | 0.026 | 1.16% | 0.17 |
| F | | 3.35 | 0.10 | 0.033 | 2.93% | 63.64 | 0.14 | 0.020 | 0.22% | 12.69 | 0.01 | 0.027 | 1.50% | 0.17 |
| F | | 3.35 | 0.10 | 0.041 | 2.91% | 63.72 | 0.22 | 0.021 | 0.34% | 12.70 | 0.00 | 0.017 | 1.57% | 0.24 |
| H | | 3.25 | 0.00 | 0.032 | 0.01% | 63.45 | 0.05 | 0.020 | −0.07% | 12.73 | 0.03 | 0.031 | 1.80% | 0.06 |
| H | | 3.31 | 0.06 | 0.039 | 1.60% | 63.47 | 0.04 | 0.022 | −0.06% | 12.80 | 0.10 | 0.054 | 2.33% | 0.12 |
| H | | 3.26 | 0.01 | 0.025 | 0.31% | 63.50 | 0.00 | 0.012 | −0.01% | 12.76 | 0.06 | 0.039 | 2.02% | 0.06 |
| H | | 3.28 | 0.03 | 0.025 | 0.74% | 63.63 | 0.13 | 0.027 | 0.20% | 12.65 | 0.05 | 0.063 | 1.13% | 0.14 |
| H | | 3.23 | 0.02 | 0.020 | −0.65% | 63.56 | 0.06 | 0.028 | 0.10% | 12.77 | 0.07 | 0.019 | 2.10% | 0.09 |
| H | | 3.26 | 0.01 | 0.010 | 0.27% | 63.76 | 0.26 | 0.055 | 0.40% | 12.74 | 0.04 | 0.023 | 1.89% | 0.26 |
| H | | 3.25 | 0.00 | 0.018 | 0.00% | 63.73 | 0.23 | 0.059 | 0.37% | 12.70 | 0.00 | 0.025 | 1.59% | 0.23 |
| V | | 3.29 | 0.04 | 0.032 | 1.20% | 63.85 | 0.35 | 0.024 | 0.55% | 12.77 | 0.07 | 0.028 | 2.08% | 0.36 |
| V | | 3.28 | 0.03 | 0.023 | 0.93% | 63.73 | 0.23 | 0.050 | 0.36% | 12.78 | 0.08 | 0.039 | 2.17% | 0.25 |
| V | | 3.27 | 0.02 | 0.020 | 0.55% | 63.85 | 0.35 | 0.024 | 0.54% | 12.75 | 0.05 | 0.019 | 1.93% | 0.35 |
| V | | 3.25 | 0.00 | 0.021 | −0.13% | 63.75 | 0.25 | 0.053 | 0.39% | 12.81 | 0.11 | 0.032 | 2.42% | 0.27 |
| V | | 3.27 | 0.02 | 0.027 | 0.58% | 63.74 | 0.24 | 0.051 | 0.37% | 12.76 | 0.06 | 0.030 | 2.02% | 0.25 |
| V | | 3.28 | 0.03 | 0.020 | 0.85% | 63.81 | 0.31 | 0.025 | 0.48% | 12.80 | 0.10 | 0.032 | 2.32% | 0.33 |
| V | | 3.25 | 0.00 | 0.021 | −0.07% | 63.79 | 0.29 | 0.017 | 0.46% | 12.80 | 0.10 | 0.032 | 2.37% | 0.31 |
Table 4.
Mean, , SE, MPE, and for HTPLA as a function of print orientation and raster angle.
Table 4.
Mean, , SE, MPE, and for HTPLA as a function of print orientation and raster angle.
| Material: HTPLA (all dimensions in mm unless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.28 | 0.03 | 0.022 | 1.00% | 63.33 | 0.17 | 0.026 | -0.27% | 12.72 | 0.02 | 0.023 | 1.75% | 0.18 |
| F | | 3.29 | 0.04 | 0.033 | 1.00% | 63.30 | 0.20 | 0.014 | -0.31% | 12.74 | 0.04 | 0.030 | 1.88% | 0.20 |
| F | | 3.28 | 0.03 | 0.029 | 0.84% | 63.54 | 0.04 | 0.043 | 0.06% | 12.74 | 0.04 | 0.023 | 1.90% | 0.06 |
| F | | 3.30 | 0.05 | 0.023 | 1.47% | 63.48 | 0.02 | 0.020 | -0.03% | 12.69 | 0.01 | 0.030 | 1.50% | 0.05 |
| F | | 3.29 | 0.04 | 0.019 | 1.19% | 63.52 | 0.02 | 0.028 | 0.04% | 12.65 | 0.05 | 0.014 | 1.20% | 0.07 |
| F | | 3.30 | 0.05 | 0.029 | 1.36% | 63.59 | 0.09 | 0.033 | 0.14% | 12.68 | 0.03 | 0.036 | 1.37% | 0.11 |
| F | | 3.27 | 0.02 | 0.033 | 0.55% | 63.63 | 0.13 | 0.019 | 0.20% | 12.68 | 0.02 | 0.013 | 1.43% | 0.13 |
| H | | 3.26 | 0.01 | 0.021 | 0.39% | 63.39 | 0.11 | 0.027 | -0.18% | 12.87 | 0.17 | 0.041 | 2.90% | 0.21 |
| H | | 3.28 | 0.03 | 0.018 | 0.80% | 63.44 | 0.06 | 0.024 | -0.10% | 12.89 | 0.19 | 0.027 | 3.01% | 0.20 |
| H | | 3.27 | 0.02 | 0.007 | 0.52% | 63.44 | 0.06 | 0.019 | -0.09% | 12.84 | 0.14 | 0.040 | 2.62% | 0.15 |
| H | | 3.24 | 0.01 | 0.010 | -0.44% | 63.53 | 0.03 | 0.011 | 0.04% | 12.86 | 0.16 | 0.036 | 2.78% | 0.16 |
| H | | 3.24 | 0.01 | 0.012 | -0.26% | 63.55 | 0.05 | 0.022 | 0.07% | 12.85 | 0.15 | 0.025 | 2.69% | 0.15 |
| H | | 3.25 | 0.00 | 0.024 | -0.17% | 63.64 | 0.14 | 0.022 | 0.22% | 12.84 | 0.14 | 0.023 | 2.67% | 0.20 |
| H | | 3.25 | 0.00 | 0.013 | -0.11% | 63.64 | 0.14 | 0.033 | 0.21% | 12.84 | 0.14 | 0.037 | 2.66% | 0.20 |
| V | | 3.29 | 0.04 | 0.019 | 1.03% | 63.71 | 0.20 | 0.077 | 0.32% | 12.69 | 0.01 | 0.019 | 1.50% | 0.21 |
| V | | 3.26 | 0.01 | 0.009 | 0.24% | 63.76 | 0.26 | 0.036 | 0.41% | 12.68 | 0.02 | 0.011 | 1.40% | 0.26 |
| V | | 3.24 | 0.01 | 0.010 | -0.29% | 63.74 | 0.24 | 0.082 | 0.38% | 12.71 | 0.01 | 0.006 | 1.64% | 0.24 |
| V | | 3.27 | 0.02 | 0.012 | 0.54% | 63.82 | 0.32 | 0.038 | 0.51% | 12.73 | 0.03 | 0.016 | 1.78% | 0.32 |
| V | | 3.23 | 0.02 | 0.012 | -0.57% | 63.80 | 0.30 | 0.061 | 0.47% | 12.70 | 0.00 | 0.018 | 1.55% | 0.30 |
| V | | 3.21 | 0.04 | 0.014 | -1.17% | 63.71 | 0.21 | 0.075 | 0.32% | 12.70 | 0.00 | 0.013 | 1.57% | 0.21 |
| V | | 3.24 | 0.01 | 0.006 | -0.44% | 63.74 | 0.24 | 0.047 | 0.38% | 12.71 | 0.01 | 0.006 | 1.63% | 0.24 |
Table 5.
Mean, , SE, MPE, and for HIPS as a function of print orientation and raster angle.
Table 5.
Mean, , SE, MPE, and for HIPS as a function of print orientation and raster angle.
| Material: HIPS (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.23 | 0.02 | 0.034 | −0.78% | 63.42 | 0.08 | 0.030 | −0.12% | 12.78 | 0.08 | 0.050 | 2.19% | 0.11 |
| F | | 3.23 | 0.02 | 0.026 | −0.77% | 63.42 | 0.09 | 0.027 | −0.13% | 12.82 | 0.12 | 0.048 | 2.45% | 0.15 |
| F | | 3.19 | 0.06 | 0.020 | −1.79% | 63.48 | 0.02 | 0.035 | −0.03% | 12.81 | 0.11 | 0.041 | 2.38% | 0.12 |
| F | | 3.22 | 0.04 | 0.022 | −1.13% | 63.42 | 0.08 | 0.030 | −0.13% | 12.78 | 0.08 | 0.041 | 2.19% | 0.12 |
| F | | 3.22 | 0.03 | 0.028 | −0.94% | 63.40 | 0.10 | 0.031 | −0.15% | 12.76 | 0.06 | 0.040 | 2.03% | 0.12 |
| F | | 3.22 | 0.03 | 0.035 | −1.13% | 63.34 | 0.16 | 0.032 | −0.26% | 12.79 | 0.09 | 0.049 | 2.22% | 0.19 |
| F | | 3.17 | 0.08 | 0.026 | −2.68% | 63.44 | 0.06 | 0.027 | −0.09% | 12.76 | 0.06 | 0.055 | 2.01% | 0.12 |
| H | | 3.25 | 0.00 | 0.011 | −0.07% | 63.49 | 0.02 | 0.023 | −0.02% | 12.68 | 0.02 | 0.028 | 1.41% | 0.03 |
| H | | 3.26 | 0.01 | 0.016 | 0.38% | 63.48 | 0.02 | 0.020 | −0.04% | 12.67 | 0.03 | 0.016 | 1.35% | 0.04 |
| H | | 3.25 | 0.00 | 0.008 | 0.06% | 63.53 | 0.03 | 0.015 | 0.05% | 12.72 | 0.02 | 0.020 | 1.70% | 0.04 |
| H | | 3.23 | 0.02 | 0.013 | −0.63% | 63.48 | 0.02 | 0.016 | −0.04% | 12.70 | 0.00 | 0.028 | 1.54% | 0.03 |
| H | | 3.24 | 0.01 | 0.007 | −0.44% | 63.46 | 0.04 | 0.016 | −0.06% | 12.72 | 0.02 | 0.026 | 1.75% | 0.05 |
| H | | 3.25 | 0.00 | 0.010 | 0.08% | 63.49 | 0.01 | 0.024 | −0.02% | 12.70 | 0.00 | 0.024 | 1.60% | 0.01 |
| H | | 3.24 | 0.01 | 0.009 | −0.25% | 63.51 | 0.01 | 0.012 | 0.01% | 12.70 | 0.00 | 0.018 | 1.57% | 0.01 |
| V | | 3.21 | 0.04 | 0.011 | −1.26% | 63.34 | 0.16 | 0.043 | −0.25% | 12.72 | 0.02 | 0.016 | 1.70% | 0.16 |
| V | | 3.25 | 0.00 | 0.008 | −0.04% | 63.35 | 0.15 | 0.045 | −0.24% | 12.77 | 0.07 | 0.023 | 2.09% | 0.17 |
| V | | 3.23 | 0.02 | 0.009 | −0.53% | 63.34 | 0.16 | 0.039 | −0.25% | 12.72 | 0.02 | 0.017 | 1.75% | 0.16 |
| V | | 3.27 | 0.02 | 0.006 | 0.49% | 63.36 | 0.14 | 0.036 | −0.22% | 12.73 | 0.03 | 0.012 | 1.83% | 0.15 |
| V | | 3.28 | 0.03 | 0.009 | 0.94% | 63.33 | 0.17 | 0.030 | −0.27% | 12.78 | 0.08 | 0.020 | 2.15% | 0.19 |
| V | | 3.30 | 0.05 | 0.015 | 1.59% | 63.31 | 0.19 | 0.028 | −0.30% | 12.75 | 0.05 | 0.024 | 1.94% | 0.20 |
| V | | 3.28 | 0.03 | 0.014 | 0.87% | 63.35 | 0.15 | 0.045 | −0.24% | 12.74 | 0.04 | 0.014 | 1.91% | 0.16 |
Table 6.
Mean, , SE, MPE, and for nylon as a function of print orientation and raster angle.
Table 6.
Mean, , SE, MPE, and for nylon as a function of print orientation and raster angle.
| Material: Nylon (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.21 | 0.04 | 0.020 | −1.41% | 63.19 | 0.31 | 0.105 | −0.49% | 12.72 | 0.02 | 0.028 | 1.73% | 0.31 |
| F | | 3.23 | 0.02 | 0.018 | −0.55% | 63.25 | 0.25 | 0.100 | −0.40% | 12.67 | 0.03 | 0.031 | 1.33% | 0.25 |
| F | | 3.27 | 0.01 | 0.016 | 0.44% | 63.34 | 0.16 | 0.086 | −0.25% | 12.75 | 0.05 | 0.028 | 1.96% | 0.17 |
| F | | 3.22 | 0.04 | 0.016 | −1.11% | 63.29 | 0.21 | 0.102 | −0.33% | 12.71 | 0.01 | 0.024 | 1.67% | 0.21 |
| F | | 3.26 | 0.01 | 0.014 | 0.38% | 63.28 | 0.22 | 0.121 | −0.35% | 12.74 | 0.04 | 0.032 | 1.87% | 0.22 |
| F | | 3.28 | 0.03 | 0.016 | 0.95% | 63.34 | 0.16 | 0.114 | −0.26% | 12.70 | 0.00 | 0.016 | 1.58% | 0.17 |
| F | | 3.22 | 0.03 | 0.015 | −0.83% | 63.24 | 0.26 | 0.103 | −0.41% | 12.71 | 0.01 | 0.038 | 1.64% | 0.26 |
| H | | 3.24 | 0.01 | 0.021 | −0.28% | 63.38 | 0.12 | 0.110 | −0.20% | 12.68 | 0.02 | 0.018 | 1.43% | 0.13 |
| H | | 3.24 | 0.01 | 0.025 | −0.36% | 63.33 | 0.17 | 0.093 | −0.27% | 12.67 | 0.03 | 0.022 | 1.37% | 0.17 |
| H | | 3.22 | 0.03 | 0.031 | −1.14% | 63.18 | 0.32 | 0.095 | −0.51% | 12.70 | 0.00 | 0.009 | 1.55% | 0.32 |
| H | | 3.26 | 0.01 | 0.017 | 0.19% | 63.31 | 0.20 | 0.100 | −0.31% | 12.66 | 0.05 | 0.021 | 1.22% | 0.20 |
| H | | 3.29 | 0.04 | 0.022 | 1.12% | 63.25 | 0.25 | 0.111 | −0.40% | 12.68 | 0.02 | 0.018 | 1.41% | 0.26 |
| H | | 3.25 | 0.00 | 0.018 | −0.03% | 63.30 | 0.20 | 0.093 | −0.32% | 12.71 | 0.01 | 0.016 | 1.66% | 0.20 |
| H | | 3.22 | 0.03 | 0.024 | −0.86% | 63.21 | 0.29 | 0.092 | −0.47% | 12.73 | 0.03 | 0.013 | 1.77% | 0.30 |
| V | | 3.26 | 0.01 | 0.019 | 0.21% | 63.38 | 0.12 | 0.061 | −0.19% | 12.66 | 0.04 | 0.012 | 1.29% | 0.12 |
| V | | 3.25 | 0.00 | 0.010 | 0.12% | 63.31 | 0.19 | 0.045 | −0.30% | 12.72 | 0.02 | 0.034 | 1.70% | 0.19 |
| V | | 3.28 | 0.03 | 0.013 | 0.93% | 63.29 | 0.21 | 0.063 | −0.34% | 12.69 | 0.01 | 0.028 | 1.49% | 0.22 |
| V | | 3.28 | 0.02 | 0.014 | 0.75% | 63.35 | 0.15 | 0.073 | −0.23% | 12.66 | 0.04 | 0.013 | 1.26% | 0.16 |
| V | | 3.25 | 0.00 | 0.009 | −0.10% | 63.41 | 0.09 | 0.054 | −0.14% | 12.67 | 0.03 | 0.025 | 1.31% | 0.09 |
| V | | 3.27 | 0.01 | 0.005 | 0.46% | 63.30 | 0.20 | 0.055 | −0.31% | 12.67 | 0.03 | 0.014 | 1.34% | 0.20 |
| V | | 3.26 | 0.01 | 0.013 | 0.35% | 63.38 | 0.12 | 0.062 | −0.19% | 12.71 | 0.01 | 0.014 | 1.65% | 0.12 |
Table 7.
Mean, , SE, MPE, and for PETG as a function of print orientation and raster angle.
Table 7.
Mean, , SE, MPE, and for PETG as a function of print orientation and raster angle.
| Material: PETG (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.21 | 0.04 | 0.023 | −1.26% | 63.45 | 0.05 | 0.042 | −0.08% | 12.70 | 0.00 | 0.015 | 1.54% | 0.07 |
| F | | 3.21 | 0.04 | 0.020 | −1.22% | 63.49 | 0.01 | 0.013 | −0.01% | 12.72 | 0.02 | 0.015 | 1.69% | 0.04 |
| F | | 3.26 | 0.01 | 0.006 | 0.18% | 63.45 | 0.05 | 0.044 | −0.08% | 12.71 | 0.01 | 0.018 | 1.61% | 0.05 |
| F | | 3.24 | 0.01 | 0.014 | −0.26% | 63.41 | 0.09 | 0.034 | −0.14% | 12.65 | 0.05 | 0.019 | 1.19% | 0.10 |
| F | | 3.27 | 0.02 | 0.010 | 0.51% | 63.29 | 0.21 | 0.036 | −0.34% | 12.68 | 0.02 | 0.013 | 1.45% | 0.21 |
| F | | 3.25 | 0.00 | 0.009 | 0.05% | 63.25 | 0.25 | 0.046 | −0.40% | 12.71 | 0.01 | 0.026 | 1.66% | 0.25 |
| F | | 3.28 | 0.02 | 0.017 | 0.74% | 63.22 | 0.28 | 0.069 | −0.44% | 12.69 | 0.01 | 0.012 | 1.48% | 0.28 |
| H | | 3.25 | 0.00 | 0.010 | −0.16% | 63.50 | 0.00 | 0.026 | 0.01% | 12.76 | 0.06 | 0.011 | 2.01% | 0.06 |
| H | | 3.24 | 0.01 | 0.013 | −0.29% | 63.52 | 0.02 | 0.024 | 0.03% | 12.69 | 0.01 | 0.018 | 1.51% | 0.02 |
| H | | 3.24 | 0.01 | 0.013 | −0.48% | 63.53 | 0.03 | 0.029 | 0.05% | 12.73 | 0.03 | 0.020 | 1.83% | 0.05 |
| H | | 3.23 | 0.02 | 0.009 | −0.72% | 63.49 | 0.01 | 0.015 | −0.01% | 12.70 | 0.00 | 0.029 | 1.54% | 0.03 |
| H | | 3.24 | 0.01 | 0.010 | −0.38% | 63.43 | 0.07 | 0.034 | −0.11% | 12.73 | 0.03 | 0.015 | 1.81% | 0.08 |
| H | | 3.23 | 0.02 | 0.011 | −0.72% | 63.44 | 0.06 | 0.056 | −0.10% | 12.73 | 0.03 | 0.028 | 1.81% | 0.08 |
| H | | 3.23 | 0.02 | 0.008 | −0.56% | 63.45 | 0.05 | 0.053 | −0.08% | 12.70 | 0.00 | 0.010 | 1.58% | 0.05 |
| V | | 3.24 | 0.01 | 0.010 | −0.32% | 63.77 | 0.27 | 0.031 | 0.42% | 12.70 | 0.00 | 0.019 | 1.55% | 0.27 |
| V | | 3.23 | 0.02 | 0.006 | −0.59% | 63.76 | 0.26 | 0.040 | 0.41% | 12.70 | 0.00 | 0.019 | 1.57% | 0.26 |
| V | | 3.21 | 0.04 | 0.013 | −1.26% | 63.80 | 0.30 | 0.042 | 0.47% | 12.68 | 0.02 | 0.021 | 1.43% | 0.31 |
| V | | 3.21 | 0.04 | 0.011 | −1.38% | 63.81 | 0.31 | 0.045 | 0.49% | 12.67 | 0.03 | 0.015 | 1.36% | 0.32 |
| V | | 3.20 | 0.05 | 0.007 | −1.50% | 63.81 | 0.31 | 0.051 | 0.48% | 12.69 | 0.01 | 0.014 | 1.53% | 0.31 |
| V | | 3.22 | 0.03 | 0.015 | −0.95% | 63.79 | 0.29 | 0.027 | 0.45% | 12.71 | 0.01 | 0.010 | 1.64% | 0.29 |
| V | | 3.22 | 0.04 | 0.017 | −1.11% | 63.82 | 0.31 | 0.019 | 0.49% | 12.72 | 0.02 | 0.024 | 1.71% | 0.32 |
Table 8.
Mean, , SE, MPE, and for PC as a function of print orientation and raster angle.
Table 8.
Mean, , SE, MPE, and for PC as a function of print orientation and raster angle.
| Material: PC (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.18 | 0.07 | 0.017 | −2.16% | 63.48 | 0.02 | 0.031 | −0.03% | 12.72 | 0.02 | 0.016 | 1.71% | 0.07 |
| F | | 3.23 | 0.02 | 0.009 | −0.66% | 63.47 | 0.03 | 0.023 | −0.04% | 12.75 | 0.05 | 0.017 | 1.94% | 0.06 |
| F | | 3.25 | 0.00 | 0.010 | −0.13% | 63.56 | 0.06 | 0.034 | 0.09% | 12.75 | 0.05 | 0.021 | 1.95% | 0.08 |
| F | | 3.25 | 0.00 | 0.010 | 0.11% | 63.49 | 0.01 | 0.030 | −0.02% | 12.73 | 0.03 | 0.013 | 1.77% | 0.03 |
| F | | 3.23 | 0.02 | 0.012 | −0.66% | 63.48 | 0.02 | 0.034 | −0.03% | 12.71 | 0.01 | 0.010 | 1.67% | 0.03 |
| F | | 3.23 | 0.02 | 0.014 | −0.70% | 63.49 | 0.01 | 0.014 | −0.01% | 12.72 | 0.02 | 0.019 | 1.73% | 0.03 |
| F | | 3.18 | 0.07 | 0.029 | −2.22% | 63.45 | 0.05 | 0.027 | −0.07% | 12.75 | 0.05 | 0.016 | 1.94% | 0.10 |
| H | | 3.25 | 0.00 | 0.004 | −0.12% | 63.48 | 0.02 | 0.015 | −0.04% | 12.62 | 0.08 | 0.031 | 0.94% | 0.08 |
| H | | 3.26 | 0.01 | 0.009 | 0.18% | 63.49 | 0.01 | 0.014 | −0.02% | 12.59 | 0.11 | 0.030 | 0.74% | 0.11 |
| H | | 3.29 | 0.04 | 0.014 | 1.14% | 63.51 | 0.01 | 0.013 | 0.02% | 12.68 | 0.02 | 0.022 | 1.41% | 0.05 |
| H | | 3.25 | 0.00 | 0.007 | 0.09% | 63.51 | 0.01 | 0.015 | 0.02% | 12.69 | 0.01 | 0.018 | 1.53% | 0.01 |
| H | | 3.26 | 0.01 | 0.009 | 0.15% | 63.46 | 0.04 | 0.029 | −0.07% | 12.71 | 0.01 | 0.014 | 1.67% | 0.05 |
| H | | 3.25 | 0.00 | 0.008 | 0.06% | 63.45 | 0.05 | 0.024 | −0.08% | 12.70 | 0.00 | 0.016 | 1.54% | 0.05 |
| H | | 3.27 | 0.02 | 0.008 | 0.51% | 63.46 | 0.04 | 0.024 | −0.06% | 12.65 | 0.05 | 0.029 | 1.15% | 0.07 |
| V | | 3.26 | 0.01 | 0.010 | 0.15% | 63.43 | 0.07 | 0.029 | −0.11% | 12.73 | 0.03 | 0.006 | 1.83% | 0.08 |
| V | | 3.26 | 0.01 | 0.006 | 0.30% | 63.41 | 0.09 | 0.022 | −0.14% | 12.73 | 0.03 | 0.008 | 1.83% | 0.09 |
| V | | 3.26 | 0.01 | 0.004 | 0.21% | 63.40 | 0.10 | 0.014 | −0.16% | 12.74 | 0.04 | 0.012 | 1.87% | 0.11 |
| V | | 3.26 | 0.01 | 0.011 | 0.42% | 63.42 | 0.08 | 0.027 | −0.12% | 12.76 | 0.06 | 0.015 | 2.04% | 0.10 |
| V | | 3.27 | 0.02 | 0.008 | 0.49% | 63.41 | 0.09 | 0.017 | −0.14% | 12.77 | 0.07 | 0.013 | 2.08% | 0.11 |
| V | | 3.28 | 0.03 | 0.012 | 0.87% | 63.37 | 0.13 | 0.032 | −0.21% | 12.75 | 0.05 | 0.013 | 1.98% | 0.14 |
| V | | 3.27 | 0.02 | 0.006 | 0.55% | 63.37 | 0.13 | 0.028 | −0.20% | 12.75 | 0.05 | 0.009 | 1.94% | 0.14 |
Table 9.
Mean, , SE, MPE, and for APLA as a function of print orientation and raster angle.
Table 9.
Mean, , SE, MPE, and for APLA as a function of print orientation and raster angle.
| Material: APLA (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.25 | 0.00 | 0.021 | −0.07% | 63.27 | 0.23 | 0.034 | −0.37% | 12.70 | 0.00 | 0.019 | 1.55% | 0.23 |
| F | | 3.26 | 0.01 | 0.023 | 0.23% | 63.30 | 0.20 | 0.031 | −0.32% | 12.71 | 0.01 | 0.028 | 1.62% | 0.20 |
| F | | 3.30 | 0.05 | 0.047 | 1.37% | 63.34 | 0.16 | 0.027 | −0.25% | 12.68 | 0.02 | 0.025 | 1.45% | 0.17 |
| F | | 3.28 | 0.03 | 0.023 | 0.96% | 63.48 | 0.02 | 0.034 | −0.03% | 12.64 | 0.06 | 0.029 | 1.10% | 0.07 |
| F | | 3.29 | 0.04 | 0.032 | 0.98% | 63.56 | 0.06 | 0.034 | 0.09% | 12.66 | 0.04 | 0.032 | 1.25% | 0.08 |
| F | | 3.30 | 0.05 | 0.031 | 1.43% | 63.56 | 0.06 | 0.019 | 0.09% | 12.66 | 0.04 | 0.029 | 1.23% | 0.09 |
| F | | 3.27 | 0.02 | 0.023 | 0.48% | 63.62 | 0.12 | 0.039 | 0.19% | 12.66 | 0.04 | 0.030 | 1.23% | 0.13 |
| H | | 3.25 | 0.00 | 0.013 | 0.05% | 63.41 | 0.09 | 0.021 | −0.14% | 12.72 | 0.02 | 0.020 | 1.74% | 0.09 |
| H | | 3.26 | 0.01 | 0.013 | 0.38% | 63.43 | 0.07 | 0.013 | −0.11% | 12.73 | 0.03 | 0.020 | 1.78% | 0.08 |
| H | | 3.26 | 0.01 | 0.013 | 0.32% | 63.51 | 0.01 | 0.016 | 0.01% | 12.75 | 0.05 | 0.026 | 1.94% | 0.05 |
| H | | 3.21 | 0.04 | 0.018 | −1.37% | 63.55 | 0.05 | 0.017 | 0.08% | 12.75 | 0.05 | 0.035 | 1.92% | 0.08 |
| H | | 3.22 | 0.03 | 0.022 | −1.04% | 63.64 | 0.14 | 0.022 | 0.22% | 12.73 | 0.03 | 0.018 | 1.78% | 0.14 |
| H | | 3.24 | 0.01 | 0.016 | −0.36% | 63.67 | 0.17 | 0.029 | 0.26% | 12.76 | 0.06 | 0.030 | 2.01% | 0.18 |
| H | | 3.24 | 0.01 | 0.027 | −0.46% | 63.77 | 0.27 | 0.022 | 0.42% | 12.72 | 0.02 | 0.025 | 1.76% | 0.27 |
| V | | 3.28 | 0.03 | 0.016 | 0.98% | 63.83 | 0.33 | 0.032 | 0.51% | 12.69 | 0.01 | 0.024 | 1.49% | 0.33 |
| V | | 3.30 | 0.05 | 0.032 | 1.34% | 63.82 | 0.32 | 0.062 | 0.50% | 12.74 | 0.04 | 0.036 | 1.90% | 0.33 |
| V | | 3.26 | 0.01 | 0.020 | 0.33% | 63.79 | 0.29 | 0.040 | 0.45% | 12.70 | 0.00 | 0.027 | 1.59% | 0.29 |
| V | | 3.26 | 0.01 | 0.022 | 0.29% | 63.80 | 0.30 | 0.041 | 0.47% | 12.75 | 0.05 | 0.028 | 1.98% | 0.30 |
| V | | 3.26 | 0.01 | 0.019 | 0.40% | 63.68 | 0.18 | 0.097 | 0.29% | 12.71 | 0.01 | 0.036 | 1.61% | 0.18 |
| V | | 3.26 | 0.01 | 0.022 | 0.26% | 63.72 | 0.22 | 0.083 | 0.35% | 12.76 | 0.06 | 0.030 | 2.03% | 0.23 |
| V | | 3.27 | 0.02 | 0.021 | 0.51% | 63.34 | 0.16 | 0.081 | −0.25% | 12.72 | 0.02 | 0.034 | 1.73% | 0.16 |
Table 10.
Mean, , SE, MPE, and for CPLA as a function of print orientation and raster angle.
Table 10.
Mean, , SE, MPE, and for CPLA as a function of print orientation and raster angle.
| Material: CPLA (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.26 | 0.01 | 0.006 | 0.37% | 63.35 | 0.15 | 0.024 | −0.24% | 12.71 | 0.01 | 0.018 | 1.64% | 0.15 |
| F | | 3.26 | 0.01 | 0.006 | 0.21% | 63.26 | 0.24 | 0.017 | −0.37% | 12.67 | 0.03 | 0.015 | 1.34% | 0.24 |
| F | | 3.25 | 0.00 | 0.013 | −0.14% | 63.45 | 0.05 | 0.016 | −0.08% | 12.67 | 0.03 | 0.014 | 1.35% | 0.06 |
| F | | 3.25 | 0.00 | 0.010 | 0.08% | 63.52 | 0.02 | 0.009 | 0.03% | 12.60 | 0.10 | 0.017 | 0.82% | 0.10 |
| F | | 3.26 | 0.01 | 0.009 | 0.30% | 63.56 | 0.06 | 0.010 | 0.09% | 12.62 | 0.08 | 0.011 | 0.97% | 0.10 |
| F | | 3.26 | 0.01 | 0.008 | 0.27% | 63.60 | 0.10 | 0.016 | 0.16% | 12.62 | 0.08 | 0.011 | 0.96% | 0.13 |
| F | | 3.25 | 0.00 | 0.007 | 0.03% | 63.68 | 0.17 | 0.021 | 0.27% | 12.68 | 0.03 | 0.016 | 1.38% | 0.18 |
| H | | 3.23 | 0.02 | 0.010 | −0.63% | 63.34 | 0.16 | 0.019 | −0.26% | 12.81 | 0.11 | 0.008 | 2.42% | 0.20 |
| H | | 3.22 | 0.04 | 0.010 | −1.10% | 63.33 | 0.17 | 0.022 | −0.27% | 12.80 | 0.10 | 0.011 | 2.31% | 0.20 |
| H | | 3.20 | 0.05 | 0.010 | −1.70% | 63.47 | 0.03 | 0.020 | −0.04% | 12.78 | 0.08 | 0.015 | 2.15% | 0.10 |
| H | | 3.19 | 0.06 | 0.007 | −1.85% | 63.60 | 0.10 | 0.027 | 0.15% | 12.73 | 0.03 | 0.008 | 1.80% | 0.12 |
| H | | 3.18 | 0.07 | 0.010 | −2.08% | 63.60 | 0.10 | 0.024 | 0.15% | 12.76 | 0.06 | 0.008 | 2.03% | 0.13 |
| H | | 3.16 | 0.09 | 0.007 | −2.88% | 63.63 | 0.13 | 0.025 | 0.21% | 12.76 | 0.06 | 0.011 | 2.03% | 0.17 |
| H | | 3.26 | 0.01 | 0.008 | 0.27% | 63.65 | 0.15 | 0.023 | 0.24% | 12.74 | 0.04 | 0.012 | 1.91% | 0.16 |
| V | | 3.27 | 0.02 | 0.010 | 0.72% | 63.72 | 0.22 | 0.023 | 0.35% | 12.67 | 0.03 | 0.010 | 1.31% | 0.23 |
| V | | 3.25 | 0.00 | 0.004 | 0.06% | 63.74 | 0.24 | 0.022 | 0.38% | 12.69 | 0.01 | 0.013 | 1.48% | 0.24 |
| V | | 3.25 | 0.00 | 0.007 | 0.00% | 63.67 | 0.17 | 0.024 | 0.26% | 12.71 | 0.01 | 0.007 | 1.68% | 0.17 |
| V | | 3.27 | 0.02 | 0.005 | 0.49% | 63.71 | 0.21 | 0.017 | 0.33% | 12.64 | 0.06 | 0.014 | 1.12% | 0.22 |
| V | | 3.28 | 0.03 | 0.030 | 0.81% | 63.67 | 0.17 | 0.020 | 0.26% | 12.70 | 0.00 | 0.012 | 1.54% | 0.17 |
| V | | 3.26 | 0.01 | 0.006 | 0.24% | 63.65 | 0.15 | 0.024 | 0.23% | 12.69 | 0.01 | 0.015 | 1.52% | 0.15 |
| V | | 3.25 | 0.00 | 0.008 | −0.07% | 63.68 | 0.18 | 0.013 | 0.28% | 12.73 | 0.03 | 0.009 | 1.81% | 0.18 |
Table 11.
Mean, , SE, MPE, and for WPLA as a function of print orientation and raster angle.
Table 11.
Mean, , SE, MPE, and for WPLA as a function of print orientation and raster angle.
| Material: WPLA (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.29 | 0.04 | 0.014 | 1.08% | 63.53 | 0.03 | 0.007 | 0.05% | 12.82 | 0.12 | 0.016 | 2.47% | 0.13 |
| F | | 3.26 | 0.01 | 0.009 | 0.36% | 63.48 | 0.02 | 0.030 | −0.03% | 12.77 | 0.07 | 0.034 | 2.09% | 0.07 |
| F | | 3.26 | 0.01 | 0.009 | 0.36% | 63.62 | 0.12 | 0.017 | 0.19% | 12.79 | 0.09 | 0.020 | 2.25% | 0.15 |
| F | | 3.25 | 0.00 | 0.015 | 0.01% | 63.55 | 0.05 | 0.022 | 0.08% | 12.73 | 0.03 | 0.014 | 1.78% | 0.06 |
| F | | 3.28 | 0.03 | 0.010 | 1.00% | 63.64 | 0.14 | 0.020 | 0.22% | 12.74 | 0.04 | 0.017 | 1.87% | 0.15 |
| F | | 3.27 | 0.02 | 0.012 | 0.66% | 63.77 | 0.27 | 0.021 | 0.42% | 12.73 | 0.03 | 0.016 | 1.79% | 0.27 |
| F | | 3.28 | 0.03 | 0.014 | 0.90% | 63.81 | 0.31 | 0.018 | 0.48% | 12.72 | 0.02 | 0.010 | 1.71% | 0.31 |
| H | | 3.30 | 0.04 | 0.013 | 1.35% | 63.36 | 0.14 | 0.052 | −0.22% | 12.70 | 0.00 | 0.021 | 1.58% | 0.14 |
| H | | 3.36 | 0.11 | 0.014 | 3.20% | 63.51 | 0.01 | 0.043 | 0.01% | 12.70 | 0.00 | 0.022 | 1.56% | 0.11 |
| H | | 3.30 | 0.04 | 0.010 | 1.36% | 63.53 | 0.03 | 0.025 | 0.05% | 12.71 | 0.01 | 0.028 | 1.65% | 0.06 |
| H | | 3.31 | 0.06 | 0.013 | 1.80% | 63.66 | 0.16 | 0.034 | 0.25% | 12.74 | 0.04 | 0.025 | 1.85% | 0.17 |
| H | | 3.25 | 0.00 | 0.015 | −0.11% | 63.63 | 0.13 | 0.049 | 0.20% | 12.71 | 0.01 | 0.017 | 1.67% | 0.13 |
| H | | 3.28 | 0.03 | 0.012 | 0.78% | 63.70 | 0.20 | 0.041 | 0.32% | 12.72 | 0.02 | 0.017 | 1.71% | 0.20 |
| H | | 3.28 | 0.03 | 0.013 | 0.96% | 63.67 | 0.17 | 0.028 | 0.26% | 12.71 | 0.01 | 0.019 | 1.66% | 0.17 |
| V | | 3.24 | 0.01 | 0.008 | −0.22% | 63.71 | 0.21 | 0.021 | 0.33% | 12.63 | 0.07 | 0.014 | 0.99% | 0.22 |
| V | | 3.23 | 0.02 | 0.011 | −0.75% | 63.75 | 0.25 | 0.025 | 0.40% | 12.68 | 0.02 | 0.015 | 1.39% | 0.26 |
| V | | 3.23 | 0.02 | 0.019 | −0.53% | 63.76 | 0.26 | 0.020 | 0.41% | 12.70 | 0.00 | 0.019 | 1.57% | 0.26 |
| V | | 3.22 | 0.03 | 0.008 | −1.00% | 63.75 | 0.25 | 0.015 | 0.39% | 12.73 | 0.03 | 0.018 | 1.79% | 0.25 |
| V | | 3.21 | 0.04 | 0.013 | −1.32% | 63.73 | 0.23 | 0.020 | 0.36% | 12.65 | 0.05 | 0.018 | 1.20% | 0.24 |
| V | | 3.21 | 0.04 | 0.010 | −1.32% | 63.79 | 0.29 | 0.025 | 0.45% | 12.69 | 0.01 | 0.014 | 1.47% | 0.29 |
| V | | 3.21 | 0.04 | 0.017 | −1.34% | 63.72 | 0.22 | 0.015 | 0.35% | 12.74 | 0.04 | 0.017 | 1.91% | 0.23 |
Table 12.
Mean, , SE, MPE, and for CFPLA as a function of print orientation and raster angle.
Table 12.
Mean, , SE, MPE, and for CFPLA as a function of print orientation and raster angle.
| Material: CFPLA (all dimensions inmmunless otherwise specified) |
| PO | Angle | Z () | C () | E () | |
| | SE | MPE | | | SE | MPE | | | SE | MPE |
| F | | 3.24 | 0.01 | 0.019 | −0.37% | 63.29 | 0.21 | 0.035 | −0.33% | 12.71 | 0.01 | 0.016 | 1.67% | 0.21 |
| F | | 3.25 | 0.00 | 0.022 | −0.01% | 63.38 | 0.13 | 0.028 | −0.20% | 12.72 | 0.02 | 0.024 | 1.72% | 0.13 |
| F | | 3.26 | 0.01 | 0.019 | 0.19% | 63.36 | 0.14 | 0.033 | −0.22% | 12.68 | 0.02 | 0.035 | 1.42% | 0.14 |
| F | | 3.24 | 0.01 | 0.020 | −0.47% | 63.44 | 0.06 | 0.022 | −0.09% | 12.67 | 0.03 | 0.044 | 1.29% | 0.07 |
| F | | 3.29 | 0.04 | 0.025 | 1.04% | 63.53 | 0.03 | 0.033 | 0.05% | 12.68 | 0.02 | 0.027 | 1.44% | 0.05 |
| F | | 3.29 | 0.04 | 0.025 | 1.22% | 63.62 | 0.12 | 0.020 | 0.19% | 12.68 | 0.02 | 0.020 | 1.45% | 0.13 |
| F | | 3.27 | 0.02 | 0.028 | 0.61% | 63.65 | 0.15 | 0.025 | 0.23% | 12.68 | 0.02 | 0.021 | 1.42% | 0.15 |
| H | | 3.25 | 0.00 | 0.015 | 0.04% | 63.41 | 0.09 | 0.032 | −0.14% | 12.83 | 0.13 | 0.035 | 2.54% | 0.15 |
| H | | 3.25 | 0.00 | 0.011 | 0.02% | 63.39 | 0.11 | 0.030 | −0.17% | 12.82 | 0.12 | 0.031 | 2.51% | 0.16 |
| H | | 3.24 | 0.01 | 0.007 | −0.19% | 63.50 | 0.01 | 0.025 | −0.01% | 12.84 | 0.14 | 0.025 | 2.62% | 0.14 |
| H | | 3.21 | 0.04 | 0.008 | −1.22% | 63.52 | 0.02 | 0.048 | 0.03% | 12.81 | 0.11 | 0.031 | 2.41% | 0.12 |
| H | | 3.21 | 0.04 | 0.012 | −1.23% | 63.56 | 0.06 | 0.045 | 0.09% | 12.79 | 0.09 | 0.026 | 2.23% | 0.11 |
| H | | 3.22 | 0.03 | 0.008 | −1.00% | 63.55 | 0.05 | 0.048 | 0.07% | 12.78 | 0.08 | 0.028 | 2.17% | 0.10 |
| H | | 3.20 | 0.05 | 0.007 | −1.57% | 63.66 | 0.16 | 0.042 | 0.25% | 12.81 | 0.11 | 0.030 | 2.45% | 0.20 |
| V | | 3.25 | 0.00 | 0.017 | −0.03% | 63.75 | 0.25 | 0.053 | 0.39% | 12.67 | 0.03 | 0.018 | 1.35% | 0.25 |
| V | | 3.22 | 0.03 | 0.008 | −0.81% | 63.73 | 0.23 | 0.040 | 0.36% | 12.66 | 0.04 | 0.021 | 1.28% | 0.23 |
| V | | 3.28 | 0.03 | 0.023 | 0.84% | 63.64 | 0.14 | 0.088 | 0.22% | 12.62 | 0.08 | 0.019 | 0.96% | 0.16 |
| V | | 3.21 | 0.04 | 0.011 | −1.38% | 63.75 | 0.25 | 0.037 | 0.39% | 12.69 | 0.01 | 0.019 | 1.50% | 0.25 |
| V | | 3.23 | 0.02 | 0.016 | −0.73% | 63.75 | 0.25 | 0.039 | 0.40% | 12.66 | 0.04 | 0.024 | 1.28% | 0.26 |
| V | | 3.24 | 0.01 | 0.020 | −0.44% | 63.72 | 0.21 | 0.052 | 0.34% | 12.70 | 0.00 | 0.013 | 1.54% | 0.22 |
| V | | 3.20 | 0.05 | 0.017 | −1.72% | 63.73 | 0.23 | 0.036 | 0.35% | 12.68 | 0.02 | 0.017 | 1.45% | 0.23 |
Table 13.
Specimen manufacturing parameters.
Table 13.
Specimen manufacturing parameters.
| Material | Velocity (mm/s) | Jerk (mm/s) | (C) | (C) | Nozzle Type | Environment |
|---|
| ABS | 50 | 8 | 225 | 90 | mm Brass | Enclosed (XYZ) |
| PLA | 60 | 8 | 200 | 50 | mm Steel | Open (Prusa) |
| HTPLA | 60 | 8 | 245 | 50 | mm Steel | Open (Prusa) |
| HIPS | 60 | 8 | 240 | 90 | mm Brass | Enclosed (XYZ) |
| Nylon | 50 | 8 | 250 | 70 | mm Brass | Enclosed (XYZ) |
| PETG | 60 | 8 | 240 | 80 | mm Steel | Open (Prusa) |
| PC | 30 | 8 | 260 | 90 | mm Brass | Enclosed (XYZ) |
| APLA | 60 | 8 | 200 | 50 | mm Steel | Open (Prusa) |
| CPLA | 60 | 8 | 205 | 50 | mm Steel | Open (Prusa) |
| WPLA | 60 | 8 | 210 | 50 | mm Steel | Open (Prusa) |
| CFPLA | 40 | 8 | 200 | 50 | mm Steel | Open (Prusa) |
Table 14.
Effective Filament Diameter and Consistency (nominal diameter mm).
Table 14.
Effective Filament Diameter and Consistency (nominal diameter mm).
| Material | Mean (mm) | Stdev (mm) |
|---|
| ABS | 1.742 | 0.008 |
| PLA | 1.746 | 0.017 |
| HTPLA | 1.746 | 0.005 |
| HIPS | 1.746 | 0.011 |
| Nylon | 1.712 | 0.015 |
| PETG | 1.806 | 0.015 |
| PC | 1.716 | 0.011 |
| APLA | 1.742 | 0.011 |
| CPLA | 1.742 | 0.013 |
| WPLA | 1.738 | 0.011 |
| CFPLA | 1.752 | 0.013 |