Metallurgical Analysis of Chip Forming Process when Machining High Strength Bainitic Steels
Abstract
1. Introduction
2. Materials and Methods
2.1. Work Material Characterization
- The fine microstructure cannot be studied with optical micrographs: trials of indexing the colors and estimating the phases quantities failed.
- No M/A islands were found in SEM imaging for SB contrary to the optic approach that showed small brown areas.
- Microstructural features (i.e., ferrite morphologies) cannot be identified similarly to the methods used in the works of Navarro-López et al. [25]. An EBSD mapping is necessary and will take place in the next stages of the study but will not be part of this document.
2.2. Tool Material Couple
2.3. Operating Range
- At feed rate f = 0.25 mm/rev, the cutting speeds ranged from 50 m/min to 650 m/min.
- At cutting speed Vc = 200 m/min, the feed varied from 0.05 to 0.4 mm/rev
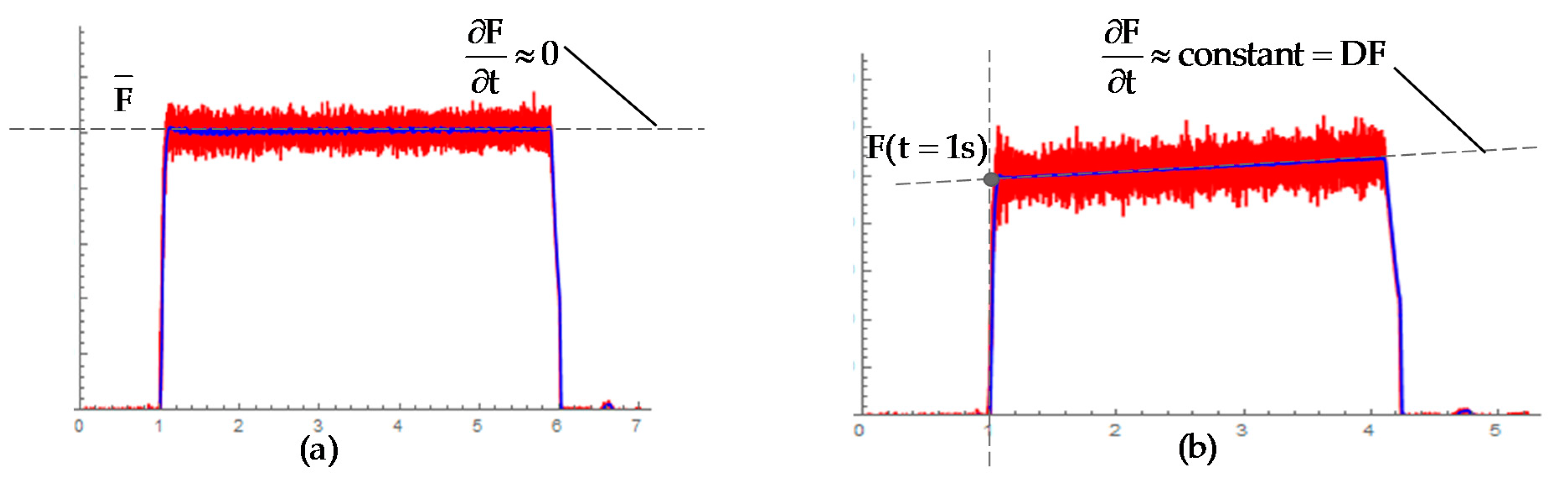
2.4. Signal Processing and Correlation
3. Results
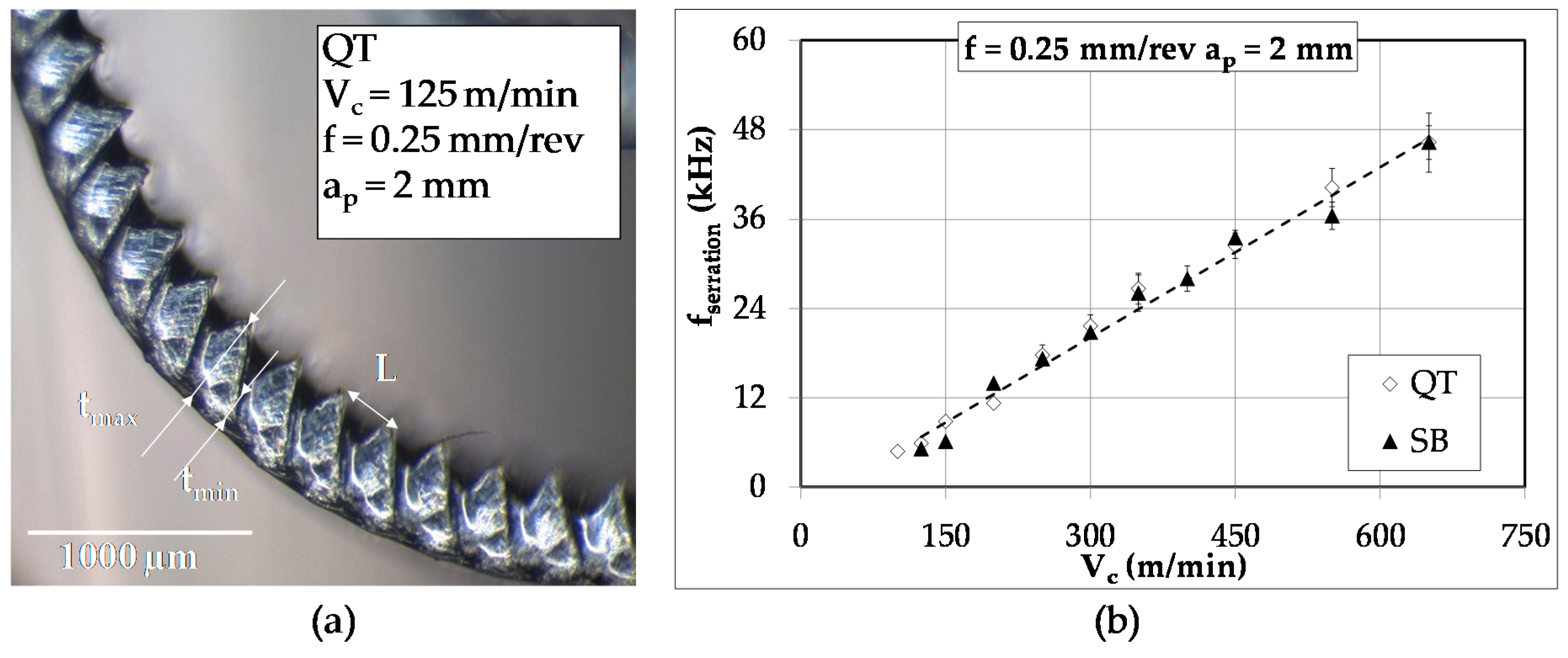
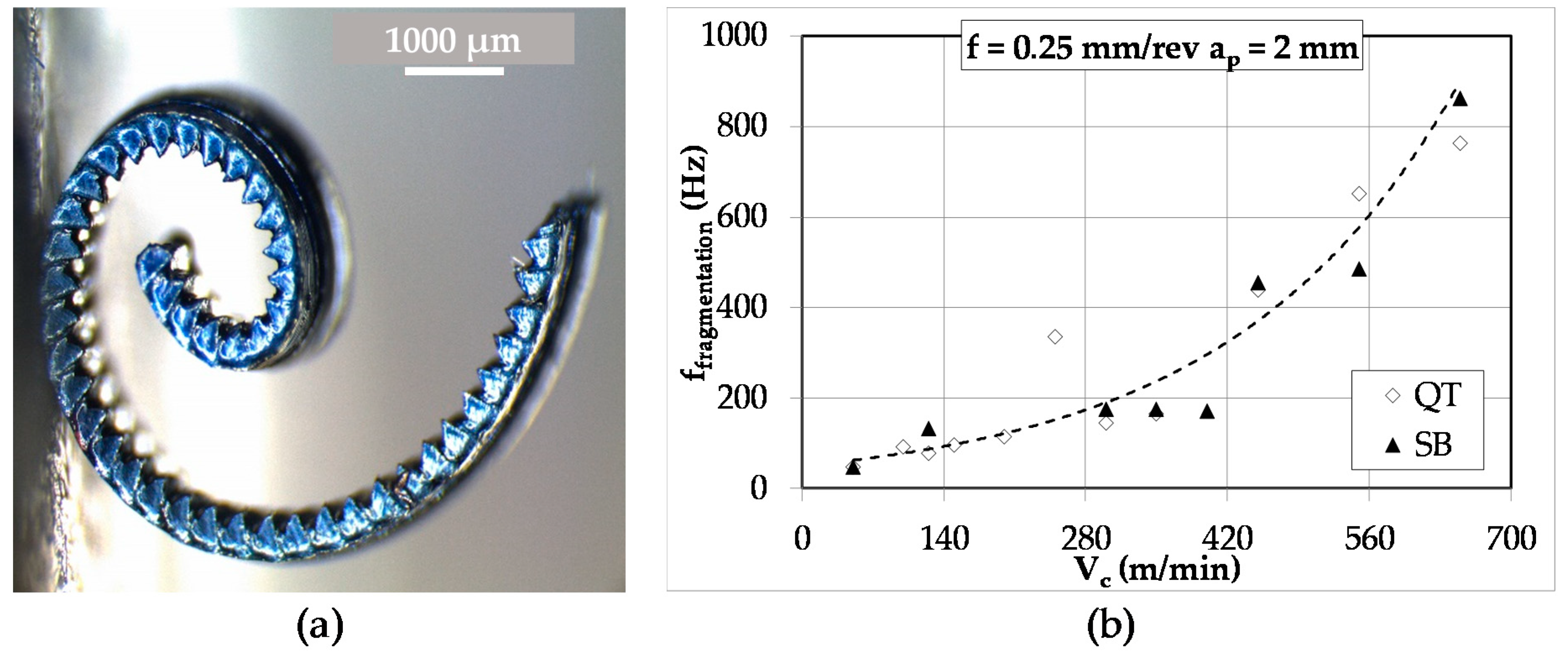
3.1. Chip Analysis
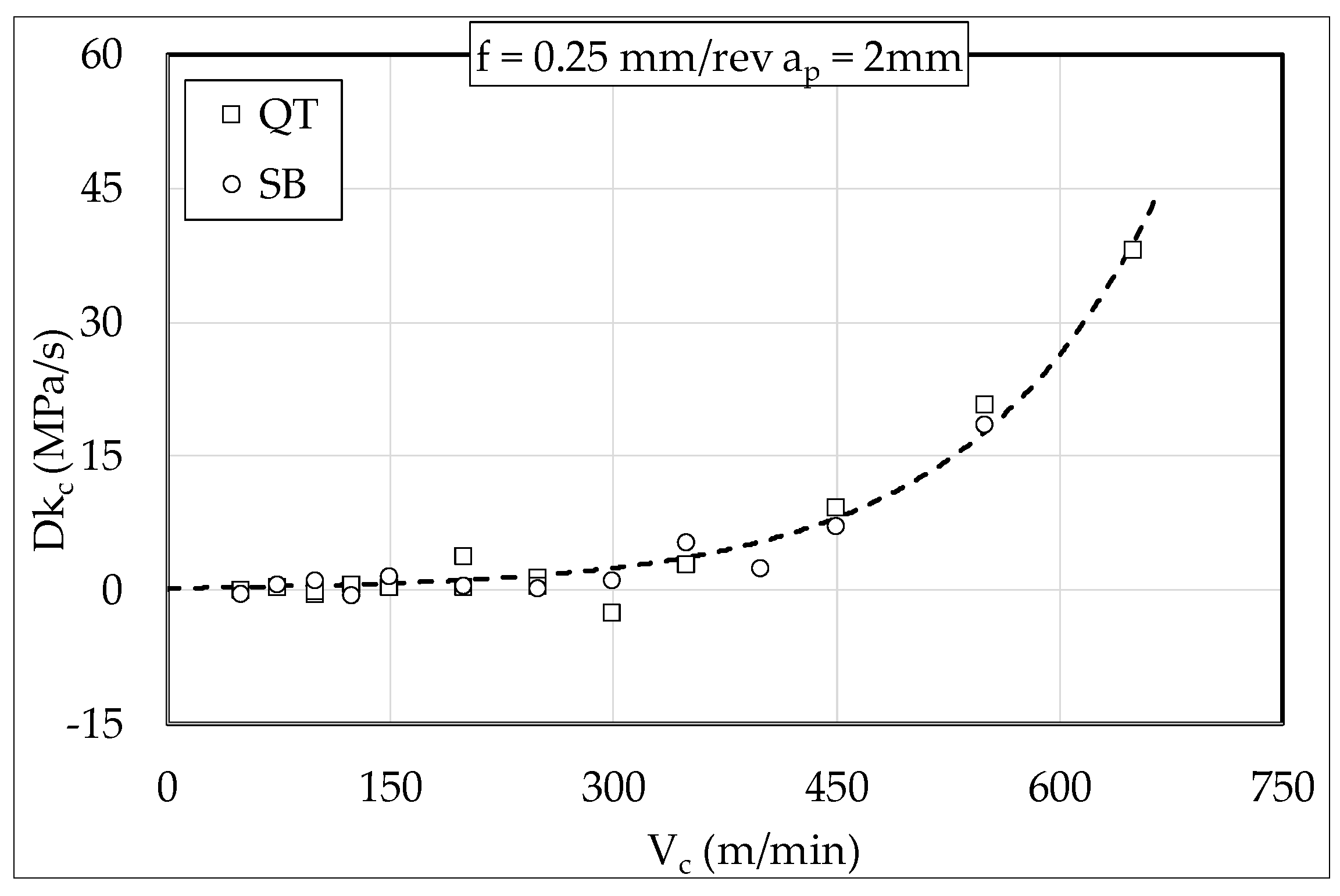
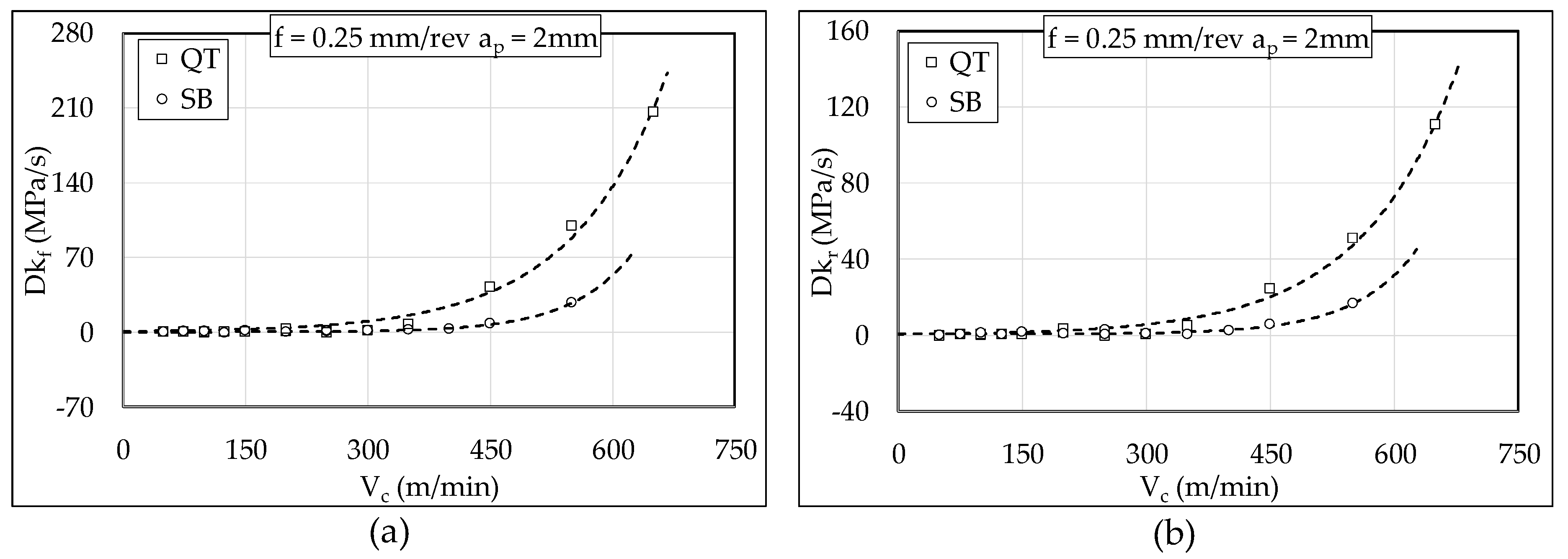
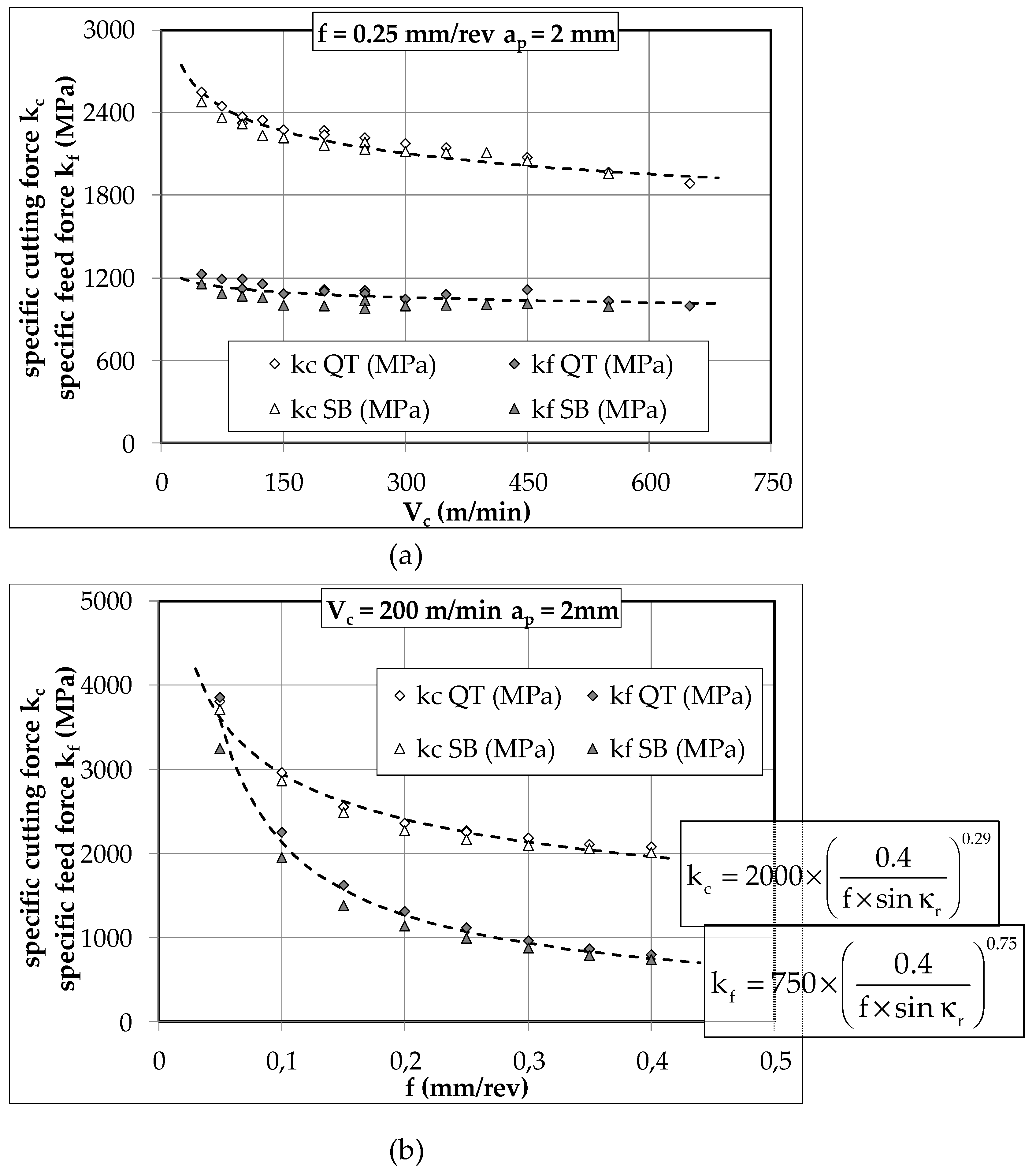
3.2. Cutting Forces Analysis
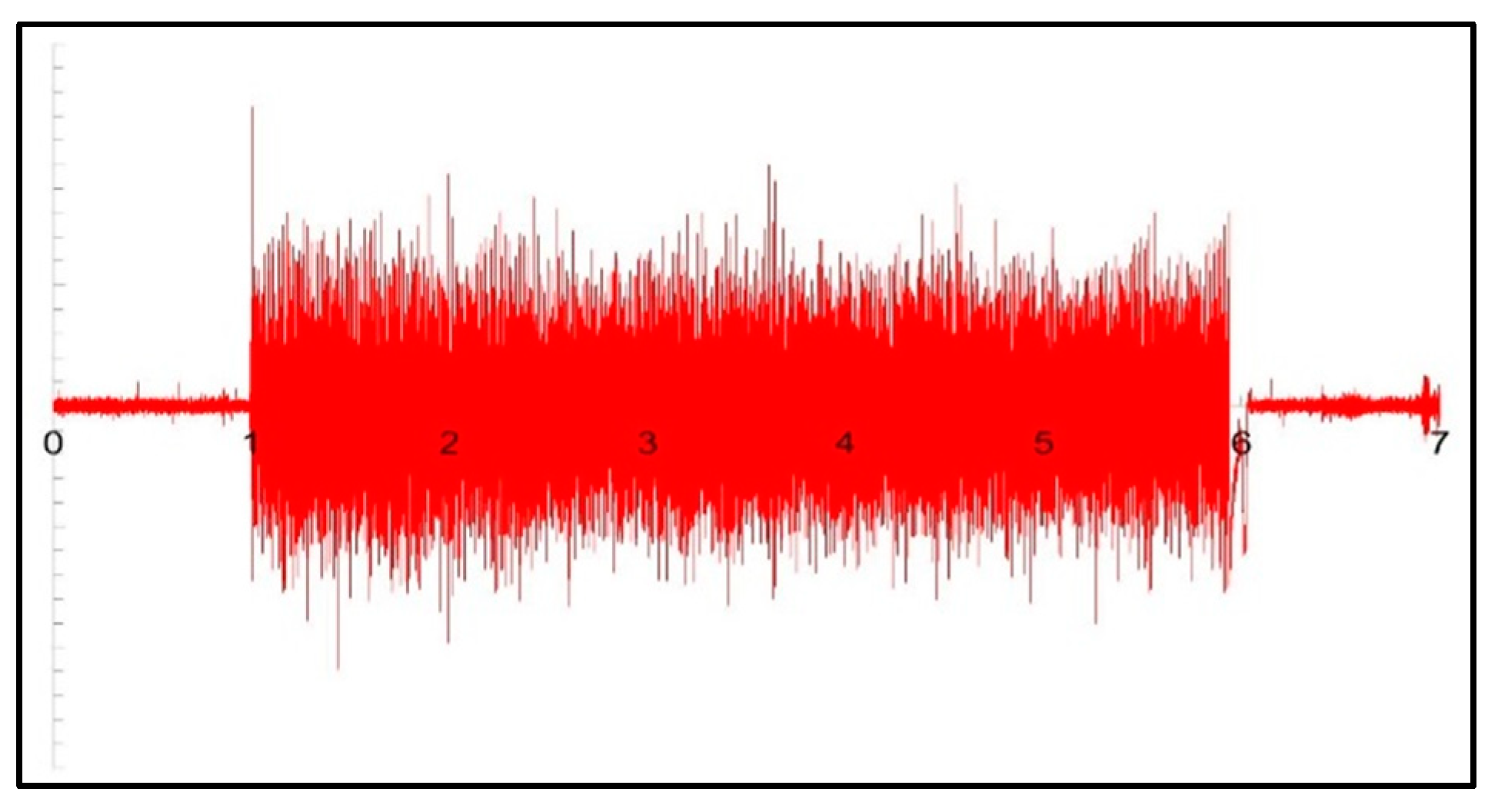
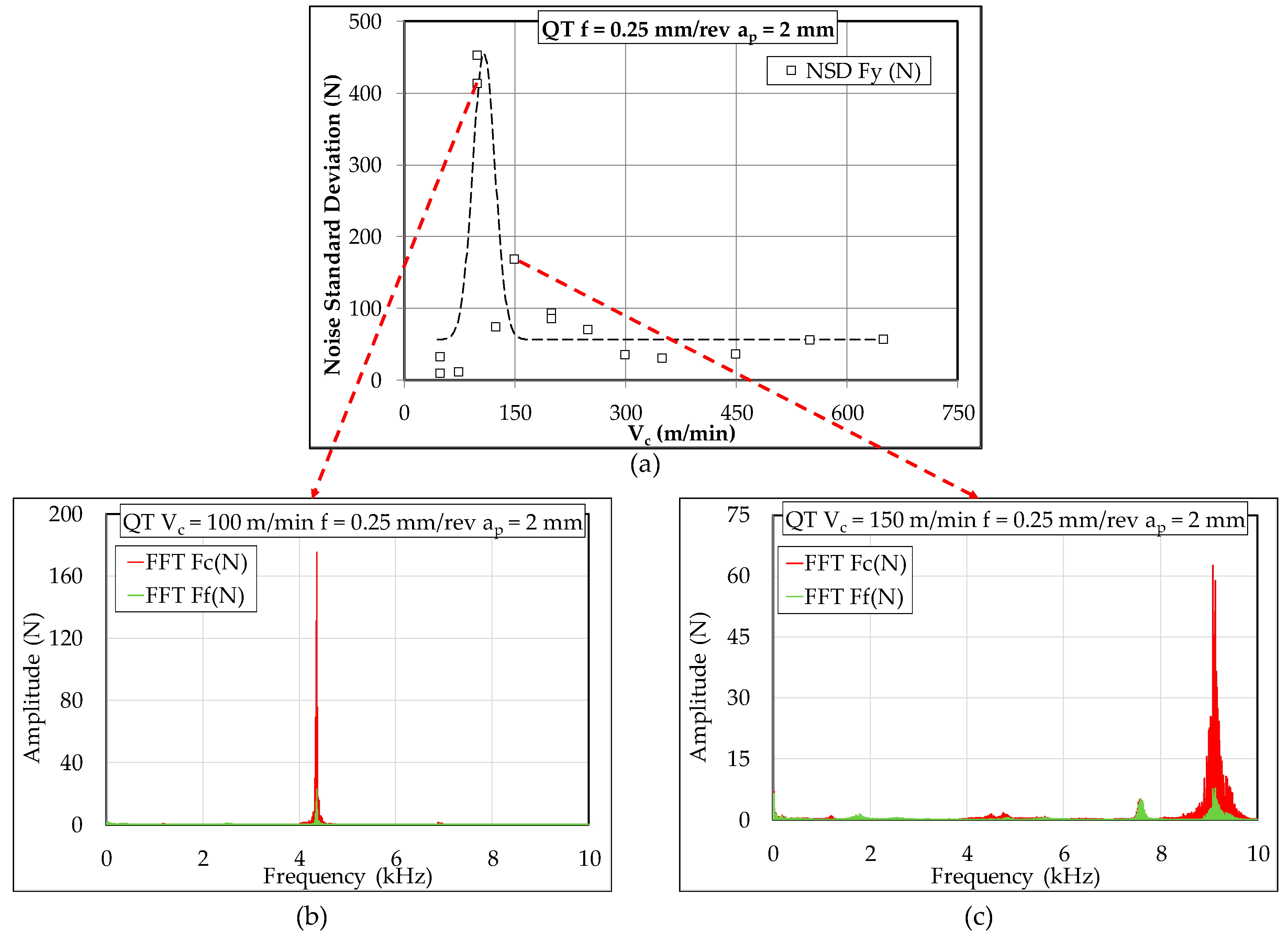
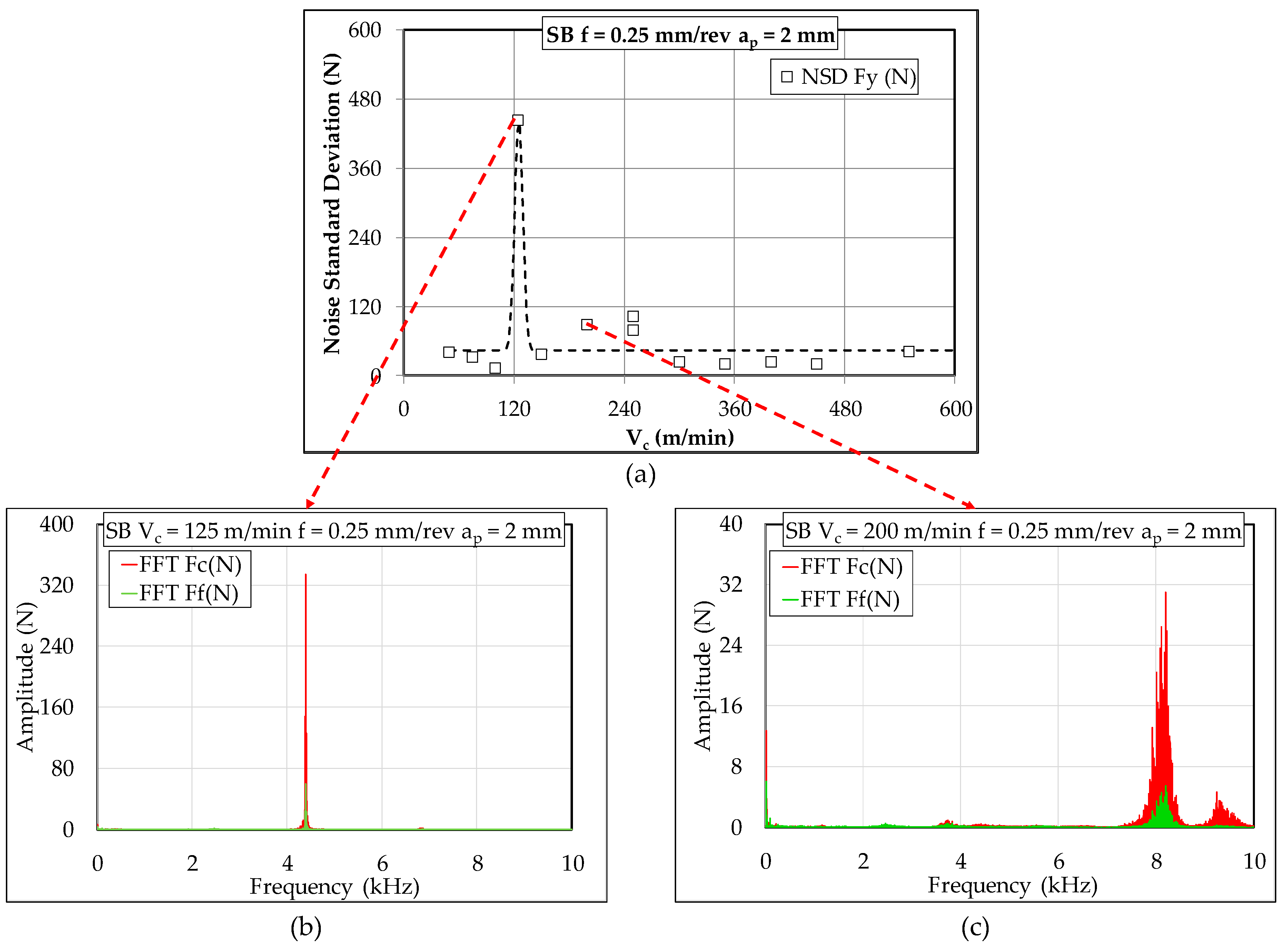
3.3. High Frequency Analysis
- Frequencies below 10 kHz will appear normally on the FFT spectrum
- Frequencies between 10 and 20 kHz will figure on their symmetric value with respect to 10 kHz (ex: a frequency of 17 kHz will show its peak on 3 kHz)
- Frequencies above 20 kHz exceed our sampling rate and cannot be properly identified
4. Discussion
- Results concerning chip fragmentation are quite different of those proposed by Hartmann [12]. The steels investigated have a huge difference in ductility (i.e., Z% was about 28.5% for the bainitic grade and 55.9% for the martensitic grade). The experiments performed in the current study seem to show that microstructure has no influence on the chip length when steel ductility (estimated through Z%) is similar. Further investigation should be performed to enhance the quantitative description of the metallurgy of steels being machined. Knowledge of the overall microstructure (martensite or bainite) or the mechanical performances is unsatisfactory.
- Investigations involving workmaterial characterization observations in the rolling plane and direction using X-ray diffraction, SEM and optical microscope showed that difference between SB and QT is primarily due to carbide precipitations. This inspection should be further developed to include image analysis like in the works of Abbaszadeh et al. [29] or manual point count and microindentation hardness measurements [30]. Eventually, an EBSD analysis will take place. It is crucial in comparing samples, as it provides important data ranging from grains and subgrains misorientations (mainly to differentiate lower and upper bainite) to the shapes of ferrite lattes and M/A constituents [31,32,33].
- The chips produced during turning of 42CrMo4 exhibit regularly spaced serrated teeth above certain cutting speeds. The values of these Vc depended on the microstructure. These teeth are formed due to the adiabatic nature of the shear process. The frequency of these serrated teeth increases with cutting speed and each time their values approached the value of natural frequency of the system chatter occur and high forces were registered.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buchmayr, B. Critical Assessment 18: Bainitic forging steels. Mater. Sci. Technol. 2016, 32, 517–522. [Google Scholar] [CrossRef]
- Hartmann, H.; Biermann, D.; Engineer, S.; Merkel, C. Investigations on machining of high strength bainitic steels. In Proceedings of the Future Trends in Steel Development, Processing Technologies and Applications, Braunschweig, Germany, 15–19 June 2014; pp. 149–156. [Google Scholar]
- Bhadeshia, H.K.D.H. Bainite in Steels Transformations, Microstructure, 2nd ed.; IOM Communications: Cambridge, UK, 2001; ISBN 1-86125-112-2. [Google Scholar]
- Desaigues, J.-E. Contribution à L’étude de L’amélioration de L’usinabilité des Aciers Analyse des Couches de Transferts Sélectifs (CTS) et Caractérisation des Conditions D’apparition; Arts et Metiers: Metz, Germany, 2015. [Google Scholar]
- Montero, M.C.; Albarran, J.; D’Eramo, E.; Juvonen, P.; Vogtel, P.; Lung, D.; Björk, T.; Persson, H.; Garay, A.; Arrazola, P.J.; et al. Innovative Approach for Steel Design Procedures Tailored Component Machining; European Commission: Brussels, Belgium, 2012; p. 168. [Google Scholar]
- Björk, T.; Perez-Alonso, M.; Albarran, J.; Moorthy, V.; Shaw, B.; Vogtel, P.; Lung, D. Automated Material Characterisation for Machinability Prediction (CHARMA); Directorate-General for Research and Innovation Directorate D—Key Enabling Technologies Unit D.4—Coal and Steel; European Commission: Brussels, Belgium, 2015; p. 134. [Google Scholar]
- Johansson, D.; Hägglund, S.; Bushlya, V.; Ståhl, J.-E. Assessment of Commonly used Tool Life Models in Metal Cutting. Procedia Manuf. 2017, 11, 602–609. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Rahman, S.S.; Ashraf, M.Z.I.; Dhar, N.R. Modeling of chip–tool interface temperature using response surface methodology and artificial neural network in HPC-assisted turning and tool life investigation. Int. J. Adv. Manuf. Technol. 2017, 90, 1547–1568. [Google Scholar] [CrossRef]
- Saez-de-Buruaga, M.; Soler, D.; Aristimuño, P.X.; Esnaola, J.A.; Arrazola, P.J. Determining tool/chip temperatures from thermography measurements in metal cutting. Appl. Therm. Eng. 2018, 145, 305–314. [Google Scholar] [CrossRef]
- Polvorosa, R.; Suárez, A.; López de Lacalle, L.N.; Cerrillo, I.; Wretland, A.; Veiga, F. Tool wear on nickel alloys with different coolant pressures: Comparison of Alloy 718 and Waspaloy. J. Manuf. Process. 2017, 26, 44–56. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Pérez-Bilbatua, J.; Sánchez, J.A.; Llorente, J.I.; Gutiérrez, A.; Albóniga, J. Using High Pressure Coolant in the Drilling and Turning of Low Machinability Alloys. Int. J. Adv. Manuf. Technol. 2000, 16, 85–91. [Google Scholar] [CrossRef]
- Hartmann, H. Analyse der Aussenlängsdreh- und Einlippentiefbohrbearbeitung Hochfester Bainitischer und Vergüteter Stähle; Technische Universität Dortmund: Dortmund, Germany, 2016. [Google Scholar]
- Arrazola, P.J.; Özel, T.; Umbrello, D.; Davies, M.; Jawahir, I.S. Recent advances in modelling of metal machining processes. CIRP Ann. Manuf. Technol. 2013, 62, 695–718. [Google Scholar] [CrossRef]
- Courbon, C. Vers une Modélisation Physique de la coupe des Aciers Spéciaux: Intégration du Comportement Métallurgique et des Phénomènes Tribologiques et Thermiques aux Interfaces; Université Lyon: Lyon, France, 2011. [Google Scholar]
- Lurdos, O. Lois de Comportement et Recristallisation Dynamique: Approches Empirique et Physique; Ecole Nationale Supérieure des Mines de Saint Etienne: Saint Etienne, France, 2008. [Google Scholar]
- Calamaz, M.; Coupard, D.; Girot, F. A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti–6Al–4V. Int. J. Mach. Tools Manuf. 2008, 48, 275–288. [Google Scholar] [CrossRef]
- Zemzemi, F.; Rech, J.; Bensalem, W.; Dogui, A.; Kapsa, P. Identification of a friction model at tool/chip/workpiece interfaces in dry machining of AISI4142 treated steels. J. Mater. Process. Technol. 2009, 209, 3978–3990. [Google Scholar] [CrossRef]
- Urbikain, G.; López de Lacalle, L.N.; Campa, F.J.; Fernández, A.; Elías, A. Stability prediction in straight turning of a flexible workpiece by collocation method. Int. J. Mach. Tools Manuf. 2012, 54, 73–81. [Google Scholar] [CrossRef]
- Patwari, M.A.U.; Amin, A.K.M.N.; Faris, W.F. Influence of Chip Serration Frequency on Chatter Formation During End Milling of Ti6Al4V. J. Manuf. Sci. Eng. 2011, 133, 011013. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z. Acoustic emission signal analysis during chip formation process in high speed machining of 7050-T7451 aluminum alloy and Inconel 718 superalloy. J. Manuf. Process. 2017, 27, 114–125. [Google Scholar] [CrossRef]
- Walker, P.; Tarn, W.H. (Eds.) CRC Handbook of Metal Etchants; CRC Press: Boca Raton, FL, USA, 1991; ISBN 978-0-8493-3623-2. [Google Scholar]
- Feng, J.; Frankenbach, T.; Wettlaufer, M. Strengthening 42CrMo4 steel by isothermal transformation below martensite start temperature. Mater. Sci. Eng. A 2017, 683, 110–115. [Google Scholar] [CrossRef]
- Metallography and Microstructures; Metals Handbook, New Edition; American Society for Metals: Metals Park, OH, USA, 2004; ISBN 978-0-87170-706-2.
- Bhadeshia, H.K.D.H. Bainite in Steels: Theory and Practic, 3rd ed.; Maney Publishing: Leeds, UK, 2015; ISBN 978-1-909662-74-2. [Google Scholar]
- Navarro-López, A.; Hidalgo, J.; Sietsma, J.; Santofimia, M.J. Characterization of bainitic/martensitic structures formed in isothermal treatments below the Ms temperature. Mater. Charact. 2017, 128, 248–256. [Google Scholar] [CrossRef]
- Fernández-Valdivielso, A.; López de Lacalle, L.; Urbikain, G.; Rodriguez, A. Detecting the key geometrical features and grades of carbide inserts for the turning of nickel-based alloys concerning surface integrity. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 3725–3742. [Google Scholar] [CrossRef]
- Stahl, J.-E. Metal Cutting Theories and Models, 1st ed.; Division of Production and Materials Engineering: Lund, Sweden, 2012. [Google Scholar]
- Biermann, D.; Hartmann, H.; Terwey, I.; Merkel, C.; Kehl, D. Turning of High-strength Bainitic and Quenched and Tempered Steels. Procedia CIRP 2013, 7, 276–281. [Google Scholar] [CrossRef]
- Abbaszadeh, K.; Saghafian, H.; Kheirandish, S. Effect of bainite morphology on mechanical properties of the mixed bainite-martensite microstructure in D6AC steel. J. Mater. Sci. Technol. 2012, 28, 336–342. [Google Scholar] [CrossRef]
- Schade, C.; Murphy, T.; Alan Lawley, A.; Doherty, R. Microstructure and mechanical properties of a bainitic PM Steel. Int. J. Powder Metall. 2016, 52, 35–76. [Google Scholar]
- Hofer, C.; Leitner, H.; Winkelhofer, F.; Clemens, H.; Primig, S. Structural characterization of “carbide-free” bainite in a Fe–0.2 C–1.5 Si–2.5 Mn steel. Mater. Charact. 2015, 102, 85–91. [Google Scholar] [CrossRef]
- Zajac, S.; Schwinn, V.; Tacke, K.H. Characterisation and Quantification of Complex Bainitic Microstructures in High and Ultra-High Strength Linepipe Steels. Mater. Sci. Forum 2005, 500–501, 387–394. [Google Scholar] [CrossRef]
- Zaefferer, S.; Ohlert, J.; Bleck, W. A study of microstructure, transformation mechanisms and correlation between microstructure and mechanical properties of a low alloyed TRIP steel. Acta Mater. 2004, 52, 2765–2778. [Google Scholar] [CrossRef]
- Bomont-Arzur, A.; Cenfente, M.; Bomont, O.; Schneider, E.; Lescalier, C. Influence of material structure on deep hole machinability of super high strengh steels-application to crankshaft manufacturing methodology, results and analysis. In Proceedings of the Fifth International Conference on High Speed Machining, Metz, France, 27–29 October 2006. [Google Scholar]
- Johansson, D.; Schultheiss, F.; Bushlya, V.; Zhou, J.; Stahl, J.-E. Tool life and wear model in metal cutting. Part 1—Influence of varying flank wear criterion on Colding’s tool life equation. In Proceedings of the 6th Swedish Production Symposium, Gothenburg, Sweden, 16–18 September 2014. [Google Scholar]



| Sample | Rm(MPa) | Rp0.2(MPa) | HV30 | A% | Z% | %RA | Chemical Composition (%wt) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Cr | Mn | Mo | Si | |||||||
| SB | 1039 | 783 | 340 | 14.1 | 56 | 0.01 | 0.4 | 1 | 0.75 | 0.22 | 0.4 |
| QT | 1108 | 973 | 355 | 15.9 | 54 | 0.16 | |||||
| Sample | Cutting Velocity (m/min) | |||||
|---|---|---|---|---|---|---|
| 100 | 125 | 150 | 200 | |||
| SB | continuous chips fserration = N/A | serrated chips fserration = 5 kHz | serrated chips fserration = 6.3 kHz | serrated chips fserration = 13.9 kHz | ||
| FFT: 4.3 kHz–2 N | FFT: 4.3 kHz–420 N | FFT: | 4.3 kHz–4 N 6.3 kHz–5 N | FFT: 12 kH–32 N | ||
| QT | serrated chips fserration = 4.8 kHz | serrated chips fserration = 6.0 kHz | serrated chips fserration = 8.7 kHz | serrated chips fserration = 11 kHz | ||
| FFT: 4.3 kHz–180 N | FFT: | 4.3 kHz–3 N 6.3 kHz–9N | FFT: 9 kHz–60 N | FFT: 13.7 kHz–14 N | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddad, F.; Lescalier, C.; Desaigues, J.-E.; Bomont-Arzur, A.; Bomont, O. Metallurgical Analysis of Chip Forming Process when Machining High Strength Bainitic Steels. J. Manuf. Mater. Process. 2019, 3, 10. https://doi.org/10.3390/jmmp3010010
Haddad F, Lescalier C, Desaigues J-E, Bomont-Arzur A, Bomont O. Metallurgical Analysis of Chip Forming Process when Machining High Strength Bainitic Steels. Journal of Manufacturing and Materials Processing. 2019; 3(1):10. https://doi.org/10.3390/jmmp3010010
Chicago/Turabian StyleHaddad, Fares, Christophe Lescalier, Jean-Edouard Desaigues, Anne Bomont-Arzur, and Olivier Bomont. 2019. "Metallurgical Analysis of Chip Forming Process when Machining High Strength Bainitic Steels" Journal of Manufacturing and Materials Processing 3, no. 1: 10. https://doi.org/10.3390/jmmp3010010
APA StyleHaddad, F., Lescalier, C., Desaigues, J.-E., Bomont-Arzur, A., & Bomont, O. (2019). Metallurgical Analysis of Chip Forming Process when Machining High Strength Bainitic Steels. Journal of Manufacturing and Materials Processing, 3(1), 10. https://doi.org/10.3390/jmmp3010010





