Comprehensive Analysis of Ball End Mill Geometrical Modification with Statistical Validation

Abstract

This work presents a comprehensive analysis of ball-end mill geometrical modification, with emphasis on surface quality and stability of the machining process. The study combines predictive modeling, analytical simulations, and experimental validation to evaluate the influence of cutting tool radius and process parameters on surface roughness. A composite factorial design of experiments was implemented to systematically investigate radius, stepover height, and inclination angle. Surface roughness was measured using a contact stylus profilometer, with secondary validation of selected samples by three-dimensional (3D) optical microscopy, ensuring robust verification of experimental outcomes. In addition, a two-dimensional (2D) computer-aided design (CAD)-based simulation model was developed to reconstruct toolpath overlaps and calculate roughness parameters for comparison. The predictive models were statistically compared with experimental and simulation results, showing consistent trends, while also highlighting deviations possibly due to process dynamics and cutting tool stability. Results indicate that ball-end mills with smaller radii demonstrate higher sensitivity to chatter and surface instability, while larger radii improve consistency as well as achievable roughness values. The combined methodology provides both practical and theoretical insights into optimizing cutting tool geometry for precision milling. The findings are relevant for cutting tool designers and manufacturing engineers seeking to balance productivity, cost, and surface integrity in finishing operations.

1. Introduction

Ball-end mills are among the most used cutting tools for machining free-form surfaces, molds, and dies, where complex part geometries and high surface-quality requirements are common [1,2,3]. Their hemispherical geometry allows for material removal of complex surfaces, making them highly suitable for finishing operations and precision manufacturing [4,5]. The very same geometry that makes them versatile also introduces unique challenges in surface quality, cutting tool deflection, and process optimization [6,7]. Achieving a predictable and controllable surface finish is essential for industries such as aerospace, automotive, and medical device manufacturing, where tight dimensional tolerances and high surface integrity are mandatory [8,9,10].

Cutting tools for milling operations can generally be divided into three categories based on the radius of the tool tip:

• Flat-end mills—cutting tools with zero corner radius, providing sharp edges suitable for slotting or shoulder milling but leaving distinct cusps during 3D surfacing.
• Corner radius-end mills—cutting tools with a radius smaller than the shank radius, offering improved cutting tool life and smoother transitions but still producing measurable surface scallops.
• Ball-end mills—cutting tools where the tip radius is equal to the shank radius, allowing smooth freeform surface generation and predictable scallop formation, making them the preferred choice for finishing complex geometries.

Surface roughness, often quantified by parameters such as R_a and R_z, is a key metric in assessing the quality of a machined surface in the scope of part manufacturing processes [11,12]. Numerous studies have demonstrated that roughness is influenced by a combination of cutting tool geometry, cutting parameters, and process kinematics [13,14,15]. In the case of ball-end mills, the effective cutting speed varies significantly along the cutting edge due to the changing engagement radius, resulting in variable chip thickness and sometimes unstable cutting conditions [16,17]. This phenomenon becomes even more pronounced when finishing inclined or curved surfaces, where the cutter contact point continuously shifts [18]. Consequently, predicting surface finish in such scenarios requires models that account not only for feed per tooth and radial step-over, but also for cutting tool radius, inclination angle, and machine–tool dynamics [19,20,21].

Recent research efforts have focused on response surface methodology (RSM) and statistical modeling to better understand and optimize these multi-factor interactions [22,23]. RSM provides a structured approach for designing experiments and developing empirical models capable of predicting responses within a defined parameter space [24,25]. While these models have been widely applied to conventional milling operations, their application to ball-end milling with modified cutting tool geometries remains relatively limited.

In a similar research endeavor, Zurawski tested a lens-shaped cutting tool, which by design represents a similar concept of cutting tool geometry but with a different curved cutting-edge position. The lens-shaped cutting tool had a large radius on the cutting tool end plane, reducing the number of required toolpath passes during milling. It is important to emphasize that, similar to cutting tools presented in this paper, the lens cutting tools also required an inclination angle; otherwise, they would engage in center-cutting conditions. In their study, the lens-shaped cutting tools were evaluated through an experimental model, and based on the results, a simulation model of surface topography generation was created. One of their conclusions was that, despite developing a statistically valid simulation model, further research is required to integrate additional parameters. They also noted that a purely kinematic simulation was inadequate to realistically capture the response development. Based on their findings, it can be assumed that even macro-geometric modifications of cutting tools have a significant effect on cutting processes and measurable responses such as surface quality indicators and cutting forces [26].

In another machining study, Duc et al. analyzed cutting edge geometry and its effect on surface quality when machining AISI 1055 steel in a hardened state. They employed an RSM-based Central Composite Design (CCD) experimental model, which was verified through a prediction-versus-validation approach similar to that used in the present work. Although their cutting tools were cutting inserts used in turning rather than ball-end mills, their methodology offers a valuable comparison on how different machining processes can yield analogous insights. In their ANOVA analysis, several selected factors were statistically significant; however, for the response parameter R_a, a Lack-of-Fit test value of 0.09 was reported. While technically not significant, this value was close to the critical threshold, indicating the complexity of the surface roughness response and justifying the use of higher-order models. Their secondary response, Vb (tool wear), showed a significant Lack-of-Fit result. Although such a result questions the validity of the model form, their prediction-versus-validation comparison aligned with ours in emphasizing that numerical tests should not be interpreted in isolation during model evaluation [27].

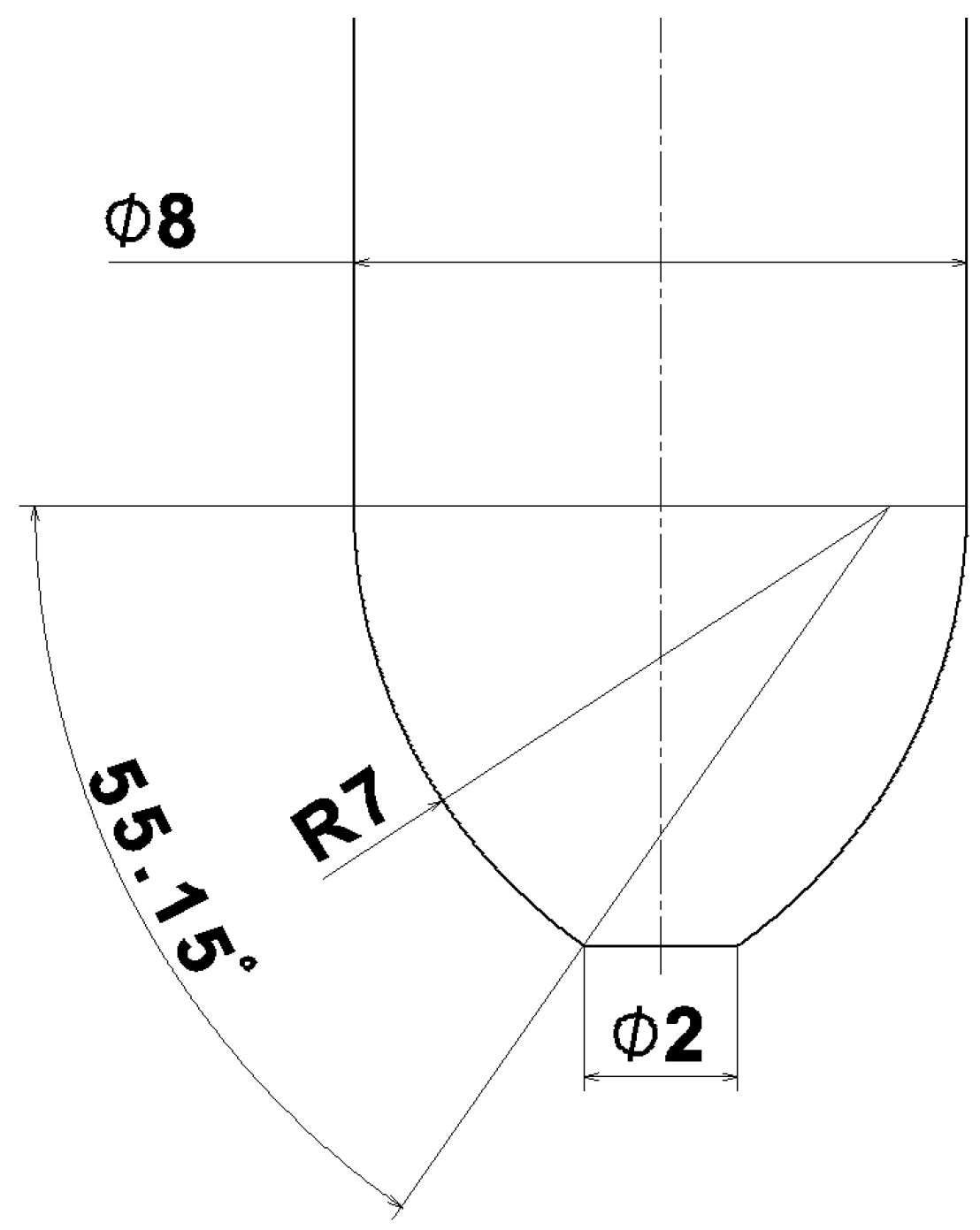
The selection of factors was determined by the characteristics of the chosen cutting tools. Parameters such as radius and stepover height are almost mandatory, as they are the two primary variables used in analytical equations for calculating R_z values found in the literature. The inclusion of inclination angle was driven by the nature of ball-end milling, where the cutting tool’s performance is significantly influenced by the effective cutting radius.

Cutting tool inclination has been widely investigated in machining research, particularly in studies analyzing surface topography formation through analytical or CAD-based simulations. Villarazo et al. examined the influence of cutting tool inclination angle on surface roughness within an interval of 15° to 60°. They utilized a MATLAB algorithm to generate analytical solutions for their experimental configuration. Similar to findings in this study, their R_a values were generally lower than the analytical predictions, while R_z values exhibited larger deviations. The authors attributed this difference primarily to plastic deformation effects. Their results reaffirm the importance of cutting tool inclination as a significant factor deserving further research attention [28].

Villarazo et al. also avoided center-cutting conditions due to the effective cutting speed reaching zero at the cutting tool tip. This reinforces the assumption that optimal conditions for machining with hemispherical cutting tools occur at specific inclination angles. Conversely, standard ball-end mills are capable of center cutting; however, it is important to consider that during cutting tool geometry definition in software such as Numroto PLUS 3.7.1, achieving cutting edges precisely at the center is challenging. Excessive grinding in this area can undesirably reduce cutting edge thickness, compromising cutting tool strength and stability. Center-cutting options on cutting tools are usually attributed to being a requirement for certain machining operations and strategies.

The present work performs a complete experimental investigation of ball-end mill geometry modifications, with a focus on surface roughness influence. A central composite design (CCD), derived from a factorial experiment, was employed. Response surface models were constructed for both R_a and R_z parameters. The statistical significance of each factor and their interactions were evaluated using ANOVA and Pareto analysis. In addition to model development, this study emphasizes verification: Model predictions were validated experimentally using both stylus-based roughness measurements and optical 3D microscopy. Furthermore, a custom 2D CAD-based analytical model was developed to reconstruct theoretical surface profiles and compare them with both predicted and experimental results. This dual-validation approach provides a deeper insight into the reliability of statistical models and highlights their limitations at extreme parameter settings.

By integrating statistical modeling, experimental validation, and CAD-based simulation, this work presents a comprehensive methodology for evaluating and optimizing ball-end mill performance. The results contribute to a better understanding of how geometrical modifications and process parameters affect surface finish, providing a foundation for improved cutting tool design and process planning in precision machining applications.

2. Materials and Methods

The experimental procedure used an RSM statistical model as the base of the experiment. As the work focuses on developing a prototype ball-end cutting tool, one of the model factors was the cutting tool radius. Additional factors were included where angle of inclination and stepover height are commonly featured in machining studies. Responses were R_a and R_z, which are also commonly featured in machining studies. Actual factor and model settings, as well as the statistical matrix, will be discussed later in this section.

2.1. Experimental Model

A central composite design was selected as the statistical model following a preliminary factor screening based on analytical CAD simulations of the selected factors and responses. The screening phase revealed curvature effects in all factors and responses, thereby justifying the use of a second-order model such as CCD. The preliminary simulations were performed in CATIA V5 R19, and multifactor ANOVA was used to assess the statistical significance of the factors using Minitab 20.2. The model was set up as a three-factor, five-level full quadratic model. Basic levels of all factors, as well as quadratic levels, can be seen in

Table 1. Basic levels of factors in uncoded units, including quadratic levels.

Factor	Symbol	−α	−1	0	1	α
Radius [mm]	R	2.97	4.00	5.50	7.00	8.02
Inclination angle [°]	A	33.18	40.00	50.00	60.00	66.82
Stepover height [mm]	S	0.43	0.50	0.60	0.70	0.76

. The experiment was set up with five replicates.

2.2. Cutting Tool Design

The primary distinction between the proposed cutting tools and standard ball-end mills lies in the tip radius. Conventional ball-end mills typically have a tip radius equal to or smaller than the shank radius. Manufacturers are constrained to use additional cutting tools or multiple operations when machining features with larger radii or curvature.

In this study, the standard design rule was intentionally broken by enlarging the tip radius—up to twice the shank radius in some cases. This geometry reduces the effective radius angle as seen in Figure 1. The small noncutting zone at the cutting tool tip was modified to a diameter 2 mm on all tools, which is known to create unfavorable cutting conditions [29]. The 2 mm diameter tool tip was not engaged in cutting during experiments. A larger tip radius also decreases the number of cutting tool passes required to achieve the same surface roughness, thereby improving process efficiency.

All cutting tools featured in the experiment were manufactured using tungsten carbide rods of nominal diameter 8h6 mm. Composition and physical data of the chosen tungsten carbide sort can be seen in

Table 2. Composition and physical data of the selected tungsten carbide rods.

ISO Group	Structure	Grain Size	Co	Hardness HV30	Hardness HRA	TRS
K20–K30	Submicron	0.7 µm	10%	1580	92.0	3800 N/mm2

. The values shown correspond to typical data specified for the K20–K30 material groups according to ISO 513 [30]. The choice of tungsten carbide was due to workpiece material properties, which will be discussed later in this study.

Cutting tools were intentionally manufactured without any surface coating or cutting edge micro-geometry modifications, as both are recognized in industry as external factors that can influence cutting tool performance. Coatings can significantly extend cutting tool life and alter chip evacuation mechanics, thereby affecting surface finish and potentially introducing variability into the experimental results [31]. Similarly, micro-geometry alterations such as edge honing modify the cutting forces and wear behavior. Cutting edge modifications were excluded to minimize data noise and isolate the influence of cutting tool macro-geometry modification [32].

Cutting-edge geometry was derived from conventional ball-end mill designs, with adjustments made to account for the geometric modifications introduced in this study. All cutting tool manufacturing processes were performed in computer-aided manufacturing (CAM) grinding software, Numroto PLUS 3.7.1. An example illustration of the manufactured cutting tool can be seen in Figure 2.

Cutting edge geometries can be seen in

Table 3. Cutting edge geometry.

Tool Radius	Helix Angle	Rake Angle	First Relief Angle	Second Relief Angle	Third Relief Angle
2.98	30	6	7	20	-
4	30	6	7–8	20–24	-
5.5	30	6–8	8	22	30
7	30	6–8	8	22	30
8.02	30	5–8	8	22	30

. Only key parameters are shown, as Numroto PLUS 3.7.1 allows for complex programming of grinding wheel toolpaths. Note that some parameters are displayed in an interval, which represents a variable cutting edge geometry.

2.3. Workpiece Material

For cutting performance testing of the designed cutting tools, a tool steel, 1.2379 according to DIN ISO 4957 [33], in the annealed state was selected. This steel grade can reach hardness levels up to 62 HRC in the hardened condition; however, due to the use of uncoated cutting tools, machining was performed in the annealed state to minimize excessive wear. The chosen tool steel is primarily used in cold forming applications owing to its relatively high chromium content (up to 12%), providing excellent wear resistance and moderate corrosion resistance [34]. The mechanical properties of 1.2379 depend on the applied heat treatment and manufacturing process. The chemical composition is shown in

Table 4. Chemical composition of 1.2379 tool steel according to DIN ISO 4957.

Element	C	Mn	P	S	Si	Cr	V	Mo
Min %	1.45	0.2	0.03	0.03	0.1	11	0.7	0.7
Max %	1.6	0.6	0.03	0.03	0.6	13	1	1

.

For the purposes of the experiment, two workpiece specimens were prepared in the form of cuboids with dimensions of 80 mm × 95 mm × 107.5 mm. Both specimens were finish-milled to achieve the target dimensions and angled using standard milling operations.

2.4. Machine Setup and Operations

The proposed cutting tools feature a non-cutting center. Machining was performed at an inclination to avoid tool–workpiece collision. While 4- or 5-axis milling could achieve this inclination directly, the associated machine kinematics can introduce additional dynamic effects such as varying engagement conditions and cutting force fluctuations [35]. For the purposes of this study, which aimed to evaluate the influence of cutting tool macro-geometry under controlled conditions, such additional variables were intentionally excluded. The required inclination angle was introduced by machining the workpiece surfaces at the target angles according to the statistical matrix. This approach allows the isolation of geometric effects while providing a stable and repeatable machining process.

The decision to use a 3-axis rather than a 5-axis machine, with a transformation of the tool inclination angle to the machined surface inclination, reduces the resource and time requirements of the experiments. The design choice provides relative insight into the cutting tool performance, despite not being influenced by dynamic effects that are part of multi-axis machining. Certain limits to the data integrity apply, as the tools are likely to perform differently if they were to be used in a true multi-axis setup. The effects on multi-axis machining with the proposed cutting tools will be further pursued in future studies. The proposed cutting tools will need further alterations with regard to geometric design, allowing true multi-axis machining.

Toolpath simulation and machining strategy setup were performed via the CAM software Autodesk PowerMill 2024. The chosen machine strategy was parallel milling with constant stepover height based on the statistical matrix. CAM setup can be seen in Figure 3a, and the toolpath simulation in Figure 3b. Toolpath connections, as well as entry and exit strategies, were set to a constant based on the chosen cutting tool. Toolpaths were programmed to be identical across the whole study, avoiding the introduction of data bias or external effects. Only key factors were changed, such as the stepover height.

All cutting tools were clamped using shrink-fit holders SCHUNK-0208131 CELSIO HSK-A63 D8x130, with a constant cutting tool overhang of 30 mm. Cutting tool clamping station can be seen in Figure 4. All machining operations were performed on a Deckel Maho DMC 635 V milling center. The workpiece was clamped in the working space of machine with a SCHUNK-0430303 KSG VS 125 machine vice. Machining direction was set downwards, and the final surface was finished with our cutting tools and a set stock material height of 0.5 mm.

2.5. Preliminary Experiment

Before the main experiment was conducted, a preliminary experiment was performed to establish suitable cutting parameters, such as cutting speed V_c and feed rate V_f. These parameters were evaluated through a combination of visual inspections and response assessment to ensure stable cutting conditions. This step ensured the avoidance of cutting tool failure or excessive wear during the main experiment. Data obtained during the preliminary trials were excluded from the main experiment’s statistical analysis. A dedicated cutting tool was used based on the center setting of the statistical matrix. A comparison of recommended ranges and the final selected cutting parameters is presented in

Table 5. Cutting parameter comparison.

Parameter	Recommended Settings	Final Settings
Vc [m/min]	40–60	150
Vf [mm/min]	650–1250	1482

. All milling operations were performed with coolant, Castrol Hysol XF, with 6% oil content.

2.6. Response Measurement

Surface roughness was measured under controlled laboratory conditions at 20 °C to eliminate temperature-related measurement error. Measurements were performed using a digital contact profilometer INSIZE ISR-C300, calibrated with the manufacturer’s reference standard. A cut-off wavelength of λ = 0.8 mm and five sampling lengths were used, resulting in a total evaluation length of 4.8 mm. Lead-in and lead-out lengths were set according to the manufacturer’s specification. Response measurements were performed perpendicularly to the feed direction, as roughness in the feed direction is mostly influenced by vibration and other similar phenomena. The stylus profilometer’s resolution and accuracy, as well as other key parameters, may be found in Appendix A.

The profilometer shown on Figure 5 was mounted in a vertically adjustable holder, and samples were clamped in a custom fixture designed to tilt the machined surfaces to a horizontal position. This configuration ensured the probe moved parallel to the machined surface, providing consistent and repeatable measurements across all inclination angles. The custom fixture was manufactured with additive technologies.

3. Results

Data collected during the main experiment were compiled and saved in accordance with the statistical matrix. Due to key differences between the responses, despite being sourced from the same specimen, they had to be analyzed individually in terms of model evaluation and testing. The design matrix with averaged responses across all five replicates can be seen in

Table 6. Design matrix with average response results based on replicates.

Run	R	A	S	Ra	Rz
1	4.00	40.00	0.50	1.76	7.36
2	7.00	40.00	0.50	1.08	5.31
3	4.00	60.00	0.50	1.01	5.39
4	7.00	60.00	0.50	0.61	3.20
5	4.00	40.00	0.70	1.96	9.62
6	7.00	40.00	0.70	1.43	8.03
7	4.00	60.00	0.70	1.50	6.80
8	7.00	60.00	0.70	0.81	3.96
9	2.98	50.00	0.60	2.31	8.75
10	8.02	50.00	0.60	0.99	4.97
11	5.50	33.18	0.60	2.00	10.17
12	5.50	66.82	0.6	1.54	6.06
13	5.50	50.00	0.43	0.51	3.54
14	5.50	50.00	0.77	1.26	5.86
15	5.50	50.00	0.60	1.17	7.10
16	5.50	50.00	0.60	1.19	6.73
17	5.50	50.00	0.60	1.12	6.74
18	5.50	50.00	0.60	1.14	6.43
19	5.50	50.00	0.60	1.17	7.20
20	5.50	50.00	0.60	1.12	6.57

; the average responses in this table are shown as a visualization of the general results of our study without statistical evaluation. Runs were not randomized due to technological limitations during machining operations.

3.1. Data Evaluation

Given the stochastic nature of machining processes, experimental data are often subject to unpredictable variations that may lie outside the expected distribution. To ensure the validity of subsequent statistical analyses, the full data set was subjected to a normality assessment using the Anderson–Darling test and to a homogeneity of variances check using Levene’s test.

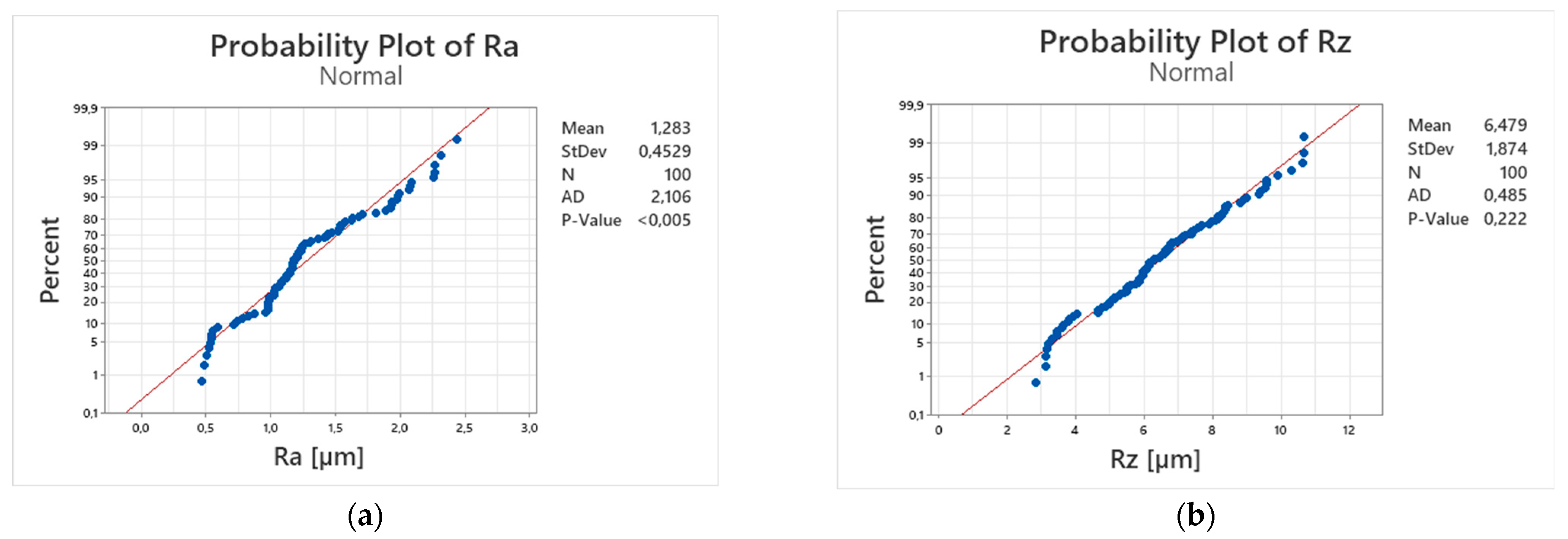
As shown in Figure 6a, the response R_a exhibits a slight deviation from normality at the 5% significance level. This is consistent with the inherent variability and dynamic nature of machining operations. While the result does not necessarily indicate model inadequacy, it warrants cautious interpretation of model diagnostics. In contrast, response R_z, as seen in Figure 6b, does not show significant departure from normality and can be considered approximately normally distributed for the purposes of regression modeling.

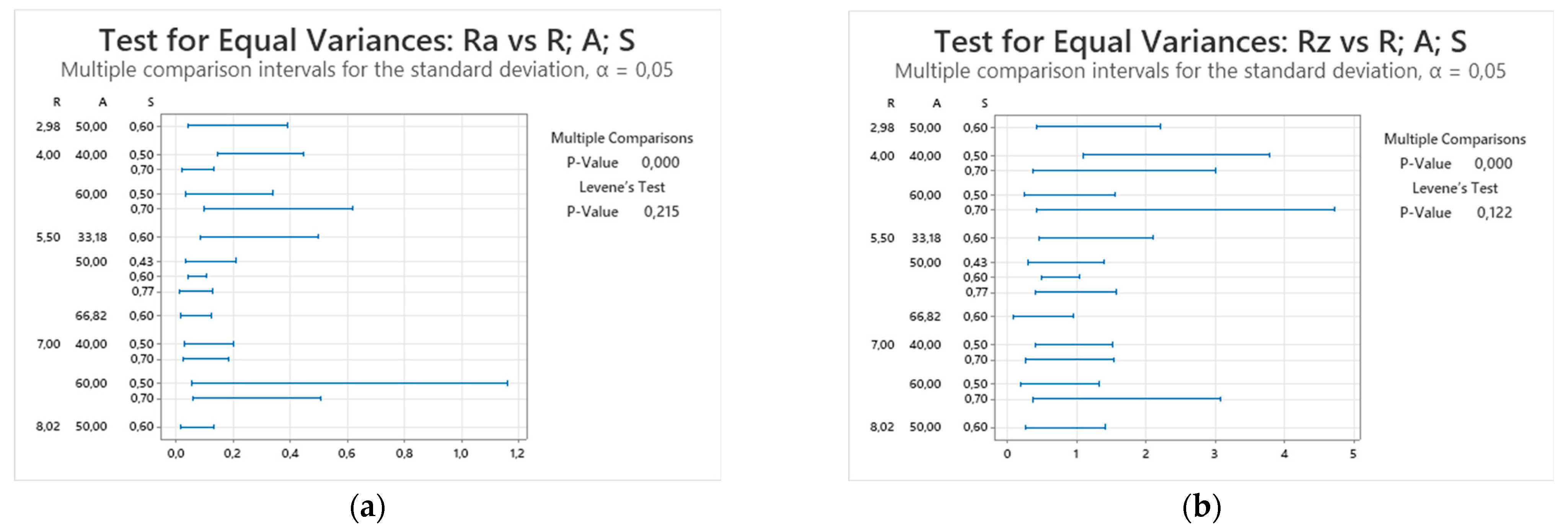
Based on Figure 7, both responses satisfy the assumption of equal variances according to Levene’s test, p > 0.05. Findings from both response tests should be considered during model diagnostics. The multiple comparison procedure flagged significant differences in variance between certain data pairs. This does not contradict the global Levene’s test result but indicates that a few factor combinations may exhibit higher variability, a phenomenon commonly observed in machining experiments due to their dynamic nature. Furthermore, some data points exhibit relatively large standard deviation intervals, which could be attributed to process instability, improper tool engagement, or tool deflection caused by certain factor combinations.

3.2. Model Analysis and Diagnostics of Response R_a

A second-order response surface model was developed for R_a using backward elimination at a 10% significance level to remove statistically insignificant terms. The final model retained all three factors, R, A, and S, and their quadratic terms, while all two-way interactions were excluded. Variance inflation factors, VIF < 1.5, for all terms confirmed the absence of multicollinearity among predictors.

Analysis of variance confirmed that the quadratic model was highly significant and captured 90.76% of the total variation in R_a. Adjusted and predicted coefficients of determination, R²_adj = 90.17% and R²_pred = 88.95%, were in close agreement, indicating good model generalization and no evidence of overfitting. ANOVA results can be seen in

Table 7. ANOVA Summary for response R_a.

Source	DF	Adj SS	Adj MS	F-Value	p-Value
Model	6	18.43	3.07	152.29	$7.54\times {10}^{-46}$
Linear	3	13.16	4.38	217.55	$6.65\times {10}^{-42}$
R	1	7.48	7.48	371.01	$3.19\times {10}^{-34}$
A	1	3.42	3.42	169.65	$1.10\times {10}^{-22}$
S	1	2.25	2.25	112.00	$1.20\times {10}^{-17}$
Square	3	5.26	1.75	87.03	$6.69\times {10}^{-27}$
$R\times R$	1	1.34	1.34	66.58	$1.57\times {10}^{-12}$
$A\times A$	1	2.33	2.33	115.98	$4.90\times {10}^{-18}$
$S\times S$	1	1.26	1.26	62.64	$5.11\times {10}^{-12}$
Error	93	1.87	0.02	-	-
Lack-of-Fit	8	1.33	0.16	26.09	$7.03\times {10}^{-20}$
Pure Error	85	0.54	$6.00\times {10}^{-3}$	-	-
Total	99	20.30	-	-	-

.

The statistically significant lack-of-fit is likely a consequence of highly consistent replicate runs, very small pure-error estimates, and the use of R_a as a mean roughness parameter, which inherently reduces variability. This leads to hypersensitive lack-of-fit statistics rather than a practical inadequacy of the fitted model. This interpretation is further supported by the absence of lack-of-fit when analyzing R_z under the same model structure.

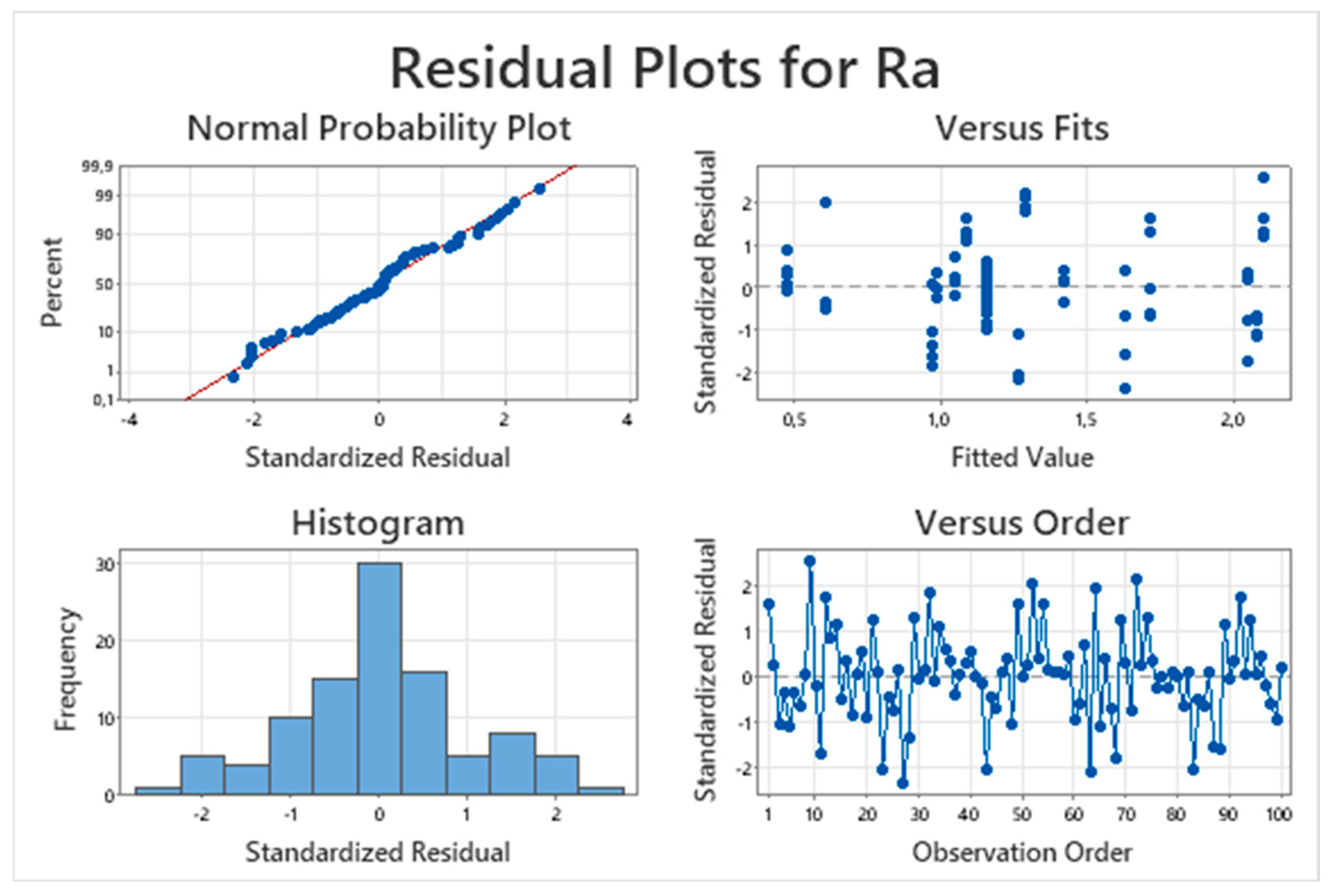
Model residuals were analyzed using normal probability plots, histograms, residual-versus-fit, and residual-versus-order plots in Figure 8. Residuals followed an approximately normal distribution, were homoscedastic, and showed no observable trends with respect to fitted values or run order. These results confirm that model assumptions were satisfied and that the quadratic model adequately describes the behavior of R_a within the experimental domain.

3.3. Model Analysis and Diagnostics of Response R_z

A second-order response surface model was also developed for R_z, including both linear and quadratic terms, as well as two-way interactions that were statistically significant at the selected 10% significance level. Unlike R_a, where all main factors and their quadratic terms were retained but two-way interactions were excluded, the R_z model required the inclusion of two interaction terms to adequately capture the behavior of the response. The quadratic term of Radius was eliminated, but the interaction between Inclination Angle and Radius, as well as Inclination Angle and Stepover height, remained in the model. Variance inflation factors (VIF < 1.5) indicated the absence of problematic multicollinearity among predictors.

The coefficients of determination for the R_z model were R²_adj = 89.12% and R²_pred = 88.14%. The close agreement among these values indicates that the model neither overfits nor underfits the data and has good predictive capability within the experimental region. The actual predictive performance will be tested after the main model analysis of both responses. ANOVA results can be seen in

Table 8. ANOVA summary for response R_z.

Source	DF	Adj SS	Adj MS	F-Value	p-Value
Model	7	312.56	44.65	116.90	$5.94\times {10}^{-43}$
Linear	3	241.415	80.47	210.67	$4.41\times {10}^{-41}$
R	1	80.48	80.48	210.70	$1.59\times {10}^{-25}$
A	1	114.46	114.46	299.67	$1.08\times {10}^{-30}$
S	1	46.46	46.46	121.65	$1.60\times {10}^{-18}$
Square	2	63.90	31.95	83.64	$1.99\times {10}^{-21}$
$\mathrm{A}\times A$	1	11.31	11.31	29.63	$4.31\times {10}^{-7}$
$S\times S$	1	47.85	47.85	125.29	$7.33\times {10}^{-19}$
2-Way interaction	2	7.24	3.62	9.49	$1.79\times {10}^{-4}$
$R\times A$	1	1.57	1.57	4.12	0.04
$A\times S$	1	5.67	5.67	14.86	$2.14\times {10}^{-4}$
Error	92	35.14	0.38	-	-
Lack-of-Fit	7	4.10	0.58	1.61	0.14
Pure Error	85	31.03	0.36	-	-
Total	99	347.70	-	-	-

.

Analysis of variance confirmed that the R_z model was statistically significant and that both the linear and quadratic components were needed. Interaction effects were also significant, supporting the inclusion of two-way terms in the final model. Importantly, the lack-of-fit test was not significant, which demonstrates that the selected model adequately represents the underlying process without missing systematic variation. This result contrasts with R_a, where the lack-of-fit test was hypersensitive due to very low pure error. The absence of significant lack-of-fit for R_z supports the conclusion that the model provides a suitable description of surface roughness variation. Another key metric that indicates that the lack-of-fit test is performing within expectation is pure error Adj MS, which, compared to lack-of-fit, does not show a major underestimation.

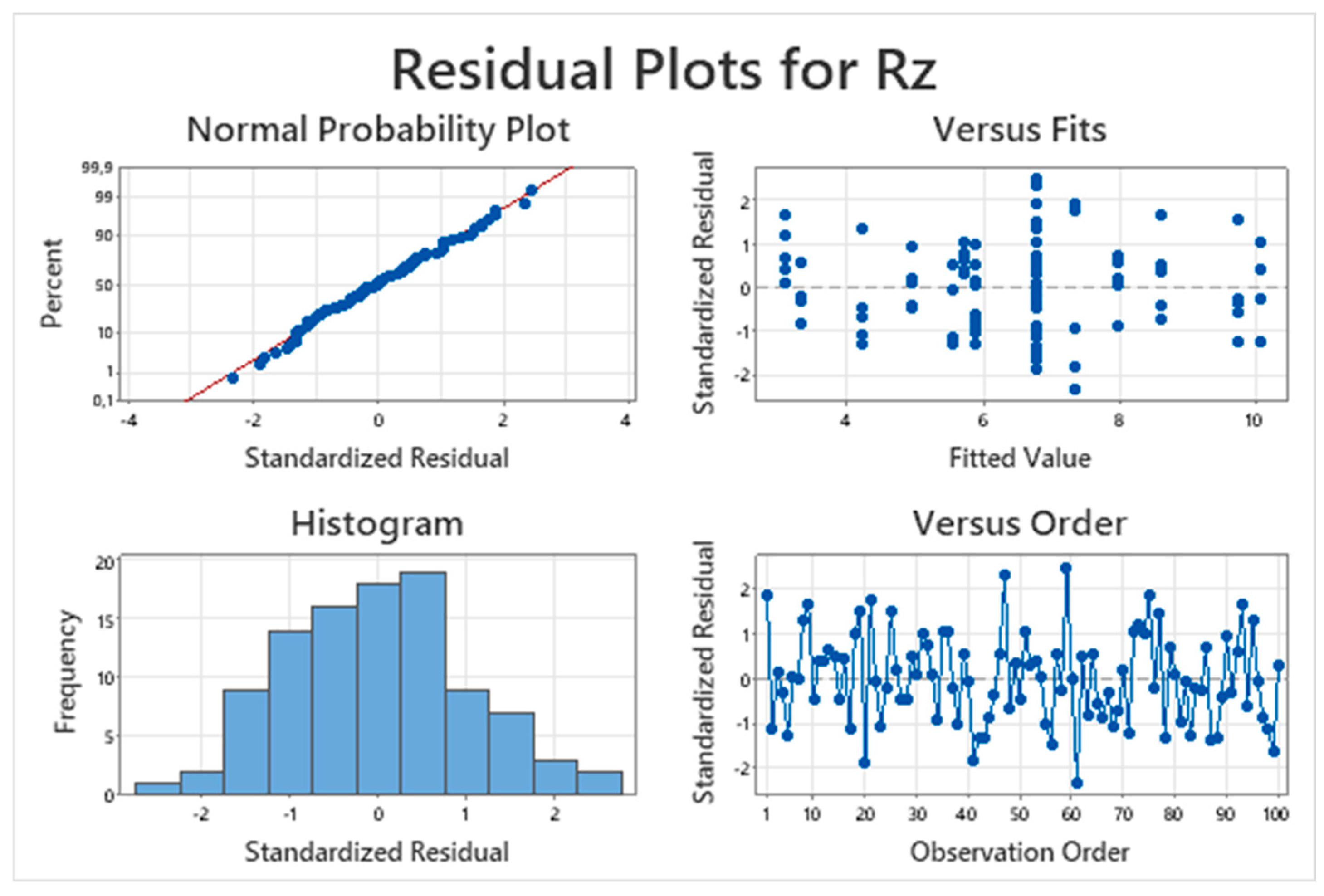
Residual diagnostics in Figure 9 confirmed that model assumptions were satisfied. Normal probability plot and histogram indicated that the residuals followed an approximately normal distribution, while residuals-versus-fits and residuals-versus-order plots showed no heteroscedasticity or systematic trends. These results confirm that the R_z model is statistically adequate.

3.4. Analysis of Standardized Effects

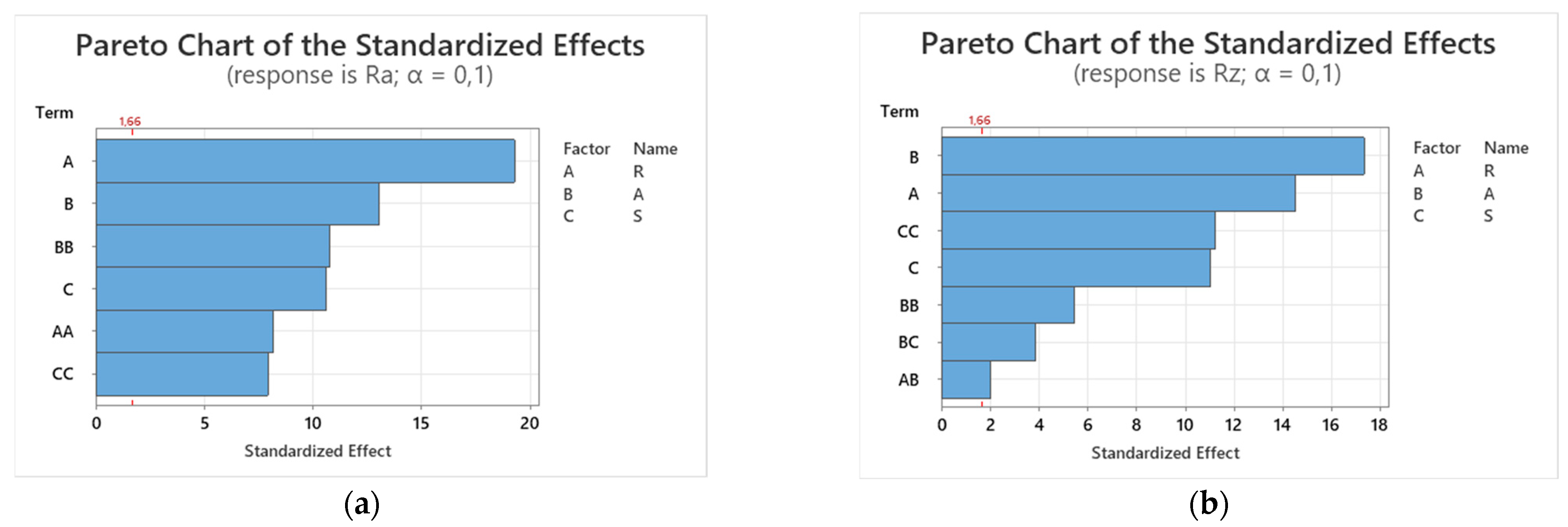
Analysis of main effects shows that the variability of response R_a is explained entirely by individual factors and their quadratic terms, with no statistically significant interactions retained in the model, as seen in Figure 10a. The dominant factor is radius, which aligns with literature findings, followed by inclination angle and stepover height. The strong effect of radius can be attributed to cusp height reduction when using larger radii at the same stepover height. Inclination angle shows a more pronounced effect than stepover height, suggesting that the dynamic component of the machining process plays a substantial role in determining R_a. This effect would likely be amplified if the experiment were conducted on a 5-axis machine with active tool inclination.

Effect analysis for response R_z in Figure 10b shows similarities but also clear differences compared to R_a. The dominant factor for R_z is inclination angle rather than radius. This can be explained by the nature of R_z, which is defined as the peak-to-valley height and is thus more sensitive to random surface phenomena and local deformations. Interestingly, Radius does not retain a quadratic term in the R_z model, indicating a certain degree of asymmetry between the R_a and R_z responses. Stepover height exhibits a comparable trend to R_a, with a quadratic term slightly stronger than its linear counterpart.

Interactions between certain factors were also present in the model; however, their overall contribution to response variability was minor. For this reason, interaction plots are not included, as they would offer limited additional insight. The interaction terms were retained in the model solely because they were statistically significant.

3.5. Contour and Surface Plots of Both Response Models

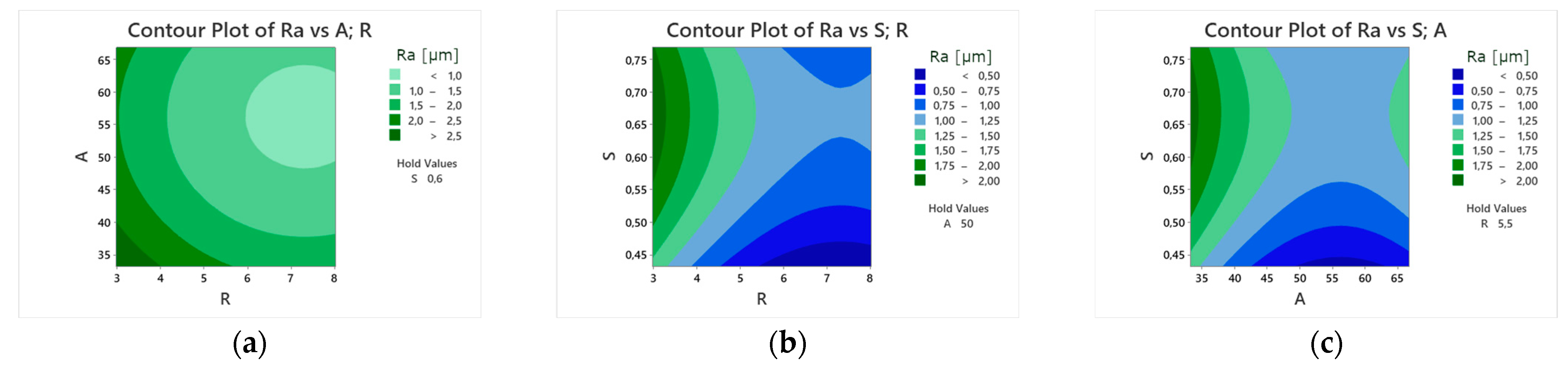
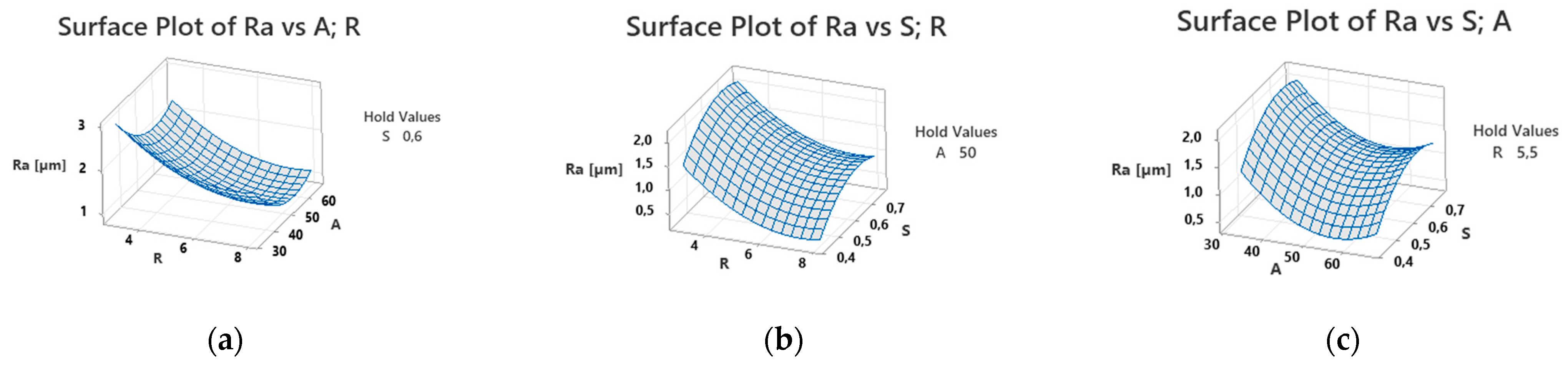
Surface plots of response R_a provide key insights into the position of the proposed model relative to the chosen response. As shown in Figure 11a, factors R and A occupy a region relatively close to a local optimum within the experimental settings. In contrast, Figure 11b,c reveals a local saddle point. This saddle point is particularly useful for guiding additional experimental steps and identifying promising directions for future research. Certain factor combinations, primarily near model edge cases, yield R_a values below 0.8 μm, suggesting that results that are lower than commonly achievable roughness levels are possible.

To provide a clearer visualization of the model results, response R_a is shown as 3D surface plots in Figure 12a–c. All factors exhibit curvature, as confirmed statistically in Table 7, and this is now visually evident. Without the quadratic terms, the model would not capture the true nature of the R_a response. The results presented in Figure 11 and Figure 12 are closely tied to the chosen experimental settings and the specially designed ball-end cutting tool. It is very likely that, if the entire experiment were conducted with R factor intervals between 10 mm and 20 mm, the results would vary significantly due to cutting dynamics.

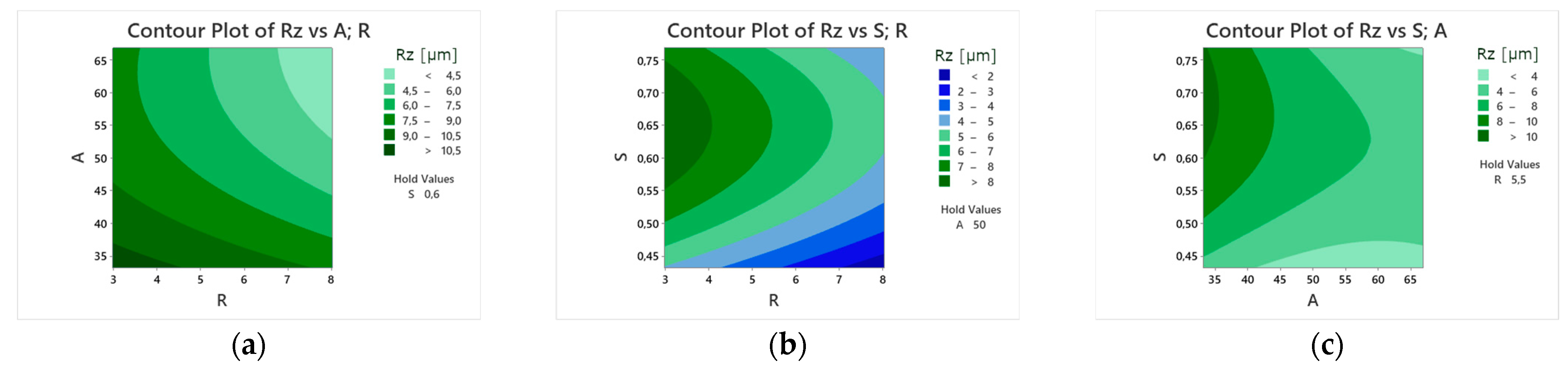
Response R_z models are visualized in Figure 13 and Figure 14 as contour and surface plots, respectively. Visual inspection confirms that factor R contributes only a linear effect, consistent with the statistical confirmation in Table 8. Similarly to response R_a, the model space lies between peak and valley points of the response surface, indicating potential directions for further research.

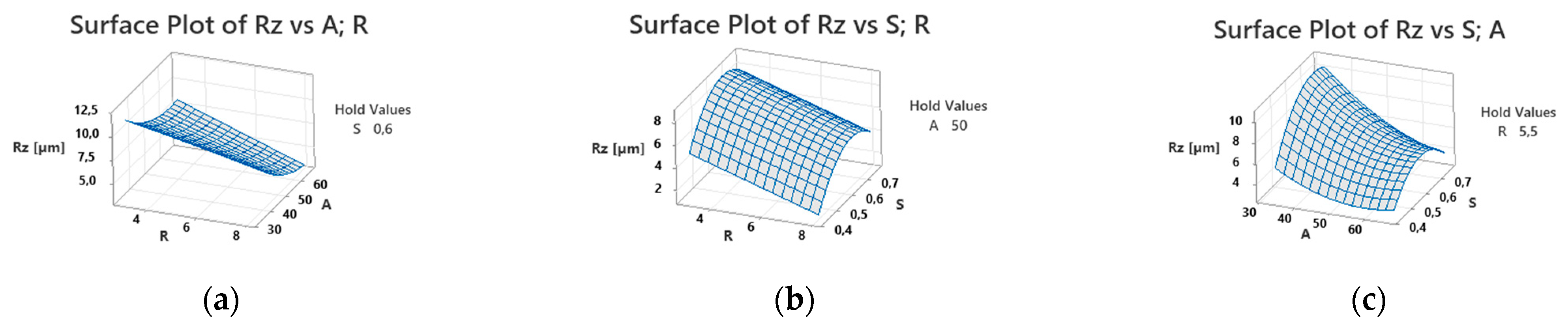
The 3D surface plots of response R_z shown in Figure 14a–c provide additional insight into the linear behavior observed for factor R. In Figure 14a, the response surface appears nearly planar along the R-axis, confirming the absence of a significant quadratic effect. The smooth nature of these surfaces also indicates that the process window explored in this study is stable, with no abrupt changes in surface quality across the tested range.

3.6. Model Validation with Prediction

Through model testing, using cutting tools from the main experiment, it was determined that statistical models are sufficiently accurate, predicting the response with an accuracy of approximately 90%. To verify the models beyond mathematical analysis, a dedicated validation experiment was designed to assess the real predictive capability of the developed models. This validation was performed under certain limitations regarding the settings of selected factors and included verification of the optimal solution.

The factor limitations applied to the designed cutting tools were as follows: All validation cutting tool samples were produced with the radius factor fixed at 7 mm. Designing a new cutting tool according to the predicted optimum would have been economically and time-demanding; therefore, the calculation of the optimum solution and the prediction of the validation values were performed with the radius factor maintained at 7 mm. Limiting the validation samples to a radius of 7 mm, affects the overall performance of the validation due to the curved nature of factor A in terms of response R_a. The authors acknowledge this design choice as a limiting factor in terms of robustness and repeatability. The remaining factors were left unrestricted. The validation comprised one optimum solution and three randomly selected predictive solutions. For the manufacturing of the optimum solution, the objective function was set to minimize response, thereby achieving the best possible surface finish within the region of our study.

Table 9. Validation experiment factor and results comparison.

Solution	R	A	S	Prediction		Validation		Error
				Ra	Rz	Ra	Rz	Ra	Rz
1	7.00	62.00	0.43	0.26	1.47	0.51	2.40	49%	39%
2	7.00	53.60	0.46	0.39	2.63	0.59	3.50	34%	25%
3	7.00	50.00	0.48	0.55	3.52	0.78	3.98	29%	12%
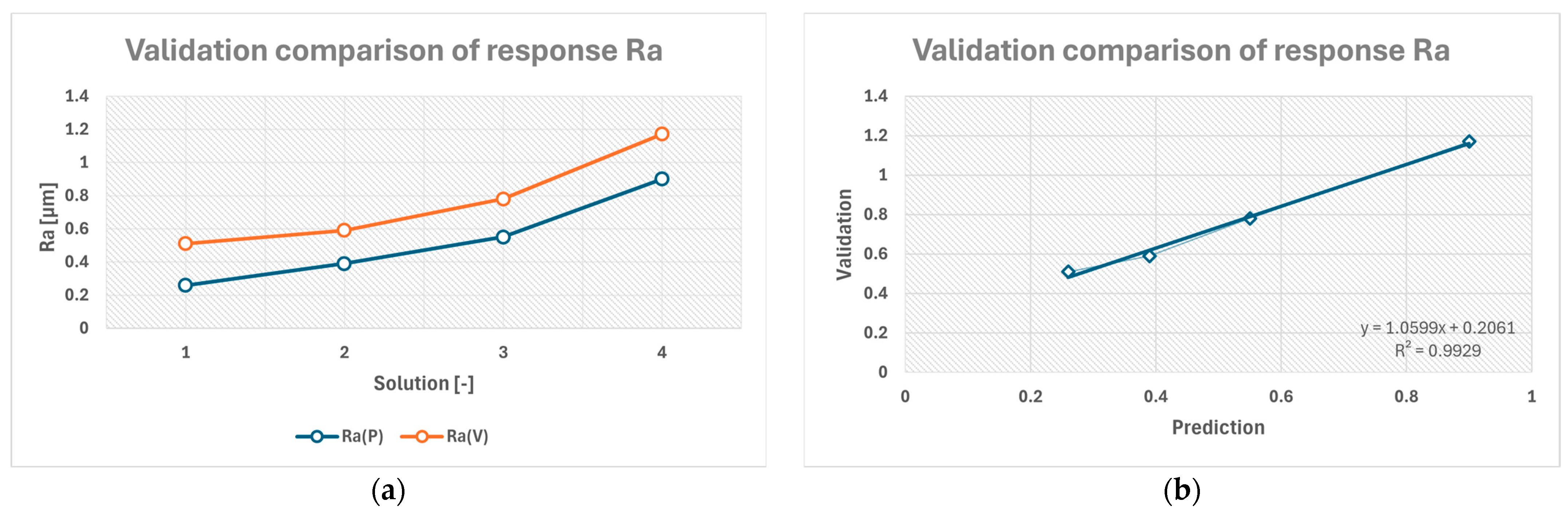
4	7.00	62.00	0.76	0.90	2.97	1.17	5.35	23%	44%

presents the factor settings based on the selected solutions together with the results of the validation compared to the model predictions. Solution 1 represents the optimum solution, while the remaining solutions correspond to random predictions.

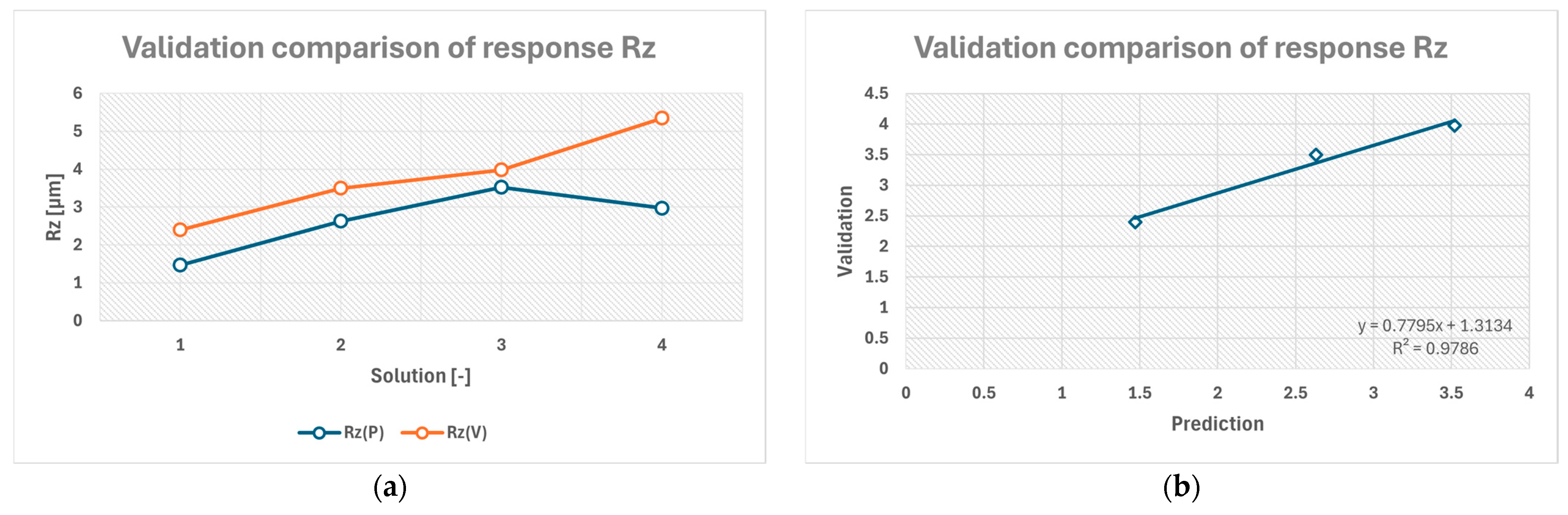
Prediction and validation data were compared both mathematically and visually. On average, the validation data points of response R_a were offset by approximately 0.24 µm above the predicted values, while R_z values were offset by 1.16 µm. As shown in Figure 15a, the predicted R_a (P) and measured values R_a (V) follow a similar trend across all four tested solutions, with a nearly parallel progression, confirming that the model correctly captures the overall shape of the response surface.

The scatter plot in Figure 15b further confirms this observation quantitatively. The data show a coefficient of determination close to 100%, indicating excellent agreement between predicted and measured values. The slight positive slope deviation reflects a small systematic overestimation of the measured response, which is expected due to process variability and measurement uncertainty.

It is important to note that prediction accuracy decreases for very low surface roughness values, where machining dynamics and surface effects dominate the response and approach limits of the measurement systems. This is particularly evident near 0.5 μm, which approaches a polished surface finish and is inherently difficult to model precisely with general cutting tools.

Prediction and validation data for response R_z were also compared visually and mathematically. As shown in Figure 16a, the overall trend of predicted and measured values is consistent for the first three solutions, with Solution 4 showing a significant deviation. This discrepancy is attributed to the extreme value of the stepover height factor, which was outside typical finishing operation conditions and likely introduced higher variability.

The scatter plot in Figure 16b excludes Solution 4 to prevent skewing of the regression fit. Even with this exclusion, the regression shows good agreement with the model predictions. The slope of 0.779 indicates that measured values tend to be slightly higher at low predictions and lower at high predictions, suggesting a mild underestimation at the lower range and overestimation at the upper range of the response. This behavior is typical for models approaching the limits of their design space and highlights the importance of avoiding extreme factor settings during finishing operations.

The average error rate between validation and prediction in terms of R_a corresponds to 34%, and for R_z, 25%, excluding the result of Solution 4. The results show that while the model captures general trends, it fails to accurately predict the actual values machined, or the predictions are slightly offset. These facts show that the models generalize poorly, which is expected due to rather large stepover heights used overall in this study, considering finishing machining operations

While the proposed response surface model provides reasonable predictions within the design space, the validation experiments revealed a non-negligible prediction error. During further analysis, it was found that applying transformations to the response improves predictive accuracy while preserving the same model structure and factor terms. This indicates that the underlying relationship between the machining parameters and the resulting surface roughness is more curved and nonlinear than initially assumed. Resulting effects due to transformations are shown on

Table 10. Effect of model transformation on predictive error.

Validation		$\mathbf{BOX}\text{-}\mathbf{COX} \mathit{\lambda }=0.5$		Error		$\mathbf{Natural} \mathbf{Log} \mathit{\lambda }=0$		Error
Ra	Rz	Ra	Rz	Ra	Rz	Ra	Rz	Ra	Rz
0.51	2.40	0.38	2.00	25%	17%	0.45	2.31	13%	4%
0.59	3.50	0.48	2.94	19%	16%	0.53	3.12	11%	12%
0.78	3.98	0.60	3.66	23%	23%	0.62	3.75	26%	6%
1.17	5.35	0.89	3.25	24%	24%	0.88	3.42	33%	56%

.

Although the transformations enhance the model’s performance, it also suggests that the physical behavior of related processes may require more comprehensive or higher-order models to fully capture the responses’ complexity. Therefore, the logarithmic model is presented as an improved statistical fit, but it also highlights potential directions for future work in refining and expanding the predictive framework.

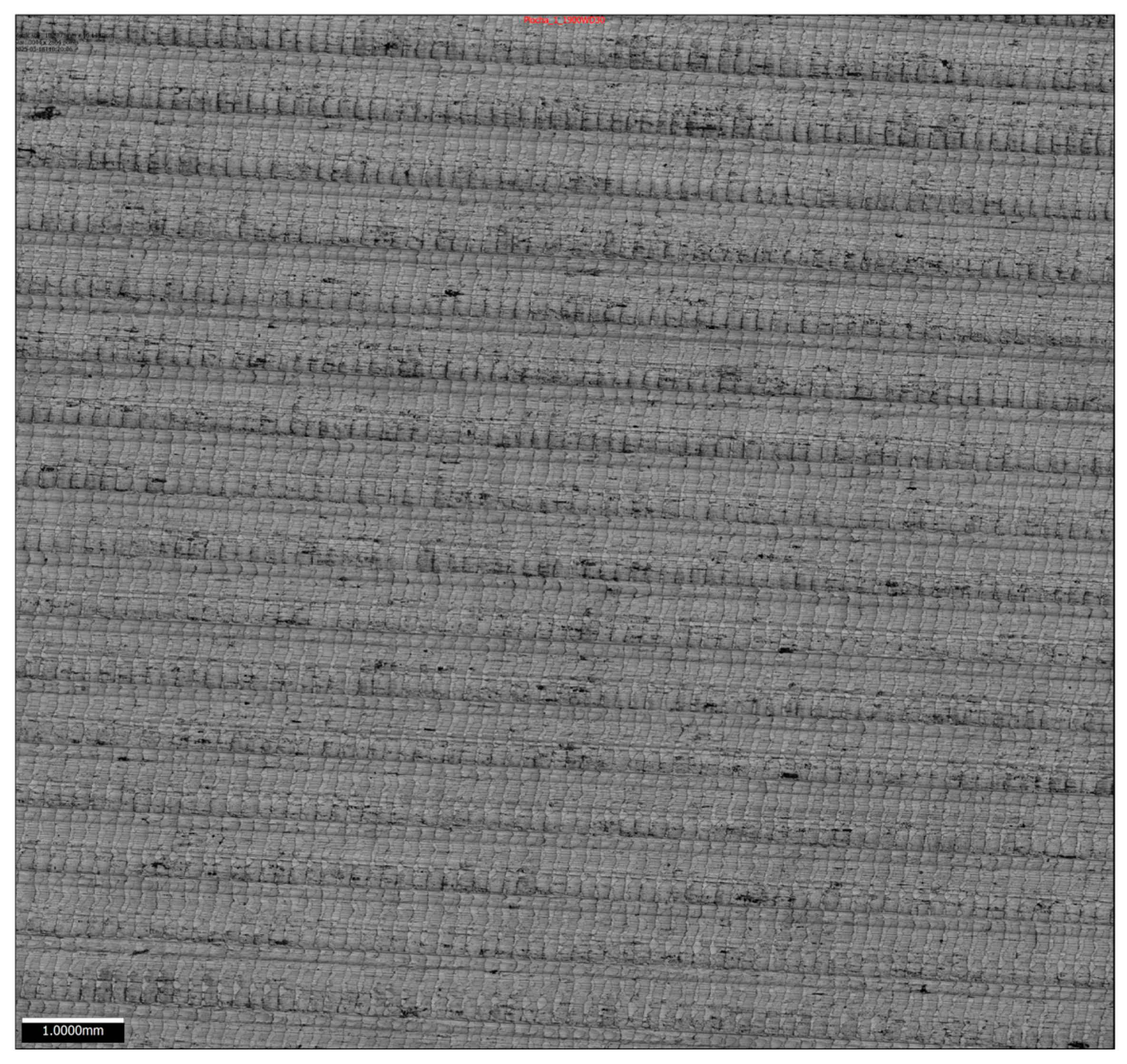
As an additional step, selected validation samples, solutions 1 and 3, were analyzed using a 3D optical measurement system Alicona Focus X(Alicona Imaging GmbH, Austria, Graz). Other solutions could not be measured due to microscope workspace size constraints. The device was employed to capture detailed surface topographies using a 1900 WD 30 lens, as shown in Figure 17. The resulting image clearly reveals the cutting tool feed marks and scallops caused by the programmed stepover height. The machining traces appear evenly distributed without abrupt changes or deformation, confirming that the process was relatively stable. Dark spots visible on the image are considered either optical artifacts or minor surface defects not representative of the overall surface texture.

To further illustrate the surface characteristics, a 2D surface roughness profile was extracted, as presented in Figure 18. The measured profile shows a characteristic pattern corresponding to the cutting tool geometrical profile, which is expected when machining with a ball-end mill. The average surface roughness R_a obtained from the Alicona measurement was approximately 0.2 μm higher than the values measured by the stylus instrument, which can be attributed to the different measurement principles and filtering methods of the optical device.

These additional measurements provide an independent confirmation of the process stability and help contextualize the experimental results by offering a complementary view of the surface topography.

3.7. Comparison with Analytical Results

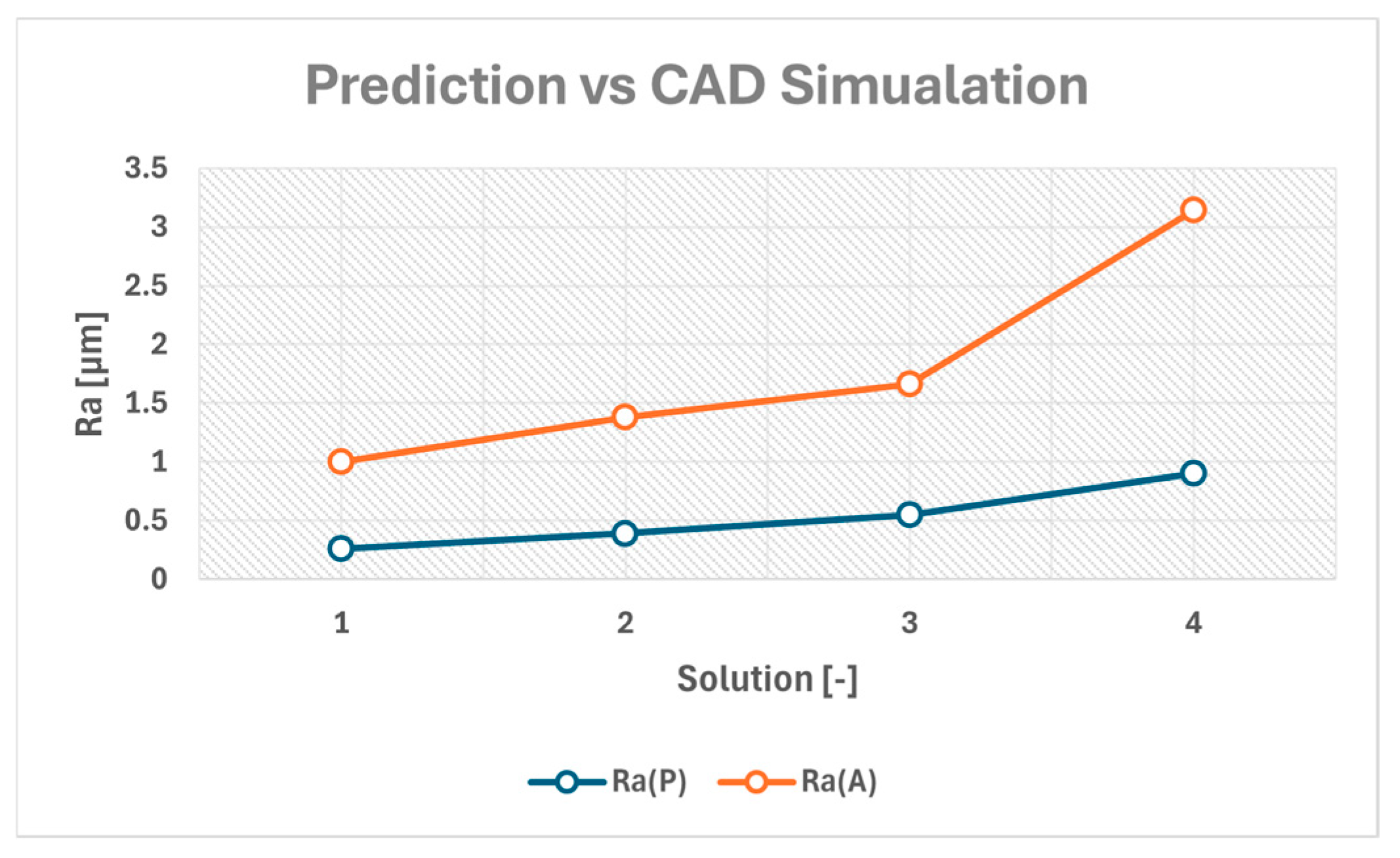
Figure 19 presents a comparison of predicted R_a values obtained from the response surface model, R_a (P), with analytically determined values from CAD simulation R_a (A), at identical factor settings. As expected, CAD simulation consistently produces higher R_a values, since it represents a purely geometric lower bound without considering machine dynamics, cutting tool edge effects, or process damping that can further smooth surfaces. The prediction model follows the same increasing trend with respect to decreasing cutting tool radius R and increasing stepover height S. The prediction model produces lower absolute results, which is consistent with real machining processes achieving better-than-ideal roughness due to burnishing and elastic recovery effects. The near-parallel nature of the two curves indicates that the prediction model is well-calibrated and captures the influence of input factors reliably, with a nearly constant offset between analytical and predicted values. This comparison strengthens confidence that the response surface model reflects the real physical process within the expected range of machining behavior.

The simulation was constructed as a 2D sketch with overlapping toolpath geometries at factor settings. While Catia V5 R19 does not have a direct feature or module to calculate resulting Ra and Rz values, it is possible to parametrically extract them via a set number of measurements from the 2D sketch profile. The number of measurements increases the accuracy of the resulting approximation; however, since this is an ideal toolpath overlap without vibration or dynamic effects, the resulting number of measurements required is low. The R_z and R_a values were obtained with a series of parametric measurements and computations, similarly to how a stylus-based measurement instrument performs computation of measured values at the microcontroller firmware level.

4. Discussion

The proposed cutting tools have achieved a satisfactory result in terms of evaluated responses R_a and R_z. Through statistical modeling using a quadratic CCD model, we have achieved a predictive model with a relative error rate. The study featured ball-end cutting tools with the factor radius in the interval of 2.98 to 8.02 mm. Cutting tools were limited to a constant stock material, a carbide rod of diameter 8h6 mm.

Residual analysis presented in Figure 8 and Figure 9 confirms that the adopted quadratic model satisfies the fundamental assumptions of normality, independence, and constant variance. Similar behavior of residuals has been reported in other machining studies employing quadratic response surface models, where increased model complexity did not lead to violations of statistical assumptions [22]. In this context, residual plots are not compared in terms of their numerical distribution but rather in terms of the absence of systematic patterns and trends. Normal probability plots serve as a diagnostic tool for identifying potential measurement errors or outliers; however, no such anomalies were observed in the present study.

Table 7 and Table 8 show the model-testing statistic lack-of-fit, while response R_a shows significant lack-of-fit, response R_z shows a non-significant lack-of-fit; however, the threshold is very close to the significance level. This might be an indication of a higher-order model requirement in the scenario of model expansion to a larger factor range. Alternatively, a logarithmic transformation might provide insight into the process, as higher-order models require many data sets as well as computational power. Higher-order models are also sensitive to response data and might start showing modeling errors. The lack-of-fit difference between responses and its effect on the results has already been discussed in Section 3, Section 2 of this article.

The present experiment was conducted without randomization due to technical constraints associated with repeated machine setup and specimen alignment. While randomization is generally recommended to minimize the influence of gradual tool wear or machine-state variations, several factors in this study limited such effects. Each cutting pass involved a very small material-removal volume, resulting in negligible wear progression over the duration of the experiment; this has not yet been experimentally validated and could be further tested in future scientific endeavors. The absence of randomization is acknowledged as a methodological limitation, especially considering the fact that the proposed cutting tools were manufactured without coatings or cutting edge modifications.

While this study focused on radius, inclination angle, and stepover height, other factors, such as feed rate, also influence surface roughness. Ginta et al. [36] reported that Feed was the dominant factor and a linear model was inadequate. Tool wear was not included in the present experiment; however, Kasim et al. [37] observed a negligible effect of flank wear on R_a in ball-end milling, indicating that wear-related effects may be limited under comparable conditions. The general literature features studies focusing on process parameters such as feed rate or cutting speed, feed etc.; the proposed study added a unique factor, as under normal circumstances, the experiment would require ball-end tools manufactured from a carbide rod of diameter 16h6 mm. Proposed cutting tools can reach similar results while preserving a relatively small cutting tool footprint. Nicola et al. used a ball-end mill of diameter 16 mm, which showed near R_a $\approx 0.6$ µm in terms of downward milling compared to run number 13 from Table 6, where we saw a similar R_a value of 0.51 µm at radius 5.5 mm. While their parameter settings were slightly different in terms of a_e, their results show how our proposed cutting tools produce similar results [38].

The cutting parameters used in this study featured similar values to optimal results from studies with coated cemented-carbide tools of diameter 20 mm, and the resulting optimal parameter settings were V_c = 159.42 m/min and f = 0.06 mm; for comparison, the cutting parameters of this study shown in Table 5 are V_c = 150 m/min and f = 0.062 mm [39].

Alternative cutting tools that can be used for finishing operations, as mentioned in this study, include toroidal endmills. Płodzień et al. found R_a values below 0.4 µm when milling with cutting inserts. The insert radius was 4 mm; the key difference lies in the measuring directions of surface roughness being along the feed direction. The surface roughness in the feed direction is mostly influenced by vibrations; our study measured the surface roughness values perpendicular to the feed direction [40].

Another study featured toroidal cutting tools with round cutting inserts milling concave and convex surfaces and varying degrees of curvature or tool inclination angle. Their findings showed that curvature mostly affect R_a values, ranging from approximately 0.25 µm from the lowest to the highest value, with varying trends. Their lowest possible values were near R_a = 0.3 µm, compared to our study’s findings, where the lowest possible value of R_a was 0.51 µm [41]. Their study featured a true five-axis setup, which affected the cutting tool and workpiece interaction. The actual difference between the curved and linear surfaces in this comparison is only viable in super finishing criterion requirements.

The tool overhang used in this study featured a constant setting of 30 mm, this value was chosen based on the required minimal clamping length of diameter 8h6 for cylindrical shanks according to DIN 6535 HA [42]. Studies have featured the tool overhang lengths as a noise control factor. Arrunda et al. found, during quadratic modeling of ball-end milling processes, a conflict between results in combination with f_z and a_e, suggesting a search for robust factor levels. This conflict suggests that the overhang length affects cutting tool deflection, which, in some cases, as per their findings, can affect surface roughness in both directions [43].

A study performed by Zhao et al. featured numerous ball-end mill solid carbide cutting tools with a Taguchi matrix. Their study featured numerous cutting radii and process parameters; however, the number of flutes varied between two and four. This was included in the design matrix as a cutting tool-specific factor, compared to our study, which featured a constant design rule of four flutes per cutting tool. Their results show a per-radius difference in obtained R_a values of almost 0.2 µm between the 2-, 3-, and 4-flute cutting tools, suggesting that the number of flutes must either be included as a factor or set as a constant. Cutting tool flutes are generally constrained by cutting tool diameter and machined material [44].

Comparable surface roughness values were reported by Varga et al. [45] for concave and convex surface machining. Their experimental setup used similar cutting parameters—a_e = 0.3 mm and f = 0.04 mm—and ball-end cutting tools. Although their study focused on tool inclination and effective radius, the best results of R_a = 0.491 μm and R_z = 2.713 μm were achieved for a convex surface. Direct comparison between inclined and curved surfaces is not appropriate; however, the results indicate that similar surface quality levels can be achieved as seen in Figure 11 and Figure 13.

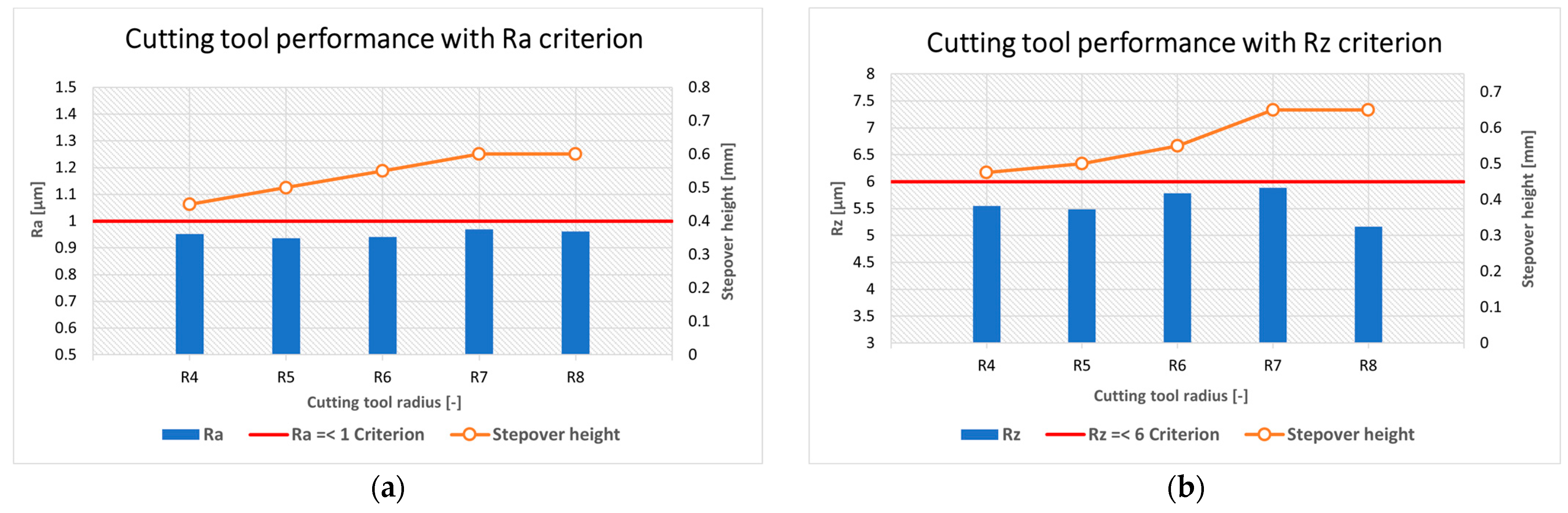
The study employed a three-factor quadratic model. From a tooling perspective, the tool radius is considered a cutting-tool-specific parameter, whereas stepover height and inclination angle are process-specific parameters defined relative to the selected machining process. Figure 20a presents a comparison of cutting tool performance for tool radii ranging from 4 to 8 mm under a surface roughness criterion of R_a ≤ 1 µm. For reference, the R4 cutting tool is considered a standard tool, as it does not incorporate the proposed cutting tool modification. All R_a values shown in Figure 20a are based on model predictions evaluated within, or near, the original design space, with the Inclination angle factor fixed at its center level.

As shown in Figure 20a, all cutting tools investigated satisfy the specified R_a criterion. The primary difference lies in the allowable stepover height. From R4 to R7, the Stepover height increases in approximately 0.05 mm increments, whereas no further increase is observed between R7 and R8, indicating a saturation effect. The total increase in allowable stepover height between R4 and R7 is 0.2 mm, corresponding to a 33.33% increase. Although the absolute magnitude of this improvement appears modest, such an increase in Stepover height can significantly enhance process efficiency in finishing operations. Larger allowable Stepover heights directly reduce toolpath density and machining time, thereby improving overall productivity and economic output in production environments. Direct economic comparison of tooling costs or cost per part is currently not feasible, as the investigated cutting tools were specifically designed for the purposes of this study and are considered special cutting tools at the present stage of development. A detailed cost-per-part analysis will be addressed in future work once the proposed cutting tool concept reaches a level of manufacturing maturity suitable for industrial deployment.

Figure 20b presents a corresponding comparison of cutting tool performance based on an R_z criterion. The overall trend is similar to the observed R_a criterion, with the primary difference occurring between the R4 and R5 cutting tools, where the change in allowable stepover height is approximately 0.025 mm. As expected, R_z values exhibit higher deviations compared to R_a, which is consistent with the general behavior of peak-to-valley roughness parameters.

Pesice et al. investigated ball-end milling processes considering lead angle modification as well as different ball-end cutting tools. Their reported results show significantly larger R_z deviations occurring at irregular intervals, strongly influenced by lead angle variation. Specifically, R_a deviation intervals ranged from ±0.01 to ±0.21 µm, whereas R_z deviation intervals ranged from ±0.03 to ±0.48 µm [46].

R_z does not contradict the observed improvement in allowable stepover height but rather reflects the higher sensitivity to stepover height change. It should be emphasized that the response values shown in Figure 20a,b are model-based predictions evaluated within the defined design space. The differences observed between individual data points are primarily driven by changes in the Stepover factor.

Consequently, Figure 20a,b does not represent a direct comparison of surface roughness stability between R_a and R_z but rather illustrates how the respective response models behave under nearly identical input conditions. A more direct assessment of R_z variability is provided by the standard deviation interval magnitudes shown in Figure 7b and by the residual distribution histogram presented in Figure 9.

5. Conclusions

This study presented a comprehensive investigation into the effects of geometrical modification of ball-end cutting tools on surface roughness and process improvement in precision milling. By systematically evaluating the influence of cutting tool radius, inclination angle, and stepover height through a Central Composite Design (CCD), a predictive framework was developed that effectively linked cutting tool geometry with measurable surface roughness parameters. The results confirmed that macro-geometric adjustments, specifically the enlargement of the cutting tool’s tip radius beyond conventional design limits, can significantly enhance the achievable surface finish while maintaining relatively stable cutting conditions. Key findings can be stated as:

• The response surface models developed for Ra and Rz demonstrated strong statistical significance, with adjusted and predicted coefficients of determination exceeding 85%. Predictive performance is rather limited due to reaching an error rate of 34% and 25% in terms of Ra and Rz, respectively. These findings were further analyzed, and by using transformations, it was possible to lower the error rate of both responses. These findings show that the experimental design space with chosen factors may be more complex than expected and hence provides additional research opportunities. The models generalize poorly in terms of variation and repeatability, especially near edge cases or extreme factor settings, which is expected of the CCD statistical models.
• Cutting tools produced significantly lower Ra and Rz values, with the lowest being Ra = 0.51 µm and Rz = 2.4 µm at factor settings of radius = 7 mm, inclination angle = 62°, and stepover height = 0.43 mm. The general trend shows major improvement in the radius factor change for Ra, while for Rz, the dominating factor was inclination angle. Based on these results, we can conclude that the Ra and Rz values are mainly influenced by factor contributions rather than interactions.
• The study analyzed a range of predicted cutting tools with radii ranging from 4 to 8 mm. Using an R4 mm ball-end cutting tool as a reference vs. R7 mm resulted in a 0.2 mm, or 33.33%, improvement in allowable stepover height at identical Ra and Rz criteria. The results show a possible increase in efficiency in machining operation times, mainly due to toolpath density reduction. All cutting tools were manufactured from constant carbide rods of diameter 8h6 mm.

In summary, the research confirms that controlled geometrical modification of ball-end mills can serve as an effective strategy for optimizing surface quality and improving overall machining efficiency. The combined methodology of statistical modeling, experimental validation, and analytical simulation establishes a reliable foundation for future cutting tool design and process optimization. Future work should extend this approach by incorporating coating effects, cutting edge micro-geometry modification, and dynamic cutting force analysis to further enhance the predictive capability and industrial relevance of the developed models.