Bounded-Gain Prescribed-Time Robust Spatiotemporal Cooperative Guidance Law for UAVs Under Jointly Strongly Connected Topologies
Abstract
1. Introduction
2. Preliminaries
2.1. Problem Formulation
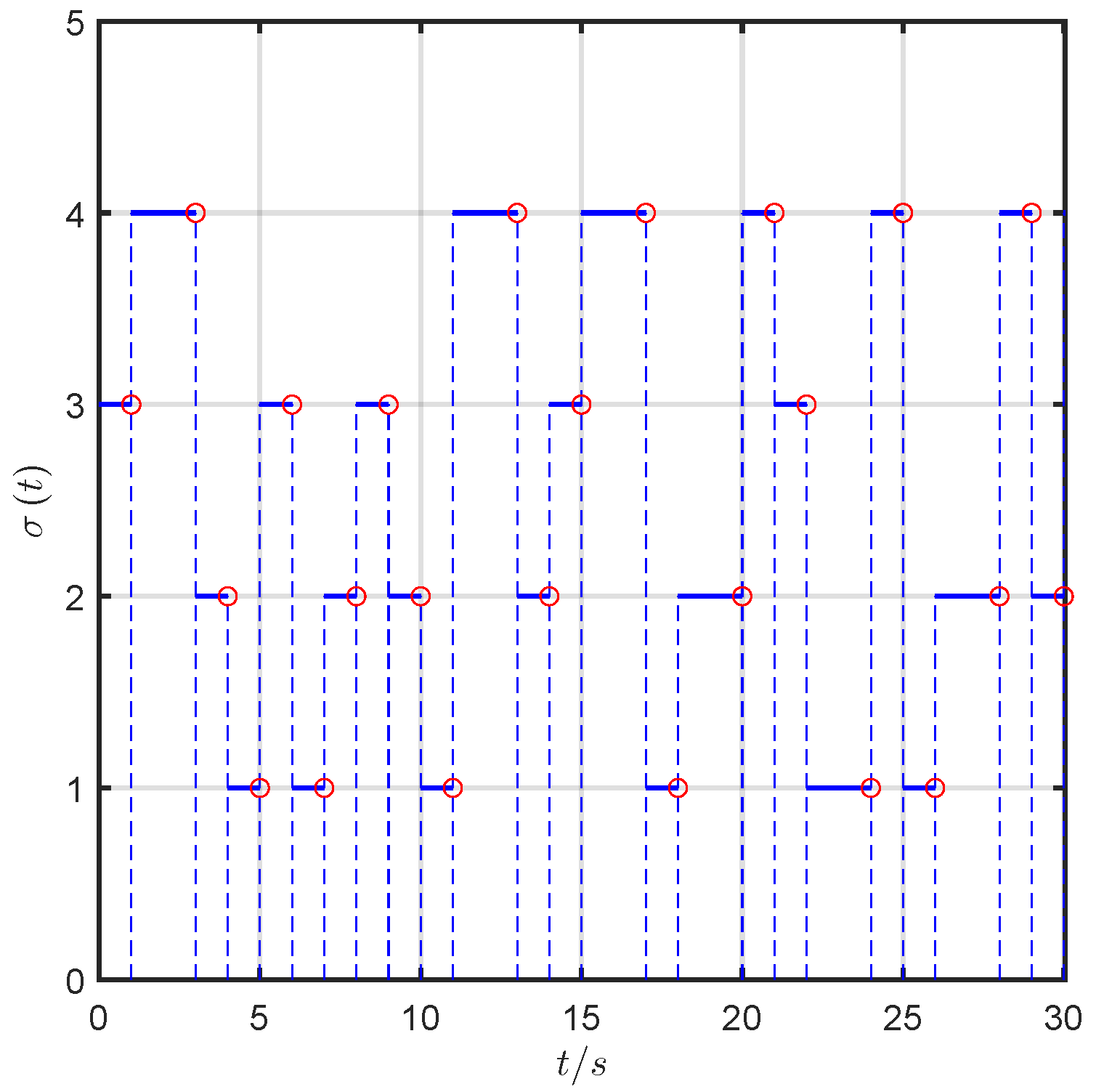
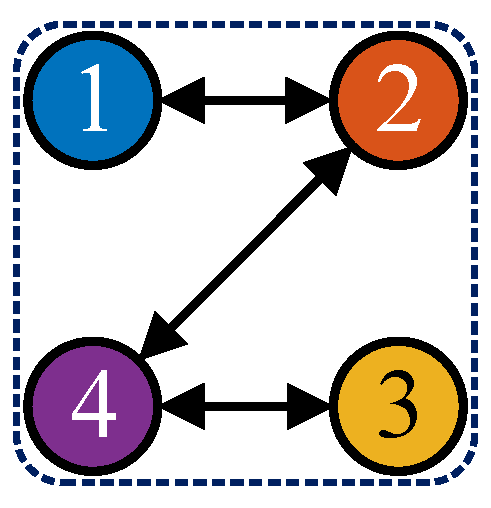
2.2. Network Topology
2.3. Bounded-Gain Prescribed-Time Stability Criterion
3. Design of the PDOs
4. Design of the PRCG Law
4.1. Tangential Acceleration Command Design
- (i)
- During phases when no UAV is faulty, the network topologies of UAVs are jointly strongly connected with ;
- (ii)
- After some UAVs become faulty, the network topologies of surviving UAVs remain jointly strongly connected.
4.2. Normal Acceleration Command Design
| Algorithm 1 The PRCG law. |
| Input: the states of the UAVs: , , , , , Output: the acceleration commands of the UAVs: , ,
|
5. Numerical Simulation
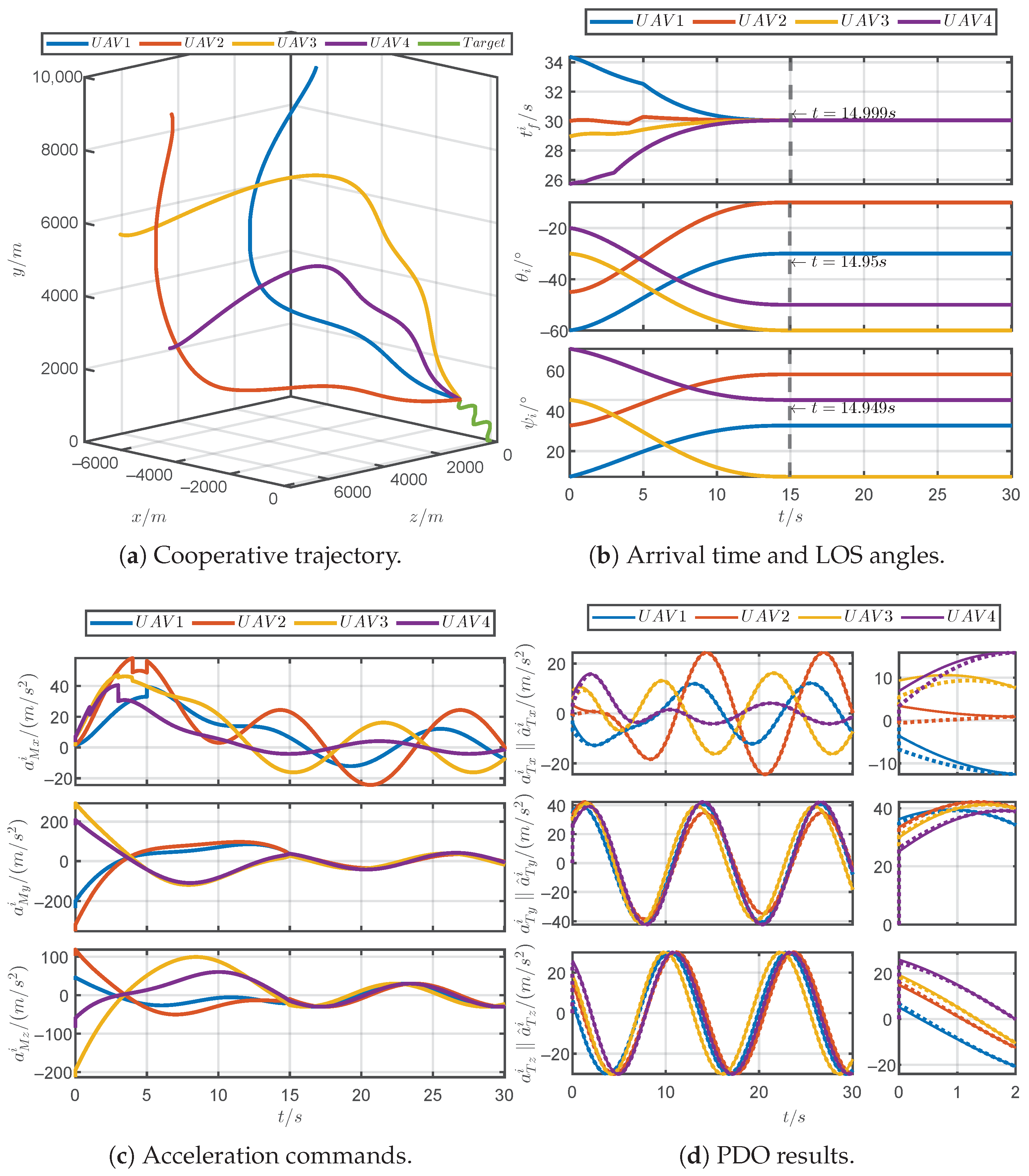
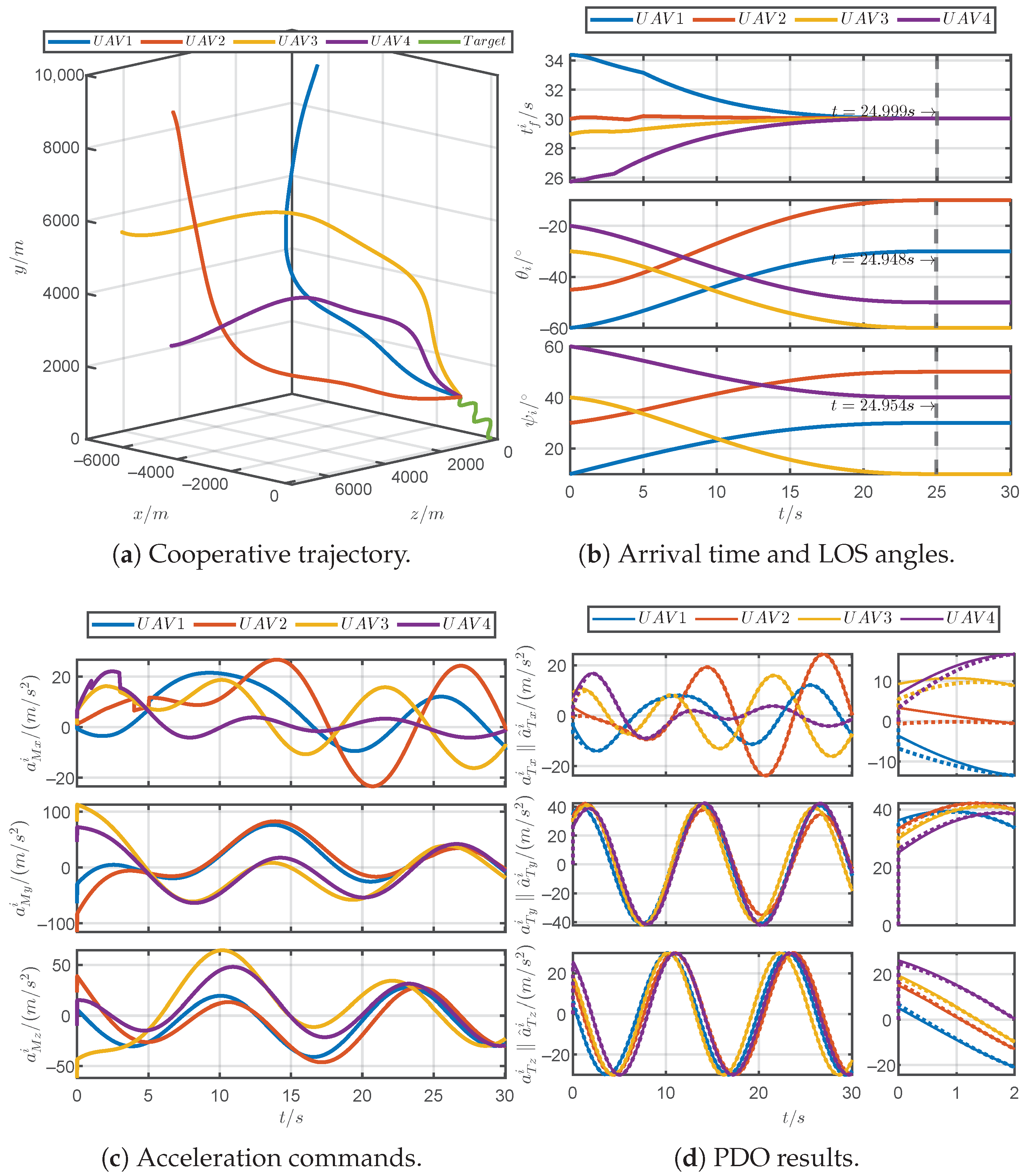
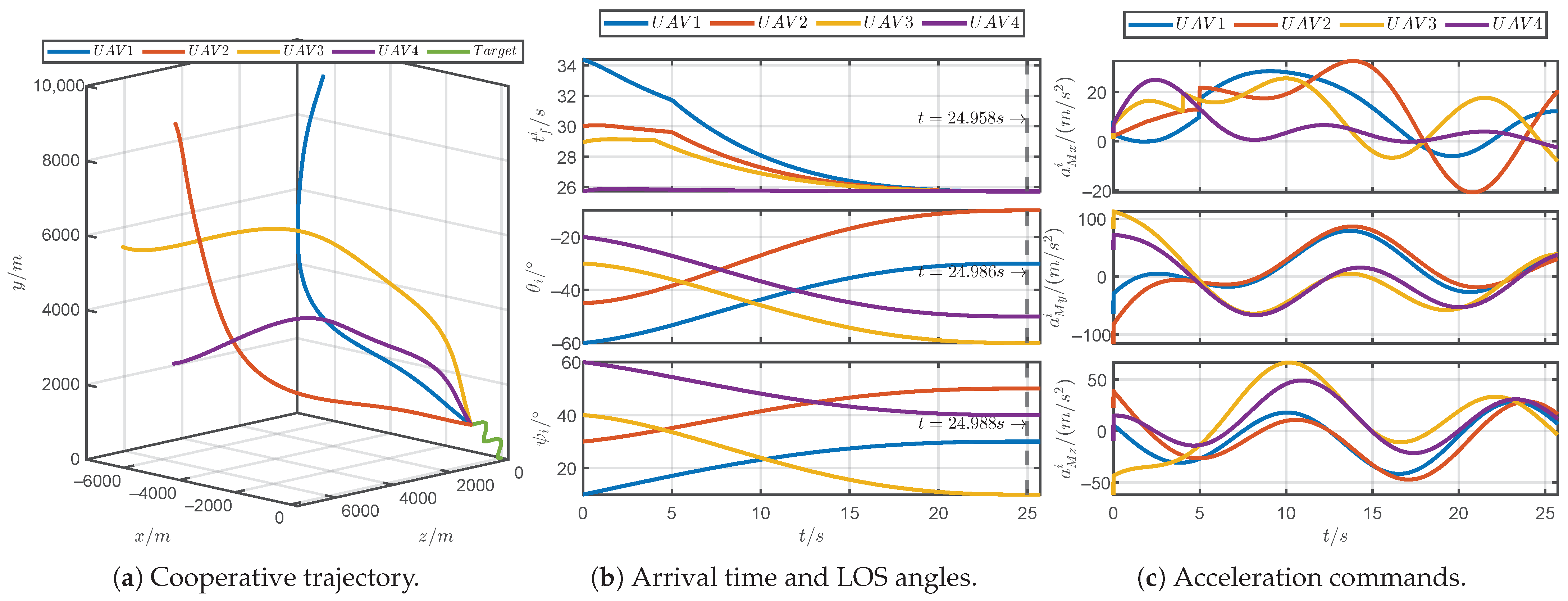
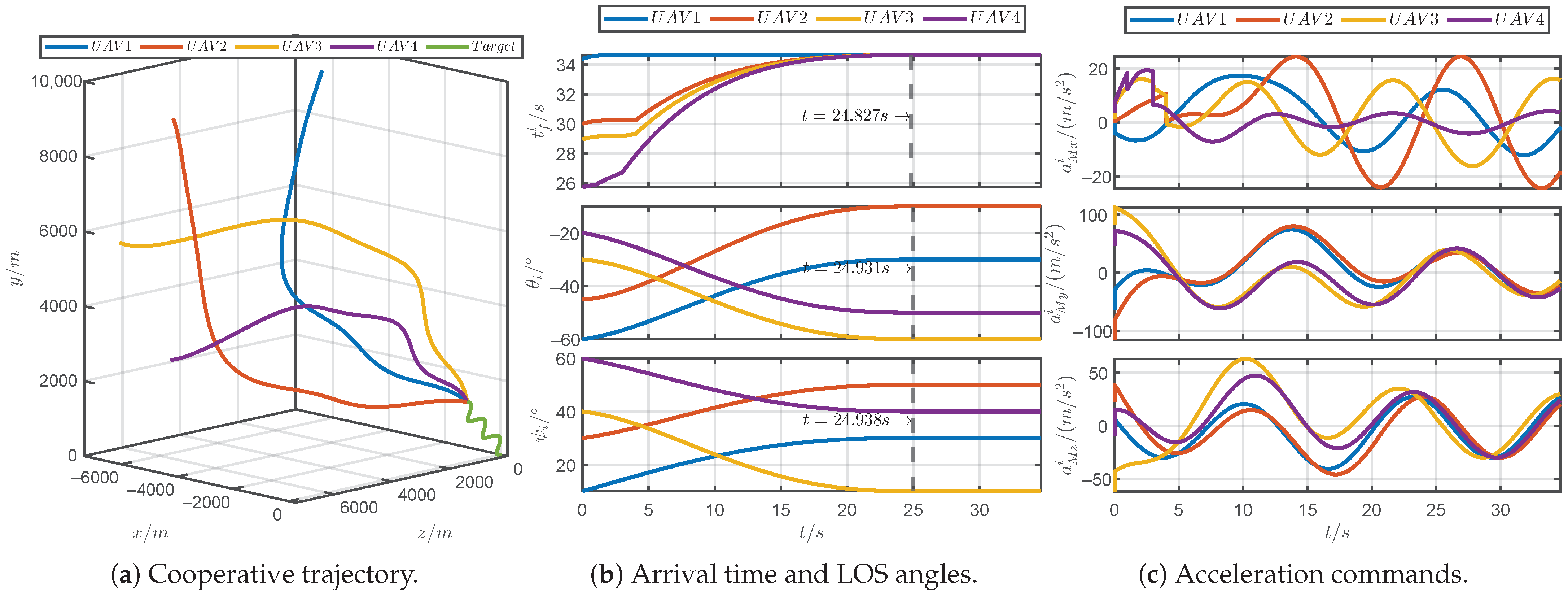
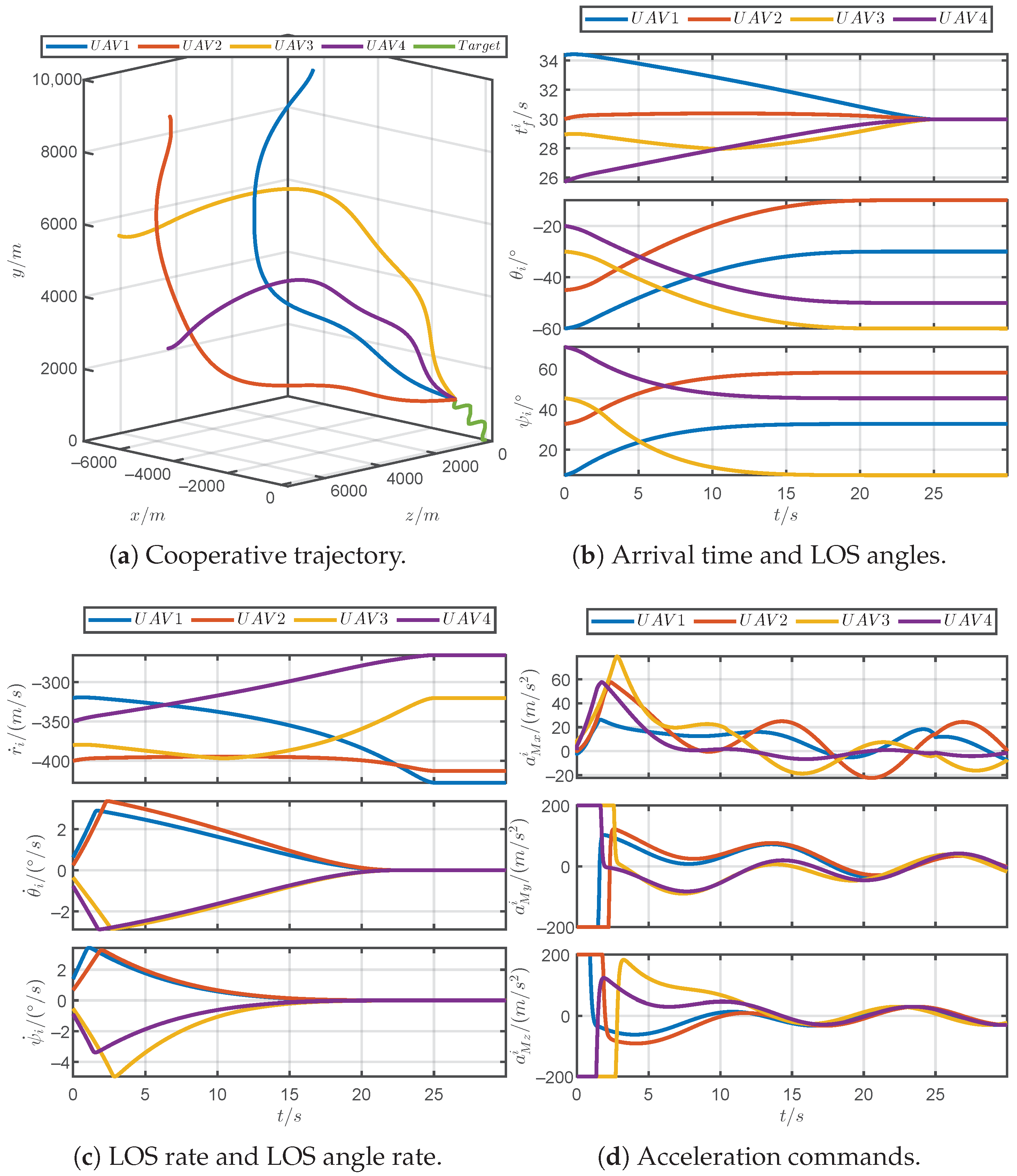
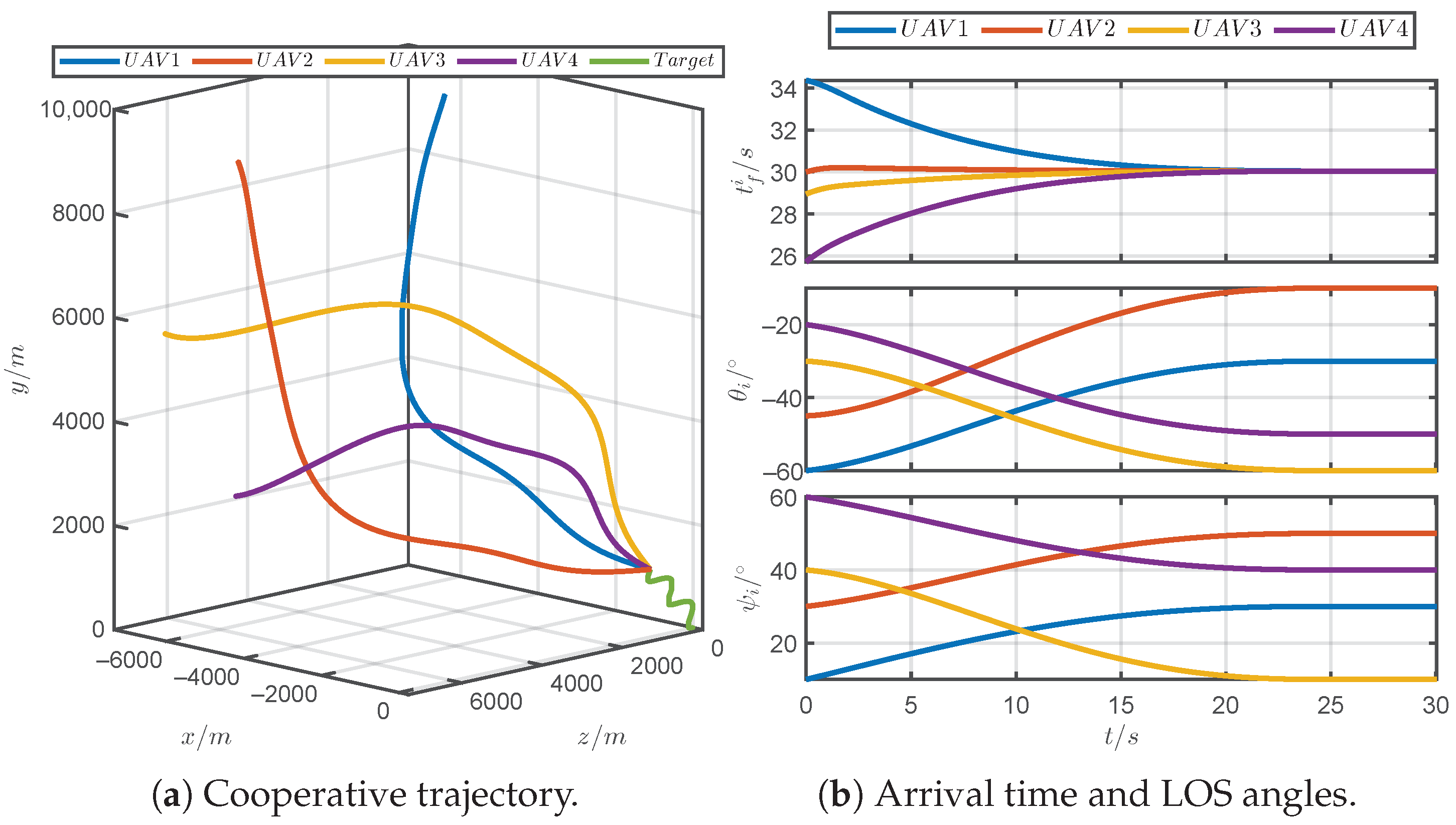
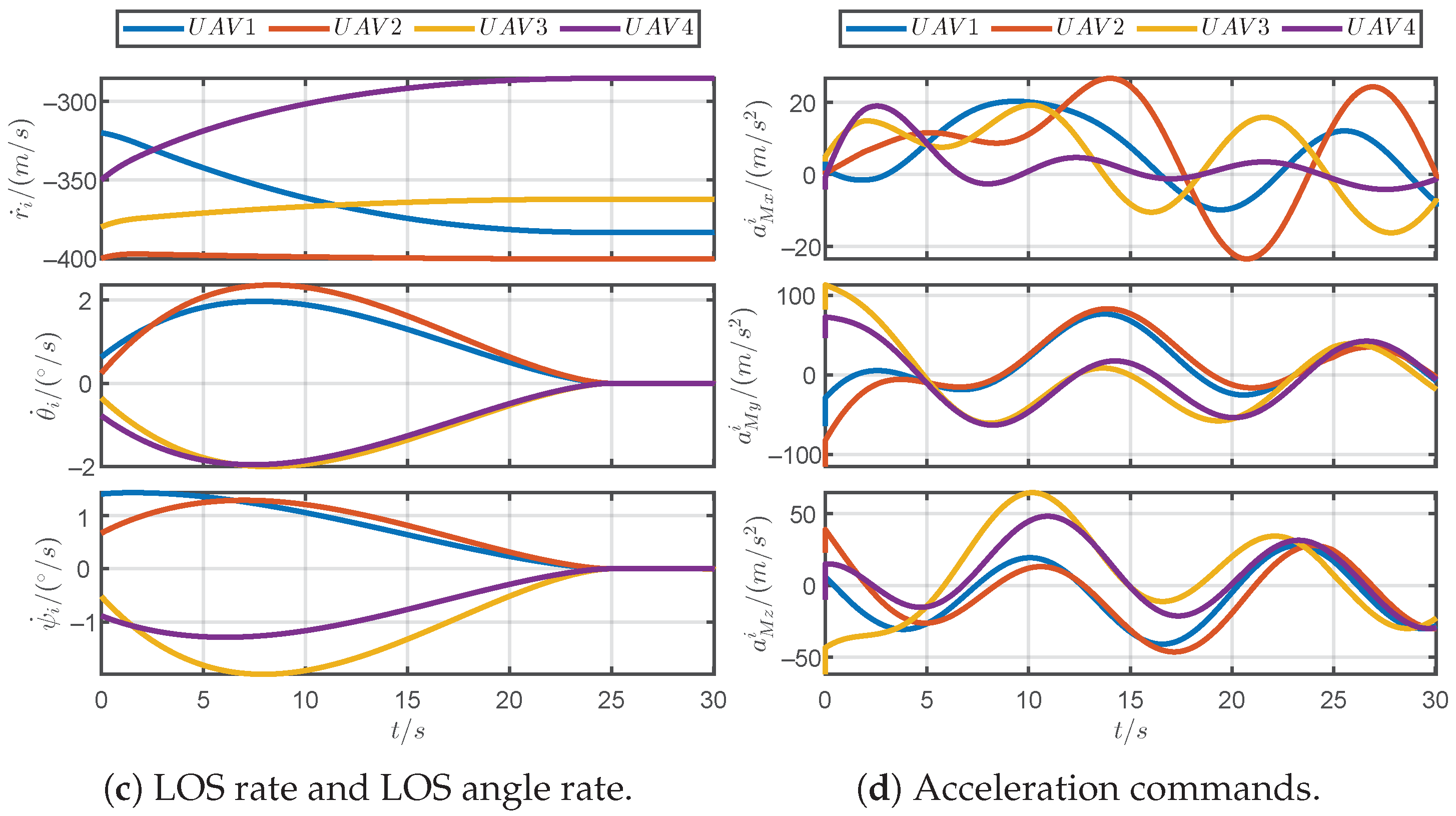
5.1. Simulations for Different Prescribed Settling Times
5.2. Simulations for Different Parameter
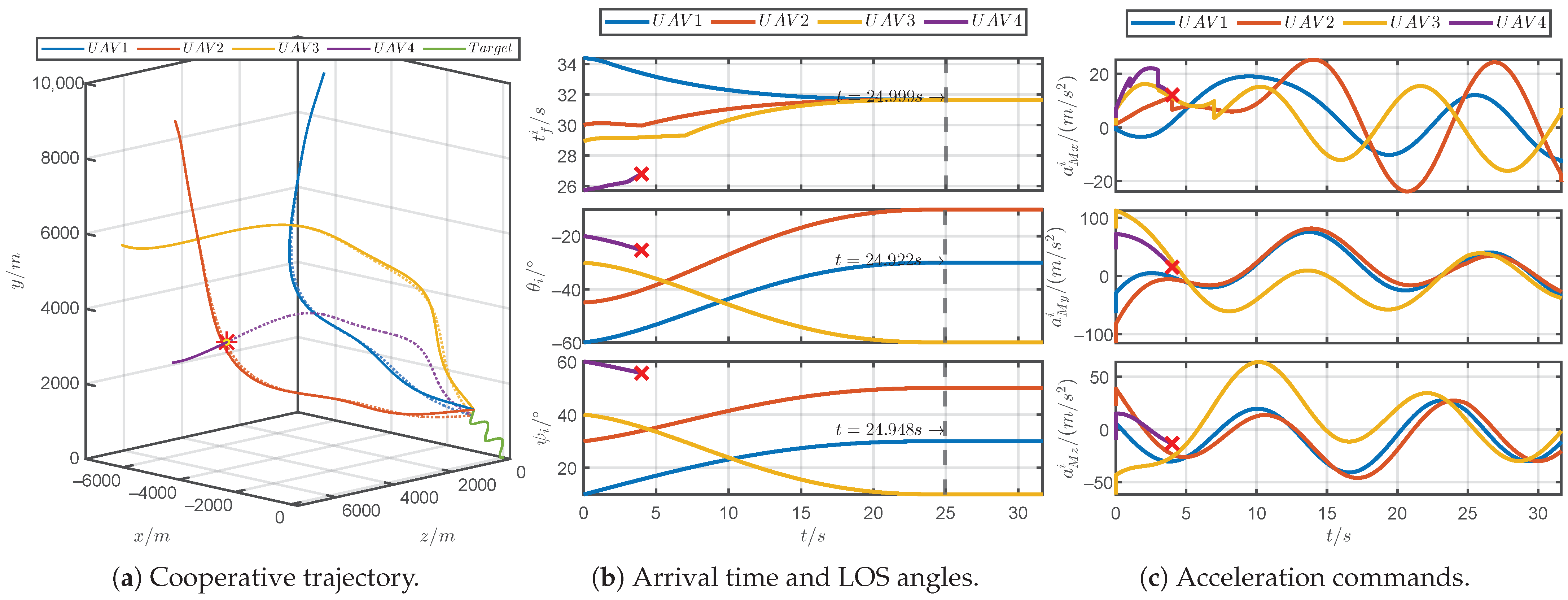
5.3. Simulations for Robustness Verification
5.4. Simulations for Comparative Verification
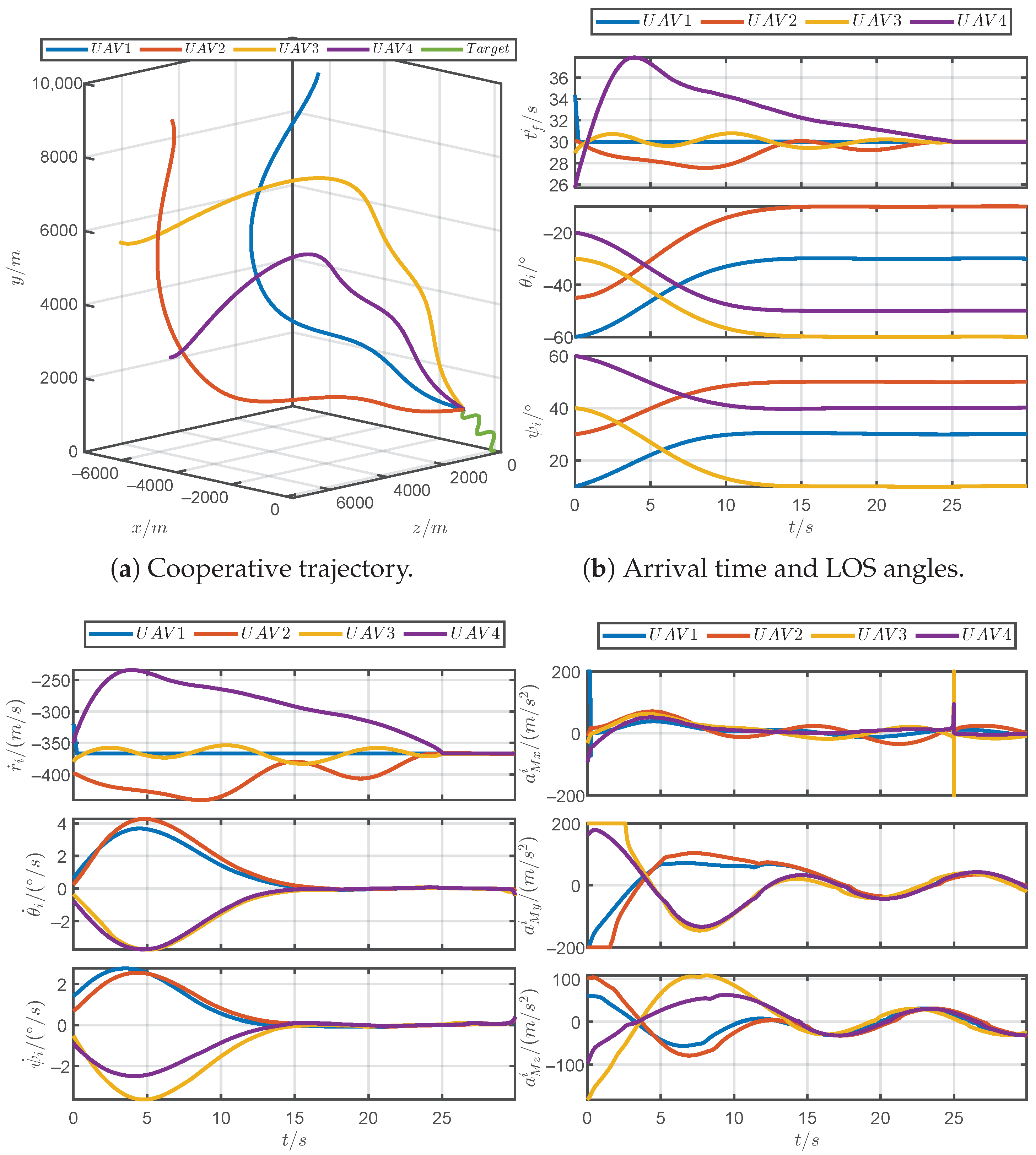
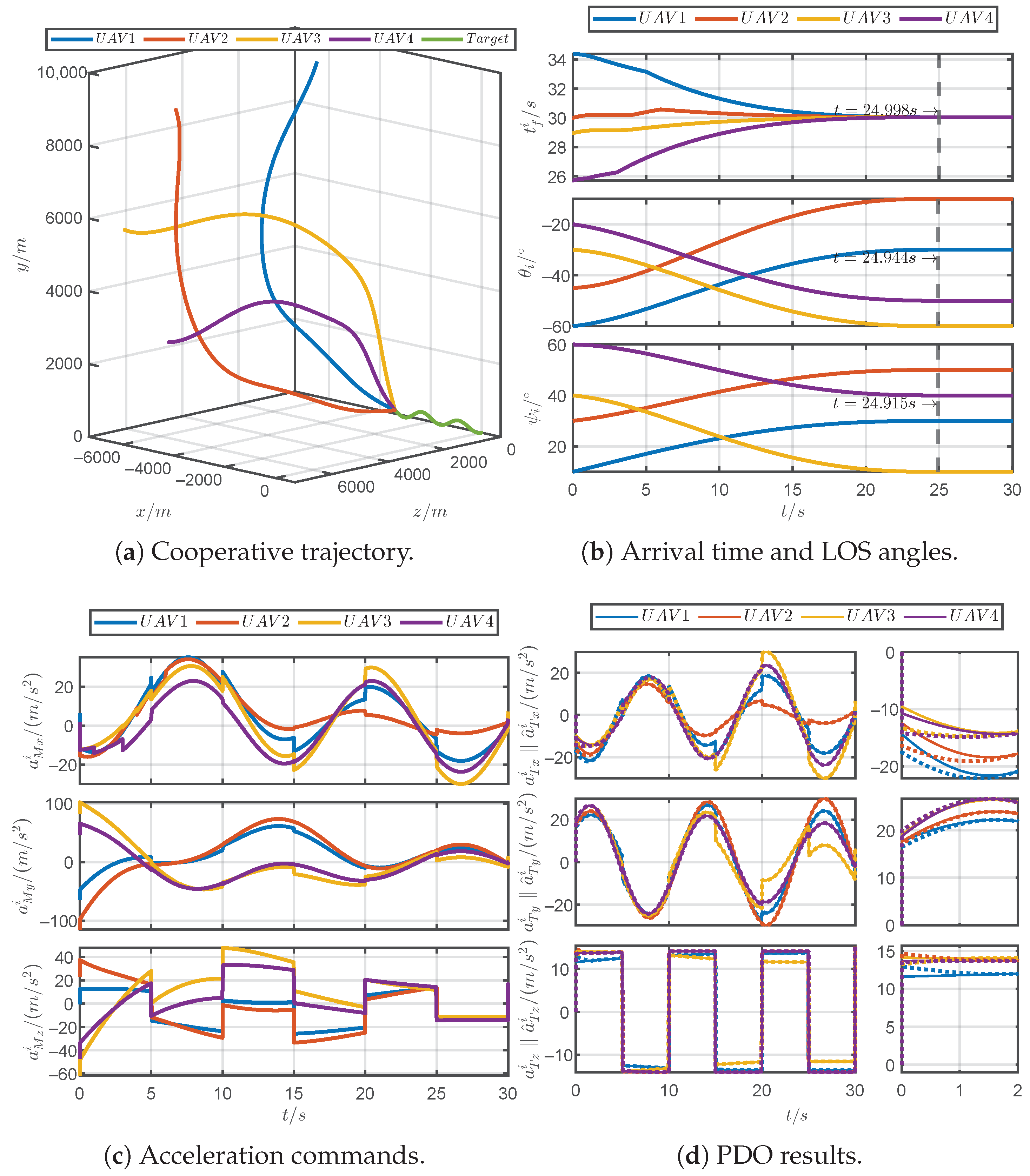
5.5. Simulations for Unpredictable Maneuvering Target
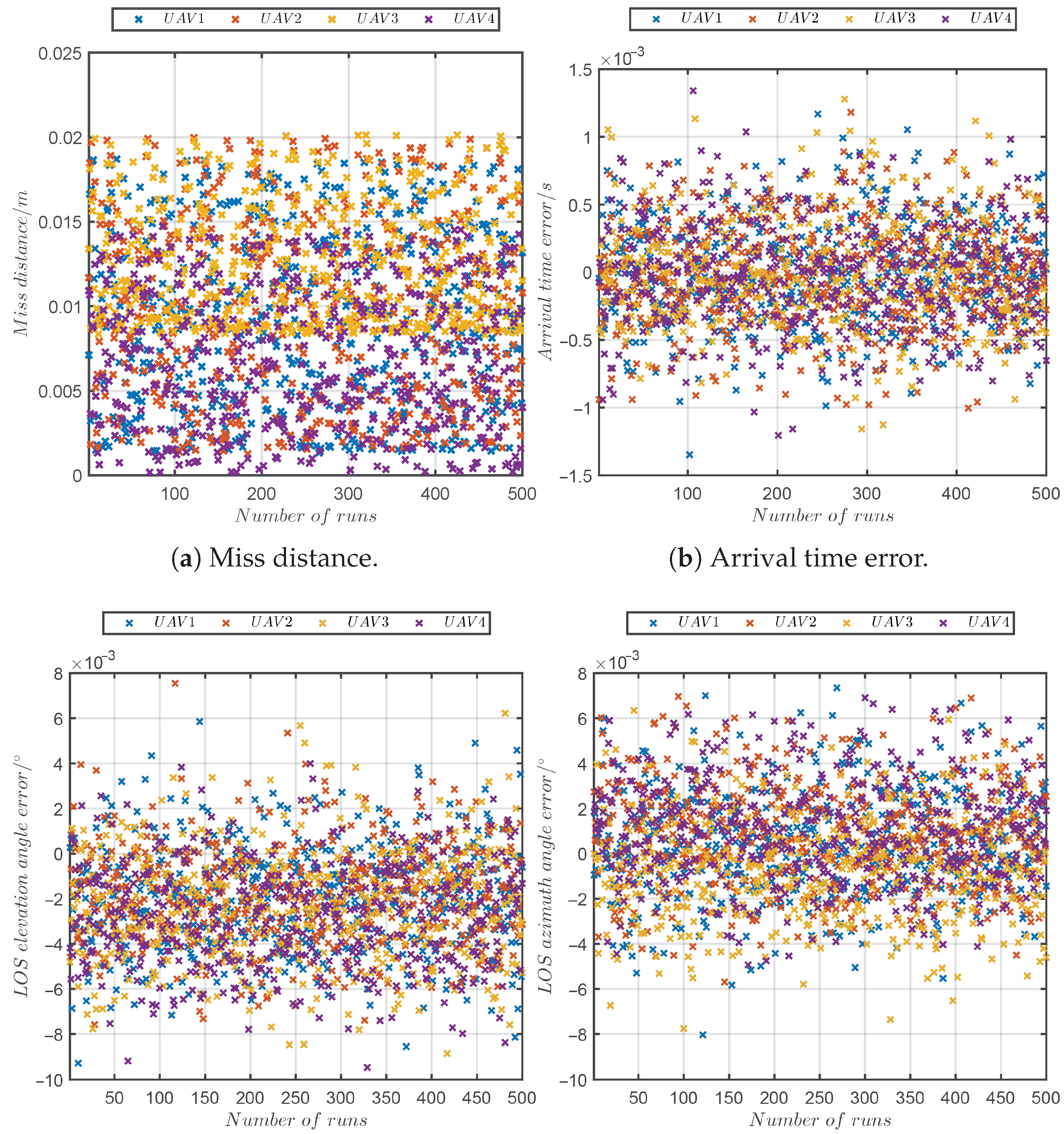
5.6. Monte Carlo Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned aerial vehicle |
| PDO | Prescribed-time disturbance observer |
| PRCG | Prescribed-time robust cooperative guidance |
| DCHO | Distributed convex hull observer |
| LOS | Line-of-sight |
References
- Zhan, Y.A.; Li, S.Y.; Zhou, D. Information Fusion-Based Three-Dimensional Two-Stage Optimal Cooperative Predictive Guidance Law. Aerosp. Sci. Technol. 2024, 155, 109533. [Google Scholar] [CrossRef]
- Wang, C.Y.; Yu, H.S.; Dong, W.; Wang, J.N. Three-Dimensional Impact Angle and Time Control Guidance Law Based on Two-Stage Strategy. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5361–5372. [Google Scholar] [CrossRef]
- Lee, J.I.; Jeon, I.S.; Tahk, M.J. Guidance Law to Control Impact Time and Angle. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 301–310. [Google Scholar]
- Liu, Z.Y.; Lei, G.; Xian, Y.; Ren, L.L.; Li, S.P.; Zhang, D.Q. Adaptive Impact-Time-Control Cooperative Guidance Law for UAVs under Time-Varying Velocity Based on Reinforcement Learning. Drones 2025, 9, 262. [Google Scholar] [CrossRef]
- Dong, W.; Wang, C.Y.; Liu, J.H.; Wang, J.N.; Xin, M. Three-Dimensional Vector Guidance Law with Impact Time and Angle Constraints. J. Frankl. Inst. 2023, 360, 693–718. [Google Scholar] [CrossRef]
- Dong, W.; Deng, F.; Wang, C.Y.; Wang, J.N.; Xin, M. Three-Dimensional Spatial-Temporal Cooperative Guidance without Active Speed Control. J. Guid. Control. Dyn. 2023, 46, 1981–1996. [Google Scholar] [CrossRef]
- Li, G.F.; Zuo, Z.Y. Robust Leader-Follower Cooperative Guidance under False-Data Injection Attacks. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4511–4524. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wang, W.L.; Dong, W.; Wang, J.N.; Deng, F. Multiple-Stage Spatial-Temporal Cooperative Guidance without Time-to-Go Estimation. Chin. J. Aeronaut. 2024, 37, S1000936124001900. [Google Scholar] [CrossRef]
- Liu, T.; Chen, Y.Y.; Li, S. Adaptive Cooperative Estimation and Guidance against Unknown Maneuvering Target. IEEE Trans. Aerosp. Electron. Syst. 2025, 1–12, early access. [Google Scholar] [CrossRef]
- Cheng, M.; Liu, H.; Xi, J.X.; Zheng, Y.S. Data-Driven Robust Optimal Guidance with Input Saturation via Differential Graphical Game Strategy for Cooperative Aerial Vehicles. IEEE Trans. Intell. Transp. Syst. 2025, 26, 8612–8621. [Google Scholar] [CrossRef]
- Li, G.F.; Tang, Q.P.; Zuo, Z.Y.; Wu, Y.J.; Lü, J.H. Resilient Cooperative Guidance for Leader-Follower Flight Vehicles against Maneuvering Target. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 6310–6324. [Google Scholar] [CrossRef]
- Jiang, Z.J.; Yang, X.X.; Wang, C.; Zhang, Y.; Yu, H. A DMPC-based Three-Dimensional Cooperative Guidance Scheme with Impact Time and Impact Angle Constraints. Meas. Control 2024, 26, 202940241269591. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y.; Liu, Z.G.; Wang, S.C.; Hu, X.X. Finite-Time Cooperative Guidance Strategy for Impact Angle and Time Control. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 806–819. [Google Scholar] [CrossRef]
- Zhan, Y.A.; Li, S.Y.; Zhou, D. Time-to-Go Based Three-Dimensional Multi-Missile Spatio-Temporal Cooperative Guidance Law: A Novel Approach for Maneuvering Target Interception. ISA Trans. 2024, 149, 178–195. [Google Scholar] [CrossRef] [PubMed]
- You, H.; Chang, X.L.; Zhao, J.F.; Wang, S.H.; Zhang, Y.H. Three-Dimensional Impact-Angle-Constrained Cooperative Guidance Strategy against Maneuvering Target. ISA Trans. 2023, 138, 262–280. [Google Scholar] [CrossRef]
- Yu, H.; Dai, K.R.; Li, H.J.; Zou, Y.; Ma, X.; Ma, S.J.; Zhang, H. Three-Dimensional Adaptive Fixed-Time Cooperative Guidance Law with Impact Time and Angle Constraints. Aerosp. Sci. Technol. 2022, 123, 107450. [Google Scholar] [CrossRef]
- You, H.; Chang, X.L.; Zhao, J.F.; Wang, S.H.; Zhang, Y.H. Three-Dimensional Impact-Angle-Constrained Fixed-Time Cooperative Guidance Algorithm with Adjustable Impact Time. Aerosp. Sci. Technol. 2023, 141, 108574. [Google Scholar] [CrossRef]
- Dong, W.; Wang, C.Y.; Wang, J.N.; Zuo, Z.Y.; Shan, J.Y. Fixed-Time Terminal Angle-Constrained Cooperative Guidance Law against Maneuvering Target. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1352–1366. [Google Scholar] [CrossRef]
- Shi, P.F.; Yu, J.L.; Dong, X.W.; Li, Q.D.; Ren, Z. Distributed Adaptive Cooperative Guidance Intercepting Maneuvering Targets with Actuator Faults. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 5556–5570. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Sinha, A.; Kumar, S.R. Cooperative Target Capture Using Predefined-Time Consensus over Fixed and Switching Networks. Aerosp. Sci. Technol. 2022, 127, 107686. [Google Scholar] [CrossRef]
- Chi, H.H.; Ding, X.H.; Zhang, G.L. Three-dimensional cooperative guidance law for multiple missiles with predefined-time convergence. J. Astronaut. 2023, 44, 1238–1250. [Google Scholar]
- Chang, Y.N.; Wang, X.Z.; Li, G.F. Prescribed-time convergent cooperative guidance method with impact time and angle constraints. J. Beijing Univ. Aeronaut. Astronaut. 2024, 1–14, early access. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, H.; Dai, K.; Yi, W.; Zhang, H.; Guan, J.; Yuan, S. Three-Dimensional Event-Triggered Predefined-Time Cooperative Guidance Law. Aerospace 2024, 11, 999. [Google Scholar] [CrossRef]
- Jimenez-Rodriguez, E.; Munoz-Vazquez, A.J.; Sanchez-Torres, J.D.; Defoort, M.; Loukianov, A.G. A Lyapunov-like Characterization of Predefined-Time Stability. IEEE Trans. Autom. Control 2020, 65, 4922–4927. [Google Scholar] [CrossRef]
- Ning, B.D.; Han, Q.L.; Zuo, Z.Y.; Ding, L.; Lu, Q.; Ge, X.H. Fixed-Time and Prescribed-Time Consensus Control of Multiagent Systems and Its Applications: A Survey of Recent Trends and Methodologies. IEEE Trans. Ind. Inform. 2023, 19, 1121–1135. [Google Scholar] [CrossRef]
- Song, Y.D.; Wang, Y.J.; Holloway, J.; Krstic, M. Time-Varying Feedback for Regulation of Normal-Form Nonlinear Systems in Prescribed Finite Time. Automatica 2017, 83, 243–251. [Google Scholar] [CrossRef]
- Ma, W.H.; Fang, Y.W.; Fu, W.X.; Liang, X.G. Three-Dimensional Prescribed-Time Impulsive Pinning Cooperative Guidance. Int. J. Aeronaut. Space Sci. 2023, 24, 1375–1388. [Google Scholar] [CrossRef]
- Tang, J.C.; Zuo, Z.Y. Cooperative Circular Guidance of Multiple Missiles: A Practical Prescribed-Time Consensus Approach. J. Guid. Control. Dyn. 2023, 46, 1799–1813. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, S.J.; Guo, J. Two-Stage Cooperative Guidance Strategy Using a Prescribed-Time Optimal Consensus Method. Aerosp. Sci. Technol. 2020, 100, 105641. [Google Scholar] [CrossRef]
- Luo, D.H.; Wang, Y.J.; Song, Y.D. Practical Prescribed Time Tracking Control with Bounded Time-Varying Gain under Non-Vanishing Uncertainties. IEEE/CAA J. Autom. Sin. 2024, 11, 219–230. [Google Scholar] [CrossRef]
- Song, Y.D.; Ye, H.F.; Lewis, F.L. Prescribed-Time Control and Its Latest Developments. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4102–4116. [Google Scholar] [CrossRef]
- Wang, X.; Cai, Y.L.; Deng, Y.F.; Jiang, H.N. Predefined-Time Spatial-Temporal Cooperative Guidance Law with Leader-Follower Strategy. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 6053–6069. [Google Scholar] [CrossRef]
- Wang, Z.K.; Fang, Y.W.; Fu, W.X.; Ma, W.H.; Wang, M.G. Prescribed-Time Cooperative Guidance Law against Manoeuvring Target with Input Saturation. Int. J. Control 2023, 96, 1177–1189. [Google Scholar] [CrossRef]
- Wang, Z.K.; Fu, W.X.; Fang, Y.W.; Zhu, S.P.; Wu, Z.H.; Wang, M.G. Prescribed-Time Cooperative Guidance Law against Maneuvering Target Based on Leader-Following Strategy. ISA Trans. 2022, 129, 257–270. [Google Scholar] [CrossRef]
- Zhang, L.; Li, D.Y.; Jing, L.; Ju, X.Z.; Cui, N.G. Appointed-Time Cooperative Guidance Law with Line-of-Sight Angle Constraint and Time-to-Go Control. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3142–3155. [Google Scholar] [CrossRef]
- Holloway, J.; Krstic, M. Prescribed-Time Observers for Linear Systems in Observer Canonical Form. IEEE Trans. Autom. Control 2019, 64, 3905–3912. [Google Scholar] [CrossRef]
- Ma, W.H.; Guo, X.W. Prescribed-Time Cooperative Guidance Law for Multi-UAV with Intermittent Communication. Drones 2024, 8, 748. [Google Scholar] [CrossRef]
- Li, Z.H.; Ding, Z.T. Robust Cooperative Guidance Law for Simultaneous Arrival. IEEE Trans. Control Syst. Technol. 2019, 27, 1360–1367. [Google Scholar] [CrossRef]
- Wang, C.Y.; Ding, X.J.; Wang, J.N.; Shan, J.Y. A Robust Three-Dimensional Cooperative Guidance Law against Maneuvering Target. J. Frankl. Inst. 2020, 357, 5735–5752. [Google Scholar] [CrossRef]
- Filippov, A.F. Differential Equations with Discontinuous Righthand Sides; Mathematics and Its Applications; Springer: Dordrecht, The Netherlands, 1988; Volume 18. [Google Scholar]
- Li, C.; Qu, Z. Distributed Finite-Time Consensus of Nonlinear Systems under Switching Topologies. Automatica 2014, 50, 1626–1631. [Google Scholar] [CrossRef]


| UAV | UAV 1 | UAV 2 | UAV 3 | UAV 4 |
|---|---|---|---|---|
| 11,000 | 12,000 | 11,000 | 9000 | |
| −320 | −400 | −380 | −350 | |
| −60 | −45 | −30 | −20 | |
| 0.630 | 0.246 | −0.355 | −0.779 | |
| −30 | −10 | −60 | −50 | |
| 10 | 30 | 40 | 60 | |
| 1.404 | 0.670 | −0.521 | −0.882 | |
| 30 | 50 | 10 | 40 |
| Indicators | PTCG Law | ATCG Law | Ours |
|---|---|---|---|
| Missing distance (m) | |||
| Arrival time error (s) | |||
| Elevation angle error | |||
| Azimuth angle error | |||
| Energy consumption |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, M.; Wang, L.; Xi, J.; Wang, C.; Luo, S. Bounded-Gain Prescribed-Time Robust Spatiotemporal Cooperative Guidance Law for UAVs Under Jointly Strongly Connected Topologies. Drones 2025, 9, 474. https://doi.org/10.3390/drones9070474
Qin M, Wang L, Xi J, Wang C, Luo S. Bounded-Gain Prescribed-Time Robust Spatiotemporal Cooperative Guidance Law for UAVs Under Jointly Strongly Connected Topologies. Drones. 2025; 9(7):474. https://doi.org/10.3390/drones9070474
Chicago/Turabian StyleQin, Mingxing, Le Wang, Jianxiang Xi, Cheng Wang, and Shaojie Luo. 2025. "Bounded-Gain Prescribed-Time Robust Spatiotemporal Cooperative Guidance Law for UAVs Under Jointly Strongly Connected Topologies" Drones 9, no. 7: 474. https://doi.org/10.3390/drones9070474
APA StyleQin, M., Wang, L., Xi, J., Wang, C., & Luo, S. (2025). Bounded-Gain Prescribed-Time Robust Spatiotemporal Cooperative Guidance Law for UAVs Under Jointly Strongly Connected Topologies. Drones, 9(7), 474. https://doi.org/10.3390/drones9070474






