Positioning Error Analysis of Distributed Random Array Based on Unmanned Aerial Vehicles in Collaborative Jamming
Abstract
1. Introduction
- A calculation method for the jamming gain is proposed based on the pattern multiplication theorem and radiation intensity, further researching the power propagation in the target area, no longer limited to the characteristics of the beam itself.
- The target azimuth JSR and effective jamming range are defined as performance evaluation parameters based on collaborative jamming scenarios, which are more matched with jamming scenarios compared to analyzing the half-power beamwidth (HPBW) and power of the array’s main lobe.
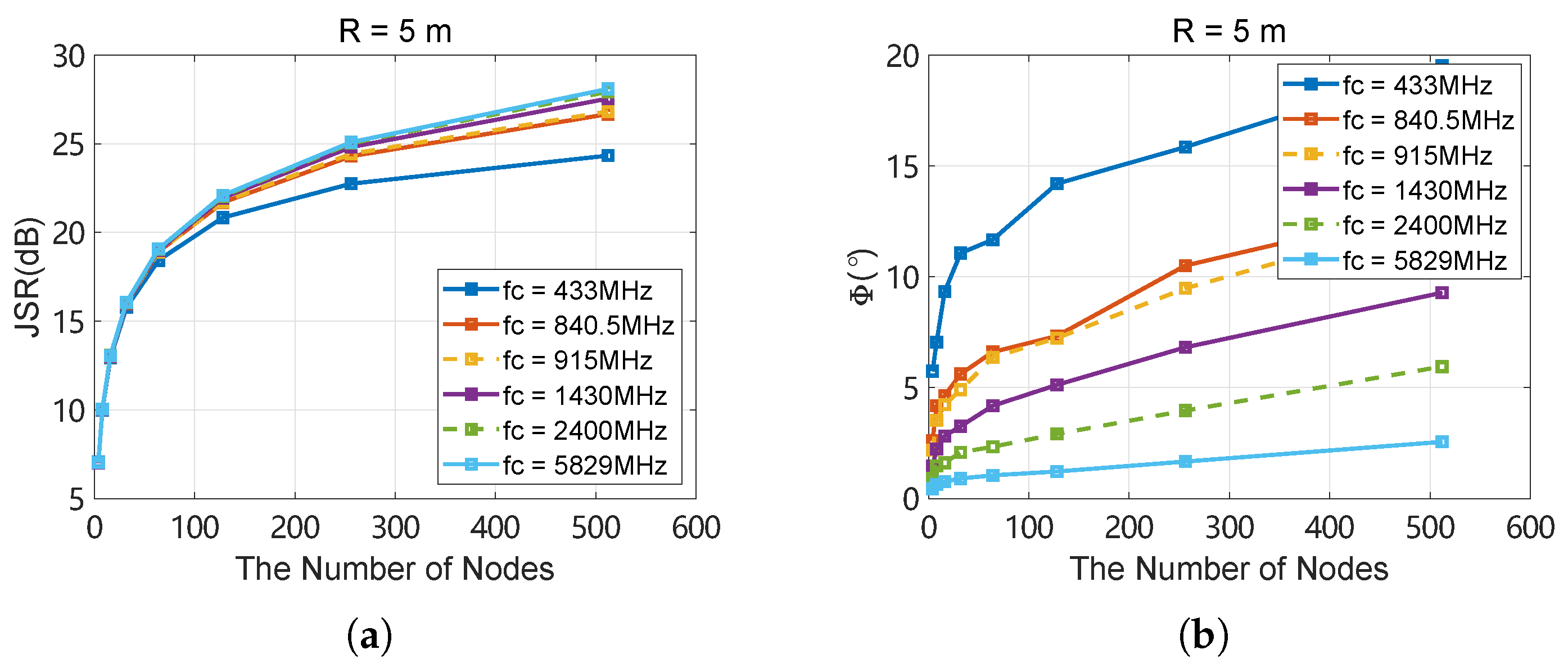
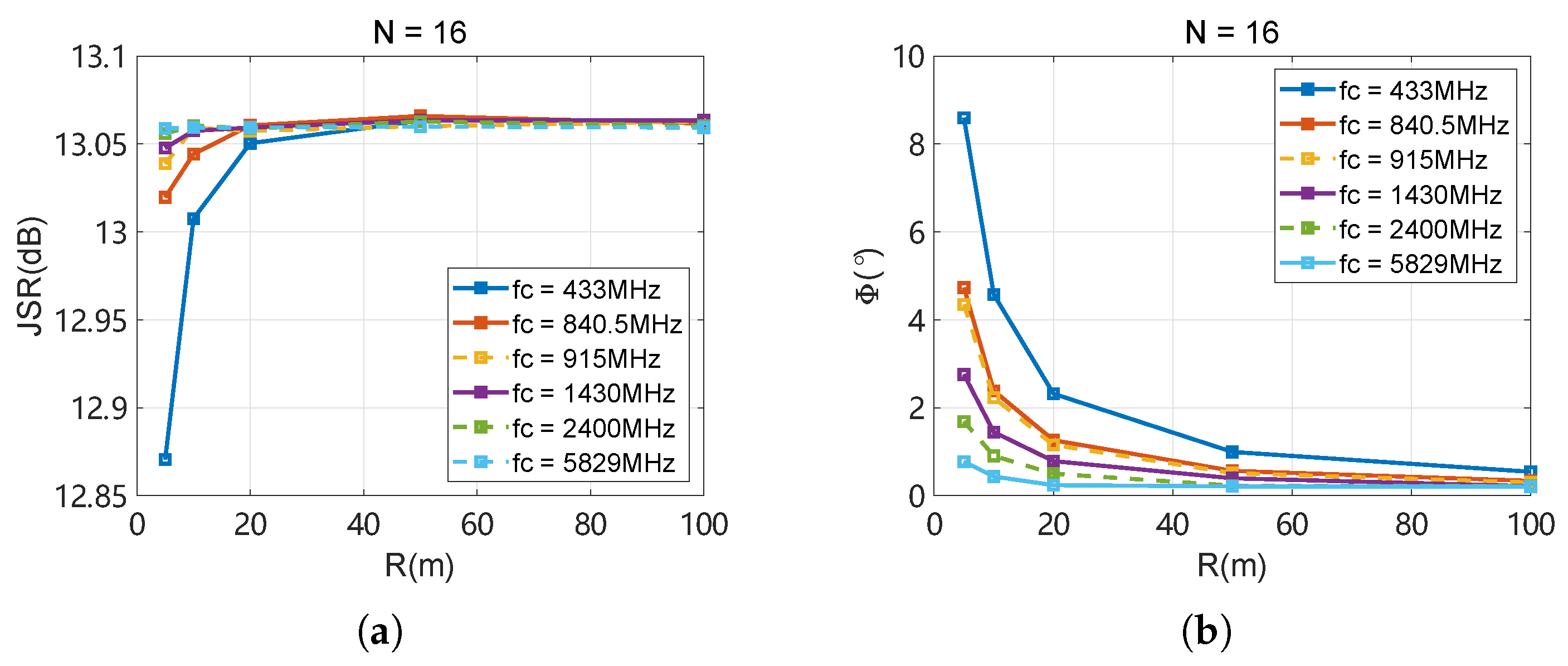
- The trend of JSR and effective range changes at different jamming frequencies is simulated under various distribution radii and numbers of nodes.
- The upper bounds of azimuth and distance errors are provided in multiple collaborative jamming scenarios where the effective jamming probability reaches 90%.
- The inter-relationship between azimuth and distance errors is analyzed under different effective jamming probabilities, providing a reference for rationally selecting the number of nodes and deploying swarms.
2. The Far-Field Condition
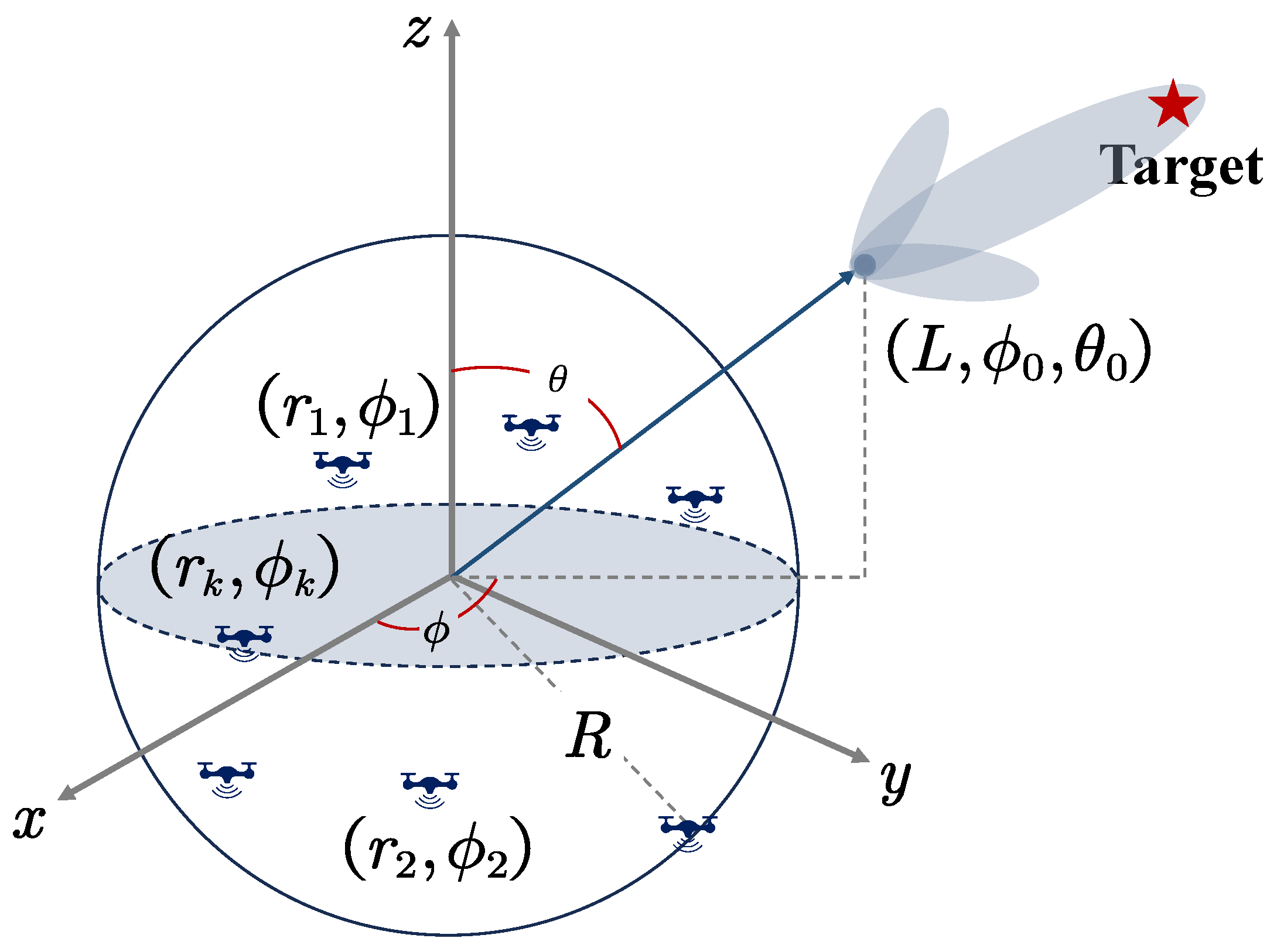
3. Collaborative Jamming Model
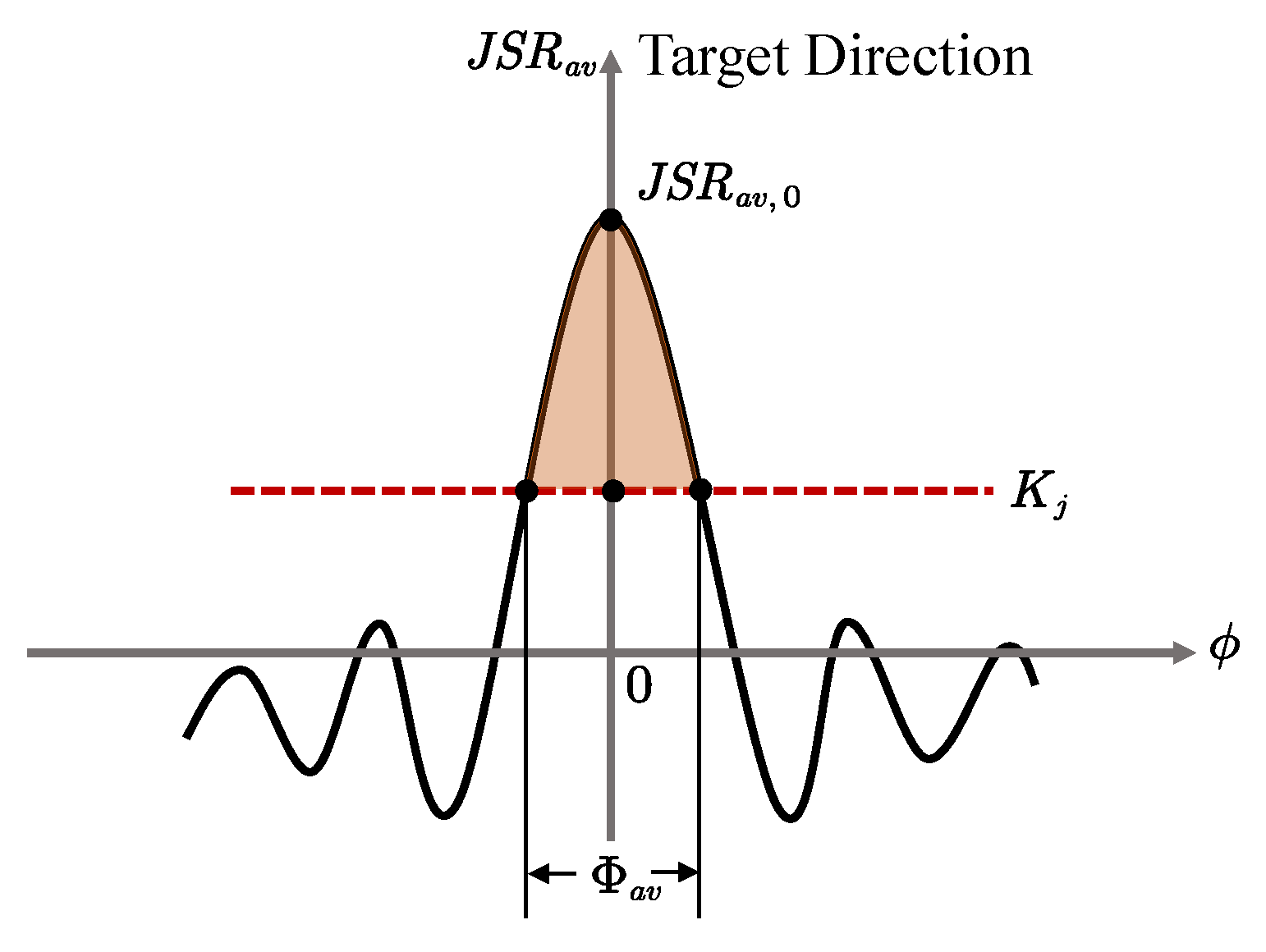
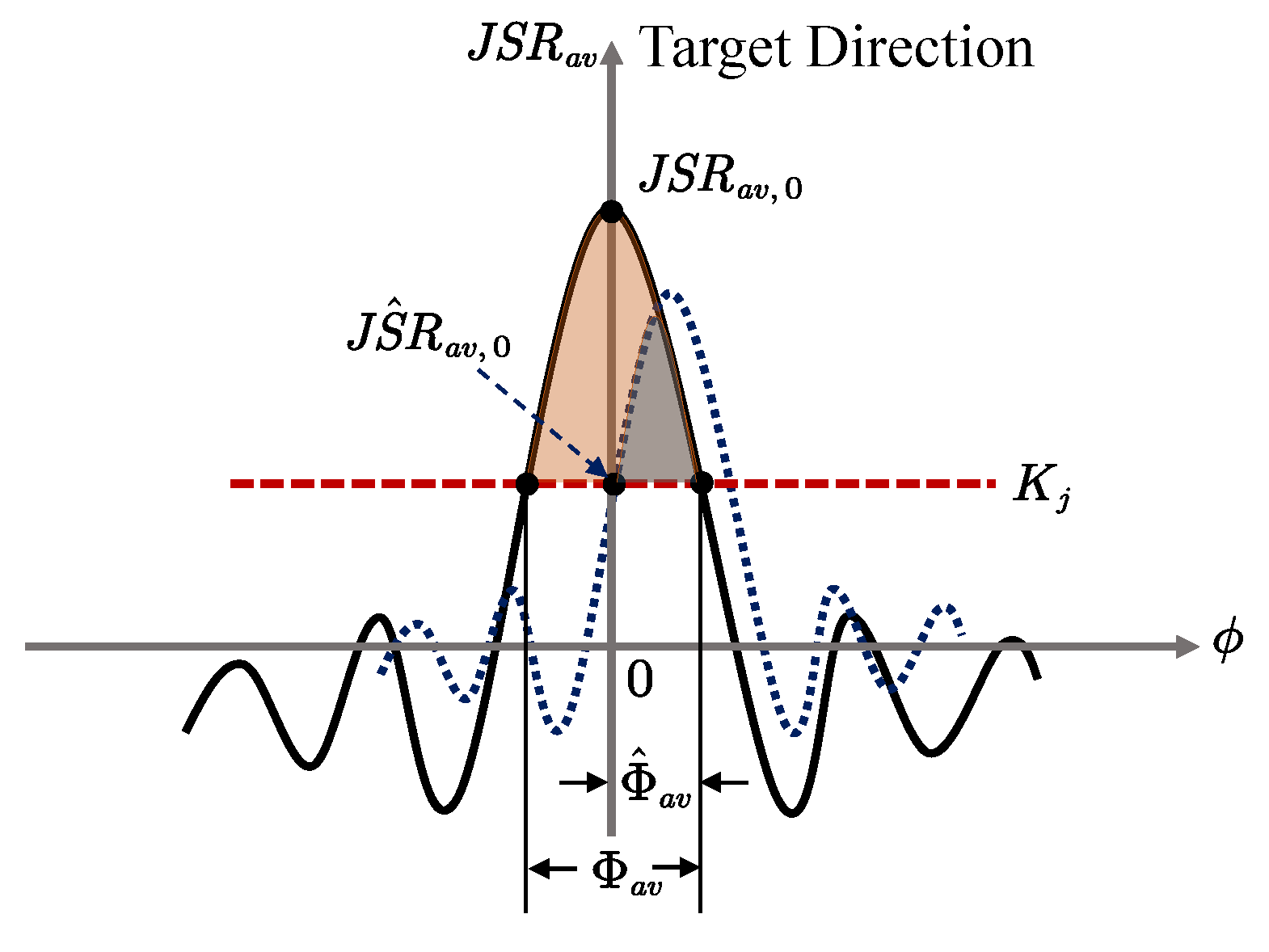
4. Jamming Effectiveness Evaluation
4.1. Ideal Jamming Effectiveness
4.2. Imperfect Jamming Effectiveness
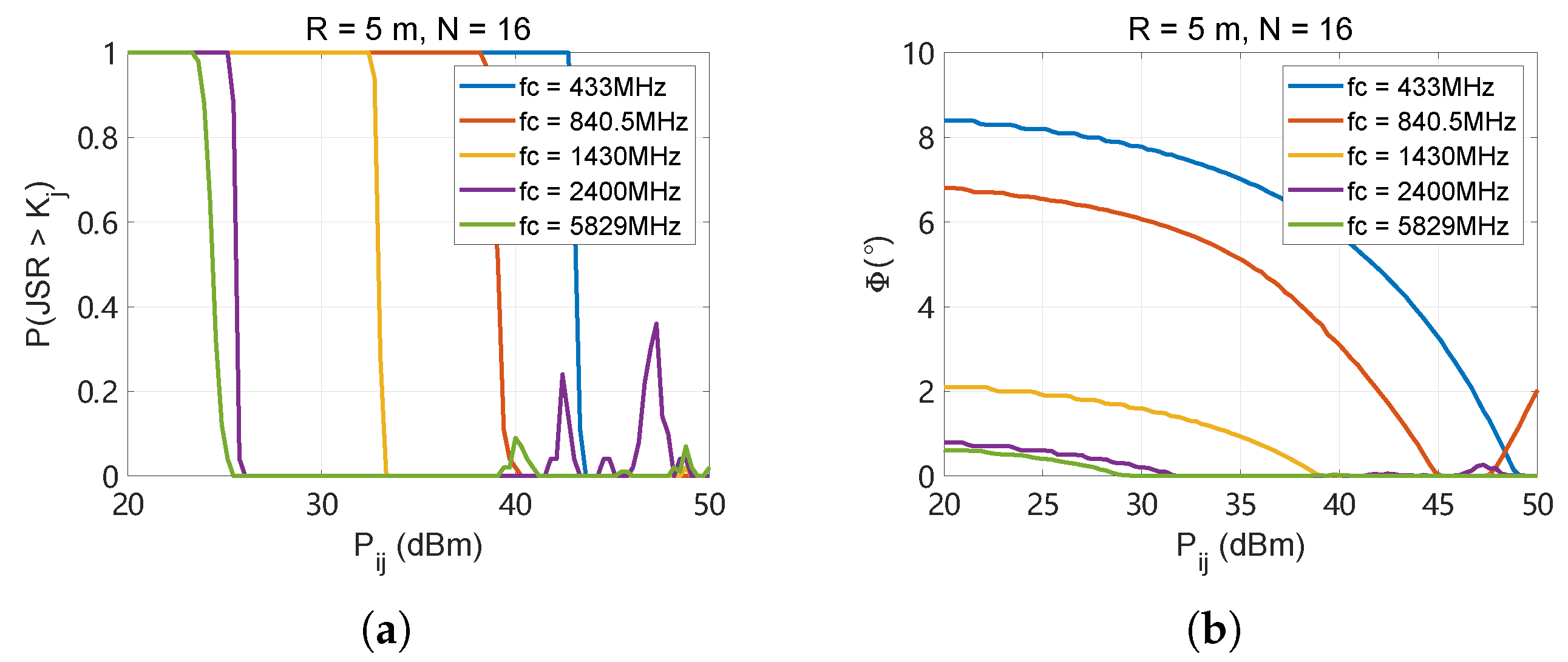
4.2.1. Jamming Performance with Azimuth Error
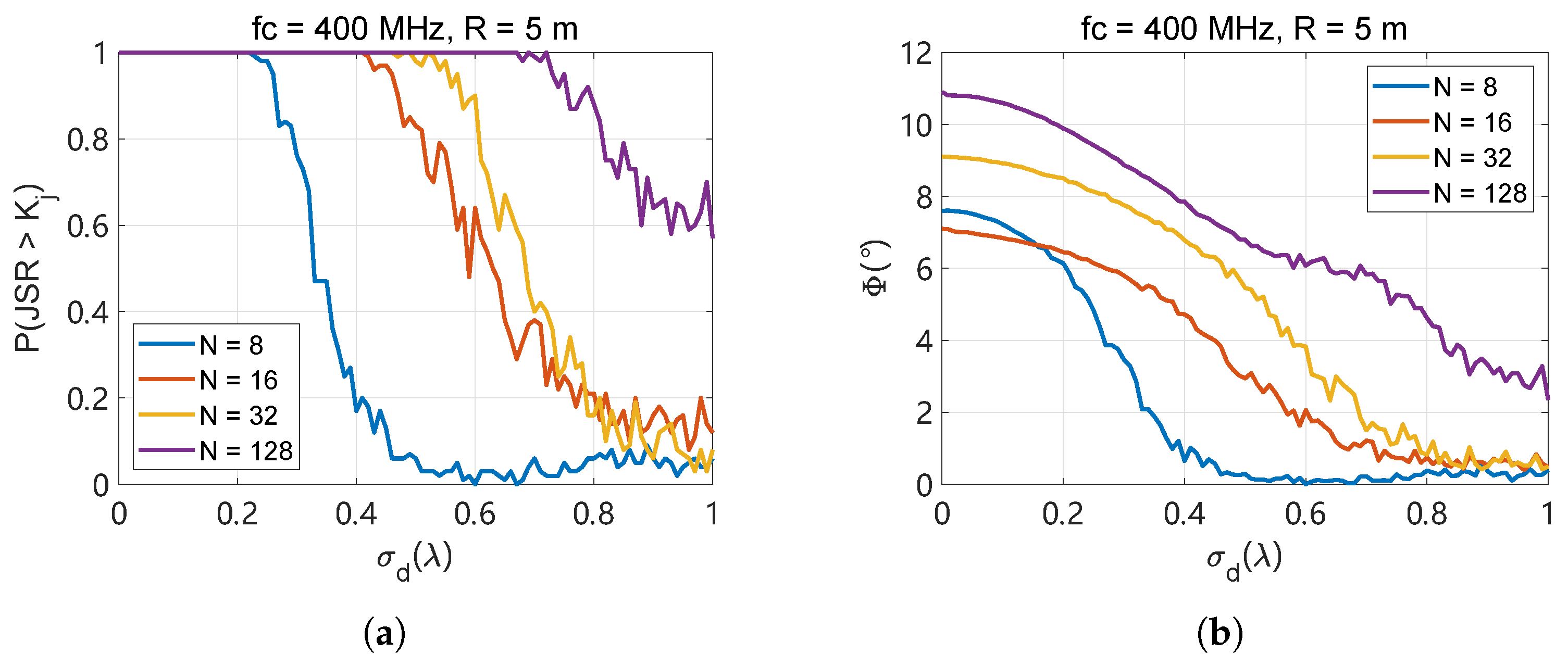
4.2.2. Jamming Performance with Distance Error
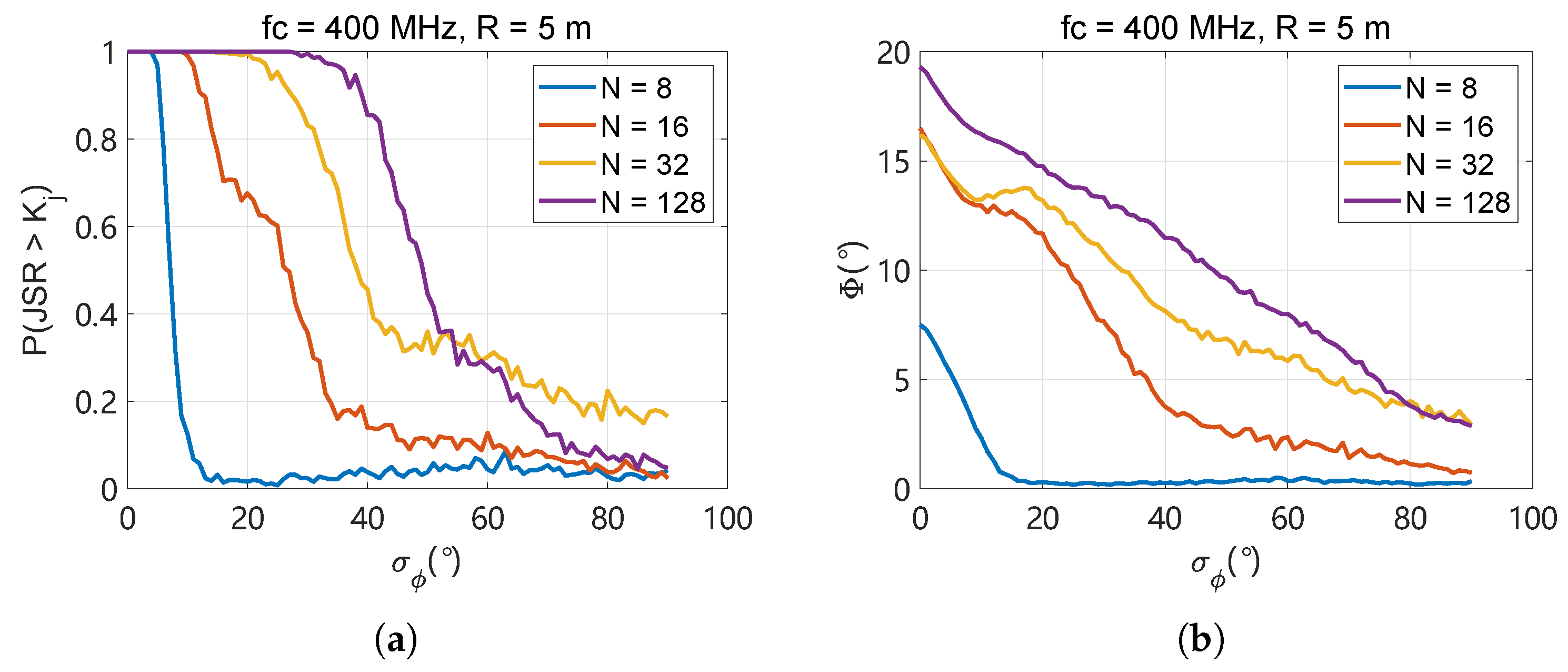
4.2.3. Joint Analysis of Positioning Errors
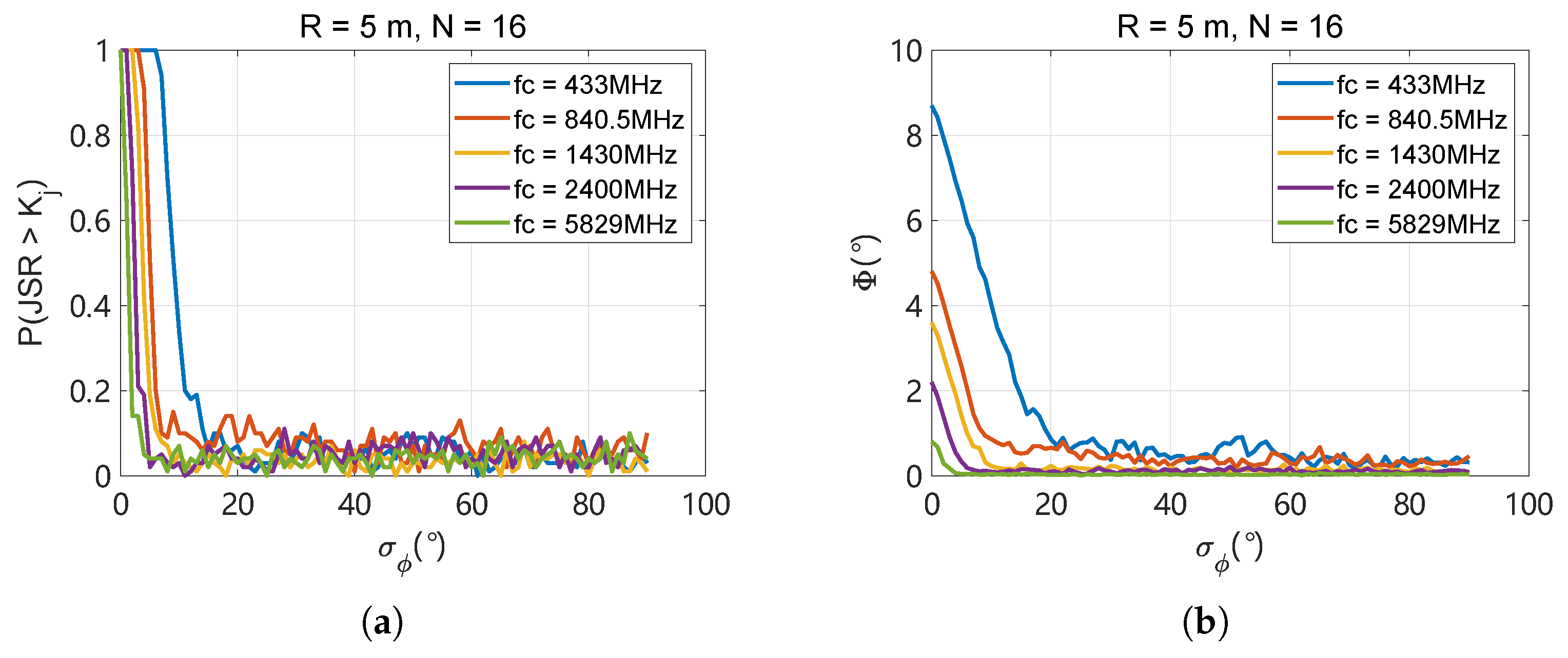
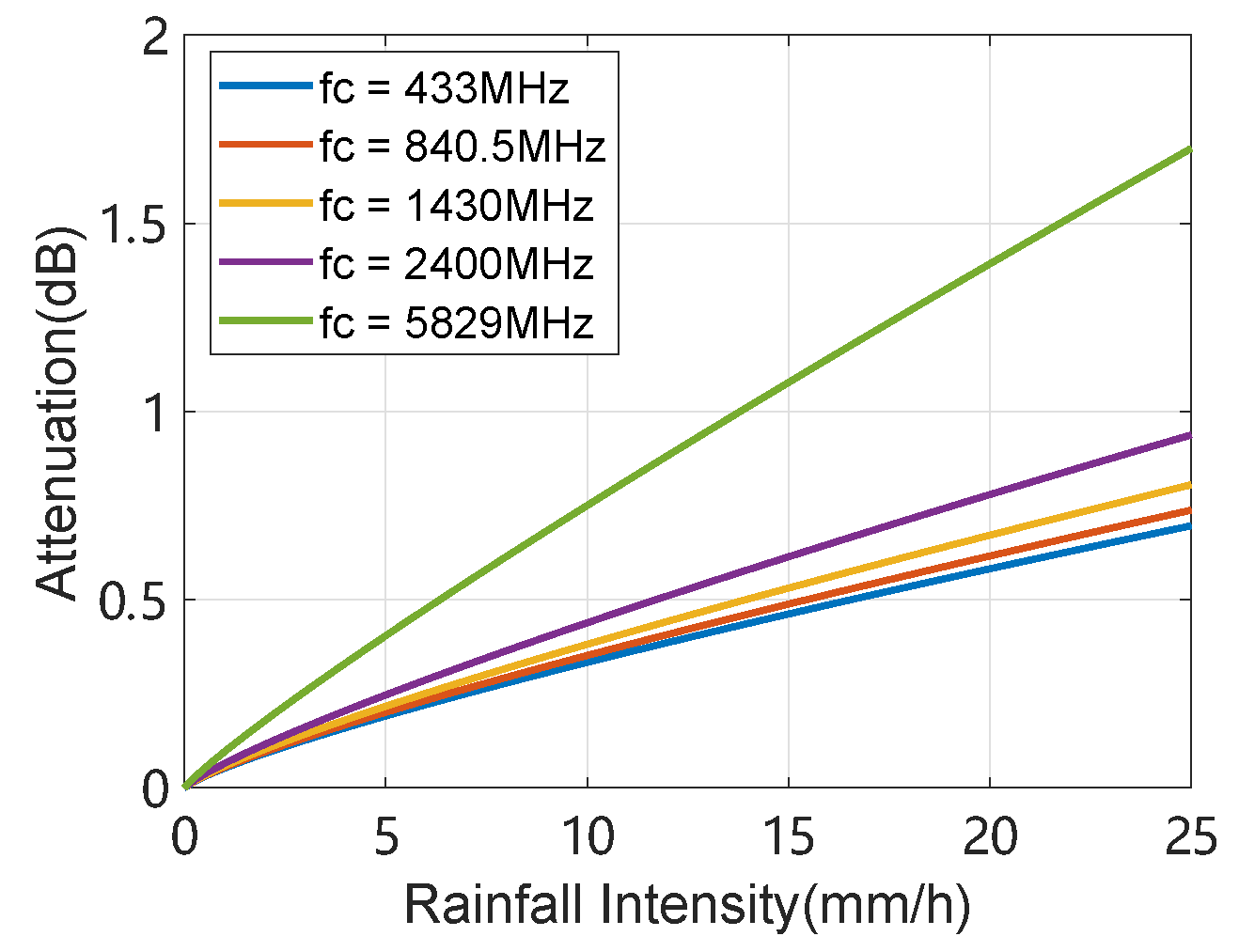
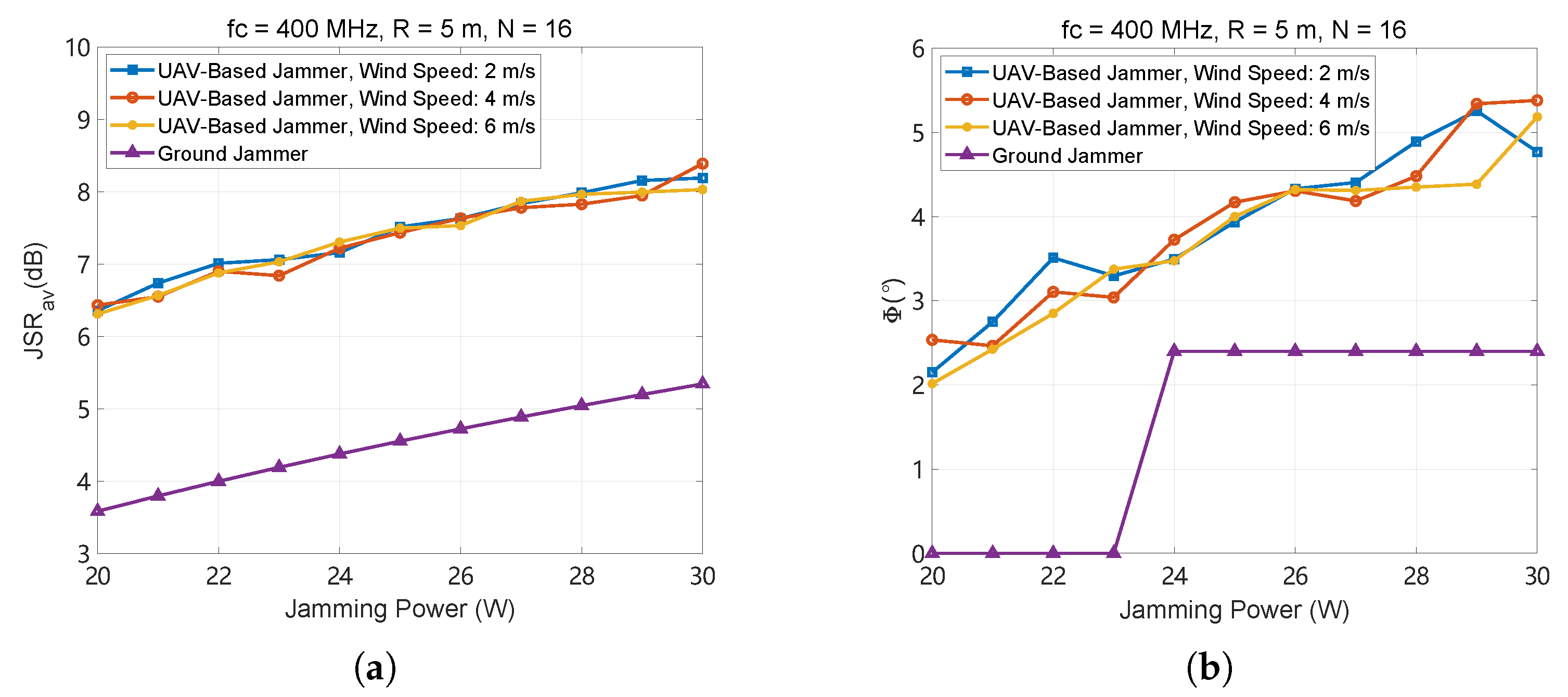
4.2.4. Jamming Performance in Different Environments
- (1)
- Wind speed
- (2)
- Rainfall intensity
- (3)
- External source of interference
5. Comprehensive Experiment
5.1. Simulation-Based Jamming Analysis in Realistic Scenarios
5.2. Comparison with Ground-Based Systems
6. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
Appendix A. Proof of Equation (24)
Appendix B. Proof of Equation (26)
References
- Moseley, R.H. A Neural Network Classifier for Fault Correlation and Root Cause Determination in an Electronic Warfare System. In Proceedings of the AIAA SciTech Forum and Exposition, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Jung, S. A Study on the Application of Artificial Intelligence for Naval Electronic Warfare. J. KNST 2020, 3, 118–124. [Google Scholar] [CrossRef]
- Li, X.; Zhao, X.; Pu, W. An approach for predicting digital material consumption in electronic warfare. Def. Technol. 2020, 16, 263–273. [Google Scholar] [CrossRef]
- Rahman, A.D.B.A.; Ghani, K.A.; Khamis, N.H.H.; Sidek, A.R.M. Unmanned Aerial Vehicle (UAV) GPS Jamming Test by using Software Defined Radio (SDR) platform. J. Phys. Conf. Ser. 2021, 1793, 012060. [Google Scholar]
- Gao, Y.; Lv, N. UAV Swarm Cooperative Situation Awareness Theory Model Construction and Scenario Analysis. J. Phys. Conf. Ser. 2023, 2504, 012013. [Google Scholar]
- Zhou, Y.; Rao, B.; Wang, W. UAV Swarm Intelligence: Recent Advances and Future Trends. IEEE Access 2020, 8, 183856–183878. [Google Scholar] [CrossRef]
- Long, X.X.; Gao, F. Cooperative attack based on small-unit UAV swarms formation with trajectory tracking. J. Intell. Fuzzy Syst. 2023, 45, 2949–2965. [Google Scholar]
- Javed, S.; Hassan, A.; Ahmad, R.; Ahmed, W.; Ahmed, R.; Saadat, A.; Guizani, M. State-of-the-Art and Future Research Challenges in UAV Swarms. IEEE Internet Things J. 2024, 11, 19023–19045. [Google Scholar] [CrossRef]
- Xu, X.; Yan, X.; Yang, W.; An, K.; Huang, W.; Wang, Y. Algorithms and applications of intelligent swarm cooperative control: A comprehensive survey. Prog. Aerosp. Sci. 2022, 135, 100869. [Google Scholar] [CrossRef]
- Abdelkader, M.; Guler, S.; Jaleel, H.; Shamma, J. Aerial Swarms: Recent Applications and Challenges. Curr. Robot. Rep. 2021, 2, 309–320. [Google Scholar] [CrossRef]
- Paulsen, L.; Hoffmann, T.; Fulton, C.; Yeary, M.; Murmann, B. Impact: A low cost, reconfigurable, digital beamforming common module building block for next generation phased arrays. In Proceedings of the Open Architecture/Open Business Model Net-Centric Systems and Defense Transformation 2015, Tysons Corner, VA, USA, 13–16 April 2015. [Google Scholar]
- Zhang, Y.; Cheng, R. Joint trajectory and power design for UAV-enabled cooperative jamming in two-way secure communication. Telecommun. Syst. Model. Anal. Des. Manag. 2023, 82, 487–498. [Google Scholar]
- Li, A.; Wu, Q.; Zhang, R. UAV-Enabled Cooperative Jamming for Improving Secrecy of Ground Wiretap Channel. IEEE Wirel. Commun. Lett. 2019, 8, 181–184. [Google Scholar] [CrossRef]
- Wu, Y.; Guan, X.; Yang, W.; Wu, Q. UAV Swarm Communication Under Malicious Jamming: Joint Trajectory and Clustering Design. IEEE Wirel. Commun. Lett. 2021, 10, 2264–2268. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Nanzer, J.A. Multiobjective Distributed Beamforming Using High-Accuracy Synchronization and Localization. IEEE Trans. Microw. Theory Tech. 2024; early access. [Google Scholar] [CrossRef]
- Deng, L.; Wu, C.; Jiang, H.; Xiao, H.; Luo, Y.; Zhang, Q.; Ye, C. Completion Time Minimization for Multiantenna UAV-Enabled Multicasting With Rank-Two Multicast Beamforming. IEEE Internet Things J. 2024, 11, 19549–19563. [Google Scholar] [CrossRef]
- Mittal, A.; Xu, Z.; Du, K.; Kumar, S.S.; Shrivastava, A. An Ultralow-Power Closed-Loop Distributed Beamforming Technique for Efficient Wireless Power Transfer. IEEE Internet Things J. 2024, 11, 31301–31316. [Google Scholar] [CrossRef]
- Hussain, K.; Oh, I.Y. Joint Radar, Communication, and Integration of Beamforming Technology. Electronics 2024, 13, 1531. [Google Scholar] [CrossRef]
- Mghabghab, S.R.; Nanzer, J.A. Impact of Localization Error on Open-Loop Distributed Beamforming Arrays. In Proceedings of the 2021 XXXIVth General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Rome, Italy, 28 August–4 September 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Nanzer, J.A.; Schmid, R.L.; Comberiate, T.M.; Hodkin, J.E. Open-Loop Coherent Distributed Arrays. IEEE Trans. Microw. Theory Tech. 2017, 65, 1662–1672. [Google Scholar] [CrossRef]
- Shi, S.; Zhu, S.; Gu, X.; Hu, R. Extendable carrier synchronization for distributed beamforming in wireless sensor networks. In Proceedings of the 2016 International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; pp. 298–303. [Google Scholar] [CrossRef]
- Mghabghab, S.R.; Nanzer, J.A. Impact of VCO and PLL Phase Noise on Distributed Beamforming Arrays with Periodic Synchronization. IEEE Access 2021, 9, 56578–56588. [Google Scholar] [CrossRef]
- Elbir, A.M.; Mishra, K.V.; Vorobyov, S.A.; Heath, R.W. Twenty-Five Years of Advances in Beamforming: From convex and nonconvex optimization to learning techniques. IEEE Signal Process. Mag. 2023, 40, 118–131. [Google Scholar] [CrossRef]
- Ding, Y.; Fusco, V.; Zhang, J. Phase error effects on distributed transmit beamforming for wireless communications. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 3100–3103. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Wang, Z.; Xu, S.; Zhang, Y. Effect of Errors in Beamforming Analysis Applied for MVDR and CBF Method. Open Electr. Electron. Eng. J. 2016, 10, 197–204. [Google Scholar]
- Chen, P.; Yang, Y.; Wang, Y.; Ma, Y. Robust Adaptive Beamforming with Sensor Position Errors Using Weighted Subspace Fitting-Based Covariance Matrix Reconstruction. Sensors 2018, 18, 1476. [Google Scholar] [CrossRef] [PubMed]
- Pirapaharan, K.; Prabhashana, W.H.S.C.; Medaranga, S.P.P.; Hoole, P.R.P.; Fernando, X. A New Generation of Fast and Low-Memory Smart Digital/Geometrical Beamforming MIMO Antenna. Electronics 2023, 12, 1733. [Google Scholar] [CrossRef]
- Wang, H.M.; Luo, M.; Yin, Q.; Xia, X.G. Hybrid Cooperative Beamforming and Jamming for Physical-Layer Security of Two-Way Relay Networks. IEEE Trans. Inf. Forensics Secur. 2013, 8, 2007–2020. [Google Scholar] [CrossRef]
- Kanatas, A.G. Spherical Random Arrays With Application to Aerial Collaborative Beamforming. IEEE Trans. Antennas Propag. 2023, 71, 550–562. [Google Scholar] [CrossRef]
- Du, J.; Guo, W.; Yan, M.; Zhao, H.; Tang, Y. Location Error Analysis for Collaborative Beamforming in UAVs Random Array. IEEE Wirel. Commun. Lett. 2024, 13, 904–907. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Z.; Guo, K.; Zhang, R.; Quek, T.Q.S. Against Mobile Collusive Eavesdroppers: Cooperative Secure Transmission and Computation in UAV-Assisted MEC Networks. IEEE Trans. Mob. Comput. 2025; early access. [Google Scholar] [CrossRef]
- Ye, R.; Peng, Y.; Al-Hazemi, F.; Boutaba, R. A Robust Cooperative Jamming Scheme for Secure UAV Communication via Intelligent Reflecting Surface. IEEE Trans. Commun. 2024, 72, 1005–1019. [Google Scholar] [CrossRef]
- Chen, P.; Li, H.; Ma, L. Distributed massive UAV jamming optimization algorithm with artificial bee colony. IET Commun. 2022, 17, 197–206. [Google Scholar]
- Zhou, Y.; Zhou, F.; Zhou, H.; Ng, D.W.K.; Hu, R.Q. Robust Trajectory and Transmit Power Optimization for Secure UAV-Enabled Cognitive Radio Networks. IEEE Trans. Commun. 2020, 68, 4022–4034. [Google Scholar] [CrossRef]
- Ge, Y.; Liu, H.; Wan, P.; Liu, C.; Liu, B.; Ren, Y. Active RIS Aided Secure UAV Communication with Cooperative Jamming. In Proceedings of the 2024 12th International Conference on Information Systems and Computing Technology (ISCTech), Xi’an, China, 8–11 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Tao, Z.; Zhou, F.; Wang, Y.; Liu, X.; Wu, Q. Resource allocation and trajectories design for UAV-assisted jamming cognitive UAV networks. China Commun. 2022, 19, 206–217. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Goldstein, H.; Poole, C.P.; Safko, J.L. Classical Mechanics, 3rd ed.; Addison-Wesley: Menlo Park, CA, USA, 2001. [Google Scholar]
- Anderson, J.D., Jr. Fundamentals of Aerodynamics. AIAA J. 2010, 48, 2983. [Google Scholar]
- White, F. Fluid Mechanics (7th Edition in SI Units); Tata Mcgraw Hill Education: Chennai, India, 2011. [Google Scholar]
- ITU-R Recommendation P.838: Specific Attenuation Model for Rain for Use in Prediction Methods; Technical Report P.838; ITU Radiocommunication Sector: Geneva, Switzerland, 2005.


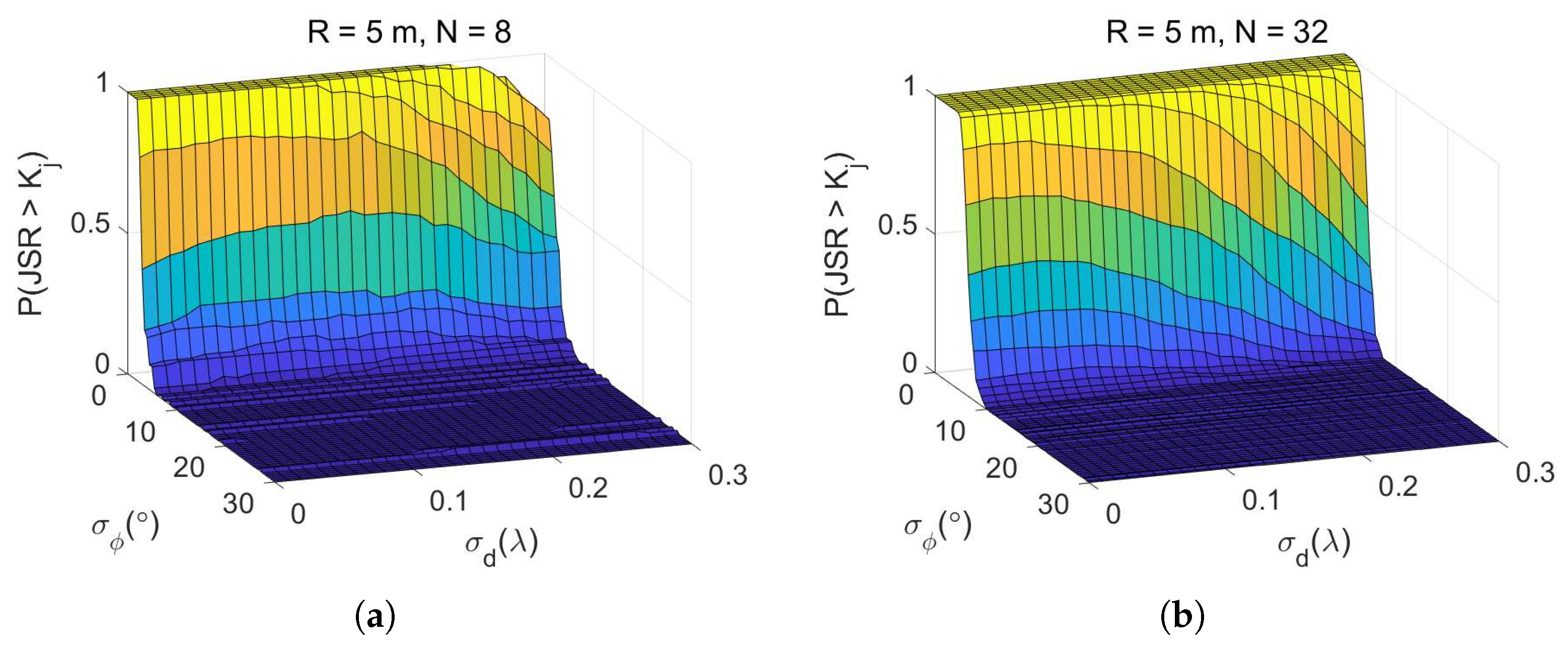
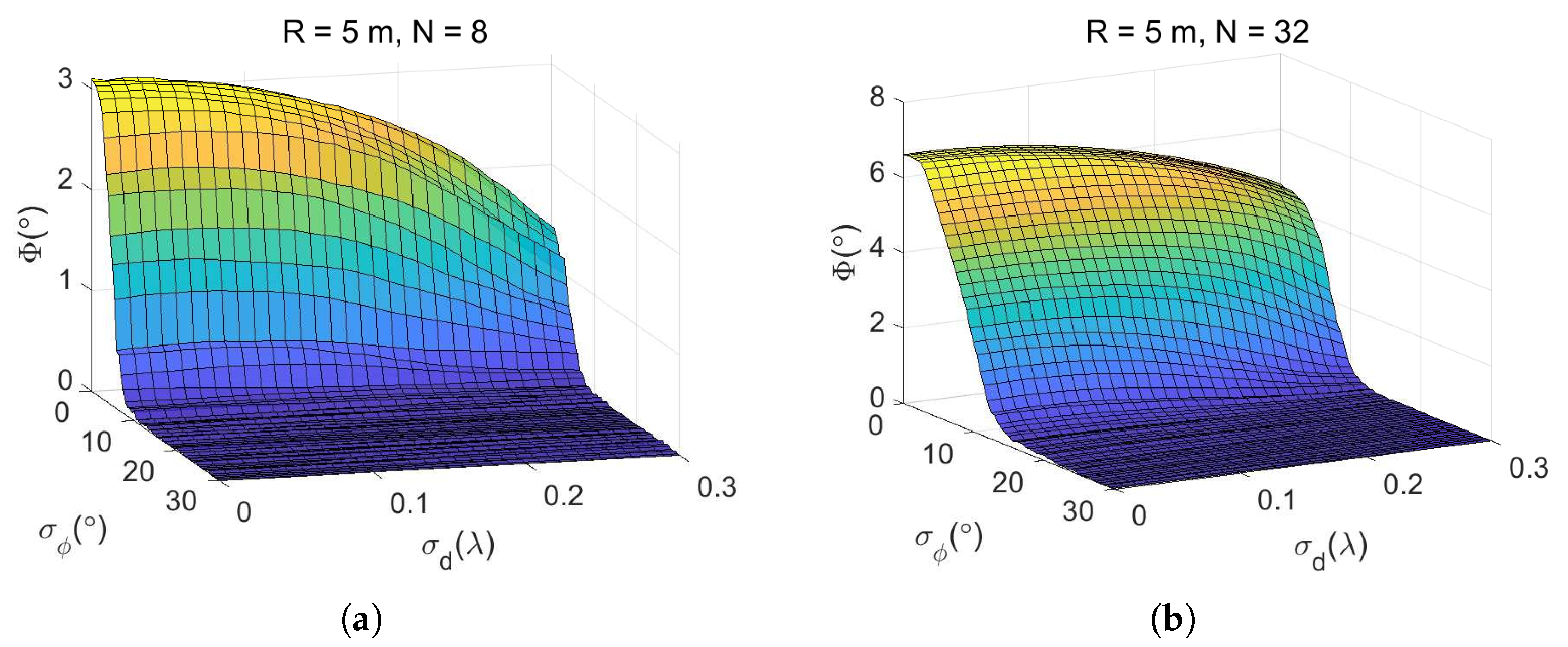
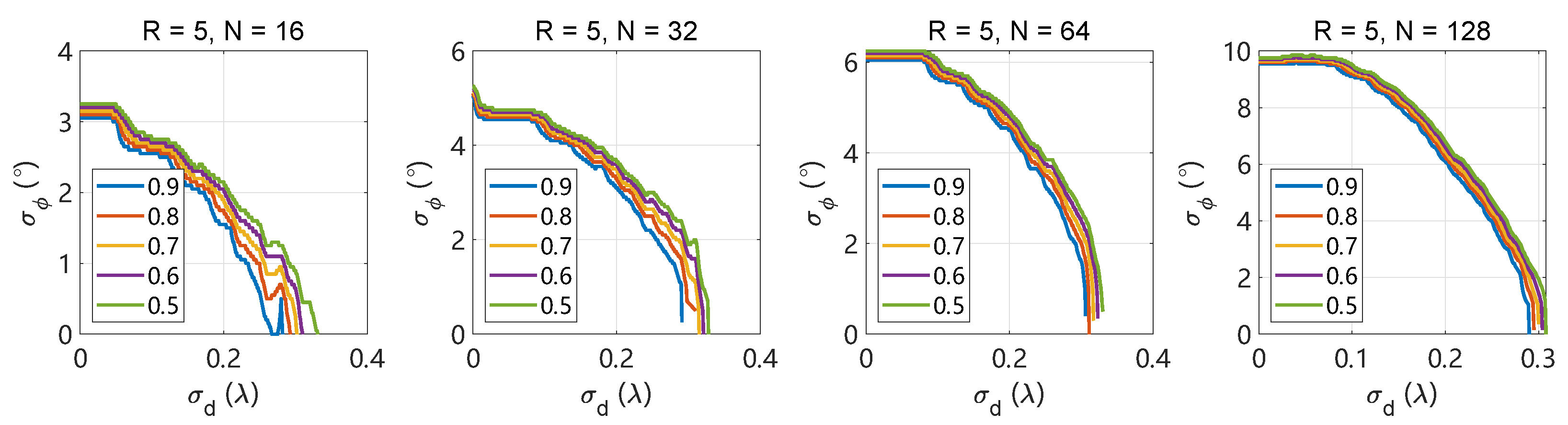
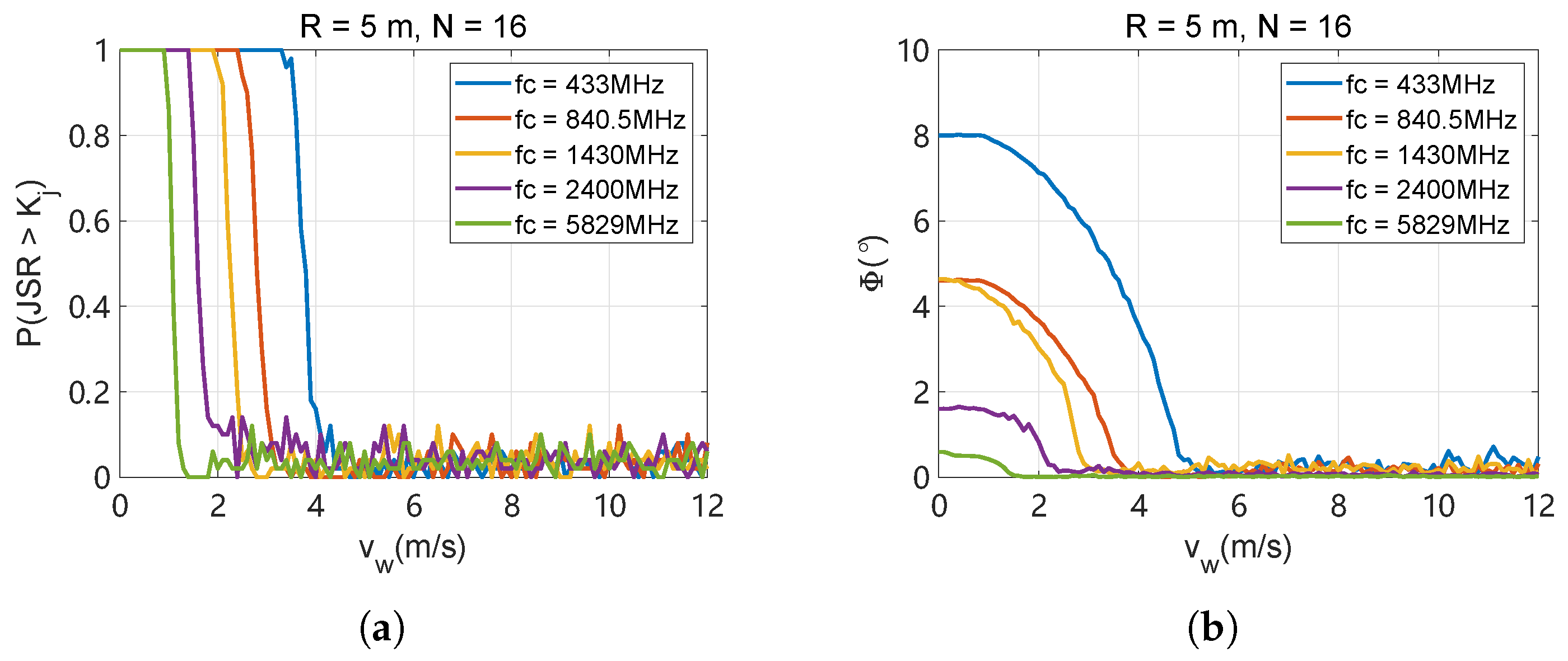

| Parameters | Data | Unit | |||
|---|---|---|---|---|---|
| 1 | 3.1 | 4.2 | 5 | ||
| 0.22 | 0.25 | 0.28 | 0.35 | ||
| 100% | 87% | 58% | 34% | / | |
| 4.9 | 4.5 | 4.0 | 2.9 | ||
| Parameters | Data | Unit | ||||
|---|---|---|---|---|---|---|
| 433 | 840.5 | 1430 | 2400 | 5829 | MHz | |
| 7.2 | 4.09 | 2.55 | 1.34 | 0.28 | ||
| 0.29 | 0.15 | 0.09 | 0.05 | 0.02 | m | |
| Parameters | Data | Unit | |||
|---|---|---|---|---|---|
| N | 8 | 16 | 32 | 128 | / |
| 5.35 | 12.65 | 27.44 | 39.05 | ||
| 0.20 | 0.35 | 0.43 | 0.57 | m | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, L.; Hu, D.; Huang, Z.; Guo, X.; Ba, J.; Huang, H.; Yuan, S.; Zhou, J. Positioning Error Analysis of Distributed Random Array Based on Unmanned Aerial Vehicles in Collaborative Jamming. Drones 2025, 9, 234. https://doi.org/10.3390/drones9040234
Zhao Y, Li L, Hu D, Huang Z, Guo X, Ba J, Huang H, Yuan S, Zhou J. Positioning Error Analysis of Distributed Random Array Based on Unmanned Aerial Vehicles in Collaborative Jamming. Drones. 2025; 9(4):234. https://doi.org/10.3390/drones9040234
Chicago/Turabian StyleZhao, Yongjie, Longqing Li, Deming Hu, Zhiping Huang, Xiaojun Guo, Junhao Ba, Honghe Huang, Shudong Yuan, and Jing Zhou. 2025. "Positioning Error Analysis of Distributed Random Array Based on Unmanned Aerial Vehicles in Collaborative Jamming" Drones 9, no. 4: 234. https://doi.org/10.3390/drones9040234
APA StyleZhao, Y., Li, L., Hu, D., Huang, Z., Guo, X., Ba, J., Huang, H., Yuan, S., & Zhou, J. (2025). Positioning Error Analysis of Distributed Random Array Based on Unmanned Aerial Vehicles in Collaborative Jamming. Drones, 9(4), 234. https://doi.org/10.3390/drones9040234








