1. Introduction
The restoration of communication networks following natural disasters is paramount in enabling the effective coordination of emergency response efforts, facilitating the delivery of humanitarian aid, and safeguarding affected populations. In such scenarios, conventional terrestrial infrastructure is frequently rendered inoperable, severing connectivity precisely when it is most urgently needed. Unmanned Aerial Vehicles (UAVs) equipped with base stations (UAV-BS) present a compelling solution, offering flexible, rapid-deployment coverage in environments where traditional systems falter. Nevertheless, the deployment of UAV-BS in disaster-affected areas poses multifaceted challenges, including the navigation of irregular terrains, the equitable provisioning of services to spatially diverse user populations, and the optimization of constrained energy resources amidst fluctuating conditions such as wind and physical obstructions.
Beyond disaster relief, UAV networks are increasingly pivotal in emerging paradigms such as the low-altitude economy (LAE), where they enable intelligent services in logistics, transportation, and urban air mobility through scalable AI deployment [
1]. Similarly, UAV-enabled Integrated Sensing and Communication (ISAC) extends these capabilities by jointly optimizing communication with ground users and target localization, enhancing spectral efficiency and adaptability in dynamic environments [
2]. Our work aligns with these timely directions by advancing RL-based UAV trajectory optimization for equitable coverage, with potential extensions to LAE and ISAC scenarios. While these domains highlight the growing role of adaptive, intelligent UAV systems, they also expose a shared limitation: traditional optimization strategies—designed for stable, predictable settings—fail to address the inherent unpredictability, user heterogeneity, and fairness demands of real-world operational environments, particularly in crisis scenarios.
Traditional optimization approaches often presuppose static user distributions or consistent environmental parameters—assumptions that do not hold in real-world crisis settings. As a result, they may fail to adequately serve isolated user groups or allocate resources inefficiently, yielding suboptimal coverage outcomes. This underscores the necessity for advanced, adaptive methodologies capable of reconciling operational efficiency with equitable service distribution, ensuring that connectivity is extended to all users irrespective of their geographic disposition. We therefore adopt reinforcement learning (RL) over traditional optimization due to the following inherent challenges in disaster environments:
Non-stationary dynamics: User locations, wind patterns, and obstacle emergence evolve unpredictably—violating static assumptions of convex optimization or MILP.
Partial observability: The UAV has limited sensing range and delayed feedback, requiring memory and sequential credit assignment—natively supported by RL.
High-dimensional action space: Nine-direction movement with variable altitude creates exponential complexity unsuitable for discretization or relaxation.
Multi-objective fairness under uncertainty: RL enables online reward shaping to balance coverage, fairness, and energy—whereas weighted-sum optimization requires known trade-offs.
These factors render classical methods intractable, motivating our LSTM-A2C framework to learn adaptive policies directly from interaction.
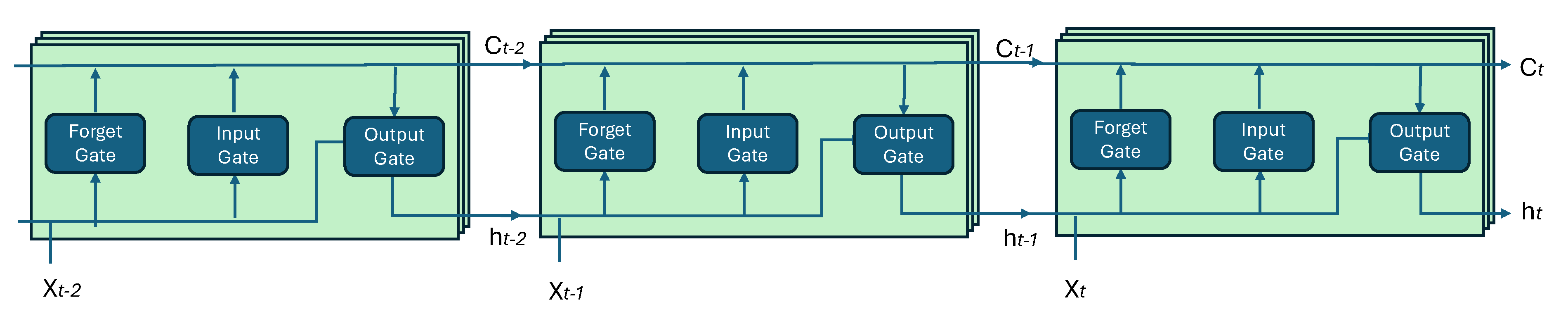
In this study, we introduce a novel reinforcement learning (RL) framework tailored to optimize UAV-BS trajectories and coverage within 6G-enabled Internet of Things (IoT) networks. Our approach is designed to maximize unique user reach while ensuring fairness in service delivery under uncertainty. At its core lies a Long Short-Term Memory (LSTM)–based Advantage Actor–Critic (A2C) model augmented with an attention mechanism. Unlike conventional LSTM-A2C frameworks, the proposed model integrates a memory-based fairness state and selective attention module, enabling the UAV to dynamically prioritize underserved or high-demand user clusters in partially observable environments. This combination allows for efficient policy learning in exponentially large state spaces while maintaining equitable coverage. Unlike prior works in UAV trajectory optimization and RL-based coverage control, which often prioritize energy minimization or basic path planning without explicitly addressing fairness disparities or attention-driven adaptability to volatile conditions (e.g., wind, obstacles—see
Section 2 for detailed comparisons), our framework uniquely integrates fairness-aware rewards, a nine-direction movement model, and an attention mechanism with LSTM. For instance, while earlier studies [
3,
4,
5] leverage recurrent networks for temporal dependencies, they do not jointly achieve memory-based user tracking, selective focus on unserved clusters, and equitable service in partially observable, high-dimensional environments—capabilities central to our design.
Our methodology pursues two principal goals: maximizing the number of unique users served and ensuring equitable coverage distribution. The attention mechanism enables the UAV to focus selectively on salient environmental cues, such as user density or coverage deficiencies, while the LSTM component captures temporal patterns to predict and respond to evolving conditions. To address the complexities of disaster environments, we propose a refined nine-direction movement model, affording the UAV enhanced maneuverability to circumvent obstacles and adapt to stochastic factors such as wind.
Key Contributions
The key contributions of this research are summarized as follows:
Novel LSTM-A2C with Attention Framework: We advance existing Actor–Critic architectures by embedding an attention mechanism into an LSTM-A2C structure. This integration allows for context-aware and temporally adaptive trajectory optimization, enabling the UAV-BS to selectively emphasize unserved user clusters and volatile regions while maintaining stable convergence in large-scale, dynamic environments.
Fairness-Aware Coverage Optimization: Beyond maximizing overall user reach, our framework explicitly incorporates fairness through memory-based user tracking and reward terms that penalize disparity. This ensures equitable service even for sparsely located users, a feature overlooked in conventional RL-based UAV-BS optimization.
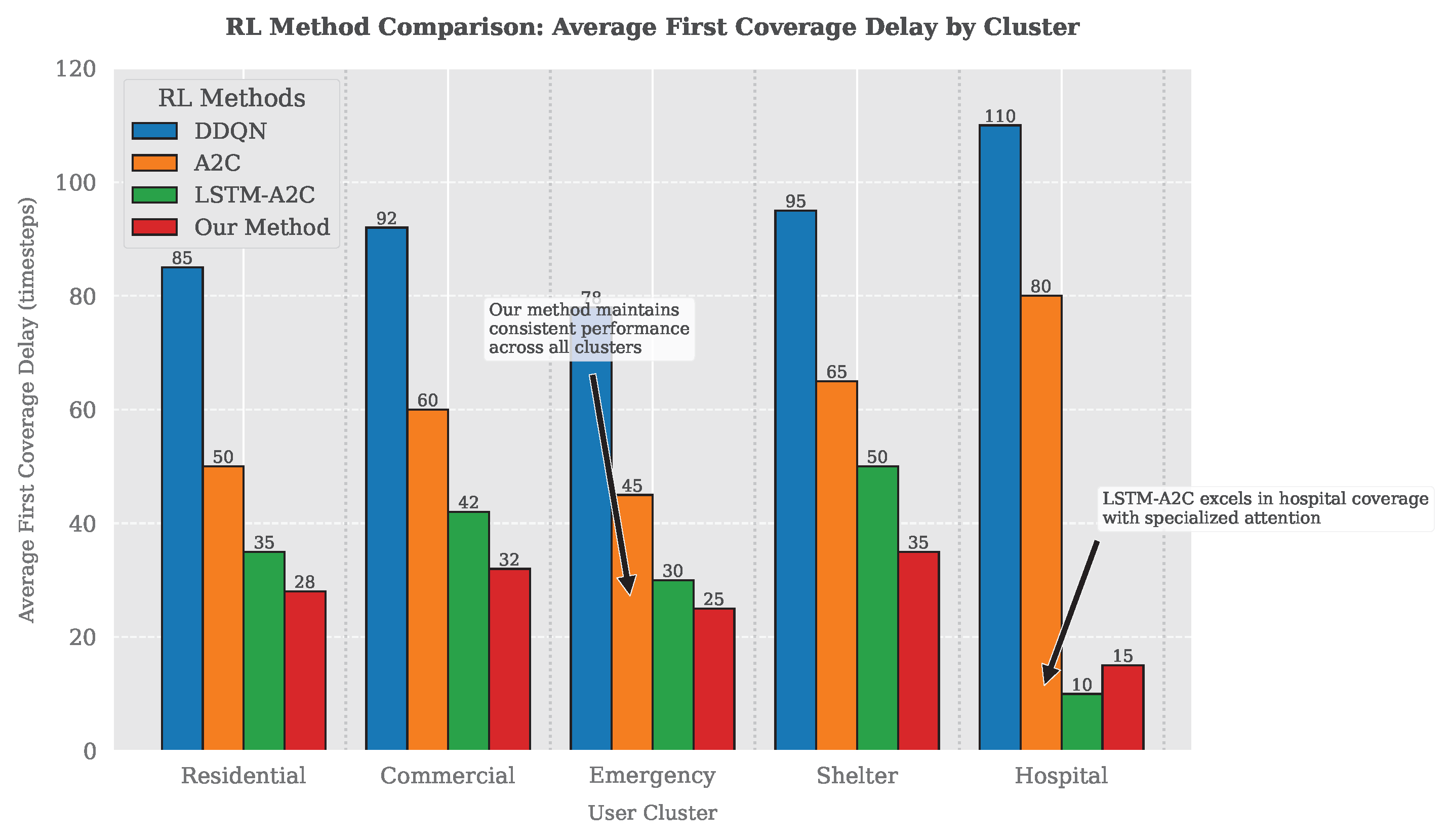
Comprehensive Evaluation and Insights: Through extensive simulations in 6G-IoT scenarios, the proposed method consistently surpasses Q-Learning, DDQN, and standard A2C in fairness (Jain’s index), coverage disparity (CDI), and energy efficiency. These results demonstrate its robustness and practical utility in disaster-response communications.
This work represents a substantial advancement in UAV-assisted communication systems by merging deep reinforcement learning with a fairness-oriented, attention-driven design to address the distinctive demands of disaster scenarios. The remainder of this paper is organized as follows:
Section 2 surveys related literature,
Section 3 outlines the system model and problem formulation,
Section 4 presents the proposed RL methodology,
Section 5 discusses simulation results, and
Section 6 concludes with key insights and future research directions.
2. Related Work
Optimizing Unmanned Aerial Vehicle (UAV) operations, particularly in terms of energy consumption and coverage, is a well-established research domain within wireless communication and Internet of Things (IoT) networks. Early efforts concentrated on traditional optimization techniques for UAV energy efficiency and deployment. Zeng et al. [
6] proposed a framework that jointly optimizes propulsion and communication energy, aiming to balance mission objectives with energy efficiency. Their method employs trajectory optimization to minimize energy use while maintaining communication coverage, but it assumes a static environment, limiting its adaptability to dynamic conditions such as moving users or shifting obstacles. Similarly, Mozaffari et al. [
7] explored adaptive deployment strategies for UAVs, enabling them to reposition dynamically based on user distribution and demand fluctuations. Their approach relies on real-time user density maps, proving effective in controlled simulations. However, it struggles with real-world unpredictability, such as sudden wind or physical barriers, due to its dependence on predefined behavioral models.
Coverage maximization is another critical aspect of UAV-based surveillance and communication systems. Cabreira et al. [
8] introduced a path-planning algorithm that segments the operational area into smaller regions to ensure comprehensive coverage. This divide-and-conquer strategy guarantees that the UAV sequentially addresses each segment, though it may compromise energy efficiency and adaptability to dynamic user distributions. In a similar vein, Jinbiao Yuan et al. [
9] developed a coverage path-planning algorithm using a genetic algorithm to optimize flight paths for maximum coverage with minimal overlap. While effective, this method’s computational intensity renders it less suitable for real-time applications or large-scale areas, highlighting the need for more scalable solutions.
Reinforcement Learning (RL) has emerged as a powerful tool for enhancing UAV decision-making in complex, dynamic environments. Traditional RL methods like Q-Learning have been widely applied to path planning and obstacle avoidance. Tu et al. [
10] demonstrated Q-Learning’s utility in a grid-based environment, enabling a UAV to navigate toward a target while avoiding obstacles. However, Q-Learning suffers from slow convergence and inefficiency in high-dimensional state spaces, limiting its practicality for intricate scenarios. To overcome these drawbacks, the Double Deep Q-Network (DDQN) was introduced, reducing overestimation bias in Q-value estimates for more stable learning. Wang et al. [
11] applied DDQN to multi-UAV coordination, achieving superior performance over traditional Q-Learning in multi-agent, dynamic settings. Additionally, Proximal Policy Optimization (PPO), another RL approach, has been explored for UAV trajectory optimization. Askaripoor et al. [
12] utilized PPO to train UAVs for coverage maximization in urban environments, demonstrating improved sample efficiency compared to Q-Learning.
Actor–Critic methods, blending policy-based and value-based RL approaches, have gained traction for their ability to manage continuous action spaces and ensure stable learning. The Advantage Actor–Critic (A2C) variant employs the advantage function to reduce variance in policy updates, enhancing training stability. Lee et al. [
5] proposed SACHER, a Soft Actor–Critic (SAC) algorithm augmented with Hindsight Experience Replay (HER) for UAV path planning. SACHER improves exploration by maximizing both expected reward and entropy, encouraging diverse action selection. However, this entropy-augmented objective may sacrifice optimality in scenarios requiring precise actions. In contrast, our study leverages LSTM-A2C, integrating Long Short-Term Memory (LSTM) networks to capture sequential dependencies in dynamic environments. This enables the UAV to base decisions on historical data, enhancing adaptability to evolving conditions such as user mobility or environmental changes.
Attention mechanisms have become increasingly prominent in RL frameworks, improving performance by allowing agents to focus on critical aspects of the state or action space. In broader contexts, Vaswani et al. [
13] introduced the Transformer architecture, which relies on self-attention to process sequential data efficiently, revolutionizing fields like natural language processing. Within RL, attention mechanisms enhance an agent’s ability to prioritize relevant information, such as high-priority regions or users in UAV applications. For instance, Kumar et al. [
4] proposed RDDQN: Attention Recurrent Double Deep Q-Network for UAV Coverage Path Planning and Data Harvesting. Their approach employs a recurrent neural network with an attention mechanism to process sequential observations, enabling the UAV to concentrate on pertinent parts of the input sequence for decision-making. This attention mechanism aids in managing long-term dependencies and boosting learning efficiency. However, RDDQN differs from our work in key ways. It utilizes a value-based DDQN framework, whereas we adopt an Actor–Critic A2C approach, combining policy and value optimization for greater flexibility. Additionally, their movement model is simpler, featuring a smaller action set that restricts UAV maneuverability in complex environments. Moreover, RDDQN does not account for harsh environmental factors like wind, nor does it address dynamic user distributions—both critical in our disaster relief scenario. Our LSTM-A2C with an attention framework, by contrast, incorporates a nine-direction movement model and considers dynamic user distributions and environmental challenges, making it more robust for real-world applications.
LSTM-A2C has been applied in various domains to leverage temporal dependencies effectively. Li et al. [
14] employed LSTM-A2C for network slicing in mobile networks, demonstrating its adaptability to user mobility and changing conditions. Similarly, Arzo et al. [
15], Jaya Sri [
16], Lotfi [
17], and Zhou et al. [
18] showcased LSTM’s effectiveness in dynamic network environments, enhancing performance and adaptability in 6G emergency scenarios, 6G-IoT, Open RAN traffic prediction, and wireless traffic prediction applications, respectively. He et al. [
19] and Xie [
20] further validated LSTM’s capability to handle long, irregular time series, emphasizing its strength in retaining temporal dependencies for UAV trajectory and information transmission optimization in IoT wireless networks. Building on these foundations, the current study extends LSTM-A2C to UAV trajectory and coverage optimization in 6G-enabled IoT networks, integrating an attention mechanism to enhance decision-making under energy and environmental constraints.
This research extends our previous work, “Deep RL for UAV Energy and Coverage Optimization in 6G-Based IoT Remote Sensing Networks” [
3]. In that study, we applied deep reinforcement learning to optimize UAV energy and coverage, focusing on static user distributions and simpler environmental conditions. The present work advances this foundation by introducing a more sophisticated nine-direction movement model, accommodating dynamic user distributions, and incorporating environmental factors such as wind and obstacles. Furthermore, we enhance the RL framework by embedding an attention mechanism within the LSTM-A2C architecture, enabling the UAV to make informed decisions based on historical data and current conditions, thus improving coverage fairness and energy efficiency in disaster relief scenarios.
While traditional RL methods like Q-Learning and DDQN have advanced UAV energy and coverage optimization, they often struggle with scalability and adaptability in real-world settings. Our novel LSTM-A2C approach with attention integrates LSTM’s temporal dependency capabilities with an attention-driven focus on critical states, offering superior performance in dynamic environments. Extensive simulations validate its effectiveness, demonstrating improvements in coverage fairness, Quality of Service (QoS), and energy utilization over baseline RL methods.
It is also worth noting that the proposed trajectory-optimization framework can be synergistic with emerging physical-layer technologies designed to enhance UAV communication efficiency. In particular, integrating the learning-based control policy with Intelligent Reflecting Surfaces (IRS) could improve signal propagation in non-line-of-sight or obstructed disaster environments by intelligently redirecting reflected waves, while advanced multiple-access schemes such as Non-Orthogonal Multiple Access (NOMA) can further increase spectral efficiency and user connectivity. Furthermore, recent advancements leverage deep reinforcement learning (DRL) to jointly optimize beamforming, power allocation, and trajectory in RSMA-IRS-Assisted ISAC systems for energy efficiency maximization [
21]. Such AI-driven coordination complements our UAV-BS trajectory framework, enabling integrated 6G systems where UAVs, IRS, and sensing coexist under dynamic constraints. Combining these physical-layer innovations with our reinforcement-learning-based trajectory optimization represents a promising direction for future research, enabling more energy-efficient and resilient UAV communication systems in 6G-enabled networks.
3. System Model and Problem Formulation
3.1. System Overview
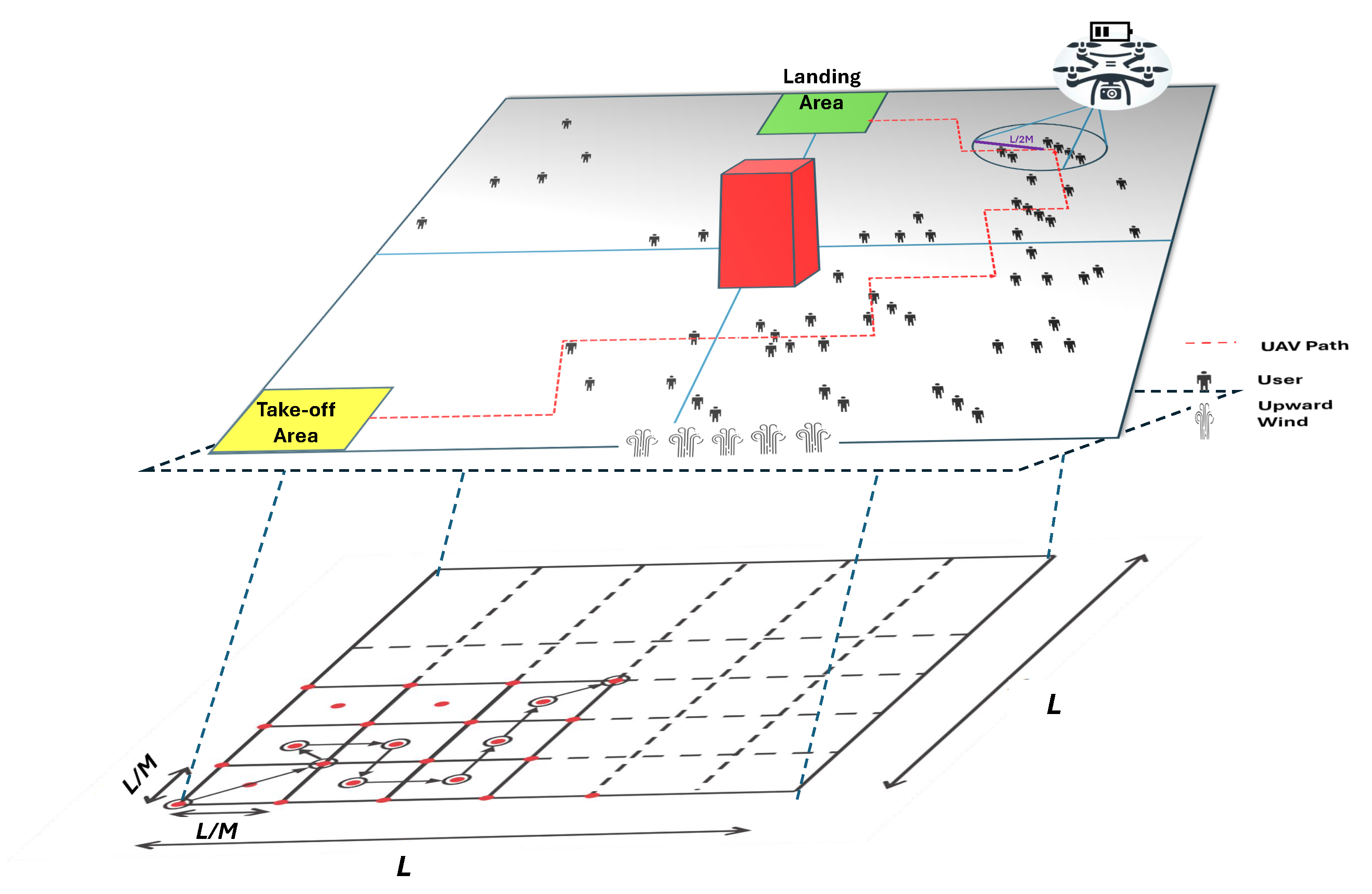
In this study, we consider a UAV-mounted base station (UAV-BS) deployed to provide emergency wireless coverage in a disaster-affected area. The operational region, as shown in
Figure 1, is modeled as an
grid divided into
smaller squares, each with side length
[
22]. The UAV-BS operates at a constant altitude of 50 m [
23] and a fixed horizontal speed, simplifying the three-dimensional motion into a two-dimensional trajectory optimization problem while maintaining physical relevance [
6]. This simplification is widely adopted in UAV-BS literature [
6,
7,
24] to focus on dynamic coverage and fairness under energy constraints while ensuring line-of-sight propagation and isolating horizontal maneuverability from altitude variations. Unlike classical 2-D path-planning tasks that focus purely on geometric shortest paths, trajectory optimization here involves sequential decision-making under temporal and stochastic dynamics (e.g., wind, energy, fairness), which substantially increases computational and modeling complexity.
Remark on Problem Complexity: Although the spatial motion occurs in two dimensions, the optimization problem remains highly nontrivial due to the joint consideration of fairness, stochastic wind perturbations, energy constraints, and partial user observability. The resulting state–action space grows exponentially as , where T is the episode length, requiring advanced RL methods for tractable policy optimization.
3.2. Communication System Model
The UAV-BS provides downlink connectivity to
N ground users randomly distributed across the operational area. To ensure equitable service distribution, a quality-of-service (QoS) framework assigns each user a minimum bandwidth of 10 MHz, with a total bandwidth of 100 MHz and up to
simultaneous connections.
where
indicates whether user
i is within the UAV’s coverage radius
at time
t, and
tracks whether the user was previously served. This binary formulation ensures fairness by rewarding coverage of newly reached users.
3.3. Channel Model
where
is the distance between the UAV and a user,
is the carrier frequency,
the speed of light, and
the line-of-sight excess loss (typically 1–3 dB). Within each coverage cell, path-loss variation remains under 3 dB, allowing constant-loss approximation for simplicity.
3.4. Mobility Model
The UAV’s movement is constrained to nine discrete actions: eight compass directions (north, northeast, east, southeast, south, southwest, west, northwest) and hovering. At each time step, the UAV moves at a constant speed, with the displacement defined relative to the grid cell length
c. For cardinal movements (north, south, east, west), the UAV travels a distance of
along one axis. For diagonal movements, it travels
along both the
x- and
y-axes simultaneously, resulting in a total Euclidean displacement of
. This ensures that the UAV reaches the diagonal vertices of each cell, maintaining geometric consistency with the layout shown in
Figure 1, while preserving constant movement speed across all directions.
Wind effects in designated regions
introduce stochastic perturbations modeled as zero-mean Gaussian random variables, with standard deviation proportional to the local wind intensity [
25]. The possible displacements are summarized as follows:
Wind-affected transitions are therefore expressed as:
where
are the wind-induced perturbations on the UAV’s motion in the
x- and
y-directions, respectively.
The energy consumption model focuses primarily on propulsion, as communication-related energy expenditure constitutes less than 5% of total power usage in typical UAV-BS deployments [
26]. The total available energy
E constrains the UAV’s operational time, requiring careful balance between coverage objectives and energy conservation.
3.5. Fairness Metric
To quantify service equity across all ground users, we employ Jain’s fairness index:
where
represents the total service time received by user
i. This metric ranges from
(worst-case unfairness) to 1 (perfect fairness), providing a normalized measure of distribution equity that is sensitive to both under-served and over-served users.
Coverage Disparity Index
To further assess spatial equity, we introduce the Coverage Disparity Index (CDI), defined as:
where
is the number of user clusters,
and
are the served and total users in cluster
, and
is the mean coverage rate. A lower CDI indicates more uniform coverage across clusters, complementing Jain’s index by focusing on geographic disparity.
3.6. Optimization Problem
The trajectory optimization problem is formulated as a multi-objective constrained optimization to maximize coverage, fairness, and efficiency:
The optimization is defined over the following key variables:
: The policy mapping current states to movement actions, guiding the UAV’s trajectory.
: The UAV’s position at time t, determining its spatial coverage.
: The propulsion energy consumed at time t, subject to the total budget E.
: The number of attached users at time t, constrained by .
Where the variables and parameters are defined as follows:
: Weighting parameters for fairness () and disparity penalty (), tuned empirically
E: Total energy budget available for the mission.
: Set of obstacle regions where the UAV cannot operate.
: Designated landing zone for the UAV at the end of the mission.
c: Grid cell side length, defining the spatial resolution.
: Maximum number of users that can be attached at any time t, ensuring QoS.
T: Total time horizon or number of decision steps.
This formulation encapsulates a complex trade-off among maximizing unique user coverage (), ensuring temporal fairness () and spatial equity (reducing ), while adhering to energy, obstacle, and movement constraints.
3.7. Computational Complexity
The problem’s combinatorial nature arises from several factors. First, the discrete grid structure creates possible positions at each time step. Second, the nine possible movement directions yield a branching factor that grows exponentially with the time horizon. Third, the user service history introduces memory dependencies that prevent Markovian decomposition. For a typical scenario with and , the state space exceeds possible configurations, rendering exhaustive search methods computationally infeasible.
This complexity motivates our machine learning approach, which can discover efficient navigation policies without explicitly enumerating all possible states. The LSTM-A2C architecture is particularly well suited to this problem because it captures temporal dependencies through its recurrent connections, effectively handles the partial observability of user distributions, and learns energy-efficient movement patterns through continuous policy optimization.
5. Simulation Framework and Experimental Setup
5.1. Grid Configuration
We model a m operational area divided into cells ( m), with key regions defined as:
Takeoff Area: Random position in ;
Landing Zone: ;
No-Fly Zone: ;
Coverage Radius: m (effective coverage per hover point).
The chosen grid resolution directly affects both the optimization granularity and computational complexity. A finer discretization (larger M) would enhance spatial precision, enabling the UAV to better target isolated users and improve fairness by distinguishing coverage gaps within clusters. However, it exponentially increases the state–action space—e.g., from at to at —significantly raising training time and memory requirements. Conversely, a coarser grid reduces complexity but risks degraded maneuverability and coverage granularity, potentially compromising equity in dense or fragmented user distributions. Our selection offers sufficient fidelity for realistic disaster scenarios while maintaining tractable computation.
In future work, we plan to treat grid resolution as a tunable parameter, enabling a systematic evaluation of the trade-off between trajectory precision and computational cost across different grid configurations. Such an analysis would further strengthen the understanding of how mission area discretization impacts real-time UAV deployment efficiency.
5.2. Hover Points and Energy Model
The number of possible hovering points is calculated as:
Energy consumption follows realistic movement constraints: The propulsion energy consumption
at each time step
t is modeled to reflect realistic power demands during UAV-BS operations in a grid-based environment. This model draws from established physics-based formulations and empirical data on rotary-wing UAVs, such as quadcopters, which align with our fixed-altitude (50 m) and discrete-movement setup. Key studies report average hovering power around 200–300 W for 1–5 kg UAVs [
27,
28,
29,
30] and cruise power around 400–600 W at constant speeds of 10–15 m/s, primarily driven by blade profile power (for rotor spin), induced power (for lift generation), and parasitic drag (air resistance increasing with speed cubed).
To adapt this for simulation efficiency in our LSTM-A2C framework, we simplify into discrete energy units, assuming constant speed v (e.g., 10 m/s) during moves, fixed drag coefficient, and no major altitude changes. This focuses energy on time spent per action, proportional to distance at fixed v. The simplification preserves key physics: base power (always on, even hovering) plus movement power (dominated by drag, scaled by time).
Under these assumptions, we normalize reported values to units as follows (
Table 2):
Hovering: units (≈200 W baseline, minimal induced power with ).
Cardinal Movement: units (≈500 W for distance ).
Diagonal Movement: units (≈1.4 × cardinal, for distance, as longer path at constant v increases time and thus energy).
Wind-affected: units adjustment, proportional to wind variance for effective drag changes (e.g., headwind raises equivalent speed, increasing drag).
This approach maintains physical proportionality—energy scales with power over time, capturing drag dominance at speed—while enabling tractable RL computations. The model ensures energy constraints integrate realistically with coverage and fairness objectives.
Total energy budget: 1500 units, calculated based on (an upper-bound approximation set for conservatism):
This creates a stringent energy constraint where:
Direct flight to landing zone costs ∼600 units;
Only ∼900 units remain for coverage tasks;
Forces intelligent energy conservation.
5.3. Wind and Obstacle Model
To emulate environmental disturbances affecting UAV navigation, we incorporate a spatially varying wind field and a central obstacle region within the simulation area. The wind primarily acts along the vertical (y) axis, producing a northward push in two narrow horizontal bands located near the southern and northern edges of the map. Specifically, a moderate upward wind is applied when the UAV position satisfies and , as well as and . These regions represent low-altitude gust corridors frequently encountered around open urban channels or valleys. In addition to the wind field, a high-rise building is modeled as a static obstacle located in the central “SB” zone. The obstacle restricts both line-of-sight connectivity and flight trajectories, forcing the UAV to plan detours while maintaining network coverage continuity.
5.4. User Distribution and Mobility Model
The ground users are grouped into five spatial clusters that correspond to representative functional zones—residential, commercial, emergency, shelter, and hospital areas—whose parameters are summarized in
Table 3. Each cluster is defined by a two-dimensional Gaussian spatial distribution centered at
with standard deviation
, as shown in the table. At the beginning of every simulation episode, user locations are randomly re-sampled from these Gaussian clusters to reflect environmental and population variability. During an episode, however, user positions remain stationary, corresponding to quasi-static conditions typically assumed in short-term UAV communication missions.
To approximate gradual mobility across multiple episodes, the cluster centers are updated following a Gaussian random-walk process with varying mean and variance, effectively shifting user groups to new nearby locations. Although this simplified mobility model does not replicate continuous user trajectories, it captures the spatial dynamics and cluster migrations observed over longer time scales, providing a practical and computationally efficient means to integrate user-position variability into the training environment.
5.5. Hyperparameters
The LSTM-A2C with attention was trained with the following configuration as shown in
Table 4. Most of the parameters are adopted from [
3] except the attention parameters.
5.6. Reward Function Weights
The multi-objective reward components were balanced as:
The overall reward function in Equation (
23) integrates multiple normalized objectives—coverage maximization, fairness enhancement (capturing both user-level and spatial fairness), and energy efficiency—each scaled to a comparable numeric range. The coefficients in the reward function were chosen to reflect mission priorities in disaster response: rapid coverage restoration is paramount (coverage weight = 1.0), fairness is important but secondary (0.7), with an additional spatial disparity penalty (
) applied through the Coverage Disparity Index (CDI) term to discourage uneven service distribution. Energy consumption is penalized moderately (0.3) to preserve mission endurance, and safety violations incur a strict penalty (5.0). The numeric magnitudes account for the natural ranges of each term (e.g.,
,
,
,
units). Coefficients were tuned with pilot/trial simulations to yield stable training and balanced trade-offs, serving as an empirical sensitivity analysis of the reward components; we plan a full hyperparameter and Pareto sensitivity analysis as part of future work.
7. Conclusions
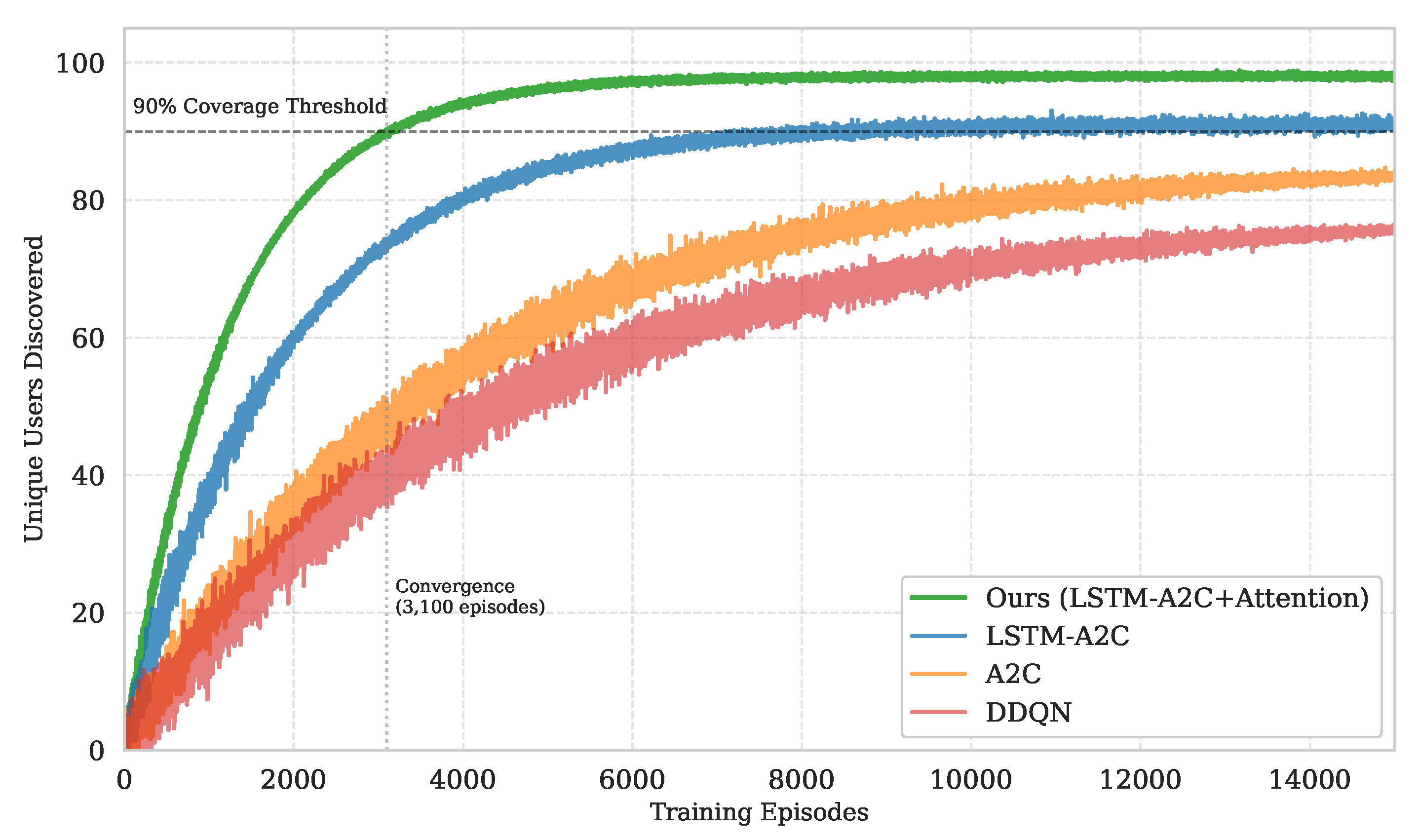
This study presents a novel reinforcement learning framework leveraging an LSTM-based Advantage Actor–Critic (A2C) model with an attention mechanism to optimize UAV-mounted base station (UAV-BS) trajectories and coverage in disaster relief scenarios. Our approach effectively addresses the challenges of dynamic environments, including obstacles, wind effects, and energy constraints, while prioritizing equitable service delivery to ground users. Simulation results demonstrate that the proposed method achieves superior performance over baseline RL techniques—such as DDQN, A2C, and vanilla LSTM-A2C—across critical metrics: it serves 98 out of 100 users (a 7.7% improvement over LSTM-A2C), attains a 92% mission completion rate, and reduces the Coverage Disparity Index (CDI) to 0.03, reflecting a 50% improvement in spatial equity. Additionally, the integration of the attention mechanism enhances adaptability by focusing on high-priority regions, while the LSTM component ensures robust temporal decision-making, resulting in a 22% reduction in energy per user compared to LSTM-A2C. These advancements underscore the potential of our framework to enhance real-time disaster response within 6G-enabled IoT networks, offering a scalable and efficient solution for restoring connectivity in crisis settings. By balancing coverage maximization, fairness, and energy efficiency, this work lays a strong foundation for next-generation UAV-assisted communication systems.
An important finding from this work is the clear computational trade-off between offline training cost and online deployment efficiency. Although the proposed LSTM-A2C with attention requires greater computational effort during training due to its sequential modeling and attention modules, this investment yields significant dividends at deployment: the trained policy enables faster real-time decision-making, reduced inference latency, and improved energy utilization. This result highlights the practical value of allocating additional offline computational resources to achieve superior operational performance and responsiveness in mission-critical environments.
While this study demonstrates significant progress in UAV-BS optimization, several avenues remain for further exploration. First, extending the framework to incorporate heterogeneous and dynamic QoS requirements could better reflect real-world disaster scenarios, where users may demand varying levels of bandwidth or latency based on their roles (e.g., emergency responders vs. civilians). This would require adapting the reward function and state representation to account for diverse service priorities. Second, transitioning from a 2D grid-based model to a 3D environment with varying UAV speeds could enhance realism and flexibility, enabling the UAV to adjust altitude and velocity dynamically in response to terrain, obstacles, or wind conditions. This extension would necessitate a more complex mobility model and increased computational resources, potentially leveraging advanced neural architectures like Transformers for improved scalability. Third, scaling the approach to multi-UAV systems offers a promising direction to increase coverage capacity and resilience, requiring coordination mechanisms to manage inter-UAV interference and task allocation. Additional future work could explore real-time environmental adaptation, such as integrating live weather data or user mobility patterns, to further enhance responsiveness.
Furthermore, a systematic investigation of hyperparameter configurations—including the learning rate, discount factor, entropy coefficient, and Actor–Critic update ratio—will be pursued in future work to identify optimal combinations that maximize policy stability, convergence efficiency, and overall mission performance. Such analysis will employ automated tuning methods (e.g., grid or Bayesian optimization) to complement the empirically tuned parameters used in this study.
Finally, validating the framework with hardware-in-the-loop simulations or field experiments could bridge the gap between simulation and practical deployment, ensuring robustness in operational settings. These enhancements aim to broaden the applicability of our approach to large-scale, complex disaster relief missions.