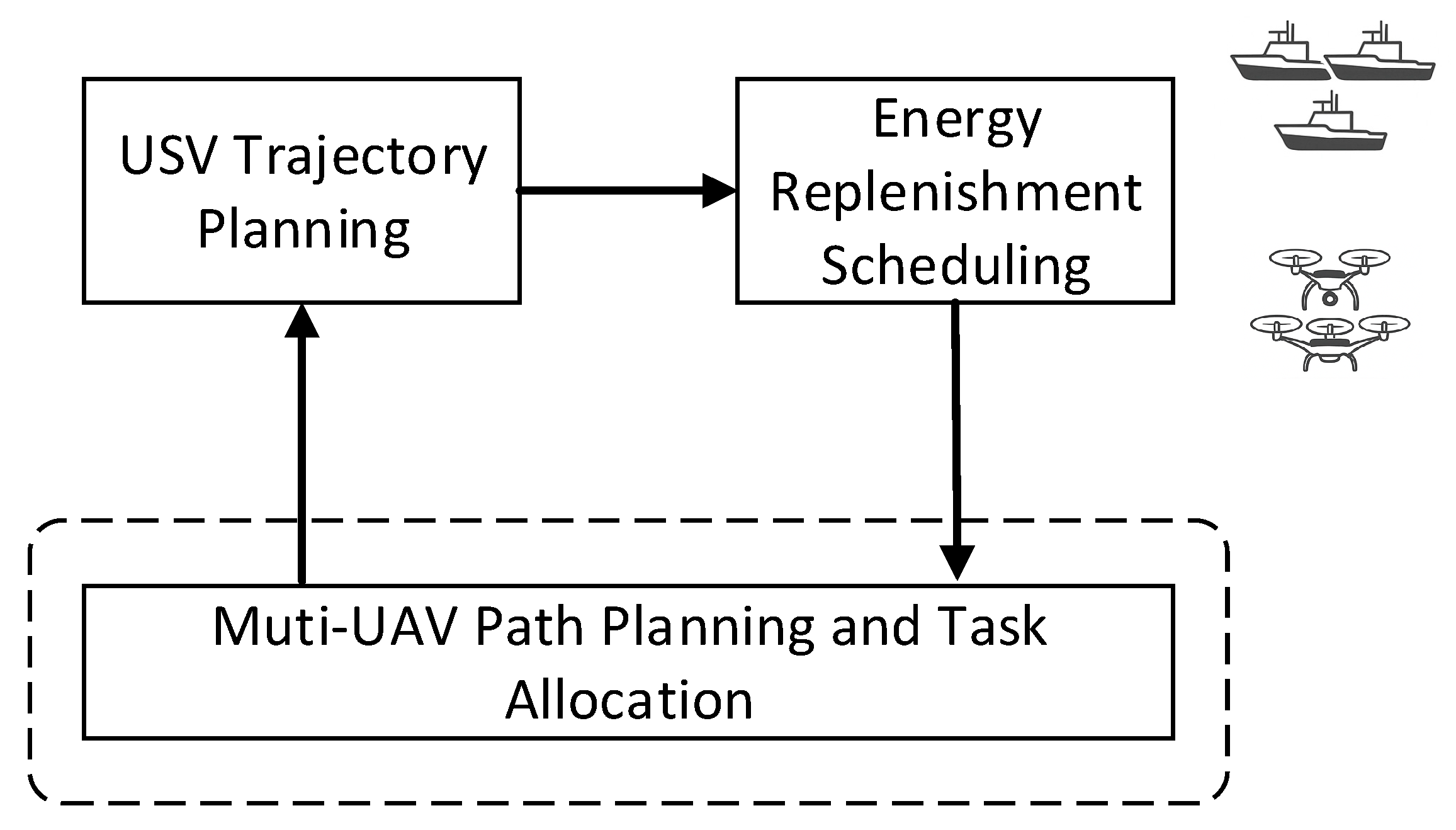
In the proposed USV–multi-UAV collaborative system, the overall framework is organized into three integrated modules that work in a coordinated manner. The first module, task planning, generates preliminary allocations based on mission requirements and priorities, ensuring that high-risk areas are addressed promptly. The second module, UAV scheduling and path optimization, computes UAV trajectories and energy management strategies, balancing mission coverage efficiency with minimal energy consumption. The third module, data fusion and monitoring, continuously collects real-time status information from both the USV and deployed UAVs, enabling dynamic adjustment of task assignments in response to operational changes. The interactions among these modules form a closed-loop process, where the outcomes of task planning guide UAV scheduling, UAV execution is synchronized with USV operations, and feedback from monitoring informs subsequent task refinement.
The path planning and energy replenishment scheduling are formulated as a multi-objective optimization problem. The objectives include minimizing the total mission time by sequencing tasks according to priority, minimizing total energy consumption, calculated as the product of UAV travel distance and an energy coefficient, and maximizing area coverage, with greater weight assigned to high-risk zones. These objectives are balanced using a weighted-sum approach, which ensures efficient allocation of tasks while maintaining overall mission effectiveness.
4.4. Results and Analysis
To verify the effectiveness of the proposed closed-loop USV–UAV cooperative optimization method based on BeiDou high-precision positioning, this section compares three methods across four dimensions—task completion rate, total mission time, energy consumption, and battery replacement waiting time: ① Baseline 1 (static path planning): the USV remains stationary while UAVs execute tasks and return independently; ② Baseline 2 (hierarchical scheduling): the USV follows a preset route and UAVs plan paths and resupply based on fixed rules; ③ Baseline 3: Game-Theoretic Multi-UAV Scheduling (GT-MUS); ④ Baseline 4: Particle Swarm Optimization-based Multi-Objective Scheduling (PSO-MO); ⑤ Proposed (this paper): the USV and UAVs jointly optimize paths and resupply through upper–lower closed-loop interaction.
- (1)
Task Completion Rate (TCR)
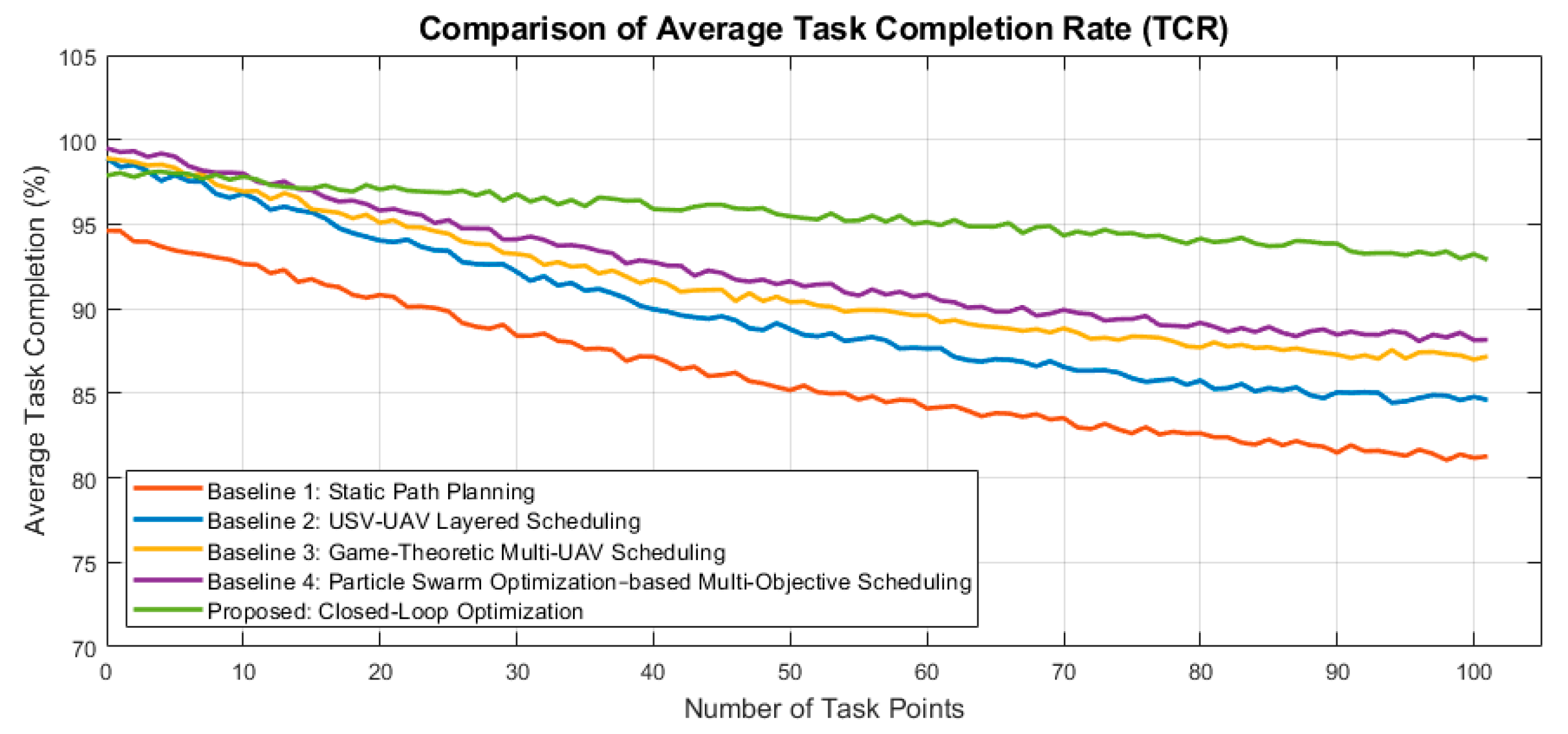
To quantitatively evaluate coverage ability, we consider three task scales: small (20 task points), medium (50), and large (100), and compute the task completion rate for all three methods. We run 10 trials and report the mean completion rate for each method. The results are shown in
Table 1, and the relationship between task scale and completion rate is plotted in
Figure 3.
Baseline 1 (SP): With 20 task points, UAVs can cover most tasks, achieving a TCR of 90.63%. As the scale increases to 50 or 100 points, battery constraints and long-range returns reduce TCR to 85.47% and 81.28%, respectively, showing a clear scale-dependent performance drop.
Baseline 2 (HS): The mobile USV provides partial resupply, improving TCR to 94.32% for 20 points, 88.75% for 50 points, and 84.54% for 100 points. However, the fixed route cannot fully adapt to UAV energy states, leaving some distant points uncovered.
Baseline 3 (GT-MUS): Cooperative game-theoretic scheduling improves UAV task allocation, resulting in TCR of 95.18% (20 points), 90.33% (50 points), and 87.20% (100 points). Decentralized negotiation enhances efficiency but without dynamic USV trajectory adaptation, full coverage for large-scale tasks is limited.
Baseline 4 (PSO-MO): Multi-objective PSO further balances coverage, energy, and battery-replacement waiting time. TCR reaches 96.02% (20 points), 91.45% (50 points), and 88.31% (100 points), showing improved coverage over GT-MUS while handling multi-objective trade-offs.
Proposed Method: Closed-loop cooperative optimization achieves TCR ≥ 93% across all scales: 97.12% (20 points), 95.61% (50 points), and 93.11% (100 points). UAVs request resupply proactively, and the USV dynamically adjusts its trajectory, ensuring nearly full coverage and high operational efficiency.
Baseline 1 (SP) shows a monotonically decreasing curve with increasing task points, dropping from 90.63% at 20 points to 81.28% at 100 points, highlighting the limitations of pure UAV path planning under energy constraints. Baseline 2 (HS) performs better, ranging from 94.32% to 84.54%, but still declines as task scale grows, indicating that a static USV route cannot fully support large-scale coverage. Baseline 3 (GT-MUS) further improves coverage with TCR values of 95.18%, 90.33%, and 87.20%, demonstrating enhanced task allocation through cooperative game-theoretic scheduling. Baseline 4 (PSO-MO) balances coverage and energy efficiency, achieving 96.02%, 91.45%, and 88.31% across small, medium, and large scales. The Proposed closed-loop cooperative method remains nearly flat, maintaining high TCRs of 97.12%, 95.61%, and 93.11%, showing robustness, scalability, and effective dynamic resupply.
- (2)
Total Mission Time (TMT)
Total mission time (
TMT) gauges overall system efficiency and reflects the time performance of USV–UAV coordination in complex scenarios. We run 10 trials and report mean
TMT for each method.
Table 2 lists the data for different numbers of task points, and the comparison of average
TMT is plotted in
Figure 4.
From the results, Baseline 1 grows almost linearly with task points and exhibits a pronounced “bottleneck” beyond 50 points due to frequent long-distance returns for resupply, which increase redundant flight and idle waiting. Baseline 2 reduces some redundant paths via a preset USV route, lowering average TMT by about 10.00–12.00% compared with Baseline 1. However, the lack of real-time interaction with UAVs results in mismatches between the USV’s route and UAV energy states, leaving resupply scheduling suboptimal.
Baseline 3 (GT-MUS) further improves scheduling by applying a game-theoretic task allocation among UAVs. This approach reduces TMT by roughly 3.00–4.00% relative to Baseline 2, but it still does not fully leverage closed-loop USV–UAV coordination, limiting responsiveness to dynamic task and energy conditions. Baseline 4 (PSO-MO) achieves multi-objective optimization across mission time, energy consumption, and battery waiting, resulting in TMT values about 1.00–2.00% lower than GT-MUS, offering more balanced performance under larger task scales.
By contrast, the Proposed closed-loop USV–UAV optimization method achieves joint upper–lower-level coordination: the USV dynamically adjusts its position and docking stops based on UAV energy states and task distribution, while UAVs adaptively plan paths and resupply requests according to the USV’s real-time status. This approach effectively avoids idle time caused by returns or waiting for resupply. At 100 task points, the average TMT is 529.39 min, which is 14.94% lower than Baseline 1, 8.41% lower than Baseline 2, 4.33% lower than Baseline 3, and 1.99% lower than Baseline 4. Across all task scales, the proposed method consistently achieves the lowest TMT, with the flattest growth curve among all methods, demonstrating strong scalability and robustness in avoiding efficiency bottlenecks that affect traditional scheduling approaches.
- (3)
Total Energy Consumption (TEC)
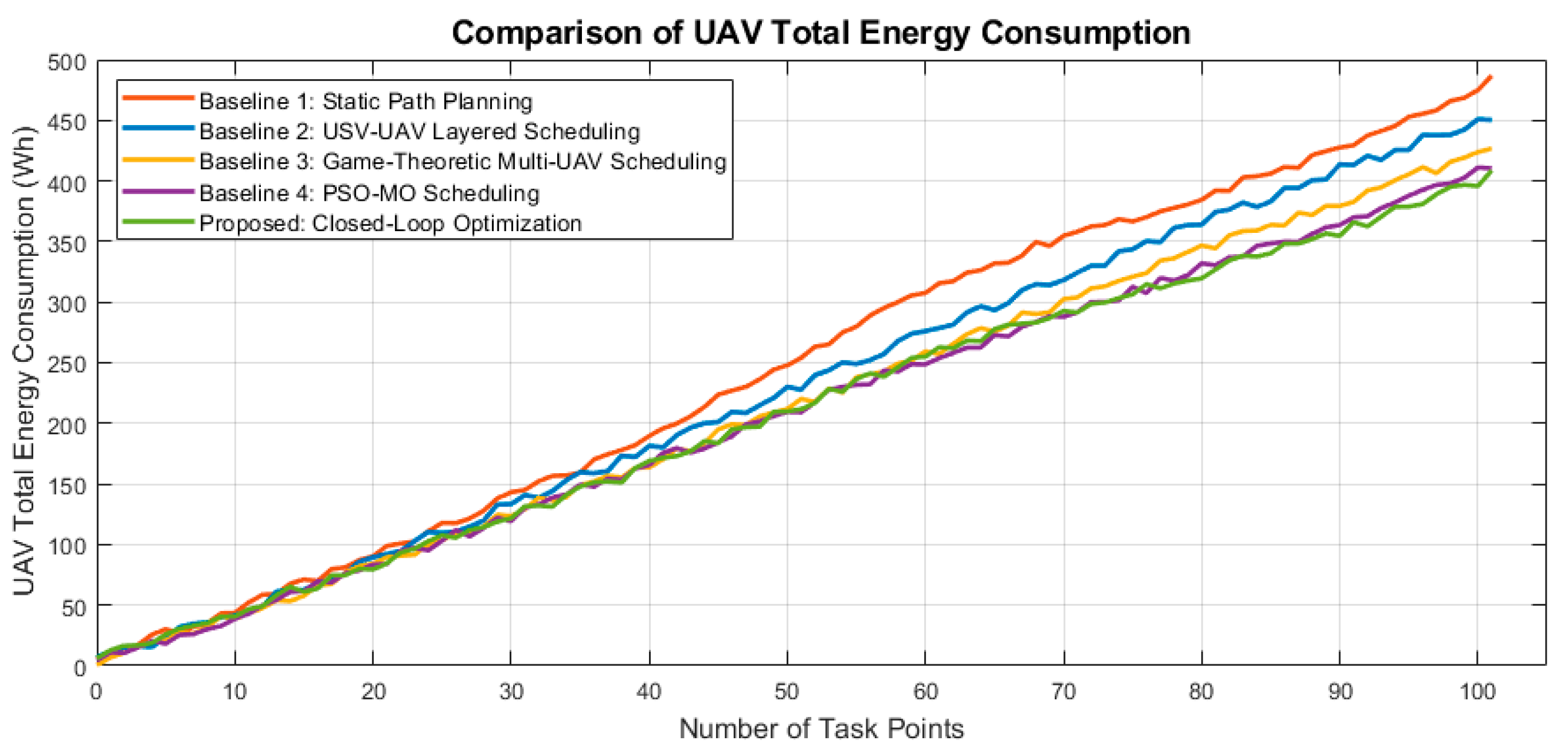
For energy analysis, we examine total UAV energy consumption under multiple task scales. We run 10 trials and report the mean for each method;
Table 3 summarizes the results, and the energy consumption of the five methods under different task scales is plotted in
Figure 5.
From the results in the table, it can be observed that:
Baseline 1 (Static Path Planning): UAVs lack dynamic support from the USV and must frequently return over long distances for resupply, leading to significantly higher energy consumption. Energy usage grows approximately linearly with the number of task points.
Baseline 2 (USV–UAV Layered Scheduling): By employing the USV as a replenishment platform, energy consumption is moderately reduced, averaging an 8.00–10.00% decrease compared with Baseline 1. However, the fixed USV trajectory cannot adapt to UAV real-time task loads, so overall energy usage remains relatively high.
Baseline 3 (GT-MUS): The game-theoretic multi-UAV scheduling balances UAV workload through decentralized negotiation, reducing redundant travel and idle times. Compared with Baseline 1 and 2, TEC is decreased by approximately 14.00% and 6.00%, respectively.
Baseline 4 (PSO-MO): Particle swarm optimization jointly minimizes mission time and energy consumption, achieving smoother energy distribution across UAVs. TEC is further reduced by 16.00% relative to Baseline 1 and 7.50% relative to Baseline 2, showing strong multi-objective optimization capability.
Proposed Method (Closed-Loop USV–UAV Optimization): By dynamically adjusting USV position and adaptively allocating UAV tasks, redundant flights and resupply trips are minimized. Average energy consumption is reduced by 13.37% compared with Baseline 1 and by 10.38% compared with Baseline 2, and by about 3.50–4.00% compared with Baseline 3 and 4. Variance in energy consumption is also significantly lower, indicating balanced multi-UAV workload and improved overall system energy efficiency.
Figure 5 presents the total energy consumption (
TEC) curves of all five methods under varying task scales. The Baseline 1 curve consistently remains at the highest level, reflecting the large energy cost caused by frequent long-distance UAV returns without dynamic USV support. Baseline 2 shows a moderate improvement due to the USV’s fixed replenishment support, but the lack of adaptive scheduling still leads to relatively high energy consumption. Baseline 3 (
GT-MUS) reduces TEC further by balancing UAV workloads via game-theoretic task allocation, while Baseline 4 (
PSO-MO) achieves even lower
TEC by optimizing multi-objective scheduling through particle swarm optimization. The Proposed closed-loop USV–UAV method consistently achieves the lowest energy consumption across all task scales, with a flatter growth curve that indicates strong scalability and effective reduction of redundant UAV flights and resupply trips. These results clearly demonstrate that the proposed cooperative optimization mechanism not only lowers average energy consumption but also improves workload balance among UAVs, validating its superior energy efficiency for large-scale maritime missions.
- (4)
Analysis of Battery Replacement Waiting Time (BWT)
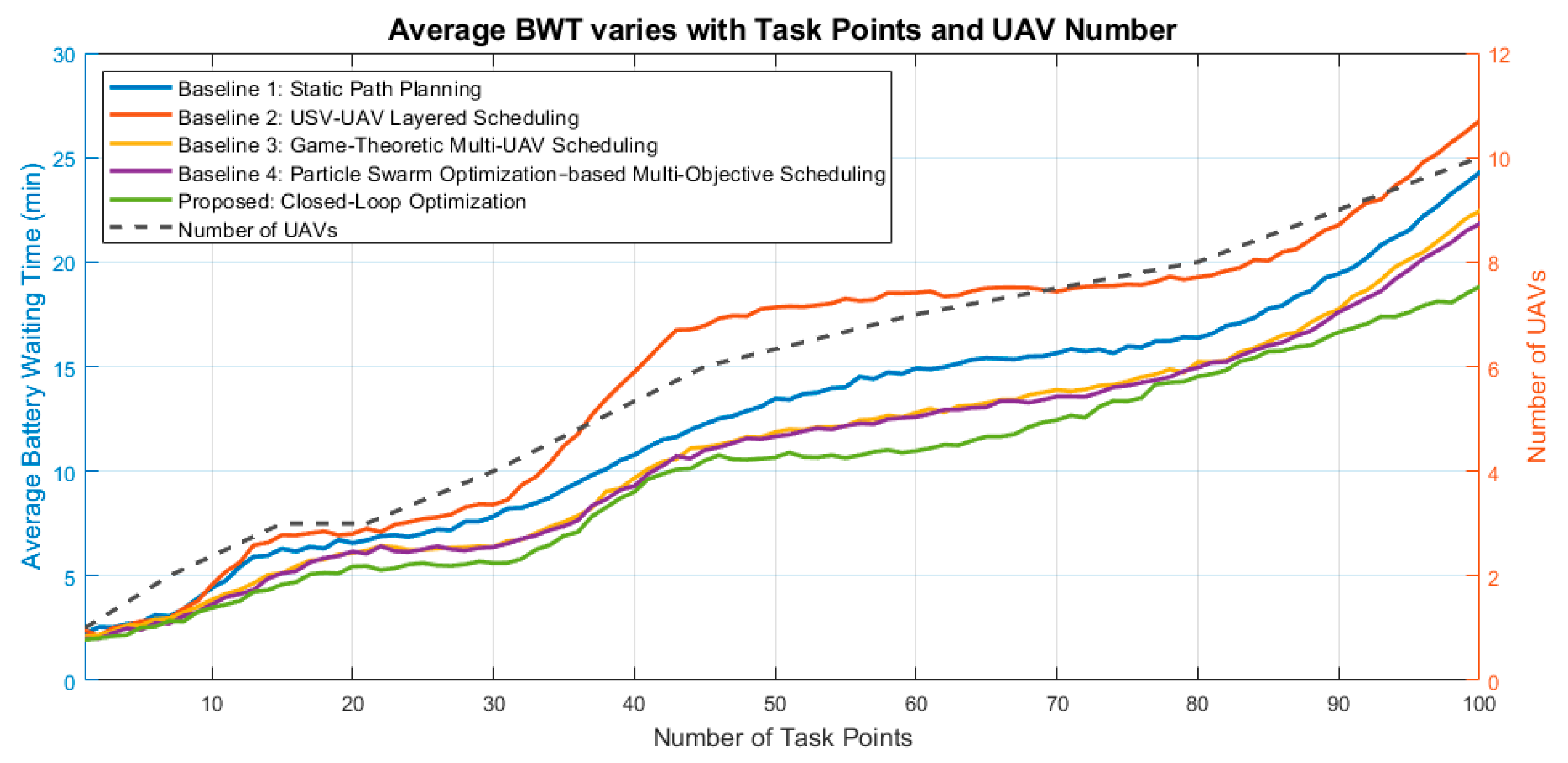
In multi-UAV concurrent operations, replenishment resources (such as battery replacement equipment on the USV) often become the critical bottleneck that constrains task efficiency. The battery replacement waiting time (BWT) directly reflects UAV queuing delays during replenishment and is therefore an important indicator for evaluating scheduling performance.
To analyze UAV battery replacement efficiency under different task scales, tasks are classified into three categories:
Small-scale tasks: 10 UAVs distributed across 1–2 operational areas, working simultaneously.
Medium-scale tasks: 10 UAVs distributed across 3–4 operational areas, with increased number of tasks and larger inter-task spacing.
Large-scale tasks: 10 UAVs distributed across 5–6 operational areas, with higher task density and more frequent returns for replenishment.
Each experiment was repeated 10 times, and the average
BWT was taken as the statistical result for the three methods.
Table 4 provides a quantitative comparison of
BWT under different task scales.
Comparison of the three methods:
Baseline 1: UAVs return to a fixed USV point. BWT increases linearly with task scale, and local congestion occurs during peaks, especially in medium and large tasks.
Baseline 2: UAVs return to a moving USV. While mobility alleviates some energy issues for small tasks, simultaneous UAV arrivals exacerbate queuing, causing BWT to increase sharply, exceeding 20% of mission time for large tasks.
Baseline 3 (GT-MUS): Game-theoretic task allocation balances UAV arrivals better than Baseline 1 and 2, reducing BWT by 5–10% for medium and large tasks.
Baseline 4 (PSO-MO): Multi-objective optimization further coordinates UAV returns, maintaining slightly lower BWT than GT-MUS under all task scales.
Proposed Method: By predicting UAV replenishment demand and dynamically allocating time slots with priority adjustments, the Proposed method maintains the lowest and most stable BWT across all scales. For example, at large-scale tasks, BWT is 11.55 min, 16.3% lower than Baseline 1 and 29.7% lower than Baseline 2.
In multi-UAV operations, replenishment resources (e.g., battery replacement equipment on the USV) remain a critical bottleneck, and BWT reflects queuing delays during replenishment, serving as a key performance metric for scheduling evaluation.
Tasks were categorized into three scales with varying UAV numbers:
Small-scale tasks: 1–2 operational areas, 2–4 UAVs, low task density, and fewer conflicts during single replenishment, resulting in relatively low BWT.
Medium-scale tasks: 3–4 operational areas, 5–7 UAVs, and moderate task density, with some UAVs returning simultaneously, leading to a sharp increase in BWT.
Large-scale tasks: 5–6 operational areas, 8–10 UAVs, high task density, and frequent simultaneous returns, causing the fastest BWT growth and potential congestion.
Each experiment was repeated 10 times, and the mean
BWT was calculated.
Table 5 summarizes the results.
Small-scale tasks: With fewer UAVs and lower task density, replenishment demand is less concentrated, so BWT remains relatively low for all methods. However, the Proposed method consistently achieves lower BWT than Baseline 2, demonstrating the effectiveness of advance time-window scheduling and dynamic priority allocation in smoothing UAV arrivals and reducing queuing.
Medium-scale tasks: As UAV numbers and inter-task distances increase, multiple UAVs often return to the USV simultaneously, sharply increasing queuing times. Baseline 2 exhibits the fastest growth in BWT, exceeding 20% of the mission duration in some cases. In contrast, the Proposed method predicts UAV replenishment demand and dynamically allocates priorities, effectively mitigating congestion and reducing BWT by approximately 30% relative to Baseline 2. Baseline 3 (GT-MUS) and Baseline 4 (PSO-MO) also improve BWT compared with Baseline 1 and 2 but to a lesser extent than the Proposed method.
Large-scale tasks: High task density and frequent simultaneous UAV returns exacerbate queuing. Both Baseline 1 and Baseline 2 suffer from severe congestion, with peak BWTs rising significantly. The Proposed method, by maintaining dynamic scheduling and priority allocation, ensures BWT remains relatively low and stable. Fluctuations across repeated trials are minimal, confirming the robustness of the strategy and its ability to maintain replenishment efficiency and fairness under heavy load.
These results confirm that the Proposed method effectively addresses resource contention in multi-UAV operations, providing both efficiency and fairness in battery replacement scheduling across different task scales, as shown in
Figure 6.
By comprehensively analyzing four key performance indicators—total mission time (TMT), task completion rate (TCR), total energy consumption (TEC), and battery replacement waiting time (BWT)—the overall effectiveness of the five scheduling methods in multi-UAV concurrent operations can be systematically evaluated.
Experimental results indicate that the Proposed method consistently achieves the best mission performance. Across small- to large-scale tasks, UAVs exhibit significantly shorter average mission completion times compared with Baseline 1 and Baseline 2, while simultaneously achieving higher task coverage rates, ensuring both comprehensiveness and reliability.
In terms of energy efficiency, Baseline 1 shows the highest consumption due to frequent long-distance returns, whereas Baseline 2 reduces energy use slightly through a mobile USV, yet fixed trajectories still constrain efficiency. In contrast, the Proposed method balances UAV workloads and employs dynamic path planning, effectively minimizing unnecessary returns and redundant flights. Consequently, total energy consumption is reduced by approximately 12–18% on average, improving operational economy.
BWT analysis further highlights scheduling efficiency: Baseline 2 suffers from severe queuing delays in medium- and large-scale tasks, whereas the Proposed method leverages time-window scheduling and dynamic priority allocation, allowing UAVs to secure replenishment slots before arrival. This reduces BWT by roughly 30% on average, alleviating the resource contention bottleneck while maintaining fairness.
In summary, across all four metrics, the Proposed method outperforms previous approaches in mission efficiency, energy economy, and replenishment scheduling. Its advantages are particularly pronounced in large-scale or high-density scenarios, demonstrating that combined time-window scheduling and dynamic priority allocation can enable efficient, energy-saving, and fair operations in multi-UAV concurrent missions.