Task Allocation and Path Planning Method for Unmanned Underwater Vehicles

Abstract

Cooperative operations of Unmanned Underwater Vehicles (UUVs) have extensive applications in fields such as marine exploration, ecological observation, and subsea security. Path planning, as a key technology for UUV autonomous navigation, is crucial for enhancing the adaptability and mission execution efficiency of UUVs in complicated marine environments. However, existing methods still have significant room for improvement in handling obstacles, multi-task coordination, and other complex problems. In order to overcome these issues, we put forward a task allocation and path planning method for UUVs. First, we introduce a task allocation mechanism based on an Improved Grey Wolf Algorithm (IGWA). This mechanism comprehensively considers factors such as target value, distance, and UUV capability constraints to achieve efficient and reasonable task allocation among UUVs. To enhance the search efficiency and accuracy of task allocation, a Circle chaotic mapping strategy is incorporated into the traditional GWA to improve population diversity. Additionally, a differential evolution mechanism is integrated to enhance local search capabilities, effectively mitigating premature convergence issues. Second, an improved RRT* algorithm termed GR-RRT* is employed for UUV path planning. By designing a guidance strategy, the sampling probability near target points follows a two-dimensional Gaussian distribution, ensuring obstacle avoidance safety while reducing redundant sampling and improving planning efficiency. Experimental results demonstrate that the proposed task allocation mechanism and improved path planning algorithm exhibit significant advantages in task completion rate and path optimization efficiency.

1. Introduction

Unmanned Underwater Vehicles (UUVs) are widely utilized in diverse fields, such as oceanic exploration, environmental surveillance, underwater rescue missions, and military applications. The enhancement of their autonomy and cooperative capabilities is crucial for the efficiency of underwater missions [1,2,3,4]. In multi-UUV systems, efficient task allocation and path planning are essential not only for the performance of individual units, but also for ensuring global system optimization and high-quality task execution. However, the underwater environment is complex and variable, with challenges such as limited communication conditions and dynamic environmental disturbances, which impose higher demands on the cooperative capabilities of UUVs [5,6]. Therefore, researching efficient methods for task allocation and path planning is of significant theoretical value and engineering importance for improving the autonomous collaborative capabilities of UUVs and enhancing mission execution reliability.

In task allocation for UUV mission planning, conventional methods involve the Hungarian algorithm and centralized linear programming techniques. Recently, with the rapid development of swarm intelligence optimization algorithms and neural network techniques, researchers have increasingly introduced intelligent optimization theories to provide new solutions for swarm task allocation. For instance, Wu et al. put forward a dynamic expanding consensus bundle algorithm based on a consensus algorithm. Extensive results demonstrated that this approach enables fast and efficient conflict-free dynamic task allocation for UUVs [7]. Yu et al. addressed the challenges of target search under limited underwater communication and dynamic environmental changes by proposing a cooperative search task planning method for UUVs based on modified k-means clustering and a dynamic consensus-based bundle algorithm (DCBBA-TICC) [8]. This method evaluates the reliability of acoustic communication links using the frame error rate and optimizes communication relay positions using the particle swarm optimization (PSO) algorithm. Li et al. introduced a multi-objective bi-level task planning approach to address the issue of dispatching UUVs to visit a series of targets [9]. Simulated annealing and a genetic algorithm were utilized to optimize task allocation and path planning simultaneously. However, as the number of UUVs increases, it becomes challenging to address load balancing between different levels. Yang et al. modeled the task of detecting potential underwater threats as a traveling salesman problem (TSP) with specified starting and ending points, and applied the ant colony optimization (ACO) algorithm to find a solution [10]. However, this approach did not fully consider complicated obstacles in UUV motion planning. To improve task efficiency and quality, Li et al. proposed a balanced task planning strategy for multi-route patrol and detection missions, aiming to reduce mission time while enhancing task performance [11].

Path planning aims to generate a short, safe, and feasible trajectory for unmanned underwater vehicles (UUVs) to reach their target locations [12,13]. To mitigate the effect of navigation errors on UUV path planning, Ma et al. introduced a hybrid approach combining quantum principles with particle swarm optimization [14]. This approach considers navigation errors and generates a time-optimal and safe trajectory, effectively mitigating the adverse effects of navigation inaccuracies. Li et al. proposed a combined strategy that merges an enhanced A* path planning algorithm with model predictive control (MPC) [15]. This method integrates path planning with trajectory tracking, greatly enhancing the real-time path planning performance of UUVs. Yu et al. proposed a cylinder-heuristic rapidly exploring random tree (termed Cyl-HRRT*) algorithm [16]. This approach enhances the likelihood of sampling feasible states by biasing the search toward cylindrical subsets, thereby yielding more optimal paths for autonomous underwater vehicles (AUVs). To solve the problem of three-dimensional path planning for UUVs, Chen et al. proposed a hybrid algorithm that combines particle swarm optimization with ant colony optimization (PSO-ACO) [17]. Li et al. developed the PQ-RRT* algorithm (Potential-Quick Rapidly-exploring Random Tree Star) to overcome the challenges of path planning for UUVs in complicated environments [18]. Experimental results show that this algorithm improves the convergence speed and path quality of UUV path planning, and effectively balances the efficiency and optimality of search. Experimental results show that this combined approach improves the global search efficiency and reduces search time. In recent years, deep reinforcement learning has shown unique advantages in path planning due to its autonomous learning and decision-making optimization capabilities [19,20,21]. For instance, Wang et al. addressed issues such as large oscillations and low learning efficiency in traditional actor-critic reinforcement learning algorithms during the initial training phases, and put forward a multi-actor-critic reinforcement learning approach for path planning of AUVs [21]. The simulation results demonstrate that the proposed method enhances adaptive learning capabilities in dynamic scenarios and increases the effectiveness of AUV obstacle avoidance.

Motivated by the above work, we put forward a task allocation and path planning approach for UUVs. By integrating an Improved Grey Wolf Algorithm (IGWA) into the task allocation process, the proposed approach enhances the efficiency of UUVs in reaching their target locations. Furthermore, an improved GR-RRT* algorithm is introduced to address path planning challenges in complicated underwater environments. The simulation results confirm the effectiveness and flexibility of the proposed method. The key contributions of our work are as follows:

• An Improved Grey Wolf Optimization (IGWA) algorithm is proposed for task allocation in multi-UUV systems, providing an optimized foundation for subsequent path planning.
• We introduce a circle chaotic mapping mechanism into the GWA method to mitigate the issue of uneven initial population distribution. Additionally, a differential evolution mechanism is incorporated to enhance local search capability and prevent premature convergence.
• A modified RRT*-based path planning algorithm is developed, featuring a goal-guided sampling strategy that ensures obstacle avoidance while reducing excessive sampling, thereby improving planning efficiency.

The structure of the paper is as follows: In Section 2, the scenario tasks are briefly introduced and a simulation environment model is established. In Section 3, the improved task allocation method and path planning algorithm are introduced. In Section 4, the simulation results under various simulation environments and the real boat experimental results are analyzed. Finally, a summary is given in Section 5.

2. Overview of the Basic Scenario

2.1. Problem Description

This study focuses on the collaborative operation of UUVs in complex marine environments. The objective is to achieve rapid and optimized task allocation for UUV target points while generating safe and feasible optimal navigation paths. In real underwater environments, UUVs must navigate around various irregularly shaped and unevenly distributed obstacles, such as coral reefs, underwater mountains, and shipwreck debris. To ensure safe navigation, all obstacle regions are uniformly defined as inaccessible regions, which must be strictly avoided. To address this challenge, a task scenario is designed in which path planning is conducted in obstacle-rich environments. The study emphasizes both the efficiency of UUV target allocation and the adaptability of UUVs in dynamically adjusting their paths during obstacle avoidance, ensuring mission safety and feasibility in complex underwater conditions.

2.2. Environmental Modeling

Underwater obstacles often exhibit complex shapes and varying sizes, typically categorized into convex and concave types. To facilitate algorithm validation, the obstacle environment is simplified in the simulation setup, as shown in Figure 1. Specifically, a 400 m × 400 m water area is designed, where black regions represent obstacle zones. Irregular obstacles are transformed into relatively regular shapes while preserving their key characteristics. In addition, four initial points (A, B, C, D) and four target points are randomly distributed around the obstacles to cover various path planning scenarios. It is noteworthy that the four target points possess different values, and the UUVs are assumed to require different capabilities. Therefore, a target-specific initial task allocation is designed to establish a solid foundation for subsequent path planning.

3. Task Allocation Approach for UUVs

The problem of assigning tasks to UUVs can be characterized as follows: Within a specified mission context, numerous UUVs having distinct performance attributes are delegated to carry out various tasks. At the same time, it is essential to make sure that every task is carried out by a UUV. Meanwhile, it must be ensured that each task is executed by a UUV. Nevertheless, in the actual task allocation process, some factors will affect the allocation results, such as the ocean environment, path cost, task success rate and UUV damage probability. Thus, it is essential to develop an optimization model for task allocation to ensure an efficient allocation solution. In this way, it ensures that each UUV is allocated an appropriate target, thereby maximizing the overall benefits and minimizing the operational costs for the entire UUVs. Drawing inspiration from the hunting behavior of wolves, we employ the GWA algorithm to allocate tasks for UUVs, aiming to derive the optimal task distribution solution.

Specifically, we use a five-tuple model $\{\mathrm{T}, \mathrm{U}, \mathrm{C}, \mathrm{O}, \mathrm{E}\}$ to construct the task allocation model. In this model, T represents the task set, U represents the UUV set, C represents the constraints in task allocation, O represents the objective function in task allocation, and E represents the marine environmental factors. In order to ensure that each UUV can achieve efficient allocation efficiency, the following aspects need to be comprehensively considered during the task allocation process to ensure the flexibility and feasibility of the assigned tasks.

3.1. Constraints

In terms of AUV task distribution, it is necessary to ensure that each task is executed by only one UUV, and each UUV is assigned one task. Assuming M UUVs and N targets, the constraint can be mathematically formulated as follows:

$$\sum _{i=1}^M\sum _{j=1}^N{x}_{ij}=1$$

(1)

$$dList=\left\{U_i\in U,T_j\in T,\mid U_i\to T_j\right\}$$

(2)

In Formula (1), $x_{ij}$ represents a binary decision variable, indicating whether $U_i$ is assigned to perform the task. If $x_{ij}=1$, it means that $U_i$ is assigned to perform the task, and if $x_{ij}=0$, it means that UUV i is not assigned to perform the task. Formula (2) represents the UUV and target allocation result.

3.2. Target Benefit

In UUV task allocation, target utility computation serves as a fundamental metric for assessing the effectiveness of the allocation strategy. This utility not only includes the direct result of the task but also embodies task execution efficiency and the optimal allocation of resources. Given the differences in the performance of each UUV, the success probability and benefits of the same task will be different when it is performed by different unmanned boats. Assume that $P_{ij}$ represents the probability that the UUV $U_i$ completes the task target $T_j$, and ${\mathrm{Value}}_{ij}$ represents the benefit that the $U_i$ can obtain by executing the task target $T_j$. Moreover, ${\mathrm{Value}}_u$ represents the value of UUV, and ${\mathrm{Value}}_t$ represents the value of the target. The value of UUV lies mainly in its ability to perform tasks, while the target value quantifies the priority of the task goals and the demand for resource allocation. Therefore, the total task benefit function of all UUVs can be expressed as:

$$\left\{\begin{array}{c}\mathrm{Value}={\lambda }_1·P_{ij}·{\mathrm{Value}}_{ij}+{\lambda }_2·{\mathrm{Value}}_u+{\lambda }_3·{\mathrm{Value}}_{\mathrm{t}}\hfill \\ {\lambda }_1+{\lambda }_2+{\lambda }_3=1\hfill \end{array}\right.$$

(3)

where ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are normalized weight coefficients.

3.3. Comprehensive Loss

In the process of UUVs performing mission objectives, they can not only obtain benefits, but also incur certain damage costs, which mainly include the range cost, damage cost, and resource cost. However, to simplify the complexity of the model in this work, the time cost and damage cost are not taken into consideration. This study only focuses on the range cost and environmental cost incurred by a UUV when performing different tasks.

Specifically, the UUV’s voyage cost can be understood as the UUV’s navigation loss caused by the complex environment, which is determined by the total distance from the UUV to the target. We adopt the Euclidean distance between two points to approximate the voyage between them. i is the UUV number, j is the target number, and the voyage cost function is expressed as:

$$\mathrm{costdis}=f\left({\mathrm{distance}}_i^j\right)=\sqrt{{\left(x_i^{\mathrm{uuv}}-x_j^{\mathrm{target}}\right)}^2+{\left(y_i^{\mathrm{unv}}-y_j^{\mathrm{target}}\right)}^2}$$

(4)

In addition, the environmental cost indicates that in the actual mission execution process, marine environmenta factors will affect the navigation of the UUV to a certain extent, and the fixed cost calculation formula may be too idealized and difficult to generalize to the real mission scenario. Therefore, in order to simulate the uncertainty in the actual mission execution, it is necessary to add noise to simulate the random disturbance in reality, so that the task allocation is more robust, thereby improving the feasibility of the algorithm in real applications. Environmental impacts on the UUV are simulated by adding noise characterized by a normal distribution, and the environmental cost function is expressed as:

$$costenv=\omega \left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}exp\left(-{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }^2}}\right)$$

(5)

where $\mu =0$ and $\sigma$=50.

Based on the above functions for different cost costs, we design the cost function for the multi-UUV task allocation problem as follows:

$$\left\{\begin{array}{c}\mathrm{Cost}={\gamma }_1·\mathrm{costdis}+{\gamma }_2·\mathrm{costen}v\hfill \\ {\gamma }_1+{\gamma }_2=1\hfill \end{array}\right.$$

(6)

where ${\gamma }_1$ and ${\gamma }_2$ are normalized weight coefficients.

3.4. Objective Function

When assigning UUVs to target tasks, the goal is to lay a solid foundation for subsequent path planning, with the allocation strategy comprehensively considering multiple factors. On one hand, it is crucial to minimize the loss value, ensuring that the wear and tear on UUVs during task execution is kept to a minimum. On the other hand, the strategy should emphasize maximizing the benefit value to ensure the effectiveness of the allocation scheme. Therefore, the allocation process requires a strategy that balances both loss and benefit, aiming to minimize the cost incurred during the approach phase. The specific formulation of the objective function F is described as follows:

$$F=\mathrm{Value}-\mathrm{Cost}$$

(7)

It should be emphasized that task allocation and path planning are closely interconnected rather than independent processes. The designated target location for a UUV directly influences the difficulty of its path planning, while the feasibility of the planned path should also be considered during task assignment.

• The influence of task allocation on path planning: If a UUV is assigned to a target that is far from its initial position and surrounded by obstacles, it may lead to an increase in the time consumption of path planning or a deterioration in the quality of the path. Therefore, in the objective function of task allocation, in addition to considering the target value and distance, the pre-assessment indicators of path planning can be implicitly introduced as constraints.
• Path planning feedback on task allocation: For certain targets for which it is difficult to plan feasible paths, the task allocation needs to be adjusted, and they should be assigned to UUVs with stronger obstacle avoidance capabilities or better initial positions.

Although the IGWA algorithm in this paper indirectly considers some spatial factors by integrating the cost function, an explicit linkage mechanism between task allocation and path planning has not yet been established. The in-depth modeling of this coupling relationship will be an important direction for future research. For example, by constructing a joint optimization framework, the difficulty of path planning can be predicted during the task allocation stage, and the allocation strategy can be dynamically adjusted to achieve global collaborative optimization.

3.5. Improved Grey Wolf Algorithm

The Grey Wolf Algorithm (GWA) [22] is a swarm intelligence optimization method inspired by the cooperative behavior of grey wolves during hunting. To further strengthen its ability to achieve the global optimal solution, the algorithm requires continued refinement and improvement. Therefore, we improved the Grey Wolf Algorithm from two key aspects. First, we replace the original random initialization of the wolf group method with initialization using Circle chaotic mapping [23]. Compared with random number generation, chaotic mapping shows superior characteristics in the optimization search process, especially in solving the global optimal solution problem. The advantage of chaotic mapping is that it can fully cover the search space to avoid missing potential solution areas, effectively avoid local optimal traps to expand the scope of solution space exploration. At the same time, this mechanism maintains the optimization direction to a certain extent, thereby accelerating the convergence process of the algorithm.

Specifically, the expression formula of Circle mapping is as follows:

$$x_{i+1}=mod\left(x_i+a-\left({\displaystyle \frac{b}{2\pi }}\right)\sin \left(2\pi x_i\right),1\right)$$

(8)

where $x_i$ denotes the state variable of the current iteration, $x_{i+1}$ denotes the state variable of the next iteration, $a=0.5$ and $b=0.2$ are control parameters.

In the realm of differential evolution and related optimization algorithms, parameter selection is of the utmost importance. The parameter a in the Circle mapping formula plays a crucial role in determining the basic step—like movement of the state variable from one iteration to the next. A value of $0.5$ provides a moderate offset that helps in balancing global exploration. It is large enough to encourage the algorithm to explore new regions of the search space, yet not so large as to cause erratic and unproductive jumps.

Parameter b influences the oscillatory component of the mapping through its role in the $sin$ function term. This relatively small value means that the sinusoidal perturbation has a subdued impact. It allows for a gentle modulation of the state variable’s progression, facilitating local exploitation. By choosing $b=0.2$, the algorithm can fine-tune its search around promising areas while still maintaining enough randomness to avoid becoming trapped in local optima. Overall, these parameter values work in tandem to enhance the algorithm’s ability to balance exploration and exploitation, improving its effectiveness in optimization tasks.

Although the current parameter configuration has achieved performance improvement through empirical methods, the quantitative impact of these parameters on population diversity and convergence speed is still not fully clear. Therefore, it is planned to design orthogonal experiments in subsequent work to provide a theoretical basis for the adaptive parameter adjustment of the algorithm in different task scenarios.

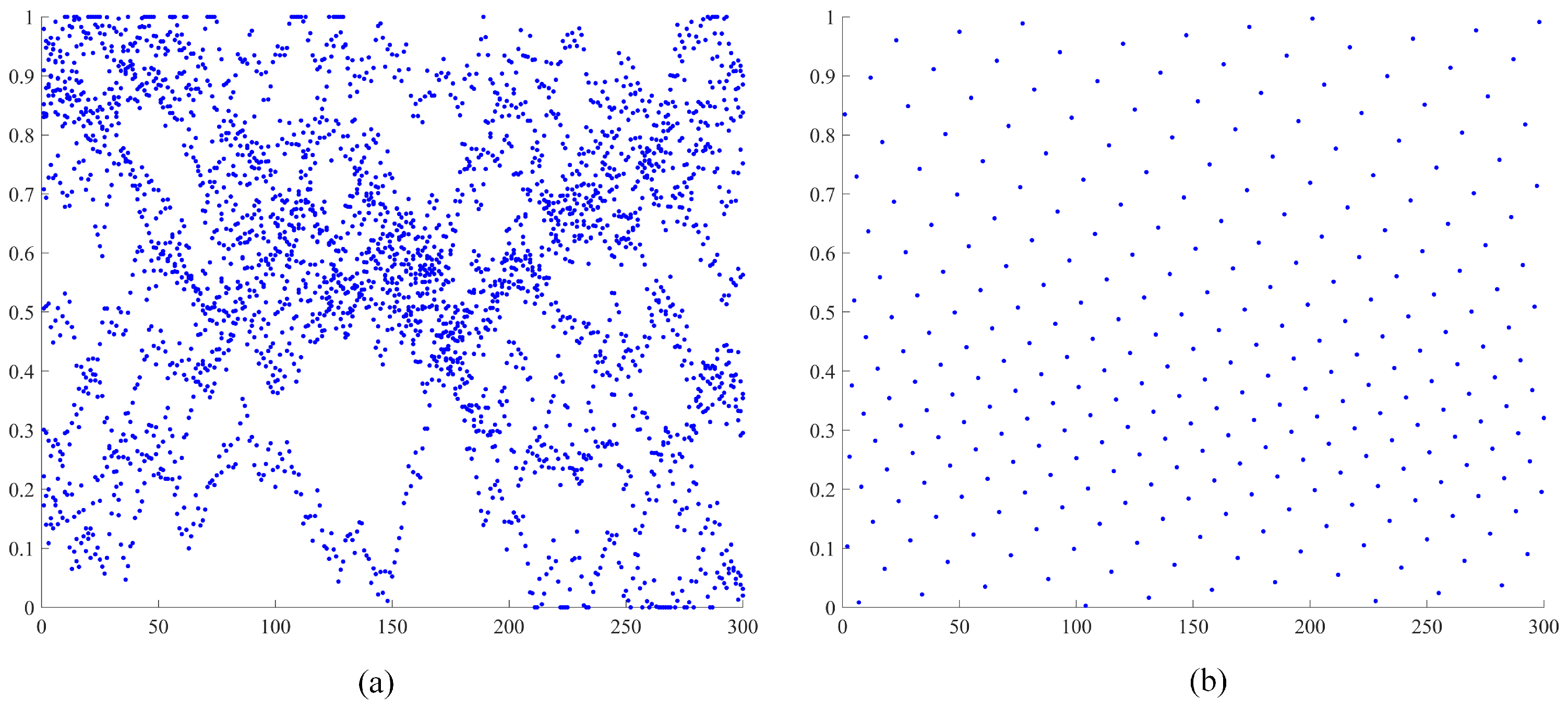
As illustrated in Figure 2, the traditional Grey Wolf Algorithm relies on random initialization of the wolf pack, which may lead to uneven distribution of initial individuals, potentially limiting the algorithm’s global search capability. By incorporating Circle chaotic mapping during initialization, a more diverse and evenly distributed initial population is generated, enhancing both the algorithm’s global exploration ability and optimization efficiency.

In the position update process of the Grey Wolf Optimization Algorithm, individuals with lower fitness continue to follow the original update mechanism, while those with higher fitness are updated using the differential evolution strategy (randk). This approach helps balance the algorithm’s global exploration and local exploitation capabilities, ultimately enhancing overall optimization performance. As a population-based global optimization method, differential evolution generates new candidate solutions through mutation and crossover operations, effectively improving the algorithm’s search depth. Specifically, the integration of differential evolution strengthens the Grey Wolf Optimization Algorithm through the following mutation and crossover mechanisms: Mutation operation: Differential operations among individuals in the population introduce randomness, expand the search space, and enhance global exploration capability. In this way, it helps to solve the problem of grey wolves escaping from local optimality. As a key stage in the differential evolution algorithm, differential mutation generates new candidate solutions by utilizing individuals from the current population. It promotes information exchange among population members and guides the search process toward the global optimum. The specific operation is to randomly select three different individuals $x_{r1}$, $x_{r2}$, $x_{r3}$ and generate a new mutation vector $v_i$, which is expressed as follows:

$$v_i=x_{r1}+F·\left(x_{r2}-x_{r3}\right)$$

(9)

where F is the scaling factor, typically $F\in [0,2]$.

Crossover operation: Crossover generates new candidate solutions by combining traits from multiple high-quality individuals, enhancing the algorithm’s local exploitation capability. This operation maintains diversity within the search space. The mutated individuals undergo crossover with the current population to produce candidate solutions. The crossover probability CR ($CR\in (0,1)$) determines whether the solution from the mutated individual is accepted, promoting a balance between exploration and exploitation. Binomial crossover is usually used to generate the vector $u_i$, which is described as follows:

$$u_{i,j}=\left\{\begin{array}{cc}{v}_{i,j}\hfill & \mathrm{if}\mathrm{rand}(0,1)\le CR,\hfill \\ x_{i,j}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(10)

In this context, CR stands for the crossover probability, which regulates the mixing proportion between the mutation vector and the original solution. The symbol $u_{i,j}$ signifies the jth dimensional component of the test vector created after crossover, $v_{i,j}$ represents the jth dimensional component of the mutation vector, and $x_{i,j}$ indicates the value of the original individual in the jth dimension.

4. Improved Path Planning Algorithm for UUVs

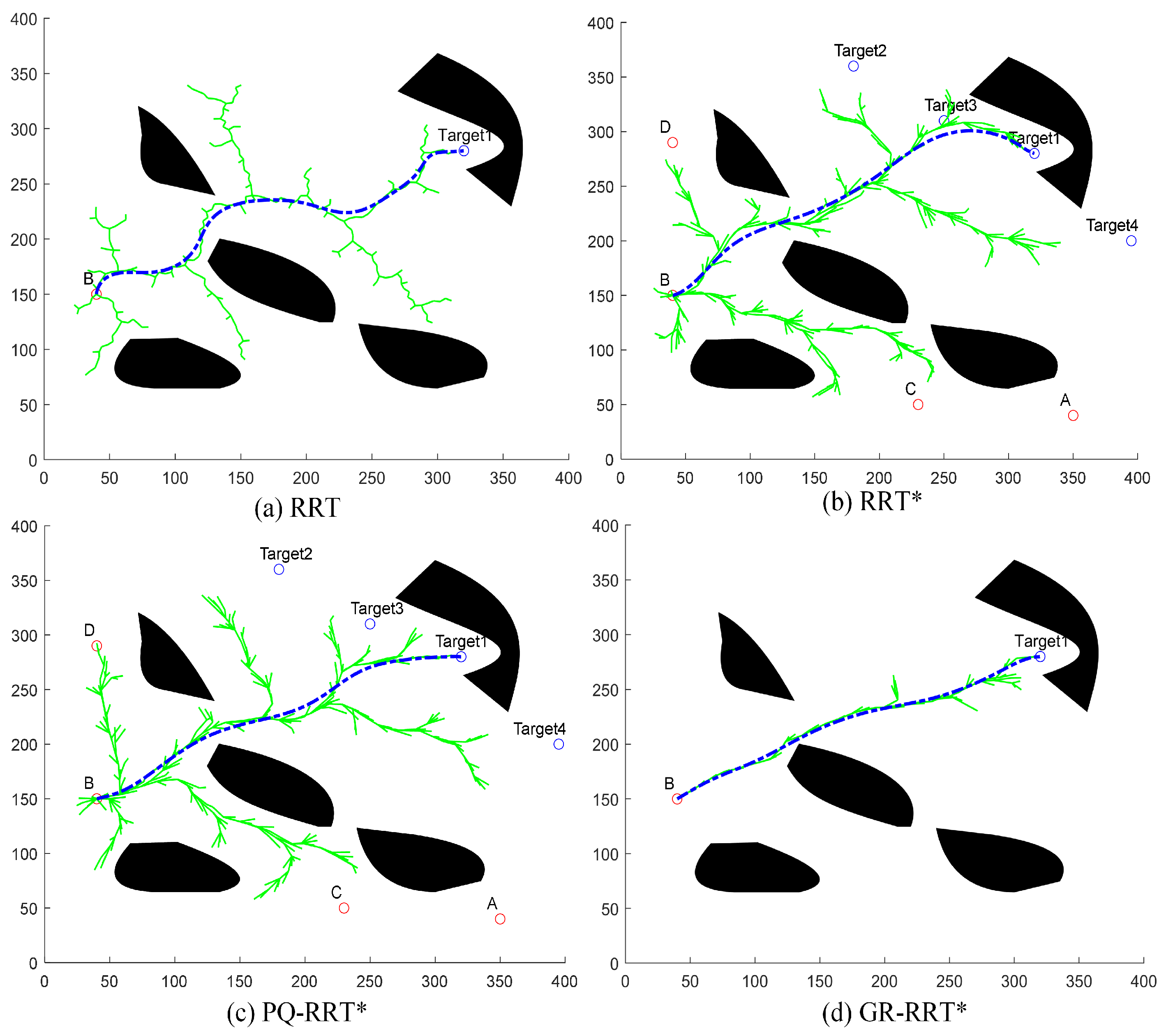
We propose an improved version of the RRT* algorithm in this section [24], termed Goal-Region Guided RRT (GR-RRT*), designed to achieve more efficient path planning. Traditional RRT* algorithms generate sampling points uniformly across the entire map, ensuring global search coverage. However, the presence of numerous redundant points significantly reduces convergence efficiency. To address this issue, our algorithm introduces an innovative goal-oriented regional sampling strategy. Specifically, instead of distributing random sampling points uniformly across the entire space, sampling is restricted to a dynamically adjusted region around the target point, following a normal distribution. This approach effectively reduces the number of redundant samples and directs the search process toward the target region, enhancing convergence speed.

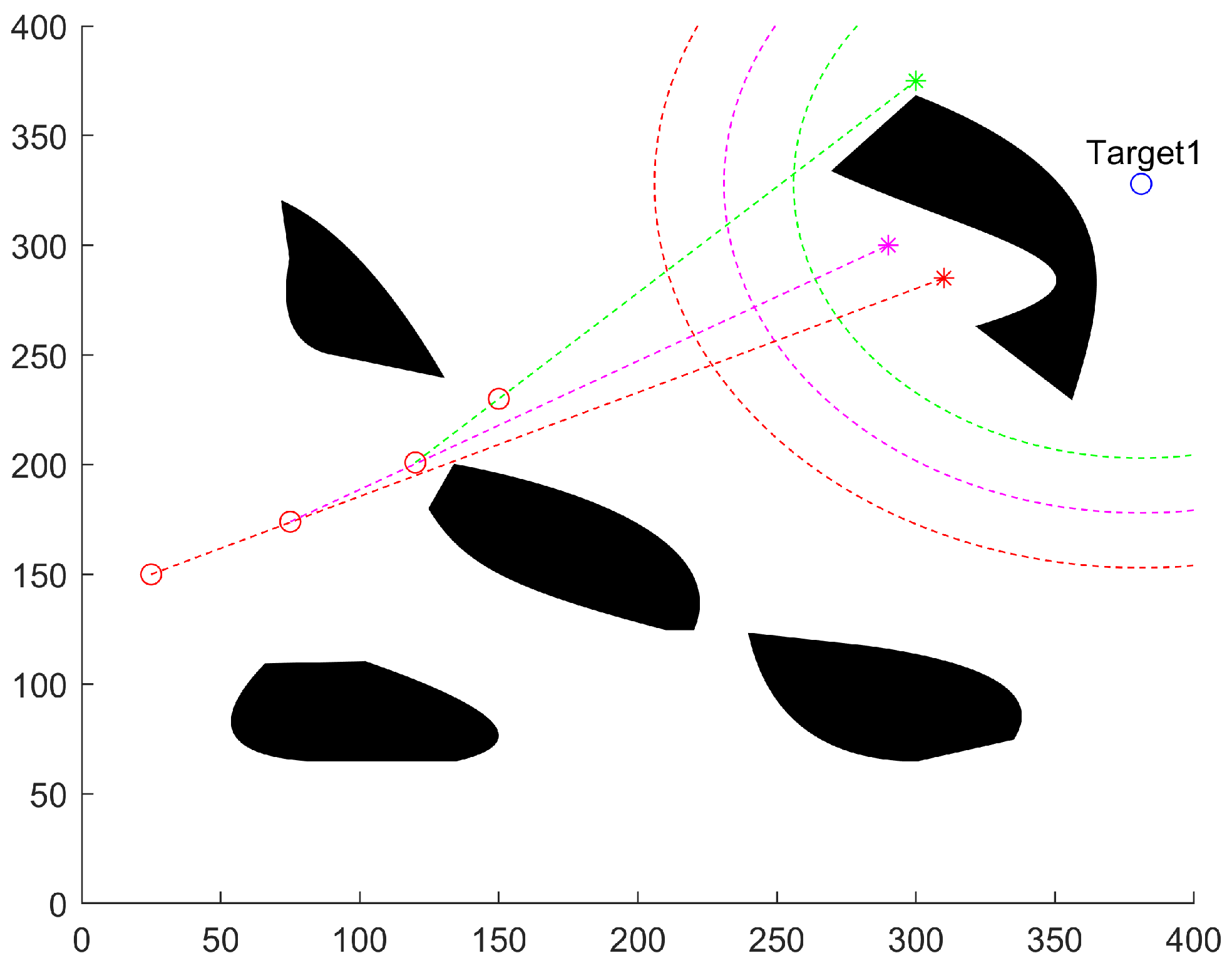
As illustrated in Figure 3, the dynamic evolution of the sampling region can be observed through three sampling iterations. When the existing nodes are far from the target point, the sampling region remains relatively large to ensure the random tree explores the environment thoroughly, avoids obstacles, and prevents premature convergence to suboptimal paths. As nodes gradually approach the target, the sampling region contracts, accelerating fine-tuned exploration and final convergence. This adaptive sampling mechanism ensures a balance between exploration and exploitation, improving both search efficiency and path quality compared to traditional RRT* algorithms.

The research in this paper focuses on 2D UUV path planning, where the proposed algorithm generates random sampling points around the target point, modeled as a 2D normal distribution problem. If random variables follow a bivariate normal distribution, the probability density function is expressed as:

$$f(x,y)={\displaystyle \frac{1}{2\pi {\sigma }_x{\sigma }_y\sqrt{1-{\rho }^2}}}exp\left(-{\displaystyle \frac{1}{2\left(1-{\rho }^2\right)}}\left[{\displaystyle \frac{{\left(x-{\mu }_x\right)}^2}{{\sigma }_x^2}}+{\displaystyle \frac{{\left(y-{\mu }_y\right)}^2}{{\sigma }_y^2}}-{\displaystyle \frac{2\rho \left(x-{\mu }_x\right)\left(y-{\mu }_y\right)}{{\sigma }_x{\sigma }_y}}\right]\right)$$

(11)

$$\left\{\begin{array}{c}{\sigma }_x={\displaystyle \frac{d_{\min }}{d_{\mathrm{init}}}}\left({\sigma }_{x\max }\right)\hfill \\ {\sigma }_y={\displaystyle \frac{d_{\min }}{d_{\mathrm{init}}}}\left({\sigma }_{y\max }\right)\hfill \end{array}\right.$$

(12)

where $f(x,y)$ is the generation probability of the sampling point at $(x,y)$ position in the map. The variances are ${\sigma }_x$, ${\sigma }_y$, and $\rho$ (set to 0) is the correlation coefficient of two variables. ${\mu }_x$ and ${\mu }_y$ are the location information of the target point. ${\sigma }_x$ and ${\sigma }_y$ are related to the surrounding environment of the target point and the shortest distance from all nodes to the target point. In Formula (12), $d_{\min }$ represents the minimum distance from all the existing nodes to the target point, $d_{\mathrm{init}}$ is the distance from the starting point to the target point, ${\sigma }_{x\max }$ and ${\sigma }_{y\max }$ represent the initial variances. Their values are empirically determined, with adjustments made based on the surrounding environment of the target point. The initial variances should be set to ensure that the resulting high-probability region adequately covers obstacles near the target, facilitating effective exploration and improving path planning robustness.

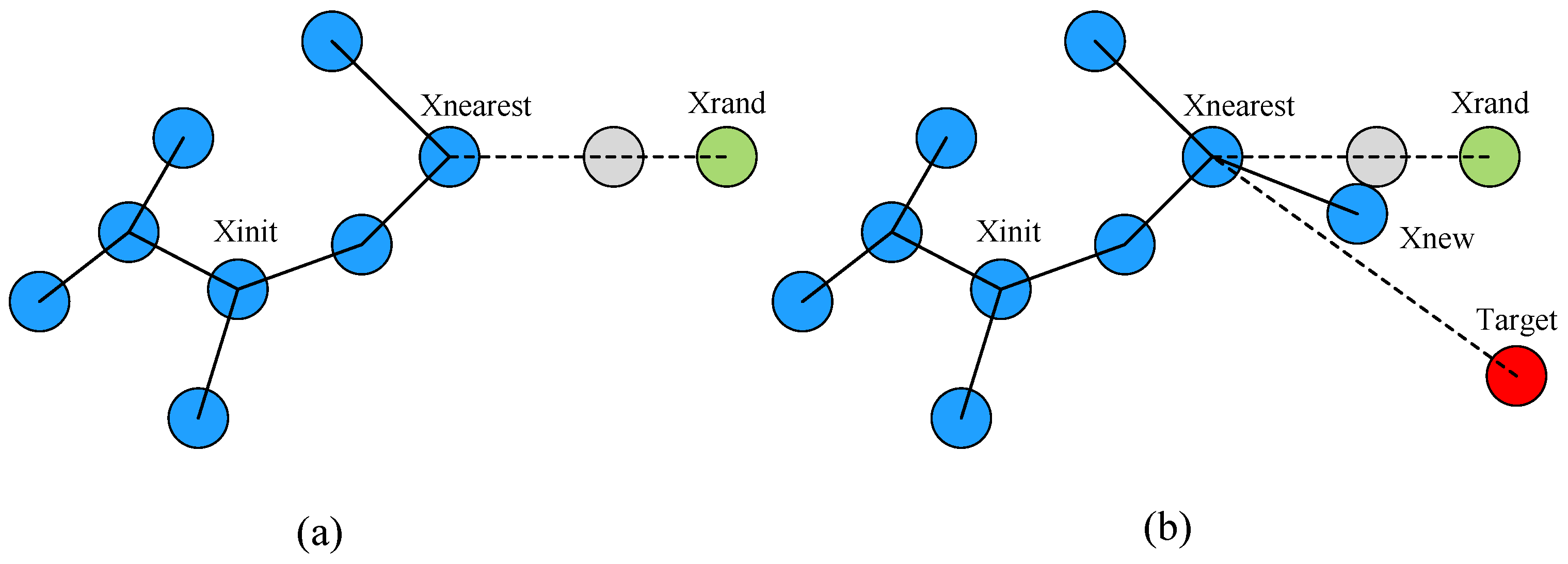
To address the limitations of traditional RRT* algorithms, which select the nearest node to the random sampling point and generate new nodes based solely on their positional relationship, we incorporate the concept of attractive potential from the Artificial Potential Field (APF) approach to improve planning efficiency.

In contrast to the traditional APF method, the enhanced GR-RRT* algorithm focuses solely on the gravitational effect of the target point, disregarding the repulsive influence of obstacles. This design can not only effectively avoid falling into the local minimum area or the problem of unreachable target during path planning, but also significantly accelerate the convergence speed of the algorithm. The conceptual diagram of this idea is shown in Figure 4b, which clearly shows the guiding effect of the gravity of the target point on the direction of new node generation. By introducing this goal-oriented gravitational mechanism, the algorithm can significantly reduce redundant searches and improve overall planning efficiency while ensuring path quality.

Specifically, the new node calculation formula based on the above concept graph idea is as follows:

$$\left\{\begin{array}{c}{x}_{\mathrm{new}}=x_{\mathrm{nearest}}+L^{*}\left(\cos {\theta }_{\mathrm{rand}}+K\cos {\theta }_{\mathrm{targ}et}\right)\hfill \\ y_{\mathrm{new}}=y_{\mathrm{nearest}}+L^{*}\left(\sin {\theta }_{\mathrm{rand}}+K\sin {\theta }_{\mathrm{targ}et}\right)\hfill \end{array}\right.$$

(13)

$$L=\left\{\begin{array}{cc}\mathrm{step}\hfill & L_{r-n}\ge \mathrm{step}\hfill \\ L_{r-n}\hfill & L_{r-n}<\mathrm{step}\hfill \end{array}\right.$$

(14)

where $x_{\mathrm{new}}$ and $y_{\mathrm{new}}$ represent the location information of the new node, and $L(L\le \mathrm{step})$ is the distance from the new node to $X_{\mathrm{nearest}}$. As shown in Formula (14), when the distance $L_{r-n}$ between the sampling point and its nearest point is longer than or equal to the fixed step size, the value of L is the step size. On the contrary, the value of L is $L_{r-n}$. ${\theta }_{\mathrm{rand}}$ and ${\theta }_{t\arg et}$ represent the angle between $X_{\mathrm{rand}}$ and $X_{\mathrm{nearest}}$, and $X_{target}$ and $X_{\mathrm{nearest}}$. K is the migration parameter of the new node.

The pseudo-code of the algorithm GR-RRT* is shown in Algorithm 1, and the functions of some key functions are explained as follows: RandPoint represents the sampling point generation function, which generates points around the target based on a bivariate normal distribution with a given initial variance; Nearest represents the function that finds the node closest to the sampling point among all current nodes; Newpoint represents the new node generation function, which generates a new node by incorporating the target’s attractive influence according to the node generation strategy; CollisionFree represents the collision-checking function, which determines whether the newly generated node collides with any obstacles; Near represents the neighboring node search function, which identifies nodes within a given radius R around the new node; ChooseParent represents the parent re-selection function, which selects the node with the lowest path cost among neighboring nodes as the new node’s parent; Rewire represents the rewiring function, which updates the paths from other nodes to the new node to ensure all nodes maintain the minimum path cost; and Distance represents the distance calculation function, which computes the Euclidean distance between two nodes.

Algorithm 1 GR-RRT* algorithm (init, target, obstacle, ${\sigma }_x,{\sigma }_y,\mathrm{K}$)

1: T.init();   2: for $\mathrm{i}=1$ to N do   3:      if dynamic environment then   4:         Obstacle handling;   5:      end if   6:      $x_{\mathrm{rand}}\leftarrow$ Randpoint(target, ${\sigma }_x,{\sigma }_y$);   7:      $x_{\mathrm{nearest}}\leftarrow Nearest\left(x_{\mathrm{rand}},\mathrm{T}\right)$;   8:      $x_{\mathrm{new}}\leftarrow$ Newpoint$\left(x_{\mathrm{rand}},x_{\mathrm{nearest}}\right.$, target, K, StepSize);   9:      if CollisionFree(obstacle, $x_{\mathrm{new}}$) then 10:         $X_{\mathrm{near}}\leftarrow$ Near$\left(\mathrm{T},x_{\mathrm{new}}\right.$, Neighbor R); 11:         $x_{\min }\leftarrow$ ChooseParent$\left(X_{\mathrm{near}},x_{\mathrm{nearest}},x_{\mathrm{new}}\right)$; 12:         T.addNode$\left(x_{\min },x_{\mathrm{new}}\right)$; 13:         TRewire(T, $x_{\mathrm{new}}$); 14:          if $\mathrm{Distance}(x_{\mathrm{new}}$, target$) <$ error then 15:               Success(); 16:               T.addNode(target); 17:          end if 18:      end if 19: end for 20: Optimization; 21: return(T);

5. Experiments

This section evaluates the performance of the proposed method through simulation experiments. It begins with a description of the experimental setup, followed by the task allocation outcomes obtained using the enhanced Grey Wolf Algorithm. Finally, the UUV path planning process is presented based on the assigned tasks.

5.1. Execution Details

The simulation tests were carried out on a Windows 10 system, employing MATLAB 2023a as the simulation environment. The hardware setup consists of an Intel(R) Core(TM) i5—1135G7 processor (Intel, Santa Clara, CA, USA) running at a clock rate of 2.40 GHz and 16 GB of RAM. The simulations center on UUVs, with the operational zone specified by $x\in [0,400],y\in [0,400]$, where x and y denote the length and width of the underwater mission area, respectively. The detailed parameter configurations are as shown in

Table 1. Parameter settings for task allocation and path planning scenarios.

Parameter	Numerical Value
Mission area	400 × 400
Number of UUVs	4
Number of targets	4
Positions of targets	A (350,40) B (40,150) C (230,50) D (40,290)
Positions of UUVs	Target1 (320,280) Target2 (180,360) Target3 (250,310) Target4 (395,200)
UUV value	A: 6 B: 6 C: 5 D: 9
Target value	Target1: 6 Target2: 5 Target3: 4 Target4: 4

:

5.2. Task Assignment Result

This section presents a comparison of the performance between the Grey Wolf Optimization Algorithm (GWA) and the Improved Grey Wolf Optimization Algorithm (IGWA). The fitness curve serves as a key metric for evaluating optimization algorithm performance, as it captures the algorithm’s dynamic behavior in the search space. The primary objective of this study is to achieve task allocation at minimal cost, with the objective function value directly reflecting the fitness value used to assess the quality of each algorithm’s solution. As illustrated in Figure 5, the optimal fitness values obtained by the GWA and IGWA are 230.3 and 221.0, respectively. Given that the GWA is a stochastic optimization algorithm, its results may be influenced by random factors. To ensure the reliability and fairness of the experimental results, we conducted 10 independent simulations for each algorithm and used the average of these results for final evaluation.

Table 2. Comparison of 10 simulation results and average best fitness values of algorithms GWA(#1) and IGWA(#2).

T	1	2	3	4	5	6	7	8	9	10	Average
#1	251.4	230.3	228.9	238.9	222.7	238.4	232.3	225.5	237.4	233.1	233.9
#2	221.0	220.2	238.0	212.4	218.1	234.0	216.5	248.1	248.7	209.8	226.7

displays the detailed results of the 10 simulations and their average optimal fitness values. In the experiments, the initial population size was set to 100, with 1000 iterations per simulation. Here, T denotes the number of simulations, and “fitness” refers to the optimal fitness value obtained in each experiment. The results indicate that IGWA demonstrates superior convergence speed and adaptability compared to GWA. Notably, IGWA achieves higher-quality solutions with fewer iterations, yielding a significantly lower final fitness value. This advancement enhances resource utilization while boosting the efficiency and accuracy of UUV task execution, offering a more effective approach to addressing complex task allocation problems.

Finally, the results of the UUVs path planning target allocation are shown in

Table 3. The final allocation results.

Target Number	Assigned UUVs
Target 1	B
Target 2	D
Target 3	C
Target 4	A

. Based on the prediction results of the IGWA algorithm, our UUVs numbered A, B, C, and D are assigned to target 4, target 1, target 3, and target 2, respectively. This allocation scheme fully considers the performance differences of each UUV, the spatial layout of the target area, and the overall mission efficiency, ensuring the optimal utilization of resources and minimization of mission completion time. In this way, the efficiency and accuracy of UUVs mission execution are further improved.

5.3. Path Planning Results

To evaluate the performance of the proposed algorithm, comparative experiments on path planning were conducted. The simulation environment was configured with predefined start and goal positions, where different algorithms were tested to generate optimal paths. The planning results of each algorithm are shown in Figure 6, where the blue lines represent the planned paths, and the green lines depict the search trees generated by the algorithms to reach the target point. It can be seen that the path planned by RRT* has significantly improved compared to RRT. In contrast, the GR-RRT* algorithm shows unique advantages in complex obstacle environments: by introducing a goal-oriented mechanism, it effectively avoids the redundant branches generated by random sampling in traditional RRT-based algorithms. In terms of planning time, the RRT, RRT*, and PQ-RRT* algorithms, respectively, require 29.08 s, 22.32 s, and 17.66 s. The planning time of the proposed GR-RRT* algorithm is 16.35 s, which is 43.78%, 26.75%, and 8% less than RRT and RRT*, respectively. Moreover, the path planned by GR-RRT meets the navigation requirements of the UUV.

In addition, we conducted multi-path planning experiments based on task allocation. According to the results of task allocation, multiple unmanned underwater vehicles simultaneously planned paths to the target point, and the planning results are shown in Figure 7. As shown in

Table 4. Different algorithms plan path time (unit: s) and length (unit: m).

Methods	Average Time	Minimum Time	Maximum Time	Average Path	Shortest Path	Longest Path
RRT	23.86	15.12	31.40	279.34	179.57	383.16
RRT*	16.18	12.10	21.24	240.15	169.92	339.14
PQ-RRT*	13.12	10.46	15.28	238.33	165.42	328.66
GR-RRT*	11.34	7.43	16.35	226.11	163.96	311.03

, different path planning algorithms exhibited significant performance differences, specifically in terms of planning time and path length. Firstly, in terms of planning time, GR-RRT* showed a significant advantage, with an average planning time of only 11.34 s, which was 52.45%, 29.91%, and 13.57% shorter than RRT (23.86 s), RRT* (16.18 s), and PQ-RRT* (13.12 s), respectively. This indicates that GR-RRT has higher search efficiency in complex environments. Further observation of the shortest and longest planning times revealed that the shortest planning time of GR-RRT* was only 7.43 s, significantly lower than RRT (15.12 s), RRT (12.10 s), and PQ-RRT* (10.46 s), reflecting its ability to quickly generate effective paths. At the same time, its longest planning time was also controlled at 16.35 s, significantly better than RRT (31.40 s) and RRT* (21.24 s), demonstrating stable time performance and robustness. It can maintain low time consumption in various complex obstacle scenarios, ensuring the real-time and reliability of path generation. In terms of path length, GR-RRT* also demonstrated excellent path optimization capabilities, with an average path length of 226.11 m, which was 19.05%, 5.85%, and 5.13% shorter than RRT (279.34 m), RRT* (240.15 m), and PQ-RRT* (238.33 m), respectively, effectively avoiding the path redundancy and detours caused by random sampling in traditional RRT algorithms. At the same time, in the shortest path indicators, the optimal path length generated by GR-RRT* was 163.96 m, significantly better than RRT (179.57 m), RRT* (169.92 m), and PQ-RRT* (165.42 m), further verifying its path planning efficiency. In the worst case, the longest path length of GR-RRT was only 311.03 m, significantly shorter than RRT (383.16 m), RRT* (339.14 m), and PQ-RRT* (311.03 m), indicating that even in complex obstacle environments, GR-RRT* can maintain high path optimization capabilities and avoid the problem of path expansion caused by ineffective exploration. In summary, by introducing a target guidance mechanism, GR-RRT* overcomes the search blind zone problem caused by pure random sampling in traditional RRT algorithms, which not only greatly improves the path planning efficiency but also significantly shortens the planning path length, demonstrating better convergence and stability.

6. Conclusions

In this study, we propose an efficient task allocation and path planning approach specifically designed for UUVs. First, task allocation is optimized by considering factors such as the target value, distance, and UUV capability constraints, ensuring a rational and effective distribution of tasks across the UUVs. The Improved Grey Wolf Algorithm (IGWA) is used for task allocation, which combines circular chaotic mapping to increase population diversity and differential evolution mechanism. In this way, the overall efficiency of task allocation is improved. Second, for UUV path planning, an enhanced RRT* algorithm is employed. A guiding strategy is implemented, where the sampling probability near target points follows a variable two-dimensional Gaussian distribution, effectively reducing redundant sampling and improving planning efficiency.

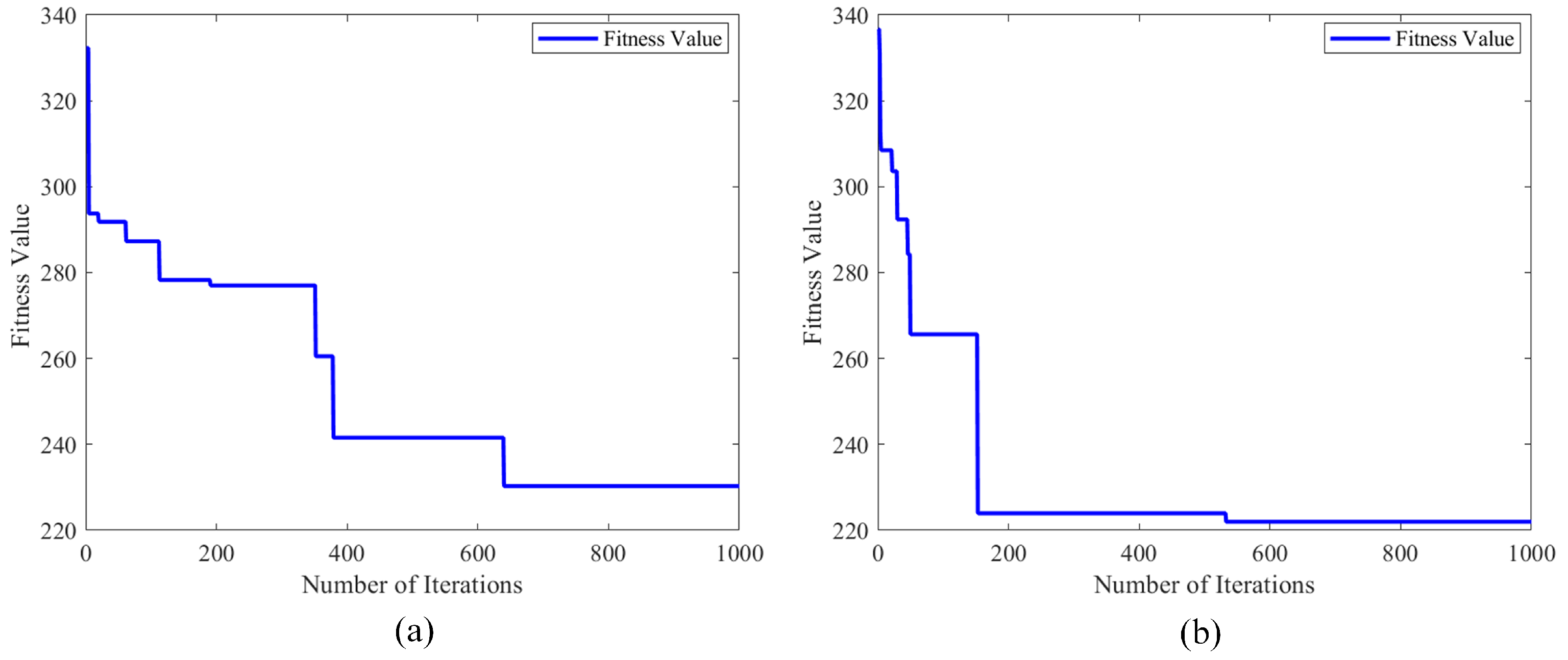
To evaluate the effectiveness of the proposed strategies, a series of simulation experiments were conducted. The results show: (1) The enhanced IGWA algorithm achieves dual optimization through the initialization of Circle chaotic mapping and the differential evolution mechanism; compared with the original GWA, its optimal fitness value decreased from 230.3 to 221.0, the average fitness value improved from 233.9 to 226.7, and the total cost of task allocation decreased by 7.2%. This indicates that integrating the Circle chaotic initialization and the differential evolution mechanism into GWA can significantly enhance its global optimization ability and convergence efficiency. (2) The improved GR-RRT* algorithm introduces a goal-oriented algorithm to alleviate the blind search behavior caused by purely random sampling in the traditional RRT algorithm. It breaks through the limitations of traditional RRT through the goal-guided two-dimensional Gaussian sampling strategy and the gravitational superposition mechanism, reducing the generation of redundant nodes by 58%. This enhancement not only significantly improves the path planning efficiency but also significantly shortens the overall path length.

However, our work has certain limitations. For example, it assumes that obstacles in the ocean environment are static. In practical operational scenarios, the marine environment may change dynamically, and obstacle positions may shift over time. Furthermore, the existing studies are limited to two-dimensional planar environments and fail to fully consider the three-dimensional characteristics of real marine scenes. In the future, our research can explore the following directions: (1) Adaptive extension of algorithms in dynamic three-dimensional environments: Incorporating reinforcement learning into path planning strategies to adaptively adjust paths based on real-time environmental features, enhancing algorithm stability in dynamic and complex environments; (2) Distributed optimization of the multi-UUV three-dimensional cooperative mechanism: Expanding multi-UUV cooperative planning mechanisms by integrating game theory or distributed cooperative control strategies to enable information sharing and task reallocation among multiple agents, thereby improving the efficiency and robustness of path planning in cooperative search and other cluster tasks.