Enhanced Dynamic Obstacle Avoidance for UAVs Using Event Camera and Ego-Motion Compensation

Highlights

What are the main findings?

• An enhanced warping function for ego-motion compensation, integrating IMU and depth data, accurately filters background events from rotational and translational UAV motions, outperforming linear methods in reducing false positives during dynamic obstacle detection.
• Motion-aware adaptive thresholding on normalized mean timestamp images, combined with an enhanced 3D Artificial Potential Field incorporating rotational force, enables robust segmentation of moving obstacles and generates smooth, collision-free paths in cluttered environments.

What are the implications of the main findings?

• The proposed framework improves real-time UAV navigation safety and efficiency in dynamic indoor settings like warehouses, minimizing missed detections for reliable autonomous operations.
• It advances event camera-based perception for UAVs, facilitating broader applications in challenging conditions with varying illumination and high-speed maneuvers, with potential for hardware validation in physical platforms.

Abstract

To navigate dynamic environments safely, UAVs require accurate, real time onboard perception, which relies on ego motion compensation to separate self-induced motion from external dynamics and enable reliable obstacle detection. Traditional ego-motion compensation techniques are mainly based on optimization processes and may be computationally expensive for real-time applications or lack the precision needed to handle both rotational and translational movements, leading to issues such as misidentifying static elements as dynamic obstacles and generating false positives. In this paper, we propose a novel approach that integrates an event camera-based perception pipeline with an ego-motion compensation algorithm to accurately compensate for both rotational and translational UAV motion. An enhanced warping function, integrating IMU and depth data, is constructed to compensate camera motion based on real-time IMU data to remove ego motion from the asynchronous event stream, enhancing detection accuracy by reducing false positives and missed detections. On the compensated event stream, dynamic obstacles are detected by applying a motion aware adaptive threshold to the normalized mean timestamp image, with the threshold derived from the image’s spatial mean and standard deviation and adjusted by the UAV’s angular and linear velocities. Furthermore, in conjunction with a 3D Artificial Potential Field (APF) for obstacle avoidance, the proposed approach generates smooth, collision-free paths, addressing local minima issues through a rotational force component to ensure efficient UAV navigation in dynamic environments. The effectiveness of the proposed approach is validated through simulations, and its application for UAV navigation, safety, and efficiency in environments such as warehouses is demonstrated, where real-time response and precise obstacle avoidance are essential.

1. Introduction

Unmanned aerial vehicles (UAVs) equipped with autonomous navigation and environmental perception capabilities are being rapidly developed. While most UAVs are designed for outdoor usage and benefit from the availability of GPS, indoor autonomous navigation capabilities of UAVs remain largely unexplored in industrial settings [1]. The real-world indoor scenarios present challenges including the change in lighting conditions, and unexpected obstacles may impede the UAV’s path [2]. Conventional visual cameras heavily rely on ambient light to capture imagery; hence, devoid of any source of illumination renders visual navigation virtually impossible [3]. This limitation necessitates the use of additional lighting systems or alternative sensors, which often adds complexity, weight, and power requirements [4]. LiDAR provides high-resolution 3D geometry data at rapid update rates and exhibits strong robustness to varying illumination conditions, making it highly effective for real-time detection and tracking of dynamic obstacles in complex environments. However, its high cost, larger size, weight, and power consumption pose challenges for lightweight UAVs, while limitations like failure to detect transparent or specular surfaces (e.g., glass) and susceptibility to environmental interference (e.g., dust or fog) restrict its versatility in indoor settings [5]. Radar sensors offer complementary advantages with long-range detection (up to hundreds of meters), invariance to lighting and weather, and the ability to penetrate certain obscurants like smoke or foliage. With recent advancements in low-complexity, low-power radar-based detectors are enabling applications such as indoor drone avoidance and airborne collision prevention in multi-agent dynamic scenes; nonetheless, radar’s lower resolution, difficulty in distinguishing fine details or static objects, and potential for false positives from clutter remain key drawbacks [6]. Ultrasonic sensors, on the other hand, are cost-effective, compact, and provide directional near-field ranging suitable for basic dynamic obstacle avoidance in confined spaces. However, these sensors are prone to errors due to environmental factors like temperature or humidity variations, limiting their reliability in noisy or cluttered indoor UAV operations [7].

The effectiveness of conventional obstacle detection systems can be greatly impeded by obstacles present in the surrounding landscape. As many navigation frameworks reliant on visual perception heavily rely on extracting distinctive features, sudden appearances or movements of obstacles may disrupt the coherence of these characteristics, resulting in possible failures during navigation [8]. This is especially true when UAVs are confronted with dynamic real-time situations encountered during obstacle avoidance scenarios. Under such circumstances, event cameras emerge as a highly promising alternative due to their bio-inspired nature that differentiates them from traditional frame cameras [9].

In contrast to conventional cameras that capture images at a fixed frame rate, event-based cameras produce a continuous stream of autonomous and independent events that signify changes in light intensity at the individual pixel level. This unique characteristic allows event cameras to naturally record the perception of movement which makes them highly suitable for UAVs performing tasks like obstacle avoidance [9]. Event cameras represent an innovative solution by measuring per-pixel brightness changes asynchronously, resulting in a high-resolution stream of events with microsecond precision. This significantly reduces latency compared to standard cameras, which inherently suffer from physical latency. However, the unique output of event cameras requires specialized algorithms for effective utilization in obstacle avoidance tasks.

An event camera detects changes in brightness at the pixel level, meaning it only transmits data from pixels where a change has occurred. When the camera is stationary, it primarily detects movement in the environment, capturing events from pixels corresponding to moving obstacles. Although some noise may be present, it is typically minimal and can be easily filtered out. With a static camera, dynamic obstacle detection is straightforward because the events mostly pertain to moving obstacles [10]. Thus, analyzing the event data and its locations allows for the identification of dynamic obstacles and their paths. However, when a UAV is in flight, event camera may perceive significant background events even in the absence of dynamic obstacles. To accurately identify and track moving obstacles, it is necessary to filter out these background events caused by the camera’s motion. This filtering process, known as “ego-motion compensation,” is essential for distinguishing between the motion of the UAV and the motion of the dynamic obstacles in the scene [11]. Addressing background events caused by both rotation and translation, ego-motion compensation is essential for reliable detection and tracking of dynamic obstacles. One reported approach is to minimize error functions derived from the spatial gradient of the mean-time image to fit a parametric motion model [12]. Another method maximizes variance, representing local contrast in the compensated image, which enhances event-based detection by improving the distinction between moving obstacles and background noise [13]. An alternative utilizes energy function minimization for a more precise optimization-based method [14]. However, the high computational cost of this approach introduces latency, potentially leading to failures in obstacle avoidance scenarios [15]. Another method employs the IMU’s average angular velocity for rotational ego-motion compensation, which is less computationally demanding and suitable for onboard flights, though it may lack accuracy in forward flights [16].

With background motion filtered out, the remaining issue is how to exploit the compensated event stream for reliable obstacle detection. Event cameras are widely investigated for dynamic obstacle detection due to their ability to provide high temporal resolution and negligible motion blur [9]. Still, the initial challenge is how to exploit the compensated event stream for reliable dynamic obstacle detection. Existing algorithms fall into two main categories: clustering events from different obstacles and tracking features on time surface frames [17,18]. Clustering-based methods intuitively align with event mechanisms but are sensitive to noise and often overlook the critical time information necessary for event-based detection [17]. One such clustering technique is the Density-Based Spatial Clustering of Applications with Noise (DBSCAN), which has been widely used for clustering tasks involving noisy, dense data [19]. DBSCAN is advantageous as it does not require the number of clusters to be pre-specified and is robust to outliers, making it suitable for event-based data, where the exact number of obstacles is often unknown [20]. However, despite these strengths, DBSCAN employs fixed parameters, which limit its adaptability in dynamic environments with varying event density and motion characteristics, as is commonly encountered in real-time UAV applications. On the other hand, tracking features on time surface frames involves creating a 2D map that only includes the latest event’s timestamp for each pixel, ignoring recently triggered events [16]. Some researchers have proposed a mean-time image representation, which averages the timestamps of events [21]. This method is less computationally demanding and more suitable for obstacle detection tasks as moving obstacles can be identified by simply thresholding the mean-time image, particularly desirable for UAV obstacle detection. However, mean-time images treat all recent events the same and are sensitive to self-motion and illumination flicker. Also, fixed thresholding on a mean time image often fails during rapid UAV motion or changing light.

Despite these advances, several key research gaps persist in dynamic obstacle avoidance for UAVs in indoor environments. Traditional ego-motion compensation techniques, such as optimization-based methods [12,13,14], are computationally intensive, limiting real-time onboard use, while simpler IMU-based approaches [16] lack precision during translational or aggressive flights, leading to residual background events and false positives. Obstacle detection on compensated streams often relies on clustering [17,19,20] or fixed-threshold mean-time images [21], which are sensitive to noise, self-motion, illumination variations, and varying event density, resulting in missed detections in dynamic settings. Moreover, avoidance algorithms like classical APF [22,23] or roll-command methods [24] struggle with local minima, abrupt maneuvers, and adaptability in cluttered, multi-obstacle scenarios. This study fills these gaps by proposing an integrated framework with efficient nonlinear ego-motion compensation fusing IMU and depth data, motion-aware adaptive thresholding for robust detection, and an enhanced 3D-APF with rotational force for smooth, collision-free paths in real-time warehouse navigation.

In this work, we propose an ego-motion compensation technique, which is designed to enhance the precision of motion correction using event camera data for UAVs performing aggressive movements. The proposed technique involves capturing 3D rotational data and constructing a nonlinear warping function to adjust for ego-motion. By leveraging rigid body kinematics principles, we align batch events with real-time IMU data within a specific time window. This nonlinear warping function offers superior correction for both rotational and translational movements by seamlessly combining depth and IMU data to provide comprehensive compensation for both types of motion. After compensation, we isolate dynamic regions from the compensated events, separating moving obstacles from the static scene.

We detect obstacles by first forming a normalized mean timestamp image on the ego motion compensated events, then applying a motion aware adaptive threshold whose sensitivity is tied to the image’s spatial mean and standard deviation and to the UAV’s current angular and linear velocities from the IMU which making the threshold more conservative at high speeds and decreasing it in slow flight. The resulting dynamic regions are converted into obstacles by fitting an oriented rectangle. Then, the method utilizes depth data in conjunction with the detected dynamic obstacles to estimate their 3D trajectory in real time. The trajectory estimation enables the system to predict potential collisions by mapping the obstacle’s movement through 3D space. The next phase of the proposed approach is obstacle avoidance, which is essential for the UAV to autonomously navigate through complex and dynamic environments. In this phase, a 3D-APF is integrated into the system to generate collision-free paths around the detected obstacles. This technique involves calculating attractive forces toward the destination and repulsive forces that push the UAV away from obstacles. To address common challenges such as local minima, where the UAV might become stuck due to competing forces, a rotational component is added to the APF, helping the UAV escape these traps and ensuring smooth navigation.

Therefore, the proposed framework introduces several key innovations to address the challenges and advance dynamic obstacle avoidance for UAVs. First, we develop a novel nonlinear warping function for ego-motion compensation that leverages rigid body kinematics and real-time IMU data within a fixed time window. This enables precise alignment of asynchronous events while seamlessly integrating depth information to correct for both rotational and translational UAV motions. It surpasses traditional optimization-based methods in computational efficiency and accuracy during aggressive maneuvers. Second, on the compensated event stream, we introduce a motion-aware adaptive thresholding mechanism applied to the normalized mean timestamp image. The threshold is dynamically derived from the image’s spatial mean and standard deviation and modulated by the UAV’s angular and linear velocities. This innovation mitigates sensitivity to self-motion and illumination variations inherent in fixed-threshold approaches. It ensures robust dynamic obstacle isolation without prior knowledge of obstacle size. Finally, we enhance the 3D Artificial Potential Field (APF) with a dedicated rotational force component that proactively resolves local minima traps common in classical APFby inducing yaw adjustments toward viable escape paths, leading to the generation of smoother and collision-free trajectories in cluttered dynamic environments. These contributions collectively enable real-time, onboard perception with reduced false positives, improved generalization to uncertain conditions, and superior navigation safety.

The rest of the paper is organized as follows. In Section 2, we introduce the proposed novel ego-motion compensation method that corrects for UAV movement during obstacle detection, using rotational and translational inputs from the IMU and depth cameras. In Section 3, we present a lightweight obstacle-detection framework that builds a normalized mean-timestamp image on the compensated event stream, applies a motion-aware adaptive threshold to robustly segment moving obstacles. Section 4 addresses UAV obstacle avoidance through a modified 3D Artificial Potential Field (APF) approach. Section 5 presents the simulation results that demonstrate the robustness of our approach in dynamic environments, validating the proposed method’s effectiveness in handling complex UAV movements and enhancing obstacle avoidance performance. Section 6 provides conclusions.

2. Ego-Motion Compensation

In this section, we introduce a nonlinear warping function that captures the intricate, nonlinear connection between the rotation of the camera and the shift in pixel positions. Unlike simpler linear models, this method employs nonlinear equations to more precisely depict how these two factors relate. This technique considers the starting locations of the pixels, which is crucial since the impact of the camera’s rotation differs across the image, affecting pixels at various locations in unique ways. The approach enhances motion compensation, particularly in situations with swift or significant UAV rotations, where traditional linear models may fail.

2.1. Preliminaries

An event camera operates based on the principle of cumulative brightness change. When the brightness change in a pixel reaches a certain threshold, it triggers a data stream known as Address-Event Representation (AER). This stream includes the pixel’s coordinates X = (x, y)^T, the timestamp t of the event, and the polarity p (indicating whether the brightness increased or decreased). Each pixel in an event camera independently detects changes in the scene’s brightness. For a pixel at coordinates X at time t, a change in the surrounding scene’s brightness causes a shift in the pixel’s logarithmic intensity:

∆L(X, t) = log I(X, t) − log I(X, t∆t)

(1)

where ∆L(X, t) represents the change in intensity at the pixel located at X over the time interval ∆t that elapsed since the last event at the same pixel, and I(X, t) represents the intensity of the pixel at location X and time t. When this change in intensity reaches a contrast sensitivity threshold T defined as

$$∆\mathrm{L}\left(\mathrm{X},\mathrm{t}\right)=\mathrm{p}\mathrm{Ͳ}$$

(2)

where $\mathrm{p} ϵ \{+1,-1\}$ the pixel outputs an event e = { X, t, p}, where p indicates whether the pixel has brightened (+1) or darkened (−1). This mechanism allows each pixel in the event camera to independently and asynchronously detect changes in brightness, facilitating real-time, high-resolution data acquisition for dynamic scene analysis.

2.2. Data Association Between IMU and Events

Camera rotation is modeled as rotation about the camera’s body axes. Under a pinhole projection, such motion induces a 2D image transform comprising an in-plane rotation and an image translation. The IMU is co-located with the camera so that both share approximately the same center of rotation. Angular-rate measurements about the x, y, and z axes are integrated over a short window Δt to obtain the incremental angles.

For each event with pixel address X = (x, y)^T, the event timestamp is aligned to the IMU samples within Δt. Over short windows, the rotation R about the camera axis is modeled as a 2 × 2 in-plane image rotation about the principal point c0, while rotations about the x- and y-axes (roll/pitch) are modeled as a 2D image-plane translation vector denoted as T. Here T refers to translation of the image on the pixel plane; it is not 3D translation of the camera through space. The explicit forms of R and T are provided in Section 2.3.

2.3. Ego-Motion Compensation Method

Events can be generated by obstacles in motion, the camera’s own movement or the change in lighting conditions in the environment. To accurately segment obstacles, it is necessary to first filter out events caused by ego-motion, which represent background information. Previous studies have developed ego-motion compensation algorithms [25], but they often lack the sufficient accuracy to fully filter out the background events, particularly under complex multi-axis rotations, high angular velocities, or sensor noise in real UAV operations. Such methods often use simplified or linearized motion models, which fail to capture the true dynamics of a fast-moving UAV. As a result, residual background events remain, causing false detections of moving obstacles and reducing the reliability of obstacle segmentation.

Our proposed ego-motion compensation is based on more accurately modeling both rotational and translational components, thereby minimizing background-event residuals and improving overall obstacle detection performance. The proposed approach aims to improve ego-motion compensation accuracy under demanding flight conditions like abrupt multi-axis rotations and quick maneuvers. By capturing the nonlinearities associated with fast UAV maneuvers and incorporating depth-based scaling, the proposed method reduces false positives and enhances reliability in dynamic obstacle detection.

For each incoming event at time t, the proposed algorithm applies a warping function φ: R³ → R³ as (x′, y′, t) = φ(x, y, t) to compensate for the camera’s motion over the interval Δt. Specifically, the function maps (x, y, t) to (x′, y′, t), where (x′, y′) is the corrected pixel location. Using the IMU integrated angles over Δt, we compensate each event by applying a rotation then translation transform about the principal point. Therefore, this warping equation compensates pixel coordinates X to X’ by applying rotation matrix R (for yaw ψ) and displacement vector T (for roll/pitch shifts) around principal point ${\mathrm{c}}_0$. It reprojects events to a motion-free reference, filtering ego-motion for accurate obstacle isolation. For an event at time t, X = (x, y)^T:

$${\mathrm{X}}^{\prime }=\left[\mathrm{R}\right(\mathrm{X}-{\mathrm{c}}_0)-\mathrm{T}]+{\mathrm{c}}_0$$

(3)

where X’ and X are the compensated and original pixel coordinates, respectively, and c₀ ∈ R² is the coordinates of the center of the pixel plane. R ∈ R^{(2 × 2)} is an image-plane rotation matrix about the z-axis corresponding to yaw angle ψ. T ∈ R² is a two-dimensional image-plane translation vector due to rotation about the x-axis and y-axis. In Equation (3), determining T requires approximating the pixel shifts from roll and pitch using the camera’s focal length f and pixel size p based on the small-angle approximation. Therefore, the following linear relationship for T is obtained as [26]:

$$\mathrm{T}=\mathrm{K}\mathsf{\Theta }$$

(4)

where parameter K is a constant that translates angular changes Θ into sensor displacements, determined by the camera’s pixel size and focal length. The vector $\mathsf{\Theta }$ comprises the camera’s rotation angles around the x-axis and y-axis, defined as

$$\mathsf{\Theta }=[ɸ, \mathsf{\theta }{]}^{\mathrm{T}}, \mathrm{K}={\displaystyle \frac{1}{{\tan }^{-1}\left(\frac{p}{\mathrm{f}}\right)}}$$

(5)

where the pixel size p and the focal length f determine how angular changes Θ translate into T which refers to translation of the image on the pixel plane. ɸ is the camera’s rotation angle around the x-axis and θ is the camera’s rotation angle around the y-axis. In scenarios where the camera’s movements are subtle, this linear approximation can yield satisfactory results for ego-motion compensation. However, with more vigorous movements, the rapid rotations result in significant alterations to the incidence angle, defined as the angle between the incoming light from an obstacle and the camera’s optical axis, leading to larger apparent shifts in the imaging surface. This change can introduce substantial errors in the approximation (4).

Furthermore, it is important to factor in the original position of the pixel when applying the warping function, particularly for those located far from the image center. Linear methods often assume small and uniform angles of incidence, overlooking the fact that off-center pixels can experience larger angular shifts if the camera rotates. Incorporating the actual incidence angle ensures that pixel displacements due to rotation are corrected more accurately across the entire sensor.

Our proposed compensation for pixel displacements is derived by modeling the geometric transformations caused by camera motion. The method begins by determining the initial angle of incidence α for each pixel, based on its position in the image plane. When the camera undergoes a rotational shift, the pixel’s apparent position changes according to the new incidence angle β. To correct for this shift, a transformation function is applied to update each pixel’s coordinates. This function accounts for both rotational and translational components, ensuring that the displacement varies according to the pixel’s distance from the image center. The compensation is performed dynamically, adjusting event positions in real-time based on the computed motion parameters.

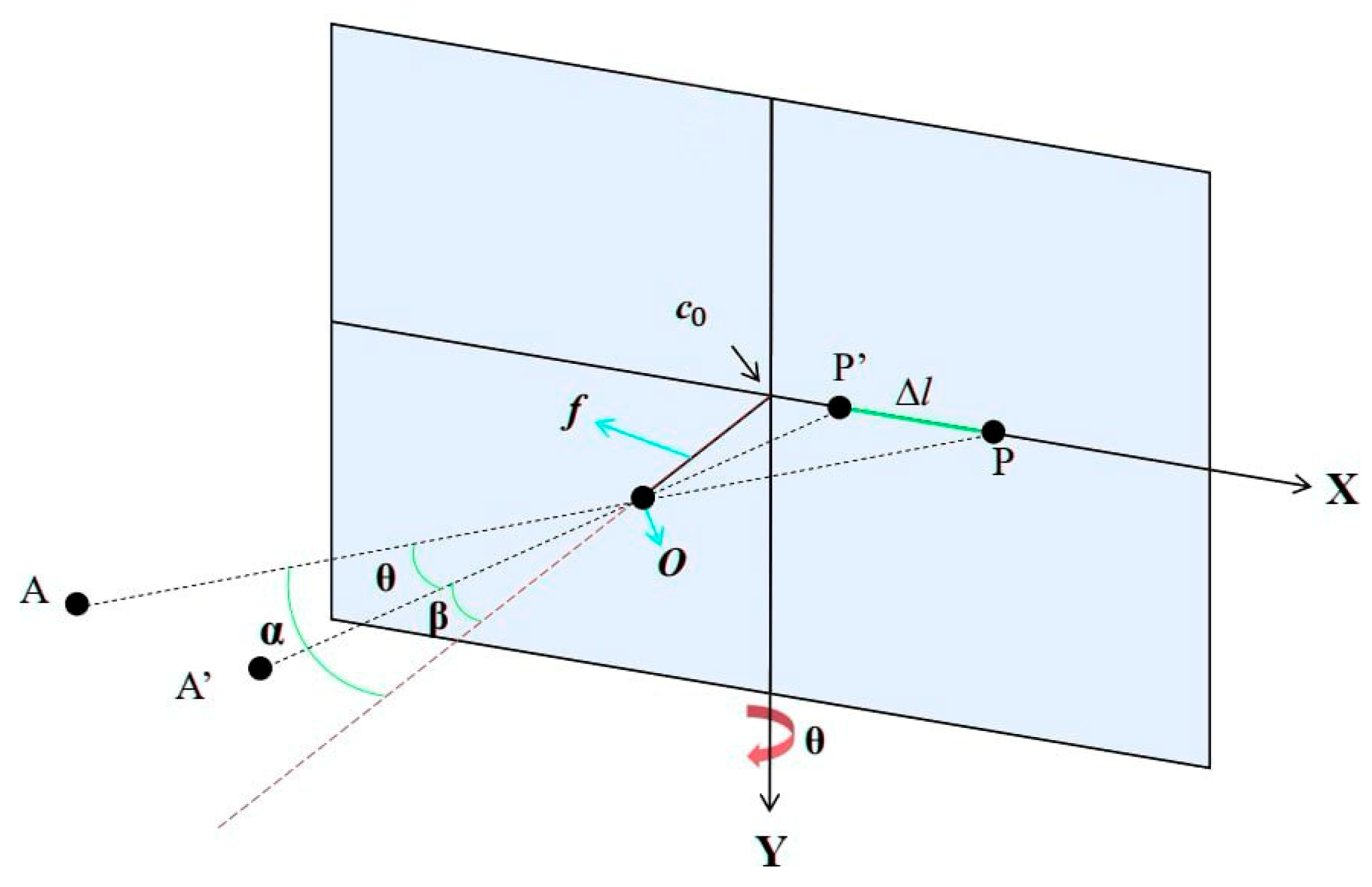
To illustrate the concept behind the ego-motion approach, suppose that the camera rotates primarily about its y-axis by an angle θ (Figure 1) [27]. For an event located at pixel coordinates (x, y), which lie mainly along the x-axis in the image plane, we begin by computing the original angle of incidence α:

$$\alpha ={\tan }^{-1}\left(\mathrm{x}{\displaystyle \frac{p}{\mathrm{f}}}\right)$$

(6)

where p defines the pixel size and f is the focal length of the camera. After the camera rotates around the y-axis, the new angle β is determined. The horizontal pixel coordinate $x$ represents the displacement from the optical axis. The angle $\alpha$ is derived from the tangent of the triangle formed by the focal length (opposite side) and the projected distance $xp$ (adjacent side) on the image plane. The horizontal angle of incidence after a rotation θ around the y-axis is obtained by

$$\mathsf{\beta }=\mathsf{\alpha }-\mathsf{\theta }$$

(7)

To compensate for the nonlinear displacement, the shift in the pixel on the x-axis is calculated as follows:

$$∆\mathrm{l}=\mathrm{x}-\mathsf{\rho }\tan \left(\mathsf{\beta }\right)$$

(8)

where ∆l specifies the change in pixel position because of the camera’s rotation around the y-axis. The term $\mathsf{\rho }\mathrm{t}\mathrm{a}\mathrm{n}\left(\mathsf{\beta }\right)$ represents the projected displacement of the obstacle point on the image plane after rotation. The original pixel coordinate $\mathrm{x}$ is adjusted by subtracting this projected shift to determine $\Delta \mathrm{l}$, the new pixel position after compensation. ρ represents the distance from the camera to the obstacle point along the optical axis, defined as

$$\mathsf{\rho }={\displaystyle \frac{\mathrm{f}}{p}}$$

(9)

The resulting translation vector T is obtained as

$$\mathrm{T}=\left(\mathrm{X}-{\mathrm{c}}_0\right)-\mathsf{\rho }\tan \left(\mathsf{\beta }\right)+\mathsf{\eta }{\left(\mathrm{X}-{\mathrm{c}}_0\right)}^2$$

(10)

where η is a nonlinear correction coefficient that accounts for higher-order variations in displacement, which linear models may not capture, and X is the original pixel coordinate before compensation. The rotation matrix R is defined as follows:

$$\mathrm{R}=\left[\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathsf{\psi }\right)& -\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathsf{\psi }\right)\\ \mathrm{s}\mathrm{i}\mathrm{n}\left(\mathsf{\psi }\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\mathsf{\psi }\right)\end{array}\right]$$

(11)

By substituting the nonlinear translation T and rotation R from (10), (11) into (3), we obtain the warping function φ, which produces the compensated event coordinates (x′, y′, t).

$${\mathrm{X}}^{\prime }=\phi \left(\mathrm{X}\right)=\phi \left(\mathrm{x},\mathrm{y},\mathrm{t}\right)=({\mathrm{x}}^{\prime },{\mathrm{y}}^{\prime },\mathrm{t})$$

(12)

To explicitly express the transformation applied to each event coordinate, we expand the warping function by incorporating the computed rotation and translation components. This results in the final compensated event coordinates given by:

$$\begin{gathered} {\mathrm{x}}^{\prime }=\cos \left(\mathsf{\psi }\right) \left(x-{\mathrm{c}}_{0\mathrm{x}}\right)-\sin \left(\mathsf{\psi }\right)\left(y-{\mathrm{c}}_{0\mathrm{y}}\right)+\left(x-{\mathrm{c}}_{0\mathrm{x}}\right)-\mathsf{\rho }.\tan \left(\mathsf{\beta }\right)+\mathsf{\eta }{\left(\mathrm{X}-{\mathrm{c}}_0\right)}^2+{\mathrm{c}}_{0\mathrm{x}} \\ {\mathrm{y}}^{\prime }=\sin \left(\mathsf{\psi }\right)\left(x-{\mathrm{c}}_{0\mathrm{x}}\right)+\cos \left(\mathsf{\psi }\right) \left(y-{\mathrm{c}}_{0\mathrm{y}}\right)+{\mathrm{c}}_{0\mathrm{y}} \end{gathered}$$

(13)

Figure 1 [27] illustrates the compensation geometry for a rotation primarily about the camera y-axis by an angle theta. The camera center is O and the principal point is ${\mathrm{c}}_0$. A scene point A projects to pixel P at time t. After the camera rotates by θ about the y-axis, the same scene point projects to P’. The pre- and post-rotation incidence angles with respect to the optical axis are $\alpha$ and $\mathsf{\beta }$, respectively. The required compensation on the image plane is the red segment $∆\mathrm{l}$ between P and P’. This schematic clarifies why our image-plane model applies a rotation about ${\mathrm{c}}_0$ followed by a translation term T, and why the displacement varies across pixels under y-axis rotation.

In reality, the impact of camera motion on event displacement in the image plane depends on obstacle depth. For the same camera move, obstacles that are close to the camera appear to move more than distant obstacles. By incorporating depth information into the compensation process, each pixel’s movement can be adjusted based on its actual distance from the camera.

To achieve more accurate camera motion compensation, a depth scaling function S(D(x, y)) is introduced to enhance the compensation for each pixel based on its depth from the camera. The scaling function can be defined as

$$\mathrm{S}\left(\mathrm{D}(\mathrm{x},\mathrm{y},\mathrm{t})\right)=1+\mathsf{\gamma }({\displaystyle \frac{1}{\mathrm{D}(\mathrm{x},\mathrm{y},\mathrm{t})+\mathsf{ϵ}}}-{\displaystyle \frac{1}{{\mathrm{D}}_{max}+\mathsf{ϵ}}})$$

(14)

where D(x, y, t) represents the depth of the obstacle at pixel (x, y) and time t, which is used to scale the warping function and handle obstacles at different distances from the camera, γ is a scaling constant that determines the influence of depth on the compensation, ϵ is a small coefficient to ensure numerical stability, and D_max represents the maximum depth value.

This function adjusts the degree of pixel displacement compensation by scaling up for pixels representing closer obstacles and scaling down for those representing distant obstacles. By integrating this scaling function with the existing warping function φ(x, y, t), the final compensated position of each pixel becomes a product of the original warping output and the depth scaling factor:

$$({\mathrm{x}}^{\prime },{\mathrm{y}}^{\prime },\mathrm{t})=\phi \left(\mathrm{x},\mathrm{y},\mathrm{t}\right)\mathrm{S}\left(\mathrm{D}\right(\mathrm{x},\mathrm{y},\mathrm{t}\left)\right)$$

(15)

3. Obstacle Detection

When events are warped to compensate for camera motion, only the spatial coordinates are adjusted while the event timestamps remain unchanged. This means each event retains its original occurrence time, preserving the temporal ordering of the data. Consequently, background events which are caused purely by camera motion are now aligned in the image plane, but their timestamps are around the same moments in time. Meanwhile, independently moving obstacles tend to produce events at distinct times or over broader time windows. By examining average timestamps of the warped events, one can distinguish foreground from background motion. This difference in timing is a powerful cue for segmenting and detecting moving obstacles [21,25], enabling more reliable dynamic obstacle identification in event-based camera systems.

3.1. Normalized Mean Timestamp

The normalized mean timestamp N(x, y) is essential for distinguishing between pixels belonging to moving obstacles and those belonging to the background in an event-based camera system. First, for each pixel location (x, y) in the warped event image, two key quantities are computed:

Event-Count C(x, y): This represents the total number of events detected at the pixel (x, y). It is essentially a count of how many times an event (i.e., a change in brightness) has been registered at that pixel.

Time-Pixel T(x, y): This is the sum of the timestamps of all events detected at pixel (x, y). It captures the cumulative time information for events occurring at that specific location.

With the event count and time-pixel values calculated, the mean timestamp is determined for each pixel (x, y) as

$$\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{T}\left(\mathrm{x},\mathrm{y}\right)\right)={\displaystyle \frac{\mathrm{T}(\mathrm{x},\mathrm{y})}{\mathrm{C}(\mathrm{x},\mathrm{y})}}$$

(16)

This mean timestamp represents the average time at which events occurred at pixel (x, y), providing a temporal measure of event activity at that location. Then, the average timestamp of all events is computed across the entire warped image:

$$\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{T}\right)={\displaystyle \frac{\sum _{x,y}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{T}\left(\mathrm{x},\mathrm{y}\right)\right)}{\sum _{x,y}\mathrm{C}(\mathrm{x},\mathrm{y})}}$$

(17)

where T is the sum of timestamps for all events in the image. This average timestamp serves as a global reference point, indicating the overall timing of events in the scene.

The normalized mean timestamp for each pixel (x, y) is then calculated by subtracting the global average timestamp from the mean timestamp of that specific pixel:

$$\mathrm{N}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{T}\left(\mathrm{x},\mathrm{y}\right)\right)-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{T}\right)$$

(18)

The value of N(x, y) reflects the time difference in events at pixel (x, y) compared to the overall average. The normalized mean timestamp is used to differentiate between static and dynamic obstacles in the scene. By applying a threshold to N(x, y), pixels associated with moving obstacles can be distinguished from those associated with the static background. This thresholding process effectively segments the image into regions representing dynamic and static elements, facilitating accurate detection and analysis of moving obstacles.

3.2. Dynamic Obstacle Segmentation with Motion-Aware Thresholding

After compensating for ego-motion, we introduce an adaptive segmentation method that integrates normalized mean timestamps and vehicle motion dynamics within the event stream. As part of this method, the segmentation process compares the normalized mean timestamp at each pixel to the dynamically determined threshold, classifying values above or below it as moving obstacles and the rest as background. The proposed method considers the variability in event density across the image plane, as well as the influence of the vehicle’s motion dynamics. The adaptive threshold θ(x, y) is formulated as

$$\mathsf{\theta }\left(\mathrm{x},\mathrm{y}\right)=\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{N}\left(\mathrm{x},\mathrm{y}\right)\right)+\mathsf{\mu }·\mathsf{\sigma }\left(\mathrm{N}\left(\mathrm{x},\mathrm{y}\right)\right)+\mathsf{\gamma }·\mathrm{f}(\mathsf{\omega },\mathrm{v})$$

(19)

where N(x, y) is the normalized mean timestamp, σ(N(x, y)) is the standard deviation of the normalized mean timestamp, and f(ω, v) is a function of the vehicle’s rotational velocity ω and linear velocity v. The parameters μ and γ are tunable constants that control the sensitivity of the threshold based on local image statistics and motion dynamics. The function f(ω, v) is intended to represent a combination of the vehicle’s angular velocity ω and linear velocity v, tailored to adjust the segmentation threshold dynamically which is defined as

$$\mathrm{f}\left(\mathsf{\omega },\mathrm{v}\right)=\mathrm{a}\left|\mathsf{\omega }\right|+\mathrm{b}\left|\mathrm{v}\right|+\mathrm{c}$$

(20)

where |ω| represents the magnitude of the angular velocity of the vehicle, |v| represents the magnitude of the linear velocity, and a and b are scaling factors that adjust the influence of the angular and linear velocities on the threshold. The bias term c offers an additional degree of fine-tuning, ensuring that the segmentation threshold accurately reflects the level of motion-induced noise. The function f(ω, v) is designed to adapt the thresholding process by taking into account how the vehicle’s motion affects the perceived movement of obstacles in the environment. For example, if the vehicle is rotating quickly (|ω| is large), the threshold might need to be higher to account for the increased relative motion, thereby reducing the chance of misclassifying background noises as moving obstacles. Similarly, faster linear movement (|v| is large) may require adjustment to maintain accurate segmentation.

This proposed adaptive approach allows for more precise segmentation by dynamically adjusting to variations in both the event stream and the vehicle’s motion, ensuring that moving obstacles are more accurately detected without being overshadowed by background noise.

After segmenting the image, the next step is to estimate the position of each detected obstacle by fitting a rotated rectangle around its points, defining a Region of Interest (ROI) to encompass the obstacle.

4. Position Estimation and Obstacle Avoidance

After fitting a rotated rectangle around obstacles, the four corner points and the center position in the image plane are determined. This step simplifies the obstacle representation and prepares the data for accurate 3D position estimation. Given the availability of a depth sensor alongside the event camera, depth estimation is performed using direct depth measurements for each point in the image plane, including the center and corner points of the fitted rectangle. This depth information is used to calculate the 3D positions of the obstacles in the camera’s frame, following the method described in [25]. Based on this method, using the depth information, the detected rectangle’s corner and center points are projected into 3D space using the perspective projection model. This projection involves the intrinsic camera matrix and transformation matrices that account for the camera’s position relative to the UAV and the world frame. The depth data provides a reliable 3D representation of the environment. To estimate the obstacle’s velocity, the algorithm matches newly detected obstacles with previously tracked ones, based on the proximity of their center positions in 3D space. The velocity of the obstacle is then estimated using an extended Kalman filter, which smooths the position signals from the depth sensor, resulting in an adequately precise and reliable velocity estimate.

Obstacle Avoidance

Obstacle avoidance in dynamic environments poses a significant challenge for UAV navigation where moving obstacles can unpredictably intersect the UAV’s path; traditional methods often struggle to react quickly to these dynamic obstacles, risking collisions or inefficient detours, necessitating advanced path planning strategies to ensure safe and efficient navigation, necessitating advanced path planning strategies to ensure safe and efficient navigation. For instance, in [28], a navigation method is proposed that leverages velocity fields to guide UAVs around dynamic obstacles in both 2D and 3D scenarios. To enhance obstacle avoidance in dynamic environments, we propose a novel 3D Artificial Potential Field (APF) approach for path generation around moving obstacles, extending the traditional APF framework by introducing a rotational force component to address the local minima problem. In our formulation, the APF generates an attractive force that draws the UAV toward its target destination and a repulsive force that pushes it away from obstacles, ensuring a safe distance is maintained [22,23]. Additionally, to counteract the common issue of local minima where the attractive and repulsive forces might cancel out and trap the UAV, our novel contribution incorporates a rotational force component that acts perpendicular to the repulsive force, inducing a circular motion around the obstacle. This rotational force ensures the UAV escapes equilibrium points by steering it along a new collision-free path, significantly improving navigation reliability in dynamic settings.

The overall potential field is described as

$$U\left(X\right)=U_{att}\left(X\right)+U_{rep}\left(X\right)$$

(21)

where X ∈ R³ denotes the UAV’s position in the Cartesian space. The attractive potential U_att(X) and the repulsive potential U_rep(X) are defined as follows:

$$\begin{gathered} U_{att}\left(X\right)={\displaystyle \frac{C_{p1}}{2}}{‖X-X_{des}‖}^2, \\ {U}_{rep}\left(X\right)=\left\{\begin{array}{c}{\displaystyle \frac{C_{p2}}{2}}{\left({\displaystyle \frac{1}{d_s}}-{\displaystyle \frac{1}{d_m}}\right)}^2, d_s<d_m\\ 0 , d_s\ge d_m\end{array}\right., \end{gathered}$$

(22)

where d_m is the thickness of the inadmissible layer on the surface and C_Pi,I = 1, 2, 3, are positive constants, X_des is the coordinates of the destination point and d_s = ‖X − X_n‖ is the normal distance from the UAV position to the surface of the obstacle. X_n is the point on the surface, which has the minimum distance to UAV’s position X. The overall potential force is calculated as follows:

$$F\left(X\right)=F_{att}\left(X\right)+F_{rep}\left(X\right)$$

(23)

where F_att(X) and F_rep(X) are the attractive and repulsive potential forces can be obtained as follows:

$$\begin{gathered} F_{att}=C_{p1}\left(X_{des}-X\right) \\ {F}_{rep}=\left\{\begin{array}{c}{C}_{p2}{\displaystyle \frac{1}{d_s^2}}\left({\displaystyle \frac{1}{d_s}}-{\displaystyle \frac{1}{d_m}}\right){\nabla }_{d_s}, d_s<d_m\\ 0 , d_s\ge d_m\end{array}\right. \end{gathered}$$

(24)

In this formulation, the attractive force directs the UAV toward the destination, while the repulsive force is activated only when the UAV is within the influence distance d_m of an obstacle to effectively push the UAV away from potential collisions.

However, a major challenge of APF is the occurrence of local minima, where the attractive and repulsive forces cancel each other, trapping the UAV in place. To overcome this, we introduce a rotational force to the potential field, modifying the APF to include a rotational component that helps the UAV escape local minima. The rotational force is defined as

$$F_{rot}\left(X\right)={\displaystyle \frac{\tan \left({\alpha }_{rot}\right)·F_{rep}\left(X\right)·\left(F_{rep}\left(X\right)\times N_{rot}\right)}{‖F_{rep}\left(X\right)\times N_{rot}‖}}$$

(25)

where N_rot is the vector normal to the plane that passes through the departure and destination points and is fixed with a specific angle β_rot. α_rot represents an angle that determines how strongly the UAV is pushed to rotate around the obstacle. An example of the rotational force in 3D space is depicted in the figure. Therefore, the overall potential force can be rewritten as follows:

$$F\left(X\right)=F_{att}\left(X\right)+F_{rep}\left(X\right)+F_{rot}\left(X\right)$$

(26)

The inclusion of the rotational force provides an additional corrective action that counteracts the local minima problem by introducing a component to the overall force. This force effectively breaks the equilibrium between the attractive and repulsive forces, steering the UAV out of potential traps and ensuring smooth, collision-free navigation in dynamic environments.

5. Simulations and Evaluation

The proposed strategy is tested within a comprehensive simulation framework integrating Gazebo, ROS, and Prometheus to model and evaluate autonomous UAV navigation and obstacle avoidance. Gazebo provides a realistic physics-based simulation environment, utilizing the open-source aws-robomaker-small-warehouse-world package to create a warehouse setting with shelves, walls, and dynamic obstacles (e.g., balls moving at 10 m/s). The P230 UAV model, provided by Prometheus, is equipped with an event camera (simulated via the Gazebo DVS plugin) and a depth sensor (emulating an Intel RealSense D435i) (Figure 2). These sensors generate event streams and depth maps, visualized in Figure 3a (depth map showing obstacle distances) and Figure 3b (event data capturing dynamic changes).

The depth sensor is emulated as an Intel RealSense D435i in the Gazebo model, providing depth measurements with a typical precision of ±1% of the measured distance (e.g., ±0.01 m at 1 m range), resolution of 240 × 180 pixels, and effective range of 0.5–18 m, as configured in the SDF plugin. This sensor operates at an update rate of 60 Hz, ensuring sufficient data for fusion in dynamic UAV scenarios. Time synchronization handles the asynchronous event streams (microsecond resolution) and depth frames by using ROS message filters for approximate time alignment, associating the nearest depth frame to event batches within a 25 ms window to minimize latency. Spatial calibration is performed offline using tools like Kalibr on a checkerboard pattern to compute intrinsics (focal length 199.37 px, principal point Cx = 133.75, Cy = 113.99, and distortion coefficients k1 = −0.383, k2 = 0.189, k3 = 0, p1 = −0.001, p2 = −0.001) and extrinsics (relative pose: depth at 0.1, 0, −0.03 m; event camera at 0.1, 0, 0 m from base_link), ensuring pixel-level registration before applying depth scaling in the warping function.

ROS serves as the middleware, facilitating communication between simulation components through topics and services. Sensor data (events, depth, and IMU) are published as ROS topics, while control commands (e.g., velocity and yaw) are sent to the simulated flight controller (emulating PX4). Our control strategy comprising nonlinear ego-motion compensation, motion-aware adaptive thresholding for obstacle detection, and modified 3D-APF for avoidance is implemented as custom ROS nodes within the Prometheus framework. These nodes subscribe to sensor topics from Gazebo, process data in real-time to detect dynamic obstacles and publish velocity and yaw commands to the flight controller.

The IMU data reliability is enhanced through a robust averaging technique used to mitigate noise in the angular velocity measurements, ensuring accurate ego-motion compensation. This method involves collecting IMU readings over a recent time window and computing an average angular velocity, which serves as a stable estimate of the camera’s rotational motion. This averaged value is then integrated over discrete 1-millisecond intervals to generate a rotation vector, effectively adjusting event positions to counteract rotational ego-motion while reducing the influence of high-frequency noise; it uses the average angular velocity from IMU data, updated every millisecond, to build a rotation matrix and warp events, which helps reduce noise. By focusing on a limited set of the most recent samples, typically up to the last 10 readings, the approach minimizes the accumulation of random fluctuations, providing a smoother and more reliable attitude estimate for dynamic UAV maneuvers.

As the UAV flies through the warehouse environment, events are generated due to both dynamic obstacles and variations in illumination. In our warehouse environment, shelves and walls naturally obstruct the overhead lights, creating areas of higher and lower illumination. As the UAV maneuvers between shelves, it transitions in and out of these partially shaded regions, causing moderate yet noticeable changes in the light intensity recorded by the event camera. These variations, along with motion-induced events, are captured and processed to differentiate between background and dynamic obstacles.

5.1. Performance Comparison of Ego-Motion Compensation

In this subsection, the evaluation of the proposed ego-motion compensation method is presented, in comparison with the linear method [26], discussed in (4), (5). The UAV operates in the Gazebo/ROS environment with a flight speed of 3 m/s and a maximum acceleration of 2 m/s² to simulate typical indoor maneuvers while dynamic obstacles move at 10 m/s along straight trajectories.

The comparison is focused on assessing the compensation performance for UAV motions and detection of dynamic obstacles in real-time, including scenarios involving rapid UAV motion with both rotational and translational movements that are often associated with noise or event misinterpretation. In comparison to linear technique, the proposed approach with the nonlinear warping function demonstrated improved accuracy in both motion compensation and dynamic obstacle detection, as shown in the following.

A pixel event density metric was used to quantify the performance of the motion compensation, which is calculated as

$${\mathrm{d}}_{∆\mathrm{t}}=\sum {\mathrm{C}}_{\mathrm{i}\mathrm{j}}.{\mathrm{P}}_{\mathrm{i}\mathrm{j}}$$

where d_∆t represents the density of compensated events within a specific time window ∆t, and P_ij represents the pixels triggered by the warped events.

$${\mathrm{P}}_{\mathrm{i}\mathrm{j}}=\left\{\begin{array}{cc}1& \mathrm{if} \mathrm{pixel} (\mathrm{i},\mathrm{j}) \mathrm{is} \mathrm{triggered} \mathrm{by} \mathrm{warped} \mathrm{events} \mathrm{within} \Delta \mathrm{t}\\ 0& \mathrm{otherwise}\end{array}\right.$$

A higher value of d_∆t indicates better compensation performance, as more events are concentrated into fewer pixels, resulting in a more spatially coherent event distribution.

Table 1. Comparison of pixel event density for different motion scenarios (pitch, yaw, roll) between raw data, linear compensation and the proposed ego-motion compensation method with the nonlinear warping function.

	Raw Events (Events/Pixel)	Proposed Method (Events/Pixel)	Linear Method (Events/Pixel)
Pitch rotation	1.50	2.87	2.35
Yaw rotation	1.78	3.30	2.90
Roll rotation	1.22	2.46	2.05

summarizes the comparison of pixel event densities across different motion sequences. The nonlinear proposed method consistently outperformed the linear method, delivering higher density values across all motion categories:

This comparison highlights that higher pixel event density was achieved by the proposed method, leading to images with better resolution, which is essential for detecting dynamic obstacles in complex environments.

In addition to enhanced motion compensation, improvements in dynamic obstacle detection were also observed with the proposed ego-motion compensation. The algorithm was tested on a simulated environment, and demonstrated its robustness in detecting moving obstacles, even under intense UAV motion. The use of the proposed compensation method resulted in better detection reliability when compared to linear compensation method, as camera motion was effectively compensated.

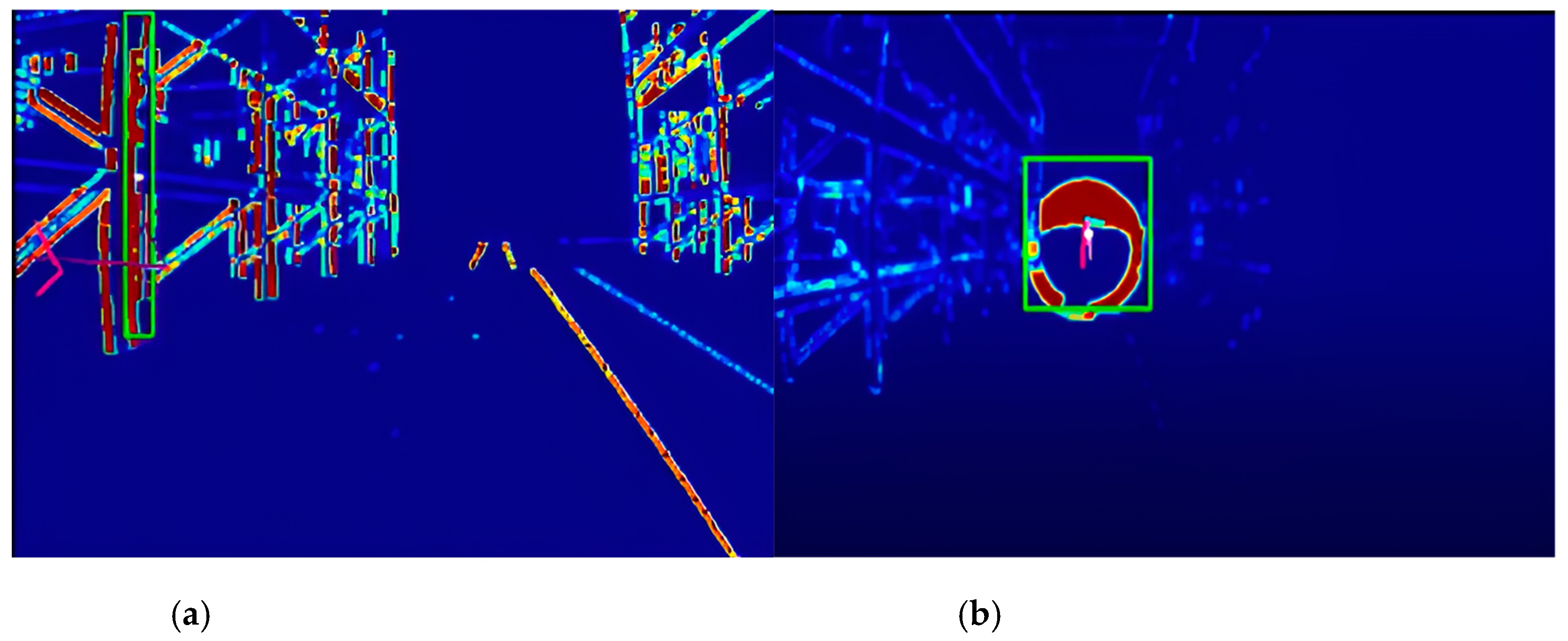
The comparative results are illustrated in Figure 4, where the linear approach as described in Equation (4) is compared with the proposed approach with the nonlinear warping function. With the Linear Approach, multiple false detections of static obstacles are observed, where parts of the static environment (e.g., warehouse shelves, walls) were mistakenly detected as dynamic obstacles (Figure 4a). These misclassifications stem from insufficient motion compensation, where background events caused by UAV motion were not effectively removed. As a result, the algorithm struggled to differentiate between actual dynamic obstacles and stationary elements in the scene, which leads to cluttered detection results and reduced accuracy in identifying moving obstacles. In contrast, Figure 4b shows more accurate results obtained using the proposed ego-motion compensation method. By employing the nonlinear method to model and compensate for both rotational and translational UAV motion, this approach accurately eliminates background noise caused by camera motion. As a result, only the true dynamic obstacles, such as the moving obstacle in the scene, are detected. This demonstrates the improved precision and reliability of the proposed method in differentiating dynamic obstacles from static background elements in complex environments, allowing the developed algorithm to focus solely on actual dynamic obstacles.

5.2. Dynamic Ball Detection and Avoidance

In this subsection, we present test results that demonstrate the effectiveness of our proposed ego-motion compensation method for dynamic obstacle detection and avoidance. A challenging scenario has been tested: the UAV was tasked with detecting and avoiding a dynamic spherical ball with unknown size moving at a speed of 10.0 m/s. As the ball approached, the event camera captured rapid brightness changes, generating a stream of asynchronous events that corresponded to the ball’s motion. The proposed ego-motion compensation filtered out background noise caused by the UAV’s own motion, isolating the dynamic events associated with the ball.

The processing pipeline computed the normalized mean timestamp and applied adaptive motion-aware thresholding to segment the ball from the static background, enabling accurate 3D position estimation and velocity tracking of the ball. Based on this real-time information, the UAV calculated the ball’s future trajectory and initiated an avoidance maneuver.

Figure 5 illustrates this process in a step-by-step manner. In the first stage, the UAV detects the approaching ball as a dynamic object distinct from the static background (Figure 5a). In the subsequent stage, the tracking algorithm identifies the ball’s position and monitors its approach (Figure 5b), estimating its future trajectory. Next, as the UAV recognizes a potential collision, it begins executing an avoidance maneuver, which is reflected in a deviation from its initial path (Figure 5c). Finally, the UAV successfully adjusts its path by applying the modified APF (Figure 5d), which combines attractive forces toward the destination, repulsive forces from the ball, and a rotational force to escape potential local minima, successfully bypassing the ball, demonstrating the effectiveness of the overall obstacle avoidance strategy.

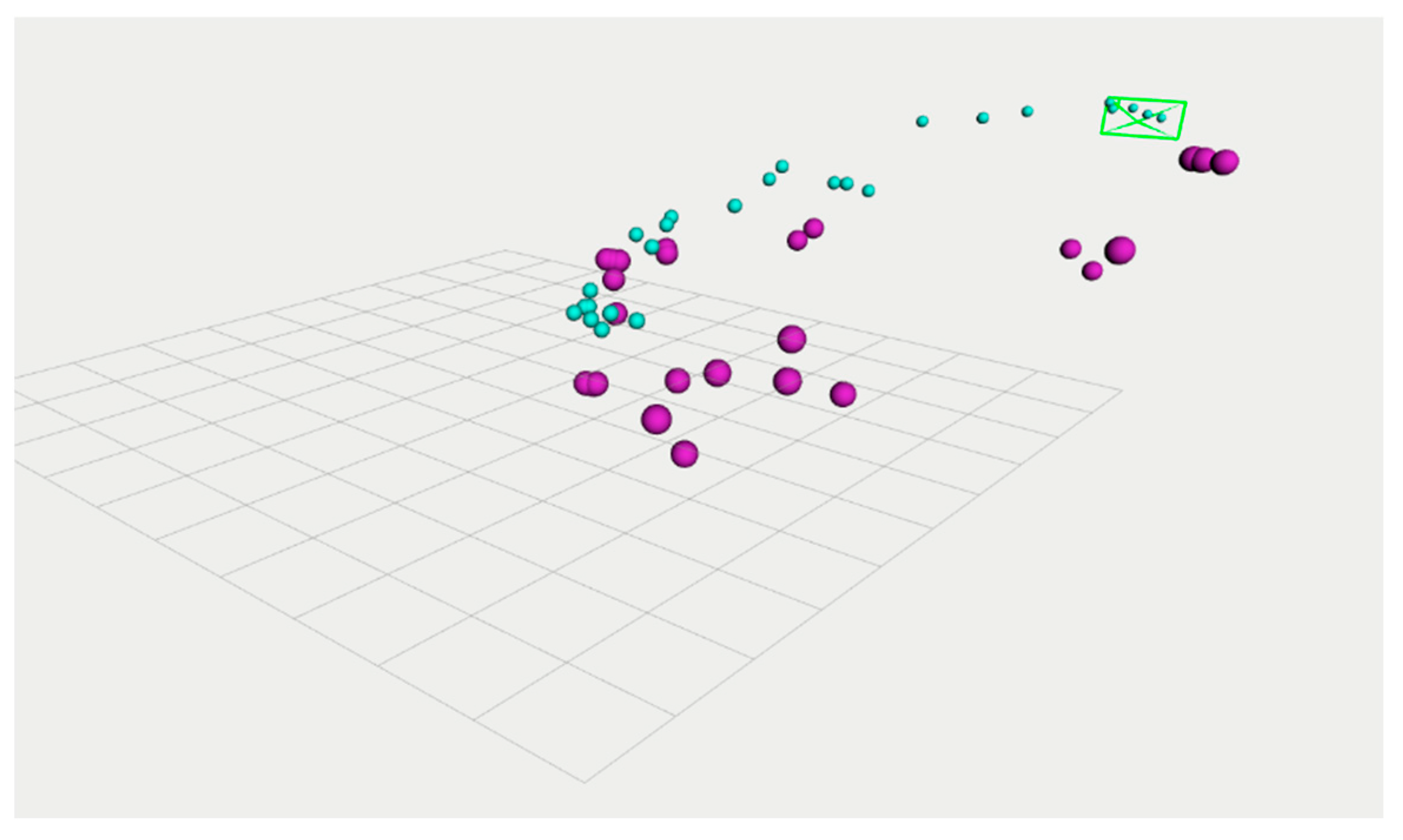
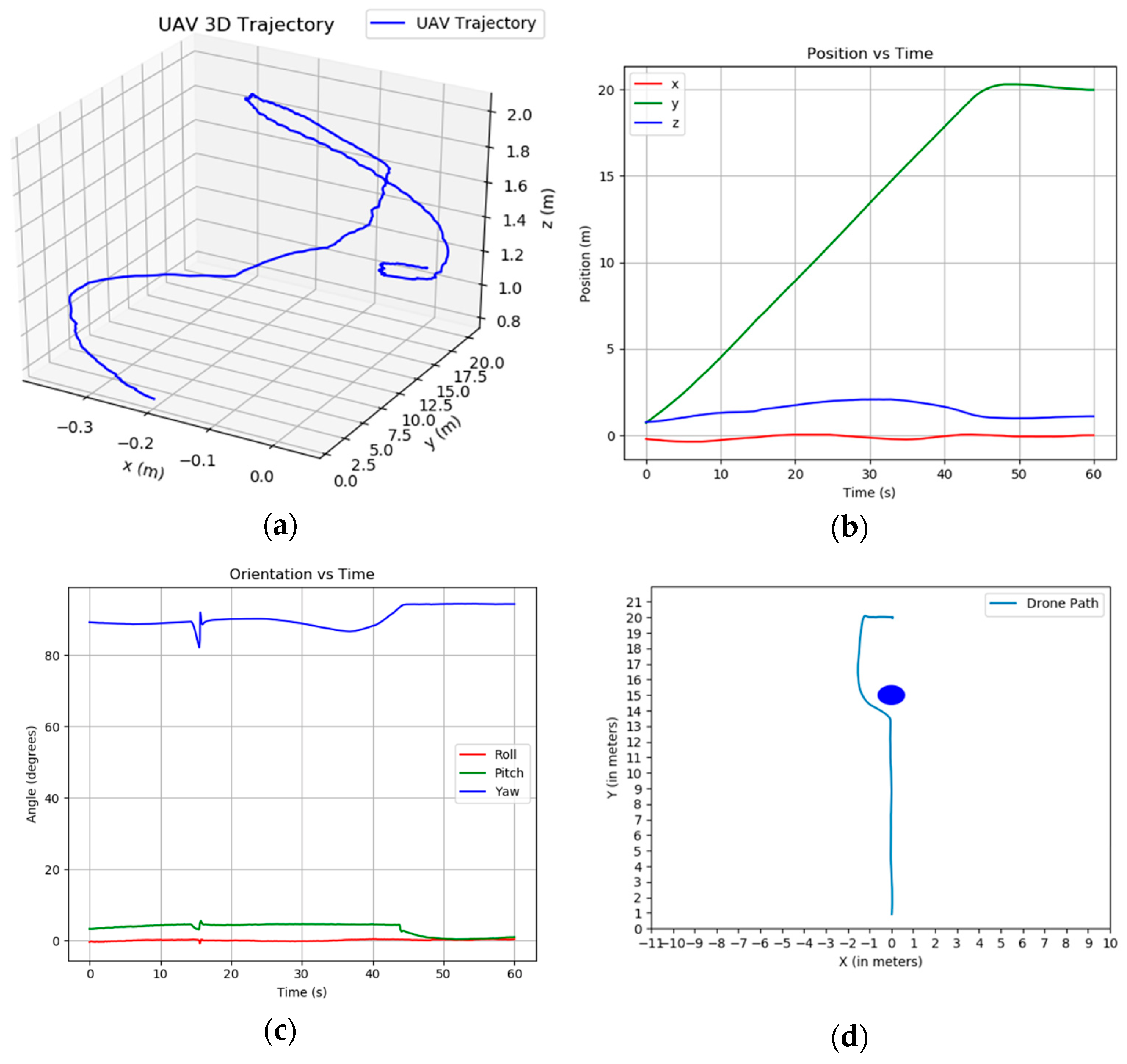
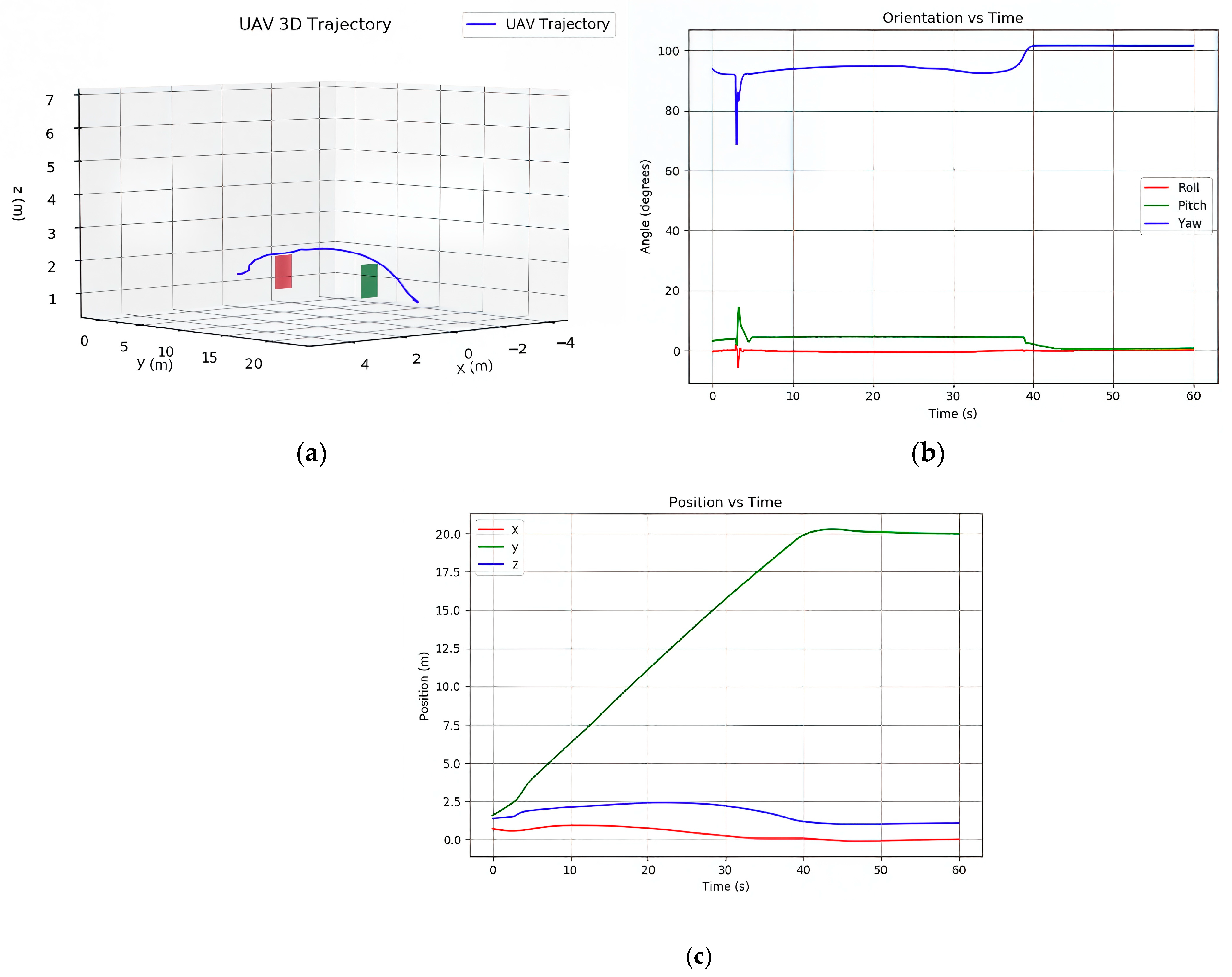
Figure 6 separates 2D obstacle detections from the 3D track of the same object. Blue points denote 2D detections on the ball in the image plane; for display, these detections are projected into the world frame using the calibrated camera pose. Purple spheres show depth-based 3D positions accumulated over time, reconstructing the ball’s approach trajectory. The UAV’s motion during this simulation is further analyzed in Figure 7, which includes three graphs: the UAV’s 3D trajectory, position vs. time, and orientation vs. time. The 3D trajectory plot (Figure 7a) shows the UAV’s path in a warehouse aisle, starting near (0, 0, 1.0) and moving along the y-axis toward the destination. Around the 30 s mark, the trajectory curves in the x and z directions, indicating an avoidance maneuver as the ball (moving at 10.0 m/s along the y-axis) approaches the UAV’s path. This smooth deviation highlights the modified APF’s ability to guide the UAV around the dynamic obstacle while maintaining progress toward the destination. The position vs. time graph in Figure 7b reveals the UAV’s progress along the y-axis (from 0 to 20 m), with small adjustments in x (between −0.3 and 0.3 m) and z (dipping to 0.8 m), corresponding to the avoidance maneuver. The orientation vs. time graph in Figure 7c) shows the UAV’s roll, pitch, and yaw angles. The yaw adjusts from 0 to 80 degrees, reflecting an initial orientation toward the destination and a slight reorientation after avoidance. These graphs illustrate the advantages of the proposed method, the ego-motion compensation ensures accurate detection of the dynamic ball by filtering out noise, and the modified APF facilitates a collision-free trajectory, enhancing the UAV’s navigation efficiency and safety in dynamic environments. In traditional obstacle avoidance approaches [24], a simple roll-command is employed after detection to execute a lateral tilt that prevents collision with the detected obstacle displayed as a blue circle, as shown in Figure 7d. However, such methods encounter several limitations: the roll-command is fixed and always triggers in a predetermined direction (e.g., left or right tilt) upon detection, which can lead to suboptimal paths in cluttered environments; it often results in abrupt maneuvers that increase mechanical stress on the UAV; and if suddenly another static or emerging element appears in that evasion direction, the method lacks the flexibility for timely readjustment, potentially causing instability or inefficient recovery.

To illustrate the effectiveness of the proposed 3D-APF method, consider a challenging scenario with two dynamic obstacles along the UAV’s path at 10 m/s, where the second is initially occluded behind the first. Using the proposed APF method, we achieve strong performance in avoiding the second obstacle as well. In this test, the complicated scenario with two dynamic obstacles moving after each other is presented to the method, and using the proposed APF, it can successfully avoid both obstacles after detecting them sequentially. The repulsive potentials first trigger an initial deviation, while the rotational force ensures the path adjusts dynamically to repel from the obstacles without trapping in local minima. The 3D trajectory using 3D-APF, orientation, and position are given in Figure 8a–c, respectively, showing smooth y-progression (0–20 m) with x/z/yaw adjustments.

5.3. Computational Performance Analysis

In this subsection, to evaluate the computational efficiency of the proposed ego-motion compensation and obstacle detection pipeline, we analyze both theoretical complexity and practical runtime performance in the Gazebo/ROS simulation environment.

Computational complexity is proportional to the number of event warping operations in the nonlinear compensation step. Assuming Ne events in a batch and incorporating depth scaling for each pixel, the complexity for warping is O(Ne), as each event is processed independently. This is bounded and more efficient than optimization-based baselines [12,14], which often require O(Ne log Ne) or higher due to iterative minimization. For adaptive thresholding, complexity is O(W H) for the normalized mean timestamp image (where W and H are image dimensions), making the overall pipeline suitable for real-time UAV applications.

Runtime measurements were conducted on a standard laptop with an Intel Core i7 CPU, using event batches of approximately 15,000 events. The ego-motion compensation step (nonlinear warping) takes about 0.5–1 s per batch. Adaptive thresholding and segmentation add 0.1 s, while the 3D-APF path planning terminates in under 0.2 s per iteration. Memory consumption is around 200 MB.

6. Conclusions

In conclusion, this paper presents a novel approach to dynamic obstacle detection and avoidance for UAVs using event camera technology combined with depth sensors. The proposed method introduces an ego-motion compensation algorithm with a nonlinear warping function, which effectively accounts for UAV motion, filtering background noise caused by translational and rotational movements. This method improves the accuracy of obstacle detection, particularly in dynamic environments. The novel APF method is integrated with the obstacle detection part to avoid detected dynamic obstacles, addressing local minima issues through a rotational force component to ensure efficient UAV navigation. The proposed method guarantees successful detection and avoidance of moving obstacles, even without prior knowledge of the obstacle’s size. The simulations have confirmed the proposed approach’s effectiveness, showcasing its superiority over linear compensation methods and traditional avoidance approaches in handling aggressive UAV movements and detecting dynamic obstacles in dynamic settings. Future work will involve real-world testing on physical UAV platforms, integrating actual event cameras, IMUs, and depth sensors like the Intel RealSense D435i, to validate the proposed methods in practical indoor environments such as warehouses with varying lighting and obstacles. This will include hardware-in-the-loop experiments to assess real-time performance, focusing on detection accuracy and avoidance success rates under aggressive maneuvers.