A Cooperative Longitudinal-Lateral Platoon Control Framework with Dynamic Lane Management for Unmanned Ground Vehicles Based on A Dual-Stage Multi-Objective MPC Approach
Abstract
Highlights
- A cooperative longitudinal–lateral platoon control framework using a dual-stage multi-objective MPC with adaptive weighting is proposed.
- A dynamic lane management mechanism enabling adaptive opening of UGV-dedicated lanes to improve platoon formation and stability is developed.
- The adaptive MPC strategy reduces the platoon formation time by 41.6% with negligible traffic speed reductions in mixed UGV–HDV traffic.
- Dynamic lane management yields longer, more stable platoons under varying penetration levels, especially in high-flow environments.
Abstract
1. Introduction
- (1)
- Limited platoon initiation: Sparse UGV distribution at early deployment stages reduces immediate platoon formation probability, constraining system efficiency gains.
- (2)
- Fragmented control architecture: Separate longitudinal or lateral control lacks an integrated system architecture to jointly optimize both trajectory dimensions in real time.
- (3)
- Rigid infrastructure usage: Incongruent lane use in high traffic flow impairs system adaptability, as dynamic management of UGV-dedicated lanes is rarely considered.
- (1)
- Adaptive platoon control: A cooperative trajectory-tracking strategy is developed for UGVs, structured into pursuit and platoon stages. This hierarchical control approach ensures coordinated tracking and robust platoon formation even under low UGV penetration.
- (2)
- Dual-stage MPC method: A novel dual-stage multi-objective MPC algorithm is developed with stage-specific objectives to coordinate longitudinal and lateral control. The adaptive weighting scheme dynamically adjusts control actions to traffic conditions, improving platoon stability and responsiveness.
- (3)
- Dynamic lane management: A traffic-aware platoon organization mechanism is proposed, allowing adaptive opening of UGV-dedicated lanes. This strategy accelerates platoon formation, sustains longer and more stable platoons, and improves traffic efficiency under congestion.
2. Literature Review
- Ad hoc Platoon Formation (APF)
- Locally coordinated Platoon Formation (LPF)
- Globally coordinated Platoon Formation (GPF)
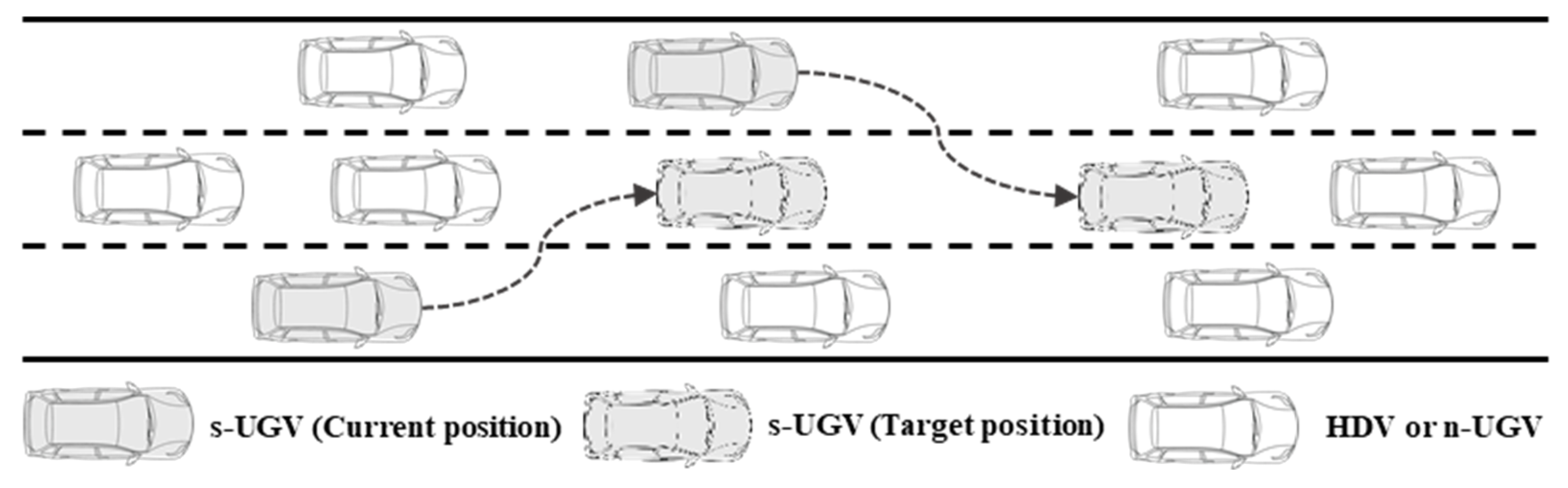
3. Problem Description
4. Vehicle Dynamics Modeling
4.1. Microscopic Dynamics Modeling of UGVs
- Case 1: Following another s-UGV
- Case 2: Following an n-UGV or HDV
4.2. Microscopic Dynamics Modeling of HDVs
4.3. Macroscopic Traffic-Flow Dynamics Modeling
5. Hybrid MPC-Based UGV Platoon Organization Framework
5.1. Generation of Reference Trajectories for UGVs
5.2. Formulation of a Multi-Objective MPC-Based Catch-Up Strategy
- Catching-up phase (): Two s-UGVs in different lanes attempt to approach each other to establish a following relationship.
- Formation phase (): The two s-UGVs stabilize their spacing and relative velocity within the same lane, thereby forming a platoon.
- MPC-I (Catching-up phase ): emphasizes minimizing spacing deviation () and establishing car following () while ignoring speed coordination ( The objective is the following:
- MPC-II (Formation phase ): once the two s-UGVs achieve a car-following mode in the same lane, the objective excludes but adds the constraint to ensure lane consistency:
5.3. Adaptive Weight Adjustment Strategy for the Hybrid MPC
- Case 1 (Congested State): Two s-UGVs travel slowly in adjacent lanes under congested traffic conditions. In this case, the control should minimize to reduce unnecessary maneuvers while still maintaining spacing via
- Case 2 (Free-flow State): Two s-UGVs travel at normal speed in adjacent lanes under free-flow conditions. Here, greater emphasis should be given to to encourage accelerations and lane changes, thereby reducing the time to complete platoon formation.
5.4. Flow-Aware Platoon Organization Strategy for Dedicated UGV Lanes
- ①
- Establish a baseline without platoon organization at a given penetration rate to determine the maximum capacity and generate speed contour plots.
- ②
- Initialize at 80% of capacity and at 22.22 m/s. For example, if the capacity at 50% UGV penetration is 2200 veh/h/lane, then = 1760 veh/h/lane.
- ③
- Simulate traffic with platoon organization under the same demand.
- ④
- If the speed contour shows a substantial reduction compared to the baseline, update the thresholds: reduce by 5% if the last update was on ; otherwise, increase by 1.39 m/s.
- ⑤
- Repeat Steps 3–4 until the speed contours under platoon organization closely match the baseline, indicating acceptable traffic efficiency.
6. Numerical Experiments and Results
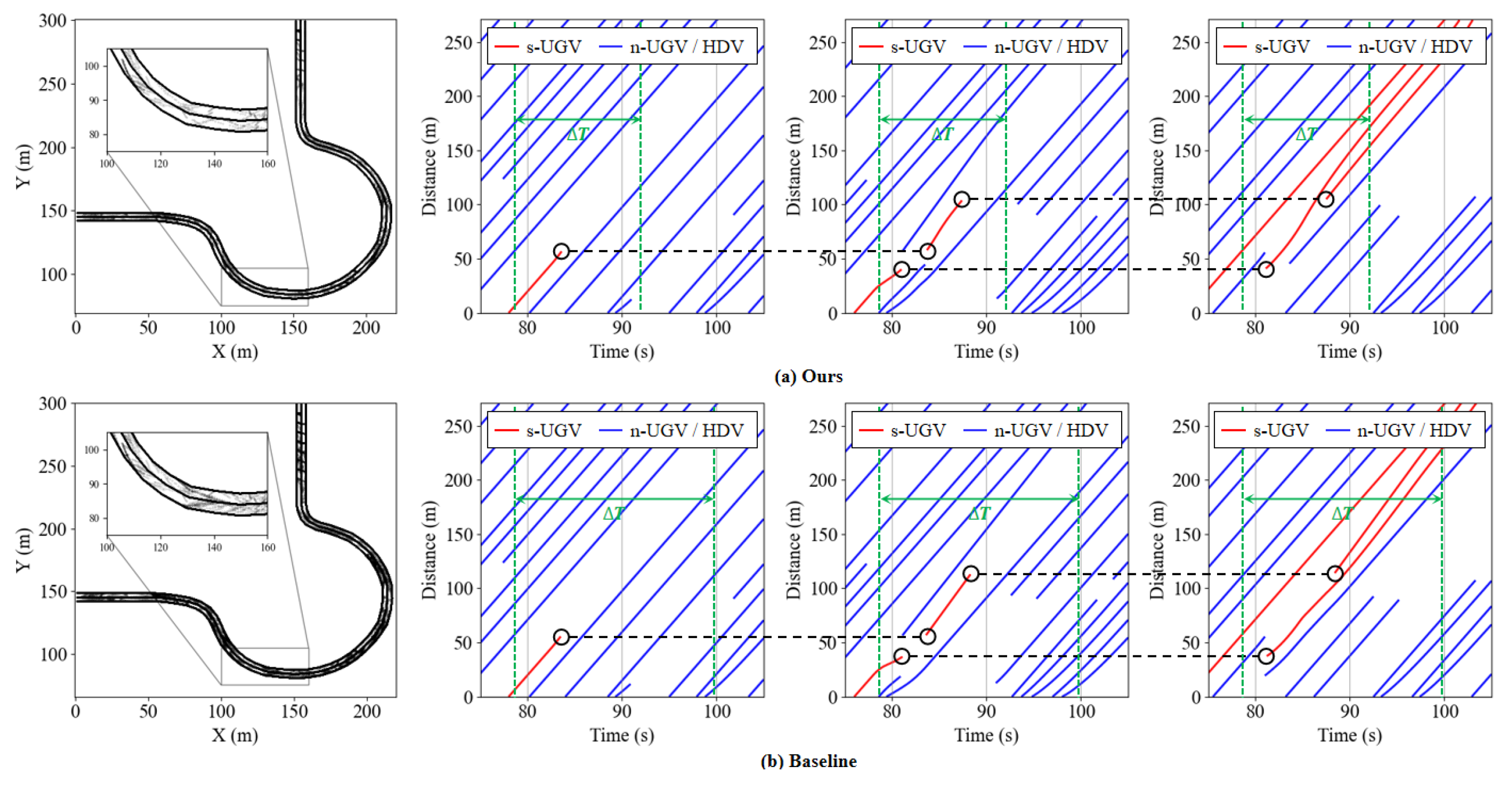
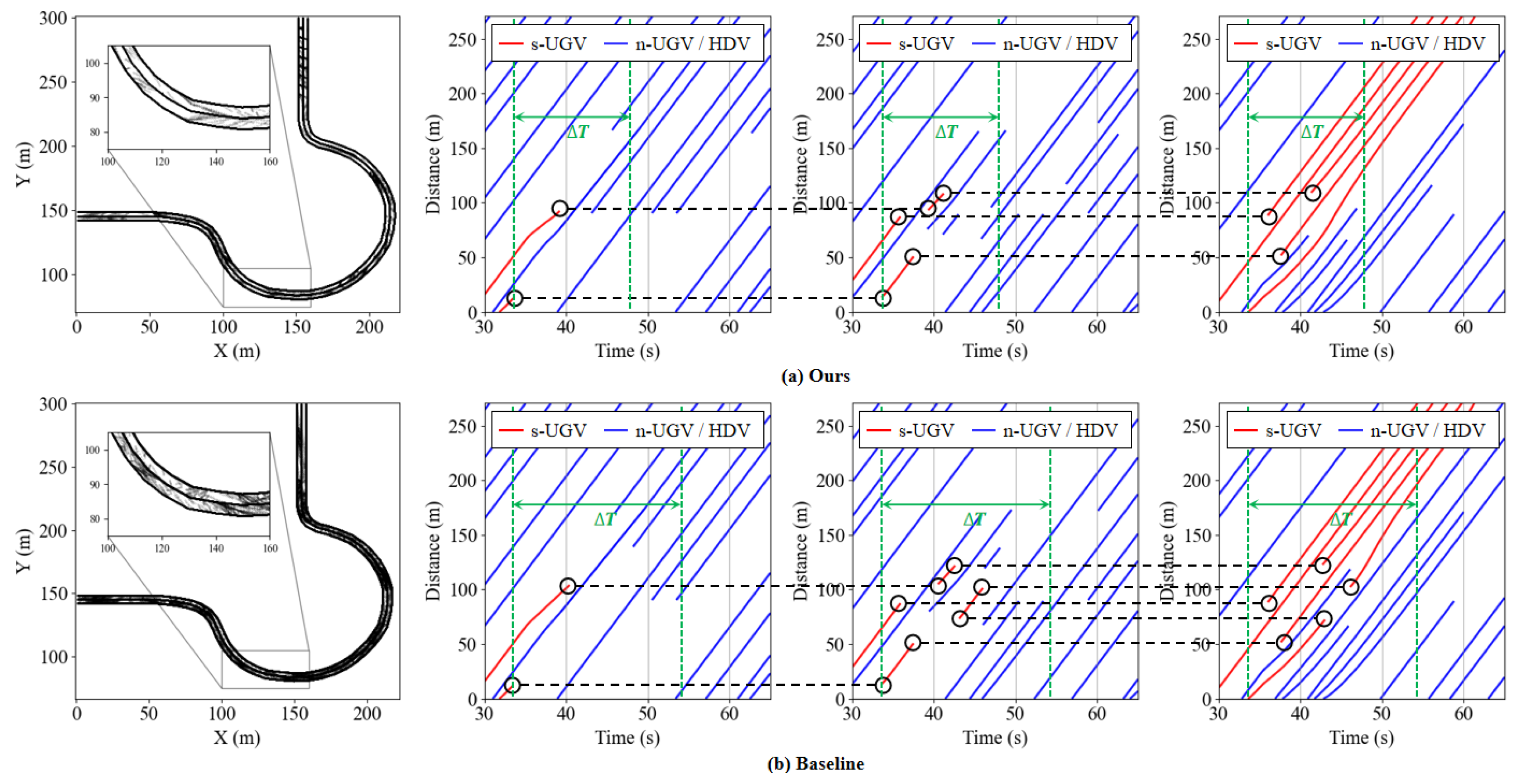
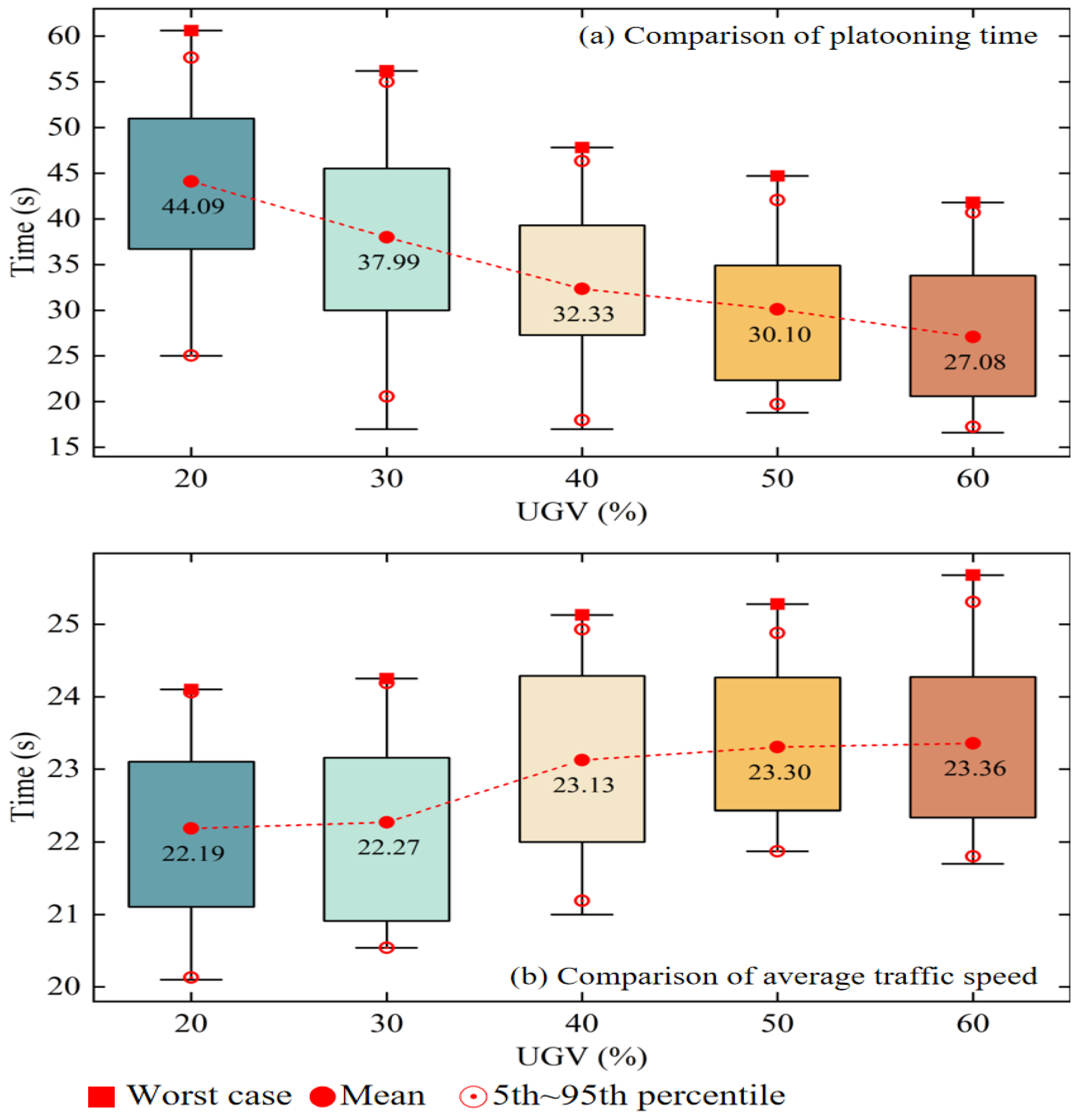
6.1. Analysis of Platoon Control Performance
- ①
- The time required for s-UGVs to complete lane changes and enter car-following mode;
- ②
- Speed coordination between s-UGVs;
- ③
- The time required to stabilize inter-vehicle spacing.
- ①
- Balanced strategy: assigns equal weights to platoon efficiency and traffic efficiency (i.e., in MPC-I or in MPC-II);
- ②
- Platoon-efficiency-first strategy: prioritizes formation efficiency by setting (or );
- ③
- Traffic-efficiency-first strategy: prioritizes traffic efficiency by setting (or );
- ④
- Adaptive strategy: dynamically adjusts weights according to Equations (37) and (39).
- Sensing noise: random deviations of 5%, 10%, and 15% were injected into vehicle perception.
- HDV cut-in: unexpected cut-in maneuvers of HDVs were introduced during the two-s-UGV platoon formation process, with the re-formation performance evaluated after disruption.
6.2. Sensitivity Analysis of Platoon Control
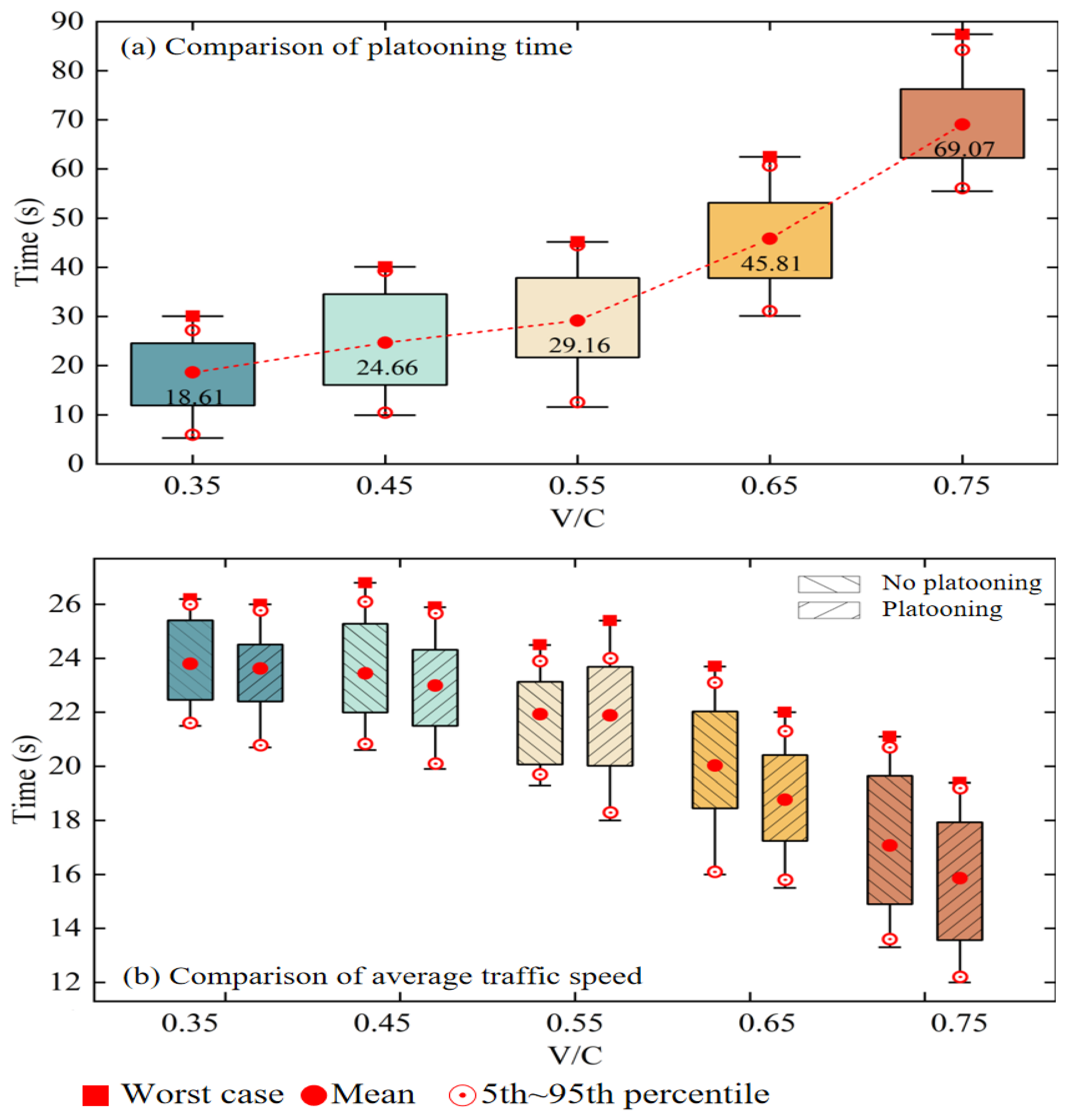
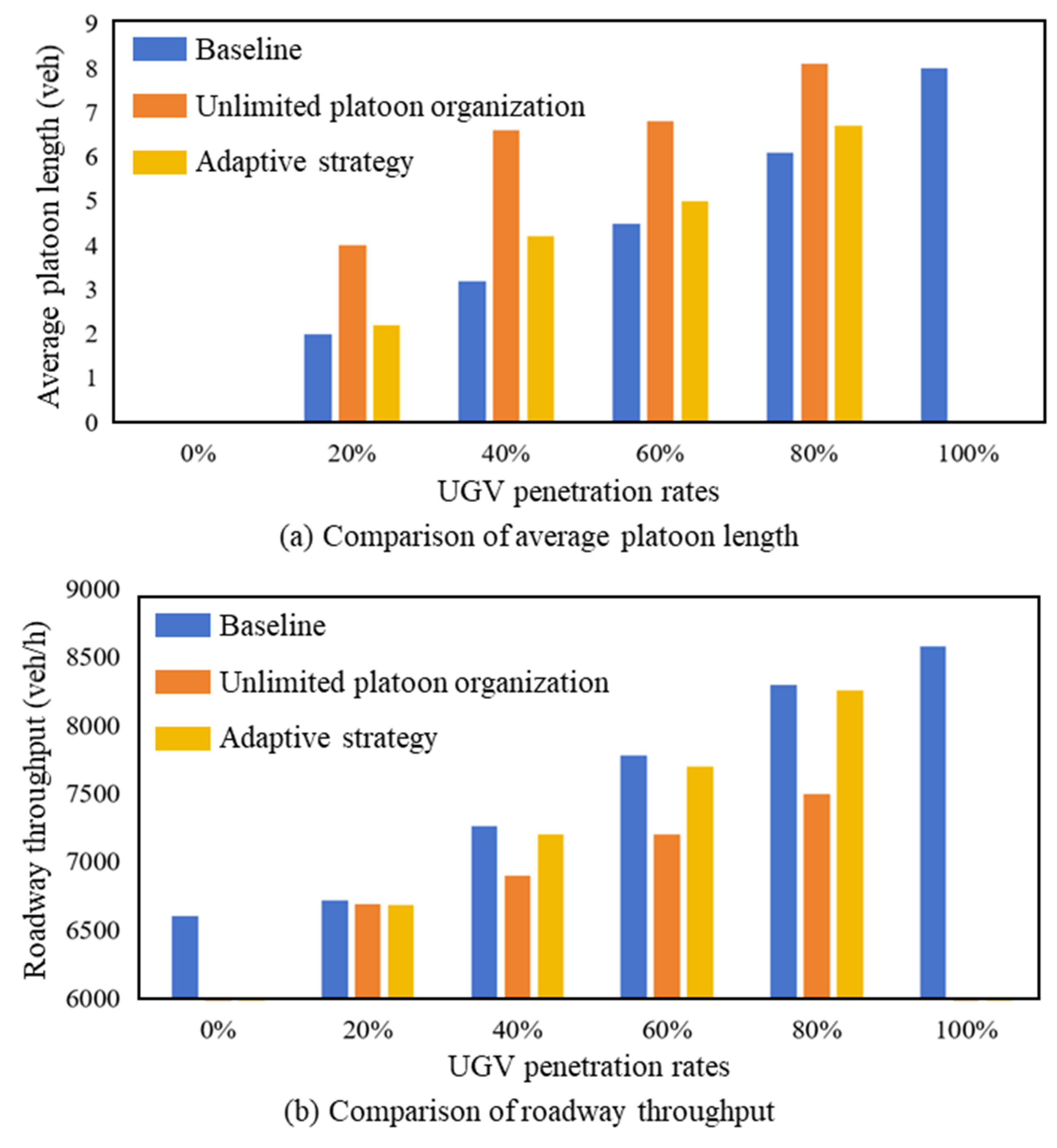
6.3. Performance Analysis of UGV Platoon Organization Strategies
- Baseline: No platoon control. To emulate real freeway conditions, HDVs follow the aggressive lane-changing rule 2, executing single discretionary lane changes.
- Dedicated UGV lane without any adaptive restriction: Based on the baseline experiment setting, the outermost lane is reserved for UGV platoon organization without any adaptive restriction.
- Dedicated UGV lane with adaptive strategy: Based on the second experiment setting, the same dedicated lane is used, but platoon organization is enabled or disabled according to the flow-aware adaptive strategy.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, S.; Hwang, S.; Kim, H.S. T–S Fuzzy Observer-Based Output Feedback Lateral Control of UGVs Using a Disturbance Observer. Drones 2024, 8, 685. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Xie, F. Robust Formation Control for Unmanned Ground Vehicles Using Onboard Visual Sensors and Machine Learning. Drones 2024, 8, 787. [Google Scholar] [CrossRef]
- Ramezani, M.; Amiri Atashgah, M.A.; Rezaee, A. A Fault-Tolerant Multi-Agent Reinforcement Learning Framework for Unmanned Aerial Vehicles–Unmanned Ground Vehicle Coverage Path Planning. Drones 2024, 8, 537. [Google Scholar] [CrossRef]
- Sui, Y.; Yang, Z.; Zhuo, H.; You, Y.; Que, W.; He, N. A Fuzzy Pure Pursuit for Autonomous UGVs Based on Model Predictive Control and Whole-Body Motion Control. Drones 2024, 8, 554. [Google Scholar] [CrossRef]
- Wang, Z.; Bian, Y.; Shladover, S.E.; Wu, G.; Li, S.E.; Barth, M.J. A survey on cooperative longitudinal motion control of multiple connected and automated vehicles. IEEE Intell. Transp. Syst. Mag. 2019, 12, 4–24. [Google Scholar] [CrossRef]
- Hu, M.; Zhao, X.; Hui, F.; Tian, B.; Xu, Z.; Zhang, X. Modeling and analysis on minimum safe distance for platooning vehicles based on field test of communication delay. J. Adv. Transp. 2021, 2021, 5543114. [Google Scholar] [CrossRef]
- Wu, J.; Ahn, S.; Zhou, Y.; Liu, P.; Qu, X. The cooperative sorting strategy for connected and automated vehicle platoons. Transp. Res. Part C Emerg. Technol. 2021, 123, 102986. [Google Scholar] [CrossRef]
- Cao, D.; Wu, J.; Wu, J.; Kulcsár, B.; Qu, X. A platoon regulation algorithm to improve the traffic performance of highway work zones. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 941–956. [Google Scholar] [CrossRef]
- Chandler, R.E.; Herman, R.; Montroll, E.W. Traffic dynamics: Studies in car following. Oper. Res. 1958, 6, 165–184. [Google Scholar] [CrossRef]
- Helly, W. Simulation of bottlenecks in single-lane traffic flow. In Proceedings of the Symposium on Theory of Traffic Flow, Research Laboratories, General Motors; Herman, R., Ed.; General Motors: New York, NY, USA, 1959; pp. 207–238. [Google Scholar]
- Schuhl, A. The probability theory applied to distribution of vehicles on two-lane highways. In Eno Found; Technical Report; Highway Traffic Control: Washington, DC, USA, 1955; pp. 59–75. [Google Scholar]
- Yao, H.; Li, Q.; Li, X. A study of relationships in traffic oscillation features based on field experiments. Transp. Res. Part A Policy Pract. 2020, 141, 339–355. [Google Scholar] [CrossRef]
- Zhou, F.; Li, X.; Ma, J. Parsimonious shooting heuristic for trajectory design of connected automated traffic part I: Theoretical analysis with generalized time geography. Transp. Res. Part B Methodol. 2017, 95, 394–420. [Google Scholar] [CrossRef]
- Li, Q.; Li, X.; Huang, Z.; Halkias, J.; McHale, G.; James, R. Simulation of mixed traffic with cooperative lane changes. Comput.-Aided Civ. Infrastruct. Eng. 2022, 37, 1978–1996. [Google Scholar] [CrossRef]
- Guo, G.; Yue, W. Autonomous platoon control allowing range-limited sensors. IEEE Trans. Veh. Technol. 2012, 61, 2901–2912. [Google Scholar] [CrossRef]
- Maiti, S.; Winter, S.; Kulik, L. A conceptualization of vehicle platoons and platoon operations. Transp. Res. Part C Emerg. Technol. 2017, 80, 1–19. [Google Scholar] [CrossRef]
- Liang, K.Y.; Mårtensson, J.; Johansson, K.H. Heavy-duty vehicle platoon formation for fuel efficiency. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1051–1061. [Google Scholar] [CrossRef]
- Tuchner, A.; Haddad, J. Vehicle platoon formation using interpolating control: A laboratory experimental analysis. Transp. Res. Part C Emerg. Technol. 2017, 84, 21–47. [Google Scholar] [CrossRef]
- Stankovic, S.S.; Stanojevic, M.J.; Siljak, D.D. Decentralized overlapping control of a platoon of vehicles. IEEE Trans. Control Syst. Technol. 2000, 8, 816–832. [Google Scholar] [CrossRef]
- Gehring, O.; Fritz, H. Practical results of a longitudinal control concept for truck platooning with vehicle to vehicle communication. In Proceedings of the Conference on Intelligent Transportation Systems, Boston, MA, USA, 12 November 1997; pp. 117–122. [Google Scholar]
- Shladover, S.E. Truck automation operational concept alternatives. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010; pp. 1072–1077. [Google Scholar]
- Kunze, R.; Ramakers, R.; Henning, K.; Jeschke, S. Organization and operation of electronically coupled truck platoons on German motorways. In Automation, Communication and Cybernetics in Science and Engineering 2009/2010; Springer: Berlin/Heidelberg, Germany, 2011; pp. 427–439. [Google Scholar]
- Tsugawa, S. Results and issues of an automated truck platoon within the energy ITS project. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 642–647. [Google Scholar]
- Shladover, S.E.; Su, D.; Lu, X.Y. Impacts of cooperative adaptive cruise control on freeway traffic flow. Transp. Res. Rec. 2012, 2324, 63–70. [Google Scholar] [CrossRef]
- Maiti, S.; Winter, S.; Kulik, L.; Sarkar, S. Ad-hoc platoon formation and dissolution strategies for multi-lane highways. J. Intell. Transp. Syst. 2023, 27, 161–173. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, S.; Yao, Z.; Zhao, B.; Wang, Y. A cellular automata model for mixed traffic flow considering the driving behavior of connected automated vehicle platoons. Phys. A Stat. Mech. Its Appl. 2021, 582, 126262. [Google Scholar] [CrossRef]
- Chang, X.; Li, H.; Rong, J.; Zhao, X.; Li, A.R. Analysis on traffic stability and capacity for mixed traffic flow with platoons of intelligent connected vehicles. Phys. A Stat. Mech. Its Appl. 2020, 557, 124829. [Google Scholar] [CrossRef]
- Zhou, J.; Zhu, F. Modeling the fundamental diagram of mixed human-driven and connected automated vehicles. Transp. Res. Part C Emerg. Technol. 2020, 115, 102614. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Zhu, H.B.; Guo, M.M.; Zhou, J.L. Impact of CACC vehicles’ cooperative driving strategy on mixed four-lane highway traffic flow. Phys. A Stat. Mech. Its Appl. 2020, 540, 122721. [Google Scholar] [CrossRef]
- Songchitruksa, P.; Bibeka, A.; Lin, L.I.; Zhang, Y. Incorporating Driver Behaviors into Connected and Automated Vehicle Simulation; Center for Advancing Transportation Leadership and Safety (ATLAS Center): Ann Arbor, MI, USA, 2016. [Google Scholar]
- Wang, Z.; Wu, G.; Hao, P.; Boriboonsomsin, K.; Barth, M. Developing a platoon-wide eco-cooperative adaptive cruise control (CACC) system. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1256–1261. [Google Scholar]
- Papadoulis, A.; Quddus, M.; Imprialou, M. Evaluating the safety impact of connected and autonomous vehicles on motorways. Accid. Anal. Prev. 2019, 124, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Oh, C. A methodology to establish operational strategies for truck platoonings on freeway on-ramp areas. J. Korean Soc. Transp. 2018, 36, 67–85. [Google Scholar] [CrossRef]
- Besselink, B.; Turri, V.; Van De Hoef, S.H.; Liang, K.Y.; Alam, A.; Mårtensson, J.; Johansson, K.H. Cyber–physical control of road freight transport. Proc. IEEE 2016, 104, 1128–1141. [Google Scholar] [CrossRef]
- Shao, B. Scheduling Plan Optimization of Truck Platooning Considering Ecological Benefits Under Connected Vehicle Environment. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Bolton, W. Instrumentation and Control Systems; Newnes: Oxford, UK, 2021. [Google Scholar]
- Klančar, G.; Matko, D.; Blažič, S. Wheeled mobile robots control in a linear platoon. J. Intell. Robot. Syst. 2009, 54, 709–731. [Google Scholar] [CrossRef]
- Turri, V.; Kim, Y.; Guanetti, J.; Johansson, K.H.; Borrelli, F. A model predictive controller for non-cooperative eco-platooning. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 2309–2314. [Google Scholar]
- Chan, E. SARTRE automated platooning vehicles. Towards Innov. Freight Logist. 2016, 2, 137–150. [Google Scholar]
- Eilers, S.; Mårtensson, J.; Pettersson, H.; Pillado, M.; Gallegos, D.; Tobar, M.; Johansson, K.H.; Ma, X.; Friedrichs, T.; Borojeni, S.S.; et al. COMPANION—Towards Co-operative Platoon Management of Heavy-Duty Vehicles. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 1267–1273. [Google Scholar]
- Kazemi, A.; Sharifi, I.; Talebi, H.A. Longitudinal and lateral control of vehicle platoons using Laguerre-based and robust MPC with merge and exit maneuvers. Control Eng. Pract. 2024, 142, 105737. [Google Scholar] [CrossRef]
- Nilsson, J.; Brännström, M.; Fredriksson, J.; Coelingh, E. Longitudinal and lateral control for automated yielding maneuvers. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1404–1414. [Google Scholar] [CrossRef]
- Tian, D.; Zhou, J.; Han, X.; Lang, P. Robust platoon control of mixed autonomous and human-driven vehicles for obstacle collision avoidance: A cooperative sensing-based adaptive model predictive control approach. Engineering 2024, 42, 244–266. [Google Scholar] [CrossRef]
- Newell, G.F. A simplified car-following theory: A lower order model. Transp. Res. Part B Methodol. 2002, 36, 195–205. [Google Scholar] [CrossRef]
- Li, H.; Pang, H.; Xia, H.; Huang, Y.; Zeng, X. Research on Trajectory Planning Method Based on Bézier Curves for Dynamic Scenarios. Electronics 2025, 14, 494. [Google Scholar] [CrossRef]
- Feinstein, Z.; Kleiber, M.; Weber, S. Stochastic cell transmission models of traffic networks. arXiv 2023, arXiv:2304.11654. [Google Scholar]
- Huang, Y.-S.; Weng, Y.-S.; Shih, C.-Y. Utilizing Cell Transmission Models to Alleviate Accident-Induced Traffic Congestion in Two-Way Grid Networks. Algorithms 2025, 18, 193. [Google Scholar] [CrossRef]
- Ogbemhe, J.; Mpofu, K.; Tlale, N.S. Continuous trajectory planning for welding of complex joints using Bezier curve. Procedia Manuf. 2019, 33, 685–692. [Google Scholar] [CrossRef]
- Hua, Z.; Zhang, W. Obstacle-Avoidance Path Planning for Autonomous Vehicles Based on Bezier Curves. Automot. Dig. 2021, 3, 46–49. [Google Scholar]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M. Model Predictive Control: Theory, Computation, and Design; Nob Hill Publishing: Madison, WI, USA, 2017. [Google Scholar]
- Al-Jumaili, M.H.; Özok, Y.E. New control model for autonomous vehicles using integration of Model Predictive and Stanley based controllers. Sci. Rep. 2024, 14, 19872. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tian, B.; Xu, Z.; Gong, S.; Gao, Y.; Cui, Z.; Chen, X. A local traffic characteristic based dynamic gains tuning algorithm for cooperative adaptive cruise control considering wireless communication delay. Transp. Res. Part C Emerg. Technol. 2022, 142, 103766. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, J.; Xu, H.; He, Z. T3C: A traffic-communication coupling control approach for autonomous intersection management system. Transp. Res. Part C Emerg. Technol. 2024, 169, 104886. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Wang, B.; Li, M. Collision avoidance motion planning for connected and automated vehicle platoon merging and splitting with a hybrid automaton architecture. IEEE Trans. Intell. Transp. Syst. 2023, 25, 1445–1464. [Google Scholar] [CrossRef]
- Ali, Y.; Zheng, Z.; Bliemer, M.C.J. Calibrating lane-changing models: Two data-related issues and a general method to extract appropriate data. Transp. Res. Part C Emerg. Technol. 2023, 152, 104182. [Google Scholar] [CrossRef]
- Li, R.; Sun, S.; Wu, Y.; Hao, H.; Wen, X.; Yao, Z. Fundamental diagram of mixed traffic flow considering time lags, platooning intensity, and the degradation of connected automated vehicles. Phys. A Stat. Mech. Its Appl. 2023, 627, 129130. [Google Scholar] [CrossRef]
- Li, R.; Jiang, B.; Zong, Y.; Lu, N.; Guo, L. Event-Triggered Collaborative Fault Diagnosis for UAV–UGV Systems. Drones 2024, 8, 324. [Google Scholar] [CrossRef]
- Wang, N.; Li, X.; Suo, Z.; Fan, J.; Wang, J.; Xie, D. Traversability Analysis and Path Planning for Autonomous Wheeled Vehicles on Rigid Terrains. Drones 2024, 8, 419. [Google Scholar] [CrossRef]




| Performance | Objective | Criterion | Description |
|---|---|---|---|
| Traffic performance | Penalty | Penalize frequent acceleration, deceleration, and lane changes by s-UGVs, discouraging abrupt maneuvers that disrupt traffic flow. | |
| Reward | Reward s-UGVs for maintaining speeds not lower than the surrounding traffic, preventing obstruction during catch-up. | ||
| Reward | Reward higher upstream throughput by promoting increased downstream outflow during platoon formation. | ||
| Platooning performance | Reward | Reward successful platoon formation through lane changing, reflected in a sustained car-following state between two s-UGVs. | |
| Penalty | Penalize large relative speed differences between s-UGVs, encouraging speed harmonization. | ||
| Penalty | Penalize deviations in inter-vehicle gaps from the desired spacing, promoting stable platoon distances. |
| Stage | Weight | Balance | Platooning Efficiency First | Traffic Efficiency First | Adaptive Weights |
|---|---|---|---|---|---|
| MPC-I | 0.30 | 0.20 | 0.40 | Adaptive | |
| 0.30 | 0.30 | 0.30 | 0.30 | ||
| MPC-II | 0.35 | 0.20 | 0.50 | Adaptive | |
| 0.35 | 0.35 | 0.35 | 0.35 |
| Scenarios | Minimum TTC (s) | Violation Rate of Headway (%) | Recovery Time (s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Min | Mean | Max | Min | Mean | Max | ||
| Sensing noise | 5% | 3.1 | 4.3 | 6.7 | 0.0 | 0.4 | 0.9 | 21.5 | 34.3 | 46.8 |
| 10% | 2.7 | 3.9 | 6.1 | 0.2 | 1.1 | 2.3 | 26.3 | 39.6 | 52.4 | |
| 15% | 2.1 | 3.3 | 5.6 | 0.8 | 2.5 | 4.3 | 37.9 | 48.4 | 69.0 | |
| V2X latency | 50 ms | 2.9 | 4.1 | 6.3 | 0.1 | 0.6 | 1.4 | 17.6 | 29.9 | 46.1 |
| 100 ms | 2.5 | 3.8 | 5.9 | 0.7 | 1.5 | 2.8 | 19.5 | 33.4 | 52.6 | |
| 150 ms | 2.1 | 3.3 | 5.4 | 1.9 | 4.1 | 6.5 | 25.8 | 39.7 | 68.2 | |
| HDV cut-in | 2.3 | 3.9 | 6.0 | 0.6 | 1.8 | 3.2 | 38.4 | 57.6 | 88.5 | |
| Demand (veh/h/lane) | ANOLC (count/veh) | APL (veh) | POPF | ROF (veh/h/lane) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Reference | Platoon | Reference | Platoon | Reference | Platoon | Reference | Platoon | Impact Ratio | |
| 1000 | 0 | 0.49 | 2.6 | 5.0 | 0.73 | 0.88 | 1000 | 998 | −0.20% |
| 1500 | 0 | 0.51 | 2.8 | 5.1 | 0.74 | 0.85 | 1500 | 1468 | −2.13% |
| 2000 | 0 | 0.53 | 2.7 | 5.1 | 0.74 | 0.87 | 2000 | 1922 | −3.90% |
| 2500 | 0 | 0.56 | 3.1 | 5.4 | 0.78 | 0.90 | 2487 | 2200 | −11.54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wu, Z.; Su, Y. A Cooperative Longitudinal-Lateral Platoon Control Framework with Dynamic Lane Management for Unmanned Ground Vehicles Based on A Dual-Stage Multi-Objective MPC Approach. Drones 2025, 9, 711. https://doi.org/10.3390/drones9100711
Wang S, Wu Z, Su Y. A Cooperative Longitudinal-Lateral Platoon Control Framework with Dynamic Lane Management for Unmanned Ground Vehicles Based on A Dual-Stage Multi-Objective MPC Approach. Drones. 2025; 9(10):711. https://doi.org/10.3390/drones9100711
Chicago/Turabian StyleWang, Shunchao, Zhigang Wu, and Yonghui Su. 2025. "A Cooperative Longitudinal-Lateral Platoon Control Framework with Dynamic Lane Management for Unmanned Ground Vehicles Based on A Dual-Stage Multi-Objective MPC Approach" Drones 9, no. 10: 711. https://doi.org/10.3390/drones9100711
APA StyleWang, S., Wu, Z., & Su, Y. (2025). A Cooperative Longitudinal-Lateral Platoon Control Framework with Dynamic Lane Management for Unmanned Ground Vehicles Based on A Dual-Stage Multi-Objective MPC Approach. Drones, 9(10), 711. https://doi.org/10.3390/drones9100711






