Research on Multi-UAV Cooperative Dynamic Path Planning Algorithm Based on Conflict Search
Abstract
1. Introduction
- (1)
- The flight coordination constraints and conflicts of multiple UAVs in the three-dimensional space environment are comprehensively analyzed, and a CBS-based framework for a multi-UAV cooperative dynamic path planning algorithm is constructed;
- (2)
- A sparse D* algorithm for UAV dynamic path planning in complex environments is proposed, which reduces the time of path search in case of sudden threats;
- (3)
- The search efficiency is improved by heuristic information, and a dynamic response mechanism is designed to realize the dynamic path planning of multiple UAVs facing sudden threats.
2. Problem Description
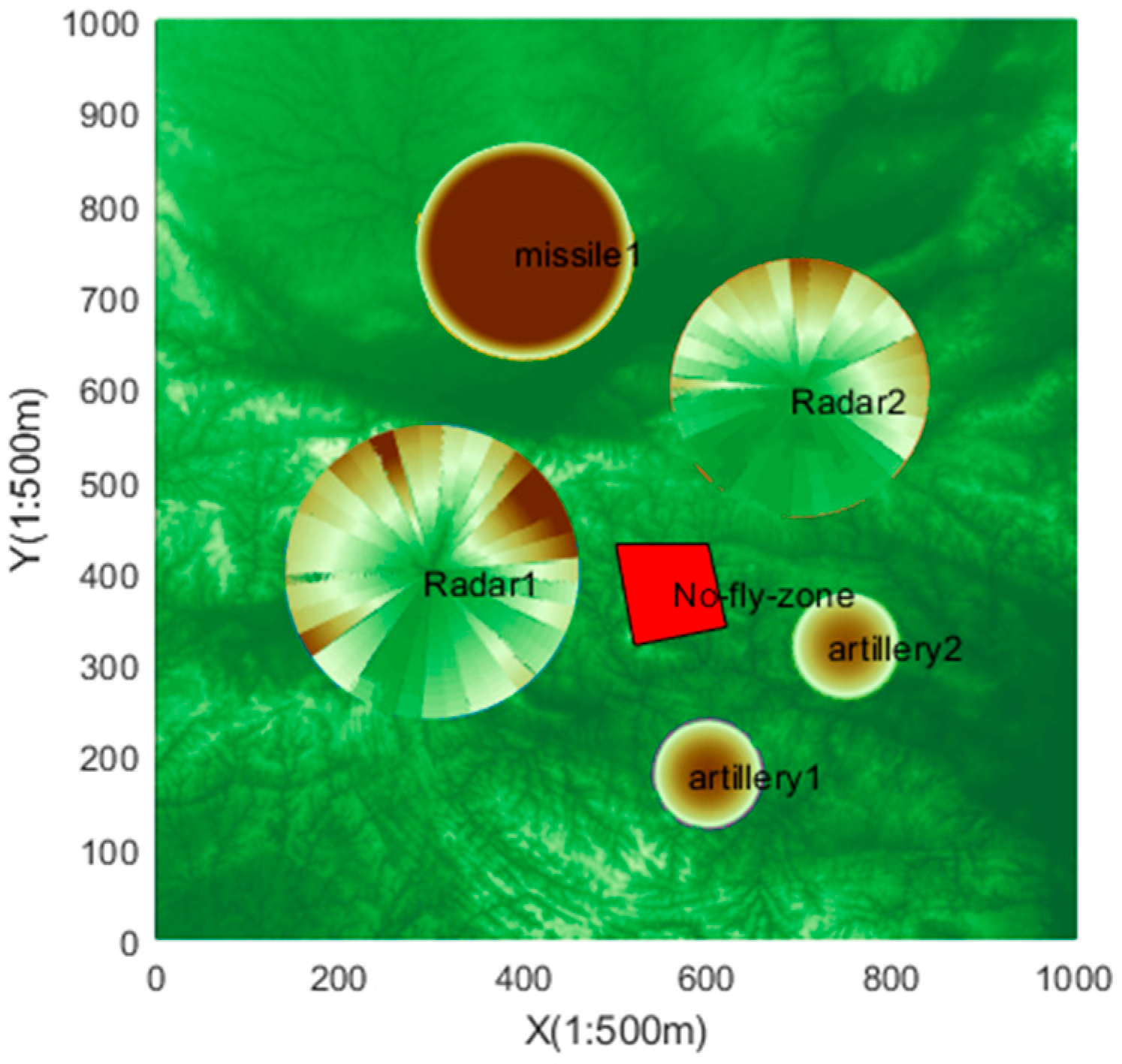
2.1. Environmental Threat Analysis
2.2. Flight Constraint Analysis
- (1)
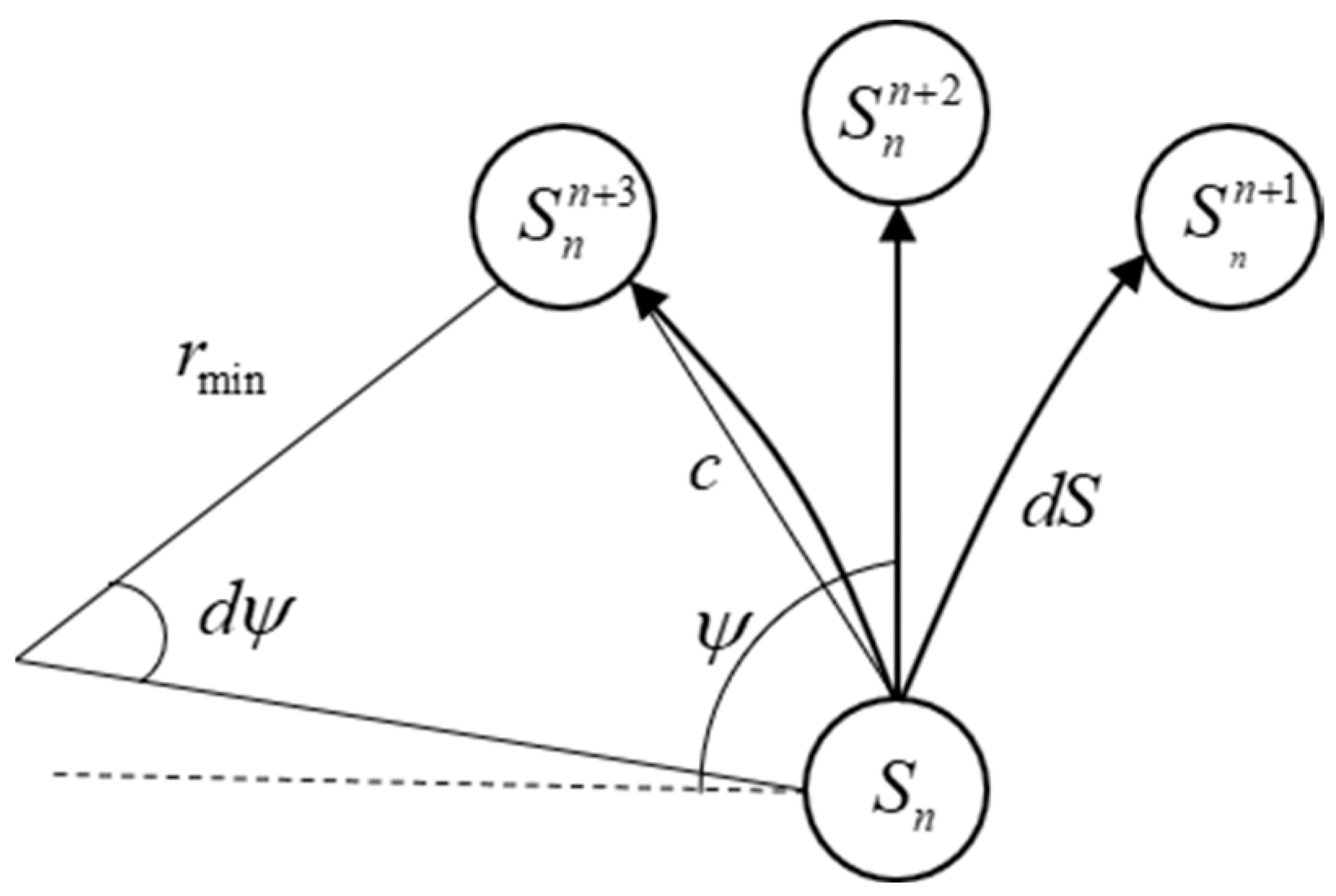
- Minimum turning radius constraint r: Due to the constraints of maneuvering conditions, the turning radius of the UAV needs to be greater than the minimum turning radius;
- (2)
- Minimum path segment length constraint dS: The minimum path segment length is the minimum distance that the UAV must fly before changing its flight attitude during flight. In path planning, the unit step size of the planned path can be set to be greater than the minimum path segment length so as to meet the minimum path segment length constraint;
- (3)
- Maximum path slope angle constraint θ: Because the UAV is constrained by engine performance and flight safety, the ascending and diving angles of the path in the vertical direction are also restricted, so the planned flight path of the UAV must meet the maximum path slope angle constraint within the unit path step size;
- (4)
- Minimum ground clearance constraint z: In order to ensure the safe flight of the UAV and avoid collision with the ground or low-altitude obstacles, the minimum ground clearance constraint needs to be set to make the flight height of the UAV greater than the minimum ground clearance and ensure flight safety;
- (5)
- Average speed constraint v: Considering the control optimization of the speed system, the flight speed of the UAV can be adjusted quickly. Therefore, the average speed of each UAV passing through different path segments is set to be the same in this paper; that is, it takes the same time to pass through different path segments.
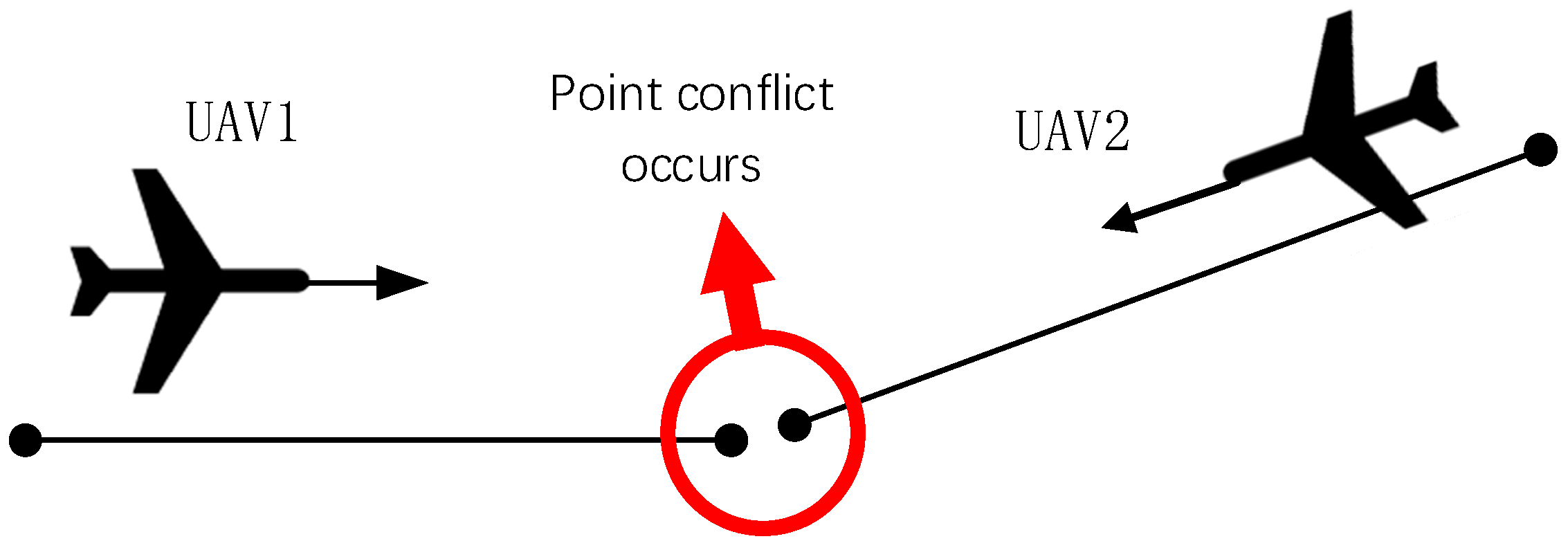
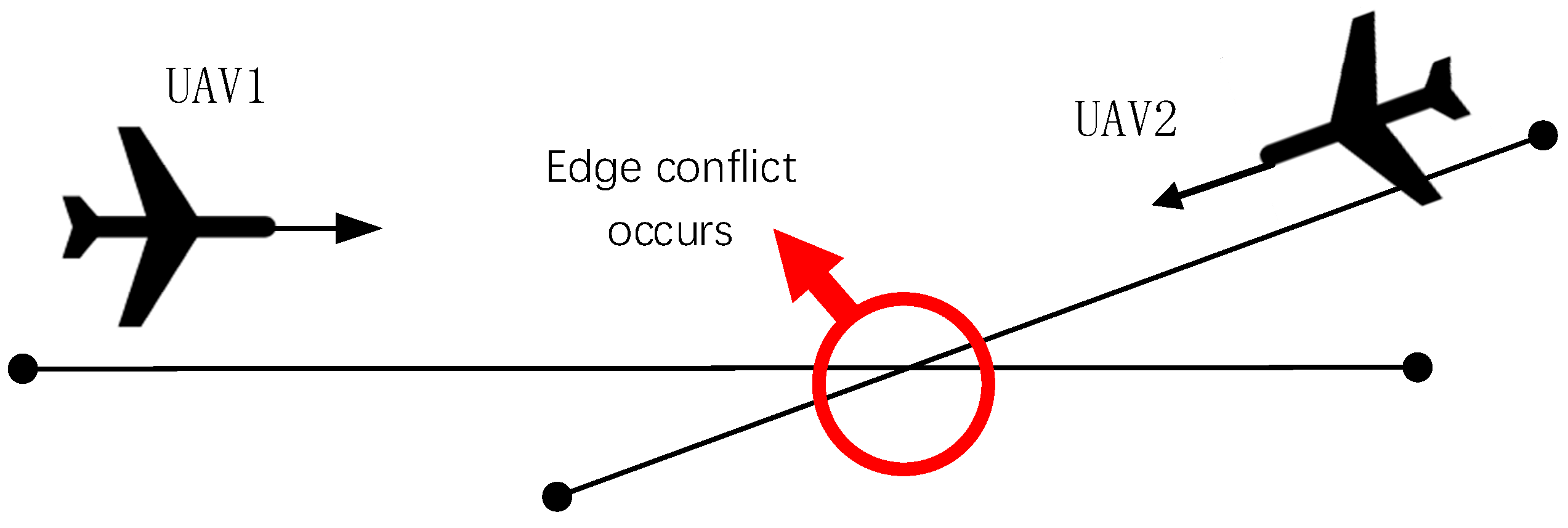
2.3. Cooperative Constraint and Conflict Analysis
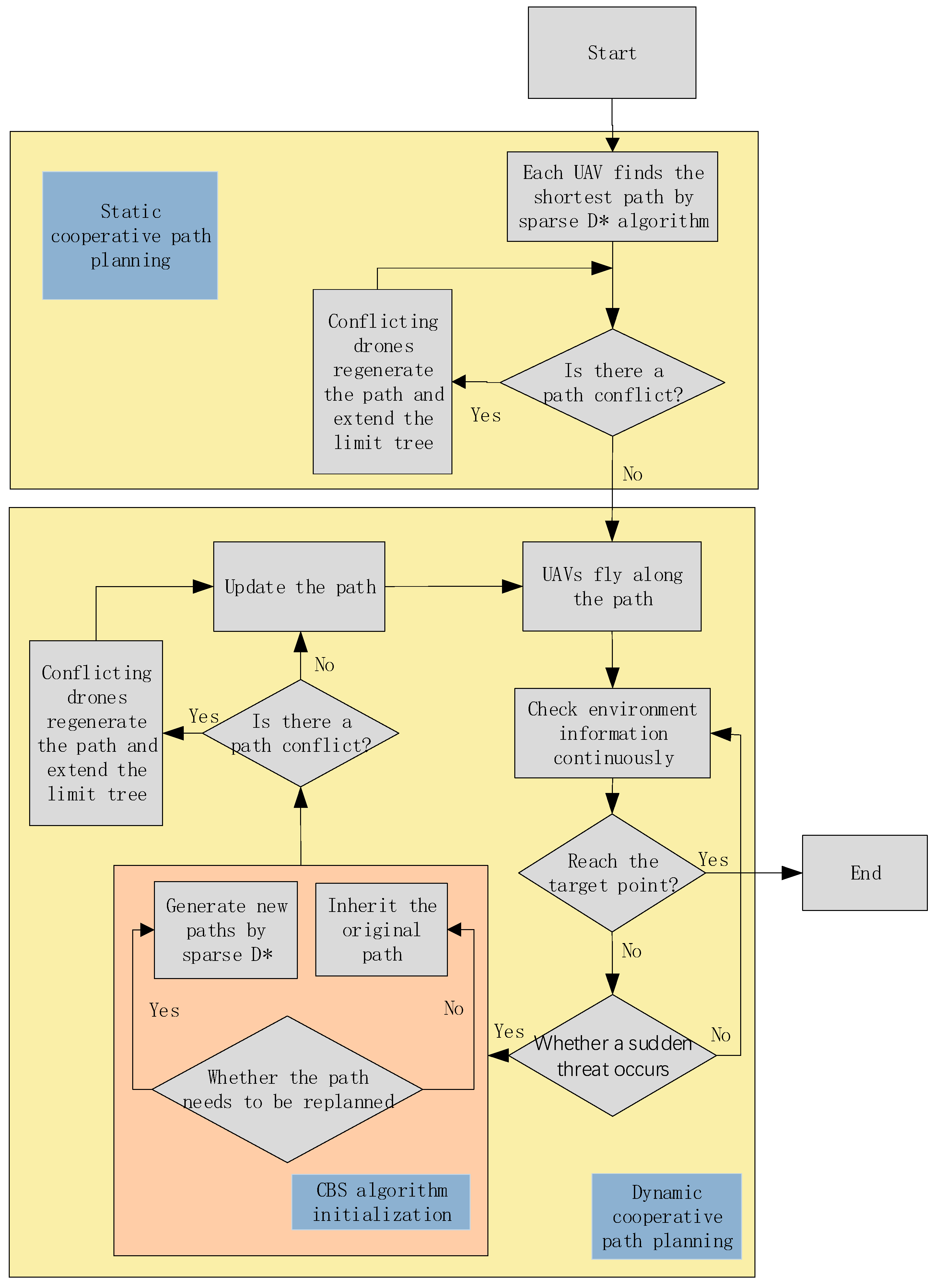
3. Design of Multi-UAV Dynamic Path Planning Algorithm Based on CBS-D*
3.1. Low-Layer Planning Design Based on Improved Sparse D* Algorithm
- (1)
- Waypoint search method design
- (2)
- Path research
3.2. High-Layer Planning and Design Based on Search Algorithm
- (1)
- Cost function design
- (2)
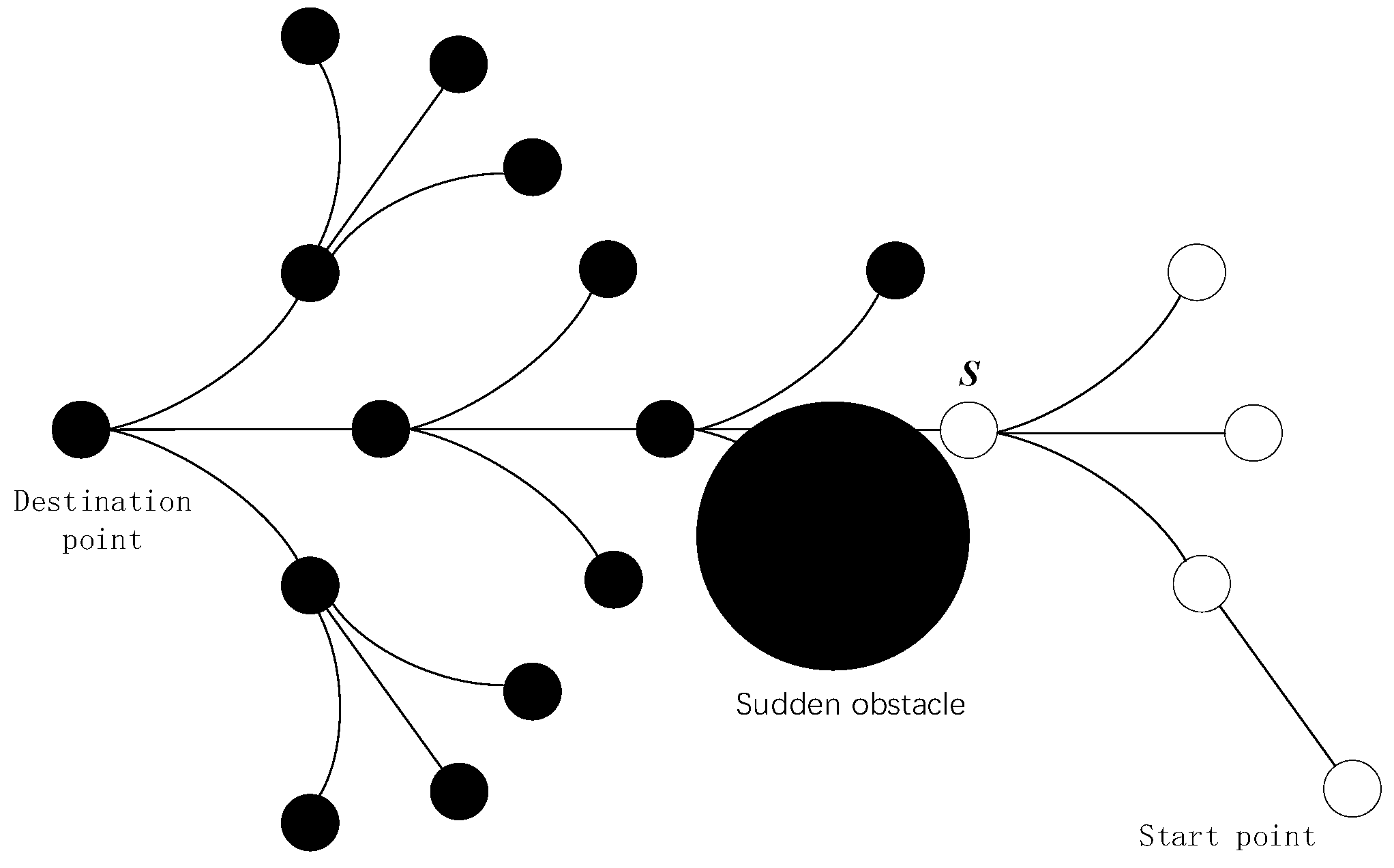
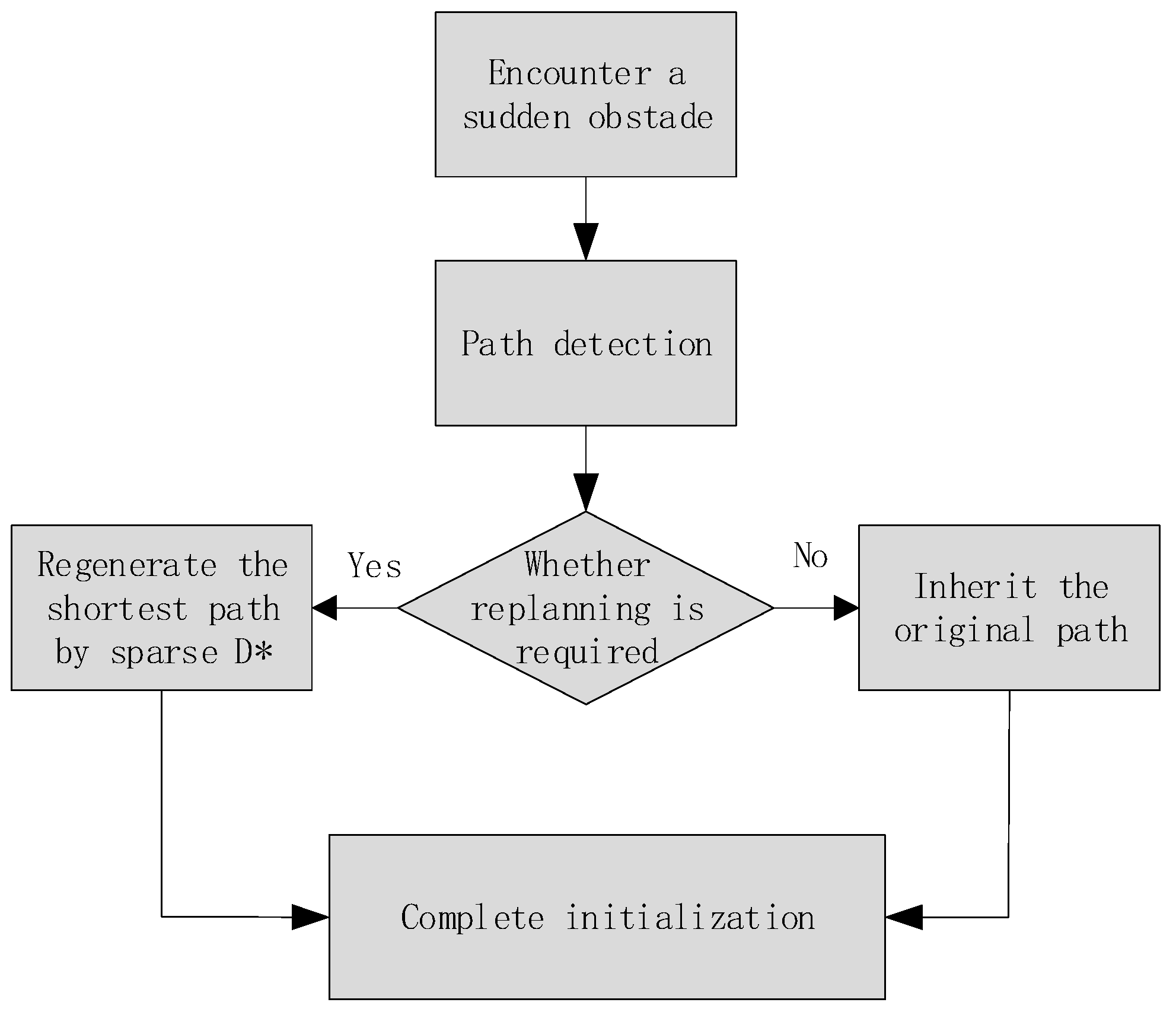
- Dynamic response mechanism design
3.3. Design of Dynamic Cooperative Path Planning Algorithm
4. Simulation Analysis
4.1. Simulation Condition Design
4.2. Improved Sparse D* Algorithm Validity Verification Analysis
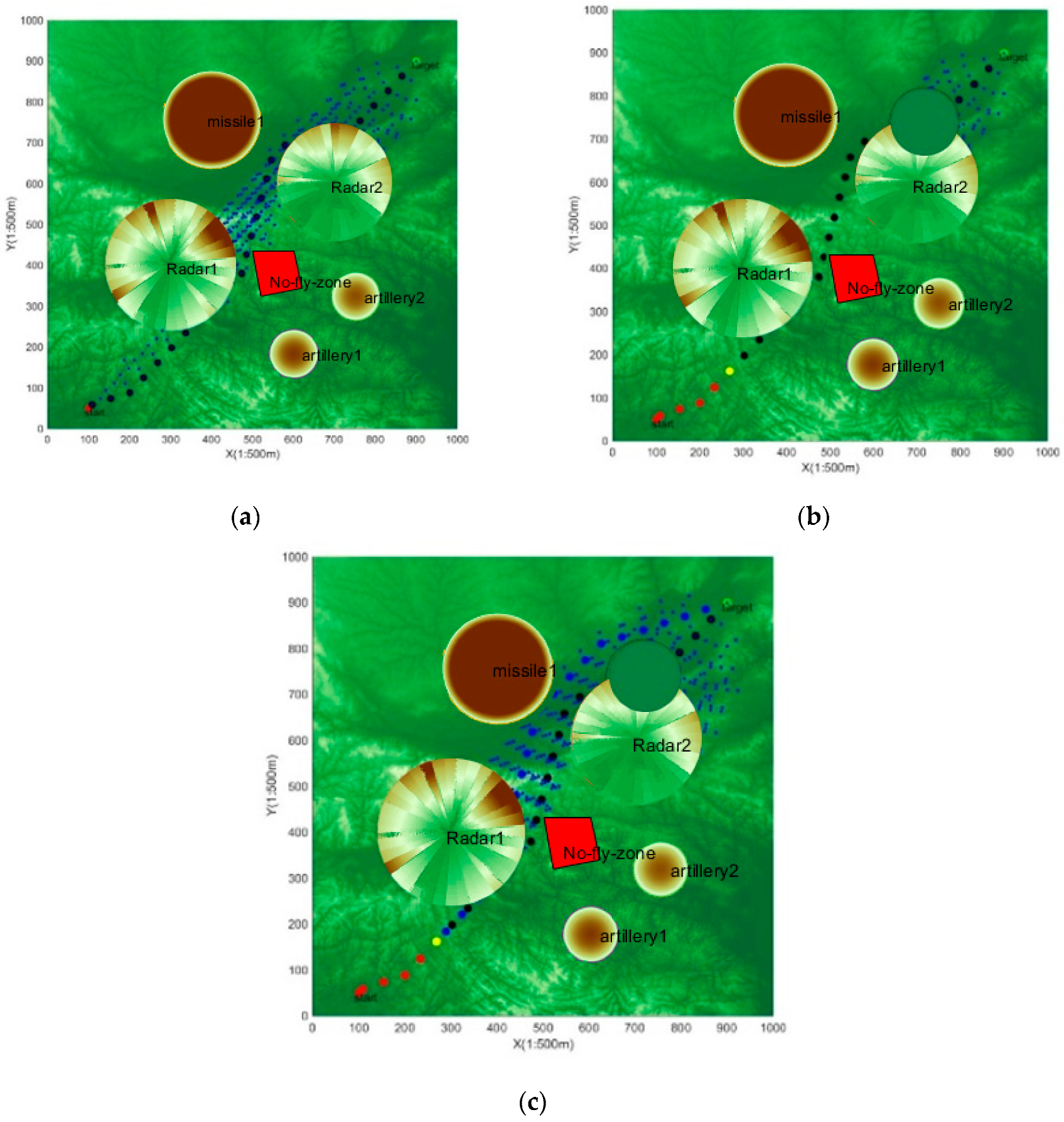
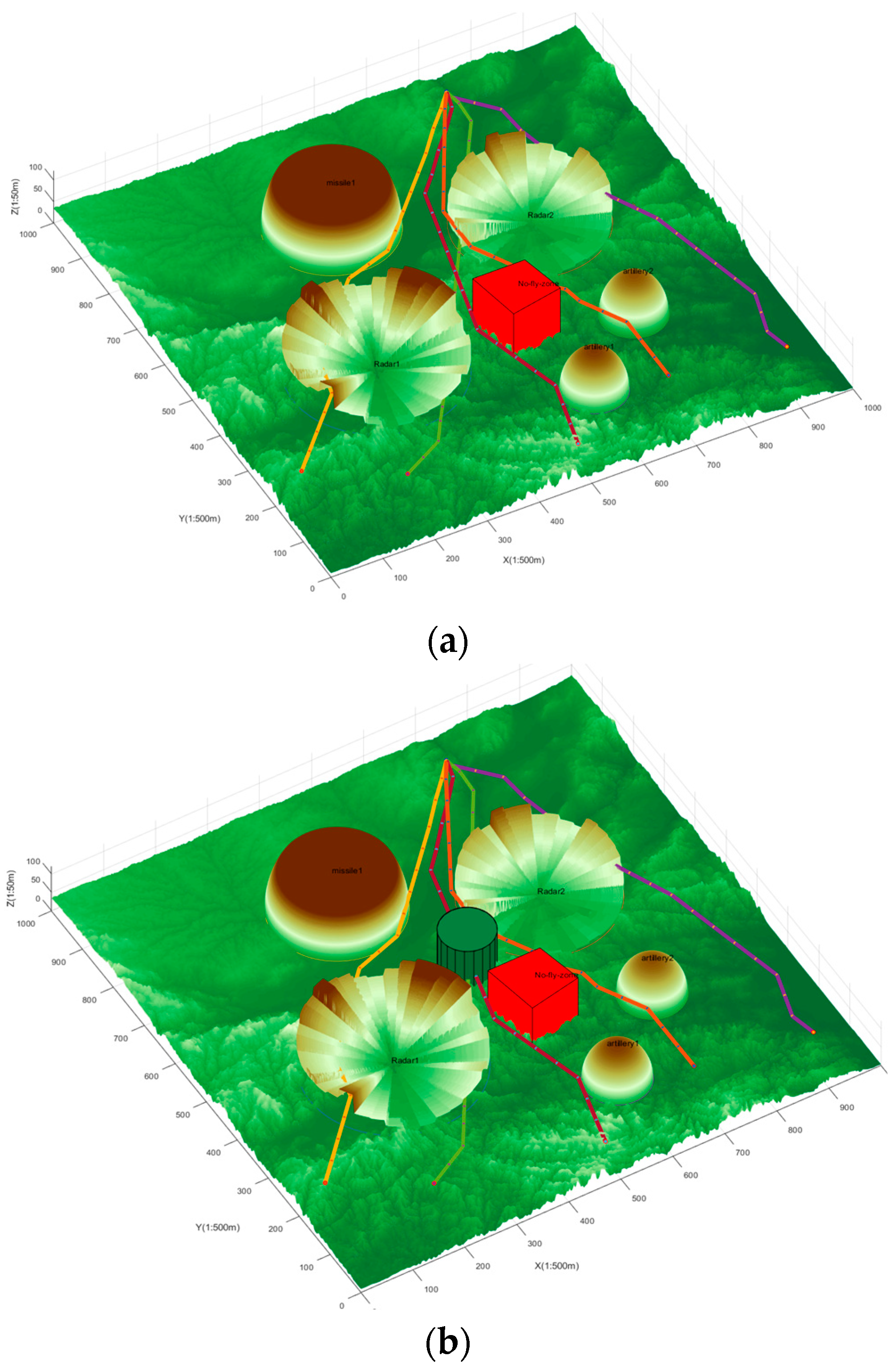
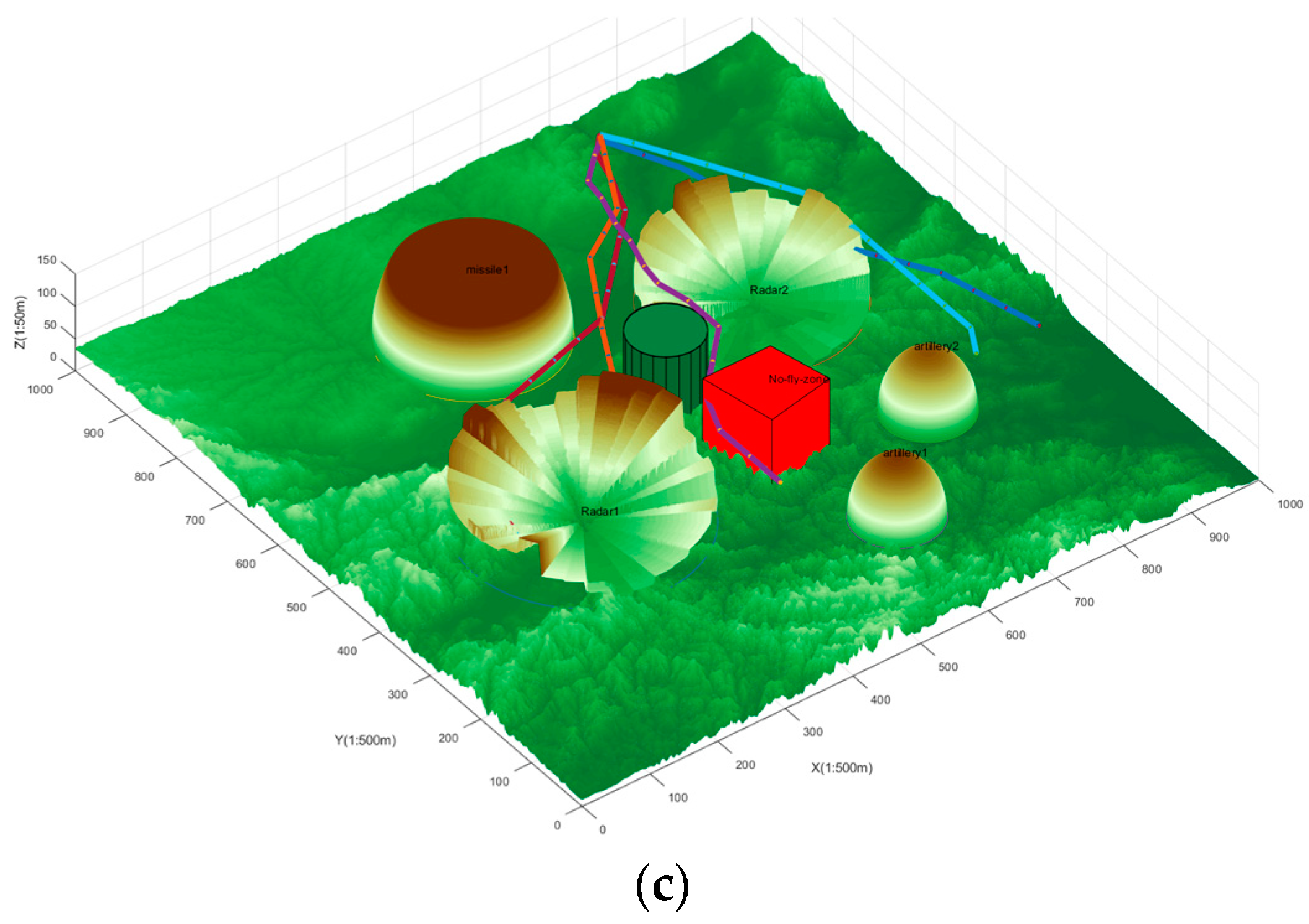
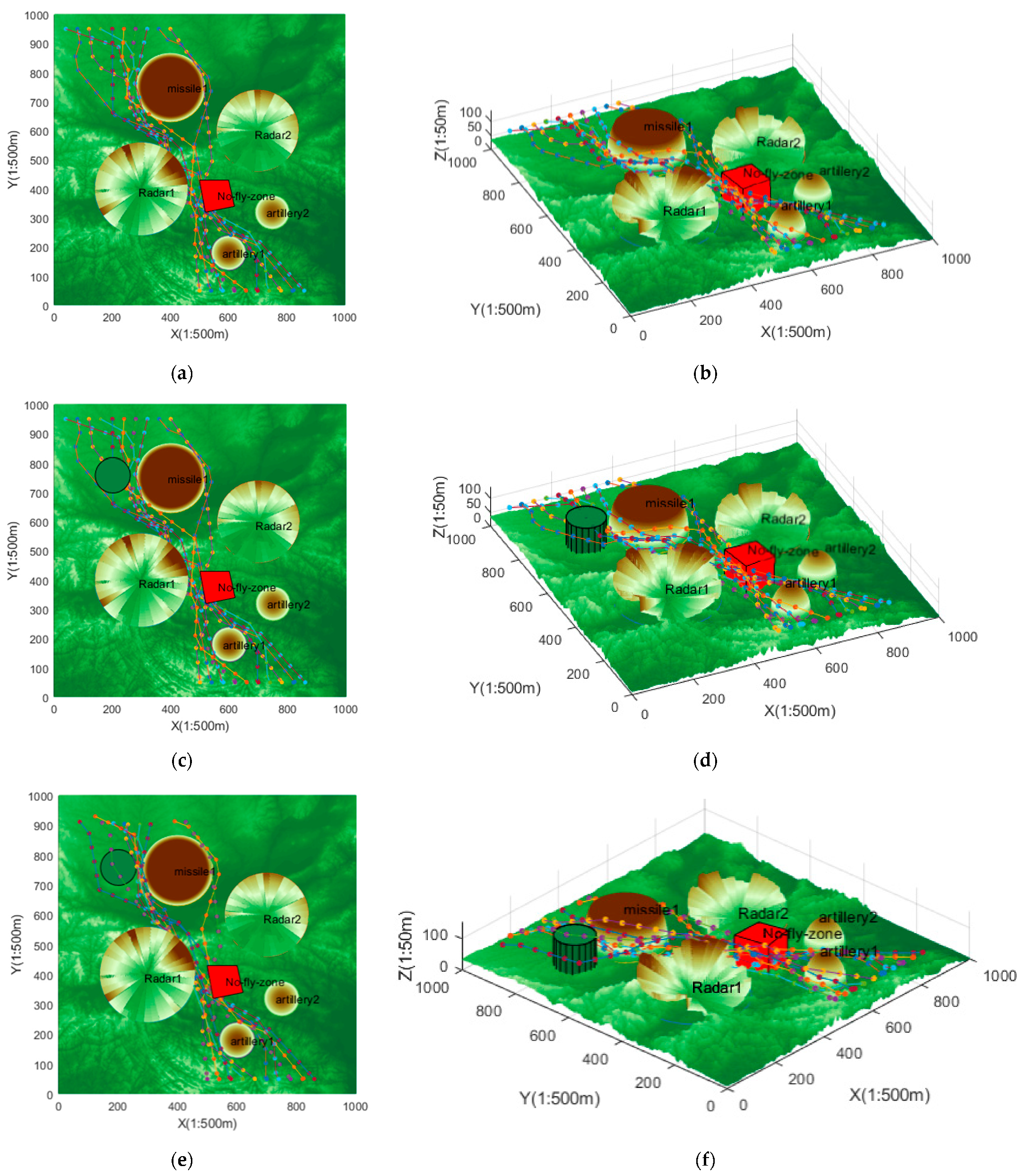
4.3. Sparse CBS-D* Algorithm Validity Verification Analysis
- Simulation verification 1. Cooperative path planning for five UAVs
- Simulation verification 2. Cooperative path planning for ten UAVs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Suh, J.; Gong, J.; Oh, S. Fast sampling-based cost-aware path planning with nonmyopic extensions using cross entropy. IEEE Trans. Robot. 2017, 33, 1313–1326. [Google Scholar] [CrossRef]
- Wang, R.; Wei, W.; Yang, M.; Liu, W. Task allocation of multiple UAVs considering cooperative route planning. Acta Aeronaut. Astronaut. Sin. 2020, 41, 724234. [Google Scholar]
- Ma’Arif, A.; Rahmaniar, W.; Vera, M.A.M.; Nuryono, A.A.; Majdoubi, R.; Çakan, A. Artificial potential field algorithm for obstacle avoidance in uav quadrotor for dynamic environment. In Proceedings of the 2021 IEEE International Conference on Communication, Networks and Satellite (COMNETSAT), Purwokerto, Indonesia, 17–18 July 2021; pp. 184–189. [Google Scholar]
- Lee, H.; Lee, D.; Shim, D.H. Receding horizon-based RRT* algorithm for a UAV real-time path planner. In Proceedings of the AIAA Information Systems-AIAA Infotech@ Aerospace, Grapevine, TX, USA, 9–13 January 2017; p. 0676. [Google Scholar]
- Guo, J.; Huo, X.; Guo, S.; Xu, J. A Path Planning Method for the Spherical Amphibious Robot Based on Improved A-star Algorithm. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8–11 August 2021; pp. 1274–1279. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, J.; Dai, J.; He, C. A novel real-time penetration path planning algorithm for stealth UAV in 3D complex dynamic environment. IEEE Access 2020, 8, 122757–122771. [Google Scholar] [CrossRef]
- Zu, W.; Fan, G.; Gao, Y.; Ma, Y.; Zhang, H.; Zeng, H. Multi-UAVs Cooperative Path Planning Method based on Improved RRT Algorithm. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 1563–1567. [Google Scholar] [CrossRef]
- Wu, Y.; Nie, M.; Ma, X.; Guo, Y.; Liu, X. Co-Evolutionary Algorithm-Based Multi-Unmanned Aerial Vehicle Cooperative Path Planning. Drones 2023, 7, 606. [Google Scholar] [CrossRef]
- Zhu, J.; Zhao, S.; Zhao, R. Path Planning for Autonomous Underwater Vehicle Based on Artificial Potential Field and Modified RRT. In Proceedings of the 2021 International Conference on Computer, Control and Robotics (ICCCR), Shanghai, China, 8–10 January 2021; pp. 21–25. [Google Scholar] [CrossRef]
- Han, L.; Wu, X.; Sun, X. Hybrid path planning algorithm for mobile robot based on A* algorithm fused with DWA. In Proceedings of the 2023 IEEE 3rd International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 26–28 May 2023; pp. 1465–1469. [Google Scholar] [CrossRef]
- Zhang, H.; Gan, X.; Mao, Y.; Yang, C.; Xie, X. Review of UAV Obstacle Avoidance Algorithms. Aero Weapon. 2021, 28, 53–63. [Google Scholar]
- Zhou, Z.; Luo, D.; Shao, J.; Xu, Y.; You, Y. Immune genetic algorithm based multi-UAV cooperative target search with event-triggered mechanism. Phys. Commun. 2020, 41, 101103. [Google Scholar] [CrossRef]
- He, W.; Qi, X.; Liu, L. A novel hybrid particle swarm optimization for multi-UAV cooperate path planning. Appl. Intell. 2021, 51, 7350–7364. [Google Scholar] [CrossRef]
- Liang, J.-H.; Lee, C.-H. Efficient collision-free path-planning of multiple mobile robots system using efficient artificial bee colony algorithm. Adv. Eng. Softw. 2015, 79, 47–56. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, Q.; Hu, X. Review of Path Planning Techniques Based on Reinforcement Learning. Comput. Eng. 2021, 47, 16–25. [Google Scholar]
- Fan, M.; He, J.; Ding, S.; Ding, Y.; Li, M.; Jiang, L. Research and Implementation of Multi-robot Path Planning Based on Genetic Algorithm. In Proceedings of the 2021 5th International Conference on Automation, Control and Robots (ICACR), Nanning, China, 25–27 September 2021; pp. 140–144. [Google Scholar] [CrossRef]
- Xu, C.; Xu, M.; Yin, C. Optimized multi-UAV cooperative path planning under the complex confrontation environment. Comput. Commun. 2020, 162, 196–203. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, Y.; Li, W. A Deep Learning Trained by Genetic Algorithm to Improve the Efficiency of Path Planning for Data Collection With Multi-UAV. IEEE Access 2021, 9, 7994–8005. [Google Scholar] [CrossRef]
- Guni, S.; Roni, S.; Ariel, F.; Sturtevant, N.R. Conflict-based search for optimal multi-agent pathfinding. Artif. Intell. 2015, 219, 40–66. [Google Scholar]
- Li, J.; Tinka, A.; Kiesel, S.; Durham, J.W.; Kumar, T.K.S.; Koenig, S. Lifelong Multi-Agent Path Finding in Large-Scale Warehouses. In Proceedings of the AAMAS 2020, Online, 9–13 May 2020; pp. 1898–1900. [Google Scholar]
- Fatih, S.; Faruk, P. Incremental multi-agent path finding. Future Gener. Comput. Syst. 2021, 116, 220–233. [Google Scholar] [CrossRef]
- Barer, M.; Sharon, G.; Stern, R.; Felner, A. Suboptimal Variants of the Conflict-Based Search Algorithm for the Multi-Agent Pathfinding Problem. In Proceedings of the Annual Symposium on Combinatorial Search (SoCS), Prague, Czech Republic, 15–17 August 2014; pp. 19–27. [Google Scholar]
- Li, J.; Wheeler, R.; Sven, K. Eecbs: A bounded-suboptimal search for multi-agent path finding. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Virtually, 2–9 February 2021. [Google Scholar]
- Liu, X.; Su, Y.; Wu, Y.; Guo, Y. Multi-Conflict-Based Optimal Algorithm for Multi-UAV Cooperative Path Planning. Drones 2023, 7, 217. [Google Scholar] [CrossRef]

| Input: Drone swarm , Starting points set , Target point T, Battlefield environment space Begin // Static cooperative path planning ; // generate the shortest path by D*Lit ; // find a conflict-free path for the CBS algorithm of D* algorithm in low layer While // before the drone reaches the target point ; // drones fly along the cooperative path ; // Continuously monitor the battlefield environment If // a sudden threat occurs on the cooperative path ; // Find a path that is not affected by threats Initial_paths = Initial_with_D*(D,S,T,E,useful_paths); // reinitialize Paths = CBSD*(D,S,T,E,Initial_paths) ; // a conflict-free path is found End End End |
| Flight Constraint | Parameter Value (Unit: 0.5 km) |
|---|---|
| Safe distance | 15 |
| Minimum path segment length | 50 |
| Minimum turning radius | 50 |
| Minimum ground clearance | 5 |
| Algorithm | The Number of New Expanded Nodes |
|---|---|
| Sparse A* algorithm | 2485 |
| Sparse D* algorithm | 1940 |
| Type | Parameter Value |
|---|---|
| Starting point coordinates | UAV 0: [50 200 60] UAV 1: [200 100 70] UAV 2: [500 50 110] UAV 3: [700 100 80] UAV 4: [900 50 100] |
| Target point coordinates | [700 900 80] |
| Safe distance (unit: 0.5 km) | 20 |
| Algorithm | The Number of Conflicts during Initial Planning | Initial Planning Time (Unit: s) | The Number of Conflicts during Re-Planning | Re-Planning Time (Unit: s) |
|---|---|---|---|---|
| Sparse CBS | 15 | 9.8 | 9 | 6.1 |
| Sparse CBS-D* | 10 | 3.9 | 2 | 0.9 |
| Threat Type | Position Coordinate | Threat Radius (Unit: 0.5 km) |
|---|---|---|
| Radar 0 | [300,400,20] | 160 |
| Radar 1 | [700,600,25] | 140 |
| Air defense missile | [400,750,20] | 120 |
| Air defense fire 0 | [600,180,25] | 60 |
| Air defense fire 1 | [750,320,20] | 60 |
| No-fly zone | p1 = [520,320]; p2 = [620,340]; p3 = [600,430]; p4 = [520,430]. |
| Drone Number | Starting Points Coordinate | Target Points Coordinate |
|---|---|---|
| UAV 0 | [860,50,60] | [40,950,85] |
| UAV 1 | [820,50,60] | [80,950,85] |
| UAV 2 | [780,50,60] | [120,950,85] |
| UAV 3 | [740,50,60] | [160,950,85] |
| UAV 4 | [700,50,60] | [200,950,85] |
| UAV 5 | [660,50,60] | [240,950,85] |
| UAV 6 | [620,50,60] | [280,950,85] |
| UAV 7 | [580,50,60] | [320,950,85] |
| UAV 8 | [540,50,60] | [360,950,85] |
| UAV 9 | [500,50,60] | [400,950,85] |
| UAV 10 | [860,50,60] | [40,950,85] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Gong, H.; Nie, M.; Liu, X. Research on Multi-UAV Cooperative Dynamic Path Planning Algorithm Based on Conflict Search. Drones 2024, 8, 274. https://doi.org/10.3390/drones8060274
Wang Z, Gong H, Nie M, Liu X. Research on Multi-UAV Cooperative Dynamic Path Planning Algorithm Based on Conflict Search. Drones. 2024; 8(6):274. https://doi.org/10.3390/drones8060274
Chicago/Turabian StyleWang, Zhigang, Huajun Gong, Mingtao Nie, and Xiaoxiong Liu. 2024. "Research on Multi-UAV Cooperative Dynamic Path Planning Algorithm Based on Conflict Search" Drones 8, no. 6: 274. https://doi.org/10.3390/drones8060274
APA StyleWang, Z., Gong, H., Nie, M., & Liu, X. (2024). Research on Multi-UAV Cooperative Dynamic Path Planning Algorithm Based on Conflict Search. Drones, 8(6), 274. https://doi.org/10.3390/drones8060274






