Abstract
A team of unmanned surface vehicles (USVs) travels with a bounded speed in an unknown corridor-like scene containing obstacles. USVs should line up at the right angle with the corridor and evenly spread themselves out to form a densest barrier across the corridor, and this barrier should move along the corridor with a given speed. Collisions between the USVs and the corridor walls, other obstacles, and among themselves must be avoided. In the fractions of the scene containing obstacles, the line formation should be preserved, but the demand for an even distribution is inevitably relaxed. This evenness should be automatically restored after such a fraction is fully traversed. Any USV is aware of the corridor direction and measures the relative coordinates of the objects that lie within a given finite sensing distance. USVs do not know the corridor’s width and the team’s size, cannot distinguish between the team-mates and fill different roles, and do not use communication devices. A computationally cheap control law is presented that attains the posed objectives when being individually run at every USV. The robustness of this law to losses of teammates and admissions of newcomers is justified. Its performance is demonstrated by mathematically rigorous non-local convergence results, computer simulation tests, and experiments with real robots.
1. Introduction
Recently, formation control has advanced in a mature stage [1], with an ever increasing attention to the distributed control paradigm and the issue of sensorial and communication constraints. This shift of focus brings strong challenges, both algorithmic and analytical, and makes designs of control laws with rigorously justified non-local convergence a really difficult task [2].
The paper focuses on methods for the spatial self-arrangement of multiple silent mobile robots that are incapable of discerning among their peers, obtain limited sensor data on close objects, and cannot enact different roles and thus have nothing to do but individually run the same algorithm. The issue is, in fact, the generation of effective, coordinated, and cooperative action of the entire team from the separate, homogeneous, and elementary decision-making of each of its ill-informed members. In computer science, this goes hand in hand with the concept of behavior-oriented artificial intelligence [3].
The above multifaceted uniformity entails several benefits regarding cost, scalability, fault tolerance, flexibility, repair, and implementation, and is among the key topics studied under the umbrella of swarm robotics [4]. Meanwhile, that uniformity is problematically compatible with many popular approaches to decentralized formation-building control [2]. Among them, there are, e.g., methods using virtual rigid or flexible structures, either team-wide or local leaders/beacons, or designated data or command links between specially selected agents, as well as the assignment of diverse entities, like labels, tasks, goals, etc., to different team members.
The uniformity previously characterized is better consistent with behavior-based approaches [5], such as virtual forces or artificial potential methods. These often lack sufficient guarantees that the targeted formation does emerge, although exceptions are available among distributed consensus protocols [6,7] and related algorithms for formation control [8] or coverage [9] control.
This paper presents a distributed algorithm for the self-deployment of fully homogeneous robotic teams for efficient sweep coverage of an area [10]. The field of coverage control is becoming progressively important due to the growing application of robotic teams to monitoring or processing extended objects, either natural or human-made, and vast areas. In the meantime, the development of microelectronic technologies gives the practical possibility to use large-scale networks of inexpensive devices for executing such missions. Their examples include [11] automatic mine-sweeping, reconnaissance, maintenance inspection, search and rescue operations, finding the source of a pollutant, the monitoring of bush fires, environmental extremum seeking, and target seeking, to name just a few.
To effectively carry out such coverage missions, the team members should be put in appropriate, ideally optimal, locations; at a minimum, any point of the handled region should be shadowed by some member. For large teams, this may be a burdensome task when being performed by external means. Hence, the self-deployment of mobile elements is an appealing option: all and everyone should arrive at the targeted deployment autonomously and on their own. To this end, distributed navigation strategies are needed that merge the easiness of implementation, computational cheapness, and low consumption of resources with guarantees of convergence. Also, the strategy should be robust to failures and the additions of the robots, and should entrust all of them with identical roles, thus making them fully interchangeable. The satisfaction of these partly competing demands constitutes a real challenge in practice.
The paper treats the problem of not static, but dynamic coverage: this problem integrates the sweep and barrier coverage patterns [12]. Effective coverage of a priori unknown scene with a robotic team of an unknown size is handled. The coverage is troubled by unknown obstacles in the area, and so the appropriate positions of the robots in the scene cannot be pre-computed, but are to be built on-the-fly in a feedback fashion based on only very limited sensory information. The mission objectives include lining up the team across an unknown passageway (either natural or human-made, either physical or virtual), frontally moving the thus obtained straight row of the robots with a given speed, preserving the row formation even if the row is cut into pieces with an obstacle, and automatic self-distribution of the robots over the width of the current passage into the densest possible net-like barrier. (Similar requirements may arise when a regular linear formation of mobile robots has to go through a confined environment cluttered with obstacles.) All these should be achieved by a computationally cheap control rule that is common for all robots and is to be individually run on every of them.
This sort of coverage is important for various applications, including mine sweeping, the deployment of static sensor networks, ecological surveillance, sentry duty, rescue operations, and maintenance inspection, to name just a few. However, among the survey of papers on multi-robot self-organization for the sweep coverage of corridor-type scenes, the authors failed to come across one treating this issue in the presence of obstacles, in the face of the above uncertainties and limitations, and with the goal to keep a straight row formation and densest distribution over an unknown passage despite the obstacles. This paper partly fills these gaps.
Specifically, it handles the case of a polygonal corridor environment with finitely many polygonal obstacles, which are a priori unknown. There is a fully homogeneous team of speed-limited USVs, each modeled as a continuous-time integrator. Every USV senses the scene within a given finite distance and thus determines the relative positions of objects that are in direct line of sight. The USVs do not know the width of the corridor, cannot tell the difference between any two peers, cannot fill distinct roles, and do not use communication devices. The above “polygonal obstacles” may in fact be upper approximations of obstacles of more general nature with polygons.
The principal contributions of this paper are as follows. (A) The problem is solved for a fully homogeneous team of robots (in particular, without the shared numbering of them) and, moreover, in a practical situation where any robot has access to data about a peer not only if the latter is within a given “visibility range” but also if nothing obscures the view to it. (B) The proposed control rule is computationally inexpensive, partly since it is reactive: in real time, it directly converts the current observation into the control input in a reflex-like fashion. (C) The problem is solved with respect to an unknown corridor-like environment cluttered with unknown obstacles. (D) The straight-line cross-section formation of USVs and their succession in the formation are maintained even if the line formation is broken into mutually invisible pieces by obstacles. Furthermore, even spacing is automatically restored after the obstacle course is left behind. (E) The proposed control law excludes the collisions of the USVs with one another, the obstacles, and the corridor walls. (F) The situation of both losses and the additions of team members is elaborated; it is proven that, under the proposed control rule, the team automatically adapts to changes in its composition. (G) Mathematically rigorous guarantees of convergence and justification of the performance are provided. (H) The rule is proven to succeed even if there is no informational connectivity of the team at the start of the mission since it creates connectivity from nothing sooner or later. Also, the algorithm restores this connectivity after it happens to be broken due to either the dropouts of team members or the visibility-blocking effect from obstacles. (I) It is shown that whenever the tasks of even distribution across the corridor and obstacle avoidance are to be solved simultaneously, the complexity of the control system can be reduced by omitting (unlike the standard approach) a special obstacle avoidance module since its functions are automatically performed by the control module responsible for distributing the robots across the corridor. (J) Unlike most works dealing with corridor environments, we handle corridors with non-straight, polygonal walls. (K) The presented findings are based on the application of a complete set of general research techniques that include theoretical developments, computer simulation tests, and real-life experiments.
The property (B) is among the main targets of the reported design, bearing in mind applications to small and miniature robots, as well as the reservation of computational resources for basic, higher-level objectives of the mission. Whereas (I) clearly participates in (B), it is worth noting that the property (I) holds under certain circumstances (detailed in the body of the paper).
Regarding (H), we remark that, for the bulk of studies on distributed formation building methods based on local data, informational connectivity is a typical prerequisite for convergence; see, e.g., [6,13,14]. It is often merely postulated that this connectivity persists over the infinite time horizon in one form or another due to an unidentified reason. However, if data transfer is distance-dependent, execution of the main motion control law may endanger this assumption. In such a situation, some algorithms rely on initial connectivity and block the robots’ moves that cause the breakages of any existing data links; see, e.g., [15,16,17]. However, then the control goal may be unattainable (e.g., if the robots start in a tight cluster and so enjoy all-to-all visibility but have to spread over so vast an area that the distance between some robots inevitably exceeds the visibility range). Another approach preserves connectivity, while allowing the breakages of cautiously selected links [18,19,20]. The price for this is high computational and communication burdens, and the need for awareness of the global topology of data exchange. By contrast, the proposed algorithm creates informational connectivity from nothing, and does so at a minimal computational cost and based on only local data.
The body of this paper is organized as follows. Section 2 offers an overview of prior relevant research, whereas Section 3 states the problem. Section 4 presents the robots model and assumptions. Section 5 and Section 6 describe the preliminary stage of data processing and the proposed navigation law, respectively. The main theoretical results are given in Section 7. Section 8 and Section 9 report on the results of computer simulations and real-world tests, respectively. Section 10 offers conclusions. The proofs of the key results are given in Appendix A.
2. Related Work
The bulk of the literature on robotic coverage algorithms is devoted to path planning: how to build a path that passes close to any point from the area of interest; we refer the reader to [21,22,23] for recent surveys of this field. Also, an extensive body of research is concerned with the nodes’ placement and dispatch problems [24,25,26,27,28,29], where the main concern is to find out where, how many, and how nodes should be distributed. By and large, these lines of research focus on geometrical aspects of the problem, leaving the issues of self-spreading and motion control beyond elaboration.
There is also a body of research on reactive algorithms for robots’ self-distribution in coverage missions by using some sort of feedback control [23,30]. Some of these methods are stochastic, often attempt to copycat natural processes in biology, and are surpassed by the idea of the swarm intelligence [31]; see, e.g., [32,33] for representative samples. Another group consists of deterministic physicomimetic methods and draws much inspiration from the concepts of virtual forces, artificial potentials, and molecular equilibrium phenomena [23,30,34,35,36,37]. The third category is distinguished by its reliance on concepts and techniques of geometry [23,30,38]. The Voronoi tessellation is a popular tool here [29,39,40,41,42,43]. Another approach is based on the access of all robots to a common global geometric structure, like a regular grid ([9], Ch. 6) or cell decomposition [44].
For more details on the conceptual and taxonomic aspects of the area, we refer the reader to the specialized surveys, e.g., [23,30,38,45]. Overall, it mainly focuses on achieving the blanket or barrier coverage of a given structure [12], the objectives of which are critically different from forming an evenly spaced straight line formation moving in an unknown corridor. Many approaches are not at all aimed to build a regular formation, need a rather comprehensive knowledge of the environment or some pre-specified global structure (which may call for access to GPS), and necessitate a heavy computational burden. Also, rigorous guarantees of convergence are relatively rare, and the algorithm validation often comes to simulation tests and secondary theoretical facts.
Challenges of the robot’s autonomous navigation in corridor-like scenes have received substantial attention from the robotic community due to their own value and since they are common constituents of more complex environments; see, e.g., [46,47,48,49,50,51] and the literature therein. However, the respective literature largely deals with the case of a single robot, though exceptions also exist; see, e.g., [9,52,53,54]. In [9,52], an algorithm for the sweep coverage of a corridor with straight walls is presented and rigorously justified, postulating persistent informational connectivity of the team. Corridors with arbitrarily shaped walls are handled in [54], where a shared numbering of the teammates and steady designated information links between some of them are assumed (i.e., the team is not fully homogeneous), and forming a straight-line formation is not an objective. The homogeneity of the team is also violated in [53], as the algorithm employs role hierarchy among the robots. In all these works, corridors without obstacles were considered; in particular, the loss of sensorial contact and the breakage of informational connectivity because of obstacles were not addressed.
For navigation in the obstacle-free part of the corridor, we use some findings from [55]. However, they are critically insufficient to deal with obstacles, and the main focus of this paper is on the design and elaboration of respective additions to the algorithmic technology. Relative to a considerably simplified version of the scenario from this paper, some preliminary algorithmic ideas are reported (without proofs) in the conference publication [56]. As compared with it, the current text offers significant extensions regarding both the scenario and algorithm (which in fact essentially differs from that from [56]), as well as a fully renewed conceptualization of the both. In addition, this manuscript offers a complete and rigorous theoretical justification of the proposed algorithm and obtained results, discusses a whole number of extra issues (like robustness against changes in the team membership, etc.), and not only presents the results of new computer simulation studies but also logically completes the research with real-world experiments.
3. Sweep Coverage of a Corridor
We consider N point-wise planar USVs, enumerated by , which travel in an unknown planar corridor between two parallel straight lines. (Later on, corridors with non-straight walls will be addressed.) The USVs should ultimately go along the corridor with a common pre-specified speed . Furthermore, they should find themselves on a common moving cross-section oriented perpendicularly to the walls; see Figure 1. And lastly, they should evenly distribute themselves over to form the densest net across the corridor.
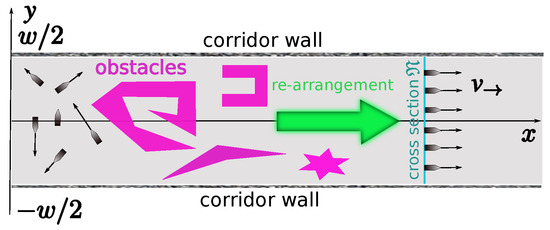
Figure 1.
Sweep coverage of a corridor with an obstacle course.
The mission is troubled by unknown obstacles inside the corridor (see Figure 1). The USVs must not collide with the corridor walls, the obstacles, and one another. Hence, the even distribution across the entire width of the corridor is possible only in its obstacle-free part: even if the team approaches the obstacle course in the ideal order, this order is then inevitably violated. The navigation law must automatically restore that order after the obstacles have been left behind.
We consider point-wise USVs with simple integrator kinematics and a given speed bound :
The velocity vector is the control input. Every USV has its own local frame of reference. In this frame, it identifies the corridor orientation and the relative coordinates of the objects, including pieces of the obstacles and the walls of the corridor, if they are within a given finite visibility distance and the line of sight to them is not blocked. We assume that no USV can fully block the sight of the peers at any obstacle due to some reason, e.g., the superiority of the obstacles over the USVs in size or since USVs can “see” the obstacles at a height above the peers.
None of the USVs use communication devices and know the number N of team members or the width w of the corridor. The team is fully homogeneous: the USVs cannot tell the peers apart, there is no hierarchy among them, and they are unable to play distinct roles and must therefore be driven by a common control rule. So, the posed tasks are to be solved in an autonomous and distributed fashion.
Formal Problem Statement
Unlike the USVs, we can use a right-handed absolute frame; its x axis goes in the targeted direction of motion parallel to the corridor walls in the middle of them; see Figure 1. Thus, the corridor walls are described by the equations . For the convenience of exposition, the x and y directions are said to be horizontal and vertical, respectively.
The location of USV i at time t is denoted by , and the polar angles are counted counterclockwise from the x axis.
To specify the problem, we introduce the symbol for the point with the abscissa and the ordinate . It is easy to see that the points evenly partition the common cross-section of the corridor described by the equation . The pursued navigation objective is in fact much disclosed in the following.
Definition 1.
The USVs are said to sweep the scene with a speed of if the following holds true:
- (i)
- Any USV i does not collide with the obstacles , the walls of the corridor , and the other USVs ;
- (ii)
- There is and an enumeration of the USVs such that .
It is needed to design a control rule that is common for all USVs and, when being independently run on every one of them, ensures the property from Definition 1, starting from occasional, though more or less reasonable, initial positions.
4. Theoretical Assumptions About the Scenario
To introduce and even more to discuss the proposed navigation algorithm, we need to first highlight some assumed properties of the scene. To streamline the exposition, we embed this material into a complete description of the assumptions underlying our theoretical analysis.
Assumption 1.
The obstacles are disjoint polygons (not necessarily convex) and lie inside the corridor.
This does not impose significant limitations on the obstacles since first, what is handled as an “obstacle” in robotics research, is often an (upper) approximation of a real obstacle with polygonal areas and second, this approximation can be made as accurate as one wishes.
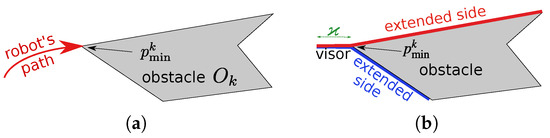
To proceed, some definitions are required. A ray (segment of a line) is said to be open if it does not contain its root (its end-points). An upward/downward ray is a vertical ray that propagates upwards/downwards. A set is said to be -free if it has no points in common with the obstacle .
Definition 2.
A upward/downward ray is said to be forward critical for if the following holds:
- (i)
- It is open and goes from the boundary of the obstacle ;
- (ii)
- This ray is not -free;
- (iii)
- To the left of and arbitrarily close to it, there is an upward/downward ray that is -free.
In Figure 2, the green rays are not O-free and are not critical, the red ones are critical, and the blue rays are O-free and are not critical. Critical rays mark either forward vertical sides of the obstacle or entrances to its “deadlock caves” (a cave of O is defined as a connected component of the set of points such that the rays issued from both upwards and downwards, respectively, intersect O). The concepts of such a ray and cave are born from the idea to bypass the obstacle by means of constantly and simultaneously (1) following its boundary and (2) progressing down the corridor . After arrival at a front vertical side, executing (2) would imply penetration into the obstacle and so is impossible. The attribute “deadlock” marks the caves such that the robots may enter but cannot leave them while following the instructions (1) and (2). Figure 2a illustrates a deadlock cave, which is entered while following the pink side of the obstacle and then cannot be left without violating (2). The caves in Figure 2b,c do not do any harm in this regard since they are not entered due to (2). When arriving at their entry points, like A in Figure 2b,c, the rule (1) brings about an instantaneous jump to point B and subsequently following another piece of the boundary to the right.
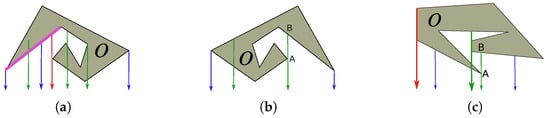
Figure 2.
Critical (red) and non-critical (other colors) downward rays. (a,c) Obstacle with critical (red) ray; (b) Obstacle without critical (red) rays.
Assumption 2.
No obstacle has forward critical rays.
Example 1.
Any convex obstacle with a unique leftmost point meets Assumption 2.
Example 2.
We orient the boundary of an obstacle so that O is to the left when traveling over , and consider the cycle C of the consecutively adjacent edges forming . Let C be cut into two (non-cyclic) chains so that the edges from a common chain are consecutively concatenated, the polar angles of the edges from one of the chains are acute (less than in absolute value), and obtuse for the other chain. Then, Assumption 2 is true.
Assumption 2 rejects the obstacles like those in Figure 2a,c. Some of them can yet be put into the framework of Assumption 2 if every robot appropriately modifies its interpretation of the scene on the fly. Some hints of such a kind will be discussed in Section 7.8.
To state the last assumptions, a few more definitions are useful.
Definition 3.
A point of the obstacle’s boundary is said to be (globally) lower/upper if is the upper/lower end of a vertical open -free (ray) segment. The closure of any set of such points is said to be (globally) lower/upper.
Remark 1.
An lower/upper side of the polygon cannot be vertical. Conversely, any non-vertical side of the polygon is either lower or upper.
The union of all globally lower/upper sides of the obstacle is called its lower/upper fence ; see Figure 3.
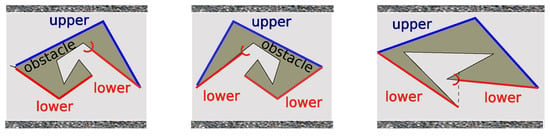
Figure 3.
Lower and upper fences.
It is clear that the abscissas of different points of differ. We orient the lower/upper fence and any its segment in the direction of the abscissa ascending. Then, the polar angle of any such segment is acute. We treat the “upper” and “lower” exterior of the corridor as obstacles with positively oriented boundaries. The fences of these obstacles are equal to the respective walls of the corridor.
Our final assumptions are concerned with the mission feasibility. First, the feedback from the distance gaps between the robots should not be lost under the targeted even deployment of the team across the corridor, which yields that . Second, the requested speed should match the capacity of the robots: . Moreover, the tactics of the boundary following may involve tracking parts of the upper or lower fences of obstacles. When doing so, the top speed of the robot’s abscissa is defined by the polar angle of the currently tracked segment and is equal to . So, the demand for the value of the horizontal speed is reasonable only if .
By slightly enhancing these necessary conditions via and introducing an upper bound on the absolute values of the polar angles of the segments in all upper and lower fences, we arrive at our final assumption:
7. Main Results
7.1. Preliminaries
To state and discuss the main results, we need to introduce some symbols and terms. The following notations will be used:
- , length of the x-scope of the compact set E, i.e., ;
- , polar angle of a non-vertical segment S oriented in the ascending direction of x;
- , collection of all globally upper/lower sides of all ’s (see Definition 3 and Figure 3).
Definition 4.
A side S of an obstacle is said to be friendly if the infinitesimal shift in the x direction brings any interior point of S to the free space. A friendly pair is a couple of adjacent friendly sides that are both globally either upper or lower for the obstacle .
The side from Figure 6c is friendly, whereas those from Figure 6a,b are not friendly. In Figure 7, only the sides from the first and third pictures are friendly.
Finally, we put:
Here, if there are no friendly pairs, and , where is taken from (2). Since all sides are not vertical by Remark 1, we infer that , , and .
7.2. Key Theoretical Result
It refers to the constant from (1), , from (2), from (4), from (5), from (6), P from (8), from Figure 4b, w from Figure 1, the number of the USVs N, and the parameters and that define the quantity (3) and the graph , respectively.
Theorem 1.
- (i)
- The control generated by the proposed navigation law always satisfies the inequality from (1), as is required;
- (ii)
- The USVs sweep the scene with a speed of , as defined in Definition 1;
- (iii)
- Their x scatter does not grow as time progresses;
- (iv)
- Any USV moves along the corridor in the targeted direction: for almost all t;
- (v)
- The USVs travel at distinct distances from the corridor walls: ;
- (vi)
- The ordering of the USVs in the vertical direction does not change with time.
The proofs of this theorem and the subsequent Remarks 2–4 are given in Appendix A.
7.3. Discussion of the Key Theoretical Result
In light of the mission objective, the initial placement of the USVs into a vertical strip is a reasonable decision. In practice, its realization often looks like putting the USVs into nearly the same place; then, in addition, no two USVs are separated by an obstacle, just like it is required in Theorem 1.
All assumptions on the initial deployment are met if, when moving along a free part of the corridor in a nearly perfect order, the team meets an obstacle course, and at this very moment, we set the clock to zero and start our consideration. In this case, the objective is to go through the obstacle course, while maintaining the line-up structure, and to restore even spacing and the required speed along the corridor after the course is left behind. In this regard, (iii) in Theorem 1 guarantees that the previously achieved “accuracy” of “lining up” never degrades, even when going through the obstacle course. By (5) and (7), the speed deviates from the desired value by at most , an observation which can be used to bound the speed error via choosing . It is worth noting that as decreases, neither of the affected requirements (13), (14), (15), and (18) from Theorem 1 is violated.
The statement (vi) means that, in the line formation, both the highest and lowest USVs retain their respective statuses. This may be of interest if there is a reason to use USVs with special roles or capabilities (e.g., those of the wall exploration or side-protection of the team) at these positions. Furthermore, no additions to the proposed control law are needed in scenarios where it is judicious to keep some special USVs hidden in the middle of the team, e.g., for protection purposes.
Theorem 1 sets forth achievable requirements. Indeed, the demands to from (13) can be satisfied due to the second inequality in (2). Inequality (16) can be met by picking small enough and , after which the last inequality in (13) can be ensured by choosing sufficiently small. By letting , we make the first inequality in (13) true and reduce (14) and (15) to and , respectively. The system of the last two inequalities has a solution if and only if
which is true by the first formula from (2) since . Hence, to meet (13)–(15), one can start with picking P and so that , and then proceed by choosing small enough. At the end, it remains to take the functions and that satisfy (5) and (6) with the just chosen parameters , and .
We also note that (17)–(20) describe a non-empty set of ’s by (6), (13), (15), and (16). For example, this set contains all small enough ’s, but not necessarily only them.
Theorem 1 remains true if the corridor width w is replaced by its upper bound in (2) and (13), the angle by its known upper bound in (15) and (19), the angle by its known lower bound in (18), and the distances and by their lower bounds in (17) and (16), (20), respectively.
Theorem 1 does not limit the choice of the parameter . If , then does not affect the control and so can be neglected everywhere since then . The idea behind the use of stems from the fact that for , the set can be essentially smaller than , which entails a reduction in the computational burden.
If, in violation of the assumptions of Theorem 1, for some , then the objective is not achieved since . (The team acts as one of a reduced size and this smaller team gains its aim.) This can be fixed by slightly altering the control law. However, we drop discussion the respective details since the easiest tactics is to ensure that via proper placement of USVs at the start of the mission. Moreover, that assumption is met with a probability of 1 if the USVs are dropped in the scene according to a continuous probability distribution.
In terms of , the control law (7) takes the form of the nonlinear nearest neighbors rule [58], which is used to achieve a consensus on the value of among multiple agents:
Its convergence needs certain connectivity of the information-flow graph (we recall that its nodes are associated with the agents, and nodes i and j are linked if and only if ). Most of consensus criteria merely assume that this graph enjoys a sort of connectivity for some reason, while leaving the reason an open issue. There are also studies on algorithms aimed at preserving the assumed initial connectivity; see, e.g., [15,16,17,18,19,20,59,60]. They are typically computationally expensive and rely on a fairly comprehensive knowledge of the scene.
On the contrary, the algorithm from this paper is computationally cheap and uses only local sensory information about the scene, whereas its convergence does not rely on the postulate of persistent connectivity or the assumption of the initial connectivity. The reason for its convergence is the proven fact that sooner or later the algorithm automatically gives birth to the connectivity.
7.4. Secondary Add-Ons to Theorem 1
Its assumptions are adopted throughout this section.
Remark 2.
This excludes sliding-mode phenomena and their associates.
Remark 3.
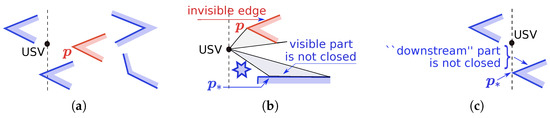
Whenever a USV is not at the front end of a visor V, the opinion of this USV on being above or below V corresponds to reality (and so the USV does not in fact displace V in its “mind”).
Now, we discuss the extension of the above findings to three special situations.
7.5. Dropout of Team Members
Suppose that, at a time , several USVs abandon the mission and the others start ignoring them. By applying Theorem 1 to , with a particular attention to (iii) and (v) at , we see that the conclusion of Theorem 1 remains true for the remaining team if its size (this keeps the second inequality in (13) true). With regard to the possibility of , the claim to shapes into and means that the loss of several teammates does not break the sensorial connectivity of the team under its even distribution across the corridor.
Similarly, the team adapts to several successive dropouts if the final team size .
7.6. Addition to the Team
We limit ourselves to a simple, though practical, scenario, where extra teammates (newcomers) are disembarked near some “old” ones (oldies). Let the newcomers appear at some time not in the caves of the obstacles and within a vertical strip that contains the oldies and has a small enough width : (17)–(20) hold with (and the updated team’s size in (20)). Theorem 1 implies that, for , its statements (i)–(vi) (and Remark 3) are valid if at the ordinates of the newcomers are pairwise different and differ from those of the oldies, and the obstacles do not obstruct the lines of sight among the USVs (in fact, the last requirement can be relaxed; we omit the respective details since they are technically involved).
7.7. Non-Straight Corridors
The above findings nearly literally extend on more general corridors. The last sentence of the paragraph following Definition 3 hints at this possibility: since the upper and lower exteriors of the corridor are handled as obstacles, it suffices that these exteriors meet our requirements to the obstacles and the structure of the corridor makes the concepts of the corridor direction and its cross-section meaningful. These ideas are detailed in the following definition. To state it, we recall that a planar set is said to be polygonal if its boundary is contained in finitely many straight lines.
Definition 5.
A directed simplistic corridor is an area such that there exists two polygonal sets and a directed straight line L with the following properties:
- (i)
- The sets are simply connected and form a partition of ;
- (ii)
- There are and such that, in a right-handed Cartesian frame whose abscissa axis is L, the parts of the sets , and lying to the right of the abscissa are described by the inequalities , and , respectively, along with ;
- (iii)
- Assumption 2 is true for and .
This definition is illustrated in Figure 9.
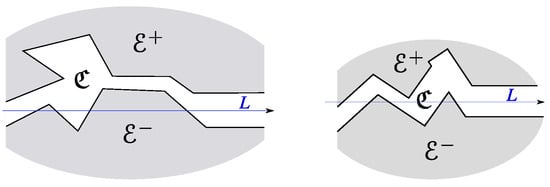
Figure 9.
Non-straight simplistic corridors.
Remark 4.
Let the corridor be simplistic. Suppose also that, in Section 7.2, all statements and formulas (including (9)–(12) and the definition of from (2)) that refer to “obstacles” take into account and . Then, Theorem 1 remains true.
The assumption of Theorem 1 on starting outside the caves can also be relaxed. We illustrate this in Section 8 by computer simulations, with omitting theoretical discussion since it is technically cumbersome.
7.8. Some Hints to Relax Assumption 2
Assumption 2 excludes the situations like those in Figure 2a,c. However, they sometimes can be reduced to a case where Assumption 2 is met. To this end, the USVs may imaginarily endow the obstacles with extra fictitious parts. The price for this is that in the opinion of the USVs, the free space shrinks.
Now, we outline the basic idea for two hints of this kind, leaving the elaboration of their details as a topic of further research. Every hint reduces the number of critical rays by one. If the obstacle has many such rays, their successive processing is recommended.
Adding a fictitious cusp to a vertical front side S of an obstacle is illustrated in Figure 10, where is a free parameter and the cusp is depicted in green.

Figure 10.
Adding a fictitious cusp in front.
The case where the both sides adjacent to S go up the corridor is of no interest: this means that the USV is in a cave, which should have been prevented by properties of the scene and algorithmic hints. To build the fictitious cusp in a timely manner, the USV must have a full view of S whenever the cusp may affect the control. So, the length s of S and should not be excessively large. Also, it is needed that the cusp points should be visible whenever they fall in the sensing range , as it is given to the controller. Hence, the USV should “see” not only these points but also the entirety of S. To create such situation, the controller may be affectedly given a value of that is lesser than the real one.
Filling up unacceptable caves is illustrated in Figure 11. In Figure 11b–d, is a free parameter. Figure 11d addresses the case where the obstacle’s side that ought to support the cusp is too short to accommodate its entirety and so the cusp is cut at the respective end of this side. The horizontal mirror images of all pictures from Figure 11 should be also included in the list of illustrations. Like in the case of vertical front sides, the USV must have the full view of the gate to the cave whenever the cave affects the control. Meanwhile, more may be needed. For example, if different obstacles are not somehow discernable (e.g., do not vary in color), then the entire cave is welcome to be visible from its entrance to differentiate it from a passage between obstacles, unless counting on luck. In Figure 11, only the cave from Figure 11d has this property.
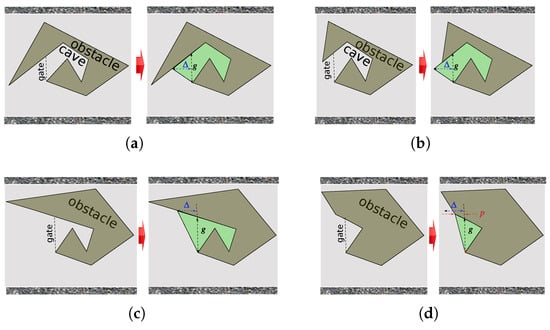
Figure 11.
Filling up an unacceptable cave. (a–c) Various examples of obstacles with caves that can fully accommodate the cusp; (d) The case where the obstacle’s side that ought to support the cusp is too short to accommodate its entirety and so the cusp is cut.
8. Computer Simulation Tests
8.1. Numerical Experiments
The experiments described in this subsection were implemented in a Jupyter Notebook using the Python programming language. For visualization and vector operations, the Pygame and NumPy libraries were used, respectively. The walls of the corridor were defined as graphs of functions of the abscissa x from Figure 1. The obstacles were described by two functions representing the “upper” and “lower” parts of their boundaries, respectively. The obstacles whose boundaries cannot be separated into such two parts (like the obstacles in Figure 11) were decomposed into sub-obstacles that allow this separation (in Figure 11, this decomposition is outlined by the little “seams” on the obstacles). The discretization of the continuous-time kinematic model of the robots (1) was performed using the Euler method; the discretization step equals the control update period shown in Table 1.

Table 1.
Numerical values used in the computer simulation tests.
Apart from the validation of the proposed control laws (7) and (8), the goals of the simulation studies described in this subsection include the assessment of its applicability in circumstances outside the bounds imposed in the theoretical part of the paper. In particular, the tests involve erroneous position measurements, controller parameters that do not quite satisfy the assumptions of Theorem 1, scenes with non-polygonal and moving obstacles, obstacles with vertical front sides, and situations where robots start in the caves of the obstacles. Meanwhile, the employed kinematic model is close to the theoretical model (1). Testing the algorithm against the challenges from more complex dynamics and other imperfections of the real world is discussed in Section 8.2 and Section 9. Various validation means (numerical simulation, Gazebo simulation, real-life experiments) are applied independently, with the main objective to cover a wider range of scenarios.
The numerical values of the key parameters used in the tests from Section 8.1 are shown in Table 1. We employed a linear function with saturation at the threshold , Table 1 displays only its linear part, as well as the control update period . The parameters from Table 1 are not fully compliant with the assumptions of Theorem 1; this is done to show that the domain of practical convergence of the offered control law is wider than its region of convergence unveiled theoretically.
Position measurements were plagued with unbiased additive noises uniformly distributed within a radius of 0.01 m. This is a fairly big inaccuracy relative to the typical inter-USV distances of ≈0.3–1.0 m observed in our experiments: e.g., many present-day sensors ensure a precision of several mm in that range of measurements. The multimedia of all experiments are available at https://drive.google.com/drive/folders/1ngTYqiY1V-2-sEI6EjcMrFmMAEFSMWuM?usp=sharing (accessed on 16 February 2025).
In Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19, the positions of the USVs and the orientations of their velocities are demonstrated with the triangles; the time step between the snapshots equals s; the trajectories of the USVs are shown as blue lines, while the boundaries of the corridor and obstacles are shown as green lines. Except for the first snapshot, the robotic team clusters near a cross-section of the corridor, which makes the snapshots easily recognizable. These snapshots allow us to evaluate the speeds of the USVs.
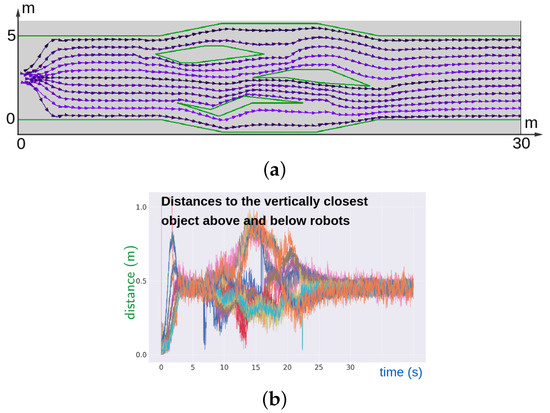
Figure 12.
Eight USVs traverse an obstacle course. (a) USVs trajectories with snapshots in the corridor with obstacles; and (b) Graph of the distances to the vertically closest object above and below USVs.
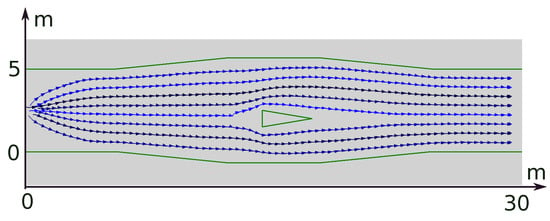
Figure 13.
Eight robots, one obstacle with a vertical front side.
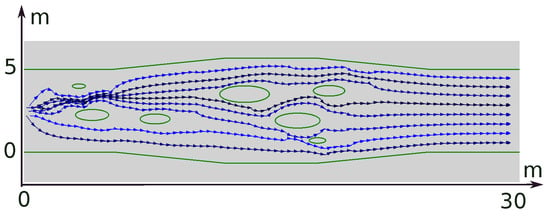
Figure 14.
Eight robots, scenario with oval obstacles.
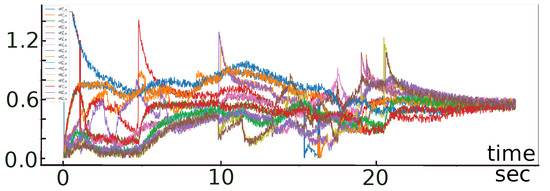
Figure 15.
Graph of the lateral distance to the nearest upper/lower object .
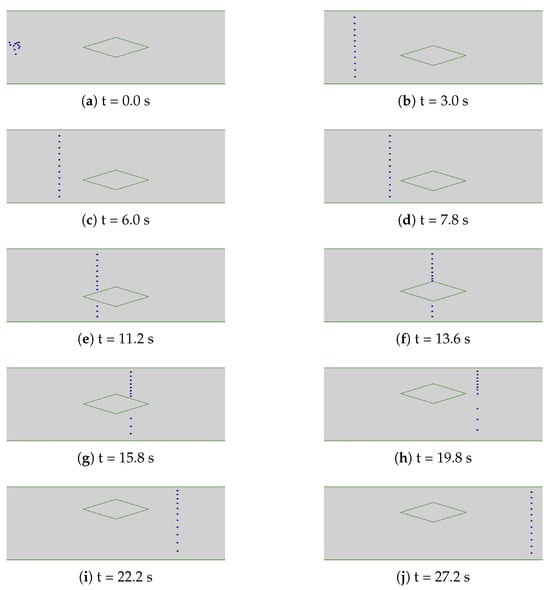
Figure 16.
Scenario with a moving obstacle.

Figure 17.
Starting in caves, twelve USVs.
Figure 18.
A team of eleven USVs unexpectedly loses five ones.
Figure 19.
Five USVs join a team of six ones.
In Figure 12, eleven USVs are tasked with performing a dense sweep of a corridor with slightly broken walls and three obstacles. Beginning from an initial patch of the corridor with a diameter of ≈1.5 m, the team accelerates to the desired speed, aligns across the corridor, and achieves an even self-distribution within about 4.0 s. This distribution remains stable until around 7.0 s, at which time the USVs encounter the first obstacle. While navigating through the obstacle course, the USVs maintain their “line-up” formation and targeted horizontal speed, in spite of the fact that USVs separated by obstacles lose information about one another. Meanwhile, the team dynamically breaks into subgroups, each utilizing different pathways through the obstacles. The number and composition of the subgroups change over time, following the sequence: {11} → {2, 9} → {2, 7, 2} → {2, 3, 4, 2} → {5, 4, 2} → {5, 6} → {11}. This progression involves both splitting and merging of subgroups. As shown in Figure 12, the USVs do not collide with the walls of the corridor, the obstacles, and one another. By approximately 30 s, the team re-establishes the “cross-section” formation and maintains the requested horizontal speed , despite the disruptions caused by obstacles. Thus, the posed objective is attained with high accuracy.
The purpose of the experiment from Figure 13 is to test the hint of adding a fictitious cusp; this hint is illustrated in Figure 10a and aims to handle obstacles with a vertical front side. In the opinion of the controller, the sensing range of the robot was artificially reduced down to 65% of its true value. Starting their mission in a circle with a diameter of ≈1.5 m, the robots achieve the required speed and uniformly distribute themselves across the width of the corridor in ≈5.0 s, having traveled ≈5.0 m along the corridor. This uniform distribution is maintained until ≈15.0 s, when the robots encounter an obstacle with a vertical front side. To avoid a collision, the concerned robots independently expand the obstacle by adding an imaginary cusp to this side, as shown in Figure 10a, and move along the boundary of this cusp. After bypassing the obstacle, it takes ≈10 s to restore the formation. The results of this experiment do not significantly differ from those described above, and the control objective is again achieved with a good precision.
In the scenario from Figure 14, a group of eight robots has to pass through a corridor with oval obstacles. At the start of the mission, the robots do not have enough space and time to attain the required speed and even distribution over a cross-section of the corridor, so long as they almost immediately stumble upon the first band of three obstacles. It takes ≈10 s for them to overcome this band. Then, they once again do not have enough time and space to distribute themselves uniformly across the corridor, this is due to the second band of obstacles. Overcoming this band takes ≈10 s, after which the robots achieve uniform self-distribution across the corridor in ≈5 s, and then stably maintain the required formation, as confirmed by Figure 15. The interest in this experiment partly stems from the fact that the oval obstacles violate Assumption 1. However, the obtained results demonstrate that the algorithm is applicable to scenarios with non-polygonal obstacles and may attain the control objective with good exactness.
Figure 16 illustrates an experiment in which 11 robots should sweep a corridor with an obstacle that oscillates across the corridor. At 3.0 s, the group lines up across the corridor and achieves a nearly even inter-robot spacing; in the meantime, the obstacle is displaced slightly downward. At 7.8 s, the group begins to notice the obstacle, whereas the latter reaches its lowest position and starts changing direction. By 11.2 s, the group splits into two subgroups: three robots “decide” to bypass the obstacle from below, and the rest of the team prefers to go above it; during the entire obstacle avoidance maneuver, the obstacle moves upward. As a result, the free space available to the upper group of eight robots becomes considerably constricted at 13.6 s. At 19.8 s, the group finishes bypassing the obstacle and merges into a single unit. Finally, at 27.2 s, the group restores an uniform distribution across the corridor, thereby achieving the control objective. Thus, we observe that the mission is successfully accomplished even in the presence of a moving obstacle.
The experiment addressed by Figure 17 illustrates the remark from the last paragraph in Section 7.7: the algorithm maintains efficiency in situations where USVs start inside caves. Initially, twelve USVs are distributed in three groups out of four. Two of them start in the caves of the obstacles and , respectively, and the third group is launched in between and . In ≈2 s, a nearly perfect alignment across the corridor is achieved within each group, along with an approximately even distribution of each group over the width of the currently used “left-to-right passage” between the obstacles’ components. Meanwhile, the sensorial contact between the groups is blocked by the obstacles. As a result, there is no progress in narrowing the x gaps among the groups (these gaps are highlighted with dashed pink rectangles). At 7 s, the “upper” and “middle” groups merge, and ≈2 s later, they appear to be close to a common moving cross-section of the corridor. Meanwhile, their alignment with the “lower” group still remains at the nearly initial level and poor. This does not come as a surprise since that group is still out of the sensorial contact. At 11 s, the united “upper” group splits into two subgroups and , which “decide” to bypass the obstacle from above and below, respectively. Initially, is out of contact with (first because of the blocking effect of and then since the gap between and exceeds the sensing distance). During this period, and retain a nearly perfect mutual alignment across the corridor, though they are separated with . The control law stimulates and to reduce the gap between them. As a result, they come into contact and the resulting united group aligns across the corridor and achieves a nearly even self-distribution over the width of the employed passage at 13.0 s. A side effect of these is that loses the alignment with . Only after the obstacle course is left behind (at 19 s) and the gap between and the remainder of the team is reduced to below the sensing range (at 21 s), the alignment of the entire team and its even self-distribution across the corridor is attained at 25 s. Once more, we observe that the mission is carried out successfully and with a good accuracy.
The last two experiments test the capacity of the algorithm to cope with changes in the team membership. In the scenario from Figure 18, the team of 11 USVs loses 5 USVs in the middle of the corridor length. After this happens, the remaining six USVs run the control rule “as usual”, ignoring the missed peers. By Figure 18, the result successfully traverses the obstacle course and achieves optimal (for the downsized team) self-spreading across the corridor. In Figure 19, six USVs encounter five motionless red “newcomers”. As soon as a newcomer detects that a USV overtakes it (in projection onto the x axis), it starts running the control rule and so begins to move. At the “time of meeting”, obstacles block the line of sight between some USVs. As can be seen, this does not bring any trouble: the united team reasonably uses the available passages between the obstacles, eventually leaves the obstacle course behind, and achieves the optimal deployment across the corridor. Thus, the algorithm demonstrates robustness to changes in the team membership.
8.2. Gazebo Experiments
To test the control law against the challenges from the more complex dynamics of the robots, some experiments were carried out using the realistic 3D robotics simulator Gazebo 11 (https://gazebosim.org/home, accessed on 16 February 2025) and ROS 2 (https://www.ros.org/, accessed on 16 February 2025). This simulator provides high-quality physics engines for modeling the robot and environment and emulates realistic sensor readings.
Two-wheeled differential drive robots are used as the robotic platform. To model it, the DiffBot package https://github.com/ros-mobile-robots/diffbot (accessed on 16 February 2025) is employed; it has been slightly modified subject to the considered application scenarios. A two-level control system was designed to control each robot. The control law (7) and (8) acts at the higher level to generate the desired velocity vector. This vector is then fed into the lower-level control module, whose role is to generate control signals for the left and right wheels in order to achieve the desired velocity. This module is based on PD controllers and is developed using standard control system design methods.
Partly in order to better exhibit the region of the control law convergence and to examine its robustness against controller tuning errors, some parameters of the algorithm and scenario are altered in Section 8.2 as compared with Section 8.1.
The parameter values used in Gazebo simulation are reported in Table 2.

Table 2.
Numerical values used for simulations with Gazebo.
The results of a typical experiment are shown in Figure 20.
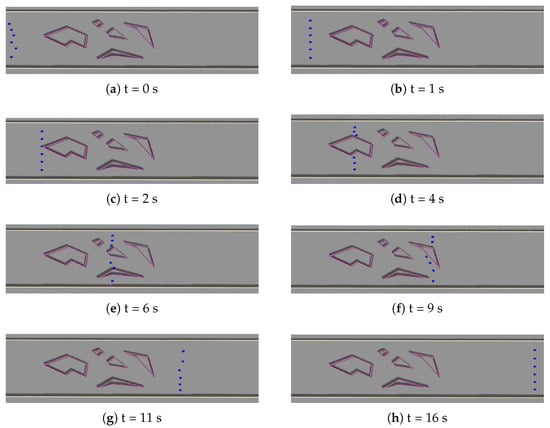
Figure 20.
Six differential drive robots passing through a band of five obstacles.
The robots achieve the required speed and uniform distribution across the corridor in just ≈1.0 s; see Figure 20b. The group of robots encounters the band of obstacles at ≈3.0 s, as seen in Figure 20b. While overcoming the band of obstacles, the number of subgroups changes over time as follows: (6) ↦ (3-3) ↦ (6) ↦ (3-2-1) ↦ (5-1) ↦ (3-2-1) ↦ (2-4) ↦ (6). Meanwhile, Figure 20c–f shows that, during the traversal of the obstacle band, the robots never collided with an obstacle; they also did not collide with each other or with the corridor walls throughout the experiment. Although the robots are noticeably disorganized upon exiting the obstacle band in Figure 20g, they quickly restore perfect order in Figure 20h. Thus, the experiment demonstrated that, for robots with more complex kinematics, the proposed control law is suitable as a high-level control module within a hierarchical two-level control system.
A video recording of the experiment is available at the following link: https://drive.google.com/drive/folders/1ngTYqiY1V-2-sEI6EjcMrFmMAEFSMWuM?usp=sharing (accessed on 16 February 2025).
The one in Figure 21a is mounted on the Rover 5 USV platform (https://www.sparkfun.com/products/retired/10336, accessed on 16 February 2025); the USV in Figure 21b is similar in architecture to the DiffBot (https://github.com/ros-mobile-robots/diffbot, accessed on 16 February 2025). Simple gearbox and motors are mounted on the wheeled chassis. Under a low stall torque situation, the acceleration of the chassis as a whole proved to be inappropriately small, presumably due to features of the employed simple gearbox. This entails a visible problems with the USV performance. To compensate for this effect, a special control loop is included in the above situation, which artificially increases the average current in the motor coil.

Figure 21.
Laboratorial USV with (a) crawler and (b) wheeled chassis.
9. Results of Real-World Tests
These were performed using the two USVs shown in Figure 21.
Every USV is equipped with two (i.e., left and right) DC brush motors, and only the motors differ between the USVs. One of them employs the motor driver L298N, the other makes use of the Motor Shield (https://amperka.com/). The algorithm (7) and (8) is implemented onboard on the basis of a Raspberry Pi 4B+ computer running under Linux. The motors are driven with voltage pulse signals; their pulse amplitude is maximal. Meanwhile, the speed profile generated in accordance with (7) and (8) is converted into the pulse ratio for every motor by means of a simple low-level regulator. Thus, the two USVs are subjected to a common higher-level control rule, whose hardware implementation is different for them. As a result, the experiments somewhat examine the robustness of the rule (7) and (8) against such a difference. The basic parameters of the control law are taken from Table 1.
Each USV uses a range measuring scanning laser Slamtec RPLidar A1. It is mounted on the top of the USV in order to avoid blind spots. The Lidar readings are updated with a frequency of 10 Hz, and the motor control loop operates at a frequency of 50 Hz (this imbalance aids to smoothen the USVs’ path). The computer, motors, and Lidar are separately powered by their own batteries. This separation is partly motivated by the wish to avoid knocking down the work of the Lidar because of disturbances from the motor sharing the same power source. The control software was implemented in the Thonny programming environment using the Python programming language. The pyrplidar library was used to obtain data from the LiDAR, and the RPi.GPIO library was used for motor control. At the level of the software implementation of the basic control law, extra measures were taken to encourage the robots to align with the direction of the corridor.
The multimedia of four real-life experiments are available at https://drive.google.com/drive/folders/1pRoDqK7XrvcZExlk-PTmdw_nc3zVeTBt?usp=share_link (accessed on 16 February 2025).
In Figure 22, the USVs go through a corridor with two obstacles made of corrugated white paper. Their initial deployment differs from the desired one. At s, they achieve a nearly even distribution over the width of the corridor but have not had enough time to equalize their coordinates along . A little later, the wheeled USV starts bypassing obstacle 1 from the right, so that, at 10.0 s, the USVs find themselves within a common passageway between obstacle 1 and the right side of . At 15.0 s, this obstacle is left behind, the USVs nearly line up across , and are in the process of increasing the distances between themselves and to the right side of , which is needed to achieve an even distribution across . This process is interrupted when the line of sight between the USVs becomes blocked by obstacle 2. Then, the USVs do not “see” each other, and the control law has to drive each of them to the center of the employed passageway. This goal is achieved with good precision at 18.0 s. After obstacle 2 is left behind, the progression towards the even distribution resumes. As a result, at 32.0 s, the targeted formation is built with good accuracy; from this time forth, it is stably maintained.

Figure 22.
Two USVs go through a corridor with two obstacles.
These facts are confirmed by Figure 23, which exhibits (slightly post-processed) telemetry data from the two Lidars. In Figure 23, the blue and orange graphs display the distance from the USV to the nearest object (either a corridor wall, or an obstacle, or another USV) to the left and right, respectively, that is found in the narrow beam issued from the USV perpendicularly to the corridor direction. Though these data are somewhat damaged by experimental artifacts and brief disruptions in the regular operation of the distance evaluation system (which are manifested as short large spikes in the graphs), it confirms that, first, the USVs do not collide with each other, the corridor walls, and the obstacles and second, evenly distribute themselves across the width of the corridor (with the maximal positional error ≲4.0 cm) after the obstacle course is left behind. Thus, the control law copes with the mission and demonstrates a reasonable performance.
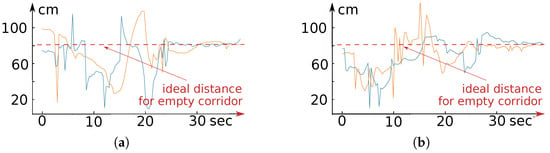
Figure 23.
Telemetry data for (a) crawled and (b) wheeled USVs.
Overall, these and our other experiments (reported at the previously indicated site) demonstrated the robustness of the proposed control law against real-life non-idealities, including sensor noises, actuator errors, and mismatches between the theoretical model of the USV and its real-world kinematics and dynamics.
10. Conclusions and Future Work
A distributed and computationally cheap control rule was offered such that, when it is individually run by every USV from a team of an unknown size, the team autonomously organizes itself into the densest net-like straight barrier across an unknown corridor. This holds even if the corridor is partly cluttered with unknown polygonal obstacles. Moreover, the rule guarantees that, eventually, the barrier goes along the corridor with a pre-specified speed and in the given direction, and the USVs evenly distribute themselves across the width of the corridor in its obstacle-free parts. Furthermore, the straight cross-section formation of the robots is not broken in all parts of the corridor, including those cluttered with obstacles. The suggested control law uses only local sensory data within a finite distance. By directly converting the observations into control in a reflex-like fashion, this law demands minimal computational resources. Regarding the simplification of the control system architecture, it was demonstrated that, under certain circumstances, the task of obstacle avoidance can be entrusted to the control module responsible for distributing the robots across the width of the corridor. The proposed algorithm was shown to be robust against the dropouts of teammates and admissions of newcomers. It was also proven that its convergence does not rely on the postulate of persistent informational connectivity of the team or the assumption on the initial connectivity. Its convergence and performance were justified via mathematically rigorous non-local convergence results and were confirmed via intensive computer simulation tests and real-world experiments. This validation was performed and the applicability of the proposed approach was demonstrated for a whole variety of scenarios, including those outside the bounds of the theoretical analysis. In particular, the method works well in certain scenarios with moving or non-polygonal obstacles, and if USVs start in “caves” inside obstacles; also, it is somewhat robust against controller tuning errors.
The practical design of navigation laws often follows through a two-stage hierarchy, where control at the kinematic level generates a reference signal, which is then tracked by standard, more or less, controllers. The developments of this paper are attributed to the first stage and are, to a certain extent, about to set forth a sort of paradigm and provide a proof of concept. Implementation issues concerned with the second stage in a context somewhat similar in spirit to that from this paper are addressed in, e.g., [61,62].
Future work includes the elaboration of the details concerned with higher-order models of the USVs and relaxation of the assumptions about the obstacles. Our agenda also includes studies of scenarios where several barriers should be formed that consecutively follow one another with a given step. Extensions to 3D environments are also on the way.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/drones9030161/s1, Video S1: animation of the experiment from Figure 17; Video S2: animation of the experiment from Figure 19; Video S3: animation of the experiment from Figure 18; Video S4: animation of the experiment from Figure 22.
Author Contributions
P.K.: Conceptualization, software, validation, formal analysis, investigation, writing—original draft preparation. A.M.: Conceptualization, methodology, data curation, formal analysis, writing—review and editing, supervision, project administration, funding acquisition. K.G.: software, validation, visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the grant of the state program of the “Sirius” Federal Territory “Scientific and technological development of the “Sirius” Federal Territory” (Agreement №18-03 date 9 October 2024).
Data Availability Statement
Data are contained within the article and Supplementary Materials.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| USV | Unmanned surface vehicle |
| a.a. | “for almost all” |
| Conventions and notations | |
| Positive angles | counted counterclockwise |
| “is defined to be”, “is used to denote” | |
| “segment of a line” | its part between two points |
| “segment” | “segment of a straight line” |
| segment bridging the points | |
| minus | |
| minus | |
| minus and | |
| number of elements in the set A | |
| signum function, | |
| boundary of the set O | |
| coordinates of point | |
| ∅ | empty set |
| handled corridor | |
| w | width of the corridor |
| N | number of the robots |
| kth obstacle | |
| location of robot i | |
| coordinates of robot i | |
| velocity vector of robot i | |
| upper bound on the robot’s speeds | |
| desired speed | |
| sensing distance | |
| upper/lower fences of obstacle | |
| upper bound on the polar angles of the segments in upper and lower fences | |
| controller parameters | |
| functions used to build the controller | |
Appendix A. Proof of Theorem 1 and Remarks 2, 3, and 4
We study the motion of the team driven by the proposed control law. The assumptions of Theorem 1 are adopted throughout the appendix. Furthermore, the x distance is the distance between the abscissas of two points; the y distance is defined likewise.
Lemma A1.
The statement (i) of Theorem 1 is true.
Proof.
To state the next lemma, we put and note that thanks to (13).
Lemma A2.
The statements (iii) and (iv) of Theorem 1 are true. Moreover, a.a. t.
Proof.
(iii) We start with invoking the notation from (22). By virtue of the Danskin’s theorem [63], the function is absolutely continuous and a.a. t, where is a maximizer for . By (7) and the definition of the Filippov’s solution [57], lies in the convex hull of the values that are the limits of
as the perturbed system’s state goes to the true one, respecting certain restrictions. However, they cannot influence the limit values of the addends, which are exactly as shown in (A1) and are nonpositive by (5). Hence, a.a. t and is a non-increasing function. Likewise, is a non-decreasing function. It remains to note that .
Corollary A1.
, where γ is taken from Theorem 1.
Lemma A3.
If USV i is on a visor V at time τ, then for , it is outside V and is actually on the side of V that was downloaded at random into its “mind” at .
Proof.
Let USV i “think” that it is below V at ; the opposite case is handled likewise. Then, and due to (3) and (4). It remains to invoke (6) and (8) and observe that
□
Lemma A4.
Let be a time interval during which the USV i does not collide with the obstacles: . Then, the following statements hold:
- (i)
- For , USV i is not in the caves of any obstacle ;
- (ii)
- If there is a point of an obstacle that lies above (below) , the closest of such points belongs to the lower (upper) fence of .
Proof.
(i) Suppose that (i) is untrue. Since USV i is initially outside the caves by the assumptions of Theorem 1, there is time and an obstacle such that is in a cave of , whereas is not in its caves for . By invoking the definition of the cave, we see that the ray does not intersect for , or the same is true for the ray . We focus on the first situation, and the second one is treated likewise. We vertically extend down from until hitting at some point and thus obtain an -free upward ray . Since is in a cave, both rays intersect . Hence, the ray is not -free, whereas arbitrarily close to it, there is the upward ray that is -free and also lies to the left of by Lemma A2 (in the part addressing iv) of Theorem 1). By Definition 2, this means that the ray is forward critical for , in violation of Assumption 2. This contradiction completes the proof of (i).
(ii) This is immediate from (i) and Definition 3. □
A right cape of the obstacle is a pair of its sides with a common point such that they lie to the left of (see Figure A1).

Figure A1.
Right capes and feasible options for two non-empty bases.
Lemma A5.
The following statements hold:
- (i)
- No more than one obstacle affects the bases and of USV i.
- (ii)
- No more than one base is not empty.
Proof.
(i) An obstacle influences base building only if vertically below/above its point there is an edge of the graph at a distance . By the definition of , the y distance from to does not exceed ; the x distance does not exceed by Corollary A1. By taking into account the imaginary visor, we infer that the x distance to the true obstacle does not exceed . Overall, the Euclidian distance between and does not exceed , where is the l.h.s. of (20). If building the bases of USV i is affected by different obstacles, the distance between them is, therefore, not greater than , in violation of (20). This completes the proof of (i).
(ii) Suppose that and , and pick . Vertically below/above , there is a point of , where by (i). Due to Corollary A1 and (17), (1) the x scope of fully covers the x scope of no side of the polygon , and (2) if lies on the left to a visor of , any node of to the right of is in the x scope of the visor. Due to (i) in Lemma A4 and the definition of , there exist two sides and of such that they form a right cape, and is vertically above , whereas is below ; also, ; see Figure A1.
Based on Figure A1, it is easy to see that, in any case, either (B.3) or (B.2) in the definition of the base (given in Section 5) is violated either for or for . This contradiction completes the proof. □
The left end of the visor is called its tip. The visored obstacle deprived of the visor’s tips is said to be blunt.
Lemma A6.
The USVs do not hit the blunt obstacles.
Figure A2.
Three ways to hit an obstacle: hitting an obstacle’s side with (a) a positive slope, (b) zero slope, (c) negative slope.
Proof.
Let be the set of times when the USVs and the blunt obstacles have no points in common. By Lemma A3, the set is non-empty and open, and its leftmost connected component has the form , where . We have to show that .
Suppose that and limit our attention to . With the aid of Lemma A3, we infer that, for such t’s, the USVs are outside the visored obstacles, and there are robot i and obstacle such that is in the blunt obstacle , and is either (1) always below or (2) always above . We focus on (1), and case (2) is handled likewise. It is easy to see that there exists a side S of such that and is below S; see Figure A2. Let stand for the point of S that is vertically above . We put and examine the cases from Figure A2 separately.
Corollary A2.
The USVs do not collide with the real obstacles and the corridor walls.
By the assumptions of Theorem 1, the USVs start outside the caves. Then, (i) in Lemma A4 yields the following.
Corollary A3.
The USVs do not visit the caves.
By invoking Lemma A3 and A2, we also come to the following two conclusions, respectively.
Corollary A4.
Remark 3 is true.
Corollary A5.
The times when USV i is in the x scope of any obstacle form a finite interval (maybe, empty). During this interval, USV i is either always above or always below .
For any USVs , we put . A time is said to be touching for the pair and the obstacle if , and arbitrarily close to there exists such that and have no common points.
Lemma A7.
Let τ be a touching time for the pair of robots and the obstacle .
Then, the following statements are true:
- (i)
- Either one and only one of the locations lies in the x scope of the obstacle , or the both lie there and are vertically aligned ;
- (ii)
- Any is either the left end of a visor or a right cape (see Figure A3e–g);
Figure A3.
Feasible options at a touching time : (a) the x-scopes of the sides and do not overlap, the slopes of the sides are opposite in sign, (b) the x-scopes of the sides do not overlap, the slopes of the sides are nonnegative, (c) the x-scopes of the sides do not overlap, the slopes of the sides are negative, (d,e) the x-scopes of the sides overlap, (f,g) the point is the tip of a visor.
Proof.
We start by noting that the interior of does not intersect with , and the locations and do not belong to the blunt obstacle by Lemma A6. So, Corollary A1 and (17) imply that the intersection contains a single point , which is a vertex of the polygon . Let and be the sides of adjacent to . By taking into account (17) and Lemma A2, we see that the cases feasible at are either those featured in Figure A3 or their mirror reflections with respect to the horizontal line. We focus on the first group of the cases; the second group is handled likewise.
We invoke from (2) and the notation introduced in the beginning of Section 7, and first focus on the cases (a–d) from Figure A3. By Lemmas A4 and A6 and Figure A3, for . So, Corollary A1 yields that
by (17) and the last inequality from (13). Hence, for , nodes i and j are linked in in the graphs and , and . Also, Lemma A5 and (4) imply that in the cases (a), (b), (d), whereas in the case (c).
In Figure A3, the side lies on the straight line described by with some c. Also, , where . We put , . Then, (A2) holds and
In the cases (a), (b), and (d), we have
in violation of (A2). This shows that (a,b,d) do not occur.
In the case (c) from Figure A3, the sides and form a forward pair and so by (11) and the definition of from (2). Hence, , and then (3), (17) and Corollary A1 entail that for . Hence,
Like in cases (a,b,d), we thus see that (c) does not hold.
In all other cases (e–g) from Figure A3, the statements (i) and (ii) are trivially true. □
Lemma A8.
If an obstacle separates USVs i and j, they cannot be both above and cannot be both below .
Proof.
Suppose to the contrary that there is time such that the obstacle separates and , whereas USVs i and j are either both above or both below . The set of times for which does not separate and contains 0 (by the assumptions of Theorem 1), and the time is touching. Due to Lemmas A2 and A7, some of the cases (e–g) from Figure A3 (or its horizontal mirror refection) hold at (maybe, with ). Among them, the case (e) from Figure A3 does not occur: otherwise, the forward USV would not be in the x scope of the obstacle at by Lemma A2.
Suppose that . Since the locations and are in the x scope of , at , the segment is vertical in Figure A3f,g. So, one of the USVs is above and the other is below at , in violation of the definition of . Hence, .
As t runs from towards , the forward USV from Figure A3f,g keeps its position with respect to (below/above) unchanged thanks to Corollary A5. Due to Corollary A1 and the inequality from (17), no later than this USV leaves the x scope of the visor, the other USV enters this scope. Let be the time when this occurs. Then, , and at , the “other” USV is on the other side of the visor since . By Corollary A5, it remains on the other side of until , in violation of the definition of . This contradiction completes the proof. □
By the assumption of Theorem 1, the USVs can be enumerated so that, at ,
Lemma A9.

Figure A4.
Options feasible at time when the ordinates of two USVs become equal: (a) Point lies below the obstacle and , (b) point lies below the obstacle and , (c) point lies to the right of the scope of the obstacle.
Proof.
(1) The segment intersects a blunt obstacle at . By Lemma A5, the respective obstacle is unique. Among the locations and , there is at least one that lies (strictly) inside the x scope of , as follows from (17). We focus on the case where is above ; the opposite case is handled likewise. By Lemma A8, the other of the above two locations is not above . Since the segment is horizontal by (A5) and does not exceed in length by Lemma A2, whereas is less than the length of the visor by (17), the abscissa cannot lie to the left of the x scope of . Thus, either lies below the obstacle or to the right of its x-scope. We shall handle these two cases separately.
(1.a) Point lies below . By the assumptions of Theorem 1, . Due to Lemma A7 and (e–g) in Figure A3, at the time when the segment touches for the first time, either USV is above or USV is below . With regard to Corollary A5, it follows that lies below and lies above . Let s be the side of that contains the point such that the segment is vertical and does not intersect . Depending on whether the polar angle of s is non-negative or negative, the situations featured in Figure A4a,b, respectively, occur.
Case from Figure A4a. Like in the proof of Lemma A7, we see that for , USV is an evader and , . Also, (10) and Corollary A1 imply that . So for , the following relations hold:
in violation of (A2). So the case from Figure A4a does not hold.
Case from Figure A4b. Like in the previous case, we see that, for , USV is an evader and , whereas . Also, . The proof is completed as before and results in the conclusion that the case from Figure A4b does not hold.
Hence, the overall case (1.a) does not occur.
(1.b) Point lies to the right of the scope of . Let be the set of times for which the obstacle does not separate USVs i and j. Then, by the assumptions of Theorem 1, the set is open in , and . So, the leftmost connected component of has the form , where is a touching time for and . Due to Lemmas A2, A7, and (e–g) in Figure A3, at the USV with the greater ordinate cannot be below . By Corollary A5 and Lemma A8, it cannot dive below while traveling through the x scope of . Thus, we see that and ; see Figure A4c. By arguing like in the situation from Figure A4a, we arrive at the conclusion that the case (1.b) and so the overall case (1) do not occur.
Now, we pass on to consider the remaining option.
(2) Segment does not intersect the blunt obstacles. Since this segment is horizontal, it is also disjoint with the visored obstacles. The USVs and are in direct sight of each other and
whereas (A2) holds. Once again, we examine the feasible cases separately.
(2.a) . Then,
Then, the arguments stated just after (A3) result in contradiction to (A2) and show that the situation (2.a) does not occur.
(2.b) It follows that some of the following options holds:
- (b.1)
- , where ;
- (b.2)
- for .
(b.1) By (4) and Lemma A5, a unique obstacle affects building any nonzero angle among . By shrinking , we arrive at a situation where, for all , the angle assumes a common value , a common obstacle influences , and if , a common obstacle does the same for . If , the arguments from the proof of i) in Lemma A5 show that the distance from any USV to a point of the related obstacle does not exceed the l.h.s. of (20). Then, (20) implies that both angles are triggered by a common obstacle .
Let . Then, USV is an evader with the main base . By (4) with , there is a node in the connected component of the graph such that , a side s of can be found vertically below a point at a distance , and the plane-parallel infinitesimal shift of the segment and point in the x direction does not increase the vertical distance from to and from to s. So the polar angle of the side s is positive. If all nodes from are in direct view of USV , then . This and Lemma A5 imply that USV is also an evader with the main base , in violation of (4) and (b.1). It follows that there is a node invisible by USV . Then, necessarily, and so .
By Corollary A1, the abscissas , and lie in an interval that is less than in length. So, (17) implies that cannot lie on the left to or in the x scope of a visor of . By taking into account the first inequality from (17), we infer that lies above .
By the assumptions of Theorem 1, does not separate USVs and initially. The time when starts separating them is touching for and , and does not exceed t. Let stand for the maximum touching time that does not exceed t. By Lemma A7, the situation from Figure A3g,f holds for . In Figure A3g,f, and so long as implies that . As time goes from to t, the segment bridging the locations of USVs and constantly intersects . Hence, USV is below at the first time when it finds itself in the x scope of . By Corollary A5, USV remains below until t, in violation of the foregoing.
As a result, we see that the case (b.1) does not hold.
(b.2) Similarly, we see that this case also does not occur.
Thus, assuming that the failure of the lemma leads to a contradiction in any case, this completes the proof. □
Now, we introduce such that the associated concluding part of the corridor is free from the obstacles. The foregoing implies the following.
Corollary A6.
The team safely goes through the obstacle course, then enters the concluding part of the corridor, and goes inside afterwards.
From now on, we consider the respective part of the team’s motion and assign to its beginning. We put , and
Lemma A10.
The following function does not decrease:
Proof.
By the Danskin theorem [63], the function is absolutely continuous, and for almost all t,
where is a minimizer for . It suffices to show that a.a. t. In the first case from (A7), this is clear. Let the second case hold. We consider three possible options separately.
Then, . Since , we infer that . Hence, due to (13), the last inequality from (17), and Corollary A1. So , , and
Here by (3) since . Also, and by (3). Overall, by (6).
. Likewise, . Due to (12) and (20), the angle cannot be influenced by the upper wall of the corridor since USV 1 is close to the lower wall. Hence, and
. Similar arguments show that . □
By putting , we arrive at the following.
Corollary A7.
.
Lemma A11.
The derivatives are bounded: there exists a constant such that,
Proof.
For , we have ,
For , we have
The case is considered likewise. □
We consider the function and recall that its ω-limit point is the limit born by an unbounded sequence . Since the components of are bounded , the collection of all -limit points is a compact non-empty set. The elements of this collection are called the limit deployments. By Corollary A7, .
Lemma A12.
The following inequality holds for any limit deployment :
Proof.
First of all, we introduce the continuous mapping
Suppose to the contrary to the conclusion of the lemma that (A12) fails to be true for some limit deployment . Then, the minimum of the function over the compact set is less than . Let be a respective minimizer. By (A13), for some i, but not for all i’s since
By noting that , we infer that there exists i for which either
By definition, the limit deployment is born by some “parent-sequence” . By thinning this sequence, if necessary, we ensure that . Furthermore,
Case (A15). In this case, the following inequality holds if is small enough
Furthermore, the symbol (maybe, with indices) is used to denote k-dependent quantities that converge to zero as . Borrowing c from Lemma A11, we see that, for and , the following holds:
Suppose first that . If , the graph contains a node at a distance from the upper wall of the corridor. This distance upper estimates , where by the foregoing. Hence, and so and . Similarly, . It follows that, in any case, and so
So, by properly reducing (if necessary), one can guarantee that for all and large enough k. Therefore,
The bounded sequence has a convergent subsequence. Its limit is a limited deployment for which the related quantity (A13) is less than the value taken by this quantity at the deployment : this holds due to (A17) (where and ) and (A19). However, this contradicts the definition of as the minimizer of (A13). This contradiction completes the proof if .
In the case (A15), it remains to examine the situation where . Then, for any , we have
Hence,
The proof is completed like in the case where .
Case (A16) is handled likewise, by systematically replacing the intervals of the form by and picking a convergent subsequence from the sequence . □
Corollary A8.
The following equality is true for any limit deployment: ,
Lemma A13.
For any ,
Proof.
By (A12) and (A20), any limit deployment satisfies the following equations:
Let us consider an -limit point of the mapping . Then, there exists an unboundedly increasing time-sequence such that . Furthermore, we note that the bounded sequence has a convergent subsequence. Its limit is a limit deployment whose ith entry is equal to . Hence, and we see that all -limit points of the bounded function are the same and equal . This implies (A21) [64] (Ch. VII, Corollary 1.1) and completes the proof. □
Corollary A9.
For all sufficiently large t, the graph introduced just after (22) is connected; moreover, its nodes i and are connected with an edge for any .
Proof of Theorem 1.
Corollary A9 and (5), (22) imply that there is for which as [58,65]. This, Definition 1, Corollary A2, Lemma A9, and (A21) ensure (ii) in Theorem 1. Its statements (i) and (iii,iv) hold by Lemma A1 and A2, respectively. The statement (v) holds by Lemma A9; the statement (vi) is immediate from (v). □
Remark 3 is justified by Corollary A4.
Proof of Remark 2.
The discontinuities could hold either due to the effects of the obstacles or in a situation where or for some . However, this cannot occur for all sufficiently large times due to ii) of Theorem 1, Definition 1, the second inequality in (13), Lemma A2, and Corollary A6. □
Proof of Remark 4.
This proof is performed via the inspection of the proof of Theorem 1 and observing that all arguments remain valid. Starting from Corollary A6, it is important that a concluding part is bounded by two parallel straight lines by (ii) in Definition 5. □
References
- Xing, T.; Liu, Y.; Chen, L. Survey of robot formation control methods. Acad. J. Sci. Technol. 2022, 4, 58–61. [Google Scholar] [CrossRef]
- Oh, K.; Park, M.; Ahn, H. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Werger, B. Cooperation without deliberation: A minimal behavior-based approach to multi-robot teams. Artif. Intell. 1999, 110, 293–320. [Google Scholar] [CrossRef]
- Abdelli, A.; Amamra, A.; Yachir, A. Swarm Robotics: A Survey. In Advances in Computing Systems and Applications; Senouci, M., Boulahia, S., Benatia, M., Eds.; Springer: Cham, Switzerland, 2022; pp. 153–164. [Google Scholar]
- Xu, D.; Zhang, X.; Zhu, Z.; Chen, C.; Yang, P. Behavior-Based Formation Control of Swarm Robots. Math. Probl. Eng. 2014, 2014, 205759. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R. Distributed Consensus in Multi-Vehicle Cooperative Control: Theory and Applications; Springer: London, UK, 2008. [Google Scholar]
- Li, Y.; Tan, C. A survey of the consensus for multi-agent systems. Syst. Sci. Control. Eng. 2019, 7, 468–482. [Google Scholar] [CrossRef]
- Maghenem, M.; Loria, A.; Nuno, E.; Panteley, E. Consensus-based formation control of networked nonholonomic vehicles with delayed communications. IEEE Trans. Autom. Control. 2021, 66, 2242–2249. [Google Scholar] [CrossRef]
- Savkin, A.; Cheng, T.; Xi, Z.; Javed, F.; Matveev, A.; Nguyen, H. Decentralized Coverage Control Problems for Mobile Robotic Sensor and Actuator Networks; Wiley and IEEE Press: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wu, W.; Zhang, Z.; Lee, W.; Du, D. Sweep-Coverage. In Optimal Coverage in Wireless Sensor Networks; Springer Optimization and Its Applications; Springer: Berlin/Heidelberg, Germany, 2020; Volume 261, pp. 183–192. [Google Scholar]
- Huang, H.; Savkin, A.; Ding, M.; Huang, C. Mobile robots in wireless sensor networks: A survey on tasks. Comput. Netw. 2019, 148, 1–19. [Google Scholar] [CrossRef]
- Gage, D. Command control for many-robot systems. In Proceedings of the the 19th Annual AUVS Technical Symposium, Hunstville, AL, USA, 22–24 June 1992; Volume 4, pp. 22–24. [Google Scholar]
- Ding, L.; Han, Q.; Ge, X.; Zhang, X. An overview of recent advances in event-triggered consensus of multiagent systems. IEEE Trans. Cybern. 2018, 48, 1110–1123. [Google Scholar] [CrossRef]
- Wen, G.; Yu, X.; Yu, W.; Lu, J. Coordination and control of complex network systems with switching topologies: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6342–6357. [Google Scholar] [CrossRef]
- Ji, M.; Egerstedt, M. Distributed coordination control of multiagent systems while preserving connectedness. IEEE Trans. Robot. 2007, 23, 693–703. [Google Scholar] [CrossRef]
- Dimarogonas, D.; Kyriakopoulos, K. Connectedness preserving distributed swarm aggregation for multiple kinematic robots. IEEE Trans. Robot. 2008, 24, 1213–1223. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, Y.; Constantinescu, D. Connectivity-preserving synchronization of time delay Euler–Lagrange networks with bounded actuation. IEEE Trans. Cybern. 2019, 51, 3469–3482. [Google Scholar] [CrossRef] [PubMed]
- Zavlanos, M.; Pappas, G. Distributed connectivity control of mobile networks. IEEE Trans. Robot. 2008, 24, 1416–1428. [Google Scholar] [CrossRef]
- Kan, Z.; Navaravong, L.; Shea, J.; Pasiliao, E.; Dixon, W. Graph matching-based formation reconfiguration of networked agents with connectivity maintenance. IEEE Trans. Control. Netw. Syst. 2015, 2, 24–35. [Google Scholar] [CrossRef]
- Poonawala, H.; Spong, M. Preserving strong connectivity in directed proximity graphs. IEEE Trans. Autom. Control. 2017, 62, 4392–4404. [Google Scholar] [CrossRef]
- Lin, H.; Huang, Y. Collaborative complete coverage and path planning for multi-robot exploration. Sensors 2021, 11, 3709. [Google Scholar] [CrossRef]
- Ni, J.; Gu, Y.; Tang, G.; Ke, C.; Gu, Y. Cooperative coverage path planning for multi-mobile robots based on improved K-means clustering and deep reinforcement learning. Electronics 2024, 13, 944. [Google Scholar] [CrossRef]
- Muhsen, D.; Sadiq, A.; Raheem, F. A survey on swarm robotics for area coverage problem. Algorithms 2024, 17, 3. [Google Scholar] [CrossRef]
- Heo, N.; Varshney, P. Energy-efficient deployment of intelligent mobile sensor networks. IEEE Trans. Syst. Man Cybern. Part A 2005, 35, 78–92. [Google Scholar] [CrossRef]
- Chao, H.; Chen, Y.; Ren, W. A study of grouping effect on mobile actuator sensor networks for distributed feedback control of diffusion process using central Voronoi tessellations. Int. J. Robot. Res. 2006, 11, 185–190. [Google Scholar]
- Wang, Y.; Tseng, Y. Distributed deployment schemes for mobile wireless sensor networks to ensure multilevel coverage. IEEE Trans. Parallel Distrributed Syst. 2008, 19, 1280–1294. [Google Scholar] [CrossRef]
- Deif, D.; Gadallah, Y. Classification of wireless sensor networks deployment techniques. IEEE Commun. Surv. Tutor. 2014, 16, 834–855. [Google Scholar] [CrossRef]
- Chang, C.; Chin, Y.; Chen, C.; Chang, C. Impasse-aware node placement mechanism for wireless sensor networks. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1225–1237. [Google Scholar] [CrossRef]
- Zhou, M.; Li, J.; Wang, C.; Wang, J.; Wang, L. Applications of Voronoi diagrams in multi-robot coverage: A Review. J. Mar. Sci. Eng. 2024, 12, 1022. [Google Scholar] [CrossRef]
- Sadeghi, M.; Shahrabi, A.; Ghoreyshi, S.; Alfouzan, F. Distributed node deployment algorithms in mobile wireless sensor networks: Survey and challenges. ACM Trans. Sens. Netw. 2023, 19, 91. [Google Scholar]
- Houssein, E.; Saad, M.; Djenouri, Y.; Hu, G.; Ali, A.; Shabah, H. Metaheuristic algorithms and their applications in wireless sensor networks: Review, open issues, and challenges. Clust. Comput. 2024, 27, 13643–13673. [Google Scholar] [CrossRef]
- Wei, C.; Ji, Z.; Cai, B. Particle swarm optimization for cooperative multi-robot task allocation: A multi-objective approach. IEEE Robot. Autom. Lett. 2020, 5, 2530–2537. [Google Scholar] [CrossRef]
- Rossides, G.; Metcalfe, B.; Hunter, A. Particle swarm optimization—An adaptation for the control of robotic swarms. Robotics 2021, 10, 58. [Google Scholar] [CrossRef]
- Spears, W.; Spears, D.; Heil, R.; Kerr, W.; Hettiarachchi, S. An overview of physicomimetics. In Proceedings of the International Workshop on Swarm Robotics, Santa Monica, CA, USA, 17 July 2004; Şahin, E., Spears, W.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 84–97. [Google Scholar]
- Schwager, M.; Rus, D.; Slotine, J. Decentralized, adaptive coverage control for networked robots. Int. J. Robot. Res. 2009, 28, 357–375. [Google Scholar] [CrossRef]
- Razafindralambo, T.; Simplot-Ryl, D. Connectivity preservation and coverage schemes for wireless sensor networks. IEEE Trans. Autom. Control. 2011, 56, 6819–6820. [Google Scholar] [CrossRef]
- Rout, M.; Roy, R. Self-deployment of randomly scattered mobile sensors to achieve barrier coverage. IEEE Sens. J. 2016, 16, 6819–6820. [Google Scholar] [CrossRef]
- Chowdhury, T.J.; Elkin, C.; Devabhaktuni, V.; Rawat, D.B.; Oluoch, J. Advances on localization techniques for wireless sensor networks: A survey. Comput. Netw. 2016, 110, 284–305. [Google Scholar] [CrossRef]
- Bartolini, N.; Ciavarella, S.; Silvestri, S.; Porta, T.L. On the vulnerabilities of Voronoi-based approaches to mobile sensor deployment. IEEE Trans. Mob. Comput. 2016, 15, 3114–3128. [Google Scholar] [CrossRef]
- Mahboubi, H.; Aghdam, A. Distributed deployment algorithms for coverage improvement in a network of wireless mobile sensors: Relocation by virtual force. IEEE Trans. Control. Netw. Syst. 2017, 4, 736–748. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, Z.; Bandyopadhyay, S.; Schwager, M. Fast, on-line collision avoidance for dynamic vehicles using buffered Voronoi cells. IEEE Robot. Autom. Lett. 2017, 2, 1047–1054. [Google Scholar] [CrossRef]
- Elmokadem, T.; Savkin, A. Computationally-efficient distributed algorithms of navigation of teams of autonomous UAVs for 3D coverage and flocking. Drones 2021, 5, 124. [Google Scholar] [CrossRef]
- Eledlebi, K.; Ruta, D.; Hildmann, H.; Saffre, F.; Al Hammadi, Y.; Isakovic, A.F. Coverage and energy analysis of mobile sensor nodes in obstructed noisy indoor environment: A Voronoi-approach. IEEE Trans. Mob. Comput. 2022, 21, 2745–2760. [Google Scholar] [CrossRef]
- Bartolini, N.; Calamoneri, T.; Ciavarella, S.; La Porta, T.; Silvestri, S. Autonomous mobile sensor placement in complex environments. ACM Trans. Auton. Adapt. Syst. 2017, 12, 7. [Google Scholar] [CrossRef]
- Priyadarshi, R.; Gupta, B.; Anurag, A. Deployment techniques in wireless sensor networks: A survey, classification, challenges, and future research issues. J. Supercomput. 2022, 76, 7333–7373. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, T.; Wu, D.; Yu, C. Corridor navigation and obstacle distance estimation for monocular vision mobile robots. Int. J. Digit. Content Technol. Its Appl. 2011, 5, 192–202. [Google Scholar]
- Keshavan, J.; Gremillion, G.; Alvarez-Escobar, H.; Humbert, J. Autonomous vision-based navigation of a quadrotor in corridor-like environments. Int. J. Micro Air Veh. 2015, 7, 111–123. [Google Scholar] [CrossRef]
- Gupta, S.; Sangeeta, R.; Mishra, R.; Singal, G.; Badal, T.; Garg, D. Corridor segmentation for automatic robot navigation in indoor environment using edge devices. Comput. Netw. 2020, 178, 107374. [Google Scholar] [CrossRef]
- Pang, Y.; Zhou, L.; Lin, B.; Lv, G.; Zhang, C. Generation of navigation networks for corridor spaces based on indoor visibility map. Int. J. Geogr. Inf. Sci. 2020, 34, 177–201. [Google Scholar] [CrossRef]
- Padhy, R.; Ahmad, S.; Verma, S.; Bakshi, S.; Sa, P. Localization of unmanned aerial vehicles in corridor environments using deep learning. In Proceedings of the the 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 9423–9428. [Google Scholar]
- Aneesh, P.; Singh, R.; Dash, R. Autonomous UAV navigation in indoor corridor environments by a depth estimator based on a deep neural network. In Proceedings of the the 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024; pp. 1–5. [Google Scholar]
- Cheng, T.; Savkin, A. Decentralized control for mobile robotic sensor network self-deployment: Barrier and sweep coverage problems. Robotica 2011, 29, 283–294. [Google Scholar] [CrossRef]
- Chen, C.; Liu, S.; Zhong, C.; Zhang, B. Multiple robot formation control strategy in corridor environments. In Proceedings of the the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 8507–8512. [Google Scholar]
- Shi, M.; Qin, K.; Liu, J. Cooperative multi-agent sweep coverage control for unknown areas of irregular shape. IET Control. Theory Appl. 2018, 12, 1983–1994. [Google Scholar] [CrossRef]
- Matveev, A.; Konovalov, P. Distributed reactive motion control for dense cooperative sweep coverage of corridor environments by swarms of non-holonomic robots. Int. J. Control. 2023, 96, 554–567. [Google Scholar] [CrossRef]
- Matveev, A.; Konovalov, P.; Gordievich, K.; Gusev, S. Distributed reactive navigation of robotic teams for sweep coverage of a corridor environment with an obstacle course. In Proceedings of the the 7th International Conference on Robotics and Automation Engineering (ICRAE), Singapore, 18–20 November 2022; pp. 210–214. [Google Scholar]
- Filippov, A. Differential Equations with Discontinuous Righthand Sides; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Lin, Z.; Francis, B.; Maggiore, M. State agreement for continuous-time coupled nonlinear systems. SIAM J. Control. Optim. 2007, 46, 288–307. [Google Scholar] [CrossRef]
- Zavlanos, M.; Egerstedt, M.; Pappas, G. Graph-theoretic connectivity control of mobile robot networks. Proc. IEEE 2011, 99, 1525–1540. [Google Scholar] [CrossRef]
- Kan, Z.; Dani, A.; Shea, J.; Dixon, W. Network connectivity preserving formation stabilization and obstacle avoidance via a decentralized controller. IEEE Trans. Autom. Control. 2012, 57, 1827–1832. [Google Scholar] [CrossRef]
- Matveev, A.; Wang, C.; Savkin, A. Real-time navigation of mobile robots in problems of border patrolling and avoiding collisions with moving and deforming obstacles. Robot. Auton. Syst. 2012, 60, 769–788. [Google Scholar] [CrossRef]
- Matveev, A.; Hoy, M.; Katupitiyac, J.; Savkin, A. Nonlinear sliding mode control of an unmanned agricultural tractor in the presence of sliding and control saturation. Robot. Auton. Syst. 2013, 61, 973–987. [Google Scholar] [CrossRef]
- Danskin, J. The theory of min-max, with applications. SIAM J. Appl. Math. 1966, 14, 641–644. [Google Scholar] [CrossRef]
- Hartman, P. Ordinary Differential Equations, 2nd ed.; Birkhäuzer: Boston, MA, USA, 1982. [Google Scholar]
- Matveev, A.; Novinitsyn, I.; Proskurnikov, A. Stability of continuous-time consensus algorithms for switching networks with bidirectional interaction. In Proceedings of the 2013 European Control Conference, Zurich, Switzerland, 17–19 July 2013; pp. 1872–1877. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).