Probabilistic Chain-Enhanced Parallel Genetic Algorithm for UAV Reconnaissance Task Assignment
Abstract
1. Introduction
- 1.
- We enhance UAV task assignment by designing probabilistic chains, modeling corresponding chromosome coding, and refining genetic algorithm operations for crossovers and mutations based on these probabilistic chains.
- 2.
- We design an adaptive fitness-based crossover operator to enhance the solution quality.
- 3.
- We implement a Bayesian network to optimize the parameters of the heuristic algorithm, enhancing its effectiveness.
- 4.
- This research establishes a parallel acceleration structure for genetic algorithms, significantly enhancing their computational speed at the hardware level.
2. Related Work
2.1. Linear Optimization Algorithms
2.2. Contract Network Protocols
2.3. Heuristic Algorithms
2.3.1. Particle Swarm Optimization
2.3.2. Enhanced Heuristic and Combination Approaches
2.3.3. Genetic Algorithms
2.4. Proposed Solution: PC-EPGA Algorithm
3. MDTSP: UAV Reconnaissance Task Assignment Model
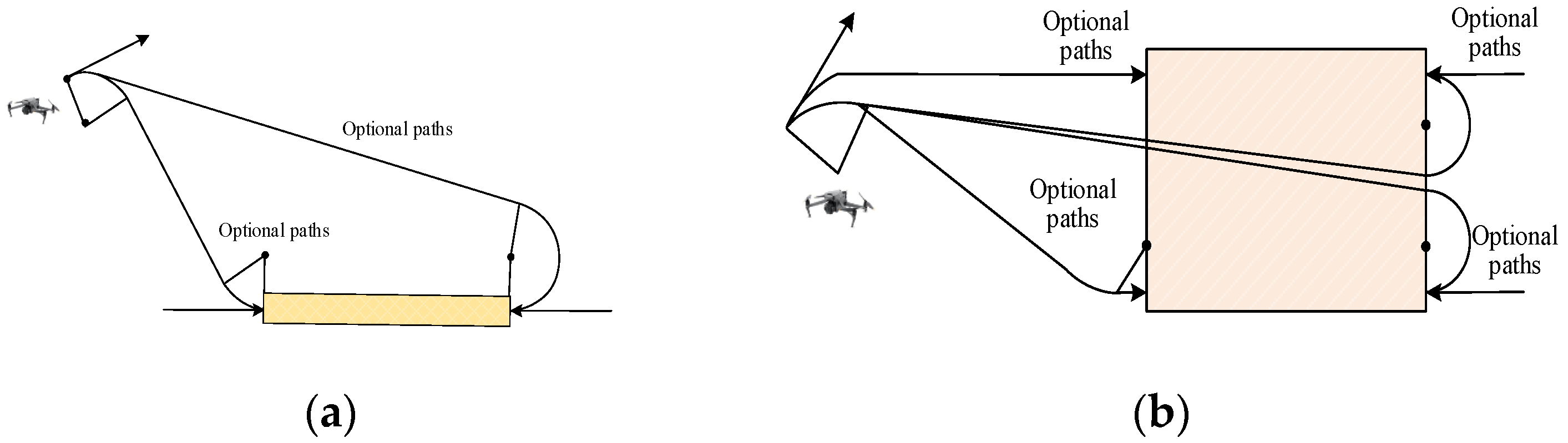
3.1. Assignment Constraints
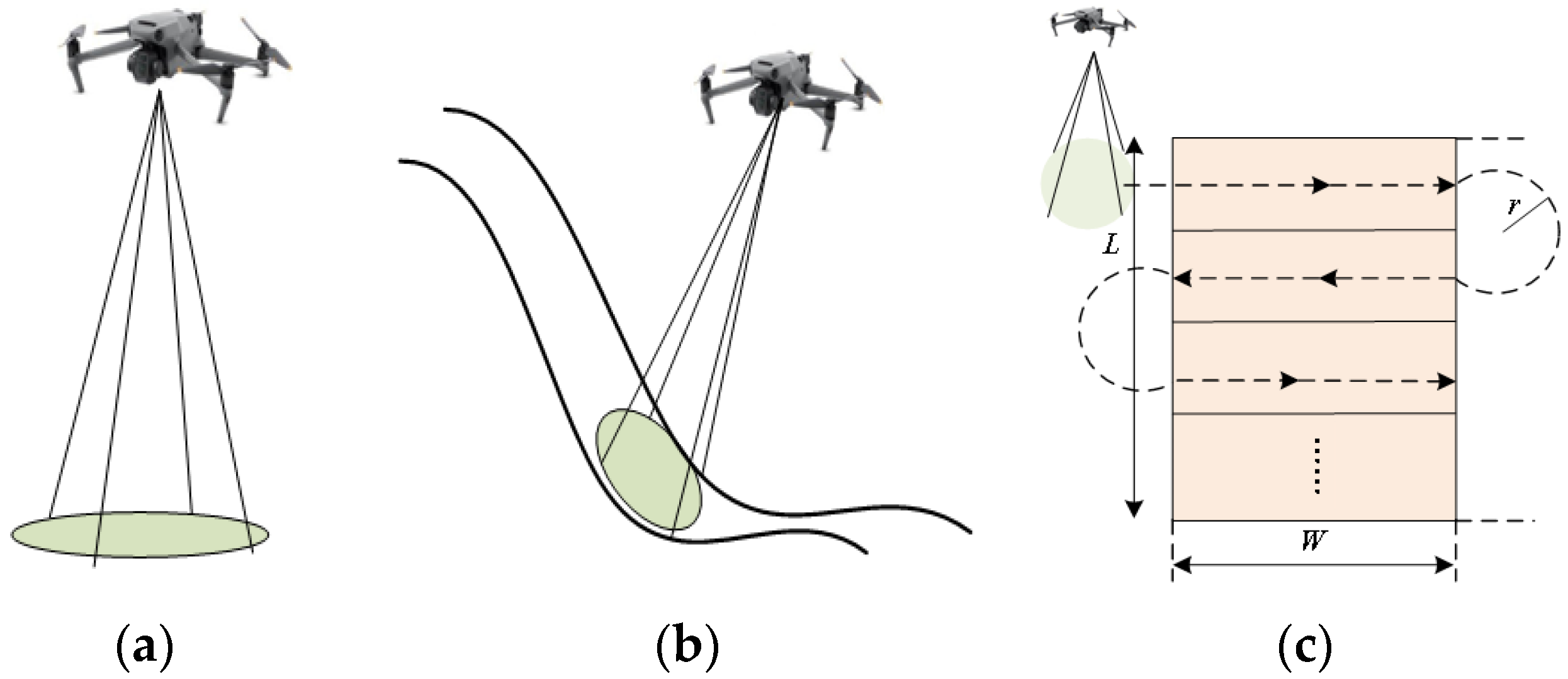
3.2. Motion Trajectory Model
3.3. Target Model
3.4. Evaluation Model
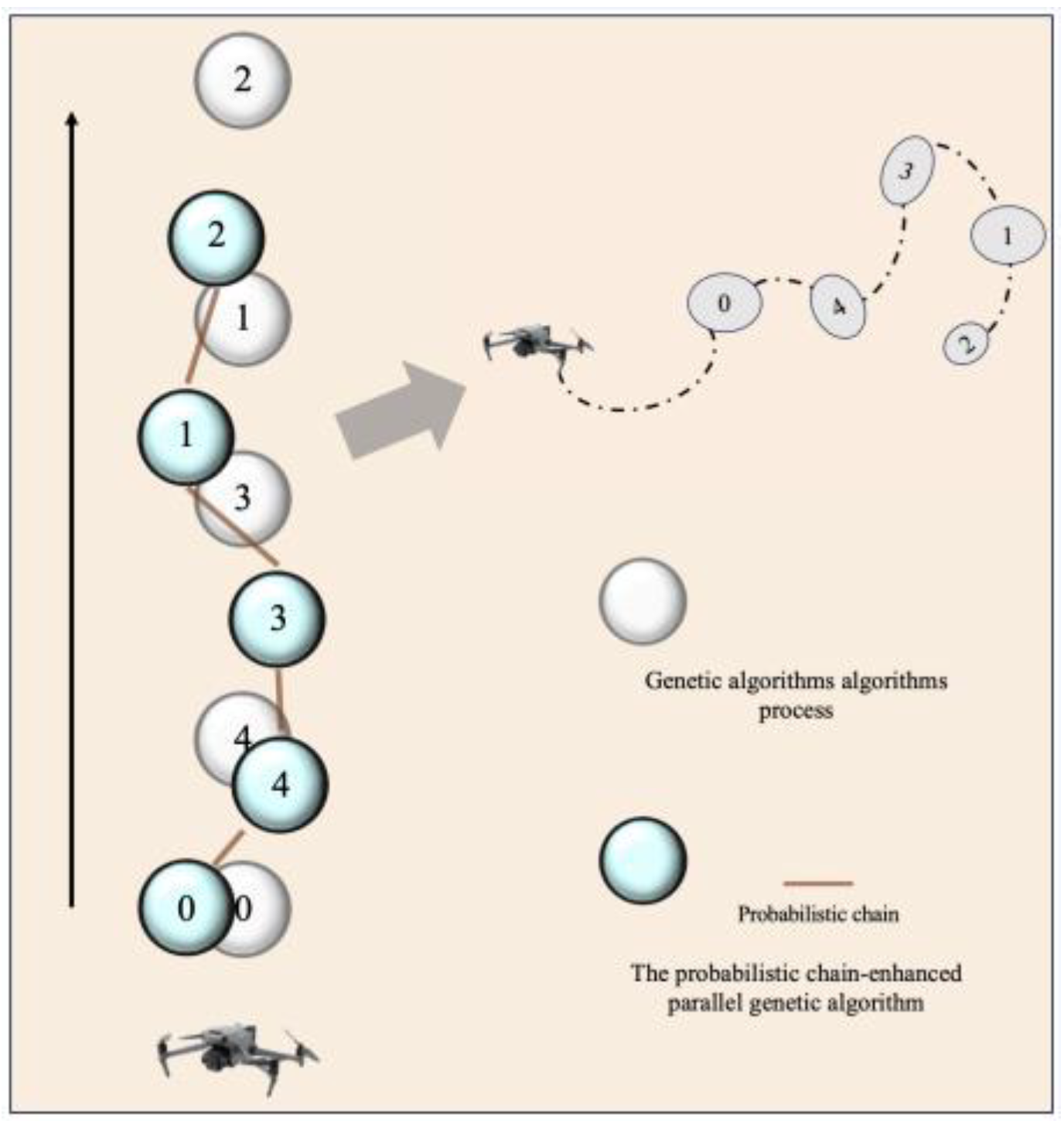
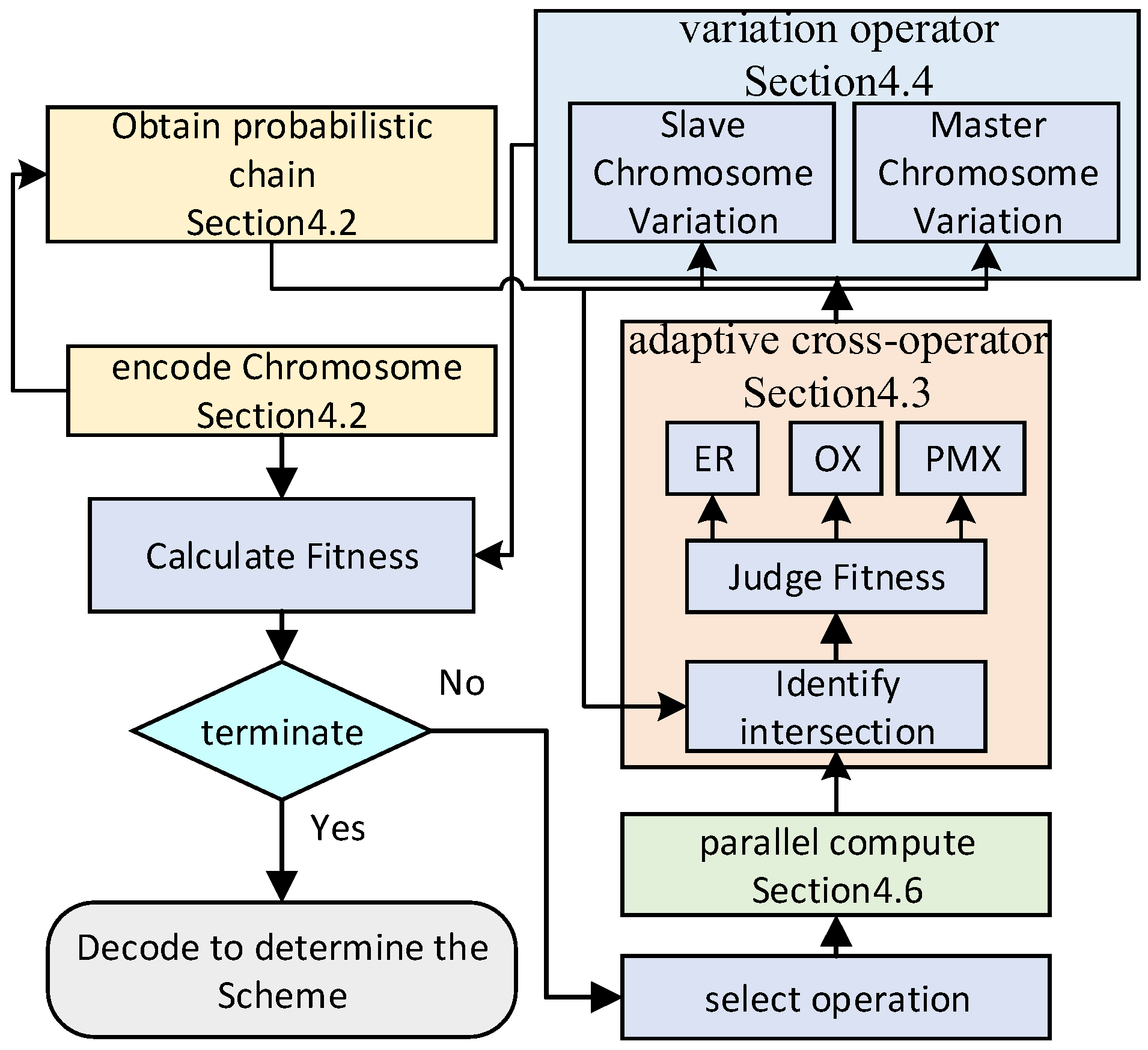
4. PC-EPGA: Probabilistic Chain-Enhanced Parallel Genetic Algorithm
4.1. PC-EPGA Model
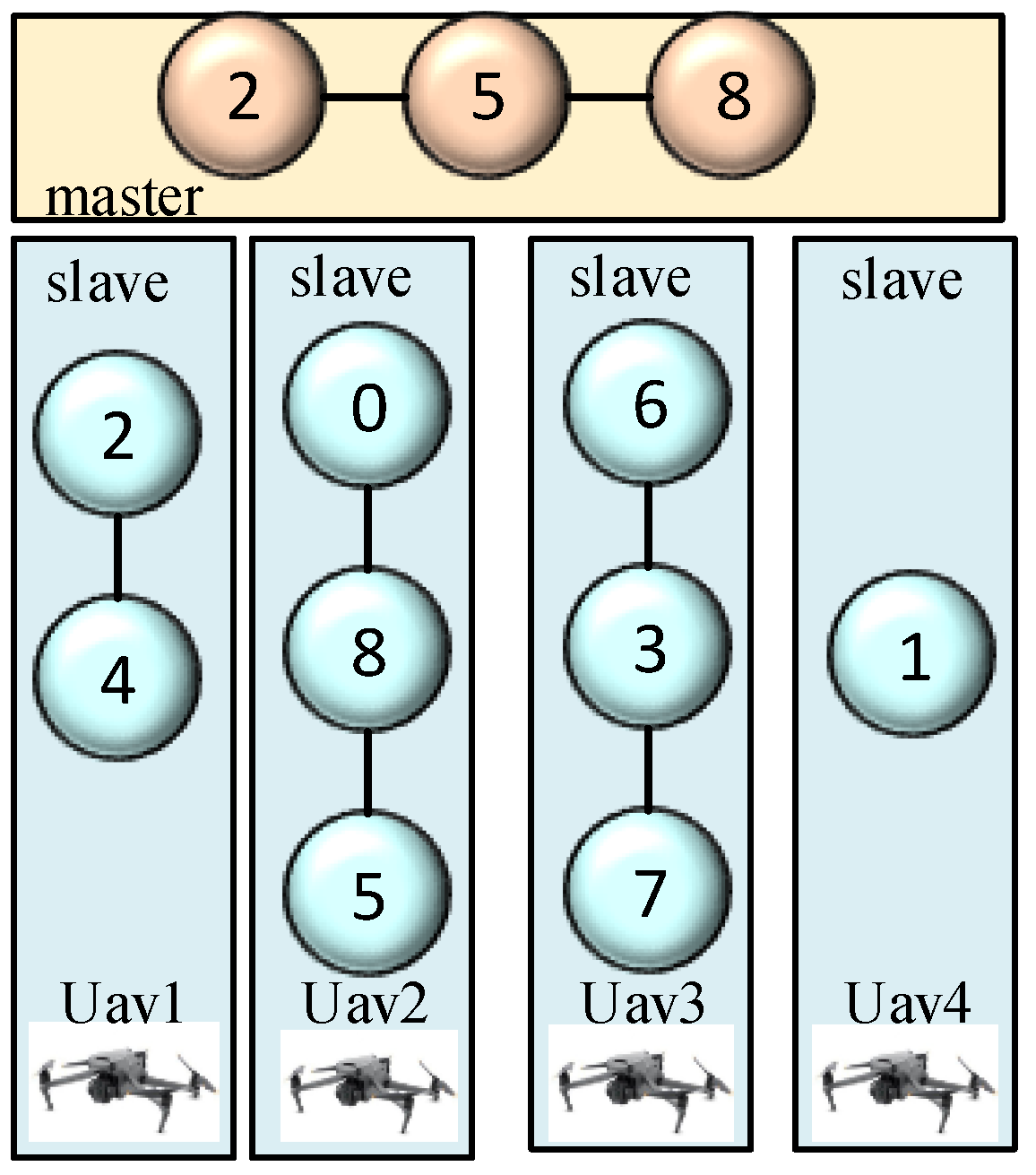
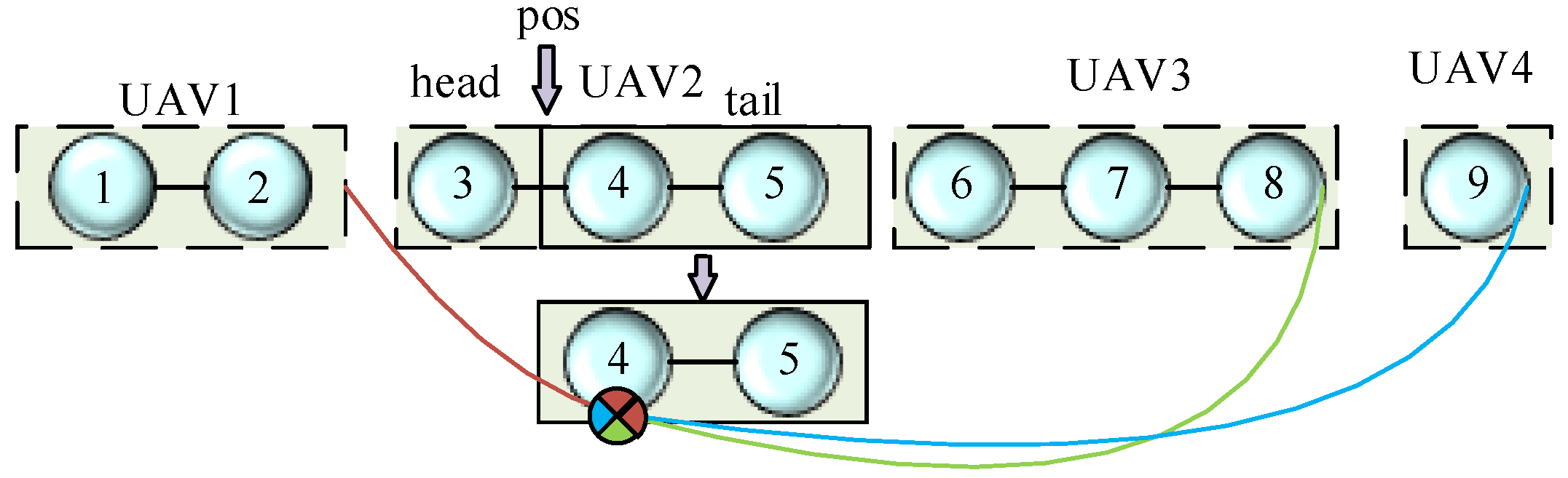
4.2. Encode Chromosome
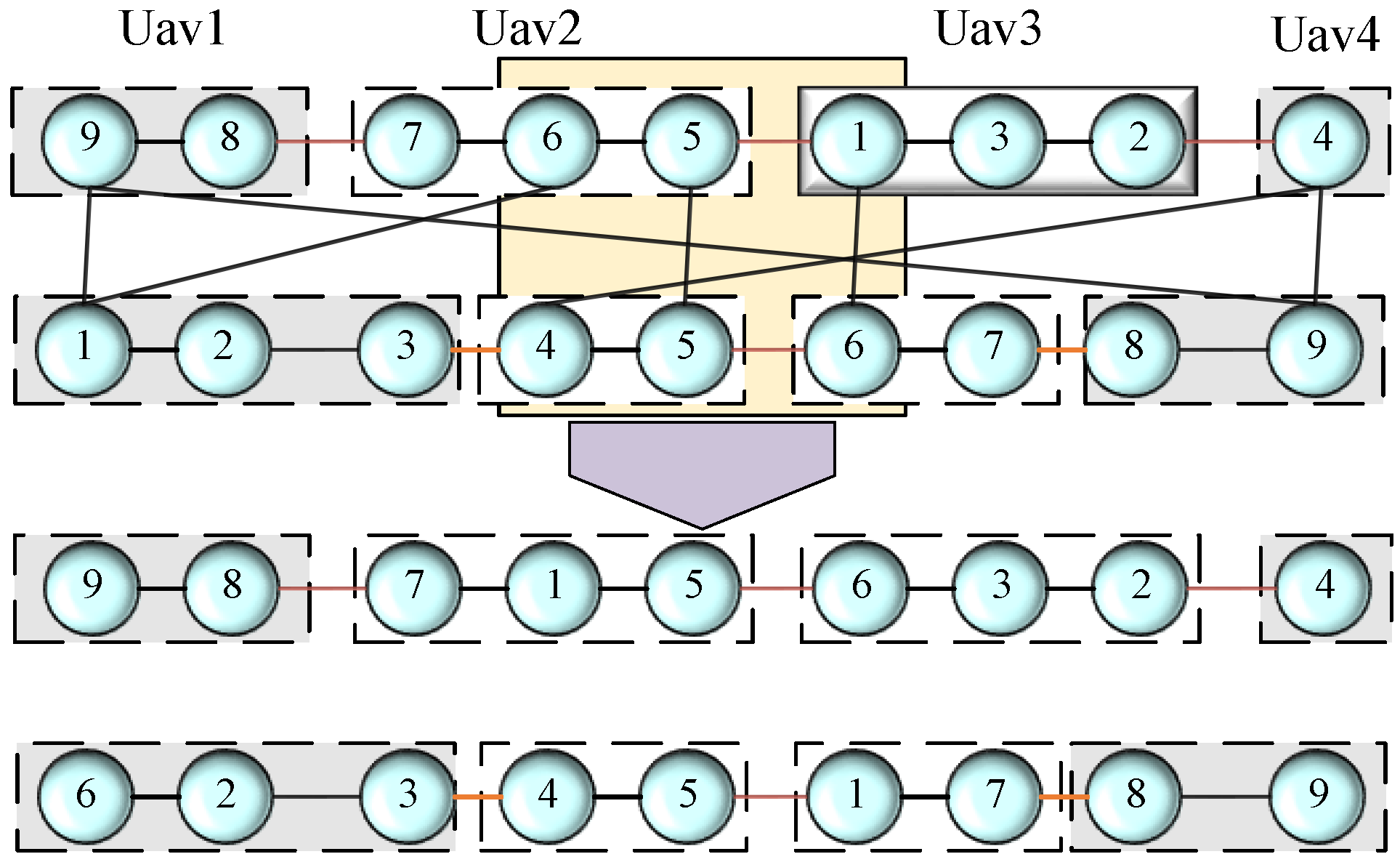
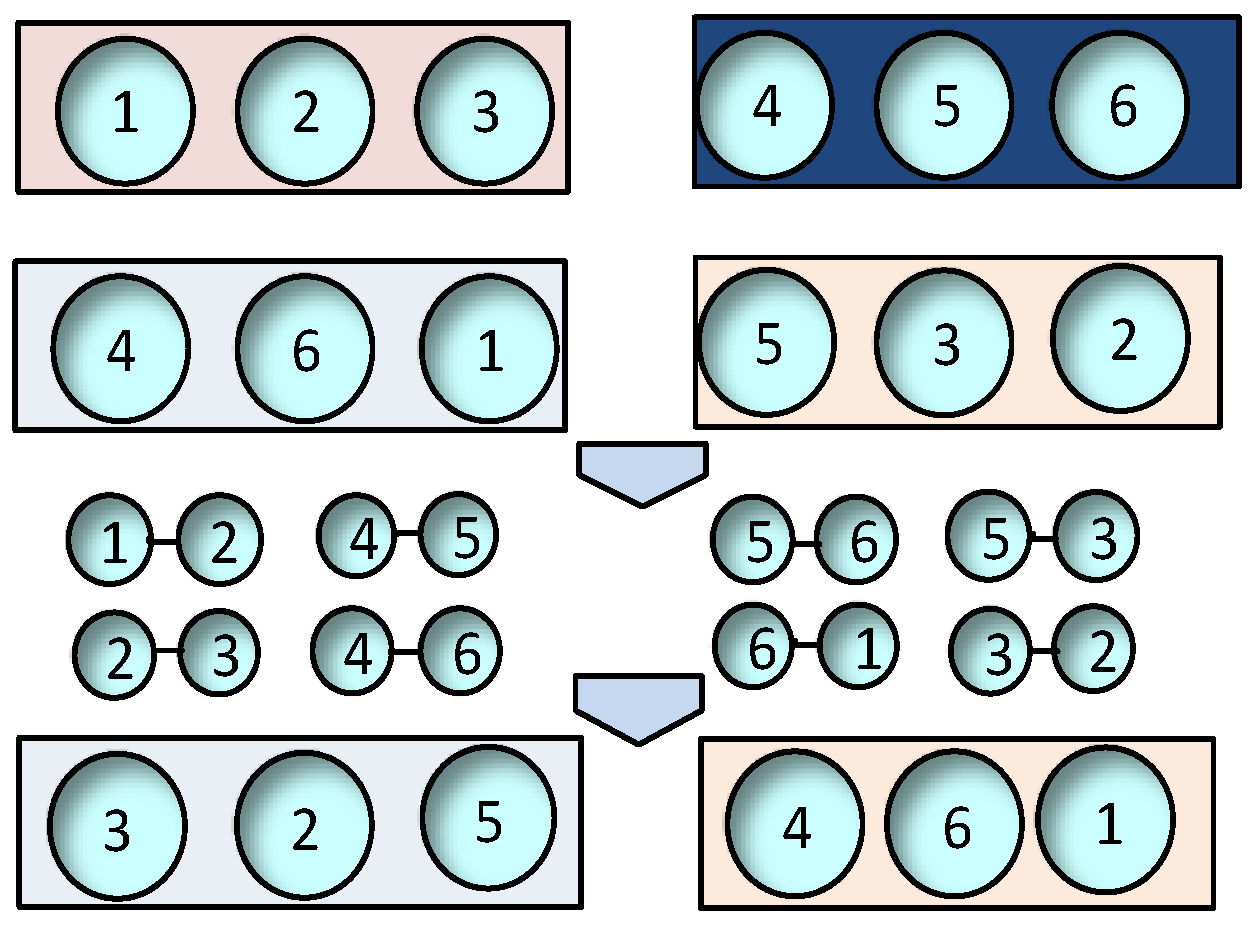
4.3. PC-EPGA Algorithm Cross-Operator
- Intra-chromosomal (IC): This category involves probabilistic chains within the same slave chromosome.
- Inter-chromosomal (XC): This category involves chains between different slave chromosomes.
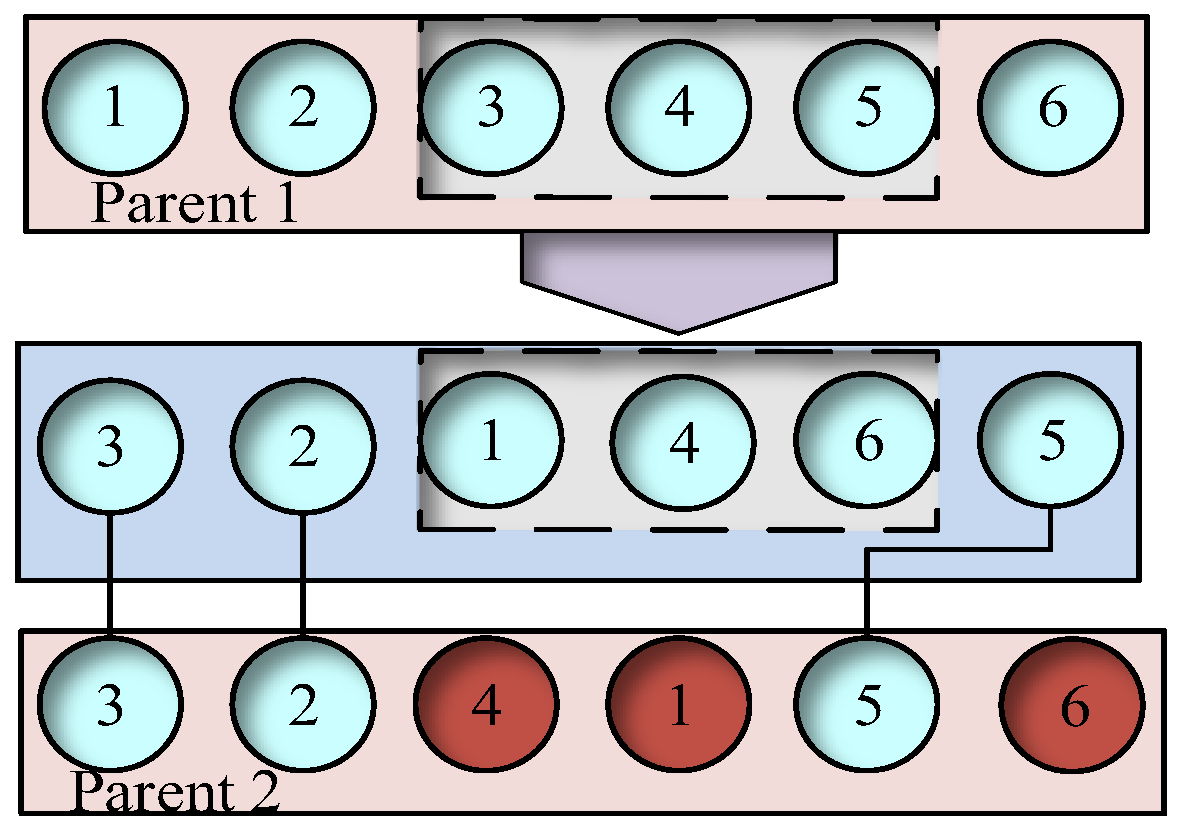
4.4. PC-EPGA Variation Operator
4.5. Bayesian Network Optimization Operator
4.6. Parallel Acceleration of Chained Genetic Algorithms
5. Simulation Experiment
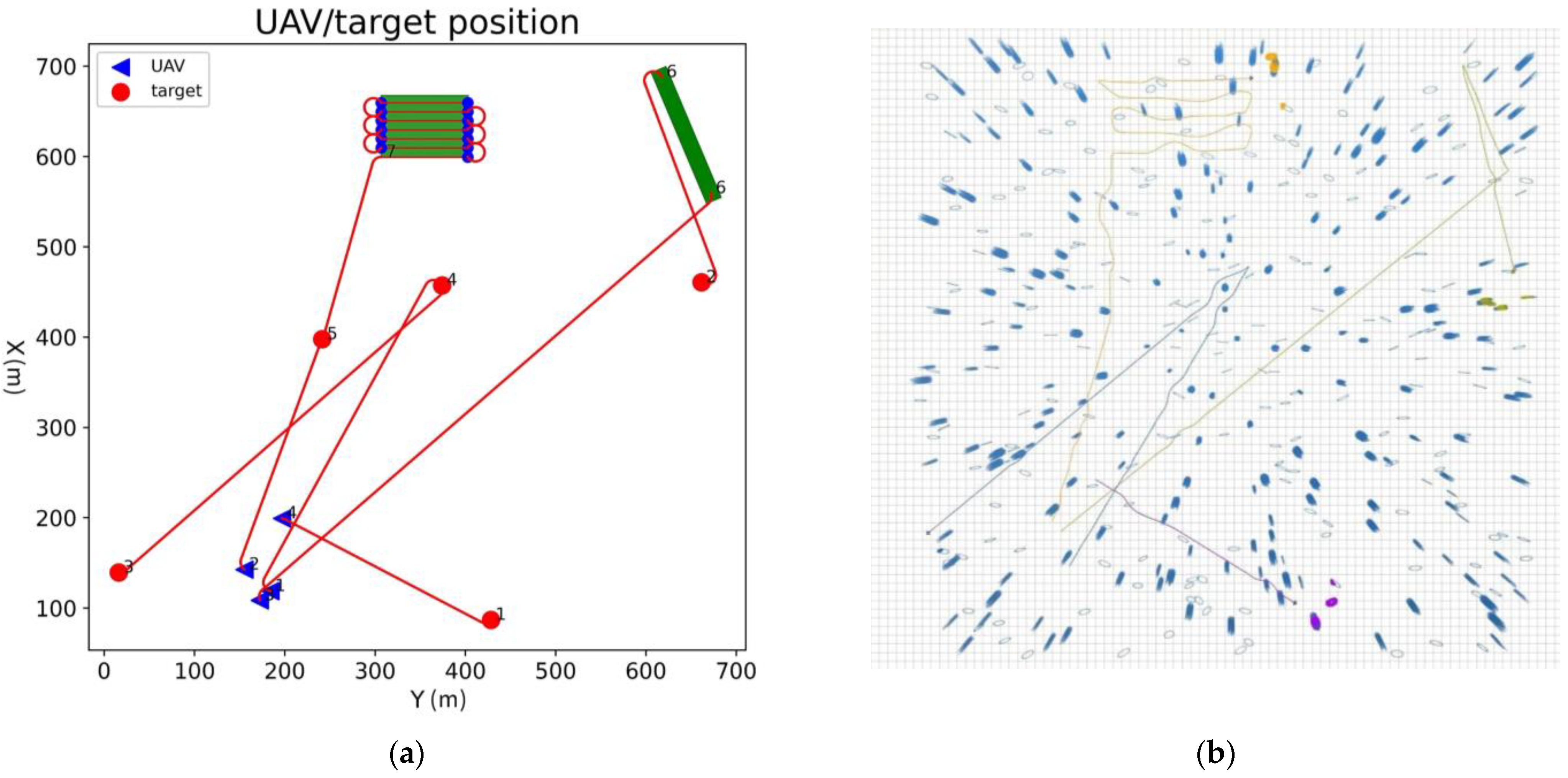
5.1. Simulation Environment
5.2. Comparative Experiment
5.2.1. Comparative Analysis of Solution Quality
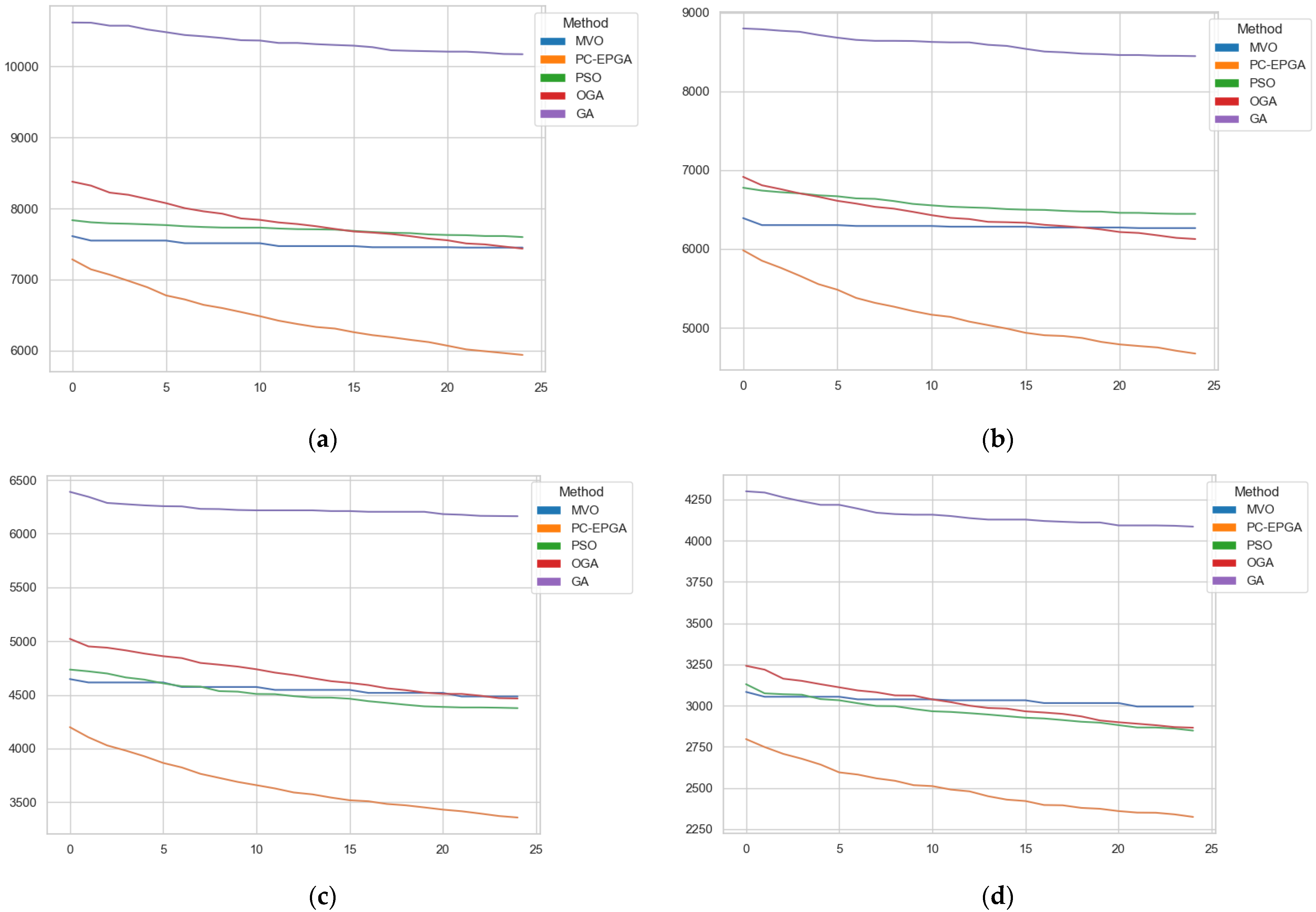
5.2.2. Comparative Analysis of Iterative Convergence Speed
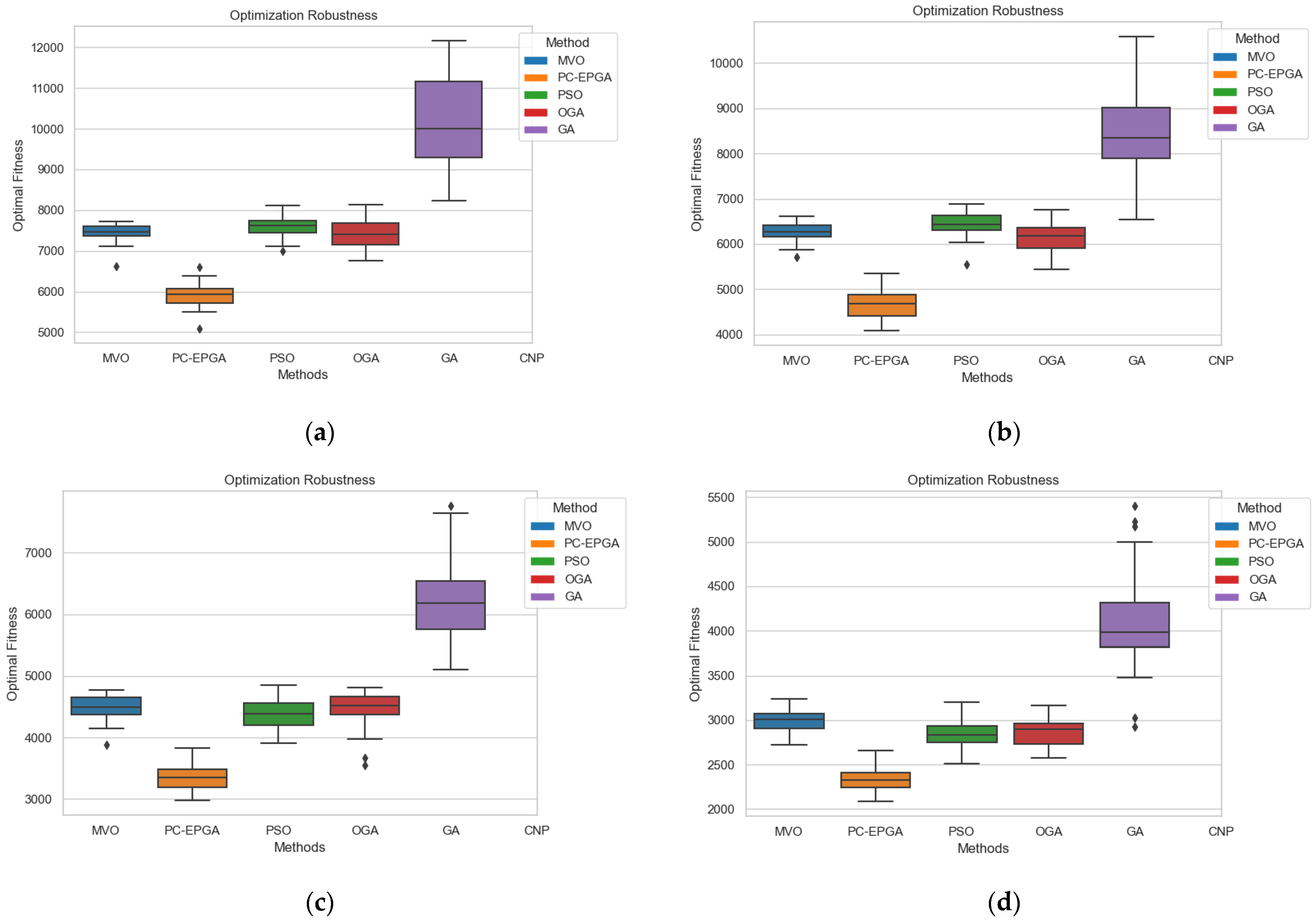
5.2.3. Comparative Assessment of Optimization Robustness
5.3. Ablation Study
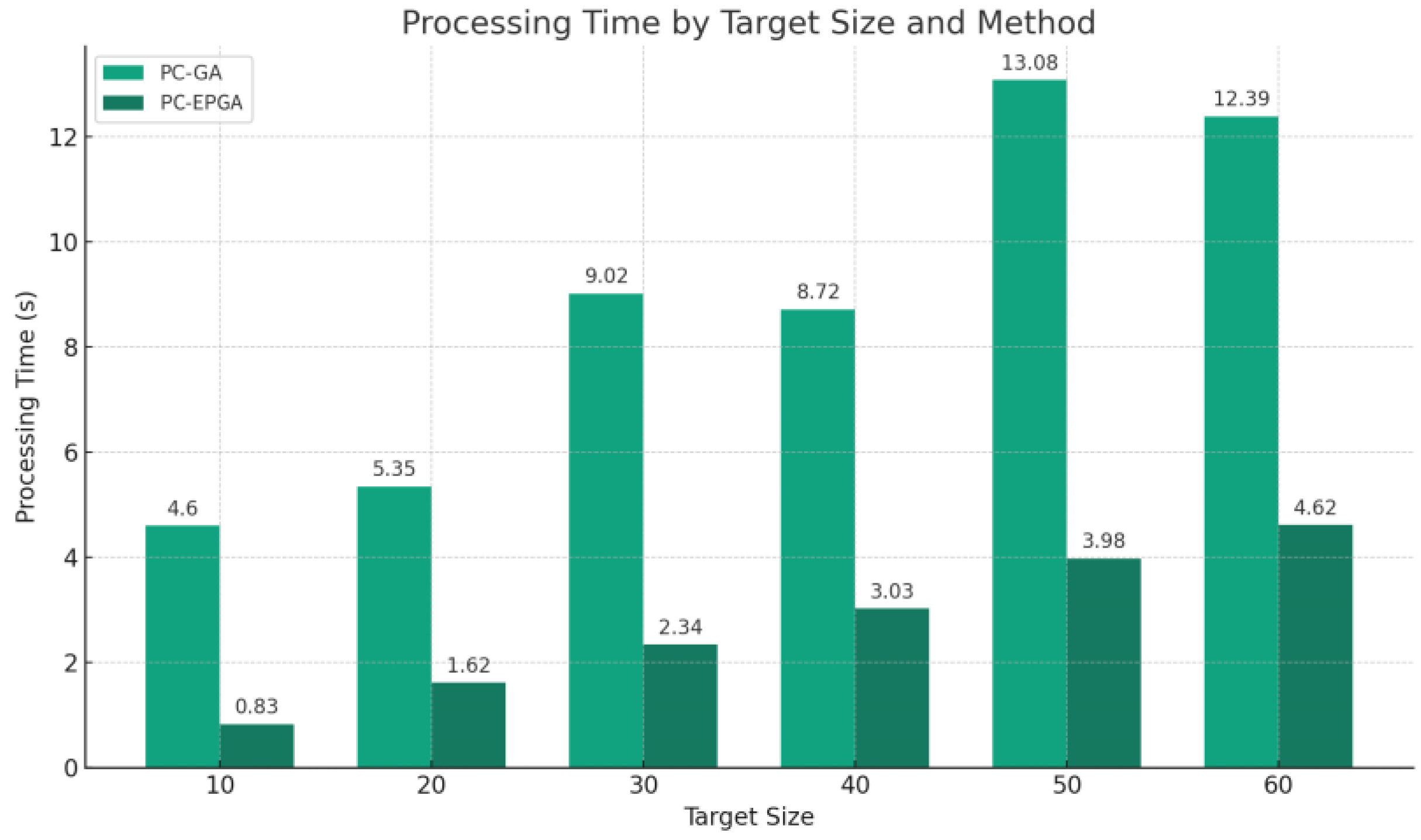
5.4. Parallel Acceleration Speed Improvement Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lou, W. Research on Obstacle Avoidance Control of Multiple UAV Formation Based on Genetic Algorithm. In Proceedings of the 6th International Conference on Computer Engineering, Information Science & Application Technology (ICCIA 2023), Hong Kong, China, 11–12 March 2023. [Google Scholar]
- Halder, S.; Ghosal, A.; Conti, M. Dynamic Super Round-Based Distributed Task Scheduling for UAV Networks. IEEE Trans. Wirel. Commun. 2023, 22, 1014–1028. [Google Scholar] [CrossRef]
- Kiliç, F.; Hardt, W. Low Latency Reliable Data Sharing Mechanism for UAV Swarm Tasks. In Proceedings of the International Symposium on Computer Science and Educational Technology, Tashkent, Uzbekistan, 24–26 October 2022. [Google Scholar]
- Liu, J.; Ji, N. A Bright Spot Detection and Analysis Method for Infrared Photovoltaic Panels Based on Image Processing. Front. Energy Res. 2022, 10, 978247. [Google Scholar] [CrossRef]
- McEnroe, P.; Wang, S.; Liyanage, M. A Survey on the Convergence of Edge Computing and AI for UAVs: Opportunities and Challenges. IEEE Internet Things J. 2022, 17, 15435–15459. [Google Scholar] [CrossRef]
- Zhang, R.; Dou, L.; Wang, Q.; Xin, B.; Ding, Y. Ability-Restricted Indoor Reconnaissance Task Planning for Multiple UAVs. Electronics 2022, 11, 4227. [Google Scholar] [CrossRef]
- Alazzam, H.; Alsmady, A.; Mardini, W. Solving Multiple Traveling Salesmen Problem Using Discrete Pigeon Inspired Optimizer. In Proceedings of the 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020; pp. 209–213. [Google Scholar]
- Bai, X.; Ye, Y.; Zhang, B.; Ge, S.S. Efficient Package Delivery Task Assignment for Truck and High Capacity Drone. IEEE Trans. Intell. Transp. Syst. 2023, 24, 13422–13435. [Google Scholar] [CrossRef]
- Salama, M. Hybrid Truck-UAV Systems for Last-Mile Delivery Logistics. Ph.D. Thesis, Industrial and Manufacturing Systems Engineering, University of Missouri, Columbia, MO, USA, 2022. [Google Scholar]
- Böther, W. What’s Wrong with Deep Learning in Tree Search for Combinatorial Optimization. arXiv 2022, arXiv:2201.10494v1. [Google Scholar]
- Vincent, T.; Seipp, F.; Ruzika, S. Multiple Objective Branch and Bound for Mixed 0–1 Linear Programming: Corrections and Improvements for the Biobjective Case. Comput. Oper. Res. 2013, 40, 498–509. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, Y.; He, H. Linear and Dynamic Programming Algorithms for Real-Time Task Scheduling with Task Duplication. J. Supercomput. 2019, 75, 494–509. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Liu, C.; Li, J. Task Assignment of UAV Swarms Based on Auction Algorithm in Poor Communication Environments. J. Adv. Comput. Intell. Intell. Inform. 2023, 27, 1142–1150. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, H.; Wu, G. A Dynamic Task Scheduling Method for Multiple UAVs Based on Contract Net Protocol. Sensors 2022, 22, 4486. [Google Scholar] [CrossRef]
- Gao, C.; Ma, J.; Li, T.; Shen, Y. Hybrid Swarm Intelligent Algorithm for Multi-UAV Formation Reconfiguration. J. Intell. Fuzzy Syst. 2022, 9, 1929–1962. [Google Scholar] [CrossRef]
- Geng, N.; Gong, D.W.; Zhang, Y. PSO-Based Robot Path Planning for Multisurvivor Rescue in Limited Survival Time. Math. Probl. Eng. 2014, 2014, 187370. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L. Improved Multi-Objective Particle Swarm Optimization Algorithm Based on Area Division with Application in Multi-UAV Task Assignment. IEEE Access 2023, 11, 123519–123530. [Google Scholar]
- Gong, D.W.; Zhang, Y.; Qi, C.L. Localising Odour Source Using Multi-Robot and Anemotaxis-Based Particle Swarm Optimisation. IET Control Theor. Appl. 2012, 6, 1661–1670. [Google Scholar] [CrossRef]
- Geng, N.; Chen, Z.; Nguyen, Q.A.; Gong, D. Particle Swarm Optimization Algorithm for the Optimization of Rescue Task Assignment with Uncertain Time Constraints. J. Intell. Fuzzy Syst. 2021, 7, 873–890. [Google Scholar]
- Cui, Y. An Improved Chaotic Self-Adapting Monkey Algorithm for Multi-UAV Task Assignment. IEEE J. Miniaturization Air Space Syst. 2023, 5, 9–15. [Google Scholar] [CrossRef]
- Su, W.W.; Gao, M.; Gao, X.; Xuan, Z. Collaborative Attack Task Assignment for Distributed UAV Swarm Using Competition Cooperation Mechanism. In Proceedings of the 3rd International Conference on Advanced Algorithms and Signal Image Processing (AASIP 2023), Kuala Lumpur, Malaysia, 30 June–2 July 2023. [Google Scholar]
- Wang, K.; Zhang, X.; Qiao, X.; Li, X.; Cheng, W.; Cong, Y.; Liu, K. Adjustable Fully Adaptive Cross-Entropy Algorithms for Task Assignment of Multi-UAVs. Drones 2023, 7, 204. [Google Scholar] [CrossRef]
- Wubben, J.; Hernández, D.; Cecilia, J.M.; Imberon, B.; Calafate, C.; Cano, J.-C.; Manzoni, P.; Toh, C. Assignment and Take-Off Approaches for Large-Scale Autonomous UAV Swarms. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4836–4847. [Google Scholar] [CrossRef]
- Zhang, R.; Feng, Y.; Yang, Y.; Li, X. A Deadlock-Free Hybrid Estimation of Distribution Algorithm for Cooperative Multi-UAV Task Assignment with Temporally Coupled Constraints. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3329–3344. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, X. Multi-UAVs Cooperative Reconnaissance Task Assignment under Heterogeneous Target Values. IEEE Access 2022, 10, 70955–70963. [Google Scholar] [CrossRef]
- Gao, S.; Wu, J. Multi-UAV Reconnaissance Task Assignment for Heterogeneous Targets Using Grouping Ant Colony Optimization Algorithm. Soft Comput. 2021, 25, 7155–7167. [Google Scholar] [CrossRef]
- Edison, E.; Shima, T. Integrated Task Assignment and Path Optimization for Cooperating Uninhabited Aerial Vehicles Using Genetic Algorithms. Comput. Oper. Res. 2011, 38, 340–356. [Google Scholar] [CrossRef]
- Deng, Q.B.; Yu, J.Q.; Wang, N.F. Cooperative Task Assignment of Multiple Heterogeneous Unmanned Aerial Vehicles Using a Modified Genetic Algorithm with Multi-Type Genes. Chin. J. Aeronaut. 2013, 26, 1238–1250. [Google Scholar] [CrossRef]
- Wang, Z.; Li, L.; Long, T.; Wen, Y. Multi-UAV Reconnaissance Task Assignment for Heterogeneous Targets Using an Opposition-Based Genetic Algorithm with Double-Chromosome Encoding. Chin. J. Aeronaut. 2018, 31, 339–350. [Google Scholar] [CrossRef]
- Savla, K.; Frazzoli, E.; Bullo, F. Traveling Salesperson Problems for the Dubins Vehicle. IEEE Trans. Autom. Control 2008, 53, 1378–1391. [Google Scholar] [CrossRef]
- Cui, Y.; Dong, W.; Hu, D. The Application of Improved Harmony Search Algorithm to Multi-UAV Task Assignment. Electronics 2022, 11, 1171. [Google Scholar] [CrossRef]
- Larranaga, P.; Kuijpers, C.M.H.; Murga, R.H.; Inza, I.; Dizdarevic, S. Genetic Algorithms for the Travelling Salesman Problem: A Review of Representations and Operators. Artif. Intell. Rev. 1999, 13, 129–170. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; pp. 2546–2554. [Google Scholar]
- Davis, L. Applying Adaptive Algorithms to Epistatic Domains. In Proceedings of the 9th International Joint Conference on Artificial Intelligence, Los Angeles, CA, USA, 18–23 August 1985; pp. 162–164. [Google Scholar]
- Nguyen, V. Bayesian Optimization for Accelerating Hyper-Parameter Tuning. In Proceedings of the IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), Sardinia, Italy, 3–5 June 2019; pp. 302–305. [Google Scholar]
- Rana, S.; Li, C.; Gupta, S.; Nguyen, V.; Venkatesh, S. High Dimensional Bayesian Optimization with Elastic Gaussian Process. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 2883–2891. [Google Scholar]



| Probabilistic Chain Parallel Accelerated Genetic Algorithm |
| Create chromosome populations For I in generation: Populations sorted by fitness cluster compute For chromo in population: Obtain probabilistic chains If crossover: Determine intersections based on probabilistic chain adaptive crossover If mutation: The master chromosome and slave chromosome are mutated paired with each other to select the best solution to retain Obtain the optimal solution |
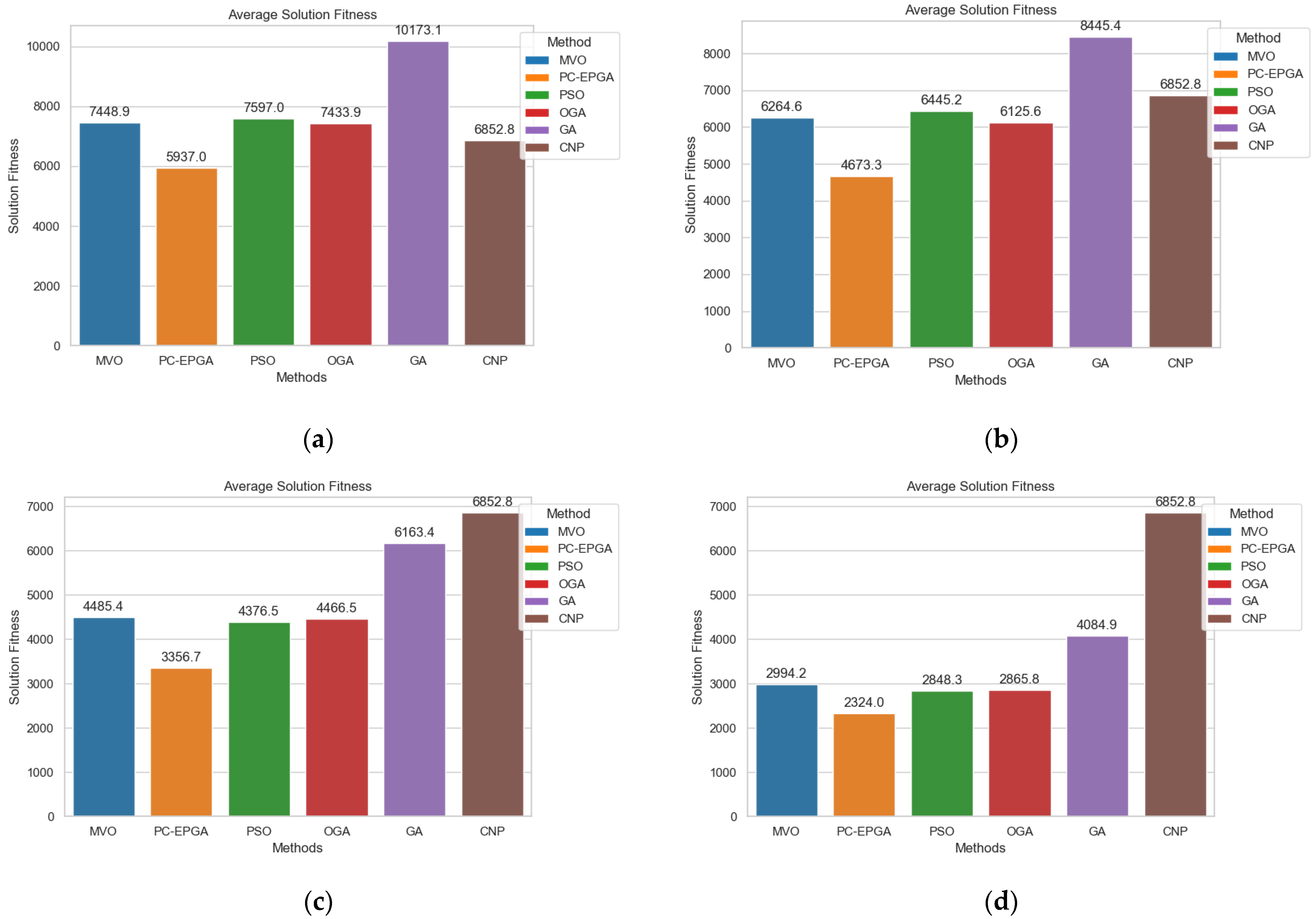
| Algorithm | TAPSO [17] | OGA [29] | GA | CNP [19] | MVO [25] | PC-EPGA | |
|---|---|---|---|---|---|---|---|
| Targetnum | |||||||
| 20 | 2848.28 | 2865.78 | 4084.93 | 6852.75 | 2994.24 | 2324.02 | |
| 30 | 4376.48 | 4466.49 | 6163.37 | 7616.26 | 4485.42 | 3356.73 | |
| 40 | 6445.21 | 6125.61 | 8445.39 | 8217.35 | 6264.58 | 4673.29 | |
| 50 | 7596.97 | 7433.87 | 10,173.13 | 12,611.20 | 7448.93 | 5937.03 | |
| Algorithm | TAPSO | OGA | GA | CNP | MVO | PC-EPGA | |
|---|---|---|---|---|---|---|---|
| Targetnum | |||||||
| 20 | 182.02 | 232.63 | 499.81 | - | 159.84 | 164.97 | |
| 30 | 364.97 | 295.64 | 775.40 | - | 279.96 | 302.42 | |
| 40 | 335.08 | 465.31 | 1125.50 | - | 242.16 | 469.81 | |
| 50 | 281.33 | 520.12 | 1861.62 | - | 242.60 | 343.73 | |
| Probabilistic Chain | PMX Cross-Operator | ER Cross-Operator | OX Cross-Operator | ADAPTIVE Cross-Operator | 20 Tasks | 30 Tasks | 40 Tasks | 50 Tasks | |
|---|---|---|---|---|---|---|---|---|---|
| A | 4084.93 | 6163.37 | 8445.39 | 10,173.13 | |||||
| B | √ | √ | 2412.51 | 3454.84 | 4860.81 | 6277.29 | |||
| C | √ | √ | 2516.58 | 3643.51 | 5200.57 | 6418.65 | |||
| D | √ | √ | 2430.25 | 3546.51 | 5105.67 | 6288.34 | |||
| E | √ | √ | 2324.02 | 3356.73 | 4673.29 | 5937.03 |
| Probabilistic Chain | PMX Cross-Operator | ER Cross-Operator | OX Cross-Operator | ADAPTIVE Cross-Operator | 20 Tasks | 30 Tasks | 40 Tasks | 50 Tasks | |
|---|---|---|---|---|---|---|---|---|---|
| A | 499.84 | 775.40 | 1125.50 | 1861.62 | |||||
| B | √ | √ | 144.09 | 256.30 | 419.34 | 471.30 | |||
| C | √ | √ | 131.06 | 316.42 | 492.30 | 340.54 | |||
| D | √ | √ | 182.67 | 407.18 | 276.85 | 568.04 | |||
| E | √ | √ | 164.97 | 302.42 | 469.81 | 343.73 |
| Target Size | 10 | 20 | 30 | 40 | 50 | 60 |
|---|---|---|---|---|---|---|
| PC-GA | 4.60 s | 5.35 s | 9.02 s | 8.72 s | 13.08 s | 12.39 s |
| PC-EPGA | 0.83 s | 1.62 s | 2.34 s | 3.03 s | 3.98 s | 4.62 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Liu, D.; Wang, Q.; Li, J.; Sun, J. Probabilistic Chain-Enhanced Parallel Genetic Algorithm for UAV Reconnaissance Task Assignment. Drones 2024, 8, 213. https://doi.org/10.3390/drones8060213
Tang J, Liu D, Wang Q, Li J, Sun J. Probabilistic Chain-Enhanced Parallel Genetic Algorithm for UAV Reconnaissance Task Assignment. Drones. 2024; 8(6):213. https://doi.org/10.3390/drones8060213
Chicago/Turabian StyleTang, Jiaze, Dan Liu, Qisong Wang, Junbao Li, and Jinwei Sun. 2024. "Probabilistic Chain-Enhanced Parallel Genetic Algorithm for UAV Reconnaissance Task Assignment" Drones 8, no. 6: 213. https://doi.org/10.3390/drones8060213
APA StyleTang, J., Liu, D., Wang, Q., Li, J., & Sun, J. (2024). Probabilistic Chain-Enhanced Parallel Genetic Algorithm for UAV Reconnaissance Task Assignment. Drones, 8(6), 213. https://doi.org/10.3390/drones8060213







