Co-Evolutionary Algorithm-Based Multi-Unmanned Aerial Vehicle Cooperative Path Planning
Abstract
:1. Introduction
- (1)
- Considering the collaborative relationship between multiple unmanned aerial vehicles, the constrained optimization model is established for the multi-UAV collaborative path planning problem.
- (2)
- A co-evolutionary optimization framework is provided to tackle the multi-UAV cooperative path planning problem. The co-evolutionary algorithm reduces the complexity of the multi-UAV collaborative path planning problem through decomposition.
- (3)
- Two information-sharing strategies are designed with the global optimal and local optimal information. The two strategies guide the search direction of the population to the potential optimal solutions with the purpose of quickly finding the optimum solution and improving the efficiency of the proposed algorithm.
2. Cooperative Path Planning Problem Analysis and Modeling
2.1. Objective Function
2.2. Constraints
- A.
- UAV flight constraints
- (1)
- Minimum turning radius constraint:
- (2)
- Minimum path segment length constraint:
- (3)
- Maximum path slope angle constraint
- (4)
- Minimum ground clearance constraint:
- B.
- UAV cooperative constraints
3. Co-Evolutionary Algorithm-Based Multi-UAV Cooperative Path Planning Algorithm
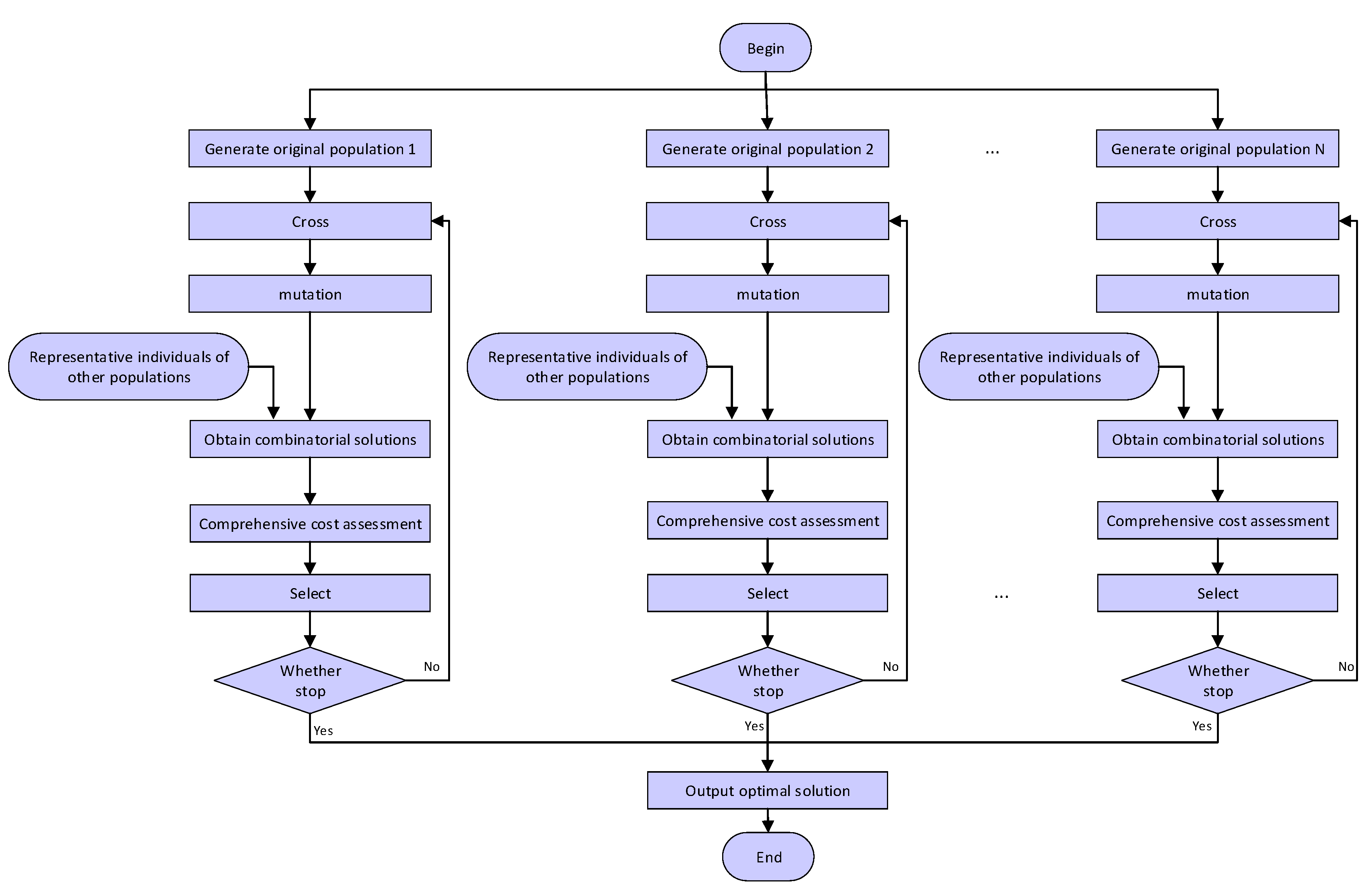
3.1. Overall Algorithm Framework Design
3.2. Constraint Processing and Comprehensive Cost of Cooperative Paths
- (1)
- Time cooperative violation
- (2)
- Spatial cooperative violation
- (3)
- UAV flight constraint violation
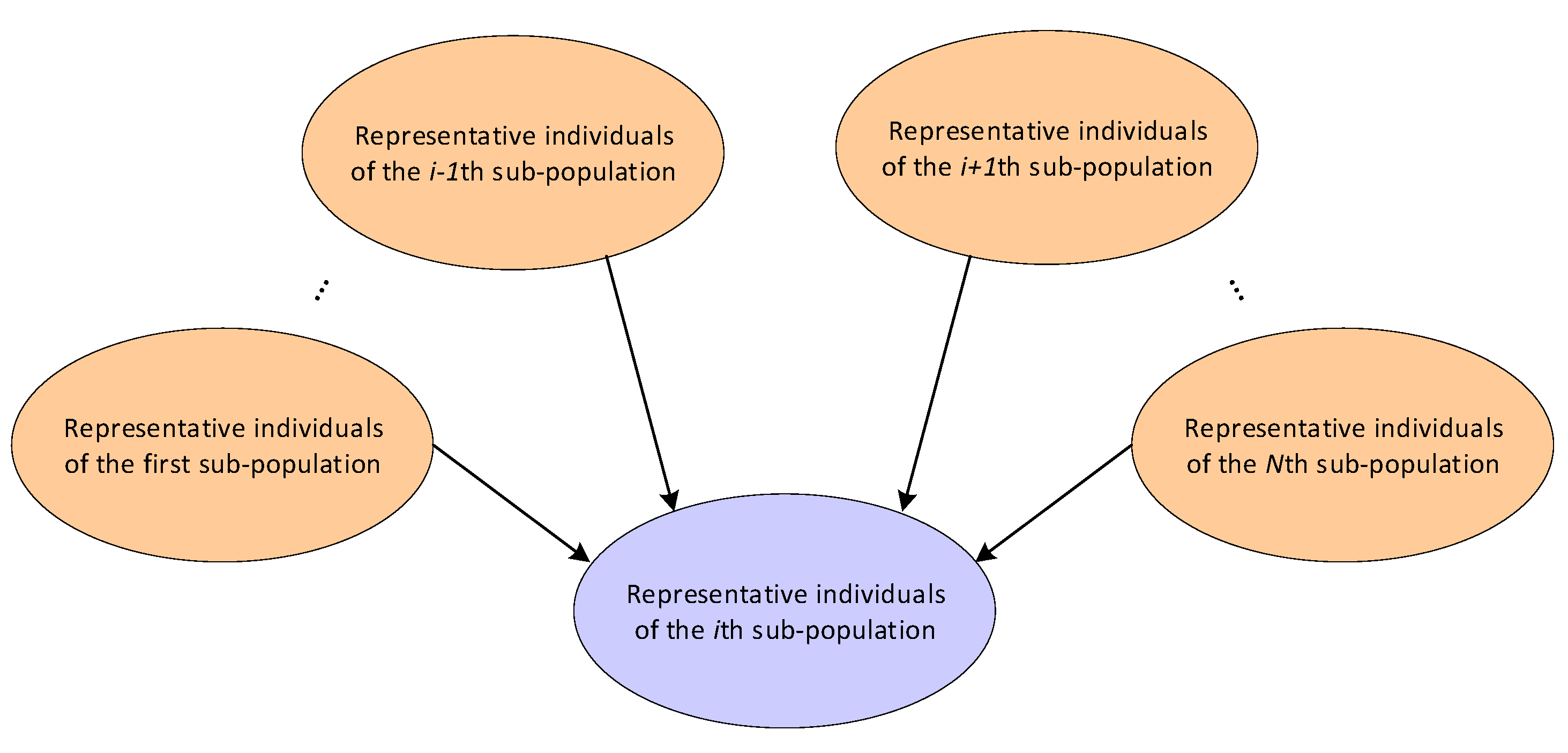
3.3. Information Sharing Methods Design
- (1)
- Best individual selection method (recorded as Bs-): Select the individual with the best overall cost () for each sub-population as the representative individual for information exchange, which has the advantage of retaining the optimal combination.
- (2)
- Mass selection method (recorded as Hs-): Select the individual with the best comprehensive cost () for each sub-population and the individual with the best single machine path cost () for each sub-population as representative individuals. Compared with Bs -, the selection of representative individuals has been added to enhance the search for the smallest neighborhood of a single UAV path.
3.4. Co-Evolutionary Algorithm-Based Multi-UAV Cooperative Path Planning Algorithm (CCEA-CPP)
| Algorithm 1. Pseudo-code of co-evolutionary algorithm-based multi-UAV cooperative path planning algorithm (CCEA-CPP). |
| Begin For each path planning subproblem //Generate initial sub-populations of paths for each UAV End ;//individual While termination criteria not satisfied//If the termination condition is not met, loop continuously For each path planning subproblem //Obtaining combinatorial solutions //According to Equations (10)–(13), calculate the constraint violation and comprehensive cost //Selecting the next-generation population //select representative individuals with Bs- or Hs- methods and update B End End End |
4. Simulation Studies
4.1. Environmental and Parametric
4.2. Algorithm Analysis
- (1)
- Analysis of simulation results for five-UAV cooperative path planning
- (2)
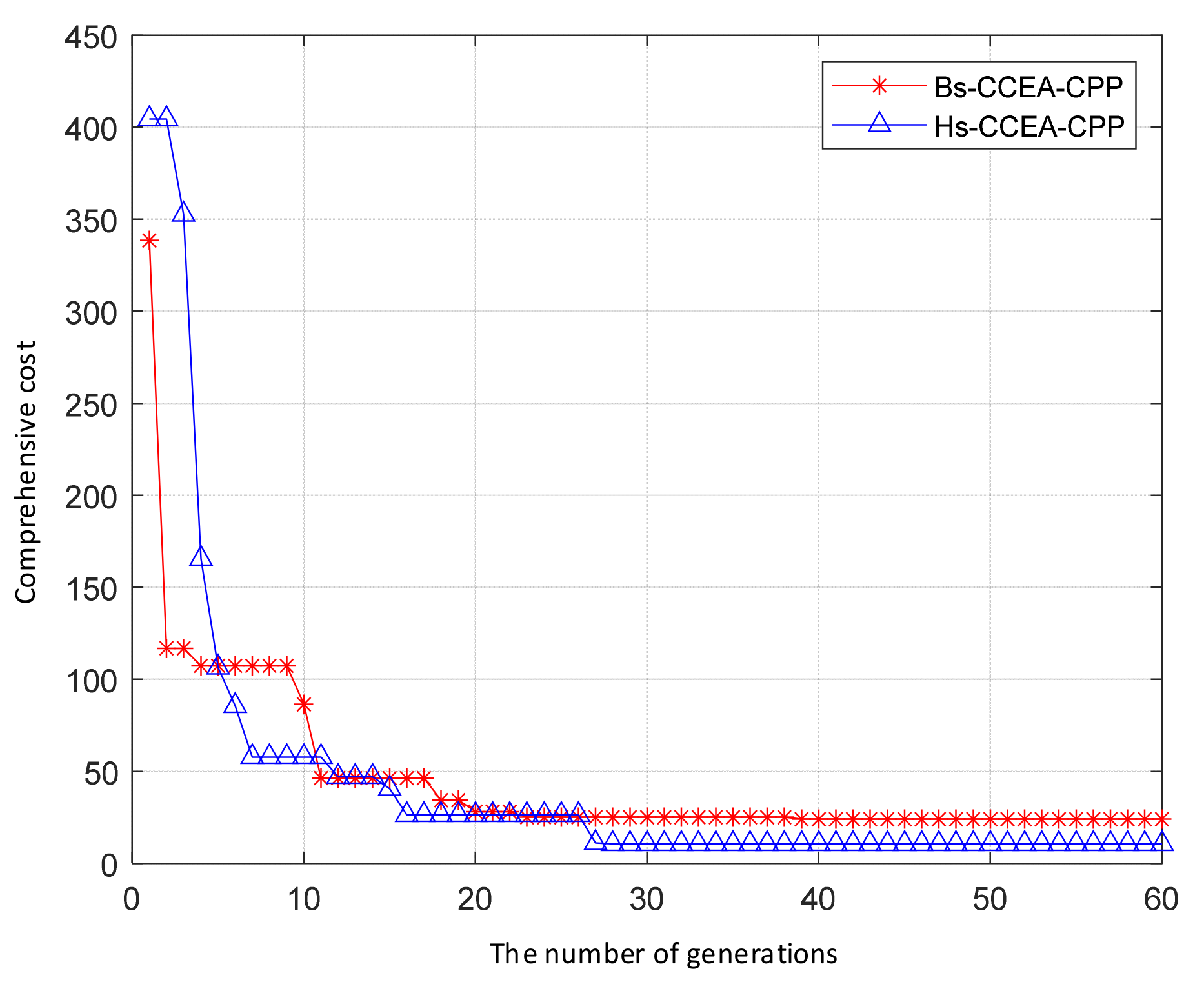
- Simulation verification of algorithm convergence stability
- (3)
- Analysis of cooperative constraints
- (4)
- Compared experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, H.; Xin, B.; Dou, L.H.; Chen, J.; Hirota, K. A review of cooperative path planning of an unmanned aerial vehicle group. Front. Inf. Technol. Electron. Eng. 2020, 21, 1671–1694. [Google Scholar] [CrossRef]
- Kent, T.; Richards, A.; Johnson, A. Homogeneous Agent Behaviours for the Multi-Agent Simultaneous Searching and Routing Problem. Drones 2022, 6, 51. [Google Scholar] [CrossRef]
- Xiong, T.; Liu, F.; Liu, H.; Ge, J.; Li, H.; Ding, K.; Li, Q. Multi-Drone Optimal Mission Assignment and 3D Path Planning for Disaster Rescue. Drones 2023, 7, 394. [Google Scholar] [CrossRef]
- Ma, X.L.; Li, X.D.; Zhang, Q.F.; Tang, K.; Liang, Z.P.; Xie, W.X.; Zhu, Z.X. A survey on cooperative Co-Evolutionary algorithms. IEEE Trans. Evol. Comput. 2019, 23, 421–441. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, P.; Li, X.; Zhang, K. Multi objective optimization algorithm based cooperative path planning of Multi-UAV. Syst. Eng. Electron. Technol. 2017, 39, 782–787. [Google Scholar]
- Madridano, Á.; Al-Kaff, A.; Martín, D.; de la Escalera, A. Trajectory planning for multi-robot systems: Methods and applications. Expert Syst. Appl. 2021, 173, 114660. [Google Scholar] [CrossRef]
- Wang, H.; Chen, W. Multi-Robot Path Planning with Due Times. IEEE Robot. Autom. Lett. 2022, 7, 4829–4836. [Google Scholar] [CrossRef]
- An, S.; Park, M.; Oh, H. Receding-horizon RRT-Infotaxis for autonomous source search in urban environments. Aerosp. Sci. Technol. 2022, 120, 107276. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, F.; Cai, S. Cluster Genetic based multi-UAV path planning. Fire Command. Control 2011, 36, 163–166+170. [Google Scholar]
- Zheng, C.; Ding, M.; Zhou, C.; Su, K.; Yuan, H.; Kim, R. Multi vehicle coordinated route planning method. J. Astronaut. Astronaut. 2003, 2, 115–120. [Google Scholar]
- Nikolos, I.K.; Brintaki, A.N. Coordinated UAV path planning using differential evolution. In Proceedings of the 2005 IEEE International Symposium on, Mediterrean Conference on Control and Automation Intelligent Control, Limassol, Cyprus, 27–29 June 2005; pp. 549–556. [Google Scholar]
- Wang, Z. Research on Key Technologies of Multi-UAV Cooperative Planning and Control; Beijing Institute of Technology: Beijing, China, 2017. [Google Scholar]
- Xiao, Z.; Yuan, D.; Qu, Y. A~* fixed length search algorithm based cooperative multiple-UAVs path planning. Aircr. Flight Mech. 2012, 30, 92–96. [Google Scholar]
- Yang, Z.; Fang, Z.; Li, P. Bio-Inspired Collision-Free 4D Trajectory Generation for UAVs Using Tau Strategy. J. Bionic Eng. 2016, 13, 84–97. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, X.; Shan, Y.; Zhao, Y.; Cui, N. Improved particle swarm optimization algorithm based collaborative path planning of aircraft. J. Autom. 2022, 48, 2670–2676. [Google Scholar]
- Lu, J. Research on Multi Aircraft Cooperative Penetration Path Planning Method Based on Improved Ant Colony Optimization Algorithms; National University of Defense Science and Technology: Changsha, China, 2011. [Google Scholar]
- Huang, L.; Qu, H.; Ji, P.; Liu, X.; Fan, Z. A novel coordinated path planning method using k-degree smoothing for multi-UAVs. Appl. Soft Comput. 2016, 48, 182–192. [Google Scholar] [CrossRef]
- Sun, J.Y.; Tang, J.; Lao, S.Y. Collision avoidance for cooperative UAVs with optimized artificial potential field algorithm. IEEE Access 2017, 5, 18382–18390. [Google Scholar] [CrossRef]
- Shao, Z.; Yan, F.; Zhou, Z.; Zhu, X. Path planning for multi-UAV formation rendezvous based on distributed cooperative particle swarm optimization. Appl. Sci. 2019, 9, 2621. [Google Scholar] [CrossRef]
- Zhang, D.F.; Duan, H.B. Social-class pigeon-inspired optimization and time stamp segmentation for multi-UAV cooperative path planning. Neurocomputing 2018, 313, 229–246. [Google Scholar] [CrossRef]
- Ma, P.; Mao, Y.; Zhang, H.; Su, X. 3DSAS based cooperative planning and search method for multiple constraints and multiple Tracks. Syst. Eng. Electron. Technol. 2011, 33, 1527–1533. [Google Scholar]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, J.; Mei, Y.; Zhang, S.; Ai, X.; Jia, Z. Trajectory optimization of multiple quad-rotor UAVs in collaborative assembling task. Chin. J. Aeronaut. 2016, 29, 184–201. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.J.; Zhang, Y.; Guan, X. Collision free 4D path planning for multiple UAVs based on spatial refined voting mechanism and PSO approach. Chin. J. Aeronaut. 2019, 32, 1504–1519. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Long, T. Minimum-time trajectory planning for multi-unmanned-aerial-vehicle cooperation using sequential convex programming. J. Guid. Control Dyn. 2017, 40, 2972–2978. [Google Scholar] [CrossRef]
- Radmanesh, M.; Kumar, M.; Sarim, M. Grey wolf optimization based sense and avoid algorithm in a Bayesian framework for multiple UAV path planning in an uncertain environment. Aerosp. Sci. Technol. 2018, 77, 168–179. [Google Scholar] [CrossRef]
- Skorobogatov, G.; Barrado, C.; Salamì, E. Multiple UAV systems: A survey. Unmanned Syst. 2020, 8, 149–169. [Google Scholar] [CrossRef]
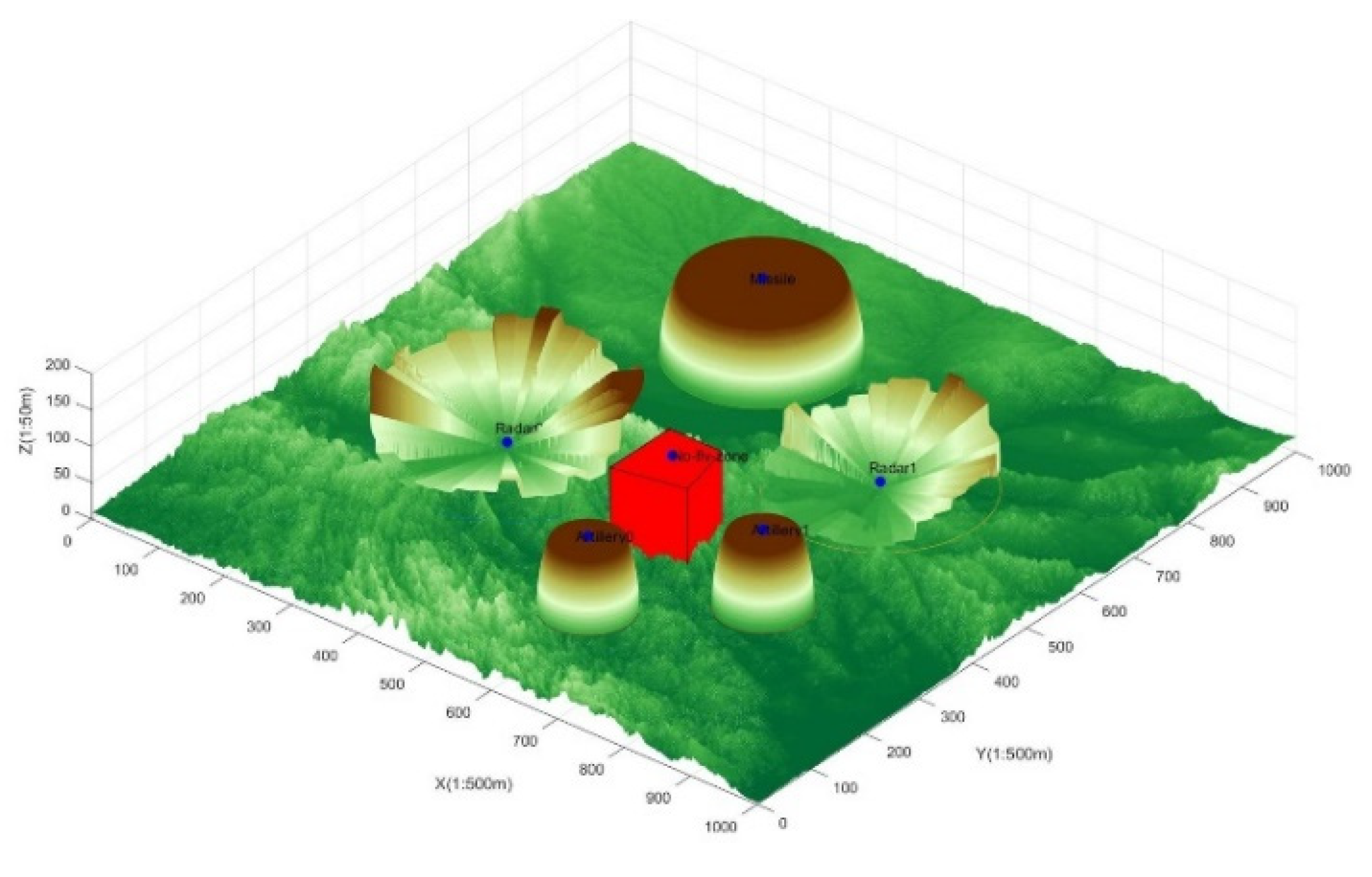



| Type of Threat | Attributes | ||
|---|---|---|---|
| Radar Number | Coordinates | Radius | |
| Air defense | radar 0 | (300, 400, 20) | 80 km |
| radar | radar 1 | (700, 600, 25) | 70 km |
| Surface-to-air | Missile Number | Coordinates | Radius |
| missile | missile 0 | (400, 750, 20) | 60 km |
| Anti-aircraft | Artillery Number | Coordinates | Radius |
| artillery | artillery 0 | (600, 180, 25) | 30 km |
| artillery 1 | (750, 320, 20) | 30 km | |
| No-fly zone | p1 = (520, 320); | Vertex Coordinates | p2 = (620, 340); |
| p3 = (600, 430); | p4 = (520, 430); |
| Parameter | Value |
|---|---|
| Minimum path segment length constraints | 50 |
| Maximum path slope angle constraint | 10 |
| Minimum ground clearance constraint | 10 |
| Minimum turning radius constraint | 85 |
| Penalty factor | 0.2 |
| Penalty factor | 1 |
| Algorithm Type | Flight Track Length/km | Cooperative Arrival Time Window/h | Spatial Cooperative Relationship |
|---|---|---|---|
| Hs-CCEA-CPP | D0: 499.18 D1: 499.09 D2: 479.18 D3: 479.81 D4: 484.20 | (1.597, 2.496) | meet |
| Hs-CCEA-CPP | D0: 501.14 D1: 501.01 D2: 492.15 D3: 498.88 D4: 490.20 | (1.593, 2.451) | meet |
| Algorithm Type | Maximum Value | Minimum Value | Average Value | Variance |
|---|---|---|---|---|
| Bs-CCEA-CPP | 21.6830 | 5.1230 | 11.2546 | 14.2146 |
| Hs-CCEA-CPP | 12.5050 | 3.5160 | 5.3216 | 10.4141 |
| Algorithm Type | Non-Zero Occurrences of Spatial Cooperative Violations | Success Rate of Spatial Collaboration |
|---|---|---|
| Bs-CCEA-CPP | 2 | 93.3% |
| Hs-CCEA-CPP | 0 | 100% |
| Algorithm Type | Maximum Time Window Length | Minimum Time Window Length | Number of Occurrences of Empty Sets | Success Rate of Time Collaboration |
|---|---|---|---|---|
| Bs-CCEA-CPP | 0.7551 | 0.5570 | 0 | 100% |
| Hs-CCEA-CPP | 0.7545 | 0.5970 | 0 | 100% |
| Algorithm Type | Maximum Value | Minimum Value | Average Value | Variance |
|---|---|---|---|---|
| GA | 178.1610 | 59.6750 | 151.6780 | 550.0395 |
| Ra-CCEA | 37.1960 | 8.4930 | 25.3129 | 57.8910 |
| Bs-CCEA-CPP | 21.6830 | 5.1230 | 11.2546 | 14.2146 |
| Hs-CCEA-CPP | 12.5050 | 3.5160 | 5.3216 | 10.4141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Nie, M.; Ma, X.; Guo, Y.; Liu, X. Co-Evolutionary Algorithm-Based Multi-Unmanned Aerial Vehicle Cooperative Path Planning. Drones 2023, 7, 606. https://doi.org/10.3390/drones7100606
Wu Y, Nie M, Ma X, Guo Y, Liu X. Co-Evolutionary Algorithm-Based Multi-Unmanned Aerial Vehicle Cooperative Path Planning. Drones. 2023; 7(10):606. https://doi.org/10.3390/drones7100606
Chicago/Turabian StyleWu, Yan, Mingtao Nie, Xiaolei Ma, Yicong Guo, and Xiaoxiong Liu. 2023. "Co-Evolutionary Algorithm-Based Multi-Unmanned Aerial Vehicle Cooperative Path Planning" Drones 7, no. 10: 606. https://doi.org/10.3390/drones7100606
APA StyleWu, Y., Nie, M., Ma, X., Guo, Y., & Liu, X. (2023). Co-Evolutionary Algorithm-Based Multi-Unmanned Aerial Vehicle Cooperative Path Planning. Drones, 7(10), 606. https://doi.org/10.3390/drones7100606






