Go with the Flow: Estimating Wind Using Uncrewed Aircraft
Abstract
:1. Introduction
1.1. Paper Organization
1.2. Broad Survey of Wind Estimation Methods
2. Literature Review
2.1. Approach 1: Direct Flow Measurement Using On-Board Flow Sensors
2.1.1. Pressure-Based Pitot Tubes or MHPPs
2.1.2. Ultrasonic Anemometers

2.1.3. Mounting and Flight Considerations
2.2. Approach 2: Thrust and Drag Force Estimation While Rejecting Wind
2.2.1. Classical Dynamic Modeling Approach
2.2.2. Machine Learning Method
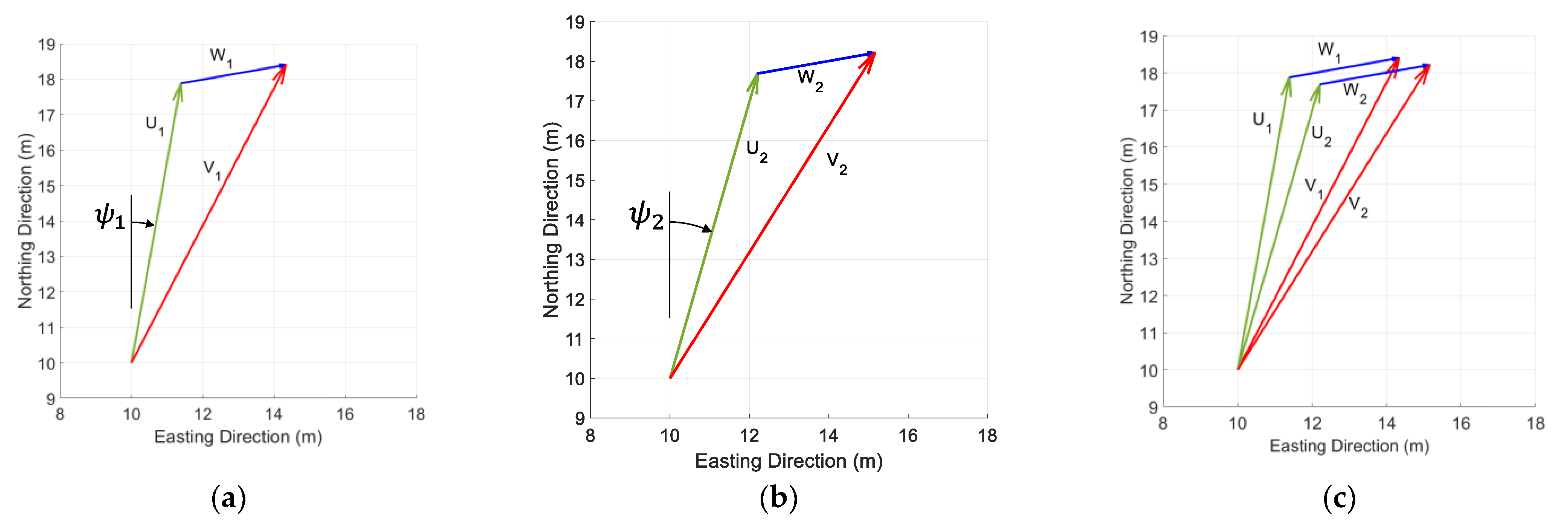
3. The Wind-Arc Method: Go with the Flow
3.1. Wind-Arc Derivation
3.2. Alias and Alibi Transformations
4. Results in Simulation
4.1. Coordinate Frames for Vehicle Dynamics and the Wind Triangle

4.2. Computing Vehicle Position Using the Wind Triangle
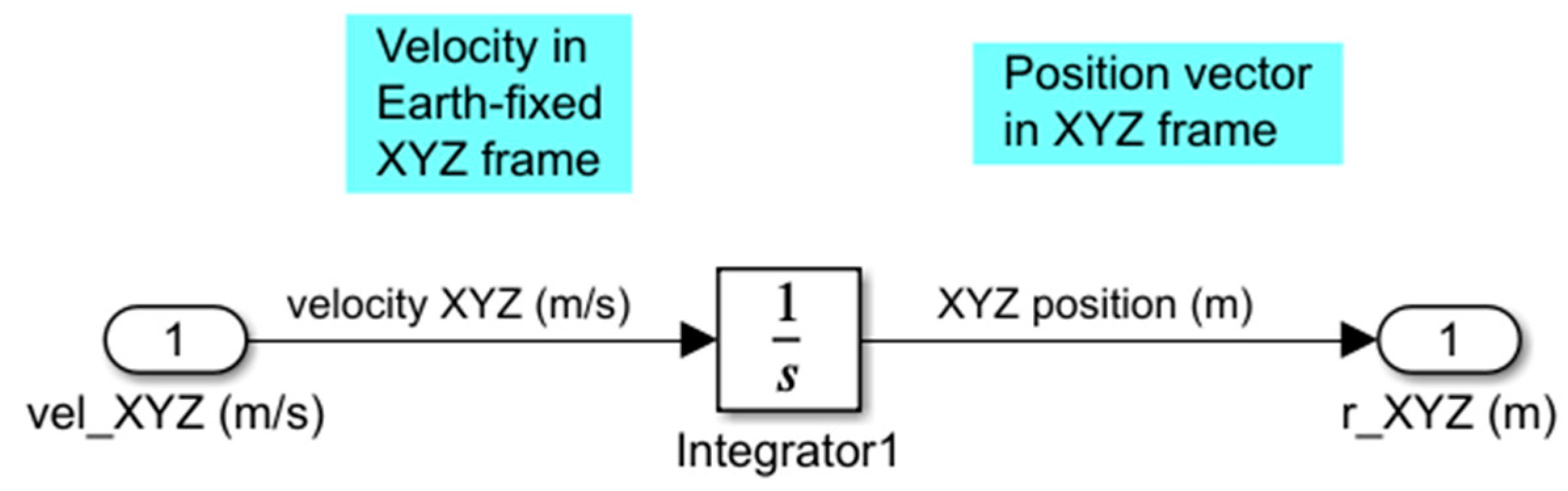
4.2.1. Standard Method for Computing Vehicle Position without Wind
- Transform the body-fixed velocity, , to velocity in the inertial or Earth-fixed frame, .
- Integrate the Earth-fixed velocity, , to achieve position in the Earth-fixed or NED frame:
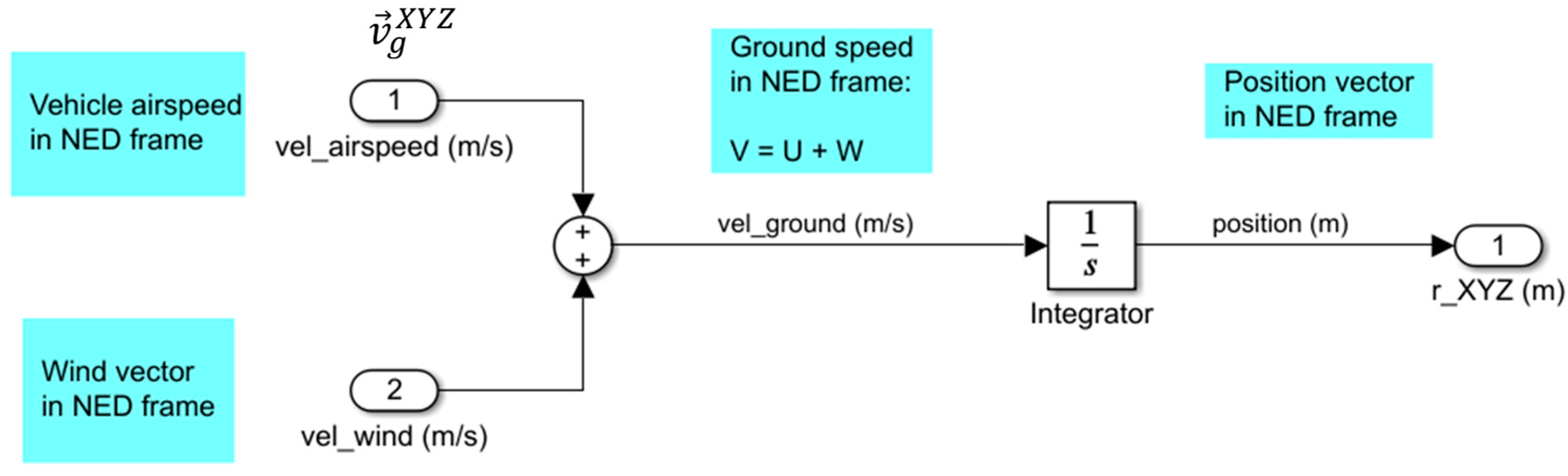
4.2.2. Modeling Vehicle Position with Influence from Wind
- Assign airspeed to vehicle velocity in the NED frame, or XYZ coordinates:
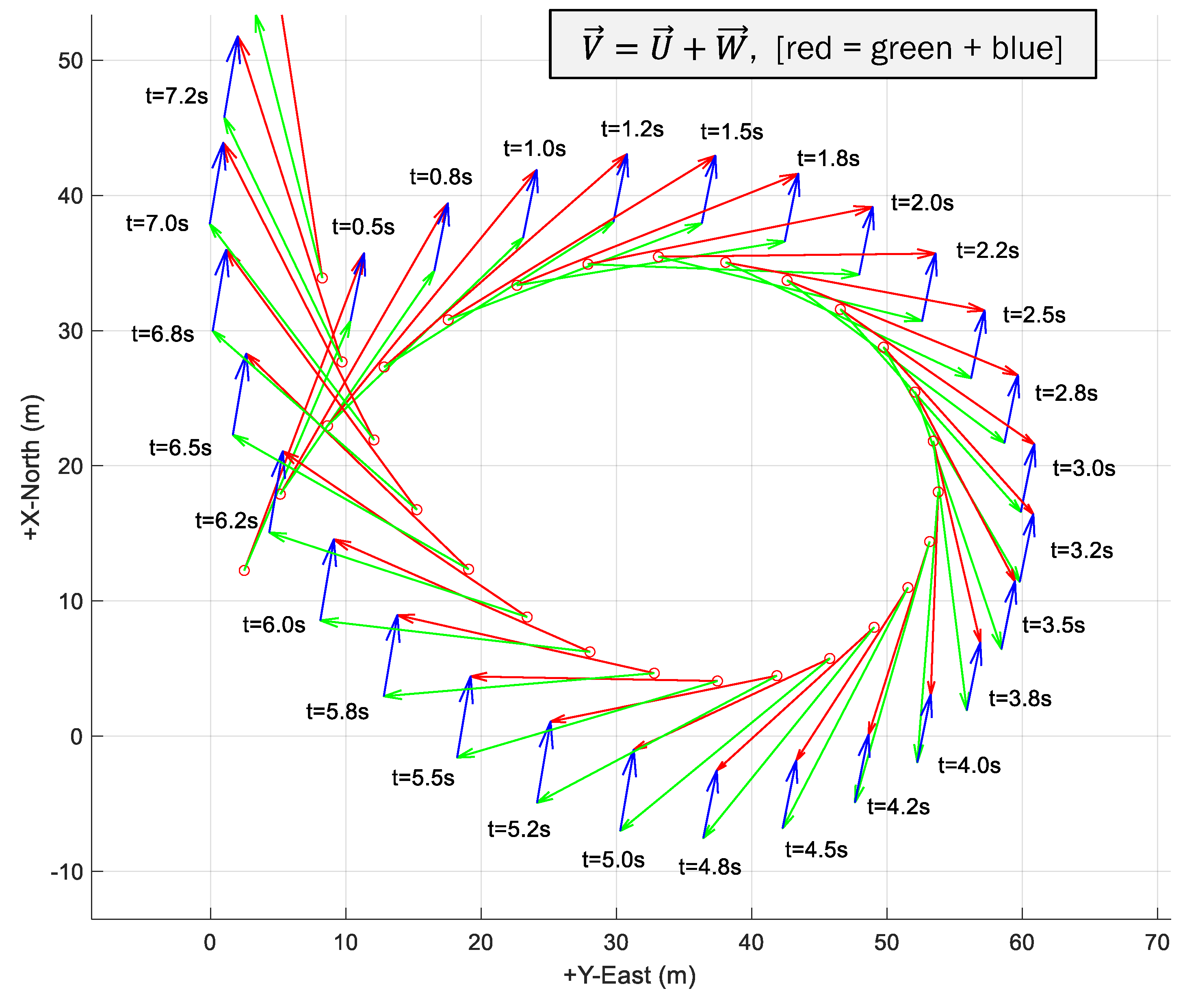
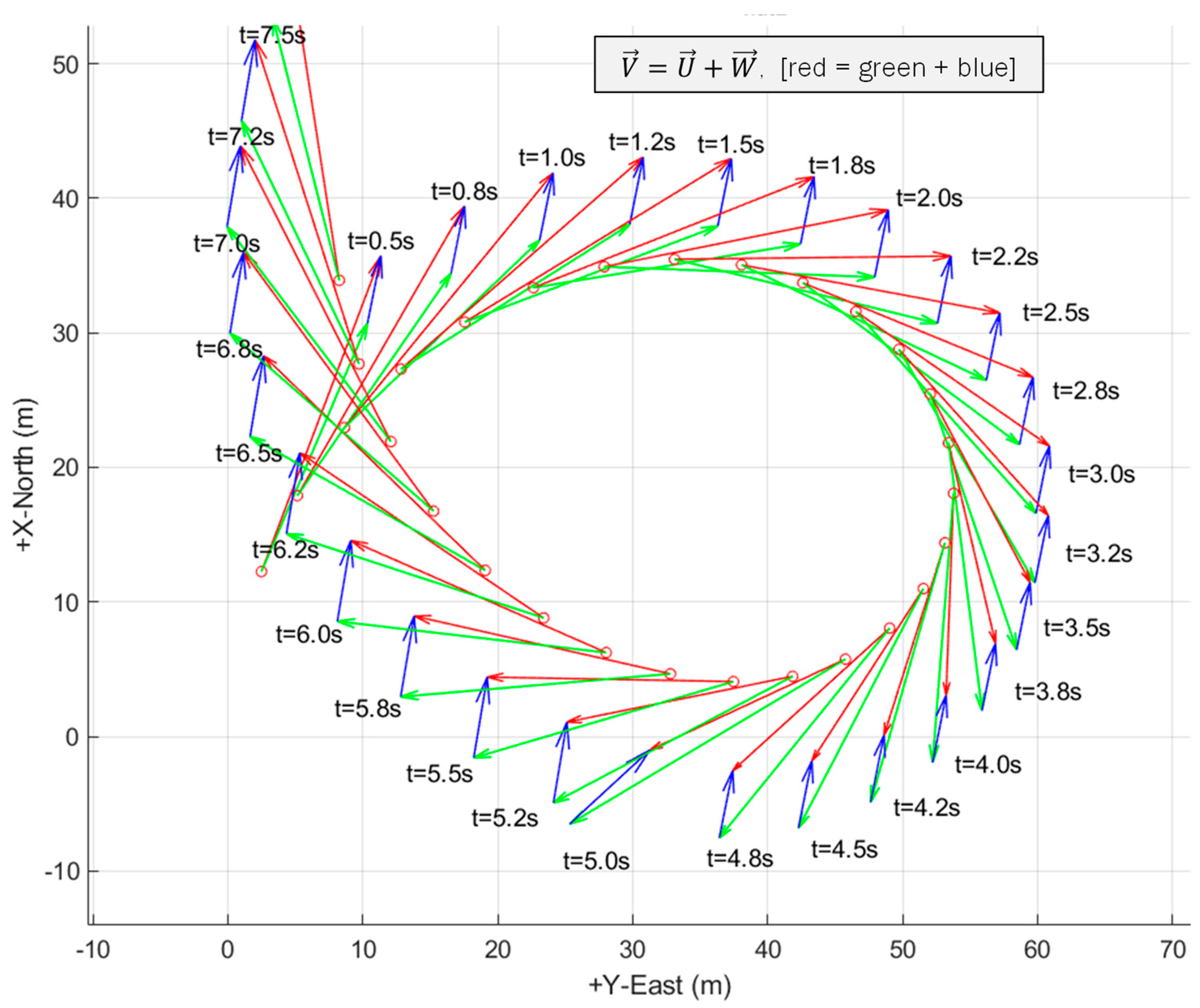
- Add the wind vector, , to vehicle airspeed, creating the wind triangle relationship:
- Integrate the new ground speed, , to achieve position in the Earth-fixed NED frame:
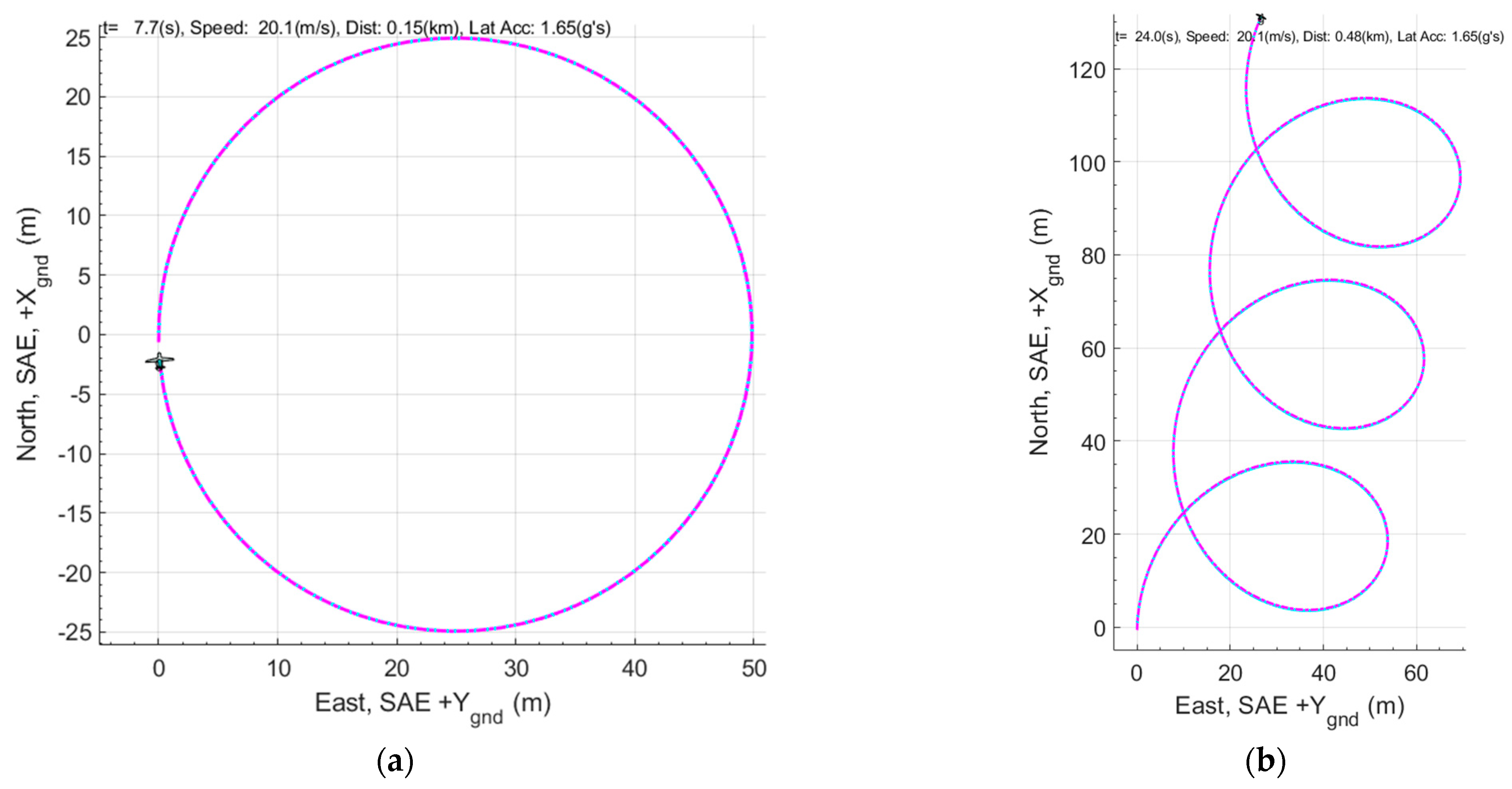
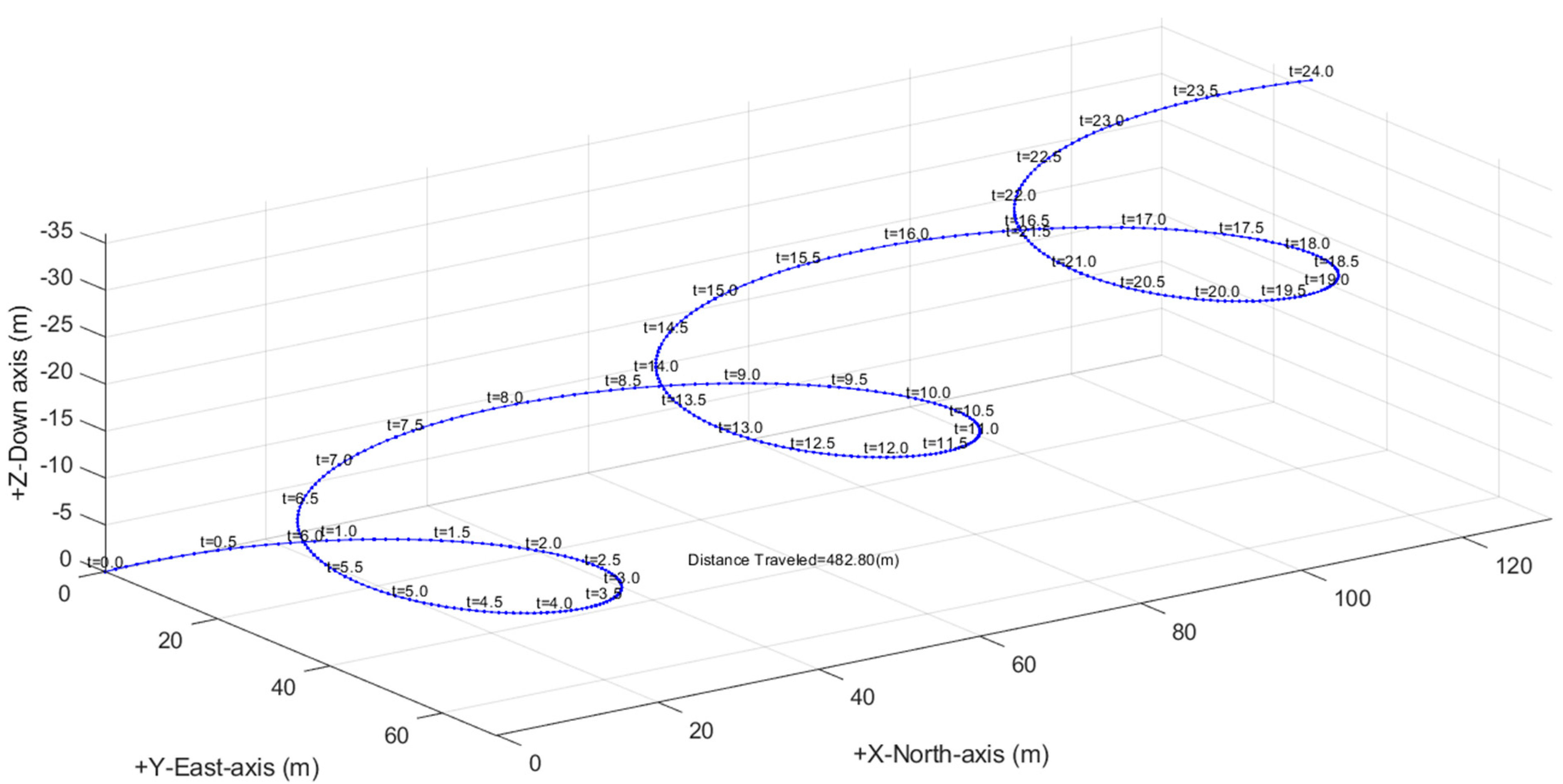
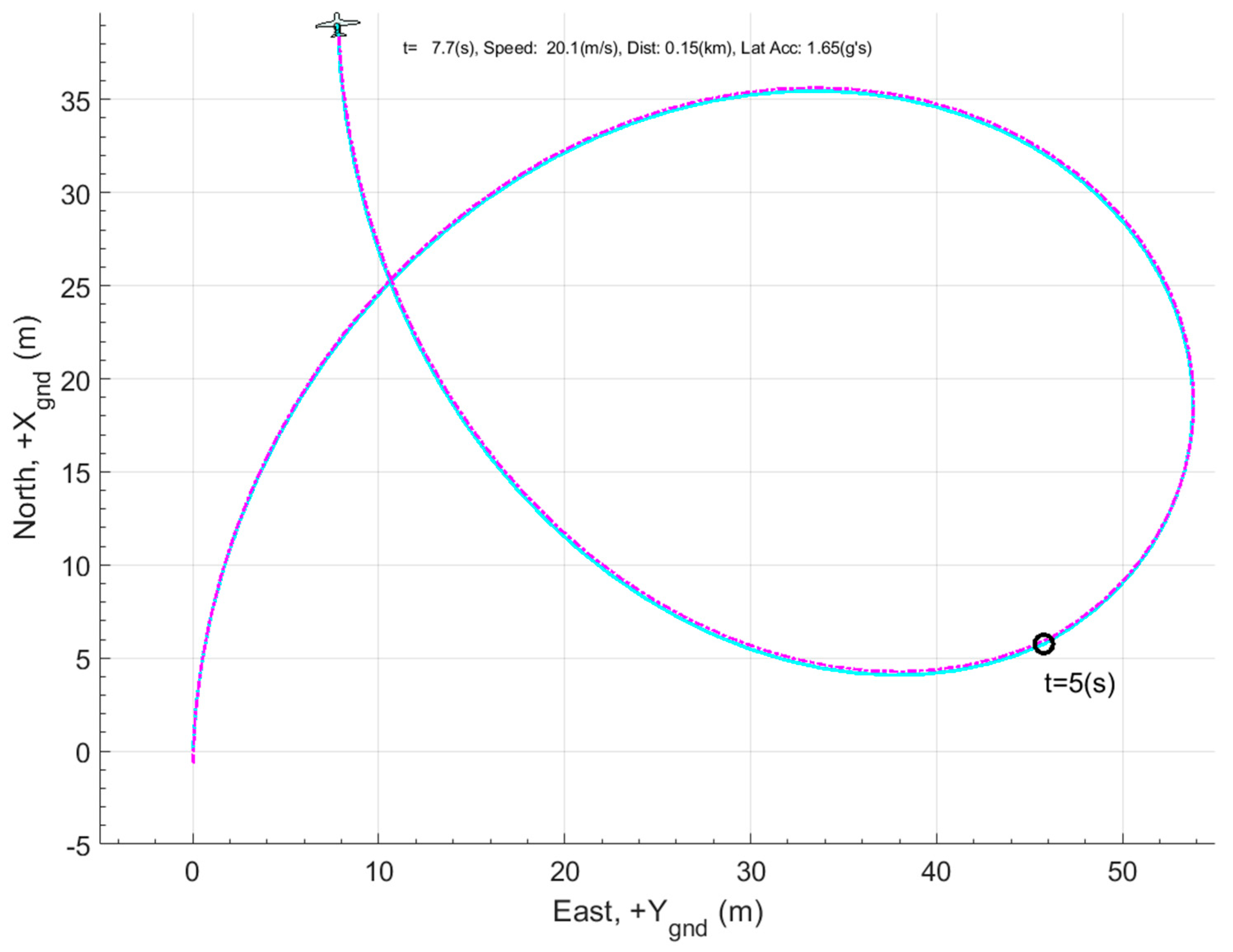
4.2.3. Simulation for Turning Motion with and without Wind
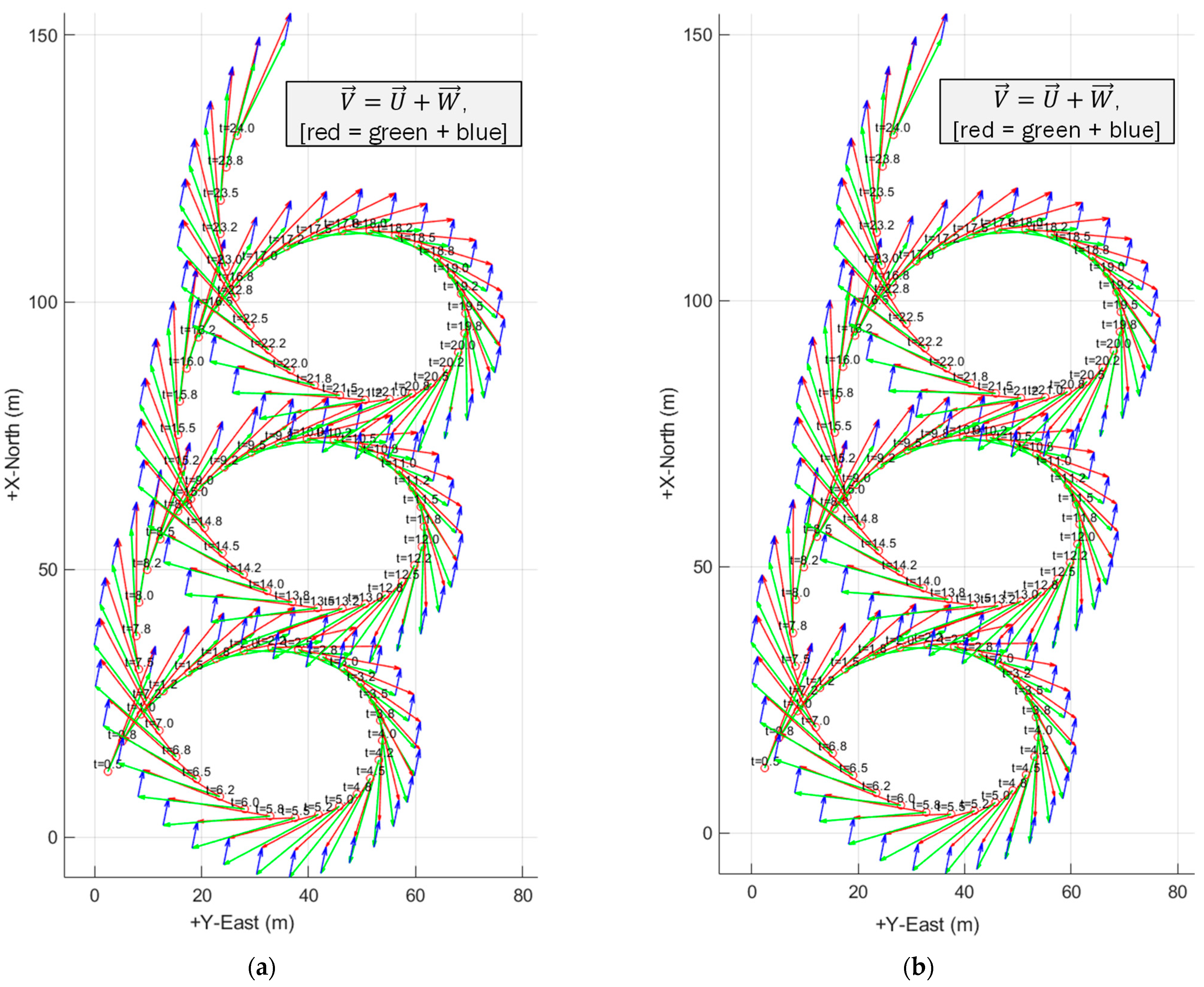
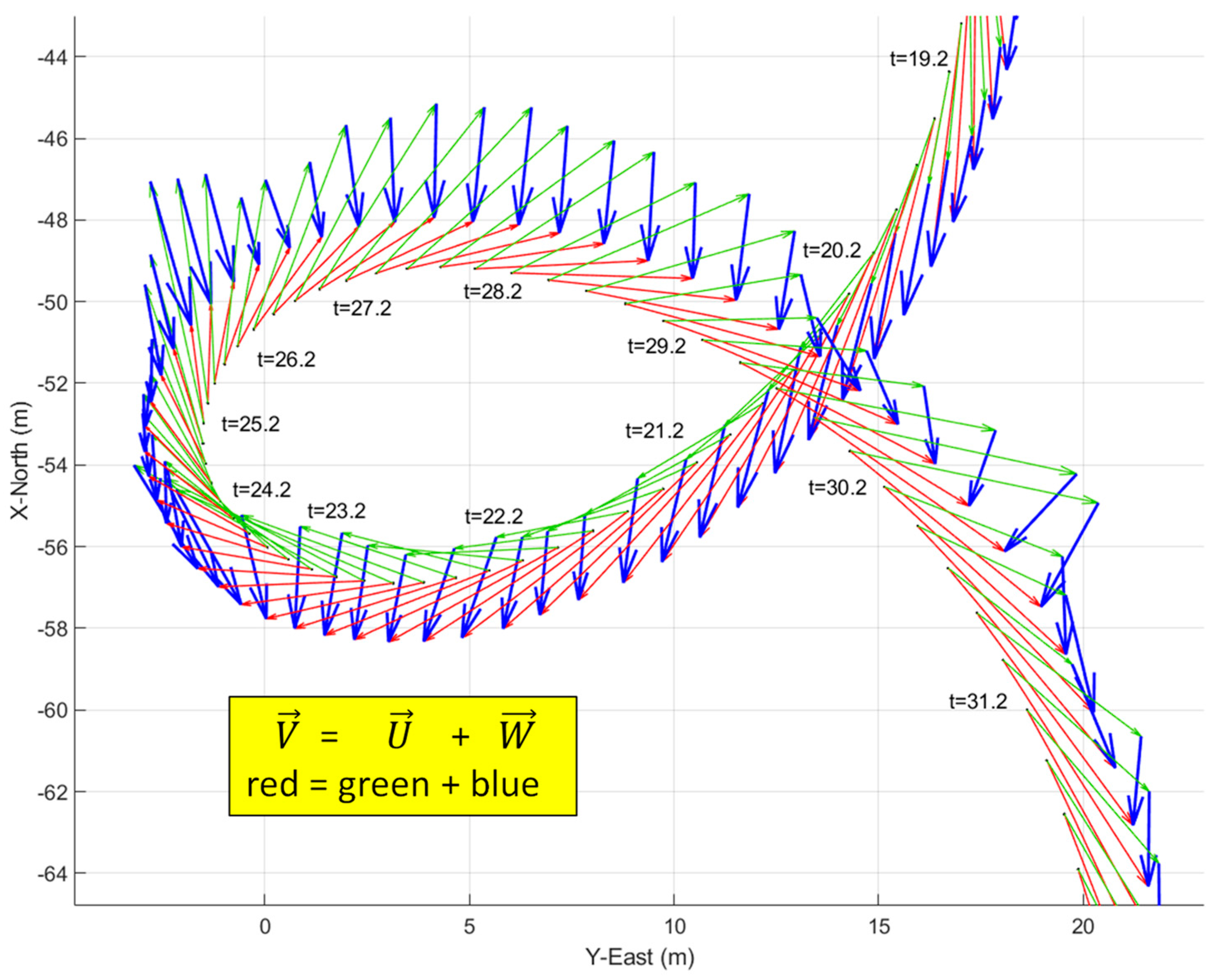
4.2.4. Simulating Wind Triangles
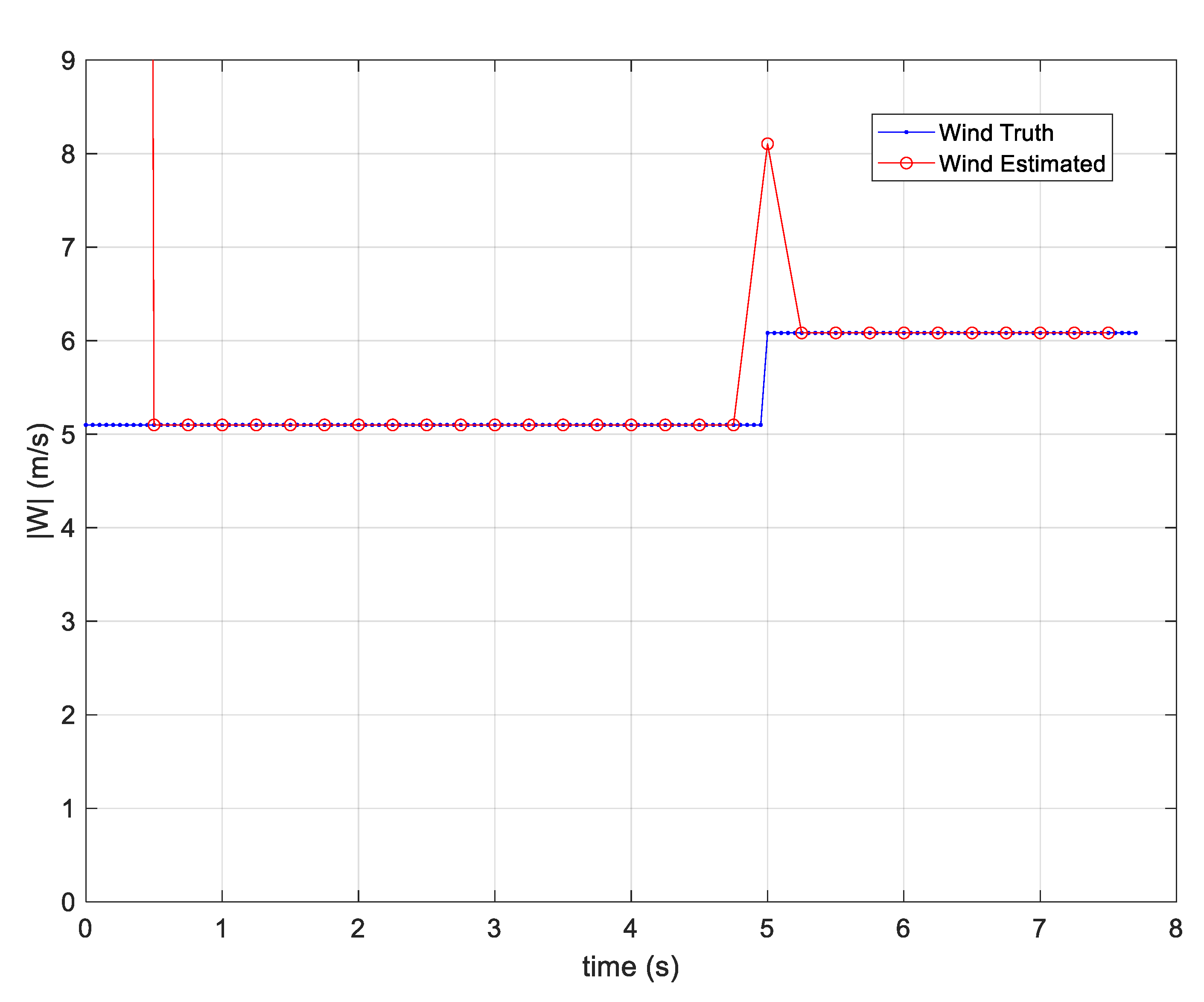
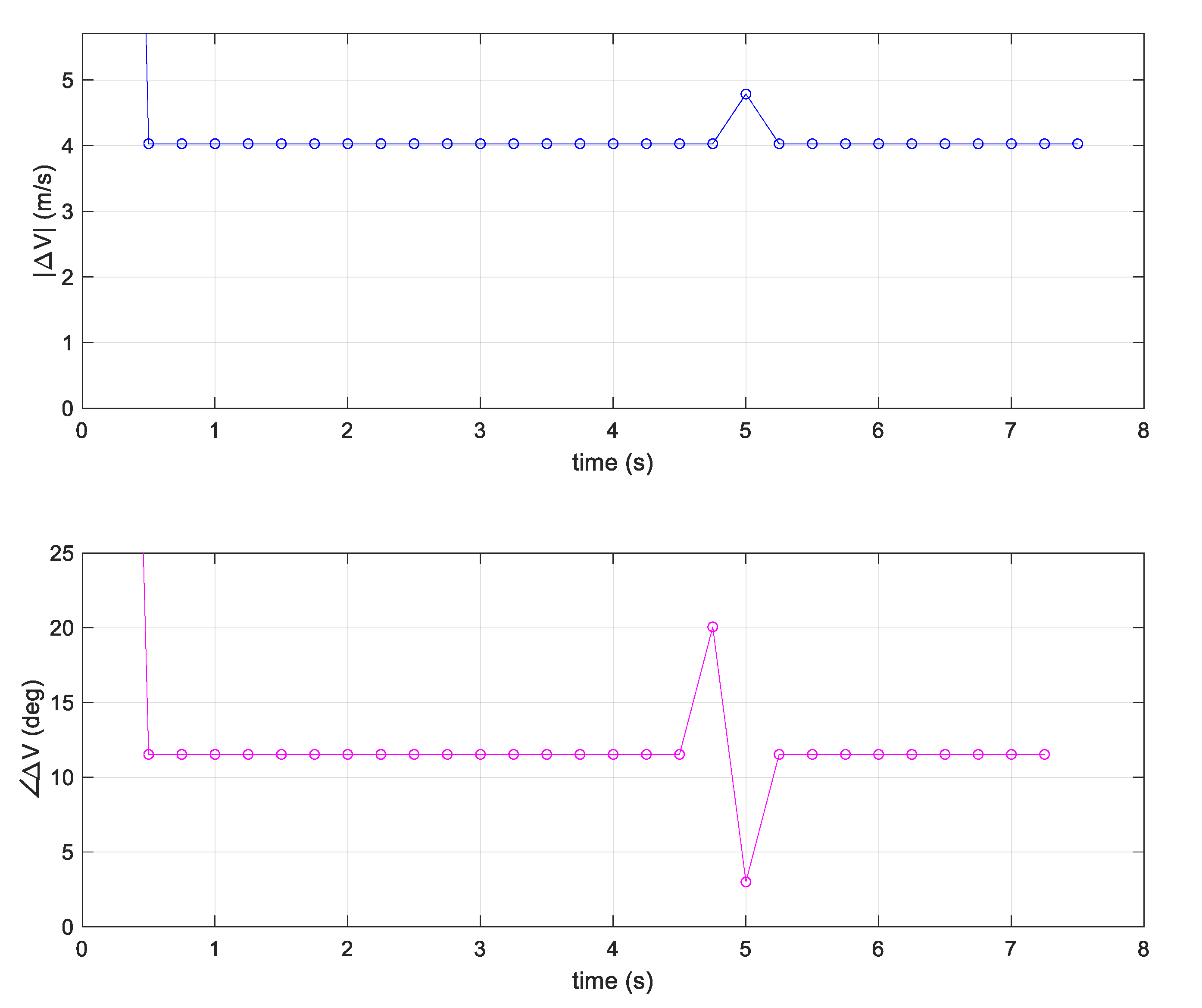
4.3. Simulation Experiment 1: Wind Vector Step Input at t = 5 s
Wind Triangle Error Analysis
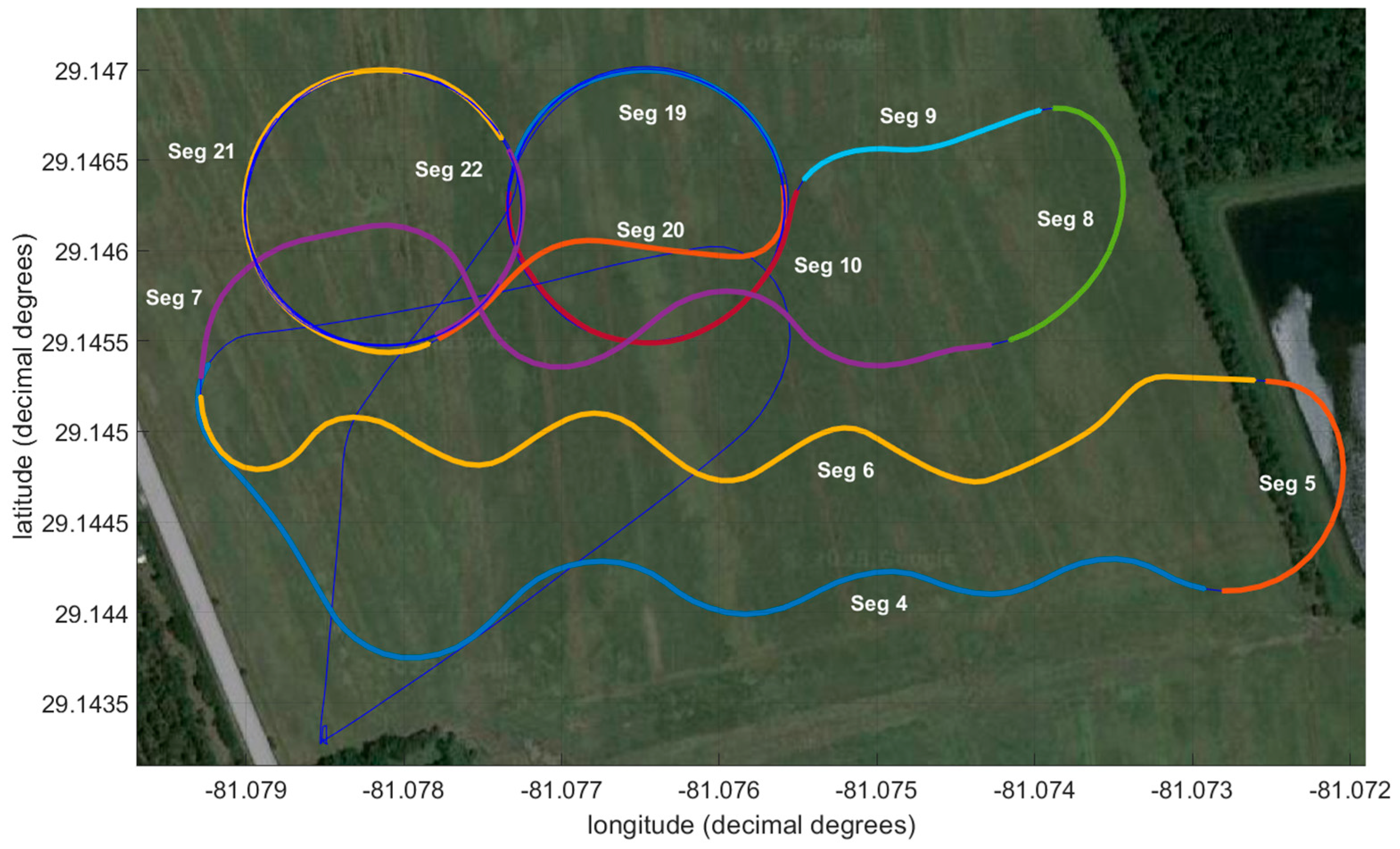
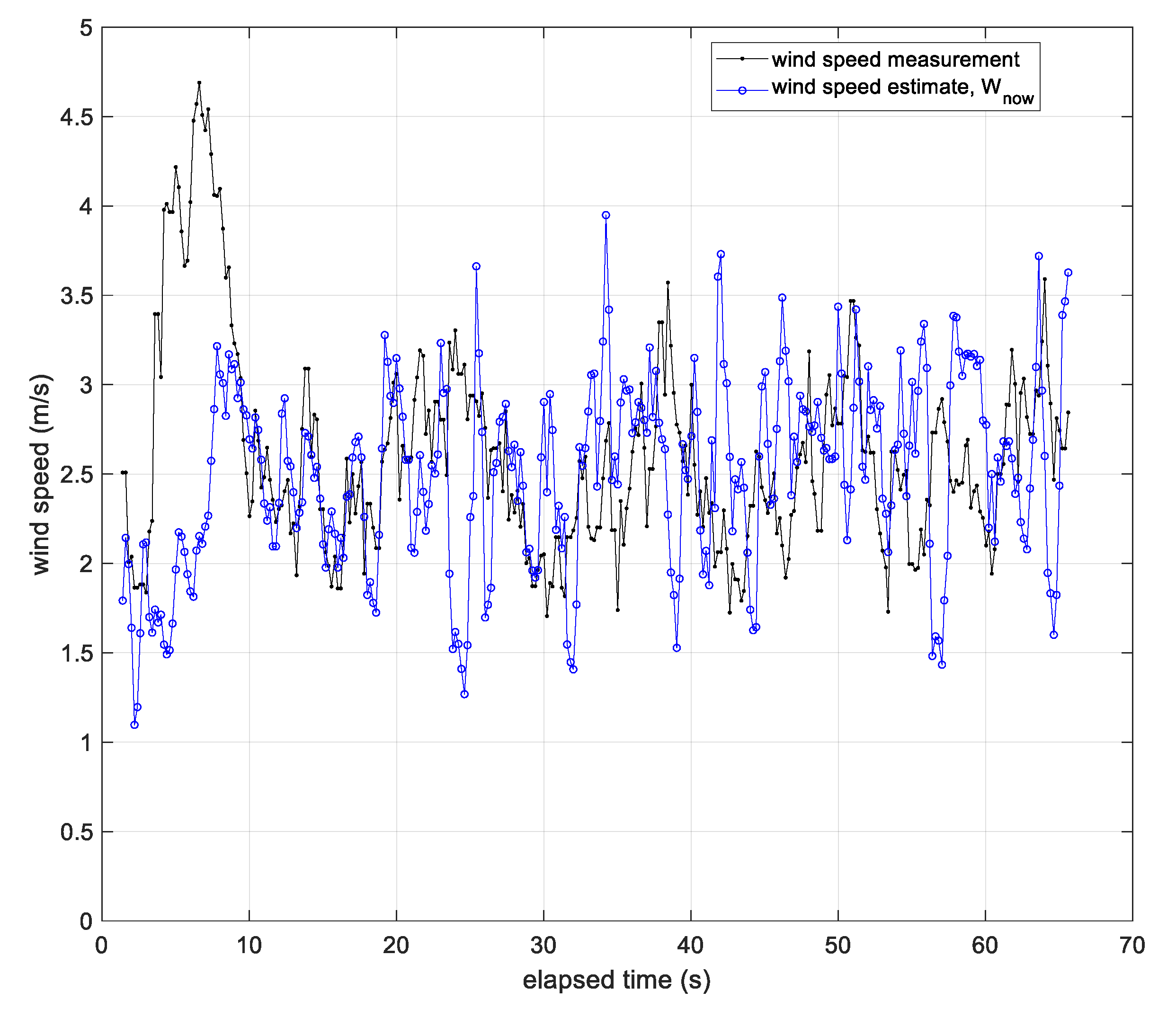
5. Results from Real Flight Tests
5.1. Experimental Vehicles and Instrumentation
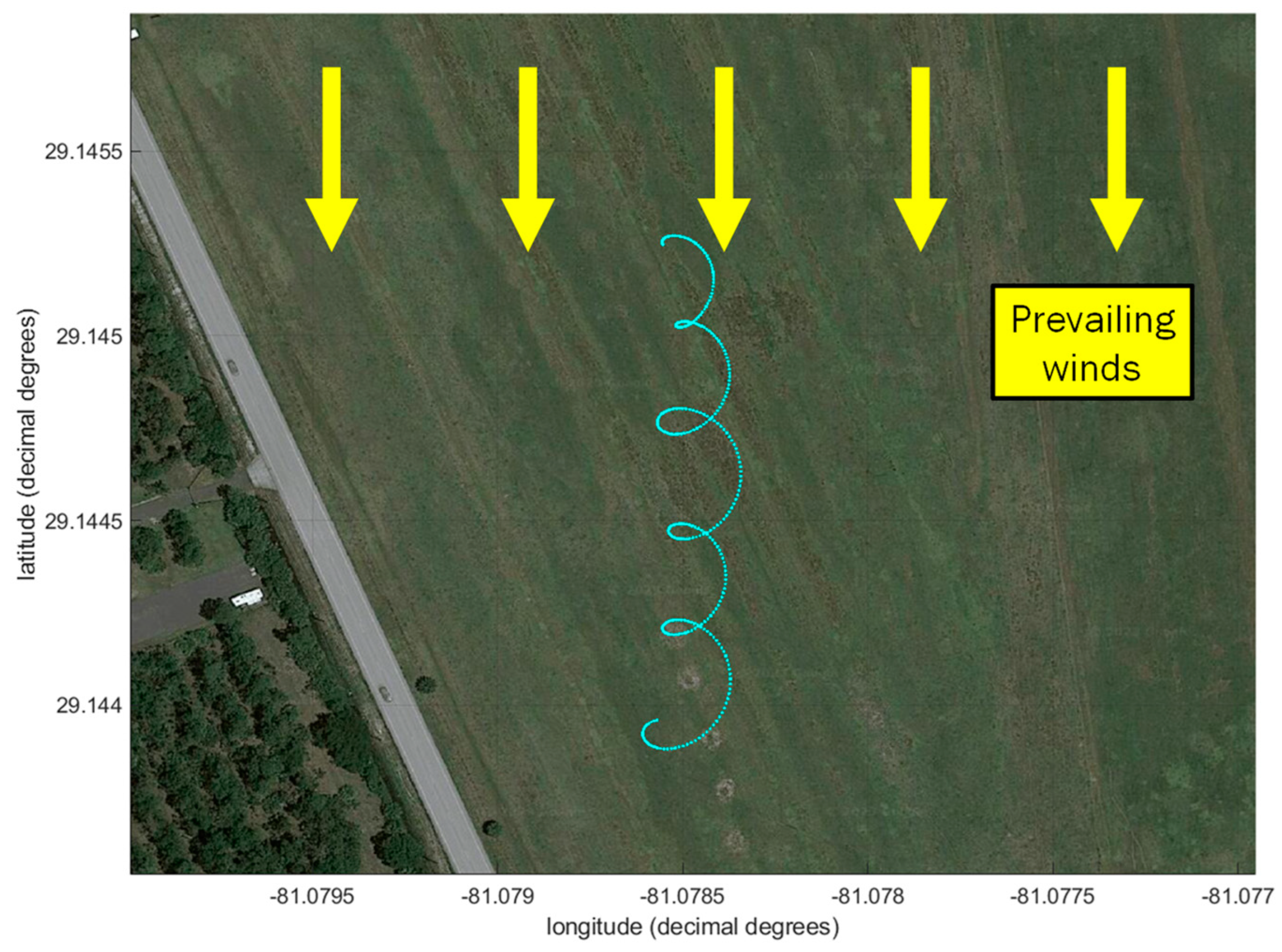
5.2. Flight Test #1 with Fixed-Wing Aircraft and Trisonica 3D Sonic Anemometer
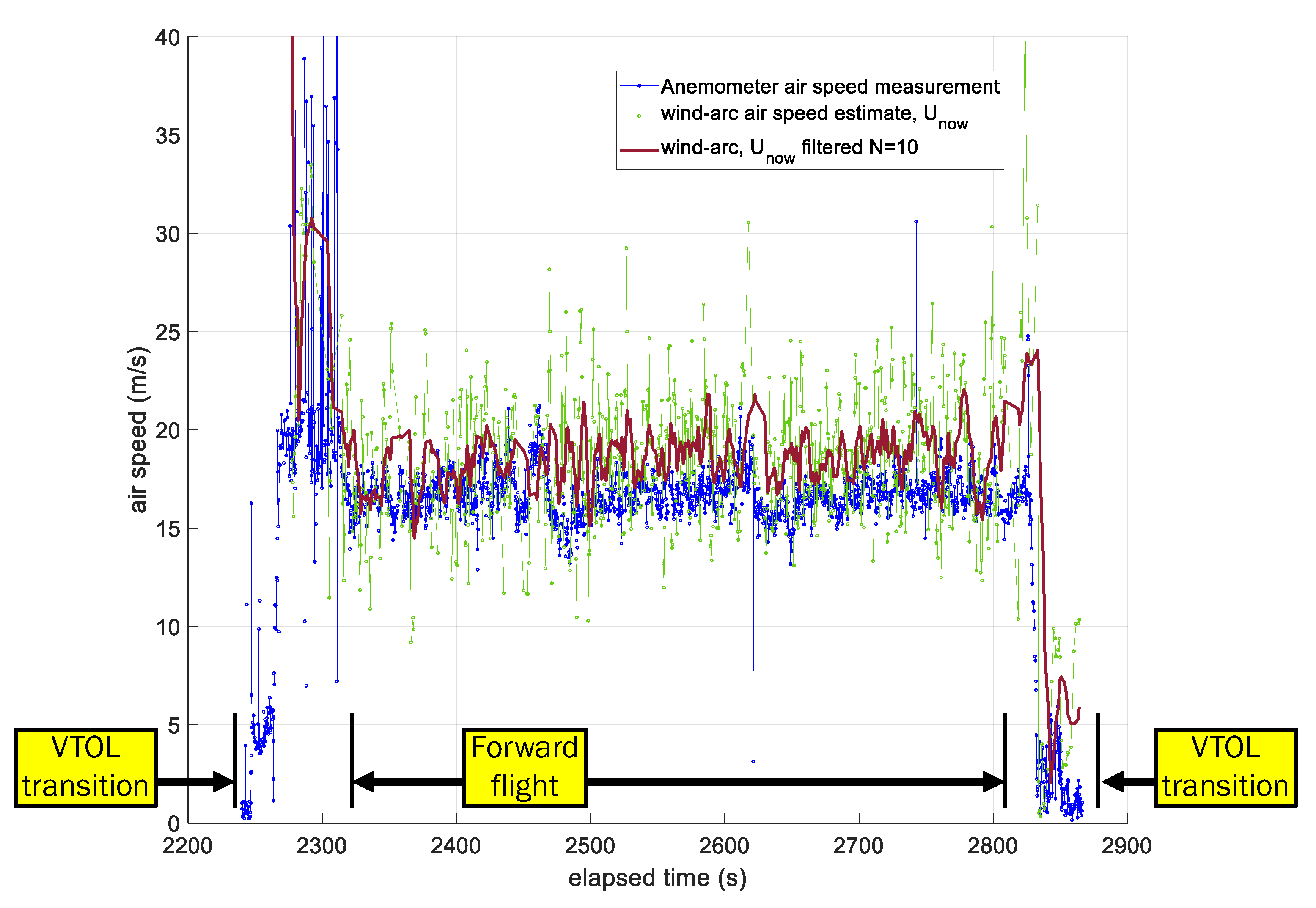
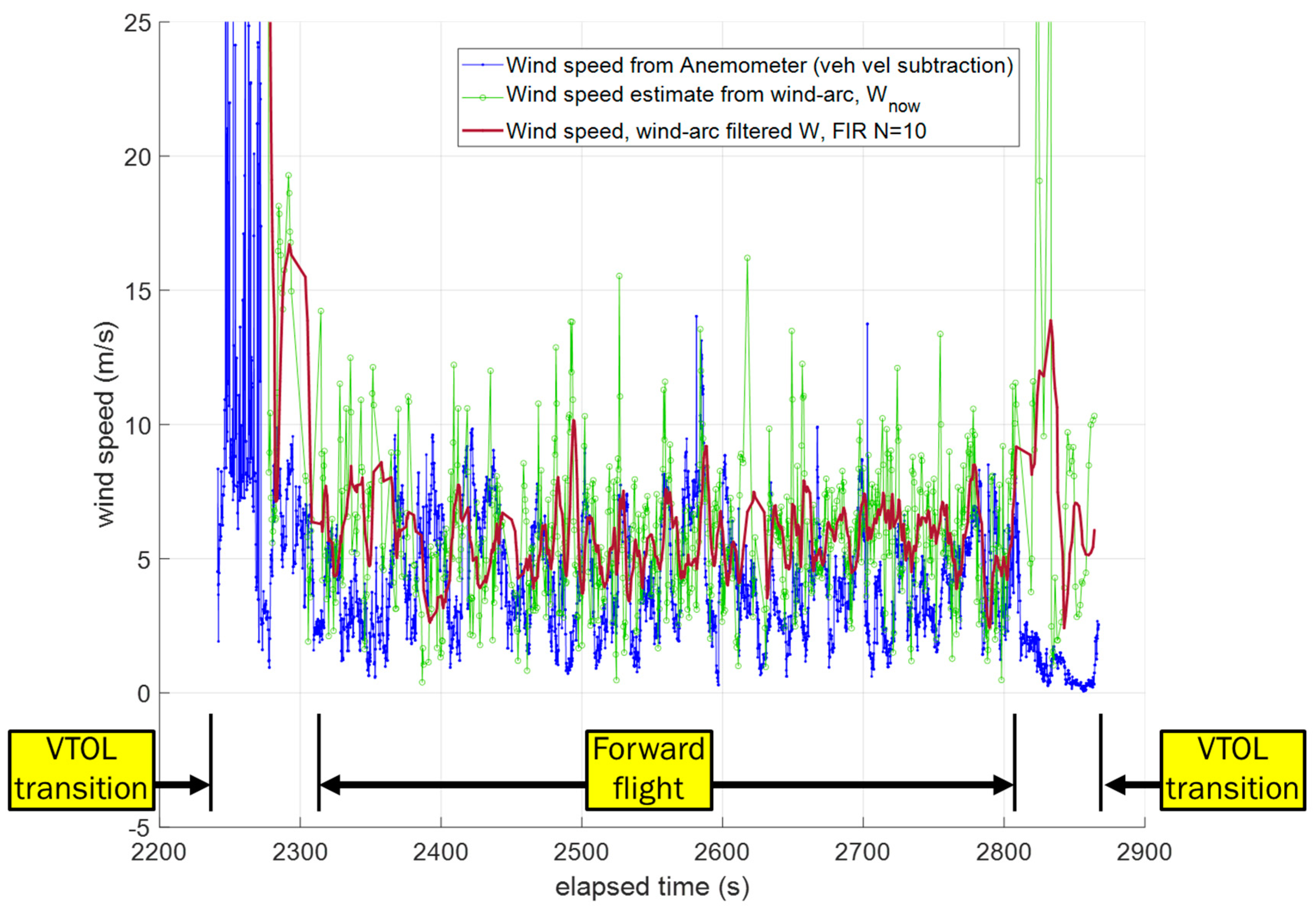
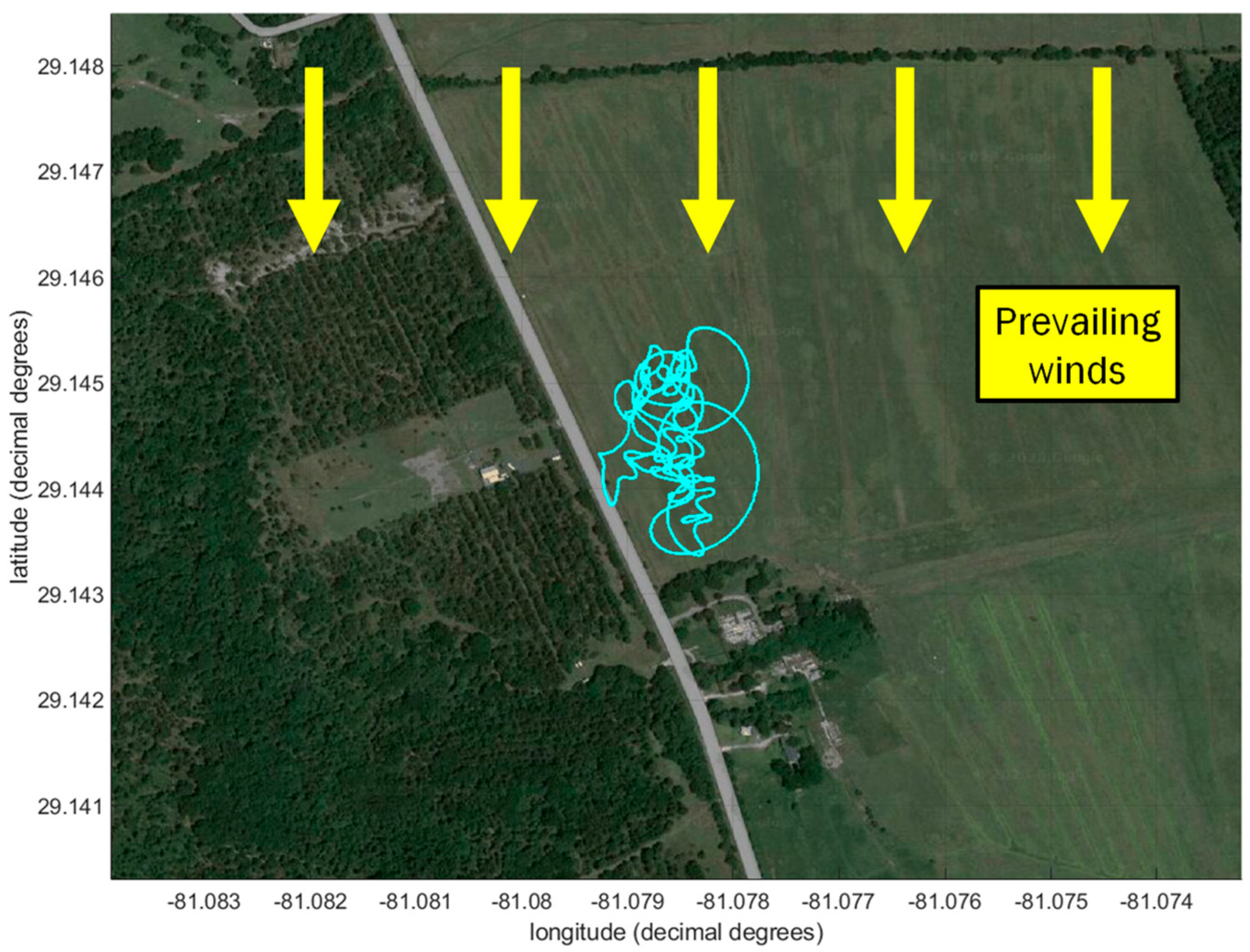
5.3. Flight Test #2 with Multi-Rotor Aircraft and FT205 2D Sonic Anemometer
6. Discussion
- The Wind-Arc method provides perfect performance both analytically and in simulation under constant wind and ideal sensor conditions. The simulation-based experiments validate the approach, underlying theory, assumptions, and performance. Under real flight tests, the method works well with some moments of unexpected magnitude and direction change.
- Anomalies in the Wind-Arc estimates are attributable to the following: (a) unmet airspeed or wind speed assumptions, (b) GPS errors, (c) heading or orientation errors, and (d) data logging delays.
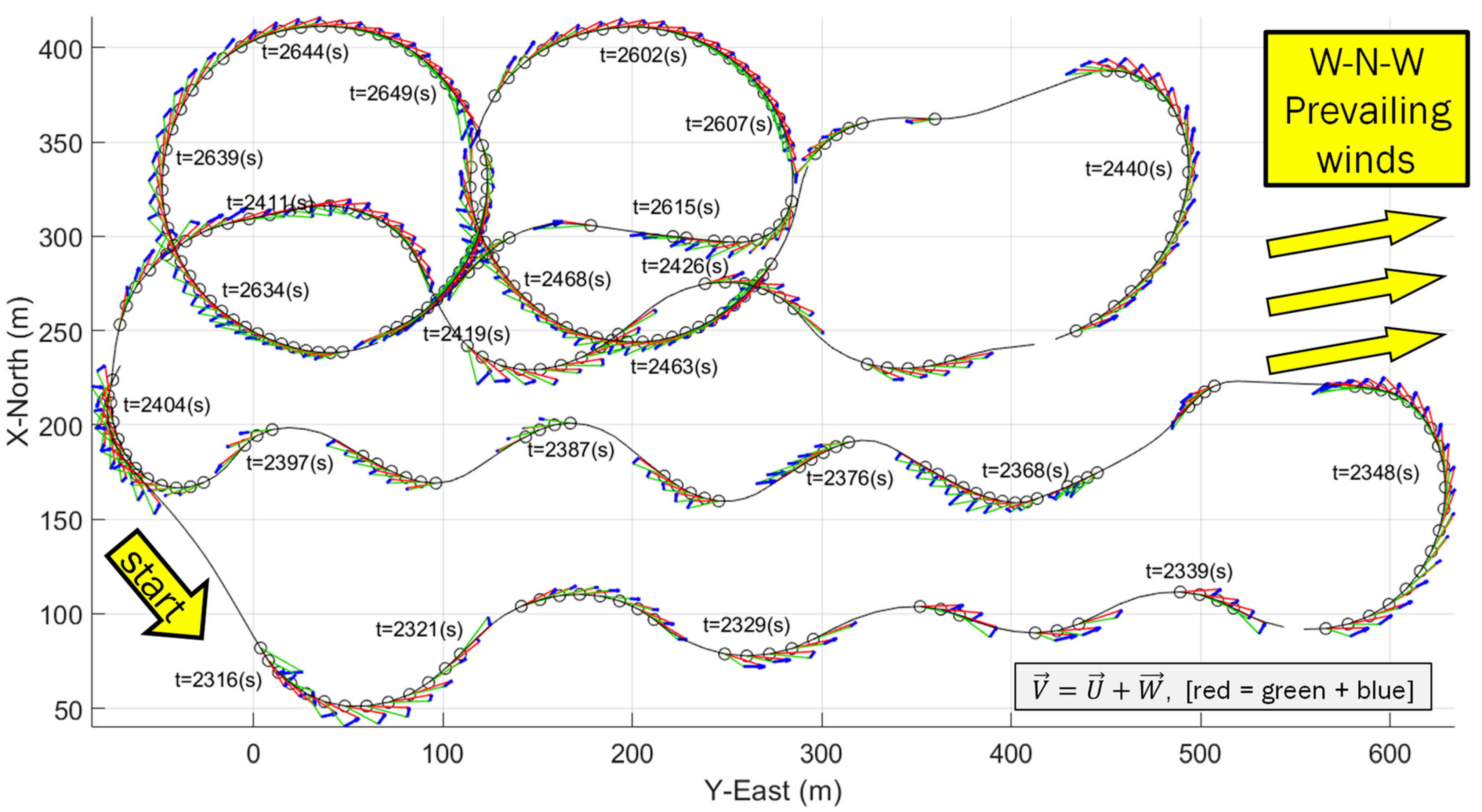
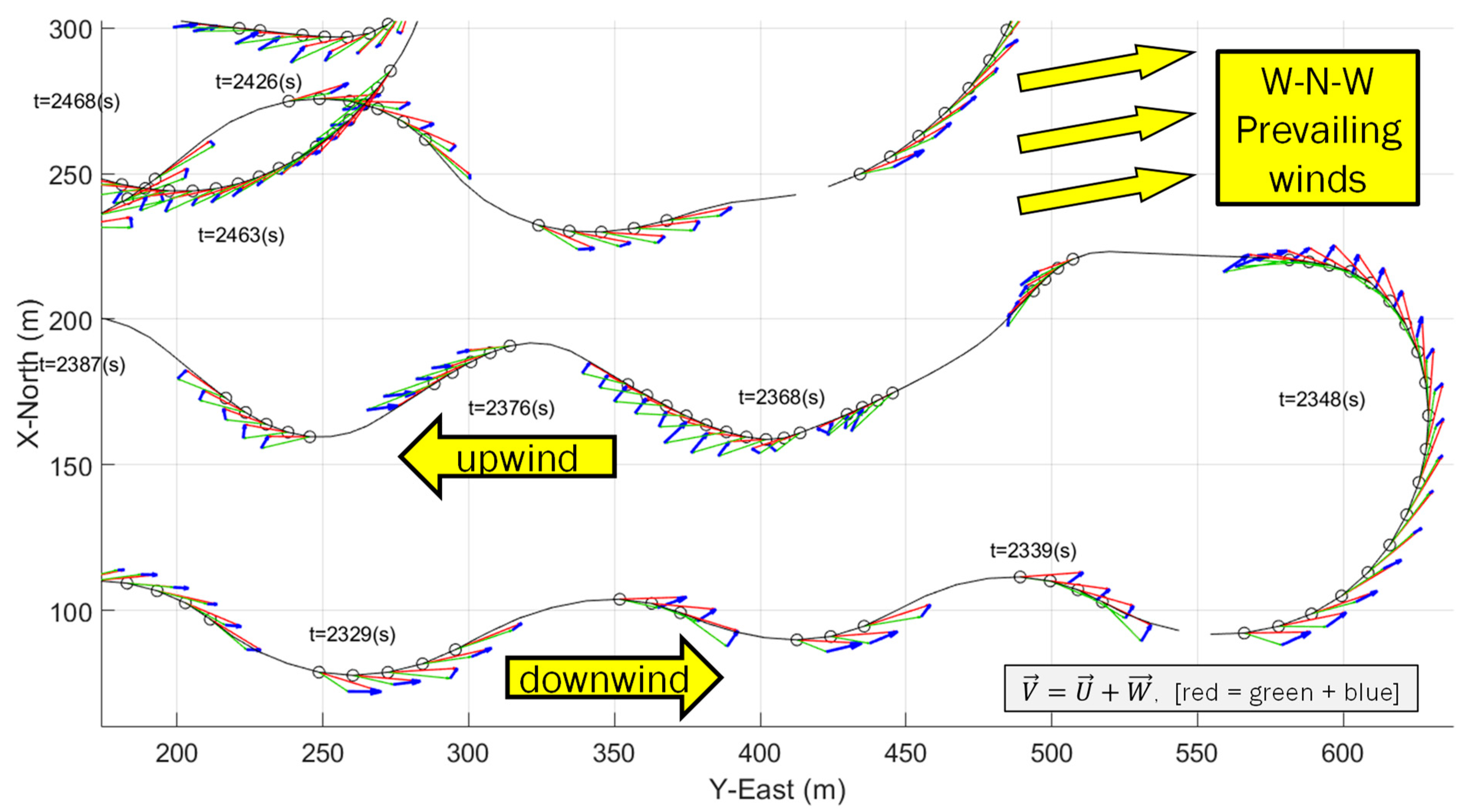
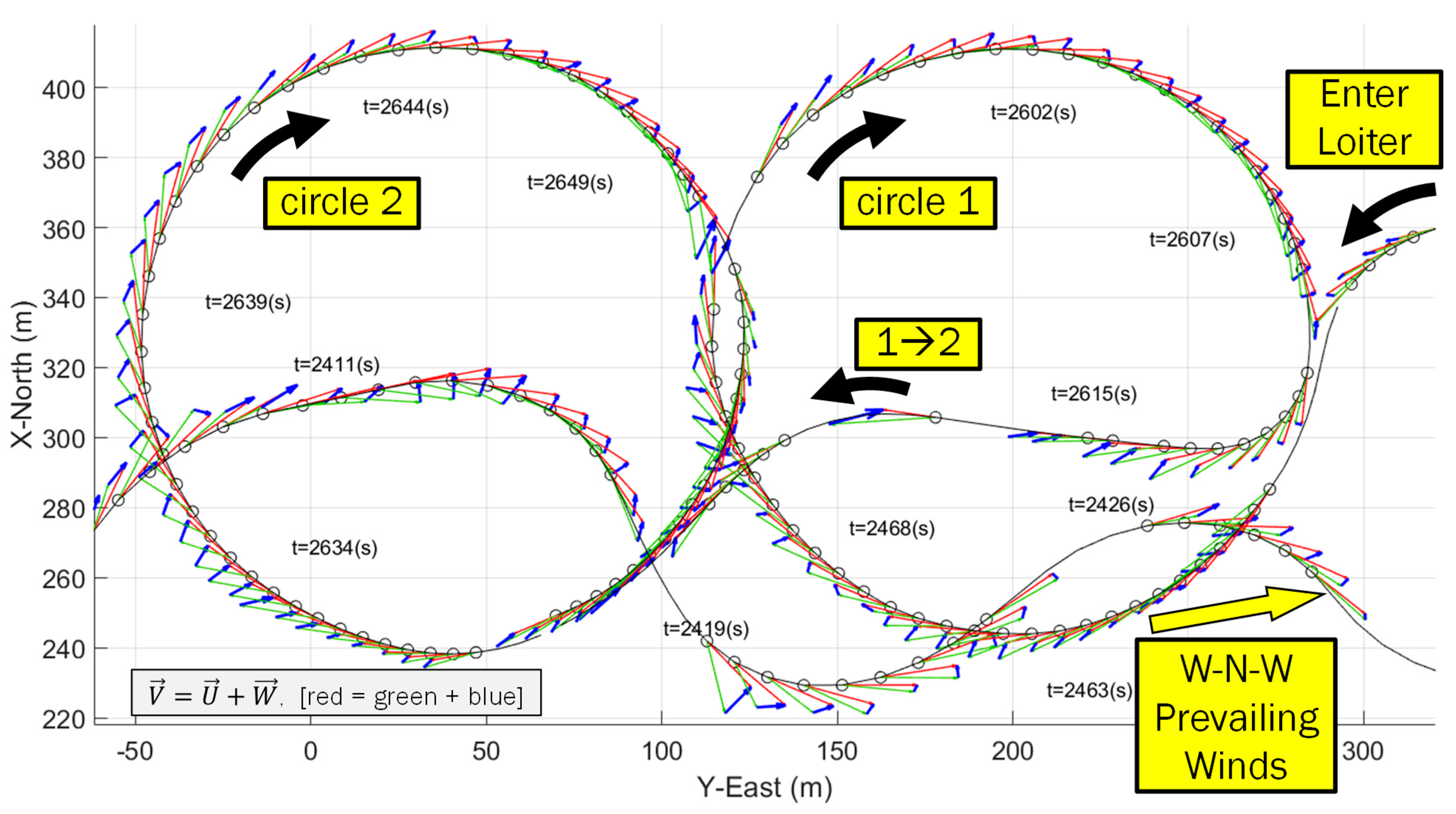
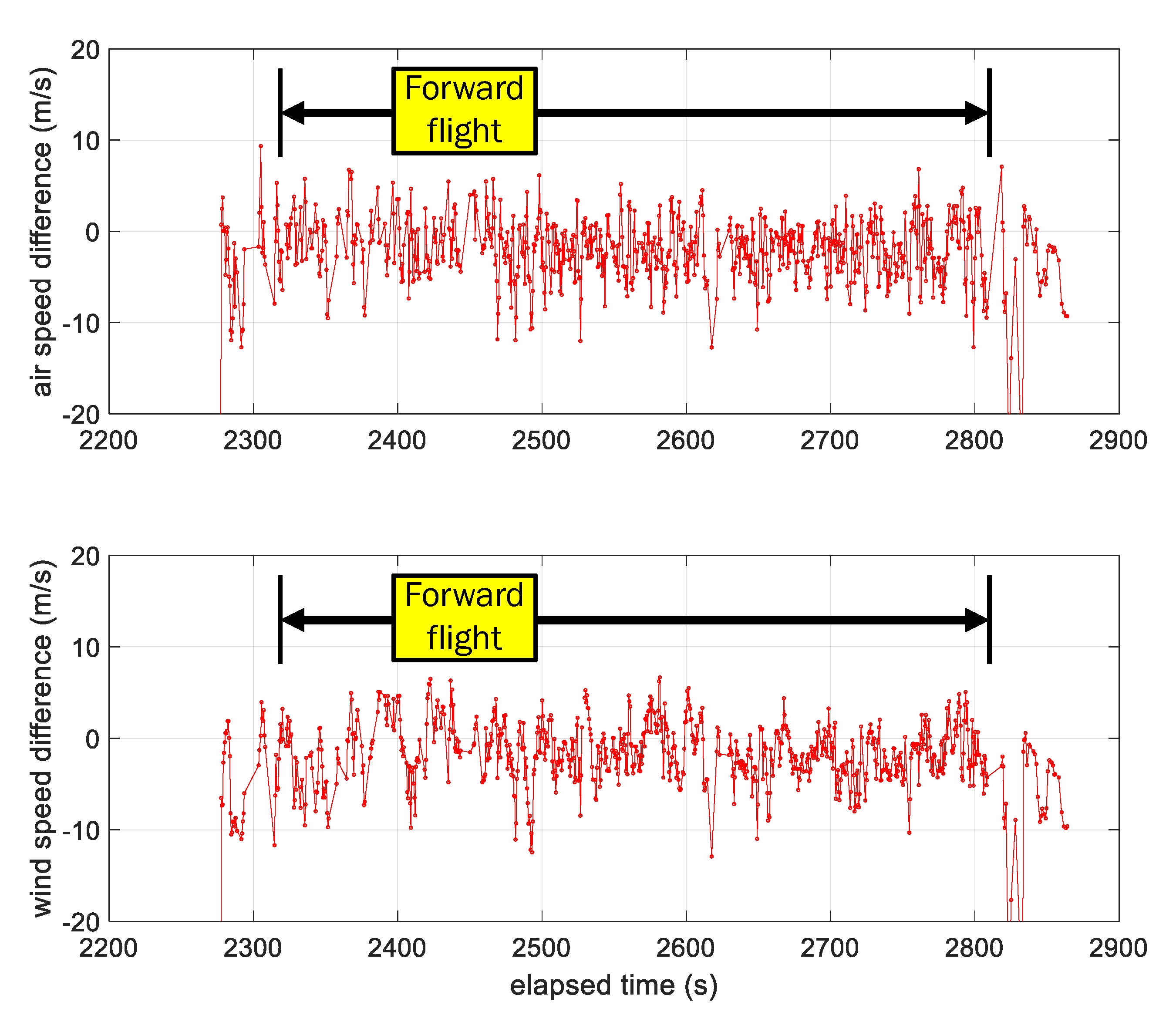
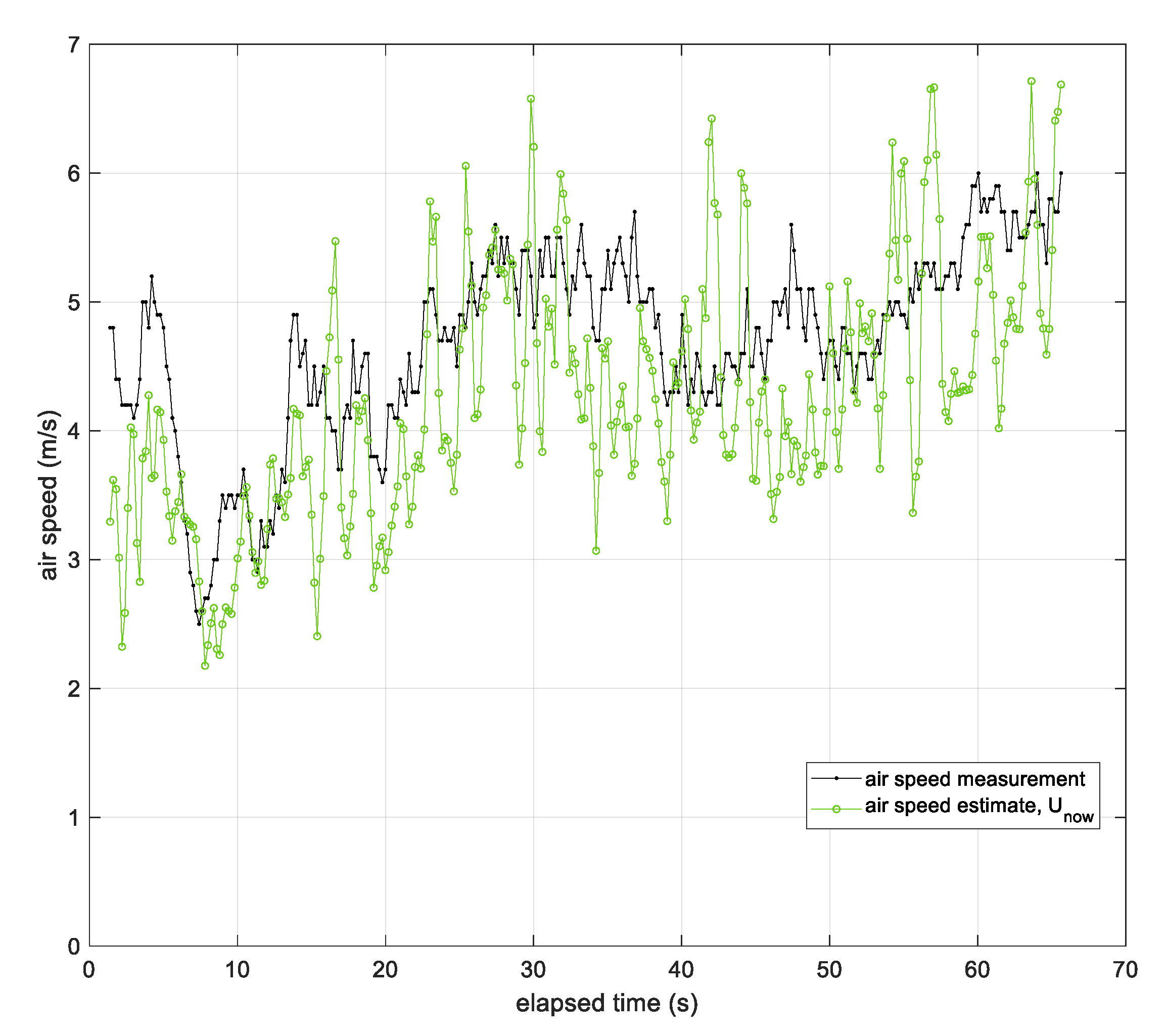
- The anemometer measuring airspeed in both experiments has some variation but is bounded around an average airspeed. This means that airspeed variation was not the dominant source of wind variation. For example, in Figure 23, the anemometer’s airspeed is approximately constant, with the exception of two locations (t = [2450 s, 2625 s]) where the vehicle changed altitude to enter and exit the first loiter circle. This indicates, for this particular example, the vehicle’s forward throttle maintained a nominal airspeed within the surrounding air mass. It also suggests the surrounding air mass moved as a coherent volume such that the entire air mass, with the vehicle, changed ground speed as the wind speed changed regardless of the vehicle’s traveling direction (upwind or downwind).
- One possible source of unexpected anomalous wind estimates is the term in Equations (14) and (15). GPS velocity is one of the most accurate sources of outdoor horizontal velocity measurements globally [65], so this term is not the most likely source of unexpected errors. But GPS error is still worth exploring using Horizontal and Vertical Dilution of Precision metrics, or HDOP and VDOP, respectively. These HDOP and VDOP values are embedded in GPS messages and can be recorded and studied in future work to determine the error associated with the term.
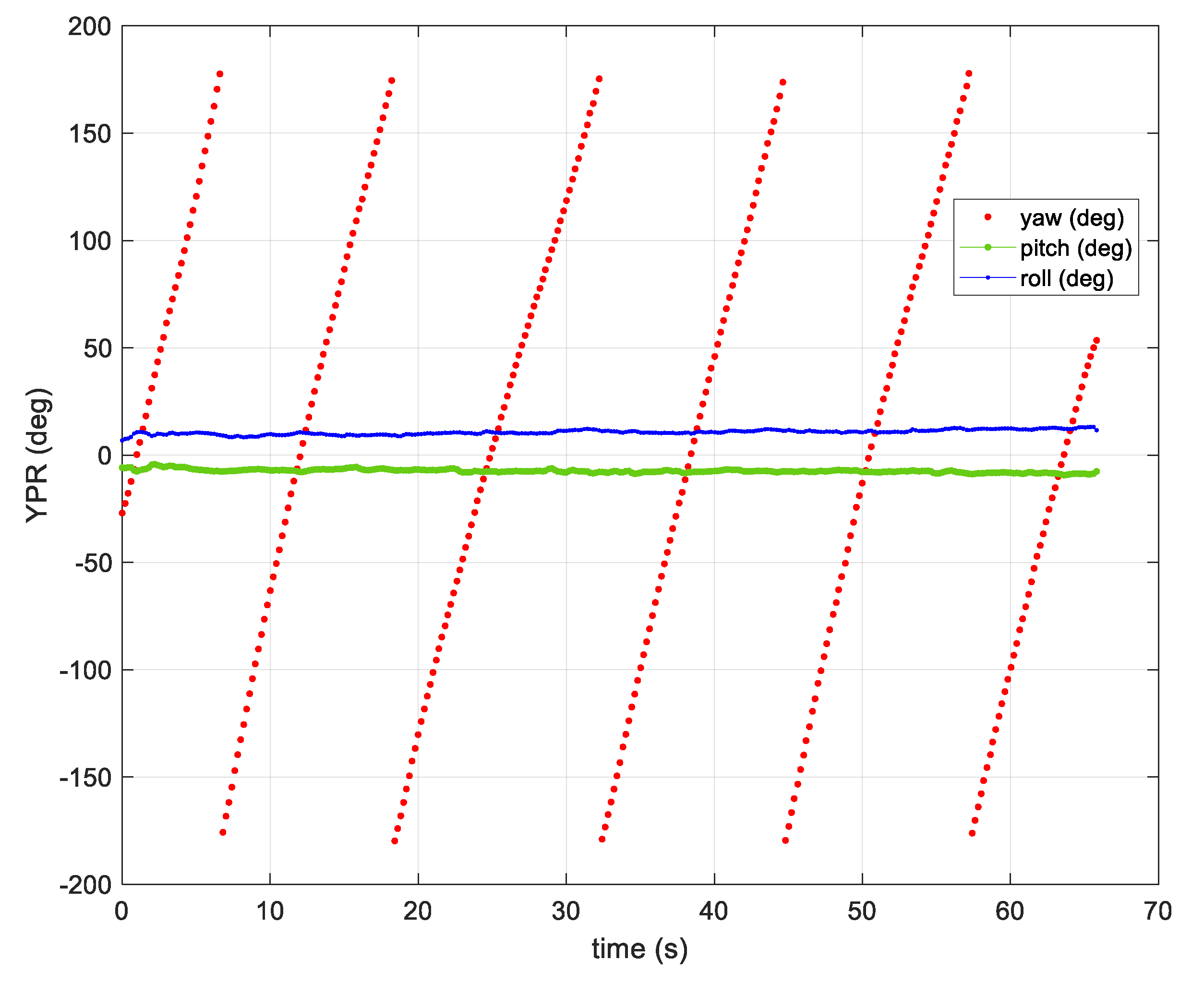
- Wind-Arc sample rates are based on state changes in the yaw angle and are not determined strictly by time. The simulation experiments and both flight tests 1 and 2 showed Wind-Arc estimates at 5 Hz, 2 Hz, and 5 Hz, respectively. This means the Wind-Arc method, from these experiments, is best suited for estimating the lowest average wind speed and is not currently a good candidate for turbulent wind measurement.
- Wind shear is defined by a velocity gradient across scales in the tens or hundreds of meters. The Wind-Arc method requires constant wind between two successive snapshots. There is no mathematical requirement for snapshot duration, but practically speaking, a shorter duration will capture the current localized wind conditions compared to a longer duration because the vehicle is moving through the air mass. Snapshot durations of the interval [0.2, 0.5] seconds were presented in two flight tests. At an average airspeed of 20 m/s, these snapshot durations correspond to 4 m to 10 m meters of vehicle travel. So, the Wind-Arc method is possibly suitable for wind shear detection across large enough spatial scales. This has not been tested.
7. Conclusions
8. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Snelling, B.; Baccheschi, N. Airspace Automation Flight Tabletop Exercise. 2023. Available online: https://ntrs.nasa.gov/citations/20230000620 (accessed on 12 July 2023).
- Sziroczak, D.; Rohacs, D.; Rohacs, J. Review of using small UAV based meteorological measurements for road weather management. Prog. Aerosp. Sci. 2022, 134, 100859. [Google Scholar] [CrossRef]
- Adkins, K.; Compere, M.; Krishnan, A.M.; Macchiarella, N.; Becker, W.; Ayyalasomayajula, S.; Lavenstein, S.; Vlachou, K.; Miller, D. Validation of the GUMP Hyperlocal Forecasting Tool Using Meteorologically Instrumented Uncrewed Aircraft; ISSARRA: Bergen, Norway, 2023. [Google Scholar]
- Adkins, K.A.; Becker, W.; Ayyalasomayajula, S.; Lavenstein, S.; Vlachou, K.; Miller, D.; Compere, M.; Muthu Krishnan, A.; Macchiarella, N. Hyperlocal Weather Predictions with the Enhanced General Urban Area Microclimate Predictions Tool. Drones 2023, 7, 428. [Google Scholar] [CrossRef]
- Mogili, U.R.; Deepak, B. Review on application of drone systems in precision agriculture. Procedia Comput. Sci. 2018, 133, 502–509. [Google Scholar] [CrossRef]
- Laksham, K.B. Unmanned aerial vehicle (drones) in public health: A SWOT analysis. J. Fam. Med. Prim. Care 2019, 8, 342. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Abraham, S.J.; Burger, B.; Christine, C.; Fraser, L.; Hoeksema, J.M.; Hwang, S.; Travnik, E.; Kumar, S.; Scheirer, W.; et al. The next generation of human-drone partnerships: Co-designing an emergency response system. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems, Honolulu, HI, USA, 25–30 April 2020; pp. 1–13. Available online: https://dl.acm.org/doi/pdf/10.1145/3313831.3376825 (accessed on 12 July 2023).
- Daud, S.M.S.M.; Yusof, M.Y.P.M.; Heo, C.C.; Khoo, L.S.; Singh, M.K.C.; Mahmood, M.S.; Nawawi, H. Applications of drone in disaster management: A scoping review. Sci. Justice 2022, 62, 30–42. [Google Scholar] [CrossRef]
- Cracknell, A.P. UAVs: Regulations and law enforcement. Int. J. Remote Sens. 2017, 38, 3054–3067. [Google Scholar] [CrossRef]
- AL-Dosari, K.; Hunaiti, Z.; Balachandran, W. Systematic Review on Civilian Drones in Safety and Security Applications. Drones 2023, 7, 210. [Google Scholar] [CrossRef]
- Lee, C. The role of culture in military innovation studies: Lessons learned from the US Air Force’s adoption of the Predator Drone, 1993–1997. J. Strateg. Stud. 2023, 46, 115–149. [Google Scholar] [CrossRef]
- Shahmoradi, J.; Talebi, E.; Roghanchi, P.; Hassanalian, M. A comprehensive review of applications of drone technology in the mining industry. Drones 2020, 4, 34. [Google Scholar] [CrossRef]
- Hill, A.C. Economical drone mapping for archaeology: Comparisons of efficiency and accuracy. J. Archaeol. Sci. Rep. 2019, 24, 80–91. [Google Scholar] [CrossRef]
- Adamopoulos, E.; Rinaudo, F. UAS-based archaeological remote sensing: Review, meta-analysis and state-of-the-art. Drones 2020, 4, 46. [Google Scholar] [CrossRef]
- Macchiarella, N.D.; Robbins, J.; Cashdollar, D. Rapid Virtual Object Development Using Photogrammetric Imagery Obtained with Small Unmanned Aircraft Systems-Applications for Disaster Assessment and Cultural Heritage Preservation. In Proceedings of the AIAA SciTech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2019; p. 1974. Available online: https://arc.aiaa.org/doi/pdf/10.2514/6.2019-1974 (accessed on 14 July 2023).
- Tang, L.; Shao, G. Drone remote sensing for forestry research and practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- Banu, T.P.; Borlea, G.F.; Banu, C. The use of drones in forestry. J. Environ. Sci. Eng. B 2016, 5, 557–562. [Google Scholar]
- Benarbia, T.; Kyamakya, K. A literature review of drone-based package delivery logistics systems and their implementation feasibility. Sustainability 2021, 14, 360. [Google Scholar] [CrossRef]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Ayamga, M.; Akaba, S.; Nyaaba, A.A. Multifaceted applicability of drones: A review. Technol. Forecast. Soc. Change 2021, 167, 120677. [Google Scholar] [CrossRef]
- Khan, M.A.; Alvi, B.A.; Safi, A.; Khan, I.U. Drones for good in smart cities: A review. In Proceedings of the International Conference on Electrical, Electronics, Computers, Communication, Mechanical and Computing (EECCMC), Vaniyambadi, India, 28–29 January 2018; pp. 1–6. Available online: https://www.researchgate.net/profile/Muhammad-Khan-716/publication/316846331_Drones_for_Good_in_Smart_CitiesA_Review/links/5a27c404aca2727dd883c881/Drones-for-Good-in-Smart-CitiesA-Review.pdf (accessed on 31 August 2023).
- How to Read a Wind Cone/Windsock? Aviation Renewables, LED Airfield Lighting and Power Solutions. 2022. Available online: https://aviationrenewables.com/how-to-read-a-wind-cone-windsock/ (accessed on 5 July 2023).
- Summers Walker, J. What am I? Blowing in the Wind, Here’s the Answer, My Friend. 1 September 2017. Available online: https://www.aopa.org/news-and-media/all-news/2017/september/flight-training-magazine/what-am-i-windsock (accessed on 5 July 2023).
- Ground Reference Maneuvers. CFI Notebook.Net-“Higher Education,” N.D. Available online: https://www.cfinotebook.net/notebook/maneuvers-and-procedures/ground/ground-reference-maneuvers (accessed on 5 July 2023).
- Administration, F.A. Airplane Flying Handbook (FAA-H-8083-3A); Skyhorse Publishing Inc.: New York, NY, USA, 2011. [Google Scholar]
- Altino, K.; Barbré, R. Applications of Meteorological Tower Data at Kennedy Space Center. In Proceedings of the 1st AIAA Atmospheric and Space Environments Conference, San Antonio, TX, USA, 22–25 June 2009; p. 3533. [Google Scholar]
- Baker, W.E.; Atlas, R.; Cardinali, C.; Clement, A.; Emmitt, G.D.; Gentry, B.M.; Hardesty, R.M.; Källén, E.; Kavaya, M.J.; Langland, R.; et al. Lidar-measured wind profiles: The missing link in the global observing system. Bull. Am. Meteorol. Soc. 2014, 95, 543–564. [Google Scholar] [CrossRef]
- Käsler, Y.; Rahm, S.; Simmet, R.; Kühn, M. Wake measurements of a multi-MW wind turbine with coherent long-range pulsed Doppler wind lidar. J. Atmos. Ocean. Technol. 2010, 27, 1529–1532. [Google Scholar] [CrossRef]
- Werner, C. Doppler Wind Lidar. In Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Springer: Berlin/Heidelberg, Germany, 2005; pp. 325–354. [Google Scholar]
- Reitebuch, O. Wind Lidar for Atmospheric Research. In Atmospheric Physics: Background–Methods–Trends; Springer: Berlin/Heidelberg, Germany, 2012; pp. 487–507. [Google Scholar]
- Richwine, D.M.; Curry, R.E.; Tracy, G.V. A Smoke Generator System for Aerodynamic Flight Research. 1989, NASA Technical Memorandum 1.15:4137. Available online: https://ntrs.nasa.gov/citations/19900004056 (accessed on 31 August 2023).
- Federal Aviation Administration Washington DC Flight Standards Service. Vortex Wake Turbulence. Flight Tests Conducted During 1970. 1971, FAA-FS-71. Available online: https://apps.dtic.mil/sti/citations/AD0724589, (accessed on 31 August 2023).
- Garodz, L.J.; Miller, N.J.; Lawrence, D. The Measurement of the DC-7 Trailing Vortex System Using the Tower Fly-by Technique. 1973. Available online: https://trid.trb.org/view/14311 (accessed on 31 August 2023).
- C-5A Wing Vortices Tests at NASA Langley Research Center. 1971. Available online: https://www.youtube.com/watch?v=RadGavdgKAk (accessed on 5 July 2023).
- Varentsov, M.; Stepanenko, V.; Repina, I.; Artamonov, A.; Bogomolov, V.; Kuksova, N.; Marchuk, E.; Pashkin, A.; Varentsov, A. Balloons and quadcopters: Intercomparison of two low-cost wind profiling methods. Atmosphere 2021, 12, 380. [Google Scholar] [CrossRef]
- Johansen, E.S.; Rediniotis, O.K.; Jones, G. The compressible calibration of miniature multi-hole probes. J. Fluids Eng. 2001, 123, 128–138. [Google Scholar] [CrossRef]
- Stainback, P.; Nagabushana, K. Review of hot-wire anemometry techniques and the range of their applicability for various flows. Electron. J. Fluids Eng. Trans. ASME 1993, 1, 4. [Google Scholar]
- Westerweel, J.; Elsinga, G.E.; Adrian, R.J. Particle image velocimetry for complex and turbulent flows. Annu. Rev. Fluid Mech. 2013, 45, 409–436. [Google Scholar] [CrossRef]
- Shinder, I.I.; Moldover, M.R.; Hall, J.; Duncan, M.; Keck, J. Airspeed calibration services: Laser Doppler anemometer calibration and its uncertainty. In Proceedings of the 8th International Symposium for Fluid Flow Measurement, Colorado Springs, CO, USA, 20–22 June 2012. [Google Scholar]
- Bean, V.E.; Hall, J.M. New primary standards for air speed measurement at NIST. In Proceeding of the 1999 NCSL Workshop and Symposium, Charlottle, NC, USA, 11–15 July 1999; Available online: https://www.nist.gov/system/files/documents/calibrations/ncsl_055.pdf (accessed on 31 August 2023).
- Arain, B.; Kendoul, F. Real-time wind speed estimation and compensation for improved flight. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1599–1606. [Google Scholar] [CrossRef]
- de Boer, G.; Borenstein, S.; Calmer, R.; Cox, C.; Rhodes, M.; Choate, C.; Hamilton, J.; Osborn, J.; Lawrence, D.; Argrow, B.; et al. Measurements from the university of colorado raaven uncrewed aircraft system during atomic. Earth Syst. Sci. Data 2022, 14, 19–31. [Google Scholar] [CrossRef]
- Van den Kroonenberg, A.; Martin, T.; Buschmann, M.; Bange, J.; Vörsmann, P. Measuring the wind vector using the autonomous mini aerial vehicle M2AV. J. Atmos. Ocean. Technol. 2008, 25, 1969–1982. [Google Scholar] [CrossRef]
- Starnes, M.W. The Study of an Acoustic Resonance Anemometer. PhD Thesis, Imperial College, London, UK, 2010. [Google Scholar]
- Kapartis, S. Anemometer Employing Standing Wave Normal to Fluid Flow and Travelling Wave Normal to Standing Wave. Google Patents Patent Number: US5877416A, 2 March 1999. [Google Scholar]
- Shimura, T.; Inoue, M.; Tsujimoto, H.; Sasaki, K.; Iguchi, M. Estimation of wind vector profile using a hexarotor unmanned aerial vehicle and its application to meteorological observation up to 1000 m above surface. J. Atmos. Ocean. Technol. 2018, 35, 1621–1631. [Google Scholar] [CrossRef]
- Adkins, K.; Wambolt, P.; Sescu, A.; Swinford, C.; Macchiarella, N.D. Observational Practices for Urban Microclimates Using Meteorologically Instrumented Unmanned Aircraft Systems. Atmosphere 2020, 11, 2020. [Google Scholar] [CrossRef]
- Palomaki, R.T.; Rose, N.T.; van den Bossche, M.; Sherman, T.J.; De Wekker, S.F. Wind estimation in the lower atmosphere using multirotor aircraft. J. Atmos. Ocean. Technol. 2017, 34, 1183–1191. [Google Scholar] [CrossRef]
- Schroeder, R.; Adkins, K.; James, C.; Kaplan, M.; Koch, S.; Ivanova, D.; Sinclair, M.; Compere, M.; Macchiarella, N.; Merkt, J.; et al. Detection of Convective Initiation and Suppression in Northern Arizonas Complex Terrain with Unmanned and Manned Aerial Systems. In Proceedings of the AGU Fall Meeting 2021, New Orleans, LA, 13–17 December 2021; p. A15G-1731. [Google Scholar]
- Vitalle, R.F.; Sunvold, D.; Dickinson, R.; Compere, M.; Krishnan, A.M.; Adkins, K. Final Report for Portable Traffic Management Tool for Wildfire Operations. Improving Aviation, LLC, 22-1-A3.04-2854, February 2023. Available online: https://sbir.nasa.gov/SBIR/abstracts/22/sbir/phase1/SBIR-22-1-A3.04-2854.html (accessed on 5 July 2023).
- Neumann, P.P.; Bartholmai, M. Real-time wind estimation on a micro unmanned aerial vehicle using its inertial measurement unit. Sens. Actuators Phys. 2015, 235, 300–310. [Google Scholar] [CrossRef]
- Meier, K.; Hann, R.; Skaloud, J.; Garreau, A. Wind Estimation with Multirotor UAVs. Atmosphere 2022, 13, 551. [Google Scholar] [CrossRef]
- Abichandani, P.; Lobo, D.; Ford, G.; Bucci, D.; Kam, M. Wind measurement and simulation techniques in multi-rotor small unmanned aerial vehicles. IEEE Access 2020, 8, 54910–54927. [Google Scholar] [CrossRef]
- González-Rocha, J.; Woolsey, C.A.; Sultan, C.; De Wekker, S.F. Sensing wind from quadrotor motion. J. Guid. Control Dyn. 2019, 42, 836–852. [Google Scholar] [CrossRef]
- Allison, S.; Bai, H.; Jayaraman, B. Wind estimation using quadcopter motion: A machine learning approach. Aerosp. Sci. Technol. 2020, 98, 105699. [Google Scholar] [CrossRef]
- Wang, L.; Misra, G.; Bai, X. AK Nearest neighborhood-based wind estimation for rotary-wing VTOL UAVs. Drones 2019, 3, 31. [Google Scholar] [CrossRef]
- Premerlani, W. Wind Estimation without an Airspeed Sensor. 29 January 2010. Available online: https://diydrones.com/forum/topics/wind-estimation-without-an (accessed on 31 August 2023).
- Premerlani, W. IMU Wind Estimation (Theory). 12 December 2009. Available online: https://storage.ning.com/topology/rest/1.0/file/get/3690830434?profile=original (accessed on 27 June 2023).
- Premerlani, W.; Bizard, P. Direction Cosine Matrix Imu: Theory. 17 May 2009. Available online: https://wiki.paparazziuav.org/w/images/e/e5/DCMDraft2.pdf (accessed on 27 June 2023).
- Mayer, S.; Hattenberger, G.; Brisset, P.; Jonassen, M.O.; Reuder, J. A ‘no-flow-sensor’ wind estimation algorithm for unmanned aerial systems. Int. J. Micro Air Veh. 2012, 4, 15–29. [Google Scholar] [CrossRef]
- Chitsaz, H.; LaValle, S.M. Time-optimal paths for a Dubins airplane. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 2379–2384. [Google Scholar]
- Liang, J.; Wang, S.; Wang, B. Online Motion Planning for Fixed-Wing Aircraft in Precise Automatic Landing on Mobile Platforms. Drones 2023, 7, 324. [Google Scholar] [CrossRef]
- SBG Systems. Reference Coordinate Frames. Available online: https://support.sbg-systems.com/sc/kb/latest/underlying-maths-conventions/reference-coordinate-frames (accessed on 5 July 2023).
- Censys Technologies. Censys Technologies, Sentaero 5. N.D. Available online: https://censystech.com/sentaero-5/ (accessed on 5 July 2023).
- Bevly, D.M.; Ryu, J.; Gerdes, J.C. Integrating INS sensors with GPS measurements for continuous estimation of vehicle sideslip, roll, and tire cornering stiffness. IEEE Trans. Intell. Transp. Syst. 2006, 7, 483–493. [Google Scholar] [CrossRef]

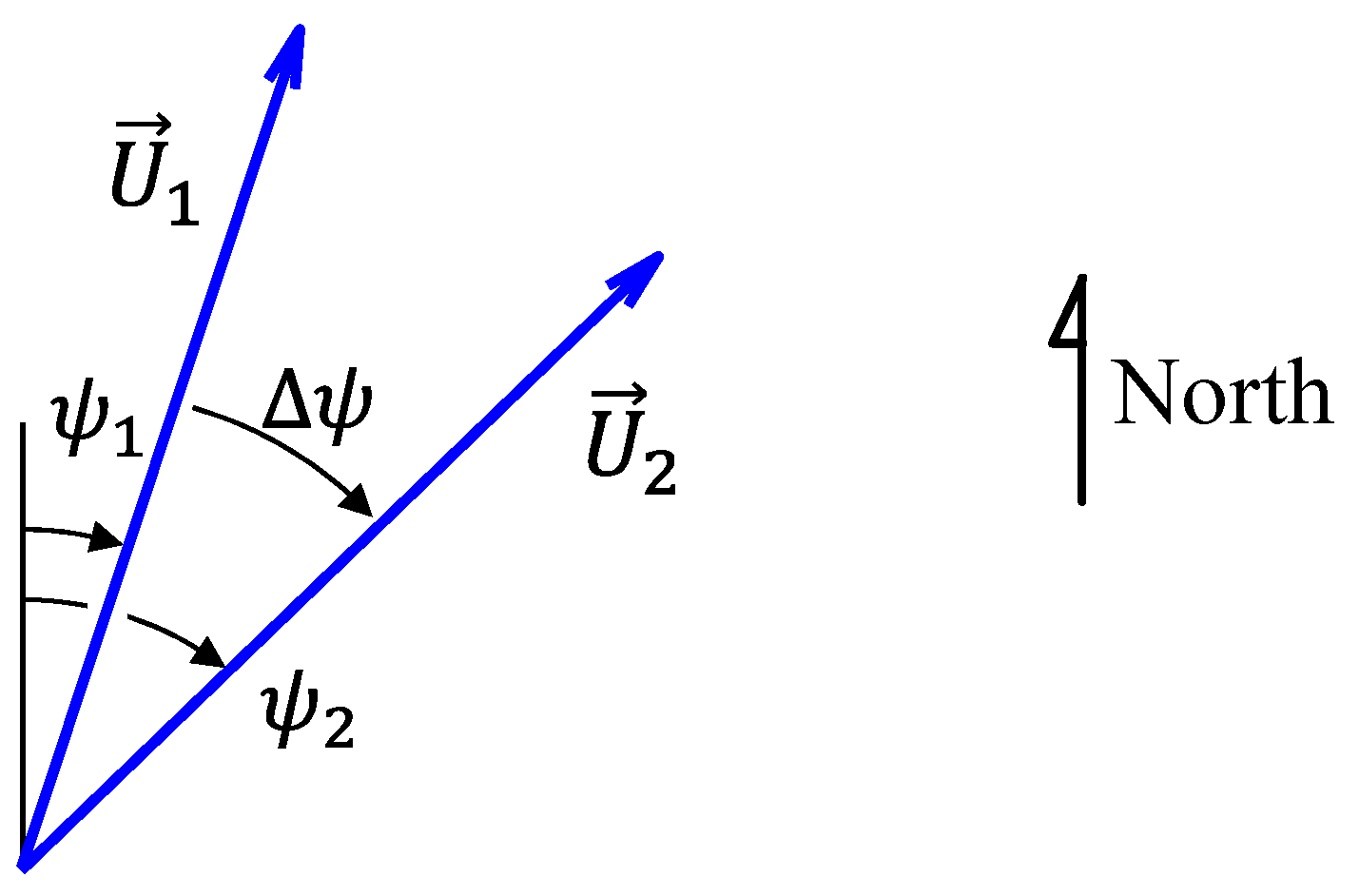





| Parameters | Value |
|---|---|
| Glide path angle, | 4.3° |
| Wingspan | 94 in (2.4 m) |
| Length | 50 in (1.3 m) |
| Cruise velocity | 45 mph (21 m/s) |
| Elevation rate, | 300 ft/min (1.5 m/s) |
| Flow Sensor Methods | Thrust and Drag Force Methods | Wind-Arc Method | |
|---|---|---|---|
| Hardware simplicity and generality | Low | Low to Moderate | High |
| Software simplicity and generality | Low | Low | High |
| Scalability, cost effectiveness | Low | Low | High |
| Accuracy for average wind speeds | Moderate to High | Moderate to High | Moderate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Compere, M.D.; Adkins, K.A.; Muthu Krishnan, A. Go with the Flow: Estimating Wind Using Uncrewed Aircraft. Drones 2023, 7, 564. https://doi.org/10.3390/drones7090564
Compere MD, Adkins KA, Muthu Krishnan A. Go with the Flow: Estimating Wind Using Uncrewed Aircraft. Drones. 2023; 7(9):564. https://doi.org/10.3390/drones7090564
Chicago/Turabian StyleCompere, Marc D., Kevin A. Adkins, and Avinash Muthu Krishnan. 2023. "Go with the Flow: Estimating Wind Using Uncrewed Aircraft" Drones 7, no. 9: 564. https://doi.org/10.3390/drones7090564
APA StyleCompere, M. D., Adkins, K. A., & Muthu Krishnan, A. (2023). Go with the Flow: Estimating Wind Using Uncrewed Aircraft. Drones, 7(9), 564. https://doi.org/10.3390/drones7090564







