Disturbance Interval Observer-Based Robust Constrained Control for Unmanned Aerial Vehicle Path Following
Abstract
1. Introduction
- A specific DIOB is developed for the position kinematics of the UAV. Through the appropriate use of the information in the inertial framework, it is capable of providing interval estimation of the wind disturbances and providing more robustness for the feedforward compensation;
- The Serret–Frenet frame is introduced to transform the path-following problem of the UAV into a general stabilizing control one. By improving the dynamic surface control technique, the resulting flight control design can address the non-affine nonlinearity of the UAV kinematics;
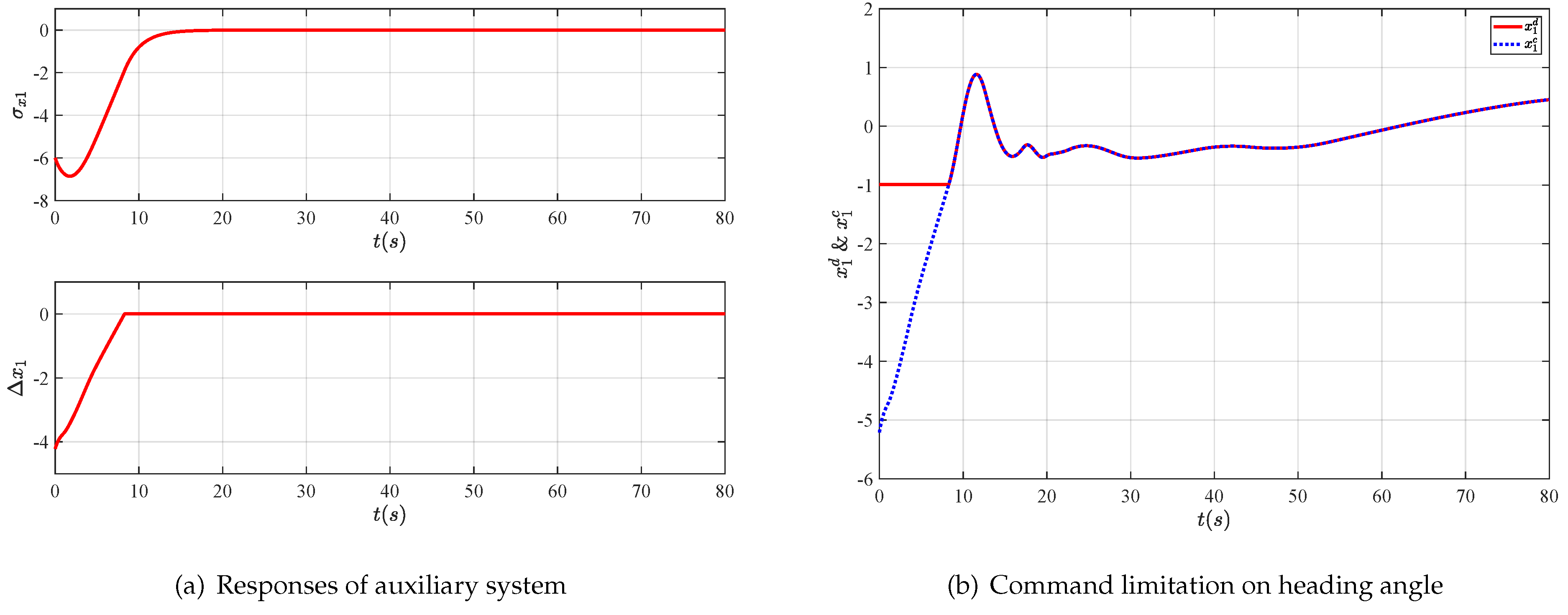
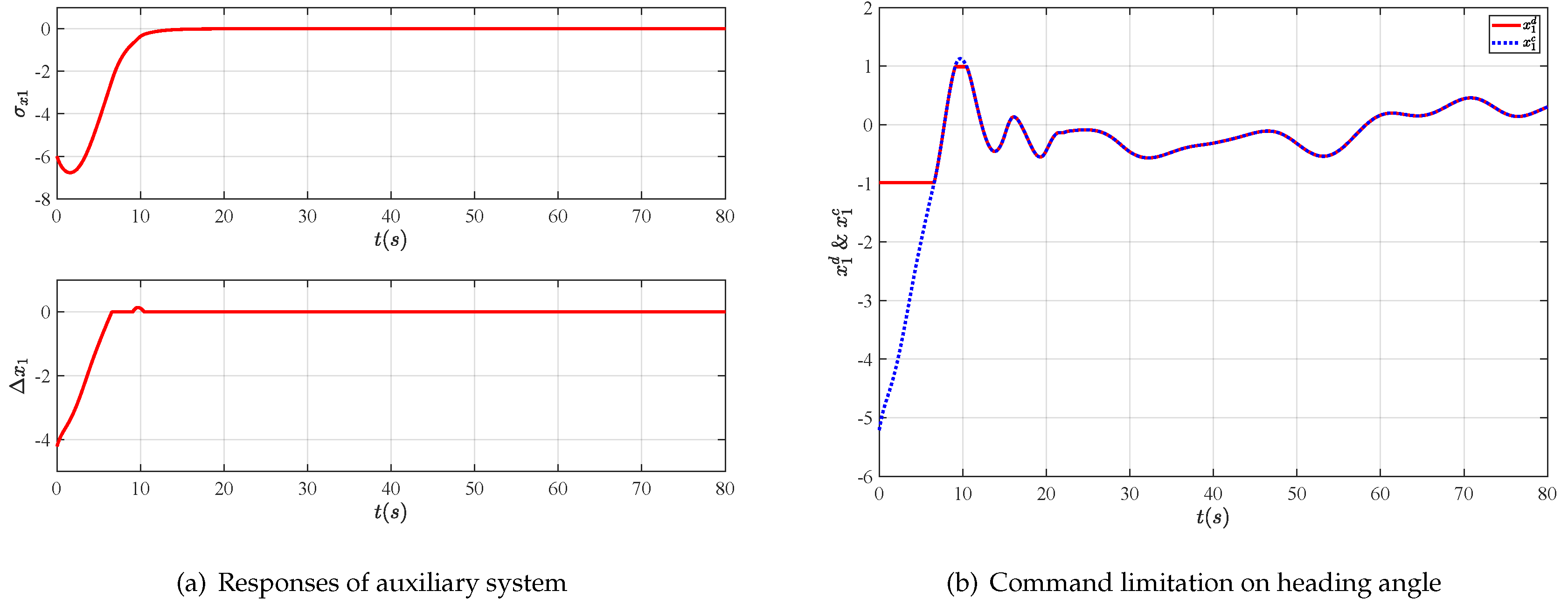
- An auxiliary system is employed to address the command limitation on the heading angle of the UAV. Specifically, the stiff saturation nonlinearity is replaced with a saturation-like smooth nonlinear, which guarantees the differentiability of the virtual control law.
- denotes the real number set, is an n-dimensional Euclidean space; meanwhile, and ;
- For the given matrix or vector , define , and ;
- For given matrices or vectors and , denotes that for any have ;
- For the given real symmetric matrix , and represent that the matrix is positive or negative definite, respectively;
- For the given real symmetric matrix , represents the maximum characteristic root of matrix ;
- For the given matrix or vector , denotes the transpose matrix of ;
- For the given vector , denotes the Euclidean norm of .
2. Problem Formulation and Preliminaries
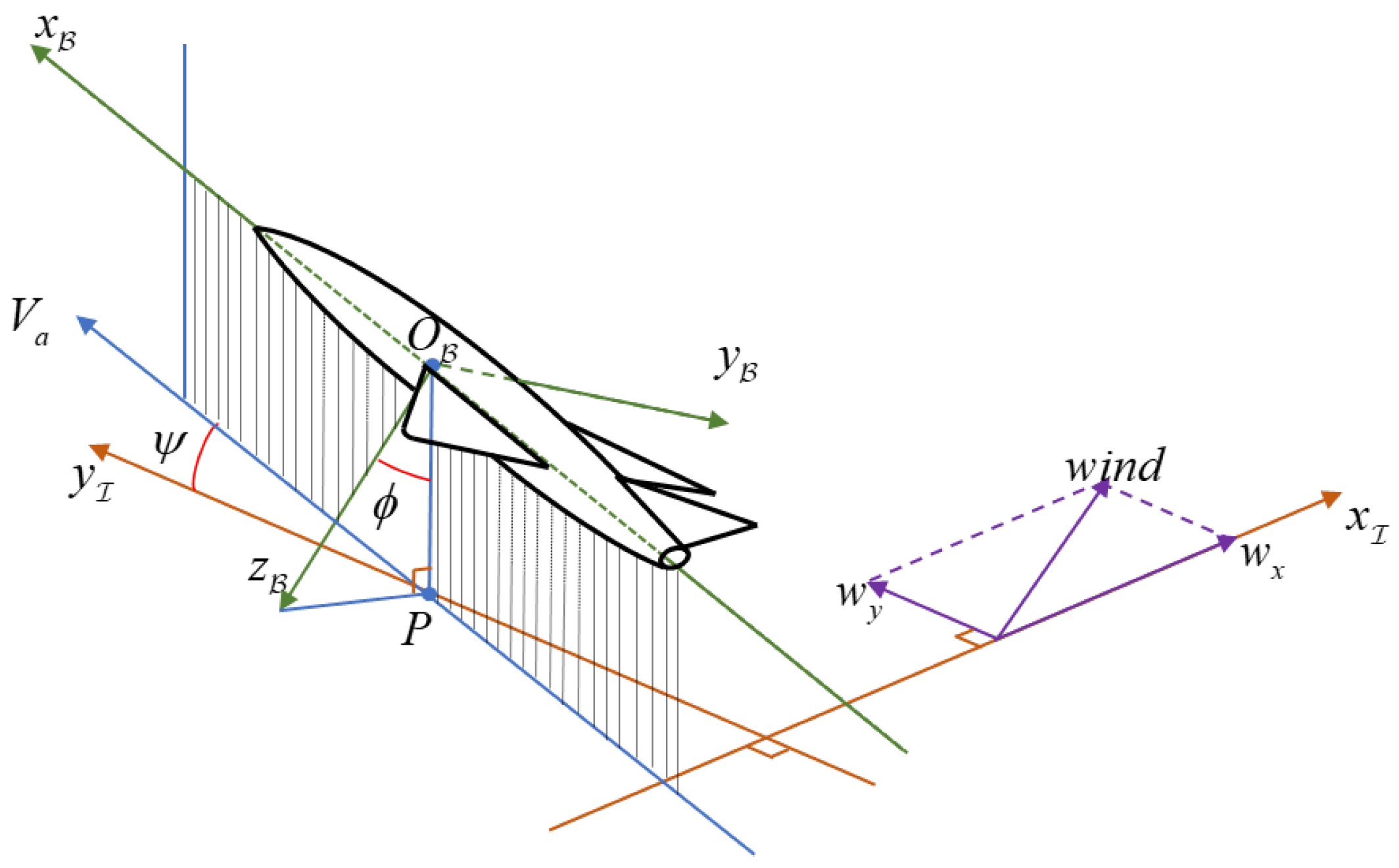
2.1. UAV Kinematics in Inertial Frame
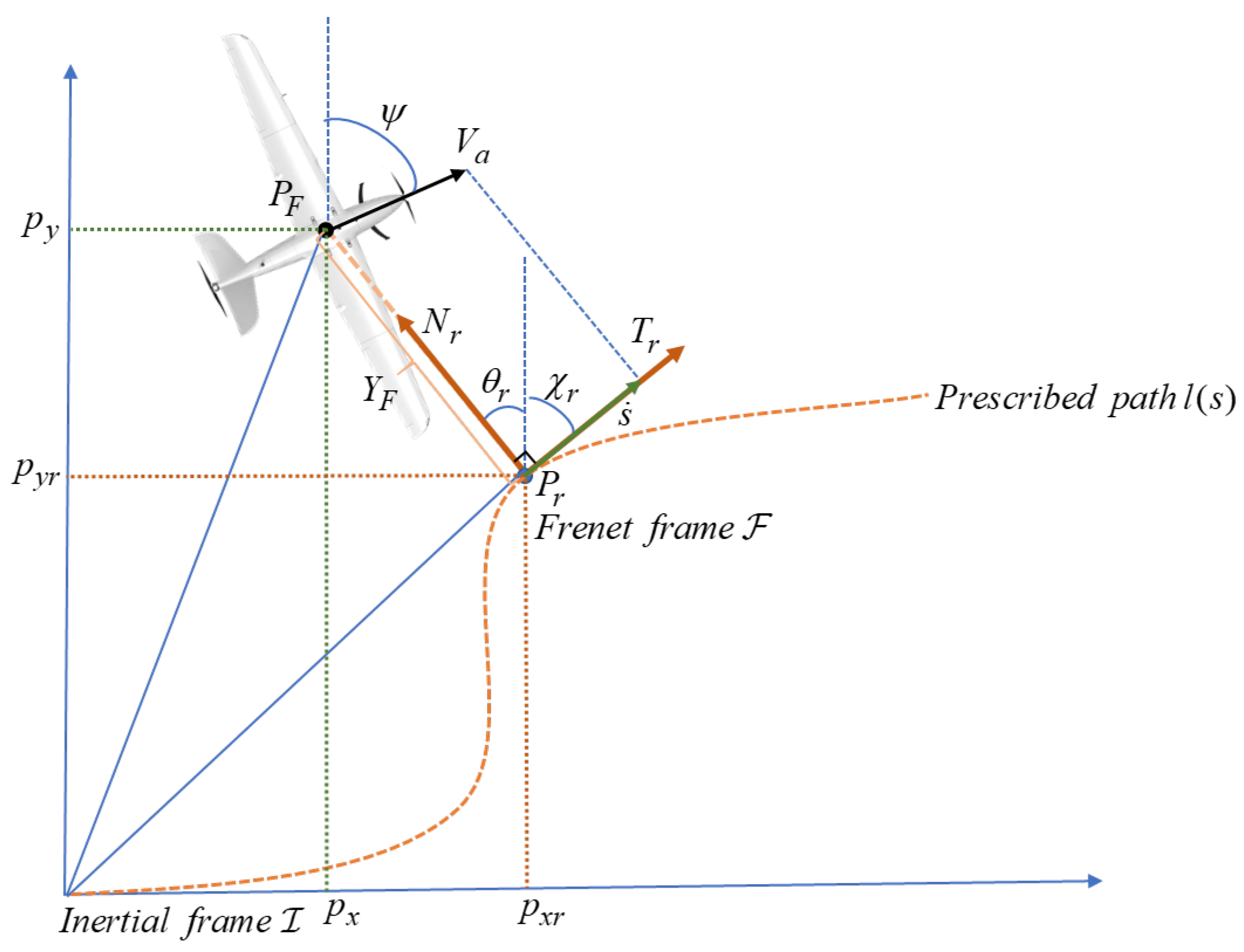
2.2. Path Following Based on the Serret–Frenet Frame
2.3. Control Objective
3. Control Design and Stability Analysis
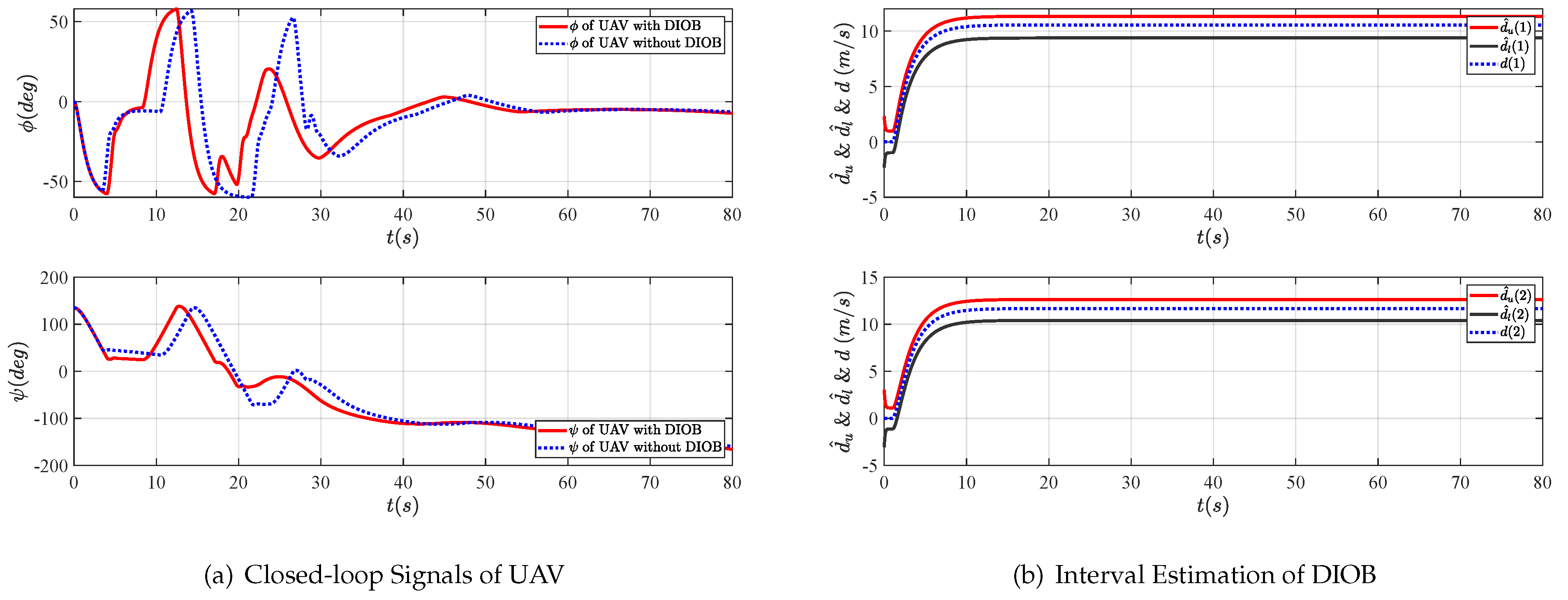
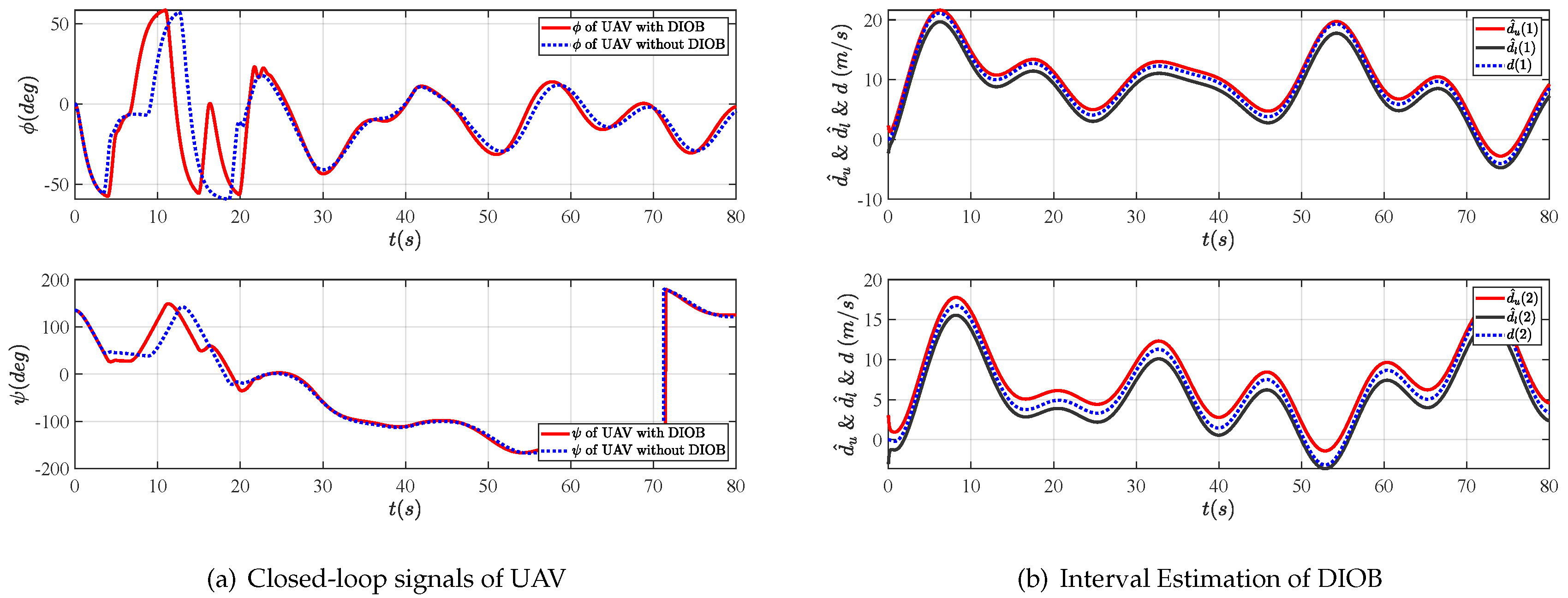
3.1. Disturbance Interval Observer Design
- If the designed matrices and make be simultaneously Metzler and Hurwitz;
- If the initial conditions of and satisfy .
3.2. Robust Constrained Control Design
3.3. Stability Analysis
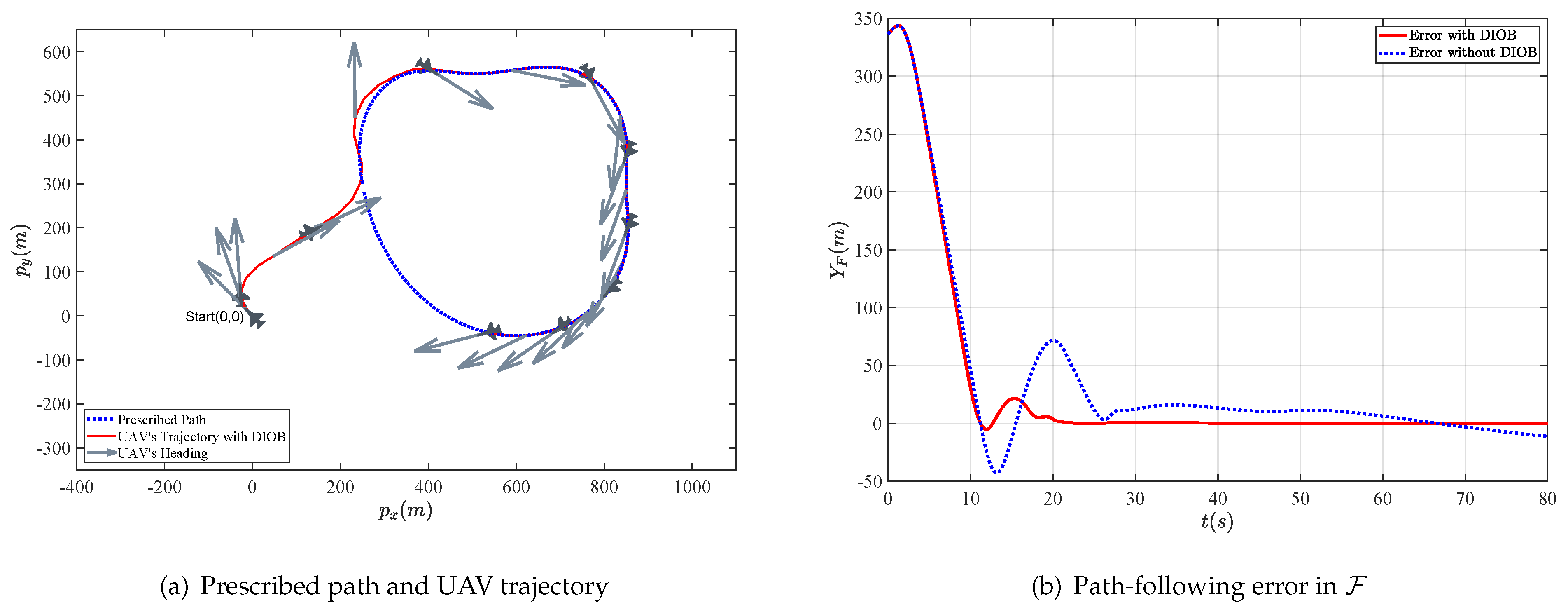
4. Simulations
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Yong, K. Disturbance interval observer-based carrier landing control of unmanned aerial vehicles using prescribed performance. Sci. Sin. Informationis 2022, 52, 1711. [Google Scholar] [CrossRef]
- Chen, M.; Xiong, S.; Wu, Q. Tracking flight control of quadrotor based on disturbance observer. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1414–1423. [Google Scholar] [CrossRef]
- Ye, H.; Chen, M.; Zeng, Q. Horizontal motion tracking control for an underwater vehicle with environmental disturbances. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 4952–4957. [Google Scholar] [CrossRef]
- Yong, K.; Chen, M.; Wu, Q. Immersion and invariance-based integrated guidance and control for unmanned aerial vehicle path following. Int. J. Syst. Sci. 2019, 50, 1052–1068. [Google Scholar] [CrossRef]
- Beard, R.W.; Ferrin, J.; Humpherys, J. Fixed wing UAV path following in wind with input constraints. IEEE Trans. Control. Syst. Technol. 2014, 22, 2103–2117. [Google Scholar] [CrossRef]
- Aguiar, A.P.; Hespanha, J.P.; Kokotovic, P.V. Path-following for nonminimum phase systems removes performance limitations. IEEE Trans. Autom. Control 2005, 50, 234–239. [Google Scholar] [CrossRef]
- Aguiar, A.P.; Hespanha, J.P. Trajectory-tracking and path-following of underactuated autonomous vehicles with parametric modeling uncertainty. IEEE Trans. Autom. Control 2007, 52, 1362–1379. [Google Scholar] [CrossRef]
- Park, S.; Deyst, J.; How, J.P. Performance and lyapunov stability of a nonlinear path following guidance method. J. Guid. Control Dyn. 2007, 30, 1718–1728. [Google Scholar] [CrossRef]
- Kaminer, I.; Pascoal, A.; Xargay, E.; Hovakimyan, N.; Cao, C.; Dobrokhodov, V. Path following for small unmanned aerial vehicles using L1 adaptive augmentation of commercial autopilots. J. Guid. Control Dyn. 2010, 33, 550–564. [Google Scholar] [CrossRef]
- Nelson, D.R.; Barber, D.B.; McLain, T.W.; Beard, R.W. Vector field path following for miniature air vehicles. IEEE Trans. Robot. 2007, 23, 519–529. [Google Scholar] [CrossRef]
- Chen, H.; Chang, K.; Agate, C.S. UAV path planning with tangent-plus-Lyapunov vector field guidance and obstacle avoidance. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 840–856. [Google Scholar] [CrossRef]
- Frew, E.W.; Lawrence, D. Tracking dynamic star curves using guidance vector fields. J. Guid. Control Dyn. 2017, 40, 1488–1495. [Google Scholar] [CrossRef]
- Xargay, E.; Kaminer, I.; Pascoal, A.; Hovakimyan, N.; Dobrokhodov, V.; Cichella, V.; Aguiar, A.P.; Ghabcheloo, R. Time-critical cooperative path following of multiple unmanned aerial vehicles over time-varying networks. J. Guid. Control Dyn. 2013, 36, 499–516. [Google Scholar] [CrossRef]
- Furieri, L.; Stastny, T.; Marconi, L.; Siegwart, R.; Gilitschenski, I. Gone with the wind: Nonlinear guidance for small fixed-wing aircraft in arbitrarily strong windfields. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 4254–4261. [Google Scholar] [CrossRef]
- Gavilan, F.; Vazquez, R.; Camacho, E.F. An iterative model predictive control algorithm for UAV guidance. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2406–2419. [Google Scholar] [CrossRef]
- Fan, Y.; Zou, X.; Wang, G.; Mu, D. Robust Adaptive Path Following Control Strategy for Underactuated Unmanned Surface Vehicles with Model Deviation and Actuator Saturation. Appl. Sci. 2022, 12, 2696. [Google Scholar] [CrossRef]
- Huang, Y.; Shi, X.; Huang, W.; Chen, S. Internal Model Control-Based Observer for the Sideslip Angle of an Unmanned Surface Vehicle. J. Mar. Sci. Eng. 2022, 10, 470. [Google Scholar] [CrossRef]
- Yong, K.; Chen, M.; Wu, Q. Noncertainty-equivalent observer-based noncooperative target tracking control for unmanned aerial vehicles. Sci. China Inf. Sci. 2022, 65, 152202. [Google Scholar] [CrossRef]
- Manchester, I.R.; Savkin, A.V. Circular navigation missile guidance with incomplete information and uncertain autopilot model. J. Guid. Control Dyn. 2004, 27, 1078–1083. [Google Scholar] [CrossRef]
- Feng, Z.; Pan, Z.; Chen, W.; Liu, Y.; Leng, J. USV Application Scenario Expansion Based on Motion Control, Path Following and Velocity Planning. Machines 2022, 10, 310. [Google Scholar] [CrossRef]
- Patrikar, J.; Makkapati, V.R.; Pattanaik, A.; Parwana, H.; Kothari, M. Nested saturation based guidance law for unmanned aerial vehicles. J. Dyn. Syst. Meas. Control 2019, 141, 071008. [Google Scholar] [CrossRef]
- Kukreti, S.; Kumar, M.; Cohen, K. Genetically tuned LQR based path following for UAVs under wind disturbance. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 267–274. [Google Scholar] [CrossRef]
- Liang, Y.; Jia, Y.; Wang, Z.; Matsuno, F. Combined vector field approach for planar curved path following with fixed-wing UAVs. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 5980–5985. [Google Scholar] [CrossRef]
- Rucco, A.; Aguiar, A.P.; Pereira, F.L.; de Sousa, J.B. A predictive path-following approach for fixed-wing unmanned aerial vehicles in presence of wind disturbances. In Proceedings of the Robot 2015: Second Iberian Robotics Conference, Lisbon, Portugal, 19–21 November 2015; Springer: Cham, Switzerland, 2016; pp. 623–634. [Google Scholar] [CrossRef]
- Gao, J.; Wang, P.; Tang, Z. An Accurate Path Following Algorithm of UAVs Under Crosswind Disturbance. Int. Conf. Auton. Unmanned Syst. 2021, 1717–1727. [Google Scholar] [CrossRef]
- Tanaka, K.; Tanaka, M.; Takahashi, Y.; Iwase, A.; Wang, H.O. 3-D flight path tracking control for unmanned aerial vehicles under wind environments. IEEE Trans. Veh. Technol. 2019, 68, 11621–11634. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Sun, M.; Zhang, X. Trajectory tracking control of a quadrotor UAV based on sliding mode active disturbance rejection control. Nonlinear Anal. Model. Control 2019, 24, 545–560. [Google Scholar] [CrossRef]
- Cabecinhas, D.; Cunha, R.; Silvestre, C. A globally stabilizing path following controller for rotorcraft with wind disturbance rejection. IEEE Trans. Control Syst. Technol. 2014, 23, 708–714. [Google Scholar] [CrossRef]
- Brezoescu, A.; Espinoza, T.; Castillo, P.; Lozano, R. Adaptive trajectory following for a fixed-wing UAV in presence of crosswind. J. Intell. Robot. Syst. 2013, 69, 257–271. [Google Scholar] [CrossRef]
- Chen, M.; Chen, W.H. Sliding mode control for a class of uncertain nonlinear system based on disturbance observer. Int. J. Adapt. Control Signal Process. 2010, 24, 51–64. [Google Scholar] [CrossRef]
- Li, R.; Chen, M.; Wu, Q. Adaptive neural tracking control for uncertain nonlinear systems with input and output constraints using disturbance observer. Neurocomputing 2017, 235, 27–37. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J.; Dong, Z. Neuroadaptive learning algorithm for constrained nonlinear systems with disturbance rejection. Int. J. Robust Nonlinear Control 2022. [Google Scholar] [CrossRef]
- Liu, C.; McAree, O.; Chen, W.H. Path-following control for small fixed-wing unmanned aerial vehicles under wind disturbances. Int. J. Robust Nonlinear Control 2013, 23, 1682–1698. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M. Robust discrete-time fractional-order control for an unmanned aerial vehicle based on disturbance observer. Int. J. Robust Nonlinear Control 2022, 32, 4665–4682. [Google Scholar] [CrossRef]
- Yang, G. Asymptotic tracking with novel integral robust schemes for mismatched uncertain nonlinear systems. Int. J. Robust Nonlinear Control 2022, 33, 1988–2002. [Google Scholar] [CrossRef]
- Yong, K.; Chen, M.; Shi, Y.; Wu, Q. Hybrid estimation strategy-based anti-disturbance control for nonlinear systems. IEEE Trans. Autom. Control 2020, 66, 4910–4917. [Google Scholar] [CrossRef]
- Yong, K.; Chen, M.; Wu, Q. Anti-disturbance control for nonlinear systems based on interval observer. IEEE Trans. Ind. Electron. 2019, 67, 1261–1269. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, L. Robust path-following control of a container ship based on Serret–Frenet frame transformation. J. Mar. Sci. Technol. 2020, 25, 69–80. [Google Scholar] [CrossRef]
- Liu, C.; McAree, O.; Chen, W.H. Path following for small UAVs in the presence of wind disturbance. In Proceedings of the 2012 UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 613–618. [Google Scholar] [CrossRef]
- Murray, R.M.; Li, Z.; Sastry, S.S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zhao, S.; Wang, X.; Zhang, D.; Shen, L. Curved path following control for fixed-wing unmanned aerial vehicles with control constraint. J. Intell. Robot. Syst. 2018, 89, 107–119. [Google Scholar] [CrossRef]
- Poksawat, P.; Wang, L.; Mohamed, A. Gain scheduled attitude control of fixed-wing UAV with automatic controller tuning. IEEE Trans. Control. Syst. Technol. 2017, 26, 1192–1203. [Google Scholar] [CrossRef]
- Polycarpou, M.M.; Ioannou, P.A. A robust adaptive nonlinear control design. In Proceedings of the 1993 American Control Conference, San Francisco, CA, USA, 2–4 June 1993; pp. 1365–1369. [Google Scholar] [CrossRef]
- Gouzé, J.L.; Rapaport, A.; Hadj-Sadok, M.Z. Interval observers for uncertain biological systems. Ecol. Model. 2000, 133, 45–56. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S.; Ren, B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints. Automatica 2011, 47, 452–465. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, X. Command filter and universal approximator based backstepping control design for strict-feedback nonlinear systems with uncertainty. IEEE Trans. Autom. Control 2019, 65, 1310–1317. [Google Scholar] [CrossRef]
- Wang, R.; Jing, H.; Hu, C.; Yan, F.; Chen, N. Robust H∞ Path Following Control for Autonomous Ground Vehicles With Delay and Data Dropout. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2042–2050. [Google Scholar] [CrossRef]
- Valavanis, K.P.; Vachtsevanos, G.J. Handbook of Unmanned Aerial Vehicles; Springer: Berlin/Heidelberg, Germany, 2015; Volume 1. [Google Scholar]


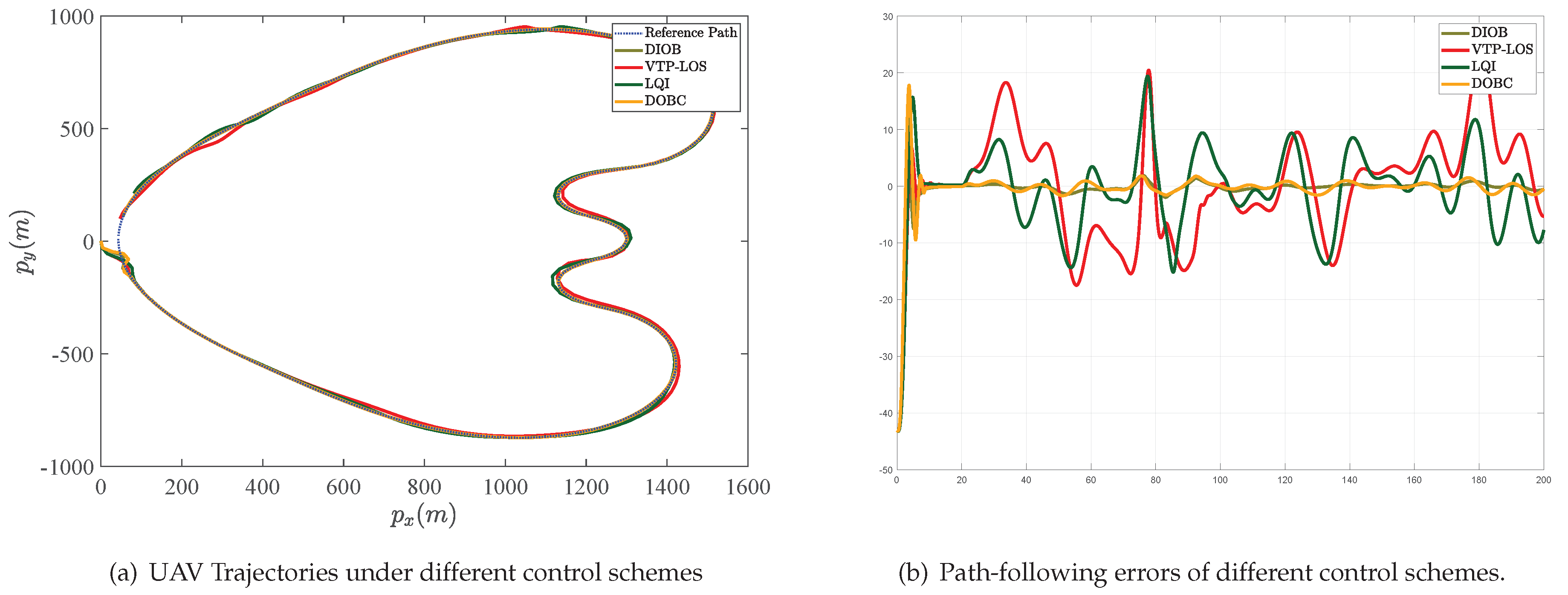
| Names of Methods | ||
|---|---|---|
| DIOB | 176.0 | 65.1 |
| VTP | 1448.6 | 62.6 |
| LQI | 1044.2 | 65.8 |
| DOBC | 230.6 | 67.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Yong, K.; Wang, X. Disturbance Interval Observer-Based Robust Constrained Control for Unmanned Aerial Vehicle Path Following. Drones 2023, 7, 90. https://doi.org/10.3390/drones7020090
Song Y, Yong K, Wang X. Disturbance Interval Observer-Based Robust Constrained Control for Unmanned Aerial Vehicle Path Following. Drones. 2023; 7(2):90. https://doi.org/10.3390/drones7020090
Chicago/Turabian StyleSong, Yaping, Kenan Yong, and Xiaolong Wang. 2023. "Disturbance Interval Observer-Based Robust Constrained Control for Unmanned Aerial Vehicle Path Following" Drones 7, no. 2: 90. https://doi.org/10.3390/drones7020090
APA StyleSong, Y., Yong, K., & Wang, X. (2023). Disturbance Interval Observer-Based Robust Constrained Control for Unmanned Aerial Vehicle Path Following. Drones, 7(2), 90. https://doi.org/10.3390/drones7020090







