Abstract
Clustering is an effective solution to improve the management efficiency of large-scale systems. One one hand, UAVs performing the same task have a similar moving tendency. One the other hand, the network topology of the UAV swarms is dynamically changing. Considering the above two aspects, our main contributrons are designing a group-oriented distributed clustering algorithm based on the coalition game that couples task attributes and communication attributes. The clustering goal is to divide UAVs performing the same task into one cluster and make each cluster have more UAVs under the cluster size limits, thus improving communication efficiency. The proposed algorithm comprehensively considers the task group information and communication link stability as the coalition value. UAVs decide whether to leave their current coalition based on coalition values. Through periodic parallel switch operations selection, UAVs are divided into the desired clustering structure. Simulations verify that our clustering algorithm is effective and better than the existing ones, especially in communication link stability, cluster numbers, and load balance.
1. Introduction
With low development and maintenance costs, ease of deployment, and high flexibility, UAV swarms have been used in various complex missions, including area surveillance [1], search and rescue [2], and relay communication [3]. In these applications, the information transmission and task collaboration among UAVs require real-time and reliable communication networks.
Multi-UAV networks are one form of mobile ad hoc networks (MANET) [4]. In the case of infrastructure absence (e.g., disaster areas), there is an urgent need to build a reliable and secure communication network between UAVs [5,6]. Based on the network architecture, UAV networks include flat and hierarchical networks [7]. A flat network is composed of homogeneous UAVs with similar responsibilities. Multi-hop communication is adopted in data transmission of the flat network, which increases the end-to-end delay and consumes more energy [8]. Therefore, the scalability and performance of the flat topology network will decrease for large UAV swarms. In the hierarchical network, the UAVs are divided into several clusters through clustering algorithms. Each cluster includes the cluster head (CH) and cluster member nodes. The cluster head aggregates the data of cluster members and sends it to the sink node directly or through another cluster head.
Compared with the flat network structure, the hierarchical network has more efficient topology management and better network performance which are often used when UAVs cooperate to perform tasks [9,10]. Therefore, we need to solve the clustering problem of the UAV swarm efficiently to get a hierarchical network.
Many works focus on the clustering problem for UAVs without particular organizations. However, UAVs are often allocated to different task groups in some applications, such as target tracking, search and rescue, and round-up. Ref. [11] proposes a topology management mechanism for hierarchical group-oriented networks to enable nodes to be organized into multiple interest groups in the same geographic area. Ref. [12] defined the structured network with an internal hierarchy in which nodes belong to operation groups, e.g., squad, section. Multi-UAV networks are typically structured networks as UAVs often need to perform collaborative tasks. Nodes with the same task have similar moving tendencies and need to frequently exchange information. For these two reasons, to provide a more stable network and better end-to-end quality of service (QoS), designing a clustering algorithm that considers group information is necessary.
1.1. Related Work
Table 1 shows some studies on the clustering of UAV swarms in the last few years. Many works are dedicated to solving clustering problems efficiently. The performance of a clustering algorithm depends on the number and distribution of CHs in the network. Most existing clustering methods first select some nodes as cluster heads according to one or more specific indicators, such as residual energy, mobility, energy efficiency, distance, and node degree. LEACH (Low-Energy Adaptive Clustering Hierarchy) [13] is one of the most classic cluster-based routing protocols, which ensures balanced energy utilization through random cluster head selection. As most LEACH-based protocols give no guarantee that cluster heads are uniformly distributed in the network, Ref. [14] propose a BN-LEACH protocol to select cluster heads using a Bayesian Network (BN) model, which can distribute cluster heads uniformly, while [15] adopts the multiple criteria decision-making method of an intuitionistic fuzzy Analytic Hierarchy Process (AHP) and hierarchical fuzzy integration for cluster head selection to obtain the energy-balanced cluster structure.

Table 1.
Related works on clustering for the UAV swarm.
Once the cluster heads are selected, non-CH nodes need to decide which clusters to join. In the cluster formation process, the node regards its distance to CH as the main criterion while utilizing the strength of the received signal for the distance estimation [22]. Many works incorporate other parameters, including the energy of CH, the distance between CH and the base station, cluster size, and mobility. The dynamic mobility-based multi-hop clustering (DMMHC) algorithm in [16] utilizes moving direction, relative position, and link lifetime estimation to improve cluster stability and reduce maintenance and communication costs. In addition, some studies treat clustering as an NP-hard problem and apply optimization algorithms to different clustering processes, such as CH selection, cluster formation, and finding the optimal cluster numbers [17].
Game theory has recently been applied in many fields, such as resource allocation, network formation, and interference. In addition, there are some works that use game theory to solve the clustering problem. A clustering protocol employing the evolutionary game is proposed in [18] considering node mobility, residual energy, and channel availability for cluster head selection. In [23], a link-weight function (based on a combination of link-stability and link-connectivity ratio functions) is adopted in the minimum connected weighted inner edge spanning tree (MWIEST) game to find an approximate solution for clustering. Ref. [19] combined non-cooperative game theory techniques with a decentralized clustering algorithm to maximize the network lifetime. Ref. [20] proposed the coalitional game-theoretic clustering (CGTC) algorithm, which partitioned the entire network area into two regions (far and vicinity) to reduce energy consumption and improve throughput. Therefore, employing the game theory to design a clustering algorithm for the self-organizing UAV network is natural. Based on group information and node mobility, Ref. [21] designed a distributed coalition game clustering algorithm for Multi-UAV networks. Therefore, employing the game theory to design a clustering algorithm for the self-organizing UAV network is natural.
1.2. Main Work and Contributions
Based on the mobility and group information of UAV swarms, this paper proposes a distributed clustering algorithm that considers communication link stability and task attributes. Our work employs the coalition game theoretical framework to solve the group-oriented clustering problem in multi-UAV networks. Extensive simulations show that our algorithm outperforms other clustering algorithms for group-oriented clustering problems in communication link stability and load balance. In addition, our method can ensure that UAVs in the same group are divided into one cluster, which is better than comparison algorithms. The main contributions are as follows:
- Defining a compound correlation combines multiple indicators of the clustering problem into a single indicator, thus easing the analysis of cluster rewards. The compound correlation combines communication link stability and task group information by designing the adaptive weights based on the information of cluster members.
- A distributed clustering algorithm is designed based on the coalition game for the network management of large-scale UAV swarms. UAV nodes are the game participants, and each cluster refers to one coalition. The total compound correlation value of the cluster is the coalition reward. Through a series of switch operations of nodes, a stable coalition structure is achieved.
- A distributed parallel clustering mechanism is designed based on cellular automata. UAVs switch between idle and busy states, and only idle nodes can participate in new switch operations, which improves clustering efficiency.
1.3. Organization
The rest of this paper is organized as follows. Section 2 describes the problem formulation and defines the group-oriented structured clustering problem. In Section 3, the optimization goal of the clustering problem is given based on the proposed compound correlation. Section 4 details the design of the distributed parallel structured clustering algorithm based on the coalition game. Section 5 shows the comparative simulations and corresponding performance evaluation. Finally, Section 6 concludes the paper.
2. Problem Formulation
N UAVs that include M task groups are deployed in mission areas. denotes the set of all UAVs. The group set of UAVs is defined as , while the size of group is . In most applications, UAVs in the same group need to share detection information frequently. Figure 1 shows that the UAV swarm with M task groups is divided into several clusters to perform missions cooperatively.
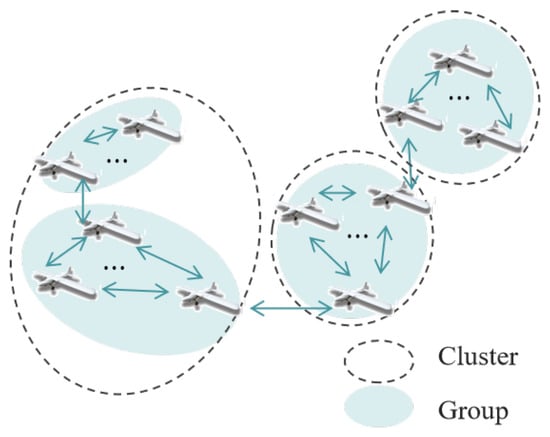
Figure 1.
The network of UAV swarms consisted of several clusters with different task groups.
Assume that the UAV network is an undirected graph where represents the vertex set and denotes the edge set related to N UAVs. UAVs i and j are neighbors if , representing that the two nodes are within the communication range of each other. Let denote the neighbor set of node i. In order to promote the management of the communication network, the clustering approach divides the UAV swarm into K disjoint clusters denoted . denotes the kth cluster with the corresponding UAV set . The size of cluster is , while and the corresponding edge set form the subgraph . Table 2 shows the list of major notations used throughout this paper.

Table 2.
Major notations.
2.1. Clustering Constraints
This paper adopts multi-hop communication for intra-cluster information exchange, supported by intra-cluster Radio Resource Allocation (RRA). The performance of intra-cluster RRA is directly related to the cluster topology, such as network topology connectivity, number of cluster members, and cluster diameter. The cluster diameter is the diameter of the cluster network topology. Cluster connectivity can ensure that any pair of nodes in the cluster communicates through intra-cluster links. However, more cluster members will make the resource load of the cluster larger, while adding the cluster diameter will increase communication delay and cost.
Therefore, we impose some constraints on the topology of each cluster as follows:
- (1)
- The network topology of cluster is connected.
- (2)
- The number of nodes () in cluster can be at most , namely .
- (3)
- The diameter of cluster cannot exceed the maximum diameter , that is, .
2.2. Communication Link Correlation
In this part, we define the communication link correlation according to the relative mobility of UAVs. First, we need to obtain the relative states between each UAV and its neighbors. To estimate the relative state information, Ref. [24] designs a distributed predefined-time state observer. In addition, Ref. [25] adopts two consecutive HELLO information to estimate the relative velocity. In this paper, we simply assume that UAVs can get the speed of others through multi-hop communication. Then, UAV can calculate the relative speed between its neighbors and itself.
The relative movement model between UAV i and UAV j is shown in Figure 2. A is the current position of UAV i, while UAV j is located at B and moves towards C with velocity relative to UAV i. Assume that the relative movement velocity remains for a short period. We define the communication link correlation between UAVs i and j as follows:
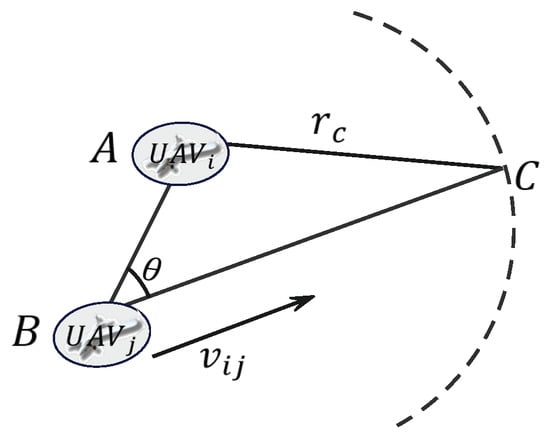
Figure 2.
The diagram of the relative movement between two UAVs.
is the link lifetime threshold. denotes the distance between positions B and C, which can be calculated from the geometric relationship in Figure 2:
The greater the communication link correlation, the more stable the communication link is.
2.3. Group-Oriented Structured Clustering Problem
Clustering is essentially a swarm partition problem. On the one hand, too many clusters will increase the communication delay and cost between different clusters of the UAV swarm. On the other hand, UAVs performing the same task frequently exchange information and should be divided into one cluster. In addition, considering the mobility of UAVs, gathering UAVs with high communication link correlation into one cluster can make the clustering structure more stable. Based on the above analysis, we define the group-oriented structured clustering problem of the UAV swarm as follows.
Definition 1
(Group-oriented structured clustering problem). Given the UAV swarm with task group , finding the clustering structure that divides N UAVs of the swarm into K disjoint clusters so that the following goals can be realized under the premise of satisfying the constraints in Section 2.1:
- Goal 1:
- The number of UAVs in one cluster should achieve as high a maximum as possible.
- Goal 2:
- UAVs in the same task group should be in one cluster.
- Goal 3:
- The clustering structure should have high total intra-cluster communication link correlation.
Remark 1.
The total inter-cluster communication link correlation is the smallest, and the corresponding total intra-cluster communication link correlation is the largest.
3. Clustering Rewards Based on Compound Correlation
In this section, the three goals of the group-oriented structured clustering problem are fused by proposing the concept of compound correlation. Moreover, we also give the optimal objective function of the clustering problem.
3.1. Compound Correlation
The compound correlation between UAVs i and j that couples the communication link correlation and group information is defined:
where and are the corresponding weights. denotes the group correlation between UAVs i and j:
is the group to which UAV i belongs.
The total intra-cluster compound correlation of cluster is the following:
Theorem 1 shows that the merge of two clusters can always increase the intra-cluster communication link correlation as long as the clustering constraints are satisfied, which means that clusters with maximal size can be built. Therefore, Goals 1 and 3 in Definition 1 can be fused, then Goal 1 can be ignored in subsequent analysis.
Theorem 1.
The merge of two clusters will increase the intra-cluster communication link correlation as long as the clustering constraints are satisfied.
Proof.
See Appendix A. □
We combine Goals 2 and 3 by building the compound correlation indicator in (3). It is proven in Theorem 2 that the more UAVs in the cluster belong to the same group, the higher the total intra-cluster compound correlation.
Theorem 2.
When more UAVs belong to the same group divided into one cluster, the total intra-cluster compound correlation will be higher.
Proof.
See Appendix B. □
Through the above analysis, we have fused the three goals of the structured clustering problem into a compound correlation indicator. Therefore, we can build a clustering structure that fulfills the desired goals by aggregating UAVs with higher compound correlation.
3.2. Adaptive Weight
To optimize the clustering result, in this part, we utilize the information of the cluster members to design the adaptive weights of the group correlation and communication link correlation in the compound correlation.
According to Goal 2 of the clustering problem, we hope that each cluster has more UAVs belonging to the same group. For group to which UAV i belongs, we define the adaptive weight of the group correlation item as the following:
is the size of group and is the number of UAVs belonging to in cluster . It indicates that the more UAVs belonging to the same group in the cluster, the larger the group weight is, which further verifies the rationality of the defined compound correlation.
For Goal 3 of the clustering problem, aggregating UAVs with higher communication link correlations to one cluster will increase the total intra-cluster communication link correlation. We give the adaptive weight of the communication link correlation item by the maximum and the average communication link correlation in the cluster, that is:
is the average communication link correlation of cluster . When the cluster size keeps constant, the high average communication link correlation of the cluster indicates that the total intra-cluster link correlation is also large.
3.3. The Objective Function of Clustering
The objective of clustering is to find the partition that maximizes the intra-cluster compound correlation of all clusters, which can fulfill the desired three goals in Definition 1.
We formulate the objective function of the group-oriented structured clustering problem as (8).
Finding the optimal partition is not easy when the network size increases; in this case, we focus on finding a feasible suboptimal solution in this paper. In addition, the centralized clustering method encounters the problems of high computational complexity and large control cost for large-scale UAV swarms. Therefore, designing a distributed cluster formation approach where each UAV can make autonomous cluster decisions based on local information is necessary.
4. Distributed Clustering Algorithm for the UAV Swarm
The coalition game, also known as a cooperative game, refers to the process in which players form stable coalitions cooperatively. The goal in the coalition game is consistent with that of the clustering problem.
4.1. Clustering Model Based on Coalition Game
In the coalition game clustering approach, coalitions are equivalent to clusters, while each cluster corresponds to one coalition. The UAV swarm will eventually form multiple disjoint coalitions, called coalition partition (or coalition structure). Definition 2 gives the concept of coalition partition.
Definition 2.
A coalition structure is defined as , which consists of K disjoint coalitions with and .
Then, we establish a coalition game model for the clustering problem of the UAV swarm. is the set of game participants. The coalition revenue u is:
Since the coalition revenue u only depends on the cluster members, the proposed coalition formation game is with transferable utility (TU).
The optimization objective of the coalition game clustering problem is:
is the best coalition partition.
According to the coalition revenue, the coalition game of the clustering problem exhibits different characteristics in static and dynamic networks. For a static network, the communication link correlation between two neighboring UAVs is 1. Thus, the adaptive weight is 1. Then we can verify that:
It shows that the designed coalition game is superadditive. Furthermore, the designed game is convex, which tends to the formation of large-size coalitions. However, the cluster constraints limit the formation of grand coalitions.
For the dynamic network, the coalition revenue is related to the average communication link correlation of the cluster. Therefore, the coalition revenue of the clustering problem for the mobile network is not monotonic. The coalition game is not convex and does not have superadditivity. However, UAVs in the same group or having high correlation will merge to form stable clusters.
4.2. Selection of the Best Switch Operation
Transferring UAVs from one coalition to another can update the coalition structure of the clustering problem. Next, we review the definition of switch operation in [12].
Definition 3.
A switch operation is defined as transferring players from the current coalition to . Hence, .
According to the coalition revenue, we can define the gain of the switch operations as follows:
In order to facilitate the evaluation of switch operations, the preference relation is introduced.
Definition 4.
The preference relation ≻ over switch operations and can be expressed as:
It indicates that when the gain of switch operation is greater than , the game participants prefer to choose the switch operation .
Then, based on the concept of switch operation and the corresponding switch gain, the definition of Nash-stable partition is given below.
Definition 5.
The coalition partition is Nash stable, if , .
Nash stable partition means that no UAV wants to deviate from the current coalition unilaterally. When no switch operations can increase the total revenue of all coalitions, the partition is stable, which is the corresponding suboptimal solution to the clustering problem.
Theorem 3.
For a static network, starting from any initial coalition partition in which all clusters satisfy the clustering constraints, the clustering structure can converge to a final coalition partition in a finite number of iterations when UAVs periodically select the switch operations with positive gains.
Proof.
See Appendix C. □
For a fixed network topology, Theorem 3 indicates that a stable coalition partition can be constructed in a finite number of iterations when UAVs periodically select the switch operations with positive gains. We detail the specific process of selecting the best switch operation in Algorithm 1.
| Algorithm 1 The best switch operation selection of the ith UAV, which is in cluster and group |
Output: The best switch operation selection of UAV i // Selection of candidate switch set
|
In Algorithm 1, assuming that UAV i belongs to group and is in cluster , we first select the candidate set of UAV i. The candidate switch set consists of two types and can be selected through heuristic rules. Denote the neighbors of i in the same cluster and the same group as .
- (1)
- The singleton can be one candidate set.
- (2)
- Each and its neignbors can form a candidate set.
The candidate switch set should at least contain the UAV itself. The second type of candidate switch set aims for the UAVs belonging to the same task group to transfer together. After obtaining the candidate switch set, select the switch operations with positive gains that satisfy the cluster constraints to construct the switch operation set . The switch operation with the largest switch operation gain is the best one, which is denoted as .
4.3. Distributed Parallel Clustering Algorithm
In this part, we mainly focus on the design of a distributed parallel clustering algorithm. Multiple UAVs can choose the switch operations in parallel during each decision-making cycle, thus reducing the iterations of clustering.
In order to resolve the conflict in parallel decision-making, we assign UAV two states: idle and busy.
- (1)
- Idle state: The UAV is not involved in any current selected switch operations.
- (2)
- Busy state: The UAV is involved in a switch operation initiated by itself or another UAV.
The state transition process of UAVs is depicted in Figure 3.
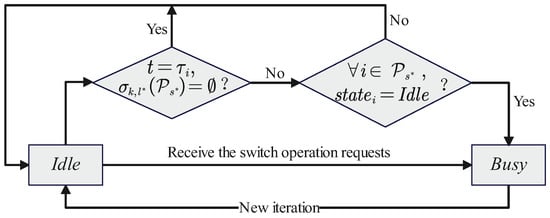
Figure 3.
State transition model for UAVs in the parallel clustering algorithm.
Moreover, we adopt the CSMA mechanism for conflict avoidance to assist the state transition of UAVs. Algorithm 2 describes the details of the designed distributed parallel clustering algorithm.
| Algorithm 2 The distributed parallel clustering algorithm based on coalition game |
// UAV i belonging to group and cluster , starts a decision-making process at time
|
In Algorithm 2, each UAV is initially in an idle state and randomly chooses a waiting time on the uniform distribution . If the UAV is idle and receives a switch operation request from another UAV, it will change to the busy state and then participate in this switch operation. When UAV i is still idle after in the decision cycle, the UAV calculates the optimal switch operation according to Algorithm 1. If all UAVs involved in the optimal switch operation are idle, the switch operation is valid. UAV i changes to the busy state and sends the switch operation request to related UAVs. In this way, conflicts in parallel decision-making are effectively avoided by introducing the two states of idle and busy.
5. Simulation Results
In this section, we simulate the proposed group-oriented clustering algorithm and evaluate the clustering performance. There are few related studies on structured clustering. We compare our algorithm with the COG (clustering with operational groups) algorithm [12] with no mobility prediction and its predictive version in [21]. In the following comparison, we call the clustering algorithm proposed in [21] CMPOG (i.e., clustering with mobility prediction and operational groups). The COG algorithm only considers the number of UAVs in each group and cluster without the mobility prediction. The CMPOG algorithm considers the prediction of node mobility besides the cluster size and group size. However, these two algorithms focus on group attributes rather than jointly considering the communication attributes and group attributes.
5.1. Simulation Setup
Assuming that the task groups of the UAV cluster have been assigned, deploy UAVs in a square area with 2.5 km × 2.5 km. The flight altitude of UAVs is about m. Assuming that the task groups of the UAV cluster have been assigned, deploy UAVs in a square area. For mobile networks, UAVs in different task groups track their respective reference points as they move. UAVs run the clustering algorithm in each decision cycle to adapt to changes in the network topology. The reference points of each group move randomly within the mission area, while UAVs adjust their moving speed and direction to track the reference point. All the results are obtained through 100 independent Monte Carlo simulations. Table 3 lists the simulation parameters.

Table 3.
The simulation parameters.
5.2. Cluster Performance for Static Networks
In order to exhibit the effectiveness of the designed clustering method for static networks, Figure 4 shows the clustering results of 50 UAVs with a total of four clusters formed in the 3D version and the XY axis version.
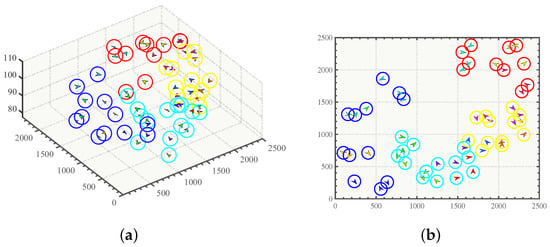
Figure 4.
Clustering results for 50 UAVs with 15 groups. (a) shows the 3D version, while (b) represents the XY axis version.
In Figure 4, UAVs in the same color belong to the same group. In addition, UAVs with the same color circle around belong to the same cluster. The clustering results show that our clustering method can effectively control the number of clusters and divide UAVs belonging to the same task group into one identical cluster.
5.2.1. Convergence
Figure 5 displays the number of iterations of these clustering methods with different scales of the UAV swarm. To make the comparison fair, the comparison algorithms and our algorithm all adopt the parallel decision-making mechanism described in Section 4.3.
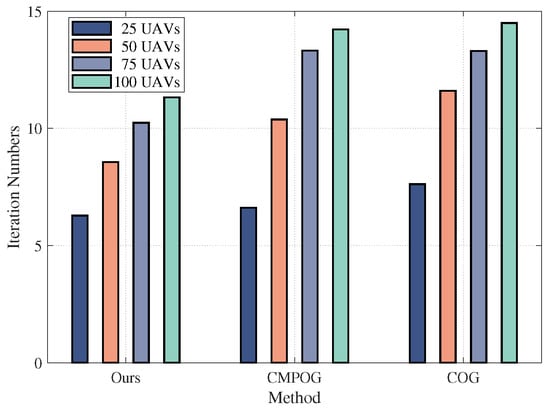
Figure 5.
The number of iterations under different scales of the UAV swarm for our algorithm and the comparison algorithms.
As can be seen from Figure 5, our clustering algorithm has fewer iterations as our method includes more candidate switch operations than the COG and CMPOG. In addition, with the cluster size growth, the number of iterations required to converge for the clustering algorithm gradually increases. Large-size UAV swarm has high density, which brings similar relations among UAVs that make the swarm challenging to partition and need more iterations.
5.2.2. Performance Evaluation
In this part, we verify whether the clustering algorithm can meet the three goals defined in the structured clustering problem through the following performance indicator: cluster count, the average number of clusters for UAVs in the same group, and the total inter-cluster communication correlation. In addition, we add the load balance indicator, defined as the ratio of UAV numbers in the smallest cluster to the average UAV numbers in all clusters:
In a given task area, the larger the swarm size, the more difficult to partition the UAV swarm. We compare the clustering effects under different sizes of the UAV swarm. The number of UAVs in each task group is in . The scale of the UAV swarm varies between 25, 50, 75, and 100.
Figure 6 displays the cluster numbers under different swarm sizes. The number of clusters in our algorithm is slightly higher than the COG algorithm and significantly less than the CMPOG algorithm.
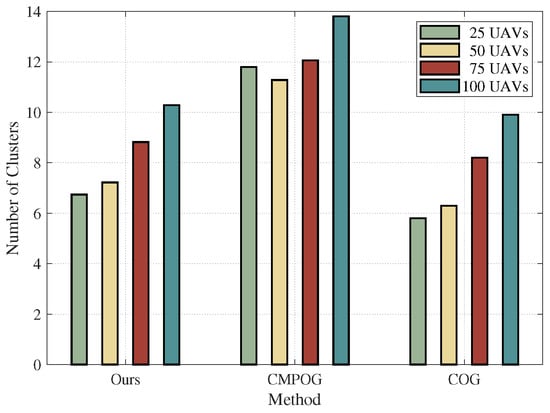
Figure 6.
The number of clusters for the final clustering structure under different scales of the UAV swarm.
The clustering load balance of each algorithm is exhibited in Figure 7. Although our algorithm has slightly more clusters, the number of UAVs for each cluster is more balanced, which avoids the generation of small clusters.
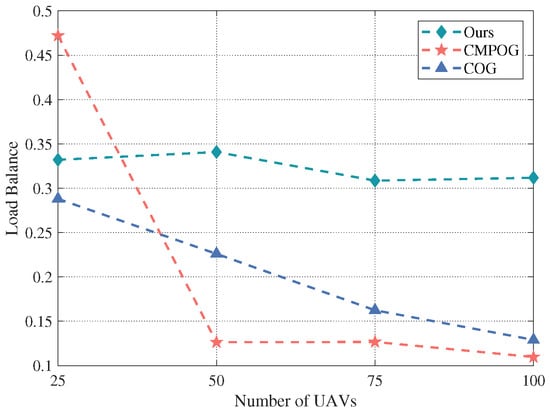
Figure 7.
The clustering load balance for the UAV swarms with different scales.
Figure 8 shows the average number of corresponding clusters for UAVs belonging to the same task group. When the swarm size is 25 and 50, both our algorithm and the comparison algorithm can divide the UAVs in the same task group into one identical cluster. When the swarm size increases, the UAVs are distributed too densely, and occasionally the UAVs of the same task group are divided into different clusters. Compared with the COG and CMPOG algorithms, there are fewer UAVs belonging to the same task group divided into different clusters in our algorithm.
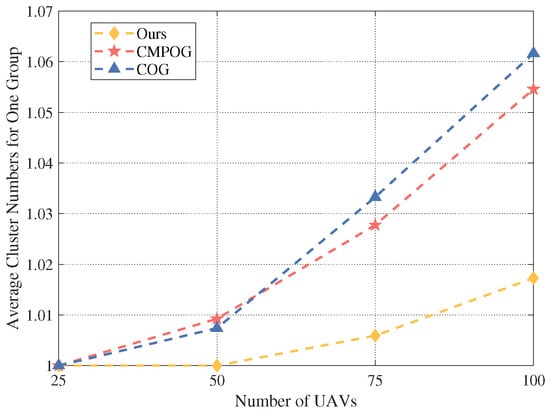
Figure 8.
The average number of clusters corresponding to one group under different scales of the UAV swarm.
The total inter-cluster communication link correlation is indicated in Figure 9. Our algorithm has the smallest total inter-cluster communication link correlation compared with the comparison algorithm under different swarm sizes. Additionally, our algorithm has more advantages in terms of the total inter-cluster communication link correlation with the increased swarm size.
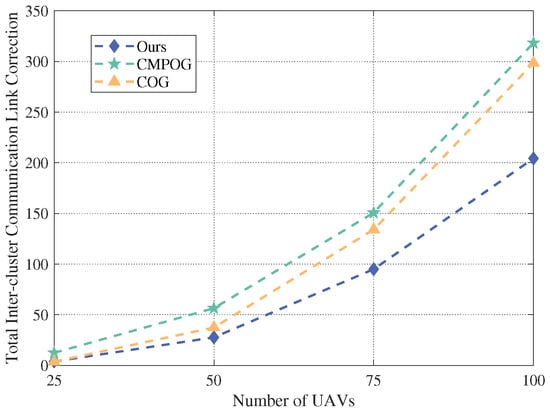
Figure 9.
The total inter-cluster communication link correlation for the UAV swarm with different numbers of UAVs.
Next, we compare the clustering performance under different group numbers of the UAV swarm. The number of UAVs is fixed as , while the group number is set as and 30. The group size will be smaller when more groups are in the swarm.
Figure 10 displays the cluster numbers under different numbers of groups. The clustering load balance of each algorithm is shown in Figure 11. Our algorithm divides the swarm into fewer clusters and has the best load balance. In addition, Figure 11 illustrates that load balance increases when the group numbers reduce (i.e., each task group contains more UAVs). As UAVs belonging to the same group tend to be divided into the same cluster, each cluster may contain only one task group when the group numbers are small. Thus, the number of UAVs in each cluster is more balanced. Our algorithm also has better load balance than COG and CMPOG.
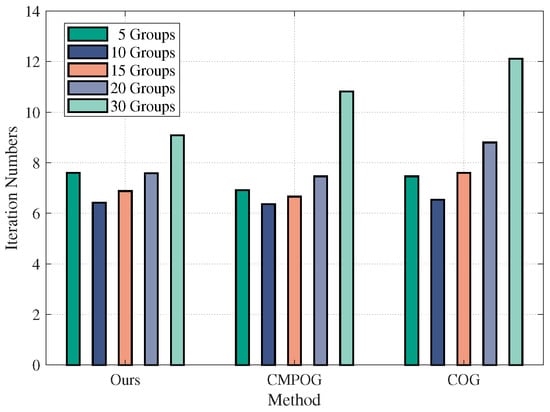
Figure 10.
The number of clusters in the clustering results under different numbers of groups.
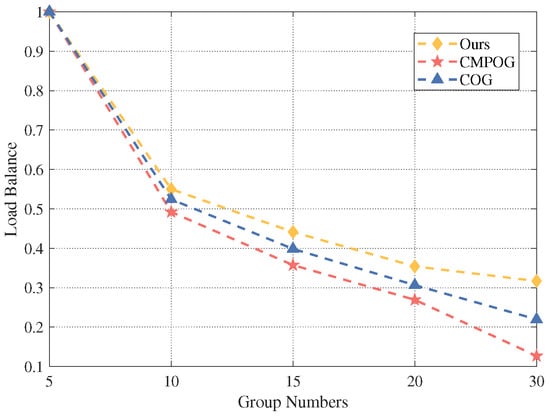
Figure 11.
The load balance for each algorithm under different numbers of groups.
Figure 12 exhibits the average number of corresponding clusters for UAVs belonging to the same task group under different group counts. When there are more groups, UAVs in the same task group may appear in different clusters. However, only one group is assigned to different clusters on average when the group count is 30. It shows that our algorithm has fewer average cluster numbers for one group than the comparison algorithms and can assign UAVs performing the same task to one identical cluster regardless of the number of groups.
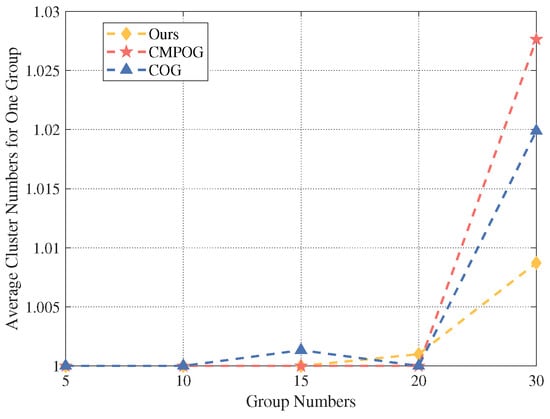
Figure 12.
The average number of clusters corresponding to one group under different numbers of groups.
The total inter-cluster communication link correlation under different group counts is shown in Figure 13. Our algorithm has the best inter-cluster communication link correlation. Moreover, with the increase of the group number, the total inter-cluster communication link correlation is gradually declining. The reason is that the distribution of UAVs is more dispersed when more groups are in the swarm.
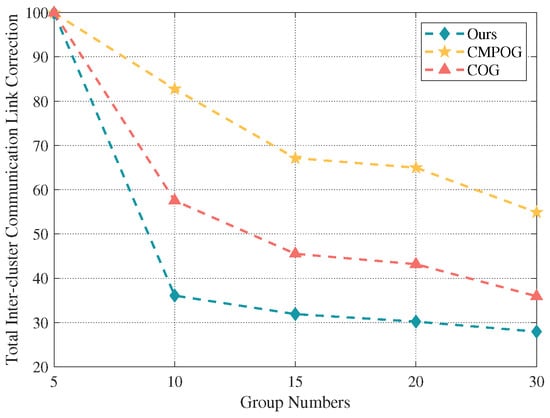
Figure 13.
The total inter-cluster communication link correlation for UAV swarms with different numbers of groups.
The above simulation results illustrate that our algorithm achieves the three goals proposed in the group-oriented structured clustering problem with a good load balance.
5.3. Cluster Performance for Mobile Networks
We now consider mobile networks for which the coordinates of UAVs are updated once every second according to the group reference points. In the following simulation, the speed of UAVs varies in the ranges of m/s, m/s, m/s, and m/s separately while the group is fixed as .
The bar graph of Figure 14 shows the number of cluster adjustments performed per interval of with our group-oriented clustering algorithm under different velocities. The cluster adjustment numbers are vast at the initialization clustering phase. After the initial adjustment period, the cluster adjustment numbers gradually stabilize and fluctuate within a small range, illustrating that our clustering algorithm has certain stability in mobile networks. Furthermore, the UAV swarm with higher speed will have more cluster adjustments.
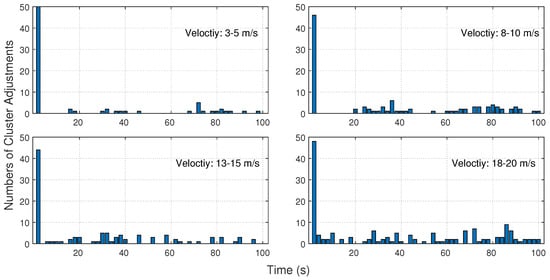
Figure 14.
The number of cluster adjustments with our group-oriented clustering algorithm under different velocities.
The total number of cluster adjustments during the whole clustering process under different velocities is shown in Figure 15. Our algorithm has the least number of adjustments than the COG and CMPOG algorithms, which indicates that our algorithm is more stable for dynamic network clustering.
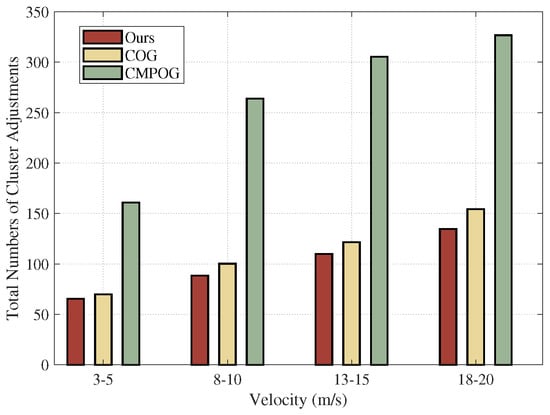
Figure 15.
The total number of cluster adjustments in one clustering process under different velocities.
In addition, the number of groups will influence the stability of dynamic network clustering. Assuming the speed of UAVs varies in the range of , Figure 16 displays the cluster adjustment numbers when the group numbers are 5, 10, and 20.
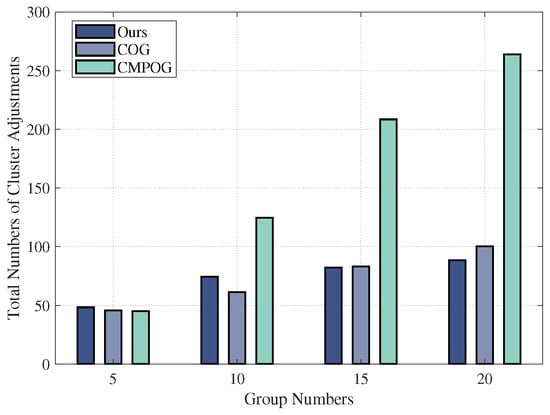
Figure 16.
The total number of cluster adjustments in one clustering process under different group numbers.
The smaller the number of groups, the fewer cluster adjustments during the moving process, indicating that dividing the nodes belonging to the same group into one identical cluster can make the cluster structure more stable. Additionally, the clustering result is more stable when the group size is closer to the maximum number of UAVs in one cluster.
6. Conclusions
This paper designs a distributed clustering algorithm for large-scale UAV swarms consisting of some groups. We first establish the group-oriented structure clustering problem, which considers the cluster topology constraints. Thus, the goals that the clustering problem should achieve are formulated. Then, we obtain the communication link correlation through the movement prediction mechanism to measure the stability of the communication link. The compound correlation is designed to comprehensively consider the group information and the communication link correlation.
We adopt the coalition game framework to solve the clustering problem. The best switch operation is chosen through some heuristic rules which consider the coalition revenue based on the compound correlation. Through state automata, we introduce the distributed parallel clustering mechanism. Extensive simulations demonstrate that the proposed algorithm performs better than the comparison algorithm and is suitable for the group-oriented structure clustering problem. However, the proposed clustering algorithm is based on the assumption of an ideal communication environment without considering the impact of communication delay, interruption, and packet loss in practical application. In the future, we will focus on dealing with the clustering problem under different communication qualities.
Author Contributions
Methodology, M.Z.; validation, M.Z.; formal analysis, X.W. (Xinning Wu); data curation, X.W. (Xinning Wu); writing—original draft preparation, M.Z.; writing—review and editing, J.L. and X.W. (Xiangke Wang); supervision, J.L.; funding acquisition, X.W. (Xiangke Wang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China under Grant 61973309.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of Theorem 1
Goal 1 indicates that we want to build clusters that include as many UAVS as possible (limited by ). To achieve Goal 1, the merge of two clusters should always increase the intra-cluster communication link correlation. Given cluster with UAVs, then the intra-cluster communication link correlation of cluster is . Adding another cluster with UAVs to cluster , then we have . It can be decomposed as . After simplification, we obtain that . Since , we can deduce that , thus concludes the proof.
Appendix B. Proof of Theorem 2
Given two different clusters and . The number of UAVs in that belongs to group is denoted as . is a subset of . Suppose that (i.e., has more UAVs belongs to than ). We also assume that both and satisfy the cluster limits. We need to prove that the total intra-cluster compound correlation will increase after transferring from to .
According to the proof of Theorem 1, we have and . Then we can deduce that . Since , then .
For the communication link correlation, we also have . If , then must . When , we can set a lower weight for the communication link correlation, which can make .
Then we obtain that when transferring UAVs to the cluster with more UAVs belonging to the same group as , the total intra-cluster compound correlation will be higher.
Appendix C. Proof of Theorem 3
Given the initial coalition partition , each switch operation transforms the current coalition partition into another partition. Besides, switch operations with positive gains can increase the total coalition values. After any switch operation with positive gain, the total coalition values strictly increase, meaning that the same partition can never be visited twice. Therefore, given the fact that the number of partitions of the UAV swarm is finite, the coalition structure will always converge to a final coalition partition in a finite number of iterations, which completes the proof.
References
- Scherer, J.; Rinner, B. Multi-UAV Surveillance With Minimum Information Idleness and Latency Constraints. IEEE Robot. Autom. Lett. 2020, 5, 4812–4819. [Google Scholar] [CrossRef]
- Liang, Y.; Xu, W.; Liang, W.; Peng, J.; Jia, X.; Zhou, Y.; Duan, L. Nonredundant Information Collection in Rescue Applications via an Energy-Constrained UAV. IEEE Internet Things J. 2019, 6, 2945–2958. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, H.; Wu, W.; Wei, J. Deployment Algorithms for UAV Airborne Networks Toward On-Demand Coverage. IEEE J. Sel. Areas Commun. 2018, 36, 2015–2031. [Google Scholar] [CrossRef]
- Gupta, L.; Jain, R.; Vaszkun, G. Survey of Important Issues in UAV Communication Networks. IEEE Commun. Surv. Tutor. 2016, 18, 1123–1152. [Google Scholar] [CrossRef]
- Hassija, V.; Chamola, V.; Agrawal, A.; Goyal, A.; Luong, N.C.; Niyato, D.; Yu, F.R.; Guizani, M. Fast, Reliable, and Secure Drone Communication: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2021, 23, 2802–2832. [Google Scholar] [CrossRef]
- Krichen, M.; Adoni, W.Y.H.; Mihoub, A.; Alzahrani, M.Y.; Nahhal, T. Security Challenges for Drone Communications: Possible Threats, Attacks and Countermeasures. In Proceedings of the 2022 2nd International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 9–11 May 2022; pp. 184–189. [Google Scholar]
- Al-Sulaifanie, A.; Al-Sulaifanie, B.; Biswas, S. Recent trends in clustering algorithms for wireless sensor networks: A comprehensive review. Comput. Commun. 2022, 191, 395–424. [Google Scholar] [CrossRef]
- Wang, X.; Mi, Z.; Wang, H.; Zhao, N. Performance test and analysis of multi-hop network based on UAV Ad Hoc network experiment. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; pp. 1–6. [Google Scholar]
- Shafiq, M.; Ali, Z.A.; Alkhammash, E.H. A Cluster-Based Hierarchical-Approach for the Path Planning of Swarm. Appl. Sci. 2021, 11, 6864. [Google Scholar] [CrossRef]
- Ali, Z.; Han, Z.; Masood, R. Collective Motion and Self-Organization of a Swarm of UAVs: A Cluster-Based Architecture. Sensors 2021, 21, 3820. [Google Scholar] [CrossRef] [PubMed]
- Câmara, D.; Bonnet, C.; Nikaein, N. Topology management for group oriented networks. In Proceedings of the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Istanbul, Turkey, 26–30 September 2010; pp. 2739–2744. [Google Scholar]
- Massin, R.; Le Martret, C.J.; Ciblat, P. A Coalition Formation Game for Distributed Node Clustering in Mobile Ad Hoc Networks. IEEE Trans. Wirel. Commun. 2017, 16, 3940–3952. [Google Scholar] [CrossRef]
- Heinzelman, W.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; Volume 2, p. 10. [Google Scholar]
- Ghasemzadeh, H.; Rezaeian, M.; Dehghan Touranposhti, F.; Ghasemian, M.M. BN-LEACH: An improvement on LEACH protocol using Bayesian networks for energy consumption reduction in wireless sensor networks. In Proceedings of the 7’th International Symposium on Telecommunications (IST’2014), Tehran, Iran, 9–11 September 2014; pp. 1138–1143. [Google Scholar]
- Song, X.; Sun, W.; Zhang, Q. A Dynamic Hierarchical Clustering Data Gathering Algorithm Based on Multiple Criteria Decision Making for 3D Underwater Sensor Networks. Complexity 2020, 2020, 8835103. [Google Scholar] [CrossRef]
- Kumar, D.N.S.R.; Barani, S. Dynamic Mobility Based Multi Hop Clustering Algorithm in Vehicular Ad Hoc Networks. Int. J. Adv. Sci. Technol. 2020, 29, 4495. [Google Scholar]
- Mohan, P.; Subramani, N.; Alotaibi, Y.; Alghamdi, S.; Khalaf, O.; Ulaganathan, S. Improved Metaheuristics-Based Clustering with Multihop Routing Protocol for Underwater Wireless Sensor Networks. Sensors 2022, 22, 1618. [Google Scholar] [CrossRef] [PubMed]
- Rai, P.; Ghose, M.; Deva Sarma, H. Game theory based node clustering for cognitive radio wireless sensor networks. Egypt. Inform. J. 2022, 23, 315–327. [Google Scholar] [CrossRef]
- Kassan, S.; Gaber, J.; Lorenz, P. Game theory based distributed clustering approach to maximize wireless sensors network lifetime. J. Netw. Comput. Appl. 2018, 123, 80–88. [Google Scholar] [CrossRef]
- Afsar, M.M.; Crump, R.T.; Far, B.H. Energy-Efficient Coalition Formation in Sensor Networks: A Game-Theoretic Approach. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–6. [Google Scholar]
- Xing, N.; Zong, Q.; Dou, L.; Tian, B.; Wang, Q. A Game Theoretic Approach for Mobility Prediction Clustering in Unmanned Aerial Vehicle Networks. IEEE Trans. Veh. Technol. 2019, 68, 9963–9973. [Google Scholar] [CrossRef]
- Rahman, G.M.E.; Wahid, K.A. LDCA: Lightweight Dynamic Clustering Algorithm for IoT-Connected Wide-Area WSN and Mobile Data Sink Using LoRa. IEEE Internet Things J. 2022, 9, 1313–1325. [Google Scholar] [CrossRef]
- Tran, T.N.; Nguyen, T.V.; Shim, K.; An, B. A Game Theory Based Clustering Protocol to Support Multicast Routing in Cognitive Radio Mobile Ad Hoc Networks. IEEE Access 2020, 8, 141310–141330. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Y.; Liang, K. Predefined-time formation control of the quadrotor-UAV cluster’ position system. Appl. Math. Model. 2022, 116, 45–64. [Google Scholar] [CrossRef]
- Yu, Y.; Ru, L.; Fang, K. Bio-inspired mobility prediction clustering algorithm for ad hoc UAV networks. Eng. Lett. 2016, 24, 328–337. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).