Deep Learning Architecture for UAV Traffic-Density Prediction
Abstract
1. Introduction
- The paper adapted an intrinsic complexity metric based on the linear dynamical system model to assess congestion in UTM operations. In this context, the study developed an optimal air traffic assignment model that computes and measures air traffic flow complexity in the neighborhood of a UAV at a given time. The proposed strategy explicitly considers operational differences between ATM and UTM systems, such as dynamic flow structures, airspace density, separation requirements, and standards.
- To validate the proposed model, three different practical drone-delivery scenarios were conducted in the simulation-scenario environment. The missions spanned a wide range of applications with variable numbers of UAVs. Furthermore, the effects of airspace-structural configurations, such as static NFZs, airfields with variable availability for drone flights, recreational areas, emergency UTM operations, and environmental constraints such as weather conditions were studied.
- The study found that the existing literature in this field covers either trajectory prediction or conflict detection and resolution, with limited research on the prediction of air traffic flow for UTM systems. To address this gap and improve the safety and efficiency of UAVs operated in urban areas, the present study proposed a learning-based model to predict air traffic congestion over a period of three minutes. The proposed model was adapted to make it suitable in terms of the look-ahead time horizon of the UTM applications (such as drone delivery services, emergency operations, and inspection-related UAV tasks). With the information supplied by such a congestion prediction system, it will also be possible to plan a safe flight trajectory in advance.
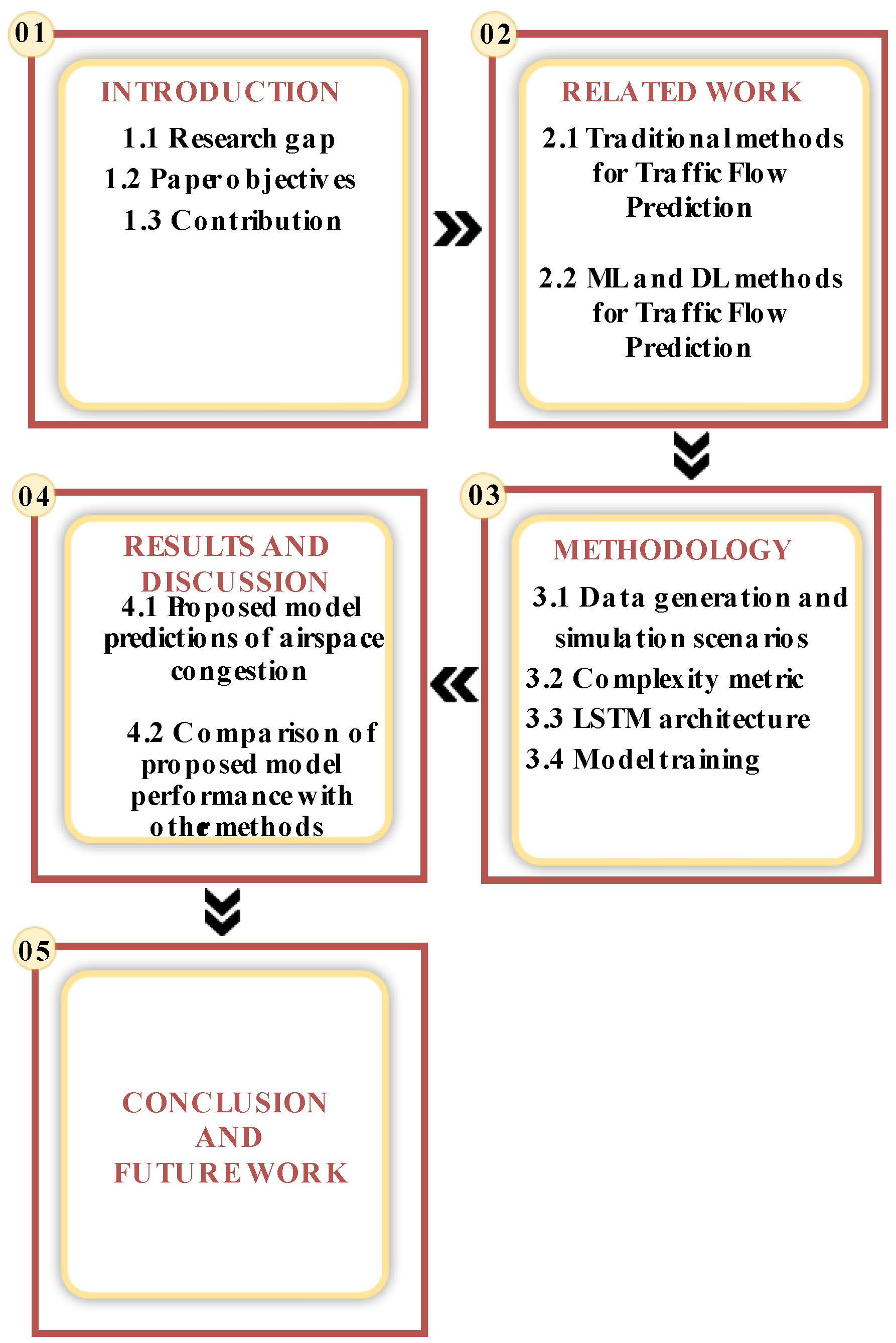
- A critical aspect of UTM operations centers on complexity assessment, and the computational effort that the latter entails. This is particularly true for on-board applications. A key goal of the present research, therefore, is to render the traffic prediction model significantly ‘smaller’ without surrendering any notable degree of predictive accuracy. In terms of methodology, the study took deep learning-based predictive models from other fields and reconfigured them. These models included ATFP for aircraft and road traffic prediction. Finally, a DL model comprising both LSTM and 1-D convolutional neural networks (1D-CNNs) is recommended. Indeed, the capacity of the proposed model to extract spatiotemporal components from UAV flight data, and to do so within an acceptable computing timeframe, is confirmed by the experimental findings. The structure of this study is depicted in Figure 1.
2. Related Work
3. Methodology
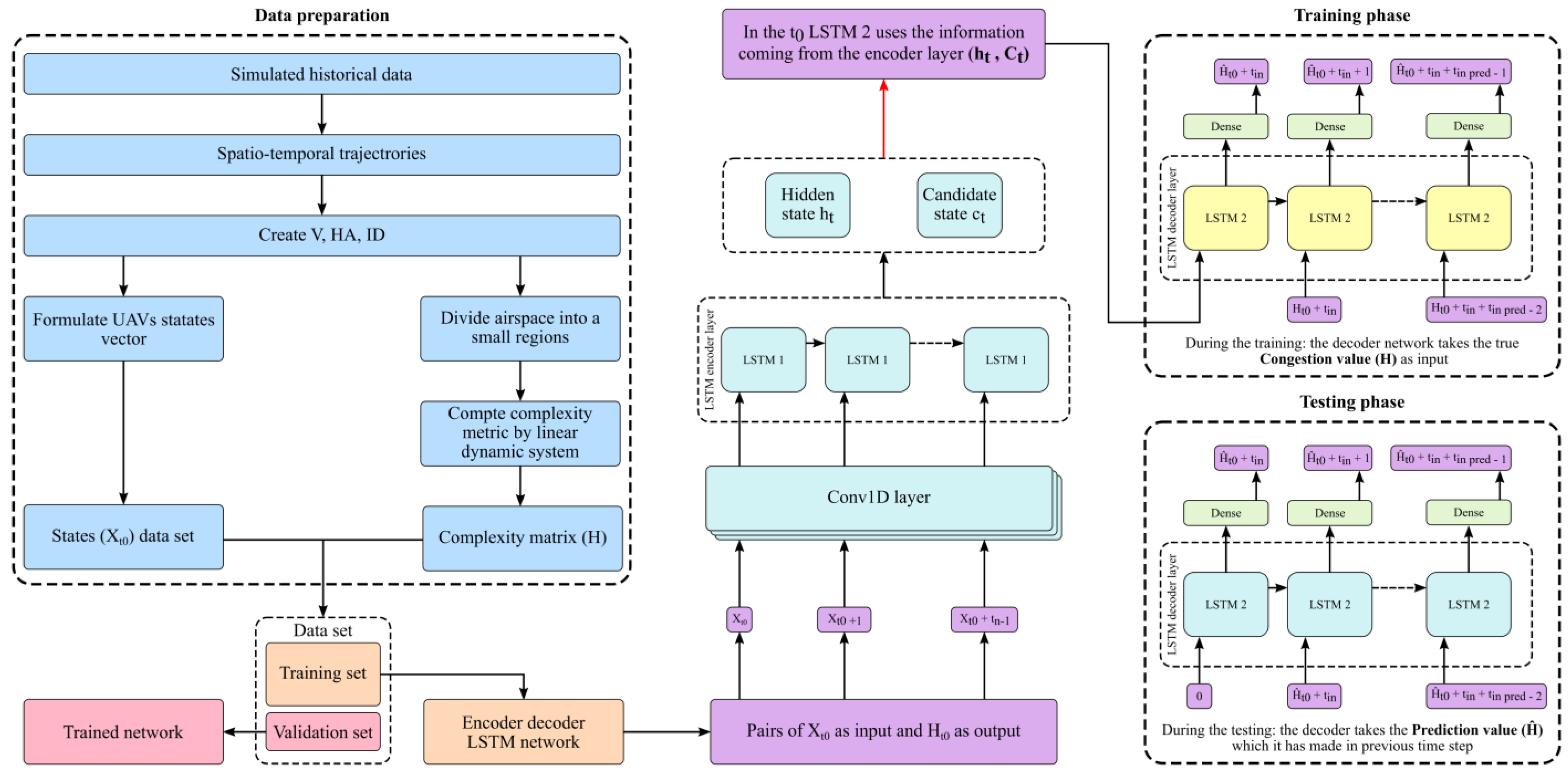
3.1. Data Generation and Simulation Scenarios
- Fixed positions: Starting and ending within this simulation, the start and end positions for the UAV missions were calibrated to imitate real emergency services and typical daily operations.
- Levels of priority: A priority service level was allocated to each flight, ranging from Level 5 (lowest priority) to Level 1 (highest priority). The various levels are described below:
- Fire surveillance and emergency services
- Delivery of COVID-19 test samples to multiple clinics
- Delivery of packages to assorted post offices
- Scheduled railway track inspection missions
- Random flights for hobbyists (single-leg missions)
- Dynamic NFZs: Some of the recreational areas and airfields incorporated in the simulation were dynamic in character, at least at certain times. This dynamism was random, rendering some areas available and others unavailable throughout the simulation hours.
- Random times of departure: For each one-hour simulation period, to make the exercise more realistic, the precise time of departure for each hobbyist’s UAV was placed randomly between one and ten minutes.
- ‘Ambiguous’ weather: Varying weather conditions, including ‘severe’ and ‘adverse’, were addressed. This study [73] presented details regarding the implementation of weather effects.
- Strategy for deconfliction: Within the simulation setting, ground delay was deployed as a deconflicting strategy.
- 1.
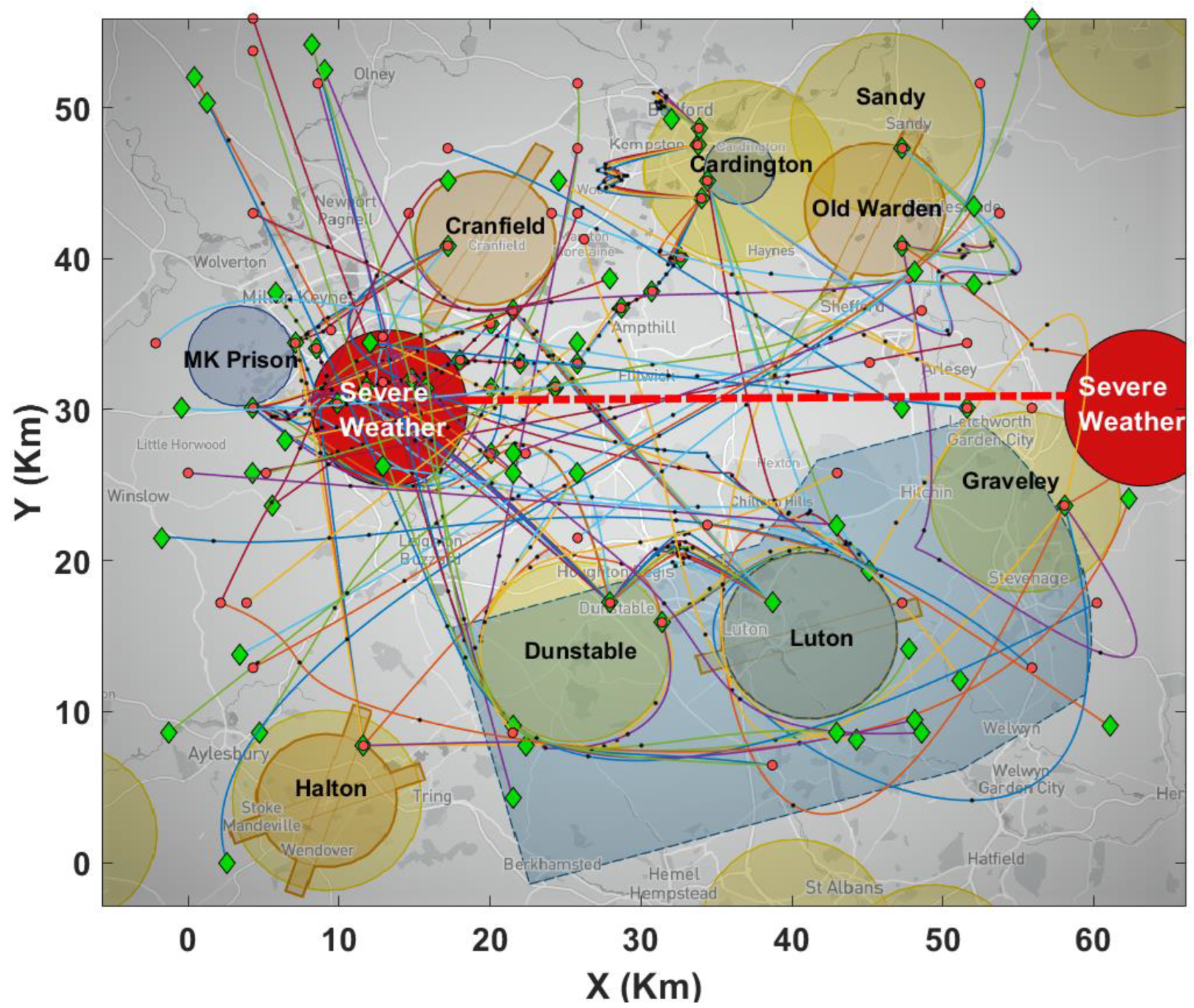
- First simulation scenario: This simulation ran between 9:00 am and 10:00 am. In this scenario, all nine NFZs were static without any dynamic obstacles and weather constraints. As a result of this constraint, no UAV could fly over them during this hour. Moreover, this scenario was conducted by 100 UAV trajectories. The railway track inspection mission by UAVs was not considered in this scenario.
- 2.
- Second simulation scenario: This simulation ran between 10:00 am and 11:00 am. The difference between this and the first scenario was that more complexity was added to the Bedfordshire airspace by considering Railway Infrastructure Monitoring operations and increasing the number of UAV trajectories to 150. The effects of adverse rain and wind were considered in this scenario.
- 3.
- Third simulation scenario: 200 UAVs’ trajectories in airspace were considered in this simulation that ran between 11:00 am and 12:00 pm. In this scenario, airfields were dynamic, while all four recreational areas and the prison were kept static. Among the four airfields, Luton and Cranfield were available, and therefore, recreational users of UAVs could fly over Luton and Cranfield at some points. This scenario also incorporated severe weather effects. The scheduled inspections of railway tracks by UAV operations were considered in this scenario.
3.2. UAVs States Formulation
3.3. Computation of Complexity Metric: Spatio-Temporal Correlation
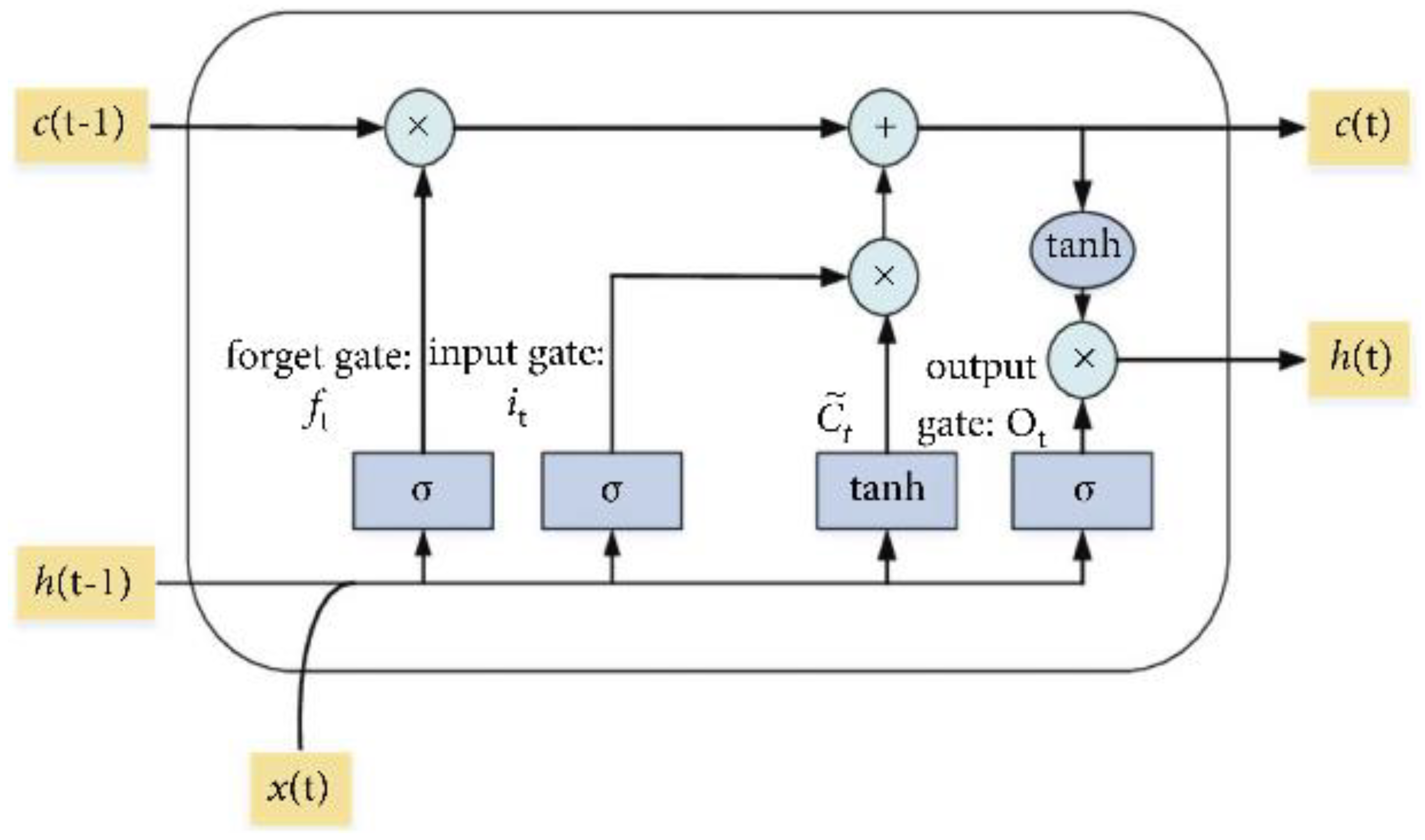
3.4. Implementation of Encoder-Decoder LSTM Model
3.5. Model Training
4. Results and Discussion
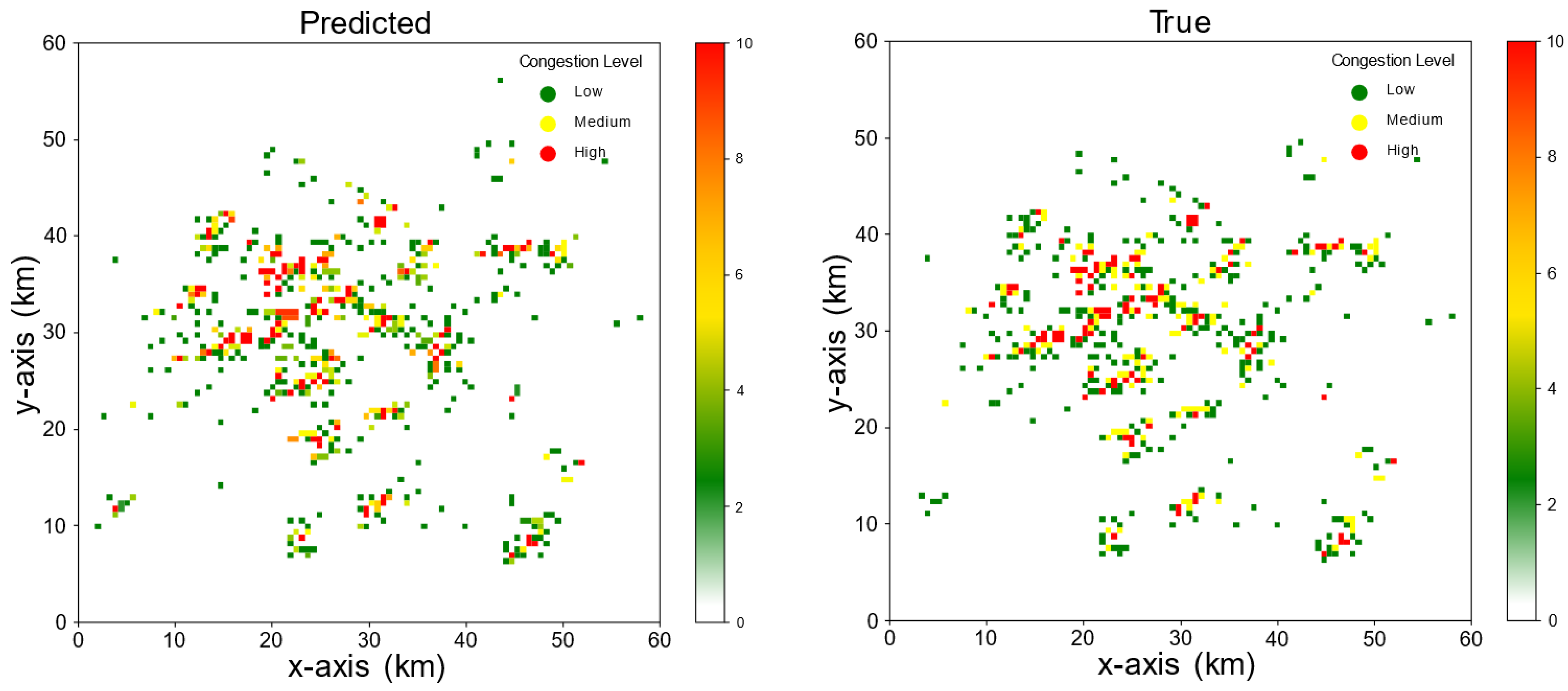
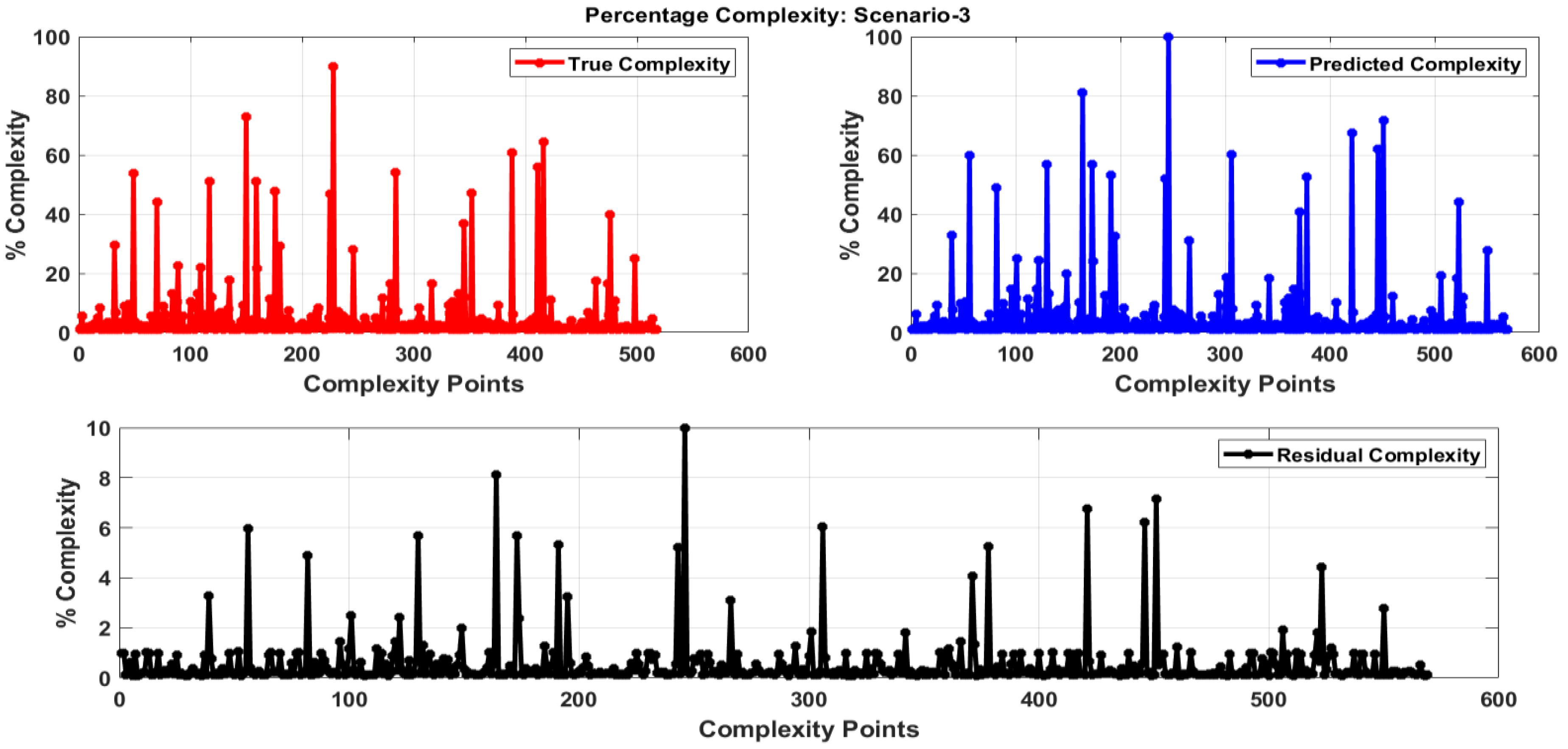
4.1. Prediction Result
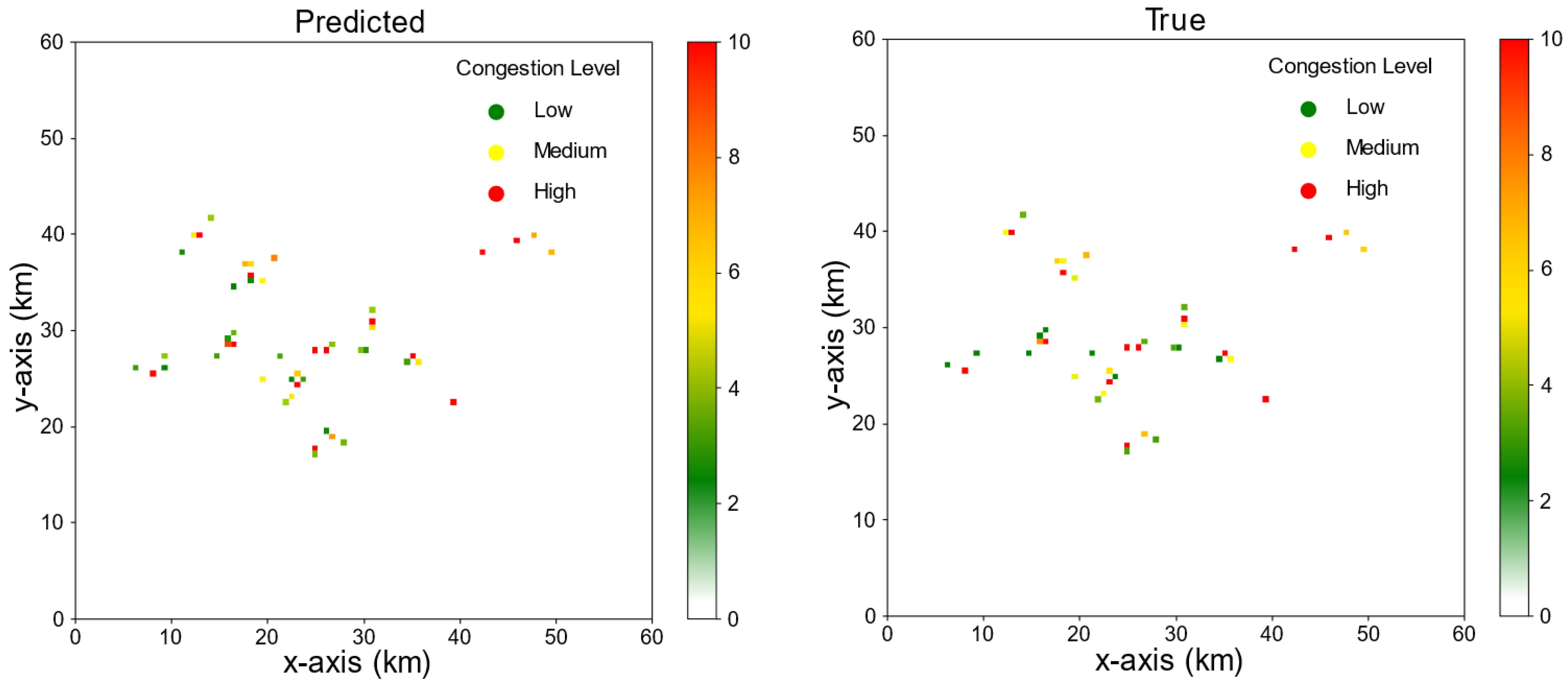
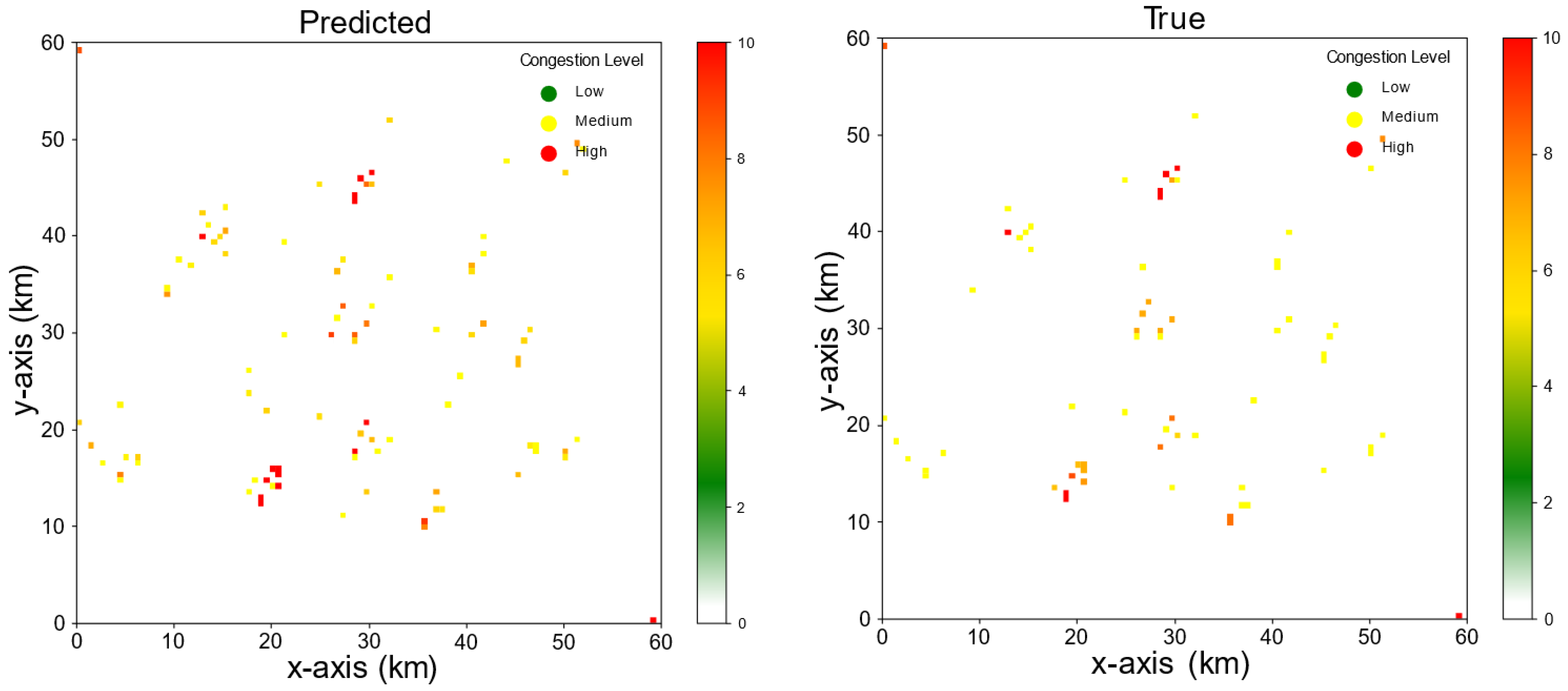
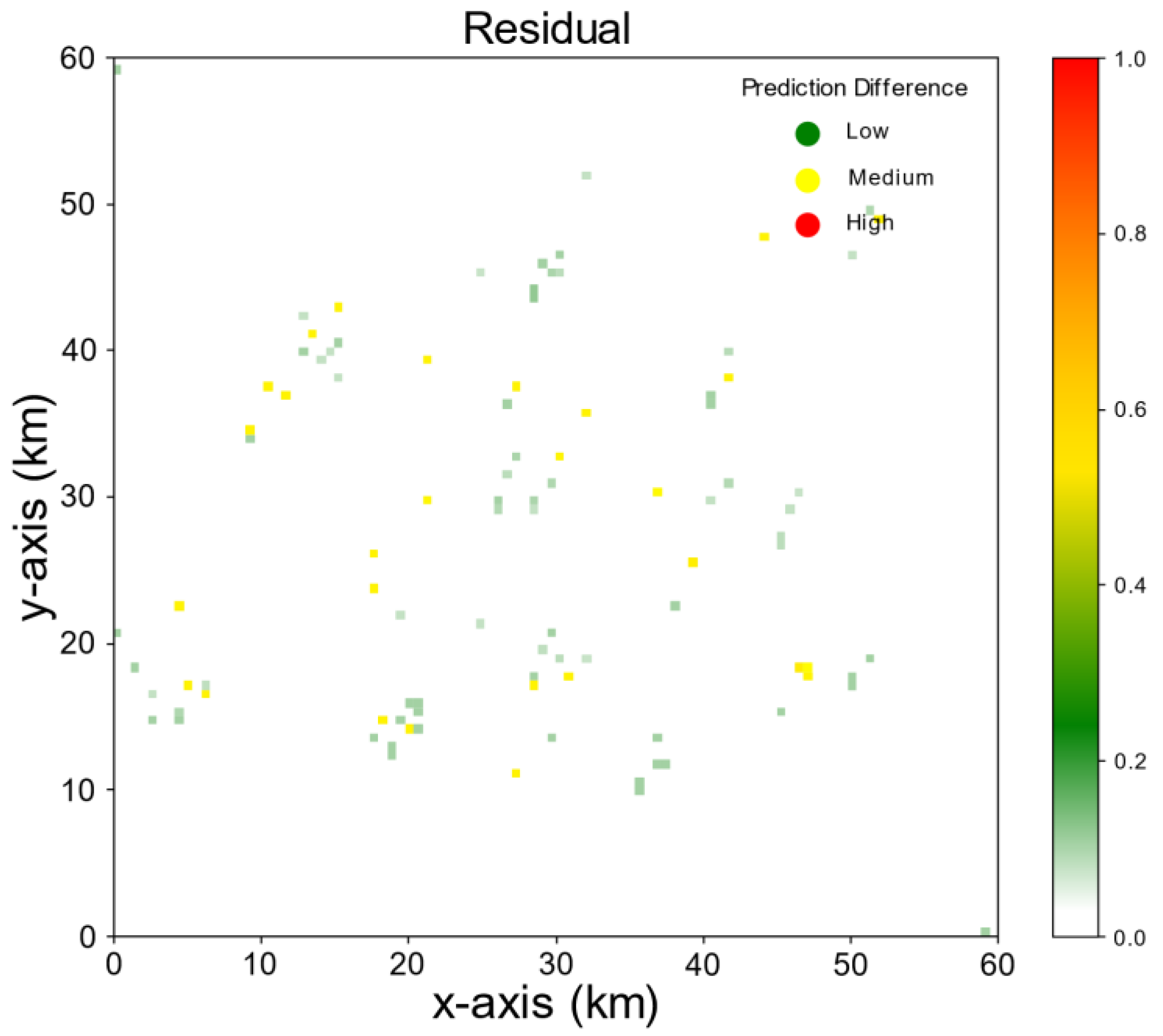
4.1.1. First Scenario Simulation
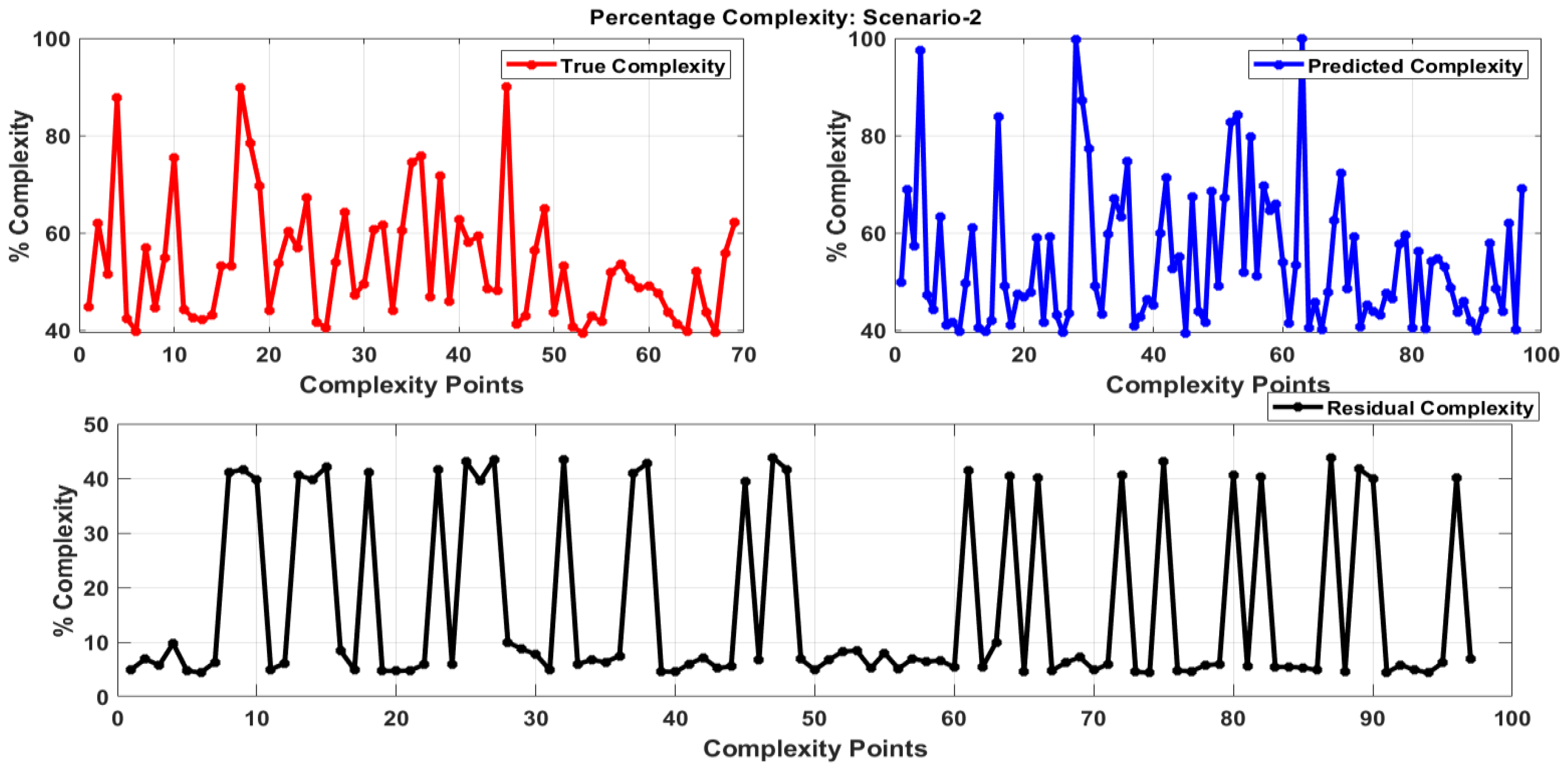
4.1.2. Second Scenario Simulation
4.1.3. Third Scenario Simulation
4.2. Comparison between Existing Approaches and the Proposed Model
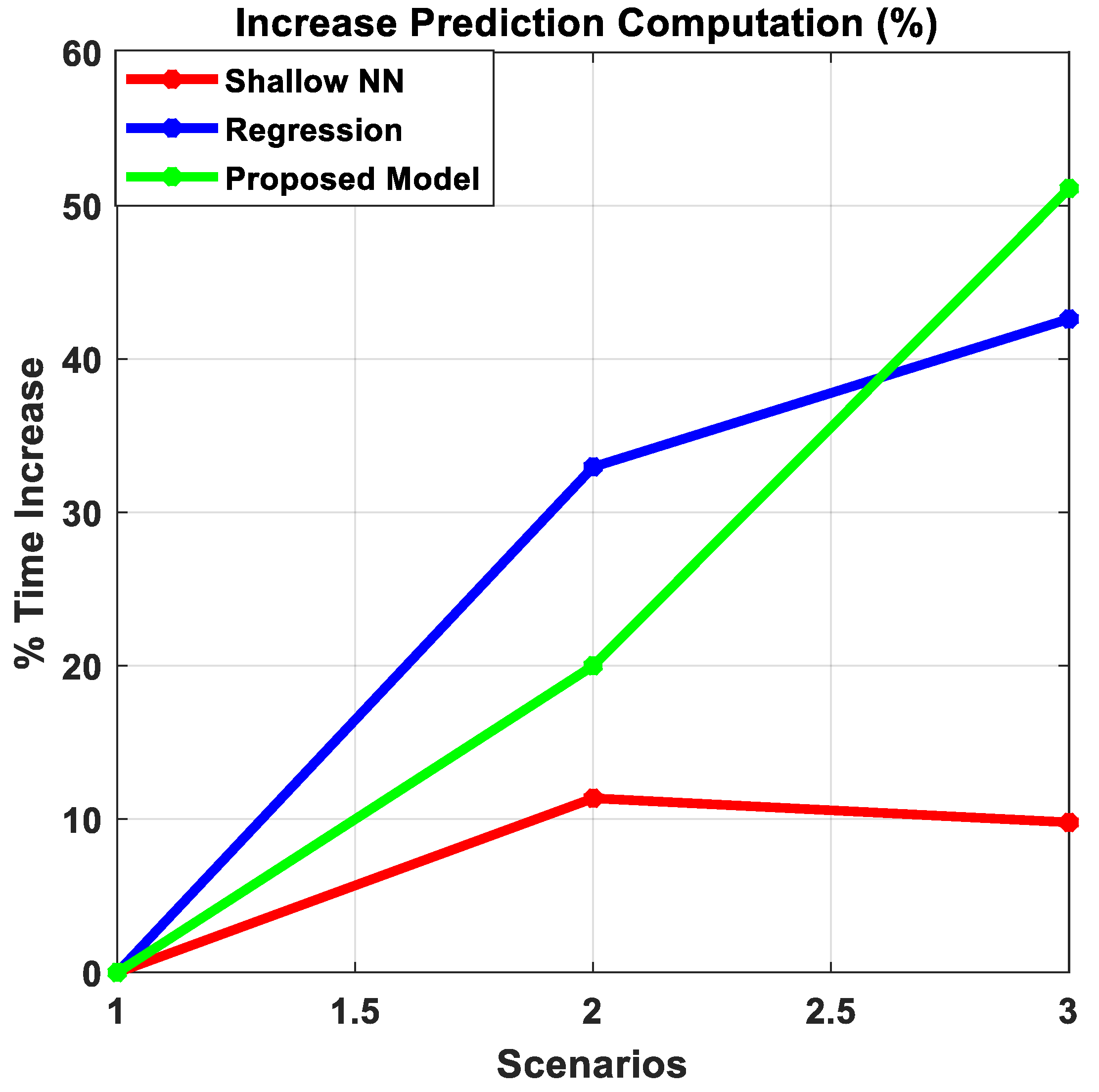
4.3. Comparison between Existing Approaches and the Proposed Model: Performance vs. Time
5. Comparison between Existing Approaches and the Proposed Model: Computation Speed
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hayes, P.B.; Mahon, T. The Market for UAV Traffic Management Services—2020–2024; Unmanned Airspace: Hove, UK, 2022; pp. 1–371. [Google Scholar]
- Circular 328 AN/190; Unmanned Aircraft Systems (UAS). ICAO: Montreal, QC, Canada, 2011.
- Shrestha, R.; Oh, I.; Kim, S. A Survey on Operation Concept, Advancements, and Challenging Issues of Urban Air Traffic Management. Front. Future Transp. 2021, 2, 626935. [Google Scholar] [CrossRef]
- Bauranov, A.; Rakas, J. Designing airspace for urban air mobility: A review of concepts and approaches. Prog. Aerosp. Sci. 2021, 125, 100726. [Google Scholar] [CrossRef]
- Scott, B.I.; Trimarchi, A. Convention on International Civil Aviation; Routledge: London, UK, 2019; pp. 31–56. [Google Scholar]
- Euteneuer, E.A.; Papageorgiou, G. UAS insertion into commercial airspace: Europe and US standards perspective. In Proceedings of the IEEE/AIAA 30th Digital Avionics Systems Conference, Seattle, WA, USA, 16–20 October 2011; pp. 1–12. [Google Scholar] [CrossRef]
- Davies, L.; Bolam, R.C.; Vagapov, Y.; Anuchin, A. Review of Unmanned Aircraft System Technologies to Enable beyond Visual Line of Sight (BVLOS) Operations. In Proceedings of the 2018 10th International Conference on Electrical Power Drive Systems, ICEPDS, Novocherkassk, Russia, 3–6 October 2018; pp. 2–7. [Google Scholar] [CrossRef]
- Civil Aviation Authority. Beyond Visual Line of Sight in Non-Segregated Airspace; CAP 1861; The UK Civil Aviation Authority: London, UK, 2020; pp. 1–11. [Google Scholar]
- Davies, L.; Vagapov, Y.; Grout, V.; Cunningham, S.; Anuchin, A. Review of Air Traffic Management Systems for UAV Integration into Urban Airspace. In Proceedings of the 2021 28th International Workshop on Electric Drives: Improving Reliability of Electric Drives, IWED, Moscow, Russia, 27–29 January 2021. [Google Scholar] [CrossRef]
- Bayen, A.; Grieder, P.; Tomlin, C. A control theoretic predictive model for sector-based air traffic flow. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002. [Google Scholar]
- Kopardekar, P.; Rios, J.; Prevot, T.; Johnson, M.; Jung, J.; Robinson, J.E. Unmanned aircraft system traffic management (UTM) concept of operations. In Proceedings of the AIAA Aviation and Aeronautics Forum (Aviation 2016), Washington, DC, USA, 13–17 June 2016; pp. 1–16. [Google Scholar]
- Mueller, E.R.; Kopardekar, P.H.; Goodrich, K.H. Enabling airspace integration for high-density on-demand mobility operations. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017; p. 3086. [Google Scholar]
- González-Arribas, D.; Soler, M.; López-Leonés, J.; Casado, E.; Sanjurjo-Rivo, M. Automated optimal flight planning based on the aircraft intent description language. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 233, 928–948. [Google Scholar] [CrossRef]
- Doc, I. 4444—Procedures for Air Navigation Services—Air Traffic Management; The International Civil Aviation Organization (ICAO): Montreal, QC, Canada, 2016. [Google Scholar]
- Bertsimas, D.; Patterson, S.S. The Air Traffic Flow Management Problem with Enroute Capacities. Oper. Res. 1998, 46, 406–422. [Google Scholar] [CrossRef]
- Crespo, A.M.F.; Weigang, L.; de Barros, A.G. Reinforcement learning agents to tactical air traffic flow management. Int. J. Aviat. Manag. 2012, 1, 145–161. [Google Scholar] [CrossRef]
- Kistan, T.; Gardi, A.; Sabatini, R.; Ramasamy, S.; Batuwangala, E. An evolutionary outlook of air traffic flow management techniques. Prog. Aerosp. Sci. 2017, 88, 15–42. [Google Scholar] [CrossRef]
- Gardi, A.; Sabatini, R.; Ramasamy, S. Multi-objective optimisation of aircraft flight trajectories in the ATM and avionics context. Prog. Aerosp. Sci. 2016, 83, 1–36. [Google Scholar] [CrossRef]
- Prevot, T.; Rios, J.; Kopardekar, P.; Robinson Iii, J.E.; Johnson, M.; Jung, J. UAS Traffic Management (UTM) Concept of Operations to Safely Enable Low Altitude Flight Operations. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Vascik, P.D.; Balakrishnan, H.; Hansman, R.J. Assessment of air traffic control for urban air mobility and unmanned systems. In Proceedings of the ICRAT 2018: 8th International Conference on Research in Air Transportation, Barcelona, Spain, 25–29 June 2018. [Google Scholar]
- Radmanesh, M.; Kumar, M.; Nemati, A.; Sarim, M. Dynamic optimal UAV trajectory planning in the National Airspace System via mixed integer linear programming. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 230, 1668–1682. [Google Scholar] [CrossRef]
- Liu, H.; Lin, Y.; Chen, Z.; Guo, D.; Zhang, J.; Jing, H. Research on the Air Traffic Flow Prediction Using a Deep Learning Approach. IEEE Access 2019, 7, 148019–148030. [Google Scholar] [CrossRef]
- Zhao, Z.; Luo, C.; Solomon, A.; Basti, F.; Caicedo, C.; Gursoy, M.C.; Qiu, Q. Machine Learning-Based Traffic Management Model for UAS Instantaneous Density Prediction in an Urban Area. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 11–15 October 2020; pp. 1–10. [Google Scholar]
- Lin, Y.; Zhang, J.-W.; Liu, H. Deep learning based short-term air traffic flow prediction considering temporal–spatial correlation. Aerosp. Sci. Technol. 2019, 93, 105113. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.Y.; Wang, K.; Lin, W.H.; Xu, X.; Chen, C. Data-Driven Intelligent Transportation Systems: A Survey. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1624–1639. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic Flow Prediction With Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Akhtar, M.; Moridpour, S. A Review of Traffic Congestion Prediction Using Artificial Intelligence. J. Adv. Transp. 2021, 2021, 8878011. [Google Scholar] [CrossRef]
- Yuan, H.; Li, G. A Survey of Traffic Prediction: From Spatio-Temporal Data to Intelligent Transportation. Data Sci. Eng. 2021, 6, 63–85. [Google Scholar] [CrossRef]
- Delahaye, D.; García, A.; Lavandier, J.; Chaimatanan, S.; Soler, M. Air traffic complexity map based on linear dynamical systems. Aerospace 2022, 9, 230. [Google Scholar] [CrossRef]
- Delahaye, D.; Puechmorel, S. Air traffic complexity: Towards intrinsic metrics. In Proceedings of the 3rd USA/Europe Air Traffic Management R&D Seminar, Napoli, Italy, 13–16 June 2000. [Google Scholar]
- Delahaye, D.; Puechmorel, S. Air traffic complexity based on dynamical systems. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 2069–2074. [Google Scholar]
- Wang, Z.; Delahaye, D.; Farges, J.-L.; Alam, S. Air Traffic Assignment for Intensive Urban Air Mobility Operations. J. Aerosp. Inf. Syst. 2021, 18, 860–875. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, J.-w.; Liu, H. An algorithm for trajectory prediction of flight plan based on relative motion between positions. Front. Inf. Technol. Electron. Eng. 2018, 19, 905–916. [Google Scholar] [CrossRef]
- Tian, W.; Hu, M. Study of Air Traffic Flow Management Optimization Model and Algorithm Based on Multi-objective Programming. In Proceedings of the 2010 Second International Conference on Computer Modeling and Simulation, Sanya, China, 22–24 January 2010; pp. 210–214. [Google Scholar]
- Mehrmolaei, S.; Keyvanpour, M.R. Time series forecasting using improved ARIMA. In Proceedings of the 2016 Artificial Intelligence and Robotics (IRANOPEN), Qazvin, Iran, 9 April 2016; pp. 92–97. [Google Scholar]
- Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Heard, C. Wind Speed Prediction Using a Univariate ARIMA Model and a Multivariate NARX Model. Energies 2016, 9, 109. [Google Scholar] [CrossRef]
- Xie, P.; Li, T.; Liu, J.; Du, S.; Yang, X.; Zhang, J. Urban flow prediction from spatiotemporal data using machine learning: A survey. Inf. Fusion 2020, 59, 1–12. [Google Scholar] [CrossRef]
- Sun, S.; Chen, J.; Sun, J. Traffic congestion prediction based on GPS trajectory data. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719847440. [Google Scholar] [CrossRef]
- Karlaftis, M.G.; Vlahogianni, E.I. Statistical methods versus neural networks in transportation research: Differences, similarities and some insights. Transp. Res. Part C Emerg. Technol. 2011, 19, 387–399. [Google Scholar] [CrossRef]
- Nadeem, K.M.; Fowdur, T.P. Performance analysis of a real-time adaptive prediction algorithm for traffic congestion. J. Inf. Commun. Technol. 2018, 17, 493–511. [Google Scholar] [CrossRef]
- Ito, T.; Kaneyasu, R. Predicting traffic congestion using driver behavior. Procedia Comput. Sci. 2017, 112, 1288–1297. [Google Scholar] [CrossRef]
- Zhang, H.-h.; Jiang, C.-p.; Yang, L. Forecasting traffic congestion status in terminal areas based on support vector machine. Adv. Mech. Eng. 2016, 8, 1687814016667384. [Google Scholar] [CrossRef]
- Reza, S.; Oliveira, H.S.; Machado, J.J.M.; Tavares, J.M.R.S. Urban Safety: An Image-Processing and Deep-Learning-Based Intelligent Traffic Management and Control System. Sensors 2021, 21, 7705. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.Y.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. Adv. Neural Inf. Process. Syst. 2014, 4, 3104–3112. [Google Scholar]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2022. [Google Scholar]
- Rosindell, J.; Wong, Y. Biodiversity, the Tree of Life, and Science Communication. In Phylogenetic Diversity: Applications and Challenges in Biodiversity Science; Scherson, R.A., Faith, D.P., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 41–71. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM—A tutorial into long short-term memory recurrent neural networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal Recurrent Convolutional Networks for Traffic Prediction in Transportation Networks. Sensors 2017, 17, 1501. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Y.; Qi, Y.; Shu, F.; Wang, Y. Short-term traffic flow prediction based on spatio-temporal analysis and CNN deep learning. Transp. A Transp. Sci. 2019, 15, 1688–1711. [Google Scholar] [CrossRef]
- Bogaerts, T.; Masegosa, A.D.; Angarita-Zapata, J.S.; Onieva, E.; Hellinckx, P. A graph CNN-LSTM neural network for short and long-term traffic forecasting based on trajectory data. Transp. Res. Part C Emerg. Technol. 2020, 112, 62–77. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 753–763. [Google Scholar]
- Jiang, W.; Luo, J. Graph neural network for traffic forecasting: A survey. Expert Syst. Appl. 2022, 207, 117921. [Google Scholar] [CrossRef]
- Cai, K.; Shen, Z.; Luo, X.; Li, Y. Temporal attention aware dual-graph convolution network for air traffic flow prediction. J. Air Transp. Manag. 2023, 106, 102301. [Google Scholar] [CrossRef]
- Jiang, Y.; Niu, S.; Zhang, K.; Chen, B.; Xu, C.; Liu, D.; Song, H. Spatial-Temporal Graph Data Mining for IoT-Enabled Air Mobility Prediction. IEEE Internet Things J. 2022, 9, 9232–9240. [Google Scholar] [CrossRef]
- Shi-Garrier, L.; Delahaye, D.; Bouaynaya, N.C. Predicting Air Traffic Congested Areas with Long Short-Term Memory Networks. In Proceedings of the Fourteenth USA/Europe Air Traffic Management Research and Development Seminar (ATM 2021), New Orleans, MS, USA, 15 September 2021. [Google Scholar]
- Wei, W.; Wu, H.; Ma, H. An AutoEncoder and LSTM-Based Traffic Flow Prediction Method. Sensors 2019, 19, 2946. [Google Scholar] [CrossRef]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; pp. 324–328. [Google Scholar]
- Duan, Z.; Yang, Y.; Zhang, K.; Ni, Y.; Bajgain, S. Improved Deep Hybrid Networks for Urban Traffic Flow Prediction Using Trajectory Data. IEEE Access 2018, 6, 31820–31827. [Google Scholar] [CrossRef]
- Jiber, M.; Mbarek, A.; Yahyaouy, A.; Sabri, M.A.; Boumhidi, J. Road Traffic Prediction Model Using Extreme Learning Machine: The Case Study of Tangier, Morocco. Information 2020, 11, 542. [Google Scholar] [CrossRef]
- Nguyen, G.; Dlugolinsky, S.; Bobák, M.; Tran, V.; López García, Á.; Heredia, I.; Malík, P.; Hluchý, L. Machine Learning and Deep Learning frameworks and libraries for large-scale data mining: A survey. Artif. Intell. Rev. 2019, 52, 77–124. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef]
- Erdelj, M.; Natalizio, E. UAV-assisted disaster management: Applications and open issues. In Proceedings of the 2016 International Conference on Computing, Networking and Communications (ICNC), Kauai, HI, USA, 15–18 February 2016; pp. 1–5. [Google Scholar]
- Radzki, G.; Golinska-Dawson, P.; Bocewicz, G.; Banaszak, Z. Modelling Robust Delivery Scenarios for a Fleet of Unmanned Aerial Vehicles in Disaster Relief Missions. J. Intell. Robot. Syst. 2021, 103, 63. [Google Scholar] [CrossRef]
- Larrabee, T.; Chao, H.; Rhudy, M.; Gu, Y.; Napolitano, M.R. Wind field estimation in UAV formation flight. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 5408–5413. [Google Scholar]
- Bijjahalli, S.; Sabatini, R.; Gardi, A. Advances in intelligent and autonomous navigation systems for small UAS. Prog. Aerosp. Sci. 2020, 115, 100617. [Google Scholar] [CrossRef]
- Besiou, M.; Pedraza-Martinez, A.J.; Van Wassenhove, L.N. OR applied to humanitarian operations. Eur. J. Oper. Res. 2018, 269, 397–405. [Google Scholar] [CrossRef]
- Koohi, I.; Groza, V.Z. Optimizing Particle Swarm Optimization algorithm. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, ON, Canada, 4–7 May 2014; pp. 1–5. [Google Scholar]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Alharbi, A.; Poujade, A.; Malandrakis, K.; Petrunin, I.; Panagiotakopoulos, D.; Tsourdos, A. Rule-Based Conflict Management for Unmanned Traffic Management Scenarios. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 11–15 October 2020; pp. 1–10. [Google Scholar]
- Alharbi, A.; Petrunin, I.; Panagiotakopoulos, D. Identification and Characterization of Traffic Flow Patterns for UTM application. In Proceedings of the 2021 IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021; pp. 1–10. [Google Scholar]
- Hilburn, B. Cognitive Complexity in Air Traffic Control: A Literature Review; Eurocontrol: Brussels, Belgium, 2004; pp. 1–80. [Google Scholar]
- Prandini, M.; Piroddi, L.; Puechmorel, S.; Brazdilova, S.L. Toward Air Traffic Complexity Assessment in New Generation Air Traffic Management Systems. IEEE Trans. Intell. Transp. Syst. 2011, 12, 809–818. [Google Scholar] [CrossRef]
- Pfleiderer, E.M.; Manning, C.A.; Goldman, S.M. Relationship of Complexity Factor Ratings with Operational Errors; Civil Aerospace Medical Institute: Oklahoma City, OK, USA, 2007. [Google Scholar]
- Histon, J.M.; Hansman, R.J.; Aigoin, G.; Delahaye, D.; Puechmorel, S. Introducing Structural Considerations into Complexity Metrics. Air Traffic Control Q. 2002, 10, 115–130. [Google Scholar] [CrossRef]
- Delahaye, D.; Puechmorel, S. Modeling and Optimization of Air Traffic; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Juntama, P.; Chaimatanan, S.; Alam, S.; Delahaye, D. A Distributed Metaheuristic Approach for Complexity Reduction in Air Traffic for Strategic 4D Trajectory Optimization. In Proceedings of the 2020 International Conference on Artificial Intelligence and Data Analytics for Air Transportation (AIDA-AT), Singapore, 3–4 February 2020; pp. 1–9. [Google Scholar]
- Wang, Z.; Delahaye, D.; Farges, J.-L.; Alam, S. Complexity optimal air traffic assignment in multi-layer transport network for Urban Air Mobility operations. Transp. Res. Part C Emerg. Technol. 2022, 142, 103776. [Google Scholar] [CrossRef]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Analysis of conflict resolution methods for manned and unmanned aviation using fast-time simulations. In Proceedings of the 9th SESAR Innovation Days, Athens, Greece, 2–6 December 2019. [Google Scholar]
- Widiputra, H.; Mailangkay, A.; Gautama, E. Multivariate CNN-LSTM Model for Multiple Parallel Financial Time-Series Prediction. Complexity 2021, 2021, 9903518. [Google Scholar] [CrossRef]
- Lu, L.; Zhang, X.; Renais, S. On training the recurrent neural network encoder-decoder for large vocabulary end-to-end speech recognition. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 5060–5064. [Google Scholar]
- Rafi, S.; Das, R. RNN Encoder And Decoder With Teacher Forcing Attention Mechanism for Abstractive Summarization. In Proceedings of the 2021 IEEE 18th India Council International Conference (INDICON), Guwahati, India, 19–21 December 2021; pp. 1–7. [Google Scholar]
- Williams, R.J.; Zipser, D. A Learning Algorithm for Continually Running Fully Recurrent Neural Networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980, p. 15. [Google Scholar]
- Geng, R.; Cui, D.; Xu, B. Support vector machine-based combinational model for air traffic forecasts. J. Tsinghua Univ. Sci. Technol. 2008, 48, 1205–1208. [Google Scholar]
- Li, Q.-F.; Song, Z.-M. High-performance concrete strength prediction based on ensemble learning. Constr. Build. Mater. 2022, 324, 126694. [Google Scholar] [CrossRef]
- Xie, Y.; Gardi, A.; Sabatini, R. Reinforcement Learning-Based Flow Management Techniques for Urban Air Mobility and Dense Low-Altitude Air Traffic Operations. In Proceedings of the 2021 IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021; pp. 1–10. [Google Scholar]
- Zhong, G.; Zhang, H.; Zhou, J.; Zhou, J.; Liu, H. Short-Term 4D Trajectory Prediction for UAV Based on Spatio-Temporal Trajectory Clustering. IEEE Access 2022, 10, 93362–93380. [Google Scholar] [CrossRef]
- Abedin, S.F.; Munir, M.S.; Tran, N.H.; Han, Z.; Hong, C.S. Data Freshness and Energy-Efficient UAV Navigation Optimization: A Deep Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5994–6006. [Google Scholar] [CrossRef]
- Komatsu, R.; Bechina, A.A.A.; Güldal, S.; Şaşmaz, M. Machine Learning Attempt to Conflict Detection for UAV with System Failure in U-Space: Recurrent Neural Network, RNNn. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 78–85. [Google Scholar]
- Yang, S.; Meng, Z.; Chen, X.; Xie, R. Real-time obstacle avoidance with deep reinforcement learning three-dimensional autonomous obstacle avoidance for uav. In Proceedings of the RICAI 2019: International Conference on Robotics, Intelligent Control and Artificial Intelligence, Shanghai, China, 20–22 September 2019; pp. 324–329. [Google Scholar]
- Zhang, Z.; Luo, C.; Gursoy, M.C.; Qiu, Q.; Caicedo, C.; Solomon, A.; Basti, F. Neural Network Architecture Search and Model Compression for Fast Prediction of UAS Traffic Density. In Proceedings of the 2021 Integrated Communications Navigation and Surveillance Conference (ICNS), Dulles, VA, USA, 19–23 April 2021; pp. 1–9. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Barredo Arrieta, A.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Xie, Y.; Pongsakornsathien, N.; Gardi, A.; Sabatini, R. Explanation of Machine-Learning Solutions in Air-Traffic Management. Aerospace 2021, 8, 224. [Google Scholar] [CrossRef]








| Airspace Class | Type of Flight | Separation Provided by ATC | Comm. to ATC | Subject to ATC Clear | |
|---|---|---|---|---|---|
| Controlled airspace | A | IFR only | All aircraft | Cont. 2-way | Yes |
| B | IFR | All aircraft | Cont. 2-way | Yes | |
| VFR | All aircraft | Cont. 2-way | Yes | ||
| C | IFR | IFR from IFR IFR from VFR | Cont. 2-way | Yes | |
| VFR | VFR from IFR | Cont. 2-way | Yes | ||
| D | IFR | IFR from IFR | Cont. 2-way | Yes | |
| VFR | No | Cont. 2-way | Yes | ||
| E | IFR | IFR from IFR | Cont. 2-way | Yes | |
| VFR | No | Not required | No | ||
| Uncontrolled airspace | F | IFR | IFR from IFR as far as practical | Cont. 2-way | No |
| VFR | No | Not required | No | ||
| G | IFR | No | Cont. 2-way | No | |
| VFR | No | Not required | No |
| Mission | COVID-19 Samples | Package Delivery | Emergency Operation | Railway Inspection |
| UAV fleet | UAV1, UAV2 and UAV3 | UAV4 and UAV5 | UAV 6 | UAV7 and UAV8 |
| Priority | 2 | 3 | 1 | 4 |
| Route | Luton | UAV4 | UAV6 available at | UAV7 |
| Cranfield | Cardington | Milton Keynes | Bedford rail station | |
| Milton Keynes | Graveley | Prison Fire Station | to Ridgmont | |
| Dunstable | Old Warren | |||
| Sandy | UAV8 Milton Keynes (MK) central rail station to Bletchley | |||
| UAV5 | ||||
| Cranfield | ||||
| Dunstable | ||||
| Halton | ||||
| Milton Keynes | ||||
| Scenario planning | All scenarios | All scenarios | All scenarios | Scenario 2 and 3 |
| Parameters of UAVs | Value | Unit |
|---|---|---|
| UAV type | Rotary wing | -- |
| Payload capacity | 25 | kg |
| Flight time | 30 | minutes |
| Cruise speed | 90 | km/h |
| Wind resistance | 10 | m/s |
| Parameter | Description |
|---|---|
| A unique code is assigned to a single aircraft UAV to identify flight mission | |
| The UAV mission priority | |
| The timestep when the UAV is passing the waypoint | |
| UAV Velocity | |
| Heading Angle | |
| UAV States | State = [Timestamp, Longitude, Latitude, Velocity, Heading Angle] |
| Complexity Metric | The complexity metric is a linear dynamic system model that identifies a complexity parameter in the vicinity of a UAV for a specified period of time. |
| Parameter | Value |
|---|---|
| Batch size | 128 |
| (1-D) kernel width d | 3 |
| (1-D) filter f | 512 |
| Hidden layers (LSTM) | 128 |
| Activation | ReLU |
| Optimizer | Adam optimizer [86] |
| Learning rate | 0.001 |
| Epochs | 500 |
| Loss function | RMSE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, A.; Petrunin, I.; Panagiotakopoulos, D. Deep Learning Architecture for UAV Traffic-Density Prediction. Drones 2023, 7, 78. https://doi.org/10.3390/drones7020078
Alharbi A, Petrunin I, Panagiotakopoulos D. Deep Learning Architecture for UAV Traffic-Density Prediction. Drones. 2023; 7(2):78. https://doi.org/10.3390/drones7020078
Chicago/Turabian StyleAlharbi, Abdulrahman, Ivan Petrunin, and Dimitrios Panagiotakopoulos. 2023. "Deep Learning Architecture for UAV Traffic-Density Prediction" Drones 7, no. 2: 78. https://doi.org/10.3390/drones7020078
APA StyleAlharbi, A., Petrunin, I., & Panagiotakopoulos, D. (2023). Deep Learning Architecture for UAV Traffic-Density Prediction. Drones, 7(2), 78. https://doi.org/10.3390/drones7020078










