Optimization Schemes for UAV Data Collection with LoRa 2.4 GHz Technology in Remote Areas without Infrastructure
Abstract
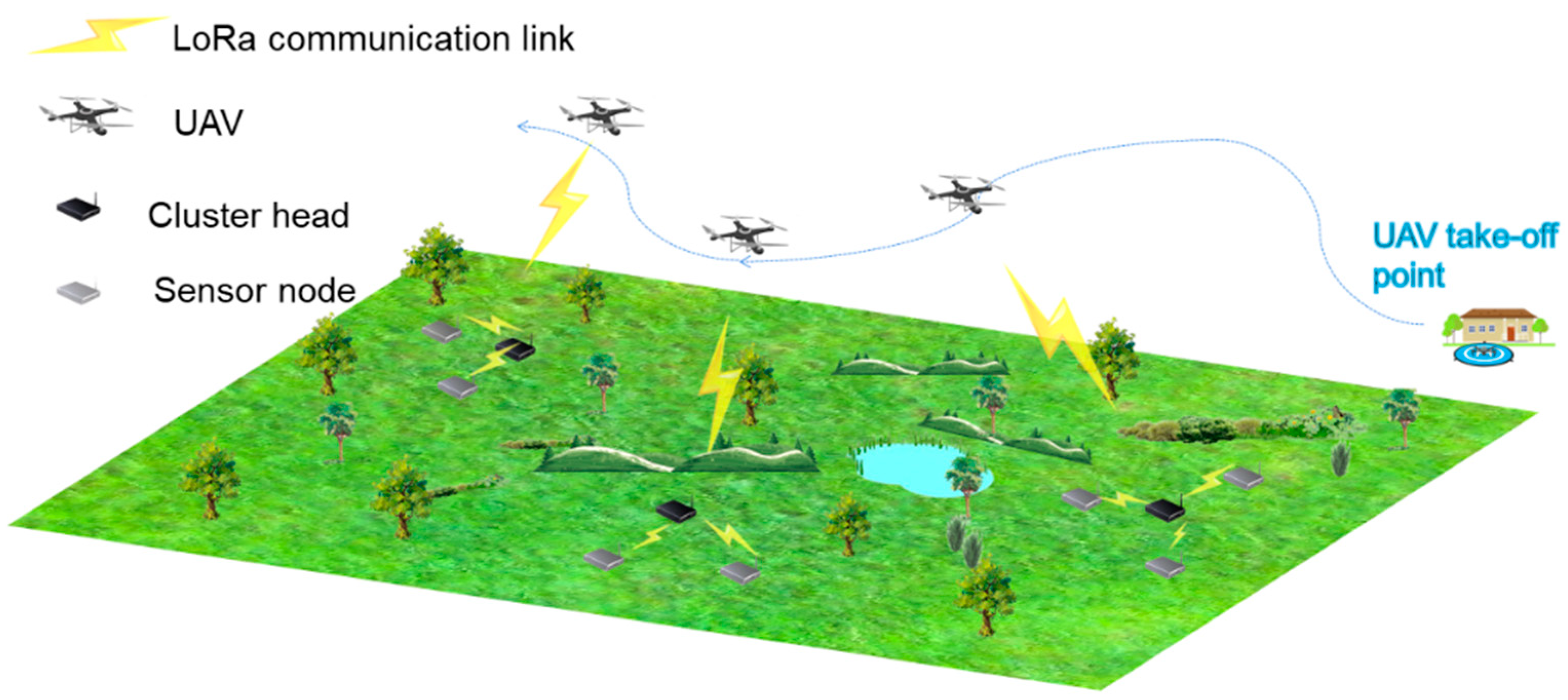
:1. Introduction
2. Related Work
- (1)
- An improved clustering algorithm for the LoRa network is proposed, which considers the influence of distance between the cluster heads and the UAV take-off point.
- (2)
- We present an improved Genetic Algorithm to obtain the optimal access path of a UAV, which introduces the Teaching–Learning-based Optimization and local search optimization algorithms to improve convergence rate and the path solution.
- (3)
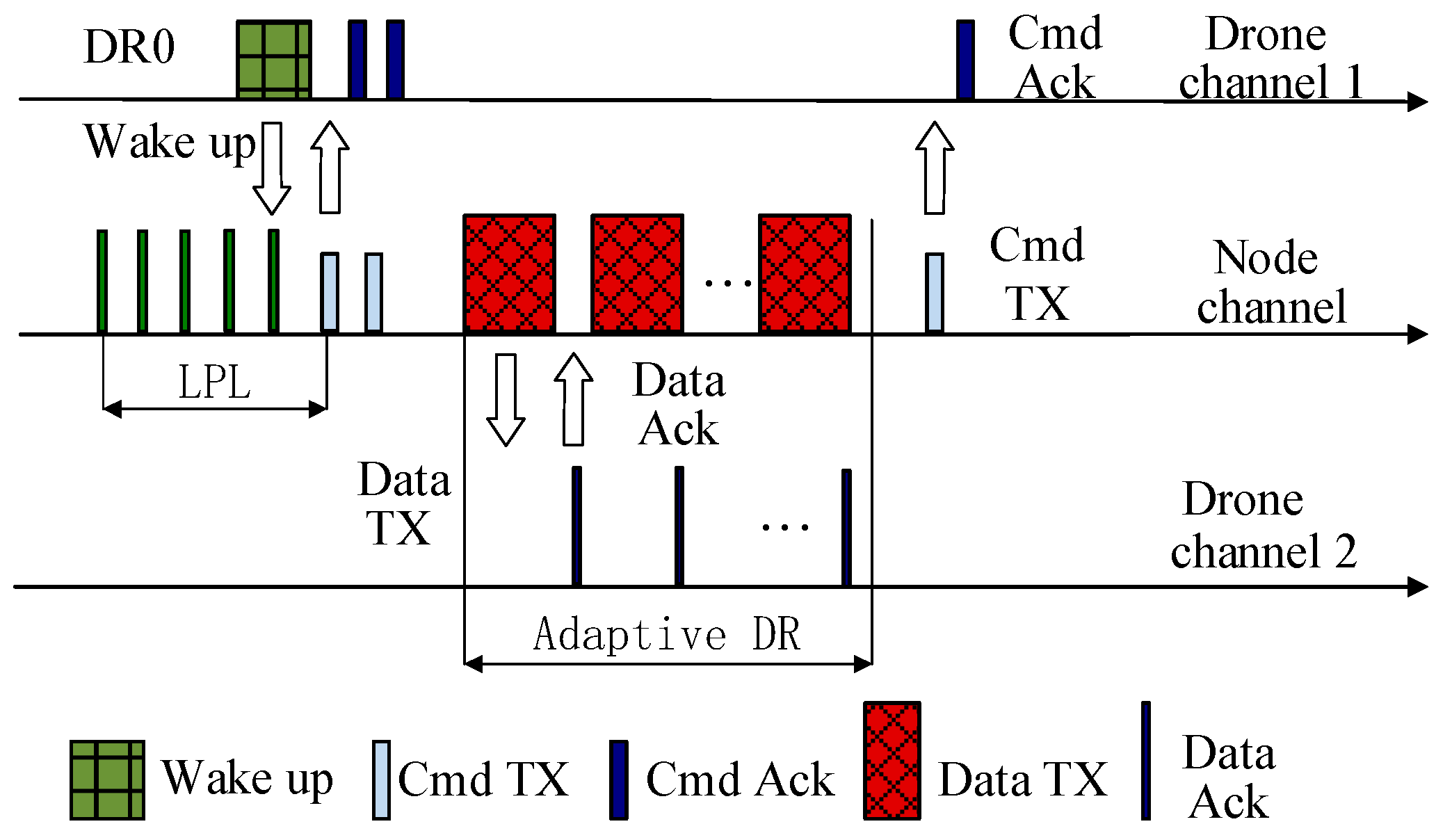
- A LoRa 2.4 GHz adaptive data rate strategy with a dual channel is designed based on distance and link quality, to reduce the data transmitting time between the UAV and the cluster head nodes.
- (4)
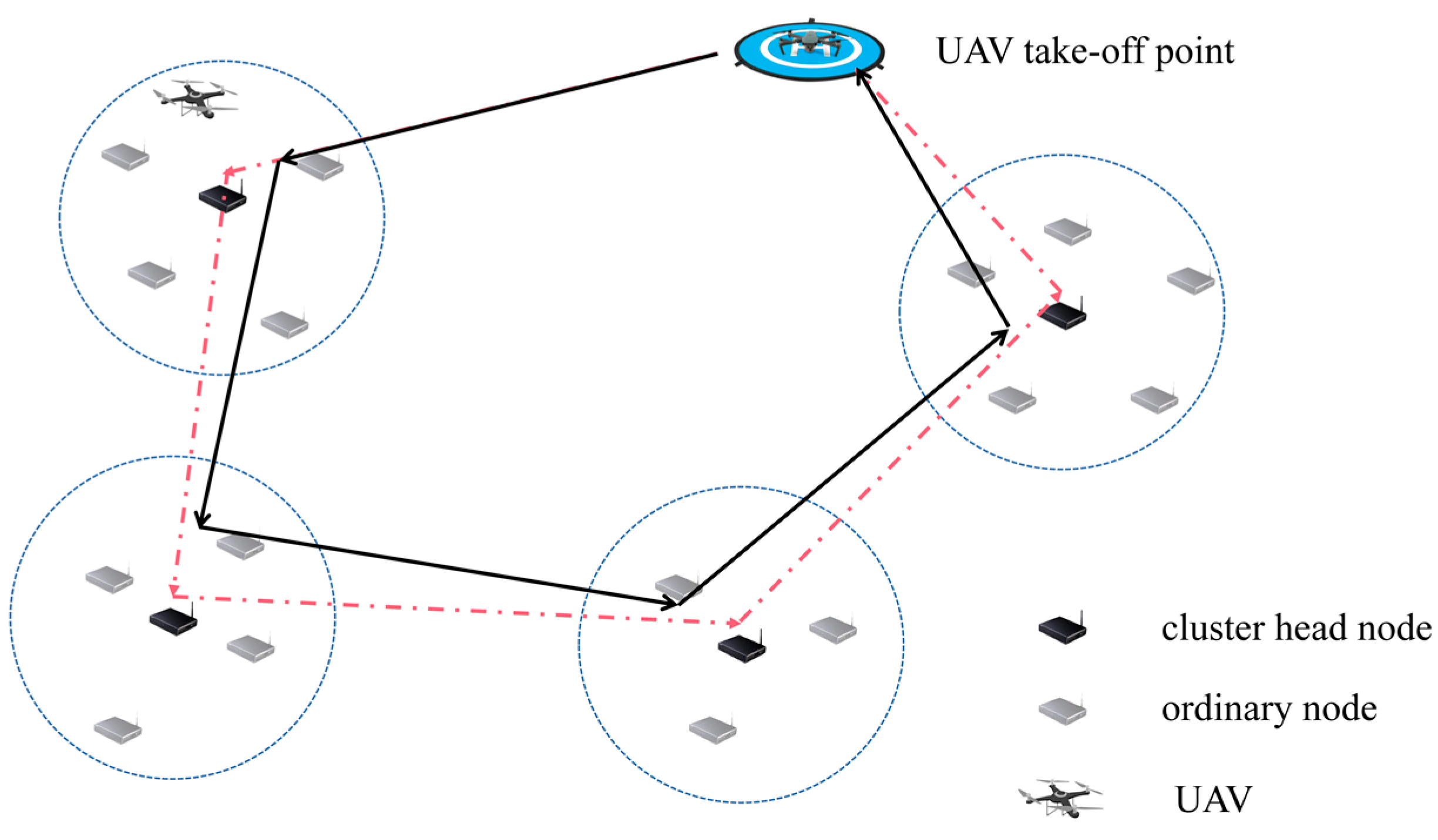
- The UAV’s moving status can be adjusted based on data gathering completion status of each cluster head to avoid meaningless flight distances. Real UAV flight paths are obtained to reduce the time of data acquisition tasks.
3. Model Formulation and Scheme Design
3.1. Model Formulation
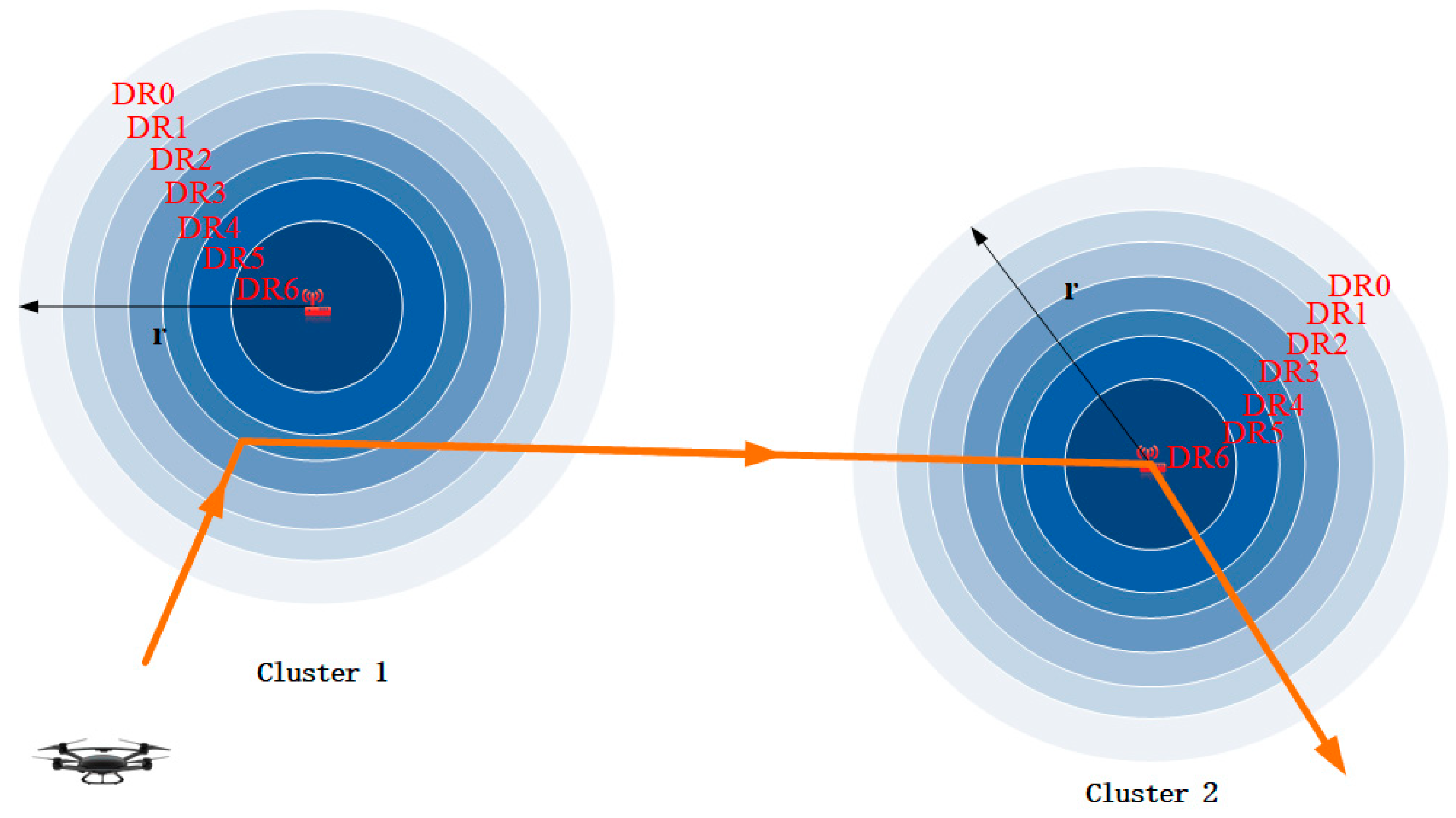
3.2. Improved Clustering Algorithm
3.3. Path Optimization
3.3.1. Path Optimization Model
3.3.2. Description of the TGA Algorithm
| Algorithm 1 Implementation of the TGA algorithm |
| Input: Maximum number of iterations, all cluster head nodes , UAV take-off point , population size, crossover probability , probability of variation Output: The optimal transportation route.
|
3.4. Communication Strategy
3.4.1. LoRa Adaptive Data Rate Strategy
3.4.2. Adjustment of the UAV’s Moving Status
4. Field Test
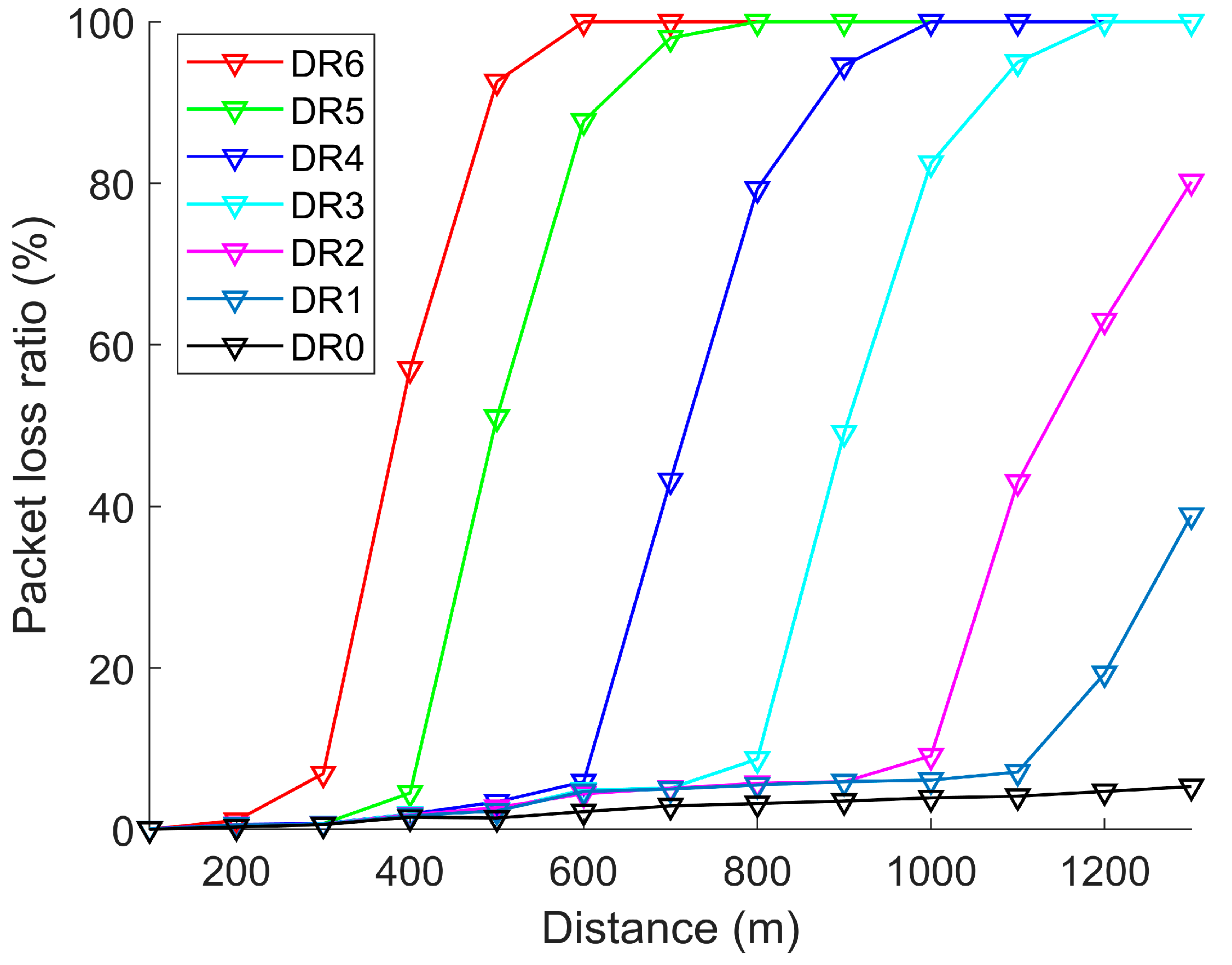
4.1. Threshold Test
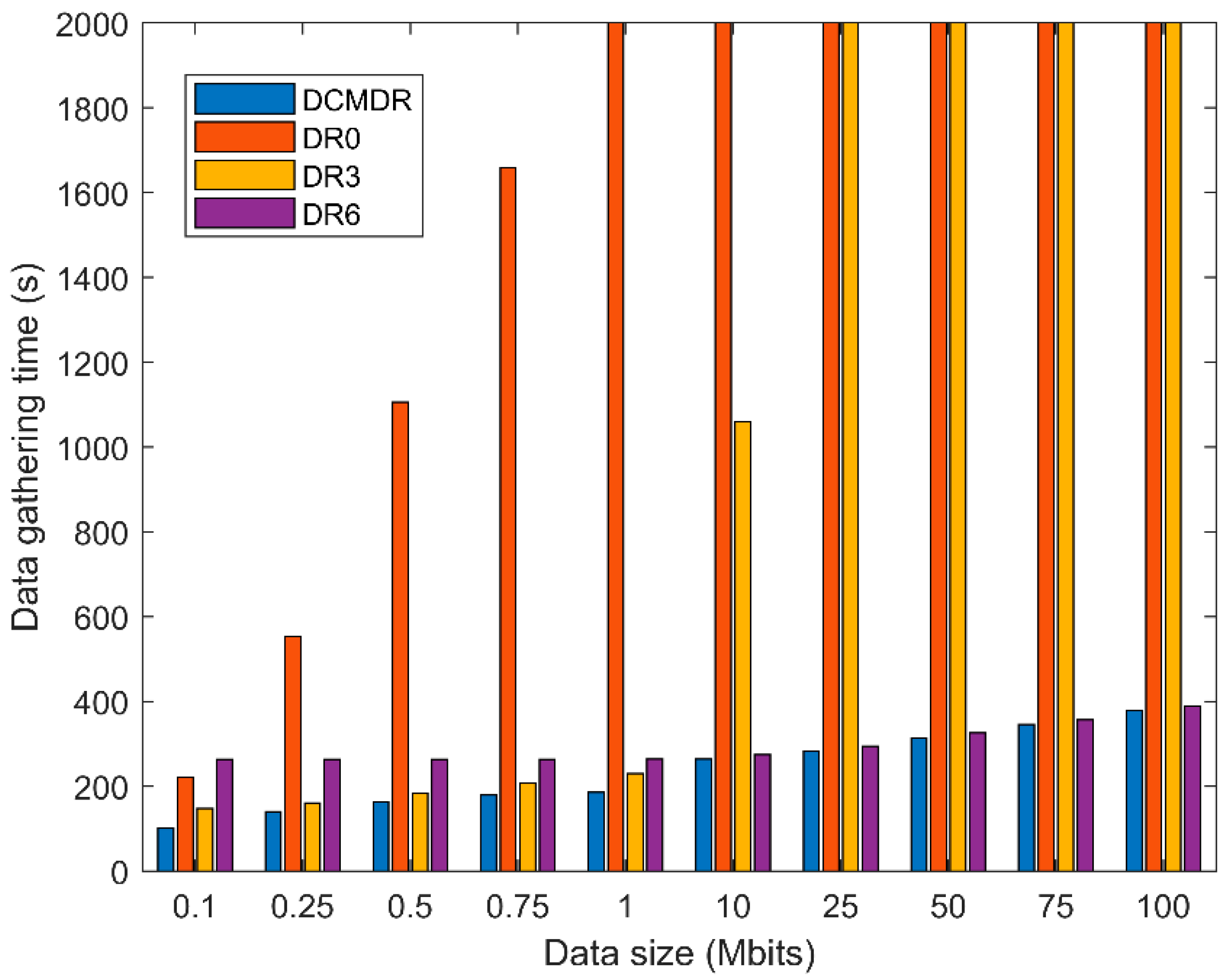
4.2. Data Gathering Time Test
5. Simulation and Experiment
5.1. Simulation
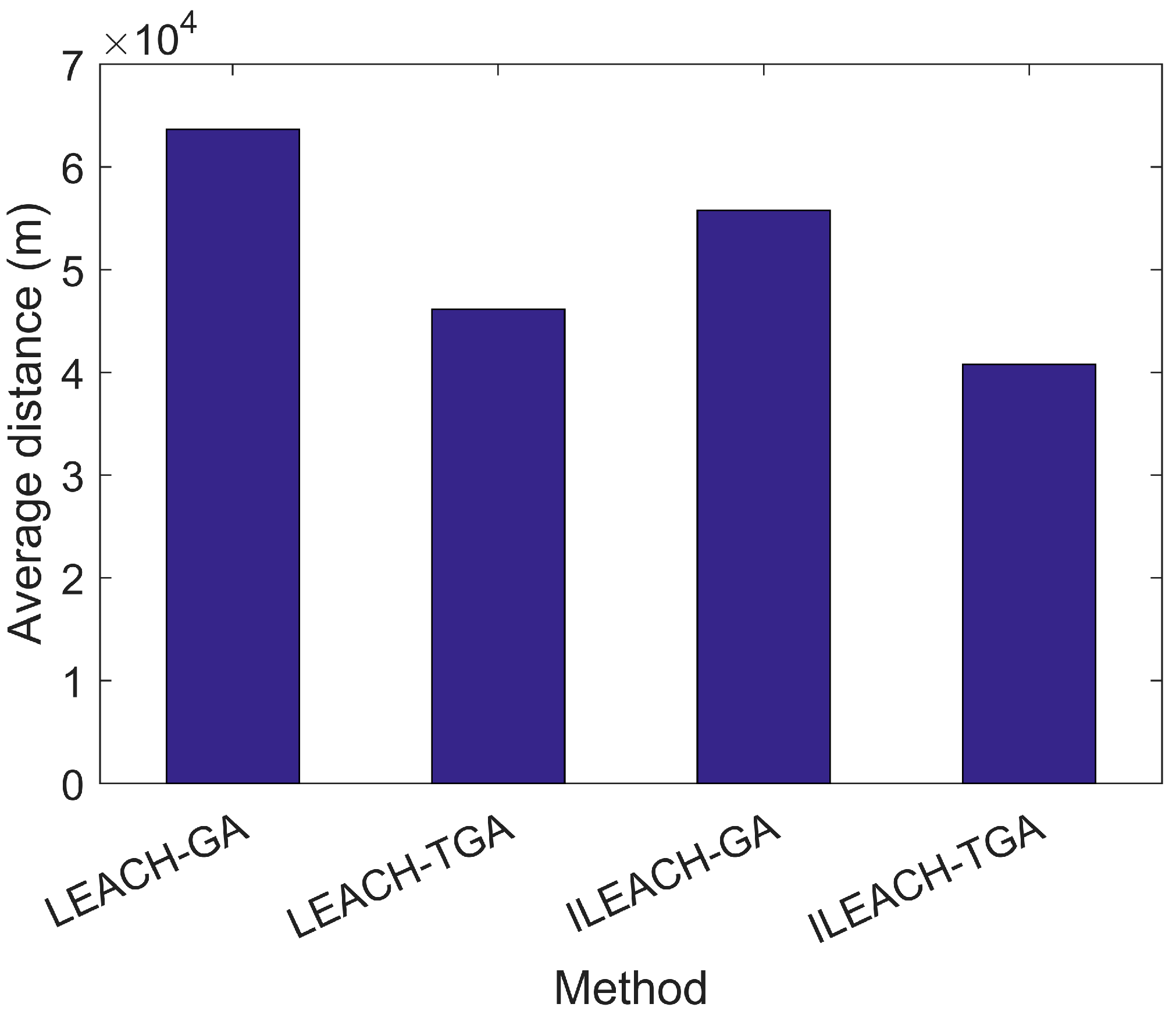
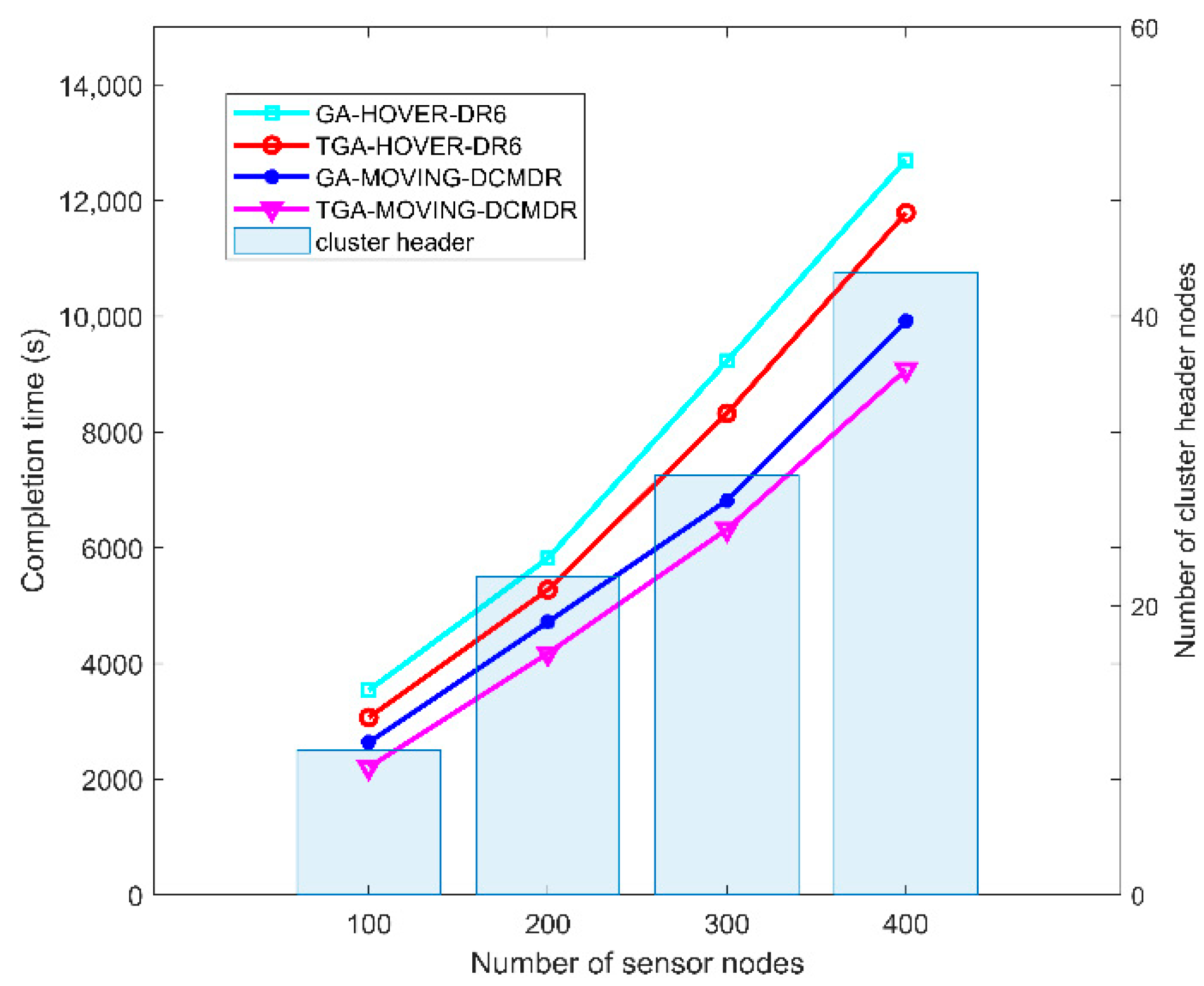
5.1.1. Simulation and Analysis of ILEACH and TGA Algorithms
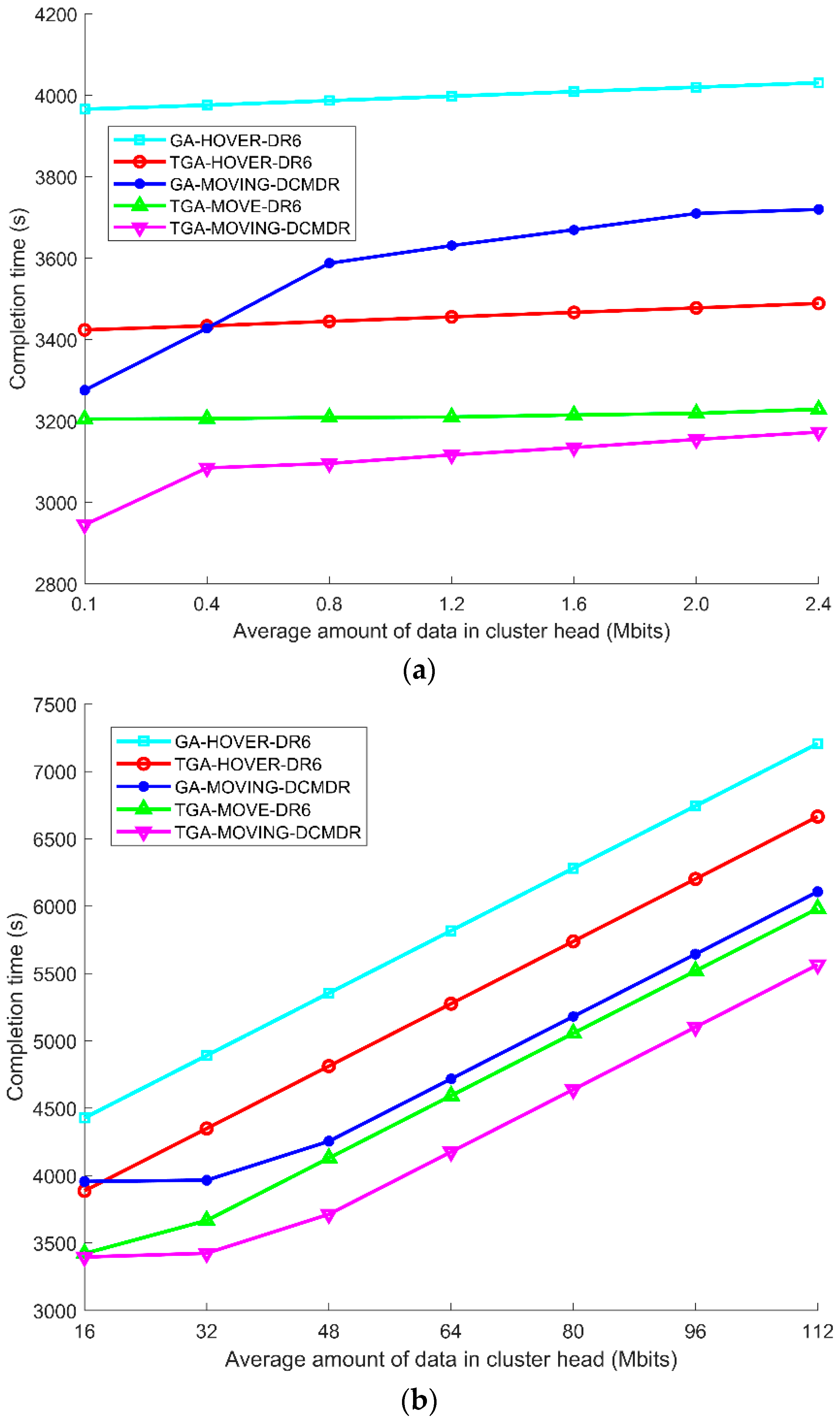
5.1.2. Simulation and Analysis of TGA-MOVING-DCMDR
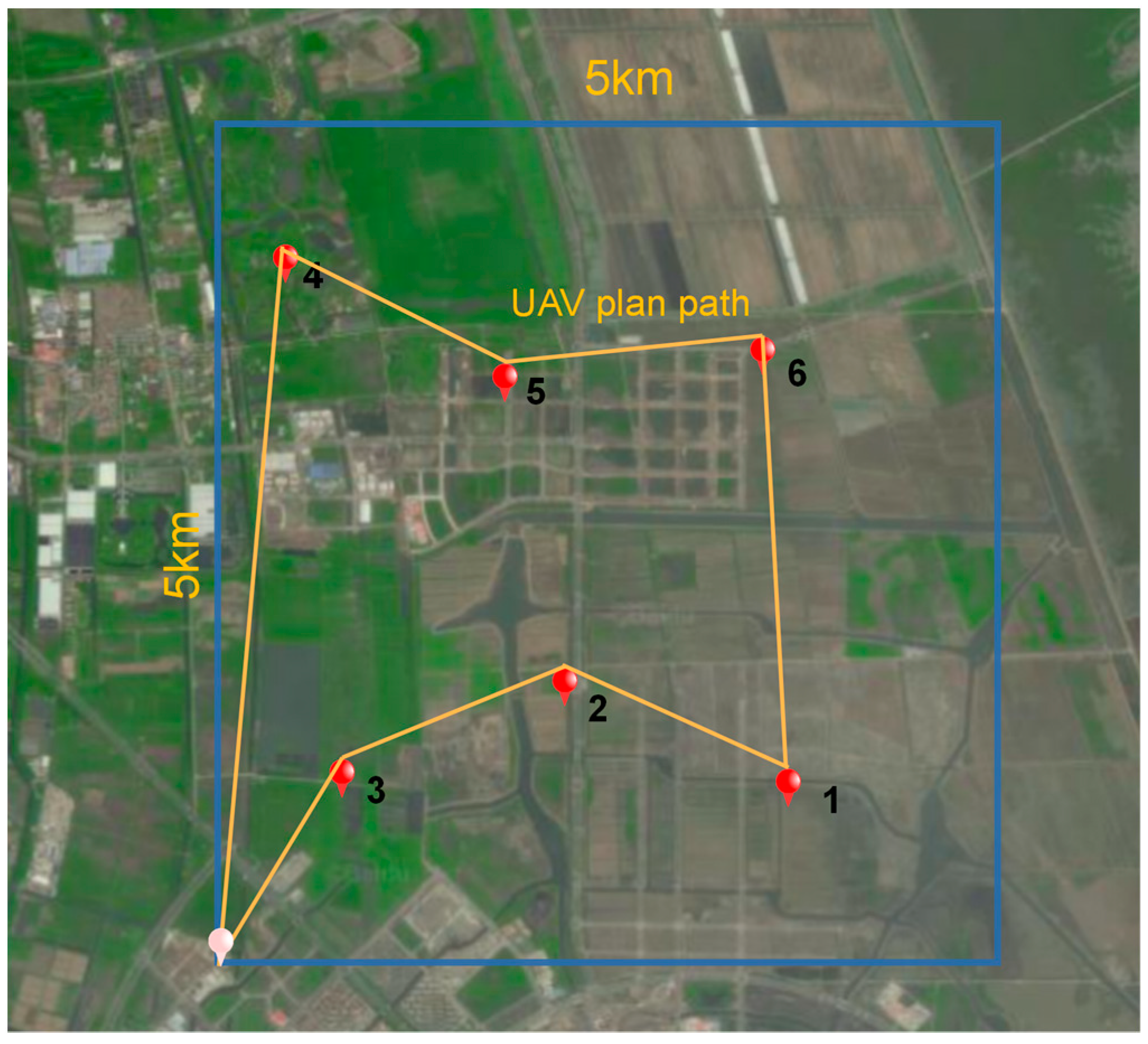
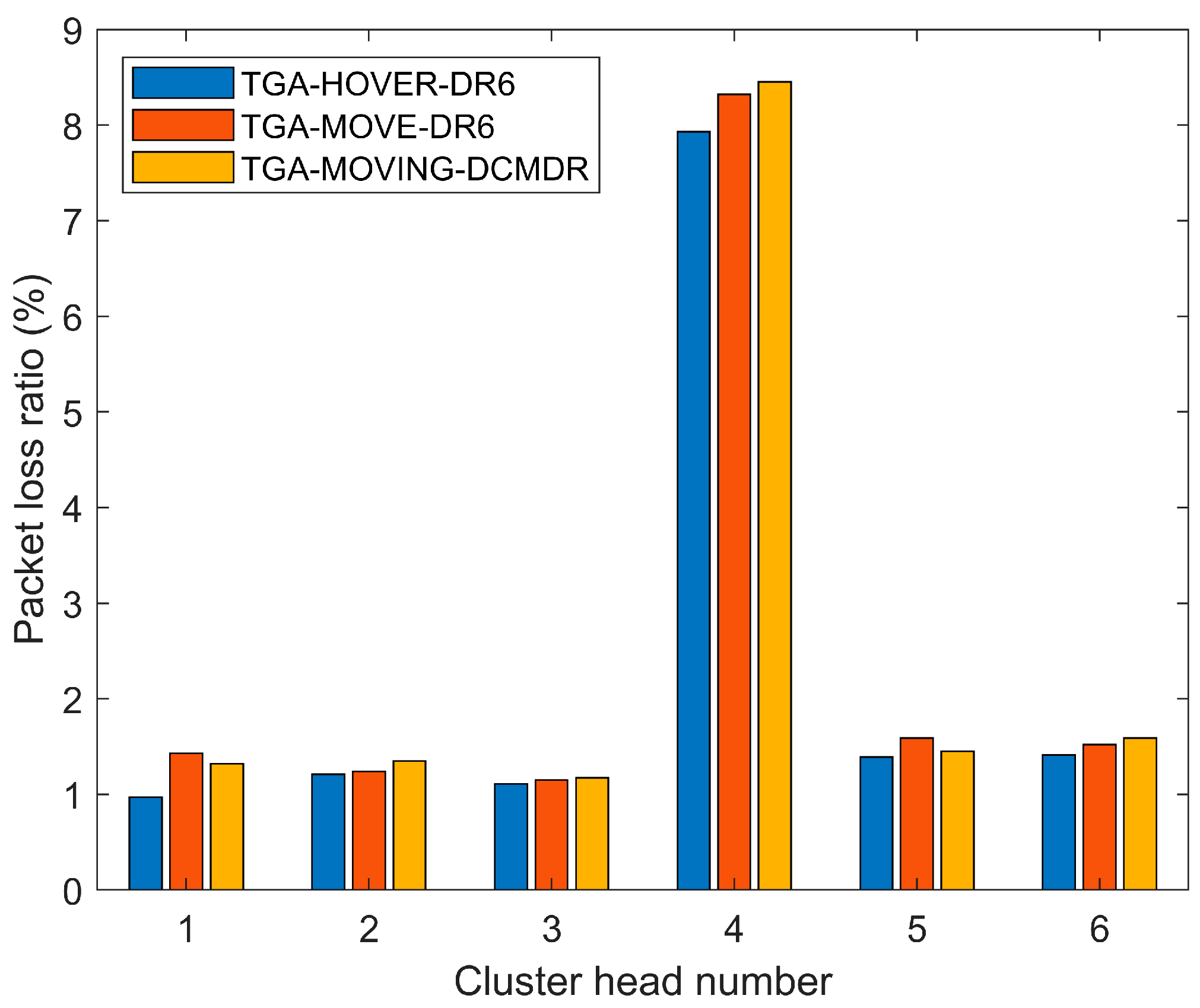
5.2. Experiment
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Yan, F.; Mao, S.; Shen, F.; Xia, W.; Wu, Y.; Shen, L. Efficient data collection in large-scale UAV-aided wireless sensor networks. In Proceedings of the IEEE International Conference on WCSP, Xi’an, China, 23–25 October 2019; pp. 1–5. [Google Scholar]
- Ge, J.; Chao, F.; He, Z.; Shi, W. Research on Water Monitoring Information Acquisition System of UAV Based on Wireless Sensor Network. In Proceedings of the 11th International Conference on Modelling, Identification and Control, Tianjin, China, 13–15 July 2019; pp. 969–977. [Google Scholar]
- Tao, M.; Li, X.; Yuan, H.; Wei, W. UAV-Aided trustworthy data collection in federated-WSN-enabled IoT applications. Inf. Sci. 2020, 532, 155–169. [Google Scholar] [CrossRef]
- Carcelle, X.; Heile, B.; Chatellier, C.; Pailler, P. Next WSN applications using ZigBee. In Home Networking; Springer: Boston, MA, USA, 2008; pp. 239–254. [Google Scholar]
- Bembe, M.; Abu-Mahfouz, A.; Masonta, M.; Ngqondi, T. A survey on low-power wide area networks for IoT applications. Telecommun. Syst. 2019, 71, 249–274. [Google Scholar] [CrossRef]
- Sinha, R.S.; Wei, Y.; Hwang, S.-H. A survey on LPWA technology: LoRa and NB-IoT. Ict Express 2017, 3, 14–21. [Google Scholar] [CrossRef]
- Behjati, M.; Noh, A.M.; Alobaidy, H.; Zulkifley, M.; Nordin, R.; Abdullah, N. LoRa Communications as an Enabler for Internet of Drones towards Large-Scale Livestock Monitoring in Rural Farms. Sensors 2021, 21, 5044. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.-S.; Baccelli, F.; De Veciana, G. Modeling and Analysis of Data Harvesting Architecture Based on Unmanned Aerial Vehicles. IEEE Trans. Wirel. Commun. 2019, 19, 1825–1838. [Google Scholar] [CrossRef] [Green Version]
- Gallego-Madrid, J.; Molina-Zarca, A.; Sanchez-Iborra, R.; Bernal-Bernabe, J.; Santa, J.; Ruiz, P.; Skarmeta-Gómez, A. Enhancing Extensive and Remote LoRa Deployments through MEC-Powered Drone Gateways. Sensors 2020, 20, 4109. [Google Scholar] [CrossRef]
- Saraereh, O.A.; Alsaraira, A.; Khan, I.; Uthansakul, P. Performance Evaluation of UAV-Enabled LoRa Networks for Disaster Management Applications. Sensors 2020, 20, 2396. [Google Scholar] [CrossRef]
- Zhang, M.; Li, X. Drone-Enabled Internet-of-Things Relay for Environmental Monitoring in Remote Areas Without Public Networks. IEEE Internet Things J. 2020, 7, 7648–7662. [Google Scholar] [CrossRef]
- Hung, C.-C.; Hsieh, C.-C. Big data management on wireless sensor networks. In Big Data Analytics for Sensor-Network Collected Intelligence; Elsevier: Amsterdam, The Netherlands, 2017; pp. 99–116. [Google Scholar]
- Sun, G.; Li, J.; Liu, Y.; Liang, S.; Kang, H. Time and Energy Minimization Communications Based on Collaborative Beamforming for UAV Networks: A Multi-Objective Optimization Method. IEEE J. Sel. Areas Commun. 2021, 39, 3555–3572. [Google Scholar] [CrossRef]
- Babu, N.; Virgili, M.; Papadias, C.B.; Popovski, P.; Forsyth, A.J. Cost-and Energy-Efficient Aerial Communication Networks with Interleaved Hovering and Flying. IEEE Trans. Veh. Technol. 2021, 70, 9077–9087. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Karunanithy, K.; Velusamy, B. Energy efficient cluster and travelling salesman problem based data collection using WSNs for Intelligent water irrigation and fertigation. Measurement 2020, 161, 107835. [Google Scholar] [CrossRef]
- Ho, D.-T.; Grøtli, E.I.; Sujit, P.; Johansen, T.A.; Sousa, J.B. Optimization of wireless sensor network and UAV data acquisition. J. Intell. Robot. Syst. 2015, 78, 159–179. [Google Scholar] [CrossRef]
- Wang, G.; Lee, B.-S.; Ahn, J.Y. UAV-assisted cluster head election for a UAV-based wireless sensor network. In Proceedings of the IEEE 6th International Conference on Future Internet of Things and Cloud, Barcelona, Spain, 6–8 August 2018; pp. 267–274. [Google Scholar]
- Alemayehu, T.S.; Kim, J.-H. Efficient Nearest Neighbor Heuristic TSP Algorithms for Reducing Data Acquisition Latency of UAV Relay WSN. Wirel. Pers. Commun. 2017, 95, 3271–3285. [Google Scholar] [CrossRef]
- Alemayehu, T.S.; Kim, J.-H.; Yoon, W. Fault-Tolerant UAV Data Acquisition Schemes. Wirel. Pers. Commun. 2020, 114, 1669–1685. [Google Scholar] [CrossRef]
- Xiao-Ting, J.; Hai-Bin, X.; Li, Z.; Sheng-De, J. Flight path planning based on an improved genetic algorithm. In Proceedings of the Third International Conference on Intelligent System Design and Engineering Applications, Hong Kong, China, 16–18 January 2013; pp. 775–778. [Google Scholar]
- Yang, T.; Hu, Y.; Yuan, X.; Mathar, R. Genetic algorithm based UAV trajectory design in wireless power transfer systems. In Proceedings of the IEEE Wireless Communications and Networking Conference, Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Nasution, T.H.; Siregar, I.; Yasir, M. UAV telemetry communications using ZigBee protocol. J. Phys. Conf. Ser. 2017, 914, 012001. [Google Scholar] [CrossRef]
- Yu, L.; Fei, Q.; Geng, Q. Combining Zigbee and inertial sensors for quadrotor UAV indoor localization. In Proceedings of the IEEE International Conference on Control and Automation, Hangzhou, China, 12–14 June 2013; pp. 1912–1916. [Google Scholar]
- Khalifeh, A.F.; AlQudah, M.; Tanash, R.; Darabkh, K.A. A simulation study for UAV-aided wireless sensor network utilizing ZigBee protocol. In Proceedings of the 14th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Limassol, Cyprus, 15–17 October 2018; pp. 181–184. [Google Scholar]
- Sidek, O.; Abdullah, A.; Za'bah, U.; Amran, N.; Jafar, H.; Hadi, M.A.; Nikmat, F.; Halim, Z.; Mansor, M. Development of prototype system for monitoring and computing greenhouse gases with unmanned aerial vehicle (uav) deployment. In Proceedings of the International Symposium on Technology Management and Emerging Technologies, Bandung, Indonesia, 27–29 May 2014; pp. 98–101. [Google Scholar]
- Tan, Z.; Yang, X.; Pang, M.; Gao, S.; Li, M.; Chen, P. UAV-Assisted Low-Consumption Time Synchronization Utilizing Cross-Technology Communication. Sensors 2020, 20, 5134. [Google Scholar] [CrossRef]
- Augustin, A.; Yi, J.; Clausen, T.; Townsley, W.M. A Study of LoRa: Long Range & Low Power Networks for the Internet of Things. Sensors 2016, 16, 1466. [Google Scholar]
- Wendt, T.; Volk, F.; Mackensen, E. A benchmark survey of long range (LoRaTM) spread-spectrum-communication at 2.45 GHz for safety applications. In Proceedings of the 16th Annual Wireless and Microwave Technology Conference (IEEE WAMICON), Cocoa Beach, FL, USA, 13–15 April 2015; pp. 1–4. [Google Scholar]
- Trasviña-Moreno, C.A.; Blasco, R.; Casas, R.; Asensio, A. A network performance analysis of LoRa modulation for LPWAN sensor devices. In Ubiquitous Computing and Ambient Intelligence; Springer: Cham, Switzerland, 2016; pp. 174–181. [Google Scholar]
- Kim, D.K.; Son, H.S.; Yang, S.H. LoRa Communication and Smartphone Technology to Share Locations of Drones. Trans. Korean Soc. Mech. Eng. A 2019, 43, 903–909. [Google Scholar] [CrossRef]
- da Silva, R.I.; Nascimento, M.A. On best drone tour plans for data collection in wireless sensor network. In Proceedings of the 31st annual ACM Symposium on Applied Computing, Pisa, Italy, 4–8 April 2016; pp. 703–708. [Google Scholar]
- Rezende, J.D.C.V.; Da Silva, R.I.; Souza, M.J.F. Gathering Big Data in Wireless Sensor Networks by Drone. Sensors 2020, 20, 6954. [Google Scholar] [CrossRef]
- Lawler, E.L.; Lenstra, J.K.; Kan, A.R.; Shmoys, D.B. The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Heinzelman, W.R. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000. [Google Scholar]
- Manjeshwar, A.; Agrawall, D.P. TEEN: A routing protoeol for enhanced efficiency in wireless sensor networks. In Proceedings of the 15th Parallel and Distributed Proeessing Symposium, San Francisco, CA, USA, 23–27 April 2001. [Google Scholar]
- Lindsey, S.; Raghavendra, C.S. PEGASIS: Power Efficient Gathering in Sensor Information Systems. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; Volume 3, pp. 1130–1152. [Google Scholar]
- Moghaddam, B.F.; Ruiz, R.; Sadjadi, S.J. Vehicle routing problem with uncertain demands: An advanced particle swarm algorithm. Comput. Ind. Eng. 2012, 62, 306–317. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agent. IEEE Trans. Syst. Man Cybern. Part B-Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, Z.; Zhu, Y.; Wang, Y.; Du, X.; Guizani, M.; Tian, Z. Applying artificial bee colony algorithm to the multidepot vehicle routing problem. Softw. Pract. Exp. 2020, 52, 756–771. [Google Scholar] [CrossRef]
- Wang, C.L.; Li, S.W. Hybrid fruit fly optimization algorithm for solving multi-compartment vehicle routing problem in intelligent logistics. Adv. Prod. Eng. Manag. 2018, 13, 466–478. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, F. An effective tabu search approach with improved loading algorithms for the 3L-CVRP. Comput. Oper. Res. 2015, 55, 127–140. [Google Scholar] [CrossRef]
- Zarandi, M.H.F.; Hemmati, A.; Davari, S.; Turksen, I.B. A simulated annealing algorithm for routing problems with fuzzy constrains. J. Intell. Fuzzy Syst. 2014, 26, 2649–2660. [Google Scholar] [CrossRef] [Green Version]
- SINTEF Research Institutes. Solomon Benchmark Datasets (R201, C201, and RC201). Available online: https://www.sintef.no/projectweb/top/vrptw/solomon-benchmark/ (accessed on 19 December 2021).







| Notation | Descriptions |
|---|---|
| DCP | The points directly above each cluster head are data collection points (DCP) |
| ILEACH | Improved cluster head selection algorithm based on LEACH |
| TGA | Improved genetic algorithm based on TLBO |
| DCMDR | Dual Channel Multiple Data Rate |
| DR | Data Rate |
| The average distance factor of neighbor nodes | |
| The number of nodes covered factor | |
| The remaining energy factor | |
| The distance factor from the node to the UAV take-off point | |
| L | Path length of UAV traversing cluster head |
| Binary variable, if UAV goes to cluster head j after arriving at cluster head i, = 1, otherwise is 0 | |
| Distance from cluster head i to j | |
| Fitness function | |
| The teaching factor, which determines the degree to which the average value is changed, typically 1 or 2, | |
| A random vector, each element of which is a random number in the range of [0, 1]. | |
| The correlation formula between cluster head i and j | |
| Current solution | |
| Updated solution | |
| The UAV’s flight speed | |
| The data rate obtained from ACK | |
| The data size stored by the cluster head |
| Data Rate (DR) | DR6 | DR5 | DR4 | DR3 | DR2 | DR1 | DR0 |
|---|---|---|---|---|---|---|---|
| Bandwidth (kHz) | 1200 | 300 | 812 | 812 | 812 | 406 | 203 |
| Mode | FLRC | FLRC | SF7 | SF9 | SF11 | SF12 | SF12 |
| Physical Bit Rate (kb/s) | 1040 | 260 | 44.41 | 14.27 | 4.36 | 1.19 | 0.595 |
| Receiver Sensitivity (dBm) | −100 | −106 | −112 | −117 | −123 | −128 | −130 |
| DR | SNR | RSSI | Dist (m) |
|---|---|---|---|
| 6 | 0 | −85 | 250 |
| 5 | 0 | −95 | 380 |
| 4 | 0 | −112 | 600 |
| 3 | −5 | −114 | 750 |
| 2 | −10 | −119 | 950 |
| 1 | −15 | −120 | 1100 |
| Datasets | TGA | GA | ||||
|---|---|---|---|---|---|---|
| Optimal Solution (m) | Average Solution (m) | Average Convergence Algebra | Optimal Solution (m) | Average Solution (m) | Average Convergence Algebra | |
| R201 | 707.5 | 712.1 | 60 | 2011.6 | 2517.3 | 164.7 |
| C201 | 723.3 | 735.4 | 79.3 | 2084.5 | 2615.5 | 159.7 |
| RC201 | 696.5 | 701.6 | 87.5 | 2646.2 | 2737.2 | 194.3 |
| Methods | Cluster Head Data (Mbits) | |||||
|---|---|---|---|---|---|---|
| 32 | 48 | 64 | 80 | 96 | 112 | |
| TGA-HOVER-DR6 | 1469 | 1584 | 1700 | 1815 | 1930 | 2045 |
| TGA-MOVE-DR6 | 1257 | 1285 | 1404 | 1512 | 1631 | 1743 |
| TGA-MOVING-DCMDR | 1239 | 1251 | 1347 | 1472 | 1577 | 1692 |
| Methods | Cluster Head Data (Mbits) | |||
|---|---|---|---|---|
| 0.25 | 0.5 | 0.75 | 1.0 | |
| TGA-HOVER-DR3 | 1359 | 1491 | 1617 | 1743 |
| TGA-HOVER-DR6 | 1240 | 1242 | 1245 | 1249 |
| TGA-MOVE-DR3 | 1079 | 1105 | 1205 | 1301 |
| TGA-MOVE-DR6 | 1165 | 1166 | 1168 | 1170 |
| TGA-MOVING-DCMDR | 1063 | 1082 | 1107 | 1136 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhou, C.; Sheng, L.; Cao, S. Optimization Schemes for UAV Data Collection with LoRa 2.4 GHz Technology in Remote Areas without Infrastructure. Drones 2022, 6, 173. https://doi.org/10.3390/drones6070173
Zhang Z, Zhou C, Sheng L, Cao S. Optimization Schemes for UAV Data Collection with LoRa 2.4 GHz Technology in Remote Areas without Infrastructure. Drones. 2022; 6(7):173. https://doi.org/10.3390/drones6070173
Chicago/Turabian StyleZhang, Zheng, Chun Zhou, Liangcai Sheng, and Shouqi Cao. 2022. "Optimization Schemes for UAV Data Collection with LoRa 2.4 GHz Technology in Remote Areas without Infrastructure" Drones 6, no. 7: 173. https://doi.org/10.3390/drones6070173
APA StyleZhang, Z., Zhou, C., Sheng, L., & Cao, S. (2022). Optimization Schemes for UAV Data Collection with LoRa 2.4 GHz Technology in Remote Areas without Infrastructure. Drones, 6(7), 173. https://doi.org/10.3390/drones6070173






