Obstacle Avoidance-Based Autonomous Navigation of a Quadrotor System

Abstract

Livestock management is an emerging area of application of the quadrotor, especially for monitoring, counting, detecting, recognizing, and tracking animals through image or video footage. The autonomous operation of the quadrotor requires the development of an obstacle avoidance scheme to avoid collisions. This research develops an obstacle avoidance-based autonomous navigation of a quadrotor suitable for outdoor applications in livestock management. A Simulink model of the UAV is developed to achieve this, and its transient and steady-state performances are measured. Two genetic algorithm-based PID controllers for the quadrotor altitude and attitude control were designed, and an obstacle avoidance algorithm was applied to ensure the autonomous navigation of the quadrotor. The simulation results show that the quadrotor flies to the desired altitude with a settling time of 6.51 s, an overshoot of 2.65%, and a steady-state error of 0.0011 m. At the same time, the attitude controller records a settling time of 0.43 s, an overshoot of 2.50%, and a zero steady-state error. The implementation of the obstacle avoidance scheme shows that the distance threshold of 1 m is sufficient for the autonomous navigation of the quadrotor. Hence, the developed method is suitable for managing livestock with the average size of an adult sheep.

1. Introduction

Unmanned Aerial Vehicles (UAVs) have gained significant research attention from academic and industrial disciplines due to their diverse utilizations in civilian and military applications. These applications include aerial and border surveillance, mapping and photography, search and rescue operations, data acquisition and transmission, and transportation and packet delivery. Nowadays, one application of the UAVs is in agriculture, for farm and livestock management. UAVs are used in this field for monitoring, behavior recognition, counting, detection, tracking, and livestock identification [1,2,3,4,5,6,7]. These applications are sometimes achieved by harnessing other technologies such as Flying Ad hoc Networks (FANET) [8] and wireless sensor networks [9].

Depending on the application, UAVs operate as drones (with rotary wing) or aircraft (with fixed wing), either in autonomous or teleoperated mode. The rotary-wing UAVs are characterized by their hovering capability, maneuverability, and Vertical Takeoff and Landing (VTOL) capabilities within a limited space. Moreover, fixed-wing UAVs are characterized by long-range and endurance flight capabilities [10,11,12]. However, fixed-winged UAVs lack the hovering ability and require a runway and more space for horizontal takeoff and landing. Thus, rotary-winged UAVs (quadrotors) are the most commonly used flying system for research by small groups, individuals, and other civil and commercial users due to the inherent ease of deployment, maneuverability, efficient performance, and VTOL ability [12,13]. Therefore, stable, precise position control of the quadrotor system is imperative to meet the needs of various users and requirements for multiple fields of application.

Different flight controllers have been presented in the literature for the quadcopter system. These controllers could be classified into nonlinear (MPC, adaptive, sliding mode, backstepping), learning-based (fuzzy logic, neural networks, reinforcement learning), and linear (PID, LQR, gain scheduling, $H_2$ and $H_{\infty }$) flight controllers [11]. The Proportional-Integral-Derivative (PID) controller is one of the most popular control algorithms that is implemented in the industry because of its design simplicity and ease of implementation. Surveys have shown that PID accounts for over 90% of all industrial control systems [14,15,16]. It also provides satisfactory performance for most applications, depending on the values of its control parameters. For a quadrotor, these PID parameters have been tuned using various techniques in literature for altitude and attitude control. Some of these techniques include particle swarm optimization [17,18], fuzzy logic [19,20], neural network [21,22,23], heuristic technique [10] and other metaheuristic techniques [24,25], amongst others. This work optimizes the PID controller parameters using a Genetic Algorithm (GA) [26,27].

Generally, the design algorithm for the autonomous navigation of the quadrotor system with obstacle avoidance comprises three key components, as shown in Figure 1. Such algorithms, which include perception, planning, and control, improve the system’s autonomy in autonomous navigation to a defined target destination.

The three steps illustrated in Figure 1 are outlined as follows:

• Perception: This step determines the current state of the quadrotor (in terms of position and orientation) and the state of the surrounding environment (in terms of obstacle and target positions). The Global Positioning System (GPS) sensor and Inertial Measurement Unit (IMU) are primarily used to determine the state of the quadrotor system. In contrast, external sensors such as ultrasonic, LiDAR and vision cameras are used to determine the state and representation of the surrounding environment. Algorithms for object detection, object tracking, localization, and simultaneous localization and mapping are mainly developed for perception.
• Planning: This step uses the information obtained in the perception stage for decision making. Route planning and path planning algorithms are developed in this step.
• Control: This step controls the quadrotor movements and actions to ensure that it follows the path generated in the planning stage. Algorithms such as path following, obstacle avoidance, path tracking, and stability control are developed in this step.

In the autonomous navigation of quadrotors, collisions could occur due to various reasons, such as poor weather conditions, the nature of the deployment environment, and moving obstacles. Therefore, obstacle avoidance is fundamental in the autonomous navigation of the quadrotors. Thus, research efforts are ongoing to ensure collision-free autonomous navigation of UAVs [28,29].

The development of UAV obstacle avoidance algorithms in dynamic building environments has been considered in previous studies, for example, [30]. In [31], using a quadrotor dynamic simulator, a sensors-based algorithm was developed to enhance the UAV attitude and altitude estimation for improving autonomous indoor navigation or similar environments. This study focuses on the three categories of algorithm development for autonomous operation of the quadrotor system, which is achieved by first developing the model of the system in Simulink and then applying the simulation parameters obtained from [13] to the model. The control parameters of the altitude and attitude controllers of the quadrotor are tuned using GA based on two error criteria (i.e., integral square error and integral time absolute error). Their performance is compared, and the best controllers are selected based on overshoot, settling time, and steady-state error. As implemented on the quadrotor system, the controllers can ensure the successful application of the quadrotor for image collection due to improved stability and tracking performance. Additionally, the obstacle avoidance algorithm will improve the system autonomy as the quadrotor is shown to reach a defined target location by avoiding collision with obstacles in the simulation environment.

The remainder of this paper is organized as follows: Section 2 provides the essential background needed to understand the quadrotor concept and its model. Section 3 describes the methodology used in this study to obtain the results provided and discussed in Section 4. The conclusion of this paper is finally drawn in Section 5.

2. Background

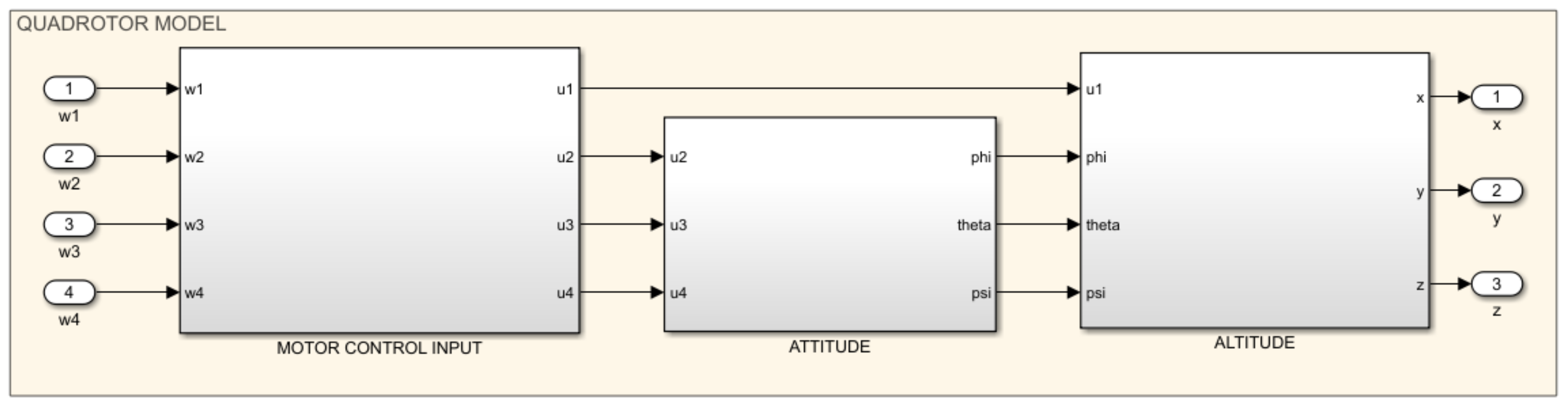
2.1. Quadrotor Model

Quadrotors are made up of four actuators equally spaced by 90° from each other. The actuators are individually controlled to generate a relative thrust. Figure 2 depicts the structure of the quadrotor with its body-fixed frame, the rotor’s angular speed and the thrust forces acting on it.

Where $f_i$ is the thrust force acting on the rotor and ${\mathsf{\omega }}_i$ is the angular velocity of the rotor. The thrust force $f_i$ and the rotor torque ${\tau }_i$ are proportional to the square of the angular velocity of the rotor as shown in Equation (1):

$$\left.\begin{array}{c}{f}_i=b{\omega }_i^2\\ {\tau }_i=d{\omega }_i^2\end{array}\right\}$$

(1)

2.1.1. Control Input

To achieve the desired motion of the quadrotor in a plus configuration, the thrust generated by the four motors is expressed as [13,32]:

$$\left.\begin{array}{l}{U}_1=b\left({\mathsf{\omega }}_1^2+{\mathsf{\omega }}_2^2+{\mathsf{\omega }}_3^2+{\mathsf{\omega }}_4^2\right)\hfill \\ U_2=b\left({\mathsf{\omega }}_4^2-{\mathsf{\omega }}_2^2\right)\hfill \\ U_3=b\left({\mathsf{\omega }}_3^2-{\mathsf{\omega }}_1^2\right)\hfill \\ U_4=d\left(-{\mathsf{\omega }}_1^2+{\mathsf{\omega }}_2^2-{\mathsf{\omega }}_3^2+{\mathsf{\omega }}_4^2\right)\hfill \end{array}\right\}$$

(2)

where U₁ is the total thrust generated by the propellers, U₂, U₃, and U_4,, respectively, represent the total thrust to achieve rolling, pitching, and yawing. The variables $\mathsf{\omega }$₁, $\mathsf{\omega }$₂, $\mathsf{\omega }$₃, and $\mathsf{\omega }$₄ represent the angular velocities of the respective motors.

The control action presented in Equation (2) is described in a matrix form as:

$$\left[\begin{array}{l}{U}_1\hfill \\ U_2\hfill \\ U_3\hfill \\ U_4\hfill \end{array}\right]=\left[\begin{array}{llll}b\hfill & b\hfill & b\hfill & b\hfill \\ 0\hfill & -b\hfill & 0\hfill & b\hfill \\ -b\hfill & 0\hfill & b\hfill & 0\hfill \\ -d\hfill & d\hfill & -d\hfill & d\hfill \end{array}\right]\left[\begin{array}{c}{\mathsf{\omega }}_1^2\\ {\mathsf{\omega }}_2^2\\ {\mathsf{\omega }}_3^2\\ {\mathsf{\omega }}_4^2\end{array}\right]$$

(3)

where b and d denote the thrust and drag factors, respectively. The overall residual angular velocity ($\mathsf{\omega }$_r) as the quadrotor rolls or pitches is defined as:

$${\mathsf{\omega }}_r=-{\mathsf{\omega }}_1+{\mathsf{\omega }}_2-{\mathsf{\omega }}_3+{\mathsf{\omega }}_4$$

(4)

2.1.2. Quadrotor Equation of Motion

The dynamic model of the quadrotor is presented in the form of translational and angular accelerations, as obtained through the Euler equation of motion. The translational equations of motion are expressed as [12]:

$$\left.\begin{array}{l}\ddot{x}=\frac{U_1}{m}[\cos \varphi \sin \theta \cos \psi -\sin \varphi \sin \psi ]\hfill \\ \ddot{y}=\frac{U_1}{m}\left[\cos \varphi \sin \theta \sin \psi -\sin \varphi \sin \psi \right]\hfill \\ \ddot{z}=\frac{U_1}{m}[\cos \varphi \cos \theta ]-g\hfill \end{array}\right\}$$

(5)

The Euler angle equations that define the angular accelerations of the quadrotor are expressed as [12]:

$$\left.\begin{array}{l}\ddot{\varphi }=\frac{1}{I_x}\left[\dot{\theta }\dot{\psi }\left(I_z-I_y\right)-J_r\dot{\theta }\mathsf{\Omega }+l{U}_2\right]\hfill \\ \ddot{\theta }=\frac{1}{I_y}\left[\dot{\theta }\dot{\psi }\left(I_x-I_z\right)-J_r\dot{\varphi }\mathsf{\Omega }+l{U}_3\right]\hfill \\ \ddot{\psi }=\frac{1}{I_z}\left[\dot{\theta }\dot{\psi }\left(I_y-I_x\right)+l{U}_4\right]\hfill \end{array}\right\}$$

(6)

where $\left(x, y, z\right)$ and $\left(\dot{x},\dot{y},\dot{z}\right)$ respectively denote the translational position and velocity along the axis, the variables $\left(\varphi ,\theta ,\psi \right)$ and $\left(\dot{\varphi },\dot{\theta },\dot{\psi }\right)$ denote the angular position and velocity for the roll, pitch, and yaw, respectively. The variable g is the acceleration due to gravity, $J_r$ denotes the moment of inertia of the motors, m is the mass of the quadrotor, l denotes the length from the center of mass to the rotor. I_x, I_y, and I_z, respectively, represent the moments of inertia around the x, y, and z axes. The Euler angles of the quadrotor are bounded to $–\pi /2\le \varphi \le \pi /2$, $–\pi /2\le \theta \le \pi /2$, and $–\pi \le \psi \le \pi$ to avoid singularities and excessive rotations [13].

It can be noted from the control input and the motion equations that the quadcopter model has six outputs (x, y, z, ϕ, θ, ψ) and four independent inputs. Thus, it is considered an under-actuated system.

The desired roll rotation (ϕ_d) and the desired pitch rotation (θ_d) are generated using the following equations (Ayad et al., 2019):

$$\left.\begin{array}{l}{\varphi }_d={\sin }^{-1}\left(U_x\sin {\psi }_d-U_y\cos {\psi }_d\right)\hfill \\ {\theta }_d={\sin }^{-1}\left(\frac{U_x\cos {\psi }_d+U_y\sin {\psi }_d}{\cos \varphi }\right)\hfill \end{array}\right\}$$

(7)

where $U_x$ and $U_y$ are the control signals generated by the x and y position controllers, respectively.

2.2. PID Control

The control law for the PID controller is defined as:

$$U\left(t\right)=K_{p}e\left(t\right)+K_i{{\displaystyle \int }}_0^{t}e\left(t\right)dt+K_d\frac{de\left(t\right)}{dt}$$

(8)

where $U\left(t\right)$ is the control signal, $e\left(t\right)$ is the error between the desired and actual outputs, K_p is the proportional gain, K_i is the integral gain, and K_d is the derivative gain. The values of these controller gains determine the controller’s performance and can be obtained using several tuning methods. Commonly used values are obtained based on the following error criteria:

$$ITAE={{\displaystyle \int }}_0^{t}t\left|e\left(t\right)\right|dt$$

(9a)

$$ISE={{\displaystyle \int }}_0^{t}e{\left(t\right)}^{2}dt$$

(9b)

where t is the simulation time while $e\left(t\right)$ is the error computed between the desired and the actual controlled output. The quantities defined above can be used to form an objective that can be optimized using any suitable optimization algorithm. Here, we adopt a genetic algorithm (GA).

A Genetic Algorithm (GA) was adopted in this research for tuning the PID controller parameters because it can generate an acceptable solution and utilizes minimal memory space. Optimizing typical PID controller gains using a GA involves initializing the population size, number of variables, number of generations, mutation rate, crossover rate, lower and upper boundaries, and generating the initial solution. A fitness function is then used to optimize the controller gains.

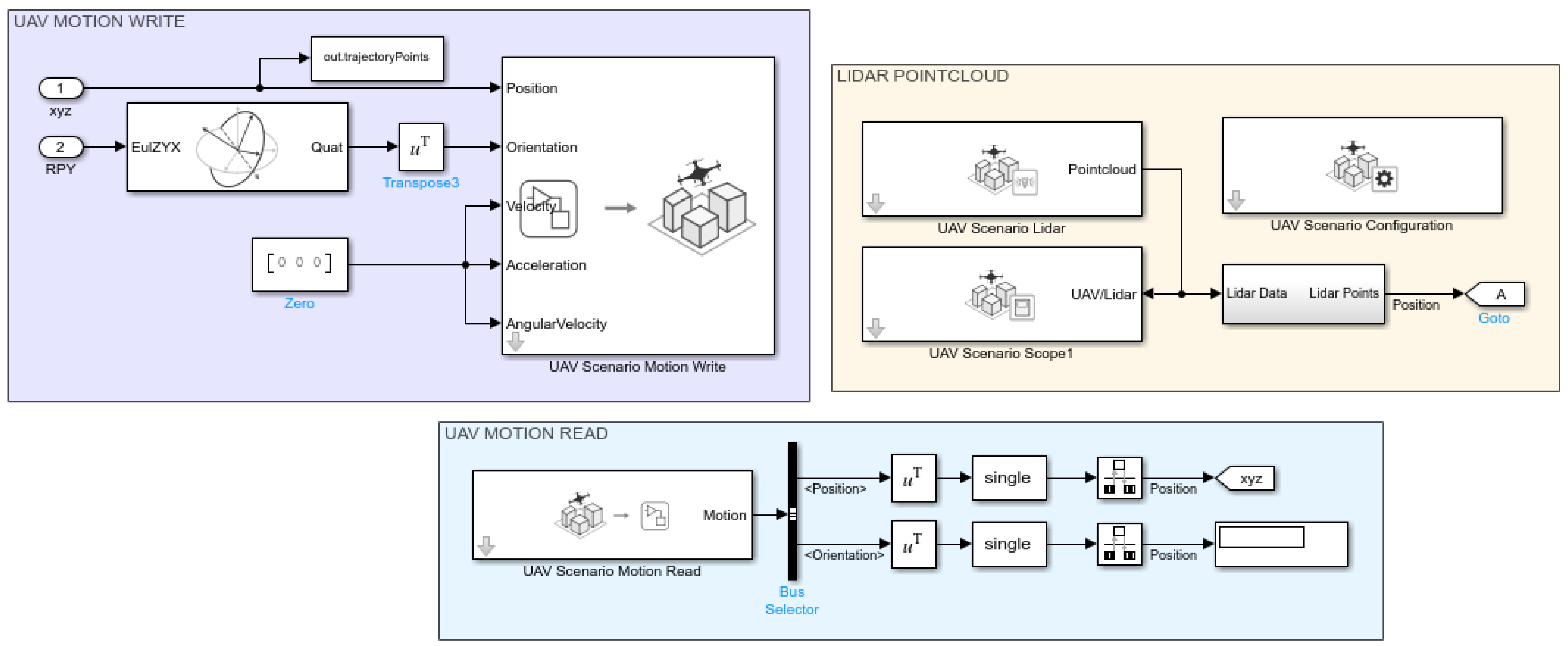
3. Methodology

The model of the quadrotor navigational system comprises the following subsystems. The path generator generates the desired trajectory, the quadrotor’s dynamic model determines the quadrotor’s actual position, and the altitude and the attitude controllers generate the manipulated signals that modify the system’s behavior to reach the desired state. Figure 3 shows the control structure of the quadrotor.

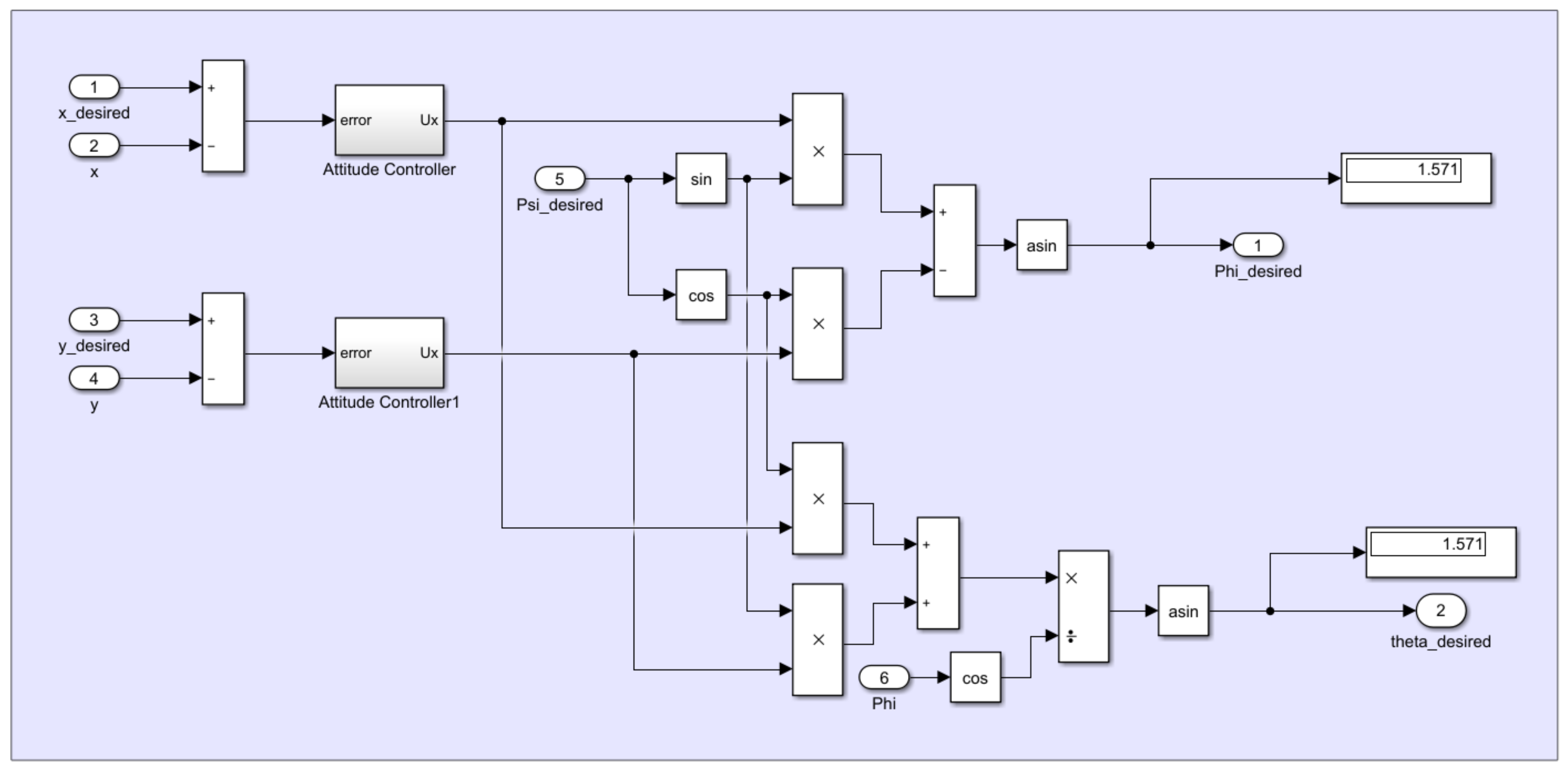
3.1. Desired Trajectory

The desired trajectory of the quadrotor system was modeled based on Equation (7), as shown in Figure 4.

The model presented in Figure 4 accepts the error between the desired position (x_d, y_d) and the actual position (x_a, y_a) of the quadrotor in the x-y plane to generate the desired roll and pitch rotations.

3.2. The Quadrotor Model

The dynamic model of the quadcopter presented in Equations (2)–(6) was modeled in Simulink to analyze the system performance without applying any control algorithms. Figure 5 shows the obtained model of the dynamic system comprising three subsystem blocks: the motor control inputs defined in Equation (2), the altitude block defined in Equation (5), and the attitude block defined in Equation (6).

The physical parameters used for studying the mathematical model of the quadrotor system are defined in

Table 1. Physical Parameters of Quadrotor.

S/N	Parameter	Symbol	Value	Units
1	Thrust factor	b	6.317 × 10−4
2	Drag factor	d	1.61 × 10−4
3	Gravity force	g	9.81	m/s2
4	Inertia around x-axis	Ix	1.453 × 10−2	Kgm2
5	Inertia around y-axis	Iy	1.453 × 10−2	Kgm2
6	Inertia around z-axis	Iz	2.884 × 10−2	Kgm2
7	Motors’ moment of inertia	Jr	2.82 × 10−7
8	Length from the rotor to the center of mass	l	0.225	m
9	Quadrotor mass	m	1.888	Kg

.

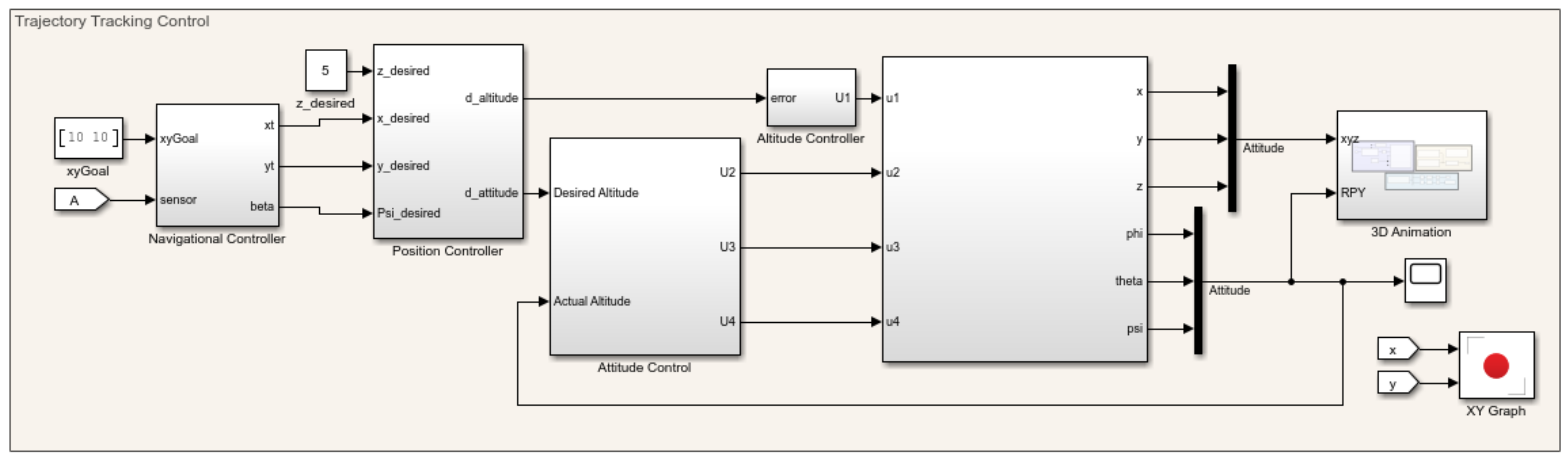
3.3. Controller Design

The PID controller was used for the altitude and attitude control of the quadrotor by optimizing the controller gains (K_p, K_i, K_d). The altitude controller accepts the error between the desired and actual altitude to generate a manipulated signal that modifies the behavior of the system based on the following control law:

$$U_1=K_p\left(z_d-z_a\right)+K_i{{\displaystyle \int }}_0^t\left(z_d-z_a\right)dt+K_d\left({\dot{z}}_d-{\dot{z}}_a\right)$$

(10)

Similarly, the attitude controller accepts the error between the desired and actual angle of the quadrotor (ϕ, θ, ψ) to drive the system to the desired target position defined in terms of x and y coordinates. The control laws for manipulating the quadrotor in terms of rolling, pitching, and yawing are presented as:

$$U_2=K_p\left({\varphi }_d-{\varphi }_a\right)+K_i{{\displaystyle \int }}_0^t\left({\varphi }_d-{\varphi }_a\right)dt+K_d\left({\dot{\varphi }}_d-{\dot{\varphi }}_a\right)$$

(11a)

$$U_3=K_p\left({\theta }_d-{\theta }_a\right)+K_i{{\displaystyle \int }}_0^t\left({\theta }_d-{\theta }_a\right)dt+K_d\left({\dot{\theta }}_d-{\dot{\theta }}_a\right)$$

(11b)

$$U_4=K_p\left({\psi }_d-{\psi }_a\right)+K_i{{\displaystyle \int }}_0^t\left({\psi }_d-{\psi }_a\right)dt+K_d\left({\dot{\psi }}_d-{\dot{\psi }}_a\right)$$

(11c)

The control laws for the x and y position controllers are given by:

$$U_x=K_p\left(x_d-x_a\right)+K_i{{\displaystyle \int }}_0^t\left(x_d-x_a\right)dt+K_d\left({\dot{x}}_d-{\dot{x}}_a\right)$$

(12a)

$$U_y=K_p\left(y_d-y_a\right)+K_i{{\displaystyle \int }}_0^t\left(y_d-y_a\right)dt+K_d\left({\dot{y}}_d-{\dot{y}}_a\right)$$

(12b)

The model of the quadrotor with the altitude and attitude controller is presented in Figure 6.

3.4. Controller Tuning

A genetic algorithm tuned the controller parameters using the procedure summarized in Figure 7. The parameters used for adjusting the PID parameters are summarized in

Table 2. GA Simulation Parameters.

S/N	Parameter	Type/Value
1	Population Size	50
2	Number of Variables	3
3	Maximum Generations	3000
4	Initialization	Uniform
5	Selection	Tournament
6	Crossover	Adaptive Feasible
7	Mutation	Arithmetic

. Extensive simulations were carried out to arrive at these parameters. Hence, these results were selected after gaining some experience and observing the performance of the controllers with different GA parameters. We note here that there is a need to develop a more systematic way of selecting the GA parameters for optimal PID tuning.

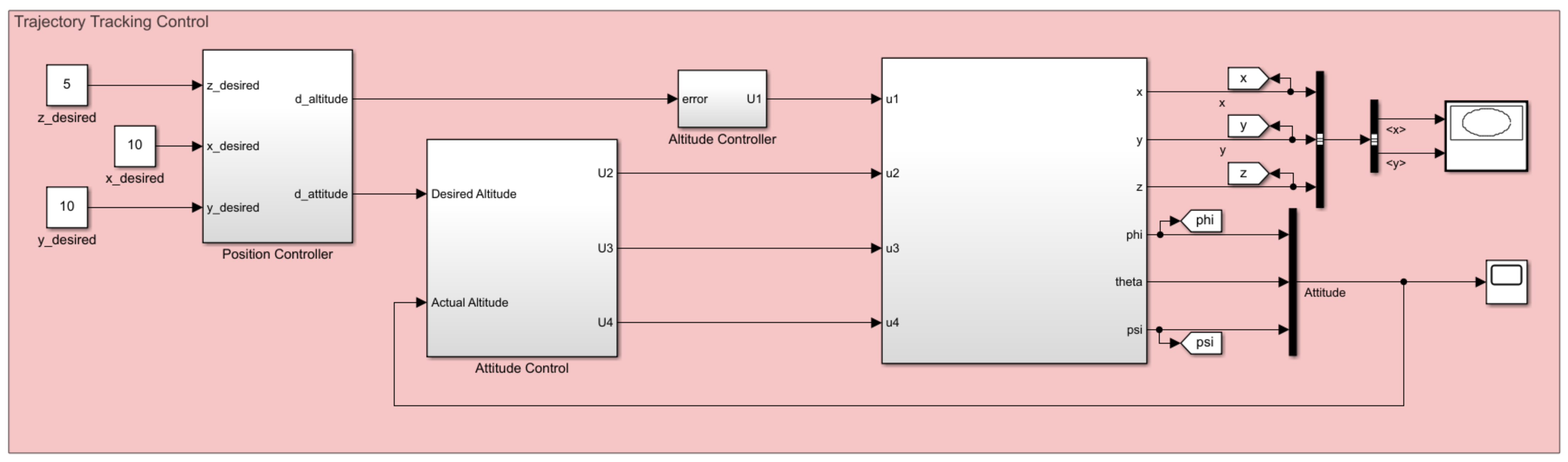
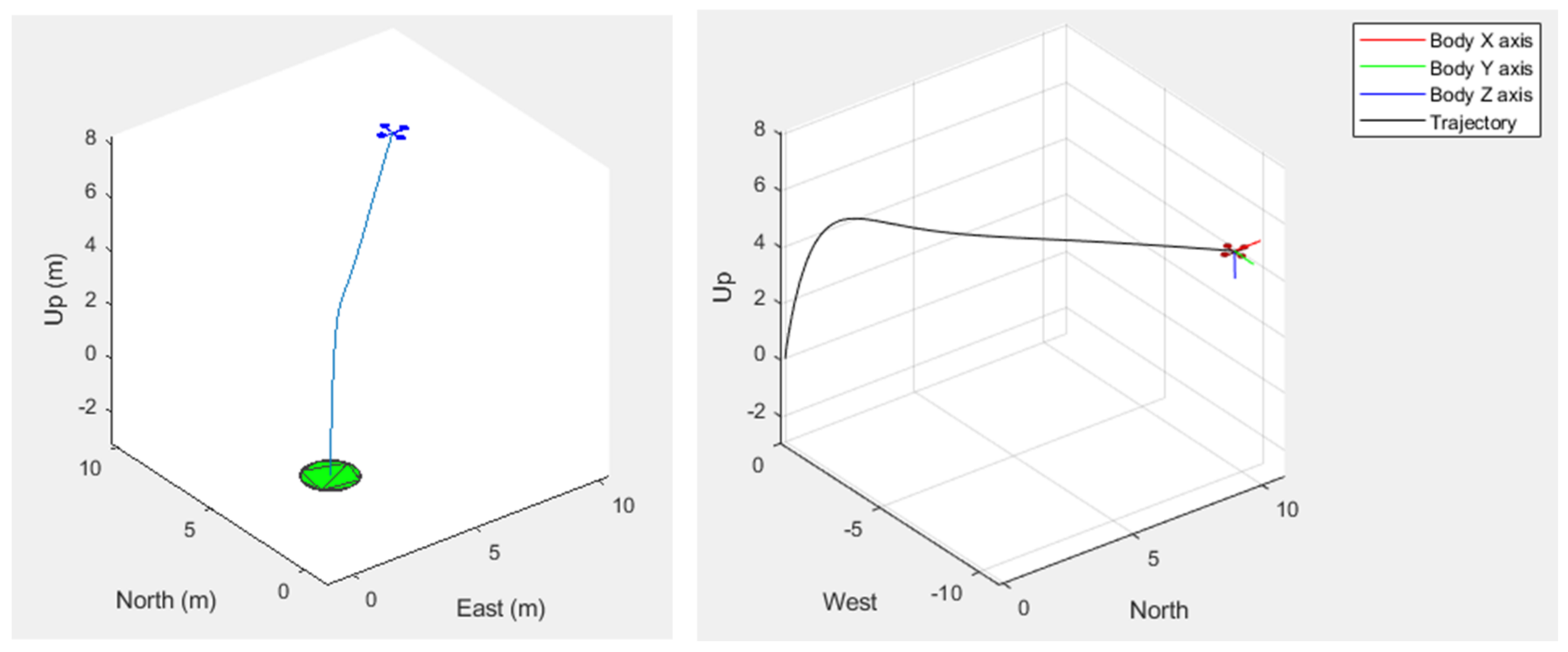
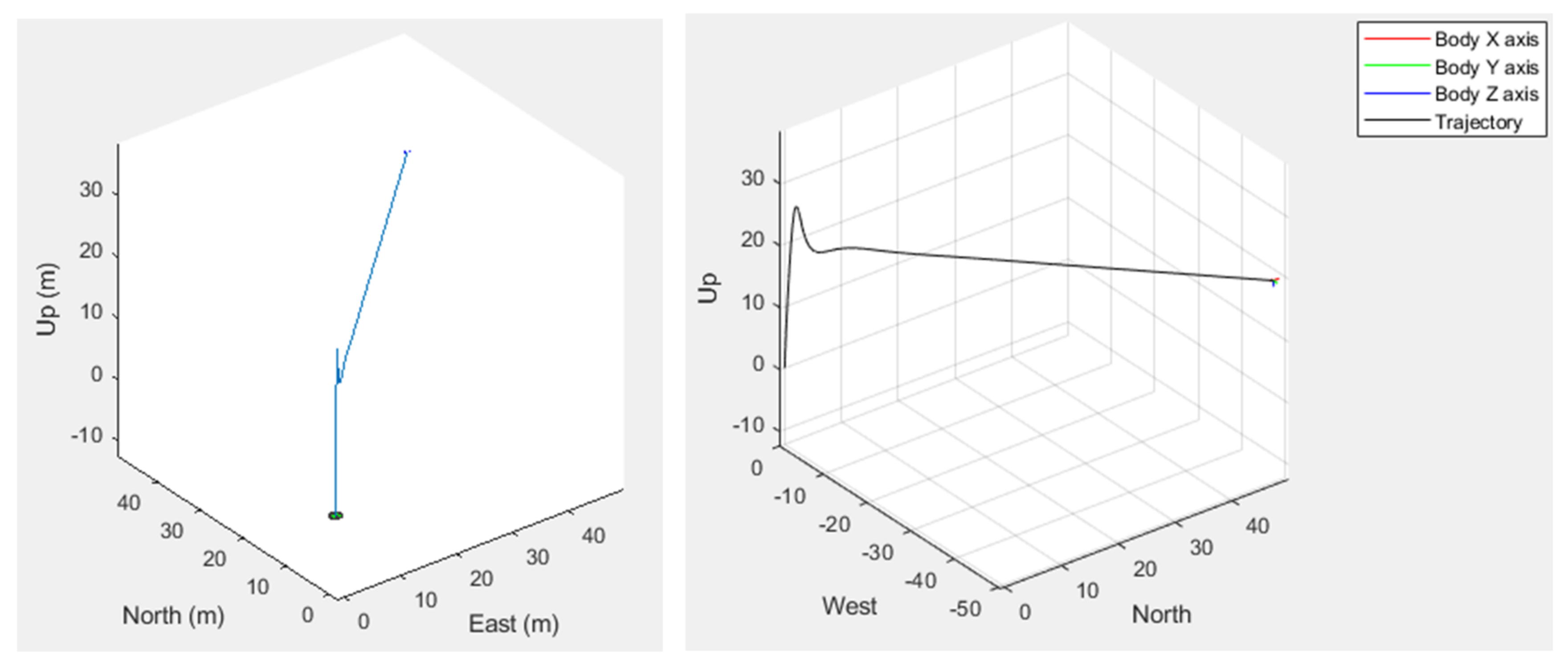
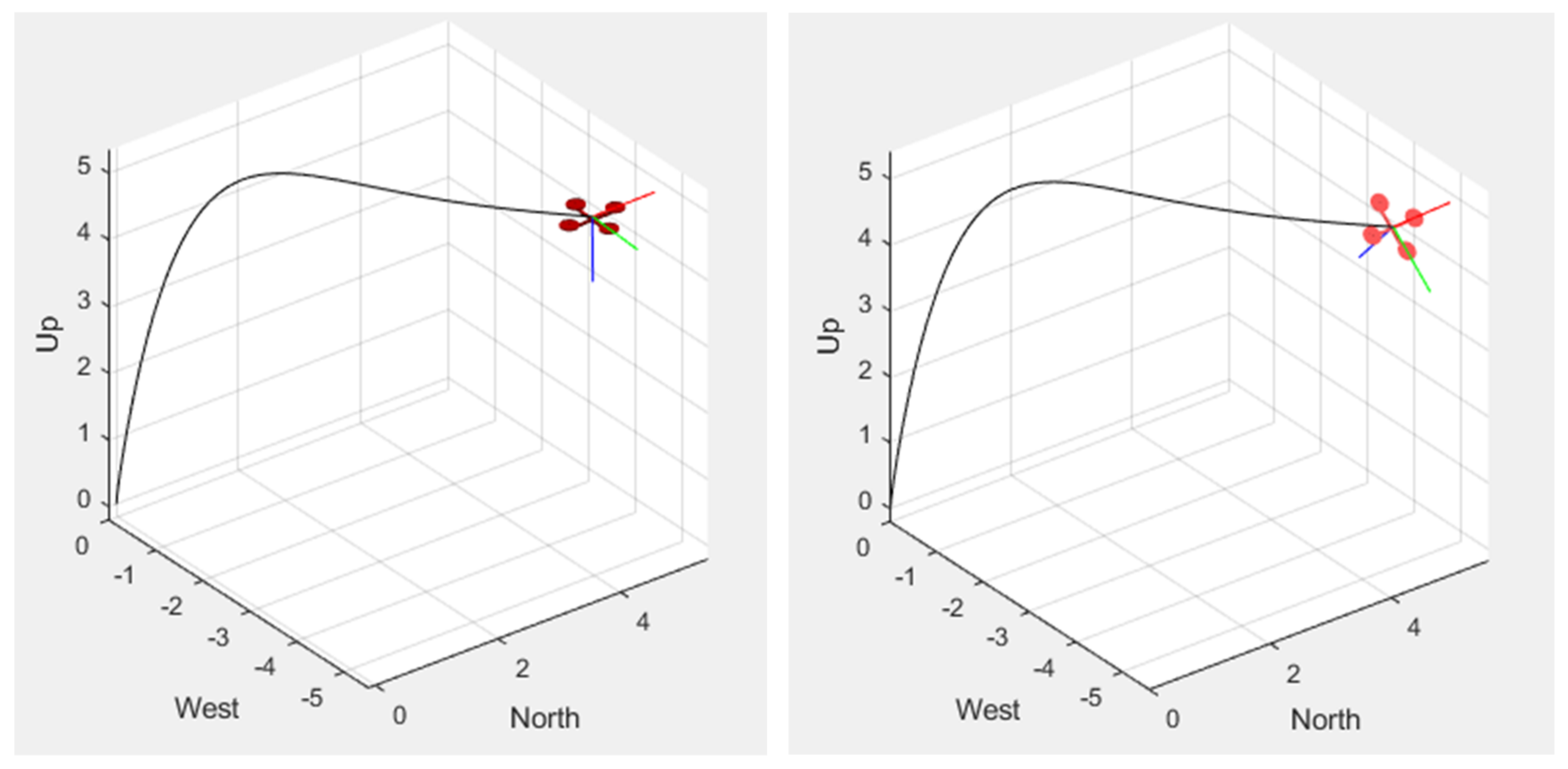
3.5. Trajectory Tracking

The designed altitude and attitude controllers were tested for trajectory tracking of the quadrotor in navigating from a defined start location to the desired target location in an environment without obstacles. The Simulink model developed is shown in Figure 8. Figure 8 contains two defined user parameters, i.e., the desired target location (x_desired, y_desired) and the desired altitude (z_desired), while the start location of the quadrotor is assumed to be at the origin (0,0). The position controller generates the desired attitude that guides the quadrotor to the goal location, in which the attitude controller minimizes the tracking error.

The Euclidean distance was used as the stopping criteria in navigating the quadrotor from a defined start location to the desired goal location while simulating over an infinite period.

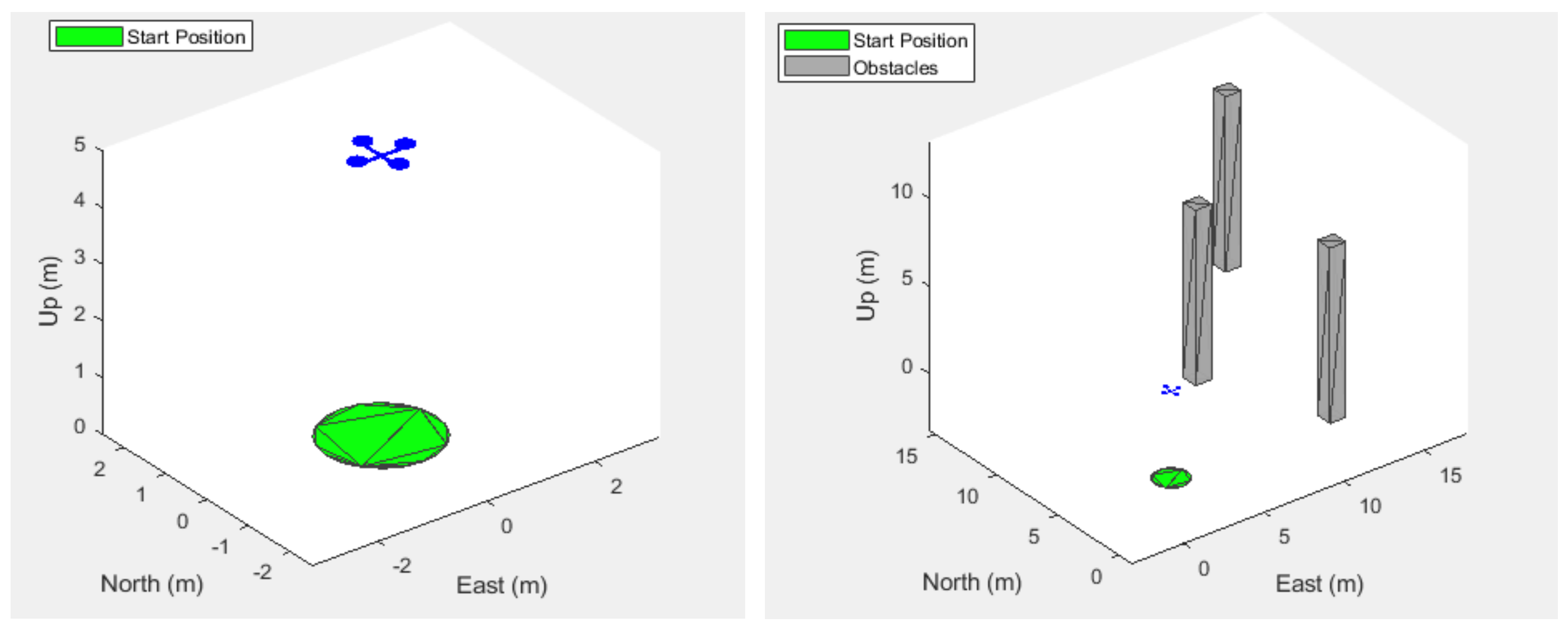
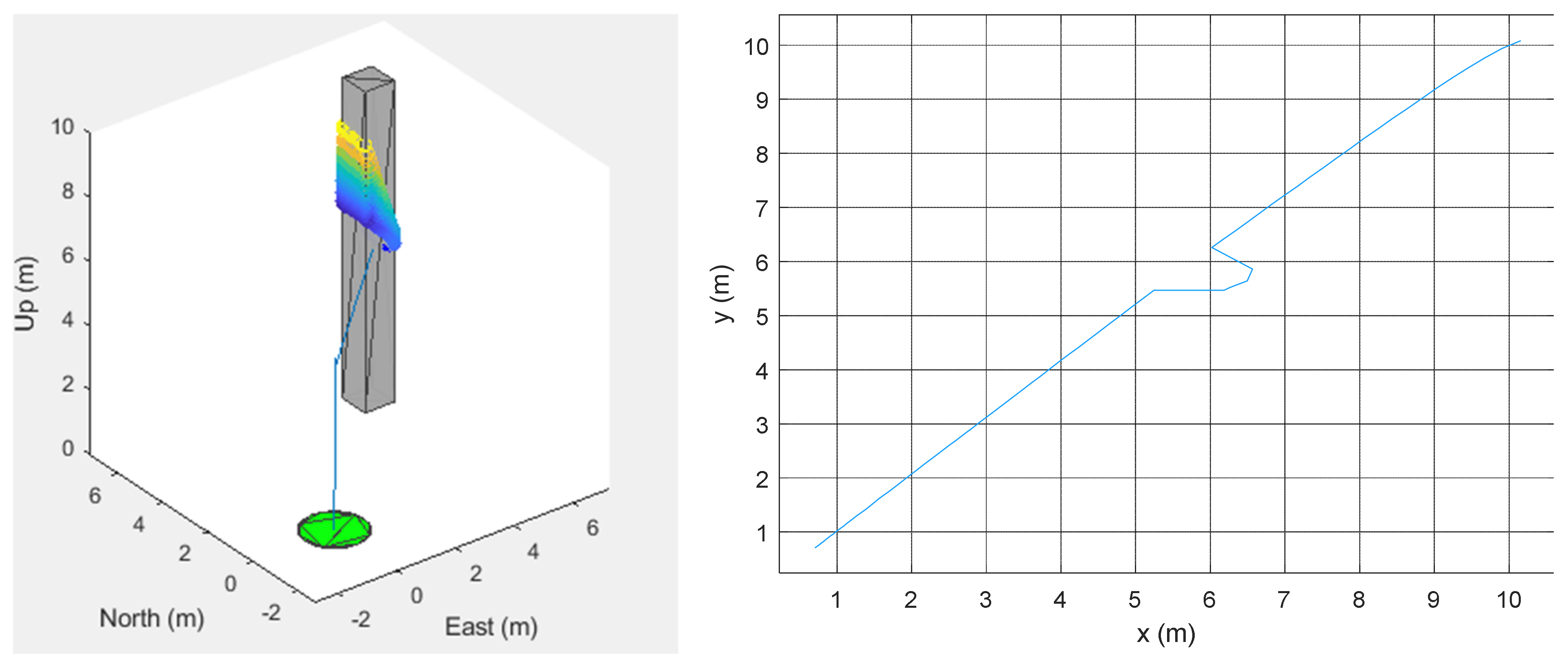
3.6. Obstacle Avoidance Model

The obstacle avoidance model comprises a quadrotor scenario environment referred to as the simulation map, the navigational controller for planning and obstacle avoidance, the quadrotor position and attitude controllers, and the 3D simulation environment. Algorithm 1 presents the control flow of the navigational controller.

Algorithm 1: Navigational Controller
	Input: desired altitude, initial position, and goal position
	Output: actual altitude and attitude.
	1	Initialize the distance threshold;
	2	while the goal location is not reached, do
	3		If $\left(sensor reading>distance threshold\right)$ then
	4		Compute the desired yaw angle;
	5		Else
	6			Execute the obstacle avoidance algorithm to obtain the best coordinate;
	7			Compute the desired yaw angle;
	8		end if
	9		Update the position of the quadrotor to move towards the goal position;
	10	end while
	11	Output the actual altitude and attitude

The quadrotor scenario was created using the MATLAB UAV Toolbox by setting its local origin at (0, 0, 0) and using a marker to indicate the start position of the quadrotor based on the NED frame. The quadrotor was positioned at (0, 0, −5) with an initial orientation of (0, 0, 0). A quadrotor platform was created in the scenario, and a quadrotor mesh was added for visualization, as shown in Figure 9 (Left). Figure 9 (Right) is the quadrotor platform with three obstacles positioned at (7, 7), (10, 0), and (15, 15), with a height of 10 m and a width of 1 m while viewing from [−37.5 30]. The quadrotor base is shown in green, and the quadrotor is presented in blue. A single LiDAR sensor with the following properties given in

Table 3. LiDAR Sensor Properties.

S/N	Parameters	Values
1	Azimuth Resolution	0.5
2	Elevation Resolution	2
3	Azimuth Limits	(−179 179)
4	Elevation Limits	(−15 15)
5	Maximum Range	7 m
6	Mounting Location	(0, 0, −0.4)
7	Mounting Angle	(0, 0, 180)

was mounted on the quadrotor system for obstacle detection.

A UAV Scenario LiDAR block was used in Simulink to simulate LiDAR measurements based on meshes in the scenario by outputting point cloud data. The LiDAR sensor uses reflected laser pulses to calculate the distance to obstacles. Moreover, LiDAR sensors have become cheaper and less cumbersome over the years and are now routinely mounted on UAVs [28]. The 3D simulation environment is shown in Figure 10.

A distance function was used to compute the distance between the quadrotor and the positions of the obstacles in the environment, as shown in Figure 10. A routing signal block, A, was used to send the obtained positions to the distance function for computation. This aids the use of the LiDAR sensor for obstacle detection in a simulation environment.

Based on the output of the function block, the obstacle avoidance algorithm is implemented in a navigational controller that accepts the coordinates of the target and current locations of the UAV to generate the next possible location and the yaw angle of the UAV. The elite opposition bat algorithm developed by [33] was adopted for the obstacle avoidance algorithm. The obstacle avoidance algorithm is executed using Equation (13) when a distance threshold is met, which is tested based on two scenarios as 0.5 m and 1 m to the nearest obstacle.

$$best=EOBA\left(\left[x, y\right], \left[xg, yg\right], obs\right)$$

(13)

where $obs$ is the distance between the current state of the UAV and the obstacle. The output of the algorithm is used to update the UAV trajectory as defined in Equation (14):

$$x_t=x+best\left(1\right)$$

(14a)

$$y_t=y+best\left(2\right)$$

(14b)

The desired yaw angle that controls the rotation of the quadcopter along the z-axis is computed as:

$${\psi }_d={\tan }^{-1}\left(\frac{y_t}{x_t}\right)$$

(15)

The simulation parameters of the obstacle avoidance algorithm are presented in

Table 4. Algorithm Simulation Parameters.

S/N	Parameters	Symbol	Value
1	Frequency Range	F	0–2
2	Initial Velocity of Bats	V	0
3	Loudness	A	0.25
4	Maximum Iteration	MaxIter	100
5	Population Size	N	25
6	Pulse Emission Rate	R	0.5
7	Search Dimension	D	2

as follows:

Algorithm 2 presents the obstacle avoidance algorithm developed based on the EOBA algorithm.

Algorithm 2: Obstacle avoidance algorithm
	Input: current state of the quadrotor, goal state, and distance to the obstacle
	Output: generate best solution
	1	Initialize the algorithm simulation parameters
	2	Initialize the bat population $\left(X\right)$ and calculate fitness;
	3	Select the best individual as elite individual $\left(X_e\right)$ from the initial solution $\left(X\right)$
	4	Update the boundaries $\left[xmj,ymj\right]$ and generate the opposite solution
	5	Select the fittest solution as a candidate for the next generation
	6	while $\left(t<maxIter\right)$ do
	7		Generate new solutions by adjusting frequency and updating velocity;
	8		if $rand>r_i$ then
	9			Select a solution among the best solutions & generate local solutions around it;
	10		end if
	11		Generate a new solution by flying randomly and evaluates fitness
	12		if $\left(rand<A_i \&f\left(x_i\right)<f\left(X^{*}\right)\right)$ then
	13		Accept the new solution and update $r_i$ and $A_i$
	14		end if
	15		Rank the bats and obtain the best solution
	16	end while
	17	Output best solution

The Simulink model for the complete obstacle avoidance system is shown in Figure 11.

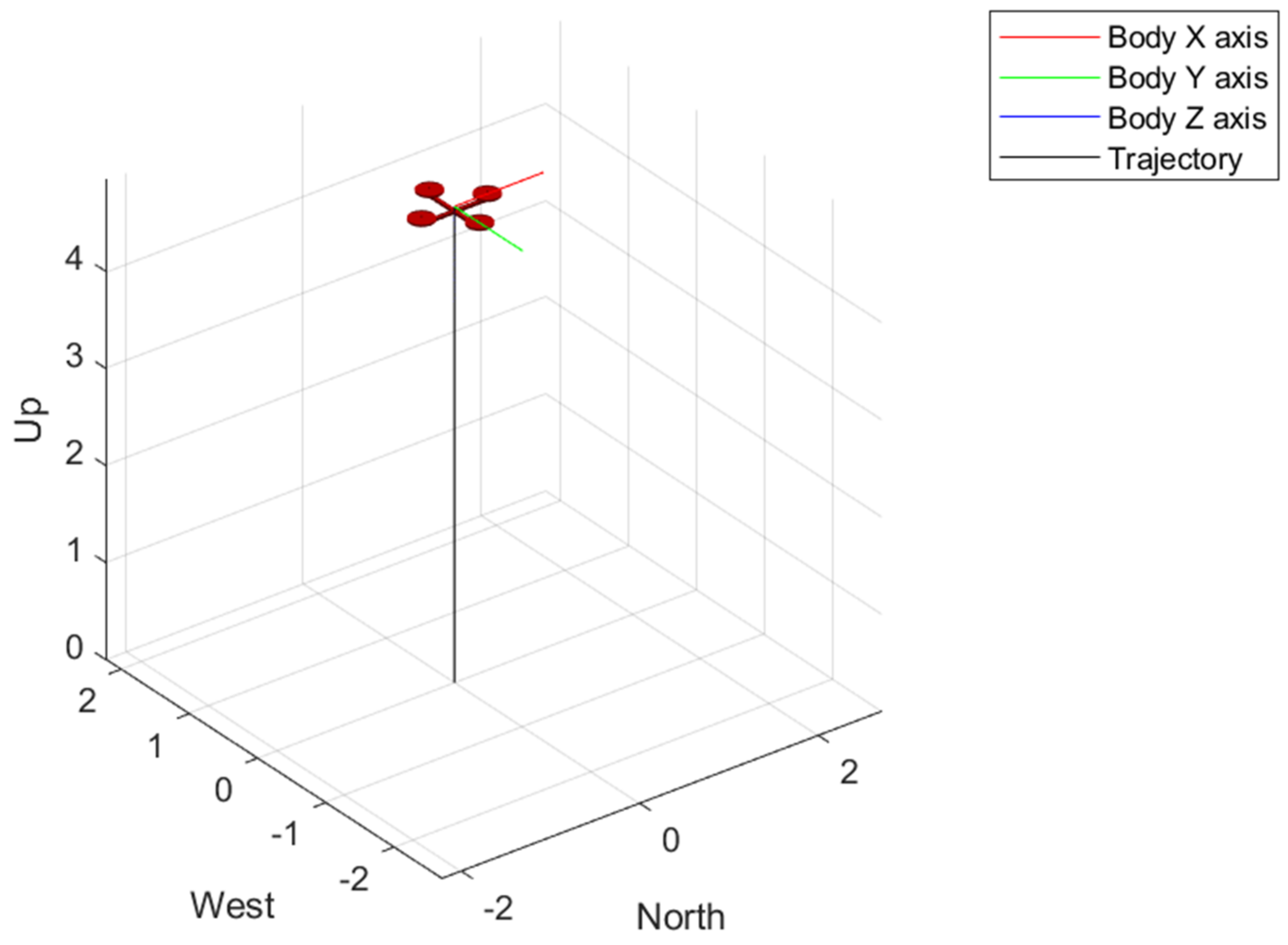
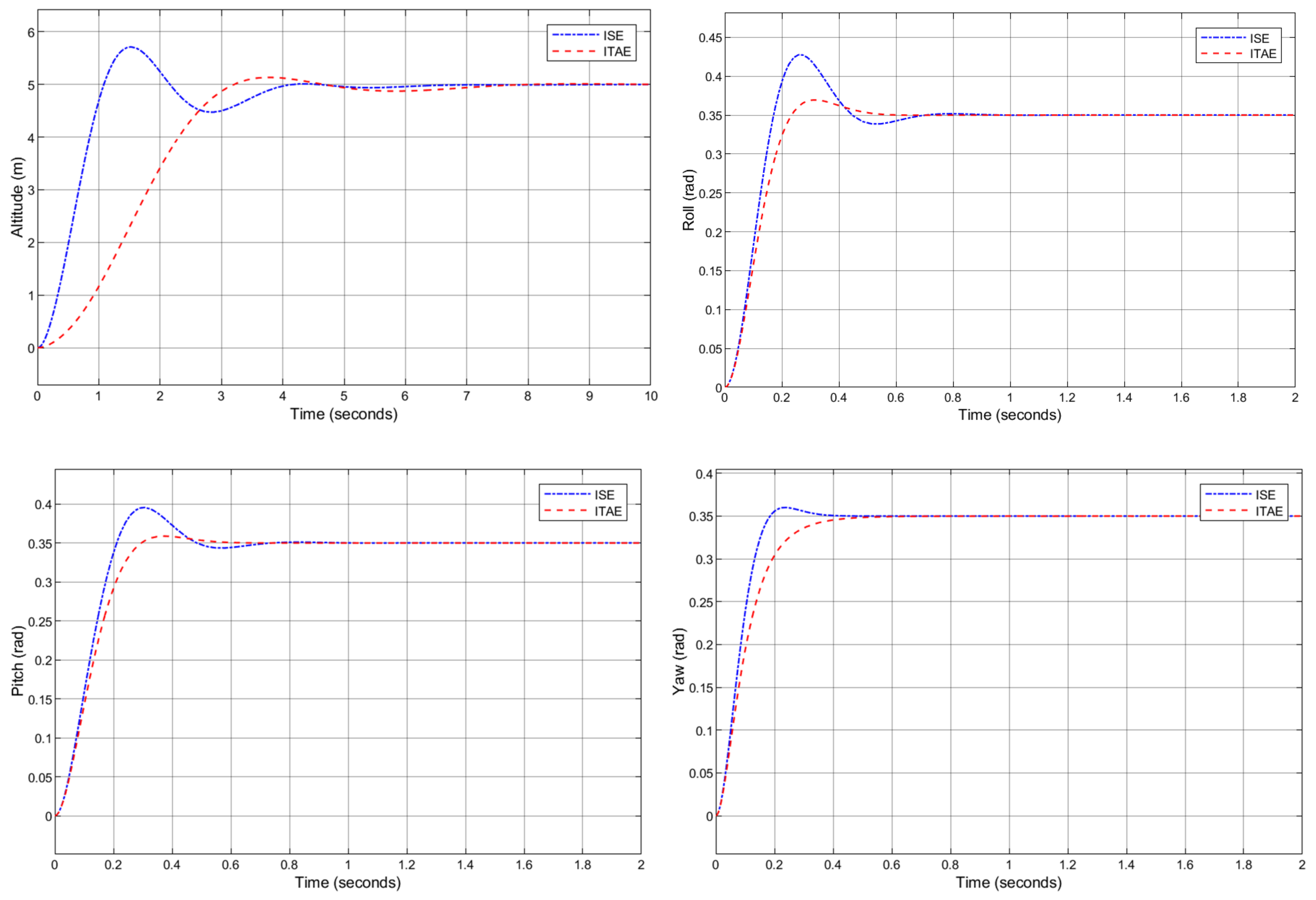
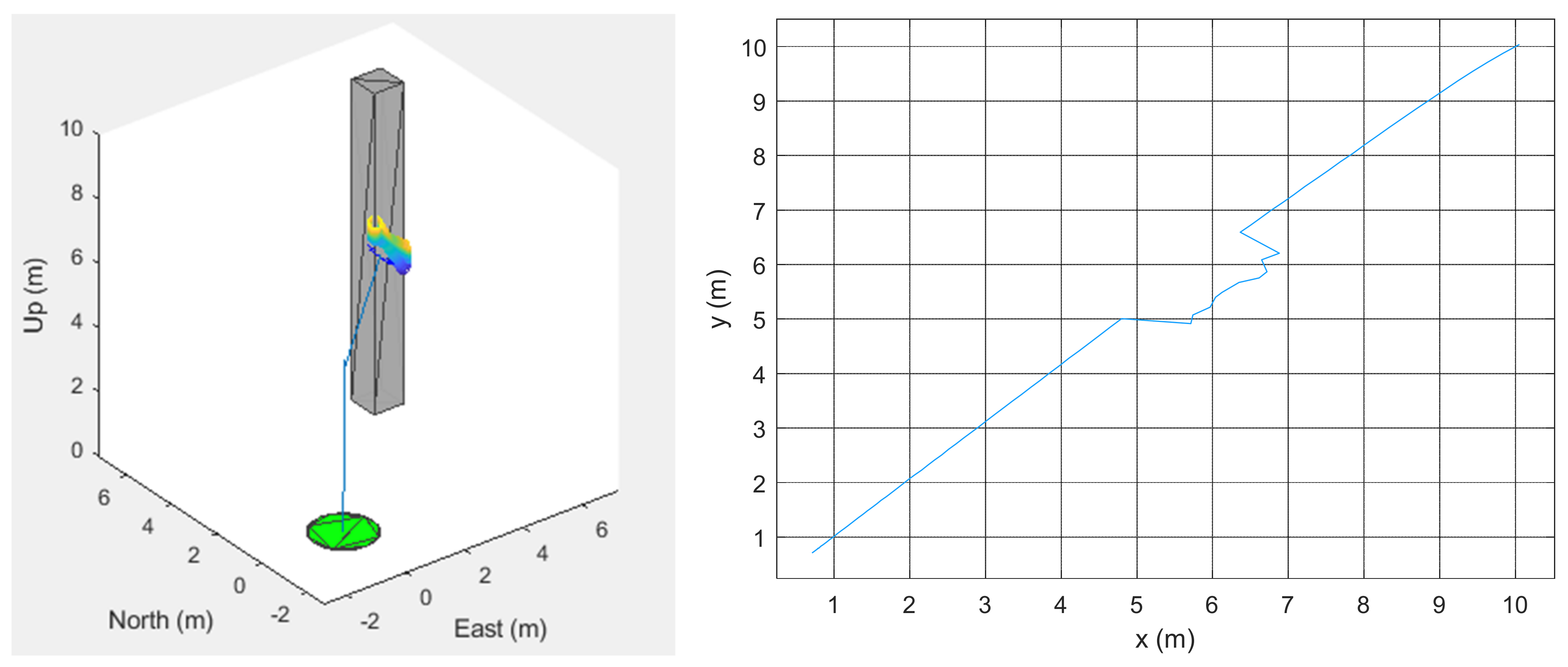
4. Results and Discussion

The quadrotor model presented in Figure 6 is simulated for 1 s by applying equal force on the system rotors to verify the model correctness through a UAV animation block in a North–East–Down (NED) coordinate frame. The results obtained are presented in Figure 12:

Figure 12 presents the quadrotor system’s response when the rotors rotate at the same angular speed due to the application of equal force of 5 N simultaneously to each motor. This resulted in the vertical takeoff of the quadrotor to an altitude of 4.2 m. It can be seen from the response that there is no motion of the quadrotor in the x and y directions as rolling, pitching, and yawing are zero. This verifies the correctness of the model with respect to the model’s response to the application of equal forces to all the motors.

The optimized PID controller gains, as recorded based on the two performance measures (ISE and ITAE), are presented in

Table 5. Optimized PID Controller Parameters.

Controller Parameters	ITAE		ISE
	Altitude Controller	Attitude Controller	Altitude Controller	Attitude Controller
Kp	5.0000	9.9995	12.8750	9.9995
Ki	2.5728	6.4267E-5	6.6843	0.0254
Kd	3.6485	1.0915	4.5464	0.7545

. The transient response of the quadrotor control system with the application of the optimized altitude and attitude controllers is shown in Figure 13.

Figure 13 presents the quadrotor system altitude (Top-Left) and attitude, comprising of the roll (Top-Right), pitch (Bottom-Left), and yaw (Bottom-Right) response with the desired height of 5 m and attitude of 0.35 rad, for all three variables (roll, pitch, and yaw). It can be seen from the figure that the quadrotor attained the desired altitude and attitude based on the ISE and ITAE performance measures with different transient properties. To evaluate the performance of the designed controllers, the transient parameters obtained for the quadrotor based on the ISE and ITAE are recorded in

Table 6. Transient Parameters of the Quadrotor Control System.

Transient Parameters	ITAE		ISE
	Altitude Controller	Attitude Controller	Altitude Controller	Attitude Controller
Overshoot (%)	2.6533	2.5028	14.2967	12.9697
Settling Time (s)	6.5088	0.4271	3.7947	0.4515
Rise Time (s)	2.0118	0.1850	0.7343	0.1440
Tracking Error	0.0011	2.343E-7	0.0021	5.657E-5

.

The results in Table 6 show that the ITAE-based controller generates a better realistic transient response than the ISE-based controller for both altitude and attitude control. Thus, the ITAE-based controller was selected for the motion control of the quadrotor system.

The control system design of the quadrotor system was tested for navigation from a start location of (0, 0) to a goal location of (10, 10) at an altitude of 5 m. The simulation result obtained is shown in Figure 14.

Figure 14 (Left) shows that the quadrotor successfully navigates to the target destination in an obstacle-free environment. The vehicle also attained the desired altitude of 5 m, as shown in Figure 15 (Right), with a slight overshoot before the system settled to navigate to the target. Similar results were obtained with a target destination of (50,50) at an altitude of 20 m, as shown in Figure 15.

When a single obstacle of width 1 m and height 10 m was placed at coordinate (5, 5) in the simulation environment, the obstacle detection result with a threshold of 0.5 m and 1 m. These thresholds were selected to define some clearance because animals, humans, and farm machinery may move towards the UAV. The width of the obstacle was determined to be 1 m, which means that the obstacle is positioned in the plane at $\pm 0.5 \mathrm{m}$ along the x and y axes. It was discovered that for the obstacles used, a threshold that has a clearance of 1 m away from the obstacle ensures the quadrotor completely avoids colliding with the obstacle despite abrupt obstacle movement. The implementation of the obstacle avoidance algorithm causes the change in orientation of the quadrotor system in the z-direction (psi angle) based on Equation (15). This is displayed in Figure 16.

From Figure 16 (Right), the quadrotor pitched down to avoid collision with the obstacle. This is because the desired pitch, as shown in Equation (8), is a function of the desired yaw angle, which is computed from the output of the obstacle avoidance algorithm.

The 2D and 3D motion of the quadrotor when the obstacle avoidance algorithm was implemented with a distance threshold of 0.5 m is presented in Figure 17.

It can be seen from Figure 17 (Left) that the quadrotor is too close to the obstacle even with the implementation of the obstacle avoidance algorithm, as the blue and yellow colors on the obstacle represent the point cloud of the LiDAR sensor. Figure 17 (Right) shows that the quadrotor has collided with the obstacle before avoiding it. This is because the yaw angle computed from the coordinate generated by the obstacle avoidance algorithm is small. Thus, it is evident in Figure 17 (Right) as the orientation of the quadrotor in the z-direction changes around the coordinate (5.2, 5.2). As the distance threshold was changed to 1 m, the 3D motion of the quadrotor shown in Figure 18 (Left) shows the change in UAV orientation around a coordinate of (4.8, 5). Thus, it can be concluded that a distance threshold of 1 m is sufficient to avoid collision without making contact with the obstacle when the width size is less than or equal to 1 m.

The performance of the obstacle avoidance algorithm was further evaluated by increasing the number of obstacles to three, with the second and third obstacles placed at (10, 0) and (10, 10), respectively. It can be seen from Figure 19 that the quadrotor system reaches the target destination of (20, 20) without collision.

5. Conclusions

This work modeled and simulated a quadrotor system’s obstacle avoidance-based autonomous navigation in MATLAB Simulink. Two genetic algorithm-based Proportional Integral Derivative (PID) controllers were developed for altitude and attitude control of the quadrotor using integral square error (ISE) and integral time absolute error (ITAE). The performance of the designed controllers was evaluated using transient parameters (i.e., settling time, rise time, and overshoot) and steady-state error. Simulation shows that the ITAE-based PID controller obtained the best realistic result for altitude control (settling time of 6.51 s, an overshoot of 2.65%, and steady-state error of 0.0011) and attitude control (settling time of 0.43 s, overshoot of 2.50%, and zero steady-state error). Two simulation scenarios were used: 5 m and 20 m for altitude control and (10,10) and (50,50) for attitude control. To improve the autonomy of the developed quadrotor control system in navigating to the desired target location from a predefined start location, an elite opposition-based bat algorithm was implemented for obstacle avoidance of the quadrotor system. The simulation results of the obstacle avoidance algorithm show that the quadrotor can effectively avoid collision with an obstacle, provided that the distance between it and the obstacle is less than or equal to the width of the obstacle. The performance of the obstacle avoidance algorithm was further evaluated by increasing the number of obstacles in the environment to three. The simulation results showed successful navigation of the quadrotor system in the environment.

Future research may consider implementing the obstacle avoidance scheme in real time to validate the performance of the simulation results. Additionally, the performance of the obstacle avoidance algorithm can be compared with that of fuzzy logic control and other metaheuristic search algorithms such as smell agent optimization. However, irrespective of the algorithm used for controller tuning, there is a need to develop systematic ways of tuning the algorithm parameters. Additionally, recent developments in swarm and collaborative robotics make the development of algorithms for the navigation of a group of UAVs collaborating on several tasks imperative.

Another area of research direction is navigation within indoor environments, where space is limited, with more obstacles, and GPS signals may be unavailable. For this application, we believe that findings in computer vision would be beneficial.