A Single-Copter UWB-Ranging-Based Localization System Extendable to a Swarm of Drones
Abstract
:1. Introduction
2. Related Work
3. Hardware Design and Integration
| Algorithm 1: Continuous Localization. |
 |
4. UWB-Ranging-Based Localization Algorithm
4.1. Problem Statement
4.2. Single Step Localization Algorithm
| Algorithm 2: Single Localization Step. |
 |
4.3. Continuous Localization
5. Experimental Evaluation
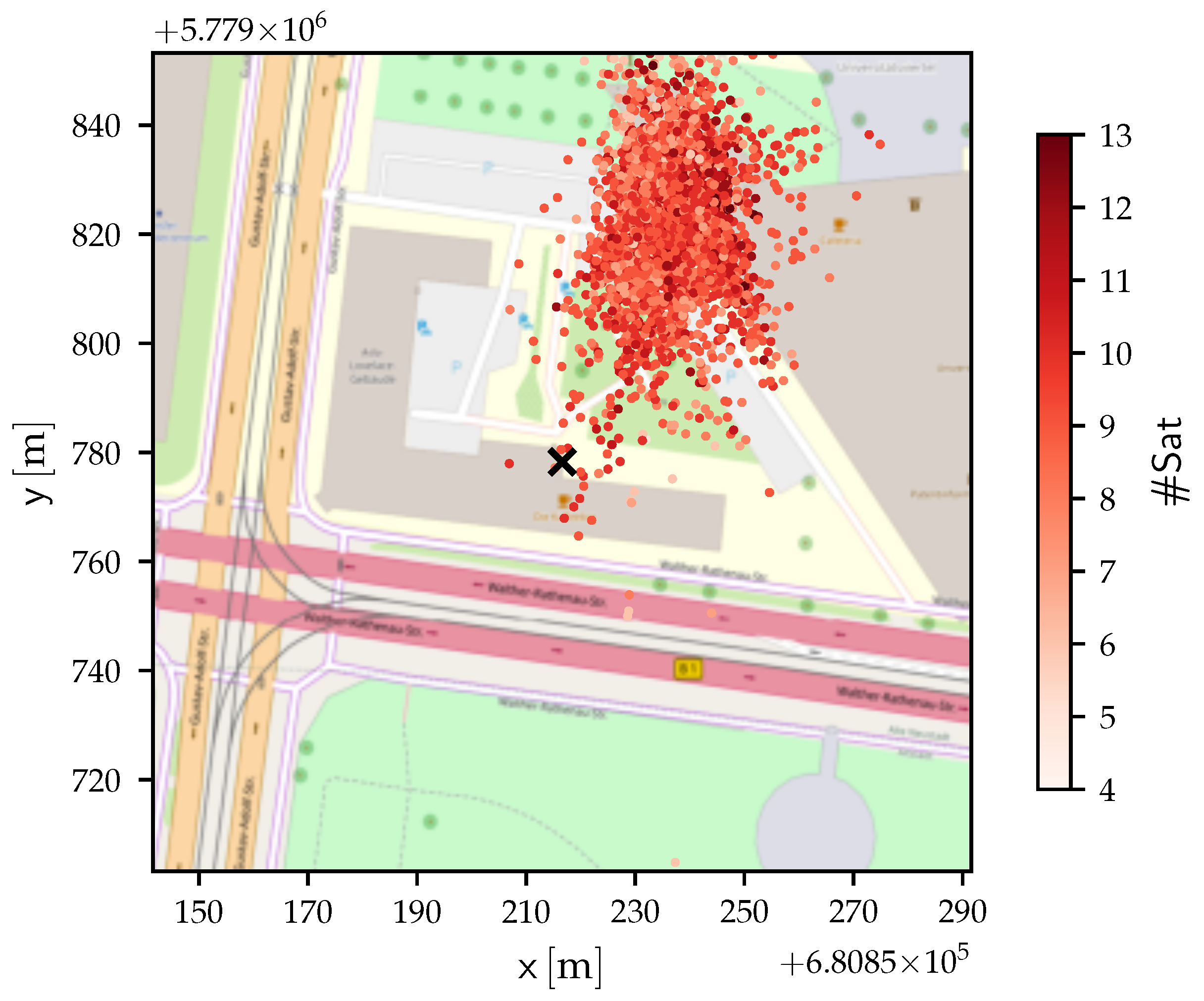
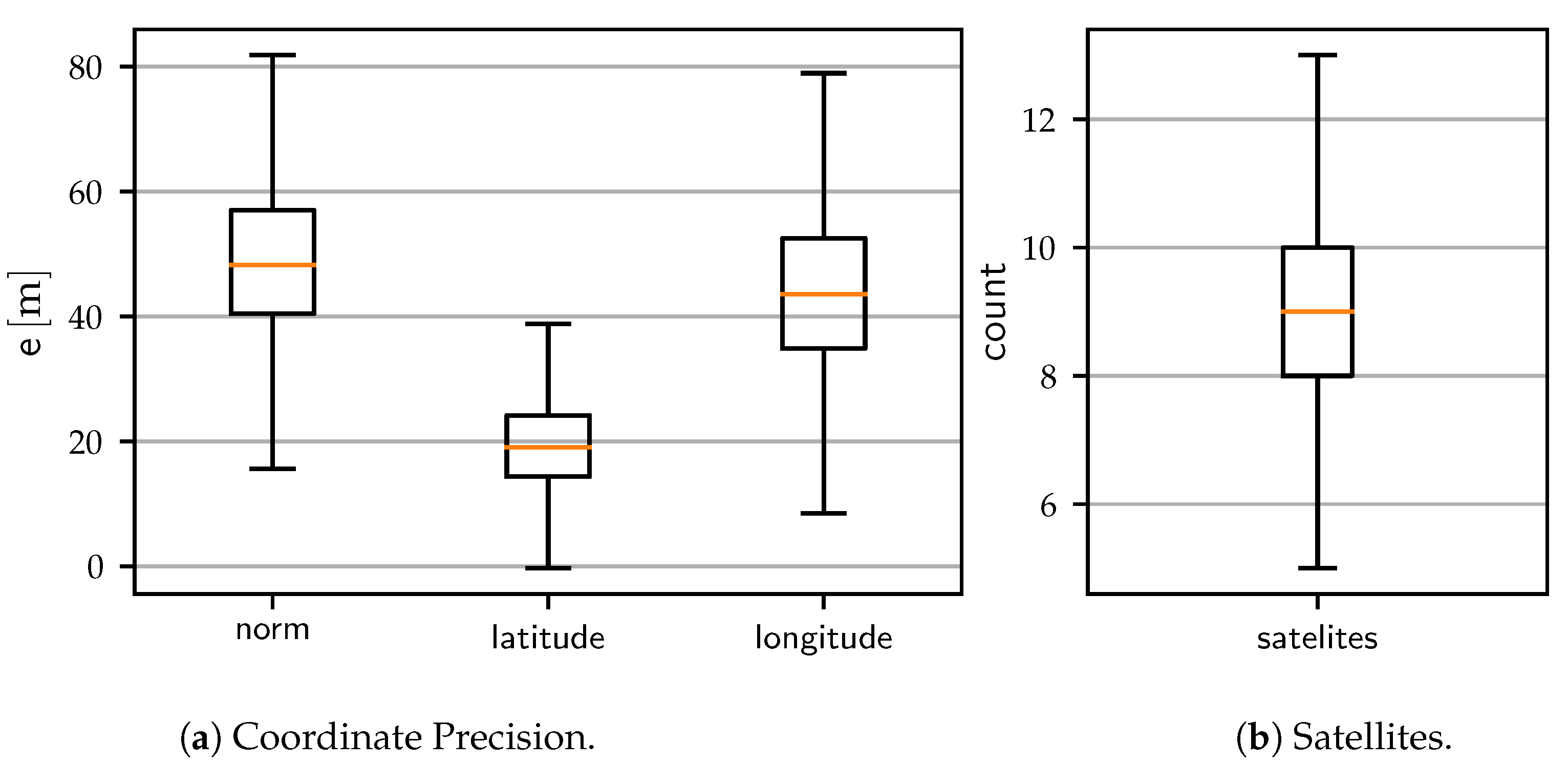
5.1. GPS Experiments
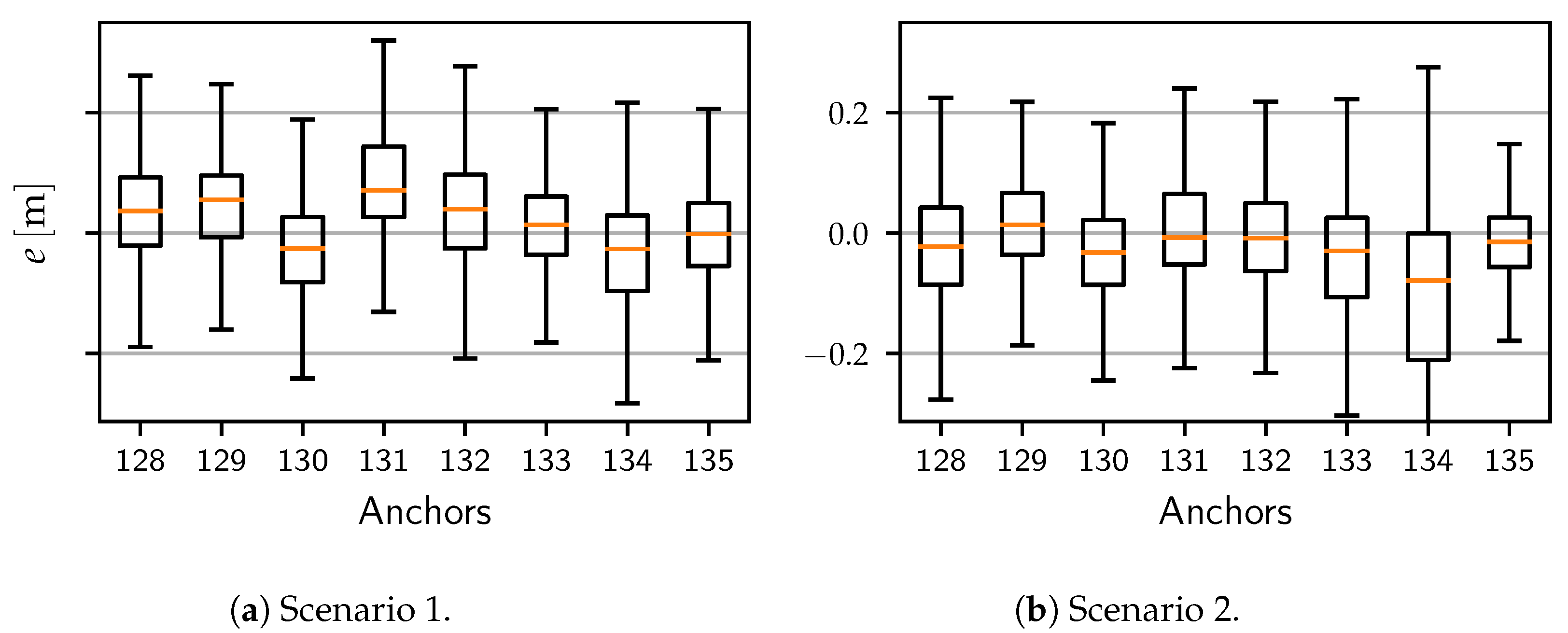
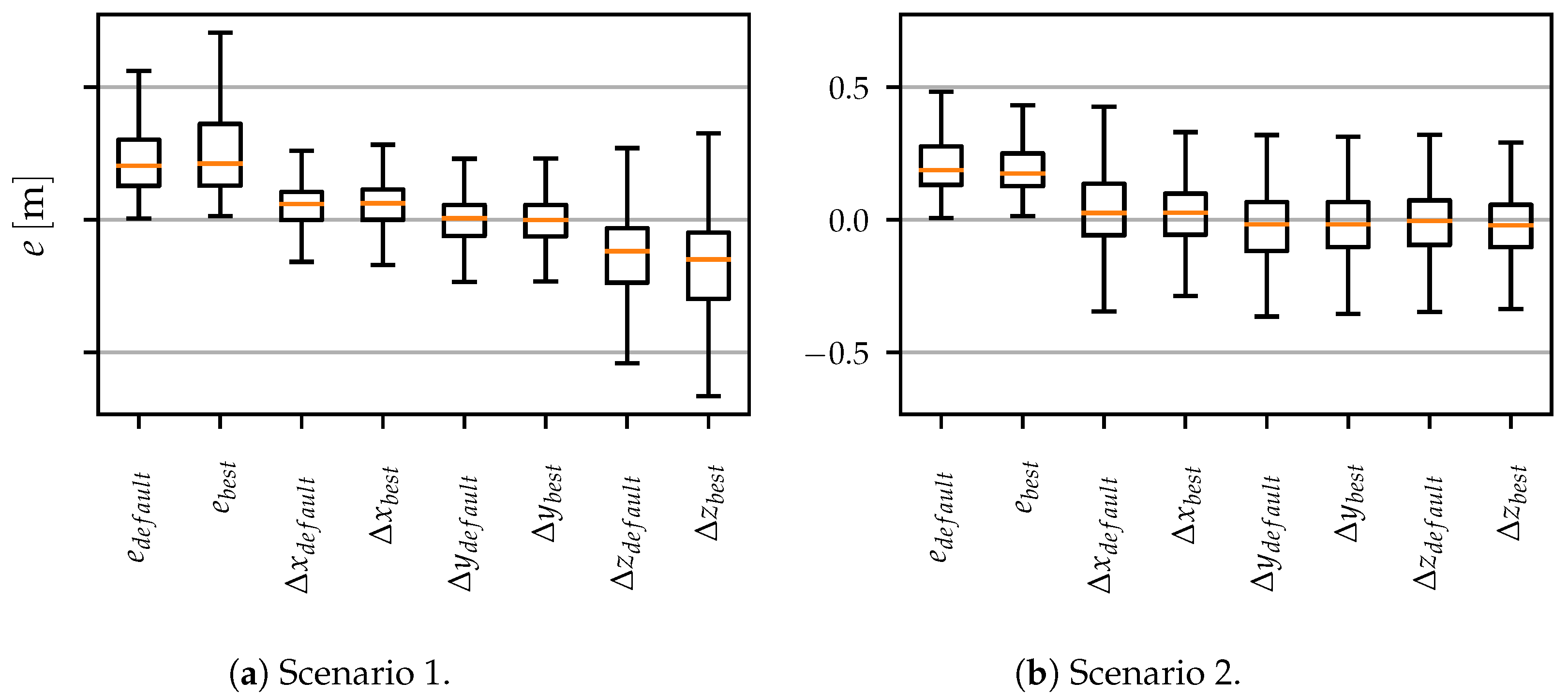
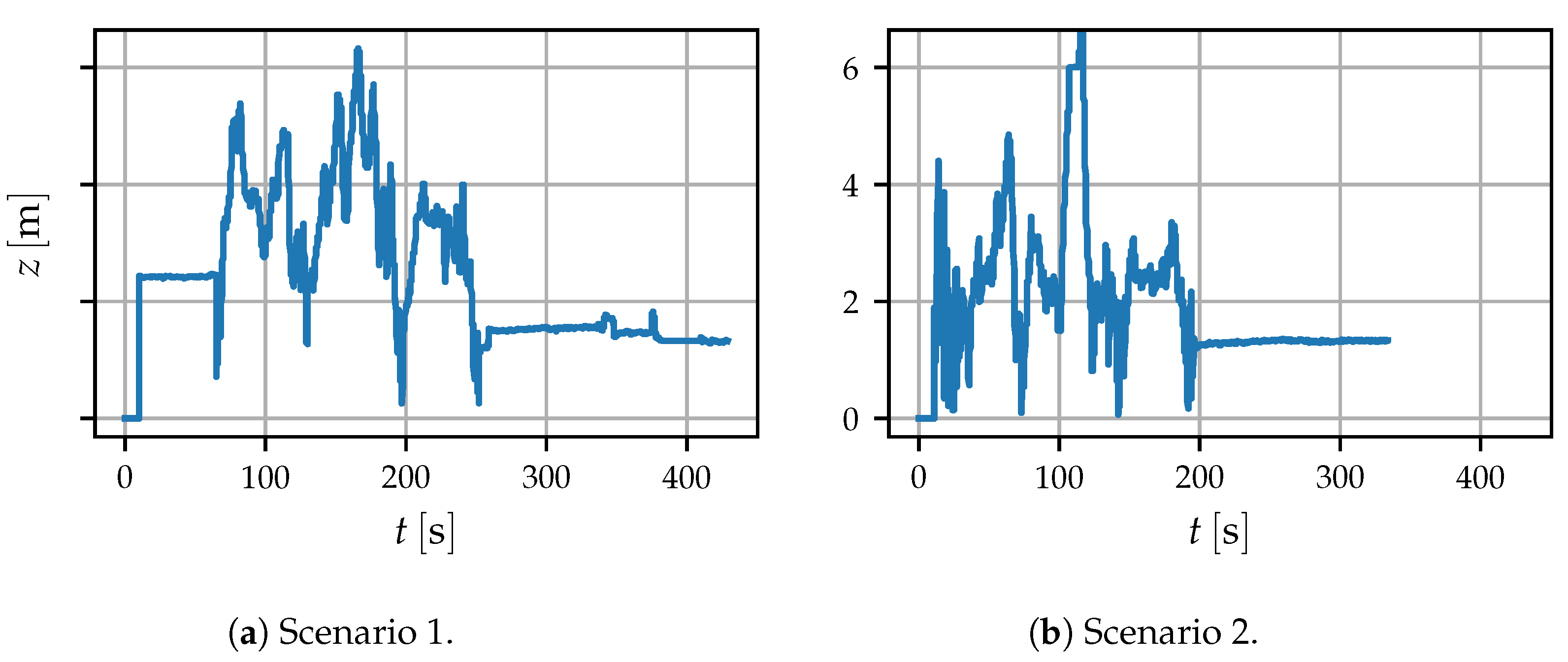
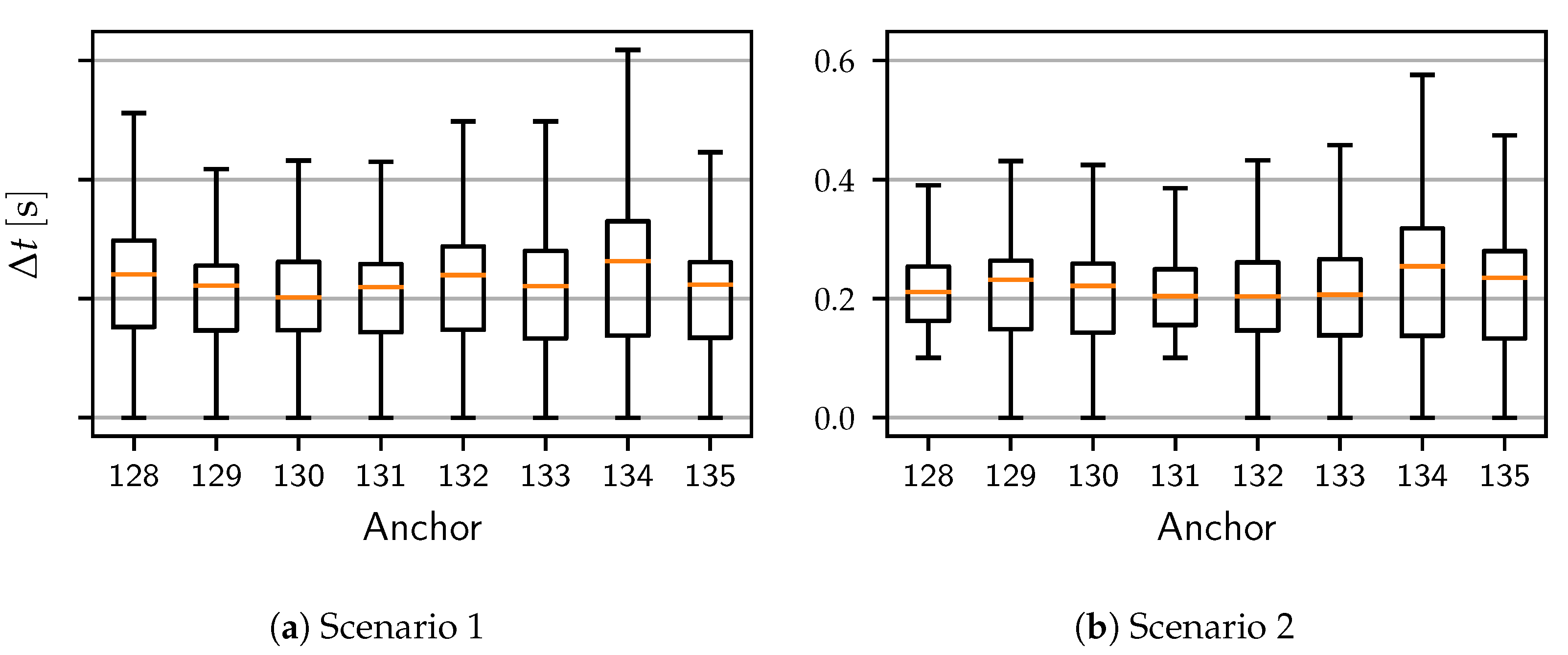
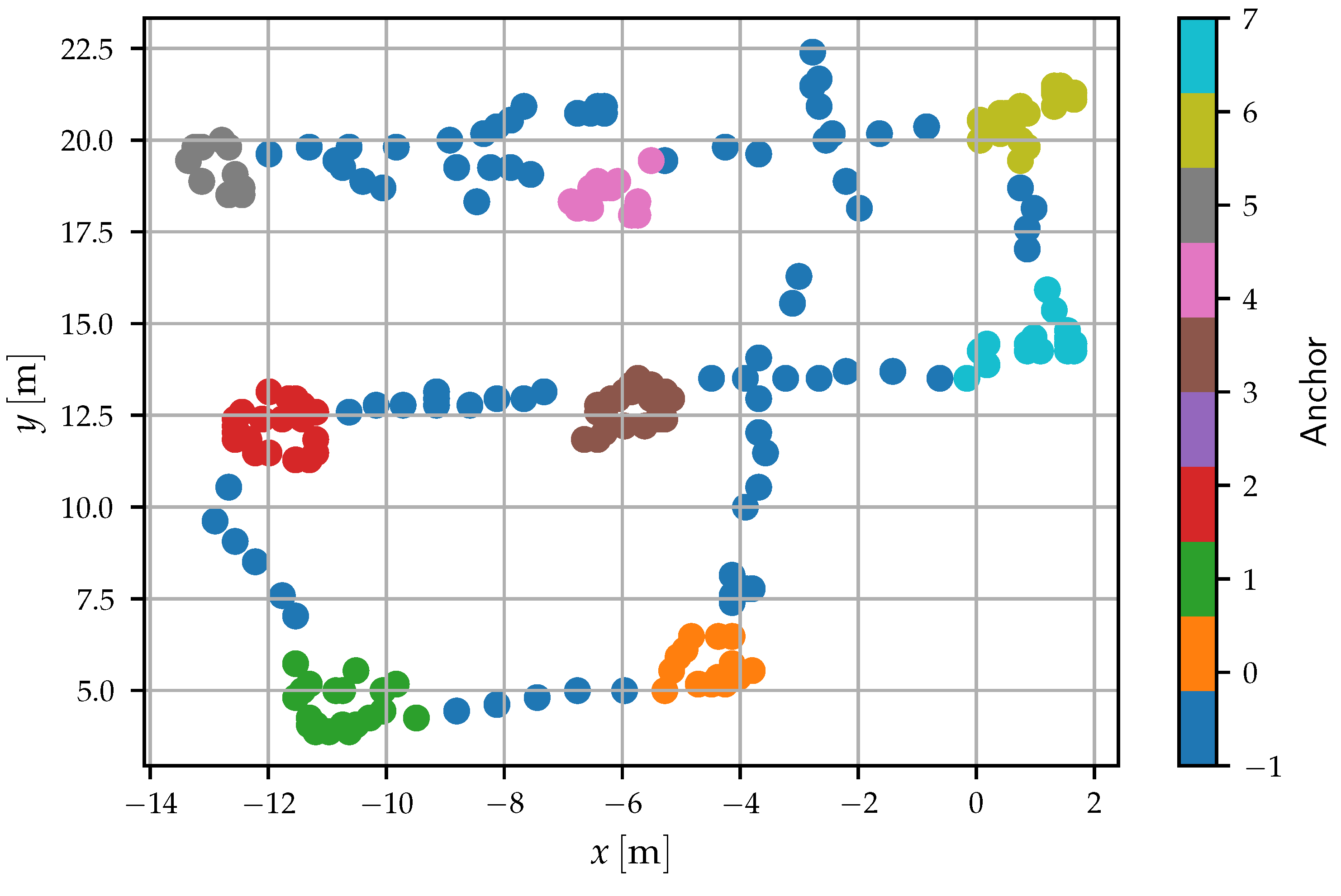
5.2. Indoor Evaluation with Precise Reference
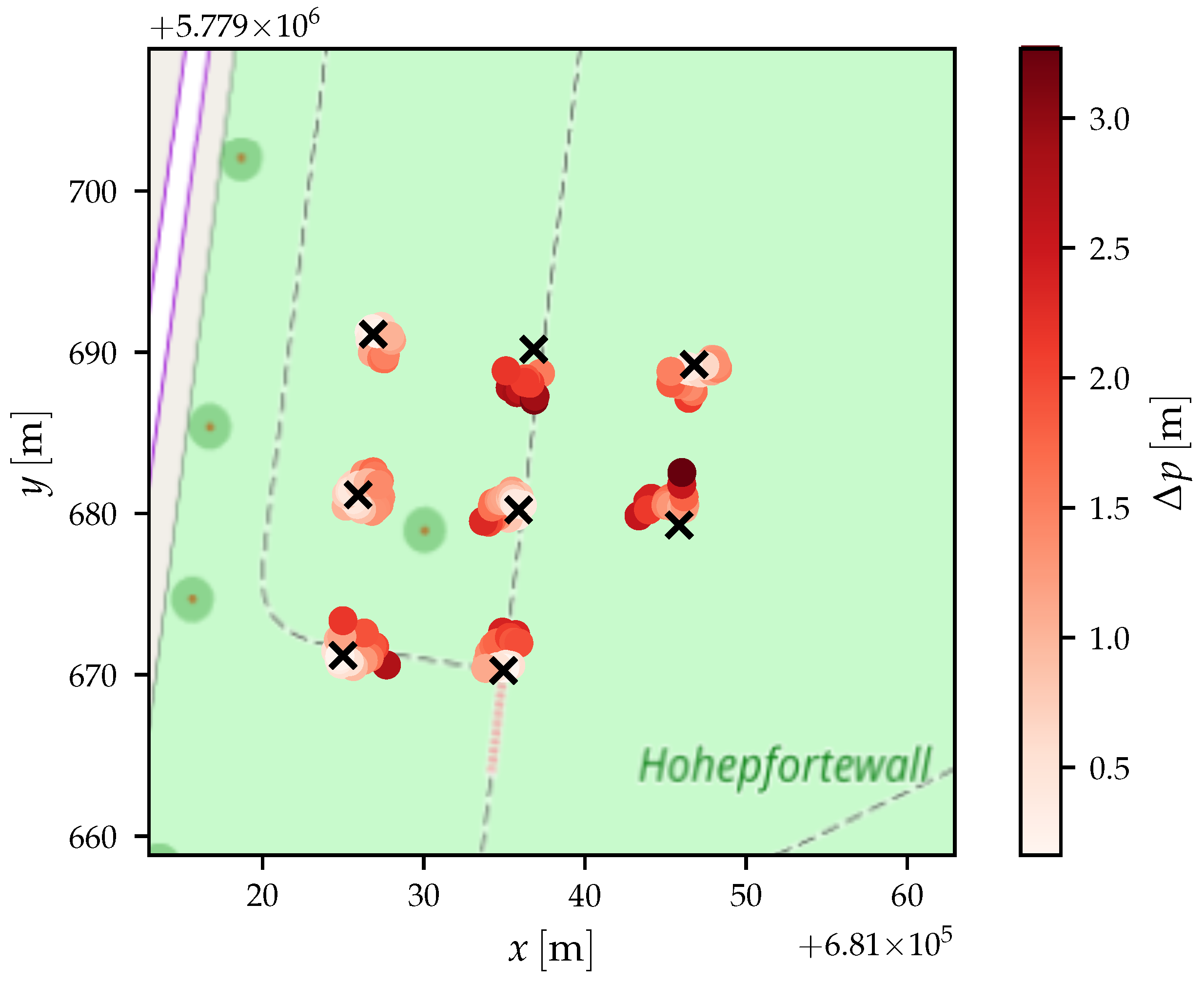
5.3. Outdoor Evaluation
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UWB | Ultrawideband |
| GPS | Global Positioning System |
| AGPS | Assisted GPS |
| D-GPS | Differential GPS |
| ToF | Time-of-Flight |
| TDoA | Time-Difference of Arrival |
| RSSI | Received Signal Strength |
| SD-Card | Secure Digital Card |
| UAV | Unmanned Aerial Vehicle |
| USART | Universal Serial Asynchronous Receiver Transmitter |
| IC | Inter-Integrated Circuit |
| NMEA | National Marine Electronics Association |
| UTM | Universal Transverse Mercator |
References
- Seo, J.; Duque, L.; Wacker, J. Drone-enabled bridge inspection methodology and application. Autom. Constr. 2018, 94, 112–126. [Google Scholar] [CrossRef]
- Shihavuddin, A.; Chen, X.; Fedorov, V.; Nymark Christensen, A.; Andre Brogaard Riis, N.; Branner, K.; Bjorholm Dahl, A.; Reinhold Paulsen, R. Wind turbine surface damage detection by deep learning aided drone inspection analysis. Energies 2019, 12, 676. [Google Scholar] [CrossRef] [Green Version]
- Erdelj, M.; Król, M.; Natalizio, E. Wireless Sensor Networks and Multi-UAV systems for natural disaster management. Comput. Netw. 2017, 124, 72–86. [Google Scholar] [CrossRef]
- Dorigo, M.; Floreano, D.; Gambardella, L.M.; Mondada, F.; Nolfi, S.; Baaboura, T.; Birattari, M.; Bonani, M.; Brambilla, M.; Brutschy, A.; et al. Swarmanoid: A novel concept for the study of heterogeneous robotic swarms. IEEE Robot. Autom. Mag. 2013, 20, 60–71. [Google Scholar] [CrossRef] [Green Version]
- Zelazo, D.; Franchi, A.; Bülthoff, H.H.; Robuffo Giordano, P. Decentralized rigidity maintenance control with range measurements for multi-robot systems. Int. J. Robot. Res. 2015, 34, 105–128. [Google Scholar] [CrossRef] [Green Version]
- Stirling, T.; Roberts, J.; Zufferey, J.C.; Floreano, D. Indoor navigation with a swarm of flying robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 4641–4647. [Google Scholar]
- Jatmiko, W.; Jovan, F.; Dhiemas, R.; Sakti, A.M.; Ivan, F.M.; Fukuda, T.; Sekiyama, K. Robots implementation for odor source localization using PSO algorithm. WSEAS Trans. Circuits Syst. 2011, 10, 115–125. [Google Scholar]
- Marchant, W.; Tosunoglu, S. Rethinking Wildfire Suppression With Swarm Robotics. In Proceedings of the 29th Florida Conference on Recent Advances in Robotics, Miami, FL, USA, 12–13 May 2016; pp. 186–191. [Google Scholar]
- Bayat, B.; Crasta, N.; Crespi, A. Environmental Monitoring using Autonomous Vehicles: A Survey of Recent Searching Techniques. Curr. Opin. Biotechnol. 2017, 45, 76–84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landau, H.; Chen, X.; Klose, S.; Leandro, R.; Vollath, U. Trimble’s Rtk and Dgps Solutions in Comparison with Precise Point Positioning. Observing Our Changing Earth; Sideris, M.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 709–718. [Google Scholar] [CrossRef]
- Shao, M.; Sui, X. Study on Differential GPS Positioning Methods. In Proceedings of the 2015 International Conference on Computer Science and Mechanical Automation (CSMA), Hangzhou, China, 23–25 October 2015; pp. 223–225. [Google Scholar] [CrossRef]
- Merriaux, P.; Dupuis, Y.; Boutteau, R.; Vasseur, P.; Savatier, X. A Study of Vicon System Positioning Performance. Sensors 2017, 17, 1591. [Google Scholar] [CrossRef] [PubMed]
- Hoyer, L.; Steup, C.; Mostaghim, S. A Robot Localization Framework Using CNNs for Object Detection and Pose Estimation. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bengaluru, India, 18–21 November 2018; pp. 1388–1395. [Google Scholar]
- Mautz, R.; Tilch, S. Survey of optical indoor positioning systems. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Zhao, Y.; Liu, Y.; Cuthbert, L. Bluetooth positioning using RSSI and triangulation methods. In Proceedings of the 2013 IEEE 10th Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2013; pp. 837–842. [Google Scholar] [CrossRef]
- Yang, C.; Shao, H. WiFi-based indoor positioning. IEEE Commun. Mag. 2015, 53, 150–157. [Google Scholar] [CrossRef]
- Sidorenko, J.; Schatz, V.; Scherer-Negenborn, N.; Arens, M.; Hugentobler, U. Decawave UWB clock drift correction and power self-calibration. Sensors 2019, 19, 2942. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kempke, B.; Pannuto, P.; Dutta, P. PolyPoint: Guiding Indoor Quadrotors with Ultra-Wideband Localization. In Proceedings of the 2nd International Workshop on Hot Topics in Wireless, Paris, France, 11 September 2015; ACM Press: Paris, France, 2015; pp. 16–20. [Google Scholar] [CrossRef] [Green Version]
- Mai, S. Simultaneous Localisation and Optimisation Towards Swarm Intelligence in Robots. Master’s Thesis, Otto-von-Guericke University, Magdeburg, Germany, 2018. [Google Scholar]
- Xu, H.; Zhang, Y.; Zhou, B.; Wang, L.; Yao, X.; Meng, G.; Shen, S. Omni-swarm: A Decentralized Omnidirectional Visual-Inertial-UWB State Estimation System for Aerial Swarm. arXiv 2021, arXiv:2103.04131. [Google Scholar]
- Steup, C.; Mai, S.; Mostaghim, S. Evaluation Platform for Micro Aerial Indoor Swarm Robotics; Technical Report FIN-003-2016; Otto-von-Guericke-Universität: Magdeburg, Germany, 2016. [Google Scholar]
- Mantilla-Gaviria, I.A.; Leonardi, M.; Balbastre-Tejedor, J.V.; de los Reyes, E. On the application of singular value decomposition and Tikhonov regularization to ill-posed problems in hyperbolic passive location. Math. Comput. Model. 2013, 57, 1999–2008. [Google Scholar] [CrossRef]
- Murphy, W.; Hereman, W. Determination of a Position in Three Dimensions Using Trilateration and Approximate Distances; Technical Report 7; Department of Mathematical and Computer Sciences, Colorado School of Mines: Golden, CO, USA, 1995. [Google Scholar]




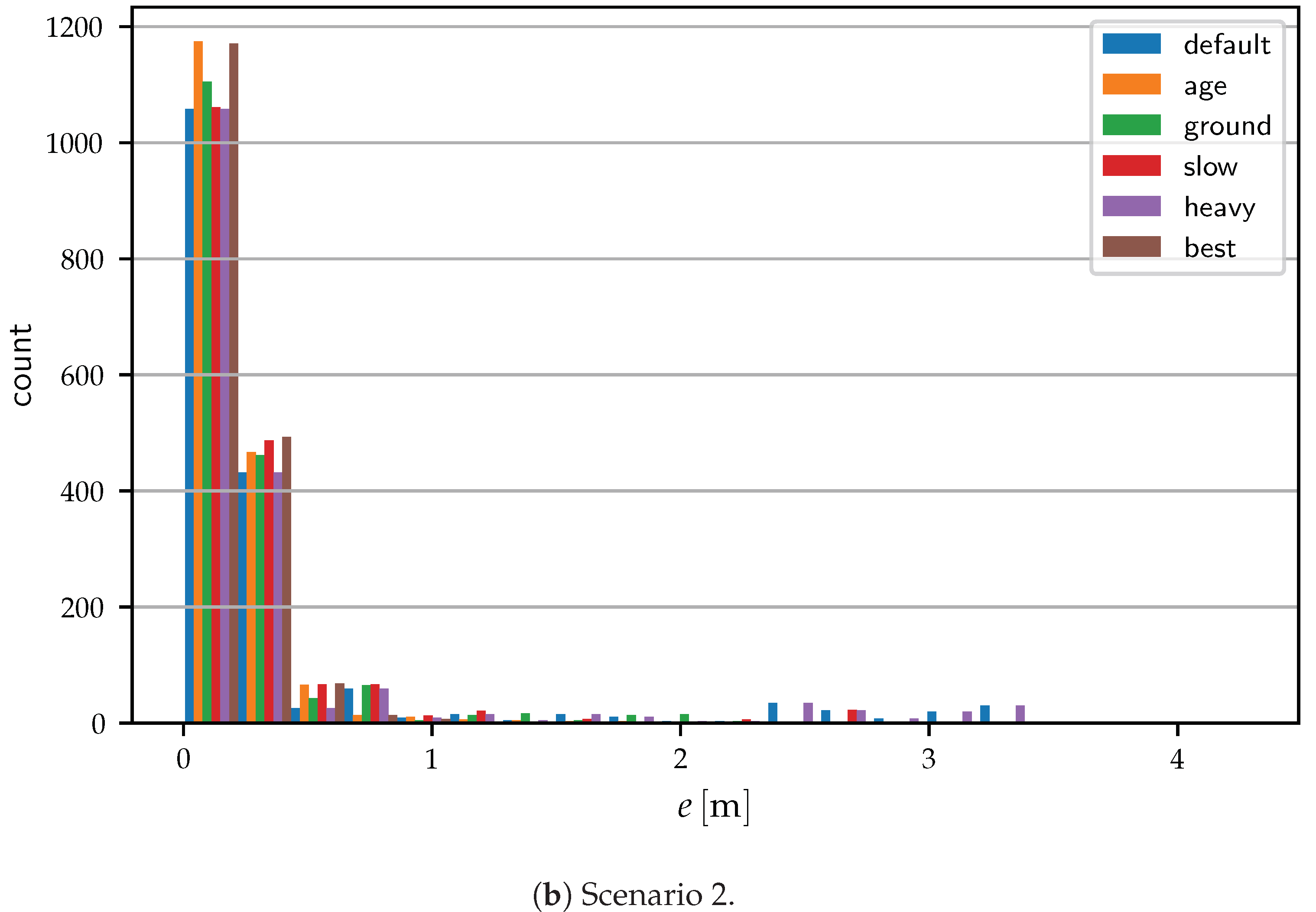



| Config | Algorithm 2 Parameters | Algorithm 1 Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| [m] | [m] | [m] | n | [m/s] | a | b | [s] | ||
| default | 0.1 | 0.2 | 0.1 | 100 | 20 | 1.01 | 1 | 0.1 | |
| age | 0.1 | 0.2 | 0.1 | 100 | 20 | 1.01 | 2 | 0.1 | |
| ground | 0.1 | 0.0 | 0.1 | 100 | 20 | 1.01 | 1 | 0.1 | |
| slow | 0.1 | 0.2 | 0.1 | 100 | 5 | 1.1 | 1 | 0.1 | |
| heavy | 0.1 | 0.2 | 0.01 | 1000 | 20 | 1.01 | 1 | 0.1 | |
| best | 0.1 | 0.0 | 0.1 | 100 | 5 | 1.1 | 2 | 0.1 | |
| Configuration | |||||
|---|---|---|---|---|---|
| Parameters | |||||
| default | −0.426 | 0.0 | −0.439 | 0.0 | |
| age | −0.459 | 0.0 | −0.370 | 0.0 | |
| ground | −0.447 | 0.0 | −0.327 | 0.0 | |
| slow | −0.274 | 0.0 | −0.250 | 0.0 | |
| heavy | −0.426 | 0.0 | −0.439 | 0.0 | |
| best | −0.188 | 0.0 | −0.398 | 0.0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steup, C.; Beckhaus, J.; Mostaghim, S. A Single-Copter UWB-Ranging-Based Localization System Extendable to a Swarm of Drones. Drones 2021, 5, 85. https://doi.org/10.3390/drones5030085
Steup C, Beckhaus J, Mostaghim S. A Single-Copter UWB-Ranging-Based Localization System Extendable to a Swarm of Drones. Drones. 2021; 5(3):85. https://doi.org/10.3390/drones5030085
Chicago/Turabian StyleSteup, Christoph, Jonathan Beckhaus, and Sanaz Mostaghim. 2021. "A Single-Copter UWB-Ranging-Based Localization System Extendable to a Swarm of Drones" Drones 5, no. 3: 85. https://doi.org/10.3390/drones5030085
APA StyleSteup, C., Beckhaus, J., & Mostaghim, S. (2021). A Single-Copter UWB-Ranging-Based Localization System Extendable to a Swarm of Drones. Drones, 5(3), 85. https://doi.org/10.3390/drones5030085







