Accuracy of 3D Landscape Reconstruction without Ground Control Points Using Different UAS Platforms
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. UASs and Camera Systems Tested
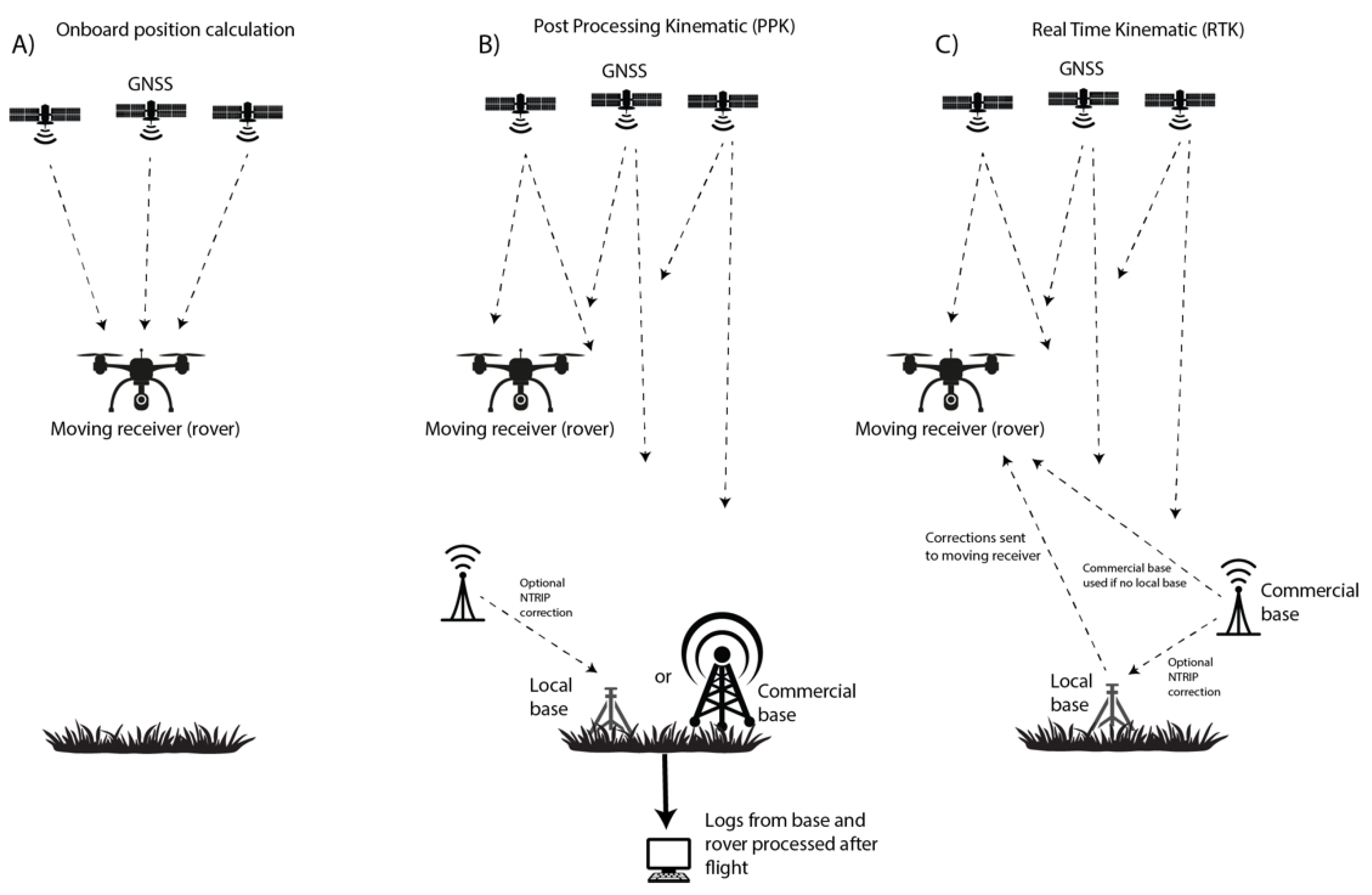
2.3. Photograph Geotagging
2.4. Checkpoint Position Measurement
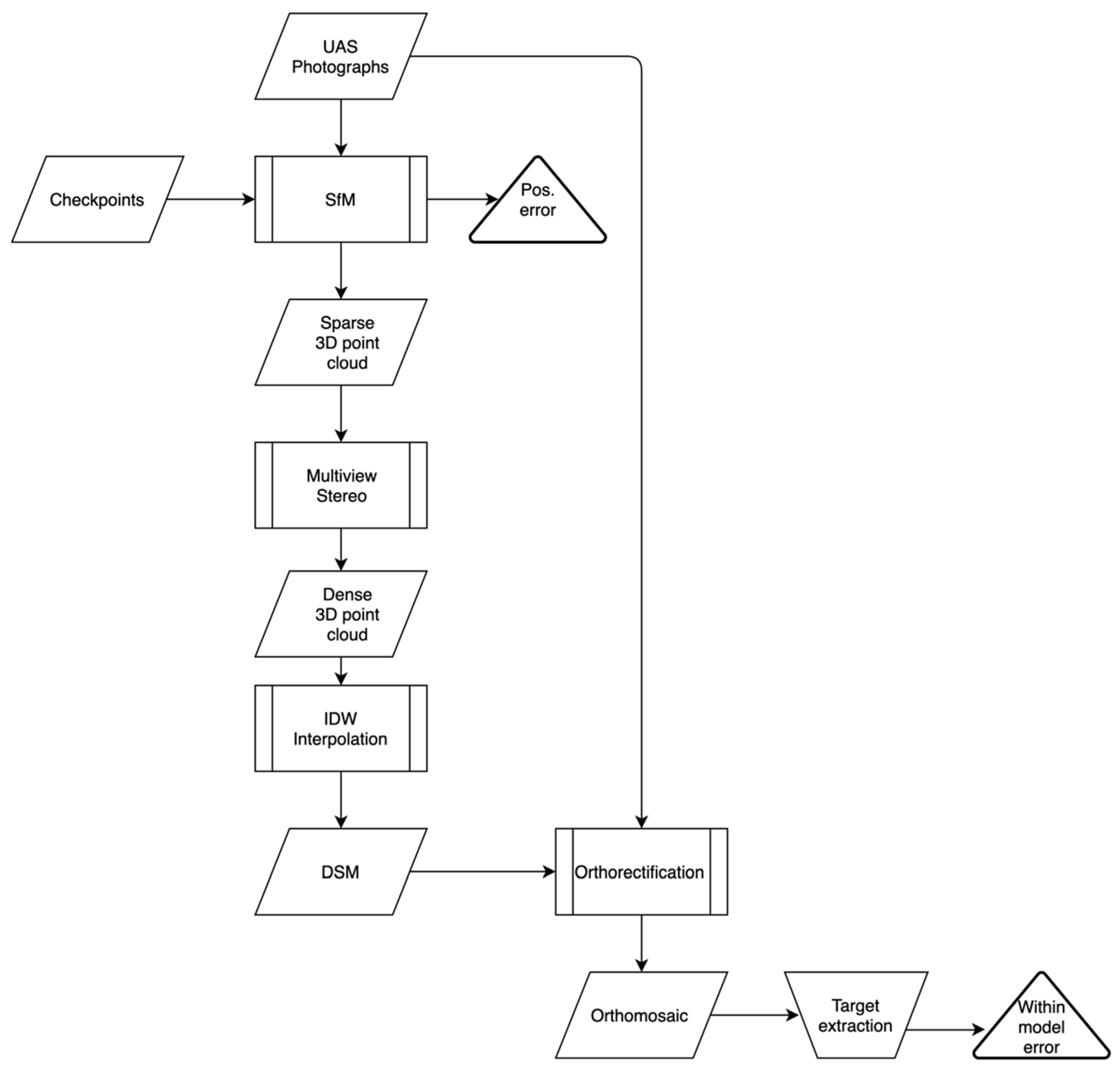
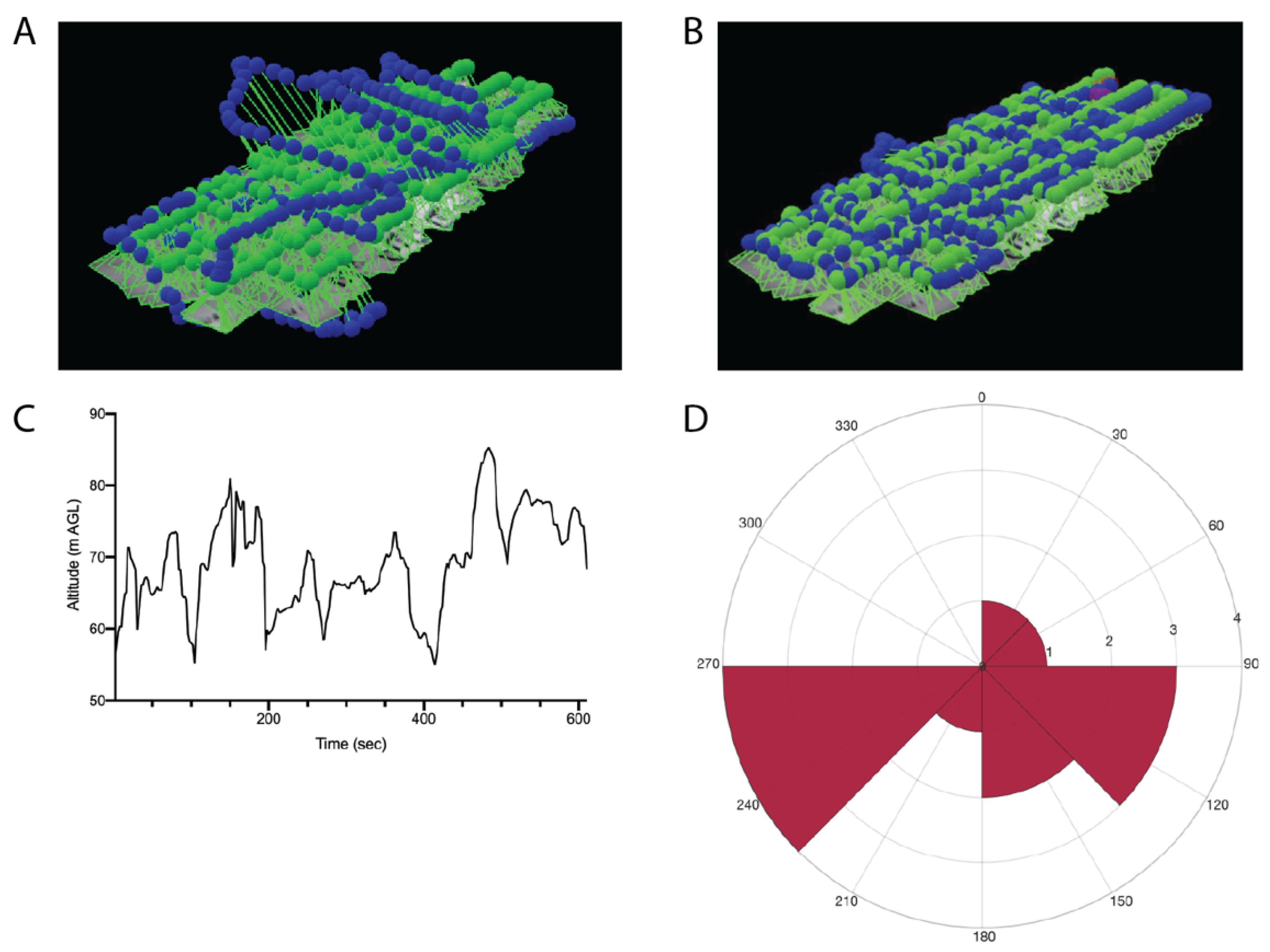
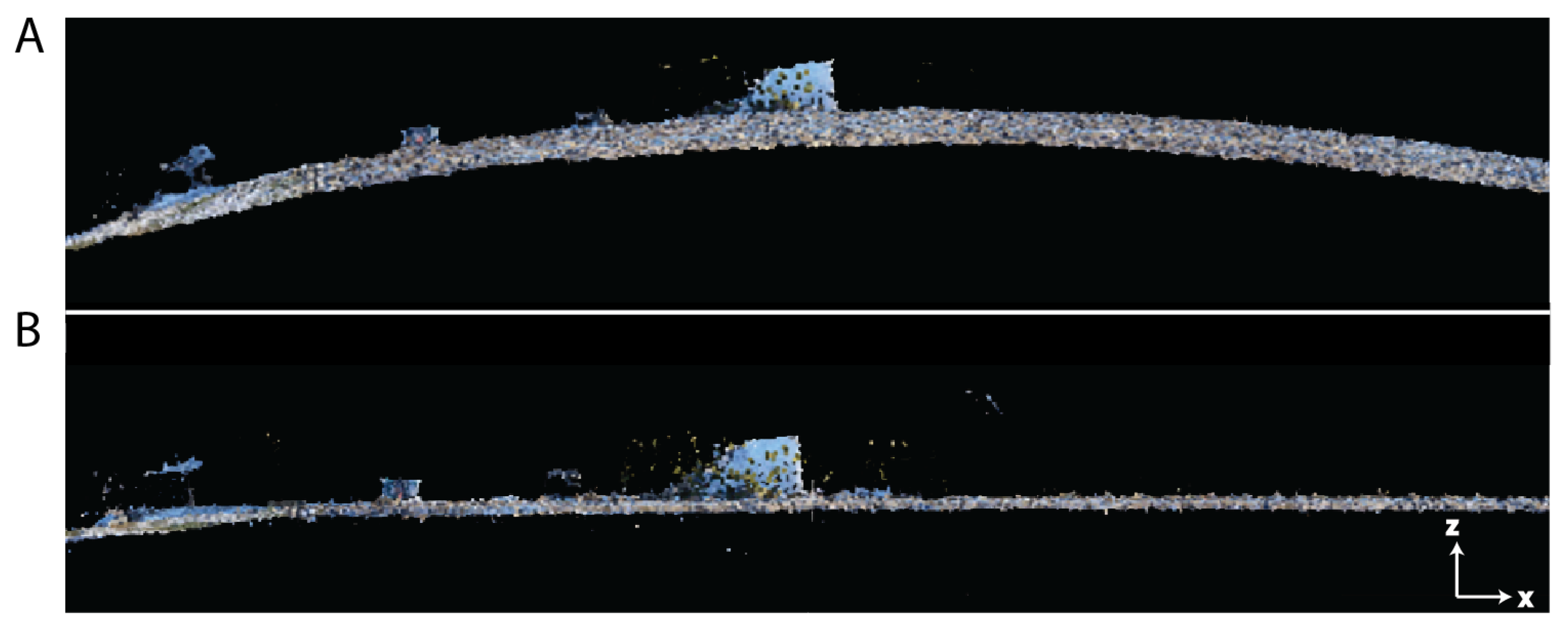
2.5. Structure from Motion–Multiview Stereo (SfM-MVS) Processing
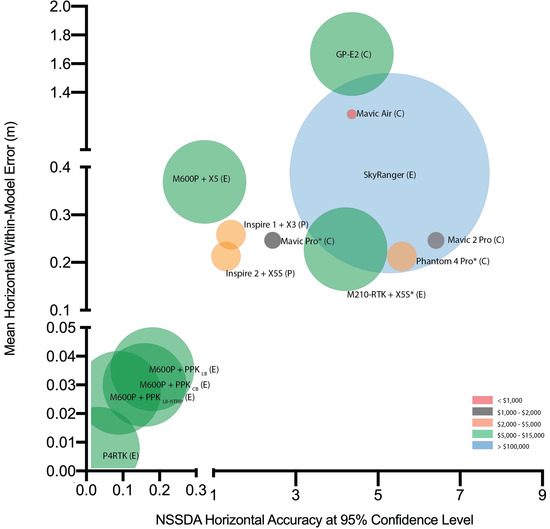
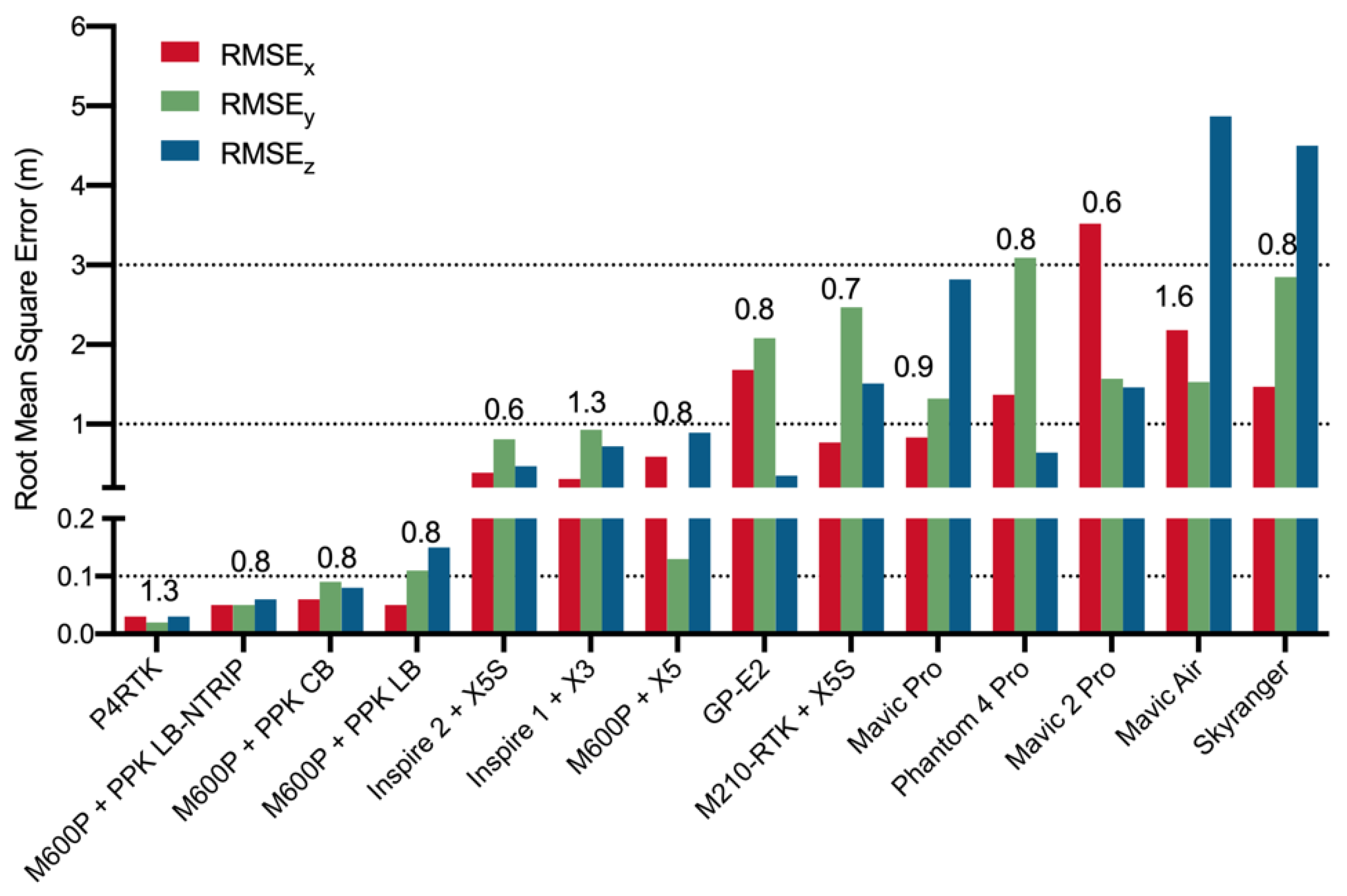
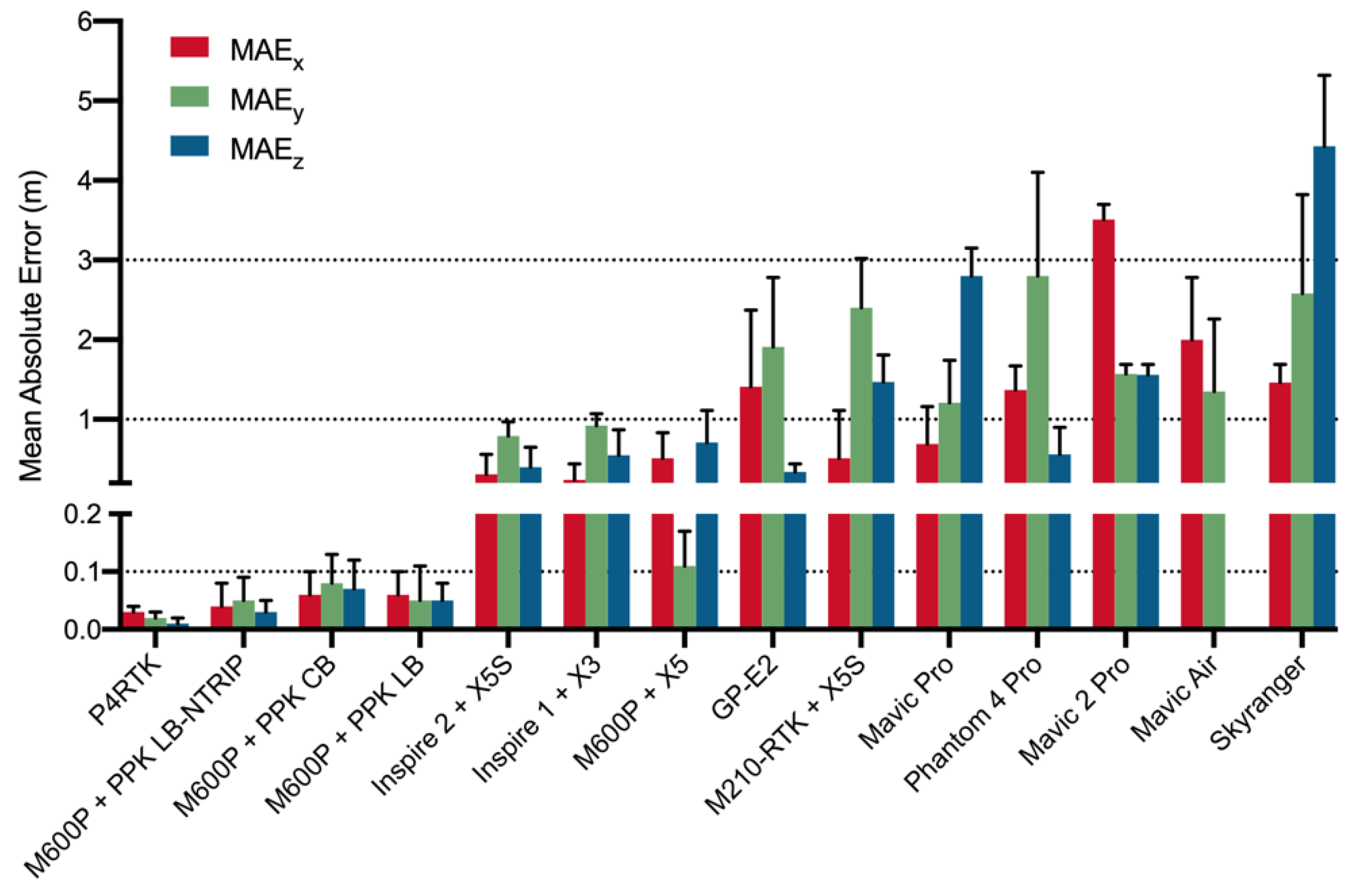
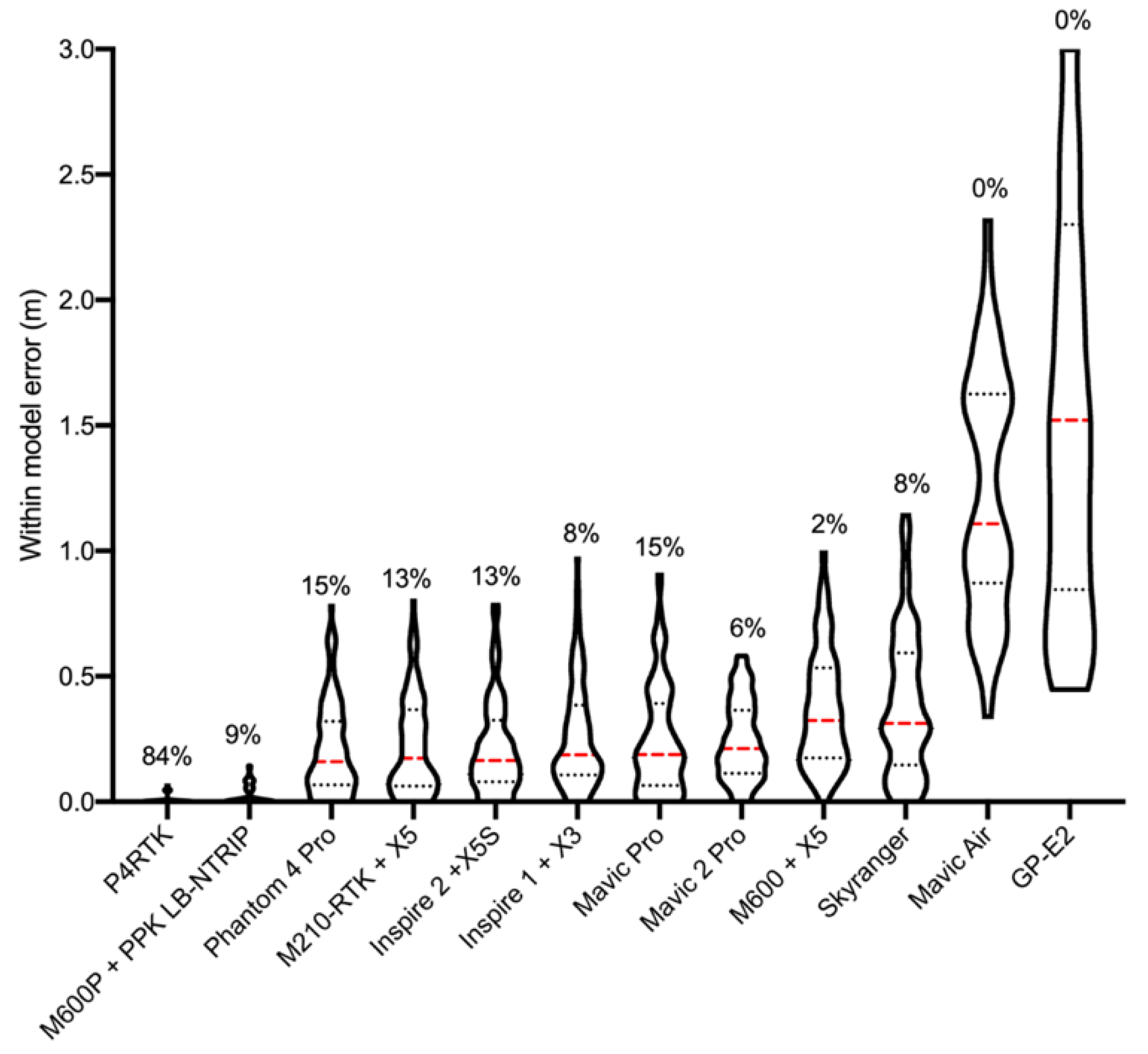
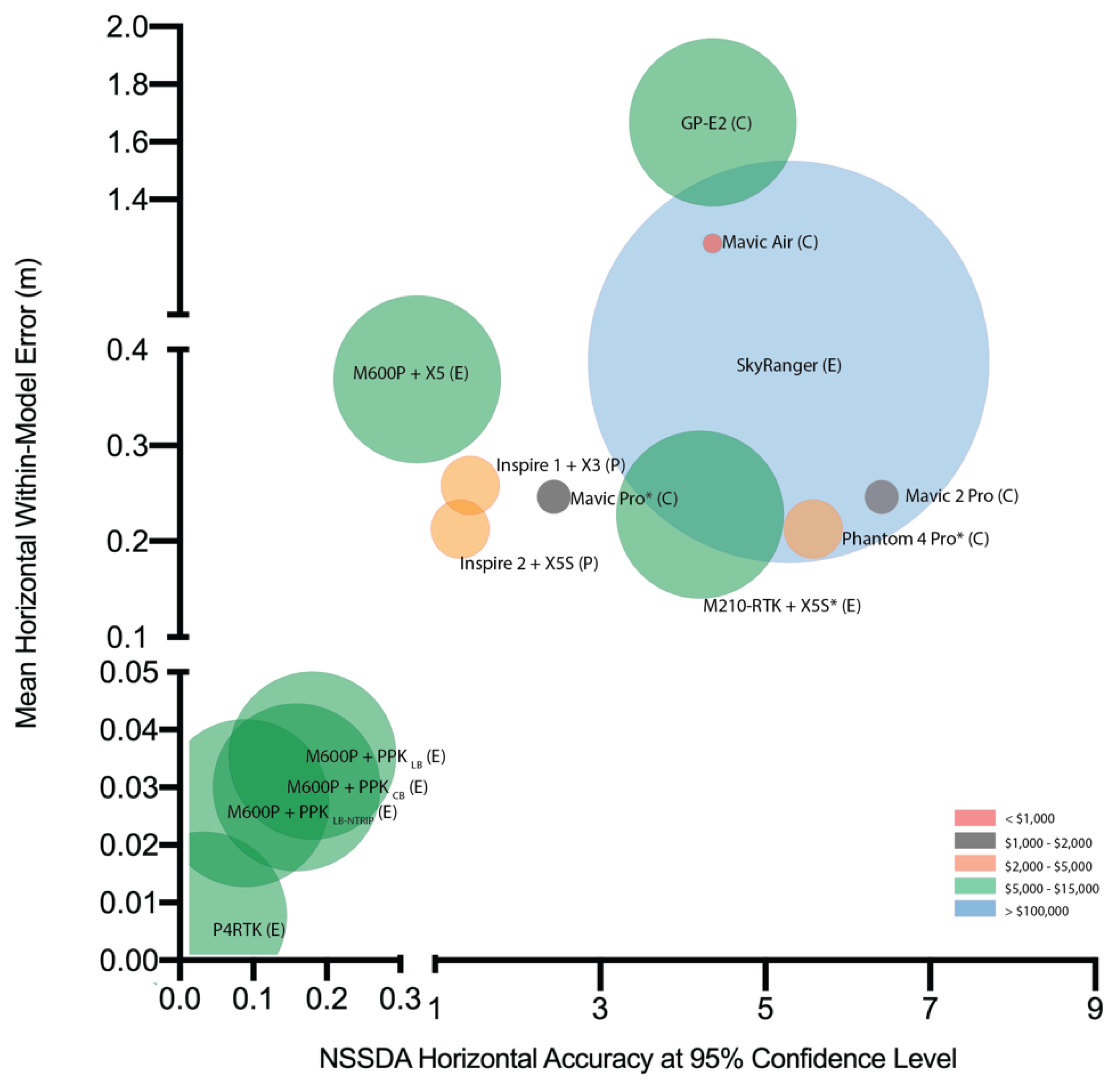
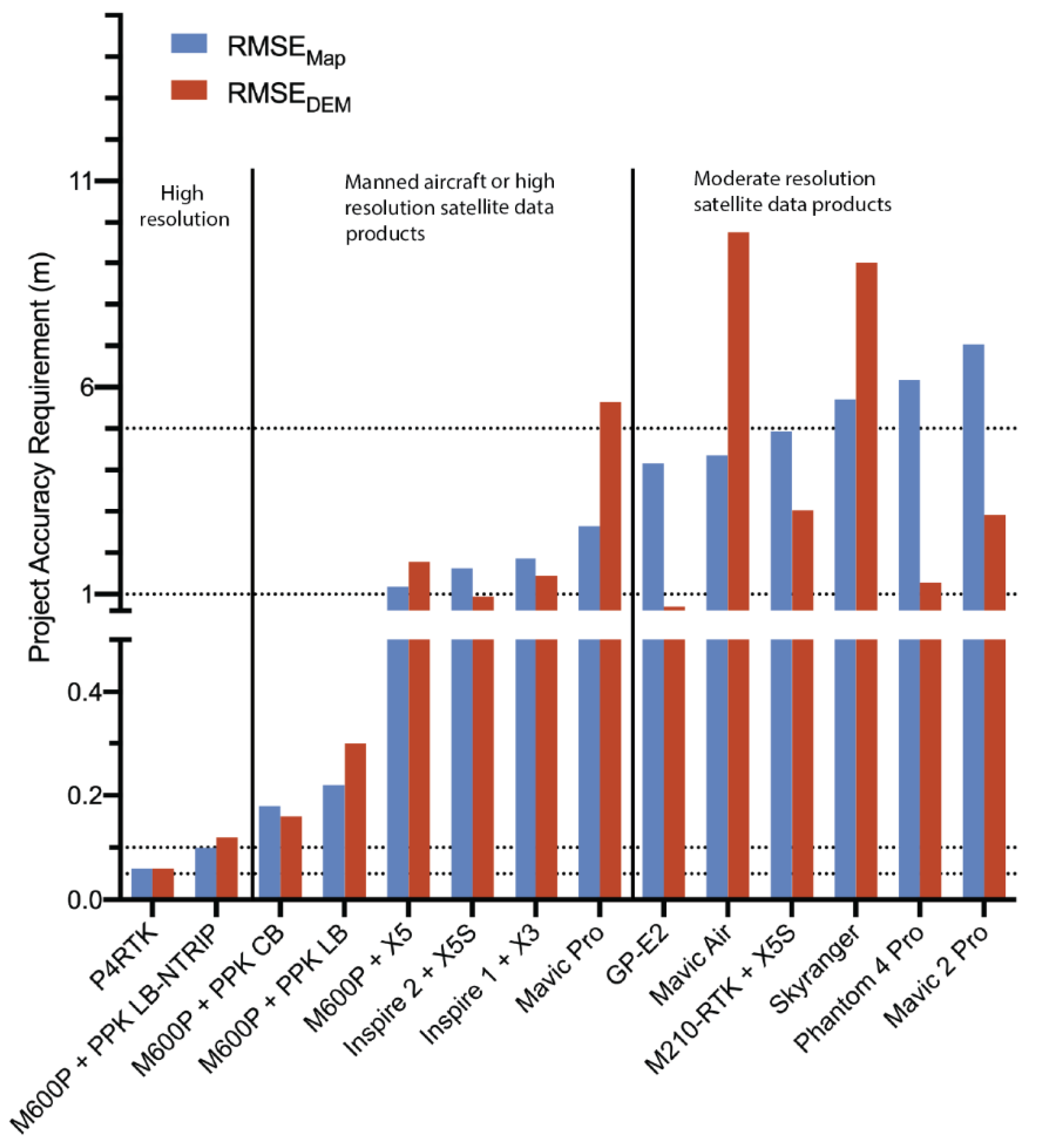
2.6. Model Accuracy Assessment
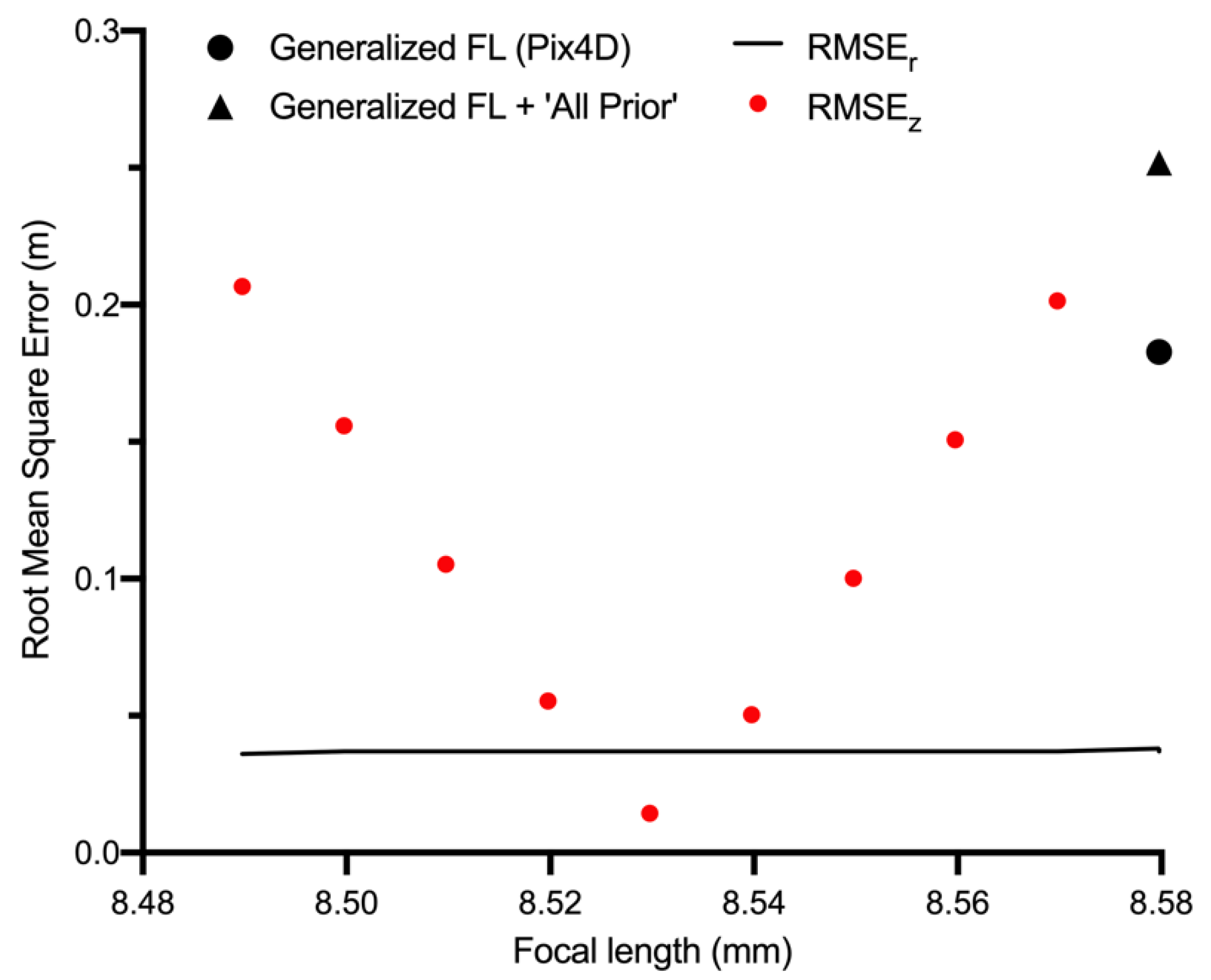
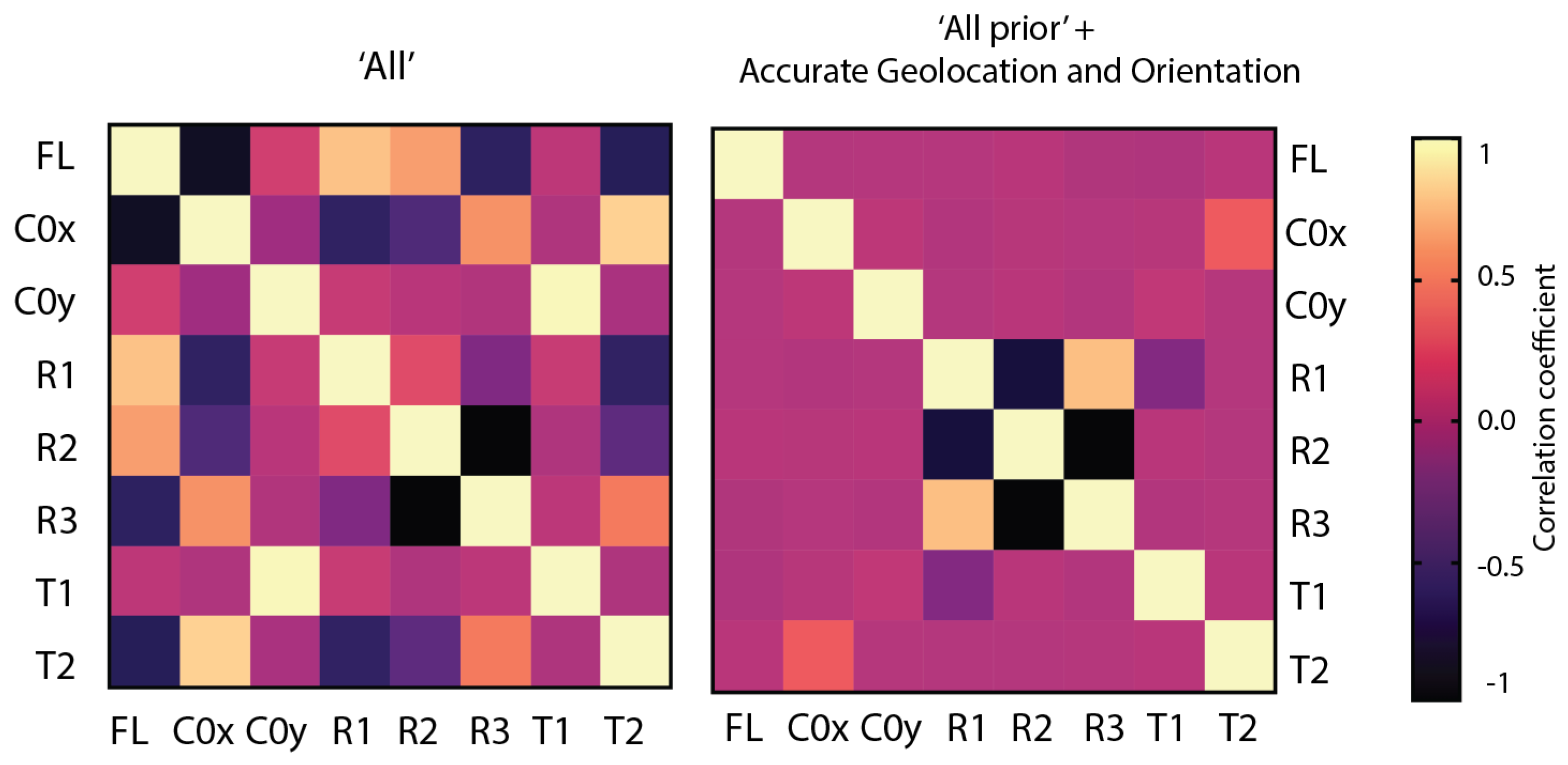
2.7. Camera Focal Length Considerations for the Phantom 4 RTK
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rokhmana, C.A. The Potential of UAV-based Remote Sensing for Supporting Precision Agriculture in Indonesia. Procedia Environ. Sci. 2015, 24, 245–253. [Google Scholar] [CrossRef]
- Hunt, E.R.; Daughtry, C.S.T. What good are unmanned aircraft systems for agricultural remote sensing and precision agriculture? Int. J. Remote Sens. 2018, 39, 5345–5376. [Google Scholar] [CrossRef]
- Carvajal-Ramírez, F.; Navarro-Ortega, A.D.; Agüera-Vega, F.; Martínez-Carricondo, P.; Mancini, F. Virtual reconstruction of damaged archaeological sites based on Unmanned Aerial Vehicle Photogrammetry and 3D modelling. Study case of a southeastern Iberia production area in the Bronze Age. Measurement 2019, 136, 225–236. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Soura, K.; Koukouvelas, I.K.; Argyropoulos, N.G. UAV vs classical aerial photogrammetry for archaeological studies. J. Archaeol. Sci.-Rep. 2017, 14, 758–773. [Google Scholar] [CrossRef]
- Li, J.; Yang, B.; Cong, Y.; Cao, L.; Fu, X.; Dong, Z. 3D Forest Mapping Using A Low-Cost UAV Laser Scanning System: Investigation and Comparison. Remote Sens. 2019, 11, 717. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Di Gennaro, S.F.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: A review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Valkaniotis, S.; Papathanassiou, G.; Ganas, A. Mapping an earthquake-induced landslide based on UAV imagery; case study of the 2015 Okeanos landslide, Lefkada, Greece. Eng. Geol. 2018, 245, 141–152. [Google Scholar] [CrossRef]
- Zanutta, A.; Lambertini, A.; Vittuari, L. UAV Photogrammetry and Ground Surveys as a Mapping Tool for Quickly Monitoring Shoreline and Beach Changes. J. Mar. Sci. Eng. 2020, 8, 52. [Google Scholar] [CrossRef]
- Danhoff, B.M.; Huckins, C.J. Modelling submerged fluvial substrates with structure-from-motion photogrammetry. River Res. Appl. 2020, 36, 128–137. [Google Scholar] [CrossRef]
- Joyce, K.E.; Duce, S.; Leahy, S.M.; Leon, J.; Maier, S.W. Principles and practice of acquiring drone-based image data in marine environments. Mar. Freshw. Res. 2019, 70, 952–963. [Google Scholar] [CrossRef]
- Kalacska, M.; Lucanus, O.; Sousa, L.; Vieira, T.; Arroyo-Mora, J.P. Freshwater Fish Habitat Complexity Mapping Using Above and Underwater Structure-From-Motion Photogrammetry. Remote Sens. 2018, 10, 1912. [Google Scholar] [CrossRef]
- Mohamad, N.; Abdul Khanan, M.F.; Ahmad, A.; Md Din, A.H.; Shahabi, H. Evaluating Water Level Changes at Different Tidal Phases Using UAV Photogrammetry and GNSS Vertical Data. Sensors 2019, 19, 3778. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.; Michanowicz, D.R.; Jia, C. Developing a Modular Unmanned Aerial Vehicle (UAV) Platform for Air Pollution Profiling. Sensors 2018, 18, 4363. [Google Scholar] [CrossRef] [PubMed]
- Son, S.W.; Yoon, J.H.; Jeon, H.J.; Kim, D.W.; Yu, J.J. Optimal flight parameters for unmanned aerial vehicles collecting spatial information for estimating large-scale waste generation. Int. J. Remote Sens. 2019, 40, 8010–8030. [Google Scholar] [CrossRef]
- Fettermann, T.; Fiori, L.; Bader, M.; Doshi, A.; Breen, D.; Stockin, K.A.; Bollard, B. Behaviour reactions of bottlenose dolphins (Tursiops truncatus) to multirotor Unmanned Aerial Vehicles (UAVs). Sci. Rep. 2019, 9, 8558. [Google Scholar] [CrossRef]
- Hu, J.B.; Wu, X.M.; Dai, M.X. Estimating the population size of migrating Tibetan antelopes Pantholops hodgsonii with unmanned aerial vehicles. Oryx 2020, 54, 101–109. [Google Scholar] [CrossRef]
- Lethbridge, M.; Stead, M.; Wells, C. Estimating kangaroo density by aerial survey: A comparison of thermal cameras with human observers. Wildl. Res. 2019, 46, 639–648. [Google Scholar] [CrossRef]
- Raoult, V.; Tosetto, L.; Williams, J. Drone-Based High-Resolution Tracking of Aquatic Vertebrates. Drones 2018, 2, 37. [Google Scholar] [CrossRef]
- Pádua, L.; Sousa, J.; Vanko, J.; Hruška, J.; Adão, T.; Peres, E.; Sousa, A.; Sousa, J. Digital Reconstitution of Road Traffic Accidents: A Flexible Methodology Relying on UAV Surveying and Complementary Strategies to Support Multiple Scenarios. Int. J. Environ. Res. Public Health 2020, 17, 1868. [Google Scholar] [CrossRef]
- Pix4D. A New Protocol of CSI for the Royal Canadian Mounted Police; Pix4D: Prilly, Switzerland, 2014. [Google Scholar]
- Liénard, J.; Vogs, A.; Gatziolis, D.; Strigul, N. Embedded, real-time UAV control for improved, image-based 3D scene reconstruction. Measurement 2016, 81, 264–269. [Google Scholar] [CrossRef]
- Arroyo-Mora, J.P.; Kalacska, M.; Inamdar, D.; Soffer, R.; Lucanus, O.; Gorman, J.; Naprstek, T.; Schaaf, E.S.; Ifimov, G.; Elmer, K.; et al. Implementation of a UAV–Hyperspectral Pushbroom Imager for Ecological Monitoring. Drones 2019, 3, 12. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Ribeiro-Gomes, K.; Hernández-López, D.; Ortega, J.F.; Ballesteros, R.; Poblete, T.; Moreno, M.A. Uncooled Thermal Camera Calibration and Optimization of the Photogrammetry Process for UAV Applications in Agriculture. Sensors 2017, 17, 2173. [Google Scholar] [CrossRef] [PubMed]
- Forsmoo, J.; Anderson, K.; Macleod, C.J.A.; Wilkinson, M.E.; DeBell, L.; Brazier, R.E. Structure from motion photogrammetry in ecology: Does the choice of software matter? Ecol. Evol. 2019, 9, 12964–12979. [Google Scholar] [CrossRef]
- Bemis, S.P.; Micklethwaite, S.; Turner, D.; James, M.R.; Akciz, S.; Thiele, S.T.; Bangash, H.A. Ground-based and UAV-Based photogrammetry: A multi-scale, high-resolution mapping tool for structural geology and paleoseismology. J. Struct. Geol. 2014, 69, 163–178. [Google Scholar] [CrossRef]
- Jorayev, G.; Wehr, K.; Benito-Calvo, A.; Njau, J.; de la Torre, I. Imaging and photogrammetry models of Olduvai Gorge (Tanzania) by Unmanned Aerial Vehicles: A high-resolution digital database for research and conservation of Early Stone Age sites. J. Archaeol. Sci. 2016, 75, 40–56. [Google Scholar] [CrossRef]
- Kalacska, M.; Chmura, G.L.; Lucanus, O.; Berube, D.; Arroyo-Mora, J.P. Structure from motion will revolutionize analyses of tidal wetland landscapes. Remote Sens. Environ. 2017, 199, 14–24. [Google Scholar] [CrossRef]
- Angel, Y.; Turner, D.; Parkes, S.; Malbeteau, Y.; Lucieer, A.; McCabe, M. Automated Georectification and Mosaicking of UAV-Based Hyperspectral Imagery from Push-Broom Sensors. Remote Sens. 2019, 12, 34. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; et al. An integrated UAV-borne lidar system for 3D habitat mapping in three forest ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Davies, L.; Bolam, R.C.; Vagapov, Y.; Anuchin, A. Review of Unmanned Aircraft System Technologies to Enable Beyond Visual Line of Sight (BVLOS) Operations. In Proceedings of the 2018 X International Conference on Electrical Power Drive Systems (ICEPDS), Novocherkassk, Russia, 3–6 October 2018; pp. 1–6. [Google Scholar]
- Abeywickrama, H.V.; Jayawickrama, B.A.; He, Y.; Dutkiewicz, E. Comprehensive Energy Consumption Model for Unmanned Aerial Vehicles, Based on Empirical Studies of Battery Performance. IEEE Access 2018, 6, 58383–58394. [Google Scholar] [CrossRef]
- Fang, S.X.; O’Young, S.; Rolland, L. Development of Small UAS Beyond-Visual-Line-of-Sight (BVLOS) Flight Operations: System Requirements and Procedures. Drones 2018, 2, 13. [Google Scholar] [CrossRef]
- Zmarz, A.; Rodzewicz, M.; Dąbski, M.; Karsznia, I.; Korczak-Abshire, M.; Chwedorzewska, K.J. Application of UAV BVLOS remote sensing data for multi-faceted analysis of Antarctic ecosystem. Remote Sens. Environ. 2018, 217, 375–388. [Google Scholar] [CrossRef]
- De Haag, M.U.; Bartone, C.G.; Braasch, M.S. Flight-test evaluation of small form-factor LiDAR and radar sensors for sUAS detect-and-avoid applications. In Proceedings of the 2016 IEEE/AIAA 35th Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–29 September 2016; pp. 1–11. [Google Scholar]
- Pfeifer, C.; Barbosa, A.; Mustafa, O.; Peter, H.-U.; Rümmler, M.-C.; Brenning, A. Using Fixed-Wing UAV for Detecting and Mapping the Distribution and Abundance of Penguins on the South Shetlands Islands, Antarctica. Drones 2019, 3, 39. [Google Scholar] [CrossRef]
- Ullman, S. The interpretation of structure from motion. Proc. Royal Soc. Lond. Ser. B 1979, 203, 405–426. [Google Scholar]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Straightforward reconstruction of 3D surfaces and topography with a camera: Accuracy and geoscience application. J. Geophys. Res.-Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Ferreira, E.; Chandler, J.; Wackrow, R.; Shiono, K. Automated extraction of free surface topography using SfM-MVS photogrammetry. Flow Meas. Instrum. 2017, 54, 243–249. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Photo tourism: Exploring photo collections in 3D. ACM Trans. Graph. 2006, 25, 835–846. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from motion photogrammetry in physical geography. Prog. Phys. Geogr.-Earth Environ. 2016, 40, 247–275. [Google Scholar] [CrossRef]
- Mosbrucker, A.; Major, J.; Spicer, K.; Pitlick, J. Camera system considerations for geomorphic applications of SfM photogrammetry. Earth Surf. Process. Landf. 2017, 42, 969–986. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Domingo, D.; Ørka, H.O.; Næsset, E.; Kachamba, D.; Gobakken, T. Effects of UAV Image Resolution, Camera Type, and Image Overlap on Accuracy of Biomass Predictions in a Tropical Woodland. Remote Sens. 2019, 11, 948. [Google Scholar] [CrossRef]
- Fraser, B.T.; Congalton, R.G. Issues in Unmanned Aerial Systems (UAS) Data Collection of Complex Forest Environments. Remote Sens. 2018, 10, 908. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; Borra-Serrano, I.; Peña, J.M. Assessing UAV-collected image overlap influence on computation time and digital surface model accuracy in olive orchards. Precis. Agric. 2018, 19, 115–133. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, B.; Wei, Z.; Wang, C.; Huang, Q. Lightweight integrated solution for a UAV-borne hyperspectral imaging system. Remote Sens. 2020, 12, 657. [Google Scholar] [CrossRef]
- Gauci, A.; Brodbeck, C.; Poncet, A.; Knappenberger, T. Assessing the Geospatial Accuracy of Aerial Imagery Collected with Various UAS Platforms. Trans. ASABE 2018, 61, 1823–1829. [Google Scholar] [CrossRef]
- Koci, J.; Jarihani, B.; Leon, J.X.; Sidle, R.C.; Wilkinson, S.N.; Bartley, R. Assessment of UAV and Ground-Based Structure from Motion with Multi-View Stereo Photogrammetry in a Gullied Savanna Catchment. ISPRS Int. Geo-Inf. 2017, 6, 23. [Google Scholar] [CrossRef]
- Tonkin, T.N.; Midgley, N.G. Ground-Control Networks for Image Based Surface Reconstruction: An Investigation of Optimum Survey Designs Using UAV Derived Imagery and Structure-from-Motion Photogrammetry. Remote Sens. 2016, 8, 786. [Google Scholar] [CrossRef]
- Shahbazi, M.; Sohn, G.; Théau, J.; Menard, P. Development and Evaluation of a UAV-Photogrammetry System for Precise 3D Environmental Modeling. Sensors 2015, 15, 27493–27524. [Google Scholar] [CrossRef]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Accuracy of Digital Surface Models and Orthophotos Derived from Unmanned Aerial Vehicle Photogrammetry. J. Surv. Eng. 2017, 143, 04016025. [Google Scholar] [CrossRef]
- Chudley, T.R.; Christoffersen, P.; Doyle, S.H.; Abellan, A.; Snooke, N. High-accuracy UAV photogrammetry of ice sheet dynamics with no ground control. Cryosphere 2019, 13, 955–968. [Google Scholar] [CrossRef]
- Daakir, M.; Pierrot-Deseilligny, M.; Bosser, P.; Pichard, F.; Thom, C.; Rabot, Y.; Martin, O. Lightweight UAV with on-board photogrammetry and single-frequency GPS positioning for metrology applications. ISPRS J. Photogramm. Remote Sens. 2017, 127, 115–126. [Google Scholar] [CrossRef]
- Suzuki, T.; Takahasi, U.; Amano, Y. Precise UAV position and attitude estimation by multiple GNSS receivers for 3D mapping. In Proceedings of the 29th International technical meeting of the satellite division of the Institute of Nativation (ION GNSS+ 2016), Portland, OR, USA, 12–15 September 2016; pp. 1455–1464. [Google Scholar]
- Gautam, D.; Lucieer, A.; Malenovský, Z.; Watson, C. Comparison of MEMS-based and FOG-based IMUs to determine sensor pose on an unmanned aircraft ssytem. J. Surv. Eng.-ASCE 2017, 143, 04017009. [Google Scholar] [CrossRef]
- Zhang, H.; Aldana-Jague, E.; Clapuyt, F.; Wilken, F.; Vanacker, V.; Van Oost, K. Evaluating the potential of post-processing kinematic (PPK) georeferencing for UAV-based structure- from-motion (SfM) photogrammetry and surface change detection. Earth Surf. Dyn. 2019, 7, 807–827. [Google Scholar] [CrossRef]
- Fazeli, H.; Samadzadegan, F.; Dadrasjavan, F. Evaluating the potential of RTK-UAV for automatic point cloud generation in 3D rapid mapping. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41B6, 221. [Google Scholar] [CrossRef]
- American Society for Photogrammetry and Remote Sensing (ASPRS). ASPRS Positional Accuracy Standards for Digital Geospatial Data (2014); ASPRS: Bethesda, MD, USA, 2015; pp. A1–A26. [Google Scholar]
- Drone Industry Insights. Top 10 Drone Manufacturers’ Market Shares in the US.; Drone Industry Insights UG: Hamburg, Germany, 2019. [Google Scholar]
- Transport Canada. Choosing the Right Drone. Available online: https://www.tc.gc.ca/en/services/aviation/drone-safety/choosing-right-drone.html#approved (accessed on 19 March 2020).
- Vautherin, J.; Rutishauser, S.; Scheider-Zapp, K.; Choi, H.F.; Chovancova, V.; Glass, A.; Strecha, C. Photogrammatetric accuracy and modeling of rolling shutter cameras. In Proceedings of the XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. In Proceedings of the International symposium on GPS/GNSS, Jeju Province, Korea, 11 April 2009; pp. 4–6. [Google Scholar]
- Bäumker, M.; Heimes, F.J. New Calibration and Computing Method for Direct Georeferencing of Image and Scanner Data Using the Position and Angular Data of an Hybrid Inertial Navigation System. In Proceedings of the OEEPE Workshop on Integrated Sensor Orientation, Hanover, Germany, 17–18 September 2001; pp. 197–212. [Google Scholar]
- Pix4D. Yaw, Pitch, Roll and Omega, Phi, Kappa Angles and Conversion. Pix4D Pproduct Documentation; Pix4D: Prilly, Switzerland, 2020; pp. 1–4. [Google Scholar]
- Pix4D. 1. Initial Processing > Calibration. Available online: https://support.pix4d.com/hc/en-us/articles/205327965-Menu-Process-Processing-Options-1-Initial-Processing-Calibration (accessed on 19 March 2020).
- Strecha, S.; Küng, O.; Fua, P. Automatic mapping from ultra-light UAV imagery. In Proceedings of the 2012 European Calibration and Orientation Workshop, Barcelona, Spain, 8–10 February 2012; pp. 1–4. [Google Scholar]
- Strecha, C.; Bronstein, A.M.; Bronstein, M.M.; Fua, P. LDAHash: Improved Matching with Smaller Descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 66–78. [Google Scholar] [CrossRef]
- Strecha, C.; von Hansen, W.; Van Gool, L.; Fua, P.; Thoennessen, U. On Benchmarking camera calibration and multi-view stereo for high resolution imagery. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Pix4D. Processing DJI Phantom 4 RTK Datasets with Pix4D. Available online: https://community.pix4d.com/t/desktop-processing-dji-phantom-4-rtk-datasets-with-pix4d/7823 (accessed on 17 March 2020).
- Natural Resources Canada’s Canadian Geodetic Survey. TRX Coordinate Transformation Tool. Available online: https://webapp.geod.nrcan.gc.ca/geod/tools-outils/trx.php?locale=en (accessed on 17 March 2020).
- Natural Resources Canada. Adopted NAD83(CSRS) Epochs. Available online: https://www.nrcan.gc.ca/earth-sciences/geomatics/canadian-spatial-reference-system-csrs/adopted-nad83csrs-epochs/17908 (accessed on 24 March 2020).
- Thomas, O.; Stallings, C.; Wilkinson, B. Unmanned aerial vehicles can accurately, reliably, and economically compete with terrestrial mapping methods. J. Unmanned Veh. Syst. 2019, 8, 57–74. [Google Scholar] [CrossRef]
- Nolan, M.; Larsen, C.; Sturm, M. Mapping snow depth from manned aircraft on landscape scales at centimeter resolution using structure-from-motion photogrammetry. Cryosphere 2015, 9, 1445–1463. [Google Scholar] [CrossRef]
- Gautam, D.; Lucieer, A.; Bendig, J.; Malenovský, Z. Footprint Determination of a Spectroradiometer Mounted on an Unmanned Aircraft System. IEEE Trans. Geosci. Remote Sens. 2019, 1–12. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landforms 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Pix4D. Internal Camera Parameters Correlation. Available online: https://support.pix4d.com/hc/en-us/articles/115002463763-Internal-Camera-Parameters-Correlation (accessed on 20 March 2020).
- Stamatopoulus, C.; Fraser, C.; Cronk, S. Accuracy aspects of utilizing RAW imagery in photogrammetric measurement. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B5, 387–392. [Google Scholar] [CrossRef]
- Tisse, C.-L.; Guichard, F.; Cao, F. Does Resolution Really Increase Image Quality? SPIE: Bellingham, WA, USA, 2008; Volume 6817. [Google Scholar]
- Jaud, M.; Passot, S.; Le Bivic, R.; Delacourt, C.; Grandjean, P.; Le Dantec, N. Assessing the Accuracy of High Resolution Digital Surface Models Computed by PhotoScan® and MicMac® in Sub-Optimal Survey Conditions. Remote Sens. 2016, 8, 8060465. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Wallace, L. Direct Georeferencing of Ultrahigh-Resolution UAV Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2738–2745. [Google Scholar] [CrossRef]



| UAS | Takeoff Weight (kg) | Study Site | Geotagging | Cost Category ($US) at Time of Purchase | Altitude AGL (m) | GNSS | Flight Controller Software |
|---|---|---|---|---|---|---|---|
| DJI Mavic Air | 0.430 | IGB | Onboard | <1000 | 45 | GPS L1, GLONASS F1 | Pix4D Capture |
| DJI Mavic Pro | 0.734 | MB | Onboard | <2000 | 35 | GPS L1, GLONASS F1 | DJI GSP |
| DJI Mavic 2 Pro + Hasselblad L1D-2C | 0.907 | MB | Onboard | <2000 | 35 | GPS L1, GLONASS F1 | DJI GSP |
| DJI Phantom 4 Pro | 1.39 | MB | Onboard | 2000–5000 | 35 | GPS L1, GLONASS F1 | DJI GSP |
| DJI Phantom 4 RTK ** | 1.39 | IGB | RTK | 5000–15,000 | 45 | GPS L1/L2 GLONASS F1/F2, Beidou B1/B2, Galileo E1/E5A | DJI GS RTK |
| Aeryon SkyRanger R60 + Sony DSC-QX30U | 2.4 | MB | Onboard | >100,000 | 35 | GPS L1 | Aeryon Flight Manager |
| DJI Inspire 1 + X3 | 3.06 | MB | Onboard | 2000–5000 | 30 | GPS L1 | DJI GSP |
| DJI Inspire 2 + X5S | 3.44 | MB | Onboard | 2000–5000 | 30 | GPS L1, GLONASS F1 | DJI GSP |
| DJI Matrice 210 RTK * | 5.51 | MB | Onboard | 5000–15,000 | 35 | GPS L1/L2 GLONASS F1/F2 | DJI GSP |
| DJI Matrice 600 Pro RTK * + X5 | 10 | Rigaud | Onboard | 5000–15,000 | 35 | GPS L1/L2 GLONASS F1/F2 | DJI GSP |
| DJI Matrice 600 Pro RTK * + DSLR | 14 | Rigaud | GP-E2 | 5000–15,000 | 45 | GPS L1 | DJI GSP |
| DJI Matrice 600 Pro RTK * + DSLR | 14 | Rigaud | PPKLB | 5000–15,000 | 45 | GPS L1/L2 GLONASS F1/F2 | DJI GSP |
| DJI Matrice 600 Pro RTK * + DSLR | 14 | Rigaud | PPKCB | 5000–15,000 | 45 | GPS L1/L2 GLONASS F1/F2 | DJI GSP |
| DJI Matrice 600 Pro RTK* + DSLR | 14 | Rigaud | PPKLB-NTRIP | 5000–15,000 | 45 | GPS L1/L2 GLONASS F1/F2 | DJI GSP |
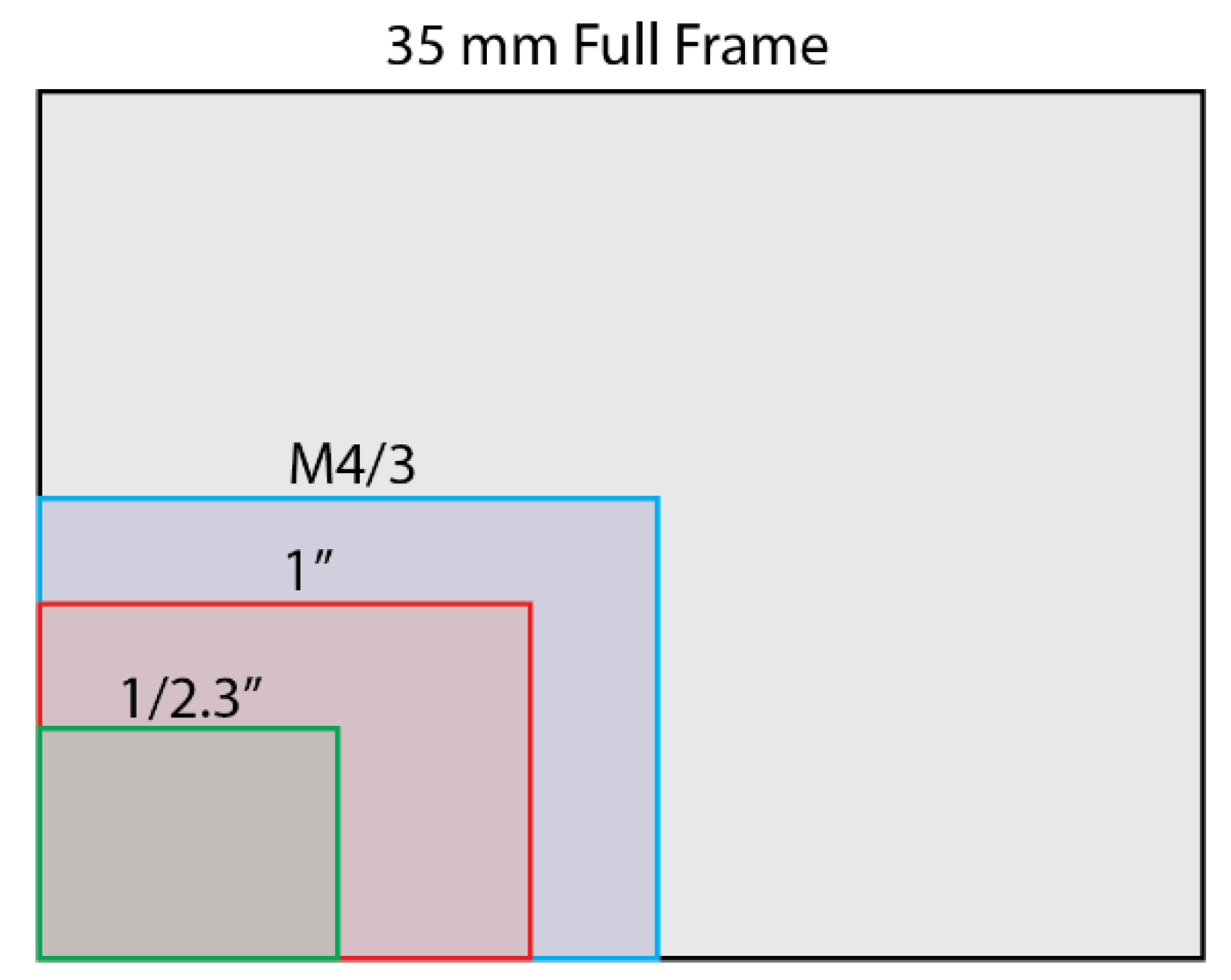
| UAS Camera | Sensor Size | Sensor Resolution (MP) | Image Size (px) | Pixel Size (μm) | FOV (°) |
|---|---|---|---|---|---|
| DJI Mavic Air | 1/2.3” | 12 | 4056 × 3040 | 1.50 | 85 |
| DJI Mavic Pro | 1/2.3” | 12 | 4000 × 3000 | 1.58 | 78.8 |
| X3 | 1/2.3” | 12.4 | 4000 × 3000 | 1.57 | 94 |
| Sony DSC-QX30U | 1/2.3” Exmor R | 20.2 | 5184 × 3888 | 0.99 * | 68.6 |
| Hasselblad L1D-2C | 1” | 20 | 5472 × 3648 | 2.35 | 77 |
| DJI Phantom 4 Pro | 1” | 20 | 4864 × 3648 | 2.35 | 84.8 |
| DJI Phantom 4 RTK | 1” | 20 | 5472 × 3648 | 2.35 | 84 |
| X5S | M4/3 | 20.8 | 5280 × 3956 | 3.3 | 72 |
| X5 | M4/3 | 16 | 4608 × 3456 | 3.8 | 72 |
| Canon 5D Mark III | FF 36 × 24 mm CMOS sensor | 22.1 | 5760 × 3840 | 6.25 | 84 |
| Trial | Calibration | Initial FL (mm) | Optimized FL (mm) | RMSEx (m) | RMSEy (m) | RMSEr (m) | RMSEz (m) |
|---|---|---|---|---|---|---|---|
| 1 | All | 8.57976 * | 8.494 | 0.028558 | 0.022756 | 0.037 | 0.182723 |
| 2 | All prior | 8.57976 * | 8.576 | 0.029126 | 0.023656 | 0.038 | 0.251885 |
| 3 | All prior | 8.56976 | 8.567 | 0.029048 | 0.023551 | 0.037 | 0.201478 |
| 4 | All prior | 8.55976 | 8.557 | 0.028982 | 0.023446 | 0.037 | 0.150739 |
| 5 | All prior | 8.54976 | 8.547 | 0.02891 | 0.023342 | 0.037 | 0.100179 |
| 6 | All prior | 8.53976 | 8.538 | 0.028852 | 0.023239 | 0.037 | 0.050315 |
| 7 | All prior | 8.52976 | 8.528 | 0.028788 | 0.023137 | 0.037 | 0.0144 |
| 8 | All prior | 8.51976 | 8.518 | 0.028724 | 0.023037 | 0.037 | 0.055332 |
| 9 | All prior | 8.50976 | 8.509 | 0.028661 | 0.022939 | 0.037 | 0.105318 |
| 10 | All prior | 8.49976 | 8.499 | 0.028598 | 0.02284 | 0.037 | 0.15587 |
| 11 | All prior | 8.48976 | 8.489 | 0.028536 | 0.022743 | 0.036 | 0.20669 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalacska, M.; Lucanus, O.; Arroyo-Mora, J.P.; Laliberté, É.; Elmer, K.; Leblanc, G.; Groves, A. Accuracy of 3D Landscape Reconstruction without Ground Control Points Using Different UAS Platforms. Drones 2020, 4, 13. https://doi.org/10.3390/drones4020013
Kalacska M, Lucanus O, Arroyo-Mora JP, Laliberté É, Elmer K, Leblanc G, Groves A. Accuracy of 3D Landscape Reconstruction without Ground Control Points Using Different UAS Platforms. Drones. 2020; 4(2):13. https://doi.org/10.3390/drones4020013
Chicago/Turabian StyleKalacska, Margaret, Oliver Lucanus, J. Pablo Arroyo-Mora, Étienne Laliberté, Kathryn Elmer, George Leblanc, and Andrew Groves. 2020. "Accuracy of 3D Landscape Reconstruction without Ground Control Points Using Different UAS Platforms" Drones 4, no. 2: 13. https://doi.org/10.3390/drones4020013
APA StyleKalacska, M., Lucanus, O., Arroyo-Mora, J. P., Laliberté, É., Elmer, K., Leblanc, G., & Groves, A. (2020). Accuracy of 3D Landscape Reconstruction without Ground Control Points Using Different UAS Platforms. Drones, 4(2), 13. https://doi.org/10.3390/drones4020013