Driving and Sensing M/NEMS Flexural Vibration Using Dielectric Transduction ^†

Abstract

We show that nanometer-scale dielectric thin films can act as efficient electromechanical transducers to simultaneously drive and sense the vibration of the first flexural mode of micro/nano-cantilevers. Here, 16 μm-long, 5 μm-wide and 350 nm-thick cantilevers are actuated by a 15 nm-thick silicon nitride layer, and electrically detected by charge measurement at megahertz frequencies. The displacement was also checked by optical interferometry, and the electromechanical transduction efficiency is extracted and compared to an analytical modelling.

1. Introduction

NEMS devices offer great opportunities for applications in metrology and fundamental science, particularly when used as resonators [1]. However as the size is reduced, devices face the challenge of the efficiency of the electromechanical transduction. Capacitive and piezoelectric principles are commonly used in MEMS devices for both actuation and detection. At nanometer scale, issues are met. For example, piezoelectric actuation is dramatically impacted when the layer thickness is reduced under 100 nm, leading to a decrease in efficiency by orders of magnitude compared to the one expected from the bulk piezoelectric properties [2]. Besides, capacitive transduction strongly depends on the airgap width and a trade-off has to be made between efficiency and risk of failure due to stiction resulting from narrow air gaps. Conversely, high-K materials made for example by Atomic Layer Deposition (ALD) techniques are available in very thin films (<10 nm) and with a high quality. Such materials are compatible with silicon microtechnologies fabrication processes and make dielectric transduction a promising alternative for sensing and driving displacements at nanoscale. Actuation and detection have first been reported separately on cantilevers at a millimeter scale [3]. Recently, actuation has also been observed for micrometer scale devices [4]. Here, we report the simultaneous actuation and detection of MEMS/NEMS cantilever devices using high-K thin films as the electromechanical transducer.

2. Materials and Methods

In the present study, we used a 15 nm-thick low-stress silicon nitride film as the dielectric active layer. Its dielectric constant ε_d is about 8 and its Poisson’s ratio υ_d is 0.23. It was deposited using low-pressure chemical vapor deposition (LPCVD) on a doped silicon-on-insulator wafer etched beforehand to create air bridges along the signal paths to reduce extra parasitic capacitances to ground. A 20 nm-thick chromium layer was used as a top electrode. The 5 μm-wide and 16 μm-long cantilevers were patterned from this stack using chemical and reactive ion etchings and released by chemical etching of the buried oxide.

We perform actuation of the device using a bias voltage V_DC added to an alternative signal V_AC applied to the chromium electrode, across the dielectric thin film. Frequency of the alternative signal varies close to the fundamental mode resonance frequency. Simultaneously, we use differential excitation (−V_AC) of a reference cantilever to subtract from the signal the parasitic coupling due to the cantilever static capacitance. Resulting motional charges are then detected and amplified with a 10 V/pC gain and the resulting signal is processed using a network analyzer. To validate the charge detection, we also measure the resonance frequency by Fabry-Perot interferometry: a laser beam is reflected both by the vibrating resonator and the substrate. The resulting interferometry signal is modulated by the vibration, and detected by a photodiode for frequency response analysis. All the measurements are made at room temperature and under vacuum (P = 2.10⁻¹ mBar). Schematic cross-section, example of a fabricated device and measurement set-up are shown in Figure 1.

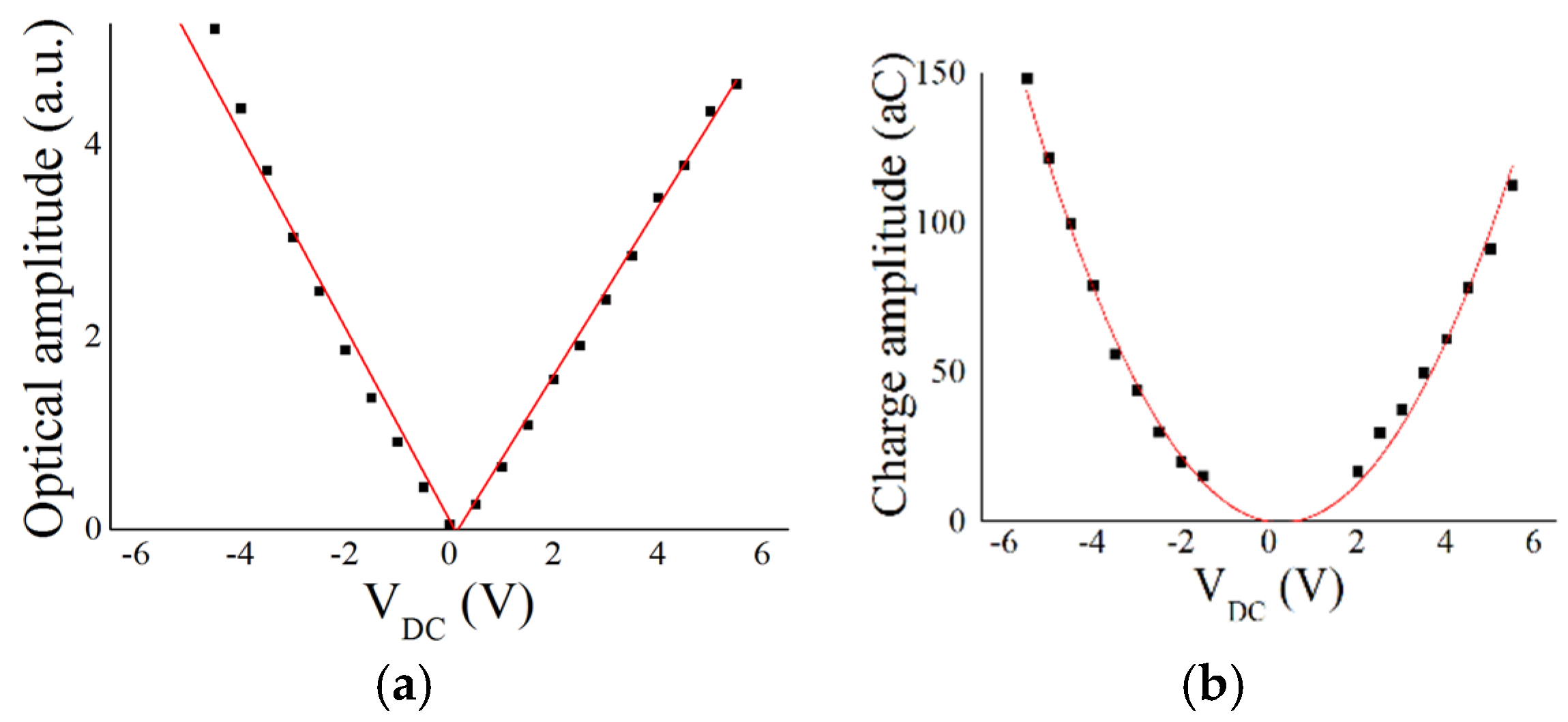
3. Results

The 5 μm × 16 μm device is tested applying a 600 mV V_AC signal and a V_DC bias ranging from −5 to 5 V. Optical and capacitive measurements have similar features: a 1.441 MHz resonance frequency, and a quality factor Q of 2200. Figure 2 shows an example of capacitive and optical amplitude and phase measurements for V_DC = −5 V (a), and optical (b) and capacitive (c) amplitude frequency responses in magnitude versus V_DC.

4. Discussion

The dielectric actuation exploits electrostatic pressure on the dielectric film, which depends on the square of the voltage applied across the film. As we use a superposition of V_DC and V_AC, we expect the vibration amplitude at resonance frequency to be linear with V_DC. Similarly, as the electrical detection principle is based on the variation of charges in the capacitor formed by the device, the detected charge is proportional to the V_DC bias. Consequently, during simultaneous actuation and detection, the measured charge variation has a parabolic dependence versus the bias. The Figure 3 shows the optical and charge measurements fitted with linear and parabolic functions respectively.

For V_DC = −5 V and V_AC = 600 mV, and taking into account the oxide over etching, the expected variation of charge is 195 aCI as calculated by an analytical approach inspired from Reference [5]:

$$Q_m\left(f_{res}\right)=\frac{Q}{K_{eff}}{\left[0.68\frac{ew}{t}\frac{{\nu }_d}{1-{\nu }_d}{ϵ}_0{ϵ}_d{V}_{DC}\right]}^2{V}_{AC}$$

(1)

where the thickness and width of the cantilever are respectively e = 320 nm and w = 5 µm, and the thickness, Poisson ratio, and dielectric coefficient of the silicon nitride layer are t = 15 nm, υ_d = 0.23, and ε_d ≈ 8 respectively.

The measured charge for these driving conditions is 125 ± 25 aC, which is slightly lower than the theoretical value. From this measurement, and using a calibration of the optical set-up based on the thermomechanical noise method, we can calculate the transduction efficiency of the device, defined as the ratio between the beam displacement and its charge: 𝜂 = 361 ± 70 pN/V. Again, the result is comparable to the theoretical value, 452 pN/V, obtained using the Reference [5] approach:

$$\eta =0.68\frac{ew}{Lt}\frac{{\nu }_d}{1-{\nu }_d}{ϵ}_0{ϵ}_d{V}_{DC}.$$

(2)

The 20% difference between the two values can be explained by measurements uncertainties and by the fact that the chromium electrode does not cover exactly the whole cantilever surface.

Table 1. Summary of the device and dielectric transducer parameters.

Cantilever Parameters		Transducer Parameters
Length	16 µm	Material	Si nitride
Width	5 µm	Thickness	15 nm
Si thickness	320 nm	Permittivity	εd ≈ 8
Eff. stiffness	1.38 N/m	Transducer efficiency theoret.	452 pN/V at VDC = −5 V
fres analytic.	1.45 MHz
fres experim.	1.441 MHz	Transducer efficiency exp.	361 pN/V at VDC = −5 V
Q factor	2200
Qm theror. Charge at VDC = −5 V, VAC = 600 mV	195 aC
Qm exp.charge at VDC =−5 V, VAC = 600 mV	125 aC

summarizes the results and the main parameters of the cantilever device and its dielectric transducer.

5. Conclusions

To conclude, simultaneous dielectric actuation and detection were successfully demonstrated for flexural devices with a nanometer scale active layer thickness. Results are in a good agreement with theoretical calculations, including the transduction efficiency. Using high-K thin-film materials with higher dielectric constants such as Al₂O₃ (ε_d = 9) and HfO₂ (ε_d = 20) would be a promising way to achieve efficient actuation and detection with even greater efficiencies. Such devices are currently under fabrication and will be presented in a later study.