Ensemble Mean Dynamics of the ENSO Spatiotemporal Oscillator with Fractional Stochastic Forcing

Abstract

This study investigates the impact of long-term memory stochastic forcing on the ensemble mean dynamics of the El Niño–Southern Oscillation (ENSO) by incorporating a fractional Ornstein-Uhlenbeck (FOU) process as external forcing into an ENSO spatiotemporal oscillator (STO) conceptual model. Unlike the classic Ornstein-Uhlenbeck (OU) process, the FOU process exhibits a slow power-law decay in auto-correlation and can trigger an anomalous growth rate that persistently influences the divergence/dissipation of the ensemble mean system. Furthermore, theoretical and quantitative analyses verify that the anomalous growth rate is determined by the ensemble mean of the FOU process, reflecting the cumulative nature of long-memory forcing. Crucially, the anomalous growth rate is positive and thus induces system divergence when the FOU process exhibits a positive ensemble mean, whereas it is negative and induces dissipation when the ensemble mean is negative. Also, the anomalous growth rate intensifies with decreasing fractional order. On the other hand, FOU forcing can also modulate the phase of the ensemble mean oscillation for ENSO. When the phases of the natural and forced oscillations are in phase alignment, the phase of the ensemble mean oscillation leads relative to the natural oscillation. Conversely, when the phases of the natural and forced oscillations are in anti-phase alignment, the phase of the ensemble mean oscillation lags behind relative to the natural oscillation. Future work would address the case when the external forcing has a spatial structure and seek observational validation of the identified growth rate signatures and phase shifts.

1. Introduction

Atmospheric activities, characterized by rapid and high-frequency variability, are generally considered stochastic forcing of the El Niño Southern Oscillation (ENSO) and play a significant role in influencing ENSO development [1,2,3]. To date, numerous studies support the hypothesis that the diversity, asymmetry, and irregularity of ENSO are closely linked to these atmospheric forcings [4,5,6,7]. Meanwhile, atmospheric activities such as Westerly Wind Bursts (WWBs) can not only advect warm water equatorward and eastward, extending the eastern edge of the warm pool, but also excite eastward downwelling equatorial Kelvin waves, which lead to surface warming in the eastern equatorial Pacific [8,9]. Therefore, investigating the interactions between atmospheric stochastic forcing and ENSO is of significant scientific value.

A common approach in theoretical analyses involves integrating the Ornstein-Uhlenbeck (OU) process, a Gaussian process characterized by an exponentially decaying ensemble mean and auto-correlation function that represent short-memory characteristics, into the ENSO conceptual recharge oscillator (RO) model as stochastic forcing [10,11,12]. Specifically, Jin et al. demonstrated that such forcing can significantly alter the evolution of the ENSO system, amplify ensemble spread, and induce systematic drift in the ensemble mean state [10]. Building upon this theoretical framework, they further explored noise-induced instability and irregularity of ENSO [11,12]. These advancements have greatly enhanced our understanding of ENSO temporal complexity. However, two key questions remain unresolved.

The first unresolved issue is that the OU process cannot adequately represent all types of real-world random forcings, particularly those exhibiting long-term memory (LTM) [13,14]. In fact, LTM is widely observed in climate variability [15,16,17,18], indicating that current climatic states may exert persistent influences on the distant future, especially when modulated by slow-response systems such as the oceans [19]. Under such conditions, the OU process often fails to accurately simulate complex climatic time series. For instance, recent research has shown that interannual timescale climate memory plays a crucial role in the arising of the early warningwarning signals during Pacific Decadal Oscillation phase transitions [20].

Thus, investigating the impacts of LTM processes on ENSO is highly significant and necessitates the development of a new mathematical framework. Recently, the fractional OU (FOU) process has been integrated into the classic RO model to examine the influence of stochastic processes with LTM [21]. Theoretical analysis demonstrates that the non-zero ensemble mean of the FOU process over the integration period significantly affects the ensemble mean dynamics of the RO model.

The second limitation is that the RO framework cannot address the inherent spatial complexity of ENSO due to its lack of spatial variability. To comprehensively capture the spatiotemporal complexity, a spatiotemporal oscillator (STO) model for ENSO has been developed [22]. The model is built on comprehensive thermodynamics and thermocline depth dynamics of the equatorial Pacific, effectively ensuring the spatiotemporal continuity of the ENSO system and providing robust physical explanations for its quasi-quadrennial (QQ) and quasi-biennial (QB) modes [22], as well as phase-locking [23].

Based on the STO model, we had established a stochastic STO model by incorporating a state-dependent OU process as external forcing [24]. Theoretical analysis indicates that the spatiotemporal OU process modulates ensemble mean dynamics through two distinct mechanisms: (i) persistent harmonic oscillations with frequencies matching the natural frequency of the original deterministic STO model; and (ii) transient damping oscillations that only affect short sub-seasonal timescales and become negligible for longer-term variability. This noise-induced drift in the ENSO ensemble mean bridges scale interactions from synoptic-scale stochastic forcing to interannual variability, providing a novel capability to simulate ENSO’s characteristic amplitude-phase modulations within a unified dynamical framework.

Note that previous studies either focused on LTM characteristics while neglecting spatial structure [21] or emphasized spatiotemporal variability without considering LTM features [24]. By combining the strengths of these two approaches, this paper further explores the influence of LTM stochastic forcing on ENSO ensemble mean dynamics by integrating the FOU process into the STO model. Following this introduction, Section 2 describes the stochastic STO model forced by the FOU process. Section 3 presents the results generated by our modeling framework. Section 4 provides quantitative analysis of the anomalous growth rate induced by the FOU process, while Section 5 offers theoretical explanations of its phase modulation effects. Finally, Section 6 concludes with summary remarks.

2. Method

Consistent with our previous investigation [21], we focus on the FOU process obtained from the fractional Langevin equation (e.g., [25,26]) by replacing the time derivative with a Caputo-type fractional derivative of order $\alpha$, that is

$${\mathrm{d}}^{\left(\alpha \right)}\xi =-r\xi \mathrm{d}t+\mathrm{d}W\left(t\right),$$

(1)

where $\xi \left(t\right)$ denotes the FOU process. $r>0$ is a constant damping coefficient. $W\left(t\right)$ represents standard Brownian motion (or called the Wiener process), and $\mathrm{d}W$ denotes Gaussian white noise. ${\mathrm{d}}^{\left(\alpha \right)}\xi$ indicates the Caputo-type fractional derivative with respect to time $t$ where the superscript $\alpha$ ($0<\alpha <1$) denotes the fractional derivative order. Specifically, if $\alpha =1$, Equation (1) reduces to the classic Langevin equation and the FOU process reduces to the classic OU process. Referring to [27], the solution to Equation (1) is

$$\xi \left(t\right)={\xi }_0{E}_{\alpha ,1}\left(-r{t}^{\alpha }\right)+{\displaystyle {\int }_0^t{\left(t-s\right)}^{\alpha -1}{E}_{\alpha ,\alpha }\left[-r{\left(t-s\right)}^{\alpha }\right]dW\left(s\right)},$$

(2)

where ${\xi }_0=\xi \left(0\right)$ is the initial value and $E_{\alpha ,\beta }\left(z\right)\triangleq {\displaystyle \sum _{k=0}^{\infty }\frac{z^k}{\Gamma \left(\alpha k+\beta \right)}}$ $z,\alpha ,\beta \in C,\mathrm{Re}\left(\alpha \right)>0$ where $C$ denotes the set of complex numbers and $\mathrm{Re}\left(\alpha \right)$ denotes the real part of $\alpha$ is the Mittag-Leffler function with $\alpha ,\beta$ as two parameters [27] and $\Gamma \left(z\right)\triangleq {\displaystyle {\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt}$ is Gamma function.

Incorporating the FOU process as the external forcing, the stochastic STO model can be written as following:

$$\left\{\begin{array}{l}{\displaystyle \frac{𝜕T}{𝜕t}}+\hspace{0.33em}{K}_{h}h=\sigma \xi G\hspace{0.33em}\\ {\displaystyle \frac{𝜕h}{𝜕t}}+\hspace{0.33em}Hb{\displaystyle \frac{{𝜕}^{2}T}{𝜕x^2}}=0\hspace{0.33em}\end{array}\right.,$$

(3)

where $T$ and $h$ represent the sea surface temperature anomaly (SSTA) and the thermocline depth anomaly (TDA), respectively; $K_h$ represents the delayed response of the thermocline depth anomaly to the local wind stress forcing; $H$ is the climatological mean depth of the mixed layer and $b$ is the coupling coefficient between the zonal ocean current anomaly and SSTA gradients. $\xi \left(t\right)$ here denotes a dimensionless FOU process with weight coefficient $\sigma$ (the unit is ${\mathrm{K} \mathrm{s}}^{-1}$); $G=1+BT$ determines the nature of the external forcing: when $B=0$ the system is forced by additive noise while when $B\ne 0$ (typically set to one) the system is forced by multiplicative noise [10]. It is important to note that Equation (3) fundamentally differs from the previous stochastic RO model [21], despite both employing the same FOU process as external forcing. The inherent difference arises from the distinction between the RO model and the STO model, with the latter being considered a spatial extension of the former.

Due to the introduction of multiplicative noise, deriving an analytic solution to Equation (3) is challenging. Consequently, ensemble mean dynamics become a useful technique for conducting semi-theoretical analysis. Therefore, we derive the ensemble mean solution to the equation by separating variables into ensemble means and departures as follows:

$$T=〈T〉+T^{\prime },h=〈h〉+h^{\prime }.$$

(4)

Substituting Equation (4) into Equation (3) and taking the ensemble mean, we can derive the ensemble mean equations as following:

$$\left\{\begin{array}{l}{\displaystyle \frac{𝜕〈T〉}{𝜕t}}+K_h〈h〉=\sigma \left(〈\xi 〉+B〈\xi 〉〈T〉+B〈\xi T^{\prime }〉\right)\\ {\displaystyle \frac{𝜕〈h〉}{𝜕t}}+Hb{\displaystyle \frac{{𝜕}^2〈T〉}{𝜕x^2}}=0\end{array}\right..$$

(5)

The system remains unclosed due to the presence of the second-order moment $〈\xi T^{\prime }〉$, whose governing equation displays damped oscillation behavior (cf. [24]). This oscillation may still exert its influence if the ensemble mean of the FOU process ($〈\xi 〉$ and $B〈\xi 〉〈T〉$ terms) can be neglected, as was done in the previous investigation [24]. However, according to Equation (2)

$$〈\xi 〉={\xi }_0{E}_{\alpha ,1}\left(-r{t}^{\alpha }\right),$$

(6)

which suggests that the ensemble mean of the FOU process converges to zero with a power-law decay as time increases, in contrast to the OU process ensemble mean, which exhibits exponential decay. This implies that the FOU process ensemble mean can exert influence over longer timescales, rather than being discarded as in the case of the OU process [24]. Moreover, the persistent forcing effect of the FOU ensemble mean surpasses the second-order moment, rendering it negligible. Consequently, we close the system by disregarding the second-order moment. This methodology is akin to expanding the means as a Taylor series in time and retaining only the most significant terms (e.g., [28]). We also conduct a 500-member Monte Carlo simulation on Equation (3) to verify this second-order moment closure scheme.

By eliminating $〈h〉$ from Equation (5), we can readily derive a wave equation for $〈T〉$ as

$${\displaystyle \frac{{𝜕}^2〈T〉}{𝜕t^2}}-\sigma B〈\xi 〉{\displaystyle \frac{𝜕〈T〉}{𝜕t}}-c^2{\displaystyle \frac{{𝜕}^2〈T〉}{𝜕x^2}}-\sigma B{\displaystyle \frac{𝜕〈\xi 〉}{𝜕t}}〈T〉=\sigma {\displaystyle \frac{𝜕〈\xi 〉}{𝜕t}},$$

(7)

where $c=\sqrt{K_{h}Hb}$ is the constant wave speed. According to Equation (7), the ensemble mean of the FOU process influences the ensemble mean oscillation through two distinct mechanisms: firstly, it directly forces the ensemble mean oscillation as an external forcing term (the right-hand side (RHS) term); secondly, it modulates the constitutive properties of the ensemble mean oscillation by altering the coefficients.

According to Li [22], the free boundary conditions are set to:

$${\left.{\displaystyle \frac{𝜕〈T〉}{𝜕x}}\right|}_{x=0,L}=0,$$

(8)

where $L$ is the basin width of the equatorial Pacific. The initial values are set to:

$${\left.T\right|}_{t=0}=F\left(x\right),{\left.h\right|}_{t=0}=G\left(x\right),$$

(9)

where $F$ and $G$ are known functions. To seek analytic solution, we expand $〈T〉$ as

$$〈T〉={\displaystyle \frac{1}{2}}{T}_0\left(t\right)+{\displaystyle \sum _{n=1}^{\infty }{T}_n\left(t\right)}\cos {\lambda }_{n}x,$$

(10)

where ${\lambda }_n=n\pi /L$, $n=1,2,\cdots$ is the eigenvalue and $T_n\left(t\right)$ is the temporally variation in the n-th eigenmode. Substituting Equation (10) into Equation (7), we can easily derive a second-order ordinary differential equation for $T_n,n=1,2,\cdots$, that is

$${\displaystyle \frac{{\mathrm{d}}^2{T}_n}{\mathrm{d}{t}^2}}-\sigma B〈\xi 〉{\displaystyle \frac{\mathrm{d}{T}_n}{\mathrm{d}t}}+\left({\omega }_n^2-\sigma B{\displaystyle \frac{\mathrm{d}〈\xi 〉}{\mathrm{d}t}}\right)T_n=0.$$

(11)

where ${\omega }_n=c{\lambda }_n$ is the time-independent natural frequency of the original STO model. Note that this second-order ordinary differential equation features time-dependent stiffness and damping terms that are associated with the ensemble mean of the FOU process and its derivative. Due to the complex form, it is impossible to derive the analytic solution to Equation (11). Therefore, we thereafter resort to numerical solutions using the Runge–Kutta method.

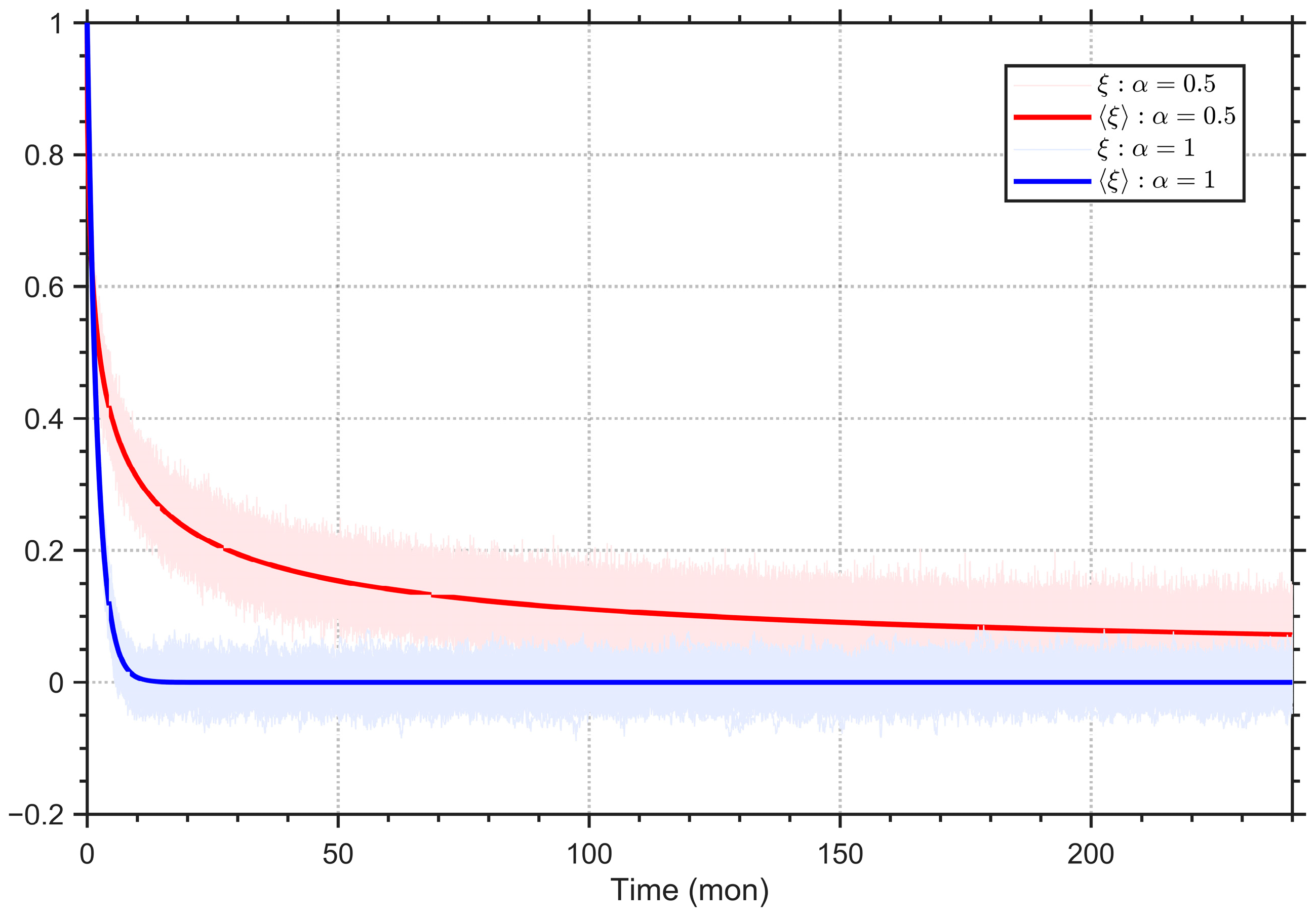
Prior to this, we first elaborate on the key distinctions between the classic OU and FOU processes from two perspectives. Although both processes exhibit a decaying trend (Figure 1), they exhibit fundamentally divergent dynamical properties. The classic OU process undergoes exponential decay toward zero, whereas the FOU process follows power-law decay kinetics and maintains persistent oscillations around a non-zero mean level over extended timescales. 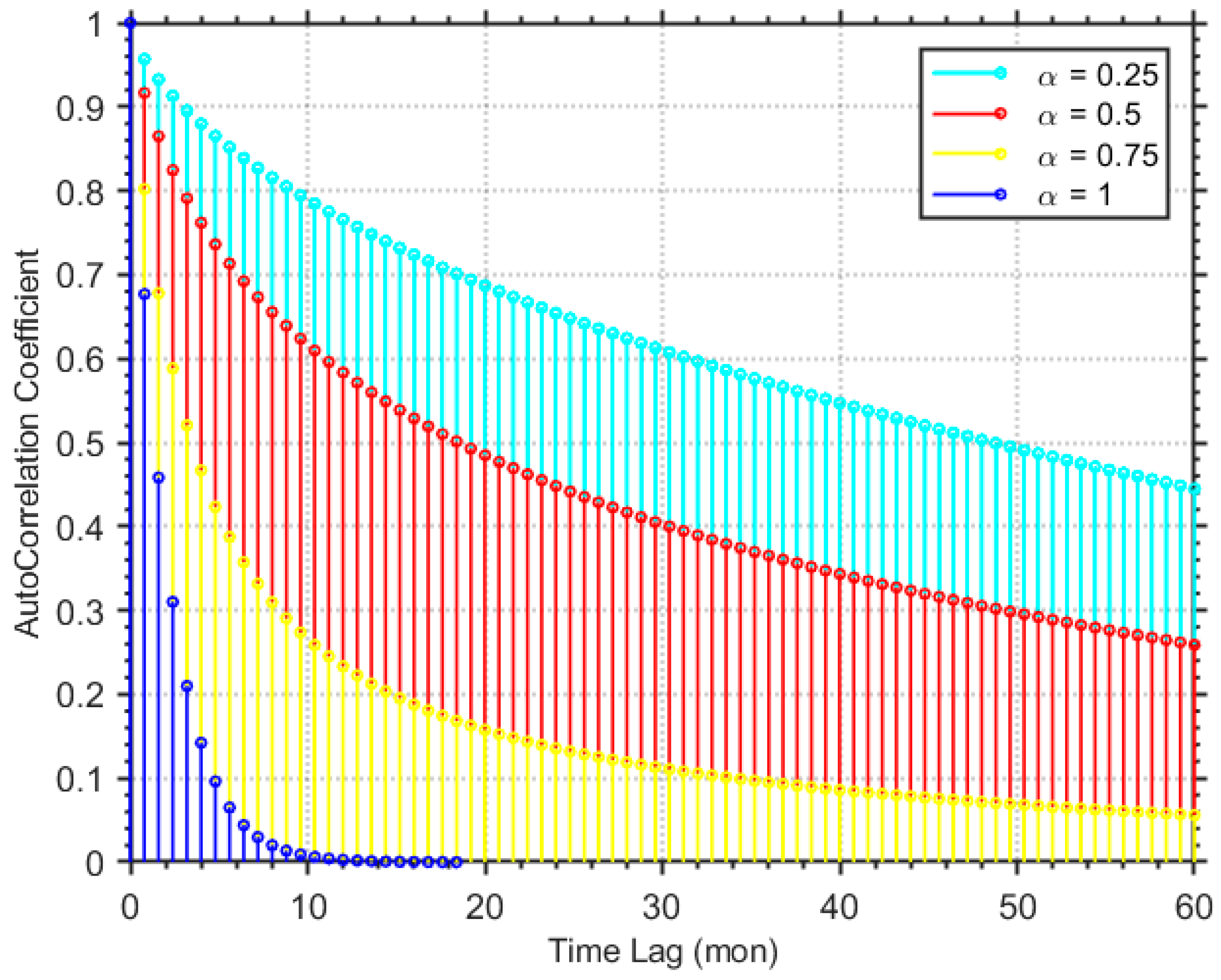Distinct auto-correlation properties constitute another key different feature between them (Figure 2). The persistent long-range auto-correlation inherent to FOU processes serves as a fundamental manifestation of their long-memory characteristics, contrasting sharply with the rapidly decaying auto-correlation exhibited by classical OU process.

3. Results

According to Equation (11), the influence of the ensemble mean of the FOU process is universally applicable to all eigenmodes. Consequently, we concentrate exclusively on the most dominant mode ($n=1$), which signifies the SSTA contrast between the eastern and western Pacific. The initial values for $〈T〉$ and $〈h〉$ are set to 1 K and 0 m, respectively. The value of parameter $B$ is set to 1 K⁻¹, representing a composite of both additive and multiplicative stochastic forcing effects.

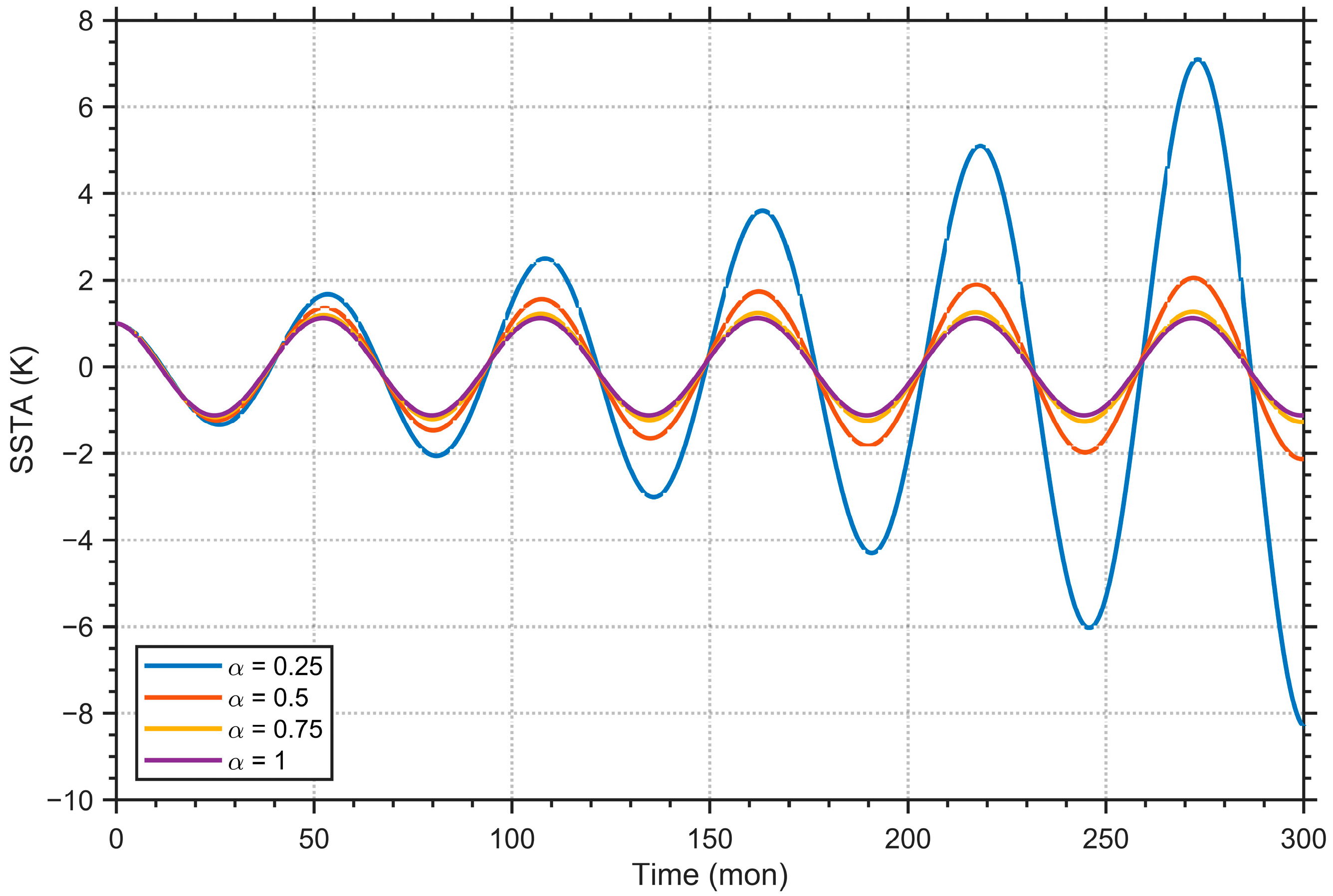
Figure 3 illustrates the temporal evolution of the first eigenmode ($T_1$) under the influence of various FOU processes, each characterized by a fixed fractional order $\alpha =1/2$ but with different initial values ${\xi }_0$. It shows that the introduction of the FOU process can cause an anomalous growth rate, the sign of which is dictated by the sign of ${\xi }_0$. Positive anomalous growth rates can lead to system divergence, whereas negative values result in dissipation. The stable regime (${\xi }_0=0$) serves as the critical transitional state that bridges these opposing behaviors. It is also notable that the introduction of the FOU process results in distinct phase modulation. Compared to the unforced baseline case, the forced outcomes display symmetric phase shifts: phase advance in the case of divergence and phase lag for dissipation. To validate the second-order moment closure scheme, the results of a 500-member Monte Carlo simulation that directly solves Equation (5) are also depicted in Figure 3. The results from the two methods show near-perfect agreement across three different initial values, strongly supporting the omission of second-moment terms as an accurate simplification within our framework.

As shown in Figure 4, the anomalous growth rate is modulated by the fractional order. When compared to the classic OU process (equivalent to $\alpha =1$), a smaller fractional order results in a more pronounced anomalous growth rate. Notably, the significantly stronger amplitude for the $\alpha =1/4$ case (the blue curve in Figure 4) further indicates a nonlinear relationship between the anomalous growth rate and the fractional order.

Generally speaking, the implementation of the FOU process primarily alters amplitude and phase characteristics; furthermore, the modifications to amplitude are more pronounced than those observed in our previous research [24], which utilized the OU process to drive the STO model. This difference can be clearly attributed to the FOU process, aligning with our intuitive expectation that long-memory processes may exert stronger effects than their short-memory counterparts. To further quantitatively characterize these effects, we next develop theoretical explanations for the anomalous growth rates and phase shifts.

4. Quantifying Anomalous Growth Rate

As previously established, the introduction of the FOU process initiates an anomalous growth rate that exhibits an intrinsic quantitative dependence on the fractional order $\alpha$. In fact, this anomalous growth rate is quantitatively linked to the FOU process itself, thereby inheriting its dependence on the fractional order $\alpha$.

If we perform a transformation for $T_n$ as

$$T_n\left(t\right)=A\left(t\right)u_n\left(t\right),$$

(12)

where

$$A\left(t\right)=\exp \left({\displaystyle {\int }_0^t\frac{\sigma B〈\xi \left(\tau \right)〉}{2}d\tau }\right).$$

(13)

By substituting Equation (13) into Equation (11), we can transform Equation (11) to

$${\displaystyle \frac{{\mathrm{d}}^2{u}_n}{\mathrm{d}{t}^2}}+{\omega }_d^2\left(t\right)u_n=0,$$

(14)

where ${\omega }_d=\sqrt{{\omega }_n^2-{\displaystyle \frac{\sigma B}{2}}{\displaystyle \frac{\mathrm{d}〈\xi 〉}{\mathrm{d}t}}-{\displaystyle \frac{{\sigma }^2{B}^2}{4}}{〈\xi 〉}^2}$ is the time-varying frequency. To make sure oscillatory solution, ${\omega }_d^2$ should be larger than zero. When time is sufficiently large, ${\omega }_d\to {\omega }_n$ such that Equation (14) asymptotically approaches a standard wave equation with a time-independent natural frequency ${\omega }_n$. On the other hand, $A\left(t\right)$ functions to modulate the amplitude envelope. According to Equation (13), the anomalous growth rate induced by the FOU process can be quantitatively defined as

$$\epsilon \left(t\right)\triangleq {\displaystyle \frac{\sigma B}{2}}〈\xi 〉={\displaystyle \frac{\sigma B}{2}}{\xi }_0{E}_{\alpha ,1}\left(-r{t}^{\alpha }\right).$$

(15)

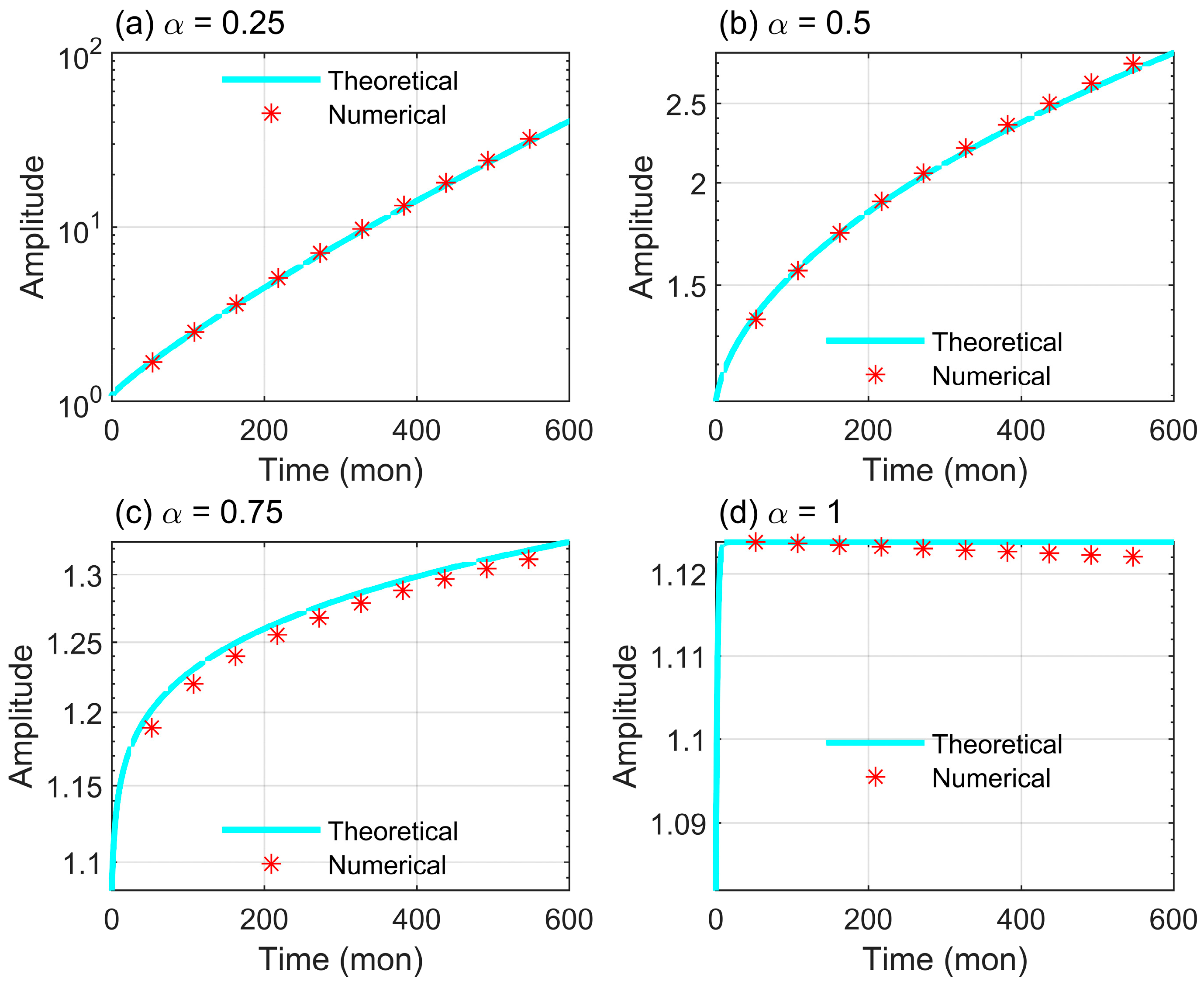
Since $E_{\alpha ,1}\left(-r{t}^{\alpha }\right)$ is strictly positive for $t>0$, the sign of $\epsilon$ is solely determined by the sign of ${\xi }_0$. This implies that the positivity or negativity of the initial value of the FOU process dictates whether the system exhibits divergence or dissipation. Additionally, since both $\sigma$ and $B$ are constants, the temporal variation in the anomalous growth rate is merely the ensemble mean of the FOU process, which exhibits a power-law decay feature as time increases. At this juncture, we establish a direct coupling between the anomalous growth rate and the ensemble mean of the FOU process. To verify the aforementioned theoretical analysis, we further compare the cumulative amplitude growth computed via Equation (13) with the numerical values in Figure 4. The results (Figure 5) demonstrate excellent agreement between theoretical analysis and numerical calculation. Physically, the cumulative amplitude growth reflects the persistent forcing exerted by the FOU process on ENSO ensemble mean dynamics. Such forcing resists rapid decay due to the power-law decay characteristic of the FOU process ensemble mean, thereby manifesting as progressively intensifying dynamical disorder.

5. Phase Shift

We further develop a theoretical elaboration for the phase shift induced by variations in the initial values of the FOU process. According to Equation (14), $T_n$ can be decomposed into a quasi-sinusoidal oscillation $u_n$ upon excluding amplitude envelope fluctuation $A\left(t\right)$. Furthermore, $u_n$ will asymptotically converge to a standard sinusoidal oscillation with frequency ${\omega }_n$ and phase ${\varphi }_n$, labeled as $T_n^s$ for convenience. Building on our previous investigation [24], we can further decompose $T_n^s$ into two components: (i) a standard sinusoidal oscillation with frequency ${\omega }_n$ and phase ${\theta }_n$, which represents the intrinsic oscillation in the absence of stochastic forcing (hereafter referred to as the natural oscillation); and (ii) a standard sinusoidal oscillation that characterizes the influence of stochastic forcing (hereafter referred to as the forced oscillation). For the forced oscillation, its initial phase ${\phi }_n$ will be modulated to ${\phi }_n+\pi /2$ as demonstrated in our previous investigation [24]. With these preliminaries, we express

$$T_n^s\sim {\Phi }_n\sin \left({\omega }_{n}t+{\varphi }_n\right)=D_n\sin \left({\omega }_{n}t+{\theta }_n\right)+X_n\sin \left({\omega }_{n}t+{\phi }_n+\pi /2\right),$$

(16)

where ${\Phi }_n,D_n,X_n$ are amplitudes for $T_n^s$ and its natural and forced components, respectively.

We can easily obtain the following relationships:

$${\Phi }_n^2=D_n^2+X_n^2+2D_n{X}_n\sin \left({\theta }_n-{\phi }_n\right),$$

(17)

$${\varphi }_n=\arccos {\displaystyle \frac{D_n\cos {\theta }_n-X_n\sin {\phi }_n}{{\Phi }_n}}.$$

(18)

The phase of natural oscillation has been set to ${\theta }_n=\pi /2$ (denoted by $T_n\left(0\right)=1,h_n\left(0\right)=0$). It is challenging to specify the initial phase of forced oscillation directly. Here, we identify it through physical understanding. When the initial value of the FOU process is set to ${\xi }_0=1$, we understand that the ensemble mean of the FOU process will monotonically decrease. Then, both time series (natural oscillation and the ensemble mean of the FOU process) decline from the maxima in the first half period of the natural oscillation, making them appear to have the same phase. Consequently, we might assign the same initial phase to the forced oscillation, that is, ${\phi }_n=\pi /2$. We further define the natural oscillation and the forced oscillation as being positively correlated. Then Equation (18) reduces to

$${\varphi }_{n\_s}=\arccos {\displaystyle \frac{-X_n}{\sqrt{D_n^2+X_n^2}}}>{\displaystyle \frac{\pi }{2}}.$$

(19)

According to Equation (19), the phase exceeds $\pi /2$, manifesting a phase-lead state. Correspondingly, when the initial phase of the forced oscillation is just opposite (${\phi }_n=-\pi /2$) so that they are defined negatively correlated, we can derive

$${\varphi }_{n\_d}=\arccos {\displaystyle \frac{X_n}{\sqrt{D_n^2+X_n^2}}}<{\displaystyle \frac{\pi }{2}}.$$

(20)

The theoretical estimated value falls below $\pi /2$, implying a phase-lag state. Equations (19) and (20) suggest that ${\varphi }_{n\_s}$ and ${\varphi }_{n\_d}$ are symmetric with respect to $\pi /2$. Moreover, they reveal a particularly significant relationship:

$${\varphi }_{n\_s}+{\varphi }_{n\_d}=\pi .$$

(21)

To verify the above inferences, we calculate the phases of the asymptotic solutions ($T_n^s\sim \sin \left({\omega }_{n}t+{\varphi }_n\right)$) for the ensemble mean oscillations. As shown in

Table 1. Phases of the ensemble mean oscillations under different fractional orders and initial values for the FOU process.

Fractional Order	Phase (${\mathit{\xi }}_0=1$)	Phase (${\mathit{\xi }}_0=-1$)	Phase Sum
$\alpha =1/4$	1.811	1.289	3.10
$\alpha =1/2$	1.849	1.269	3.12
$\alpha =3/4$	1.857	1.243	3.10

, with different fractional orders, the estimated phase values are approximately symmetric about $\pi /2$, and the sums of the phases are all close to $\pi$, further providing conclusive evidence for the theoretical analysis above.

6. Conclusions and Discussions

This paper investigates the impact of LTM stochastic processes on ENSO by incorporating the FOU process into the recently proposed STO conceptual model for ENSO. It analyzes the system behavior within the framework of ensemble mean dynamics. Compared to the persistent forcing from the non-zero ensemble mean of the FOU process during integration, the second-order moment forcing can be neglected without introducing significant errors. The validity of this second-order closure scheme is further verified via a 500-member Monte Carlo simulation that directly solves the original equations. Our model suggests that incorporating the FOU process alters the ensemble mean amplitude envelope and phase by introducing an anomalous amplitude growth rate and a phase modulation mechanism.

The anomalous growth rate is positive and induces divergence when the FOU process exhibits a positive ensemble mean. Conversely, it becomes negative and induces system dissipation when the ensemble mean is negative. Theoretical and numerical analyses further indicate that the anomalous growth rate is proportional to the ensemble mean of the FOU process, which is the Mittag-Leffler function with the fractional order of the FOU process as its parameter. Smaller fractional orders lead to slower decay of the FOU ensemble mean, thereby enhancing the FOU process’s influence on the ENSO ensemble mean amplitude.

The FOU process modulates the phase of the ensemble mean oscillation by altering the phase of the forced oscillation, which superimposes on the natural oscillation to form the total ensemble mean oscillation. Specifically, theoretical and numerical analyses demonstrate that positively correlated natural and forced oscillations advance the phase of the ensemble mean oscillation, while negative correlations delay it. Additionally, the leading and lagging phases are symmetric around the natural oscillation phase, with their average equal to the natural oscillation phase.

The results further extend our previous investigation, which forced the STO model with the classic OU process [24]. When the fractional order equals unity, the FOU process reduces to the classic OU process, whose ensemble mean decays exponentially and can thus be neglected. Correspondingly, the anomalous growth rate vanishes, allowing second-order moment forcing to dominate. This scenario is consistent with the theoretical framework established in our prior work. Additionally, they extend our previous investigation [21], which forced the RO model with the FOU process. In that study, while the amplified amplitude and modulated phase were identified, the explicit mechanisms remained incompletely understood.

The mechanisms of the phase modulation and anomalous growth rate uncovered in this study have significant implications for ENSO prediction models and early warning systems. On one hand, the phase shifts caused by the FOU process indicate that traditional models, which are based on short-term stochastic processes, may underestimate the LTM effect of initial stochastic perturbations on ENSO phase evolution. Consequently, it is essential to integrate LTM stochastic processes into prediction models to enhance the accuracy of ENSO onset timing (e.g., lead time for El Niño events). On the other hand, noise-induced anomalous growth rates imply that current warning systems may undervalue the amplifying effect of stochastic forcing on ENSO intensity. For example, the power-law decay characteristic of the FOU process can prolong the influence window of perturbations, resulting in systematic biases in intensity predictions of extreme events (e.g., strong El Niño) by traditional short-term noise parameterization schemes.

Future efforts should focus on developing prediction models coupled with spatiotemporal stochastic dynamical frameworks, which quantify phase-amplitude feedback mechanisms of LTM processes to optimize multi-timescale (seasonal-to-interannual) warning thresholds, thereby enhancing early warning capabilities for ENSO-related climate disasters (e.g., droughts and floods). Additionally, future work should also focus on validating phase-amplitude feedback mechanisms with real-world ENSO dynamics by incorporating observational data comparisons. For instance, observed ENSO events might be categorized into two types, those with and without stochastic atmospheric forcing, to compare the phase and amplitude differences between these two types of events.

Finally, when comparing with observational data or numerical predictions, the spatial distribution of the FOU process must be taken into account. Although incorporating the spatial distribution of the FOU process into the simple STO model presents significant theoretical challenges, we can numerically solve the system to further detect signatures of the anomalous growth rate or phase shifts identified in the present investigation. This also represents a critical direction for future research.