Quantitative Analysis of Multi-Angle Correlation Between Fractal Dimension of Anthracite Surface and Its Coal Quality Indicators in Different Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Geological Background
2.2. Experimental Methods
2.2.1. Proximate Analysis and Vitrinite Reflectance
2.2.2. Maceral Measurement
2.2.3. Atomic Force Microscope Experiment
3. Results and Discussion
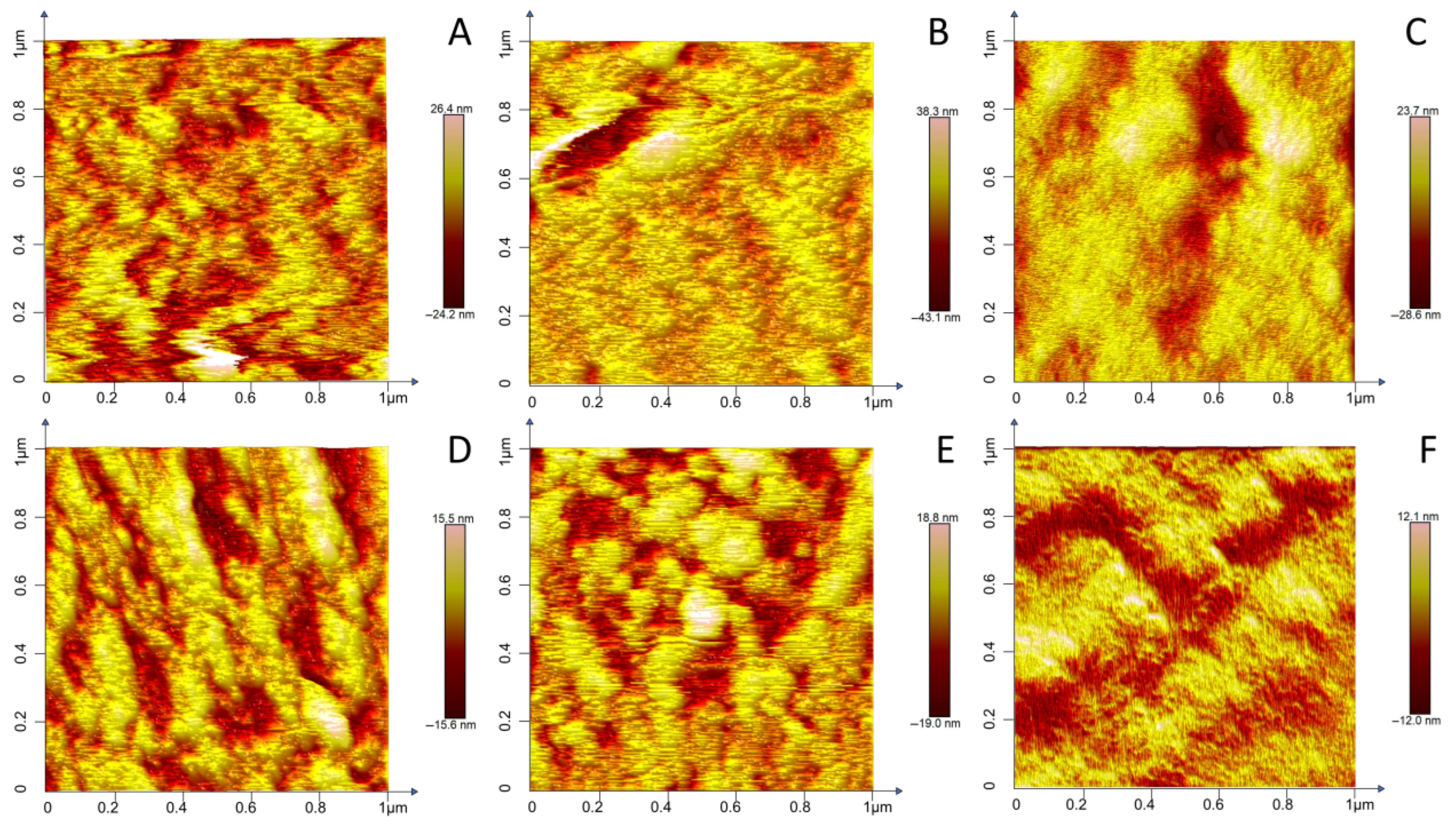
3.1. AFM Image Analysis
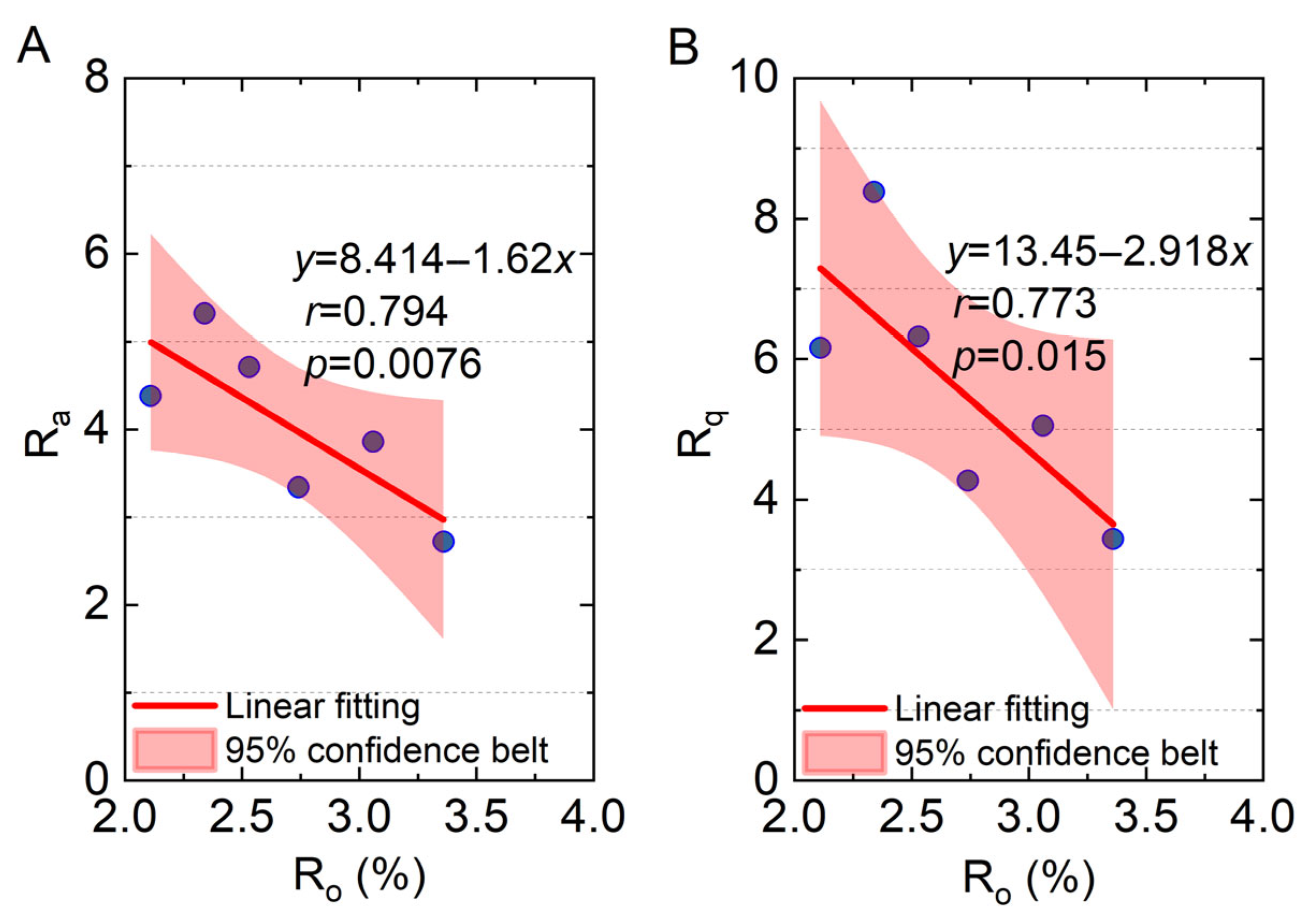
3.2. Surface Roughness Analysis
3.3. Analysis of Nanopore Structure Parameters
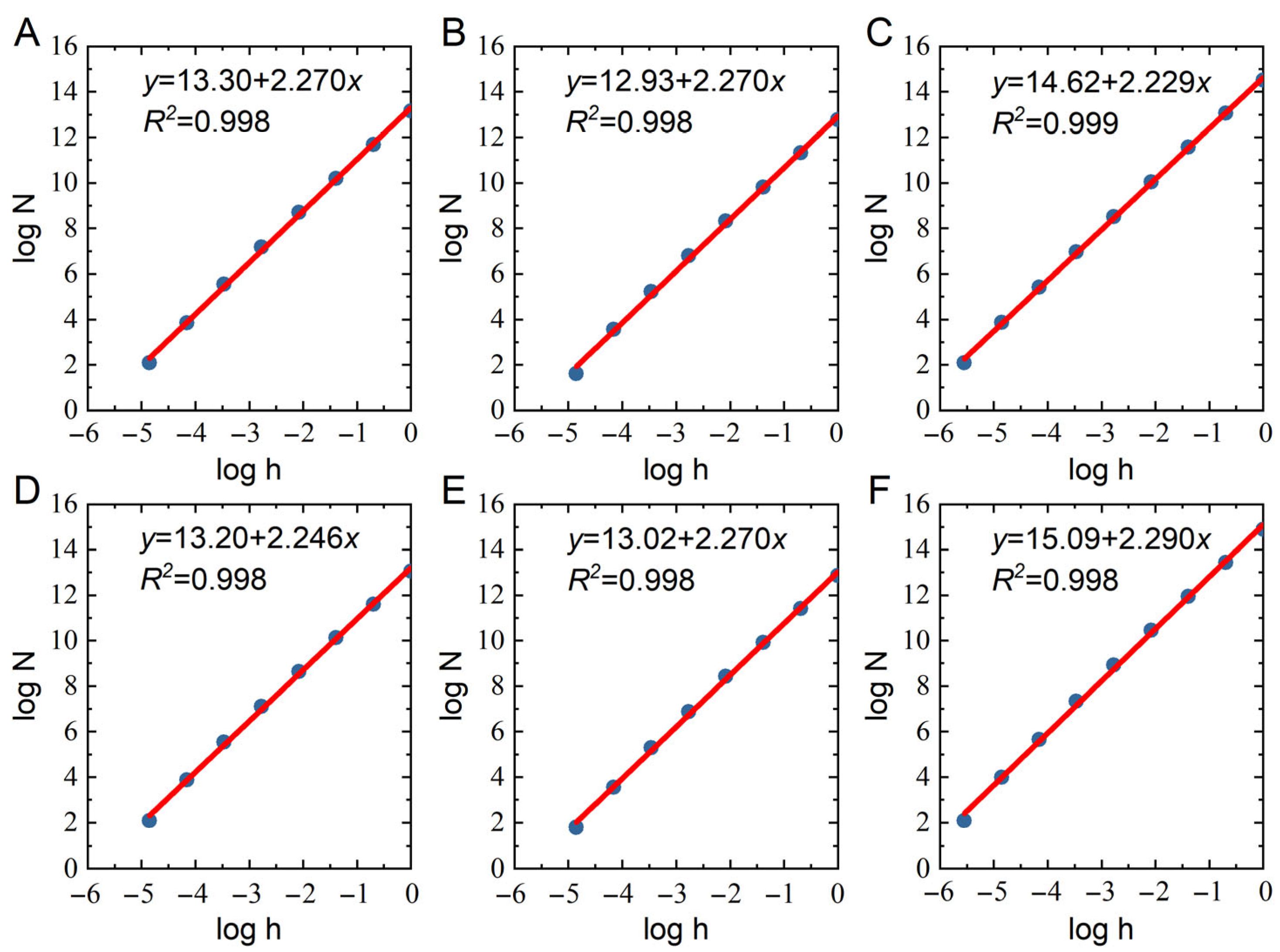
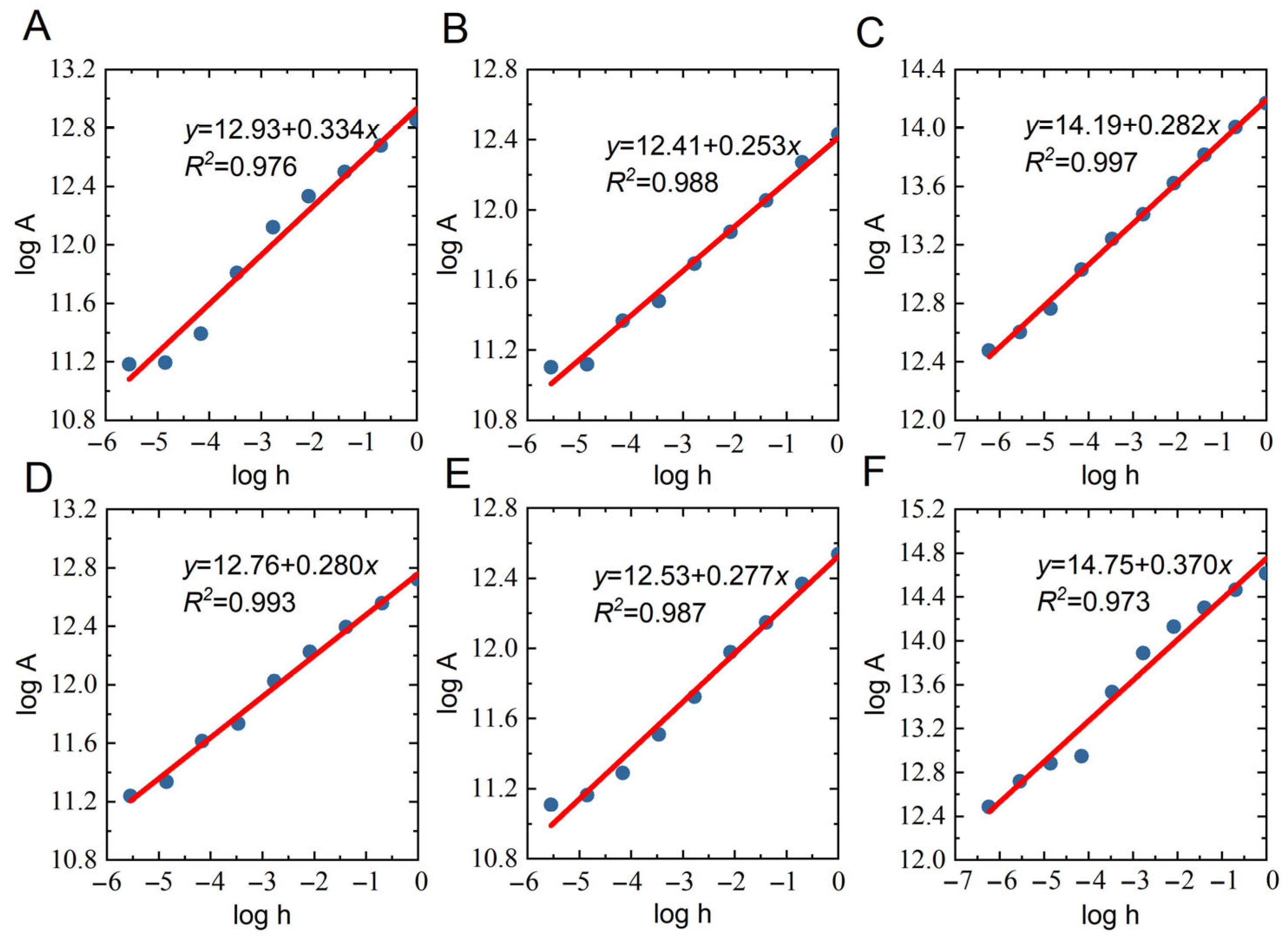
3.4. Fractal Dimension Analysis
3.4.1. Cube-Counting Method
3.4.2. Triangulation Method
3.4.3. Variance Partitioning Method
3.4.4. Power Spectral Method
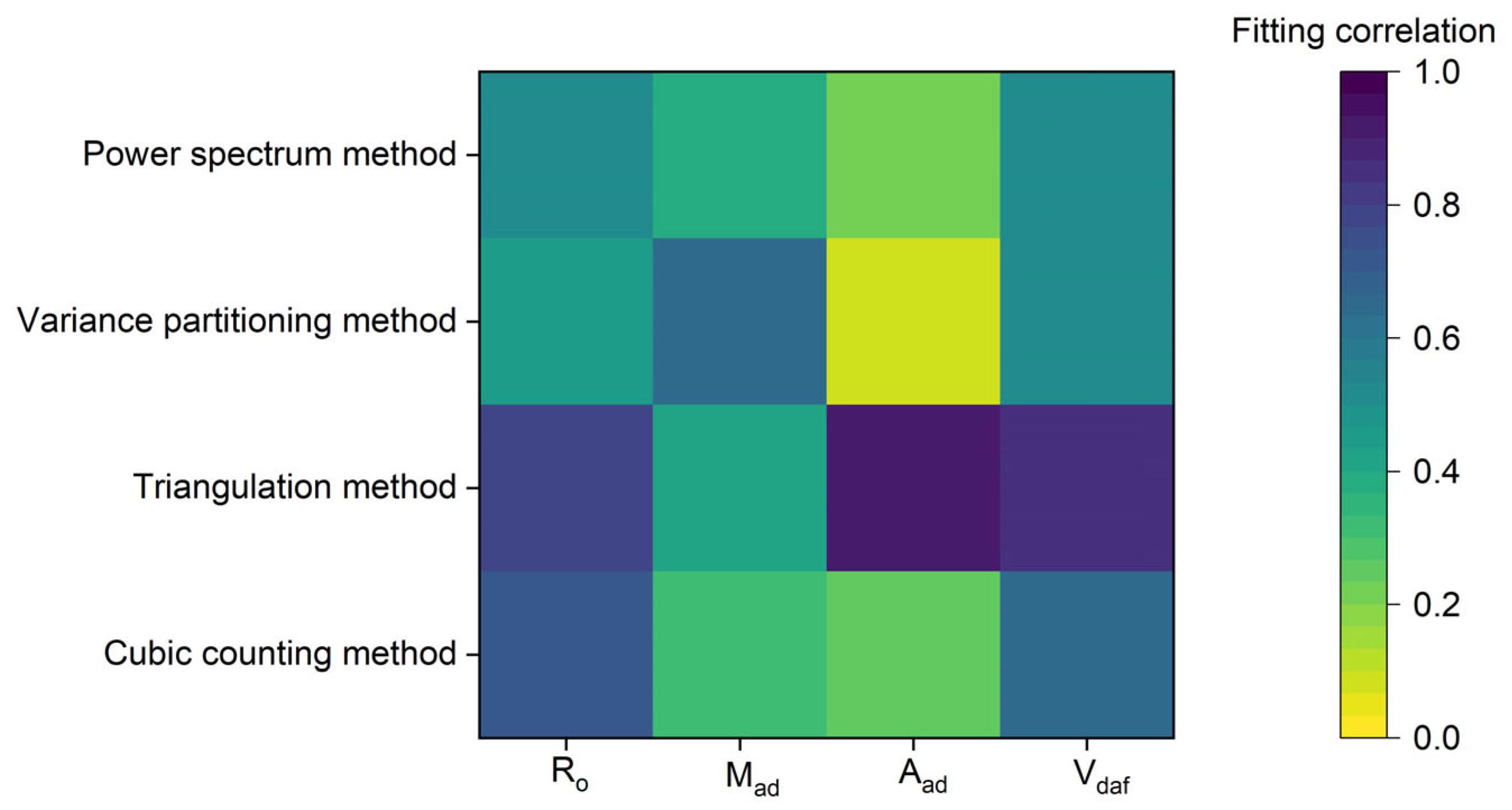
3.5. Factors Influencing Fractal Dimension
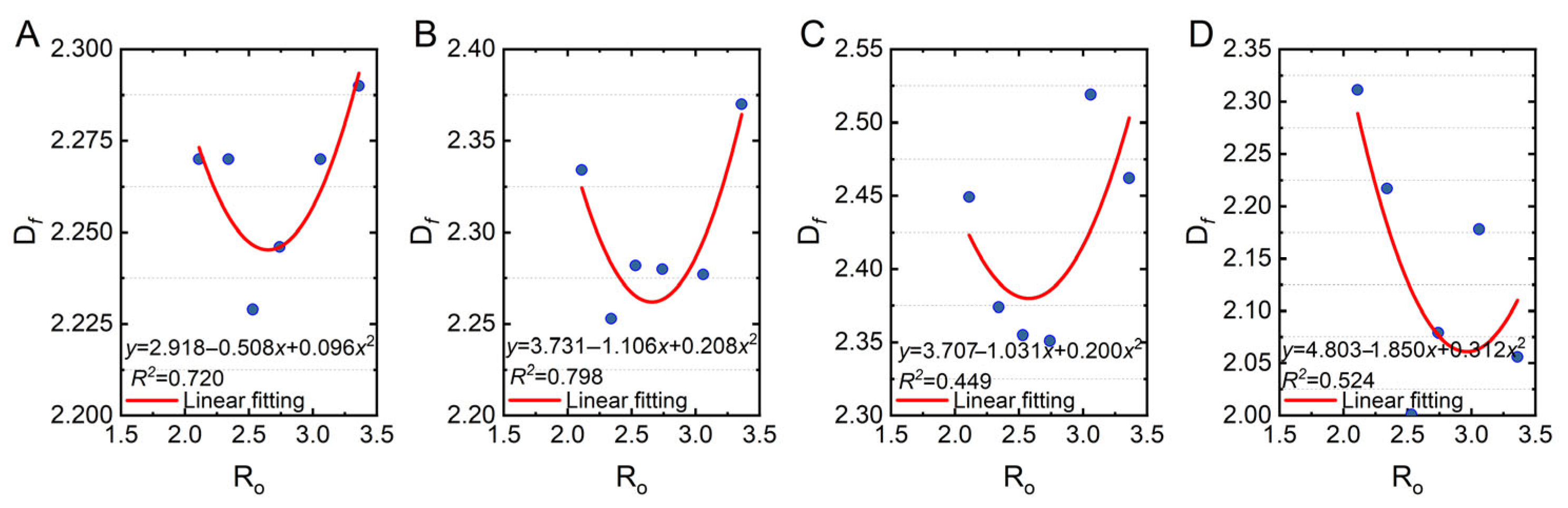
3.5.1. Metamorphic Grade
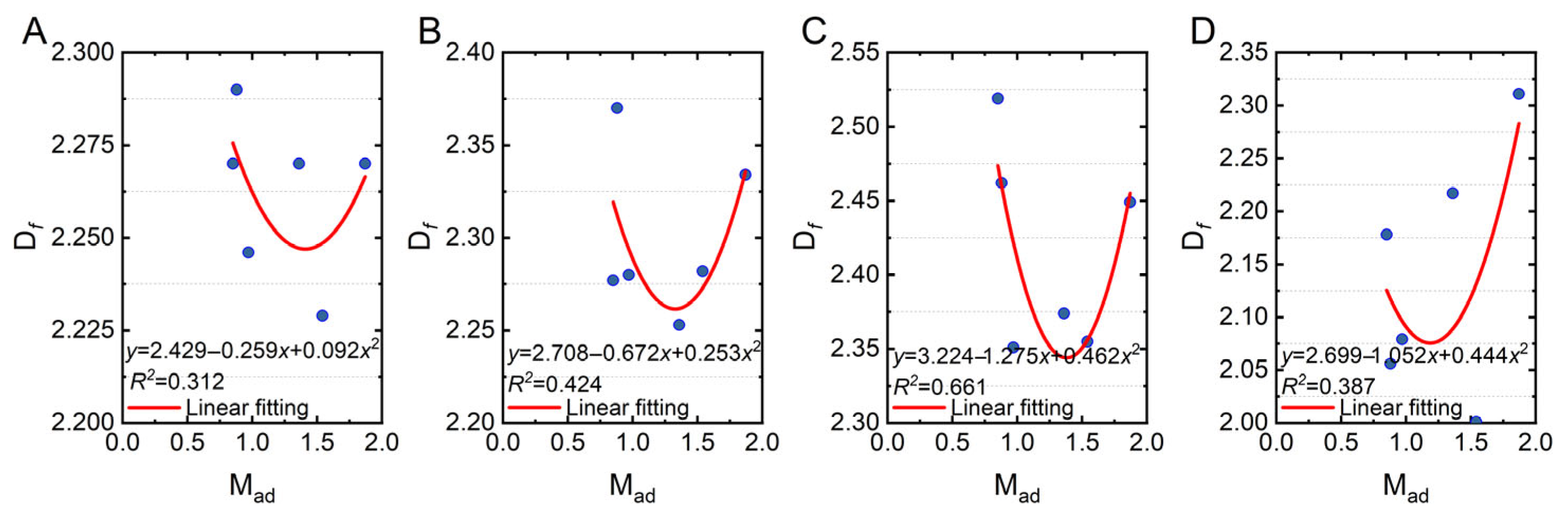
3.5.2. Moisture
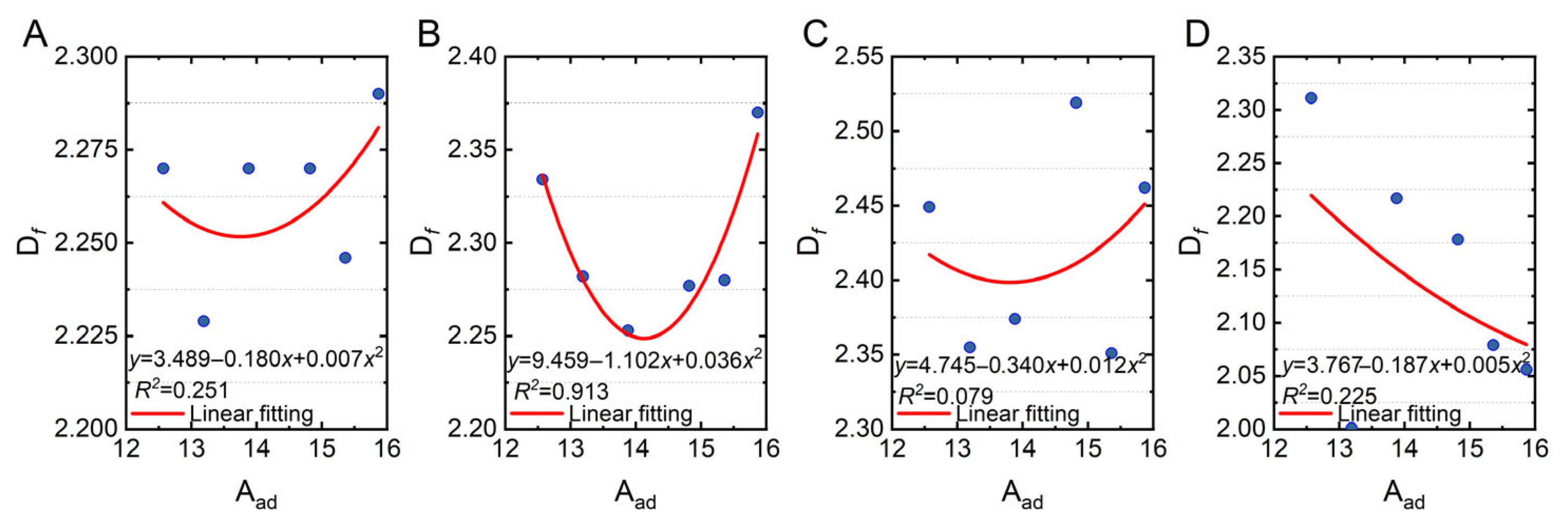
3.5.3. Ash Content
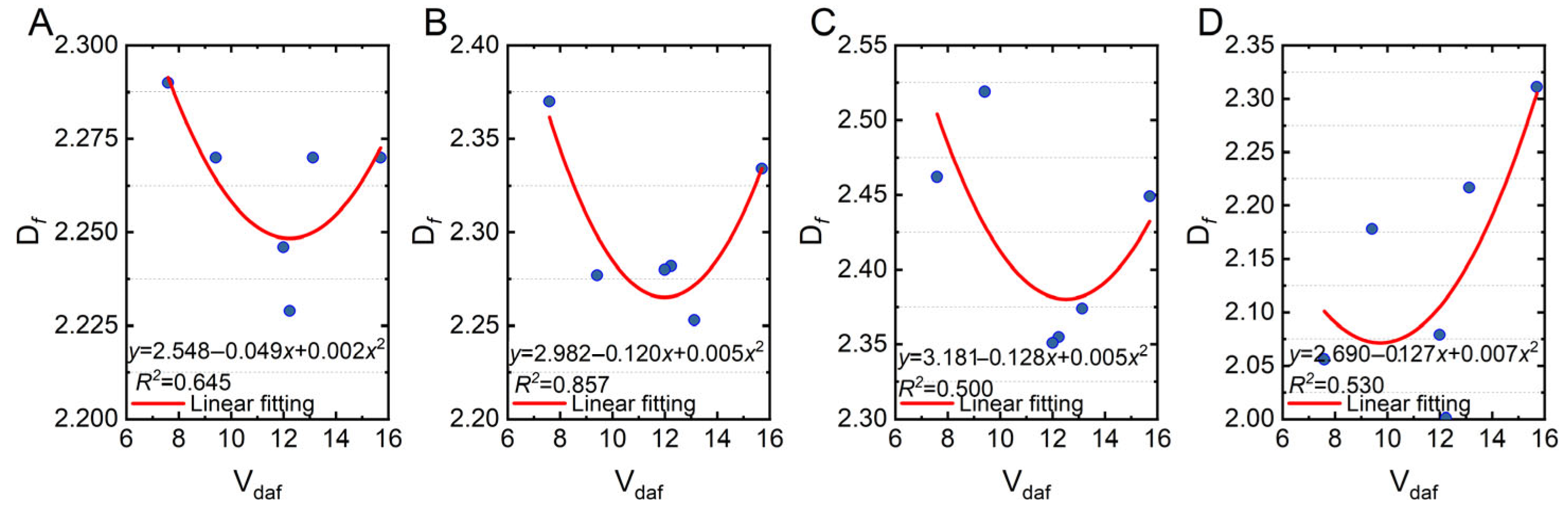
3.5.4. Volatile Matter
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, Z.H.; Ning, Z.; Zhang, H.; Yang, H.Q.; Chang, S.J. A generalized Faustmann model with multiple carbon pools. For. Policy Econ. 2024, 169, 103363. [Google Scholar] [CrossRef]
- Yu, Z.H.; Ning, Z.; Chang, W.Y.; Chang, S.J.; Yang, H.Q. Optimal harvest decisions for the management of carbon sequestration forests under price uncertainty and risk preferences. For. Policy Econ. 2023, 151, 102957. [Google Scholar] [CrossRef]
- Li, B.; Wang, X.; Khurshid, A.; Saleem, S.F. Environmental governance, green finance, and mitigation technologies: Pathways to carbon neutrality in European industrial economies. Int. J. Environ. Sci. Technol. 2025. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, Y.Y.; Khurshid, A.; Saleem, S.F. E-governance and policy efforts advancing carbon neutrality and sustainability in European countries. Public Money Manag. 2025. [Google Scholar] [CrossRef]
- Wang, X.Y.; Su, H.Y.; Liu, X. The Impact of Green Technological Innovation on Industrial Structural Optimization Under Dual-Carbon Targets: The Role of the Moderating Effect of Carbon Emission Efficiency. Sustainability 2025, 17, 6313. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, X.; He, N.; Song, F.H.; Wang, X. Investigation on novel deep eutectic solvents with high carbon dioxide adsorption performance. J. Environ. Chem. Eng. 2025, 13, 117870. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.F.; Zhang, S.R.; Wu, J.; Bi, J.J.; Meng, S.Z.; Tao, C.Q. Gas bearing system difference in deep coal seams and corresponded development strategy. J. China Coal Soc. 2023, 48, 900–917. [Google Scholar]
- Guo, T.; Jin, X.B.; Wu, D.D.; Xie, F.; Liu, J.X. Accumulation characteristics and exploration prospects of deep coalbed methane in the Longtan Formation of the Nanchuan block on the southeastern margin of the Sichuan Basin. Coal Geol. Explor. 2024, 52, 60–67. [Google Scholar] [CrossRef]
- Jiang, J.Y.; Yang, W.H.; Cheng, Y.P.; Zhao, K.; Zheng, S.J. Pore structure characterization of coal particles via MIP, N2 and CO2 adsorption: Effect of coalification on nanopores evolution. Powder Technol. 2019, 354, 136–148. [Google Scholar] [CrossRef]
- He, L.; Cao, J.; Lu, J.; Lin, B.; Lu, Y.; Shi, S.; Liu, M. Effect of microwave-assisted cyclic oxidation on the coal internal and surface structure based on NMR and AFM. Energy 2024, 288, 129872. [Google Scholar]
- Zeng, F.; Dong, C.; Lin, C.; Tian, S.; Wu, Y.; Lin, J.; Zhang, X. Pore structure characteristics of reservoirs of Xihu Sag in East China Sea Shelf Basin based on dual resolution X-ray computed tomography and their influence on permeability. Energy 2022, 239, 122386. [Google Scholar] [CrossRef]
- Zang, J.; Liu, J.L.; He, J.B.; Zhang, X.P. Characterization of the pore structure in Chinese anthracite coal using FIB-SEM tomography and deep learning-based segmentation. Energy 2023, 282, 128686. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Liu, S.M.; Elsworth, D.; Jiang, Y.D.; Zhu, J. Pore structure characterization of coal by synchrotron small-angle X-ray scattering and transmission electron microscopy. Energy Fuels 2014, 28, 3704–3711. [Google Scholar] [CrossRef]
- Yu, X.L.; Li, L.L.; Jiang, H.; Lu, L.F.; Du, C.J. Application of sparry grain limestone petrographic analysis combining image processing and deep learning. Pet. Geol. Exp. 2023, 45, 1026–1038. [Google Scholar] [CrossRef]
- Collinson, D.W.; Nepal, D.; Zwick, J.; Dauskardt, R.H. Gas cluster etching for the universal preparation of polymer composites for nano chemical and mechanical analysis with AFM. Appl. Surf. Sci. 2022, 599, 153954. [Google Scholar] [CrossRef]
- Gojzewski, H.; Van Drongelen, M.; Imre, B.; Hempenius, M.A.; Check, C.; Chartoff, C.; Wurm, F.R.; Vancso, G.J. AFM monitoring of the cut surface of a segmented polyurethane unveils a microtome-engraving induced growth process of oriented hard domains. Polym. Test. 2023, 120, 107961. [Google Scholar] [CrossRef]
- Flechsig, H.; Ando, T. Protein dynamics by the combination of high-speed AFM and computational modeling. Curr. Opin. Struct. Biol. 2023, 80, 102591. [Google Scholar] [CrossRef]
- Lostao, A.; Lim, K.S.; Pallarés, M.C.; Ptak, A.; Marcuello, C. Recent advances in sensing the inter-biomolecular interactions at the nanoscale–A comprehensive review of AFM-based force spectroscopy. Int. J. Biol. Macromol. 2023, 238, 124089. [Google Scholar] [CrossRef]
- Liu, X.F.; Song, D.Z.; He, X.Q.; Wang, Z.P.; Zeng, M.R.; Deng, K. Nanopore structure of deep-burial coals explored by AFM. Fuel 2019, 246, 9–17. [Google Scholar] [CrossRef]
- Lawrie, G.A.; Gentle, I.R.; Fong, C.; Glikson, M. Atomic force microscopy studies of Bowen Basin coal macerals. Fuel 1997, 76, 1519–1526. [Google Scholar] [CrossRef]
- Liu, J.X.; Jiang, X.M.; Huang, X.Y.; Wu, S.H. Morphological characterization of super fine pulverized coal particle. Part 2. AFM investigation of single coal particle. Fuel 2010, 89, 3884–3891. [Google Scholar] [CrossRef]
- Xie, H.G.; Li, X.J. Microstructure and nanomechanical characterization of tectonic coal based on SEM, AFM, XRD and DSI. Surf. Interfaces 2024, 46, 104158. [Google Scholar] [CrossRef]
- Qiao, P.; Ju, Y.W.; Yu, K.; Ju, L.T.; Xiao, L.; Feng, H.Y.; Yao, Y.B.; Nie, B.S.; Li, X.; Tian, J.J.; et al. Nanoscale quantitative characterization of microstructure evolution of partly graphitized high rank coal: Evidence from AFM and HRTEM. Fuel 2022, 324, 124802. [Google Scholar] [CrossRef]
- Chen, S.B.; Li, X.Y.; Chen, S.; Wang, Y.; Gong, Z.; Zhang, Y.K. A new application of atomic force microscopy in the characterization of pore structure and pore contribution in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2021, 88, 103802. [Google Scholar] [CrossRef]
- Li, Z.B.; Ren, T.; Li, X.C.; Qiao, M.; Yang, X.H.; Tan, L.H.; Nie, B.S. Multi-scale pore fractal characteristics of differently ranked coal and its impact on gas adsorption. Int. J. Min. Sci. Technol. 2023, 33, 389–401. [Google Scholar] [CrossRef]
- Liu, Z.; Li, R.R.; Yang, H.; Tian, F.C.; Zhu, D.L. A new fractal model of coal permeability based on the increasing fractal construction method of the menger sponge. Fractals 2021, 29, 2150187. [Google Scholar] [CrossRef]
- Cai, Y.D.; Liu, D.M.; Yao, Y.B.; Li, J.Q.; Liu, J.L. Fractal characteristics of coal pores based on classic geometry and thermodynamics models. Acta Geol. Sin. 2011, 85, 1150–1162. [Google Scholar] [CrossRef]
- Zhang, S.H.; Tang, S.H.; Tang, D.Z.; Huang, W.H.; Pan, Z.J. Determining fractal dimensions of coal pores by FHH model: Problems and effects. J. Nat. Gas Sci. Eng. 2014, 21, 929–939. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, L.; Li, B.; Kataza, N.N. Geochemical study on nitrogen isotope composition, speciation distribution, and influencing factors of vitrinite-rich coal seams during the Late Carboniferous. Sci. Rep. 2025, 15, 19095. [Google Scholar] [CrossRef]
- Wu, D.; Liu, G.J.; Sun, R.Y.; Chen, S.C. Influences of magmatic intrusion on the macromolecular and pore structures of coal: Evidences from Raman spectroscopy and atomic force microscopy. Fuel 2014, 119, 191–201. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, G.F.; Lin, J.; Barakos, G.; Chang, P. Fractal evolution characteristics on the three-dimensional fractures in coal induced BY CO2 phase transition fracturing. Fractal Fract. 2024, 8, 273. [Google Scholar] [CrossRef]
- Chang, Y.M.; Yang, H.G.; Ma, T.; Fan, L.; Zhang, H. Study of the Coal Micro-Structure Based on AFM. Mod. Sci. Instrum. 2006, 16, 71–72. [Google Scholar]
- Li, Y.; Yang, J.H.; Pan, Z.J.; Tong, W.S. Nanoscale pore structure and mechanical property analysis of coal: An insight combining AFM and SEM images. Fuel 2020, 260, 116352. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Mastalerz, M.; Schimmelmann, A. Characterization of chemical functional groups in macerals across different coal ranks via micro-FTIR spectroscopy. Int. J. Coal Geol. 2012, 104, 22–33. [Google Scholar] [CrossRef]
- Bruening, F.A.; Cohen, A.D. Measuring surface properties and oxidation of coal macerals using the atomic force microscope. Int. J. Coal Geol. 2005, 63, 195–204. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.F.; Guo, F.Y.; Luo, J.Q.; Ding, S.H.; Cao, Y.J.; Xing, Y.W.; Gui, X.H. Effect of surface roughness on floatability of coal slime. Coal Sci. Technol. 2019, 47, 253–258. [Google Scholar] [CrossRef]
- Morga, R. Changes of semifusinite and fusinite surface roughness during heat treatment determined by atomic force microscopy. Int. J. Coal Geol. 2011, 88, 218–226. [Google Scholar] [CrossRef]
- Yu, H.; Shen, R.; Guo, H.K.; Wang, G.D.; Shao, G.Y.; Shang, Z.H. Application progress of atomic force microscopy in shale reservoir characterization. Appl. Chem. Ind. 2023, 52, 511–516. [Google Scholar]
- Li, C.X.; Ostadhassan, M.; Guo, S.L.; Gentzis, T.; Kong, L.Y. Application of PeakForce tapping mode of atomic force microscope to characterize nanomechanical properties of organic matter of the Bakken Shale. Fuel 2018, 233, 894–910. [Google Scholar] [CrossRef]
- Poon, C.Y.; Bhushan, B. Nano-asperity contact analysis and surface optimization for magnetic head slider/disk contact. Wear 1996, 202, 83–98. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Open Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Soroushian, P.; Elzafraney, M. Morphological operations, planar mathematical formulations, and stereological interpretations for automated image analysis of concrete microstructure. Cem. Concr. Compos. 2005, 27, 823–833. [Google Scholar] [CrossRef]
- Xue, K.S.; Pu, H.; Li, M.; Luo, P.; Liu, D.J.; Yi, Q.Y. Fractal-based analysis of stress-induced dynamic evolution in geometry and permeability of porous media. Phys. Fluids. 2025, 37, 036630. [Google Scholar] [CrossRef]
- Pu, H.; Xue, K.S.; Wu, Y.; Zhang, S.J.; Liu, D.J.; Xu, J.C. Estimating the permeability of fractal rough rock fractures with variable apertures under normal and shear stresses. Phys. Fluids. 2025, 37, 036635. [Google Scholar] [CrossRef]
- Du, S.W.; Li, Y.T. Fractal characteristics and microstructure evolution of magnetron sputtering Cu thin films. Chin. J. Mech. Eng. 2013, 26, 137–143. [Google Scholar] [CrossRef]
- Mannelquist, A.; Almqvist, N.; Fredriksson, S. Influence of tip geometry on fractal analysis of atomic force microscopy images. Appl. Phys. A Mater. Sci. Process. 1998, 66, S891–S896. [Google Scholar] [CrossRef]
- Shrivastava, S.C.; Shrivastava, R.; Priyanka. Comparative analysis of fractal dimension of CdS, CdZnS and CdZnS: Ce thin films. Indian J. Phys. 2023, 97, 757–765. [Google Scholar] [CrossRef]
- Roman, H.E.; Cesura, F.; Maryam, R.; Levchenko, I.; Alexander, K.; Riccardi, C. The fractal geometry of polymeric materials surfaces: Surface area and fractal length scales. Soft Matter 2024, 20, 3082–3096. [Google Scholar] [CrossRef]
- Shao, L.Y.; Li, J.X.; Wang, S.; Hou, H.H.; Li, J.A.; Zhu, M.Y. Pore structures and fractal characteristics ofliquid nitrogen adsorption pores in lignite in the Hailar Basin. Nat. Gas Ind. 2020, 40, 15–25. [Google Scholar]
- Lin, H.F.; Cheng, B.; Zeng, Q.; Yan, M.; Zhang, C. The experimental study on the fractal characteristies of coal adsorbed porein Fukang mining district of Xinjiang. China Coal 2016, 42, 103–108. [Google Scholar]
- Qin, X.L. Study on the fractal feature of coal pore structure with different ranks and its influencing factors in Xishan coal field. China Min. Mag. 2021, 30, 157–161. [Google Scholar] [CrossRef]





| Sample Number | Origin | Ro | Proximate Analysis (wt%) | Macerals (%) | ||||
|---|---|---|---|---|---|---|---|---|
| Mad | Aad | Vdaf | Vitrinite | Liptinite | Inertinite | |||
| M-1 | Hebei Xingtai | 2.11 | 1.87 | 12.57 | 15.7 | 92.36 | 5.15 | 2.49 |
| M-2 | Hebei Xingtai | 2.34 | 1.36 | 13.88 | 13.12 | 93.53 | 4.33 | 2.14 |
| M-3 | Shanxi Jincheng | 2.53 | 1.54 | 13.19 | 12.23 | 93.71 | 3.51 | 2.78 |
| M-4 | Shanxi Jincheng | 2.74 | 0.97 | 15.36 | 11.99 | 92.54 | 3.97 | 3.49 |
| M-5 | Shanxi Jincheng | 3.06 | 0.85 | 14.82 | 9.41 | 94.33 | 2.72 | 2.95 |
| M-6 | Shanxi Jincheng | 3.36 | 0.88 | 15.87 | 7.59 | 93.69 | 3.36 | 2.95 |
| Sample Number | Ro | Nanopore Parameters | Surface Roughness | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Pore Quantity | Average Pore Diameter (nm) | Areal Porosity (%) | Form Factor (ff) | Ra (nm) | Rq (nm) | Rsk (nm) | Rku (nm) | ||
| M-1 | 2.11 | 3568 | 13.56 | 5.73 | 0.64 | 4.38 | 6.16 | 0.508 | 7.56 |
| M-2 | 2.34 | 4638 | 10.28 | 8.35 | 0.75 | 5.32 | 8.38 | −0.354 | 15.90 |
| M-3 | 2.53 | 4966 | 12.47 | 7.38 | 0.72 | 4.71 | 6.32 | −0.576 | 5.04 |
| M-4 | 2.74 | 4714 | 8.84 | 9.17 | 0.84 | 3.34 | 4.27 | −0.143 | 3.48 |
| M-5 | 3.06 | 5174 | 6.57 | 11.48 | 0.81 | 3.86 | 5.05 | −0.052 | 4.4 |
| M-6 | 3.36 | 6887 | 7.37 | 9.83 | 0.86 | 2.72 | 3.44 | −0.060 | 3.22 |
| Sample Number | Ro | Proximate Analysis (wt%) | Fractal Dimension | |||||
|---|---|---|---|---|---|---|---|---|
| Mad | Aad | Vdaf | Cubic Counting Method | Triangulation Method | Variance Partition Method | Power Spectrum Method | ||
| M-1 | 2.11 | 1.87 | 12.57 | 15.7 | 2.270 | 2.334 | 2.449 | 2.311 |
| M-2 | 2.34 | 1.36 | 13.88 | 13.12 | 2.270 | 2.253 | 2.374 | 2.217 |
| M-3 | 2.53 | 1.54 | 13.19 | 12.23 | 2.229 | 2.282 | 2.355 | 2.001 |
| M-4 | 2.74 | 0.97 | 15.36 | 11.99 | 2.246 | 2.280 | 2.351 | 2.079 |
| M-5 | 3.06 | 0.85 | 14.82 | 9.41 | 2.270 | 2.277 | 2.519 | 2.178 |
| M-6 | 3.36 | 0.88 | 15.87 | 7.59 | 2.290 | 2.370 | 2.462 | 2.056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Wu, D. Quantitative Analysis of Multi-Angle Correlation Between Fractal Dimension of Anthracite Surface and Its Coal Quality Indicators in Different Regions. Fractal Fract. 2025, 9, 538. https://doi.org/10.3390/fractalfract9080538
Zhao S, Wu D. Quantitative Analysis of Multi-Angle Correlation Between Fractal Dimension of Anthracite Surface and Its Coal Quality Indicators in Different Regions. Fractal and Fractional. 2025; 9(8):538. https://doi.org/10.3390/fractalfract9080538
Chicago/Turabian StyleZhao, Shoule, and Dun Wu. 2025. "Quantitative Analysis of Multi-Angle Correlation Between Fractal Dimension of Anthracite Surface and Its Coal Quality Indicators in Different Regions" Fractal and Fractional 9, no. 8: 538. https://doi.org/10.3390/fractalfract9080538
APA StyleZhao, S., & Wu, D. (2025). Quantitative Analysis of Multi-Angle Correlation Between Fractal Dimension of Anthracite Surface and Its Coal Quality Indicators in Different Regions. Fractal and Fractional, 9(8), 538. https://doi.org/10.3390/fractalfract9080538





