Investigation of Stress Wave Propagation and Crack Propagation Characteristics in Intersecting-Joint Mass Under Blasting
Abstract
1. Introduction
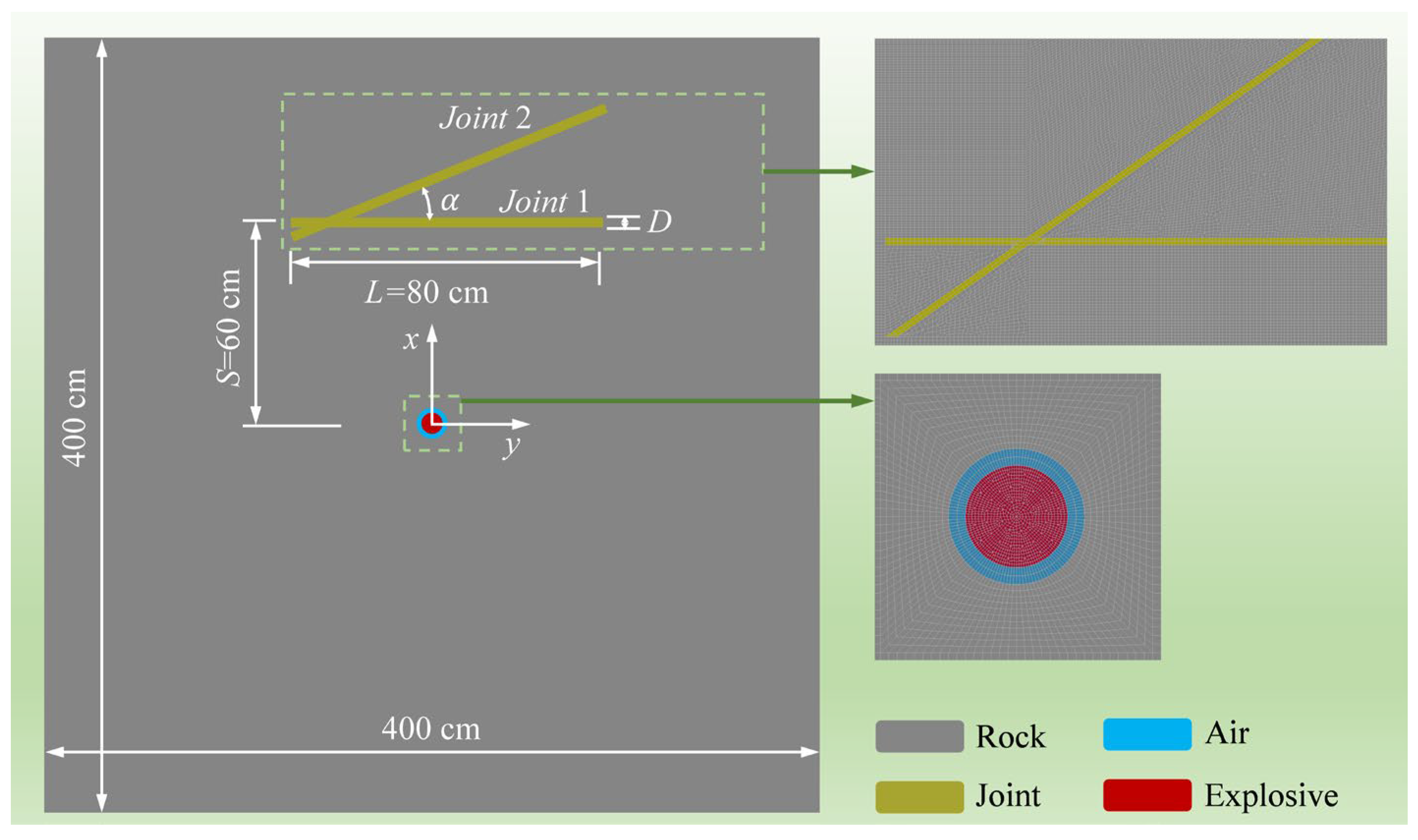
2. Numerical Simulation of Blasting in Intersecting-Joint Rock Mass
2.1. Numerical Model Development
2.2. Parameters of Materials
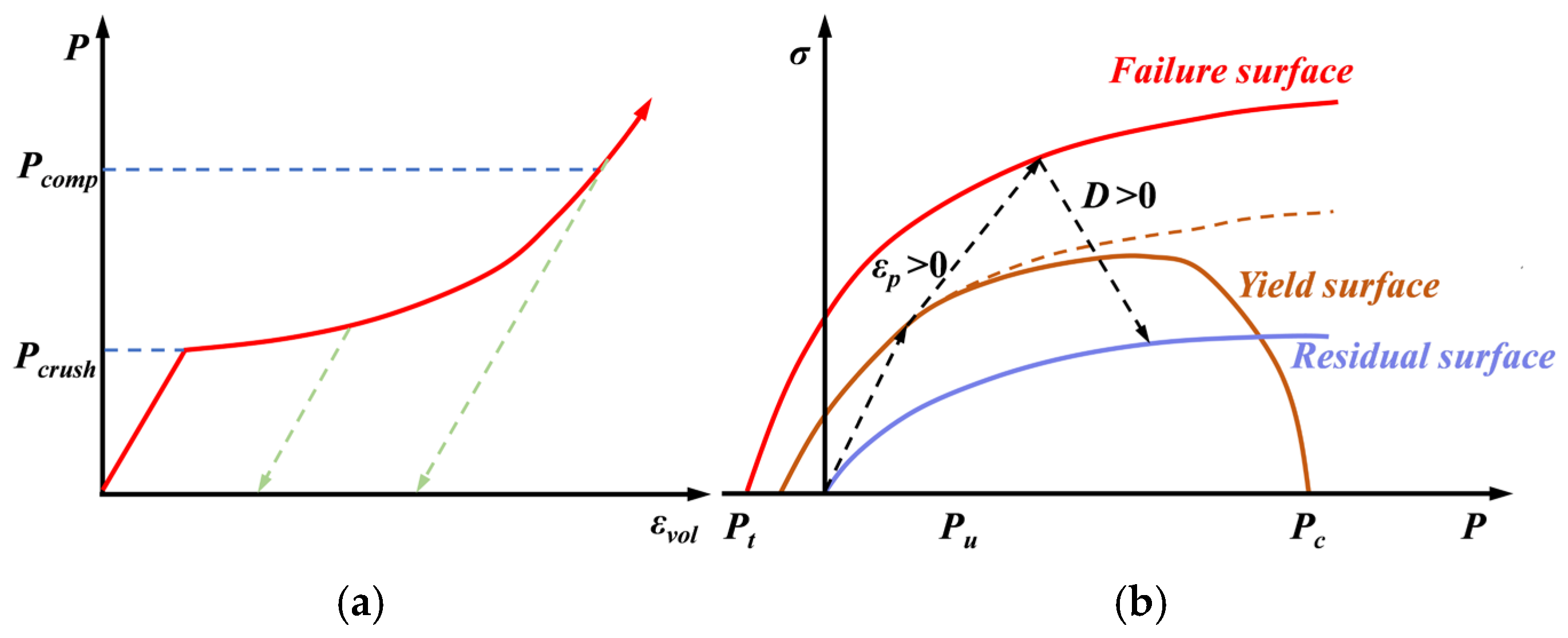
2.2.1. RHT Model
2.2.2. Parameters of Explosive
2.2.3. Parameters of the Filled Joints
2.2.4. Parameters of Air
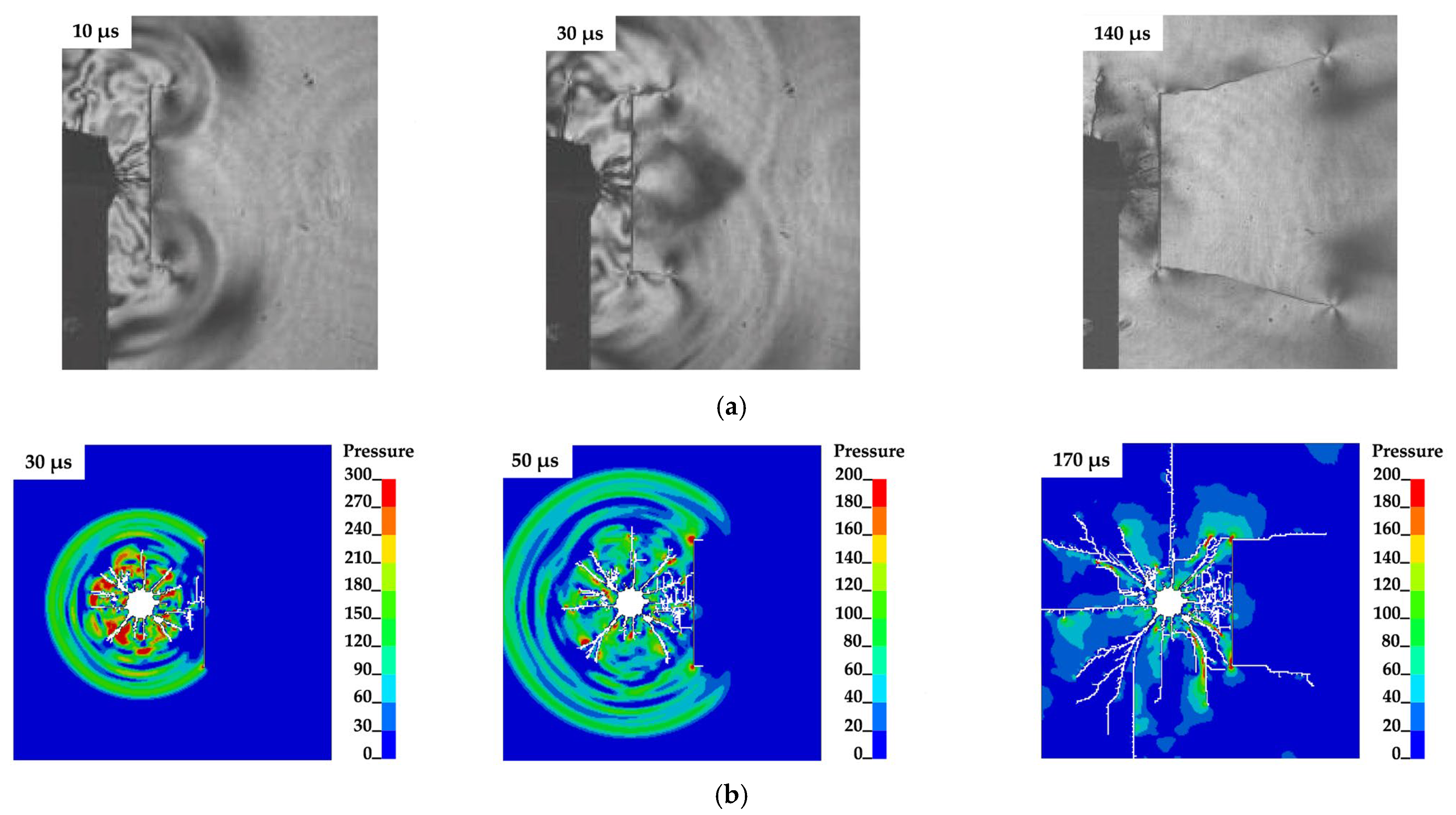
2.3. Validation of the Numerical Simulation
3. Analysis of Numerical Simulation Results
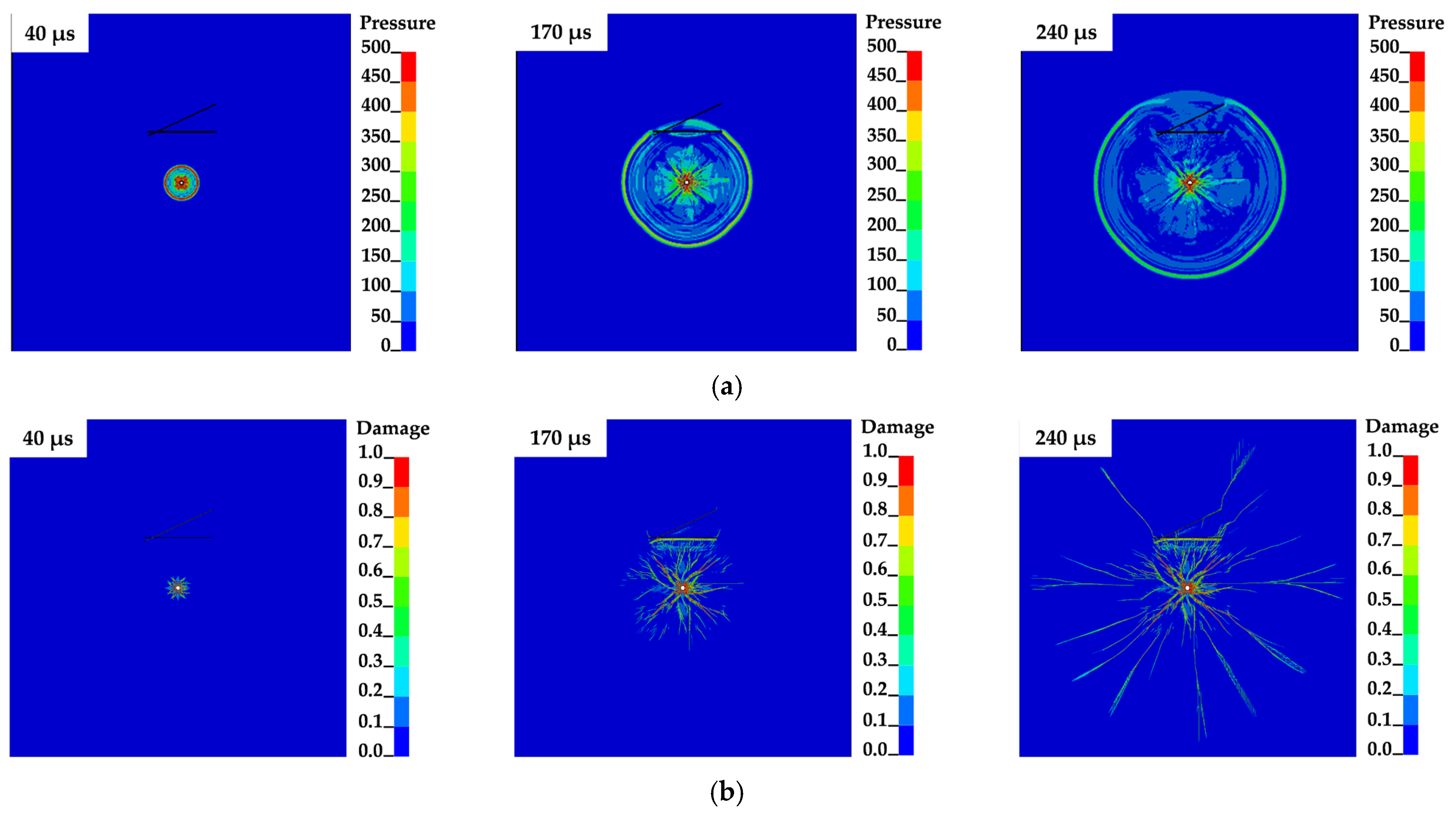
3.1. Propagation of Blasting-Induced Cracks
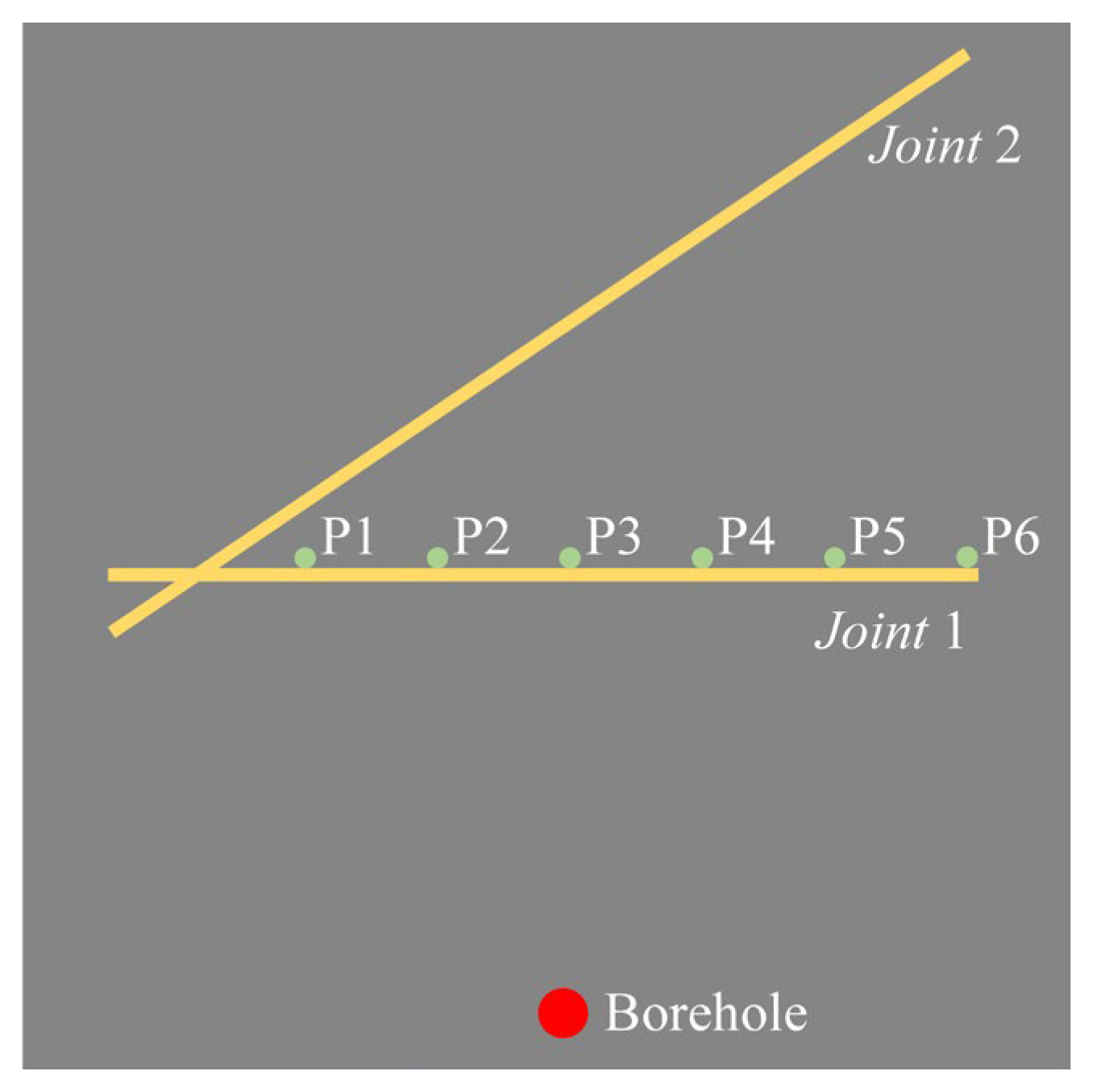
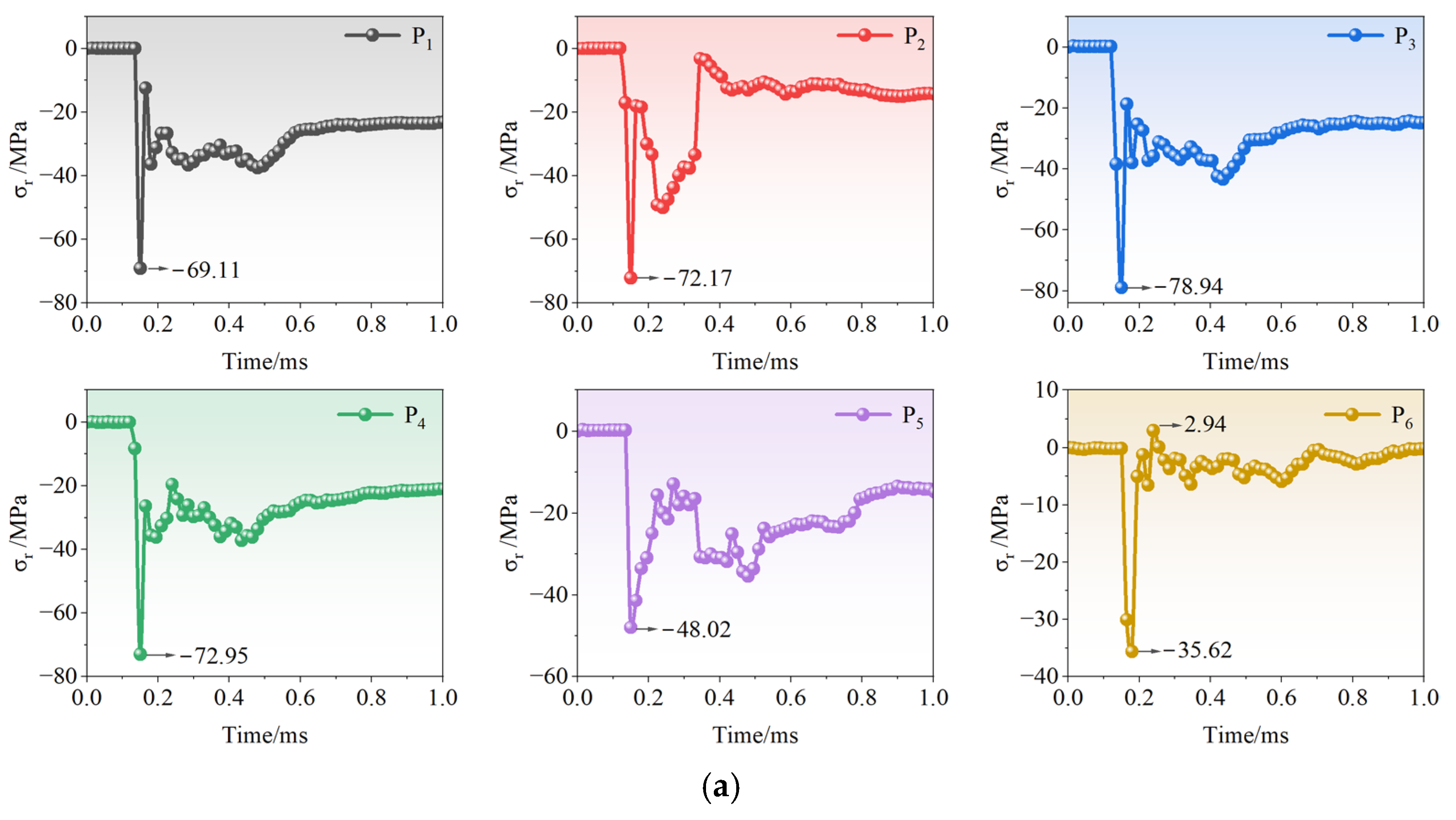
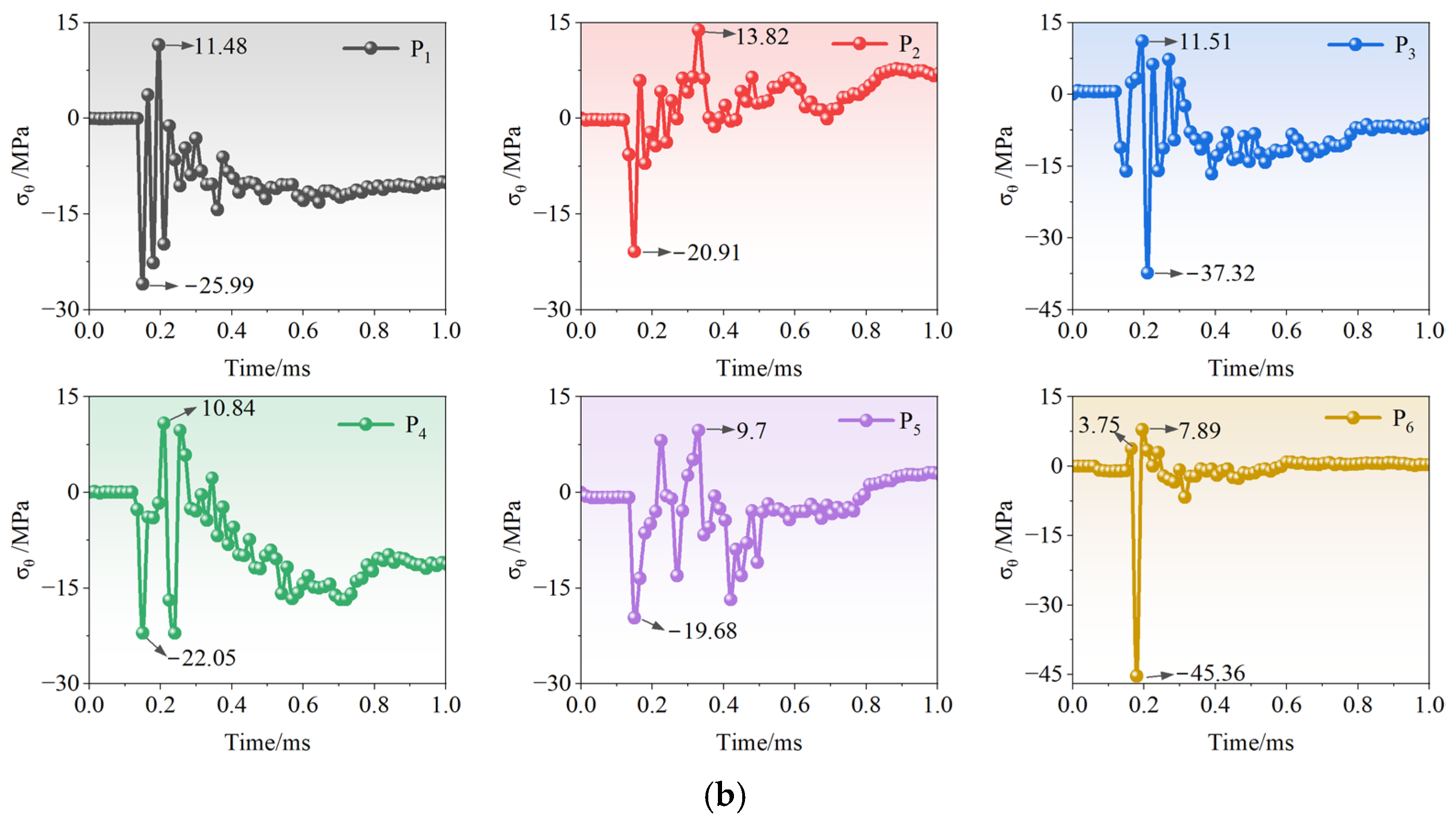
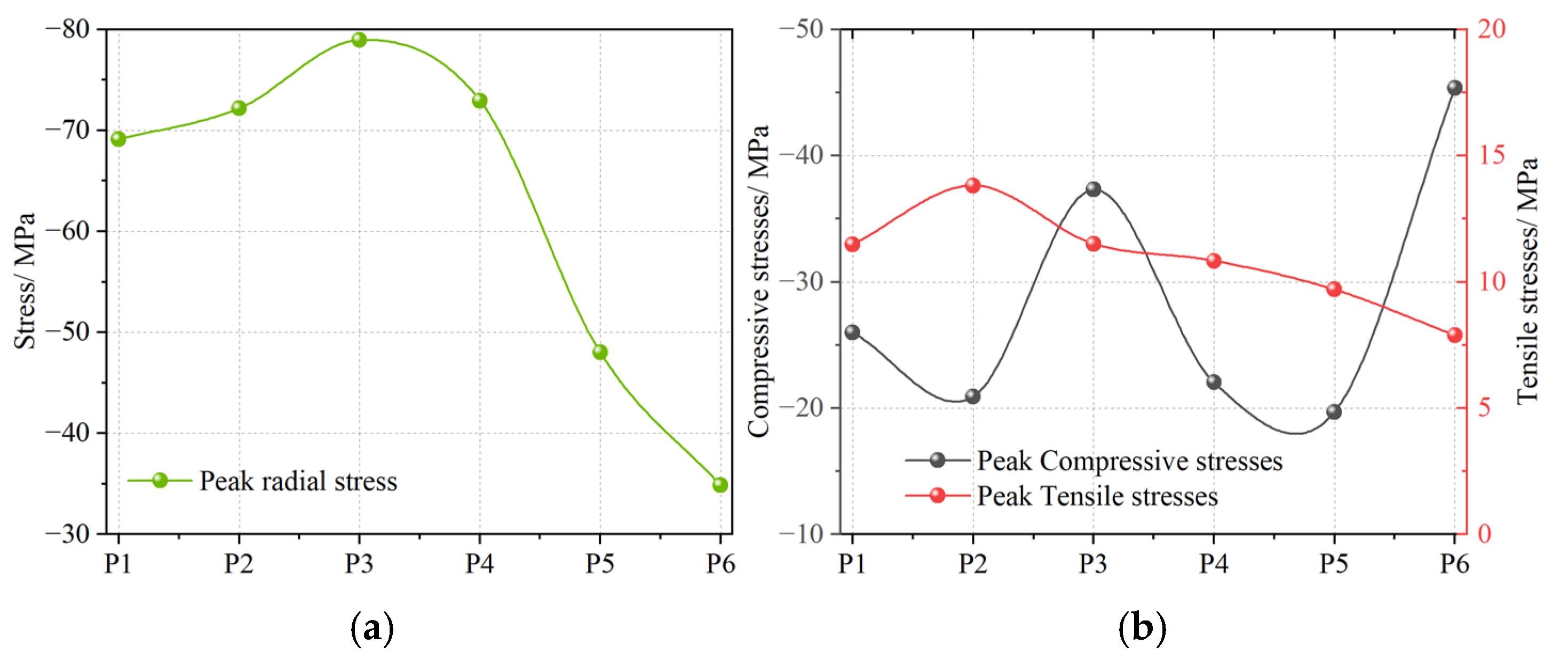
3.2. Effect of Joint Angle on Stress Wave Propagation
3.3. Effect of Joint Thickness on Stress Wave Propagation
4. Analysis of Blasting-Induced Crack Propagation in Jointed Rock Mass
4.1. Crack Propagation in Jointed Rock Under Blasting with Varying Joint Characteristics
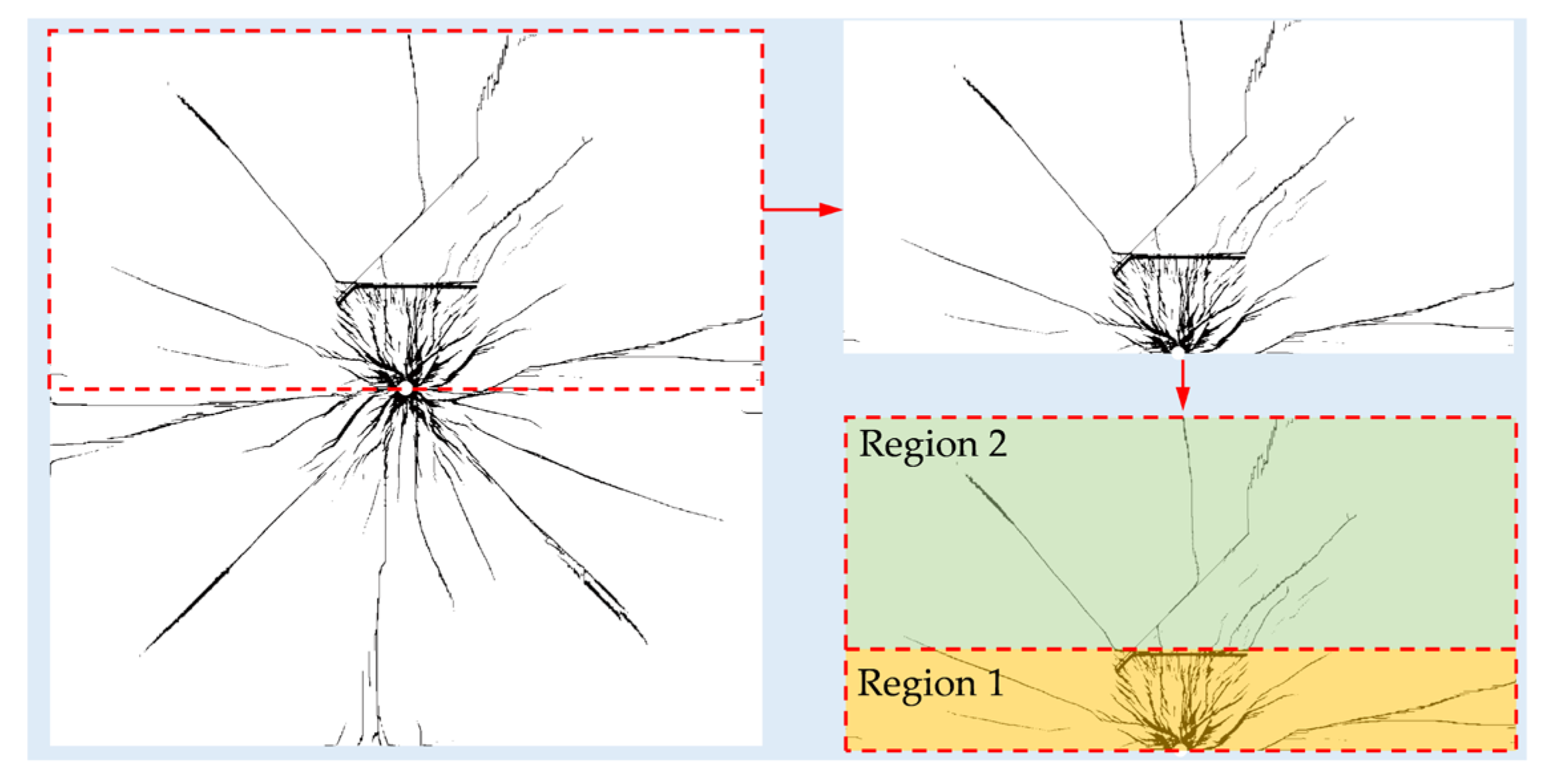
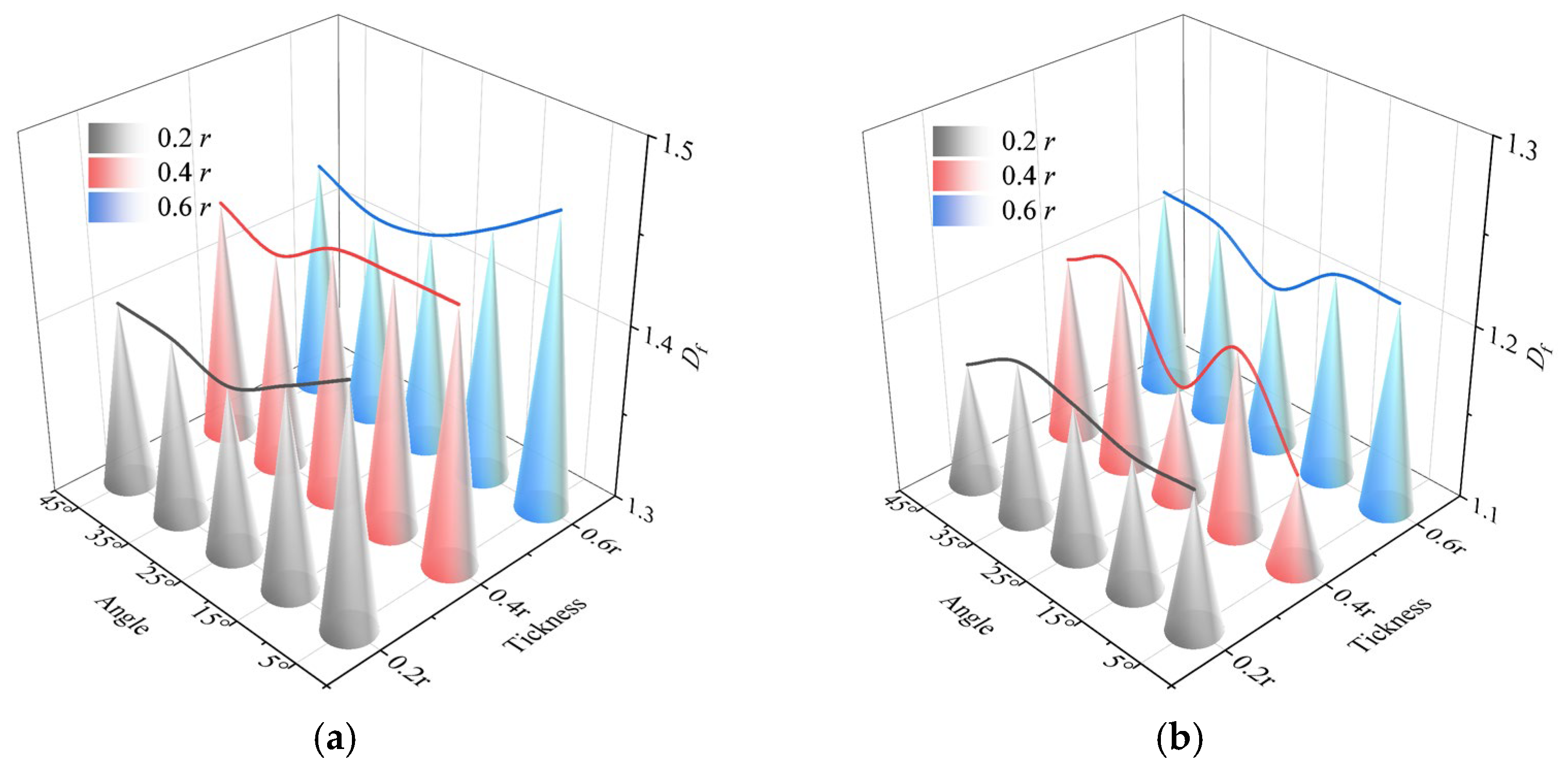
4.2. Statistical Analysis of Blasting-Induced Crack Distribution in Rock Mass
4.3. Crack Distribution in Blasted Rock Mass with Varying Joint Configurations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Silva, J.; Worsey, T.; Lusk, B. Practical Assessment of Rock Damage due to Blasting. Int. J. Min. Sci. Technol. 2019, 29, 379–385. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Zhu, Z.; Wu, Y.; Yu, H.; Gao, W.; Lv, B. Detonation Dynamics and Damage Behavior of Segmented Tunnel Charges with Shaped Liners. Buildings 2025, 15, 2815. [Google Scholar] [CrossRef]
- Dotto, M.S.; Pourrahimian, Y. The Effect of Initiation Time Delay and Sequencing on Rock Damage in Multi-Hole Blasting. Mining 2025, 5, 22. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, X.; Li, Z.; Gao, W.; Xu, Z.; Zhang, Y.; Zhou, J. Effects of In-Situ Stress on Damage and Fractal during Cutting Blasting Excavation. Fractal Fract. 2024, 8, 450. [Google Scholar] [CrossRef]
- Li, J.; Ma, G.; Huang, X. Analysis of Wave Propagation through a Filled Rock Joint. Rock Mech. Rock Eng. 2010, 43, 789–798. [Google Scholar] [CrossRef]
- Li, F.; Yang, G.; Guo, D.; Liu, X.; Wang, X.; Hu, G. Toward Sustainable Geohazard Assessment: Dynamic Response and Failure Characteristics of Layered Rock Slopes under Earthquakes via DEM Simulations. Sustainability 2025, 17, 7374. [Google Scholar] [CrossRef]
- Luo, Z.; Gao, Z.; Liu, G.; Du, C.; Liu, W.; Wang, Z. Research on the Damage Mechanism and Shear Strength Weakening Law of Rock Discontinuities under Dynamic Load Disturbance. Symmetry 2025, 17, 569. [Google Scholar] [CrossRef]
- Jiang, X.; Xue, Y.; Kong, F.; Gong, H.; Fu, Y.; Zhang, W. Dynamic Responses and Damage Mechanism of Rock with Discontinuity Subjected to Confining Stresses and Blasting Loads. Int. J. Impact Eng. 2023, 172, 104404. [Google Scholar] [CrossRef]
- Liang, X.; Ding, C.; Zhu, X.; Zhou, J.; Chen, C.; Guo, X. Visualization Study on Stress Evolution and Crack Propagation of Jointed Rock Mass under Blasting Load. Eng. Fract. Mech. 2024, 296, 109833. [Google Scholar] [CrossRef]
- Shen, Y.; Lin, B.; Lin, M.; Liu, T.; Zhang, X.; Yang, W.; Zhang, C. Experiments and Discrete Element Simulations on the Influence of Symmetrical Forms of Joints on the Propagation of Blasting Cracks. Eng. Fract. Mech. 2025, 320, 111072. [Google Scholar] [CrossRef]
- Xu, P.; Yang, R.; Guo, Y.; Guo, Z. Investigation of the Blasting-induced Crack Propagation Behavior in a Material Containing an Unfilled Joint. Appl. Sci. 2020, 10, 4419. [Google Scholar] [CrossRef]
- Li, J.; Ma, G. Analysis of Blast Wave Interaction with a Rock Joint. Rock Mech. Rock Eng. 2010, 43, 777–787. [Google Scholar] [CrossRef]
- Li, J.C.; Wu, W.; Li, H.; Zhu, J.; Zhao, J. A Thin-Layer Interface Model for Wave Propagation through Filled Rock Joints. J. Appl. Geophys. 2013, 91, 31–38. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Jiao, Y.; Liu, Y.; Xia, X.; Yu, C. Analysis for Oblique Wave Propagation across Filled Joints Based on Thin-Layer Interface Model. J. Appl. Geophys. 2014, 102, 39–46. [Google Scholar] [CrossRef]
- Miller, R.K. An Approximate Method of Analysis of the Transmission of Elastic Waves through a Frictional Boundary. J. Appl. Math. 1977, 44, 652–656. [Google Scholar] [CrossRef]
- Schoenberg, M. Elastic Wave Behavior across Linear Slip Interfaces. J. Acoust. Soc. Am. 1980, 68, 1516–1521. [Google Scholar] [CrossRef]
- Desai, C.; Zaman, M.; Lightner, J.; Siriwardane, H. Thin-Layer Element for Interfaces and Joints. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 19–43. [Google Scholar] [CrossRef]
- Duanying, W.; Zheming, Z.; Ruifeng, L.; Bang, L. Effect of Two Parallel Cracks on Main Propagating Cracks under Blasting. Explos. Shock. Waves 2019, 39, 083105. (In Chinese) [Google Scholar]
- Al-Yaari, A.; Ching, D.L.C.; Sakidin, H.; Muthuvalu, M.S.; Zafar, M.; Haruna, A.; Merican, Z.M.A.; Yunus, R.B.; Al-Dhawi, B.N.S.; Jagaba, A.H. The effects of nanofluid thermophysical properties on enhanced oil recovery in a heterogenous porous media. Case Stud. Chem. Environ. Eng. 2024, 9, 100556. [Google Scholar] [CrossRef]
- Zhai, J.; Wang, Z.; Wang, J.; Feng, C.; Li, S. Numerical Study on Blast Dynamic Response of Jointed Rock Mass under High Geostress Field. Int. J. Geomech. 2025, 25, 04025005. [Google Scholar] [CrossRef]
- Li, J.C. Wave Propagation across Non-Linear Rock Joints Based on Time-Domain Recursive Method. Geophys. J. Int. 2013, 193, 970–985. [Google Scholar] [CrossRef]
- Zhang, Q. The Transmission Process of Stress Waves at Joints. Chin. J. Geotech. Eng. 1986, 8, 99–105. (In Chinese) [Google Scholar]
- Johnson, G.R.; Holmquist, T.J. An Improved Computational Constitutive Model for Brittle Materials. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 1994; Volume 309, pp. 981–984. [Google Scholar]
- Borrvall, T.; Riedel, W. The RHT Concrete Model in LS-DYNA. In Proceedings of the 8th European LS-DYNA User Conference, Strasbourg, France, 23–24 May 2011; pp. 23–24. [Google Scholar]
- Bornstein, H.; Kuznetsov, V.; Lu, J.-P.; Stojko, S.; Freundt, J. Characterisation and Validation of the JWL Equation of State Parameters for PE4. Int. J. Impact Eng. 2022, 164, 104190. [Google Scholar] [CrossRef]
- Yang, J.; Peng, C.; Ye, Z.; Yao, C.; Zhang, X.; Ma, Y.; Zhou, C. Study on the Efficiency of Energy Transfer in the Blasting with Different Coupling Mediums for Deep Rock Mass Excavation. Eng. Fract. Mech. 2025, 319, 111048. [Google Scholar] [CrossRef]
- Sharma, K.; Desai, C. Analysis and Implementation of Thin-Layer Element for Interfaces and Joints. J. Eng. Mech. 1992, 118, 2442–2462. [Google Scholar] [CrossRef]
- Wei, X.; Zhao, Z.; Gu, J. Numerical Simulations of Rock Mass Damage Induced by Underground Explosion. Int. J. Rock Mech. Min. Sci. 2009, 46, 1206–1213. [Google Scholar] [CrossRef]
- Xiao, C.; Yang, R.; Ma, X.; Wang, Y.; Ding, C. Damage Evaluation of Rock Blasting Based on Multi-Fractal Study. Int. J. Impact Eng. 2024, 188, 104953. [Google Scholar] [CrossRef]
- Li, K.; Cheng, Y.; Fan, X. Roles of Model Size and Particle Size Distribution on Macro-Mechanical Properties of Lac du Bonnet Granite Using Flat-Joint Model. Comput. Geotech. 2018, 103, 43–60. [Google Scholar] [CrossRef]
- Ding, C.; Yang, R.; Yang, L. Experimental Results of Blasting-induced Cracking Fractal Characteristics and Propagation Behavior in Deep Rock Mass. Int. J. Rock Mech. Min. Sci. 2021, 142, 104772. [Google Scholar] [CrossRef]
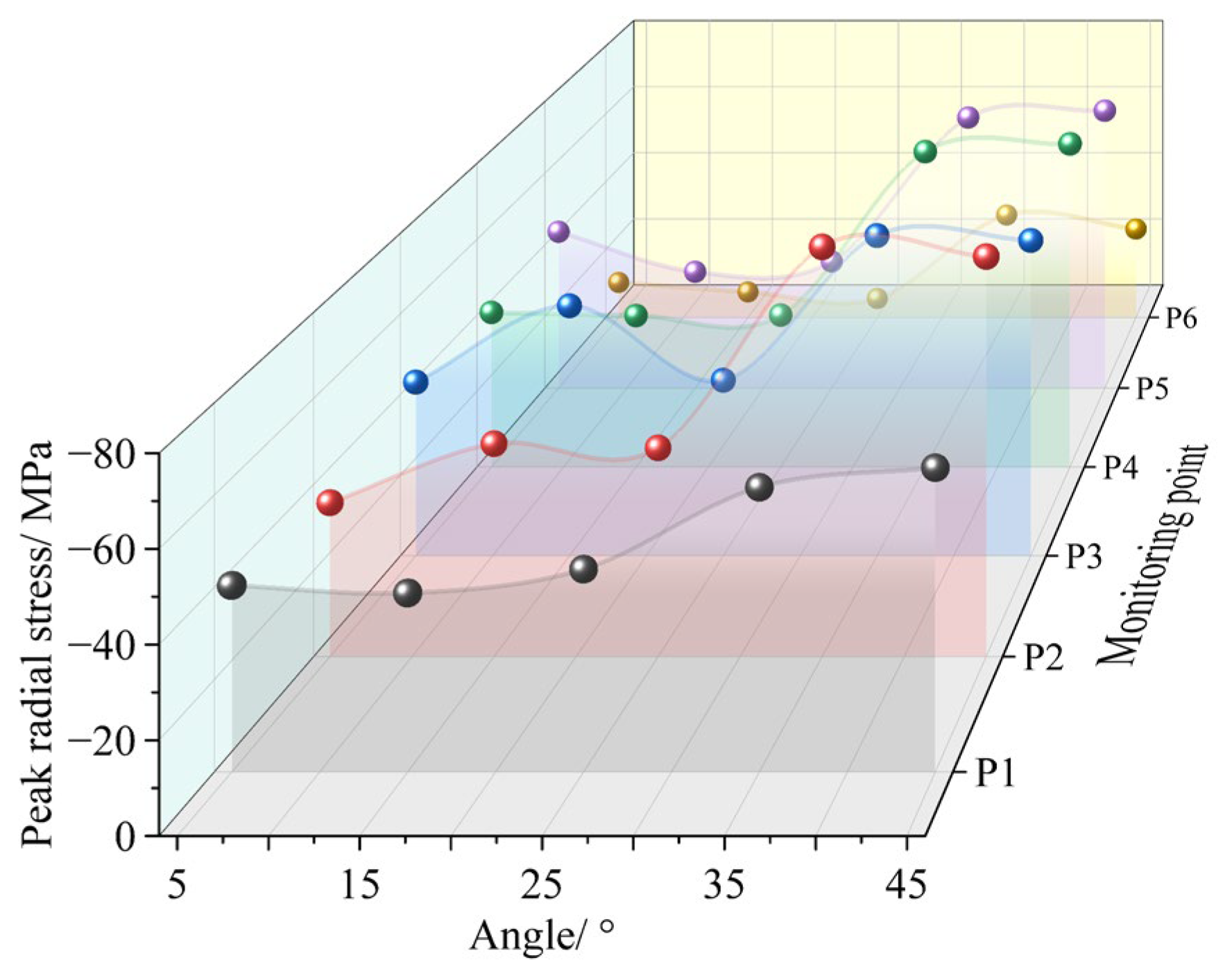
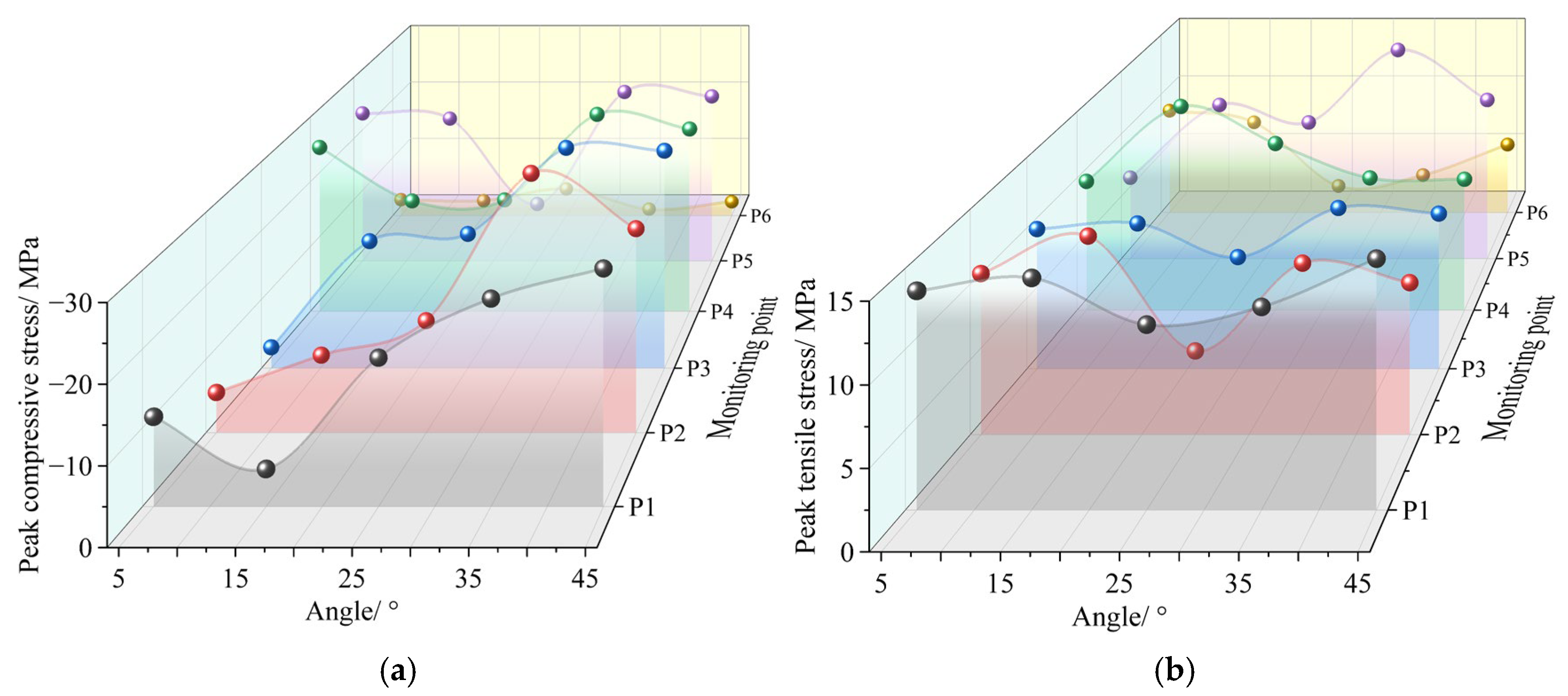
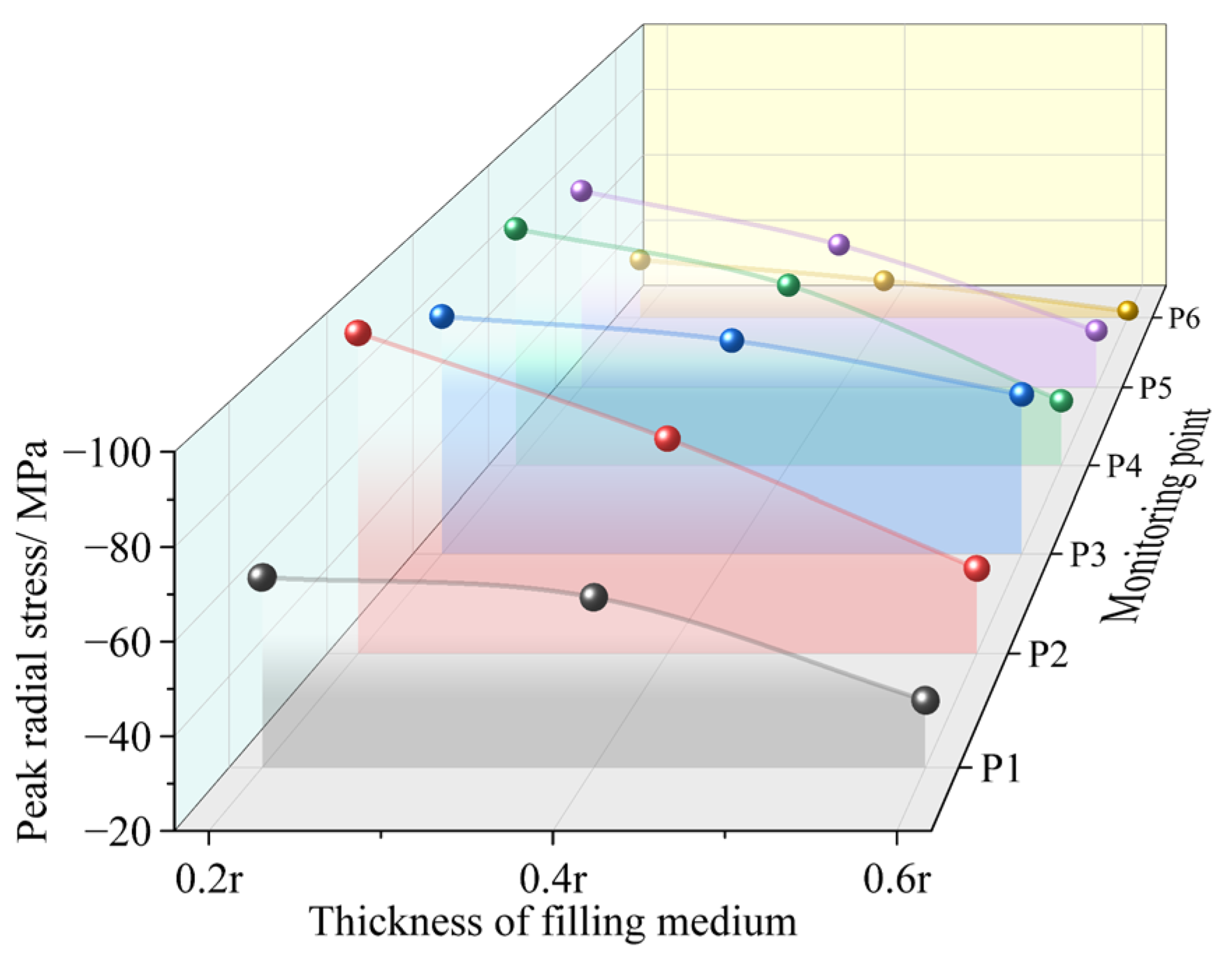
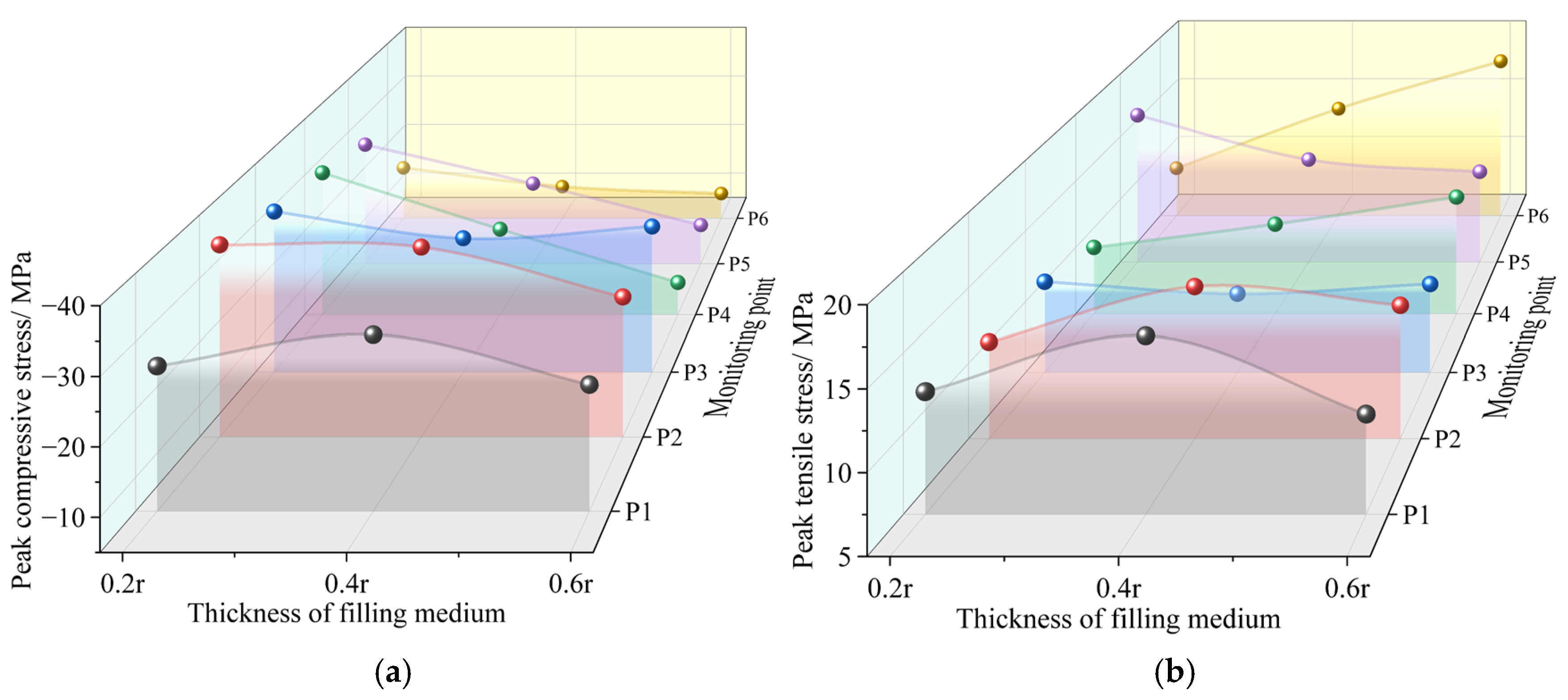
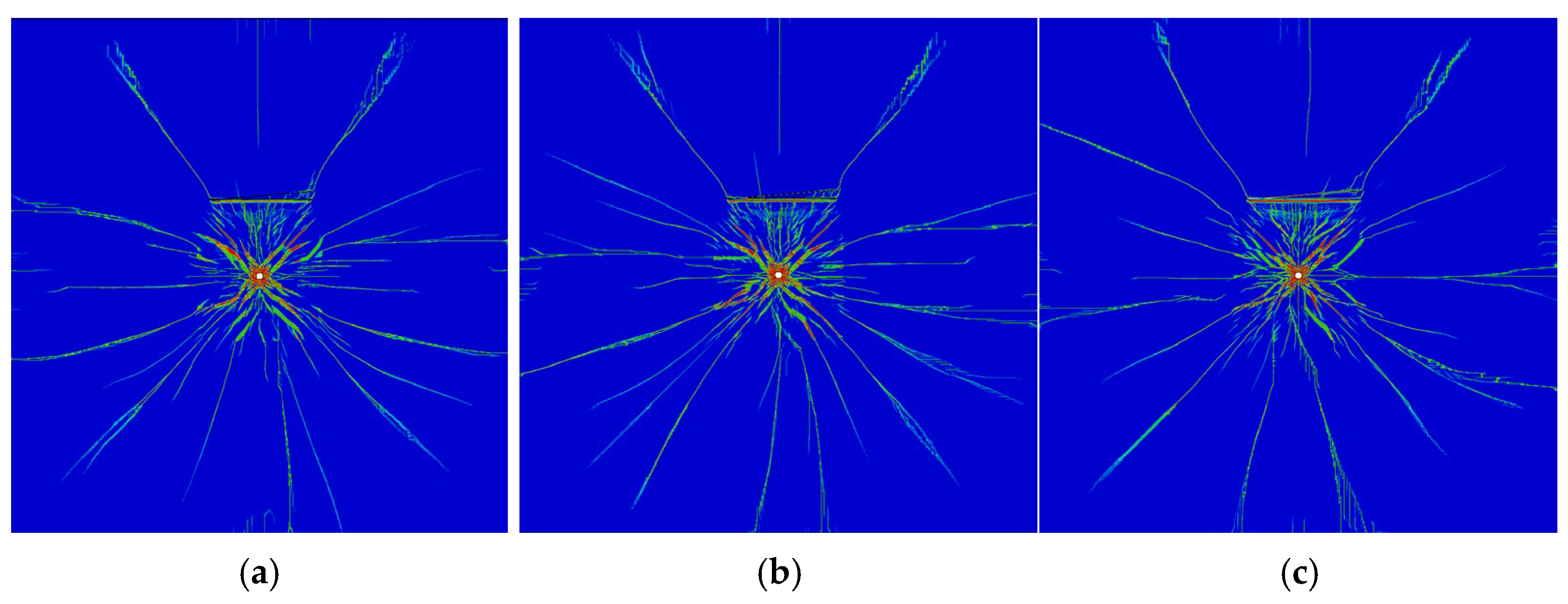
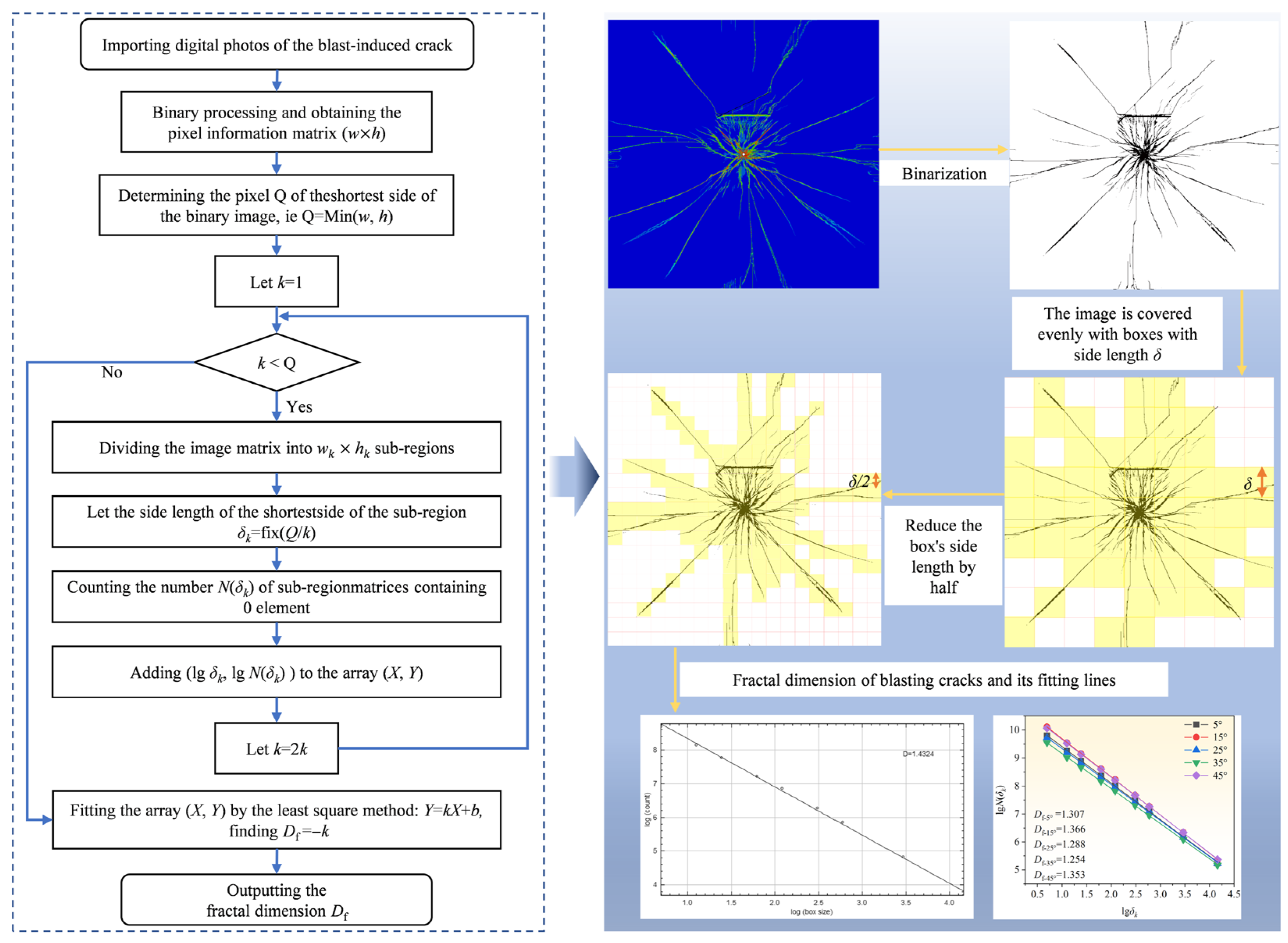
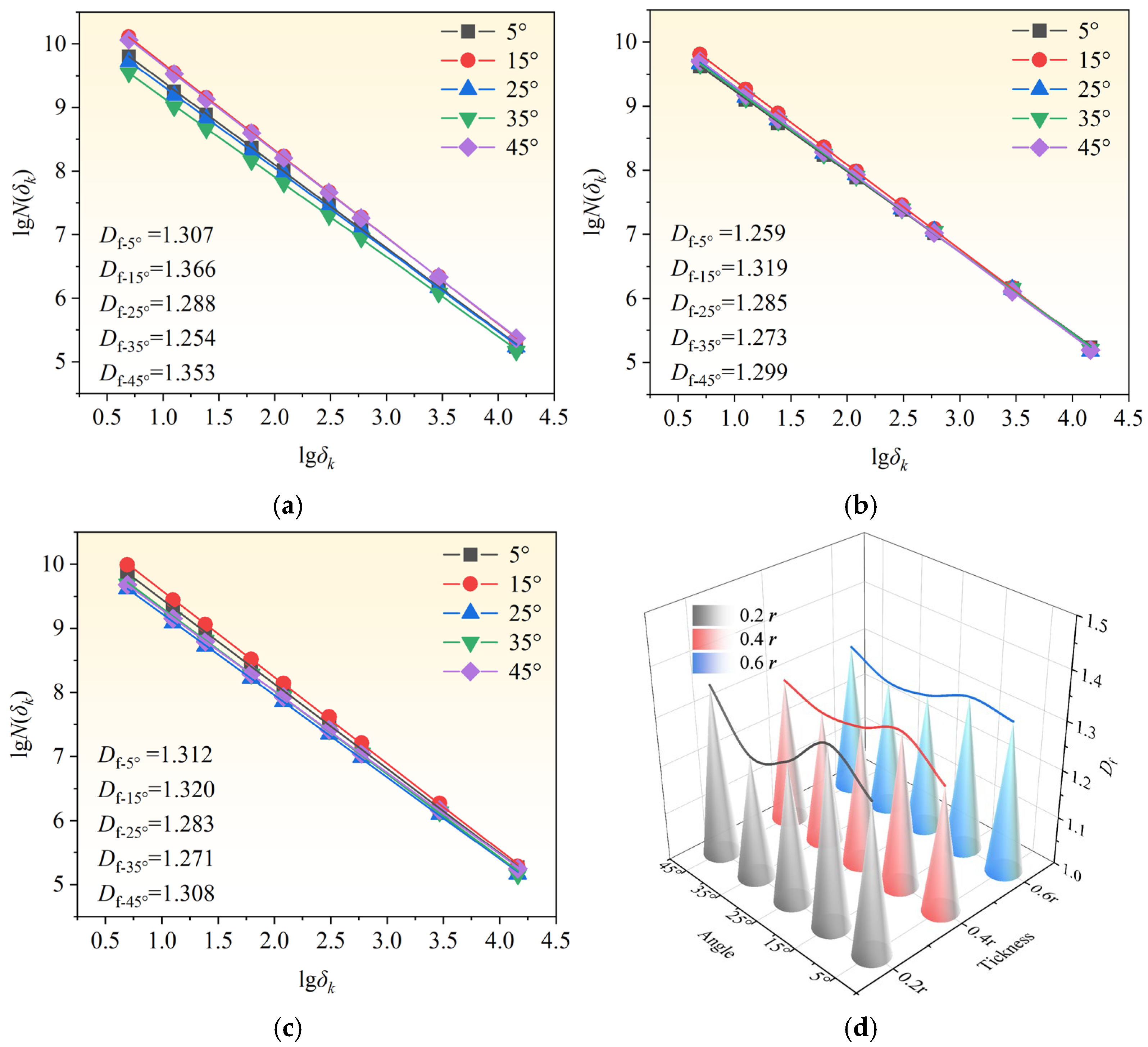
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Mass density ρ0/g/cm3 | 2.62 | Elastic shear modulus G/GPa | 8.65 |
| Compressive strength fc/GPa | 0.112 | Compaction pressure Pco/GPa | 6.00 |
| Damage parameter D1 | 0.04 | Damage parameter D2 | 1.0 |
| Relative shear strength fs* | 0.11 | Relative tensile strength ft* | 0.12 |
| Parameter for polynomial EOS T2 | 0 | Parameter for polynomial EOS B0 | 1.22 |
| Tensile yield surface parameter Gt* | 0.68 | Tensile strain rate dependence exponent βt | 0.10 |
| Initial porosity α0 | 1.00 | Break tensile strain rate /s−1 | 3 × 1025 |
| Failure surface parameter A | 1.60 | Parameter for polynomial EOS B1 | 1.22 |
| Crush pressure Pel/GPa | 0.07 | Tensile strain rate dependence exponent βc | 0.20 |
| Failure surface parameter N | 0.61 | Break compressive strain rate /s−1 | 3 × 1025 |
| Parameter for polynomial EOS T1/GPa | 55.44 | Compressive yield surface parameter Gc* | 0.53 |
| Hugoniot polynomial coefficient A1/GPa | 55.44 | Hugoniot polynomial coefficient A2/GPa | 67.64 |
| Hugoniot polynomial coefficient A3/GPa | 32.44 | Reference tensile strain rate /s−1 | 3 × 10−5 |
| Reference compressive strain rate /s−1 | 3 × 10−6 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Density ρ/g/cm3 | 1.3 | Detonation velocity D/m/s | 4000 | Initial pressure PCJ | 1.60 |
| Material constant B/GPa | 0.182 | Material constant R1 | 4.2 | Material constant R2 | 0.9 |
| Material constant A/GPa | 214.4 | Material constant ω | 0.15 | Relative volume Ve | 1.0 |
| Internal energy per unit volume E0/GPa | 4.192 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Density ρ/g/cm3 | 1.16 | Elastic modulus Ej/GPa | 22.00 | Shear modulus Et/GPa | 4.00 |
| Yield strength σy/GPa | 2.50 | Poisson’s ratio υ | 0.30 | Hardening parameter βj | 0.9 |
| α | Radial Stress | Circumferential Stress | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Compressive Stress | Compressive Stress | Tensile Stress | |||||||
| 0.2 r | 0.4 r | 0.6 r | 0.2 r | 0.4 r | 0.6 r | 0.2 r | 0.4 r | 0.6 r | |
| 15° | −27.04 | 51.78 | 79.95 | −6.56 | 51.18 | 87.23 | −11.39 | 55.69 | 68.60 |
| 25° | −45.70 | 30.74 | 98.52 | 67.13 | 144.66 | 249.23 | −73.95 | 8.84 | 6.05 |
| 35° | 192.92 | 200.66 | 112.98 | −1.11 | 449.45 | 312.91 | −63.25 | 62.79 | 109.30 |
| 45° | 152.82 | −12.98 | −33.25 | −12.98 | 370.64 | 331.01 | −33.25 | 33.83 | 65.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, X.; Wu, Y.; Li, Z.; Gao, W.; Wang, F.; Zhang, Y. Investigation of Stress Wave Propagation and Crack Propagation Characteristics in Intersecting-Joint Mass Under Blasting. Fractal Fract. 2025, 9, 693. https://doi.org/10.3390/fractalfract9110693
Yang X, Zhang X, Wu Y, Li Z, Gao W, Wang F, Zhang Y. Investigation of Stress Wave Propagation and Crack Propagation Characteristics in Intersecting-Joint Mass Under Blasting. Fractal and Fractional. 2025; 9(11):693. https://doi.org/10.3390/fractalfract9110693
Chicago/Turabian StyleYang, Xian, Xiaojun Zhang, Yongbo Wu, Zhuo Li, Wenxue Gao, Feng Wang, and Yang Zhang. 2025. "Investigation of Stress Wave Propagation and Crack Propagation Characteristics in Intersecting-Joint Mass Under Blasting" Fractal and Fractional 9, no. 11: 693. https://doi.org/10.3390/fractalfract9110693
APA StyleYang, X., Zhang, X., Wu, Y., Li, Z., Gao, W., Wang, F., & Zhang, Y. (2025). Investigation of Stress Wave Propagation and Crack Propagation Characteristics in Intersecting-Joint Mass Under Blasting. Fractal and Fractional, 9(11), 693. https://doi.org/10.3390/fractalfract9110693






