Pore Evolution and Fractal Characteristics of Marine Shale: A Case Study of the Silurian Longmaxi Formation Shale in the Sichuan Basin
Abstract
1. Introduction
2. Geological Setting
3. Sample and Method
3.1. Samples and Simulation Experiment
3.2. Supporting Experiments
3.3. Fractal Dimension Analysis
3.3.1. LTNA Data with FHH Model
3.3.2. HPMI Data with Capillary Bundle Model
4. Results
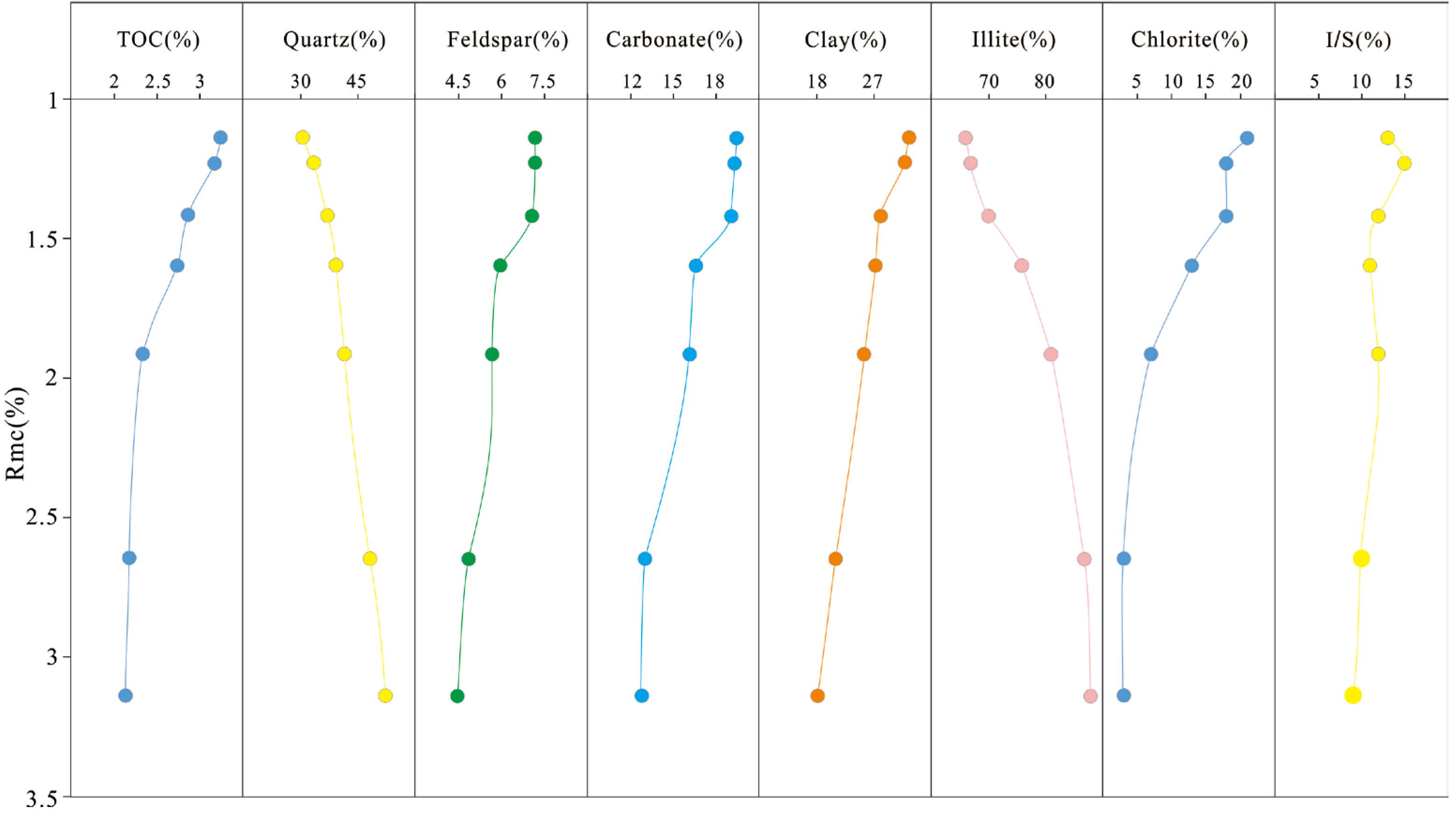
4.1. Evolution of TOC and Mineral Composition
4.2. SEM Image Analysis and Pore Morphology
4.2.1. Organic Pores
4.2.2. Inorganic Pores and Microfracture
4.3. Evolution of Shale Porosity and Pore Structures Parameter
4.3.1. Porosity Characterization
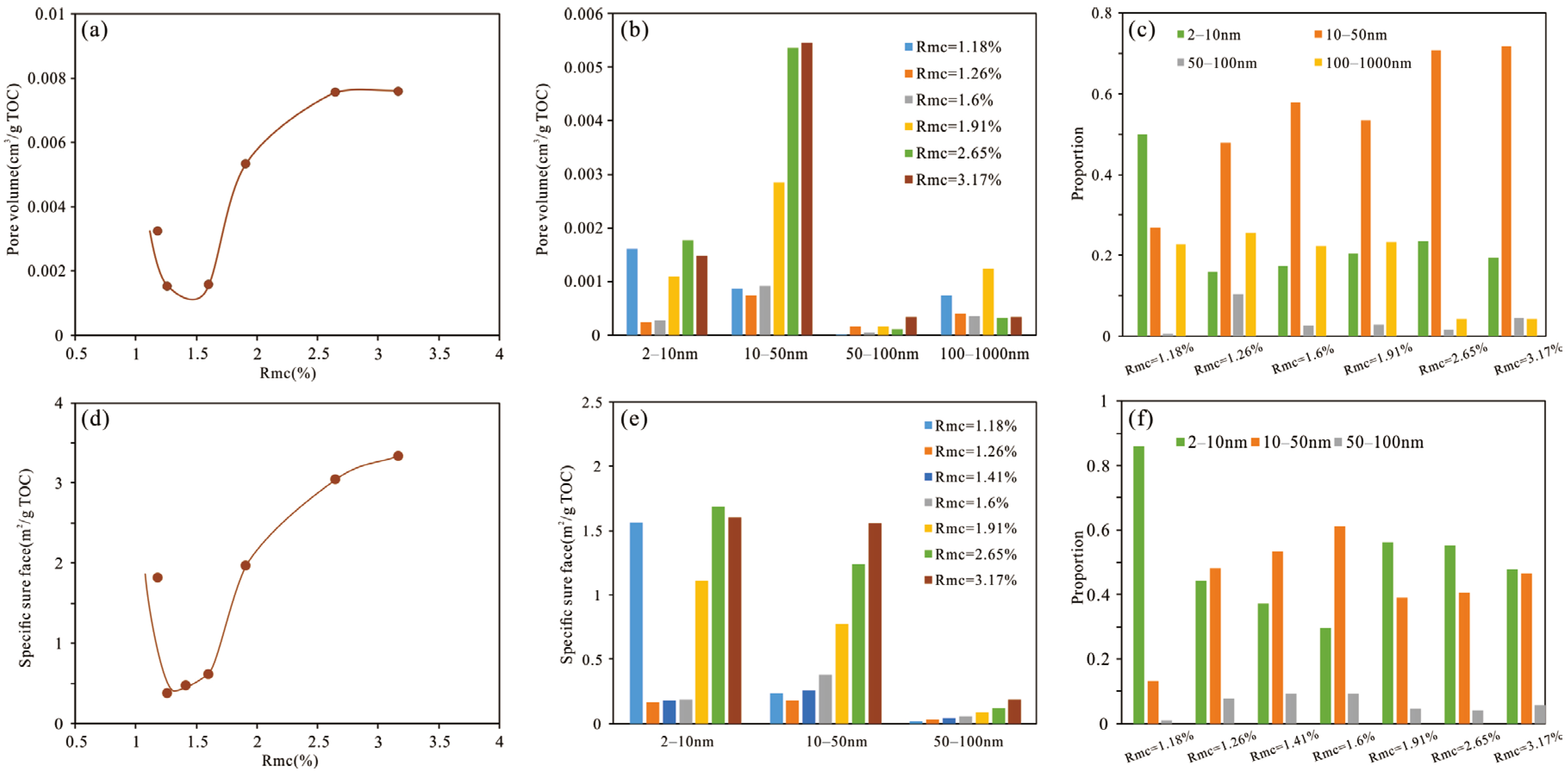
4.3.2. Pore Structure Parameter Characterization
4.4. Fractal Characteristics
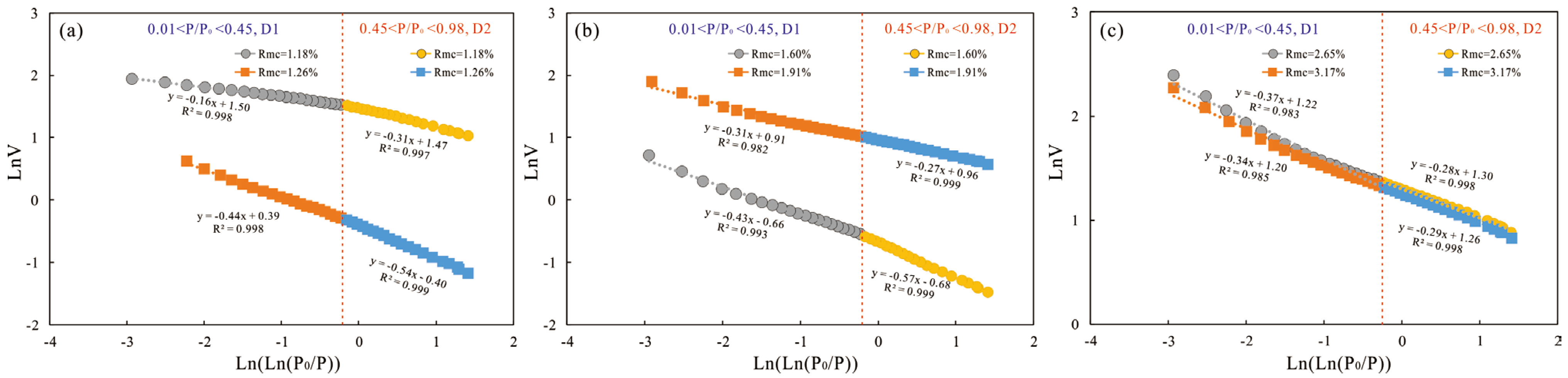
4.4.1. The Fractal Dimension Calculated by LTNA
4.4.2. The Fractal Dimension Calculated by HPMI
5. Discussion
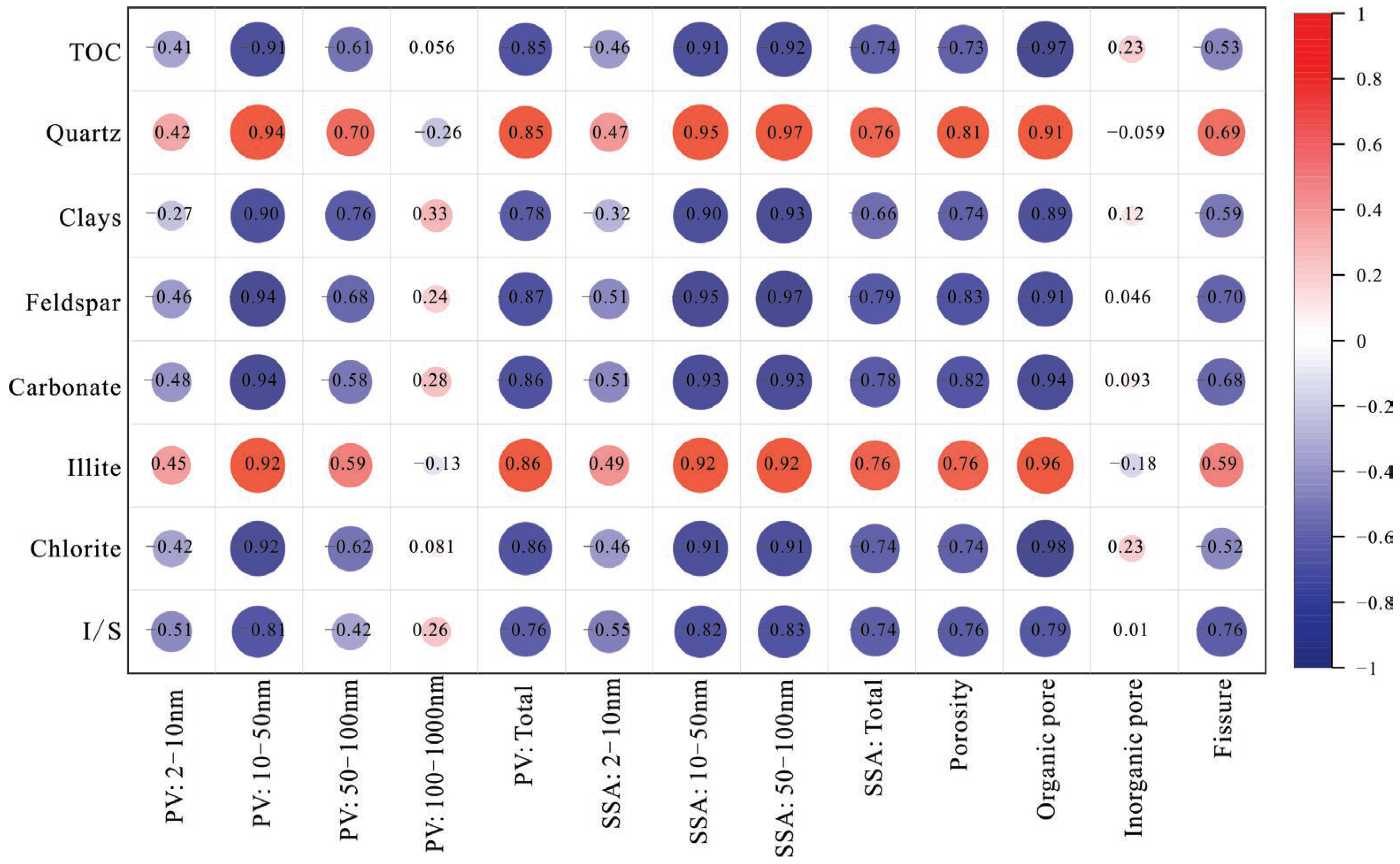
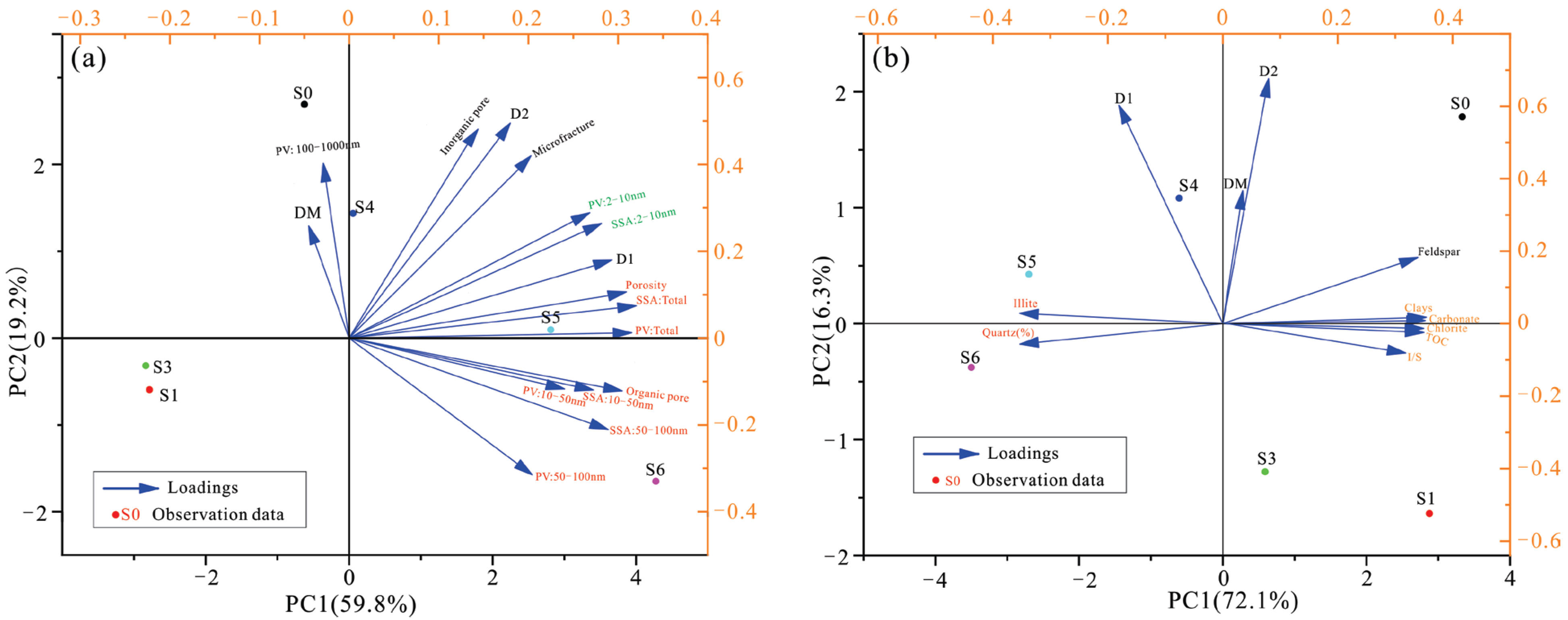
5.1. Shale Composition–Pore Structure Co-Evolution
5.2. Fractal Dimension Characteristics and Influencing Factors
5.2.1. Relationship Between Fractal Dimension and Pore Development Characteristics
5.2.2. Relationship Between Fractal Dimension and Shale Components
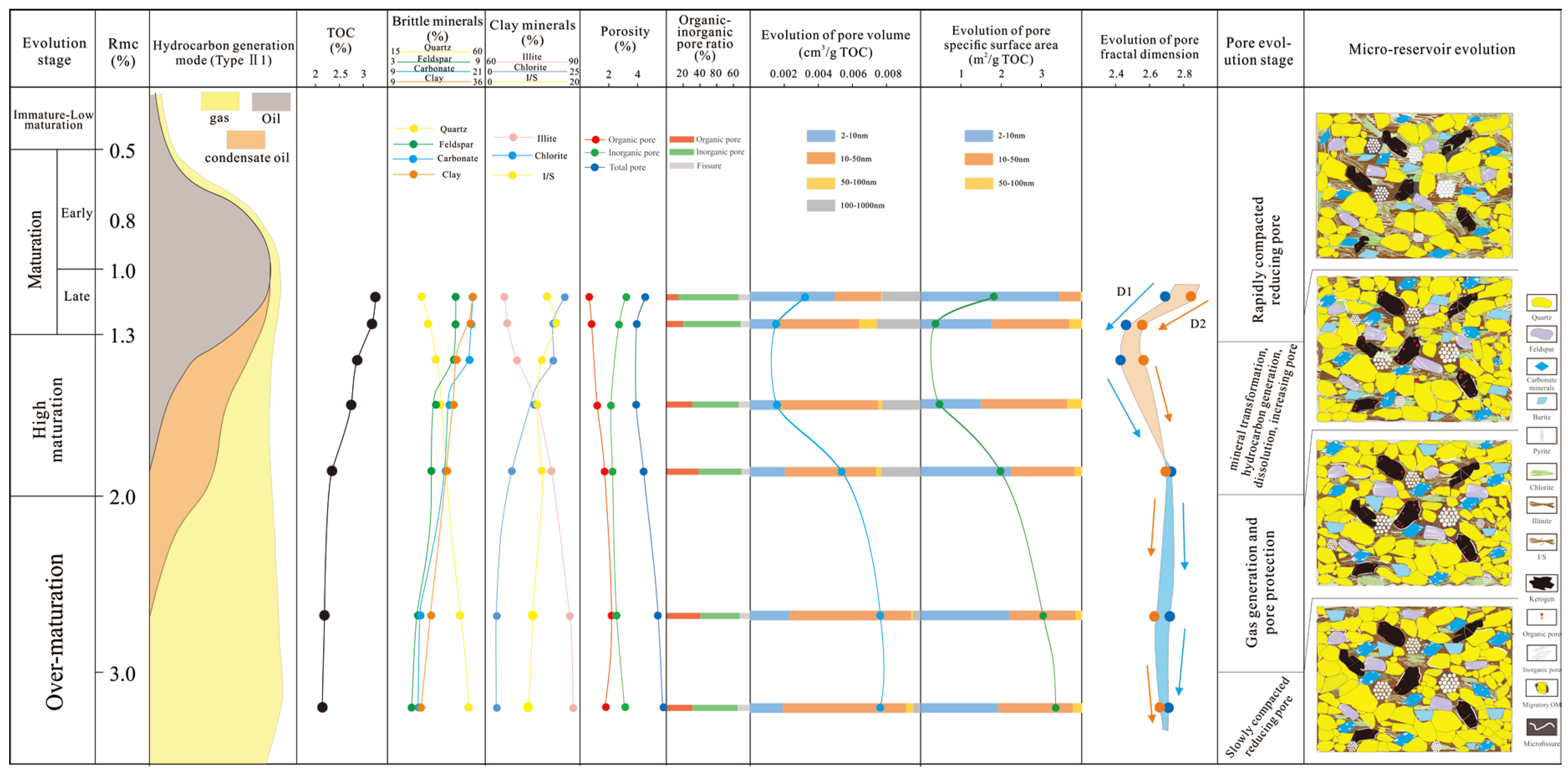
5.3. Comprehensive Evolutionary Model
- (1)
- Stage One (Rmc < 1.3%): Before organic matter reaches maturity, pore development rapidly decreases due to compaction, with residual primary intergranular pores dominating [46]. As kerogen undergoes thermal cracking and volume contraction, small organic pores and fractures begin to form on the surface and edges of the organic matter, gradually increasing the relative abundance of organic pores. However, adsorption, filling, and ongoing compaction by retained hydrocarbons continue to suppress pore development. The PV and SSA of most pores decline, especially for 2–10 nm pores. Compaction results in more regular pore geometries and smoother pore surfaces, reducing both the PV and SSA. Consequently, fractal dimension D1 decreases, indicating lower surface roughness, complexity, and higher self-similarity. Quartz content correlates positively with D1 (Figure 12b), reflecting its resistance to compaction, the enhancement of reservoir brittleness, and the promotion of pore and microfracture preservation. Retained hydrocarbons tend to smooth originally irregular pore surfaces, reducing tortuous pathways and surface heterogeneity for gas adsorption, which further lowers D1. Together, these effects suppress the development of inorganic pores and microfractures, decrease overall pore complexity, and lead to a gradual decline in fractal dimension D2.
- (2)
- Stage Two (Rmc = 1.3–2.0%): With increasing thermal maturity, kerogen and residual hydrocarbons break down into condensates and wet gas, promoting the formation of abundant nanoscale pores and reopening previously occluded inorganic pores. Consequently, the proportion of organic pores steadily increases. Organic acids released from kerogen enhance the dissolution of “depletion” components such as feldspar and carbonates, and drive clay mineral transformation, notably increasing the intensity of clay alteration. During the late high maturity stage, the porosity of inorganic pores and microfractures gradually increases, accompanied by a rise in fractal dimension D2. The proportion of pores sized 5–60 nm significantly grows, indicating enhanced pore development and a marked increase in fractal dimension D1. Dissolution produces numerous pores with rough, uneven surfaces characterized by high curvature, increasing surface complexity, tortuosity of adsorption pathways, and steepening adsorption isotherms, resulting in higher D1 values. Moreover, dissolution enlarges existing pores and opens blocked pores, enhancing pore connectivity and spatial heterogeneity. Dissolution pores in shale are typically irregular and asymmetric, forming multiscale pore systems that increase pore space complexity and contribute to a higher D2. Additionally, illitization of clay minerals forms irregular plate-like structures and alters microscopic pore morphology, promoting pore structure reorganization and pore throat expansion. This significantly increases the roughness and complexity of pore surfaces and networks, likely elevating both D1 and D2.
- (3)
- Stage Three (Rmc = 2.1–3.0%): The cracking of kerogen alkyl side chains generates C1–C3 compounds. Retained hydrocarbons and wet gas continue to crack into methane, leading to the formation of numerous spherical organic pores. Due to the “hydrocarbon generation pressure preservation” effect, both the quantity and size of organic pores peak at Ro = 2.7%. In contrast, inorganic diagenetic processes, primarily illitization and compaction, reduce the porosity of inorganic pores and microfractures. After an initial increase, pore development stabilizes, with a notable rise in pores within the 10–50 nm range. As a result, D1 initially increases before stabilizing, while D2 gradually decreases.
- (4)
- Stage Four (Rmc > 3.0%): At this stage, shale components stabilize, and organic matter evolution is limited to kerogen decarbonation reactions. Inorganic diagenesis is dominated by intense compaction. As a result, organic pores become less prevalent, while inorganic pores and microfractures increasingly dominate. Total porosity and pore development continue to decline gradually, causing D1 to decrease further. In contrast, D2 shows an increasing trend. Total PV slightly decreases due to inorganic compaction, reflecting a slow reduction in porosity and pore development. Pores smaller than 10 nm decrease significantly, whereas pores larger than 10 nm increase. Meanwhile, SSA increases, likely due to the closure of micropores caused by carbonization and compaction, while overpressure-induced microfracturing and brittle failure at organic–mineral interfaces enlarge the larger pores. These changes enhance pore heterogeneity and complexity, contributing to the rise in D2.
6. Conclusions
- (1)
- The evolution of mineral composition indicates a gradual increase in quartz content, accompanied by a decline in clay, feldspar, and carbonate minerals. The thermal evolution of organic matter is primarily reflected in the formation of organic pores and marginal shrinkage fissures on the kerogen surface, while retained hydrocarbons filling inorganic pores generate numerous nanoscale pores in the later stages. Inorganic diagenetic evolution is mainly characterized by compaction, dissolution, and clay mineral transformation.
- (2)
- Throughout the simulation, the porosity evolution exhibited distinct stages of rapid decline, notable increase, and relative stabilization. The proportion of organic pores peaked at approximately Rmc = 2.7%. Both the PV and SSA showed a trend of initial decrease followed by an increase. However, the PV declined gradually after reaching its maximum in the late overmature stage. During the entire process, the dominant pore size contributing to the PV ranged from 10–50 nm, while for the SSA, it ranged from 2–50 nm.
- (3)
- The FHH model results show that D1 (average 2.62) is lower than D2 (average 2.66), indicating that pore surface roughness across different maturity levels is less complex than the internal pore structure. DM values derived from the capillary bundle model range from 2.32 to 2.94 (average 2.69), higher than the average values of D1 and D2, suggesting that macropores possess more complex pore structures.
- (4)
- The correlation matrix reveals a co-evolutionary relationship between shale composition and pore structure. The PCA analysis demonstrates a strong association between inorganic and microfracture porosity with fractal dimension D2, whereas organic pore porosity, dominant pore diameter, PV, and SSA are closely linked to D1. D1 serves as an indicator of pore development extent and reflects changes in components that are either consumed or generated during thermal evolution. Based on shale composition, fractal dimensions, and pore structure evolution patterns, a comprehensive evolution model for pores and fractal dimensions in organic-rich shale was established.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BET | Brunauer–Emmett–Teller |
| D1 | The fractal dimension indicative of pore surface roughness, calculated using the FHH model from the low-pressure region (0.1 < P/P0 < 0.45) of N2 adsorption |
| D2 | The fractal dimension indicative of pore structure complexity, calculated using the FHH model from the high-pressure region (0.45 < P/P0 < 0.98) of N2 adsorption |
| DM | Fractal dimension indicating pore heterogeneity, calculated via the capillary bundle model from mercury intrusion over 20–1000 nm pore sizes |
| FE-SEM | Field Emission-Scanning Electron Microscope |
| FHH | Frenkel–Halsey–Hill |
| HPMI | High pressure mercury intrusion |
| LTNA | Low-Temperature Nitrogen Adsorption |
| MIP | Mercury intrusion porosimetry |
| NMR | Nuclear Magnetic Resonance |
| PC | Principal Component |
| PCA | Principal Component Analysis |
| PV | Pore Volume |
| Rmc | Reflectance estimated from Raman spectroscopy |
| SSA | Specific Surface Area |
| T2 | Transverse relaxation time from NMR |
| TOC | The Organic Carbon |
| XRD | X-ray Diffraction |
References
- Guo, X.; Hu, Z.; Li, S.; Zheng, L.; Zhu, D.; Liu, J.; Shen, B.; Du, W.; Yu, L.; Liu, Z.; et al. Progress and prospect of natural gas exploration and research in deep and ultra-deep strata. Pet. Sci. Bull. 2023, 4, 461–474. (In Chinese) [Google Scholar]
- Guo, X.; Wang, R.; Shen, B.; Wang, G.; Wan, C.; Wang, Q. Geological characteristics, resource potential, and development direction of shale gas in China. Pet. Explor. Dev. 2025, 52, 15–28. [Google Scholar] [CrossRef]
- Zou, C.; Dong, D.; Wang, S.; Li, J.; Li, X.; Wang, Y.; Li, D.; Cheng, K. Geological characteristics and resource potential of shale gas in China. Pet. Explor. Dev. 2010, 37, 641–653. [Google Scholar] [CrossRef]
- Guo, X.; Teng, B.; Wei, X.; Yu, L.; Lu, X.; Sun, L.; Wei, F. Occurrence mechanism and exploration potential of deep marine shale gas in Sichuan Basin. Acta Pet. Sin. 2022, 43, 453–468. (In Chinese) [Google Scholar]
- Li, X.; Jiang, Z.; Wang, S.; Wu, F.; Miao, Y.; Wang, X.; Wang, H.; Liu, X. Differences of marine and transitional shales in the case of dominant pore types and exploration strategies, in China. J. Nat. Gas Sci. Eng. 2022, 103, 104628. [Google Scholar] [CrossRef]
- Teng, B.; Qiu, N.; Yu, L.; Guo, T.; Feng, Q.; Shen, B.; Lu, L.; Zeng, W.; Li, H.; Chen, W.; et al. Differential preservation mechanisms of marine shale gas under varying burial conditions in southern China. Acta Geol. Sin. 2024, 98, 3285–3301. (In Chinese) [Google Scholar]
- Wei, F.; Liu, Z.; Chen, F.; Yuan, T.; Li, F. Characteristics of the deep and ultra-deep shale reservoirs of the Wufeng–Longmaxi formations in the southeastern Sichuan Basin and the significance of shale gas exploration. Pet. Geol. Exp. 2023, 45, 751–760. (In Chinese) [Google Scholar]
- Wang, D.; Jiang, Z.; Du, W.; Liu, D.; Chen, W.; Yang, Y.; Feng, X. Pore structure difference characteristics and evolution model in the process of gas reservoir uplift: A case study of the shale reservoir of Wufeng Formation- Longmaxi Formation in Sichuan basin and its surrounding areas. Acta Geol. Sin. 2025, 99, 1381–1397. [Google Scholar]
- Xu, L.; Yang, K.; Wei, H.; Liu, L.; Li, X.; Chen, L.; Xu, T.; Wang, X. Diagenetic evolution sequence and pore evolution model of Mesoproterozoic Xiamaling organic-rich shale in Zhangjiakou, Hebei, based on pyrolysis simulation experiments. Mar. Petrol. Geol. 2021, 132, 105233. [Google Scholar] [CrossRef]
- Wang, X.M. Formation and Evolution of Pores in Organic-Rich Shale and Its Controlling on Shale Gas Content. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2020. (In Chinese). [Google Scholar]
- Guo, S.; Mao, W. Division of diagenesis and pore evolution of a Permian Shanxi shale in the Ordos Basin, China. J. Petrol. Sci. Eng. 2019, 182, 106351. [Google Scholar] [CrossRef]
- Wang, F.; Feng, Z.; Wang, X.; Zeng, H. Effect of organic matter, thermal maturity and clay minerals on pore formation and evolution in the Gulong Shale, Songliao Basin, China. Geoenergy Sci. Eng. 2023, 223, 211507. [Google Scholar] [CrossRef]
- Qian, C.; Li, X.; Shen, W.; Zhang, Q.; Guo, W.; Hu, Y.; Cui, Y.; Jia, Y. Study on the Pore Structure and Fractal Characteristics of Different Lithofacies of Wufeng–Longmaxi Formation Shale in Southern Sichuan Basin, China. ACS Omega 2022, 7, 8724–8738. [Google Scholar] [CrossRef] [PubMed]
- Guan, Q.; Dong, D.; Sun, S.; Hu, L.; Qi, L.; Li, C.; Chen, C.; Chen, X. Fractal characteristics of organic-rich shale pore structure and its geological implications: A case study of the Lower Silurian Longmaxi Formation in the Weiyuan block, Sichuan Basin. Nat. Gas Ind. 2024, 44, 108–118. (In Chinese) [Google Scholar]
- Guo, X.; Huang, Z.; Zhao, L.; Han, W.; Ding, C.; Sun, X.; Yan, R.; Zhang, T.; Yang, X.; Wang, R. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Sun, W.; Zuo, Y.; Wu, Z.; Liu, H.; Xi, S.; Shui, Y.; Wang, J.; Liu, R.; Lin, J. Fractal analysis of pores and the pore structure of the Lower Cambrian Niutitang shale in northern Guizhou province: Investigations using NMR, SEM and image analyses. Mar. Pet. Geol. 2019, 99, 416–428. [Google Scholar] [CrossRef]
- Avnir, D.; Jaroniec, M. An isotherm equation for adsorption on fractal surfaces of heterogeneous porous materials. Langmuir 1989, 5, 1431–1433. [Google Scholar] [CrossRef]
- Neimark, A.V.; Unger, K.K. Method of discrimination of surface fractality. J. Colloid Interface Sci. 1993, 158, 412–419. [Google Scholar] [CrossRef]
- Pfeifer, P.; Wu, Y.; Cole, M.W.; Krim, J. Multilayer adsorption on a fractally rough surface. Phys. Rev. Lett. 1989, 62, 1997–2000. [Google Scholar] [CrossRef] [PubMed]
- Menger, K. General Spaces and Cartesian Spaces I. Communications to the Amsterdam; Academy of Sciences: 1926; Reprinted in Classics on Fractals; Edgar, G.A., Ed.; Addison-Wesley: Boston, MA, USA, 1993; pp. 3–9. [Google Scholar]
- Chang, J.; Fan, X.; Jiang, Z.; Wang, X.; Chen, L.; Li, J.; Wu, L.; Wan, C.; Chen, Z. Differential impact of clay minerals and organic matter on pore structure and its fractal characteristics of marine and continental shales in China. Appl. Clay Sci. 2022, 216, 106334. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Jiang, S.; Li, Z.; Song, Y.; Jiang, H.; Qiu, H.; Cao, X.; Miao, Y. Various controlling factors of matrix-related pores from differing depositional shales of the Yangtze Block in south China: Insight from organic matter isolation and fractal analysis. Mar. Pet. Geol. 2020, 111, 720–734. [Google Scholar] [CrossRef]
- Li, Y.; Liu, D.; Feng, X.; Zhao, F.; Chen, Y.; Wang, Y.; Lin, R.; Du, W.; Fan, Q.; Song, Y.; et al. Heterogeneity characteristics and its controlling factors of marine shale reservoirs from the Wufeng–Longmaxi Formation in the Northern Guizhou area. Geol. China 2024, 51, 780–798. (In Chinese) [Google Scholar]
- Wang, F.; Guo, S. Influential factors and model of shale pore evolution: A case study of a continental shale from the Ordos Basin. Mar. Petrol. Geol. 2019, 102, 271–282. [Google Scholar] [CrossRef]
- Lu, C.; Xiao, X.; Gai, H.; Feng, Y.; Li, G.; Meng, G.; Gao, P. Nanopore structure characteristics and evolution of type III kerogen in marine-continental transitional shales from the Qinshui basin, northern China. Geoenergy Sci. Eng. 2023, 221, 211412. [Google Scholar] [CrossRef]
- Liu, B.; Mohammadi, M.; Ma, Z.; Bai, L.; Wang, L.; Xu, Y.; Ostadhassan, M.; Hemmati-Sarapardeh, A. Evolution of porosity in kerogen type I during hydrous and anhydrous pyrolysis: Experimental study, mechanistic understanding, and model development. Energy 2023, 338, 127149. [Google Scholar] [CrossRef]
- Cao, T.; Deng, M.; Cao, Q.; Huang, Y.; Yu, Y.; Cao, X. Pore formation and evolution of organic-rich shale during the entire hydrocarbon generation process: Examination of artificially and naturally matured samples. J. Nat. Gas Sci. Eng. 2021, 93, 104020. [Google Scholar] [CrossRef]
- He, Q.; Chen, S.; Li, S.; Guo, B.; Lu, J.; Li, Y.; Li, X.; Zhao, L.; Ma, Z. Organic geochemical characteristics and hydrocarbon generation mechanism of marine-continental transitional organic-rich shale: A case study from the Shanxi formation in the eastern margin of the Ordos Basin. J. Pet. Sci. Eng. 2022, 219, 111116. [Google Scholar] [CrossRef]
- Wu, J.; Li, H.; Yang, X.; Zhao, S.; Guo, W.; Sun, Y.; Liu, Y.; Liu, Z. Types and combinations of deep marine shale laminae and their effects on reservoir quality: A case study of the first submember of Member 1 of Longmaxi Formation in Luzhou block, south Sichuan Basin. Acta Pet. Sin. 2023, 44, 1517–1531. (In Chinese) [Google Scholar]
- Gu, M.; Liu, R.; Zhang, H.; He, Y.; Li, X.; Hao, Y.; Jiang, H.; Li, W. Characteristics and geological response of Caledonian tectonic movement in the Sichuan Basin. Nat. Gas Ind. 2023, 43, 32–43. (In Chinese) [Google Scholar]
- Wang, H.; Shi, Z.; Zhou, T.; Zhao, Q.; Sun, S.; Qi, L.; Liang, P. Types and characteristics of sweet spots of marine black shale and significance for shale gas exploration: A case study of Wufeng–Longmaxi in southern Sichuan Basin. Nat. Gas Ind. 2023, 43, 1–13. (In Chinese) [Google Scholar]
- Zou, C.; Dong, D.; Wang, Y.; Li, X.; Huang, J.; Wang, S.; Guan, Q.; Zhang, C.; Wang, H.; Liu, H.; et al. Shale gas in China: Characteristics, challenges and prospects (II). Pet. Explor. Dev. 2016, 43, 166–178. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, N.; Yang, Y.; Rui, X.; Zhou, Y.; Fang, G.; Wu, H.; Shen, B.; Cheng, L.; Teng, G. Thermal Maturity of Wufeng-Longmaxi Shale in Sichuan Basin. Earth Sci. 2019, 44, 953–971. [Google Scholar]
- Li, J.; Ma, W.; Wang, Y.; Wang, D.; Xie, Z.; Li, Z.; Ma, C. Modeling of the whole hydrocarbon-generating process of sapropelic source rock. Pet. Explor. Dev. 2018, 45, 445–454. [Google Scholar] [CrossRef]
- Ma, Z.L.; Zheng, L.J.; Li, Z.M. The Thermocompression Simulation Experiment of Source Rock Hydrocarbon Generation and Expulsion in Formation Porosity. Acta Sedimentol. Sin. 2012, 30, 955–963. (In Chinese) [Google Scholar]
- Liu, D.; Xiao, X.; Tian, H.; Min, Y.; Zhou, Q.; Cheng, P.; Shen, J. Sample maturation calculated using Raman spectroscopic parameters for solid organics: Methodology and geological applications. Chin. Sci. Bull. 2013, 58, 1285–1298. [Google Scholar] [CrossRef]
- Yin, N.; Hu, Q.; Becker, S.J.; Jones, R.; Meng, M.; Zhu, X.; Liu, H. Development of an NMR workflow for determining nano-petrophysical properties of marine and lacustrine mudrocks. J. Petrol. Sci. Eng. 2022, 214, 110491. [Google Scholar] [CrossRef]
- Zhang, C.; Guan, P.; Zhang, J.; Liang, X.; Ding, X.; You, Y. A Review of the Progress on Fractal Theory to Characterize the Pore Structure of Unconventional Oil and Gas Reservoirs. Acta Sci. Nat. Univ. Pekin. 2023, 59, 897–908. (In Chinese) [Google Scholar]
- Li, P.; Zheng, M.; Bi, H.; Wu, S.; Wang, X. Pore throat structure and fractal characteristics of tight oil sandstone: A case study in the Ordos Basin, China. J. Pet. Sci. Eng. 2017, 149, 665–674. [Google Scholar] [CrossRef]
- Milliken, K.L.; Rudnicki, M.; Awwiller, D.N.; Zhang, T. Organic matter-hosted pore system, Marcellus Formation (Devonian), Pennsylvania. AAPG Bull. 2013, 97, 177–200. [Google Scholar] [CrossRef]
- Arif, M.; Zhang, Y.H.; Iglauer, S. Shale Wettability: Data Sets, Challenges, and Outlook. Energy Fuels 2021, 35, 2965–2980. [Google Scholar] [CrossRef]
- Zhou, B. The Applications of NMR Relaxometry, NMR Cryoporometry, and FFC NMR to Nanoporous Structures and Dynamics in Shale at Low Magnetic Fields. Energy Fuels 2018, 32, 8897–8904. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, D. Experimental Study on the Influence of Paramagnetic Ions on the Relaxation Response of Nuclear Magnetic Resonance and Its Application. Well Logging Technol. 2003, 27, 270–273. (In Chinese) [Google Scholar]
- Xue, J.; Lee, C.; Wakeham, S.G.; Armstrong, R. Using principal components analysis (PCA) with cluster analysis to study the organic geochemistry of sinking particles in the ocean. Org. Geochem. 2011, 42, 356–367. [Google Scholar] [CrossRef]
- Gotelli, N.J.; Ellison, A.M. A Primer of Ecological Statistics; Sinauer Associates: Sunderland, MA, USA, 2004. [Google Scholar]
- Wang, G.P.; Jin, Z.J.; Zhang, Q.; Zhu, R.K.; Tang, X.; Liu, K.Q.; Dong, L. Effects of clay minerals and organic matter on pore evolution of the early mature lacustrine shale in the Ordos Basin, China. J. Asian Earth Sci. 2023, 246, 105516. [Google Scholar] [CrossRef]

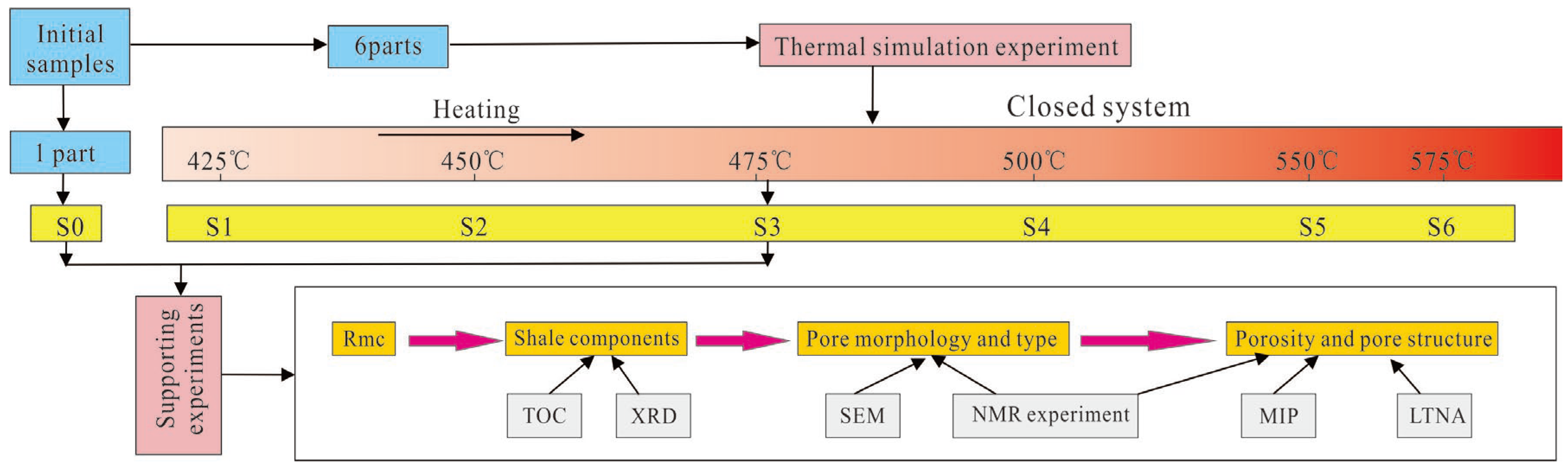





| Sample ID | Simulated Burial Depth (m) | Lithostatic Pressure (MPa) | Heating Rate (°C/min) | Final Temperature (°C) | Holding Time (h) | Rmc (%) |
|---|---|---|---|---|---|---|
| S0 | / | / | / | / | 1.18 | |
| S1 | 2500 | 62.5 | 2 | 425 | 72 | 1.26 |
| S2 | 3000 | 75 | 2 | 450 | 84 | 1.41 |
| S3 | 3500 | 90 | 2 | 475 | 96 | 1.60 |
| S4 | 4000 | 100 | 2 | 500 | 84 | 1.91 |
| S5 | 4500 | 112.5 | 2 | 550 | 168 | 2.65 |
| S6 | 5000 | 125 | 2 | 575 | 240 | 3.17 |
| Sample ID | Rmc (%) | 0.01 < P/P0 < 0.45 | 0.45 < P/P0 < 0.98 | HPMI (20 nm < r < 1000 nm) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D1 | 95% CI Half-Width | D2 | 95% CI Half-Width | DM1 | 95% CI Half-Width | DM2 | 95% CI Half-Width | DM | ||
| S0 | 1.18 | 2.69 | 0.009 | 2.84 | 0.004 | 2.67 | 0.008 | 2.97 | 0.004 | 2.74 |
| S1 | 1.26 | 2.46 | 0.002 | 2.56 | 0.005 | 2.52 | 0.028 | 2.99 | 0.004 | 2.53 |
| S3 | 1.60 | 2.43 | 0.008 | 2.57 | 0.003 | 2.62 | 0.022 | 2.92 | 0.004 | 2.75 |
| S4 | 1.91 | 2.73 | 0.002 | 2.70 | 0.010 | 2.93 | 0.004 | 2.94 | 0.002 | 2.94 |
| S5 | 2.65 | 2.72 | 0.012 | 2.63 | 0.012 | 2.87 | 0.020 | 2.98 | 0.001 | 2.90 |
| S6 | 3.17 | 2.71 | 0.01 | 2.66 | 0.003 | 2.28 | 0.098 | 2.99 | 0.001 | 2.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, H.; Jiang, Y.; Guan, Q.; Yin, X.; Gu, Y. Pore Evolution and Fractal Characteristics of Marine Shale: A Case Study of the Silurian Longmaxi Formation Shale in the Sichuan Basin. Fractal Fract. 2025, 9, 492. https://doi.org/10.3390/fractalfract9080492
Zhuang H, Jiang Y, Guan Q, Yin X, Gu Y. Pore Evolution and Fractal Characteristics of Marine Shale: A Case Study of the Silurian Longmaxi Formation Shale in the Sichuan Basin. Fractal and Fractional. 2025; 9(8):492. https://doi.org/10.3390/fractalfract9080492
Chicago/Turabian StyleZhuang, Hongzhan, Yuqiang Jiang, Quanzhong Guan, Xingping Yin, and Yifan Gu. 2025. "Pore Evolution and Fractal Characteristics of Marine Shale: A Case Study of the Silurian Longmaxi Formation Shale in the Sichuan Basin" Fractal and Fractional 9, no. 8: 492. https://doi.org/10.3390/fractalfract9080492
APA StyleZhuang, H., Jiang, Y., Guan, Q., Yin, X., & Gu, Y. (2025). Pore Evolution and Fractal Characteristics of Marine Shale: A Case Study of the Silurian Longmaxi Formation Shale in the Sichuan Basin. Fractal and Fractional, 9(8), 492. https://doi.org/10.3390/fractalfract9080492







