Numerical Investigation of the Time-Fractional Black–Scholes Problem Using the Caputo Fractional Derivative in the Financial Industry

Abstract

The present study addresses the European option pricing problem based on the Black–Scholes (B-S) model using a hybrid analytical approach known as the Sawi homotopy perturbation transform scheme (SHPTS). We formulate fractional derivatives in the Caputo sense to effectively capture the memory effects inherent in financial models. The competency and reliability of the SHPTS are demonstrated through two illustrative examples. This method produces a closed-form series solution that converges to the precise solution. We perform convergence and visual analyses to demonstrate the competency and reliability of the proposed scheme. The numerical findings further reveal that the strategy is straightforward to apply and very successful in resolving the fractional form of the B-S problem.

1. Introduction

Fractional derivatives expand the idea of ordinary differentiation to non-integer orders and offer a strong mechanism for the analysis of systems with complex, nonlocal, or memory-dependent behavior. This idea was initially proposed by Leibniz in the 17th century, with the formal mathematical foundations later developed by Liouville and Riemann and subsequently refined by Caputo [1]. The Caputo formulation has been widely adopted due to its compatibility with physically interpretable initial conditions in differential equations. This generalization to differentiation offers significant advantages in the analysis of complex, nonlocal phenomena where classical integer-order models are inadequate [2,3,4]. Among the various fractional definitions, the Riemann–Liouville and Caputo formulations are predominant, combining mathematical robustness with empirical applicability across a wide range of scientific and engineering domains [5,6]. Numerous analytical schemes have been developed to handle these fractional differential problems, such as Hirota’s bilinear method [7], the Laplace transform [8], the variational iteration approach [9], the Adomian decomposition scheme [10], the homotopy analysis technique [11], the Newton–Raphson scheme [12], and the spectral collocation technique [13].

The homotopy perturbation method (HPM) was developed by Ji-Huan He [14,15] for the solution of ordinary and partial differential problems. Later, numerous researchers employed this technique across a wide range of disciplines, including oscillators with nonlinear behavior [16], waves with nonlinear models [17], nonlinear differential models [18], fractional integro-differential problems [19], heat radiation equations [20], inverse problem of diffusion equations [21], and other fields [22,23]. Moreover, this method has been effectively integrated with the Laplace transformation to resolve more complex models of nonhomogeneous partial differential equations [24]. The advantage of the HPM lies in its capacity to regulate both the convergence domain and the rate of convergence, which makes it suitable for solving nonlinear dynamical systems [25]. Due to this flexibility and efficiency, the HPM has become a valuable tool in modeling real-world systems, including those arising in financial mathematics.

In this paper, we study the fractional Black–Scholes model, which is particularly recognized for its role in option pricing and is given by the following expression [26]:

$$\begin{array}{c}\hfill D_{\xi }^{\alpha }\Psi (\varsigma ,\xi )+{\displaystyle \frac{{\varphi }^2{\varsigma }^2}{2}}{D}_{\varsigma }^2\Psi (\varsigma ,\xi )+\phi \left(\xi \right)\varsigma D_{\varsigma }\Psi (\varsigma ,\xi )-\phi \left(\xi \right)\Psi (\varsigma ,\xi )=0,(\varsigma ,\xi )\in R^{+}\times (0,\xi ),0<\alpha \le 1.\end{array}$$

(1)

In this context, $D^{\alpha }$ is the Caputo derivative of fractional order $\alpha$, $\Psi (\varsigma ,\xi )$ represents the European call option at price $\varsigma$ and $\xi$ as the time to maturity of the option, $\phi \left(\xi \right)$ is the risk-free interest rate, and $\varphi$ refers to the volatility function of the underlying asset. The corresponding payoff functions are given by

$$\begin{array}{c}\hfill {\Psi }_c(\varsigma ,\xi )=\max (\varsigma -E,0);{\Psi }_p(\varsigma ,\xi )=\max (E-\varsigma ,0).\end{array}$$

(2)

Here, ${\Psi }_c(\varsigma ,\xi )$ and ${\Psi }_p(\varsigma ,\xi )$ denote the prices of the European call and put options, respectively. The parameter E is the strike price of the option, and the function $\max (\varsigma ,0)$ is used to determine the maximum value between $\varsigma$ and zero. Numerous researchers have explored the fractional B-S model using a wide range of mathematical and numerical methods. Ravi and Aruna [27] investigated multiple forms of solutions to the time-fractional B-S equation relevant to European option pricing in financial markets. Jena and Chakraverty [28] applied the residual power series method to derive analytical solutions for the fractional B-S equation with initial conditions for European options. Similarly, Prathumwan and Trachoo [29] utilized the Laplace homotopy perturbation method to study option price behavior in the market using a two-dimensional time-fractional B-S equation for European put options. Roul [30] used a collocation method based on quintic B-spline basis functions, using a backward Euler method for the numerical solution of the time-fractional B-S equation. Zhao and Tian [31] studied finite difference techniques to address a spatial fractional B-S problem within a finite domain. Kazmi [32] employed a computational integration plan to address the time-fractional B-S problem that governs European options. However, some of these techniques have limitations when applied to fractional problems. The Sawi transform is notably simpler to use for fractional differential problems, especially when compared to methods like the variational iteration method (VIM), Laplace transform, and homotopy analysis method (HAM). This is because the VIM requires integration and introduces a constant, the Laplace transform relies on the convolution theorem, and the HAM requires certain assumptions to be made.

The hypothesis of the present study is that the SHPTS presents greater accuracy and a reduced computational cost compared to classical methods such as the VIM, Laplace transform, and HAM. The Caputo fractional derivative is highlighted for its effectiveness, particularly in the initial value problems. The application of the Sawi transform ($\mathbb{S}$T) serves to reduce the order of the fractional derivative and transforms the differential problems into simpler recurrence relations. By integrating the homotopy perturbation method (HPM), we efficiently derive the He’s polynomials. Our proposed methodology does not rely on assumptions, constraints, or specific variable conditions. The rest of the study is organized as follows: Section 2 examines the fractional calculus literature and the $\mathbb{S}$T properties. The formulation of the SHPTS is elaborated on in Section 3. Section 4 presents an analysis of the uniqueness and convergence of the derived solution. Section 5 confirms the application of the SHPTS for the time-fractional B-S problem. Section 6 showcases some graphical representations and their absolute errors with various values of order $\alpha$. Finally, the conclusion of this study is presented in Section 7.

2. Basic Concepts and Characteristics of FC and Sawi Transform

This section provides some basic concepts and characteristics of FC and the $\mathbb{S}$T. These properties are crucial for the formulation and advancement of the proposed scheme.

Definition 1.

The Riemann–Liouville fractional integral operator for function $\Psi \left(\xi \right)$ is defined as [33]

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill J^{\alpha }\Psi \left(\xi \right)& ={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{\xi }{(\xi -\Im )}^{\alpha -1}\Psi (\Im )d\Im ,\alpha >0,\Im >0,\hfill \\ \hfill J^0\Psi \left(\xi \right)& =\Psi \left(\xi \right).\hfill \end{array}\end{array}$$

where Γ is the gamma function

$$\begin{array}{c}\hfill \Gamma \left(p\right)={\int }_0^{\infty }{e}^{-\xi }{\xi }^{p-1}d\xi ,p\in \mathbb{C}.\end{array}$$

Definition 2.

The Riemann–Liouville fractional derivative for function $\Psi \left(\xi \right)$ is defined as [33]

$$\begin{array}{c}\hfill D_{\xi }^{\alpha }\Psi \left(\xi \right)=D_{\xi }^n{j}_{\xi }^{n-\alpha }\Psi \left(\xi \right)={\displaystyle \frac{1}{\Gamma (n-\alpha )}}{\displaystyle \frac{d^n}{d{\xi }^n}}{\int }_0^{\xi }{(\xi -\Im )}^{n-\alpha -1}\Psi (\Im )d\Im ,\end{array}$$

where n is a positive number such that the condition $n-1<\alpha \le n$ holds true.

Definition 3.

The Caputo-type fractional derivative of order α for the function $\Psi \left(\xi \right)$, where $\xi >0$, is defined as follows [34]:

$$\begin{array}{c}\hfill D_{\xi }^{\alpha }\Psi (\varsigma ,\xi )={\displaystyle \frac{{\partial }^{\alpha }\Psi (\varsigma ,\xi )}{\partial {\xi }^{\alpha }}}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma (n-\alpha )}}{\int }_0^{\xi }{(\xi -\Im )}^{n-\alpha -1}{\displaystyle \frac{{\partial }^{\alpha }\Psi (\varsigma ,\Im )}{\partial {\Im }^{\alpha }}}d\Im ,\hfill & n-1<\alpha <n,\hfill \\ {\displaystyle \frac{{\partial }^{\alpha }\Psi (\varsigma ,\Im )}{\partial {\xi }^{\alpha }}},\hfill & \alpha =n\in \mathrm{N}.\hfill \end{array}\right.\end{array}$$

The primary motivation for employing the Caputo form lies in its ability to yield distinct and accurate results for the suggested framework. The Caputo definition is widely valued in aligning the fractional derivative with classical integer-order derivatives under given initial conditions and assumptions of the model:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & D^{\alpha }{\xi }^{\gamma }=0,\gamma <\alpha ,\hfill \\ \hfill & D^{\alpha }{\xi }^{\gamma }={\displaystyle \frac{\Gamma (\gamma +1)}{\Gamma (\alpha +\gamma +1)}}{\xi }^{\gamma +\alpha },\gamma \ge \alpha .\hfill \end{array}\end{array}$$

Definition 4.

The Mittag-Leffler function, $E_{\alpha }\left(z\right)$ for $\alpha >0$, is defined as [35]

$$\begin{array}{c}\hfill E_{\alpha }\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{z^n}{\Gamma (\alpha n+1)}}.\end{array}$$

Definition 5.

The Sawi transform is applicable for the function $\Psi \left(\xi \right)$, which is piecewise continuous on $[0,\infty )$, and is denoted by $\mathbb{S}$T. It is defined as follows [36]:

$$\begin{array}{c}\hfill \mathbb{S}[\Psi \left(\xi \right)]=Z\left(\eta \right)={\displaystyle \frac{1}{{\eta }^2}}{\int }_0^{\infty }\Psi \left(\xi \right)e^{-{\displaystyle \frac{\xi }{\eta }}}d\xi ,\xi \ge 0,\eta >0.\end{array}$$

Thus, the inverse $\mathbb{S}$T becomes

$$\begin{array}{c}\hfill \Psi \left(\xi \right)={\displaystyle \frac{1}{2\pi \iota }}{\int }_{c-\iota \infty }^{c+\iota \infty }Z\left(\eta \right)e^{{\displaystyle \frac{\xi }{\eta }}}d\eta .\end{array}$$

Here, c denotes a real constant and $Z\left(\eta \right)$ is the transformed function corresponding to $\Psi \left(\xi \right)$.

Proposition 1.

The basic properties of $\mathbb{S}$T are as follows [36]. Let $\mathbb{S}\left\{{\Psi }_1\left(\xi \right)\right\}=Z_1\left(\eta \right)$ and $\mathbb{S}\left\{{\Psi }_2\left(\xi \right)\right\}=Z_2\left(\eta \right)$. Thus, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{S}\{a{\Psi }_1\left(\xi \right)+b{\Psi }_2\left(\xi \right)\}& =a\mathbb{S}\left\{{\Psi }_1\left(\xi \right)\right\}+b\mathbb{S}\left\{{\Psi }_2\left(\xi \right)\right\},\hfill \\ \hfill \Rightarrow \mathbb{S}\{a{\Psi }_1\left(\xi \right)+b{\Psi }_2\left(\xi \right)\}& =a{Z}_1\left(\eta \right)+b{Z}_2\left(\eta \right).\hfill \end{array}\end{array}$$

Proposition 2.

The differential properties of $\mathbb{S}$T are expressed as follows [36,37]. If $\mathbb{S}\{\Psi (\xi \left)\right\}=Z\left(\eta \right)$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{S}\left\{{\Psi }^{\prime }\left(\xi \right)\right\}& ={\displaystyle \frac{Z\left(\eta \right)}{\eta }}-{\displaystyle \frac{\Psi \left(0\right)}{{\eta }^2}},\hfill \\ \hfill \mathbb{S}\left\{{\Psi }^{″}\left(\xi \right)\right\}& ={\displaystyle \frac{Z\left(\eta \right)}{{\eta }^2}}-{\displaystyle \frac{\Psi \left(0\right)}{{\eta }^3}}-{\displaystyle \frac{{\Psi }^{\prime }\left(0\right)}{{\eta }^2}},\hfill \\ \hfill \mathbb{S}\left\{{\Psi }^m\left(\xi \right)\right\}& ={\displaystyle \frac{Z\left(\eta \right)}{{\eta }^m}}-{\displaystyle \frac{\Psi \left(0\right)}{{\eta }^{m+1}}}-{\displaystyle \frac{{\Psi }^{\prime }\left(0\right)}{{\eta }^m}}-\dots -{\displaystyle \frac{{\Psi }^{m-1}\left(0\right)}{{\eta }^2}}.\hfill \end{array}\end{array}$$

Definition 6.

The Caputo fractional derivative in terms of $\mathbb{S}$T is [36]

$$\begin{array}{c}\hfill \mathbb{S}[D_{\xi }^{\alpha }\Psi \left(\xi \right)]={\displaystyle \frac{1}{{\eta }^{\alpha }}}\mathbb{S}[\Psi \left(\xi \right)]-\sum _{k=0}^{m-1}{\left({\displaystyle \frac{1}{\eta }}\right)}^{\alpha -(k-1)}.\end{array}$$

3. Formulation of SHPTS

In this section, we present the step-by-step formulation of the SHPTS for the solution of the fractional-order differential problem. The fractional order $\alpha$ is tackled through the application of $\mathbb{S}$T, and a corresponding series solution is obtained using the HPM. Notably, the resulting series transforms into the exact outcomes when $\alpha =1$. Here, we introduce a fractional-order differential model to analyze the SHPTS procedure,

$$\begin{array}{c}\hfill D_{\xi }^{\alpha }\Psi (\varsigma ,\xi )=L_1\Psi (\varsigma ,\xi )+L_2\Psi (\varsigma ,\xi )+g(\varsigma ,\xi ),\end{array}$$

(3)

under the subsequent condition

$$\begin{array}{c}\hfill \Psi (\varsigma ,0)=f\left(\varsigma \right).\end{array}$$

(4)

Here, $f\left(\varsigma \right)$ is considered piecewise continuous on $[0,\infty )$, $\Psi$ is a function that depends on the variables $\varsigma$ and $\xi$, and $D_{\xi }^{\alpha }={\displaystyle \frac{{\partial }^{\alpha }}{\partial {\xi }^{\alpha }}}$ denotes the Caputo fractional derivative of order $\alpha \in (0,1]$. Meanwhile, $L_1$ is a linear differential operator, while $L_2$ represents nonlinear differential operators, and $g(\varsigma ,\xi )$ serves as a homogeneous component in the model. By applying the linearity property of the $\mathbb{S}$T operator to Equation (3), we have

$$\begin{array}{c}\hfill \mathbb{S}[D_{\xi }^{\alpha }\Psi (\varsigma ,\xi )]=\mathbb{S}[L_1\Psi (\varsigma ,\xi )+L_2\Psi (\varsigma ,\xi )+g(\varsigma ,\xi )].\end{array}$$

This expression can be reformulated as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{{\eta }^{\alpha }}}Z\left(\eta \right)-{\displaystyle \frac{1}{{\eta }^{\alpha +1}}}\Psi (\varsigma ,0)=\mathbb{S}[L_1\Psi (\varsigma ,\xi )+L_2\Psi (\varsigma ,\xi )+g(\varsigma ,\xi )].\end{array}$$

The transformed function $Z\left(\eta \right)$ is evaluated as

$$\begin{array}{c}\hfill Z\left[\eta \right]={\displaystyle \frac{\Psi (\varsigma ,0)}{\eta }}+{\eta }^{\alpha }\mathbb{S}\left[L_1\Psi (\varsigma ,\xi )+L_2\Psi (\varsigma ,\xi )+g(\varsigma ,\xi )\right].\end{array}$$

Next, utilizing the inverse $\mathbb{S}$T property, we get

$$\begin{array}{cc}\hfill \Psi (\varsigma ,\xi )& =G(\varsigma ,\xi )+{\mathbb{S}}^{-1}{\displaystyle [}{\eta }^{\alpha }\mathbb{S}{\displaystyle \{}{L}_1\Psi (\varsigma ,\xi )+L_2\Psi (\varsigma ,\xi ){\displaystyle \}}{\displaystyle ]}.\hfill \end{array}$$

(5)

Equation (5) is termed a recurrence relation, in which $G(\varsigma ,\xi )$ denotes the combined effect of the subsequent condition and the homogeneous component, such as

$$\begin{array}{c}\hfill G(\varsigma ,\xi )={\mathbb{S}}^{-1}\left[{\displaystyle \frac{\Psi (\varsigma ,0)}{\eta }}+{\eta }^{\alpha }\mathbb{S}\left[g(\varsigma ,\xi )\right]\right].\end{array}$$

Consider the general form of Equation (3) as follows:

$$\begin{array}{c}\hfill \Psi (\varsigma ,\xi )=\sum _{n=0}^{\infty }{p}^n{\Psi }_n(\varsigma ,\xi ).\end{array}$$

(6)

Now, we apply the HPM to handle the operator $L_2$ of Equation (5) in the following manner:

$$\begin{array}{c}\hfill L_2\Psi (\varsigma ,\xi )=\sum _{n=0}^{\infty }{p}^n{H}_n(\Psi ),\end{array}$$

(7)

where $p\in [0,1]$ is a small perturbation parameter, and $H_n$ denotes the He polynomials of ${\Psi }_0,{\Psi }_0,\dots ,{\Psi }_n$, which can be computed by the following formula:

$$\begin{array}{c}\hfill H_n(\varsigma ,\xi )=H_n({\Psi }_0,{\Psi }_1,\dots ,{\Psi }_1)={\displaystyle \frac{1}{n!}}{\displaystyle \frac{{\partial }^n}{\partial p^n}}{\left(L_2\left(\sum _{n=0}^{\infty }{p}^n{\Psi }_n\right)\right)}_{p=0},n=0,1,2,\dots .\end{array}$$

By substituting Equations (6) and (7) into Equation (5), we have the following expression:

$$\begin{array}{c}\hfill \sum _{n=0}^{\infty }{p}^n{\Psi }_n(\varsigma ,\xi )=G(\varsigma ,\xi )+p{\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{L_1\left(\sum _{n=0}^{\infty }{p}^n{\Psi }_n(\varsigma ,\xi )\right)+\sum _{n=0}^{\infty }{p}^n{H}_n{\Psi }_n(\varsigma ,\xi )\right\}\right].\end{array}$$

Performing successive iterations and examining the relevant terms of p, we obtain

$$\begin{array}{cc}\hfill p^0& :{\Psi }_0(\varsigma ,\xi )=G(\varsigma ,\xi ),\hfill \\ \hfill p^1& :{\Psi }_1(\varsigma ,\xi )={\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\right\{L_1{\Psi }_0(\varsigma ,\xi )+H_0(\Psi )\left\}\right],\hfill \\ \hfill p^2& :{\Psi }_2(\varsigma ,\xi )={\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\right\{L_1{\Psi }_1(\varsigma ,\xi )+H_1(\Psi )\left\}\right],\hfill \\ \hfill p^3& :{\Psi }_3(\varsigma ,\xi )={\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\right\{L_1{\Psi }_2(\varsigma ,\xi )+H_2(\Psi )\left\}\right],\hfill \\ \hfill & ⋮\hfill \\ \hfill p^n& :{\Psi }_n(\varsigma ,\xi )={\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\right\{L_1{\Psi }_{n-1}(\varsigma ,\xi )+H_{n-1}(\Psi )\left\}\right].\hfill \end{array}$$

Therefore, the series described above can be written as

$$\begin{array}{c}\hfill \Psi (\varsigma ,\xi )={\Psi }_0+{\Psi }_1+{\Psi }_2+\dots =\underset{p\to \infty }{lim}\sum _{i=1}^{\infty }{\Psi }_i(\varsigma ,\xi ).\end{array}$$

(8)

This iterative process develops a convergent result for the suggested fractional framework, which clearly demonstrates the effectiveness of the SHPTS in solving various complex challenges.

4. Existence and Uniqueness Analysis of the Fractional B-S Model

Here, we demonstrate that the fractional B-S problem is unique and convergent.

4.1. Existence and Uniqueness Theorem

Theorem 1.

Let us assume that the time-fractional B-S problem using $\sigma =1$ and $r\left(\xi \right)=1$ becomes

$$\begin{array}{c}\hfill D_{\xi }^{\alpha }\Psi +{\displaystyle \frac{{\varsigma }^2}{2}}{D}_{\varsigma }^2\Psi +\varsigma D_{\varsigma }\Psi -\Psi =0,0<\alpha \le 1,\xi >0,\end{array}$$

with the condition

$$\begin{array}{c}\hfill \Psi (\varsigma ,0)=f\left(\varsigma \right).\end{array}$$

It possesses a single and unique solution given by

$$\begin{array}{c}\hfill \hslash ={\displaystyle \frac{(h_1+h_2+h_3){\xi }^{\alpha }}{\Gamma (\alpha +1)}},\end{array}$$

where $0<\hslash <1$.

Proof. 

Let $W=\left(h\right(I),\parallel ·\parallel )$ denote a Banach space of all continuous functions defined in the interval $I=[0,\Lambda ]$, endowed with the norm $\parallel ·\parallel$.

$$\begin{array}{c}\hfill \parallel \Psi \left(\xi \right)\parallel =\underset{\xi \in I}{max}|\Psi \left(\xi \right)|.\end{array}$$

Let us define a mapping $Y:W\to W$ such that

$$\begin{array}{c}\hfill Y(\Psi \left(\xi \right))=f\left(\varsigma \right)-J^{\alpha }{Q}_1(\Psi \left(\xi \right))-J^{\alpha }{Q}_2(\Psi \left(\xi \right))-J^{\alpha }{Q}_3(\Psi \left(\xi \right)).\end{array}$$

Here, $Q_1(\Psi \left(\xi \right))$ denotes the linear component of $D_{\varsigma }^2$, $Q_2(\Psi \left(\xi \right))$ defines the linear component of $D_{\varsigma }$, and $Q_3(\Psi \left(\xi \right))$ is the component of the last term. The term $Q_1(\Psi \left(\xi \right))$ demonstrates Lipschitz continuity—that is, it behaves as a Lipschitz operator under the given norm as

$$\begin{array}{c}\hfill |Q_1(\Psi )-Q_1\left(r\right)|\le h_1|\Psi -r|.\end{array}$$

Let $\Psi ,{\Psi }^{\prime }$ be elements of the space W; therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel Y(\Psi )-Y\left({\Psi }^{\prime }\right)\parallel =& \underset{\xi \in I}{max}|-J^{\alpha }{Q}_1(\Psi \left(\xi \right))-J^{\alpha }{Q}_2(\Psi \left(\xi \right))-J^{\alpha }{Q}_3(\Psi \left(\xi \right))+J^{\alpha }{Q}_1\left({\Psi }^{\prime }\left(\xi \right)\right)+J^{\alpha }{Q}_2\left({\Psi }^{\prime }\left(\xi \right)\right)+J^{\alpha }{Q}_3\left({\Psi }^{\prime }\left(\xi \right)\right)|\hfill \\ \hfill =& \underset{\xi \in I}{max}|-J^{\alpha }(Q_1\Psi -Q_1{\Psi }^{\prime })-J^{\alpha }(Q_2\Psi -Q_2{\Psi }^{\prime })-J^{\alpha }(Q_3\Psi -Q_3{\Psi }^{\prime })|\hfill \\ \hfill =& \underset{\xi \in I}{max}|J^{\alpha }(Q_1\Psi -Q_1{\Psi }^{\prime })+J^{\alpha }(Q_2\Psi -Q_2{\Psi }^{\prime })+J^{\alpha }(Q_3\Psi -Q_3{\Psi }^{\prime })|\hfill \\ \hfill \le & \underset{\xi \in I}{max}|J^{\alpha }(Q_1\Psi -Q_1{\Psi }^{\prime })|+|J^{\alpha }(Q_2\Psi -Q_2{\Psi }^{\prime })|+|J^{\alpha }(Q_3\Psi -Q_3{\Psi }^{\prime })|\hfill \end{array}\end{array}$$

Suppose that $Q_2(\Psi \left(\xi \right))$ and $Q_3(\Psi \left(\xi \right))$ also exhibit Lipschitz continuity, implying that

$$\begin{array}{c}\hfill |Q_2(\Psi )-Q_2\left(r\right)|\le h_2|\Psi -r|,\end{array}$$

and

$$\begin{array}{c}\hfill |Q_3(\Psi )-Q_3\left(r\right)|\le h_3|\Psi -r|,\end{array}$$

The constants $h_1$, $h_2$, and $h_3$ represent the Lipschitz constants for each operator. Thus,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel Y(\Psi )-Y\left({\Psi }^{\prime }\right)\parallel & \le \underset{\xi \in I}{max}\left(h_1{J}^{\alpha }|\Psi -{\Psi }^{\prime }|+h_2{J}^{\alpha }|\Psi -{\Psi }^{\prime }|+h_3{J}^{\alpha }|\Psi -{\Psi }^{\prime }|\right)\hfill \\ & \le (h_1+h_2+h_3)\parallel \Psi -{\Psi }^{\prime }\parallel {\displaystyle \frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}}\hfill \\ & \parallel Y(\Psi )-Y\left({\Psi }^{\prime }\right)\parallel \le \hslash \parallel \Psi -{\Psi }^{\prime }\parallel ,\hfill \end{array}\end{array}$$

with

$$\begin{array}{c}\hfill \hslash ={\displaystyle \frac{(h_1+h_2+h_3){\xi }^{\alpha }}{\Gamma (\alpha +1)}}.\end{array}$$

Hence, the resulting operator satisfies the contraction condition. Consequently, the Banach fixed-point theorem ensures the existence and uniqueness of the solution. □

4.2. Investigation of Convergence Behavior for the Fractional B-S Problem

Theorem 2.

Let

$$\begin{array}{c}\hfill {\Lambda }_i=\sum _{l=0}^i{\Psi }_l(\varsigma ,\xi )\end{array}$$

represent the partial sum to the $i^{\mathrm{th}}$ term. Then, our goal is to prove that $\left\{{\Lambda }_i\right\}$ forms a Cauchy sequence to Banach space Y.

Proof. 

In order to illustrate the preceding assertion, we make the following assumptions:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel {\Lambda }_{i+j}-{\Lambda }_i\parallel & =\underset{\Lambda \in I}{max}|{\Lambda }_{i+j}-{\Lambda }_i|,\hfill \\ \hfill & =\underset{\Lambda \in I}{max}\left|\sum _{l=i+1}^{i+j}{\Psi }_l(\varsigma ,\xi )\right|,\hfill \\ \hfill & =\underset{\Lambda \in I}{max}|-J^{\alpha }\sum _{l=i+1}^{i+j}{B}_1{\Psi }_{l-1}(\varsigma ,\xi )-J^{\alpha }\sum _{l=i+1}^{i+j}{B}_2{\Psi }_{l-1}(\varsigma ,\xi )-J^{\alpha }\sum _{l=i+1}^{i+j}{B}_3{\Psi }_{l-1}(\varsigma ,\xi )|,\hfill \\ \hfill & =\underset{\Lambda \in I}{max}|J^{\alpha }{B}_1{\Lambda }_{i+j-1}-B_1{\Lambda }_{i-1}+J^{\alpha }{B}_2{\Lambda }_{i+j-1}-B_2{\Lambda }_{i-1}+J^{\alpha }{B}_3{\Lambda }_{i+j-1}-B_3{\Lambda }_{i-1}|,\hfill \\ \hfill & \le \underset{\Lambda \in I}{max}{J}^{\alpha }|B_1{\Lambda }_{i+j-1}-B_1{\Lambda }_{i-1}|+\underset{\Lambda \in I}{max}{J}^{\alpha }|B_2{\Lambda }_{i+j-1}-B_2{\Lambda }_{i-1}|+\underset{\Lambda \in I}{max}{J}^{\alpha }|B_3{\Lambda }_{i+j-1}-B_3{\Lambda }_{i-1}|\hfill \\ \hfill & \le h_2\underset{\Lambda \in I}{max}{J}^{\alpha }|{\Lambda }_{i+j-1}-{\Lambda }_{i-1}|+h_3\underset{\Lambda \in I}{max}{J}^{\alpha }|{\Lambda }_{i+j-1}-{\Lambda }_{i-1}|+h_1\underset{\Lambda \in I}{max}{J}^{\alpha }|{\Lambda }_{i+j-1}-{\Lambda }_{i-1}|\hfill \\ \hfill & \le (h_1+h_2+h_3){\displaystyle \frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}}\parallel {\Lambda }_{i+j-1}-{\Lambda }_{i-1}\parallel \hfill \end{array}\end{array}$$

Consider that $\hslash =(h_1+h_2+h_3){\displaystyle \frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}}$; therefore,

$$\begin{array}{c}\hfill \parallel {\Lambda }_{i+j}-{\Lambda }_i\parallel \le \hslash \parallel {\Lambda }_{i+j-1}-{\Lambda }_{i-1}\parallel .\end{array}$$

Proceeding in a similar way, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel {\Lambda }_{i+j}-{\Lambda }_i\parallel & \le {\hslash }^2\parallel {\Lambda }_{i+j-2}-{\Lambda }_{i-2}\parallel ,\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le {\hslash }^i\parallel {\Lambda }_j-{\Lambda }_0\parallel ,\hfill \\ \hfill & \le {\hslash }^i\parallel {\Lambda }_1-{\Lambda }_0\parallel ,\mathrm{for}j=1\hfill \\ \hfill & \le {\hslash }^i\parallel {\Psi }_1\parallel .\hfill \end{array}\end{array}$$

Consider $i,l\in \mathbb{N}$ such that $i>l$,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel {\Lambda }_i-{\Lambda }_l\parallel & \le \parallel {\Lambda }_{l+1}-{\Lambda }_l\parallel +\parallel {\Lambda }_{l+2}-{\Lambda }_{l+1}\parallel +\dots +\parallel {\Lambda }_i-{\Lambda }_{i-1}\parallel ,\hfill \\ \hfill & \le ({\hslash }^l+{\hslash }^{l+1}+\dots +{\hslash }^{i-1})\parallel {\Psi }_1\parallel ,\hfill \\ \hfill & \le {\hslash }^l\left[{\displaystyle \frac{1-{\hslash }^{i-l}}{1-\hslash }}\right]\parallel {\Psi }_1\parallel .\hfill \end{array}\end{array}$$

Since $0<\hslash <1$, it follows that $1-{\hslash }^{i-l}<1$. Therefore,

$$\begin{array}{c}\hfill \parallel {\Lambda }_i-{\Lambda }_l\parallel \le {\displaystyle \frac{{\hslash }^l}{1-\hslash }}\parallel {\Psi }_1\parallel .\end{array}$$

Given the boundedness of $\Psi (\Lambda )$, the norm $\parallel {\Psi }_1\parallel$ remains finite. Hence,

$$\begin{array}{c}\hfill \underset{i\to \infty }{lim}\parallel {\Lambda }_i-{\Lambda }_l\parallel \to 0.\end{array}$$

The convergence property of the Cauchy sequence confirms that the variance among sequence parameters is less than ℏ. This indicates that the sequence will converge to a limit in a full metric space. Hence, the solution is convergent as $\left\{{\Lambda }_i\right\}$ forms a Cauchy sequence to Banach space Y. □

5. Numerical Problems

In this section, we conduct a fractional analysis of time-fractional B-S problems using the suggested approach. The resulting sequence closely approximates the exact solutions after only a few iterations, demonstrating the accuracy and efficiency of the approach. All algebraic computations and symbolic visualizations are performed using the Mathematica 11 package.

5.1. Problem 1

Consider the financial model under the fractional B-S problem [38]

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{\alpha }\Psi }{\partial {\xi }^{\alpha }}}={\displaystyle \frac{{\partial }^2\Psi }{\partial {\varsigma }^2}}+(k-1){\displaystyle \frac{\partial \Psi }{\partial \varsigma }}-k\Psi ,0<\alpha \le 1,\xi >0,\end{array}$$

(9)

with respect to the initial condition

$$\begin{array}{c}\hfill \Psi (\varsigma ,0)=\max (e^{\varsigma }-1,0).\end{array}$$

(10)

Utilizing $\mathbb{S}$T in Equation (9), we get

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\eta }^{\alpha }}}\mathbb{S}[\Psi (\varsigma ,\xi )]-{\displaystyle \frac{1}{{\eta }^{\alpha +1}}}\Psi (\varsigma ,0)& =\mathbb{S}\left[{\displaystyle \frac{{\partial }^2\Psi }{\partial {\varsigma }^2}}+(k-1){\displaystyle \frac{\partial \Psi }{\partial \varsigma }}-k\Psi \right],\hfill \\ \hfill \mathbb{S}[\Psi (\varsigma ,\xi )]={\displaystyle \frac{1}{{\eta }^{\alpha }}}\Psi (\varsigma ,0)& +{\eta }^{\alpha }\mathbb{S}\left[{\displaystyle \frac{{\partial }^2\Psi }{\partial {\varsigma }^2}}+(k-1){\displaystyle \frac{\partial \Psi }{\partial \varsigma }}-k\Psi \right].\hfill \end{array}$$

After simplification, we apply the Sawi inverse transform to derive the following result:

$$\begin{array}{c}\hfill \Psi (\varsigma ,\xi )=\Psi (\varsigma ,0)+{\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{{\displaystyle \frac{{\partial }^2\Psi }{\partial {\varsigma }^2}}+(k-1){\displaystyle \frac{\partial \Psi }{\partial \varsigma }}-k\Psi \right\}\right].\end{array}$$

(11)

By introducing the HPM, Equation (11) can be reformulated as follows:

$$\begin{array}{c}\hfill \sum _{i=0}^{\infty }{p}^i{\Psi }_i(\varsigma ,\xi )=\Psi (\varsigma ,0)+{\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{{\partial }^2{\Psi }_i}{\partial {\varsigma }^2}}+(k-1)\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{\partial {\Psi }_i}{\partial \varsigma }}-k\sum _{i=0}^{\infty }{p}^i{\Psi }_i\right\}\right].\end{array}$$

(12)

The relevant components of p are given by the following expressions:

$$\begin{array}{cc}\hfill p^0& :{\Psi }_0(\varsigma ,\xi )=\Psi (\varsigma ,0),\hfill \\ \hfill p^1& :{\Psi }_1(\varsigma ,\xi )={\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{{\displaystyle \frac{{\partial }^2{\Psi }_0}{\partial {\varsigma }^2}}+(k-1){\displaystyle \frac{\partial {\Psi }_0}{\partial \varsigma }}-k{\Psi }_0\right\}\right],\hfill \\ \hfill p^2& :{\Psi }_2(\varsigma ,\xi )={\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{{\displaystyle \frac{{\partial }^2{\Psi }_1}{\partial {\varsigma }^2}}+(k-1){\displaystyle \frac{\partial {\Psi }_1}{\partial \varsigma }}-k{\Psi }_1\right\}\right],\hfill \\ \hfill p^3& :{\Psi }_3(\varsigma ,\xi )={\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{{\displaystyle \frac{{\partial }^2{\Psi }_2}{\partial {\varsigma }^2}}+(k-1){\displaystyle \frac{\partial {\Psi }_2}{\partial \varsigma }}-k{\Psi }_2\right\}\right],\hfill \\ \hfill & ⋮.\hfill \end{array}$$

The following outcomes are derived by applying Equation (10) in the aforementioned equation:

$$\begin{array}{cc}\hfill {\Psi }_0(\varsigma ,\xi )& =\max (e^{\varsigma }-1,0),\hfill \\ \hfill {\Psi }_1(\varsigma ,\xi )& =\max (e^{\varsigma },0){\displaystyle \frac{k{\xi }^{\alpha }}{\Gamma (\alpha +1)}}-\max (e^{\varsigma }-1,0){\displaystyle \frac{k{\xi }^{\alpha }}{\Gamma (\alpha +1)}},\hfill \\ \hfill {\Psi }_2(\varsigma ,\xi )& =-\max (e^{\varsigma },0){\displaystyle \frac{k^2{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}}+\max (e^{\varsigma }-1,0){\displaystyle \frac{k^2{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}},\hfill \\ \hfill {\Psi }_3(\varsigma ,\xi )& =\max (e^{\varsigma },0){\displaystyle \frac{k^2{\xi }^{3\alpha }}{\Gamma (\alpha +1)}}-\max (e^{\varsigma }-1,0){\displaystyle \frac{k^2{\xi }^{3\alpha }}{\Gamma (\alpha +1)}},\hfill & \\ \hfill ⋮\end{array}$$

We can now express these series results as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Psi (\varsigma ,\xi )& ={\Psi }_0(\varsigma ,\xi )+{\Psi }_1(\varsigma ,\xi )+{\Psi }_2(\varsigma ,\xi )+\dots \hfill \\ \hfill \Psi (\varsigma ,\xi )& =\max (e^{\varsigma }-1,0)\left(1-{\displaystyle \frac{k{\xi }^{\alpha }}{\Gamma (\alpha +1)}}+{\displaystyle \frac{k^2{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}}-{\displaystyle \frac{k^3{\xi }^{3\alpha }}{\Gamma (3\alpha +1)}}+\dots \right)\hfill \\ & +\max (e^{\varsigma },0)\left({\displaystyle \frac{k{\xi }^{\alpha }}{\Gamma (\alpha +1)}}-{\displaystyle \frac{k^2{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}}+{\displaystyle \frac{k^3{\xi }^{3\alpha }}{\Gamma (3\alpha +1)}}+\dots \right).\hfill \end{array}\end{array}$$

(13)

For $\alpha =1$, the given series simplifies and converges to the exact closed-form expression shown below:

$$\begin{array}{c}\hfill \Psi (\varsigma ,\xi )=\max (e^{\varsigma }-1,0)e^{-2\xi }+\max (e^{\varsigma },0)(1-e^{-2\xi }).\end{array}$$

(14)

5.2. Problem 2

Consider the financial model under the fractional B-S problem [38]

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^{\alpha }\Psi }{\partial {\xi }^{\alpha }}}+0.08{(2+sin\varsigma )}^2{\varsigma }^2{\displaystyle \frac{{\partial }^2\Psi }{\partial {\varsigma }^2}}+0.06\varsigma {\displaystyle \frac{\partial \Psi }{\partial \varsigma }}-0.06\Psi =0,0<\alpha \le 1,\xi >0,\end{array}$$

(15)

with respect to the initial condition

$$\begin{array}{c}\hfill \Psi (\varsigma ,0)=\max (\varsigma -25e^{-0.06},0).\end{array}$$

(16)

Utilizing $\mathbb{S}$T in Equation (15), we get

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\eta }^{\alpha }}}\mathbb{S}[\Psi (\varsigma ,\xi )]-{\displaystyle \frac{1}{{\eta }^{\alpha +1}}}\Psi (\varsigma ,0)& =-\mathbb{S}\left[0.08{(2+sin\varsigma )}^2{\varsigma }^2{\displaystyle \frac{{\partial }^2\Psi }{\partial {\varsigma }^2}}+0.06\varsigma {\displaystyle \frac{\partial \Psi }{\partial \varsigma }}-0.06\Psi \right],\hfill \\ \hfill \mathbb{S}[\Psi (\varsigma ,\xi )]={\displaystyle \frac{1}{{\eta }^{\alpha }}}\Psi (\varsigma ,0)& -{\eta }^{\alpha }\mathbb{S}\left[0.08{(2+sin\varsigma )}^2{\varsigma }^2{\displaystyle \frac{{\partial }^2\Psi }{\partial {\varsigma }^2}}+0.06\varsigma {\displaystyle \frac{\partial \Psi }{\partial \varsigma }}-0.06\Psi \right].\hfill \end{array}$$

After simplification, we apply the Sawi inverse transform to derive the following result:

$$\begin{array}{c}\hfill \Psi (\varsigma ,\xi )=\Psi (\varsigma ,0)-{\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{0.08{(2+sin\varsigma )}^2{\varsigma }^2{\displaystyle \frac{{\partial }^2\Psi }{\partial {\varsigma }^2}}+0.06\varsigma {\displaystyle \frac{\partial \Psi }{\partial \varsigma }}-0.06\Psi \right\}\right].\end{array}$$

(17)

By introducing the HPM, Equation (17) can be reformulated as follows:

$$\begin{array}{c}\hfill \sum _{i=0}^{\infty }{p}^i{\Psi }_i(\varsigma ,\xi )=\Psi (\varsigma ,0)-{\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{0.08{(2+sin\varsigma )}^2{\varsigma }^2\sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{{\partial }^2{\Psi }_i}{\partial {\varsigma }^2}}+0.06\varsigma \sum _{i=0}^{\infty }{p}^i{\displaystyle \frac{\partial {\Psi }_i}{\partial \varsigma }}-0.06\sum _{i=0}^{\infty }{p}^i{\Psi }_i\right\}\right].\end{array}$$

(18)

The relevant components of p are given by the following expressions:

$$\begin{array}{cc}\hfill p^0& :{\Psi }_0(\varsigma ,\xi )=\Psi (\varsigma ,0),\hfill \\ \hfill p^1& :{\Psi }_1(\varsigma ,\xi )=-{\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{0.08{(2+sin\varsigma )}^2{\varsigma }^2{\displaystyle \frac{{\partial }^2{\Psi }_0}{\partial {\varsigma }^2}}+0.06\varsigma {\displaystyle \frac{\partial {\Psi }_0}{\partial \varsigma }}-0.06{\Psi }_0\right\}\right],\hfill \\ \hfill p^2& :{\Psi }_2(\varsigma ,\xi )=-{\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{0.08{(2+sin\varsigma )}^2{\varsigma }^2{\displaystyle \frac{{\partial }^2{\Psi }_1}{\partial {\varsigma }^2}}+0.06\varsigma {\displaystyle \frac{\partial {\Psi }_1}{\partial \varsigma }}-0.06{\Psi }_1\right\}\right],\hfill \\ \hfill p^3& :{\Psi }_3(\varsigma ,\xi )=-{\mathbb{S}}^{-1}\left[{\eta }^{\alpha }\mathbb{S}\left\{0.08{(2+sin\varsigma )}^2{\varsigma }^2{\displaystyle \frac{{\partial }^2{\Psi }_2}{\partial {\varsigma }^2}}+0.06\varsigma {\displaystyle \frac{\partial {\Psi }_2}{\partial \varsigma }}-0.06{\Psi }_2\right\}\right],\hfill \\ \hfill & ⋮.\hfill \end{array}$$

The following outcomes are derived by applying Equation (10) in the aforementioned equation:

$$\begin{array}{cc}\hfill {\Psi }_0(\varsigma ,\xi )& =\max (\varsigma -25e^{-0.06},0),\hfill \\ \hfill {\Psi }_1(\varsigma ,\xi )& =-0.06\varsigma {\displaystyle \frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}}+0.06\max (\varsigma -25e^{-0.06},0){\displaystyle \frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}},\hfill \\ \hfill {\Psi }_2(\varsigma ,\xi )& =-{\left(0.06\right)}^2\varsigma {\displaystyle \frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}}+{\left(0.06\right)}^2\max (\varsigma -25e^{-0.06},0){\displaystyle \frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}},\hfill \\ \hfill {\Psi }_3(\varsigma ,\xi )& =-{\left(0.06\right)}^3\varsigma {\displaystyle \frac{{\xi }^{3\alpha }}{\Gamma (3\alpha +1)}}+{\left(0.06\right)}^3\max (\varsigma -25e^{-0.06},0){\displaystyle \frac{{\xi }^{3\alpha }}{\Gamma (2\alpha +1)}},\hfill & \\ \hfill ⋮\end{array}$$

We can now express these series results as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Psi (\varsigma ,\xi )& ={\Psi }_0(\varsigma ,\xi )+{\Psi }_1(\varsigma ,\xi )+{\Psi }_2(\varsigma ,\xi )+\dots \hfill \\ \hfill \Psi (\varsigma ,\xi )& =\max (\varsigma -25e^{-0.06},0)\left(1+\left(0.06\right){\displaystyle \frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}}+{\left(0.06\right)}^2{\displaystyle \frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}}+{\left(0.06\right)}^3{\displaystyle \frac{{\xi }^{3\alpha }}{\Gamma (3\alpha +1)}}+\dots \right)\hfill \\ & -\varsigma \left(\left(0.06\right){\displaystyle \frac{{\xi }^{\alpha }}{\Gamma (\alpha +1)}}+{\left(0.06\right)}^2{\displaystyle \frac{{\xi }^{2\alpha }}{\Gamma (2\alpha +1)}}+{\left(0.06\right)}^3{\displaystyle \frac{{\xi }^{3\alpha }}{\Gamma (3\alpha +1)}}+\dots \right).\hfill \end{array}\end{array}$$

(19)

For $\alpha =1$, the given series simplifies and converges to the exact closed-form expression shown below:

$$\begin{array}{c}\hfill \Psi (\varsigma ,\xi )=\max (\varsigma -25e^{-0.06},0)E_{\alpha }(-0.06\xi )+\varsigma (1-E_{\alpha }(-0.06\xi )).\end{array}$$

(20)

6. Numerical Findings and Analysis

The following section presents graphical results based on the SHPTS technique, highlighting its effectiveness for the time-fractional B-S problem under appropriate conditions. The impact of varying the fractional order $\alpha$ is also demonstrated.

Figure 1 presents the 3D visualizations derived from the numerical analysis using the SHPTS for the time-fractional B-S problem across varying fractional orders. Specifically, Figure 1a shows the graphical visualization of the SHPTS result with $\alpha =0.50$, and Figure 1b reflects the system’s performance with $\alpha =0.75$, whereas Figure 1c shows the standard case with $\alpha =1$, and Figure 1d displays the exact result of the time-fractional B-S model (Section 5.1) within the ranges $0\le \varsigma \le 2$ and $0\le \xi \le 1$. These illustrations confirm that, as the fractional order $\alpha$ increases, the numerical results increasingly align with the exact 3D solution. Figure 2a shows the 2D behavior at $\xi =0.1$ for $\varsigma$ between 0 and 1, and Figure 2b shows the 2D behavior at $\xi =0.5$ for $\varsigma$ between 0 and 2 for the analysis of $\Psi (\varsigma ,\xi )$, using multiple values of $\alpha$, such as $\alpha$ = 0.2, 0.4, 0.6, and $0.8$. Figure 3a,b display the behavior of $\Psi (\varsigma ,\xi )$ over the ranges $0\le \varsigma \le 1$ and $0\le \varsigma \le 2$ at multiple values of $\xi =0.1$, $0.2$, $0.3$, and $0.4$, with $\alpha$ set to $0.5$ and 1, respectively. Figure 4a compares the SHPTS results to the exact solution for $\alpha =0.5$ over the range of $\varsigma$ from 0 to 1 and $\xi =0.1$, while Figure 4b presents the SHPTS results for the exact solution at $\alpha =1$ over the range of $\varsigma$ from 0 to 2 and $\xi =0.1$. Table 1 presents the absolute errors between the approximate and exact solutions for the numerical problem (Section 5.1), evaluated at fractional orders $\alpha =0.5$ and $\alpha =1$.

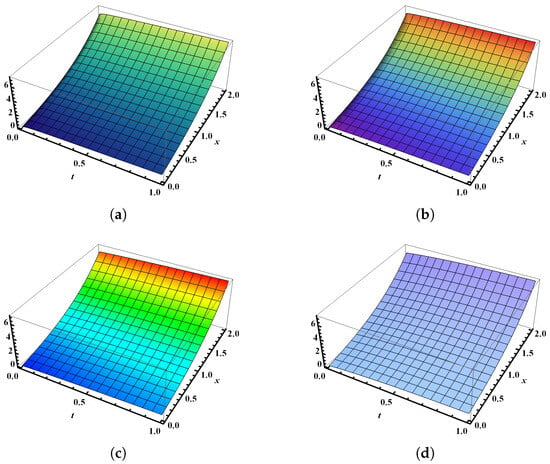
Figure 1. A three-dimensional graphical comparison of the SHPTS results and the exact solutions for $\Psi (\varsigma ,\xi )$ across various values of the fractional order $\alpha$. (a) Graphical visualization of SHPTS results for $\Psi (\varsigma ,\xi )$ with $\alpha =0.50$, (b) graphical visualization of SHPTS results for $\Psi (\varsigma ,\xi )$ with $\alpha =0.75$, (c) graphical visualization of SHPTS results for $\Psi (\varsigma ,\xi )$ with $\alpha =1$, and (d) graphical visualization of exact results for $\Psi (\varsigma ,\xi )$.

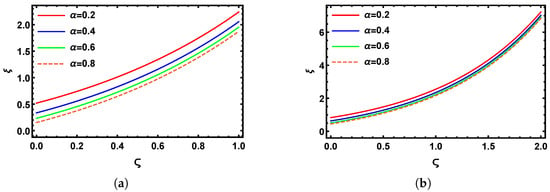
Figure 2. A two-dimensional graphical comparison of the SHPTS results across various values of $\alpha$ for (a) $0\le \varsigma \le 1$ and $\xi =0.1$; (b) $0\le \varsigma \le 2$ and $\xi =0.5$.

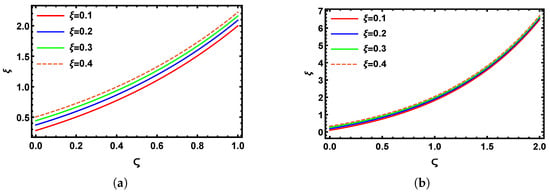
Figure 3. A two-dimensional graphical comparison of the SHPTS results across various values of $\xi$ for (a) $0\le \varsigma \le 1$ and $\alpha =0.5$; (b) $0\le \varsigma \le 2$ and $\alpha =1$.

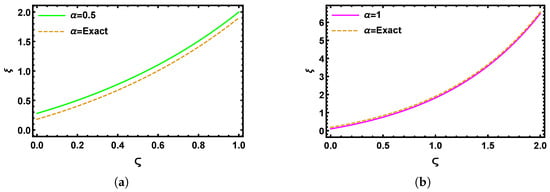
Figure 4. A two-dimensional graphical comparison of the SHPTS results and the exact solutions of $\Psi (\varsigma ,\xi )$ with $\xi =0.1$ for (a) $0\le \varsigma \le 1$ and $\alpha =0.5$; (b) $0\le \varsigma \le 2$ and $\alpha =1$.

Table 1. Absolute errors of the approximate and exact values for $\Psi (\varsigma ,\xi )$ at $\xi =0.1$ and $k=2$.

$\mathit{\varsigma }$	${\mathbf{\Psi }}_{\mathbf{approximate}}$ at ($\mathit{\alpha }=0.5$)	${\mathbf{\Psi }}_{\mathbf{approximate}}$ at ($\mathit{\alpha }=1$)	Exact ($\mathit{\alpha }=1$)	Absolute Error at ($\mathit{\alpha }=1$)
0.1	1.828630	0.737291	0.771838	0.034547
0.2	1.944860	0.853523	0.888069	0.034546
0.3	2.073320	0.981979	1.016530	0.034555
0.4	2.215290	1.123950	1.158490	0.034540
0.5	2.372180	1.280840	1.315390	0.034550
0.6	2.545580	1.454240	1.488790	0.034550
0.7	2.737210	1.645870	1.680420	0.034550
0.8	2.949000	1.857660	1.892210	0.034550
0.9	3.183060	2.091720	2.126270	0.034550
1.0	3.441740	2.350400	2.384950	0.034550

Figure 5 presents the 3D visualizations derived from the numerical analysis using the SHPTS for the time-fractional B-S problem across varying fractional orders. Specifically, Figure 5a shows the graphical visualization of the SHPTS result with $\alpha =0.50$, and Figure 5b reflects the system’s performance with $\alpha =0.75$, whereas Figure 5c shows the standard case with $\alpha =1$, and Figure 5d displays the exact result of the time-fractional B-S model (Section 5.2) within the ranges $-5\le \varsigma \le 5$ and $0\le \xi \le 1$. These illustrations confirm that, as the fractional order $\alpha$ increases, the numerical results increasingly align with the exact 3D solution. Figure 6a shows the 2D behavior at $\xi =0.1$ for $\varsigma$ between 0 and 1, and Figure 6b shows the 2D behavior at $\xi =0.5$ for $\varsigma$ between 0 and 2 for the analysis of $\Psi (\varsigma ,\xi )$, using multiple values of $\alpha$, such as $\alpha$ = 0.2, 0.4, 0.6, and $0.8$. Figure 7a,b display the behavior of $\Psi (\varsigma ,\xi )$ over the ranges $0\le \varsigma \le 2$ and $0\le \varsigma \le 1$ at multiple values of $\xi =0.1$, $0.2$, $0.3$, and $0.4$, with $\alpha$ set to $0.5$ and 1, respectively. Figure 8a compares the SHPTS results to the exact solution for $\alpha =0.5$ over the range of $\varsigma$ from 0 to 1 and $\xi =0.1$, while Figure 8b shows the SHPTS results and the exact solution at $\alpha =1$ over the range of $\varsigma$ from 0 to 2 and $\xi =0.1$. Table 2 presents the absolute errors between the approximate and exact solutions for the numerical problem (Section 5.2), evaluated at fractional orders $\alpha =0.5$ and $\alpha =1$.

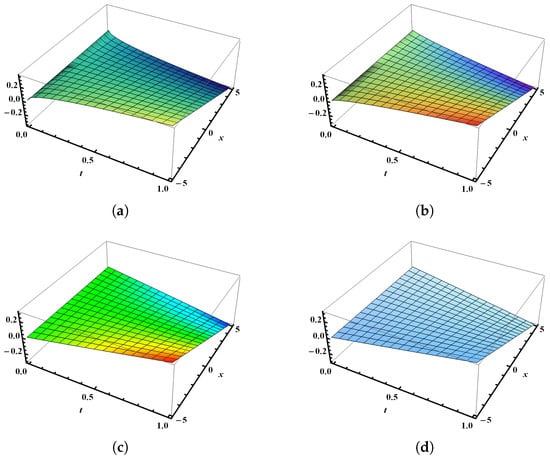
Figure 5. A three-dimensional graphical comparison of the SHPTS results and the exact solutions for $\Psi (\varsigma ,\xi )$ across various values of the fractional order $\alpha$. (a) Graphical visualization of SHPTS results for $\Psi (\varsigma ,\xi )$ with $\alpha =0.50$, (b) graphical visualization of SHPTS results for $\Psi (\varsigma ,\xi )$ with $\alpha =0.75$, (c) graphical visualization of SHPTS results for $\Psi (\varsigma ,\xi )$ with $\alpha =1$, and (d) graphical visualization of exact results for $\Psi (\varsigma ,\xi )$.

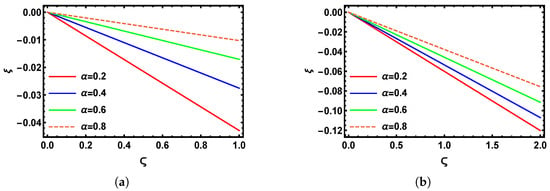
Figure 6. A two-dimensional graphical comparison of the SHPTS results across various values of $\alpha$ for (a) $0\le \varsigma \le 1$ and $\xi =0.1$; (b) $0\le \varsigma \le 2$ and $\xi =0.5$.

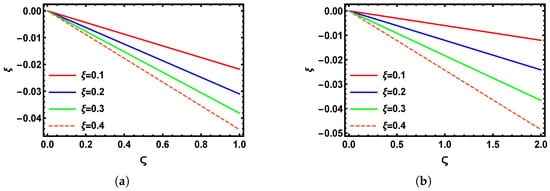
Figure 7. A two-dimensional graphical comparison of the SHPTS results across various values of $\xi$ for (a) $0\le \varsigma \le 1$ and $\alpha =0.5$; (b) $0\le \varsigma \le 2$ and $\alpha =1$.

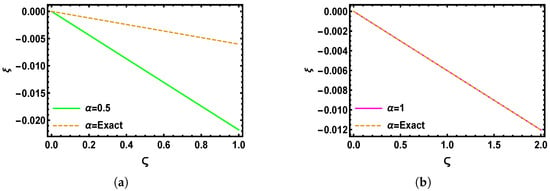
Figure 8. A two-dimensional graphical comparison of the SHPTS results and the exact solutions of $\Psi (\varsigma ,\xi )$ with $\xi =0.1$ for (a) $0\le \varsigma \le 1$ and $\alpha =0.5$; (b) $0\le \varsigma \le 2$ and $\alpha =1$.

Table 2. Absolute errors of the approximate and exact values for $\Psi (\varsigma ,\xi )$ at $\xi =0.5$.

$\mathit{\varsigma }$	${\mathbf{\Psi }}_{\mathbf{approximate}}$ at ($\mathit{\alpha }=0.5$)	${\mathbf{\Psi }}_{\mathbf{approximate}}$ at ($\mathit{\alpha }=1$)	Exact ($\mathit{\alpha }=1$)	Absolute Error at ($\mathit{\alpha }=1$)
0.1	0.089146	0.089219	0.089247	0.000028
0.2	0.178293	0.178439	0.178494	0.000055
0.3	0.267439	0.267658	0.267742	0.000084
0.4	0.356586	0.356878	0.356989	0.000111
0.5	0.445732	0.446097	0.446237	0.000140
0.6	0.534878	0.535316	0.535484	0.000168
0.7	0.624025	0.624536	0.624731	0.000195
0.8	0.713171	0.713755	0.713979	0.000224
0.9	0.802318	0.802975	0.803227	0.000252
1.0	0.891464	0.892194	0.892474	0.000280

The SHPTS method demonstrates high convergence and accuracy with minimal iterations in the classical case when $\alpha =1$. This efficiency is clearly supported by the 2D and 3D visual plots, which consistently show that the SHPTS results are close to the exact solution. These findings highlight the reliability, precision, and computational efficiency of the proposed technique in solving the time-fractional B-S problem.

7. Concluding Remarks

In our investigation, we conducted a fractional analysis of the B-S problem by employing an innovative computational approach termed the Sawi homotopy perturbation transform scheme (SHPTS). Using the fractional derivative in the Caputo sense, we addressed the complexity of systems that are not easy to handle with conventional integer-order derivatives. The Sawi transform converted the fractional parts into a Sawi space characterized by components of recurrence relations. We handled these components efficiently by employing He’s polynomials with the use of the HPM. We also provided two numerical examples to show the efficiency and applicability of the SHPTS. The present scheme produced series results that were close to the exact results using the initial condition. Finally, we presented 2D and 3D graphical visualizations of the obtained solution and compared them with the precise results. These results confirm that the SHPTS is a fast, stable, and reliable approach for a variety of fractional-order problems. In future work, we intend to broaden the scope of this methodology for more time–space-fractional models across numerous scientific and technological disciplines.