A Double-Parameter Regularization Scheme for the Backward Diffusion Problem with a Time-Fractional Derivative
Abstract
1. Introduction
2. Preliminaries
3. Convergence Analysis and Error Estimate
4. The Convergence Rate of the Corresponding Solution
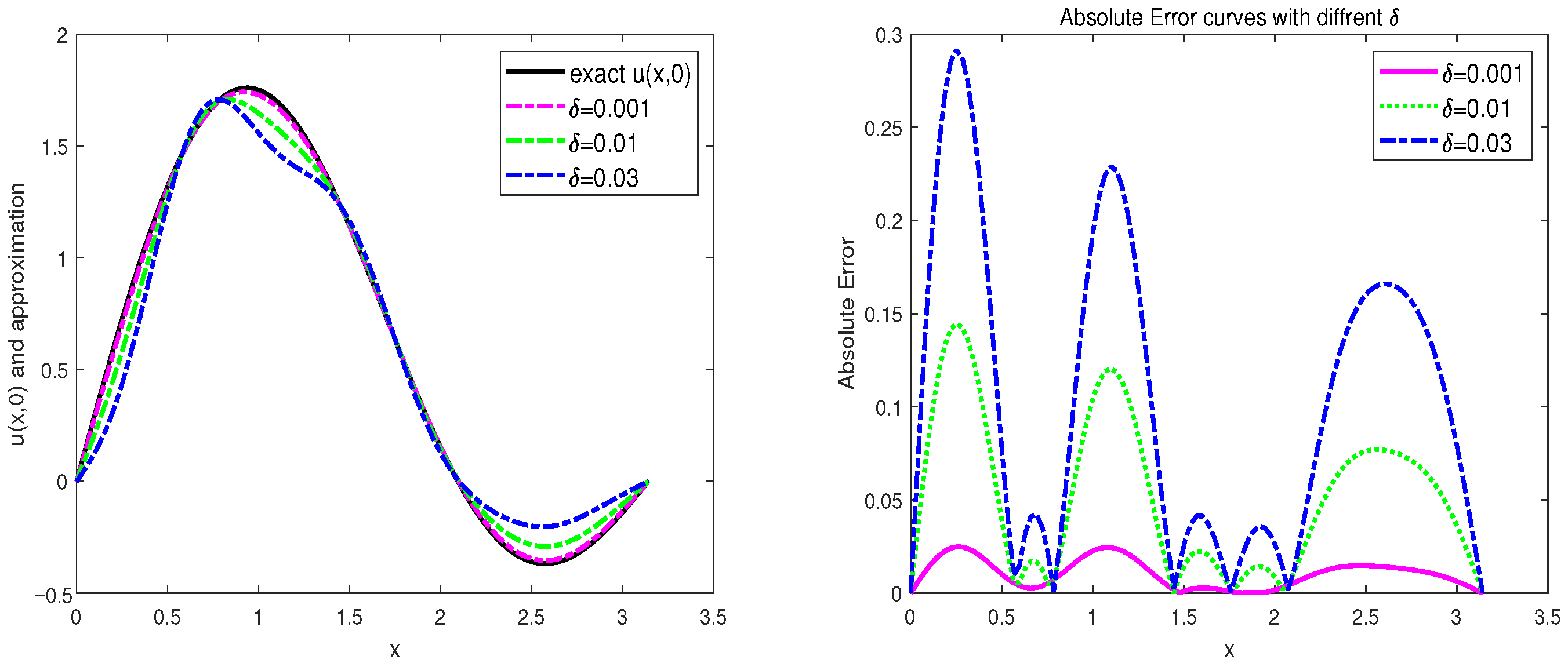
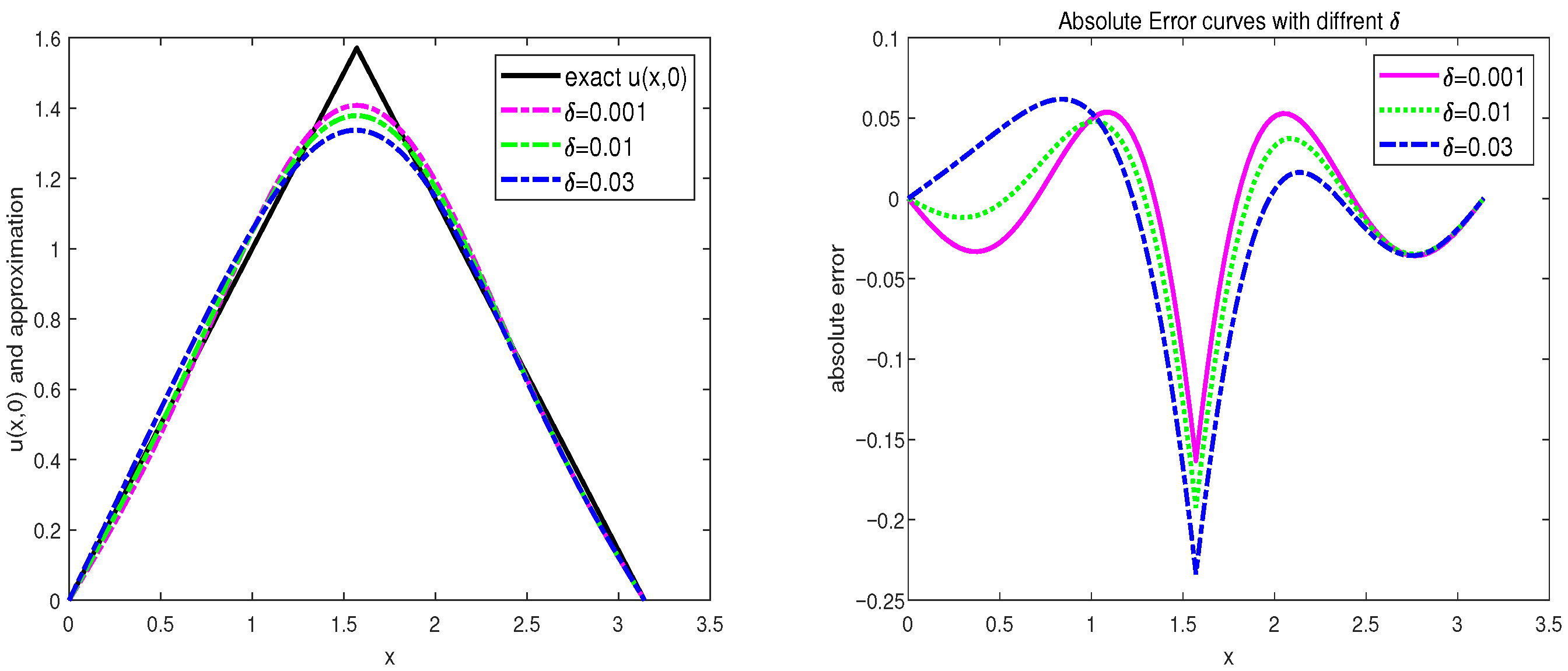
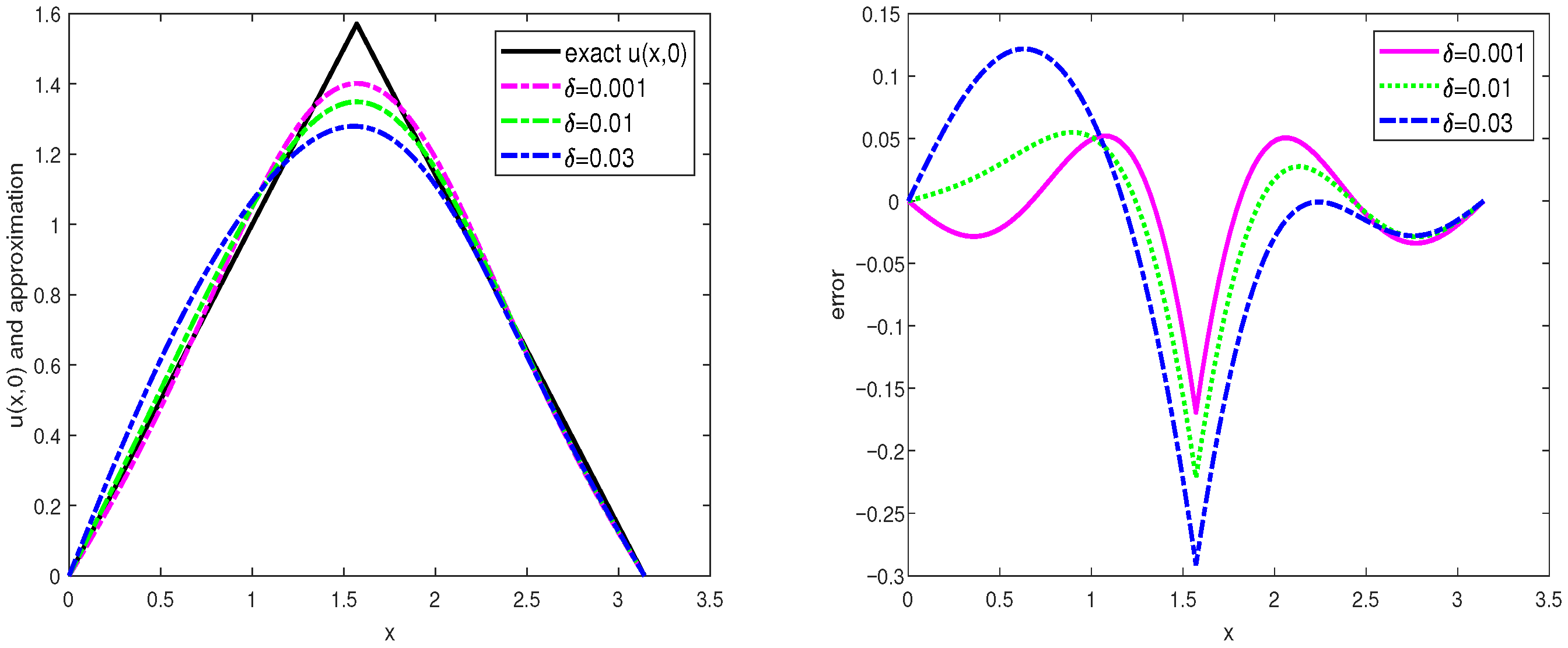
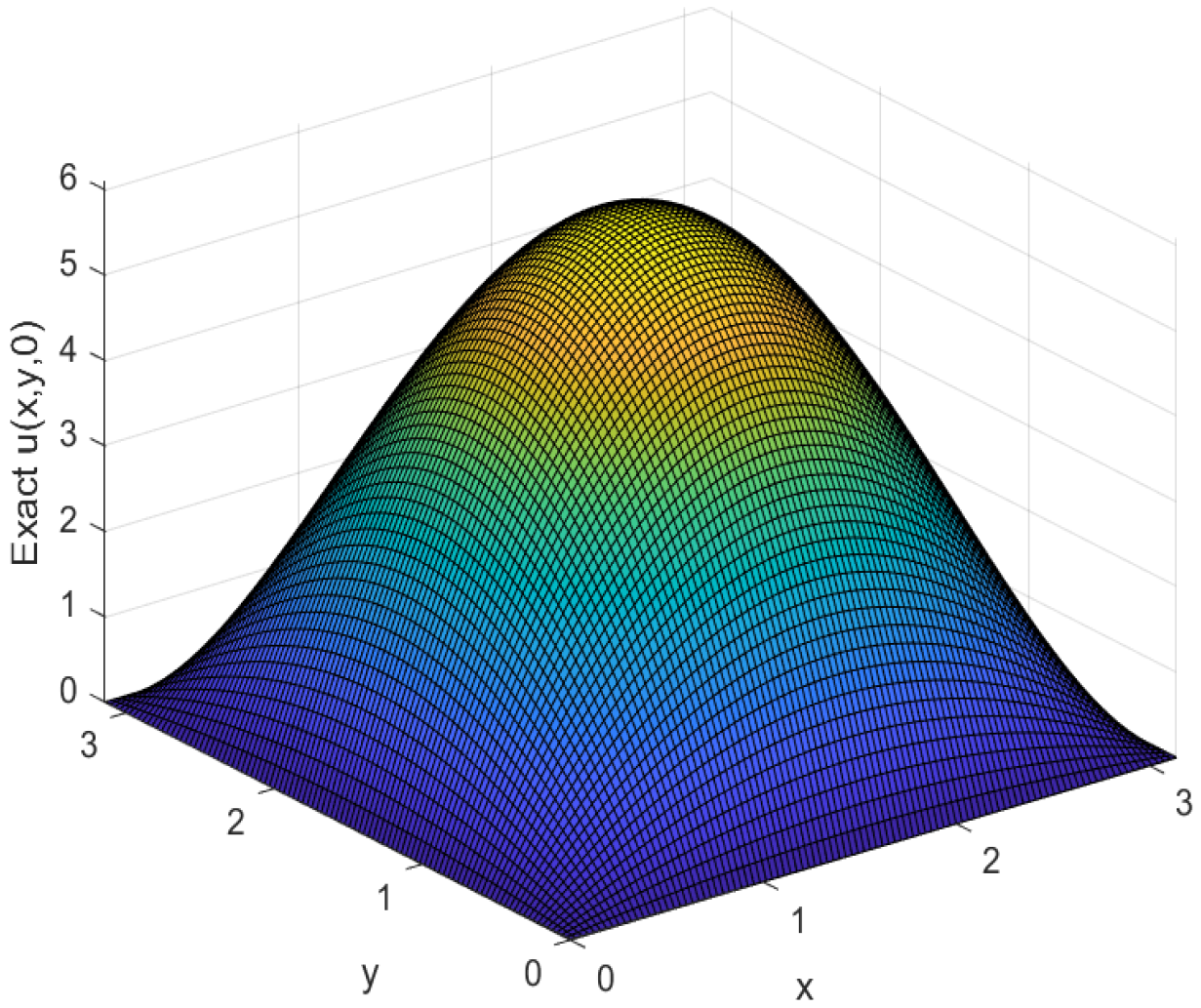
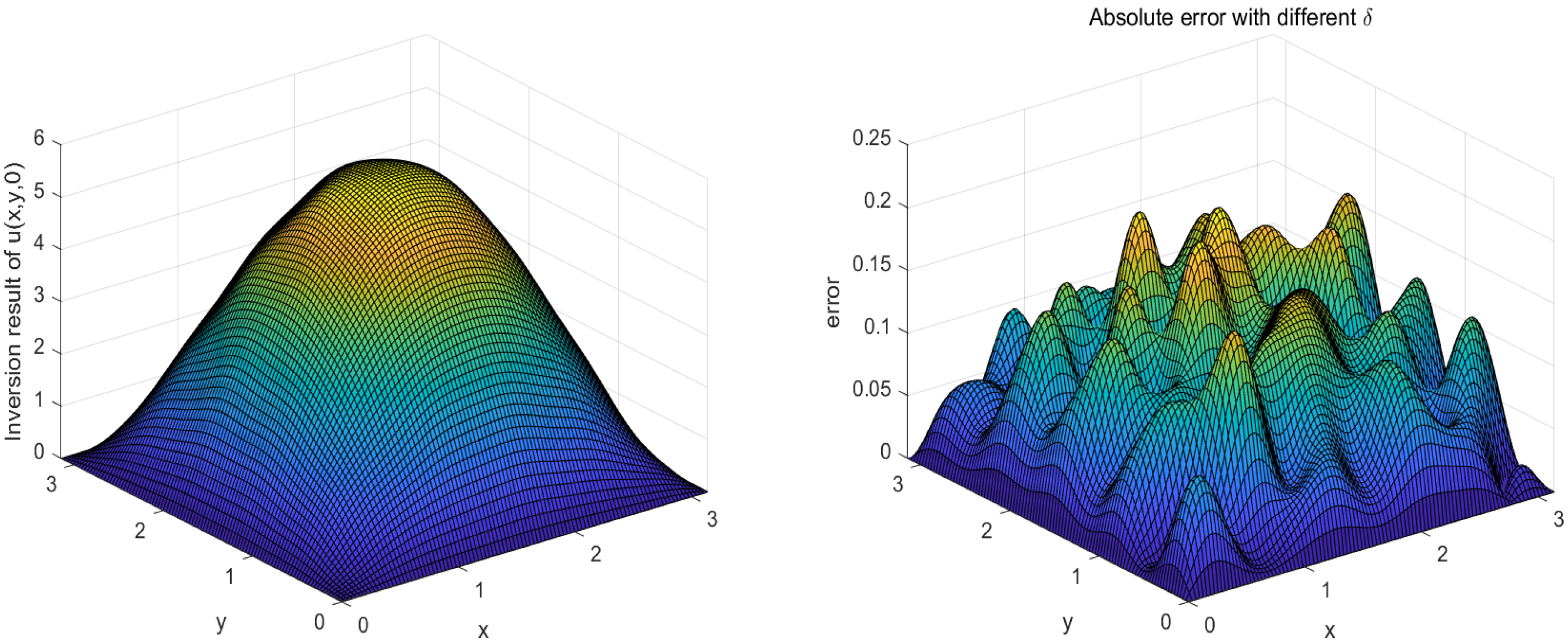
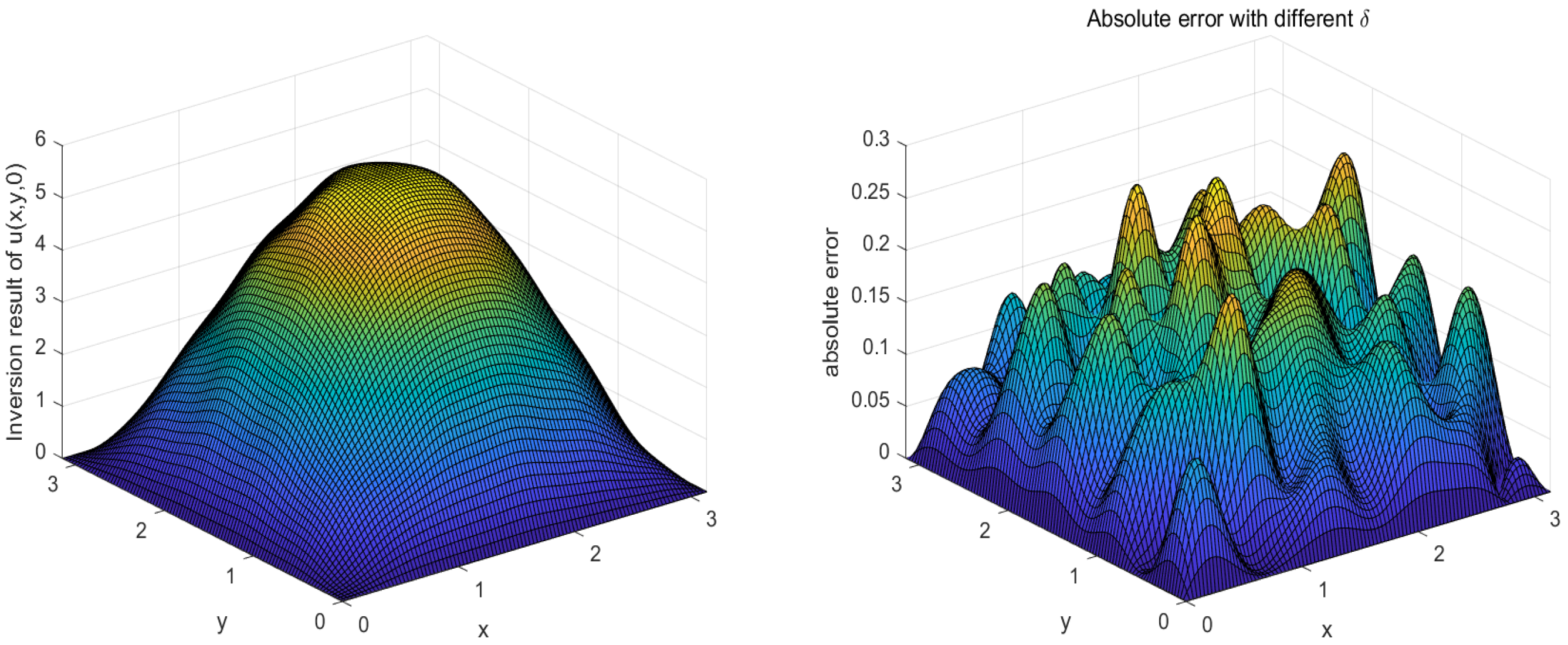
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Metzler, R.; Klafter, J. Subdiffusive transport close to thermal equilibrium: From the Langevin equation to fractional diffusion. Phys. Rev. E. 2000, 61, 6308–6311. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, I.M. Lévy flights from a continuous-time process. Phys. Rev. E. 2001, 63, 011104. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiao, F. Existence of weak solutions for time-fractional diffusion equations. J. Differ. Equ. 2010, 249, 1176–1191. [Google Scholar]
- Luchko, Y. Maximum principle and its application for the time-fractional diffusion equations. Fract. Calc. Appl. Anal. 2011, 14, 110–124. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Boyadjiev, L.; Al-Saqabi, B. Numerical treatment of fractional heat equations. Appl. Numer. Math. 2008, 58, 1212–1223. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Xu, Q.W.; Hesthaven, J.S.; Chen, F. A parareal method for time-fractional differential equations. J. Comput. Phys. 2015, 293, 173–183. [Google Scholar] [CrossRef]
- Bi, Q.L.; Lin, Z.Q.; Chen, B.R.; Lai, M.L.; Guo, Y.Y.; Lv, Y.J.; Tang, Y.L.; Huang, C.X. Super-Resolution Reconstruction of Weak Targets on Water Surfaces: A Generative Adversarial Network Approach Based on Implicit Neural Representation. Trait. Signal 2023, 40, 2701. [Google Scholar] [CrossRef]
- Sakamoto, K.; Yamamoto, M. Inverse source problem with a final overdetermination for a fractional diffusion equation. Math. Control Relat. Fields 2011, 1, 509–518. [Google Scholar] [CrossRef]
- Wang, J.G.; Ran, Y.H.; Yuan, Z.B. Uniqueness and numerical scheme for the Robin coefficient identification of the time-fractional diffusion equation. Comput. Math. Appl. 2018, 75, 4107–4114. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Z. Recovering the potential term in a fractional diffusion equation. IMA J. Appl. Math. 2017, 82, 579–600. [Google Scholar] [CrossRef]
- Wang, Z.; Qiu, Z.; Qiu, S.; Ruan, Z. Multiple Terms Identification of Time Fractional Diffusion Equation with Symmetric Potential from Nonlocal Observation. Fractal Fract. 2023, 7, 778. [Google Scholar] [CrossRef]
- Sun, L.; Yan, X.; Liao, K. Simultaneous inversion of a fractional order and a space source term in an anomalous diffusion model. J. Inverse-Ill-Posed Probl. 2022, 30, 791–805. [Google Scholar] [CrossRef]
- Jing, X.H.; Jia, J.X.; Song, X.L. Simultaneous uniqueness for the diffusion coefficient and initial value identification in a time-fractional diffusion equation. Appl. Math. Lett. 2024, 156, 109149. [Google Scholar] [CrossRef]
- Yu, S.; Wang, Z.; Yang, H. Simultaneous inversion of the space-dependent source term and the initial value in a time-fractional diffusion equation. Comput. Methods Appl. Math. 2023, 23, 767–782. [Google Scholar] [CrossRef]
- Liu, J.J.; Yamamoto, M. A backward problem for the time-fractional diffusion equation. Appl. Anal. 2010, 89, 1769–1788. [Google Scholar] [CrossRef]
- Sakamoto, K.; Yamamoto, M. Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 2011, 382, 426–447. [Google Scholar] [CrossRef]
- Wang, Y.L.; Liu, J.J. Data regularization for a backward time-fractional diffusion problem. Comput. Math. Appl. 2012, 64, 3613–3626. [Google Scholar] [CrossRef][Green Version]
- Tuan, N.H.; Long, L.D.; Tatar, S. Tikhonov regularization method for a backward problem for the inhomogeneous time-fractional diffusion equation. Appl. Anal. 2018, 97, 842–863. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhou, Y.B.; Wei, T. A posteriori regularization parameter choice rule for the quasi-boundary value method for the backward time-fractional diffusion problem. Appl. Math. Lett. 2013, 26, 741–747. [Google Scholar] [CrossRef]
- Wei, T.; Wang, J.G. A modified quasi-boundary value method for the backward time fractional diffusion problem. Math. Model. Numer. Anal. 2014, 48, 603–621. [Google Scholar] [CrossRef]
- Ren, C.X.; Xu, X.; Lu, S. Regularization by projection for a backward problem of the time-fractional diffusion equation. J. Inverse Ill-Posed Probl. 2014, 22, 121–139. [Google Scholar] [CrossRef]
- Xiong, X.; Xue, X. A fractional Tikhonov regularization method for identifying a space-dependent source in the time-fractional diffusion equation. Appl. Math. Comput. 2019, 349, 292–303. [Google Scholar] [CrossRef]
- Han, Y.; Xiong, X.; Xue, X. A fractional Landweber method for solving backward time-fractional diffusion problem. Comput. Math. Appl. 2019, 78, 81–91. [Google Scholar] [CrossRef]
- Shi, W.X.; Xiong, X.T.; Xue, X.M. A fractional-order quasi-reversibility method to a backward problem for the time fractional diffusion equation. J. Comput. Appl. Math. 2023, 394, 113552. [Google Scholar] [CrossRef]
- Fu, J.L.; Liu, J.J. Double-parameter regularization for solving the backward diffusion problem with parallel-in-time algorithm. Inverse Probl. 2024, 40, 015010. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Pollard, H. The completely monotonic character of the Mittag-Leffler function Eα(−x). Bull. Am. Math. Soc. 1948, 54, 1115–1116. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhou, Y.B.; Wei, T. A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation. Appl. Numer. Math. 2014, 78, 95–111. [Google Scholar]
- Wang, Z.; Qiu, S.; Yu, S.; Wu, B.; Zhang, W. Exponential Tikhonov Regularization method for solving an inverse source problem of time fractional diffusion equation. J. Comput. Math. 2023, 41, 173–190. [Google Scholar] [CrossRef]
- Wang, J.G.; Wei, T. Quasi-reversibility method to identify a space-dependent source for the time-fractional diffusion equation. Appl. Math. Model. 2015, 39, 6139–6149. [Google Scholar] [CrossRef]
- Podlubny, I.; Kacenak, M. *MLF—Mittag-Leffler Function* [Computer Software]. MATLAB Central File Exchange. 2009. Available online: https://www.mathworks.com/matlabcentral/fileexchange/8738 (accessed on 10 April 2025).
| 0.6864 | 0.5124 | 0.3402 | 0.2577 | 0.3428 | 0.5060 | 0.6513 | |
| 0.6186 | 0.3552 | 0.1482 | 0.0661 | 0.0685 | 0.0776 | 0.0812 | |
| 0.5410 | 0.2159 | 0.0557 | 0.0347 | 0.0418 | 0.0440 | 0.0444 | |
| 0.2215 | 0.0811 | 0.0719 | 0.0697 | 0.0686 | 0.0680 | |
| 0.0639 | 0.0190 | 0.0184 | 0.0182 | 0.0181 | 0.0181 | |
| 0.0485 | 0.0049 | 0.0047 | 0.0046 | 0.0046 | 0.0045 | |
| 0.1579 | 0.1232 | 0.1153 | 0.1109 | 0.1082 | 0.1063 | |
| 0.0401 | 0.029 | 0.0280 | 0.0270 | 0.0264 | 0.0259 | |
| 0.0091 | 0.0066 | 0.0063 | 0.0060 | 0.0058 | 0.0057 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Wang, Z. A Double-Parameter Regularization Scheme for the Backward Diffusion Problem with a Time-Fractional Derivative. Fractal Fract. 2025, 9, 459. https://doi.org/10.3390/fractalfract9070459
Chen Q, Wang Z. A Double-Parameter Regularization Scheme for the Backward Diffusion Problem with a Time-Fractional Derivative. Fractal and Fractional. 2025; 9(7):459. https://doi.org/10.3390/fractalfract9070459
Chicago/Turabian StyleChen, Qun, and Zewen Wang. 2025. "A Double-Parameter Regularization Scheme for the Backward Diffusion Problem with a Time-Fractional Derivative" Fractal and Fractional 9, no. 7: 459. https://doi.org/10.3390/fractalfract9070459
APA StyleChen, Q., & Wang, Z. (2025). A Double-Parameter Regularization Scheme for the Backward Diffusion Problem with a Time-Fractional Derivative. Fractal and Fractional, 9(7), 459. https://doi.org/10.3390/fractalfract9070459






